Spatial-Temporal Distribution Analysis of Industrial Heat Sources in the US with Geocoded, Tree-Based, Large-Scale Clustering
Abstract
1. Introduction
2. Related Works
2.1. Traditional Fire Detection Methods
2.2. Approaches for Industrial Heat Source Identification
3. Datasets and Study Area
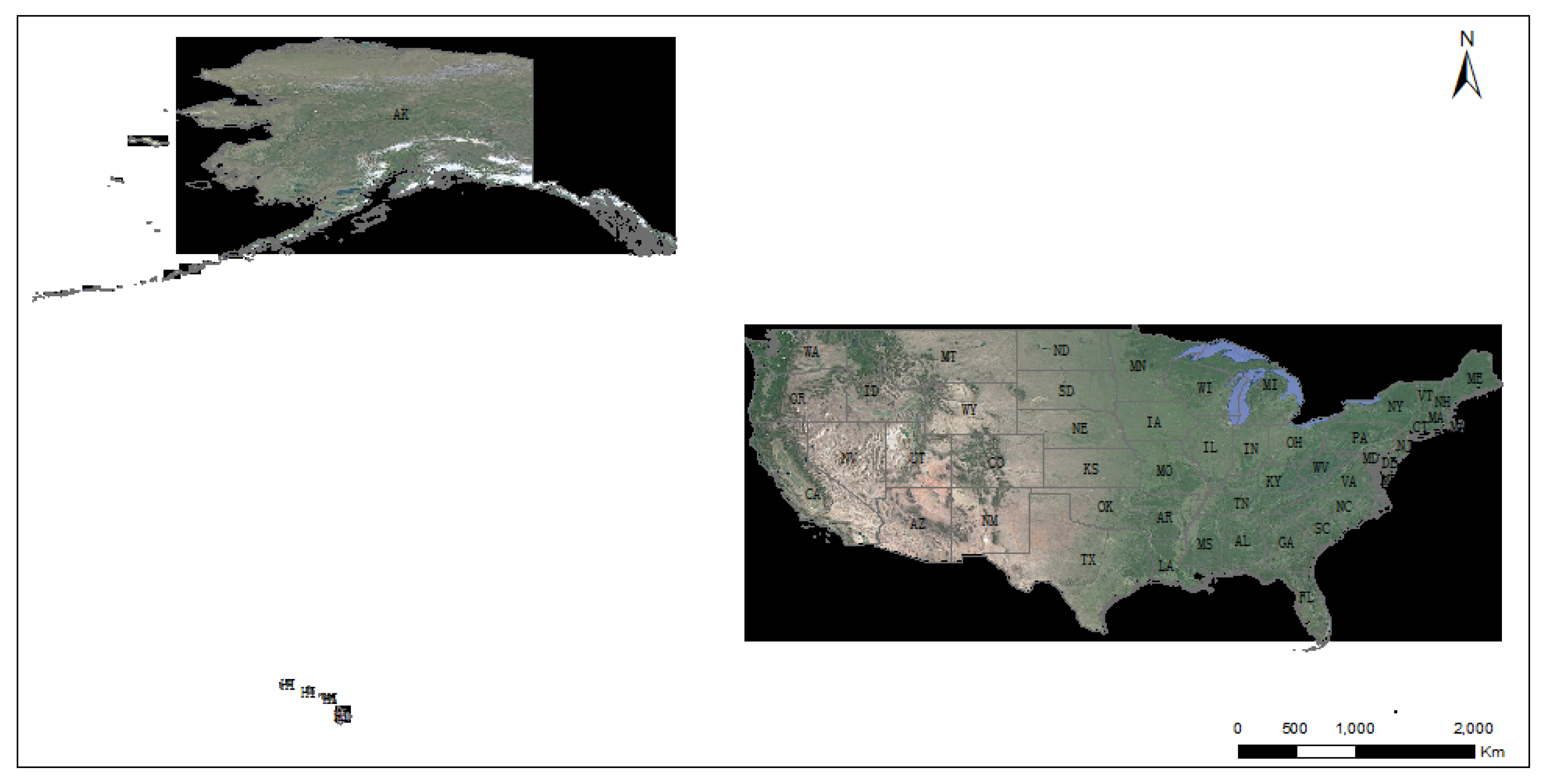
3.1. Study Area
3.2. VIIRS Active Fire Products
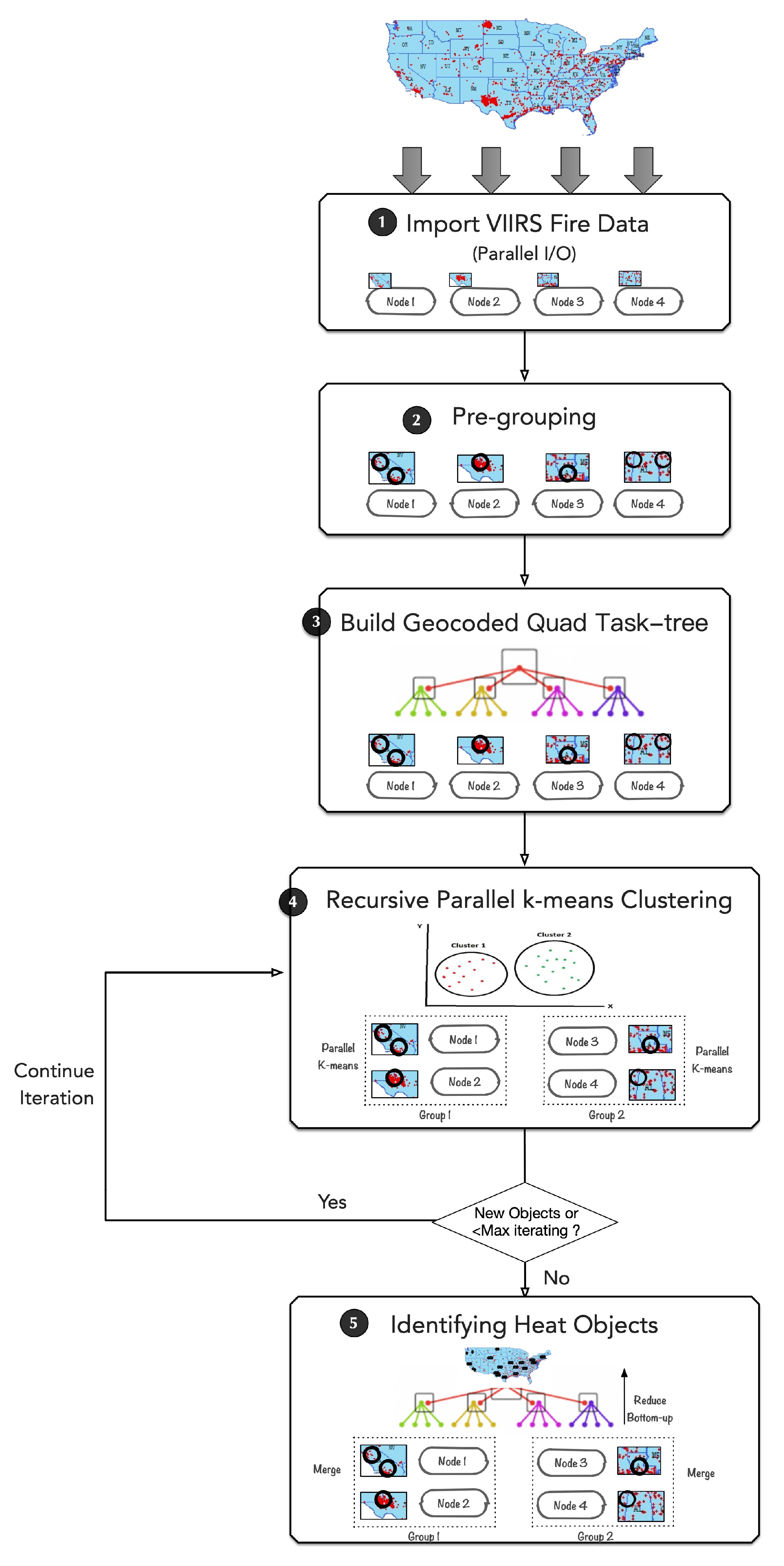
4. Methods
- -
- Data importing with Parallel I/O: Firstly, 3,461,260 time-series VIIRS active fire-point data ranging from 2012 to 2018 and covering the whole United States are extracted from the VNP14IMG global datasets. For I/O performance consideration, each computing node adopts an asynchronous parallel I/O operation to concurrently load in its own part of the data. These loaded fire data points are then imported into a heat point stack.
- -
- Building the geocoded quad task-tree: Secondly, following a GeoSOT global division, the local fire points in the stack of each computing node are geographically pre-grouped into initial grid tasks and are also regarded as the initial cluster center. Then, each pre-grouped grid task is encoded with a GeoSOT geographical code. Following binary-tree communication, a reduced operation over all the computing nodes is conducted to merge the grid tasks with the same geocode, and heat points inside are re-arranged. Thereafter, in a bottom-up way, a quad task-tree is built out of these grid tasks by connecting them with their neighbor grid tasks according to the GeoSOT code. The grid tasks in the tree are treated as bags of tasks waiting for issued for parallel computing.
- -
- Recursive parallel k-means clustering: The kernel processing step in the whole procedure. The computing nodes are divided into groups using a group communicator, and the grid tasks in the tree are treated as bags of tasks waiting for issued for parallel computing. Each group of computing nodes simultaneously implements recursive parallel k-means clustering with an empirical cluster number k of 2 on one selected grid task. During each iteration, the odd fire points that are extremely far from the cluster center are filtered out. Following that, the heat points in each grid task are recursively segmented until the recursive convergence condition shows that there are no more new cluster objects anymore. Moreover, a distributed, shared-memory-based data structure of heat objects is also built to ease and optimize the data communication across nodes. Eventually, the potential candidate industrial heat objects can be detected in each grid task.
- -
- Identifying heat objects: Finally, reduce all the grid tasks following the geocoded quad task-tree in a bottom-up way. The overlapped heat objects are merged in order to avoid fake objects result from over-segmentation. Whether the overlapped heat objects are merged or not is judged by the distance of objects and the size of the overlapping region. Finally, all the industrial heat objects can be identified.
4.1. Building a GeoSOT-Encoded Quad Task-Tree
4.1.1. Pre-Grouping Based on GeoSOT Global Division
- -
- Firstly, calculate GeoSOT code for fire hotspots to find exact grids the fires are in. Each processor calculates the GeoSOT-encoded grid ID for each fire hotspot located in a local fire hotspots stack according to the GeoSOT global division method. With the longitude and latitude values of the fire hotspots in the geographic coordinate system as well as the size of the basic grid cell, the GeoSOT-encoded grid ID can be easily determined with the GeoSOT discrete grid model. Here, we adopt a maximum level of 33 for the GeoSOT model, since a tiny grid size could always lead to over-segmentation of objects.
- -
- Then, pre-group the fire hotspots by their GeoSOT codes. The processor then creates a stack to store these fire hotspots groups and checks the tagged fire hotspots. If the GeoSOT codes of the tagged fire hotspots are totally new, then it creates a new group tagged with this GeoSOT grid ID and puts this new group into a group stack. Otherwise, if there already exists a group tagged with this GeoSOT code, then it inserts these fire hotspots into this group. Then, if the stack of fire hotspots is not empty, it goes back to calculate its GeoSOT-encoded grid ID and does the pre-grouping until all the fire hotspots are handled.
- -
- Finally, build the GeoSOT-encoded grid tasks across processors. After all the fire hotspots in each processor are locally pre-grouped, these initial fire hotspot groups with the same GeoSOT grid code are still randomly scattered across the processors. Thus, reducing these initial groups is inevitable. For performance consideration, a binary-tree communication structure is employed for reducing the fire hotspot groups. Following a bottom–top order along the binary communication tree, each processor reduces the initial fire hotspot groups with its near neighbor . In a case in which these two processors both have fire hotspot groups with the same GeoSOT grid ID, they are merged to a single group. Afterward, the reduced processor continues to reduce with the (where k is the depth of the binary-tree) until the root processor. Eventually, a GeoSOT-encoded grid task is built out from the reduced initial fire hotspot group in which all fire hotspots in the same GeoSOT grid are merged. In order to ease the data exchanging among the binary-tree communication structure, virtual distributed shared memory across processors is constructed with a one-side communication operator of MPI (Message Passing Interface). Each processor puts its initial fire hotspots group stack data into the virtual distributed shared memory for easy sharing with neighboring processors.
4.1.2. Building a Distributed, GeoSOT-Encoded Quad Task-Tree
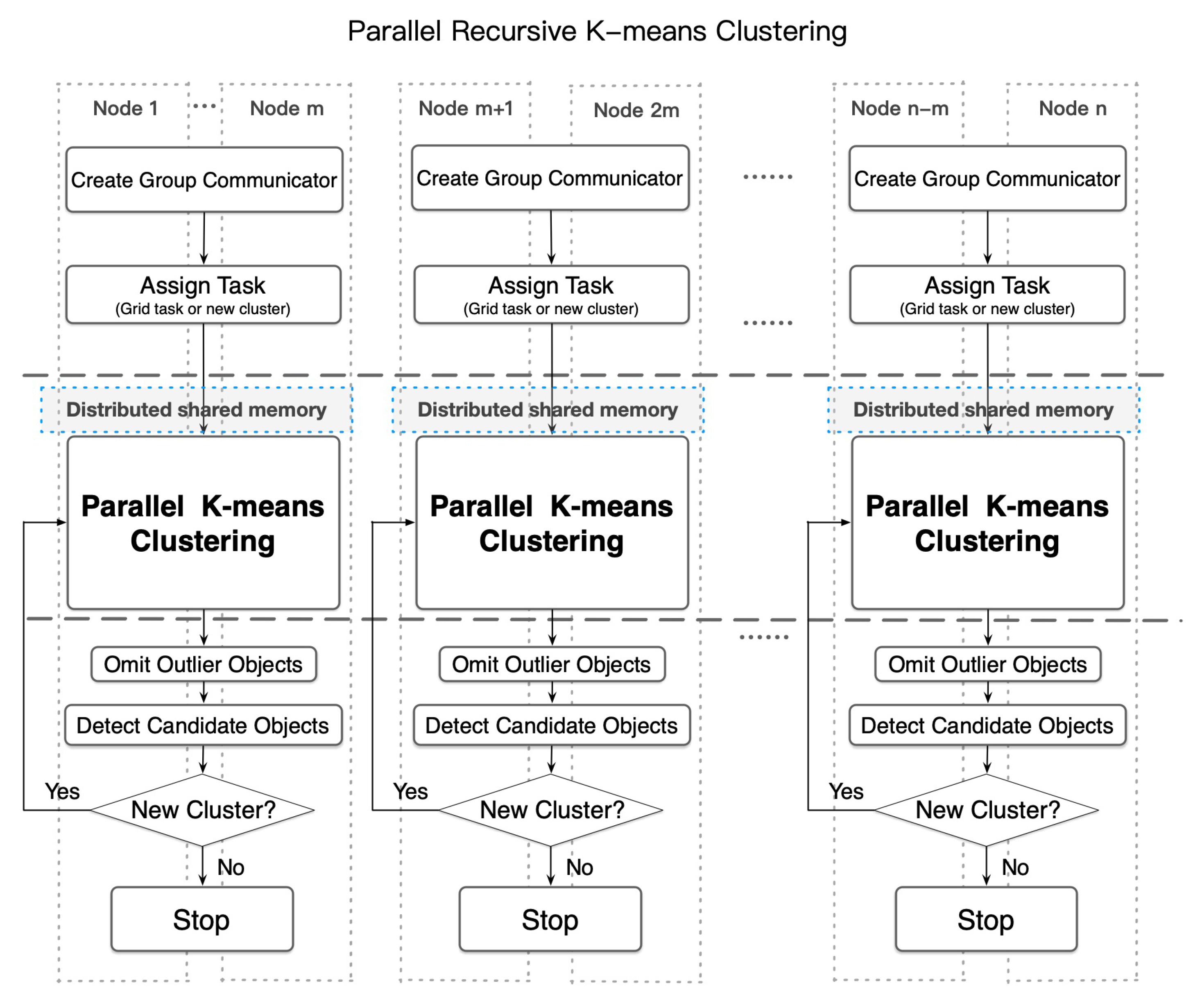
4.2. Optimized Recursive k-means Clustering in Parallel
- Divide the processors into group communicators wherein each group has a number of processors available for implementing parallel k-means data clustering.
- Choose a pre-grouped GeoSOT-encoded grid task for each processor group and take this pre-grouped fire hotspot as an initial partition for clustering.
- Each group concurrently executes a parallel k-means data clustering algorithm across a group of computing nodes inside their group communicator.
- (a)
- Distribute the fire points in across processors inside its group communicator.
- (b)
- Each processor concurrently implements a local k-means data clustering algorithm with a parameter k of to generate a new partition of sub-clusters and assign patterns to each closest cluster center. Here we choose a as four.
- (c)
- Reduce the squared error across the processors inside the group concurrently and minimize the sum of the error overall clusters.
- (d)
- Calculate the new cluster centers: .
- Omit new clusters with outlier fire points. When new clusters that cover a relatively reasonable small region also contain a small number of fire points, an outlier object check takes place or can be omitted.
- Check whether each new cluster is a valid candidate industrial heat object. New clusters that cover a relatively reasonable small region but are not outlier objects are taken as candidates for the industrial heat objects and put into candidate object stacks. Thus, these small new clusters would not be intended for further recursive clustering. The other bigger new clusters should be put into cluster stacks for further recursive parallel k-means clustering.
- Conduct the critical convergence condition. Check if the cluster stack is not empty and then pick one new cluster for further clustering, namely, ; repeat steps 3 to 5 until there are no new clusters, finally leading to the stability of the cluster membership.
4.3. Identifying Heat Objects through a Geocode-Aware Task-Tree
- Construct a binary-tree structured communication network across processors for a hierarchical merging and reducing of the candidate industrial heat objects, wherein the merging tasks namely non-leaf task nodes in the geo-encoded task tree are responsible for merging and reducing all the over-segmented industrial heat objects.
- Following a bottom-up way, each un-merged processor conducts task merging with its nearest right un-merged neighbor processor with a bigger id.
- (a)
- Reduce the geographically adjacent grid task nodes that belong to the same farther merging task which encoded with a higher level GeoSOT grid ID in the GeoSOT quad task-tree.
- (b)
- When all the four tasks required for a merging task have all found, find out the overlapping candidate objects along the boundary of grid tasks by judging the distance between objects and the size of overlapping regions.
- (c)
- Then conduct another k-means clustering a second time among all the fire points inside these overlapped candidate heat objects so as to over-come the over-segmenting problem.
- Mark this processor as a merged processor; repeat step 2 until the root of the task tree.
5. Results
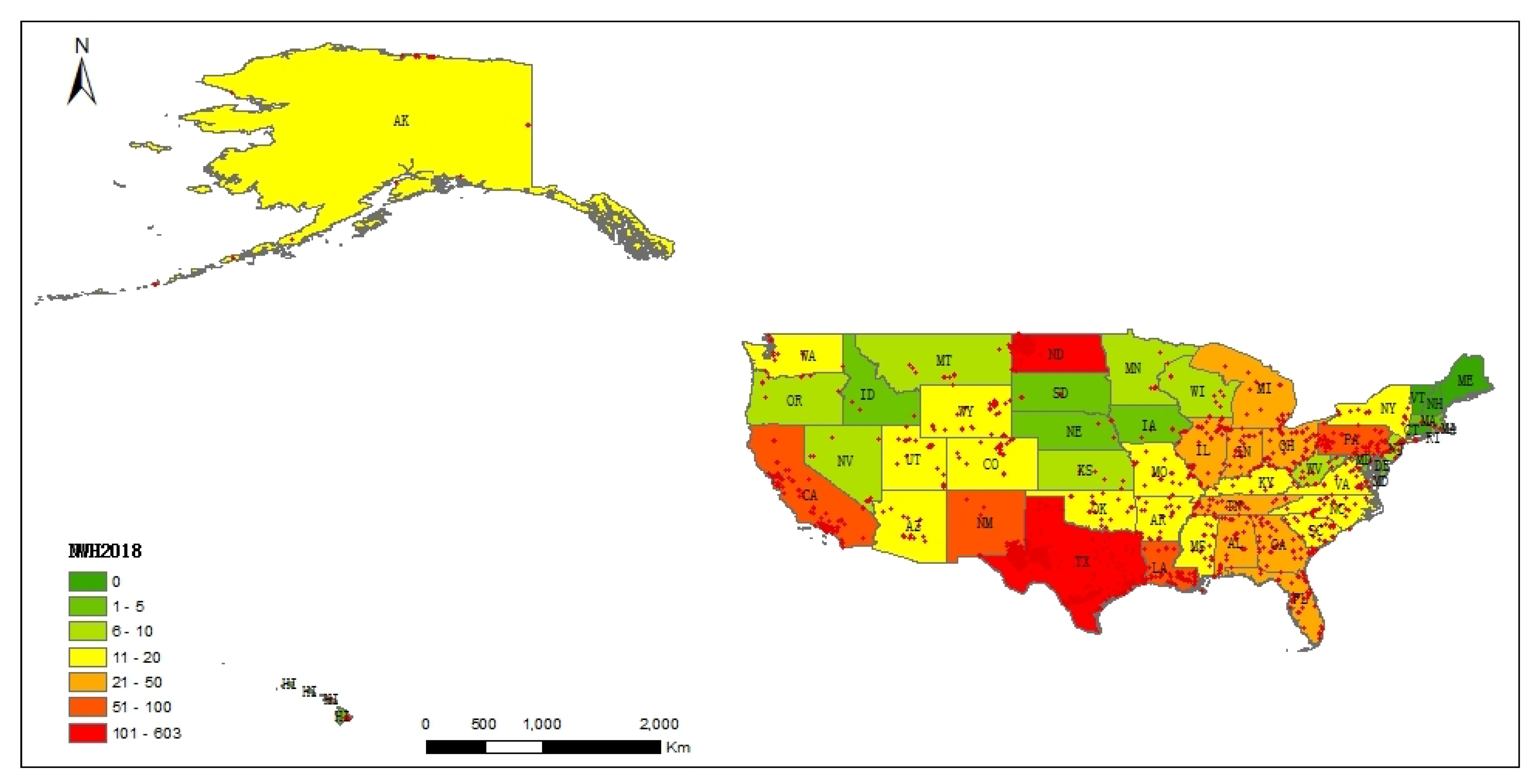
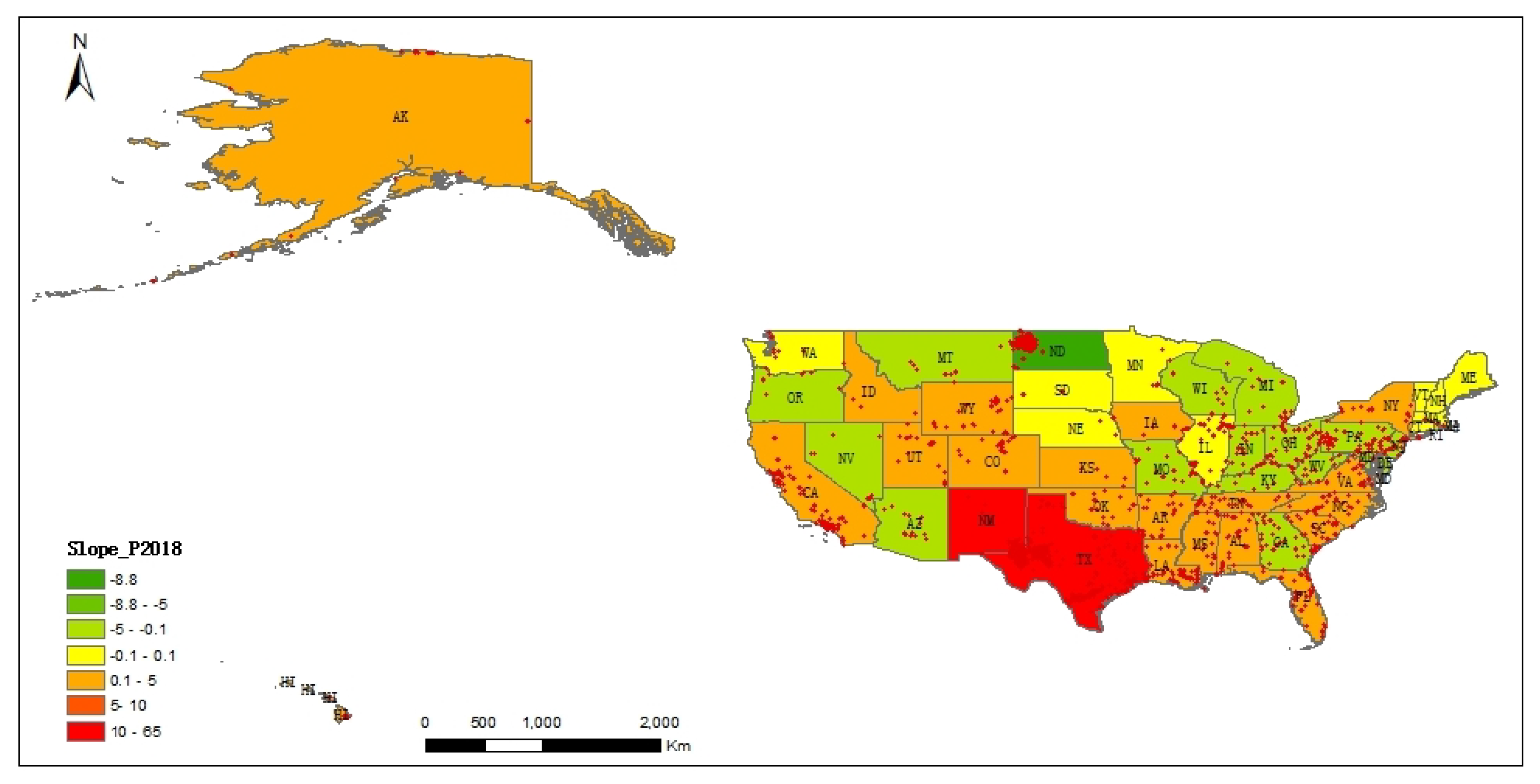
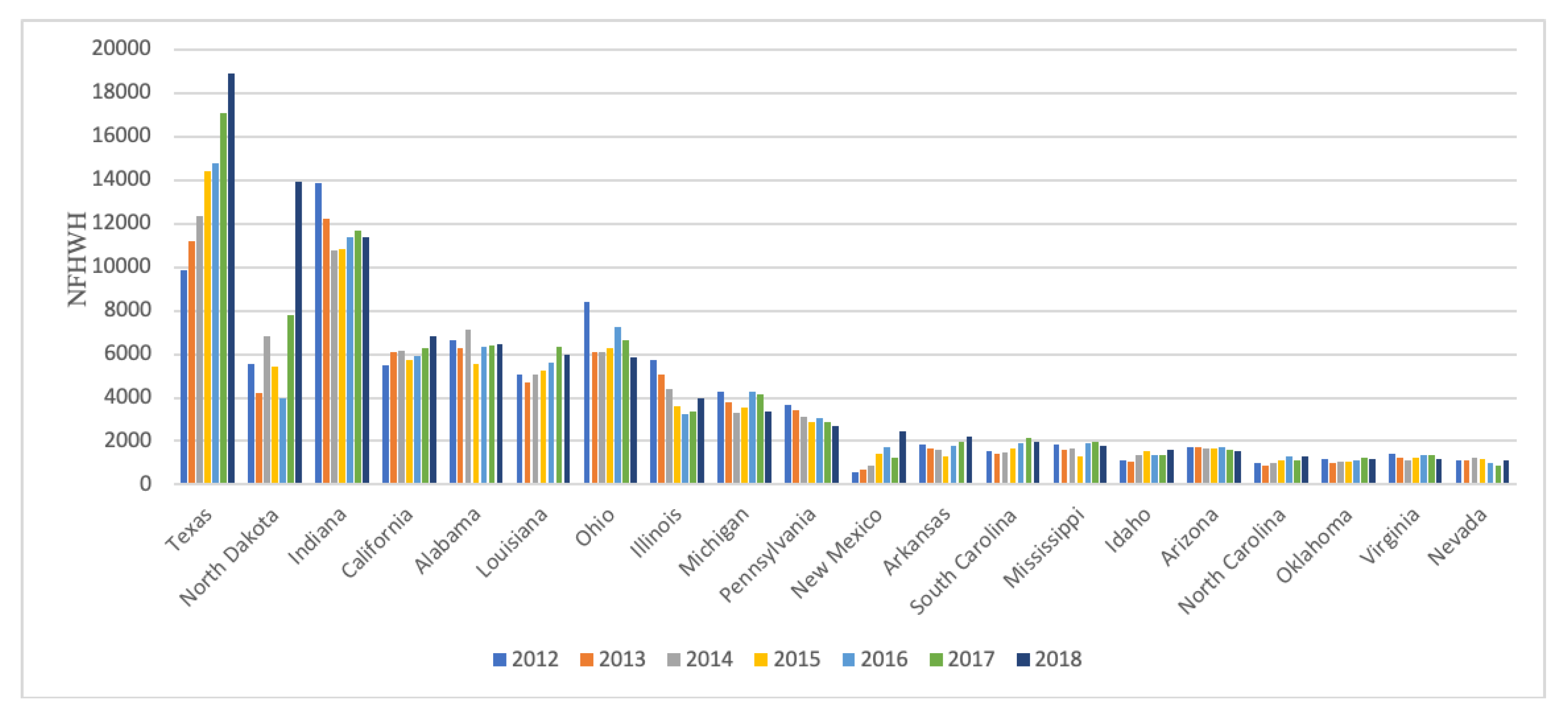
5.1. Distribution Characteristics of Heavy Industrial Heat Sources cross the United States
5.2. Spatial-Temporal Distribution Characteristics at State Scale
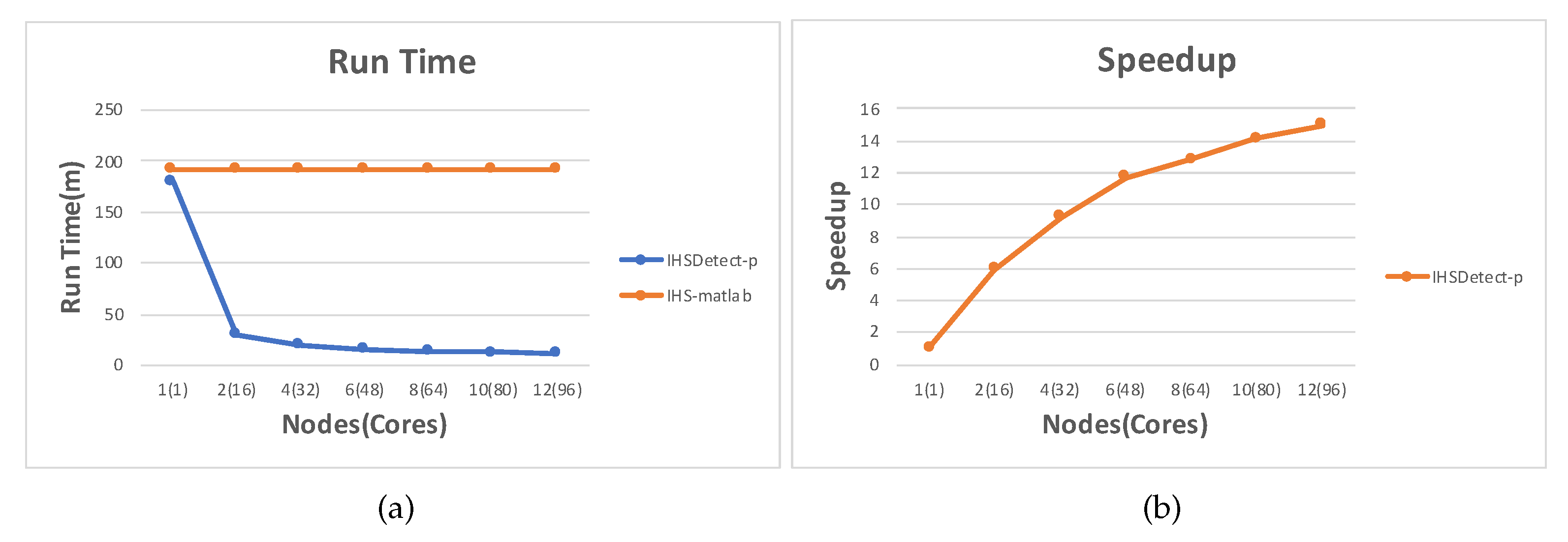
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bellevrat, K.W. Commentary: Clean and Efficient Heat for Industry. Available online: https://www.iea.org/newsroom/news/2018/january/commentary-clean-and-efficient-heat-for-industry.html (accessed on 23 January 2018).
- Kusnetz, N. U.S. Emissions Dropped in 2019: Here’s Why in 6 Charts. Available online: https://insideclimatenews.org/news/07012020/infographic-united-states-emissions-2019-climate-change-greenhouse-gas-coal-transportation (accessed on 7 January 2020).
- Climate, C.F.; Solutions, E. Projecting and Accelerating U.S. Greenhouse Gas Reductions. Available online: https://www.c2es.org/site/assets/uploads/2017/09/projecting-accelerating-us-greenhouse-gas-reductions.pdf (accessed on 10 September 2017).
- Dimitrov, R.S. The Paris agreement on climate change: Behind closed doors. Glob. Environ. Politics 2016, 16, 1–11. [Google Scholar] [CrossRef]
- Xia, H.; Chen, Y.; Quan, J. A simple method based on the thermal anomaly index to detect industrial heat sources. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 627–637. [Google Scholar] [CrossRef]
- Roberts, D. This Climate Problem is Bigger Than Cars and Much Harder to Solve. Available online: https://www.vox.com/energy-and-environment/2019/10/10/20904213/climate-change-steel-cement-industrial-heat-hydrogen-ccs (accessed on 10 October 2019).
- Hulley, G.; Malakar, N.; Hughes, T.; Islam, T.; Hook, S. Moderate Resolution Imaging Spectroradiometer (MODIS) MOD21 Land Surface Temperature and Emissivity Algorithm Theoretical Basis Document; Technical Report; Jet Propulsion Laboratory, National Aeronautics and Space: Pasadena, CA, USA, 2016.
- Sekertekin, A.; Arslan, N. Monitoring thermal anomaly and radiative heat flux using thermal infrared satellite imagery—A case study at Tuzla geothermal region. Geothermics 2019, 78, 243–254. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Baugh, K.; Zhizhin, M.; Hsu, F.C.; Ghosh, T. VIIRS night-time lights. Int. J. Remote Sens. 2017, 38, 5860–5879. [Google Scholar] [CrossRef]
- Schroeder, W.; Oliva, P.; Giglio, L.; Csiszar, I.A. The New VIIRS 375 m active fire detection data product: Algorithm description and initial assessment. Remote Sens. Environ. 2014, 143, 85–96. [Google Scholar] [CrossRef]
- Cracknell, A.P. Advanced Very High Resolution Radiometer AVHRR; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Schroeder, W.; Oliva, P.; Giglio, L.; Quayle, B.; Lorenz, E.; Morelli, F. Active fire detection using Landsat-8/OLI data. Remote Sens. Environ. 2016, 185, 210–220. [Google Scholar] [CrossRef]
- Kumar, S.S.; Roy, D.P. Global operational land imager Landsat-8 reflectance-based active fire detection algorithm. Int. J. Digit. Earth 2018, 11, 154–178. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Justice, C.; Flynn, L.; Kendall, J.; Giglio, L.; Prins, E.; Ward, D.; Menzel, P.; Setzer, A. Monitoring global fires from EOS-MODIS. J. Geophys. Res. 1998, 103, 215–239. [Google Scholar] [CrossRef]
- Casadio, S.; Arino, O.; Serpe, D. Gas flaring monitoring from space using the ATSR instrument series. Remote Sens. Environ. 2012, 116, 239–249. [Google Scholar] [CrossRef]
- Mansor, S.B.; Cracknell, A.P.; Shilin, B.; Gornyi, V. Monitoring of underground coal fires using thermal infrared data. Int. J. Remote Sens. 1994, 15, 1675–1685. [Google Scholar] [CrossRef]
- Ononye, A.E.; Vodacek, A.; Saber, E. Automated extraction of fire line parameters from multispectral infrared images. Remote Sens. Environ. 2007, 108, 179–188. [Google Scholar] [CrossRef]
- Pozo, D.; Olrno, F.; Alados-Arboledas, L. Fire detection and growth monitoring using a multitemporal technique on AVHRR mid-infrared and thermal channels. Remote Sens. Environ. 1997, 60, 111–120. [Google Scholar] [CrossRef]
- Roy, D.P.; Landmann, T. Characterizing the surface heterogeneity of fire effects using multi-temporal reflective wavelength data. Int. J. Remote Sens. 2005, 26, 4197–4218. [Google Scholar] [CrossRef]
- Li, Y.; Vodacek, A.; Kremens, R.L.; Ononye, A.; Tang, C. A hybrid contextual approach to wildland fire detection using multispectral imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2115–2126. [Google Scholar]
- Roberts, G.; Wooster, M. Development of a multi-temporal Kalman filter approach to geostationary active fire detection & fire radiative power (FRP) estimation. Remote Sens. Environ. 2014, 152, 392–412. [Google Scholar]
- Koltunov, A.; Ustin, S. Early fire detection using non-linear multitemporal prediction of thermal imagery. Remote Sens. Environ. 2007, 110, 18–28. [Google Scholar] [CrossRef]
- Zhang, P.; Yuan, C.; Sun, Q.; Liu, A.; You, S.; Li, X.; Zhang, Y.; Jiao, X.; Sun, D.; Sun, M.; et al. Satellite-Based Detection and Characterization of Industrial Heat Sources in China. Environ. Sci. Technol. 2019, 53, 11031–11042. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, C.; Zhan, W.; Sun, C.; Murch, B.; Ma, L. Identifying industrial heat sources using time-series of the VIIRS Nightfire product with an object-oriented approach. Remote Sens. Environ. 2018, 204, 347–365. [Google Scholar] [CrossRef]
- Ma, C.; Yang, J.; Chen, F.; Ma, Y.; Liu, J.; Li, X.; Duan, J.; Guo, R. Assessing heavy industrial heat source distribution in China using real-time VIIRS active fire/hotspot data. Sustainability 2018, 10, 4419. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Abubaker, M.; Ashour, W.M. Efficient data clustering algorithms: Improvements over Kmeans. Effic. Data Clust. Algorithms Improv. Kmeans 2013, 3, 37–49. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, H.; Eom, K.B. Active Deep Learning for Classification of Hyperspectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 712–724. [Google Scholar] [CrossRef]
- Liu, P.; Choo, K.K.R.; Wang, L.; Huang, F. SVM or Deep Learning? A Comparative Study on Remote Sensing Image Classification. Soft Comput. 2017, 21, 7053–7065. [Google Scholar] [CrossRef]
- Guo, H.; Nativi, S.; Liang, D.; Craglia, M.; Wang, L.; Schade, S.; Corban, C.; He, G.; Pesaresi, M.; Li, J.; et al. Big Earth Data science: An information framework for a sustainable planet. Int. J. Digit. Earth 2020, 13, 743–767. [Google Scholar] [CrossRef]
- Guo, H.; Goodchild, M.F.; Annoni, A. Manual of Digital Earth; Springer Nature: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Ma, Y.; Wu, H.; Wang, L.; Huang, B.; Ranjan, R.; Zomaya, A.; Jie, W. Remote sensing big data computing: Challenges and opportunities. Future Gener. Comput. Syst. 2015, 51, 47–60. [Google Scholar] [CrossRef]
- Liu, P.; Di, L.; Du, Q.; Wang, L. Remote Sensing Big Data: Theory, Methods and Applications. Remote Sens. 2018, 10, 711. [Google Scholar] [CrossRef]
- Li, S.; Cheng, C.; Chen, B.; Meng, L. Integration and management of massive remote-sensing data based on GeoSOT subdivision model. J. Appl. Remote Sens. 2016, 10, 034003. [Google Scholar] [CrossRef]
- Khalilian, M.; Boroujeni, F.Z.; Mustapha, N.; Sulaiman, M.N. K-means divide and conquer clustering. In Proceedings of the 2009 International Conference on Computer and Automation Engineering, Bangkok, Thailand, 8–10 March 2009; pp. 306–309. [Google Scholar]
- Li, Z.; Nadon, S.; Cihlar, J. Satellite-based detection of Canadian boreal forest fires: Development and application of the algorithm. Int. J. Remote Sens. 2000, 21, 3057–3069. [Google Scholar] [CrossRef]
- Ichoku, C.; Kaufman, Y.; Giglio, L.; Li, Z.; Fraser, R.; Jin, J.Z.; Park, W. Comparative analysis of daytime fire detection algorithms using AVHRR data for the 1995 fire season in Canada: Perspective for MODIS. Int. J. Remote Sens. 2003, 24, 1669–1690. [Google Scholar] [CrossRef]
- Ma, C.; Niu, Z.; Ma, Y.; Chen, F.; Yang, J.; Liu, J. Assessing the Distribution of Heavy Industrial Heat Sources in India between 2012 and 2018. ISPRS Int. J. Geo-Inf. 2019, 8, 568. [Google Scholar] [CrossRef]
- Schroeder, W. Visible Infrared Imaging Radiometer Suite (VIIRS) 375 m & 750 m Active Fire Detection Data Sets Based on Nasa VIIRS Land Science Investigator Processing System (SIPS) Reprocessed Data-Version 1, NASA. 2017. Available online: https://lpdaac.usgs.gov/documents/132/VNP14_User_Guide_v1.3.pdf (accessed on 1 August 2020).
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Ding, Y.; Zhao, Y.; Shen, X.; Musuvathi, M.; Mytkowicz, T. Yinyang k-means: A drop-in replacement of the classic k-means with consistent speedup. In Proceedings of the 32nd International Conference on Machine Learning, ICML 2015, Lille, France, 6–11 July 2015; pp. 579–587. [Google Scholar]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A.; Vigo-Aguiar, J. Yinyang K-means clustering for hyperspectral image analysis. In Proceedings of the 17th International Conference on Computational and Mathematical Methods in Science and Engineering, Cadiz, Spain, 4–8 July 2017; pp. 1625–1636. [Google Scholar]
- Lv, Z.; Hu, Y.; Zhong, H.; Wu, J.; Li, B.; Zhao, H. Parallel k-means clustering of remote sensing images based on mapreduce. In Proceedings of the International Conference on Web Information Systems and Mining, Sanya, China, 24–25 September 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 162–170. [Google Scholar]
- Ke, H.; Chen, D.; Shi, B.; Zhang, J.; Liu, X.; Zhang, X.; Li, X. Improving Brain E-Health Services via High-Performance EEG Classification with Grouping Bayesian Optimization. IEEE Trans. Serv. Comput. 2020, 13, 696–708. [Google Scholar] [CrossRef]
- Chen, D.; Hu, Y.; Wang, L.; Zomaya, A.Y.; Li, X. H-PARAFAC: Hierarchical Parallel Factor Analysis of Multidimensional Big Data. IEEE Trans. Parallel Distrib. Syst. 2017, 28, 1091–1104. [Google Scholar] [CrossRef]
- Chen, D.; Tang, Y.; Zhang, H.; Wang, L.; Li, X. Incremental Factorization of Big Time Series Data with Blind Factor Approximation. IEEE Trans. Knowl. Data Eng. 2019, 1–14. [Google Scholar] [CrossRef]
- Chen, K. On coresets for k-median and k-means clustering in metric and euclidean spaces and their applications. SIAM J. Comput. 2009, 39, 923–947. [Google Scholar] [CrossRef]
- Karypis, M.S.G.; Kumar, V.; Steinbach, M. A comparison of document clustering techniques. In Proceedings of the TextMining Workshop at KDD2000, Boston, MA, USA, 20–23 August 2000. [Google Scholar]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Ma, C.; Liu, P.; Yang, J.; Wang, Y.; Zhu, Y.; Du, X. Spatial-Temporal Distribution Analysis of Industrial Heat Sources in the US with Geocoded, Tree-Based, Large-Scale Clustering. Remote Sens. 2020, 12, 3069. https://doi.org/10.3390/rs12183069
Ma Y, Ma C, Liu P, Yang J, Wang Y, Zhu Y, Du X. Spatial-Temporal Distribution Analysis of Industrial Heat Sources in the US with Geocoded, Tree-Based, Large-Scale Clustering. Remote Sensing. 2020; 12(18):3069. https://doi.org/10.3390/rs12183069
Chicago/Turabian StyleMa, Yan, Caihong Ma, Peng Liu, Jin Yang, Yuzhu Wang, Yueqin Zhu, and Xiaoping Du. 2020. "Spatial-Temporal Distribution Analysis of Industrial Heat Sources in the US with Geocoded, Tree-Based, Large-Scale Clustering" Remote Sensing 12, no. 18: 3069. https://doi.org/10.3390/rs12183069
APA StyleMa, Y., Ma, C., Liu, P., Yang, J., Wang, Y., Zhu, Y., & Du, X. (2020). Spatial-Temporal Distribution Analysis of Industrial Heat Sources in the US with Geocoded, Tree-Based, Large-Scale Clustering. Remote Sensing, 12(18), 3069. https://doi.org/10.3390/rs12183069







