Retrieval of Crude Protein in Perennial Ryegrass Using Spectral Data at the Canopy Level
Abstract
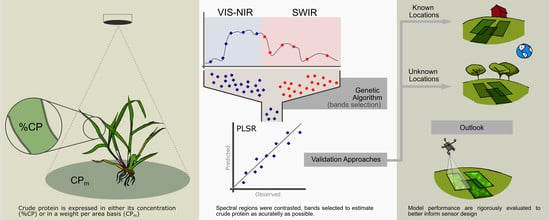
1. Introduction
2. Methods
2.1. Experimental Setup
2.2. Data Collection
2.3. Data Analysis
2.3.1. Ground Truth Analysis
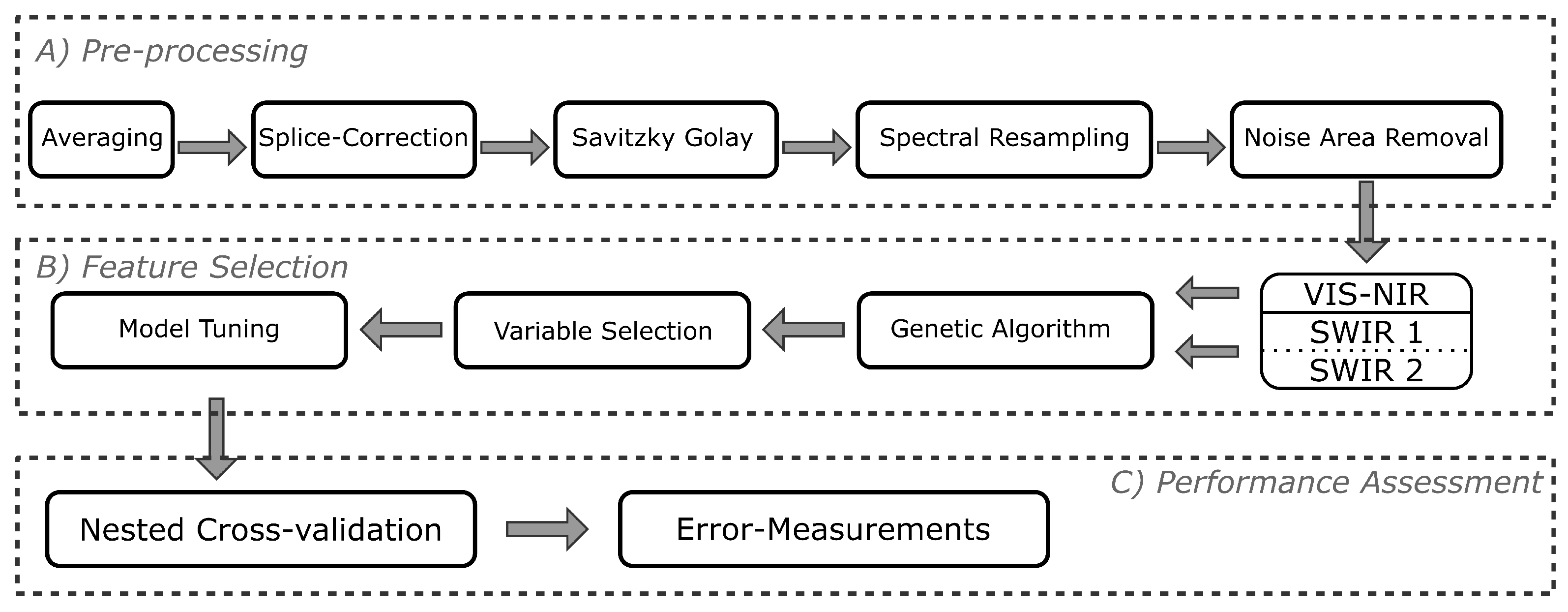
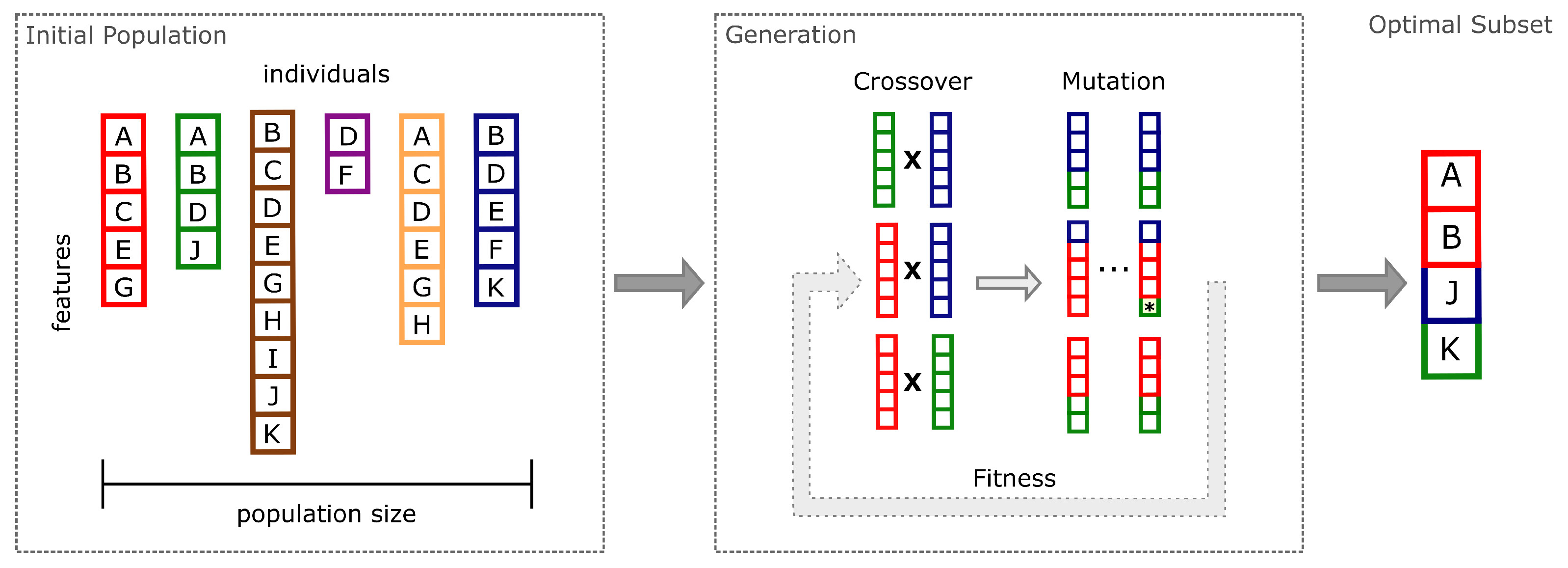
2.3.2. Spectral Analysis
- number of variables;
- variable importance in projection of the jth feature (band);
- ath component to maximum (A) number of latent components;
- the jth feature;
- sum of squares of Y;
- loading weights of the predictor matrix (i.e., features);
- mean squares (from the -test notation).
3. Results
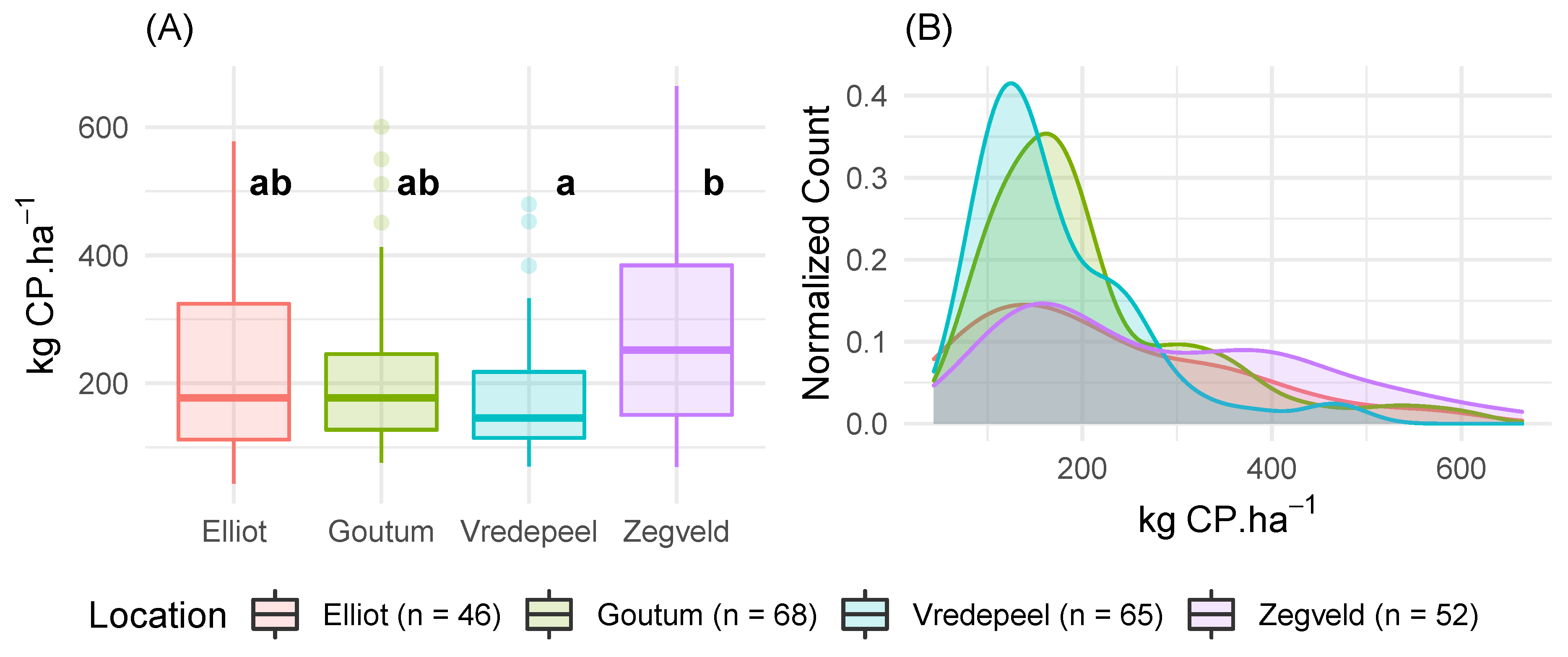
3.1. Ground Truth Analysis
3.2. Spectral Analysis
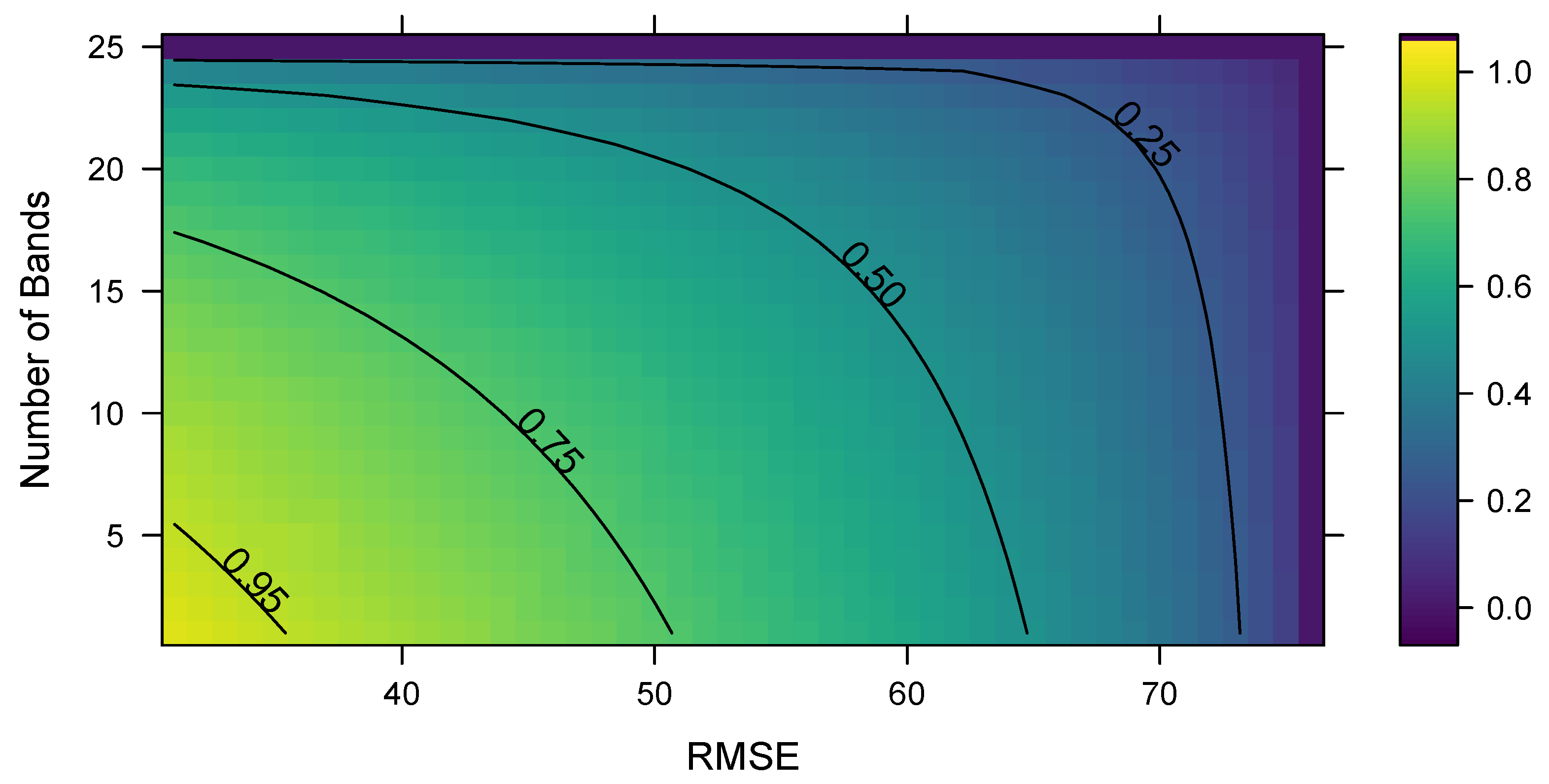
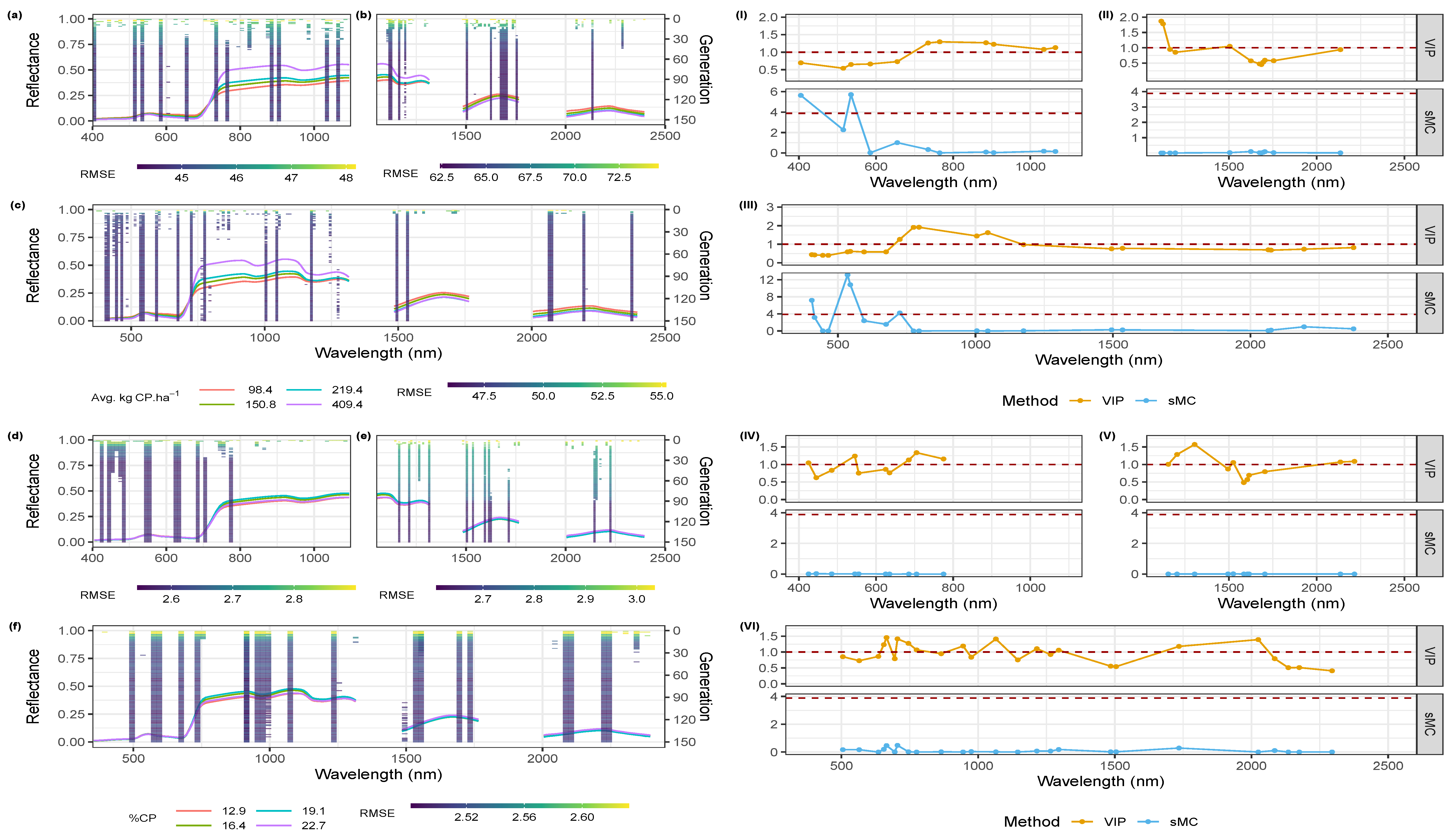
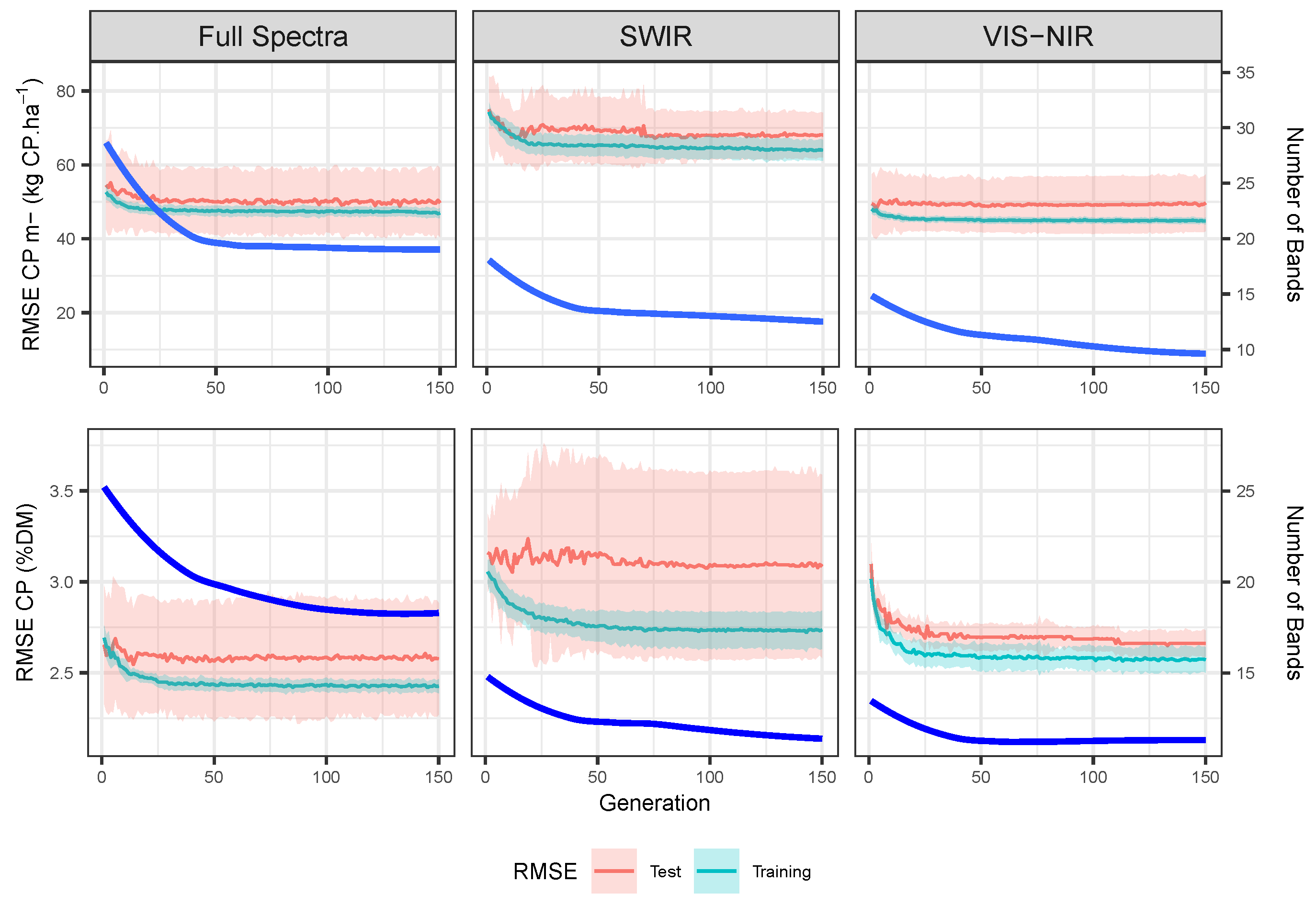
3.2.1. Feature Selection (Band) Selection
VIS-NIR Feature Selection Protocol
SWIR Feature Selection Protocol
Full Spectrum Selection Protocol
3.2.2. Variable Importance
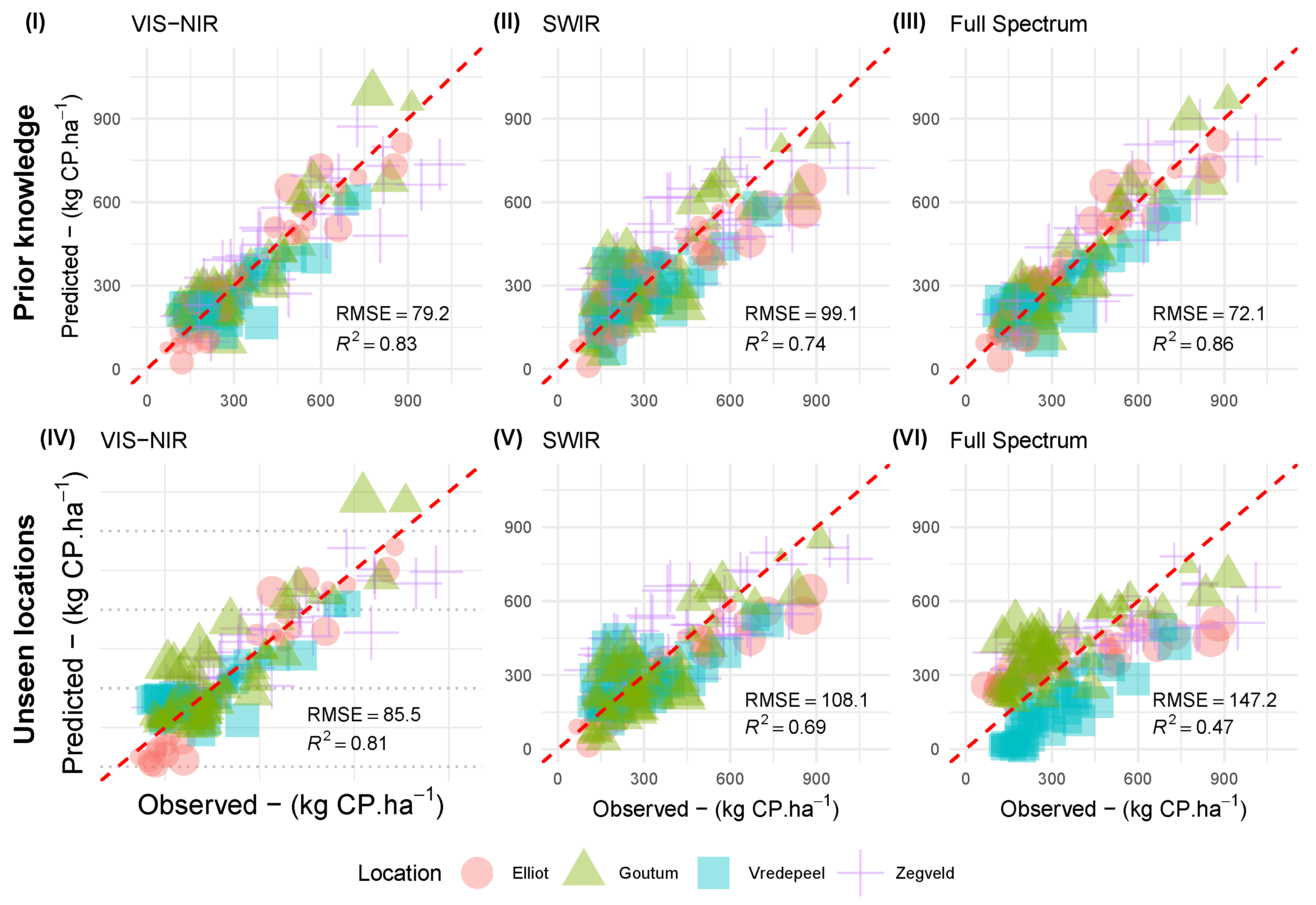
3.2.3. Performance Assessment
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CP | Crude Protein |
| CPm | Crude Protein Yield |
| Crude Protein as a Dry Matter Fraction | |
| DM | Dry Matter |
| FS | Full Spectrum |
| InGaAs | Indium Gallium Arsenide |
| LAI | Leaf Area Index |
| LAD | Leaf Angle Distribution |
| MS | Multispectral |
| N | Nitrogen |
| NIRS | Near Infrared Spectroscopy |
| PbS | Lead Sulfide |
| R | Reflectance |
| RMSE | Root Mean Square Error |
| RMSE | Root Mean Square Error Prediction |
| RS | Remote Sensing |
| Si | Silicon |
| SWIR | Shortwave Infrared |
| TOC | Top of Canopy |
| VIS–NIR | Visible and Near Infrared |
References
- Fariña, S.R.; Garcia, S.C.; Fulkerson, W.J.; Barchia, I.M. Pasture-based dairy farm systems increasing milk production through stocking rate or milk yield per cow: Pasture and animal responses. Grass Forage Sci. 2011, 66, 316–332. [Google Scholar] [CrossRef]
- Jones, G.; Wade, N.S.; Baker, J.P.; Ranck, E.M. Use of Near Infrared Reflectance Spectroscopy in Forage Testing. J. Dairy Sci. 1987, 70, 1086–1091. [Google Scholar] [CrossRef]
- Roberts, C.A.; Stuth, J.; Flinn, P. Analysis of Forages and Feedstuffs. In Near-Infrared Spectroscopy in Agriculture; Wiley Online Library: Hoboken, NJ, USA, 2004; Volume 44, pp. 229–267. [Google Scholar] [CrossRef]
- Prewer, W.E.; Bysterveldt, A.V. The Pasture Quality Poster-a learning tool for farmers. In Proceedings of the New Zealand Grassland Association; New Zealand Grassland Association: Wellington, New Zealand, 2004; pp. 183–186. [Google Scholar]
- Machado, C.F.; Morris, S.T.; Hodgson, J.; Fathalla, M. Seasonal changes of herbage quality within a New Zealand beef cattle finishing pasture. N. Z. J. Agric. Res. 2005, 48, 265–270. [Google Scholar] [CrossRef]
- Valk, H.; Leusink-Kappers, I.E.; Van Vuuren, A.M. Effect of reducing nitrogen fertilizer on grassland on grass intake, digestibility and milk production of dairy cows. Livest. Prod. Sci. 2000, 63, 27–38. [Google Scholar] [CrossRef]
- Norris, K.H.; Barnes, R.F.; Moore, J.E.; Shenk, J.S. Predicting Forage Quality by Infrared Reflectance Spectroscopy. J. Anim. Sci. 1976, 43, 889–897. [Google Scholar] [CrossRef]
- Wijesingha, J.; Astor, T.; Schulze-Brüninghoff, D.; Wengert, M.; Wachendorf, M. Predicting Forage Quality of Grasslands Using UAV-Borne Imaging Spectroscopy. Remote Sens. 2020, 12, 126. [Google Scholar] [CrossRef]
- Sanches, I.; Tuohy, M.; Hedley, M.; Mackay, A. Seasonal prediction of in situ pasture macronutrients in New Zealand pastoral systems using hyperspectral data. Int. J. Remote Sens. 2013, 34, 276–302. [Google Scholar] [CrossRef]
- Kawamura, K.; Betteridge, K.; Costall, D.; Sanches, I.D.; Tuohy, M.P.; Inoue, Y. Spectro-CAPP as a tool to estimate and map pasture biomass and mineral component in New Zealand. In Proceedings of the 29th Asian Conference on Remote Sensing 2008 (ACRS 2008), Colombo, Sri Lanka, 10–14 November 2008; Volume 2, pp. 1345–1350. [Google Scholar]
- Curran, P.J. Remote sensing of foliar chemistry. Remote Sens. Environ. 1989, 30, 271–278. [Google Scholar] [CrossRef]
- Asner, G.P. Biophysical and Biochemical Sources of Variability in Canopy Reflectance. Remote Sens. Environ. 1998, 64, 234–253. [Google Scholar] [CrossRef]
- Beer. Bestimmung der Absorption des rothen Lichts in farbigen Flüssigkeiten. Ann. Phys. Chem. 1852, 162, 78–88. [Google Scholar] [CrossRef]
- Baranoski, G.V.G.; Eng, D. An Investigation on Sieve and Detour Effects Affecting the Interaction of Collimated and Diffuse Infrared Radiation (750 to 2500 nm) With Plant Leaves. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2593–2599. [Google Scholar] [CrossRef]
- Shorten, P.R.; Leath, S.R.; Schmidt, J.; Ghamkhar, K. Predicting the quality of ryegrass using hyperspectral imaging. Plant Methods 2019, 15, 63. [Google Scholar] [CrossRef] [PubMed]
- Hadamard, J. Sur les problems aux derivees patielles et leur signification physique. Princet. Univ. Bull. 1902, 13, 49–52. [Google Scholar]
- Baret, F.; Samuel, B. Advances in Land Remote Sensing; Number November 2014; Springer: Dordrecht, The Netherlands, 2008; pp. 173–201. [Google Scholar] [CrossRef]
- Thulin, S.; Hill, M.J.; Held, A.; Jones, S.; Woodgate, P. Predicting Levels of Crude Protein, Digestibility, Lignin and Cellulose in Temperate Pastures Using Hyperspectral Image Data. Am. J. Plant Sci. 2014, 05, 997–1019. [Google Scholar] [CrossRef]
- Kawamura, K.; Watanabe, N.; Sakanoue, S.; Lee, H.J.; Inoue, Y.; Odagawa, S. Testing genetic algorithm as a tool to select relevant wavebands from field hyperspectral data for estimating pasture mass and quality in a mixed sown pasture using partial least squares regression. Grassl. Sci. 2010, 56, 205–216. [Google Scholar] [CrossRef]
- Starks, P.J.; Brown, M.A. Prediction of Forage Quality from Remotely Sensed Data: Comparison of Cultivar-Specific and Cultivar-Independent Equations Using Three Methods of Calibration. Crop Sci. 2010, 50, 2159–2170. [Google Scholar] [CrossRef]
- Biewer, S.; Fricke, T.; Wachendorf, M. Development of Canopy Reflectance Models to Predict Forage Quality of Legume-Grass Mixtures. Crop Sci. 2009, 49, 1917–1926. [Google Scholar] [CrossRef]
- Baret, F.; Houles, V.; Guerif, M. Quantification of plant stress using remote sensing observations and crop models: The case of nitrogen management. J. Exp. Bot. 2006, 58, 869–880. [Google Scholar] [CrossRef] [PubMed]
- Baret, F.; Fourty, T. Radiometric Estimates of Nitrogen Status of Leaves and Canopies. In Diagnosis of the Nitrogen Status in Crops; Springer: Berlin/Heidelberg, Germany, 1997; pp. 201–227. [Google Scholar] [CrossRef]
- Starks, P.J.; Zhao, D.; Phillips, W.A.; Coleman, S.W. Development of Canopy Reflectance Algorithms for Real-Time Prediction of Bermudagrass Pasture Biomass and Nutritive Values. Crop Sci. 2006, 46, 927–934. [Google Scholar] [CrossRef]
- Kattenborn, T.; Schiefer, F.; Zarco-Tejada, P.; Schmidtlein, S. Advantages of retrieving pigment content [μg/cm2] versus concentration [%] from canopy reflectance. Remote Sens. Environ. 2019, 230, 111195. [Google Scholar] [CrossRef]
- Kjeldahl, K.; Bro, R. Some common misunderstandings in chemometrics. J. Chemom. 2010, 24, 558–564. [Google Scholar] [CrossRef]
- Rasmussen, M.A.; Bro, R. A tutorial on the Lasso approach to sparse modeling. Chemom. Intell. Lab. Syst. 2012, 119, 21–31. [Google Scholar] [CrossRef]
- Hoving, I.E.; Starmans, D.A.J.; Booij, J.A.; Kuiper, I.; Holshof, G. Amazing Grazing: Grass Growth Measurements with Remote Sensing Techniques; Teagasc, Animal & Grassland Research and Innovation Centre: Fermoy, Irish Republic, 2018; pp. 860–862. [Google Scholar]
- Rawnsley, R.P.; Langworthy, A.D.; Pembleton, K.G.; Turner, L.R.; Corkrey, R.; Donaghy, D.J. Quantifying the interactions between grazing interval, grazing intensity, and nitrogen on the yield and growth rate of dryland and irrigated perennial ryegrass. Crop Pasture Sci. 2014, 65, 735–746. [Google Scholar] [CrossRef]
- Mac Arthur, A.; Robinson, I. A critique of field spectroscopy and the challenges and opportunities it presents for remote sensing for agriculture, ecosystems, and hydrology. In Remote Sensing for Agriculture, Ecosystems, and Hydrology XVII; Neale, C.M.U., Maltese, A., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9637, p. 963705. [Google Scholar] [CrossRef]
- Lantinga, E.A.; Nassiri, M.; Kropff, M.J. Modelling and measuring vertical light absorption within grass–clover mixtures. Agric. For. Meteorol. 1999, 96, 71–83. [Google Scholar] [CrossRef]
- Marten, G.; Shenk, J.; Barton, F. Near infrared reflectance spectroscopy (NIRS): Analysis of forage quality. In Agriculture Handbook; U.S. Department of Agriculture: Washington, DC, USA, 1989; Volume 643, pp. 1–110. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Kuhn, M.; Johnson, K. Feature Engineering and Selection: A Practical Approach for Predictive Models, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2019; p. 314. [Google Scholar] [CrossRef]
- Kuhn, M. Desirability: Function Optimization and Ranking via Desirability Functions; R Package Version 2.1.; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A review of variable selection methods in Partial Least Squares Regression. Chemom. Intell. Lab. Syst. 2012, 118, 62–69. [Google Scholar] [CrossRef]
- Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Josse, J.; Husson, F. missMDA: A Package for Handling Missing Values in Multivariate Data Analysis. J. Stat. Softw. 2016, 70. [Google Scholar] [CrossRef]
- Cao, D.S.; Deng, Z.K.; Zhu, M.F.; Yao, Z.J.; Dong, J.; Zhao, R.G. Ensemble partial least squares regression for descriptor selection, outlier detection, applicability domain assessment, and ensemble modeling in QSAR/QSPR modeling. J. Chemom. 2017, 31, e2922. [Google Scholar] [CrossRef]
- Hotelling, H. The Generalization of Student’s Ratio. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; Volume 2, pp. 54–65. [Google Scholar] [CrossRef]
- Lehnert, L.W.; Meyer, H.; Obermeier, W.A.; Silva, B.; Regeling, B.; Bendix, J. Hyperspectral Data Analysis in R: The hsdar Package. J. Stat. Softw. 2018, 89. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013; Volume 26, pp. 1–600. [Google Scholar] [CrossRef]
- Mevik, B.H.; Wehrens, R. Introduction to the Pls Package; R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
- Scrucca, L. GA: A package for genetic algorithms in R. J. Stat. Softw. 2013, 53, 1–37. [Google Scholar] [CrossRef]
- Jaccard, P. Distribution de la flore alpine dans le bassin des Dranses et dans quelques régions voisines. Bull. Soc. Vaud. Sci. Nat. 1901, 37, 241–272. [Google Scholar] [CrossRef]
- Starks, P.J.; Brown, M.A.; Turner, K.E.; Venuto, B.C. Canopy Visible and Near-infrared Reflectance Data to Estimate Alfalfa Nutritive Attributes Before Harvest. Crop Sci. 2016, 56, 484–496. [Google Scholar] [CrossRef]
- Australian Fodder Industry Association Standards. FODDERS Trading Standards—Grain Trade Australia. Available online: https://www.graintrade.org.au/sites/default/files/file/CommodityStandards/Section05-Fodder201314 (accessed on 7 June 2020).
- Mutanga, O.; Skidmore, A.K. Red edge shift and biochemical content in grass canopies. ISPRS J. Photogramm. Remote Sens. 2007, 62, 34–42. [Google Scholar] [CrossRef]
- Sandmeier, S.; Itten, K. A field goniometer system (FIGOS) for acquisition of hyperspectral BRDF data. IEEE Trans. Geosci. Remote Sens. 1999, 37, 978–986. [Google Scholar] [CrossRef]
- Guyot, G.; Baret, F. Utilisation de la haute résolution spectrale pour suivre l’état des couverts végétaux. (Use of high spectral resolution for vegetation monitoring). In Proceedings of the 4th International Colloquium on Spectral Signatures of Objects in Remote Sensing, Aussois, France, 18–22 January 1988; Volume 287, pp. 279–286. [Google Scholar] [CrossRef]
- Miller, E.J. The basic amino-acids of typical forage grass proteins. Biochem. J. 1935, 29, 2344–2350. [Google Scholar] [CrossRef] [PubMed]
- Kokaly, R. Spectroscopic Determination of Leaf Biochemistry Using Band-Depth Analysis of Absorption Features and Stepwise Multiple Linear Regression. Remote Sens. Environ. 1999, 67, 267–287. [Google Scholar] [CrossRef]
- Morimoto, S.; Scholar, V.; McClure, W.F. More on Derivatives: Resolving Overlapping Absorbance Bands. NIR News 1999, 10, 10–12. [Google Scholar] [CrossRef]
- Wang, S.; Baum, A.; Zarco-Tejada, P.J.; Dam-Hansen, C.; Thorseth, A.; Bauer-Gottwein, P.; Bandini, F.; Garcia, M. Unmanned Aerial System multispectral mapping for low and variable solar irradiance conditions: Potential of tensor decomposition. ISPRS J. Photogramm. Remote Sens. 2019, 155, 58–71. [Google Scholar] [CrossRef]
- Burkart, A.; Cogliati, S.; Schickling, A.; Rascher, U. A Novel UAV-Based Ultra-Light Weight Spectrometer for Field Spectroscopy. IEEE Sens. J. 2014, 14, 62–67. [Google Scholar] [CrossRef]
- Mamaghani, B.; Salvaggio, C. Multispectral Sensor Calibration and Characterization for sUAS Remote Sensing. Sensors 2019, 19, 4453. [Google Scholar] [CrossRef]
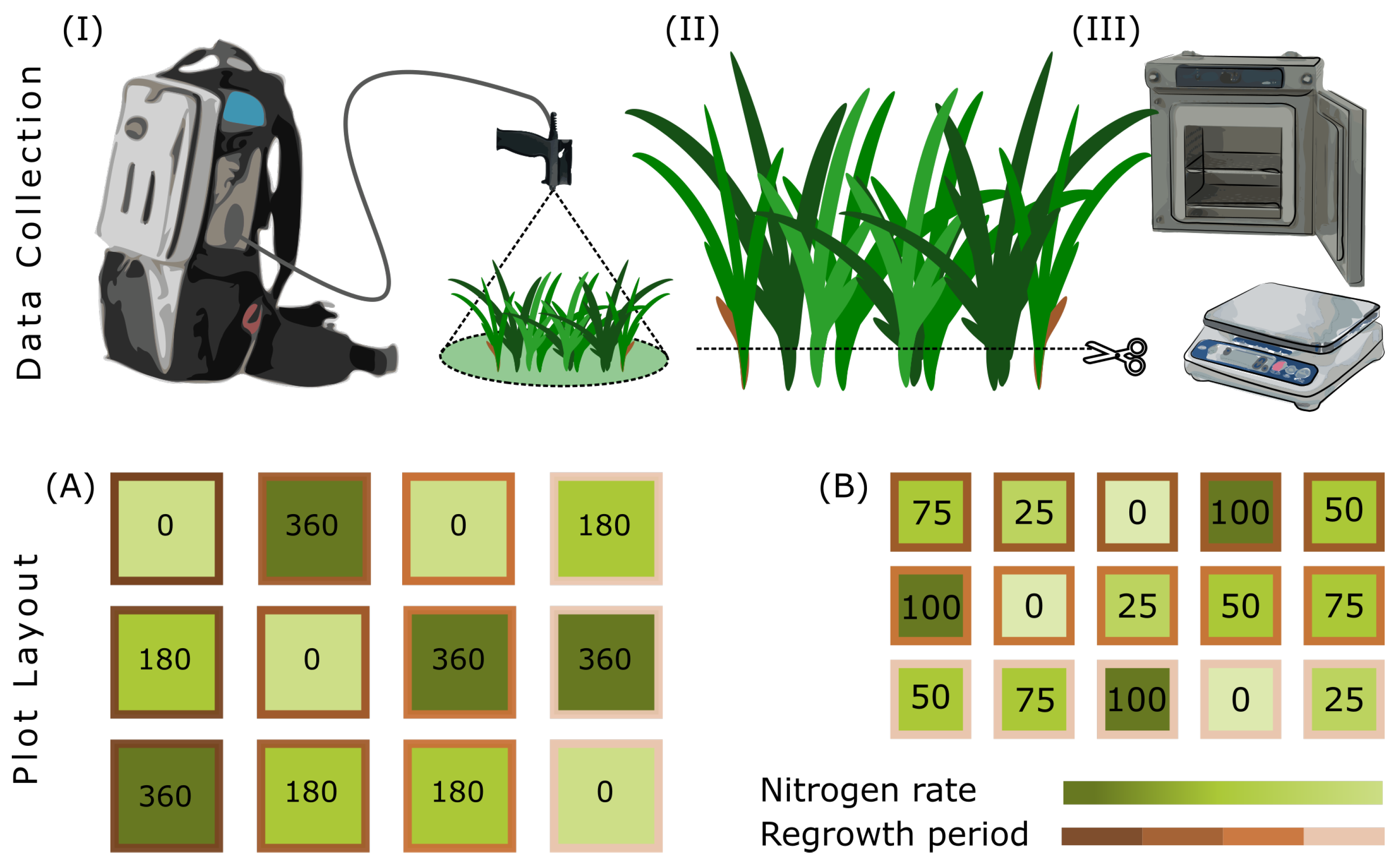
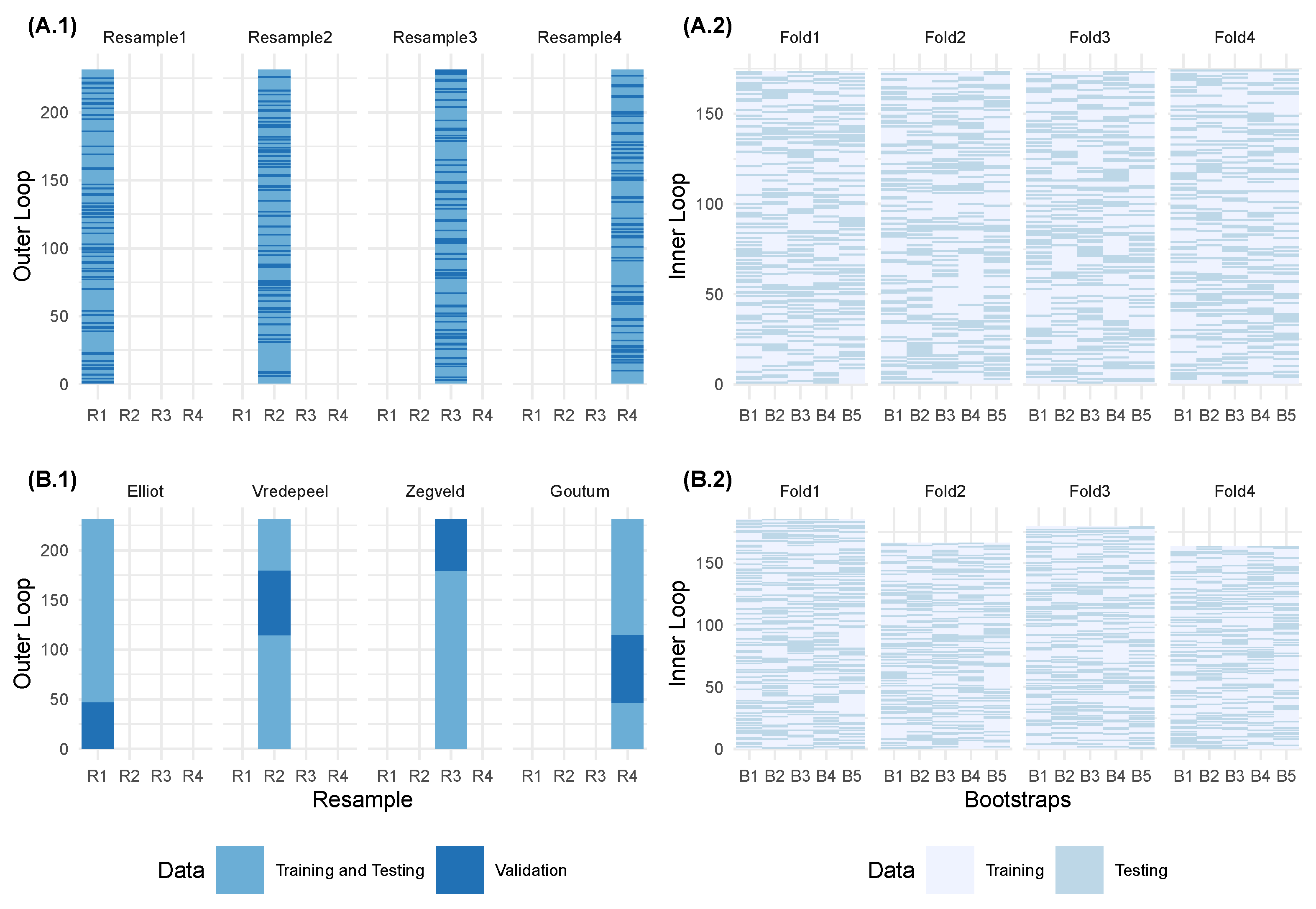

| Location | Date 1 | Date 2 | Date 3 | Instrument | Soil Type | N Rates * | Regrowth ** |
|---|---|---|---|---|---|---|---|
| Elliot (AU) | 11 November | 17 November | 24 November | FieldSpec 4 | Clay | 50–75–100 | 3 |
| Goutum (NL) | 15 May | 28 June | 05 October | FieldSpec 3 | Clay | 180–360 | 4 |
| Vredepeel(NL) | 11 June | 03 July | 27 September | FieldSpec 3 | Sandy | 180–360 | 4 |
| Zegveld (NL) | 10 May | 19 June | 10 October | FieldSpec 3 | Peat | 180–360 | 4 |
| Samples (n) | CPm (kg CP.ha−1) | % CP (% DM) | Biomass (kg DM.ha−1) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Location | Initial | Final | Mean | Min | Max | Mean | Min | Max | Mean | Min | Max | |||
| Elliot | 50 | 46 | 223 | 43 | 578 | 20 | 12.3 | 27 | 1115 | 224 | 2986 | |||
| Goutum | 72 | 68 | 208 | 76 | 601 | 16 | 9.4 | 28 | 1380 | 526 | 3282 | |||
| Vredepeel | 72 | 65 | 172 | 70 | 479 | 18 | 9.6 | 26 | 1015 | 395 | 3223 | |||
| Zegveld | 72 | 52 | 283 | 70 | 664 | 18 | 11.5 | 24 | 1566 | 592 | 3420 | |||
| Training (RMSE-kg CP.ha ) | Testing (RMSE-kg CP.ha ) | Features () | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Max | Min | Ini | Fin | Max | Min | Ini | Fin | Max | Min | ||||||||
| VIS NIR | 45 | 50 | 43 | 0.97 | 47 | 45 | 49 | 63 | 35 | 7.2 | 50 | 49 | 11 | 24 | 8 | ||
| SWIR | 65 | 79 | 60 | 3.23 | 71 | 64 | 69 | 93 | 56 | 7.6 | 71 | 68 | 14 | 33 | 9 | ||
| Full | 48 | 55 | 45 | 1.54 | 50 | 47 | 50 | 80 | 37 | 8.7 | 53 | 50 | 20 | 52 | 13 | ||
| (RMSE-%DM) | (RMSE-%DM) | () | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Max | Min | Ini | Fin | Max | Min | Ini | Fin | Max | Min | ||||||||
| VIS NIR | 2.6 | 3.2 | 2.4 | 0.09 | 2.8 | 2.6 | 2.7 | 3.5 | 2.0 | 0.38 | 2.9 | 2.7 | 12 | 21 | 8 | ||
| SWIR | 2.8 | 3.2 | 2.6 | 0.11 | 3.0 | 2.7 | 3.1 | 4.2 | 2.0 | 0.48 | 3.1 | 3.1 | 12 | 27 | 6 | ||
| Full | 2.4 | 2.8 | 2.3 | 0.06 | 2.6 | 2.4 | 2.6 | 3.3 | 1.9 | 0.31 | 2.6 | 2.6 | 20 | 41 | 12 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Togeiro de Alckmin, G.; Lucieer, A.; Roerink, G.; Rawnsley, R.; Hoving, I.; Kooistra, L. Retrieval of Crude Protein in Perennial Ryegrass Using Spectral Data at the Canopy Level. Remote Sens. 2020, 12, 2958. https://doi.org/10.3390/rs12182958
Togeiro de Alckmin G, Lucieer A, Roerink G, Rawnsley R, Hoving I, Kooistra L. Retrieval of Crude Protein in Perennial Ryegrass Using Spectral Data at the Canopy Level. Remote Sensing. 2020; 12(18):2958. https://doi.org/10.3390/rs12182958
Chicago/Turabian StyleTogeiro de Alckmin, Gustavo, Arko Lucieer, Gerbert Roerink, Richard Rawnsley, Idse Hoving, and Lammert Kooistra. 2020. "Retrieval of Crude Protein in Perennial Ryegrass Using Spectral Data at the Canopy Level" Remote Sensing 12, no. 18: 2958. https://doi.org/10.3390/rs12182958
APA StyleTogeiro de Alckmin, G., Lucieer, A., Roerink, G., Rawnsley, R., Hoving, I., & Kooistra, L. (2020). Retrieval of Crude Protein in Perennial Ryegrass Using Spectral Data at the Canopy Level. Remote Sensing, 12(18), 2958. https://doi.org/10.3390/rs12182958