Abstract
Due to spatial inhomogeneity of land-cover types and spectral confusions among them, land-cover maps suffer from misclassification errors. While much research has focused on improving image classification by re-processing source images with more advanced algorithms and/or using images of finer resolution, there is rarely any systematic work on re-processing existing maps to increase their accuracy. We propose refining existing maps to achieve accuracy gains by exploring and utilizing relationships between reference data, which are often already available or can be collected, and map data. For this, we make novel use of canonical correspondence analysis (CCA) to analyze reference-map class co-occurrences to facilitate probabilistic re-classification of map classes in CCA ordination space, a synthesized feature space constrained by map class occurrence patterns. Experiments using GlobeLand30 land-cover (2010) over Wuhan, China were carried out using reference sample data collected previously for accuracy assessment in the same area. Reference sample data were stratified by map classes and their spatial heterogeneity. To examine effects of model-training sample size on refinements, three subset samples (360, 720, and 1480 pixels) were selected from a pool of 3000 sample pixels (the full training sample). Logistic regression modeling was employed as a baseline method for comparisons. Performance evaluation was based on a test sample of 1020 pixels using a strict and relaxed definitions of agreement between reference classification and map classification, resulting in measures of types I and II, respectively. It was found that the CCA-based method is more accurate than logistic regression in general. With increasing sample sizes, refinements generally lead to greater accuracy gains. Heterogeneous sub-strata usually see greater accuracy gains than in homogeneous sub-strata. It was also revealed that accuracy gains in specific strata (map classes and sub-strata) are related to strata refinability. Regarding CCA-based refinements, a relatively small sample of 360 pixels achieved a 3% gain in both overall accuracy (OA) and F0.01 score (II). By using a selective strategy in which only refinable strata of cultivated land and forest are included in refinement, accuracy gains are further increased, with 5–11% gains in users’ accuracies (UAs) (II) and 4–10% gains in F0.01 scores (II). In conclusion, on condition of refinability, map refinement is well worth pursuing, as it increases accuracy of existing maps, extends utility of reference data, facilitates uncertainty-informed map representation, and enhances our understanding about relationships between reference data and map data and about their synthesis.
1. Introduction
Land-cover information is important for research and applications concerning environmental modeling, land change, and sustainable developments. Various land-cover information products, such as MODIS land-cover [1], GlobeLand30 [2], and the US National Land Cover Database (NLCD) [3], are developed and made available for users nowadays. They are often updated at regular intervals (e.g., every five years for NLCD). Moreover, product improvements that seek to increase accuracy are facilitated through data re-processing and algorithm refinements [1].
Along with product developments, there is continuing work on accuracy assessments and analyses [4,5]. Such work has been done for various kinds of land-cover products, either static or dynamic [5,6], categorical or fractional [7,8], as also reviewed by Stehman and Foody [9]. It has been increasingly recognized that misclassification errors are not merely random but follow certain spatial patterns, as demonstrated in the literature on spatialized (per-pixel) accuracy modeling and analyses [10,11,12,13,14,15,16,17,18].
One major common goal for map producers and users is to increase map accuracies so that they can better serve land-cover monitoring [4] and other applications [19]. For instance, a 3% accuracy increase in single-date classification likely results in a 5% increase in bi-temporal change-classification, assuming single-date maps are about 80% accurate. We may seek to increase map accuracies by using smarter classifiers, incorporating more informative features, and/or using images of finer spatial, spectral, or temporal resolution, as mentioned above. On the other hand, for existing maps (or initial image classifications), it is sensible to pursue synthesis of map data and reference data to increase map accuracies, as is the goal of this research.
We can increase map accuracies by correcting misclassification errors, especially when they exhibit certain patterns. For example, Campos and Brito [20] observed misclassifications of rocky pixels as savannah mostly in the northern parts of the study area, and of water-bodies as vegetation (grasslands and savannah) or as rocky areas (gravel floodplains and bare rock) across their study area. They applied specific protocols to the identification of rock and water pixels, using local masking for cleaning erroneous savannah pixels and water indices, respectively. More often, misclassification patterns are not so straightforward to discern. This means we need to look elsewhere for increasing map accuracies. For this, it is sensible to explore relationships between reference data and map data, given availability of reference land-cover data [7], which are usually furnished for map accuracy assessments as mentioned previously.
We refer to such processes of analyzing and utilizing relationships between reference data and map data for increasing map accuracies as map refinement, with the aforementioned misclassification correction as a special case. Reference data consist of the reference classification for each unit in a sample. By reference classification, we mean the best available assessment of ground conditions [21], to reflect the relativity of ground truthing. In this paper, reference classes and map classes refer to class labels in reference classification and map classification, respectively.
The essence of map refinements is to predict reference class probabilities based on the relationships between reference classes and map classes (and their occurrence patterns). Previous work on map data fusion [22,23] and map refinement [24] was based on various empirical modeling approaches (e.g., generalized linear modeling (GLM)). Related work on local accuracy characterization has resulted in a variety of methods explored, including conventional inverse distance-weighted interpolation, logistic regression (i.e., GLM), and kernel-based interpolation [16]; these methods may be adapted for use in map refinement, although local accuracy estimation concerns probabilities that individual map pixels are classified correctly (not those for reference class occurrences). Literature on species distribution modeling [25,26,27] and imputation (of missing true values of variables of interest) [28,29,30] may shed light on suitable methods for map refinement. Canonical analysis methods [31] are also potentially useful, as reviewed below.
There have been applications of canonical analysis methods for predictive mapping of area classes (e.g., vegetation), mostly in combination with remote-sensing images [32,33,34,35,36,37,38]. Specific canonical analysis methods used include detrended correspondence analysis (DCA) [38], non-metric multidimensional scaling (NMDS) [35], isometric feature mapping (Isomap) [39], redundancy analysis (RDA) [40], and canonical correspondence analysis (CCA) [32]. These methods were used for improved predictive mapping of vegetation [33], mapping continuous floristic gradients (variations) [34,35,37,41,42], describing fuzziness in vegetation composition/units [40] or gradual changes from one plant association to another [36], and mapping characteristic material compositions in urban areas [38]. Some of these research efforts seek to quantify and visualize uncertainty in predictive mapping of vegetation based on canonical analysis [39]. CCA followed by k-nearest neighbors (kNN) in ordination space (also known as gradient space) constitutes a method known as gradient nearest neighbors (GNN) [32,43], which is useful for imputation. The strength of CCA and other relevant multivariate approaches is that full information about species composition is used through simultaneously relating each single recorded species to the data matrix on environmental information (climate, terrain, soil, spectral, etc.). This leads to an ordination space where the ordination axes reflect the statistical relationships between species and environmental information, with species having similar relationships to the environments being put in order along the axes to facilitate interpretation and visualization [40].
However, there seems to be no reported work on using CCA and other canonical analysis methods for exploring relationships between reference data and map data in general and for map refinement in particular. This research seeks to fill this important niche by applying CCA for map refinement through analyzing relationships between reference data and map class. The advantages of using CCA for map refinement are two-fold, although this research focuses on the first one. First, correspondence between reference classification and map classification can be directly analyzed in ordination space. Predictions of reference classes at unsampled locations can then be performed non-parametrically in the ordination space via kNN (e.g., GNN [43]), which would only be possible in the form of feature space when working in the spectral domain using image data [16,17,44]. Second, CCA-based predictive mapping provides an integral framework for refining both discrete and fractional land-cover maps (since both types can be modeled with CCA); the latter type would require models which are better suited for proportional data (e.g., robust GLM [45], while conventional GLM is designed for modeling probabilities of discrete class occurrences.
2. Materials and Methods
2.1. Explanatory Variables
Map refinement is to predict reference class occurrences by exploring relationships between reference classes and map classes (and their occurrence pattern indices), given some reference samples, known as model-training samples or simply training samples. In refinement-oriented modeling, response variables are reference class indicators (denoted by I), while explanatory variables (denoted by Z) are map classes and pattern indices derived from them in different sized moving windows centered at individual pixels being considered. Explanatory variables Z include map class, class proportions, homogeneity, heterogeneity, dominance, entropy, contagion, class occurrence frequencies of first-order adjacent polygons of the polygon where a pixel falls in (and the polygonal area), and geospatial coordinates (denoted X and Y). Except for class proportions and polygonal class adjacencies, which are proposed in this paper, all other Z variables were used in Zhang et al. [46] (Smith et al. [10] used polygonal areas). Definitions and calculation for these explanatory variables are shown in Table 1 below.

Table 1.
Explanatory variables.
In this study, we computed map class occurrence pattern indices over moving window sizes of 3 by 3, 5 by 5, 7 by 7, and 9 by 9. This maximum window size of 9 was set because smaller window sizes are more informative for pixel-level reference class modeling and for reducing computational burden. A total of 63 explanatory variables are considered in model selection: map class (6), class proportions in different-sized windows (28), pattern indices computed in different-sized windows (20), polygonal adjacencies (7), and geospatial coordinates (2).
2.2. CCA vs. GLM
CCA (Ter Braak, 1987) is conventionally used to predict distributions of species in ecology. The usual steps for CCA are [31]:
- 1)
- The response variables I matrix is transformed to Q matrix consisting of () for each element pij in the sample I matrix, where and are sums of values in row i and column j, respectively.
- 2)
- Weighted multiple regression is performed (weights applied to matrix Z (i.e., the matrix of explanatory variables), which is a diagonal matrix with diagonal elements being computed as ), with coefficient vector B hence matrix of fitted values derived:
- 3)
- Principal component analysis is run based on matrix, with eigenvalues and eigenvectors U derived.
- 4)
- Site scores are computed as linear combinations of explanatory variables Z (also known as environmental variables in numerical ecology) using the estimated canonical coefficients B:
These site scores determine the canonical coordinates of each map pixel in the canonical space (also known as ordination space or gradient space) defined by the main axes.
CCA explanatory variable selection is crucial for its performance. Variable selection can be made in a stepwise approach: selection is made of those explaining successively the highest proportion of variance in the response matrix dataset as a whole, this highest proportion of explained variation is tested for significance using Monte Carlo permutation test. In this research, anova.cca function in the R package vegan (vegan: community ecology package, version 2.5-4, http://cran.r-project.org/, http://vegan.r-forge.r-project.org/) was used for forward variable selection to identify a reduced set of explanatory variables. Variables were added if significant (p < 0.01), where significance was determined by a Monte Carlo permutation test using 999 permutations. Canonical axes can also be tested for significance through successive Monte Carlo permutations [47].
After projecting pixels onto the CCA ordination space (Equation (3)), class probabilities can be estimated using k-Nearest Neighbor (kNN) algorithms, in particular, GNN [32]. The distance in GNN is calculated as: , where and are the predicted site score of target pixel i and the site score of the reference sample pixel j, respectively, and is the diagonal matrix constructed using the eigenvalues of CCA model. The inverse distance weighting is often used to assign weights to nearest neighbors in kNN: , where is the distance from the ith target pixel to the jth reference pixel, and t is the power of inverse distance weighting. k and t are often optimized through cross-validation, in which each training pixel is withheld in turn and its (reference) class membership values are predicted using all other training pixels, given a series of combinations of k (say 1 through 50) and t (say 0, 1, 2). The optimal configuration of k and t for GNN is then taken to run predictions of class probabilities at unsampled pixels. In this research, GNN-based predictive mapping was performed using the R package yaImpute [48].
On the other hand, logistic regression models are usually used to describe relationships between a binary response variable I(x) and one or more explanatory variables Zl(x) (l=1, …, L) at pixel x. For mapping probabilities of a cover type occurring at a pixel x, the response variable is an indicator I(x) for the cover type at pixel x (coded as 1 if the specific cover type is present at pixel x, and 0 otherwise). The explanatory variables are pattern indices for map class occurrences within multi-scale neighborhoods, as described above. Model predictions are probabilities of individual pixels. A logistic model is
where pj(x) is the probability of pixel x belonging to class j, and β = (β0, β1, β2 …, βL) represents the parameters to be estimated [10].
For logistic model selection, an exhaustive procedure is often applied to find the optimal model containing the largest number of significant explanatory variables based on a particular model-training sample [11]. Individual candidate explanatory variables are tested using chi-square statistics with respect to their statistical significance. This is to test if adding a candidate variable to a model already selected (i.e., a simpler model) significantly improves model-fitting (i.e., leading to a significant decrease in model deviance) (at a significance level (α) of say 0.05). We performed logistic regression analysis on the R package Survey.
After predictions of class probabilities either by CCA (GNN) or GLM, residuals of class indicator values at model-training pixels should be analyzed to see if there exists significant spatial auto-correlation. This can be done by examining Moran’s I statistic at training pixels after GNN or GLM predictions [49]. If spatial autocorrelation is significant, kriging of residuals may be performed, with resultant kriging estimates of residuals added to GNN or GLM predictions to get final predictions [18].
2.3. Sampling
In addition to suitable methods, map refinements require properly furnished reference sample data. Stratified random sampling (StRS) is recommended for reference data collection in the context of accuracy assessment and area estimation as opposed to simple random sampling (SRS) [9,50]. Given known inter-class variations in classification accuracies and the understanding that pixels at proximity of class boundaries (i.e., edge pixels or heterogeneous pixel segments) are more prone to misclassifications than those within homogeneous pixel segments (i.e., interior pixels) [51], a class-heterogeneity-stratified sample design (a special type of StRS), which was applied by Zhang et al. [46] for per-pixel accuracy mapping, were adopted for map refinement. This permits dual-purpose use of reference sample data for accuracy assessment (already completed by Zhang et al. [46]) and map refinement.
In this map class-heterogeneity-stratified sampling, stratification is first based on map classes and then heterogeneity/homogeneity. Here, homogeneity is defined as the number of pixels with the same class label as that of the center pixel in a focal neighborhood of 3 by 3 pixels. A homogeneity value of 4 is chosen as the threshold value to determine if the center pixel lies in a homogeneous sub-stratum (O) or a heterogeneous one (E) within a stratum (a certain map class). In contrast, a threshold of 8 was used for determining if the center pixel is interior (corresponding to a homogeneous sub-stratum) in Sweeney and Evans [51]. The “strata” when using Neyman allocation (i.e., optimal allocation) [52] were combinations of map classes and E/O sub-classes. In other words, the O and E sub-strata of each class were considered as different strata during sampling.
Usually, a set of reference data is used as training data for model building (Section 2.2), with another as test data for performance evaluation (Section 2.4). It is important to analyze effects of sample sizes on map refinement, because cost-effectiveness in sampling is essential. We propose selecting a few subset samples from a pool of training sample pixels previously collected by Zhang et al. [46]. Sample sizes should be allocated optimally for precision in design-based and cross-strata estimation of accuracies and areas [21]. We used proportional reduction of sample pixels in individual strata of the full sample set.
Collecting reference data is a time-consuming and costly procedure. The response design for this research was such that only primary class labels were recorded for sample pixels. In the study, the reference classes at sample pixels were obtained using visual interpretation of high spatial resolution images (i.e., Google Earth images). Interpretation was undertaken according to the standards consistent with GlobeLand30 classification system [46]. In most cases, Google Earth images were used for interpretation. When such images were not available, actual ground visits and Landsat TM image flown in temporal proximity of corresponding GlobeLand30 2010 maps were used as sources to obtain reference class labels
2.4. Refinement Accuracy Evaluation and Uncertainty Representation
Error matrices were used to assess classification accuracies of refined maps based on an independent test sample set mentioned in Section 2.3. To estimate error matrices and accuracy measures for a refined map, we need to label map classes from predicted class probabilities. It is useful to consider both the first and the second most probable map classes [14,53] to accommodate uncertainty in class memberships and, more importantly, to facilitate uncertainty-informed spatial analyses (e.g., change analyses) [4]. In addition, given existence of mixed pixels when using medium-resolution data over a highly fragmented landscape as in Wuhan, it is sensible to factor in both primary and alternate map classes in map representation and accuracy assessment. In line with the NLCD method for reference classification [5], we denote the first and second most probable map classes as primary and alternate classes, respectively. Thus, two definitions of agreement between reference and map classes are possible. The first is to check if primary map classes match reference classes. This leads to accuracy measure I. Second, an agreement is registered when the primary map class matches the reference class for a pure pixel or when either the primary or alternate map class matches the reference class for a mixed pixel, resulting in accuracy measure II, which is more objective. The threshold values for determining if a pixel is pure can be chosen by the primary map class probabilities; the greater the threshold value, the less the number of pixels deemed pure (and greater the resulting accuracy measure II, as more pixels are treated as being mixed for a more relaxed assessment). In this research, we used threshold values so that the percentage of pure pixels approximates that of sample pixels in homogeneous sub-strata (which is about 60%).
With error matrices estimated, accuracy measures, including overall, users’, and producers’ accuracies (denoted overall accuracies (OAs), users’ accuracies (UAs), and producers’ accuracies (PAs), respectively), are computed with sampling weights properly accounted for when using StRS sample data [50]. On the other hand, Fβ score is useful as a combined measure of precision and recall (which correspond to UA and PA, respectively) [54]. Fβ score is more recommendable where there are differing costs of false positives (commission errors) vs. false negatives (omission errors) or when class imbalance is a concern. The β parameter determines the relative weight of recall in computing the score. β < 1 gives more weight to precision (UA), while β > 1 favors recall (PA). As UAs are more important for map users, we used F0.01 (in combination with OA, UA, and PA) for accuracy evaluation (β = 0.01 to weigh much less on PAs). In this research, strata are map classes (E or O substrata). Strata information is explicit for the original map, while such information must be correctly transferred to a refined map. The error matrix for a refined map results from combination of stratum-specific error matrices, which are weighted properly with stratum size [5]. For estimating measures of type II, we assumed that proportions of pure vs. mixed pixels in a sample stratum are roughly representative of those in the map stratum.
With class probabilities estimated, per-pixel maximum class probabilities can be used to generate a map of certainty along with a refined map. However, that map (of certainty) is not equivalent to a map showing per-pixel classification accuracy, which would require accuracy models properly fitted with reference data [46], although this is not elaborated here. Maps showing alternate classes (for mixed pixels) in addition to primary classes can also be generated, with certainty quantified as the sum of primary and alternate class probabilities.
A flowchart is provided in Figure 1 and shows how the methods described previously in this section work through inter-related steps. It also outlines what are involved in the experiments to be described below.
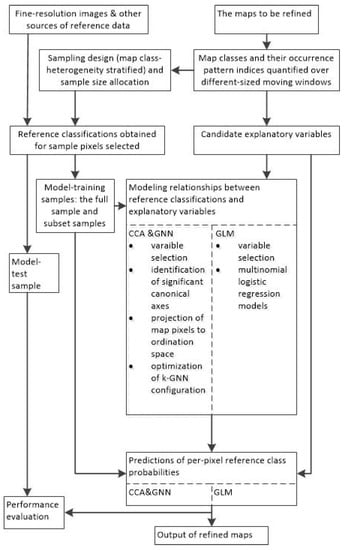
Figure 1.
Flowchart of the methodology used for map refinement.
3. Experiments of Map Refinement with Globeland30 Product
3.1. The Study Area and Experimental Datasets
GlobeLand30 (http://www.globallandcover.com) 2010 land-cover dataset for Wuhan City was used for this research. The city of Wuhan (Lat 29°58′–31°22′ N, Long 113°41′–115°05′ E) is about 8495 km2 in areal extent, located in the middle and lower reaches of the Yangtze, and is the provincial capital of China’s Hubei province, as shown in Figure 2 (the inset map of China, lower right corner). For Wuhan, of seven classes in total, the dominate class is cultivated land, occupying about 60 percent of Wuhan’s areal extent, followed by water, forest, and artificial surface, which account for 15 percent, 12 percent, and 7 percent of the total area, respectively. Grassland, wetland, and bare land together take about 6 percent of Wuhan’s areal extent. Further detail can be found in Zhang et al. [46].
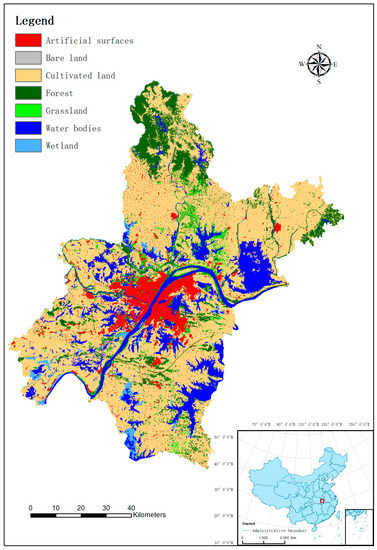
Figure 2.
GlobeLand30 2010 land-cover map of Wuhan, China.
As mentioned in Section 2.3, class-heterogeneity-StRS proposed by Zhang et al. [46] was adopted for collection of training and test sample data. The full sample size was 3000 pixels for model-training. For sample allocation shown in Table 2, the Neyman method was used [21,46]. In Table 2, Cultivt and Artfct are abbreviations for cultivated land and artificial surfaces, respectively. As shown in Table 2, sampling intensities at E sub-strata are obviously higher than at O ones, as evaluated relative to the respective population sub-strata (e.g., about 3.93% for Wetland_E, wetland stratum, E sub-stratum, but only 0.10% for Wetland_O, wetland stratum, and O sub-stratum). The test sample of 1020 pixels were also collected following class-heterogeneity-StRS design, as shown in Table 2.

Table 2.
Number of sample pixels belonging to individual sub-strata, while sampling intensities (in percentages) shown in parentheses are with respect to the total number of pixels (Nstrata) belonging to specific sub-strata (E—Heterogeneous, O—Homogeneous).
We selected three subset samples of reduced sizes from the full training sample set to test the proposed method’s effectiveness with different training sample sizes. The reduced sample sizes were 360, 720, and 1480 pixels, as preliminary tests using smaller sized samples (e.g., 120 pixels and 240 pixels) led to unsatisfactory and unstable refinements. We employed the proportional schemes for sample allocations, as described in Section 2.3. Sample allocations for the three subset samples are tabulated in Table 3, where Cultivt and Artfct are, again, abbreviations for cultivated land and artificial surfaces, respectively, as in Table 2.

Table 3.
Number of sample pixels belonging to individual sub-strata (E—Heterogeneous, O—Homogeneous) in model-training samples of different sizes.
3.2. Modeling and Predictive Mapping
Before refinement procedures, we assessed the original map to get some ideas about its accuracy and misclassification patterns. Based on the full set of 3000 training pixels, an error matrix was constructed, with accuracy measures estimated, as shown in Appendix A, Table A1. UAs shown in Table A1 indicate that water bodies and artificial surfaces (“O” sub-strata) are more accurately classified than others. As no purely systematic confusion patterns are observed in the error matrix shown in Table A1, we may not be able to correct misclassifications by one-one re-labeling of map classes, highlighting the need for modeling-based map refinement.
For the full training sample set and its three subset samples, we carried out CCA and GLM modeling. This subsection describes the procedures done, with intermediate results shown in Appendix A. Accuracy of refined maps is reported in Section 3.3.
As mentioned in Section 2.2, the vegan package supports selection of optimal explanatory variables and identification of significant canonical axes. Relevant results are shown in Appendix A, Table A2 and Table A3, respectively. It is indicated in Table A2 and Table A3 that different training samples give rises to quite different sets of optimal explanatory variables (i.e., CCA models). Proportions of variations explained by canonical axes are also different (the canonical axes obtained by the sample of 720 pixels explained the greatest proportion of variation), although number of significant canonical axes is the same. After identification of optimal configuration parameters for GNN (Appendix A, Table A4), class probabilities of individual pixels were estimated. This allowed for accuracy assessment if predictions were made at test pixels (to be shown in Section 3.3) and generation of a refined map if predictions were made over all map pixels (while reference classification were retained for training pixels). As an example, a refined map based on 3000 training pixels is shown in Figure 3a, while the by-product map of certainty in class labeling (i.e., the maximum class probabilities) is shown in Figure 3b.
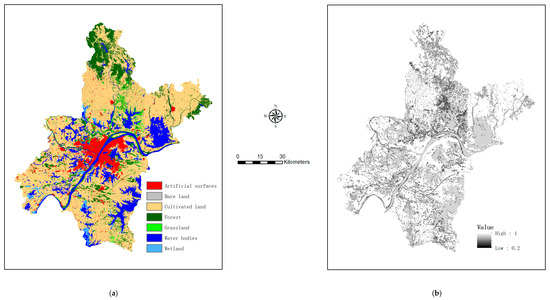
Figure 3.
Output of map refinement using 3000 model-training pixels: (a) the refined map showing the most probable class labels, and (b) the corresponding certainty surface showing the maximum class probabilities.
With class probabilities estimated for unknown pixels, we extracted their first and second most probable class labels (i.e., primary and alternate map classes). An example map depicting alternate labels for mixed pixels is shown in Figure 4a (with the map depicting primary labels shown in Figure 3a), while the map of certainty in class labeling is shown in Figure 4b.
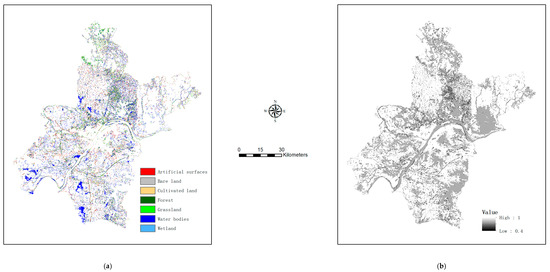
Figure 4.
Further output of map refinement (using the set of 3000 training pixels) for mixed pixels (complementing those in Figure 3): (a) the map showing the second most probable class labels, and (b) the certainty surface showing the sums of the maximum and the second maximum class probabilities.
For comparisons, GLM was also performed, again with candidate explanatory variables mentioned in Section 2. Variable selection was done following the procedure mentioned in Section 2. Intermediate results are given in Appendix A, Table A5. As for CCA modeling results, different GLM models are obtained with different training samples. Predictions were made over test pixels for performance evaluation (Section 3.3), although no maps were generated.
For both CCA and GLM, spatial autocorrelations of prediction residuals at 3000 training pixels were analyzed by using the R package spdep [49]. Moran’s I statistic was estimated and confirmed being not significant (α = 0.01) except for the class of bare land (see Appendix A, Table A6 for detail). Thus, no kriging of residuals was done. As kriging would be of lesser effects when sample pixels are more sparsely distributed for subset samples of reduced sizes, we asserted that no kriging would be necessary.
3.3. Evaluation of the Proposed Method’s Performance
First, we compare refinements obtained with CCA vs. GLM. OAs and F0.01 scores for refined maps as a whole (rows labeled “All”) vs. O and E sub-strata are estimated on the basis of the 1020 test sample pixels and shown in Table 4, where measures of types I and II described in Section 2.3 are listed. In Table 4, accuracy gains are with respect to original map’s accuracy as assessed on the test sample data (shown in Table 5 with detail; for instance, OA_E = 36.8%, OA_O = 79.8%, OA_All = 78.4%, for the original map).

Table 4.
Accuracy gains (%) (overall accuracies (OAs) vs. F0.01 scores) for all the study area (All) and the homogeneous (O) and heterogeneous I sub-areas after refinements using different training samples (see Section 2.4 for accuracy measures I and II).

Table 5.
Accuracy gains (%) (OAs vs. F0.01 scores) in map classes and their homogeneous (O) and heterogeneous (E) sub-strata for refined maps using canonical correspondence analysis (CCA) (see Section 2.4 for accuracy measures I and II).
As shown in Table 4, CCA is generally more accurate than GLM. In general, increases in sample sizes lead to increases in accuracies, although there are fluctuations in the trend, especially for GLM. There appears to be a plateau in accuracy gains achieved by CCA (measure I), when using more than 720 training pixels. Accuracy increases in E sub-strata are greater than those in O ones, as sampling densities in the former are usually much greater than in the latter (See Table 2). For CCA-based refinements, with 360 training pixels (corresponding to a sampling intensity of 0.0037% over a population of 9,535,092 map pixels in the study area), gains in OA and F0.01 score are both 3% (II), respectively.
Second, we report results of accuracy assessment for CCA-based map refinements below in more detail, after confirming CCA’s relative advantages over GLM in terms of accuracy gains. We admit, however, that comparisons between CCA and GLM above are by no means comprehensive or exhaustive. Nonetheless, we focus on CCA-based results because the objective of the paper is to promote map refinement rather than comparing CCA with a list of alternative methods.
Gains in map-wise (indicated by “All”) and strata-wise OAs and F0.01 scores are shown in Table 5, where map accuracy before refinement is also shown to facilitate comparisons. In Table 5, Cultivt and Artfct are abbreviations for cultivated land and artificial surfaces, respectively, as in Table 2. In Table 5, accuracies are estimated using measures I and II, as in Table 4.
As shown in Table 5, cultivated land, forest, wetland (E), and bare land (E) register gains in strata-wise OAs (and F0.01 scores except for wetland) consistently across different sample sizes. They are major contributors to accuracy gains. Other strata or sub-strata have positive or negative gains in accuracy. We discuss these further in Section 4.1.
For comparison, we referred to Tsendbazar et al. [23], who presented a piece of work that is closely related to this research. They showed that integration of multiple input land cover maps (i.e., Globcover-2009, Land Cover-CCI-2010, MODIS-2010, and Globeland30 maps for Africa) and reference data (3887 sample sites) resulted in 4.5–13% higher correspondence with the reference land-cover than any of the input land-cover maps. An integrated land-cover map (at a spatial resolution of 300 m at the Equator with eight harmonized general classes) and class probability maps were computed using regression kriging, which produced the highest correspondence (76%).
4. Discussion
4.1. Further Interpretations and Analyses of Modeling and Predictive Mapping for Refinement
We interpret strata-wise accuracy gains shown in Table 4 in combination with the error matrix in Table A1, Appendix A, which was estimated using the full sample of 3000 pixels (error matrices estimated using subset training samples showed similar patterns). It appears that accuracy gains are achievable only for certain strata (map classes and their sub-strata) that possess the following characteristic. For such a stratum, its commission error is dominated by its confusion with a particular different class rather than distributed among multiple candidate classes. We call it a refinable stratum.
For this research, the following strata meet the aforementioned criterion and are thus refinable: cultivated land, forest (E), wetland (E), and bare land (E). These strata are more likely confused with water bodies than with other classes, except for bare land which is more likely confused with forest. These strata achieved accuracy gains after refinements, as seen in Table 5. For example, a pixel mis-labeled as cultivated land on the map is likely re-labeled more correctly as water bodies when the predicted class probabilities say so. For other strata, accuracy gains are mostly no greater than zero, as they are essentially non-refinable.
In principle, a perfectly refinable stratum would see it being completely confused with a single different class. We could then fix this type of “perfect” misclassification by direct re-labeling, similar to Campos and Brito [20]. On the other hand, a non-refinable stratum is one that is virtually equal-probably confused with all other candidate classes. It would be infeasible to refine a map by modeling if all strata were virtually non-refinable, unless we resort to dense sampling (if not census). Although being rare in practice, there would be no need to refine a stratum should it have a UA of 100% (because the UA is already maximum). In reality, we likely have strata that are only partially refinable (in between the two aforementioned extremes), while other strata are practically non-refinable (thus accuracy measure II makes better sense), as in this research. Therefore, a map’s refinability should be analyzed on the basis of the error matrix estimated from relevant reference data before deciding on whether to proceed with refinements. Refinability is also likely to set an upper bound to achievable accuracy gain for a map, although this is yet to be investigated.
To reduce possible side effects of non-refinable strata on refinements (e.g., possible losses in UAs and PAs; however, it is more important to focus on increasing UAs from a user’s perspective), it is sensible to pursue selective refinements in which only refinable strata are treated. Such selective refinements would be straightforward to decide on (regarding which strata to include) and make perfect sense, when the themes of interest (i.e., land-cover types and/or their changes being studied) converge with refinable strata. Suppose cultivated land is refinable, as is the case for this research. If the theme of interest is cultivated land monitoring (which is very likely the case due to its importance in China), we should certainly include it for refinement. This is because accuracy in change detection and analyses concerning cultivated land is directly related to accuracies of mapped cultivated land in single-date maps, especially when change detection is based on post-classification comparisons. Obviously, accuracy gains in change detection are likely greater if cultivated land is refinable and included in refinements for single-date maps concerned. In this research, we tested a selective refinement (though for single-date land-cover), as shown below.
Given that cultivated land and forest are the two classes with the first and second greatest PAs (Table A1) and that wetland (E) and bare land (E) are of very small areal extents in the study area (Section 3.1), we tested a selective strategy by which all map classes in the original map except cultivated land and forest were left unchanged. This selective refinement strategy led to gains in OAs and UAs (for cultivated land and forest only), as shown in Table 6. For comparisons, gains in UAs without use of the aforementioned selective strategy are shown in parentheses underneath those of selective refinement in Table 6.

Table 6.
Accuracy gains (%) in OAs, users’ accuracies (UAs) (cultivated land and forest), and F0.01 scores for selective refinements (gains in UAs and F0.01 scores achieved without use of the selective strategy are in parentheses underneath).
As shown in Table 6, by applying this selective refinement strategy, accuracy gains achieved (measure I) are greater than those reported in Table 5; accuracy gains in terms of measure II were not evaluated, since only strata of cultivated land and forest were refined. Gains in UAs are also greater with selective refinements than without.
Main findings of this research are summarized below. CCA is a promising method for map refinement. Map refinability was put forward as a key concept for refinement, which is helpful for analyzing if map classes are refinable and for developing selective refinement strategies to enhance effectiveness. A modest-sized reference sample (360 pixels, at a sampling intensity of 0.0037%) achieved 3% gains in OA (map-wise) and 5–11% gains in UAs for cultivated land and forest, respectively, using a selective refinement strategy accounting for refinability of cultivated land and forest; accuracy gains in terms of F0.01 scores are 3% (map-wise) and 4–10% (cultivated land and forest). Probabilistic mapping underlying refinements helps to differentiate relatively pure pixels from mixed pixels and facilitates uncertainty-informed map representation and accuracy assessment.
4.2. Comparisons with Related Work
Although accuracy gains achieved in this research (especially in terms of type I measures) are modest in comparison with what were achieved in Tsendbazar et al. [23], some explanation is in place for this research. First, objectives and data analyses are different. Tsendbazar et al. [23] aimed for fusion of multiple input map data whereby classification harmonization was included. In this research, refinements were based on single-source map data (implying disadvantage in terms of amount of input information), with accuracy assessed without class harmonization. Second, in Tsendbazar et al. [23], data integration was performed at a coarser spatial resolution (300 m). This likely led to smoothened geographic heterogeneity and increased correspondence between maps and reference classifications. On the other hand, this research was at much finer resolution (30 m) [2] over a highly complex and fragmented landscape. This implies increased occurrences of mixed pixels, more complicated patterns of class confusions, and limited gains in refinements.
Rather than putting alternative methods in contrast, we should view them as being complementary. For example, fused maps may be further refined with reference data [22,23,55], while mapped environmental data [26,27] can be incorporated in map refinement to improve re-classification further. The proposed method can also be used as a post-processing upon initial image classifications for improving land-cover mapping, with image classification training data and/or test data readily available as reference data (e.g., Campos and Brito [20]). Similarly, map refinements are likely helpful for improving image classification over difficult-to-map classes and locations [56].
4.3. Issues of Reference Data and Sampling
Reference sample data are prerequisite for map refinement. Existing reference data should be re-used if appropriate [46], as is the case for this research. When using existing reference datasets [7,23], map legends and classification schemes should be homogenized, with spatio-temporal alignments furnished.
When planning for collection of reference data, it is important to optimize sampling. Geographic stratification may be necessary for having sampling adapted to spatial variations in map-reference class correspondence over large areas.
Progressive sampling (starting at small sample size) is recommendable for refinements as budgets permit. The certainty maps shown in Figure 3b and Figure 4b can provide useful information about where additional sampling may be targeted to reduce uncertainty. Though not for map refinement, Lin et al. [57] used co-kriging for locating additional sample sites to augment existing sample data. It is helpful to consider sampling in feature space and geographic space together [58].
As it is more objective to represent land-cover continua using class probabilities at individual pixels, reference data collection should accommodate partial and multiple memberships to reflect uncertainty in reference classification [59]. In this way, disagreement between reference and map class labeling may be further reconciled [5].
When using data from complex survey samples including StRS samples, as is the case in this research, some researchers argue for incorporating sampling weights in regression analysis modeling (both linear and logistic) [60,61]. We carried out some comparative study about relative performances of weighted vs. unweighted regression based on R package Survey [62]. Unweighted regression was found no less accurate than weighted regression, although weighted CCA (based on weighted least squares for linear regression) was only an approximation. This concurs with Winship and Radbill [63] arguing for unweighted linear regression using sample data stratified by explanatory variables included in the model; this also provides the justification for using unweighted modeling approaches in this research. Nevertheless, it is important to further clarify statistically sound ways of CCA modeling with stratified sample data.
4.4. Recommendation for Future Work
Being essentially pixel-based, the proposed method treats individual pixels separately, implying that logical consistency is yet to be checked in refined maps, although continuity in ordination space is transferred to that in predicted class probabilities. To fix this, we may undertake post-processing of refined maps, whereby logical consistency is checked: deletion of illogical class adjacencies, spatial filtering of isolated pixel segments below minimum mapping units (MMUs), consistency of primary and alternate map classes over neighborhoods, and other aspects established in the literature [64]. In change monitoring, logical consistency in multi-temporal land-cover occurrences needs also to be checked [65].
For enhancing accuracy and logic consistency of refinements, especially over O substrata, it is sensible to explore object-based approaches to modeling, with individual segments of O substrata being units of sampling and modeling to complement pixel-based approaches in E sub-strata. A refined map results from object-based refinement for O sub-strata superimposed by pixel-based refinement for E sub-strata. However, there are issues with object-based approaches [9], such as existence of inclusions and complication of boundary geometry in class labeling, which need to be investigated.
It is important to study the feasibility of applying the proposed methods to large areas, though this is beyond the scope of this paper. Direct scaling of a sampling intensity of 0.0037% (corresponding to 360 sample pixels) in this study to large-area applications seems infeasible, as affordable sampling intensities are likely in the magnitude of millionth for country-wide applications [6,18]. However, given that Wuhan features a highly fragmented landscape and is in one of the least accurately mapped regions (being in the second most inaccurately mapped region of China, with an estimated reginal OA of 73% [66], the results obtained in this research have a rather promising prospect for large-area applications. On top of this, we need to characterize GlobeLand30 map refinability to demarcate the cost-effectiveness of refinements and develop regionalized refinement strategies.
Being applicable for both categorical and fractional map refinements represents an advantage of CCA method, as response variables can include cover percentages in addition to class indicators, allowing for estimating class fractions [8,67] at unsampled pixels. Maps representing probabilistic or possibilistic class memberships [4] can also be handled in CCA. For fractional land-cover map refinement, surface metrics (rather than patch shape indices) pertaining to cover type fractions [68] may be used as explanatory variables.
5. Conclusions
Accuracy is important for land-cover map producers and users alike. From users’ perspective, there are merits in refining existing maps to increase their accuracy so that accuracy in applications that employ the maps (e.g., change monitoring and analyses) is improved. However, there has been no systematic research on map refinement. This research seeks to bridge this gap by applying CCA for map refinement through synthesis of reference data and map data.
Empirical results confirm that the CCA-based method is generally more accurate than GLM. Accuracy increases in heterogeneous sub-strata are almost an order of magnitude greater than those in homogeneous sub-strata, as sampling intensities in the former were much greater than the latter on average. Accuracy gains by CCA are incremental with increasing sample size. It was revealed that accuracy gains are only achievable for certain strata (which are called refinable strata) whose commission errors are mostly due to their confusions with single different classes, as can be observed from relevant error matrices. Strata refinability can be used to develop selective strategies; whereby, only refinable strata are included in refinement while others are left unchanged.
In terms of cost-effectiveness, a reference sample of relatively small size (360 pixels) led to a 3% accuracy gain in map-wise OA (also a 3% gain in F0.01 score) and 5–11% gains in UAs (cultivated land and forest) (4–10% gains in F0.01 scores) (measure II). Although accuracy gains are modest (especially in measure type I), we should not look down upon these gains for the following reasons. First, the original map is only of limited refinability. This means that very high accuracy gains are unlikely because misclassification errors in the map contain only limited systematic component for modeling-based corrections, although we should strive for improving refinements. Second, we should appreciate the fact that increased map accuracy along with probabilistic class memberships means added value in refined maps as they are incorporated for change monitoring and other spatial analyses while extending utility of reference data beyond accuracy assessment. Last, we should recognize that accuracy gains achieved with a relatively small sample are meaningful and make this research worthwhile.
In summary, this research has fulfilled the objective of using reference data that were collected for accuracy assessment and necessarily small-sized to have the map refined. The benefits of map refinement include increased accuracy in maps (and spatial analyses based on them), augmented information about map uncertainty (which is turn useful for refining change analyses, for instance), extended utility of reference data, and enhanced understanding about relationships between reference data and map data. To reiterate, the contribution of this research lies not only in having achieved meaningful accuracy gains but also in having advanced knowledge about synthesis (and the underlying mechanism) of reference data and maps, which are accumulating.
Author Contributions
Conceptualization, J.Z. and Y.W.; methodology, Y.W., J.Z., W.Y., and Y.T.; data, W.Y. and Y.W.; experiments, Y.W., W.Y., and J.Z.; analysis and validation, Y.W., J.Z., and W.Y.; writing, J.Z., Y.W., and Y.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the National Science Foundation of China (NSFC) (grant no. 41471375) and Ministry of Science and Technology of China (grant no. 2019YFC1520802). The paper constitutes supportive evidence for a research proposal to NSFC in 2020 (no. 4207011340).
Acknowledgments
The manuscript was drafted before and after the outbreak of respiratory illness (Covid-19). We pray for healing of all patients, containment of the plague, and safety of all people around the world. Part of the work was undertaken when Jingxiong Zhang visited University of Washington, USA in summer 2019, with Sarah Elwood and Michael Goodchild being the host. Roger Kirby (The University of Edinburgh) and Jun Chen (the National Geomatic Center of China) have been sources of inspiration for him. Matthew Gregory (Oregon State University, Corvallis) has also provided invaluable advice about related research. Comments and suggestions from anonymous reviewers are very constructive for revision of the paper and are received with thanks.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Intermediate Results of CCA and GLM-Based Modeling
We describe intermediate results of CCA and GLM modeling from using the full model-training sample and its subsets in this section. Evaluations of prediction results are described in Section 3.3 of the main text.
Classification accuracy of the original map was assessed using the set of 3000 model-training pixels. Cell proportions in the error matrix (including both homogeneous (O) and heterogeneous (E) sub-strata of different map classes) were estimated properly incorporating sample weights (Oloffson et al., 2014), as shown in Table A1, from which OA, UA (for both O and E sub-strata of individual map classes), and PA are computed. In Table A1, Cultivt and Artfct are again abbreviations for cultivated land and artificial surfaces, respectively. Clearly, water and artificial surfaces (homogeneous sub-strata) are relatively more accurately classified than other classes (with UAs > 80%), while homogeneous sub-strata have greater UAs than their corresponding heterogeneous sub-strata. There are no clear patterns for misclassifications, especially for grass, bare land, wetland, and most heterogeneous sub-strata, making it difficult to correct for them.

Table A1.
Confusion matrix and accuracy assessment for the original map based on the full model-training sample set (cell proportions and accuracy measures in %, OA = 74.0%).
Table A1.
Confusion matrix and accuracy assessment for the original map based on the full model-training sample set (cell proportions and accuracy measures in %, OA = 74.0%).
| Map Class | Reference Class | |||||||
|---|---|---|---|---|---|---|---|---|
| Artfct | Bare | Cultivt | Forest | Grass | Water | Wetland | UA | |
| Artfct (E) | 0.1 | 6.1 × 10−3 | 2.0 × 10−2 | 3.9 × 10−2 | 1.6 × 10−2 | 1.6 × 10−2 | 0 | 52.0 |
| Artfct (O) | 6.2 | 0.4 | 0.2 | 0.1 | 0.4 | 0.1 | 0 | 84.0 |
| Bare (E) | 0 | 1.3 × 10−2 | 7.2 × 10−3 | 9.6 × 10−3 | 8.2 × 10−3 | 4.8 × 10−4 | 0 | 33.8 |
| Bare (O) | 0 | 3.7 × 10−2 | 9.0 × 10−3 | 1.2 × 10−2 | 1.3 × 10−2 | 1.6 × 10−3 | 0 | 51.1 |
| Cultivt (E) | 0.1 | 2.5 × 10−2 | 0.2 | 4.5 × 10−2 | 6.4 × 10−2 | 0.1 | 3.5 × 10−2 | 36.7 |
| Cultivt (O) | 3.6 | 0.8 | 43.4 | 2.5 | 1.8 | 5.8 | 2.3 | 72.1 |
| Forest (E) | 0.1 | 3.0 × 10−2 | 0.3 | 0.4 | 0.2 | 0.4 | 0.1 | 26.4 |
| Forest (O) | 0.1 | 3.8 × 10−2 | 0.8 | 8.3 | 0.8 | 0.3 | 0.2 | 79.3 |
| Grass (E) | 3.1 × 10−2 | 6.1 × 10−3 | 0.1 | 0.1 | 0.3 | 0.1 | 3.7 × 10−2 | 38.3 |
| Grass (O) | 0.2 | 0.1 | 0.3 | 0.2 | 1.3 | 0.4 | 4.6 × 10−2 | 51.2 |
| Water (E) | 0 | 0 | 2.3 × 10−2 | 7.5 × 10−3 | 1.3 × 10−2 | 0.2 | 3.0 × 10−2 | 71.0 |
| Water (O) | 0.1 | 0.4 | 0.4 | 0.1 | 0.6 | 12.5 | 0.6 | 85.6 |
| Wetland (E) | 0 | 0 | 2.7 × 10−4 | 0 | 5.3 × 10−4 | 9.1 × 10−3 | 1.1 × 10−2 | 53.8 |
| Wetland (O) | 0 | 0 | 0.1 | 1.0 × 10−2 | 2.0 × 10−2 | 0.3 | 1.0 | 69.3 |
| PA | 59.8 | 2.9 | 95.1 | 73.0 | 29.5 | 62.8 | 22.9 | |
Variables selected for CCA are listed in Table A2, while significant canonical axes are shown in Table A3. In Table A2, abbreviations such as p“m”w“n” stand for proportions of map class coded “m” (class codes 1, 2, 5, 6, 8, and 9 stand for cultivated land, forest, grass, wetland, water, artificial surfaces, and bare land, respectively) in moving windows sized “n”. Patch”m” represents polygonal adjacency in terms of frequencies of map classes coded “m” occurring as first-order neighbors of the polygon a sample pixel falls in. As shown in Table A2, selected explanatory variables are obviously different for models trained with different samples, while numbers of significant canonical axes shown in Table A3 are relatively similar.

Table A2.
Variable selections in CCA for different model-training samples.
Table A2.
Variable selections in CCA for different model-training samples.
| Sample Sets (Sample Size Indicated by Number of Pixels) | Optimal Explanatory Variables |
|---|---|
| Full sample 3000 | cultivt + forest + grass + wetland + water + artfct + hom3 + hom5 + p1w3 + p5w3 + p6w3 + p5w5 + p8w5 + p5w7 + p9w9 + area + patch1 + patch2 + patch3 + patch4 + patch5 + patch6 |
| Subset samples | |
| 1480 | p8w3 + p1w3 + wetland + p3w3 + forest + con5 + p6w3 + grass + artfct + hom5 + water + cultivt + p1w9 + p2w9 + p5w3 + patch4 + patch6 + patch5 + p9w9 + p9w7 + dom7 + patch1 + p3w7 |
| 720 | p8w3 + p5w3 + p6w3 + p9w5 + p2w3 + p5w5 + con7 + forest + patch6 + water + patch1 + patch4 + cultivt + p2w9 + p1w5 + het7 + hom9 |
| 360 | p8w5 + p1w3 + p2w5 + p5w3 + p9w5 + p3w3 + forest + patch4 + p9w7 + con9 + patch6 + p5w7 + p9w9 |

Table A3.
Significant canonical axes in CCA (α = 0.001).
Table A3.
Significant canonical axes in CCA (α = 0.001).
| Sample Sets (Sample Size Indicated by Number of Pixels) | Significant Canonical Axes and Explained Proportions (%) of the Overall Variation | |||||
|---|---|---|---|---|---|---|
| CCA1 | CCA2 | CCA3 | CCA4 | CCA5 | CCA6 | |
| Full Sample | 9.5 | 7.4 | 7.2 | 5.0 | 4.2 | 2.5 |
| Subset Samples | ||||||
| 1480 | 9.8 | 8.2 | 7.5 | 5.6 | 4.4 | 3.2 |
| 720 | 10.2 | 8.8 | 7.8 | 7.0 | 4.5 | 2.7 |
| 360 | 10.0 | 9.2 | 7.7 | 6.0 | 3.5 | 1.7 |
The optimal values of k’s are listed in Table A4, while the optimal t is 0 all model-training samples. Clearly, optimal k values are different for different model-training samples.

Table A4.
Optimal numbers (k) of nearest neighbors for kNN in ordination space using different model-training samples.
Table A4.
Optimal numbers (k) of nearest neighbors for kNN in ordination space using different model-training samples.
| Training Sample Sets | Sample Size (Number of Pixels) | Optimal k for CCA (Unweighted) |
|---|---|---|
| Full set | 3000 | 25 |
| Subsets | ||
| 1480 | 12 | |
| 720 | 19 | |
| 360 | 23 |
Results of GLM model selection are shown in Table A5, where abbreviations are interpreted as in Table A2. Clearly, optimal explanatory variables are different for models trained with different samples, while different (reference) classes have different models as expected.

Table A5.
Optimal logistic regression models for candidate classes with corresponding significant explanatory variables using different model-training samples (size by number of pixels): (a) full sample set, and (b)–(d) subset samples.
Table A5.
Optimal logistic regression models for candidate classes with corresponding significant explanatory variables using different model-training samples (size by number of pixels): (a) full sample set, and (b)–(d) subset samples.
| Reference Classes | Significant Explanatory Variables |
|---|---|
| (a) 3000 | |
| Artfct | Grass + POINT_X + p1w3 + p2w3 + p3w3 + p6w3 + p8w3 + con3 + ent3+ patch1 + patch2 + patch3 + patch4 + patch5 + patch6 + patch7 |
| Bare | Cultivt + Forest + Grass + Water + Artfct + POINT_X + POINT_Y + p1w3 + p3w3 + p5w3 |
| Cultivt | Cultivt + Wetland + POINT_X + POINT_Y + p1w3 + p2w3 + p6w3 + p8w3 + con3 + dom3 |
| Forest | Forest + Grass + Water + Artfct + p1w3 + p3w3 + p5w3 + p6w3 + p8w3 + p9w3 |
| Grass | Cultivt + Forest + Wetland + Water + Artfct + POINT_Y + p1w3 + p3w3 + p9w3 + ent3+ patch5 + patch6 + patch7 |
| Water | Cultivt + Forest + Grass + Water + Artfct + POINT_X + POINT_Y + p1w3 + p2w3 + p3w3 + p6w3 + p8w3 + p9w3 + con3 + dom3 + het3 + patch4 + patch7 |
| Wetland | Wetland + p1w3 + p2w3 + p3w3 + p5w3 + p6w3 + het3 |
| (b) 1480 | |
| Artfct | Grass + POINT_Y + p1w3 + p2w3 + p3w3 + p6w3 + p8w3 + con3 + ent3 |
| Bare | Cultivt + Forest + Grass + Water + Artfct + POINT_Y + p1w3 + p2w3 + p5w3 + p8w3 + p9w3 + con3 |
| Cultivt | Cultivt + POINT_X + POINT_Y + p1w3 + p2w3 + p3w3 + p5w3 + p9w3 + con3 + het3 |
| Forest | Forest + Grass + Water + Artfct + p1w3 + p2w3 + p3w3 + p5w3 + p6w3 + p8w3 + p9w3 + con3 + dom3 + het3 |
| Grass | Cultivt + Forest + Water + Artfct + p1w3 + p2w3 + p5w3 + p6w3 + p9w3 + het3 |
| Water | Cultivt + Forest + Grass + Water + Artfct + POINT_X + POINT_Y + p1w3 + p2w3 + p3w3 + p5w3 + p8w3 + p9w3 + dom3 + ent3 + het3 |
| Wetland | Forest + Water + p2w3 + p3w3 + p5w3 + p6w3 + p8w3 + p9w3 + con3 + het3 |
| (c) 720 | |
| Artfct | p1w3 + p3w3 + p8w3 + ent3 |
| Bare | Cultivt + Forest + Grass + Water + p1w3 + p5w3 + p8w3 + dom3 + ent3 + het3 |
| Cultivt | Forest + Artfct + p1w3 + p2w3 + p3w3 + p8w3 + p9w3 |
| Forest | Forest + Grass + Artfct + POINT_Y + p1w3 + p2w3 + p9w3 |
| Grass | Water + p1w3 + p2w3 + p5w3 + p6w3 + p8w3 + p9w3 + hom3 |
| Water | Cultivt + Forest + Grass + Water + Artfct + p1w3 + p2w3 + p3w3 + p5w3 + p6w3 + p9w3 + dom3 + ent3 + het3 |
| Wetland | Grass + p1w3 + p5w3 + p6w3 + hom3 |
| (d) 360 | |
| Artfct | p1w3 + p2w3 + p3w3 + p6w3 + p8w3 + ent3 |
| Bare | Cultivt + Forest + Artfct + POINT_X + p1w3 + p2w3 + p8w3 + p9w3 + hom3 |
| Cultivt | Water + Artfct + p1w3 + p2w3 + p3w3 + p5w3 + p8w3 + p9w3+ area + patch1 + patch2 + patch4 + patch5 + patch6 |
| Forest | Forest + Artfct + POINT_Y + p1w3 + p2w3 + p3w3 + p6w3 + p9w3+ area + patch2 + patch4 + patch6 + patch7 |
| Grass | p1w3 + p2w3 + p3w3 + p5w3 + p6w3 + p8w3 + p9w3+ patch5 |
| Water | Cultivt + Artfct + p1w3 + p2w3 + p3w3 + p5w3 + p6w3 + p9w3 + het3 |
| Wetland | Cultivt + Grass + POINT_Y + p1w3 + p2w3 + p5w3 + p6w3 + ent3 + het3 + hom3 |
Moran’s I indices were computed using residuals from predictions by GNN (CCA followed by kNN) and GLM, as shown in Table A6 (a) and (b), respectively. These indices are shown for different classes. As shown in Table A6, except for residuals in GLM-predicted bare land occurrence probabilities, all residuals show insignificant spatial autocorrelation, implying little information gain from their spatial interpolation.

Table A6.
Moran’s I statistic and p-values for residuals from GNN (a) and GLM (b) using the sample of 3000 model-training pixels.
Table A6.
Moran’s I statistic and p-values for residuals from GNN (a) and GLM (b) using the sample of 3000 model-training pixels.
| Classes | Moran’s I | p-Value |
|---|---|---|
| (a) | ||
| Artfct | 0.02 | 0.81 |
| Bare | 0.01 | 0.70 |
| Cultivt | 0.06 | 0.24 |
| Forest | 0.06 | 0.33 |
| Grass | 0.07 | 0.31 |
| Water | 0.14 | 0.07 |
| Wetland | 0.13 | 0.06 |
| (b) | ||
| Artfct | 0.02 | 0.68 |
| Bare | 0.40 | 0 |
| Cultivt | 0.05 | 0.41 |
| Forest | 0.08 | 0.19 |
| Grass | 0.08 | 0.19 |
| Water | 0.11 | 0.06 |
| Wetland | 0.13 | 0.04 |
References
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Chen, J.; Chen, J.; Liao, A.; Cao, X.; Chen, L.; Chen, X.; He, C.; Han, G.; Peng, S.; Lu, M.; et al. Global land cover mapping at 30 m resolution: A POK-based operational approach. ISPRS J. Photogramm. Remote Sens. 2015, 103, 7–27. [Google Scholar] [CrossRef]
- Yang, L.; Jin, S.; Danielson, P.; Homer, C.; Gass, L.; Bender, S.M.; Case, A.; Costello, C.; Dewitz, J.; Fry, J.; et al. A new generation of the United States National Land Cover Database: Requirements, research priorities, design, and implementation strategies. ISPRS J. Photogramm. Remote Sens. 2018, 146, 108–123. [Google Scholar] [CrossRef]
- Christman, Z.; Rogan, J.; Eastman, J.R.; Turner, B.L. Quantifying uncertainty and confusion in land change analyses: A case study from central Mexico using MODIS data. GIScience Remote Sens. 2015, 52, 543–570. [Google Scholar] [CrossRef]
- Wickham, J.; Stehman, S.V.; Gass, L.; Dewitz, J.A.; Sorenson, D.G.; Granneman, B.J.; Poss, R.V.; Baer, L.A. Thematic accuracy assessment of the 2011 National Land Cover Database (NLCD). Remote Sens. Environ. 2017, 191, 328–341. [Google Scholar] [CrossRef] [PubMed]
- Wickham, J.; Stehman, S.V.; Homer, C.G. Spatial patterns of the united states national land cover dataset (NLCD) land-cover change thematic accuracy (2001-2011). Int. J. Remote Sens. 2018, 39, 1729–1743. [Google Scholar] [CrossRef]
- Tsendbazar, N.E.; Herold, M.; de Bruin, S.; Lesiv, M.; Fritz, S.; Van De Kerchove, R.; Buchhorn, M.; Duerauer, M.; Szantoi, Z.; Pekel, J.F. Developing and applying a multi-purpose land cover validation dataset for Africa. Remote Sens. Environ. 2018, 219, 298–309. [Google Scholar] [CrossRef]
- Wickham, J.; Stehman, S.V.; Neale, A.C.; Mehaffey, M. Accuracy assessment of NLCD 2011 percent impervious cover for selected USA metropolitan areas. Int. J. Appl. Earth Obs. Geoinf. 2020, 84, 101955. [Google Scholar] [CrossRef]
- Stehman, S.V.; Foody, G.M. Key issues in rigorous accuracy assessment of land cover products. Remote Sens. Environ. 2019, 231. [Google Scholar] [CrossRef]
- Smith, J.H.; Stehman, S.V.; Wickham, J.D.; Yang, L. Effects of landscape characteristics on land-cover class accuracy. Remote Sens. Environ. 2003, 84, 342–349. [Google Scholar] [CrossRef]
- Van Oort, P.A.J.; Bregt, A.K.; De Bruin, S.; De Wit, A.J.W.; Stein, A. Spatial variability in classification accuracy of agricultural crops in the Dutch national land-cover database. Int. J. Geogr. Inf. Sci. 2004, 18, 611–626. [Google Scholar] [CrossRef]
- Foody, G.M. Local characterization of thematic classification accuracy through spatially constrained confusion matrices. Int. J. Remote Sens. 2005, 26, 1217–1228. [Google Scholar] [CrossRef]
- Burnicki, A.C. Modeling the probability of misclassification in a map of land cover change. Photogramm. Eng. Remote Sens. 2011, 77, 39–50. [Google Scholar] [CrossRef]
- Park, N.W.; Kyriakidis, P.C.; Hong, S.Y. Spatial estimation of classification accuracy using indicator kriging with an image-derived ambiguity index. Remote Sens. 2016, 8, 320. [Google Scholar] [CrossRef]
- Comber, A.; Brunsdon, C.; Charlton, M.; Harris, P. Geographically weighted correspondence matrices for local error reporting and change analyses: Mapping the spatial distribution of errors and change. Remote Sens. Lett. 2017, 8, 234–243. [Google Scholar] [CrossRef]
- Khatami, R.; Mountrakis, G.; Stehman, S.V. Mapping per-pixel predicted accuracy of classified remote sensing images. Remote Sens. Environ. 2017, 191, 156–167. [Google Scholar] [CrossRef]
- Heydari, S.S.; Mountrakis, G. Effect of classifier selection, reference sample size, reference class distribution and scene heterogeneity in per-pixel classification accuracy using 26 Landsat sites. Remote Sens. Environ. 2018, 204, 648–658. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, W.; Mei, Y.; Yang, W. Geostatistical characterization of local accuracies in remotely sensed land cover change categorization with complexly configured reference samples. Remote Sens. Environ. 2019, 223, 63–81. [Google Scholar] [CrossRef]
- Szantoi, Z.; Geller, G.N.; Tsendbazar, N.E.; See, L.; Griffiths, P.; Fritz, S.; Gong, P.; Herold, M.; Mora, B.; Obregón, A. Addressing the need for improved land cover map products for policy support. Environ. Sci. Policy 2020, 112, 28–35. [Google Scholar] [CrossRef]
- Campos, J.C.; Brito, J.C. Mapping underrepresented land cover heterogeneity in arid regions: The Sahara-Sahel example. ISPRS J. Photogramm. Remote Sens. 2018, 146, 211–220. [Google Scholar] [CrossRef]
- Stehman, S.V. Impact of sample size allocation when using stratified random sampling to estimate accuracy and area of land-cover change. Remote Sens. Lett. 2012, 3, 111–120. [Google Scholar] [CrossRef]
- See, L.; Schepaschenko, D.; Lesiv, M.; McCallum, I.; Fritz, S.; Comber, A.; Perger, C.; Schill, C.; Zhao, Y.; Maus, V.; et al. Building a hybrid land cover map with crowdsourcing and geographically weighted regression. ISPRS J. Photogramm. Remote Sens. 2015, 103, 48–56. [Google Scholar] [CrossRef]
- Tsendbazar, N.E.; de Bruin, S.; Mora, B.; Schouten, L.; Herold, M. Comparative assessment of thematic accuracy of GLC maps for specific applications using existing reference data. Int. J. Appl. Earth Obs. Geoinf. 2016, 44, 124–135. [Google Scholar] [CrossRef]
- Yang, W.J. Local Classification Accuracy Modeling and Land-Cover Information Refinement Based on Class-Heterogeneity-Stratified Reference Sample Data; Wuhan University: Wuhan, China, 2019. [Google Scholar]
- Guisan, A.; Weiss, S.B.; Weiss, A.D. GLM versus CCA spatial modeling of plant species distribution. Plant Ecol. 1999, 143, 107–122. [Google Scholar] [CrossRef]
- Franklin, J.; Woodcock, C.E.; Warbington, R. Multi-attribute vegetation maps of Forest Service lands in California supporting resource management decisions. Photogramm. Eng. Remote Sens. 2000, 66, 1209–1217. [Google Scholar]
- Miller, J.; Franklin, J. Modeling the distribution of four vegetation alliances using generalized linear models and classification trees with spatial dependence. Ecol. Modell. 2002, 157, 227–247. [Google Scholar] [CrossRef]
- Tomppo, E.O.; Gagliano, C.; De Natale, F.; Katila, M.; McRoberts, R.E. Predicting categorical forest variables using an improved k-Nearest Neighbour estimator and Landsat imagery. Remote Sens. Environ. 2009, 113, 500–517. [Google Scholar] [CrossRef]
- Duveneck, M.J.; Thompson, J.R.; Wilson, B.T. An imputed forest composition map for New England screened by species range boundaries. For. Ecol. Manag. 2015, 347, 107–115. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Chen, Q.; Domke, G.M.; Næsset, E.; Gobakken, T.; Chirici, G.; Mura, M. Optimizing nearest neighbour configurations for airborne laser scanning-assisted estimation of forest volume and biomass. Forestry 2017, 90, 99–111. [Google Scholar] [CrossRef]
- Legendre, P.; Legendre, L. Numerical Ecology. In Biometrics; Elsevier Science: Amsterdam, The Netherlands, 1984; Volume 40, p. 280. [Google Scholar]
- Ohmann, J.L.; Gregory, M.J. Predictive mapping of forest composition and structure with direct gradient analysis and nearest-neighbor imputation in coastal Oregon, USA. Can. J. For. Res. 2002, 32, 725–741. [Google Scholar] [CrossRef]
- Dirnböck, T.; Dullinger, S.; Gottfried, M.; Ginzier, C.; Grabherr, G. Mapping alpine vegetation based on image analysis, topographic variables and Canonical Correspondence Analysis. Appl. Veg. Sci. 2003, 6, 85–96. [Google Scholar] [CrossRef]
- Schmidtlein, S.; Sassin, J. Mapping of continuous floristic gradients in grasslands using hyperspectral imagery. Remote Sens. Environ. 2004, 92, 126–138. [Google Scholar] [CrossRef]
- Thessler, S.; Ruokolainen, K.; Tuomisto, H.; Tomppo, E. Mapping gradual landscape-scale floristic changes in Amazonian primary rain forests by combining ordination and remote sensing. Glob. Ecol. Biogeogr. 2005, 14, 315–325. [Google Scholar] [CrossRef]
- Middleton, M.; Närhi, P.; Arkimaa, H.; Hyvönen, E.; Kuosmanen, V.; Treitz, P.; Sutinen, R. Ordination and hyperspectral remote sensing approach to classify peatland biotopes along soil moisture and fertility gradients. Remote Sens. Environ. 2012, 124, 596–609. [Google Scholar] [CrossRef]
- Adams, B.T.; Matthews, S.N.; Peters, M.P.; Prasad, A.; Iverson, L.R. Mapping floristic gradients of forest composition using an ordination-regression approach with landsat OLI and terrain data in the Central Hardwoods region. For. Ecol. Manag. 2019, 434, 87–98. [Google Scholar] [CrossRef]
- Jilge, M.; Heiden, U.; Neumann, C.; Feilhauer, H. Gradients in urban material composition: A new concept to map cities with spaceborne imaging spectroscopy data. Remote Sens. Environ. 2019, 223, 179–193. [Google Scholar] [CrossRef]
- Feilhauer, H.; Faude, U.; Schmidtlein, S. Combining Isomap ordination and imaging spectroscopy to map continuous floristic gradients in a heterogeneous landscape. Remote Sens. Environ. 2011, 115, 2513–2524. [Google Scholar] [CrossRef]
- Oldeland, J.; Dorigo, W.; Lieckfeld, L.; Lucieer, A.; Jürgens, N. Combining vegetation indices, constrained ordination and fuzzy classification for mapping semi-natural vegetation units from hyperspectral imagery. Remote Sens. Environ. 2010, 114, 1155–1166. [Google Scholar] [CrossRef]
- Harris, A.; Charnock, R.; Lucas, R.M. Hyperspectral remote sensing of peatland floristic gradients. Remote Sens. Environ. 2015, 162, 99–111. [Google Scholar] [CrossRef]
- Hakkenberg, C.R.; Peet, R.K.; Urban, D.L.; Song, C. Modeling plant composition as community continua in a forest landscape with LiDAR and hyperspectral remote sensing. Ecol. Appl. 2018, 28, 177–190. [Google Scholar] [CrossRef]
- Ohmann, J.L.; Gregory, M.J.; Henderson, E.B.; Roberts, H.M. Mapping gradients of community composition with nearest-neighbour imputation: Extending plot data for landscape analysis. J. Veg. Sci. 2011, 22, 660–676. [Google Scholar] [CrossRef]
- Chiang, J.L.; Liou, J.J.; Wei, C.; Cheng, K.S. A feature-space indicator Kriging approach for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4046–4055. [Google Scholar] [CrossRef]
- Cantoni, E.; Ronchetti, E. Robust inference for generalized linear models. J. Am. Stat. Assoc. 2001, 96, 1022–1030. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, W.; Zhang, W.; Wang, Y.; Liu, D.; Xiu, Y. An explorative study on estimating local accuracies in land-cover information using logistic regression and class-heterogeneity-stratified data. Remote Sens. 2018, 10, 1581. [Google Scholar] [CrossRef]
- Legendre, P.; Oksanen, J.; ter Braak, C.J.F. Testing the significance of canonical axes in redundancy analysis. Methods Ecol. Evol. 2011, 2, 269–277. [Google Scholar] [CrossRef]
- Crookston, N.L.; Finley, A.O. yaImpute: An R package for κNN imputation. J. Stat. Softw. 2008, 23, 1–16. [Google Scholar] [CrossRef]
- Bivand, R.; Piras, G. Comparing implementations of estimation methods for spatial econometrics. J. Stat. Softw. 2015, 63, 1–36. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Herold, M.; Stehman, S.V.; Woodcock, C.E.; Wulder, M.A. Good practices for estimating area and assessing accuracy of land change. Remote Sens. Environ. 2014, 148, 42–57. [Google Scholar] [CrossRef]
- Sweeney, S.P.; Evans, T.P. An edge-oriented approach to thematic map error assessment. Geocarto Int. 2012, 27, 31–56. [Google Scholar] [CrossRef]
- Cochran, W.G. Sampling Techniques, 3rd ed.; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Zhang, J.; Foody, G.M. A fuzzy classification of sub-urban land cover from remotely sensed imagery. Int. J. Remote Sens. 1998, 19, 2721–2738. [Google Scholar] [CrossRef]
- Goutte, C.; Gaussier, E. A Probabilistic Interpretation of Precision, Recall and F-Score, with Implication for Evaluation. Lect. Notes Comput. Sci. 2005, 3408, 345–359. [Google Scholar] [CrossRef]
- Feng, M.; Bai, Y. A global land cover map produced through integrating multi-source datasets. Big Earth Data 2019, 3, 191–219. [Google Scholar] [CrossRef]
- Yu, L.; Liu, X.; Zhao, Y.; Yu, C.; Gong, P. Difficult to map regions in 30 m global land cover mapping determined with a common validation dataset. Int. J. Remote Sens. 2018, 39, 4077–4087. [Google Scholar] [CrossRef]
- Lin, Y.P.; Yeh, M.S.; Deng, D.P.; Wang, Y.C. Geostatistical approaches and optimal additional sampling schemes for spatial patterns and future sampling of bird diversity. Glob. Ecol. Biogeogr. 2008, 17, 175–188. [Google Scholar] [CrossRef]
- Kilibarda, M.; Tadić, M.P.; Hengl, T.; Luković, J.; Bajat, B. Global geographic and feature space coverage of temperature data in the context of spatio-temporal interpolation. Spat. Stat. 2015, 14, 22–38. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Stehman, S.V.; Liknes, G.C.; Næsset, E.; Sannier, C.; Walters, B.F. The effects of imperfect reference data on remote sensing-assisted estimators of land cover class proportions. ISPRS J. Photogramm. Remote Sens. 2018, 142, 292–300. [Google Scholar] [CrossRef]
- Roberts, G.; Rao, N.K.; Kumar, S. Logistic regression analysis of sample survey data. Biometrika 1987, 74, 1–12. [Google Scholar] [CrossRef]
- Bollen, K.A.; Biemer, P.P.; Karr, A.F.; Tueller, S.; Berzofsky, M.E. Are Survey Weights Needed? A Review of Diagnostic Tests in Regression Analysis. Annu. Rev. Stat. Its Appl. 2016, 3, 375–392. [Google Scholar] [CrossRef]
- Lumley, T. Survey Sampling, a Guide to Analysis Using R; Wiley: New York, NY, USA, 2010. [Google Scholar]
- Winship, C.; Radbill, L. Sampling Weights and Regression Analysis. Sociol. Methods Res. 1994, 23, 230–257. [Google Scholar] [CrossRef]
- Kainz, W. Logical consistency. In Elements of Spatial Data Quality; Elsevier Science Ltd.: Amsterdam, The Netherlands, 1995; pp. 109–137. [Google Scholar]
- Abercrombie, S.P.; Friedl, M.A. Improving the Consistency of Multitemporal Land Cover Maps Using a Hidden Markov Model. IEEE Trans. Geosci. Remote Sens. 2016, 54, 703–713. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Liu, D.; Yang, W.; Zhang, W. Accuracy assessment of GlobeLand30 2010 land cover over China based on geographically and categorically stratified validation sample data. Remote Sens. 2018, 10, 1213. [Google Scholar] [CrossRef]
- DeFries, R.; Hansen, M.; Steininger, M.; Dubayah, R.; Sohlberg, R.; Townshend, J. Subpixel forest cover in central Africa from multisensor, multitemporal data. Remote Sens. Environ. 1997, 60, 228–246. [Google Scholar] [CrossRef]
- McGarigal, K.; Tagil, S.; Cushman, S.A. Surface metrics: An alternative to patch metrics for the quantification of landscape structure. Landsc. Ecol. 2009, 24, 433–450. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).