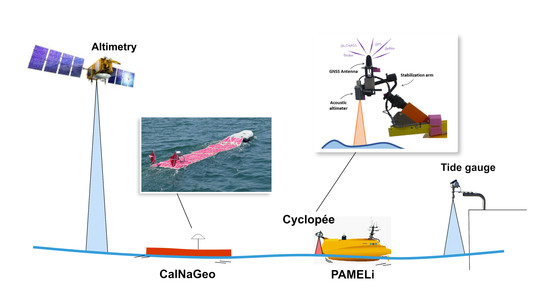
Mapping Sea Surface Height Using New Concepts of Kinematic GNSS Instruments
Abstract
1. Introduction
2. Materials and Methods
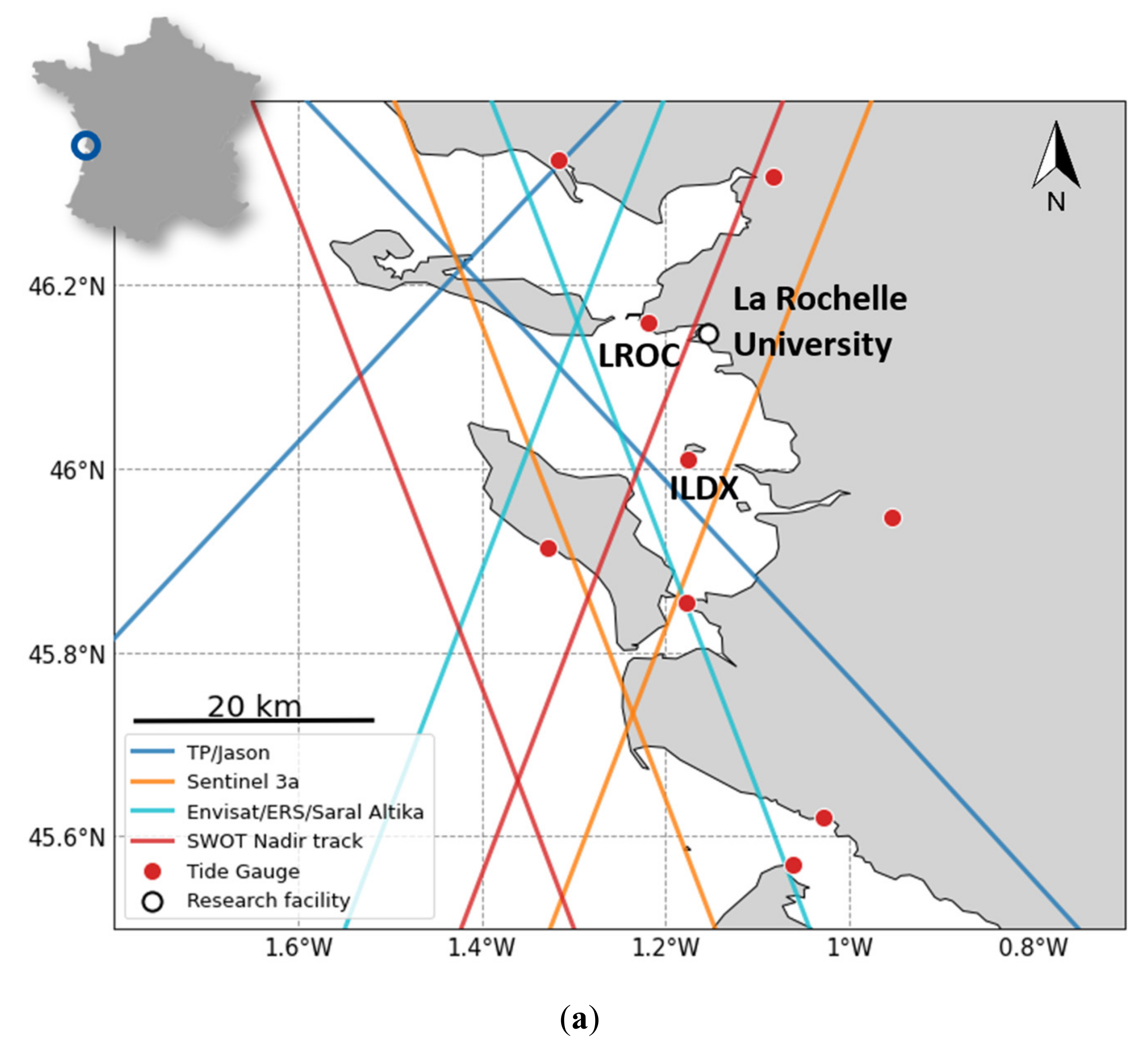
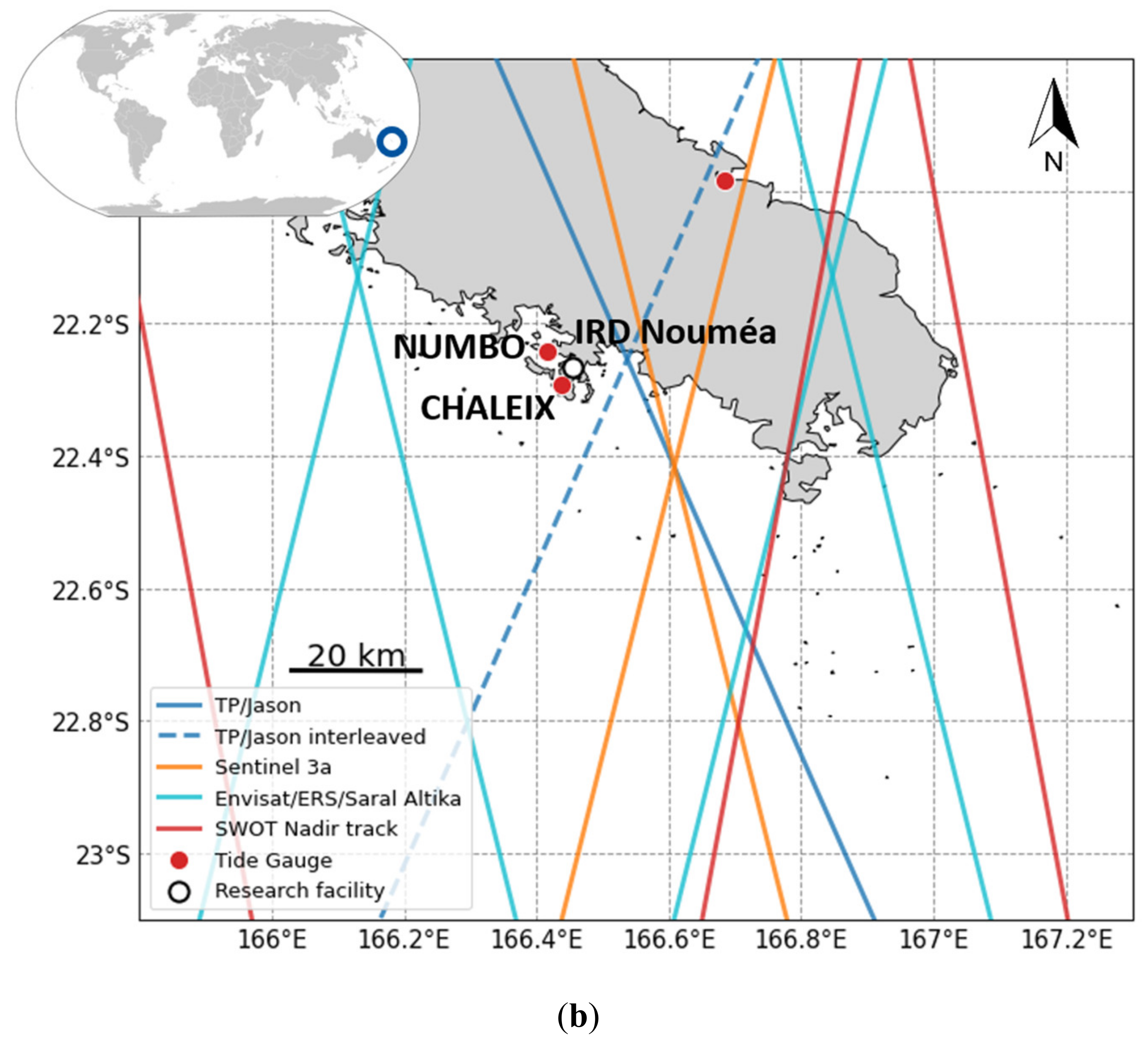
2.1. Coastal Areas for Calibration/Validation Activities
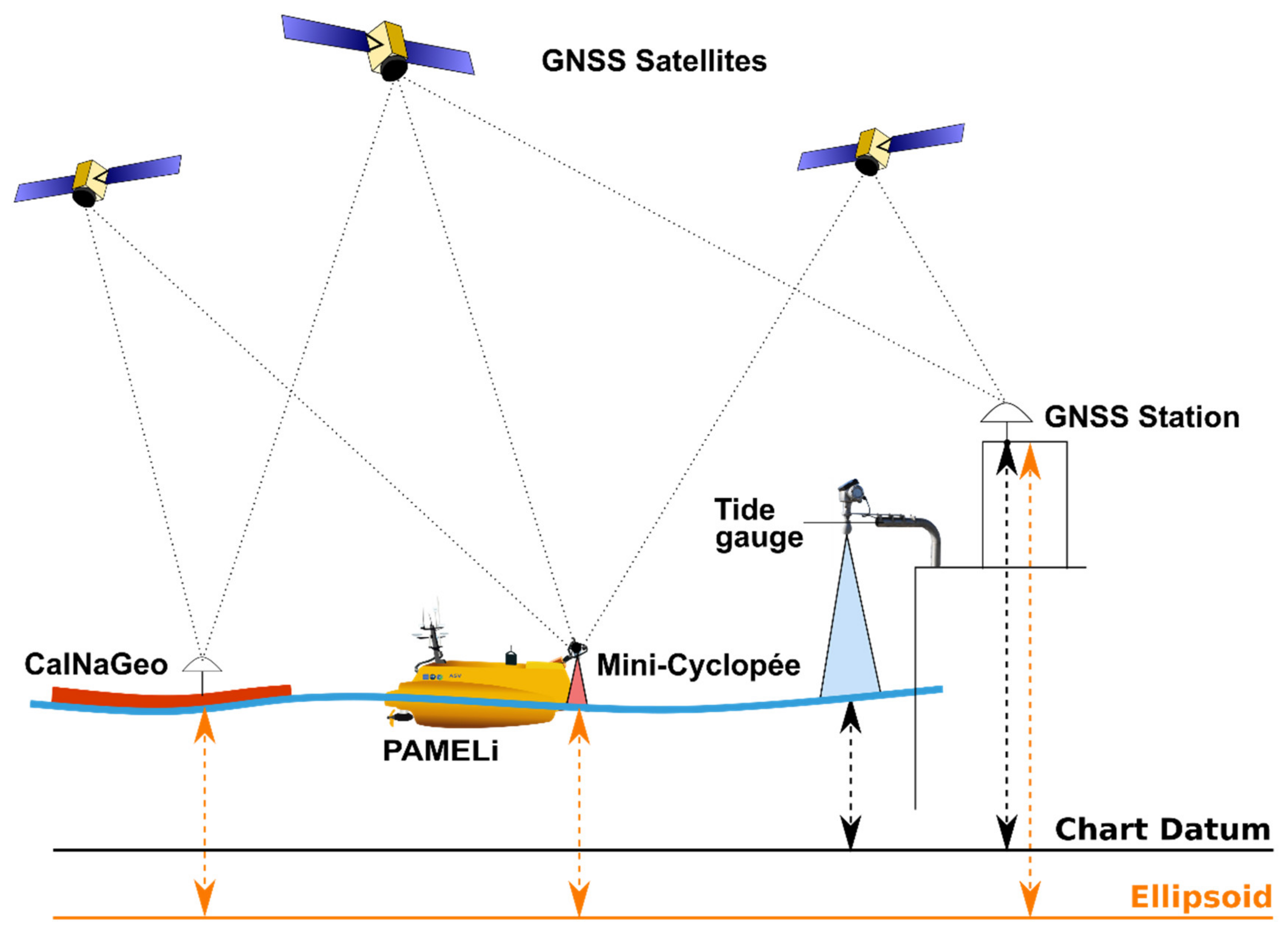
2.2. CalNaGeo GNSS Towed Carpet
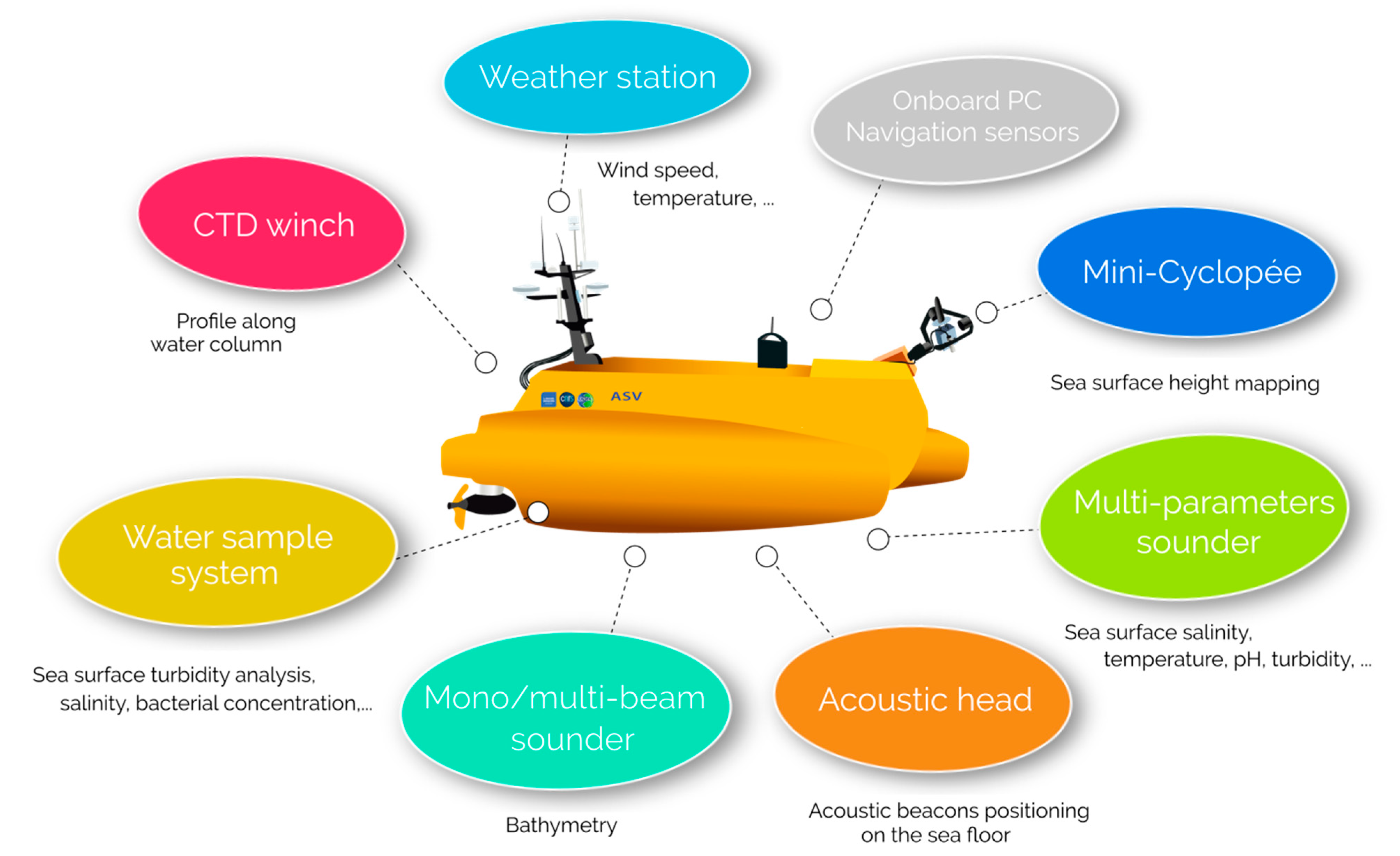
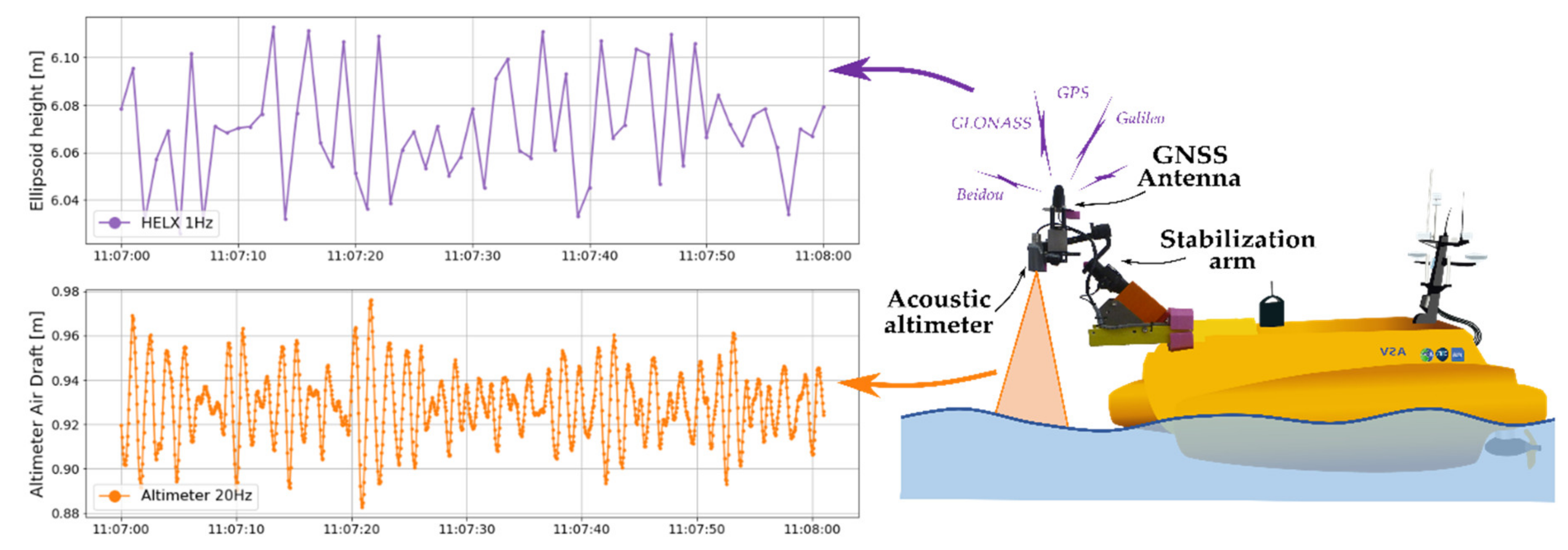
2.3. Cyclopée System with Autonomous Plateform
3. Results
3.1. Instruments Calibration
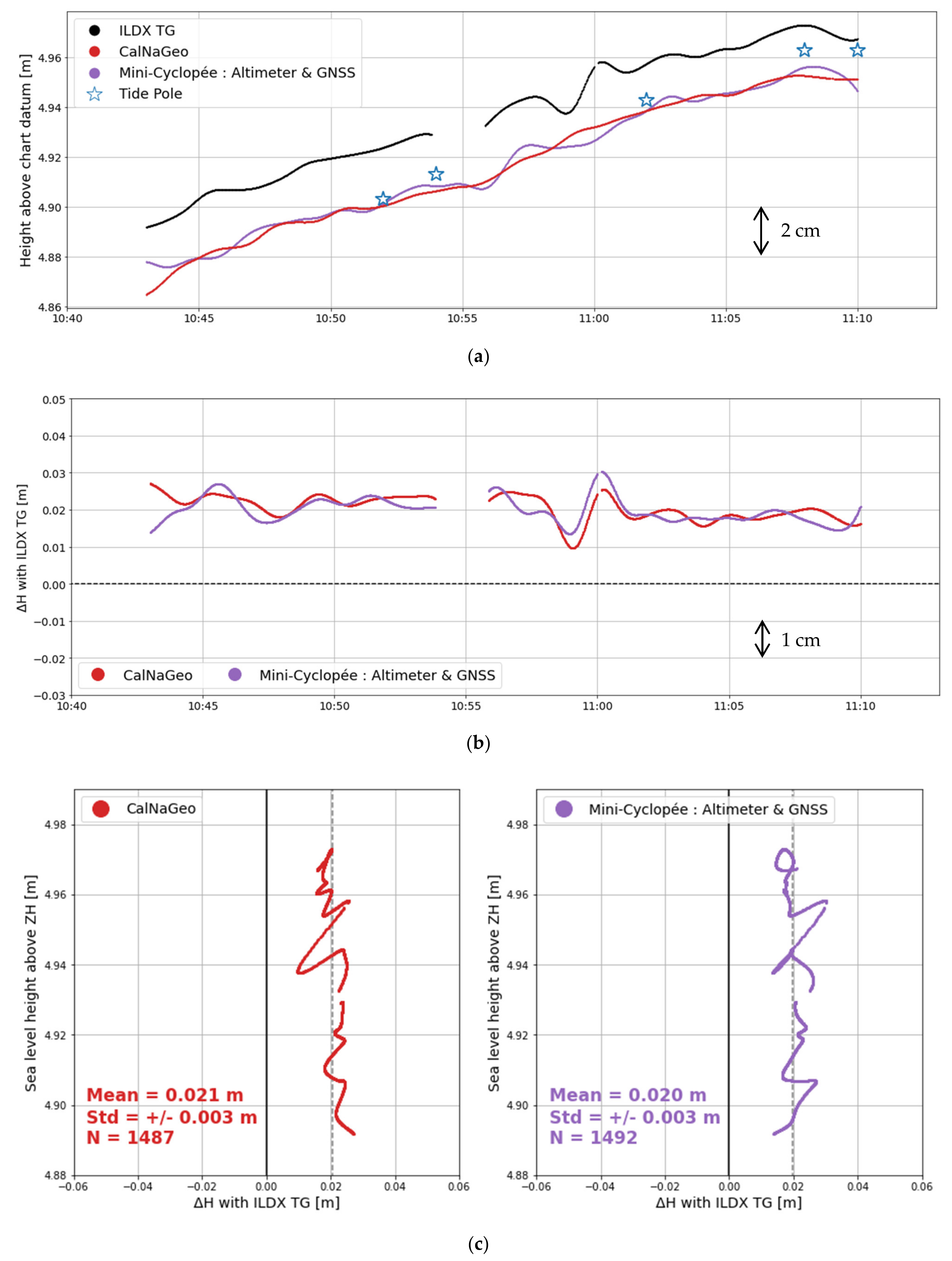
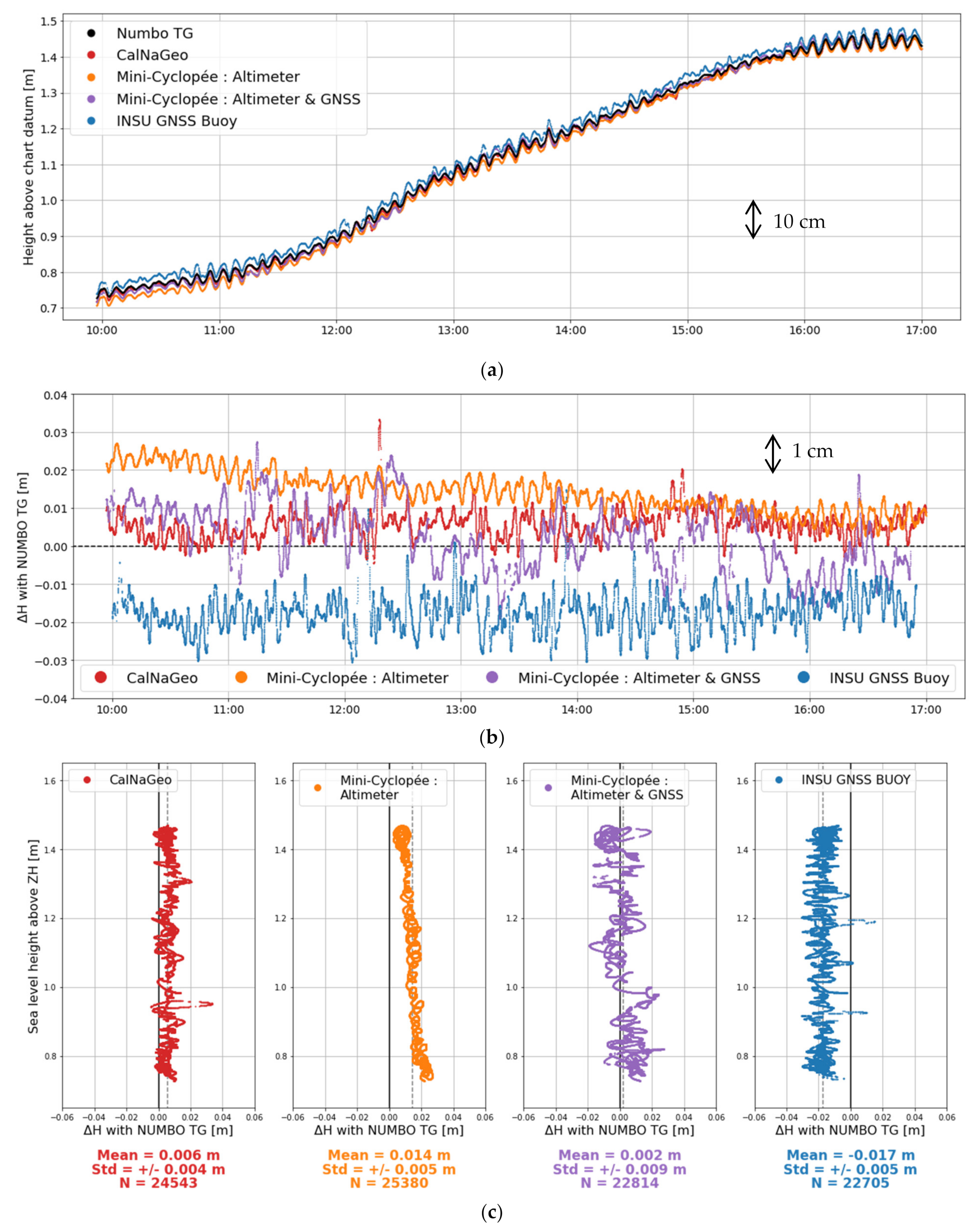
3.1.1. Static Tide Gauge Sessions
Setup of the Experiments
Comparison with Tide Gauge Observations
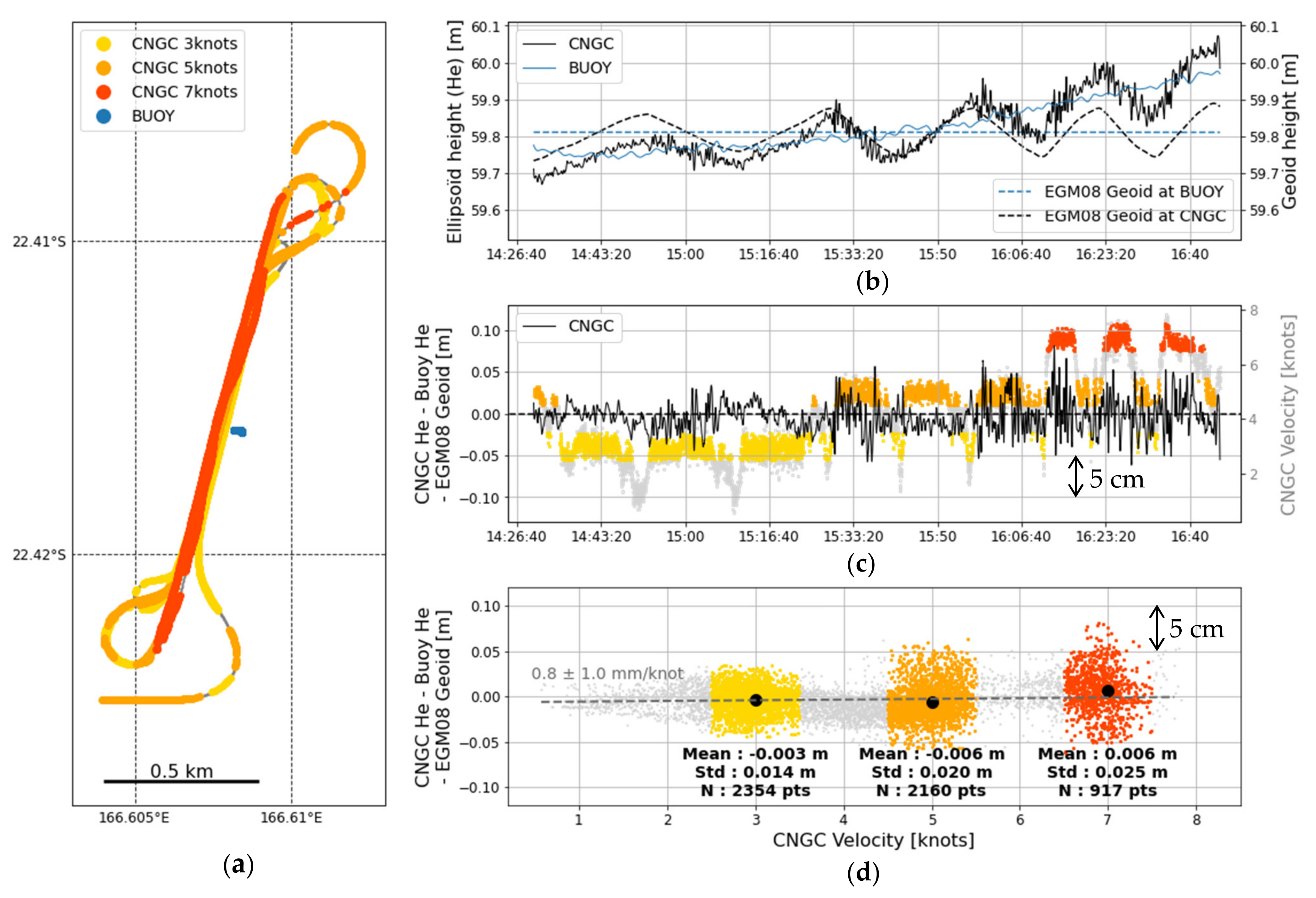
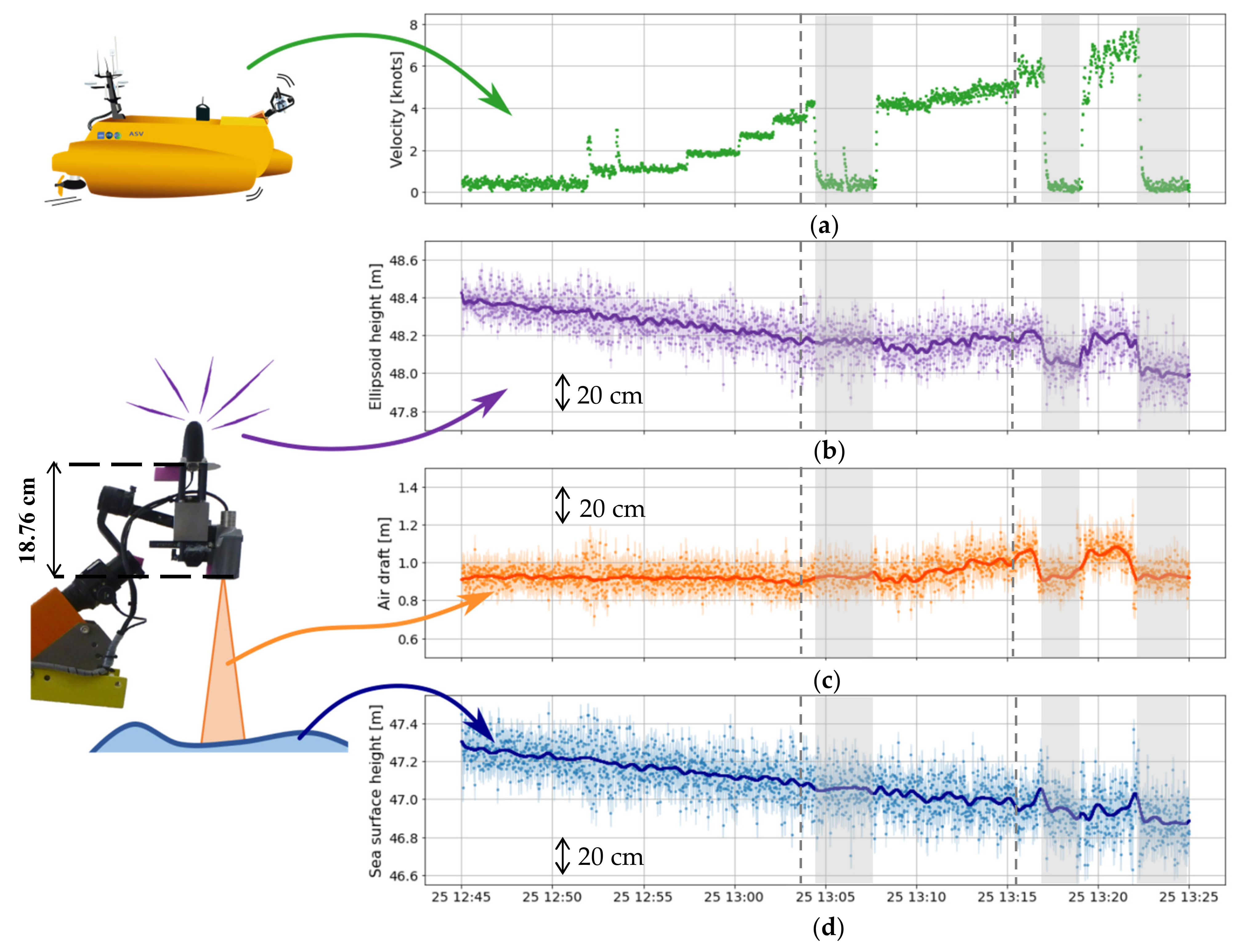
3.1.2. Effect of Speed on Water Height Measurements
CalNaGeo Experiment Setup in Noumea Lagoon
PAMELi Experiment Setup Near La Rochelle
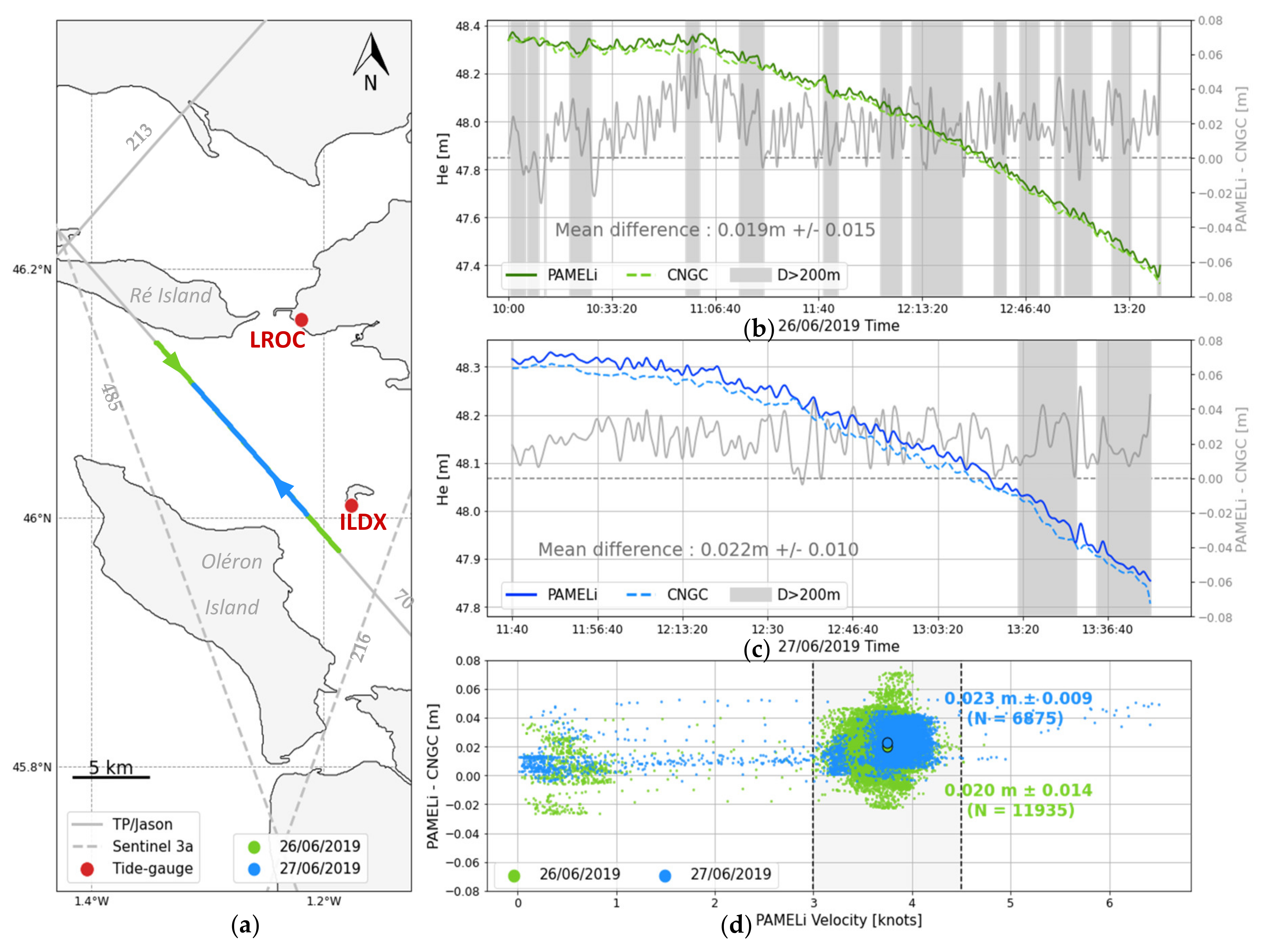
3.2. Comparison of Both Systems
Sea Surface Measurements along Track
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- −
- P. Bonnefond—SYRTE, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Univ. Paris 06, LNE, 77 avenue Denfert-Rochereau, 75014 Paris, France
- −
- O.Laurain—OCA-GEOAZUR, 250 av. A. Einstein, 06560 Valbonne, France
- −
- V. Ballu, X. Bertin, C. Chupin E. Poirier and Y-T. Tranchant—LIENSs, UMR 7266, CNRS/ La Rochelle Université, Bâtiment ILE, 2, rue Olympe de Gouges, 17000 La Rochelle, France
- −
- M.-P. Bonnet, J. Darrozes, P. Exertier, F. Frappart, F. Perosanz, G. Ramillien and A. Santamaría-Gómez—OMP-GET/GRGS, 14 av. Ed. Belin, 31000 Toulouse, France
- −
- D. Allain, M. Bergé-Nguyen, S. Calmant, J.-F. Crétaux, F. Lyard and L. Testut—LEGOS, 18 av. Ed. Belin, 31000 Toulouse, France
- −
- C. Brachet, M. Calzas, C. Drezen, A. Guillot and L.Fichen—DT INSU, Bâtiment IPEV, BP 74 29280 Plouzane, France
- −
- M. Cancet—NOVELTIS, 153 rue du Lac 31670 Labège, France
- −
- P. Schaeffer—CLS, 8-10 rue Hermes, Parc Technologique du Canal 31526 RAMONVILLE St-Agne, France
- −
- Flavien Mercier—CNES, 18, av. Ed. Belin 31401 Toulouse, France
- −
- F. Seyler—UMR—ESPACE DEV, maison de la télédétection, 500 rue Jean-François Breton, 34093 Montpellier, France
- −
- R. Abarca Del Rio—DGEO, University of Concepcion, Casilla: 160-C, Barrio Universitario S/N, Concepcion, Chili
- −
- D. Medeiros Moreira—CPRM, Av. Pasteur, 404—Urca Rio de Janeiro, RJ, Brazil 22290-255
- −
- J. Santos da Silva—CESTU/UEA, Avenida J. Batista 3578, Manaus, Brazil
References
- Bonnefond, P.; Exertier, P.; Laurain, O.; Thibaut, P.; Mercier, F. GPS-based sea level measurements to help the characterization of land contamination in coastal areas. Adv. Space Res. 2013, 51, 1383–1399. [Google Scholar] [CrossRef]
- Roblou, L.; Lamouroux, J.; Bouffard, J.; Lyard, F.; Le Hénaff, M.; Lombard, A.; Marsaleix, P.; De Mey, P.; Birol, F. Post-processing Altimeter Data Towards Coastal Applications and Integration into Coastal Models. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 217–246. ISBN 978-3-642-12796-0. [Google Scholar]
- GCOS. Systematic Observation Requirements for Satellite-Based Products for Climate 2011 Update: Supplemental Details to the Satellite-Based Component of the “Implementation Plan for the Global Observing System for Climate in Support of the UNFCCC (2010 Update); WMO: Geneva, Switzerland, 2011. [Google Scholar]
- Mitchum, G.T. An Improved Calibration of Satellite Altimetric Heights Using Tide Gauge Sea Levels with Adjustment for Land Motion. Mar. Geod. 2000, 23, 145–166. [Google Scholar] [CrossRef]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Ray, R.D.; Egbert, G.D.; Erofeeva, S.Y. Tide Predictions in Shelf and Coastal Waters: Status and Prospects. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 191–216. ISBN 978-3-642-12796-0. [Google Scholar]
- Born, G.H.; Parke, M.E.; Axelrad, P.; Gold, K.L.; Johnson, J.; Key, K.W.; Kubitschek, D.G.; Christensen, E.J. Calibration of the TOPEX altimeter using a GPS buoy. J. Geophys. Res. 1994, 99, 24517. [Google Scholar] [CrossRef]
- André, G.; Miguez, B.M.; Ballu, V.; Testut, L.; Wöppelmann, G. Measuring sea level with gps-equipped buoys: A multi-instruments experiment at Aix Island. Int. Hydrogr. Rev. 2013, 14, 26–38. [Google Scholar]
- Bonnefond, P.; Haines, B.J.; Watson, C. In situ Absolute Calibration and Validation: A Link from Coastal to Open-Ocean Altimetry. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 259–296. ISBN 978-3-642-12796-0. [Google Scholar]
- Fund, F.; Perosanz, F.; Testut, L.; Loyer, S. An Integer Precise Point Positioning technique for sea surface observations using a GPS buoy. Adv. Space Res. 2013, 51, 1311–1322. [Google Scholar] [CrossRef]
- Rocken, C.; Johnson, J.; Van Hove, T.; Iwabuchi, T. Atmospheric water vapor and geoid measurements in the open ocean with GPS. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Bouin, M.-N.; Ballu, V.; Calmant, S.; Boré, J.-M.; Folcher, E.; Ammann, J. A kinematic GPS methodology for sea surface mapping, Vanuatu. J. Geod. 2009, 83, 1203–1217. [Google Scholar] [CrossRef]
- Foster, J.H.; Carter, G.S.; Merrifield, M.A. Ship-based measurements of sea surface topography. Geophys. Res. Lett. 2009, 36, L11605. [Google Scholar] [CrossRef]
- Bonnefond, P.; Exertier, P.; Laurain, O.; Ménard, Y.; Orsoni, A.; Jeansou, E.; Haines, B.J.; Kubitschek, D.G.; Born, G. Leveling the Sea Surface Using a GPS-Catamaran. Mar. Geod. 2003, 26, 319–334. [Google Scholar] [CrossRef]
- Crétaux, J.-F.; Bergé-Nguyen, M.; Calmant, S.; Romanovski, V.V.; Meyssignac, B.; Perosanz, F.; Tashbaeva, S.; Arsen, A.; Fund, F.; Martignago, N.; et al. Calibration of Envisat radar altimeter over Lake Issykkul. Adv. Space Res. 2013, 51, 1523–1541. [Google Scholar] [CrossRef]
- Penna, N.T.; Maqueda, M.A.M.; Martin, I.; Guo, J.; Foden, P.R. Sea Surface Height Measurement Using a GNSS Wave Glider. Geophys. Res. Lett. 2018, 45, 5609–5616. [Google Scholar] [CrossRef]
- Gouriou, T.; Martín Míguez, B.; Wöppelmann, G. Reconstruction of a two-century long sea level record for the Pertuis d’Antioche (France). Cont. Shelf Res. 2013, 61–62, 31–40. [Google Scholar] [CrossRef]
- Aucan, J.; Merrifield, M.A.; Pouvreau, N. Historical Sea Level in the South Pacific from Rescued Archives, Geodetic Measurements, and Satellite Altimetry. Pure Appl. Geophys. 2017, 174, 3813–3823. [Google Scholar] [CrossRef]
- Coulombier, T.; Ballu, V.; Pineau, P.; Lachaussee, N.; Poirier, E.; Guillot, A.; Calzas, M.; Drezen, C.; Fichen, L.; Plumejeaud, C.; et al. PAMELi, un drone marin de surface au service de l’interdisciplinarité. In Proceedings of the XVèmes Journées Nationales Génie Côtier–Génie Civil, La Rochelle, France, 29–31 May 2018; pp. 337–344. [Google Scholar]
- Martín Míguez, B.; Le Roy, R.; Wöppelmann, G. The Use of Radar Tide Gauges to Measure Variations in Sea Level along the French Coast. J. Coast. Res. 2008, 4, 61–68. [Google Scholar] [CrossRef]
- Roy, R.L. Evaluation of the Quality of Radar Telemeters. Available online: https://www.sonel.org (accessed on 25 June 2020).
- Takasu, T. RTKLIB: An Open Source Program Package for GNSS Positioning. Available online: http://www.rtklib.com/ (accessed on 6 June 2020).
- Vondrak, J. Problem of Smoothing Observational Data II; Astronomicall Institue of the Czechoslovak Academy of Sciences: Praha, Czech, 1977; Volume 28, pp. 84–89. [Google Scholar]
- Gobron, K.; de Viron, O.; Wöppelmann, G.; Poirier, É.; Ballu, V.; Van Camp, M. Assessment of Tide Gauge Biases and Precision by the Combination of Multiple Collocated Time Series. J. Atmos. Ocean. Technol. 2019, 36, 1983–1996. [Google Scholar] [CrossRef]
- Miguez, B.M.; Testut, L.; Wöppelmann, G. The Van de Casteele Test Revisited: An Efficient Approach to Tide Gauge Error Characterization. J. Atmos. Oceanic Technol. 2008, 25, 1238–1244. [Google Scholar] [CrossRef]
- Bonnefond, P.; Exertier, P.; Laurain, O.; Guinle, T.; Féménias, P. Corsica: A 20-Yr multi-mission absolute altimeter calibration site. Adv. Space Res. 2019. [Google Scholar] [CrossRef]
- Marty, J.C.; Loyer, S.; Perosanz, F.; Mercier, F.; Bracher, G.; Legresy, B.; Portier, L.; Capdeville, H.; Fund, F.; Lemoine, J.M.; et al. GINS: The CNES/GRGS GNSS scientific software. In Proceedings of the ESA Proceedings WPP326, Copenhagen, Denmark, 31 August–2 September 2011. [Google Scholar]
- Calzas, M.; Brachet, C.; Drezen, C.; Fichen, L.; Guillot, A.; Téchiné, P.; Testut, L.; Bonnefond, P.; Laurain, O.; Umr, G.; et al. Mesure du geoïde marin avec le système CalNaGEO (GNSS). 2019. Available online: http://www.legos.obs-mip.fr/observations/rosame/documents/CalNaGEO_Refmar_2019.pdf?lang=fr (accessed on 12 August 2020).
| System | Pertuis Session | Noumea Session | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean Difference to TG [m] | Std [m] | Number of Data | Mean Difference to TG [m] | Std [m] | Number of Data | |||
| CalNaGeo | 0.021 | 0.003 | 1 487 | 0.006 | 0.004 | 24 543 | ||
| Mini-Cyclopée | On USV | 0.020 | 0.003 | 1 492 | - | - | - | |
| On wharf | Altimeter only | - | - | - | 0.014 | 0.005 | 25 380 | |
| Altimeter and GNSS | - | - | - | 0.002 | 0.009 | 22 814 | ||
| GNSS Buoy | - | - | - | −0.017 | 0.005 | 22 705 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chupin, C.; Ballu, V.; Testut, L.; Tranchant, Y.-T.; Calzas, M.; Poirier, E.; Coulombier, T.; Laurain, O.; Bonnefond, P.; FOAM Project, T. Mapping Sea Surface Height Using New Concepts of Kinematic GNSS Instruments. Remote Sens. 2020, 12, 2656. https://doi.org/10.3390/rs12162656
Chupin C, Ballu V, Testut L, Tranchant Y-T, Calzas M, Poirier E, Coulombier T, Laurain O, Bonnefond P, FOAM Project T. Mapping Sea Surface Height Using New Concepts of Kinematic GNSS Instruments. Remote Sensing. 2020; 12(16):2656. https://doi.org/10.3390/rs12162656
Chicago/Turabian StyleChupin, Clémence, Valérie Ballu, Laurent Testut, Yann-Treden Tranchant, Michel Calzas, Etienne Poirier, Thibault Coulombier, Olivier Laurain, Pascal Bonnefond, and Team FOAM Project. 2020. "Mapping Sea Surface Height Using New Concepts of Kinematic GNSS Instruments" Remote Sensing 12, no. 16: 2656. https://doi.org/10.3390/rs12162656
APA StyleChupin, C., Ballu, V., Testut, L., Tranchant, Y.-T., Calzas, M., Poirier, E., Coulombier, T., Laurain, O., Bonnefond, P., & FOAM Project, T. (2020). Mapping Sea Surface Height Using New Concepts of Kinematic GNSS Instruments. Remote Sensing, 12(16), 2656. https://doi.org/10.3390/rs12162656