Next Article in Journal
Intercomparison of Satellite-Derived Solar Irradiance from the GEO-KOMSAT-2A and HIMAWARI-8/9 Satellites by the Evaluation with Ground Observations
Next Article in Special Issue
GYMEE: A Global Field-Scale Crop Yield and ET Mapper in Google Earth Engine Based on Landsat, Weather, and Soil Data
Previous Article in Journal
Modeling and Multi-Temporal Characterization of Total Suspended Matter by the Combined Use of Sentinel 2-MSI and Landsat 8-OLI Data: The Pertusillo Lake Case Study (Italy)
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 12
Issue 13
10.3390/rs12132148
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Watershed Modeling with Remotely Sensed Big Data: MODIS Leaf Area Index Improves Hydrology and Water Quality Predictions

by
Adnan Rajib
1,*,
I Luk Kim
2,
Heather E. Golden
3,
Charles R. Lane
3,
Sujay V. Kumar
4,
Zhiqiang Yu
5 and
Saranya Jeyalakshmi
6
1
Department of Environmental Engineering, Frank H. Dotterweich College of Engineering, Texas A&M University, 917 W Ave B, Kingsville, TX 78363, USA
2
Rosen Center for Advanced Computing, Purdue University, West Lafayette, IN 47907, USA
3
U.S. Environmental Protection Agency, Office of Research and Development, Cincinnati, OH 45220, USA
4
NASA Goddard Space Flight Center, Hydrological Sciences Laboratory, Greenbelt, MD 20771, USA
5
Civica Infrastructure Inc., Vaughan, ON L6A 4P5, Canada
6
Department of Civil and Environmental Engineering, University of Windsor, ON N9B 3P4, Canada
*
Author to whom correspondence should be addressed.
Remote Sens. 2020, 12(13), 2148; https://doi.org/10.3390/rs12132148
Submission received: 28 May 2020 / Revised: 25 June 2020 / Accepted: 28 June 2020 / Published: 4 July 2020
(This article belongs to the Special Issue Remote Sensing for Improved Understanding of Land Surface, Hydrology, and Water Quality)
Browse Figures
Versions Notes

Abstract

:
Traditional watershed modeling often overlooks the role of vegetation dynamics. There is also little quantitative evidence to suggest that increased physical realism of vegetation dynamics in process-based models improves hydrology and water quality predictions simultaneously. In this study, we applied a modified Soil and Water Assessment Tool (SWAT) to quantify the extent of improvements that the assimilation of remotely sensed Leaf Area Index (LAI) would convey to streamflow, soil moisture, and nitrate load simulations across a 16,860 km2 agricultural watershed in the midwestern United States. We modified the SWAT source code to automatically override the model’s built-in semiempirical LAI with spatially distributed and temporally continuous estimates from Moderate Resolution Imaging Spectroradiometer (MODIS). Compared to a “basic” traditional model with limited spatial information, our LAI assimilation model (i) significantly improved daily streamflow simulations during medium-to-low flow conditions, (ii) provided realistic spatial distributions of growing season soil moisture, and (iii) substantially reproduced the long-term observed variability of daily nitrate loads. Further analysis revealed that the overestimation or underestimation of LAI imparted a proportional cascading effect on how the model partitions hydrologic fluxes and nutrient pools. As such, assimilation of MODIS LAI data corrected the model’s LAI overestimation tendency, which led to a proportionally increased rootzone soil moisture and decreased plant nitrogen uptake. With these new findings, our study fills the existing knowledge gap regarding vegetation dynamics in watershed modeling and confirms that assimilation of MODIS LAI data in watershed models can effectively improve both hydrology and water quality predictions.

1. Introduction

The big data evolution in recent years has paved the way for remote sensing-integrated watershed modeling. To limit models’ perceived tendency to give the “right answers for wrong reasons” [1,2], and therefore ensure realistic watershed management alternatives [3,4,5], the hydrogeoscience community is increasingly using remotely sensed big data. It is already evident that remotely sensed estimates of vertical water fluxes, such as soil moisture and evapotranspiration, offer realistic constraints to watershed models, leading to improved simulation of hydrologic processes [6,7,8,9,10]. However, such improved simulation is feasible despite misrepresented vegetation dynamics in the model [7,8]. Because spatiotemporal vegetation dynamics (i.e., when, where, what, and how vegetation grows on the land surface) is a primary driver of land-atmosphere interaction and hence the water-energy exchanges across the watershed [11,12], achieving the so-called improved hydrologic simulation while overlooking vegetation dynamics is not physically meaningful. Nonetheless, the implications of misrepresented vegetation dynamics on water quality simulations (e.g., in-stream nutrient load [13]) remains underexplored.
With the advent of advanced earth observation algorithms, remotely sensed Leaf Area Index (LAI; leaf surface area per unit land surface area) has emerged as an effective measure of global vegetation dynamics [11,14]. Today’s state-of-the-science biophysical models simulating gross/net primary productivity, surface wetness, crop yield, and CO2 storage often assimilate remotely sensed LAI data as the proxy for real-life vegetation dynamics [12,15,16,17,18,19,20]. However, watershed models simulating hydrology and water quality continue to rely on semiempirical LAI equations (e.g., leaf development curve) and associated biotic/abiotic user inputs (e.g., vegetation types, available solar energy, crop plantation, and harvest dates) [21,22,23,24,25]. This LAI parameterization approach lacks physical realism in many widely used watershed models (e.g., Soil and Water Assessment Tool, Variable Infiltration Capacity model) [21,22,23,24,25]. In some of these models, a vegetation/LAI development module does not exist (e.g., Hydrologic Engineering Center-Hydrologic Modeling System) [26]. Therefore, remedial measures such as modification of existing LAI equations and calibration of LAI parameters (see, e.g., [13,22,23]) are not always applicable. To address these limitations, assimilation of remotely sensed LAI data has been recently introduced in traditional watershed modeling practices [24,25,27,28,29,30].
The few recent studies which have assimilated remotely sensed LAI data in traditional watershed modeling practices invariably showed that better LAI representation improves model predictability [24,25,27,28,29,30]. Whereas these results promote a widespread use of remotely sensed LAI data in watershed modeling, we identified two major knowledge gaps that require targeted investigations:
(1)
Previous studies were predominantly focused on hydrologic processes [24,25,27,28,29]. Although studies involving water quality simulations evaluated the potential effect of improved LAI on sediment yield [30], the extent of such effects on nutrient (e.g., nitrate) loads—the most critical issue in agricultural watersheds from water quality management standpoint—is still unknown.
(2)
Evaluations conducted in the previous hydrologic studies were mostly limited to vertical water flux and storage simulations (e.g., evapotranspiration and soil moisture) [24,27,28,29], with very little emphasis on the watersheds’ cumulative response to downstream waters (i.e., streamflow) [25,30].
In this study, we intended to fill these knowledge gaps by assimilating Moderate Resolution Imaging Spectroradiometer LAI data (MODIS MCD15A3H) [31] into the Soil and Water Assessment Tool (SWAT) [21]. The specific objective of this study was to quantify the extent of improvements that the assimilation of MODIS LAI data would convey to streamflow, soil moisture, and nitrate load simulations at a daily timescale. Another unique contribution of our study was a new, highly efficient SWAT source code, which can perform multisource, multivariate assimilation of remotely sensed data regardless of watershed sizes and geolocations.

2. Methodology

We developed two contrasting model configurations to evaluate the effect assimilating MODIS LAI data on simulated streamflow, soil moisture, and nitrate load:
(1)
The basic model: LAI was simulated by the model based on input land use and associated biophysical parameters—a common approach in watershed modeling. This was our baseline to measure the degree of improvement in model results in the subsequent configuration.
(2)
The LAI assimilation model: The same setup as in the basic model, except MODIS LAI was directly inserted by replacing the simulated LAI values in each of the spatial units of the model (e.g., hydrologic response units or subbasins).
Our model testbed, the 16,860-km2 Cedar River Watershed (CRW; Figure 1), drains a major portion of eastern Iowa in the United States (Figure 1). This entire region has experienced increased flood frequency in the last two decades [32] as a result of climate and land use changes [33,34]. Studies have shown that this altered hydrologic dynamic is likely to continue in future years [35,36]. Furthermore, with more than 70% of the land area used for agricultural purposes (Figure 1a), CRW has long been noted as a water quality hotspot exporting large nitrate loads to the Mississippi River system [3,37]. Considering these challenges, CRW is frequently used as a testbed in watershed modeling and management studies [3,35,37,38,39].
Our modeling experiments were conducted using SWAT [21], which is a process-based, semidistributed tool capable of simulating landscape water balances, floods and droughts, nonpoint source water pollution, crop yield, and best management practices across different physiographic settings (see, e.g., [5,36,40,41,42,43]). Correspondingly, many previous studies addressing the heterogeneous water issues in Iowa watersheds applied SWAT as their primary research tool [3,35,37,38,39,44]. SWAT has also been used as the simulation tool in many data assimilation experiments (e.g., [7,8]). Therefore, our SWAT-based analyses to understand the effect of assimilating MODIS LAI data on hydrology and water quality simulations will have immediate applications-both to CRW and other agricultural watersheds worldwide.
In the following subsections, we describe the data and method used to set up the two contrasting model configurations (with and without MODIS LAI data assimilation) and the model calibration-verification procedure.

2.1. The Basic Model

The basic model configuration was based on the CRW model originally developed by Golden et al. [3]. The geospatial inputs, primarily weather, topography, land use, soil properties, and agricultural management data, required to setup the CRW model are summarized in Table 1. In short, a topographic analysis of flow direction and flow accumulation divided the CRW into 95 subbasins, with an average drainage area of ~176 km2. The original CRW model by Golden et al. [3] discretized the subbasins into 1860 Hydrologic Response Units (HRUs). However, to reflect the common modeling issues of limited data availability, model infidelity, and computational liability (e.g., [5,7,45]), we spatially discretized the CRW model at the subbasin level, meaning that subbasins were the smallest units of process simulation in our modeling experiments. As a result, each of the 95 subbasins functioned like a single HRU (hence, total 95 HRUs). This approach aggregated land use input data and spatially explicit information on crop types to the subbasin level, and therefore allowed us to assess the full potential of MODIS LAI data for minimizing these deficiencies in the LAI assimilation model.
Representation of landscape vegetation dynamics in our basic model configuration was based on a commonly followed semiempirical leaf development approach (e.g., [21,22,23]). Specifically, in our approach, the temporal variation of LAI was determined by plant/crop-specific biophysical parameters primarily related to heat units, radiation use efficiency, vapor pressure deficit, maximum canopy height, and input plantation and harvest schedules (for row crops) [21,22,23,24,25]. The spatial variation of these parameters, hence the spatial variability of LAI, was directly linked with the level of specificity in model’s land use representation [7]. Therefore, the best possible spatial representation of LAI in the basic model configuration was at the subbasin level.

2.2. The LAI-Assimilation Model

The LAI-assimilation model was the same as the basic model configuration, except with the integration of MODIS LAI data across the watershed. Following a well-accepted approach of earth data processing for watershed-scale modeling and analyses [7,8,9], we constructed representative LAI time series from the original gridded MODIS product. Briefly, we applied a recently developed semiautomatic web-based tool [51] to account for the heterogeneity in size, shape, and locations of any number of subbasins. The ~500-m-gridded four-day total LAI data (Table 1) [31] were first georeferenced and then assigned to respective subbasin(s) by taking an area-weighted average value from encompassing and/or intersecting MODIS grid(s). In the subsequent step, we performed a linear temporal interpolation (by averaging) [28] to transform the subbasin-level four-day total LAI values into a continuous daily LAI time series. We assimilated this spatially distributed and temporally continuous LAI data into our basic model configuration using a new SWAT source code. In each instance of simulation (days), our new source code applied the direct insertion approach (e.g., [24,25,30,52]) to replace the simulated LAI (Section 2.1) across all subbasins and all simulation time steps with the corresponding MODIS LAI data.
The new SWAT source code is an advanced version of the source code developed by Rajib et al. [7], which was initially equipped with the capacity to assimilate remotely sensed potential evapotranspiration (PET) data. In this study, we added additional features to this source code so that it was capable of assimilating both PET and LAI data simultaneously, thus allowing a holistic approach for improving SWAT’s process representations. To the best of authors’ knowledge, this is the first SWAT source-code with such functionalities.

2.3. Model Calibration

We followed an identical calibration protocol for both model configurations (basic and LAI- assimilation). The calibration length was four years (2009–2012), with a prior two-year initialization of model state (2007–2008). Both configurations were calibrated at daily time step, first using streamflow data at five gage stations throughout the watershed and then using nitrate load data at the watershed outlet (Figure 1b; Table 1). It was feasible to conduct our water quality calibration at daily time step because of the abundant in-situ nutrient concentration data in CRW [53,54]. To ensure compatibility with model simulations, we converted nitrate concentrations (mg/L) into nitrate loads (kg/day) using the corresponding daily average streamflow data (m3/s) as a multiplier (i.e., load = concentration × streamflow × 3600 × 24/1000) [3].
Both basic and LAI assimilation models used an identical set of 42 calibration parameters. We selected these calibration parameters from our previous CRW study [3]. These parameters represent hydrology and water quality (Table A1 and Table A2, respectively) while being indirectly related to vegetation dynamics. Although SWAT is relatively well equipped with many biophysical parameters and process conceptualizations that directly influence vegetation dynamics (e.g., maximum root depth, radiation use efficiency, stomatal conductance, day/nighttime thresholds of vapor pressure deficit) [7,55], other advanced watershed models are not [23,24,56]. Therefore, we excluded such parameters from our calibration [unlike previous studies, (e.g., [8,13]) to isolate the effects of MODIS LAI assimilation into the model and to maintain focus on our study’s hypothesis that assimilated LAI data can serve as a proxy for vegetation dynamics when limited (or completely absent) vegetation-related parameters and processes are available in watershed models.
We used Sequential Uncertainty Fitting version 2 (SUFI-2), which is a semiautomated calibration algorithm available inside SWAT-CUP calibration platform [57]. A weighted Kling-Gupta Efficiency (KGE) [8,58] was the objective function to measure the association between daily simulated and measured data at the stream gages. KGE decomposes Nash-Sutcliffe Efficiency and Mean Squared Error into a three-dimensional criteria space and finds out a Pareto front in terms of the shortest Euclidean distance [8,9]. KGE ranges from −∞ to 1. Model accuracy increases as KGE value moves closer to 1. To find the best parameter combination and hence the most optimal model state, SUFI-2 seeks the highest possible KGE value across all calibration locations.

2.4. Model Verification

We performed a series of tasks to assess the relative improvement of simulation accuracy between the two model configurations (with and without MODIS LAI data assimilation). These verification tasks include the following:
(1)
Assessments of hydrologic simulation:
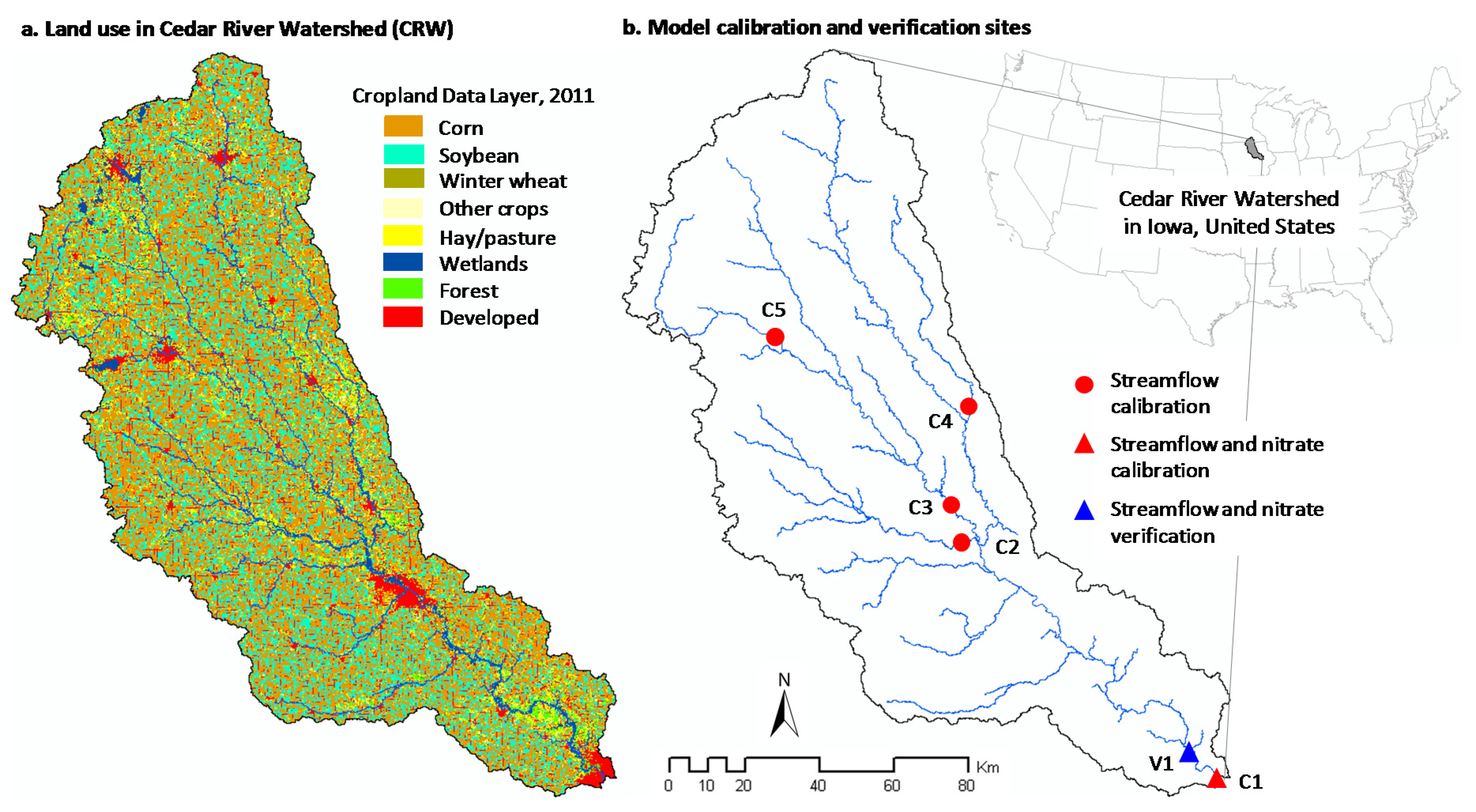
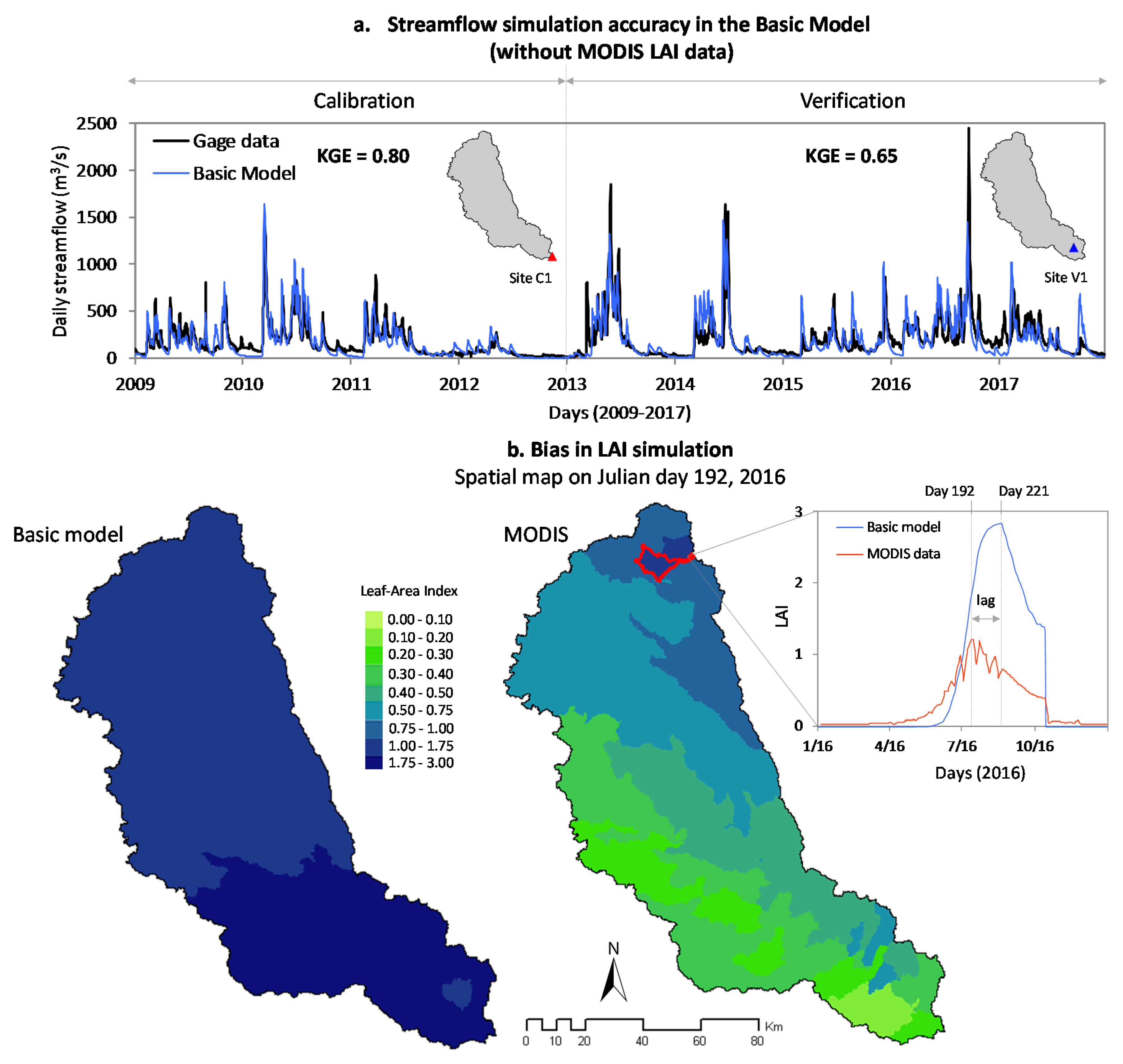
  • We assessed the accuracy of daily streamflow simulation for a five-year period (2013–2017) and at a separate gage station not included in the calibration process (for model verification) (Figure 1b).
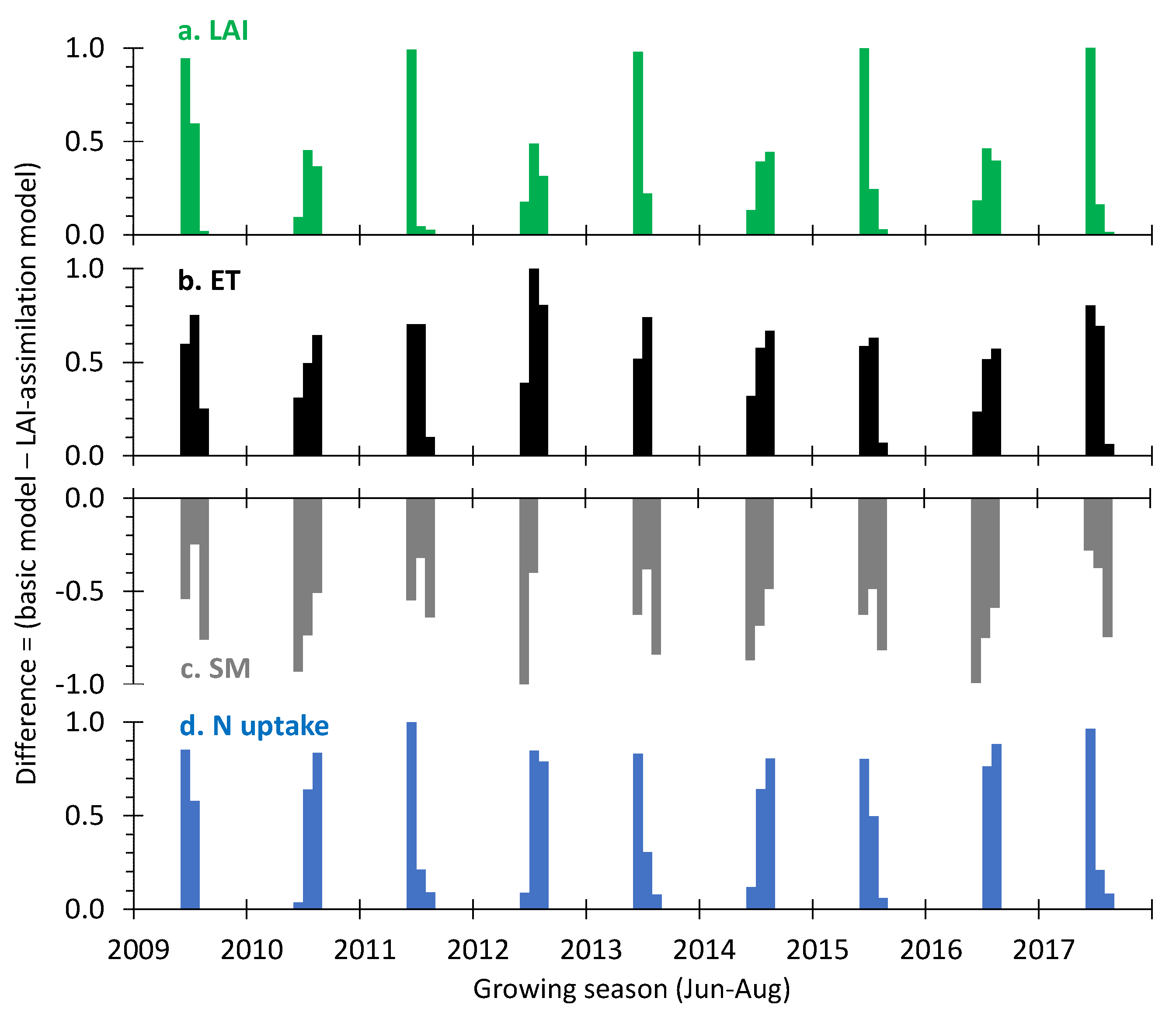
  • We then compared simulated LAI with MODIS data to identify how the calibrated models differ in their respective spatiotemporal representation of vegetation dynamics. For evaluating the spatial accuracy in LAI simulation, we considered specific day(s) in the 2016 crop growing season (June–August). We focused on crop growing season because this is the most active period in terms of vegetation growth and associated water-energy exchanges. We selected 2016 for temporal evaluation because this was a year with average precipitation, hence representative of the watershed’s general hydrologic response.
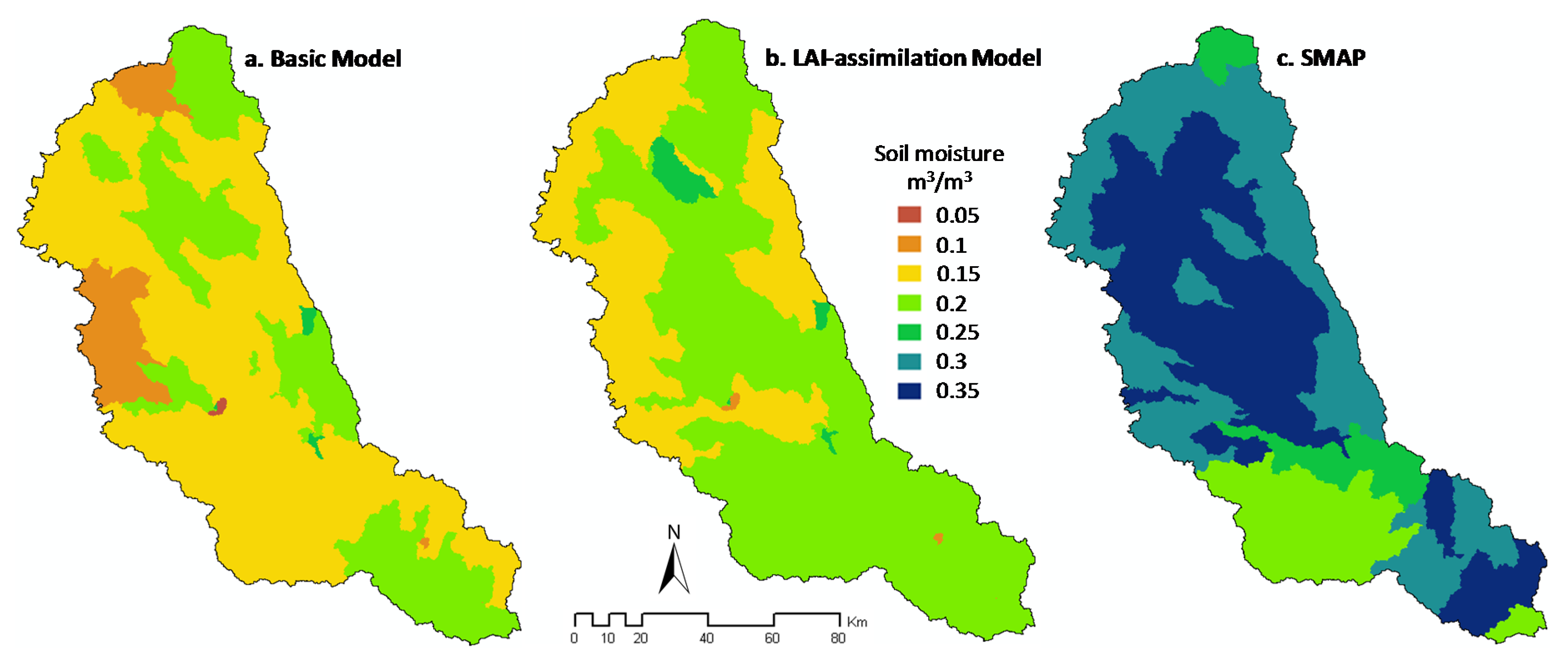
  • To further assess improvements in hydrologic simulation, we compared the spatial consistency of soil moisture between model simulations and Soil Moisture Active Passive (SMAP) mission level 4 estimates (Table 1). SMAP mission provides 9-km gridded estimates of rootzone soil moisture, which is a model-assimilated product of remotely sensed surface moisture observations [50]. Briefly, we produced subbasin-level aggregated SMAP data using the same web-based tool and areal averaging procedure described in Section 2.2, took the daily average of rootzone volumetric moisture content over the 2016 crop growing season (June–August), and subsequently generated a watershed soil moisture distribution map to enable spatial comparison with model outputs. We considered the same period for assessment of LAI and soil moisture as it would produce a consistent comparison across two mutually dependent processes. Furthermore, selecting summer months ensured that SMAP data used in our model assessments were not affected by snow cover and frozen soil—the common sources of inaccuracies in remotely sensed soil moisture [59].
(2)
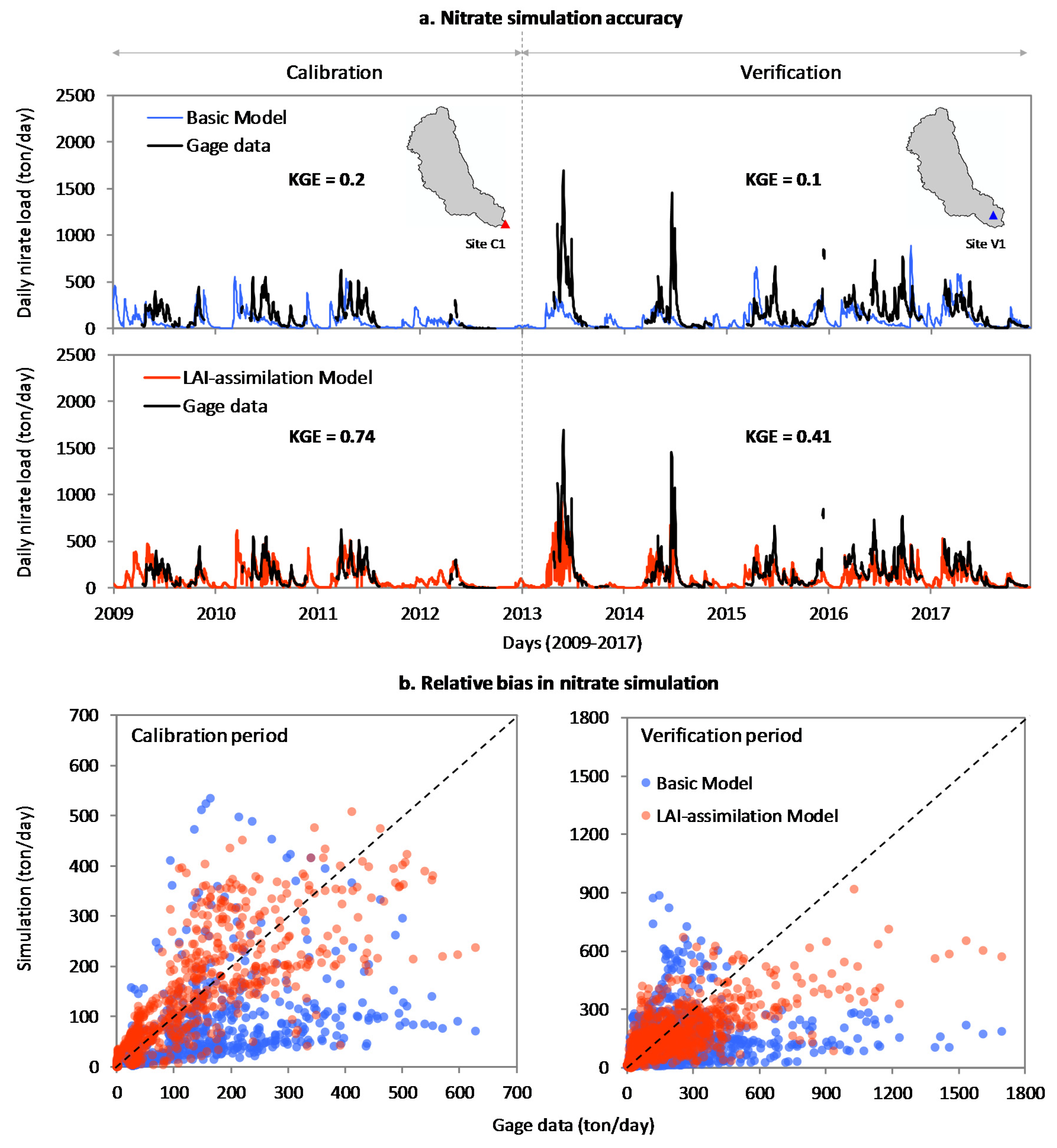
Assessment of water quality simulation:
We assessed the accuracy of daily nitrate load simulation for the same five-year period and at the same location used for streamflow verification (Figure 1b). To the best of our knowledge, this is the first study to verify the effect of LAI data assimilation on water quality simulations and that using long-term daily observations as the reference.

3. Results

3.1. Effect of LAI Data Assimilation on Hydrologic Simulation Accuracy

The basic model configuration simulated daily streamflow reasonably well (Figure 2a), with KGE = 0.8 at the watershed outlet and KGE ≥ 0.5 across all other locations (Table A2). However, such accuracy in streamflow simulation was obtained despite a poor representation of landscape vegetation dynamics. For example, simulated LAI in the basic model on a given day of the crop growing season showed little spatial variability across the watershed, differing substantially from the spatial variability of MODIS LAI data (Figure 2b). In addition to an overestimation tendency throughout the late spring and summer crop growing seasons, the temporal variability of MODIS LAI data was largely inconsistent with the basic model (time series comparison in Figure 2b; note the ~30-day lag between the respective occurrences of maximum LAI).
The LAI assimilation model increased streamflow simulation accuracy, with higher KGE values compared to the basic model at all locations (Table 2). We demonstrate this relative improvement in Figure 3 using the combined exceedance probability of streamflow at two outlet/near-outlet locations (i.e., based on a combined streamflow time series from the outlet calibration location, 2009–2012, and the near-outlet verification location, 2013–2017). Streamflow simulated by the LAI assimilation model was closer to gage data throughout the nine-year calibration-verification period (Figure 3a), with significantly improved accuracy across medium-to-low flow conditions (p < 0.05; Figure 3b). Whereas the LAI assimilation model produced improved streamflow in medium-to-high flow conditions as well, such improvements were not significant (p ≥ 0.05; Figure 3c).
The spatial pattern of rootzone soil moisture (Figure 4) afforded additional insights into how MODIS LAI data altered the model’s overall water balance. For example, despite the basic model’s reasonable accuracy in streamflow simulations, the spatial pattern of rootzone soil moisture in the model was largely inconsistent with SMAP data (comparing Figure 4a with Figure 4c). Compared to SMAP, this indicated an unrealistically “dry” condition across the watershed. However, after assimilating MODIS LAI data, the basic model showed increased spatial consistency with SMAP data, hence an overall improved water balance (comparing Figure 4b with Figure 4c).

3.2. Effect of LAI Data Assimilation on Water Quality Simulation Accuracy

The assimilation of LAI data produced considerable improvements in the model’s simulated nitrate loads (Figure 5). First, the LAI assimilation model could better reproduce the temporal variability of observed daily nitrate loads than the basic model (Figure 5a). This was also confirmed by increased KGE values (e.g., 0.20 versus 0. 74 and 0.10 versus 0.41, respectively, during calibration and verification). Second, daily nitrate loads simulated by the basic model showed noticeably large departures from gage nitrate data (1:1 line in Figure 5b). In comparison, the LAI assimilation model exhibited closer adherence to the 1:1 line, suggesting reduced bias in nitrate load simulations. Specifically, the basic model underestimated overall nitrate loads that the watershed conveyed to downstream waters. With improved LAI representation, the model reduced this bias by 47% and 17%, respectively, during the calibration (2009–2012) and verification (2013–2017) periods (Figure 5b).

4. Discussion

Our results suggest that traditional watershed modeling practices overlooking the physical realism of vegetation dynamics inadequately represent landscape water balance and nutrient loads at the daily timescale. Whereas the assimilation of remotely sensed LAI data can considerably improve hydrology and water quality simulations, three key questions remain: (1) What is the link between improved LAI data and improved model predictions? (2) Which LAI datasets are appropriate for watershed-scale modeling? and (3) What modeling factors are important to make LAI data assimilation efficient? We address these questions below.

4.1. What Is the Link between Improved LAI Data and Improved Model Predictions?

Although calibration results may indicate a high-performing model, misrepresentation of LAI drove the model state to a direction where the simulated water balance was not physically meaningful. Figure 6 explains this “pulling of model-state” [8,60] between the basic and LAI assimilation model configurations. Clearly, compared to the LAI assimilation model, higher LAI values in the basic model resulted into proportionally higher ET and lower soil moisture. The overestimation of ET was logical because higher LAI values mean lower canopy resistance (see Penman-Monteith equation in [21]), which subsequently improves the efficiency of aerodynamic processes by lowering the threshold for vapor and momentum transfers. Higher ET further indicates more water being depleted from the rootzone storage (Figure 6c), hence an unrealistic dry condition across the watershed (e.g., Figure 4). A dry rootzone explains why the basic model showed a significantly underestimated baseflow in the rivers (Figure 3a,b).
Higher LAI values in the basic model also led to higher plant nitrogen uptake, although nutrient input (i.e., fertilization; Table 1) was identical across the two model configurations. High nitrogen consumption by the vegetation resulted in smaller volumes of mineral nitrogen on the land surface, which caused the basic model to substantially (and inaccurately) underestimate nitrate loads in the rivers. The LAI assimilation model, despite being calibrated with the same reference datasets as the basic model, pulled the model state toward improved accuracy by decreasing ET, increasing soil moisture, and decreasing plant nitrogen uptake.

4.2. Which LAI Datasets Are Appropriate for Watershed-Scale Modeling?

Various multisource “fusion” LAI datasets have emerged in recent years, primarily combining the Advanced Very High-Resolution Radiometer (AVHRR) products with machine learning algorithms (e.g., AVH15C1, LAI3g, and GLASS) [61,62,63,64]. Some of these relatively new LAI datasets are available in daily timescale with short latency from present time (e.g., AVH15C1). Despite the potential high temporal resolution, almost all these datasets are available at coarse spatial resolutions (e.g., ~5 km for AVH15C1, LAI3g, and GLASS). Furthermore, studies that have assessed the quality of these relatively new datasets are still very limited. Whereas these emergent big data offer new opportunities for improved hydrology and water quality modeling at continental/global scales [28], the use of MODIS MCD15A3H LAI data [31] seems suitable for watershed-scale modeling given the reasonably high spatiotemporal resolution (~500 m; four-day total), continuous algorithm improvisations [14,65], and more importantly, well-documented quality assessments [14,66,67,68].

4.3. What Modeling Factors Are Important to Make LAI Data Assimilation Efficient?

The efficiency of any remote sensing-integrated watershed modeling approach largely depends on the interoperability between the model and remotely sensed data [69]. This interoperability is essentially a “big data problem” [7], defined in terms of the degree of automation in two fundamental tasks: (i) Processing a dataset such that it is fully compatible with a model’s geodatabase architecture, and (ii) seamlessly assimilating the processed dataset in spatiotemporal simulations. Previous studies which have showed the potential of assimilating remotely sensed LAI data in watershed models (e.g., [29,30]) did not exclusively address how these two tasks can be conducted in an interoperable (hence, efficient) way. We addressed this problem by developing a new model source code to perform task (ii) and by supplementing the source code with an open access companion tool [51] to perform task (i) (see Section 2.2). Thus, we implemented an interoperable MODIS-SWAT linkage, which made our approach highly efficient and reproducible regardless of watershed sizes and geolocations. Using our approach, SWAT modelers can efficiently assimilate MODIS LAI data without going through the learning curve of big data processing and model source code programming.

5. Summary

We applied a remote sensing-integrated watershed modeling approach assimilating MODIS LAI data across the 16,800-km2 Cedar River Watershed in Iowa, United States. We compared the two models, i.e., LAI assimilation configuration (with MODIS data) and basic configuration (with the model’s default semiempirical LAI representation), over a nine-year period and concluded the following:
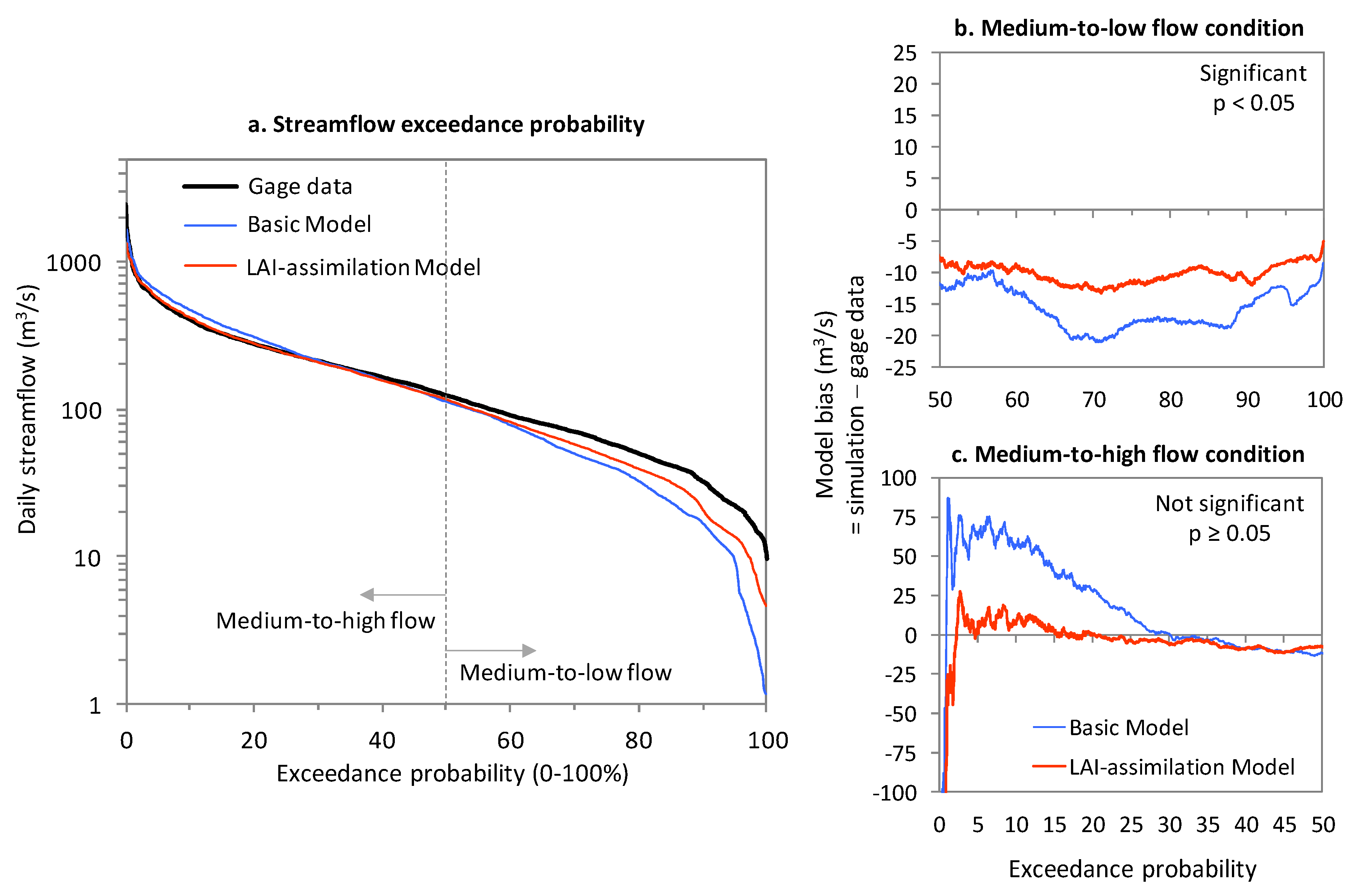
  • The basic model gave right answers for wrong reasons, with reasonably good daily streamflow simulation despite a large bias in LAI. The accuracy of daily streamflow simulation improved throughout the nine-year period. However, this improvement was significant during medium-to-low flow conditions.
  • The LAI assimilation model adopted a physically realistic water balance by increasing rootzone soil moisture storage, therefore improving the model’s spatial consistency with reference estimates (from the SMAP satellite mission).
  • Assimilation of LAI data into our watershed model substantially improved nitrate load simulations, reproducing long-term in-situ observations at a daily timescale. Our study is the first to show such an effect.
We also addressed conceptual and technical challenges associated with LAI assimilation in hydrology and water quality modeling. Conceptually, we disentangled how overestimation or underestimation of LAI cascades through watershed processes and how the model responds to it by partitioning hydrologic fluxes and nutrient pools. From a technical standpoint, we highlighted that high-quality remotely sensed global LAI datasets are becoming increasingly available. However, widespread community adoption of these emerging data resources will not be feasible without minimizing the lack of interoperability between remotely sensed big data and complex watershed models. By making SWAT model interoperable with a semiautomatic earth data processing tool, our study demonstrated how assimilation of LAI data in watershed models can be done efficiently regardless of watershed size and location. Our next step is to apply this efficient big data-driven modeling approach for watershed management decisions in various geophysical settings.

Author Contributions

A.R. developed the concept and conducted modeling experiments. H.E.G. and C.R.L. contributed to the early development of the models. S.V.K. provided expert opinion to articulate the narrative of the study. I.L.K. and Z.Y. assisted with MODIS data acquisition and data assimilation. S.J. helped with literature review. A.R. wrote the manuscript with contributions from H.E.G., C.R.L. and S.V.K. The views expressed in this article are those of the author(s) and do not necessarily represent the views or policies of the National Aeronautics and Space Administration (NASA) and U.S. Environmental Protection Agency (U.S. EPA). The U.S. EPA through the Office of Research and Development provided technical direction but did not collect, generate, evaluate, or use the environmental data described herein. All authors have read and agreed to the published version of the manuscript.

Software Availability

The modified SWAT source-code is available upon request.

Funding

This research was partially funded by the early career faculty startup grant from the Texas A&M University, Kingsville, TX, USA.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table
Table A1. Parameters included in the streamflow calibration of the Cedar River Watershed model. See supplementary information for the most optimal parameter values.
Table A1. Parameters included in the streamflow calibration of the Cedar River Watershed model. See supplementary information for the most optimal parameter values.
No.Parameter aDefinition bSpatial ScaleInitial Range c
1ALPHA_BFBaseflow recession constant (days)HRU0.001–1
2CH_K2Channel hydraulic conductivity (mm/h)Subbasin5–100
3CH_N1Tributary channel Manning’s nSubbasin0.001–0.15
4CH_N2Main channel Manning’s nSubbasin0.001–0.15
5OV_N Overland Manning’s nHRU0.12 d
6CN2Curve number (moisture condition II)HRU−0.08–0.08
7SURLAGSurface runoff lag coefficient (days)Basin0.05–10
8EPCOPlant uptake compensation factorHRU0.01–1
9ESCOSoil evaporation compensation factorHRU0.01–1
10GW_DELAYGroundwater delay (days)HRU−10–10
11GW_REVAPGroundwater “revap” coefficientHRU0.01–0.2
12GWQMNThreshold depth for return flow (mm H2O)HRU0.01–5000
13REVAPMNRe-evaporation threshold (mm H2O)HRU0.01–500
14RCHRG_DPDeep aquifer percolation fractionHRU0–1
15SOL_AWCAvailable soil water capacity (mm/mm)HRU−0.15–0.15
16SOL_KSoil hydraulic conductivity (mm/h)HRU−0.15–0.15
17TIMPSnow pack temperature lag factorBasin0–1
18SFTMPSnowfall temperature (°C)Basin0–5
19SMFMNMin snowmelt factor (mm H2O/°C-day)Basin0–10
20SMFMXMax snowmelt factor (mm H2O/°C-day)Basin0–10
21SMTMPSnowmelt base temperature (°C)Basin−2–5
a Each parameter, except CN2, SOL_AWC, SOL_K and GW_DELAY, was iterated such that the original value was replaced by a value from respective initial ranges. During every iteration, a value from GW_DELAY’s initial range was added to its original value; original value of CN2, SOL_AWC and SOL_K was multiplied by an adjustment factor (1 + a value from the initial range). b See Neitsch et al. [21] for detail description of these parameters. c Selection of parameters and their initial ranges were based on our previous study [3]. d Based on the calibration results of Hutchinson and Christiansen [37]; the value was assigned directly in the model without further iteration.
Table
Table A2. Parameters included in the nitrate calibration of the Cedar River Watershed model. See supplementary information for the most optimal parameter values a.
Table A2. Parameters included in the nitrate calibration of the Cedar River Watershed model. See supplementary information for the most optimal parameter values a.
No.Parameter aDefinition bSpatial ScaleInitial Range c
1SPCONLinear sediment routing factorBasin0.0081 d
2SPEXPExponent sediment routing factorBasin1 d
4CH_COV1Channel erodibility factorSubbasin0.22 d
3CH_COV2Channel cover factorSubbasin0.1 d
5PHOSKDPhosphorus soil partitioning coefficientBasin167 d
6PPERCOPhosphorus percolation coefficientBasin11.2 d
7SOL_ORGPInitial organic P conc. in soil layer (mg P/kg)HRU10 d
8SOL_ORGNInitial organic N conc. in soil layer (mg N/kg)HRU1–50
9SOL_NO3Initial NO3 concentration in soil layer (mg N/kg)HRU1–50
10SOL_CBNOrganic carbon content in soil layer (% weight)HRU0.05–10
11BIOMIXBiological mixing efficiencyHRU0.001–1
12CDNDenitrification exponential rateBasin0.001–3
13CMNMineralization rate of active N and PBasin0.001–0.003
14HLIFE_NGWHalf-life of nitrogen in ground water (days)Basin0–500
15NPERCONitrate percolation coefficientBasin0.001–1
16SDNCODenitrification threshold water contentBasin0.001–1.1
17ANION_EXCLFraction of porosity to exclude anionsBasin0.01–1
18BC1Biological oxidation rate (NH3) (day−1)Basin0.1–1
19BC2Biological oxidation rate (NO2-NO3) (day−1)Basin0.2–2
20BC3Biological oxidation rate (organic N-NH3) (day−1)Basin0.02–0.4
21RS4Organic N settling rate in the channel (day−1)Subbasin0.001–0.1
a Calibration of nitrate load was conducted separately, following the hydrology calibration. The gage stations (Figure 1b) provide in-situ estimates of nitrate plus nitrite as nitrogen (NO3-N + NO2-N). These estimates mainly represented NO3 in the stream because NO2 was not the dominant N species. See Golden et al. [3]. b Each parameter was iterated such that the original value was replaced by a value from respective initial ranges. See Neitsch et al. [21] for detail description of these parameters. c Selection of parameters and their initial ranges were based on our previous study [3]. d These parameters are related to sediment and phosphorus. Calibration of these parameters was not possible because of the unavailability of observed/estimated datasets. The values listed above were obtained from the calibration results of Hutchinson and Christiansen [37] and Wu and Liu [38] for a much larger watershed which included our study area. These values were therefore assigned directly in our Cedar River Watershed model without further iteration.

References

  1. Beven, K.J. Towards a Coherent Philosophy for Environmental Modelling. Royal Soc. 2002, 458, 2465–2484. [Google Scholar] [CrossRef] [Green Version]
  2. Ruddell, B.L.; Drewry, D.T.; Nearing, G.S. Information Theory for Model Diagnostics: Structural Error is Indicated by Trade-Off Between Functional and Predictive Performance. Water Resour. Res. 2019, 55, 6534–6554. [Google Scholar] [CrossRef]
  3. Golden, H.E.; Rajib, A.; Lane, C.R.; Christensen, J.R.; Wu, Q.; Mengistu, S.G. Non-floodplain Wetlands Affect Watershed Nutrient Dynamics: A Critical Review. Environ. Sci. Technol. 2019, 53, 7203–7214. [Google Scholar] [CrossRef] [PubMed]
  4. Rajib, A.; Ahiablame, L.; Paul, M. Modeling the effects of future land use change on water quality under multiple scenarios: A case study of low-input agriculture with hay/pasture production. Sustain. Water Qual. Ecol. 2016, 8, 50–66. [Google Scholar] [CrossRef] [Green Version]
  5. Du, L.; Rajib, A.; Merwade, V. Large scale spatially explicit modeling of blue and green water dynamics in a temperate mid-latitude basin. J. Hydrol. 2018, 562, 84–102. [Google Scholar] [CrossRef]
  6. Kunnath-Poovakka, A.; Ryu, D.; Renzullo, L.J.; George, B. Remotely sensed ET for streamflow modelling in catchments with contrasting flow characteristics: An attempt to improve efficiency. Stoch. Environ. Res. Risk Assess. 2018, 32, 1973–1992. [Google Scholar] [CrossRef]
  7. Rajib, A.; Merwade, V.; Yu, Z. Rationale and Efficacy of Assimilating Remotely Sensed Potential Evapotranspiration for Reduced Uncertainty of Hydrologic Models. Water Resour. Res. 2018, 54, 4615–4637. [Google Scholar] [CrossRef]
  8. Rajib, A.; Evenson, G.R.; Golden, H.E.; Lane, C.R. Hydrologic model predictability improves with spatially explicit calibration using remotely sensed evapotranspiration and biophysical parameters. J. Hydrol. 2018, 567, 668–683. [Google Scholar] [CrossRef]
  9. Rajib, A.; Merwade, V.; Yu, Z. Multi-objective calibration of a hydrologic model using spatially distributed remotely sensed/in-situ soil moisture. J. Hydrol. 2016, 536, 192–207. [Google Scholar] [CrossRef] [Green Version]
  10. Brocca, L.; Moramarco, T.; Melone, F.; Wagner, W.; Hasenauer, S.; Hahn, S. Assimilation of Surface- and Root-Zone ASCAT Soil Moisture Products into Rainfall Runoff Modeling. IEEE Trans. Geosci. Remote Sens. 2011, 50, 2542–2555. [Google Scholar] [CrossRef]
  11. Fang, H.; Liang, S. Leaf area index models. In Encyclopedia of Ecology; Fath, D., Ed.; Academic Press: Oxford, UK, 2008; pp. 2139–2148. [Google Scholar] [CrossRef]
  12. Demarty, J.; Chevallier, F.; Viovy, N.; Friend, A.D.; Piao, S.; Ciais, P. Assimilation of global MODIS leaf area index retrievals within a terrestrial biosphere model. Geophys. Res. Lett. 2007, 34, 1–6. [Google Scholar] [CrossRef]
  13. Nair, S.S.; King, K.; Witter, J.D.; Sohngen, B.L.; Fausey, N.R. Importance of Crop Yield in Calibrating Watershed Water Quality Simulation Tools1. JAWRA J. Am. Water Resour. Assoc. 2011, 47, 1285–1297. [Google Scholar] [CrossRef]
  14. Fang, H.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An Overview of Global Leaf Area Index (LAI): Methods, Products, Validation, and Applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar] [CrossRef]
  15. Qu, Y.; Zhuang, Q. Modeling leaf area index in North America using a process-based terrestrial ecosystem model. Ecosphere 2018, 9, e02046. [Google Scholar] [CrossRef] [Green Version]
  16. Ling, X.; Fu, C.; Guo, W.; Yang, Z.-L. Assimilation of Remotely Sensed LAI into CLM4CN Using DART. J. Adv. Model. Earth Syst. 2019, 11, 2768–2786. [Google Scholar] [CrossRef] [Green Version]
  17. Mokhtari, A.; Noory, H.; Vazifedoust, M. Improving crop yield estimation by assimilating LAI and inputting satellite-based surface incoming solar radiation into SWAP model. Agric. For. Meteorol. 2018, 2018, 159–170. [Google Scholar] [CrossRef]
  18. Ines, A.V.M.; Das, N.N.; Hansen, J.; Njoku, E.G. Assimilation of remotely sensed soil moisture and vegetation with a crop simulation model for maize yield prediction. Remote Sens. Environ. 2013, 138, 149–164. [Google Scholar] [CrossRef] [Green Version]
  19. Muñoz-Sabater, J.; Rüdiger, C.; Calvet, J.-C.; Fritz, N.; Jarlan, L.; Kerr, Y. Joint assimilation of surface soil moisture and LAI observations into a land surface model. Agric. For. Meteorol. 2008, 148, 1362–1373. [Google Scholar] [CrossRef] [Green Version]
  20. Barbu, A.L.; Calvet, J.-C.; Mahfouf, J.-F.; Albergel, C.; Lafont, S. Assimilation of Soil Wetness Index and Leaf Area Index into the ISBA-A-gs land surface model: Grassland case study. Biogeosciences 2011, 8, 1971–1986. [Google Scholar] [CrossRef] [Green Version]
  21. Neitsch, S.; Arnold, J.; Kiniry, J.; Williams, J. Soil & Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute Technical Report No. 406; Texas A&M University System: College Station, TX, USA, 2011; Available online: https://swat.tamu.edu/media/99192/swat2009-theory.pdf (accessed on 3 July 2020).
  22. Strauch, M.; Volk, M. SWAT plant growth modification for improved modeling of perennial vegetation in the tropics. Ecol. Model. 2013, 269, 98–112. [Google Scholar] [CrossRef]
  23. Alemayehu, T.; Van Griensven, A.; Woldegiorgis, B.T.; Bauwens, W. An improved SWAT vegetation growth module and its evaluation for four tropical ecosystems. Hydrol. Earth Syst. Sci. 2017, 21, 4449–4467. [Google Scholar] [CrossRef] [Green Version]
  24. Ford, T.W.; Quiring, S.M. Influence of MODIS-Derived Dynamic Vegetation on VIC-Simulated Soil Moisture in Oklahoma. J. Hydrometeorol. 2013, 14, 1910–1921. [Google Scholar] [CrossRef]
  25. Parr, D.; Wang, G.; Bjerklie, D. Integrating Remote Sensing Data on Evapotranspiration and Leaf Area Index with Hydrological Modeling: Impacts on Model Performance and Future Predictions. J. Hydrometeorol. 2015, 16, 2086–2100. [Google Scholar] [CrossRef]
  26. US Army Corps of Engineers. Hydrologic Modeling System User’s Manual Version 4.3; US Army Hydrologic Engineering Centre: Davis, CA, USA, 2018. Available online: https://www.hec.usace.army.mil/software/hec-hms/documentation/HEC-HMS_Users_Manual_4.3.pdf (accessed on 29 June 2020).
  27. Albergel, C.; Munier, S.; Leroux, D.J.; Dewaele, H.; Fairbairn, D.; Barbu, A.L.; Gelati, E.; Dorigo, W.; Faroux, S.; Meurey, C.; et al. Sequential assimilation of satellite-derived vegetation and soil moisture products using SURFEX_v8.0: LDAS-Monde assessment over the Euro-Mediterranean area. Geosci. Model Dev. 2017, 10, 3889–3912. [Google Scholar] [CrossRef] [Green Version]
  28. Kumar, S.V.; Mocko, D.M.; Wang, S.; Peters-Lidard, C.D.; Borak, J. Assimilation of Remotely Sensed Leaf Area Index into the Noah-MP Land Surface Model: Impacts on Water and Carbon Fluxes and States over the Continental United States. J. Hydrometeorol. 2019, 20, 1359–1377. [Google Scholar] [CrossRef]
  29. Zhang, X.; Maggioni, V.; Rahman, A.; Houser, P.; Xue, Y.; Sauer, T.; Kumar, S.; Mocko, D. The Influence of Assimilating Leaf Area Index in a Land Surface Model on Global Water Fluxes and Storages. Hydrol. Earth Syst. Sci. Discuss. 2019, 1–28. [Google Scholar] [CrossRef] [Green Version]
  30. Ma, T.; Duan, Z.; Li, R.; Song, X. Enhancing SWAT with remotely sensed LAI for improved modelling of ecohydrological process in subtropics. J. Hydrol. 2019, 570, 802–815. [Google Scholar] [CrossRef] [Green Version]
  31. Myneni, R.; Knyazikhin, Y.; Park, T. MCD15A3H MODIS/Terra+Aqua Leaf Area Index/FPAR 4-Day L4 Global 500m SIN Grid V006. 2015. Available online: https://lpdaac.usgs.gov/products/mcd15a3hv006/ (accessed on 29 June 2020).
  32. Mallakpour, I.; Villarini, G. The changing nature of flooding across the central United States. Nat. Clim. Chang. 2015, 5, 250–254. [Google Scholar] [CrossRef]
  33. Easterling, D.; Arnold, J.; Knutson, T.; Kunkel, K.; LeGrande, A.; Leung, L.; Vose, R.; Waliser, D.; Wehner, M.F. Precipitation. In Climate Science Special Report: Fourth National Climate Assessment, Volume I; Wuebbles, D.J., Fahey, D.W., Hibbard, K.A., Eds.; U.S. Global Change Research Program: Washington, DC, USA, 2017; pp. 207–230. Available online: https://science2017.globalchange.gov/chapter/7/ (accessed on 29 June 2020).
  34. Paul, M.; Rajib, A.; Ahiablame, L. Spatial and Temporal Evaluation of Hydrological Response to Climate and Land Use Change in Three South Dakota Watersheds. JAWRA J. Am. Water Resour. Assoc. 2016, 53, 69–88. [Google Scholar] [CrossRef]
  35. Wu, Y.; Liu, S.; Sohl, T.; Young, C.J. Projecting the land cover change and its environmental impacts in the Cedar River Basin in the Midwestern United States. Environ. Res. Lett. 2013, 8, 024025. [Google Scholar] [CrossRef]
  36. Rajib, A.; Merwade, V. Hydrologic response to future land use change in the Upper Mississippi River Basin by the end of 21st century. Hydrol. Process. 2017, 31, 3645–3661. [Google Scholar] [CrossRef]
  37. Hutchinson, K.; Christiansen, D. Use of the Soil and Water Assessment Tool (SWAT) for Simulating Hydrology and Water Quality in the Cedar River Basin, Iowa, 2000–10; U.S. Geological Survey Scientific Investigations Report 2013–5002; U.S. Geological Survey: Iowa City, IA, USA, 2013. Available online: https://pubs.usgs.gov/sir/2013/5002/ (accessed on 29 June 2020).
  38. Wu, Y.; Liu, S. Impacts of biofuels production alternatives on water quantity and quality in the Iowa River Basin. Biomass- Bioenergy 2012, 36, 182–191. [Google Scholar] [CrossRef]
  39. Le, L. Modeling Stream Discharge and Nitrate Loading in the Iowa-Cedar River Basin under Climate and Land Use Change. Ph.D. Thesis, University of Iowa, Iowa City, IA, USA, 2015. Available online: https://ir.uiowa.edu/etd/1872/ (accessed on 29 June 2020).
  40. Schuol, J.; Abbaspour, K.C.; Yang, H.; Srinivasan, R.; Zehnder, A.J. Modeling blue and green water availability in Africa. Water Resour. Res. 2008, 44, 1–18. [Google Scholar] [CrossRef] [Green Version]
  41. Schierhorn, F.; Faramarzi, M.; Prishchepov, A.V.; Koch, F.J.; Müller, D. Quantifying yield gaps in wheat production in Russia. Environ. Res. Lett. 2014, 9, 084017. [Google Scholar] [CrossRef]
  42. Rajib, A.; Golden, H.E.; Lane, C.R.; Wu, Q. Surface depression and wetland water storage improves major river basin hydrologic predictions. Water Resour. Res. 2020. [Google Scholar] [CrossRef]
  43. Rajib, A.; Liu, Z.; Merwade, V.; Tavakoly, A.A.; Follum, M.L. Towards a large-scale locally relevant flood inundation modeling framework using SWAT and LISFLOOD-FP. J. Hydrol. 2020, 581, 124406. [Google Scholar] [CrossRef]
  44. Ilampooranan, I.; Van Meter, K.J.; Basu, N.B. A Race Against Time: Modeling Time Lags in Watershed Response. Water Resour. Res. 2019, 55, 3941–3959. [Google Scholar] [CrossRef]
  45. Faramarzi, M.; Abbaspour, K.C.; Adamowicz, W.L.V.; Lu, W.; Fennell, J.; Zehnder, A.J.; Goss, G.G. Uncertainty based assessment of dynamic freshwater scarcity in semi-arid watersheds of Alberta, Canada. J. Hydrol. Reg. Stud. 2017, 9, 48–68. [Google Scholar] [CrossRef]
  46. US Geological Survey National Elevation Dataset (USGS-NED). National Map Viewer. Available online: http://viewer.nationalmap.gov/viewer/ (accessed on 10 October 2018).
  47. National Agricultural Statistics Service Cropland Data Layer (NASS-CDL), US Department of Agriculture CropScape. Available online: https://nassgeodata.gmu.edu/CropScape/ (accessed on 10 October 2018).
  48. Natural Resources Conservation Service. U.S. Department of Agriculture Soil Survey Staff. Available online: https://websoilsurvey.nrcs.usda.gov/ (accessed on 10 October 2018).
  49. Thornton, P.E.; Thornton, M.M.; Mayer, B.W.; Wei, Y.; Devarakonda, R.; Vose, R.S.; Cook, R.B. DAYMET: Daily Surface Weather Data on a 1-km Grid for North America, Version 3; ORNL DAAC: Oak Ridge, TN, USA, 2018. [Google Scholar] [CrossRef]
  50. Reichle, R.; De Lannoy, G.; Koster, R.D.; Crow, W.; Kimball, J.; Liu, Q. SMAP L4 Global 3-Hourly 9 km EASE-Grid Surface and Root Zone Soil Moisture Geophysical Data, Version 4; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2018. [CrossRef]
  51. Rajib, A.; Merwade, V.; Zhao, L.; Shin, J.; Smith, J.; Song, C. HydroGlobe Tool. 2018. Available online: https://mygeohub.org/resources/hydroglobetool (accessed on 9 June 2020).
  52. Meng, C.; Zhang, C.; Tang, R. Variational Estimation of Land–Atmosphere Heat Fluxes and Land Surface Parameters Using MODIS Remote Sensing Data. J. Hydrometeorol. 2013, 14, 608–621. [Google Scholar] [CrossRef]
  53. Kalkhoff, S.J. Transport of nitrogen and phosphorus in the Cedar River Basin, Iowa and Minnesota, 2000–2015. US Geol. Surv. 2018, 44. [Google Scholar] [CrossRef]
  54. Jones, C.; Davis, C.A.; Drake, C.W.; Schilling, K.E.; Debionne, S.H.; Gilles, D.W.; Demir, I.; Weber, L. Iowa Statewide Stream Nitrate Load Calculated Using In Situ Sensor Network. JAWRA J. Am. Water Resour. Assoc. 2017, 54, 471–486. [Google Scholar] [CrossRef]
  55. Holder, A.J.; Rowe, R.; McNamara, N.P.; Donnison, I.S.; McCalmont, J. Soil & Water Assessment Tool (SWAT) simulated hydrological impacts of land use change from temperate grassland to energy crops: A case study in western UK. GCB Bioenergy 2019, 11, 1298–1317. [Google Scholar] [CrossRef]
  56. Lin, P.; Rajib, A.; Yang, Z.-L.; Somos-Valenzuela, M.; Merwade, V.; Maidment, D.R.; Wang, Y.; Chen, L. Spatiotemporal Evaluation of Simulated Evapotranspiration and Streamflow over Texas Using the WRF-Hydro-RAPID Modeling Framework. JAWRA J. Am. Water Resour. Assoc. 2017, 54, 40–54. [Google Scholar] [CrossRef]
  57. Abbaspour, K.C. SWAT-CUP 2012: SWAT Calibration and Uncertainty Programs—A User Manual; Swiss Federal Institute of Aquatic Science and Technology: Dübendorf, Switzerland, 2015; Available online: http://swat.tamu.edu/media/114860/usermanual_swatcup.pdf (accessed on 9 June 2019).
  58. Gupta, H.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
  59. Reichle, R.H.; De Lannoy, G.J.; Liu, Q.; Ardizzone, J.V.; Colliander, A.; Conaty, A.; Crow, W.T.; Jackson, T.J.; Jones, L.A.; Kimball, J.S.; et al. Assessment of the SMAP Level-4 Surface and Root-Zone Soil Moisture Product Using In Situ Measurements. J. Hydrometeorol. 2017, 18, 2621–2645. [Google Scholar] [CrossRef]
  60. Efstratiadis, A.; Koutsoyiannis, D. One decade of multi-objective calibration approaches in hydrological modelling: A review. Hydrol. Sci. J. 2010, 55, 58–78. [Google Scholar] [CrossRef] [Green Version]
  61. Vermote, E. NOAA Climate Data Record (CDR) of AVHRR Leaf Area Index (LAI) and Fraction of Absorbed Photosynthetically Active Radiation (FAPAR), Version 5; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2019. [CrossRef]
  62. Claverie, M.; Matthews, J.L.; Vermote, E.F.; Justice, C.O. A 30+ Year AVHRR LAI and FAPAR Climate Data Record: Algorithm Description and Validation. Remote Sens. 2016, 8, 263. [Google Scholar] [CrossRef] [Green Version]
  63. Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.; Myneni, R. Global Data Sets of Vegetation Leaf Area Index (LAI)3g and Fraction of Photosynthetically Active Radiation (FPAR)3g Derived from Global Inventory Modeling and Mapping Studies (GIMMS) Normalized Difference Vegetation Index (NDVI3g) for the Period 1981 to 2011. Remote Sens. 2013, 5, 927–948. [Google Scholar] [CrossRef] [Green Version]
  64. Xiao, Z.; Liang, S.; Wang, J.; Chen, P.; Yin, X.; Zhang, L.; Song, J. Use of General Regression Neural Networks for Generating the GLASS Leaf Area Index Product from Time-Series MODIS Surface Reflectance. IEEE Trans. Geosci. Remote Sens. 2013, 52, 209–223. [Google Scholar] [CrossRef]
  65. Yan, K.; Park, T.; Yan, G.; Chen, C.; Yang, B.; Liu, Z.; Nemani, R.; Knyazikhin, Y.; Myneni, R. Evaluation of MODIS LAI/FPAR Product Collection 6. Part 1: Consistency and Improvements. Remote Sens. 2016, 8, 359. [Google Scholar] [CrossRef] [Green Version]
  66. Yan, K.; Park, T.; Yan, G.; Liu, Z.; Yang, B.; Chen, C.; Nemani, R.; Knyazikhin, Y.; Myneni, R. Evaluation of MODIS LAI/FPAR Product Collection 6. Part 2: Validation and Intercomparison. Remote Sens. 2016, 8, 460. [Google Scholar] [CrossRef] [Green Version]
  67. Yang, W.; Tan, B.; Huang, D.; Rautiainen, M.; Shabanov, N.; Wang, Y.; Privette, J.; Huemmrich, K.; Fensholt, R.; Sandholt, I.; et al. MODIS leaf area index products: From validation to algorithm improvement. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1885–1898. [Google Scholar] [CrossRef]
  68. Jiang, C.; Ryu, Y.; Fang, H.; Myneni, R.; Claverie, M.; Zhu, Z. Inconsistencies of interannual variability and trends in long-term satellite leaf area index products. Glob. Chang. Biol. 2017, 23, 4133–4146. [Google Scholar] [CrossRef] [PubMed]
  69. Kumar, S.; Peters-Lidard, C.; Tian, Y.; Houser, P.; Geiger, J.; Olden, S.; Lighty, L.; Eastman, J.; Doty, B.; Dirmeyeri, P.A.; et al. Land information system: An interoperable framework for high resolution land surface modeling. Environ. Model. Softw. 2006, 21, 1402–1415. [Google Scholar] [CrossRef]
Remotesensing 12 02148 g001 550
Figure 1. The 16,860-km2 Cedar River Watershed (CRW) in Iowa, United States. (a) Land use map showing the agriculture-dominated landscape in the CRW, and (b) U.S. Geological Survey (USGS) gage stations across the watershed used for model calibration and verification. The corresponding station IDs are as follows: C1 = 05464500, C2 = 05458900, C3 = 05462000, C4 = 05458000, C5 = 05459500, V1 = 05464420. Streamflow and nitrate data can be accessed from https://waterdata.usgs.gov/nwis using respective stations IDs.
Figure 1. The 16,860-km2 Cedar River Watershed (CRW) in Iowa, United States. (a) Land use map showing the agriculture-dominated landscape in the CRW, and (b) U.S. Geological Survey (USGS) gage stations across the watershed used for model calibration and verification. The corresponding station IDs are as follows: C1 = 05464500, C2 = 05458900, C3 = 05462000, C4 = 05458000, C5 = 05459500, V1 = 05464420. Streamflow and nitrate data can be accessed from https://waterdata.usgs.gov/nwis using respective stations IDs.
Remotesensing 12 02148 g001
Remotesensing 12 02148 g002 550
Figure 2. The basic model gave right answers for wrong reasons: (a) Reasonably good daily streamflow simulation despite (b) a large bias in LAI. The spatial maps correspond to a specific date when MODIS LAI peaked during the 2016 growing season (day 192). To focus on model’s temporal inconsistency, the time series correspond to a specific subbasin where simulated LAI and MODIS LAI showed minimum difference between their respective peak values relative to all other subbasins.
Figure 2. The basic model gave right answers for wrong reasons: (a) Reasonably good daily streamflow simulation despite (b) a large bias in LAI. The spatial maps correspond to a specific date when MODIS LAI peaked during the 2016 growing season (day 192). To focus on model’s temporal inconsistency, the time series correspond to a specific subbasin where simulated LAI and MODIS LAI showed minimum difference between their respective peak values relative to all other subbasins.
Remotesensing 12 02148 g002
Remotesensing 12 02148 g003 550
Figure 3. (a) Streamflow exceedance probability during 2009–2017 (Y flow being exceeded X percent of all days in the flow record) suggests improved streamflow simulation in the LAI assimilation model, as compared to gage data. (b,c) Statistical significance of changes in medium-to-low (streamflow exceedance 50–100%) and medium-to-high flow conditions (streamflow exceedance 0–50%), respectively, based on model bias.
Figure 3. (a) Streamflow exceedance probability during 2009–2017 (Y flow being exceeded X percent of all days in the flow record) suggests improved streamflow simulation in the LAI assimilation model, as compared to gage data. (b,c) Statistical significance of changes in medium-to-low (streamflow exceedance 50–100%) and medium-to-high flow conditions (streamflow exceedance 0–50%), respectively, based on model bias.
Remotesensing 12 02148 g003
Remotesensing 12 02148 g004 550
Figure 4. Comparison of daily average rootzone soil moisture across the 2016 crop growing season (June–August): (a) Basic model, (b) LAI assimilation model, and (c) SMAP data. The values represent wetness (m3/m3) in the top 100 cm of the soil profile.
Figure 4. Comparison of daily average rootzone soil moisture across the 2016 crop growing season (June–August): (a) Basic model, (b) LAI assimilation model, and (c) SMAP data. The values represent wetness (m3/m3) in the top 100 cm of the soil profile.
Remotesensing 12 02148 g004
Remotesensing 12 02148 g005 550
Figure 5. Effect of MODIS LAI data on the simulation of daily nitrate loads. (a) Improved accuracy as a result of assimilating MODIS LAI data. (b) The scatterplot shows the relative change of bias in the basic and LAI assimilation configurations separately for calibration and verification periods. Proximity to the 1:1 line indicates reduced bias relative to gage station in-situ nitrate data.
Figure 5. Effect of MODIS LAI data on the simulation of daily nitrate loads. (a) Improved accuracy as a result of assimilating MODIS LAI data. (b) The scatterplot shows the relative change of bias in the basic and LAI assimilation configurations separately for calibration and verification periods. Proximity to the 1:1 line indicates reduced bias relative to gage station in-situ nitrate data.
Remotesensing 12 02148 g005
Remotesensing 12 02148 g006 550
Figure 6. Bias in LAI (a) proportionally influenced the models’ partitioning of hydrologic fluxes (as suggested by evapotranspiration (ET) and soil moisture (SM) (b,c) and nutrient loads (as suggested by plant nitrogen uptake (d). The corresponding values (i.e., difference = basic model—LAI assimilation model) were normalized in a uniform scale (0–1) to show the proportional effect of LAI across different processes. To facilitate a focused assessment, only the growing season watershed average values were included for visualization.
Figure 6. Bias in LAI (a) proportionally influenced the models’ partitioning of hydrologic fluxes (as suggested by evapotranspiration (ET) and soil moisture (SM) (b,c) and nutrient loads (as suggested by plant nitrogen uptake (d). The corresponding values (i.e., difference = basic model—LAI assimilation model) were normalized in a uniform scale (0–1) to show the proportional effect of LAI across different processes. To facilitate a focused assessment, only the growing season watershed average values were included for visualization.
Remotesensing 12 02148 g006
Table
Table 1. Datasets used in the Cedar River Watershed (CRW) model.
Table 1. Datasets used in the Cedar River Watershed (CRW) model.
ItemDescription
Topography30-m National Elevation Dataset [46]
Land use30-m 2011 Cropland Data Layer [47]
Soil texture1:250,000 State Soil Geographic (STATSGO) dataset [48]
SlopeFive slope classes: 0–2%, 2–4%, 4–6%, 6–8%, >8% [3,39]
Subsurface drainageTile drains were assigned on low slope (<2%) with row crops and poorly drained soils (hydrologic soil group D) [3,37,38]
Agricultural management operations(a) Timing of plantation and harvest; (b) timing, type, rate, and place of fertilizer applications; (c) corn–soybean annual rotation [3,37]
PrecipitationTotal daily precipitation from 1-km gridded DAYMET product [49]
Energy-related weather forcingMinimum and maximum daily temperature from 1-km gridded DAYMET product [49]; solar radiation, wind speed and relative humidity from the historical weather generator within the SWAT source-code [21]; potential evapotranspiration (PET) estimated with built-in Penman-Monteith equation [21]
Streamflow and nitrate dataSix U.S. Geological Survey (USGS) gage stations; five for model calibration and one for model verification (Figure 1b)
Rootzone (100 cm) soil moisture dataSoil Moisture Active Passive (SMAP) mission 3-hourly L4 global 9-km rootzone soil moisture; used for model verification [50]
LAI dataMODIS MCD15A3H LAI/FPAR four-day L4 global 500 m v006 [31]; assimilated in the model replacing the model’s default LAI values
Table
Table 2. Evaluation of model performance in daily streamflow simulation. KGE = 1 means 100% agreement between simulated and reference data.
Table 2. Evaluation of model performance in daily streamflow simulation. KGE = 1 means 100% agreement between simulated and reference data.
Location aBasic ModelLAI-Assimilation Model
CalibrationC1b0.800.86
C20.840.85
C30.870.87
C40.500.51
C50.550.64
VerificationV10.650.72
aFigure 1b maps these locations across CRW’s stream network. b C1 is at the watershed outlet.

Share and Cite

MDPI and ACS Style

Rajib, A.; Kim, I.L.; Golden, H.E.; Lane, C.R.; Kumar, S.V.; Yu, Z.; Jeyalakshmi, S. Watershed Modeling with Remotely Sensed Big Data: MODIS Leaf Area Index Improves Hydrology and Water Quality Predictions. Remote Sens. 2020, 12, 2148. https://doi.org/10.3390/rs12132148

AMA Style

Rajib A, Kim IL, Golden HE, Lane CR, Kumar SV, Yu Z, Jeyalakshmi S. Watershed Modeling with Remotely Sensed Big Data: MODIS Leaf Area Index Improves Hydrology and Water Quality Predictions. Remote Sensing. 2020; 12(13):2148. https://doi.org/10.3390/rs12132148

Chicago/Turabian Style

Rajib, Adnan, I Luk Kim, Heather E. Golden, Charles R. Lane, Sujay V. Kumar, Zhiqiang Yu, and Saranya Jeyalakshmi. 2020. "Watershed Modeling with Remotely Sensed Big Data: MODIS Leaf Area Index Improves Hydrology and Water Quality Predictions" Remote Sensing 12, no. 13: 2148. https://doi.org/10.3390/rs12132148

APA Style

Rajib, A., Kim, I. L., Golden, H. E., Lane, C. R., Kumar, S. V., Yu, Z., & Jeyalakshmi, S. (2020). Watershed Modeling with Remotely Sensed Big Data: MODIS Leaf Area Index Improves Hydrology and Water Quality Predictions. Remote Sensing, 12(13), 2148. https://doi.org/10.3390/rs12132148

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop