3D Point Cloud Analysis for Damage Detection on Hyperboloid Cooling Tower Shells
Abstract
1. Introduction
1.1. Problem Statement
1.2. Related Work
- (1)
- reference planes;
- (2)
- point cloud processing, common in deformation monitoring applications;
- (3)
- local geometric features of surfaces of interest.
1.2.1. Reference Plane
1.2.2. Processed Point Clouds as in Deformation Monitoring Applications
1.2.3. Local Surface Geometric Properties
2. Materials
2.1. Test Cooling Tower
2.2. Experimental Data
- black and white Z+F Professional 6˝ targets centred and levelled over the monitoring network points (Figure 3b);
- 150 mm steel reference spheres with adapters for fixed, stable mounting, precision levelled (Figure 3c).
3. Methods
3.1. Overview of Research Methodology
3.2. Data Pre-Processing
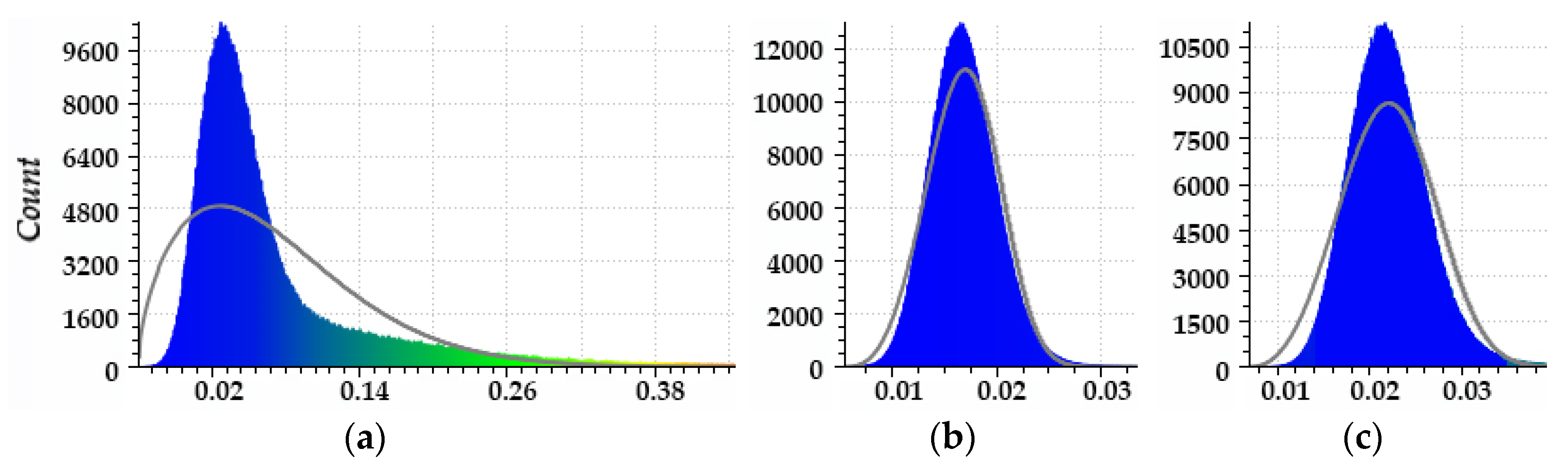
3.3. Curvature Estimation
3.4. Segmentation
| Algorithm 1: Point cloud segmentation based on curvature |
| Input: Point cloud P = p1,p2…, pn; Point curvatures C; Curvature threshold cth; Neighbour finding function F(∙) |
| Process: 1: Region list {R} ← ∅ 2: Available points list {L} ← {l..|P|} 3: While {L} is not empty do 4: Current region {Rc} ← ∅ 5: Current seeds {Sc} ← ∅ 6: Point with minimum curvature in {L} = Pmin 7: {Sc} ← {Sc} ∪ Pmin 8: {Rc} ← {Rc} ∪ Pmin 9: {L} ← {L} \ Pmin 10: For i = 0 to size ({Sc}) do 11: Find nearest neighbors of current seed point {Bc} ← F(Sc{i}) 12: For j = 0 to size ({Bc}) do 13: Current neighbor point Pj ← Bc{j} 14: If PjL and c{Pj} < cth then 15: {Sc} ← {Sc} ∪ Pj 16: {Rc} ← {Rc} ∪ Pj 17: {L} ← {L} \ Pj 18: End if 19: End for 20: End for 21: Global segment list {R} ← {R} ∪ {Rc} 22: End while 23: Return the global segment list {R} |
| Outputs: a set of homogeneous regions R = {Ri} |
3.5. Labelling
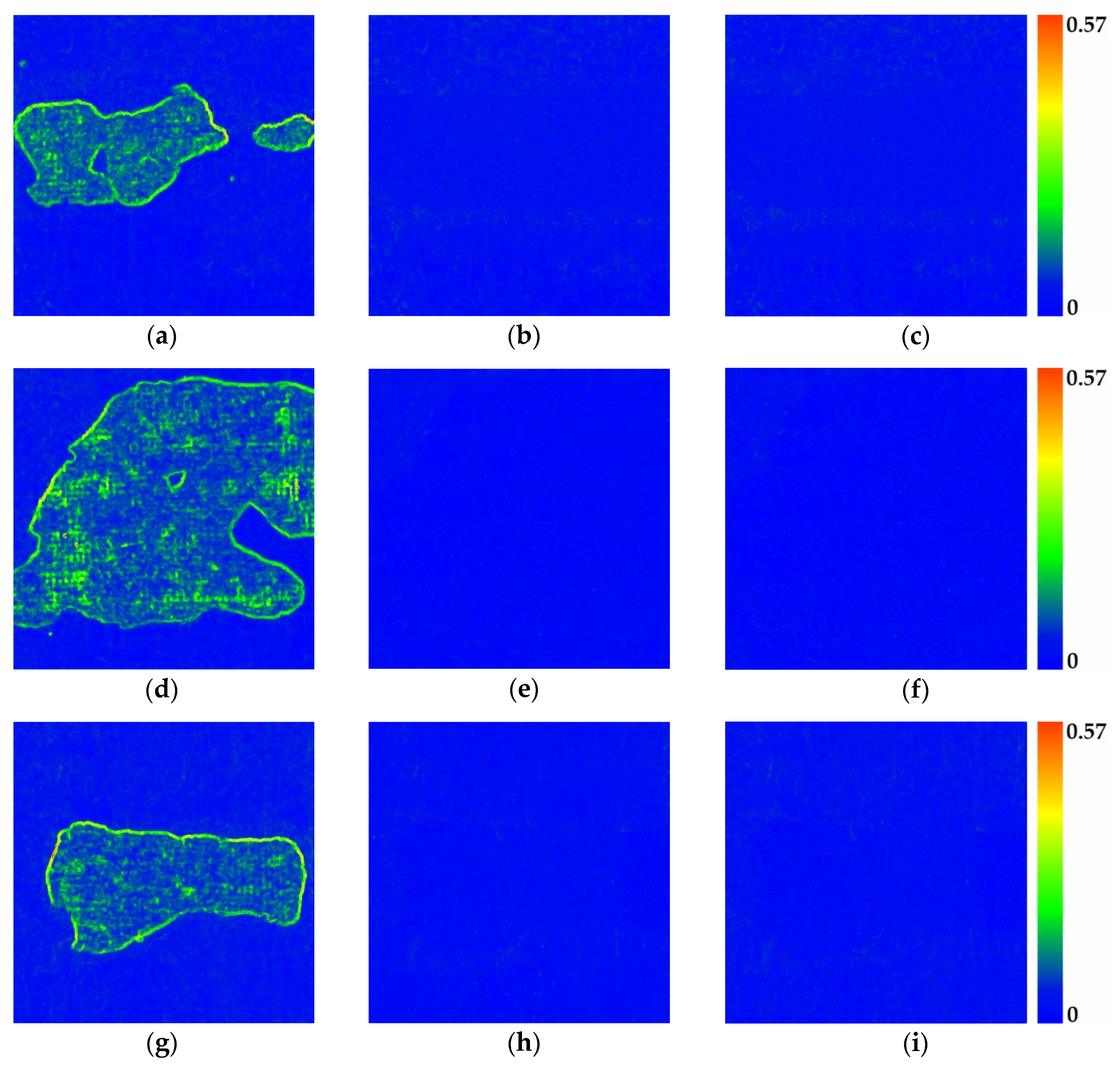
3.6. Defect Vectorisation
4. Results and Discussion
4.1. Experimental Results
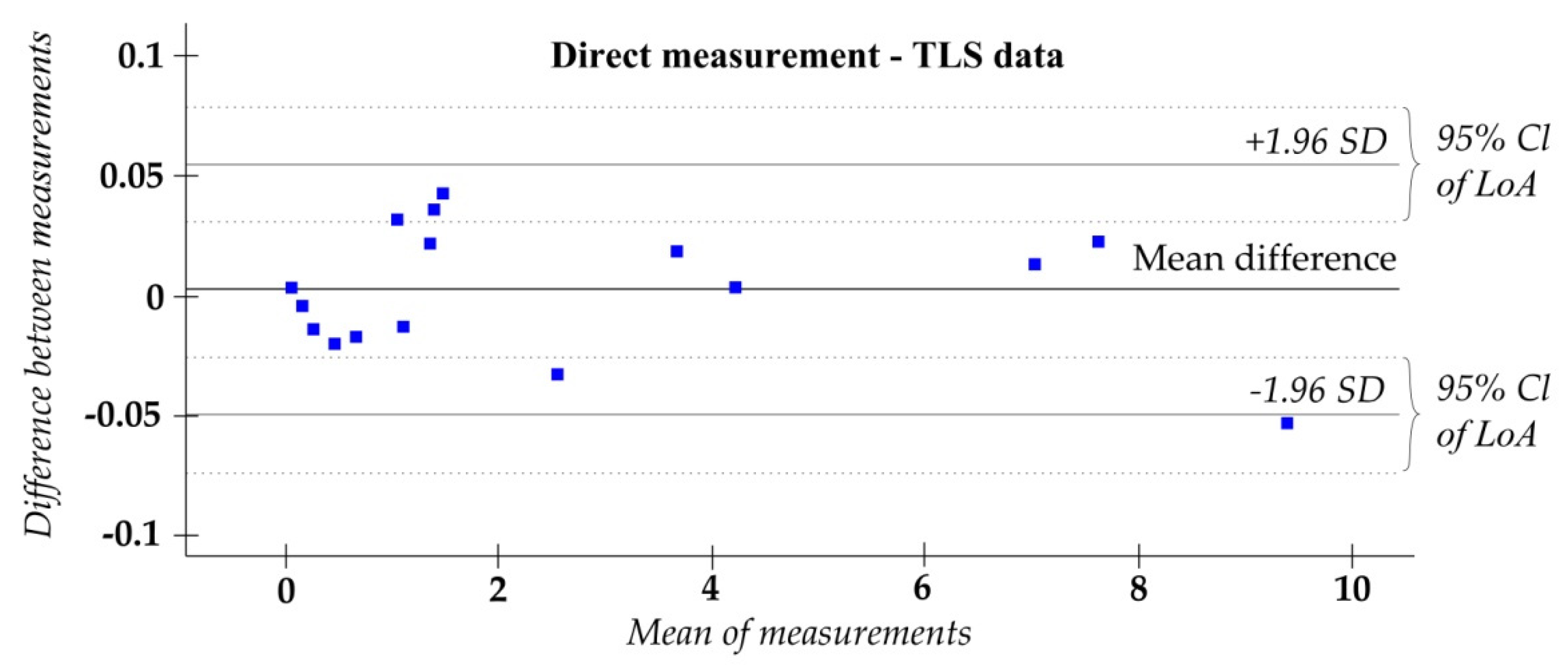
4.2. Evaluation Using Traditional Methods
4.3. Future Work
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bamu, P.C.; Zingoni, A. Damage, deterioration and the long-term structural performance of cooling-tower shells: A survey of developments over the past 50 years. Eng. Struct. 2005, 27, 1794–1800. [Google Scholar] [CrossRef]
- Konderla, P.; Kutyłowski, R.; Stefanek, K. Koncepcja wzmocnienia konstrukcji chłodni kominowej materiałem kompozytowym z matrycą cementową. [Concept for reinforcing the structure of a cooling tower with a cement matrix composite]. In Proceedings of the Construction Failures, 26th Scientific Conference, Szczecin-Miedzyzdroje, 21–24 May 2013; pp. 251–258. Available online: http://www.awarie.zut.edu.pl/files/ab2013/referaty/03_Diagnostyka_w_ocenie_bezpieczenstwa_konstrukcji/04_Konderla_P_i_inni_Koncepcja_wzmocnienia_konstrukcji_chlodni_kominowej_materialem_kompozytowym_z_matryca_cementowa.pdf (accessed on 15 January 2020).
- Etcheverry, L. Cooling Tower Repairs. Power 2004, 7–8, 17–18. Available online: http://www.chemistry.uoc.gr/demadis/pdfs/9-Scale%20Power%202004.pdf (accessed on 15 January 2020).
- Harte, R.; Krätzig, W.B.; Montag, U.; Petryna, Y.S. Damage, rehabilitation and residual life duration of natural draft cooling towers. VGB PowerTech 2005, 6, 61–65. Available online: https://www.vgb.org/en/pt_06_2005_e-p-10487.PDF (accessed on 15 January 2020).
- Zacharopoulou, A.; Zacharopoulou, E.; Batis, G. Statistics Analysis Measures Painting of Cooling Tower. Int. J. Corros. 2013, 1, 1–9. [Google Scholar] [CrossRef]
- Jawański, W.; Stefanek, K. Remonty chłodni kominowych—20 lat technologii firmy Sika w Polsce. [Cooling tower renovation. 20 years of Sika technology in Poland]. In Proceedings of the Construction Failures, 25th Scientific Conference, Szczecin-Miedzyzdroje, 24–27 May 2011, pp. 337–348. Available online: http://www.awarie.zut.edu.pl/files/ab2011/referaty/T1_03_Referaty_sponsorowane/01_Jawanski_W_i_inni_Remonty_chlodni_kominowych_20_lat_technologii_firmy_Sika_w_Polsce.pdf (accessed on 15 January 2020).
- Chung, H.W. Assessment and classification of damages in reinforced concrete structures. ConcrInt 1994, 16, 55–59. Available online: https://www.concrete.org/publications/internationalconcreteabstractsportal/m/details/id/4611 (accessed on 15 January 2020).
- Chmielewski, T.; Górski, P. O ocenie stanu technicznego chłodni kominowych. [On assessing the condition of cooling towers]. Prz. Bud. 2010, 81, 48–51. Available online: http://yadda.icm.edu.pl/baztech/element/bwmeta1.element.baztech-article-BTB2-0061-0068 (accessed on 15 January 2020).
- Kutyłowski, R. Diagnostyka Chłodni Kominowych. [Diagnostics of Cooling Towers]; Oficyna Wydawnicza Politechniki Wrocławskiej: Wrocław, Poland, 2013; pp. 5–136. [Google Scholar]
- Lechman, M.; Chruściel, W.; Lamenta, A. Program utrzymania z uwzględnieniem trwałości hiperboloidalnych chłodni kominowych po 30 latach eksploatacji. [Maintenance programme considering life expectancy for cooling towers after 30 years of service]. Prz. Bud. 2012, 5, 30–35. Available online: http://yadda.icm.edu.pl/baztech/element/bwmeta1.element.baztech-article-BTB6-0003-0036?q=bwmeta1.element.baztech-volume-0033-2038-przeglad_budowlany-2012-r__83_nr_5;5&qt=CHILDREN-STATELESS (accessed on 15 January 2020).
- Dubis, J.; Persona, M. Komputerowy system rejestracji, obróbki i przetwarzania parametrów z inwentaryzacji uszkodzeń chłodni kominowych. [Computer system for registering, treatment, and processing of parameters for cooling tower damage records]. Conf. Cool. Towers Eff. Prot. Repair Syst. 1991, 55–60. [Google Scholar]
- Kim, M.K.; Wang, Q.; Li, H. Non-contact sensing based geometric quality assessment of buildings and civil structures: A review. Autom. Constr. 2019, 100, 163–179. [Google Scholar] [CrossRef]
- Antoniszyn, K.; Hawro, L.; Konderla, P.; Kutyłowski, R. Wybrane problemy procesów modernizacji i remontów chłodni kominowych. [Selected issues with upgrading and repairing cooling towers]. Mater. Bud. 2016, 5, 24–25. [Google Scholar] [CrossRef]
- Mills, J.; Barber, D. An Addendum to the Metric Survey Specifications for English Heritage—The Collection and Archiving of Point Cloud Data Obtained by Terrestrial Laser Scanning or Other Methods; The Metric Survey Team: York, UK, 2003. [Google Scholar]
- Park, H.S.; Lee, H.M.; Adeli, H.; Lee, I. A New Approach for Health Monitoring of Structures: Terrestrial Laser Scanning. Comput. Aided Civ. Infrastruct. Eng. 2007, 22, 19–30. [Google Scholar] [CrossRef]
- Ioannidis, C.; Valani, A.; Georgopoulos, A.; Tsiligiris, E. 3D model generation for deformation analysis using laser scanning data of a cooling tower. In Proceedings of the 3rd IAG 12th FIG Symposium on Deformation Measurements, Baden, Austria; pp. 22–24. Available online: http://www.fig.net/commission6/baden_2006/ (accessed on 15 January 2020).
- Ioannidis, C.; Valani, A.; Soile, S.; Tsiligiris, E.; Georgopoulos, A. Alternative techniques for the creation of 3D models for finite element analysis—Application on a cooling tower. Proc. Opt. 3-D Meas. Tech. VIII Vol. II 2007. [Google Scholar] [CrossRef]
- Głowacki, T.; Grzempowski, P.; Sudoł, E.; Wajs, J.; Zając, M. The assessment of the application of terrestrial laser scanning for measuring the geometrics of cooling towers. Geomat. Landmanag. Landsc. 2016, 4, 49–57. [Google Scholar] [CrossRef]
- Piot, S.; Lançon, H. New Tools for the Monitoring of Cooling Towers. 6th European Workshop on Structural Health Monitoring. In Proceedings of the 6th European Workshop on Structural Health Monitoring, Germany, 2012. Available online: https://www.ndt.net/article/ewshm2012/papers/tu4b3.pdf (accessed on 15 January 2020).
- Camp, G.; Carreaud, P.; Lançon, H. Large Structures: Which Solutions for Health Monitoring? Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-5/W2, 137–141. [Google Scholar] [CrossRef]
- Laefer, D.F.; Truong-Hong, L.; Carr, H.; Singh, M. Crack Detection Limits in Unit Based Masonry with Terrestrial Laser Scanning. NDT&E Int. 2014, 62, 66–76. [Google Scholar] [CrossRef]
- Olsen, M.J.; Kuester, F.; Chang, B.J.; Hutchinson, T.C. Terrestrial laser scanning-based structural damage assessment. J. Comput. Civ. Eng. 2009, 24, 264–272. [Google Scholar] [CrossRef]
- Mosalam, K.M.; Shakhzod, M.; Park, S.T. Applications of laser scanning to structures in laboratory tests and field surveys. Struct. Control Health Monit. 2014, 21, 115–134. [Google Scholar] [CrossRef]
- Chen, S.E. Laser Scanning Technology for Bridge Monitoring. In Laser Scanner Technology; IntechOpen: London, UK, 2012; pp. 71–92. [Google Scholar] [CrossRef]
- Anil, E.B.; Akinci, B.; Garrett, J.H.; Kurc, O. Characterization of Laser Scanners for Detecting Cracks for Post-earthquake Damage Inspection. Proc. Int. Symp. Autom. Robot. Constr. Min. 2013, 313–320. [Google Scholar] [CrossRef]
- Reyno, T.; Marsden, C.; Wowk, D. Surface damage evaluation of honeycomb sandwich aircraft panels using 3D scanning technology. NDT&E Int. 2018, 97, 11–19. [Google Scholar] [CrossRef]
- Erkal, B.G.; Hajjar, J.F. Laser-based surface damage detection and quantification using predicted surface properties. Autom. Constr. 2017, 83, 285–302. [Google Scholar] [CrossRef]
- Teza, G.; Galgaro, A.; Moro, F. Contactless recognition of concrete surface damage from laser scanning and curvature computation. NDT&E Int. 2009, 42, 240–249. [Google Scholar] [CrossRef]
- Laefer, D.F.; Gannon, J.; Deely, E. Reliability of crack detection methods for baseline condition assessments. J. Infrastruct. Syst. 2010, 16, 129–137. [Google Scholar] [CrossRef]
- Tang, P.; Huber, D.; Akinci, B. Characterization of Laser Scanners and Algorithms for Detecting Flatness Defects on Concrete Surfaces. J. Comput. Civ. Eng. 2010, 25, 31–42. [Google Scholar] [CrossRef]
- Yoon, J.; Sagong, M.; Lee, J.S.; Lee, K. Feature extraction of a concrete tunnel liner from 3D laser scanning data. NDT&E Int. 2009, 42, 97–105. [Google Scholar] [CrossRef]
- Suchocki, C.; Błaszczak-Bąk, W. Down-Sampling of Point Clouds for the Technical Diagnostics of Buildings and Structures. Geosciences 2019, 9, 70. [Google Scholar] [CrossRef]
- Maalek, R.; Lichti, D.D.; Walker, R.; Bhavnani, A.; Ruwanpura, J.Y. Extraction of Pipes and Flanges from Point Clouds for Automated Verification of Pre-Fabricated Modules in Oil and Gas Refinery Projects. Autom. Constr. 2019, 103, 150–167. [Google Scholar] [CrossRef]
- Janowski, A.; Nagrodzka-Godycka, K.; Szulwic, J.; Ziolkowski, P. Remote sensing and photogrammetry techniques in diagnostics of concrete structures. Comput. Concr. 2016, 18, 405–420. [Google Scholar] [CrossRef]
- Armesto-González, J.; Riveiro Rodríguez, B.; González-Aguilera, D.; Rivas-Brea, M.T. Terrestrial laser scanning intensity data applied to damage detection for historical buildings. J. Archaeol. Sci. 2010, 37, 3037–3047. [Google Scholar] [CrossRef]
- Hancock, C.M.; Roberts, G.W.; Bisby, L.; Cullen, M.; Arbuckle, J. Detecting fire damaged concrete using laser scanning. Proc. FIG Work. Week 2012, 1–9. Available online: https://www.researchgate.net/publication/275581624_Detecting_Fire_Damaged_Concrete_Using_Laser_Scanning (accessed on 15 January 2020).
- Tsai, Y.C.J.; Li, F. Critical assessment of detecting asphalt pavement cracks under different lighting and low intensity contrast conditions using emerging 3D laser technology. J. Transp. Eng. 2012, 138, 649–656. [Google Scholar] [CrossRef]
- Xu, X.; Yang, H.; Neumann, I. Concrete Crack Measurement and Analysis Based on Terrestrial Laser Scanning Technology. Sens. Transducers 2015, 186, 168–172. [Google Scholar]
- Cho, S.; Park, S.; Cha, G.; Oh, T. Development of Image Processing for Crack Detection on Concrete Structures through Terrestrial Laser Scanning Associated with the Octree Structure. Appl. Sci. 2018, 8, 2373. [Google Scholar] [CrossRef]
- Tan, K.; Cheng, X. Correction of incidence angle and distance effects on TLS intensity data based on reference targets. Remote Sens. 2016, 8, 251. [Google Scholar] [CrossRef]
- Höfle, B.; Pfeifer, N. Correction of laser scanning intensity data: Data and model-driven approaches. ISPRS J. Photogramm. Remote Sens. 2007, 62, 415–433. [Google Scholar] [CrossRef]
- Yan, W.Y.; Shaker, A. Radiometric normalization of overlapping LiDAR intensity data for reduction of striping noise. Int. J. Digit. Earth 2016, 9, 649–661. [Google Scholar] [CrossRef]
- Kaasalainen, S.; Jaakkola, A.; Kaasalainen, M.; Krooks, A.; Kukko, A. Analysis of incidence angle and distance effects on terrestrial laser scanner intensity: Search for correction methods. Remote Sens. 2011, 3, 2207–2221. [Google Scholar] [CrossRef]
- López, M.; Martínez, J.; Matías, J.M.; Vilán, J.A.; Taboada, J. Application of a Hybrid 3D-2D Laser Scanning System to the Characterization of Slate Slabs. Sensors 2010, 10, 5949–5961. [Google Scholar] [CrossRef]
- Hildmann, H.; Kovacs, E. Review: Using Unmanned Aerial Vehicles (UAVs) as Mobile Sensing Platforms (MSPs) for Disaster Response, Civil Security and Public Safety. Drones 2019, 3, 59. [Google Scholar] [CrossRef]
- Kerle, N.; Nex, F.; Gerke, M.; Duarte, D.; Vetrivel, A. UAV-Based Structural Damage Mapping: A Review. ISPRS Int. J. Geo-Inf. 2020, 9, 14. [Google Scholar] [CrossRef]
- Morgenthal, G.; Hallermann, N. Quality Assessment of Unmanned Aerial Vehicle (UAV) Based Visual Inspection of Structures. Adv. Struct. Eng. 2014, 17, 289–302. [Google Scholar] [CrossRef]
- Na, W.S.; Baek, J. Impedance-Based Non-Destructive Testing Method Combined with Unmanned Aerial Vehicle for Structural Health Monitoring of Civil Infrastructures. Appl. Sci. 2017, 7, 15. [Google Scholar] [CrossRef]
- Yao, H.; Qin, R.; Chen, X. Unmanned Aerial Vehicle for Remote Sensing Applications—A Review. Remote Sens. 2019, 11, 1443. [Google Scholar] [CrossRef]
- Liu, W.; Chen, S.; Hauser, E. LiDAR-Based Bridge Structure Defect Detection. Exp. Tech. 2011, 35, 27–34. [Google Scholar] [CrossRef]
- Chen, X.; Li, J.A. Feasibility Study on Use of Generic Mobile Laser Scanning System for Detecting Asphalt Pavement Cracks. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B1, 545–549. [Google Scholar] [CrossRef]
- Kim, M.K.; Cheng, J.C.P.; Sohn, H.; Chang, C. A framework for dimensional and surface quality assessment of precast concrete elements using BIM and 3D laser scanning. Autom. Constr. 2014, 49, 225–238. [Google Scholar] [CrossRef]
- Law, D.W.; Silcock, D.; Holden, L. Terrestrial laser scanner assessment of deteriorating concrete structures. Struct. Control Health Monit. 2018, 25, 2156. [Google Scholar] [CrossRef]
- Jovančević, I.; Pham, H.; Orteu, J.; Gilblas, R.; Harvent, J.; Maurice, X.; Brethes, L. 3D Point Cloud Analysis for Detection and Characterization of Defects on Airplane Exterior Surface. J. Nondestruct. Eval. 2017, 36, 74. [Google Scholar] [CrossRef]
- Mizoguchi, T.; Koda, Y.; Iwaki, I.; Wakabayashi, H.; Kobayashi, Y.; Shirai, K.; Hara, Y.; Lee, H.S. Quantitative scaling evaluation of concrete structures based on terrestrial laser scanning. Autom. Constr. 2013, 35, 263–274. [Google Scholar] [CrossRef]
- Wang, M.; Tseng, Y.H. LIDAR data segmentation and classification based on octree structure. Proc. ISPRS Congr. 2004, 286–291. Available online: https://pdfs.semanticscholar.org/8523/d435f3d0772454fe7e2547ae0a51290bf59a.pdf (accessed on 15 January 2020).
- Von Hansen, W.; Michaelsen, E.; Thoennessen, U. Cluster analysis and priority sorting in huge point clouds for building reconstruction. Proc. Int. Conf. Pattern Recognit. 2006, 23–26. [Google Scholar] [CrossRef]
- Hoppe, H.; DeRose, T.; Duchamp, T.; McDonald, J.; Stuetzle, W. Surface Reconstruction from Unorganized Points. In Proceedings of the 19th Annual Conference on Computer Graphics and Interactive Techniques, 1992; pp. 71–78. Available online: http://hhoppe.com/recon.pdf (accessed on 15 January 2020).
- Pauly, M.; Gross, M.; Kobbelt, L.P. Efficient simplification of point-sampled surfaces. IEEE Vis. 2002, 163–170. [Google Scholar] [CrossRef]
- Rabbani, T.; van Den Heuvel, F.; Vosselmann, G. Segmentation of Point Clouds Using Smoothness Constraint. International Archives of Photogrammetry. Remote Sens. Spat. Inf. Sci. 2006, 36, 248–253. Available online: https://www.isprs.org/proceedings/XXXVI/part5/paper/RABB_639.pdf (accessed on 15 January 2020).
- Rusu, R.B. Semantic 3D Object Maps for Everyday Manipulation in Human Living Environments. Künstl. Intell. 2010, 24, 345–348. [Google Scholar] [CrossRef]
- Weinmann, M. Reconstruction and Analysis of 3D Scenes; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Ni, H.; Lin, X.; Ning, X.; Zhang, J. Edge Detection and Feature Line Tracing in 3D-Point Clouds by Analyzing Geometric Properties of Neighborhoods. Remote Sens. 2016, 8, 710. [Google Scholar] [CrossRef]
- CloudCompare. Available online: https://www.cloudcompare.org (accessed on 20 October 2019).
- Karhunen, J.; Joutsensalo, J. Generalizations of principal component analysis, optimization problems, and neural networks. Neural Netw. 1995, 8, 549–562. [Google Scholar] [CrossRef]
- Abdel-Qader, I.; Pashaie-Rad, S.; Abudayyeh, O.; Yehia, S. PCA-Based algorithm for unsupervised bridge crack detection. Adv. Eng. Softw. 2006, 37, 771–778. [Google Scholar] [CrossRef]
- Jollife, I.T. Principal Component Analysis; Springer: New York, NY, USA, 1986. [Google Scholar] [CrossRef]
- Shen, Y.; Lindenbergh, R.; Wang, J.; G. Ferreira, V. Extracting Individual Bricks from a Laser Scan Point Cloud of an Unorganized Pile of Bricks. Remote Sens. 2018, 10, 1709. [Google Scholar] [CrossRef]
- Maalek, R.; Lichti, D.D.; Ruwanpura, J.Y. Automatic Recognition of Common Structural Elements from Point Clouds for Automated Progress Monitoring and Dimensional Quality Control in Reinforced Concrete Construction. Remote Sens. 2019, 11, 1102. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhang, X. Estimating differential quantities from point cloud based on a linear fitting of normal vectors. Inf. Sci. 2009, 52, 431–444. [Google Scholar] [CrossRef]
- Vo, A.V.; Truong-Hong, L.; Laefer, D.F.; Bertolotto, M. Octree-based Region Growing for Point Cloud Segmentation. ISPRS J. Photogramm. Remote Sens. 2015, 104, 88–100. [Google Scholar] [CrossRef]
- Belton, D.; Lichti, D.D. Classification and segmentation of terrestrial laser scanner point clouds using local variance information. Proc. ISPRS Comm. V Symp. Image Eng. Vis. Metrol. 2006, 44–49. Available online: https://www.isprs.org/PROCEEDINGS/XXXVI/part5/paper/BELT_619.pdf (accessed on 15 January 2020).
- Morrison, D.F. Wielowymiarowa Analiza Statystyczna. [Multi-Dimensional Statistical Analysis]; Państwowe Wydawnictwo Naukowe: Warszawa, Poland, 1990. [Google Scholar]
- Bronsztejn, I.N.; Musiol, G.; Siemiendiajew, K.A. Nowoczesne Kompendium Matematyki. Nowoczesne Kompendium Matematyki [Modern Compendium of Mathematics]; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2017. [Google Scholar]
- Jaboyedoff, M.; Metzger, R.; Oppikofer, T.; Couture, R.; Derron, M.H.; Locat, J.; Durmel, D. New insight techniques to analyze rock-slope relief using DEM and 3D-imaging clouds points: COLTOP-3D software. In Rock Mechanics: Meeting Society’s Challenges and Demands; Taylor & Francis: Abingdon, UK, 2007; pp. 61–68. [Google Scholar] [CrossRef]
- Besl, P.J.; Jain, R.C. Segmentation through Variable-order Surface Fitting. IEEE Trans. Pattern Anal. Mach. Intell. 1988, 10, 167–192. [Google Scholar] [CrossRef]
- Poux, F.; Billen, R. Voxel-Based 3D Point Cloud Semantic Segmentation: Unsupervised Geometric and Relationship Featuring vs Deep Learning Methods. ISPRS Int. J. Geo-Inf. 2019, 8, 213. [Google Scholar] [CrossRef]
- Xu, Y.; Tuttas, S.; Hoegner, L.; Stilla, U. Voxel-based segmentation of 3D point clouds from construction sites using a probabilistic connectivity model. Pattern Recognit. Lett. 2018, 102, 67–74. [Google Scholar] [CrossRef]
- Wang, L.; Huang, Y.; Shan, J.; He, L. MSNet: Multi-Scale Convolutional Network for Point Cloud Classification. Remote Sens. 2018, 10, 612. [Google Scholar] [CrossRef]
- Vieira, M.; Shimada, K. Surface Extraction from Point-sampled Data through Region Growing. Int. J. CAD/CAM 2009, 5, 1–15. Available online: http://www.koreascience.or.kr/article/JAKO200503018236590.page (accessed on 15 January 2020).
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. Trans. 1951, 18, 293–297. Available online: http://www.barringer1.com/wa_files/Weibull-ASME-Paper-1951.pdf (accessed on 15 January 2020).
- Pu, S.; Vosselman, G. Automatic extraction of building features from terrestrial laser scanning. Proc. ISPRS Comm. V Symp. Image Eng. Vis. Metrol. 2006, 5–9. Available online: https://www.isprs.org/proceedings/XXXVI/part5/paper/1219_Dresden06.pdf (accessed on 15 January 2020).
- Samet, H.; Tamminen, M. Efficient Component Labeling of Images of Arbitrary Dimension Represented by Linear Bintrees. IEEE Trans. Pattern Anal. Mach. Intell. 1988, 10, 579–586. [Google Scholar] [CrossRef]
- Trevor, A.J.; Gedikli, S.; Rusu, R.B.; Christensen, H.I. Efficient organized point cloud segmentation with connected components. Semant. Percept. Map. Explor. 2013. Available online: https://cs.gmu.edu/~kosecka/ICRA2013/spme13_trevor.pdf (accessed on 15 January 2020).
- Poux, F.; Neuville, R.; Van Wersch, L.; Nys, G.-A.; Billen, R. 3D Point Clouds in Archaeology: Advances in Acquisition, Processing and Knowledge Integration Applied to Quasi-Planar Objects. Geosciences 2017, 7, 96. [Google Scholar] [CrossRef]
- De Berg, M.; Van Kreveld, M.; Overmars, M.; Schwarzkopf, O.C. Computational Geometry: Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Barber, C.B.; Dobkin, D.P.; Huhdanpaa, H. The Quickhull Algorithm for Convex Hulls. ACM Trans. Math. Softw. 1996, 22, 469–483. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. Biometrics 1945, 80–83. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef]
- Makuch, M. Application of Terrestrial Laser Scanning in the Process of Modernization of Hyperboloid Cooling Towers. Ph.D. Thesis, University of Agriculture in Krakow, Kraków, Poland, 21 March 2018. (In Polish). [Google Scholar]








| Step | Algorithm/Function | Parameters |
|---|---|---|
| 1: Data pre-processing | statistical outlier removal | k=20, 2σ |
| 2: Curvature estimation | principal component analysis, square root function | r=2rmin |
| 3: Segmentation | coefficient of variation, region growing | CVth = 30%, cth =0.02 |
| 4: Labelling | connected component labelling | o = 8, p = 10 |
| 5: Defect vectorization | convex hull | L = 0.01 m |
| Test Field | SERIES I | SERIES II | SERIES III | ||||||
|---|---|---|---|---|---|---|---|---|---|
| σ | CV | σ | CV | σ | CV | ||||
| 1: 50 m above ground | 0.029 | 0.024 | 83% | 0.021 | 0.005 | 24% | 0.022 | 0.006 | 27% |
| 2: 30 m above ground | 0.049 | 0.034 | 71% | 0.017 | 0.004 | 22% | 0.018 | 0.004 | 22% |
| 3: 10 m above ground | 0.031 | 0.021 | 68% | 0.018 | 0.004 | 22% | 0.020 | 0.005 | 25% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makuch, M.; Gawronek, P. 3D Point Cloud Analysis for Damage Detection on Hyperboloid Cooling Tower Shells. Remote Sens. 2020, 12, 1542. https://doi.org/10.3390/rs12101542
Makuch M, Gawronek P. 3D Point Cloud Analysis for Damage Detection on Hyperboloid Cooling Tower Shells. Remote Sensing. 2020; 12(10):1542. https://doi.org/10.3390/rs12101542
Chicago/Turabian StyleMakuch, Maria, and Pelagia Gawronek. 2020. "3D Point Cloud Analysis for Damage Detection on Hyperboloid Cooling Tower Shells" Remote Sensing 12, no. 10: 1542. https://doi.org/10.3390/rs12101542
APA StyleMakuch, M., & Gawronek, P. (2020). 3D Point Cloud Analysis for Damage Detection on Hyperboloid Cooling Tower Shells. Remote Sensing, 12(10), 1542. https://doi.org/10.3390/rs12101542






