1. Introduction
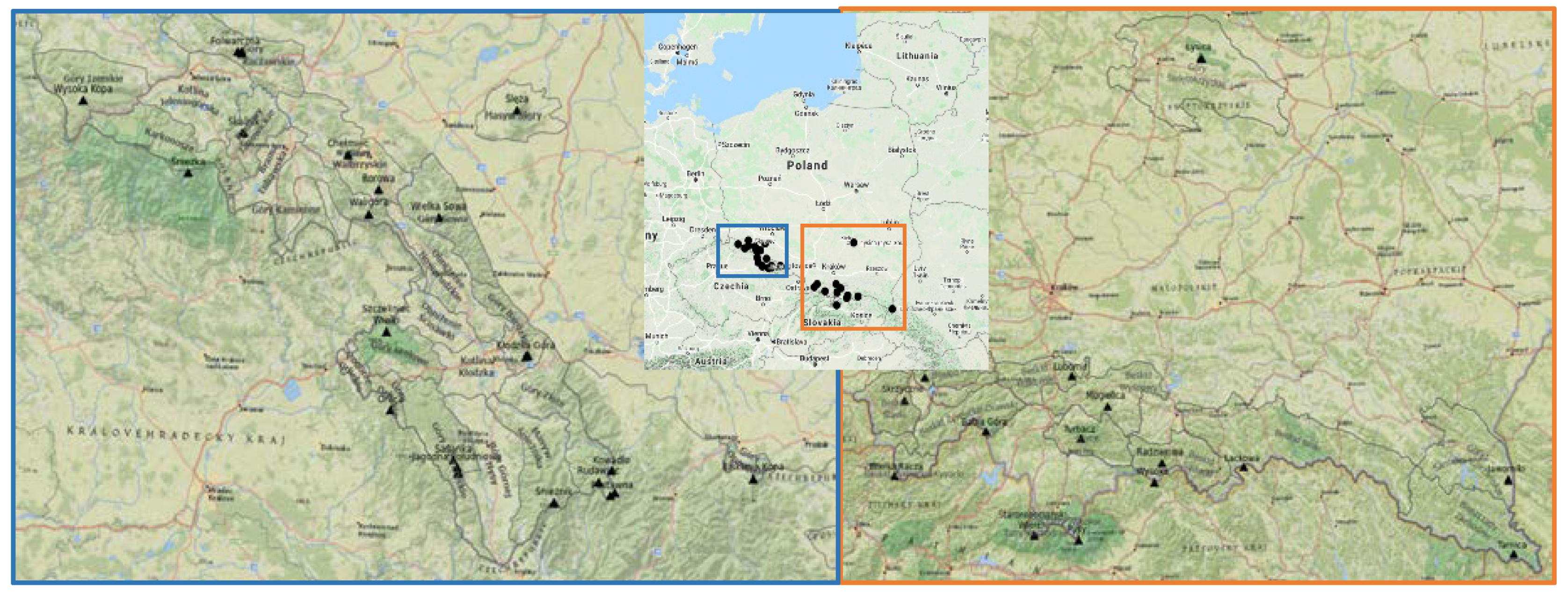
The Crown of Polish Mountains (CPM) is a list of the 28 highest peaks of the main mountain ranges (mesoregions) in Poland (
Figure 1). The concept of CPM was established in 1997 [
1]. Currently, the CPM club, a club bringing together Polish mountain enthusiasts, has over 40,000 members including over 2000 members who have summited all the 28 peaks listed (
https://kgp.info.pl/). The idea of verification of the height of the peaks included in the CPM list arose after verification of the height of two of the highest summits in Ukraine—the Hoverla and Pop Ivan peaks, where inaccuracies of up to several meters were also found [
2]. In addition, the analysis of available cartographic materials confirmed numerous inconsistencies related to the heights of mountain peaks.
Although the highest peaks of each range are frequently visited as mountain tourism destinations (e.g., Tarnica, Śnieżka or Babia Góra), in numerous materials we analyzed, including historical maps, current maps and guidebooks, and the Internet, significant discrepancies appeared, amounting to as much as several meters.
Figure 2 illustrates how the published height of Babia Góra has changed since the beginning of the 19
th century. The current height of this summit is listed as 1725 m a.s.l (above sea level). All heights in the article are shown in meters above sea level.
In addition, there is a lack of research in this area, especially for little-known and rarely frequented summits. As studies of the literature have shown, the most iconic and globally recognized peaks have already been thoroughly tested using same the GNSS technique that we used, such as Mount Everest [
4,
5,
6], Mont Blanc [
7], Aconcagua [
8] or Kilimanjaro [
9,
10]. Polish summits have also been measured in this way, but to a very limited extent; the only measurements conducted with geodetic receivers were of the peaks of Rysy [
11] and Śnieżka (
http://www.krkonose.eu/pl/aktuality/813/).
Therefore, in 2019 a project which was named ‘Setka w Koronie. Korona Gór Polski na 100-lecie AGH’ (100 in the Crown: The Crown of Polish Mountains on the 100-year anniversary of AGH University of Science and Technology in Kraków) was initiated. The aim of this project was the measurement and verification of the height of the highest peaks of individual mountain ranges in Poland using modern satellite measurement techniques.
2. Materials and Methods
2.1. Preparatory Work
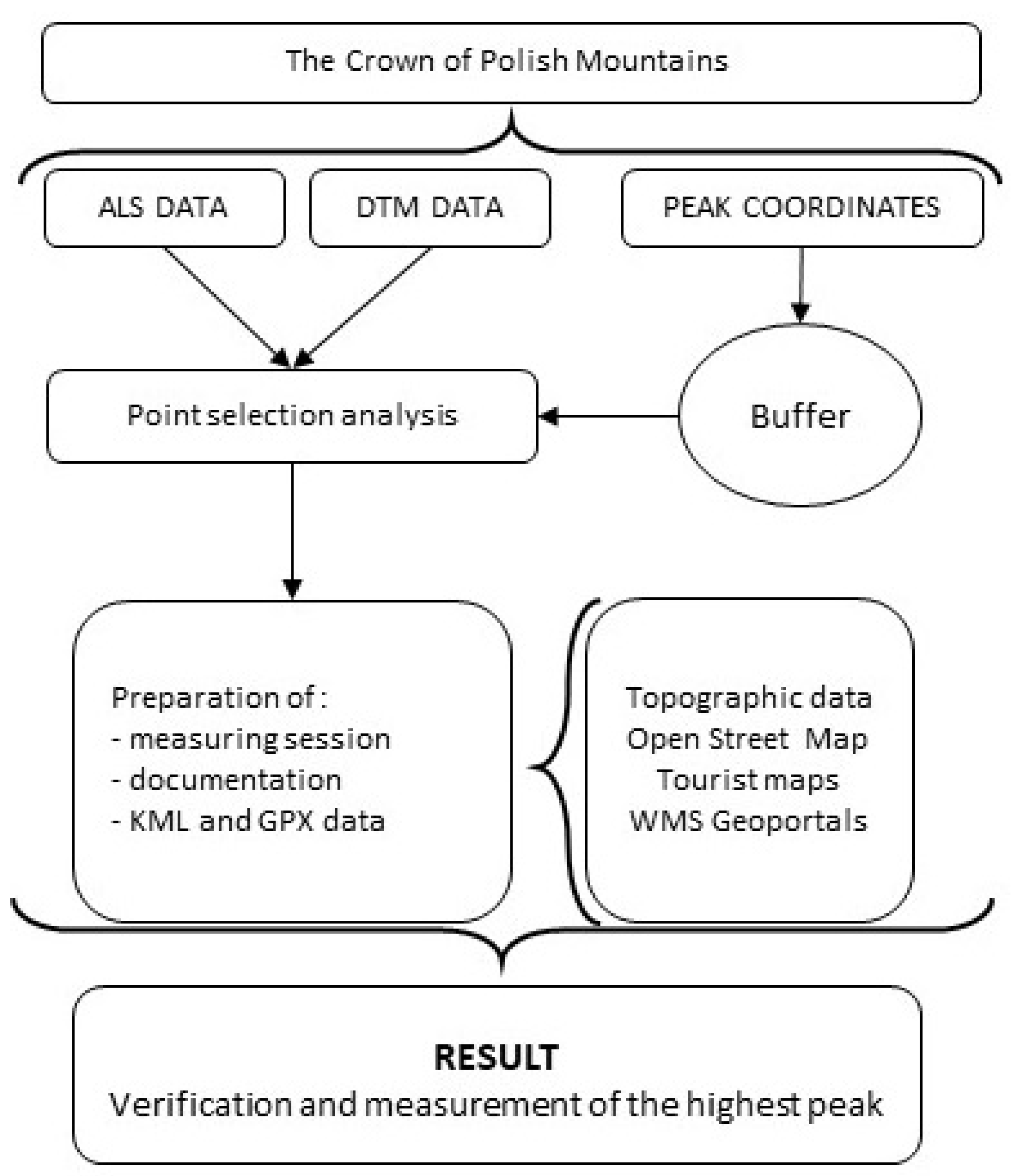
The project was implemented from May to December 2019. The objects of study were the 28 highest points on the CPM list. Based on the analysis of source materials, such as the DEM (digital elevation model), mountain forums, maps and guidebooks, as well as other sources, a list of potential peaks for height verification was determined. About 20 people participated in the measurements; a single measurement team usually consisted of 5–7 people, and more than 30 measurement expeditions were carried out in this way. The characteristics of the selected ranges and peaks had a huge impact on the course of the measurements. Some of the summits are located within national parks, which required the researchers to obtain the appropriate permits. During the implementation of the works, peaks believed to be potentially higher than their listed heights were identified. Ultimately (although there are only 28 peaks officially listed in the CPM), our measuring team verified the heights of 39 peaks. Techniques ensuring accuracy to within 10 cm, such as LIDAR (light detection and ranging) [
12] or drone measurements [
13], may provide the required accuracy, however, these techniques are susceptible to distortions due to resolution, weather conditions or plant cover. InSAR (synthetic aperture radar interferometry) is very accurate for testing relative height changes, though in the case of determining absolute values, it provides an accuracy only to within 1–2 m [
14]. Therefore, it was decided to conduct direct GNSS measurements in the field, using LIDAR data to determine the 2D position of the points considered to potentially be the highest and to determine their values. The highest points at the top of each peak were identified based on DEM analyses and data from aerial laser scanning obtained as part of the ISOK project (
https://www.isok.gov.pl/).
Figure 3 shows data and the workflow for a single peak analysis.
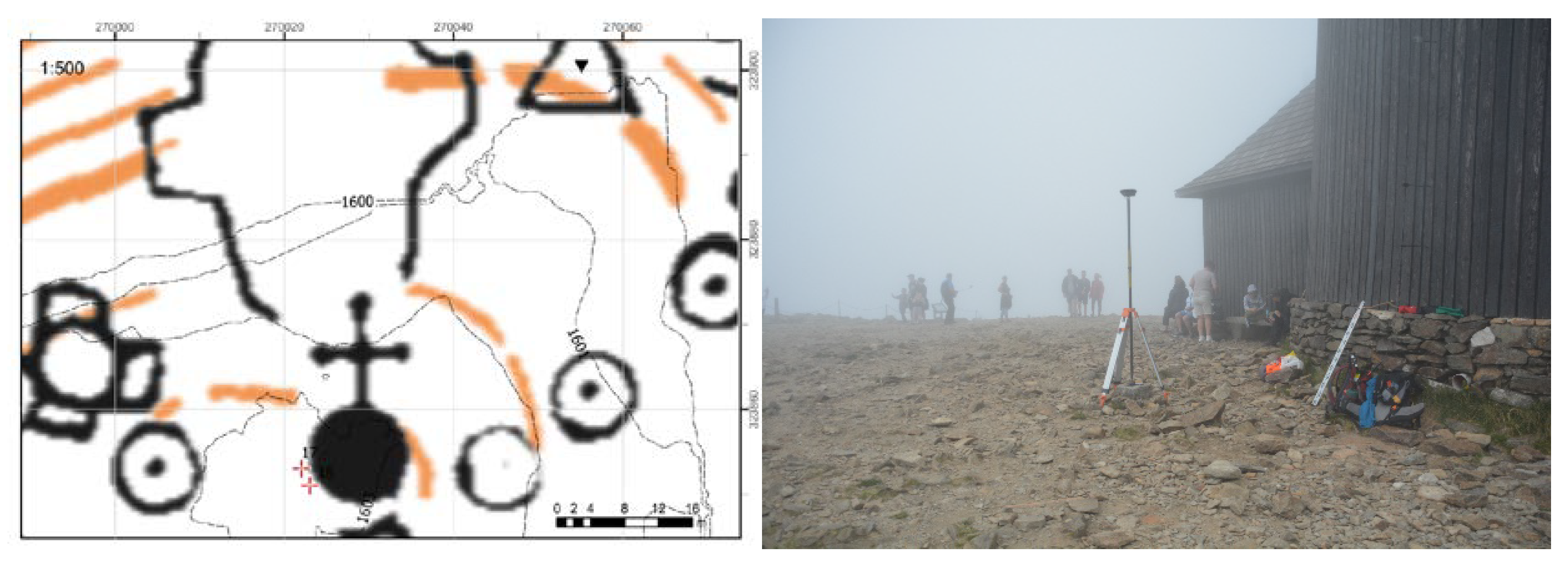
An example of such analysis and direct measurement in the field is shown in
Figure 4. Subsequently, we verified these data in the field during measurement.
2.2. GNSS Measurement
In most cases, the highest points of the peaks were clearly visible; in cases of doubt, we checked these points with a leveler, assessing differences between points which were believed to potentially be the highest. Then, we proceeded to GNSS measurement with a Leica GS16 receiver. We started with RTK using ASG-EUPOS corrections (
http://www.asgeupos.pl/), and three 30-s measurements (final height was determined as the average of these measurements) with re-initialization as a precise (ambiguity fix) solution, ensuring accuracy to within 5 cm. In cases when a precise RTK solution at the peak was not available, we conducted an hour-long static GNSS measurement with a 1-s measurement interval. As a reference, we adopted the nearest 2-4 ASG-EUPOS reference stations located closer than 100 km. At many peaks, the GNSS measurement was carried out not at the highest point (due to large aerial obstacles), but in points with good visibility of the sky. In such cases, the height was transferred by geometrical leveling. The adopted measurement methodology allowed for accuracy on the order of single centimeters to be obtained, but we decided that for the final heights an accuracy to within 10 cm would be sufficient. This level of accuracy proved to be fully sufficient; in practice, the heights of mountains are usually published with a 1 m accuracy. In several cases, the difference between the published and measured heights of the highest peaks was less than 1 m (e.g., Łysica and Skała Agaty in the Świętokrzyskie Mountains). Static observations were post-processed in Leica Geo Office using IGS final orbits; then we determined normal heights using the height anomaly from the PL-geoid-2011 quasi-geoid model on the WGS-84 ellipsoid [
15]. In the case of RTK measurements, normal heights were determined directly based on the abovementioned model. The published results are given according to the Kroonstadt 86 national height reference system, in this particular case PL-KRON86-NH [
16]. In the territory of current-day Poland, the first leveling networks were established in the 1870s, when Poland did not exist as an independent state due to its occupation by foreign powers during the period known as the Partitions and its territory was divided between three countries: Austria, Prussia and Russia. The peaks listed in the CPM are located in areas which at that time belonged to two of these powers, Austria and Prussia. At that time, height systems in Austrian and Prussian lands were related to the level of two seas [
17]: the Adriatic in the Austrian partition (as measured at Trieste) and the North Sea in the Prussian partition (as measured at Amsterdam). The differences used in this manuscript between Kroonstad-Trieste tide-gauges is 48 cm and Kroonstad-Amsterdam −14 cm, respectively [
18]. After WWI, the reference point used in Poland was the tide-gauge in Amsterdam, while after WWII in the 1950s, there was a transition to a national height system referenced to the Kroonstad tide-gauge. Therefore, the differences arising from the use of different height reference systems could have had a significant impact only on the peaks located within the Austrian partition before 1918 (referenced to the Kroonstad-Trieste tide-gauge with a 48 cm difference). In the interwar years and after WWII up until the 1950s, these differences amounted to at most at a dozen centimeters.
2.3. LIDAR Analyses
The analysis of data seeking to identify the potentially highest point at the peak was based on data from a Polish project called ISOK [
19] based on ALS (airborne laser scanning) measurements. The following products are available as part of the ISOK project:
- -
laser cloud points:
- -
density 4 pts/m2 or 6 pts/m2
- -
density 12 pts/m2 for the urban zones
- -
DTM GRID size 1.0 m
- -
DTM GRID size 0.5 m (only for 12 pts/m2)
The digital terrain model (DTM) obtained as part of the ISOK project was generated from LIDAR points as lying on the ground, as well as points in areas under water. This means that the process of filtering the remaining points (vegetation, buildings and other objects above ground level) was highly demanding. To fill in areas that were devoid of point cloud data, appropriate interpolation was performed. A numeric terrain model was developed in the PL-1992 coordinate system and the PL-KRON86-NH height system and was translated into WGS-84 geodetic coordinates (latitude and longitude. This was stored in two formats: ASCII (XYZ coordinates) and Esri GRID (ArcInfo ASCII GRID format). After obtaining the ALS and DTM data in accordance with the above-mentioned standards, analyses aimed at finding the highest points were carried out. According to research on the differences between different interpolation methods, the difference between ALS and DTM was smaller than the difference between GNSS measurement, influenced by various factors [
19,
20,
21,
22,
23,
24,
25]. In the comparisons made between the values from the DEM model and the measurements from ASL for the designated points, the differences between the field research and the DTM analysis were puzzling. As a result of the analyses, a set of highest points was obtained for each peak. Results of the analysis were obtained for 52 points, and their mean absolute deviation between ALS and DTM was 0.04 m, while the maximum difference was 0.22 m for the Ostra Mała peak (resulting from a few rocks located on the peak). For this reason, there was no indication whether the data was taken to the highest possible points at the peak from ALS or DTM (assumed resulting accuracy was 0.1 m). In
Table 1 and
Table 2, column H
D contains height values obtained from DTM analysis, columns ΔH
A–D (
Table 1) and column ΔH
N–D (
Table 2) contain values indicating the discrepancy between the measurement results and the result of the DTM analysis. The discrepancies between these values are quite significant, ranging from −4.2 m (Śnieżnik,
Table 1) to +2.4 m (Okole,
Table 2). In the case of negative differences, this is a fairly obvious problem arising from the qualification of low vegetation as ground points, or the classification of artificial embankments as soil elements. In the case of positive differences, the most likely factor affecting the result is the impact of dense stands of vegetation and soil cover at the top of the mountain [
26,
27,
28,
29].
3. Results
Table 1 summarizes all 28 CPM summits, including the heights obtained from the authors’ own measurements (H
A), from the CPM (H
C), TM websites (H
T) and DTM data (H
D), together with the differences between our results (ΔH). In addition, the last column contains the names of peaks which as a result of this study proved to be the highest in the given range and should be officially treated as such.
The results show differences of up to 19.0 m when compared to data from the CMP (14 height differences less than 1 m) and up to 8.8 m in the case of TM (18 differences less than 1 m). This indicates the need for the correction of the height of almost all the analyzed peaks; only four CPM peak heights (five in the case of TM) fit within the 10 cm measurement accuracy adopted for the purposes of this study. DTM data are the most accurate (21 differences less than 1 m), but cannot be used as a method of measuring the heights of peaks, due to low reliability. This method may be used in a supporting role for GNSS measurements.
Table 2 shows the actual measured heights and differences from currently accepted heights for seven summits which are higher than their officially recorded heights and which should be treated officially as the highest peak in each mountain range.
Interestingly, in the case of only two mountain ranges are the differences less than 1 m (Świętkorzyskie Mts and Rudawy Janowickie Mts). In the case of the remaining heights, these differences range from 3.4 m to 9.3 m. The differences between the measured heights and heights determined from DTM analysis in most cases did not exceed 1 m. The only peak for which this value exceeded 1 m is the Okole peak (Kaczawskie Mts)
for which the difference was 2.4 m. This results not from the inaccuracy of measurement, but from incorrectly adopted peaks which were until now considered to be the highest.
4. Discussion
To the best of the authors’ knowledge, no study such as the present one has been conducted so far. Modern measurement techniques have been used only for the determination of the height of individual mountain peaks, as was presented in the Introduction section. This study successfully demonstrates the necessity for verification of the heights of mountain peaks. These results indicate that the actual heights of almost every mountain range analyzed in this study were incorrect. The measurement accuracy was 10 cm, and taking into account this level of accuracy only four (14%) and five (18%) heights from the CPM and TM databases respectively were consistent with the new measurements. Due to the fact that mountain peaks generally do not have clearly defined points on the top, heights are given with an accuracy of 1 m. Taking into account this level of accuracy, the number of consistent heights increased to six (21%) and 11 (39%) for the CPM and TM databases respectively. However, in many cases, the differences exceed the measurement accuracy significantly and reach up to several meters, such as in the case of Kłodzka Góra (7.8 m and 8.8 m for the CPM and TM databases respectively), Czupel (3.3 m and 2.3 m) or Szczeliniec Wielki (2.7 m and 2.7 m).
It is the belief of the authors that the presented measurements are pioneering. Peak measurements usually refer to a single peak, e.g., the highest peak in Europe. We believe that results taking into account only ALS or DEM data for all peaks are not a satisfactory way to obtain peak height data without verification. It is necessary to understand the nature of the vegetation, buildings or residue from human activities that cover the summit. One could venture to say that the automatic transfer of peak heights from ALS or DEM data will be affected by random errors that the statistical apparatus cannot detect. According to the authors, the use of artificial intelligence may have an interesting application in this area. To this end, further measurements are needed to build an appropriate knowledge base.
This study was limited by time, human and financial resources, and thus it took almost 6 months to conduct height measurements of 40 peaks. However, this project showed the necessity of measurement and verification of all mountain peaks, especially those for which there are different heights given in existing source materials. Again, to our knowledge, no studies have questioned the heights of the highest peaks of individual mountain ranges. Our study covers Polish mountain mesoregions and shows that 25% of mountain ranges that are officially considered as the highest peaks in their ranges are in fact not the highest peaks. Differences in measured versus documented heights of almost all of them are more than 3 m and can even be up to 9.3 m (Bialskie Mts). It is to be expected that similar measurements of other, smaller (micro-regions) mountain ranges in Poland or of other mountain ranges in the world will show similar results. We hope that the conclusions presented in this paper will allow us to update the seven highest peaks of the Polish mountain mesoregions to those that are in fact the highest. In addition, this article will be useful as a reference for publication of correct values of the heights of the studied summits in future published materials, books, the Internet, etc.
5. Conclusions
This paper presents the main results of a project, which aimed to establish the correct measurement and verification of the highest peaks of all Polish mountain ranges using precise GNSS measurements. Different techniques such as LIDAR, InSAR or another non-invasive measurement would not have provided such precise, and more importantly reliable, heights. The differences between the measurements and DTM show that only 50% of the results from DTM are consistent with the measurements. In order to further analyze the reasons for these differences, individual peaks should be analyzed. For example, the difference at the summit of Śnieżnik (HA = 1423.0 m above sea level HD = 1427.2 m above sea level, i.e., a difference of 4.2 m) results from the acceptance of the ruins of a building (rubble) as natural ground. On the other hand, for the Mogielica peak (the peak is forested with an observation tower) this difference is 1.6 m and results from the filtering and classification of ALS points. Therefore, the conclusion that comes to mind is that ALS values cannot be uncritically accepted as unambiguous and exact height values for peaks.
The results showed differences between officially known and adopted heights of more than a dozen meters, with an average of several meters. These differences confirm the need to verify all the highest or most popular mountain peaks for individual mountain ranges using satellite techniques, because currently listed heights may not be valid. In addition to the alteration of the height of individual peaks in the official lists, this revision also requires a change in the peaks considered to be the highest for some mountain ranges (here 25%, 7 of 28) and this paper may provide the basis for an official change. Moreover, measurements of this type may also have an impact on mountain hiking habits, making new hiking routes the most attractive in a given range.
Author Contributions
Conceptualization, K.K. and K.M.; methodology, K.K. and K.M.; software, K.K. and K.M.; validation, K.K. and K.M.; formal analysis, K.K. and K.M.; investigation, K.K. and K.M.; resources, K.K. and K.M.; data curation, K.K. and K.M.; writing—original draft preparation, K.K. and K.M.; writing—review and editing, K.K. and K.M.; visualization, K.K. and K.M.; supervision, K.K. and K.M.; project administration, K.K. and K.M.; funding acquisition, K.K. All authors have read and agreed to the published version of the manuscript.
Acknowledgments
This paper was created as part of statutory research 16.16.150.545.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lewandowski, W.; Więckowski, M. Korona Gór Polski. Poznaj Swój Kraj 1997, 422, 17. [Google Scholar]
- Kudrys, J.; Buśko, M.; Kozioł, K.; Maciuk, K. Determination of the normal height of Chornohora summits by a precise modern measurement techniques. Maejo Int. J. Sci. Technol. 2020, 14, 2. [Google Scholar]
- Fenna, D. Jednostki Miar; Świat Książki: Warszawa, Polska, 2004; p. 328. [Google Scholar]
- Ward, M. The height of Mount Everest. Alp. J. 1995, 100, 30–33. [Google Scholar]
- Junyong, C.; Yanping, Z.; Janli, Y.; Chunxi, G.; Peng, Z. Height Determination of Qomolangma Feng (MT. Everest) in 2005. Surv. Rev. 2010, 42, 122–131. [Google Scholar] [CrossRef]
- De Graaff-Hunter, J. De Various Determinations over a Century of the Height of Mount Everest. Geogr. J. 1955, 121, 21–26. [Google Scholar] [CrossRef]
- De Beer, G. The history of the altimetry of Mont Blanc. Ann. Sci. 1956, 12, 3–29. [Google Scholar] [CrossRef]
- Poretti, G.G. America’s highest peak now measures 6962 metres! Report. Mag. Leica Geosystems 1999, 47, 28–29. [Google Scholar]
- Saburi, J.; Angelakis, N.; Jaeger, R.; Illner, M.; Jackson, P.; Pugh, K.T. Height measurement of Kilimanjaro. Surv. Rev. 2000, 35, 552–562. [Google Scholar] [CrossRef]
- TeamKILI2008. Precise Determination of the Orthometric Height of Mt Kilimanjaro. In FIG Working Week 2009; FIG: Eilat, Israel, 2009; p. 11. [Google Scholar]
- Makowska, A. Dynamika Tatr Wyznaczana Metodami Geodezyjnymi; Instytut Geodezji I Kartografii: Warszawa, Poland, 2003; No. 6. [Google Scholar]
- Chen, W.; Li, X.; Wang, Y.; Chen, G.; Liu, S. Forested landslide detection using LiDAR data and the random forest algorithm: A case study of the Three Gorges, China. Remote Sens. Environ. 2014, 152, 291–301. [Google Scholar] [CrossRef]
- Puniach, E.; Mamczarz, K.; Niewiem, W. Assessment of the Possibility of Using Unmanned Aerial Vehicles (UAVs) for the Documentation of Hiking Trails in Alpine Areas. Sensors 2018, 18, 81. [Google Scholar]
- Hejmanowski, R.; Malinowska, A.A.; Witkowski, W.T.; Guzy, A. An Analysis Applying InSAR of Subsidence Caused by Nearby Mining-Induced Earthquakes. Geosciences 2019, 9, 490. [Google Scholar] [CrossRef]
- Kadaj, R. Algorytm opracowania modelu PL-geoid-2011. In Realizacja Osnów Geodezyjnych a Problemy Geodynamiki; Politechnika Warszawska: Grybów, Poland, 2012; p. 26. [Google Scholar]
- Ministrów, R. Rozporządzenie Rady Ministrów z Dnia 15 Października 2012 r. w Sprawie Państwowego Systemu Odniesień Przestrzennych; Kancelaria Prezesa Rady Ministrów: Warszawa, Poland, 2012; p. 8.
- Balasubramanian, N. Definition and Realization of a Global Vertical Datum; Scientific Report, No.1; The Ohio State University, Department of Geodetic Science and Surveying: Columbus, OH, USA, 1994. [Google Scholar]
- Wiśniewski, B.; Giza, A.; Wolski, T. Adjustment of the European Vertical Reference System for the representation of the Baltic Sea water surface topography. Zesz. Nauk. Akad. Morska w Szczecinie 2014, 38, 106–117. [Google Scholar]
- Stereńczak, K.; Ciesielski, M.; Balazy, R.; Zawiła-Niedźwiecki, T. Comparison of various algorithms for DTM interpolation from LIDAR data in dense mountain forests. Eur. J. Remote Sens. 2016, 49, 599–621. [Google Scholar] [CrossRef]
- Graham, A.N.V.; Coops, N.C.; Tompalski, P.; Plowright, A.; Wilcox, M. Effect of ground surface interpolation methods on the accuracy of forest attribute modelling using unmanned aerial systems-based digital aerial photogrammetry. Int. J. Remote Sens. 2020, 41, 3287–3306. [Google Scholar] [CrossRef]
- Shamsoddini, A.; Turner, R.; Trinder, J.C. Improving lidar-based forest structure mapping with crown-level pit removal. J. Spat. Sci. 2013, 58, 29–51. [Google Scholar] [CrossRef]
- Godone, D.; Garnero, G. The role of morphometric parameters in Digital Terrain Models interpolation accuracy: A case study. Eur. J. Remote Sens. 2013, 46, 198–214. [Google Scholar] [CrossRef]
- Chow, T.E.; Hodgson, M.E. Effects of lidar post-spacing and DEM resolution to mean slope estimation. Int. J. Geogr. Inf. Sci. 2009, 23, 1277–1295. [Google Scholar] [CrossRef]
- Lloyd, C.D.; Atkinson, P.M. Deriving ground surface digital elevation models from LiDAR data with geostatistics. Int. J. Geogr. Inf. Sci. 2006, 20, 535–563. [Google Scholar] [CrossRef]
- Lloyd, C.D.; Atkinson, P.M. Deriving DSMs from LiDAR data with kriging. Int. J. Remote Sens. 2002, 23, 2519–2524. [Google Scholar] [CrossRef]
- Guo, Q.; Su, Y.; Hu, T.; Zhao, X.; Wu, F.; Li, Y.; Liu, J.; Chen, L.; Xu, G.; Lin, G.; et al. An integrated UAV-borne lidar system for 3D habitat mapping in three forest ecosystems across China. Int. J. Remote Sens. 2017, 38, 2954–2972. [Google Scholar] [CrossRef]
- Su, Y.; Guo, Q.; Collins, B.M.; Fry, D.L.; Hu, T.; Kelly, M. Forest fuel treatment detection using multi-temporal airborne lidar data and high-resolution aerial imagery: A case study in the Sierra Nevada Mountains, California. Int. J. Remote Sens. 2016, 37, 3322–3345. [Google Scholar] [CrossRef]
- Su, Y.; Guo, Q.; Fry, D.L.; Collins, B.M.; Kelly, M.; Flanagan, J.P.; Battles, J.J. A Vegetation Mapping Strategy for Conifer Forests by Combining Airborne LiDAR Data and Aerial Imagery. Can. J. Remote Sens. 2016, 42, 1–15. [Google Scholar] [CrossRef]
- Bigdeli, B.; Gomroki, M.; Pahlavani, P. Generation of digital terrain model for forest areas using a new particle swarm optimization on LiDAR data. Surv. Rev. 2020, 52, 115–125. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).