A Random Forest Machine Learning Approach for the Retrieval of Leaf Chlorophyll Content in Wheat
Abstract
1. Introduction
2. Materials and Methods
2.1. Greenhouse Pot Experiment
2.2. Hyperspectral Data Acquisition
2.3. Chlorophyll Determination
2.4. Hyperspectral Data Processing and Extraction of Vegetation Indices
2.5. Statistical Analysis and Machine Learning
2.5.1. Simple Univariate Regression Analysis
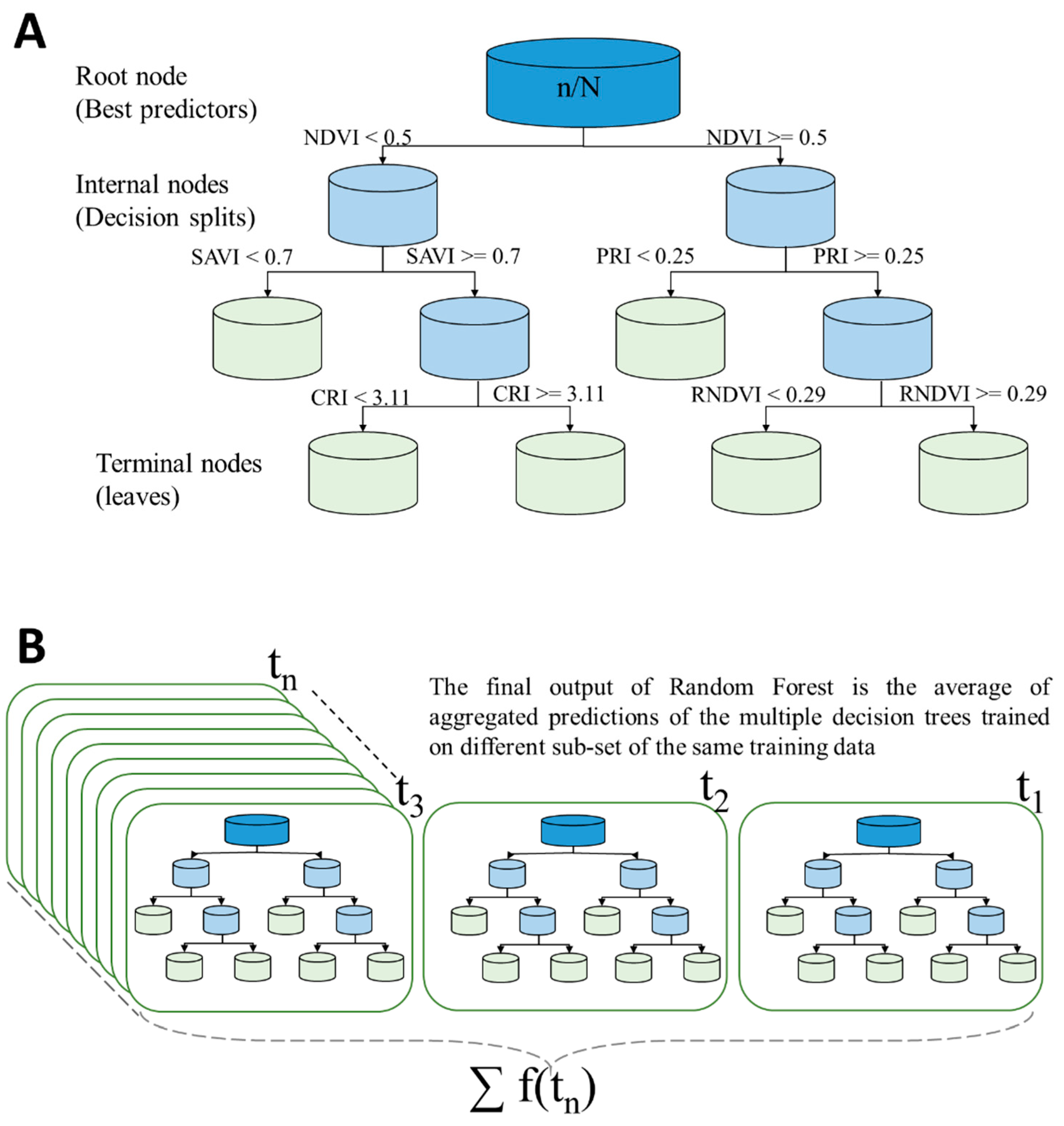
2.5.2. Description of the Random Forest Approach
2.5.3. Implementing the Random Forest Approach
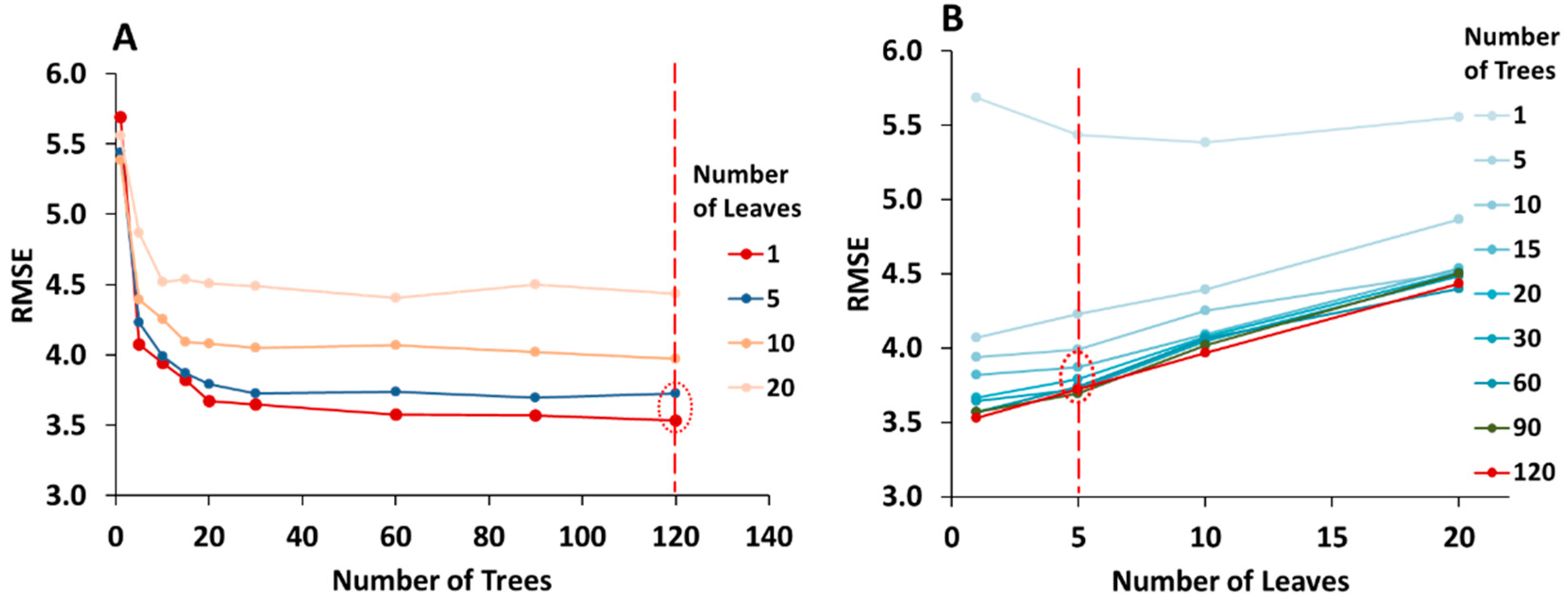
- Define the optimum number of trees (ntree) based on a bootstrapping sampling procedure.
- Optimal number of leaves (nodesize) was decided as a specified stop condition to reach during the data splitting process at all internal nodes. Leaves are the terminal nodes where the tree growth is stopped. If the trees are allowed to grow to full depth, it may be too variable (i.e., result in relatively high variance and low bias and a possible overfitting of the data). Thus, pruning of the tree is done by deciding upon the optimal number of leaves.
- At every node of the tree, the number of input variables (mtry) (i.e., number of individual bands or VIs) used for the split decisions were randomly selected out of the total (2102 individual spectral bands or 45 VIs).
- The stop condition of each tree growth in our method was determined by defining an optimum number of leaves. The number of trees and number of leaves were optimized by minimizing the RMSE. A diagram of the workflow is provided in Figure 2.
3. Results
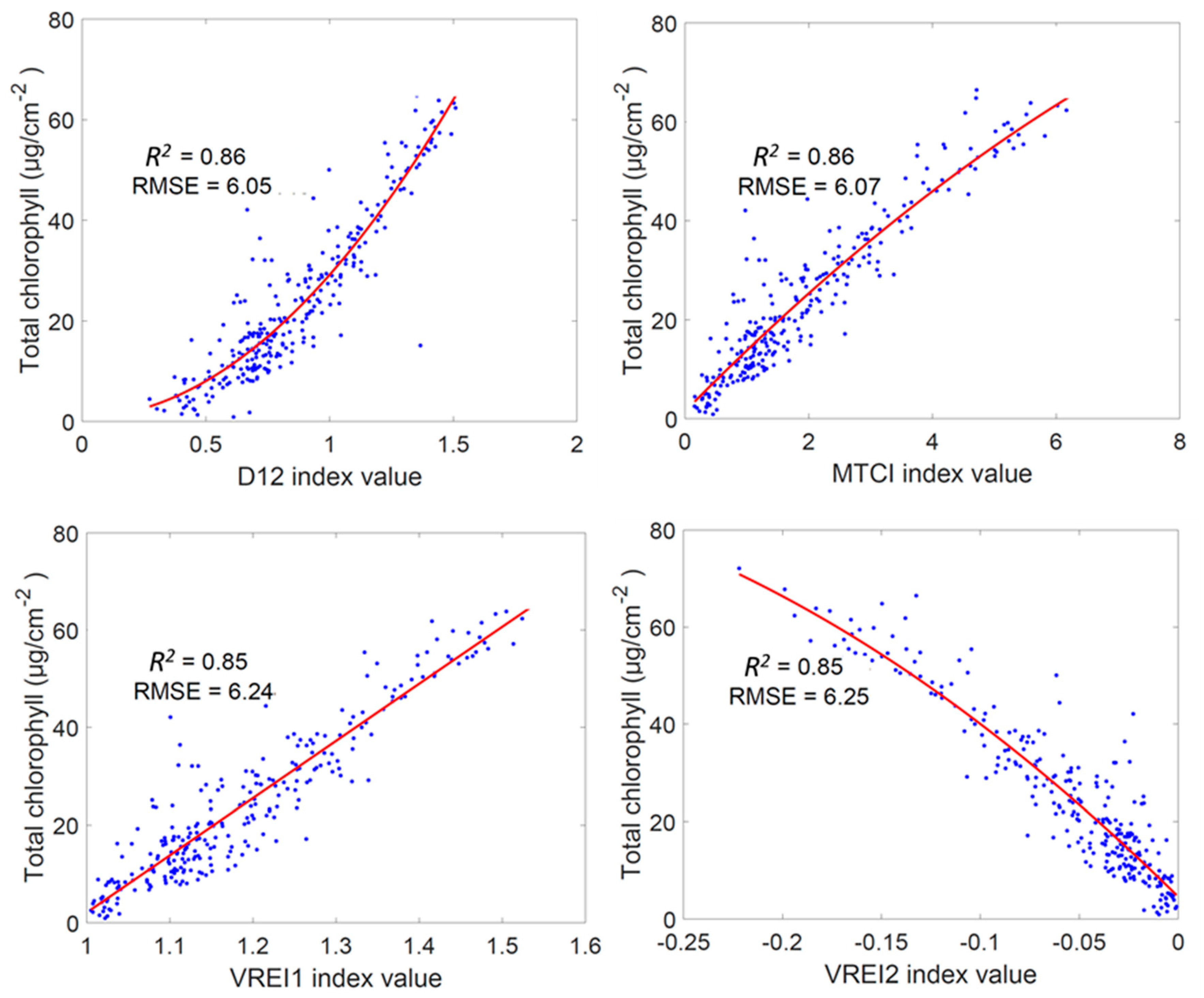
3.1. Regression Analysis Using Established Vegetation Indices for Chlt Estimation
3.2. RF Machine Learning Approach Using All Hyperspectral Bands as Input Features
3.3. Random Forest Approach Using Vegetation Indices as Input Features
3.3.1. Optimization of the Random Forest Model
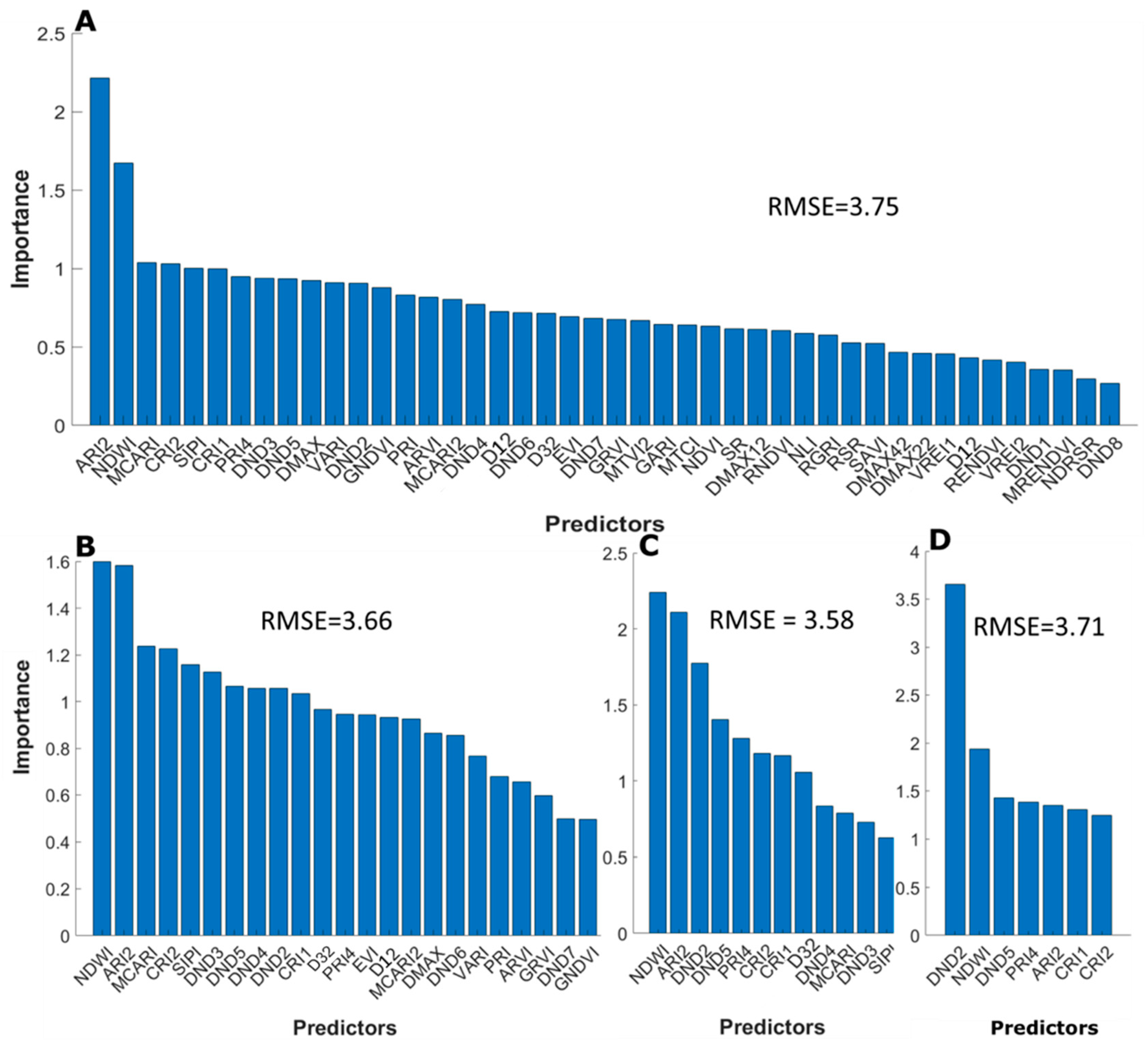
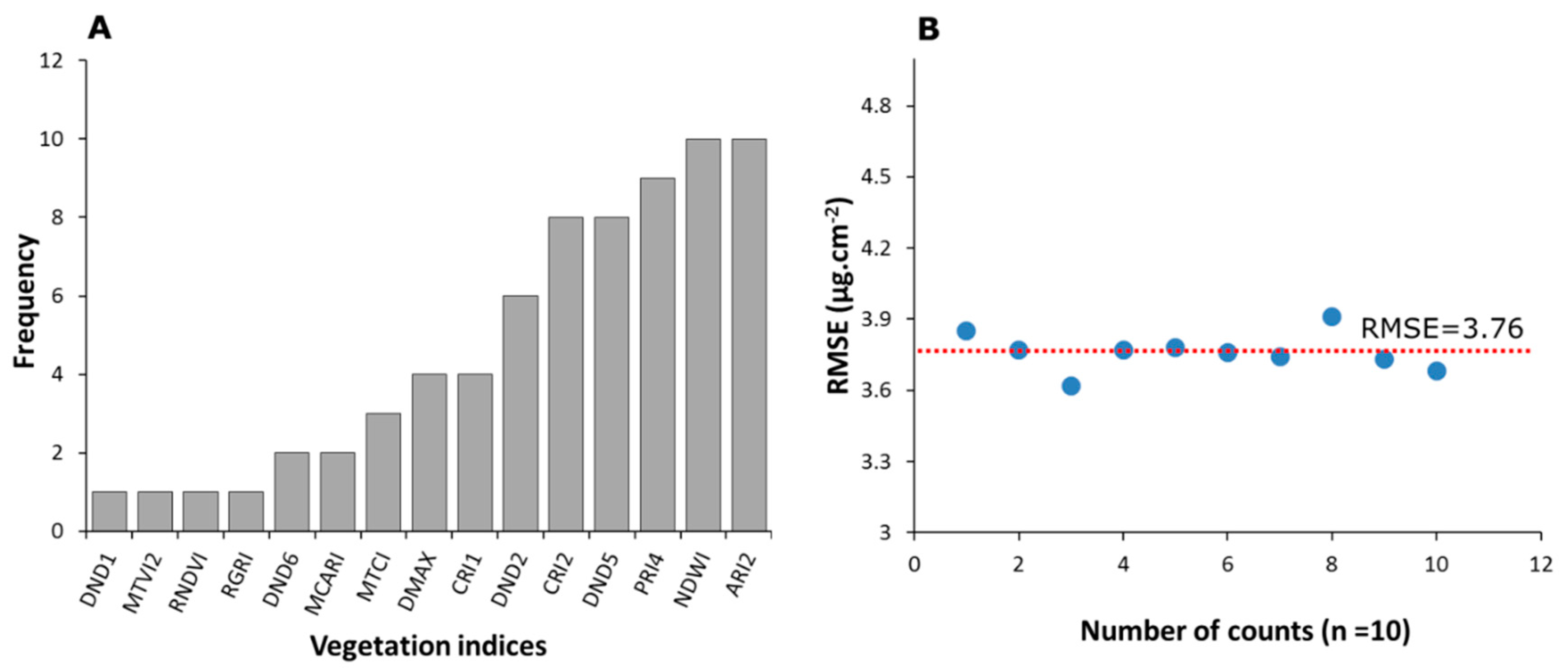
3.3.2. Selective Reduction of Important Predictors
4. Discussion
4.1. Simple Regression Analysis of the Vegetation Indices for Chlt Determination
4.2. RF Machine Learning Approach Using Hyperspectral Bands and VIs as Input Features
4.3. Selection of Important Predictors
4.4. Limitations of the Experimental and Modeling Approach
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stengel, D.B.; Connan, S.; Popper, Z.A. Algal chemodiversity and bioactivity: Sources of natural variability and implications for commercial application. Biotechnol. Adv. 2011, 29, 483–501. [Google Scholar] [CrossRef] [PubMed]
- Hosikian, A.; Lim, S.; Halim, R.; Danquah, M.K. Chlorophyll extraction from microalgae: A review on the process engineering aspects. Int. J. Chem. Eng. 2010, 2010, 1–11. [Google Scholar] [CrossRef]
- Feret, J.B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. Prospect-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Cannella, D.; Möllers, K.B.; Frigaard, N.U.; Jensen, P.E.; Bjerrum, M.J.; Johansen, K.S.; Felby, C. Light-driven oxidation of polysaccharides by photosynthetic pigments and a metalloenzyme. Nat. Commun. 2016, 7, 11134. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Peng, Y.; Arkebauer, T.J.; Schepers, J. Relationships between gross primary production, green lai, and canopy chlorophyll content in maize: Implications for remote sensing of primary production. Remote Sens. Environ. 2014, 144, 65–72. [Google Scholar] [CrossRef]
- Houborg, R.; Fisher, J.B.; Skidmore, A.K. Advances in remote sensing of vegetation function and traits. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 1–6. [Google Scholar] [CrossRef]
- Fernández-Marín, B.; Artetxe, U.; Barrutia, O.; Esteban, R.; Hernández, A.; García-Plazaola, J.I. Opening pandora’s box: Cause and impact of errors on plant pigment studies. Front. Plant Sci. 2015, 6, 148. [Google Scholar] [CrossRef] [PubMed]
- Houborg, R.; McCabe, M.F. Adapting a regularized canopy reflectance model (regflec) for the retrieval challenges of dryland agricultural systems. Remote Sens. Environ. 2016, 186, 105–120. [Google Scholar] [CrossRef]
- Gonzalez-Dugo, V.; Hernandez, P.; Solis, I.; Zarco-Tejada, P.J. Using high-resolution hyperspectral and thermal airborne imagery to assess physiological condition in the context of wheat phenotyping. Remote Sens. 2015, 7, 13586–13605. [Google Scholar] [CrossRef]
- Serbin, S.P.; Dillaway, D.N.; Kruger, E.L.; Townsend, P.A. Leaf optical properties reflect variation in photosynthetic metabolism and its sensitivity to temperature. J. Exp. Bot. 2012, 63, 489–502. [Google Scholar] [CrossRef]
- Peñuelas, J.; Filella, I. Visible and near-infrared reflectance techniques for diagnosing plant physiological status. Trends Plant Sci. 1998, 3, 151–156. [Google Scholar] [CrossRef]
- Hansen, P.M.; Schjoerring, J.K. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and partial least squares regression. Remote Sens. Environ. 2003, 86, 542–553. [Google Scholar] [CrossRef]
- Boegh, E.; Houborg, R.; Bienkowski, J.; Braban, C.F.; Dalgaard, T.; van Dijk, N.; Dragosits, U.; Holmes, E.; Magliulo, V.; Schelde, K. Remote sensing of lai, chlorophyll and leaf nitrogen pools of crop-and grasslands in five european landscapes. Biogeosciences 2013, 10, 6279–6307. [Google Scholar] [CrossRef]
- Liu, L.Y.; Huang, W.J.; Pu, R.L.; Wang, J.H. Detection of internal leaf structure deterioration using a new spectral ratio index in the near-infrared shoulder region. J. Integr. Agric. 2014, 13, 760–769. [Google Scholar] [CrossRef]
- Fletcher, R.S. Using vegetation indices as input into random forest for soybean and weed classification. Am. J. Plant Sci. 2016, 7, 2186. [Google Scholar] [CrossRef]
- Viña, A.; Gitelson, A.A.; Nguy-Robertson, A.L.; Peng, Y. Comparison of different vegetation indices for the remote assessment of green leaf area index of crops. Remote Sens. Environ. 2011, 115, 3468–3478. [Google Scholar] [CrossRef]
- Boegh, E.; Soegaard, H.; Broge, N.; Hasager, C.B.; Jensen, N.O.; Schelde, K.; Thomsen, A. Airborne multispectral data for quantifying leaf area index, nitrogen concentration, and photosynthetic efficiency in agriculture. Remote Sens. Environ. 2002, 81, 179–193. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Chen, F.; Shi, T.; Wu, G. Wavelet-based coupling of leaf and canopy reflectance spectra to improve the estimation accuracy of foliar nitrogen concentration. Agric. For. Meteorol. 2018, 248, 306–315. [Google Scholar] [CrossRef]
- Wang, L.a.; Zhou, X.; Zhu, X.; Dong, Z.; Guo, W. Estimation of biomass in wheat using random forest regression algorithm and remote sensing data. Crop J. 2016, 4, 212–219. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, T.; Zhu, Y.; Tian, Y.; Cao, W.; Yao, X.; Wang, N. Comparative analysis of vegetation indices, non-parametric and physical retrieval methods for monitoring nitrogen in wheat using uav-based multispectral imagery. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 7362–7365. [Google Scholar]
- McCabe, M.F.; Rodell, M.; Alsdorf, D.E.; Miralles, D.G.; Uijlenhoet, R.; Wagner, W.; Lucieer, A.; Houborg, R.; Verhoest, N.E.C.; Franz, T.E. The future of earth observation in hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 3879–3914. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Houborg, R.; McCabe, M.F. A hybrid training approach for leaf area index estimation via cubist and random forests machine-learning. ISPRS J. Photogramm. Remote Sens. 2018, 135, 173–188. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Abdel-Rahman, E.M.; Mutanga, O.; Adam, E.; Ismail, R. Detecting sirex noctilio grey-attacked and lightning-struck pine trees using airborne hyperspectral data, random forest and support vector machines classifiers. ISPRS J. Photogramm. Remote Sens. 2014, 88, 48–59. [Google Scholar] [CrossRef]
- Mutanga, O.; Adam, E.; Cho, M.A. High density biomass estimation for wetland vegetation using worldview-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
- Prasad, A.M.; Iverson, L.R.; Liaw, A. Newer classification and regression tree techniques: Bagging and random forests for ecological prediction. Ecosystems 2006, 9, 181–199. [Google Scholar] [CrossRef]
- Dahms, T.; Seissiger, S.; Borg, E.; Vajen, H.; Fichtelmann, B.; Conrad, C. Important variables of a rapideye time series for modelling biophysical parameters of winter wheat. Photogramm. Fernerkund. Geoinf. 2016, 2016, 285–299. [Google Scholar] [CrossRef]
- Liang, L.; Luo, X.; Sun, Q.; Rui, J.; Li, J.; Liang, J.; Lin, H. In Diagnosis the dust stress of wheat leaves with hyperspectral indices and random forest algorithm. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 6385–6388. [Google Scholar]
- Sonobe, R.; Sano, T.; Horie, H. Using spectral reflectance to estimate leaf chlorophyll content of tea with shading treatments. Biosyst. Eng. 2018, 175, 168–182. [Google Scholar] [CrossRef]
- Bashour, I.I.; Al-Mashhady, A.S.; Devi Prasad, J.; Miller, T.; Mazroa, M. Morphology and composition of some soils under cultivation in saudi arabia. Geoderma 1983, 29, 327–340. [Google Scholar] [CrossRef]
- Chuluun, B.; Shah, S.H.; Rhee, J.S. Bioaugmented phytoremediation: A strategy for reclamation of diesel oil-contaminated soils. Int. J. Agric. Biol. 2014, 16, 624–628. [Google Scholar]
- Saqib, M.; Akhtar, J.; Abbas, G.; Nasim, M. Salinity and drought interaction in wheat (Triticum aestivum L.) is affected by the genotype and plant growth stage. Acta Physiol. Plant. 2013, 35, 2761–2768. [Google Scholar] [CrossRef]
- Arnon, D.I. Copper enzymes in isolated chloroplasts. Polyphenoloxidase in beta vulgaris. Plant Physiol. 1949, 24, 1. [Google Scholar] [CrossRef]
- Wellburn, A.R. The spectral determination of chlorophylls a and b, as well as total carotenoids, using various solvents with spectrophotometers of different resolution. J. Plant Physiol. 1994, 144, 307–313. [Google Scholar] [CrossRef]
- Sonobe, R.; Wang, Q. Towards a universal hyperspectral index to assess chlorophyll content in deciduous forests. Remote Sens. 2017, 9, 191. [Google Scholar] [CrossRef]
- Filella, I.; Penuelas, J. The red edge position and shape as indicators of plant chlorophyll content, biomass and hydric status. Int. J. Remote Sens. 1994, 15, 1459–1470. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Pushnik, J.C.; Dobrowski, S.; Ustin, S.L. Steady-state chlorophyll a fluorescence detection from canopy derivative reflectance and double-peak red-edge effects. Remote Sens. Environ. 2003, 84, 283–294. [Google Scholar] [CrossRef]
- Kochubey, S.M.; Kazantsev, T.A. Derivative vegetation indices as a new approach in remote sensing of vegetation. Front. Earth Sci. 2012, 6, 188–195. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N.; Chivkunova, O.B. Optical properties and nondestructive estimation of anthocyanin content in plant leaves. Photochem. Photobiol. 2001, 74, 38–45. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanre, D. Atmospherically resistant vegetation index (arvi) for eos-modis. IEEE Trans. Geosci. Remote Sens. 1992, 30, 261–270. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Zur, Y.; Chivkunova, O.B.; Merzlyak, M.N. Assessing carotenoid content in plant leaves with reflectance spectroscopy. Photochem. Photobiol. 2002, 75, 272–281. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the modis vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from eos-modis. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Remote sensing of chlorophyll concentration in higher plant leaves. Adv. Space Res. 1998, 22, 689–692. [Google Scholar] [CrossRef]
- Sripada, R.P.; Heiniger, R.W.; White, J.G.; Meijer, A.D. Aerial color infrared photography for determining early in-season nitrogen requirements in corn. Agron. J. 2006, 98, 968–977. [Google Scholar] [CrossRef]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; de Colstoun, E.B.; McMurtrey, J.E. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green lai of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. Evaluation of the meris terrestrial chlorophyll index. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Anchorage, AK, USA, 20–24 September 2004; pp. 1–257. [Google Scholar]
- Dash, J.; Curran, P.J. Evaluation of the meris terrestrial chlorophyll index (mtci). Adv. Space Res. 2007, 39, 100–104. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Vina, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.; Deering, D. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; Prog. Rep. RSC 1978-1; Remote Sensing Center, Texas A&M Univ.: College Station, TX, USA, 1973.
- Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Goel, N.S.; Qin, W. Influences of canopy architecture on relationships between various vegetation indices and lai and fpar: A computer simulation. Remote Sens. Rev. 1994, 10, 309–347. [Google Scholar] [CrossRef]
- Gamon, J.; Serrano, L.; Surfus, J. The photochemical reflectance index: An optical indicator of photosynthetic radiation use efficiency across species, functional types, and nutrient levels. Oecologia 1997, 112, 492–501. [Google Scholar] [CrossRef]
- Goerner, A.; Reichstein, M.; Tomelleri, E.; Hanan, N.; Rambal, S.; Papale, D.; Dragoni, D.; Schmullius, C. Remote sensing of ecosystem light use efficiency with modis-based pri. Biogeosciences 2011, 8, 189–202. [Google Scholar] [CrossRef]
- Gamon, J.; Surfus, J. Assessing leaf pigment content and activity with a reflectometer. New Phytol. 1999, 143, 105–117. [Google Scholar] [CrossRef]
- Roujean, J.L.; Breon, F.M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Birth, G.S.; McVey, G.R. Measuring the color of growing turf with a reflectance spectrophotometer 1. Agron. J. 1968, 60, 640–643. [Google Scholar] [CrossRef]
- Vogelmann, J.; Rock, B.; Moss, D. Red edge spectral measurements from sugar maple leaves. Remote Sens. 1993, 14, 1563–1575. [Google Scholar] [CrossRef]
- Díaz-Uriarte, R.; Alvarez de Andrés, S. Gene selection and classification of microarray data using random forest. BMC Bioinform. 2006, 7, 3. [Google Scholar] [CrossRef]
- Strobel, J.; Hawkins, C. An exploration of design phenomena in second life. In Proceedings of the E-Learn: World Conference on E-Learning in Corporate, Government, Healthcare, and Higher Education, Vancouver, BC, Canada, 26–30 October 2009; pp. 3702–3709. [Google Scholar]
- Xiong, C.; Johnson, D.; Xu, R.; Corso, J.J. Random forests for metric learning with implicit pairwise position dependence. In Proceedings of the 18th ACM SIGKDD international conference on Knowledge discovery and data mining, Beijing, China, 12–16 August 2012; pp. 958–966. [Google Scholar]
- Rodriguez, J.D.; Perez, A.; Lozano, J.A. Sensitivity analysis of k-fold cross validation in prediction error estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 569–575. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomforest. R News 2002, 2, 18–22. [Google Scholar]
- Thenkabail, P.S.; Smith, R.B.; De Pauw, E. Hyperspectral vegetation indices and their relationships with agricultural crop characteristics. Remote Sens. Environ. 2000, 71, 158–182. [Google Scholar] [CrossRef]
- Hatfield, J.L.; Prueger, J.H. Value of using different vegetative indices to quantify agricultural crop characteristics at different growth stages under varying management practices. Remote Sens. 2010, 2, 562–578. [Google Scholar] [CrossRef]
- Ampatzidis, Y.; Partel, V. Uav-based high throughput phenotyping in citrus utilizing multispectral imaging and artificial intelligence. Remote Sens. 2019, 11, 410. [Google Scholar] [CrossRef]
- Matese, A.; Di Gennaro, F.S. Practical applications of a multisensor uav platform based on multispectral, thermal and rgb high resolution images in precision viticulture. Agriculture 2018, 8, 116. [Google Scholar] [CrossRef]
- Ollinger, S.V. Sources of variability in canopy reflectance and the convergent properties of plants. New Phytol. 2011, 189, 375–394. [Google Scholar] [CrossRef]
- Manfreda, S.; McCabe, M.F.; Miller, P.E.; Lucas, R.; Pajuelo Madrigal, V.; Mallinis, G.; Ben Dor, E.; Helman, D.; Estes, L.; Ciraolo, G. On the use of unmanned aerial systems for environmental monitoring. Remote Sens. 2018, 10, 641. [Google Scholar] [CrossRef]
- Shah, S.; Houborg, R.; McCabe, M. Response of chlorophyll, carotenoid and spad-502 measurement to salinity and nutrient stress in wheat (Triticum aestivum L.). Agronomy 2017, 7, 61. [Google Scholar] [CrossRef]
- Wójtowicz, M.; Wójtowicz, A.; Piekarczyk, J. Application of remote sensing methods in agriculture. Commun. Biom. Crop Sci. 2016, 11, 31–50. [Google Scholar]
- Vuolo, F.; Neugebauer, N.; Bolognesi, S.; Atzberger, C.; Urso, G. Estimation of leaf area index using deimos-1 data: Application and transferability of a semi-empirical relationship between two agricultural areas. Remote Sens. 2013, 5, 1274–1291. [Google Scholar] [CrossRef]
- Liang, S. Recent developments in estimating land surface biogeophysical variables from optical remote sensing. Prog. Phys. Geogr. Earth Environ. 2007, 31, 501–516. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. Prospect—A model of leaf optical-properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Berger, K.; Atzberger, C.; Danner, M.; D’Urso, G.; Mauser, W.; Vuolo, F.; Hank, T. Evaluation of the PROSAIL model capabilities for future hyperspectral model environments: A review study. Remote Sens. 2018, 10, 85. [Google Scholar] [CrossRef]


| No | Name | Vegetation Index | Application | |
|---|---|---|---|---|
| 1 | Anthocyanin Reflectance Index [40] | Carotenoids | ||
| 2 | Atmospherically Resistant Vegetation Index [41] | Vegetation | ||
| 3 | Carotenoid Reflectance Index 1 [42] | Carotenoids | ||
| 4 | Carotenoid Reflectance Index 2 [42] | Carotenoids | ||
| 5 | Enhanced Vegetation Index [43] | Vegetation | ||
| 6 | Green Atmospherically Resistant Index [44] | Chlorophyll | ||
| 7 | Green Norm. Difference Vegetation Index [45] | Chlorophyll | ||
| 8 | Green Ratio Vegetation Index [46] | Pigments | ||
| 9 | Modified Chlorophyll Absorption Ratio Index [47] | Chlorophyll | ||
| 10 | Modified Chlorophyll Absorption Ratio Index Improved [48] | Vegetation | ||
| 11 | Plant Senescence Reflectance Index [49] | Pigments | ||
| 12 | MERIS Terrestrial Chlorophyll Index [50] | Chlorophyll | ||
| 13 | MERIS Terrestrial Chlorophyll Index 2 [51] | Chlorophyll | ||
| 14 | Modified Triangular Vegetation Index Improved [48] | Vegetation | ||
| 15 | Normalized Difference Red-edge Simple Ratio [52] | Chlorophyll | ||
| 16 | Normalized Difference Vegetation Index [53] | Vegetation | ||
| 17 | Normalized Difference Water Index [54] | Leaf water | ||
| 18 | Non-Linear Index [55] | Vegetation | ||
| 19 | Photochemical Reflectance Index [56] | Pigments | ||
| 20 | Photochemical Reflectance Index Improved [57] | Pigments | ||
| 21 | Red Edge Normalized Vegetation Index [49] | Chlorophyll | ||
| 22 | Red Green Ratio Index [58] | Pigments | ||
| 23 | Renormalized Difference Vegetation Index [59] | Chlorophyll | ||
| 24 | Red-edge Simple Ratio [52] | Chlorophyll | ||
| 25 | Soil Adjusted Vegetation Index [43] | Vegetation | ||
| 26 | Structure Insensitive Pigment Index [11] | Pigments | ||
| 27 | Simple Ratio Index [60] | Vegetation | ||
| 28 | Visible Atmospherically Resistant Index [42] | Vegetation | ||
| 29 | Vogelmann Red Edge Index [61] | Chlorophyll | ||
| 30 | Vogelmann Red Edge Index Improved [61] | Chlorophyll | ||
| 31 | Derivative Simple Ratio 02 | Vegetation | ||
| 32 | Derivative Simple Ratio 32 | Vegetation | ||
| 33 | Derivative Simple Ratio 12 | Vegetation | ||
| 34 | -----NDVIs based on the first derivatives (DND) over 650–750 nm domain----- | Maximum Derivative Index | Vegetation | |
| 35 | DMAX Simple Ratio with D712 | Vegetation | ||
| 36 | DMAX Simple Ratio D722 | Vegetation | ||
| 37 | DMAX Simple Ratio D742 | Vegetation | ||
| 38 | Normalized Difference Derivative 1 | Vegetation | ||
| 39 | Normalized Difference Derivative 2 | Vegetation | ||
| 40 | Normalized Difference Derivative 3 | Vegetation | ||
| 41 | Normalized Difference Derivative 4 | Vegetation | ||
| 42 | Normalized Difference Derivative 5 | Vegetation | ||
| 43 | Normalized Difference Derivative 6 | Vegetation | ||
| 44 | Normalized Difference Derivative 7 | Vegetation | ||
| 45 | Normalized Difference Derivative 8 | Vegetation | ||
| No. | Vegetation Index | R2 | RMSE (µg cm−2) | No. | Vegetation Index | R2 | RMSE (µg cm−2) |
|---|---|---|---|---|---|---|---|
| 1 | D12 | 0.86 | 6.05 | 24 | DND3 | 0.43 | 12.41 |
| 2 | MTCI | 0.86 | 6.07 | 25 | SR | 0.39 | 12.74 |
| 3 | VREI1 | 0.85 | 6.24 | 26 | NDVI | 0.37 | 12.98 |
| 4 | VREI2 | 0.85 | 6.25 | 27 | DND4 | 0.35 | 13.22 |
| 5 | D02 | 0.85 | 6.26 | 28 | PSRI | 0.32 | 13.46 |
| 6 | MRENDVI | 0.85 | 6.34 | 29 | MCARI | 0.30 | 13.73 |
| 7 | DND1 | 0.85 | 6.36 | 30 | CRI1 | 0.27 | 13.96 |
| 8 | RSR | 0.85 | 6.38 | 31 | NLI | 0.26 | 14.03 |
| 9 | NDRSR | 0.85 | 6.39 | 32 | EVI | 0.24 | 14.22 |
| 10 | DND8 | 0.85 | 6.45 | 33 | ARI2 | 0.24 | 14.23 |
| 11 | DMAX22 | 0.85 | 6.47 | 34 | RNDVI | 0.24 | 14.25 |
| 12 | D32 | 0.83 | 6.71 | 35 | SAVI | 0.24 | 14.25 |
| 13 | DMAX42 | 0.82 | 6.91 | 36 | PRI4 | 0.24 | 14.30 |
| 14 | RENDVI | 0.82 | 6.97 | 37 | CRI2 | 0.22 | 14.49 |
| 15 | DND2 | 0.82 | 7.01 | 38 | MCARI2 | 0.20 | 14.63 |
| 16 | GRVI | 0.80 | 7.40 | 39 | MTVI | 0.20 | 14.63 |
| 17 | GNDVI | 0.79 | 7.42 | 40 | VARI | 0.17 | 14.88 |
| 18 | GARI | 0.79 | 7.55 | 41 | RGRI | 0.14 | 15.16 |
| 19 | DND7 | 0.78 | 7.64 | 42 | DMAX | 0.09 | 15.61 |
| 20 | DMAX12 | 0.62 | 10.09 | 43 | NDWI | 0.08 | 15.66 |
| 21 | PRI | 0.54 | 11.12 | 44 | DND5 | 0.02 | 16.21 |
| 22 | SIPI | 0.53 | 11.27 | 45 | DND6 | 0.01 | 16.30 |
| 23 | ARVI | 0.43 | 12.32 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, S.H.; Angel, Y.; Houborg, R.; Ali, S.; McCabe, M.F. A Random Forest Machine Learning Approach for the Retrieval of Leaf Chlorophyll Content in Wheat. Remote Sens. 2019, 11, 920. https://doi.org/10.3390/rs11080920
Shah SH, Angel Y, Houborg R, Ali S, McCabe MF. A Random Forest Machine Learning Approach for the Retrieval of Leaf Chlorophyll Content in Wheat. Remote Sensing. 2019; 11(8):920. https://doi.org/10.3390/rs11080920
Chicago/Turabian StyleShah, Syed Haleem, Yoseline Angel, Rasmus Houborg, Shawkat Ali, and Matthew F. McCabe. 2019. "A Random Forest Machine Learning Approach for the Retrieval of Leaf Chlorophyll Content in Wheat" Remote Sensing 11, no. 8: 920. https://doi.org/10.3390/rs11080920
APA StyleShah, S. H., Angel, Y., Houborg, R., Ali, S., & McCabe, M. F. (2019). A Random Forest Machine Learning Approach for the Retrieval of Leaf Chlorophyll Content in Wheat. Remote Sensing, 11(8), 920. https://doi.org/10.3390/rs11080920







