Improving the AVHRR Long Term Data Record BRDF Correction
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
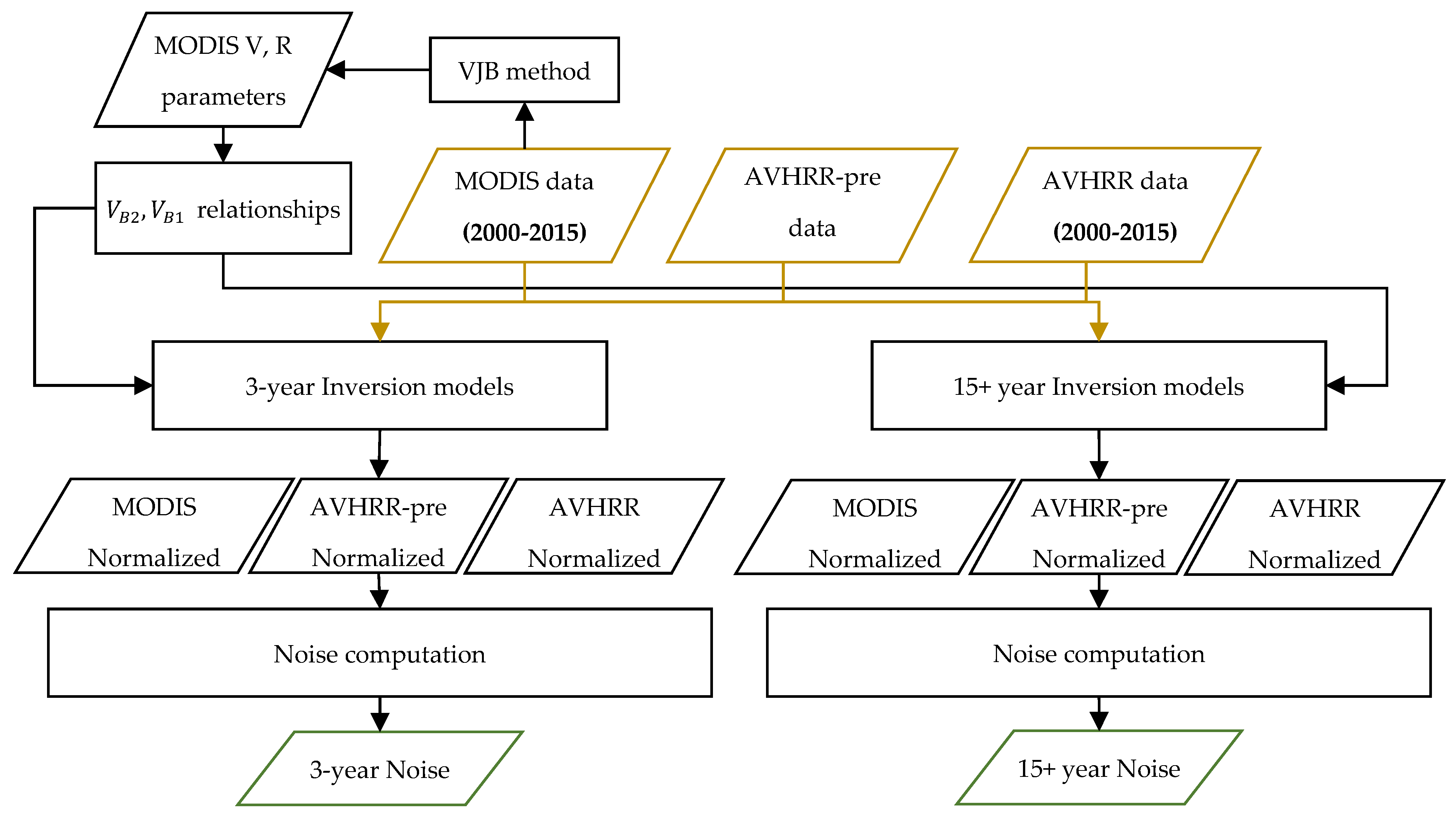
2.2. Methods
2.2.1. VJB Method
2.2.2. BRDF Parameters Relationship
2.2.3. Inversion Period
2.2.4. Inversion Models
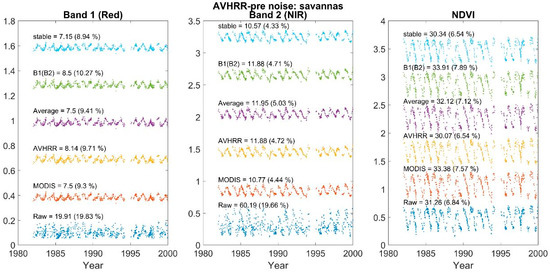
3. Results
3.1. BRDF Parameters Relationship
3.2. Inversion Period
3.3. Inversion Models
4. Discussion
4.1. BRDF Parameters Relationships
4.2. Inversion Period
4.3. Inversion Models
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vermote, E.; Claverie, M. Climate Algorithm Theoretical Basis Document (C-ATBD) AVHRR Land Bundle—Surface Reflectance and Normalized Difference Vegetation Index; University of Wisconsin-Madison: Madison, WI, USA, 2013. [Google Scholar]
- Franch, B.; Vermote, E.; Roger, J.-C.; Becker-Reshef, I.; Justice, C.O. A 30+ year AVHRR Land Surface Reflectance Climate 2 Data Record and its application to wheat yield 3 monitoring. Remote Sens. 2016, 9, 296. [Google Scholar] [CrossRef]
- Moreno Ruiz, J.A.; Riaño, D.; Arbelo, M.; French, N.H.F.; Ustin, S.L.; Whiting, M.L. Burned area mapping time series in Canada (1984–1999) from NOAA-AVHRR LTDR: A comparison with other remote sensing products and fire perimeters. Remote Sens. Environ. 2012, 117, 407–414. [Google Scholar] [CrossRef]
- Claverie, M.; Matthews, J.L.; Vermote, E.F.; Justice, C.O. A 30+ Year AVHRR LAI and FAPAR Climate Data Record: Algorithm Description and Validation. Remote Sens. 2016, 8, 263. [Google Scholar] [CrossRef]
- Verger, A.; Baret, F.; Weiss, M.; Lacaze, R.; Makhmara, H.; Vermote, E. Long term consistent global GEOV1 AVHRR biophysical products. In Proceedings of the 1st EARSeL Workshop on Temporal Analysis of Satellite Images, Mykonos, Greece, 23–25 May 2012; Volume 2325, p. 2833. [Google Scholar]
- Wang, S.; Yin, H.; Yang, Q.; Yin, H.; Wang, X.; Peng, Y.; Shen, M. Spatiotemporal patterns of snow cover retrieved from NOAA-AVHRR LTDR: a case study in the Tibetan Plateau, China. Int. J. Dig. Earth 2017, 10, 504–521. [Google Scholar] [CrossRef]
- Julien, Y.; Sobrino, J.A. Monitoring global vegetation with the Yearly Land Cover Dynamics (YLCD) method. In Proceedings of the 2011 6th International Workshop on the Analysis of Multi-Temporal Remote Sensing Images (Multi-Temp), Trento, Italy, 12–14 July 2011; pp. 121–124. [Google Scholar]
- Hu, B.; Lucht, W.; Strahler, A.H.; Barker Schaaf, C.; Smith, M. Surface Albedos and Angle-Corrected NDVI from AVHRR Observations of South America. Remote Sens. Environ. 2000, 71, 119–132. [Google Scholar] [CrossRef]
- Saunders, R.W. The determination of broad band surface albedo from AVHRR visible and near-infrared radiances. Int. J. Remote Sens. 1990, 11, 49–67. [Google Scholar] [CrossRef]
- Strugnell, N.C.; Lucht, W.; Schaaf, C. A global albedo data set derived from AVHRR data for use in climate simulations. Geophys. Res. Lett. 2001, 28, 191–194. [Google Scholar] [CrossRef]
- Trishchenko, A.P.; Luo, Y.; Khlopenkov, K.V.; Wang, S. A Method to Derive the Multispectral Surface Albedo Consistent with MODIS from Historical AVHRR and VGT Satellite Data. J. Appl. Meteor. Climatol. 2008, 47, 1199–1221. [Google Scholar] [CrossRef]
- Bates, J.J.; Privette, J.L.; Kearns, E.J.; Glance, W.; Zhao, X. Sustained Production of Multidecadal Climate Records: Lessons from the NOAA Climate Data Record Program. Bull. Am. Meteorol. Soc. 2015, 97, 1573–1581. [Google Scholar] [CrossRef]
- Hollmann, R.; Merchant, C.J.; Saunders, R.; Downy, C.; Buchwitz, M.; Cazenave, A.; Chuvieco, E.; Defourny, P.; de Leeuw, G.; Forsberg, R.; et al. The ESA Climate Change Initiative: Satellite Data Records for Essential Climate Variables. Bull. Am. Meteorol. Soc. 2013, 94, 1541–1552. [Google Scholar] [CrossRef]
- Schulz, J.; Albert, P.; Behr, H.-D.; Caprion, D.; Deneke, H.; Dewitte, S.; Dürr, B.; Fuchs, P.; Gratzki, A.; Hechler, P.; et al. Operational climate monitoring from space: The EUMETSAT satellite application facility on climate monitoring (CM-SAF). Atmos. Chem. Phys. Discuss. 2008, 8, 8517–8563. [Google Scholar] [CrossRef]
- Bojinski, S.; Verstraete, M.; Peterson, T.C.; Richter, C.; Simmons, A.; Zemp, M. The Concept of Essential Climate Variables in Support of Climate Research, Applications, and Policy. Bull. Am. Meteorol. Soc. 2014, 95, 1431–1443. [Google Scholar] [CrossRef]
- Qu, Y.; Liang, S.; Liu, Q.; He, T.; Liu, S.; Li, X. Mapping Surface Broadband Albedo from Satellite Observations: A Review of Literatures on Algorithms and Products. Remote Sens. 2015, 7, 990–1020. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.-P.; et al. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.O.; Breon, F.M. Towards a Generalized Approach for Correction of the BRDF Effect in MODIS Directional Reflectances. IEEE Trans. Geosci. Remote Sens. 2009, 47, 898–908. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.; Skakun, S.; Roger, J.-C.; Santamaria-Artigas, A.; Villaescusa-Nadal, J.L.; Masek, J. Toward Landsat and Sentinel-2 BRDF Normalization and Albedo Estimation: A Case Study in the Peruvian Amazon Forest. Front. Earth Sci. 2018, 6, 185. [Google Scholar] [CrossRef]
- Vermote, E.F. MOD09A1 MODIS Surface Reflectance 8-Day L3 Global 500m SIN Grid V006; NASA: Washington, DC, USA, 2015.
- Vermote, E.; Vermeulen, A. Atmospheric Correction Algorithm: Spectral Reflectances (MOD09); ATBD: New York, NY, USA, 1999. [Google Scholar]
- LTDR (Land Long Term Data Record) Home. Available online: https://ltdr.modaps.eosdis.nasa.gov/cgi-bin/ltdr/ltdrPage.cgi?fileName=products (accessed on 11 January 2019).
- Baret, F.; Morissette, J.T.; Fernandes, R.A.; Champeaux, J.L.; Myneni, R.B.; Chen, J.; Plummer, S.; Weiss, M.; Bacour, C.; Garrigues, S.; et al. Evaluation of the representativeness of networks of sites for the global validation and intercomparison of land biophysical products: proposition of the CEOS-BELMANIP. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1794–1803. [Google Scholar] [CrossRef]
- Villaescusa-Nadal, J.L.; Franch, B.; Roger, J.; Vermote, E.F.; Skakun, S.; Justice, C. Spectral Adjustment Model’s Analysis and Application to Remote Sensing Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 1–12. [Google Scholar] [CrossRef]
- Roujean, J.-L.; Leroy, M.; Deschamps, P.-Y. A bidirectional reflectance model of the Earth’s surface for the correction of remote sensing data. J. Geophys. Res. 1992, 97, 20455–20468. [Google Scholar] [CrossRef]
- Maignan, F.; Bréon, F.-M.; Lacaze, R. Bidirectional reflectance of Earth targets: evaluation of analytical models using a large set of spaceborne measurements with emphasis on the Hot Spot. Remote Sens. Environ. 2004, 90, 210–220. [Google Scholar] [CrossRef]
- Bréon, F.-M.; Vermote, E. Correction of MODIS surface reflectance time series for BRDF effects. Remote Sens. Environ. 2012, 125, 1–9. [Google Scholar] [CrossRef]
- Vermote, E.F.; El Saleous, N.Z.; Justice, C.O. Atmospheric correction of MODIS data in the visible to middle infrared: First results. Remote Sens. Environ. 2002, 83, 97–111. [Google Scholar] [CrossRef]
- Marticorena; Chazette, P.; Bergametti, G.; Dulac, F.; Legrand, M. Mapping the aerodynamic roughness length of desert surfaces from the POLDER/ADEOS bi-directional reflectance product. Int. J. Remote Sens. 2004, 25, 603–626. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.F.; Sobrino, J.A.; Julien, Y. Retrieval of Surface Albedo on a Daily Basis: Application to MODIS Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7549–7558. [Google Scholar] [CrossRef]
- Marticorena, B.; Kardous, M.; Bergametti, G.; Callot, Y.; Chazette, P.; Khatteli, H.; Le Hégarat-Mascle, S.; Maillé, M.; Rajot, J.-L.; Vidal-Madjar, D.; et al. Surface and aerodynamic roughness in arid and semiarid areas and their relation to radar backscatter coefficient. J. Geophys. Res. 2006, 111, F03017. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.F.; Sobrino, J.A.; Fédèle, E. Analysis of directional effects on atmospheric correction. Remote Sens. Environ. 2013, 128, 276–288. [Google Scholar] [CrossRef]
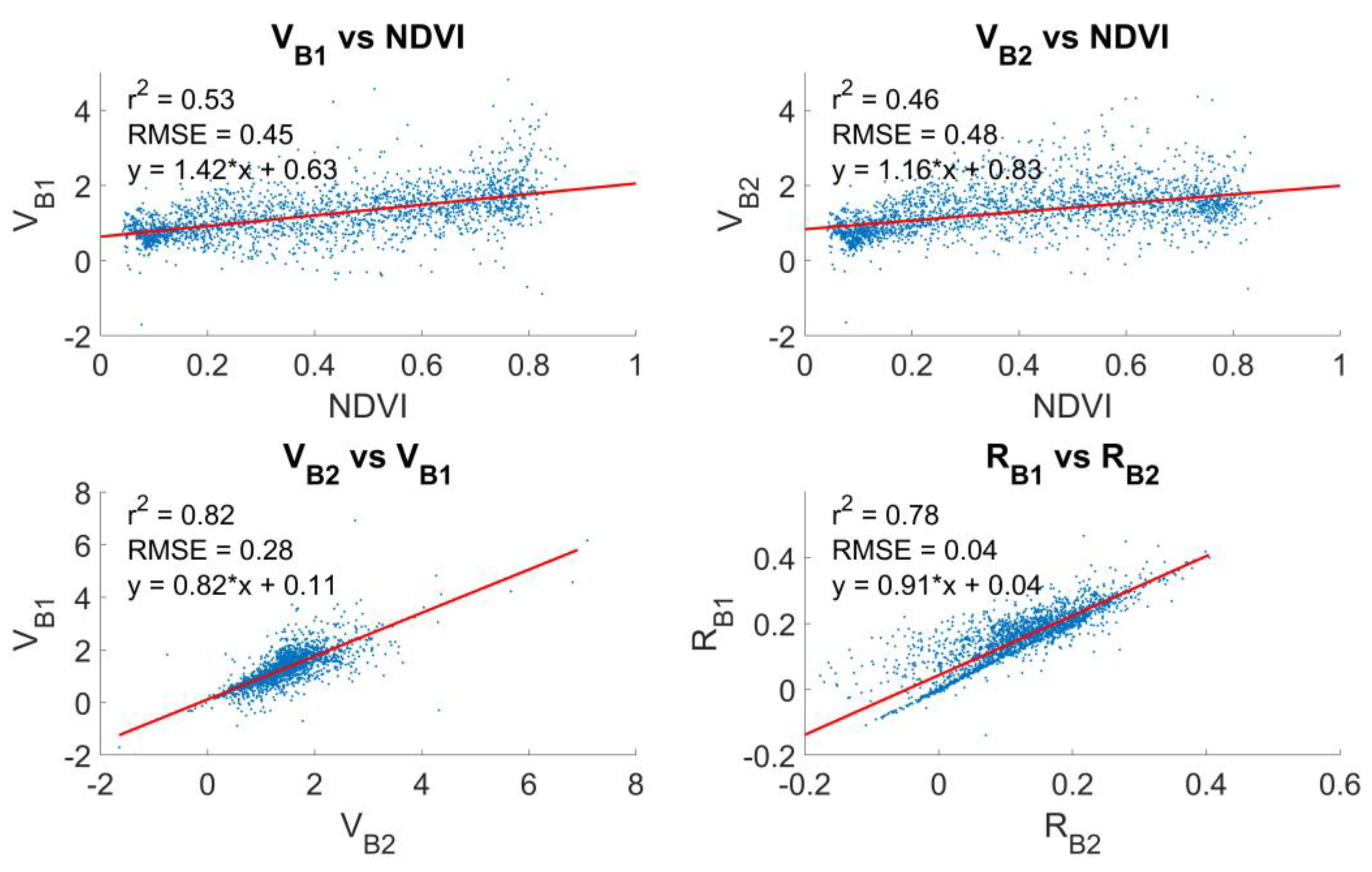
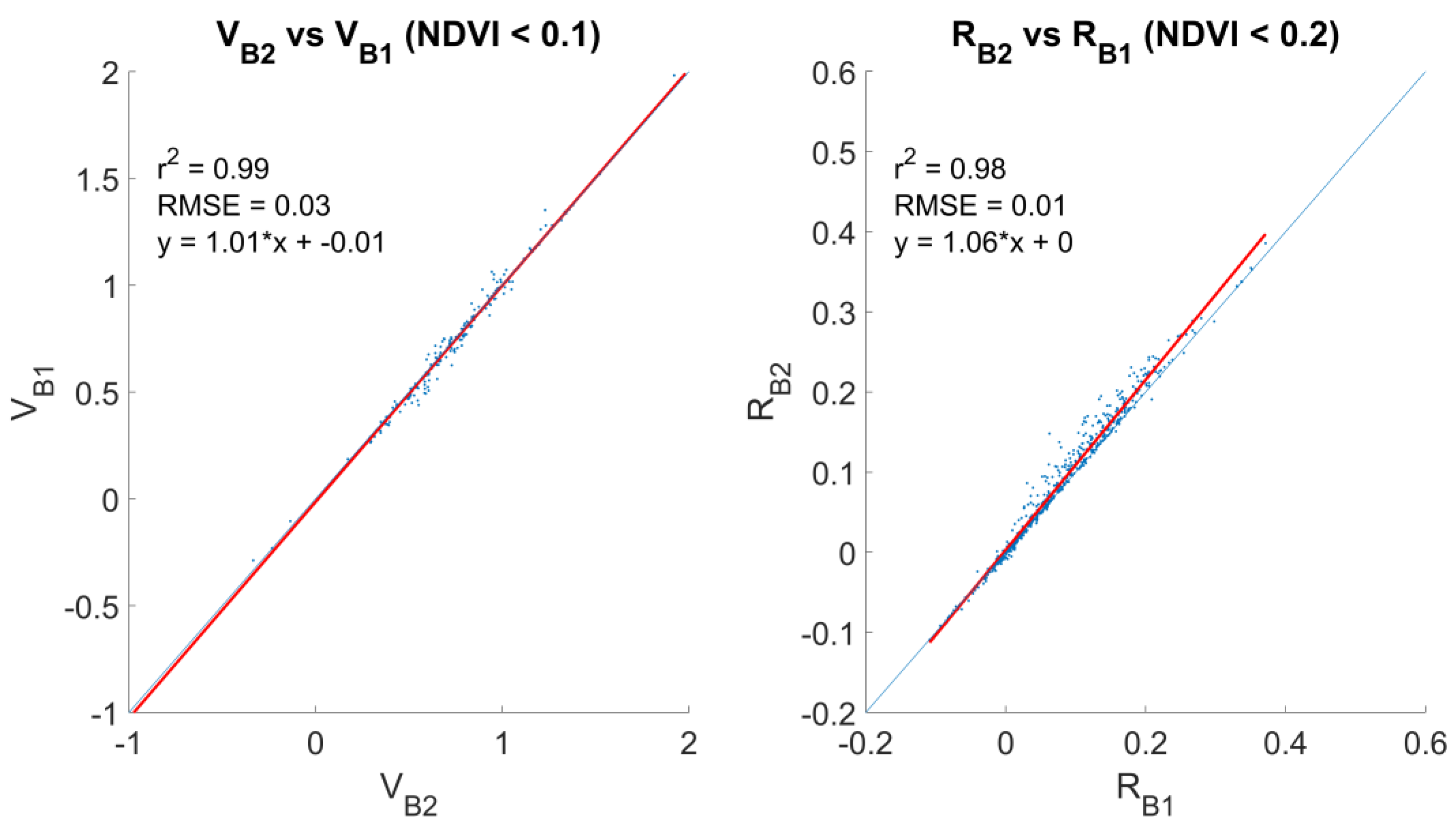
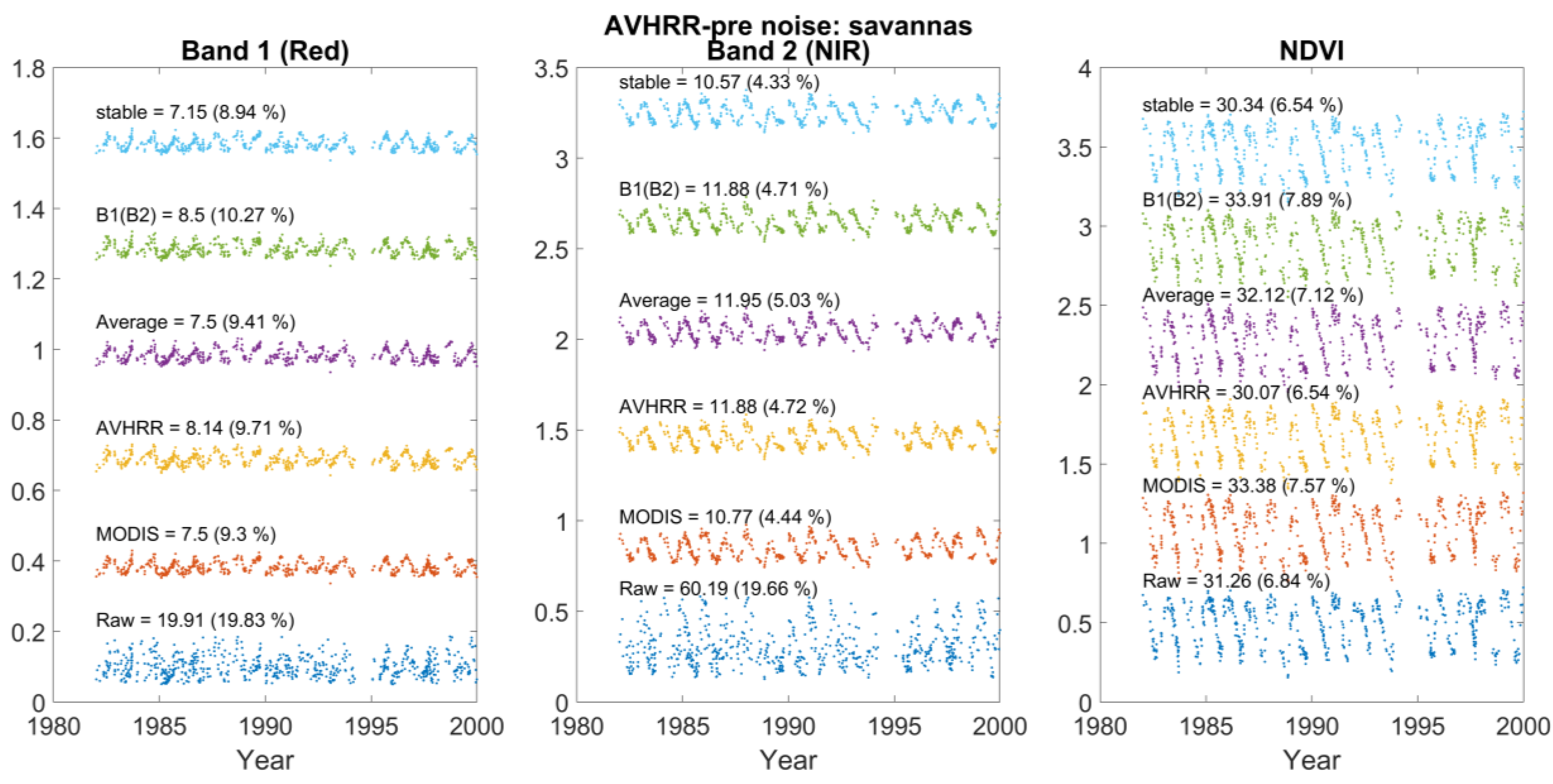
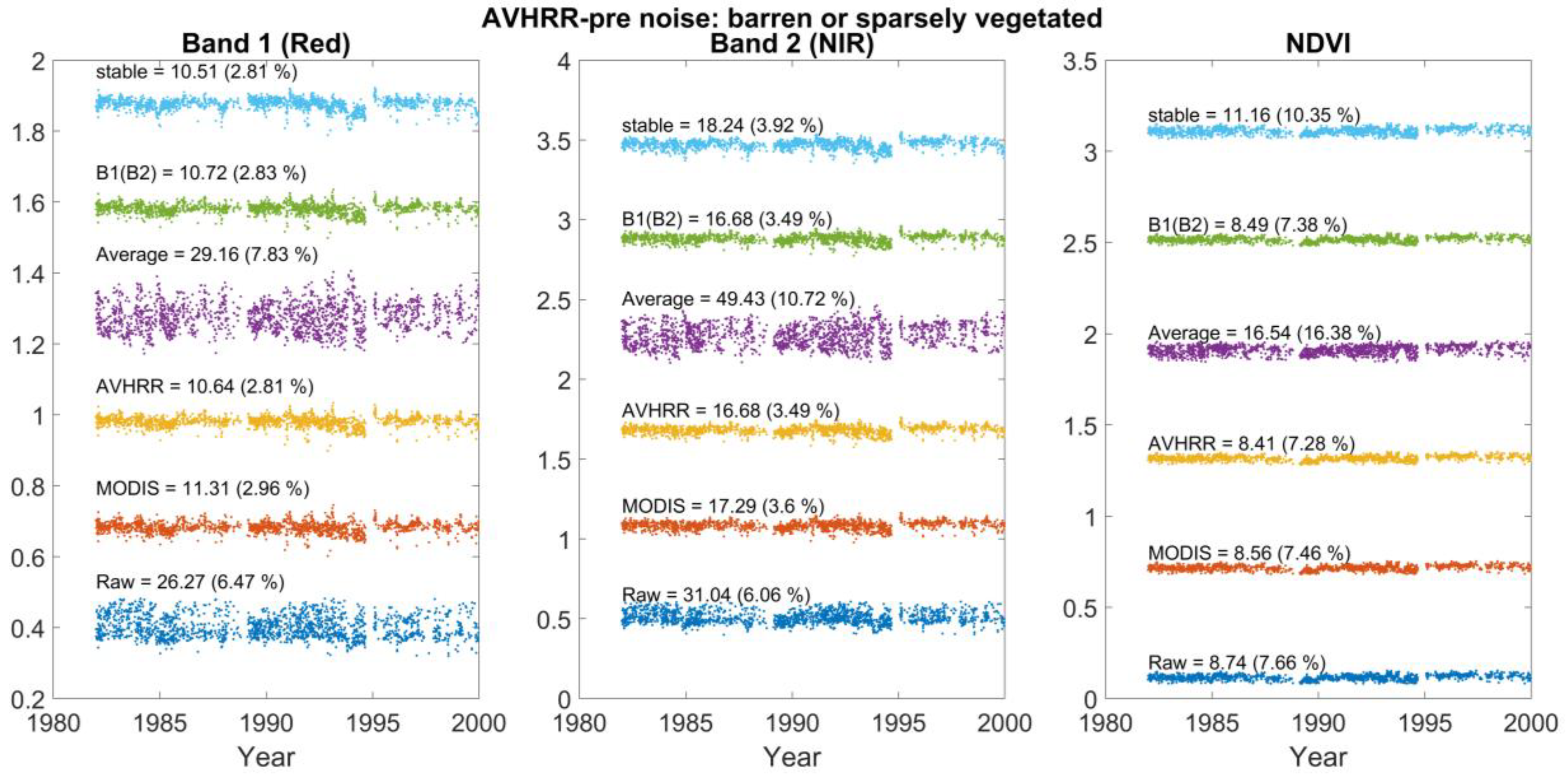
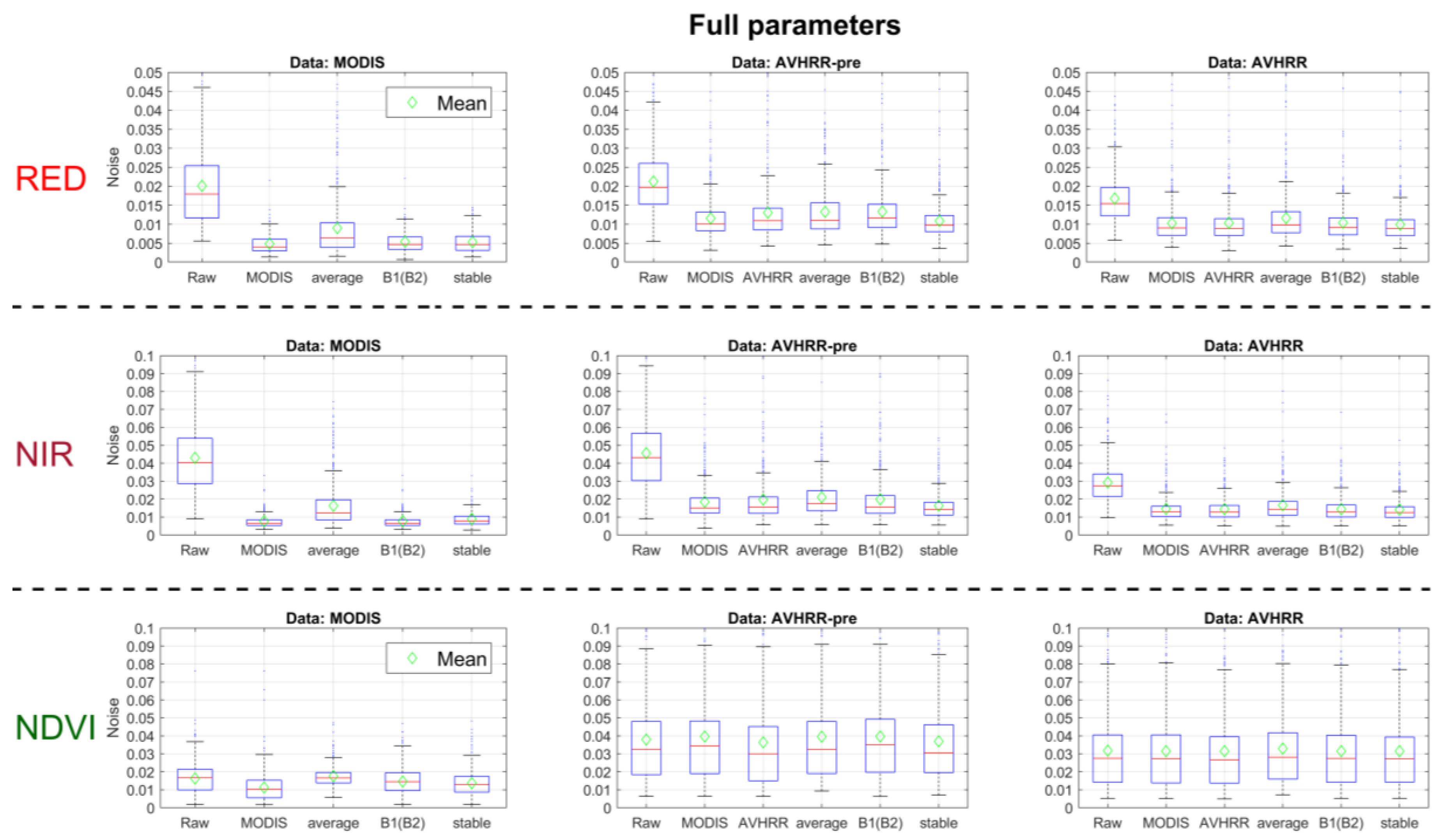
| Band 1 (red) | V = NDVI + 0.50 | R = 0.20*NDVI + 0.10 |
| Band 2 (NIR) | V = 2.00*NDVI + 0.50 | R = −0.05*NDVI + 0.15 |
| Red | NIR | NDVI | |||||
|---|---|---|---|---|---|---|---|
| Full | 3-Year | Full | 3-Year | Full | 3-Year | ||
| MODIS | Raw | 201.42 | 201.42 | 430.45 | 430.45 | 162.21 | 162.21 |
| Corrected | 48.38 (75.98%) | 53.44 (73.47%) | 76.23 (82.29%) | 107.80 (74.96%) | 113.20 (30.22%) | 121.19 (25.29%) | |
| AVHRR pre | Raw | 212.97 | 212.97 | 456.51 | 456.51 | 379.83 | 379.83 |
| Corrected | 130.46 (38.74%) | 130.16 (38.88%) | 198.10 (56.61%) | 230.63 (49.48%) | 363.58 (4.28%) | 389.08 (−2.43%) | |
| AVHRR | Raw | 168.22 | 168.22 | 292.62 | 292.62 | 317.32 | 317.32 |
| Corrected | 103.73 (38.34%) | 106.58 (36.64%) | 144.02 (50.78%) | 158.68 (45.77%) | 315.33 (0.63%) | 319.48 (−0.68%) | |
| Red | NIR | NDVI | ||
|---|---|---|---|---|
| MODIS | Raw | 201.42 | 430.45 | 162.21 |
| MODIS | 48.94 (75.70%) | 76.23 (82.29%) | 113.20 (30.22%) | |
| Average | 90.19 (55.22%) | 163.47 (62.02%) | 175.16 (−7.98%) | |
| B1(B2) | 53.28 (73.55%) | 76.28 (82.28%) | 146.00 (10.00%) | |
| Stable | 53.33 (73.52%) | 89.74 (79.15%) | 136.81 (15.66%) | |
| AVHRR pre | Raw | 212.97 | 456.51 | 379.83 |
| MODIS | 115.96 (45.55%) | 184.07 (59.68%) | 396.65 (−4.43%) | |
| AVHRR-pre | 126.98 (40.37%) | 198.10 (56.61%) | 363.58 (4.28%) | |
| Average | 132.78 (37.65%) | 210.16 (53.96%) | 394.81 (−3.94%) | |
| B1(B2) | 134.41 (36.89%) | 199.32 (56.34%) | 397.18 (−4.57%) | |
| Stable | 108.75 (48.93%) | 163.30 (64.23%) | 368.93 (2.87%) | |
| AVHRR | Raw | 168.22 | 292.62 | 317.32 |
| MODIS | 103.42 (38.52%) | 145.35 (50.33%) | 314.67 (0.84%) | |
| AVHRR | 104.08 (38.13%) | 144.02 (50.78%) | 315.33 (0.63%) | |
| Average | 116.37 (30.82%) | 166.03 (43.26%) | 329.07 (−3.70%) | |
| B1(B2) | 105.14 (37.50%) | 144.74 (50.53%) | 315.00 (0.73%) | |
| Stable | 99.28 (40.98%) | 140.84 (51.87%) | 314.92 (0.76%) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villaescusa-Nadal, J.L.; Franch, B.; Vermote, E.F.; Roger, J.-C. Improving the AVHRR Long Term Data Record BRDF Correction. Remote Sens. 2019, 11, 502. https://doi.org/10.3390/rs11050502
Villaescusa-Nadal JL, Franch B, Vermote EF, Roger J-C. Improving the AVHRR Long Term Data Record BRDF Correction. Remote Sensing. 2019; 11(5):502. https://doi.org/10.3390/rs11050502
Chicago/Turabian StyleVillaescusa-Nadal, Jose Luis, Belen Franch, Eric F. Vermote, and Jean-Claude Roger. 2019. "Improving the AVHRR Long Term Data Record BRDF Correction" Remote Sensing 11, no. 5: 502. https://doi.org/10.3390/rs11050502
APA StyleVillaescusa-Nadal, J. L., Franch, B., Vermote, E. F., & Roger, J.-C. (2019). Improving the AVHRR Long Term Data Record BRDF Correction. Remote Sensing, 11(5), 502. https://doi.org/10.3390/rs11050502