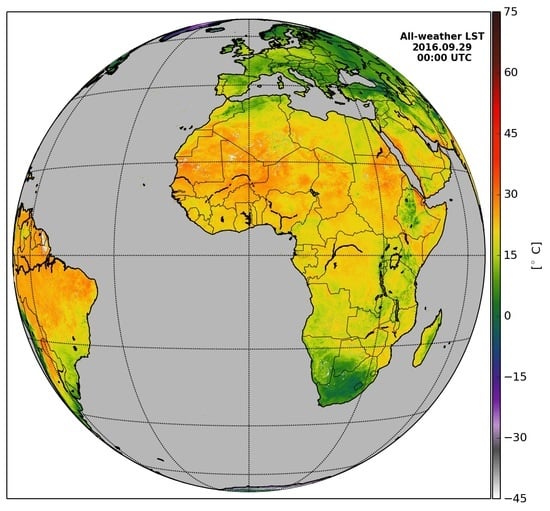
An All-Weather Land Surface Temperature Product Based on MSG/SEVIRI Observations
Abstract
1. Introduction
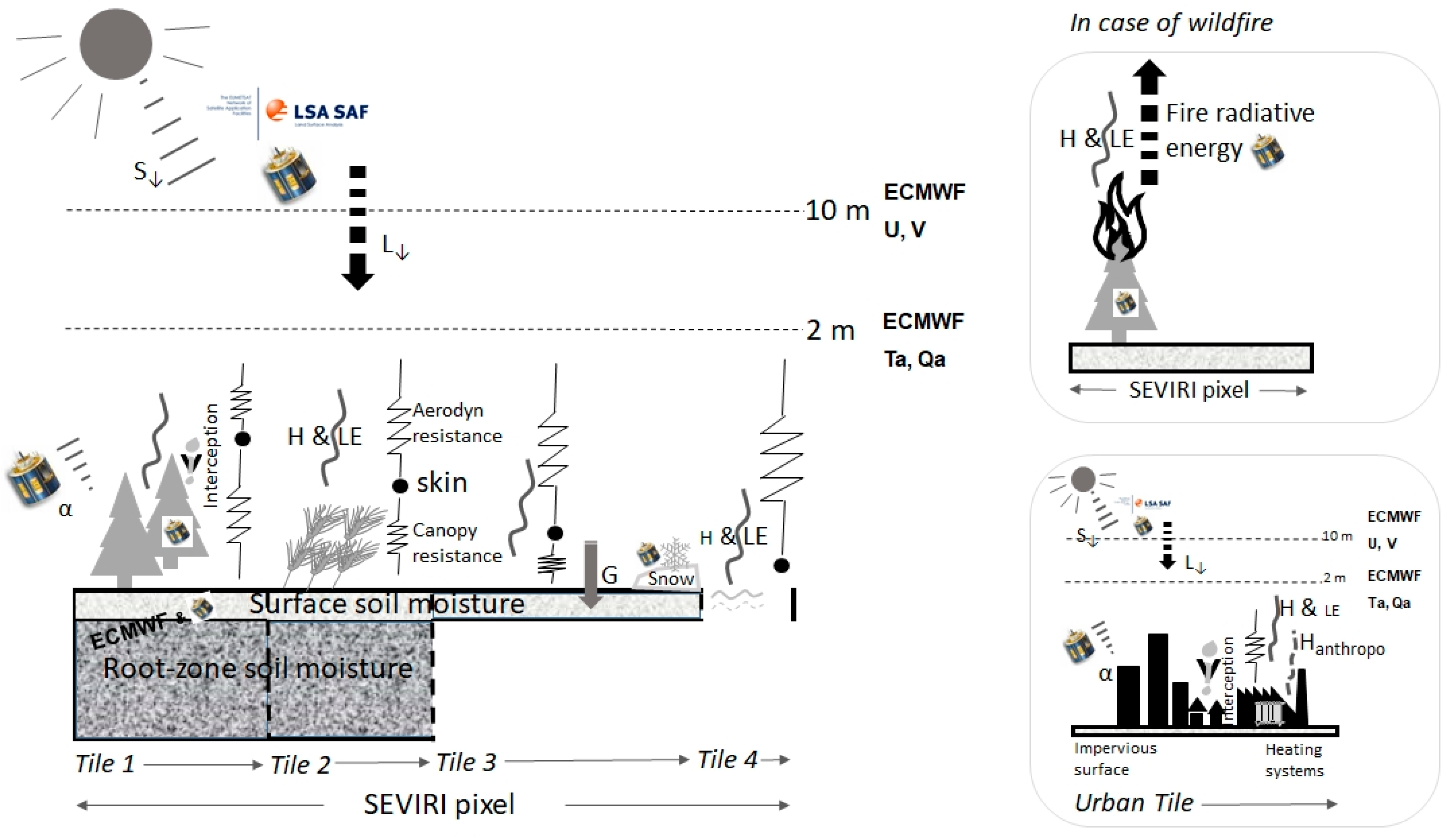
2. Methodology and Datasets
2.1. Satellite Application Facility on Land Surface Analysis (LSA-SAF) All-Weather Land Surface Temperature (LST)
2.1.1. Clear Sky
2.1.2. Cloudy Sky
2.2. Microwave-Based Advanced Microwave Scanning Radiometer-Earth Observing System (AMSR-E) LST
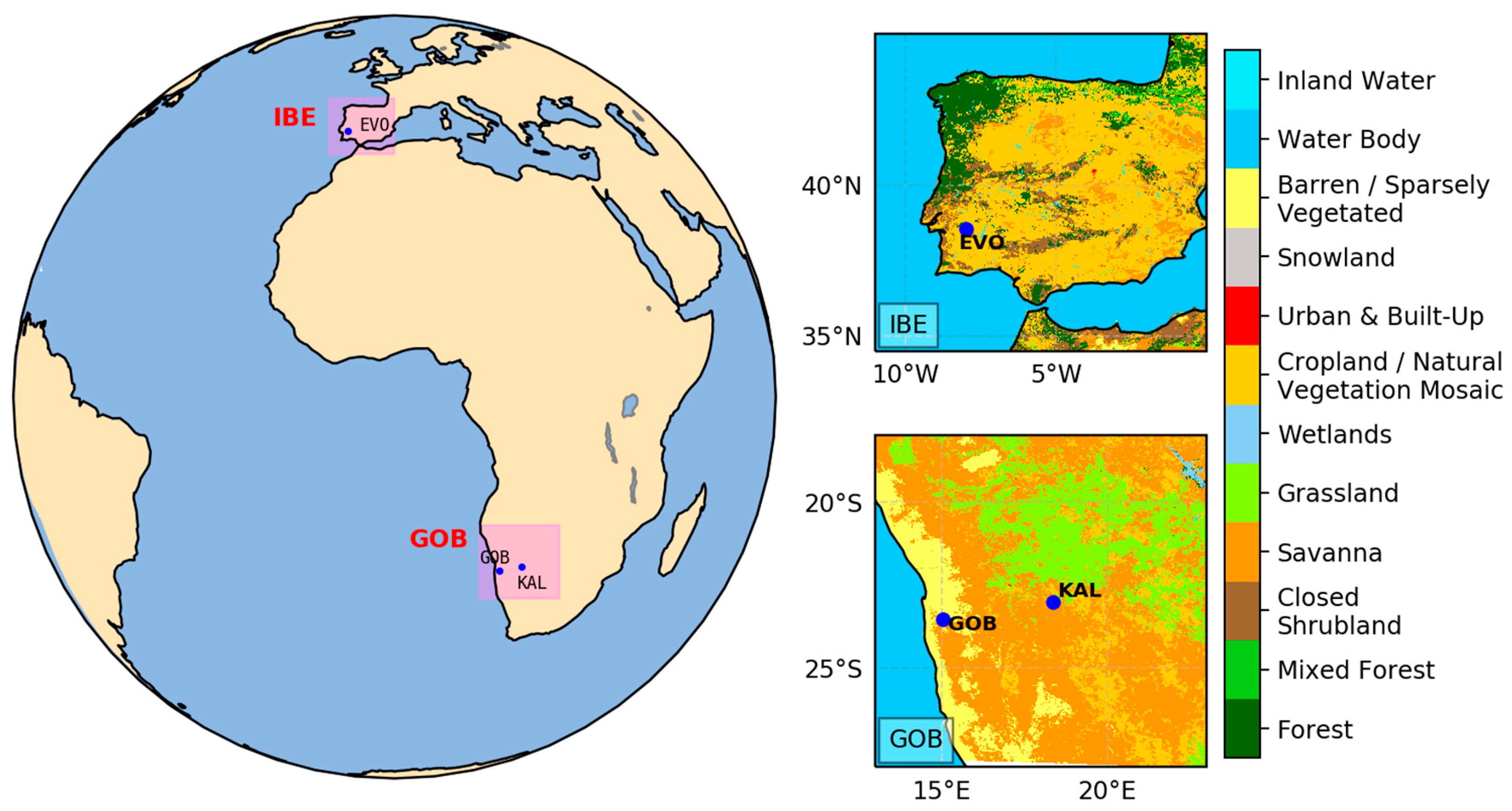
2.3. In Situ LST
2.4. Statistical Metrics
3. Results
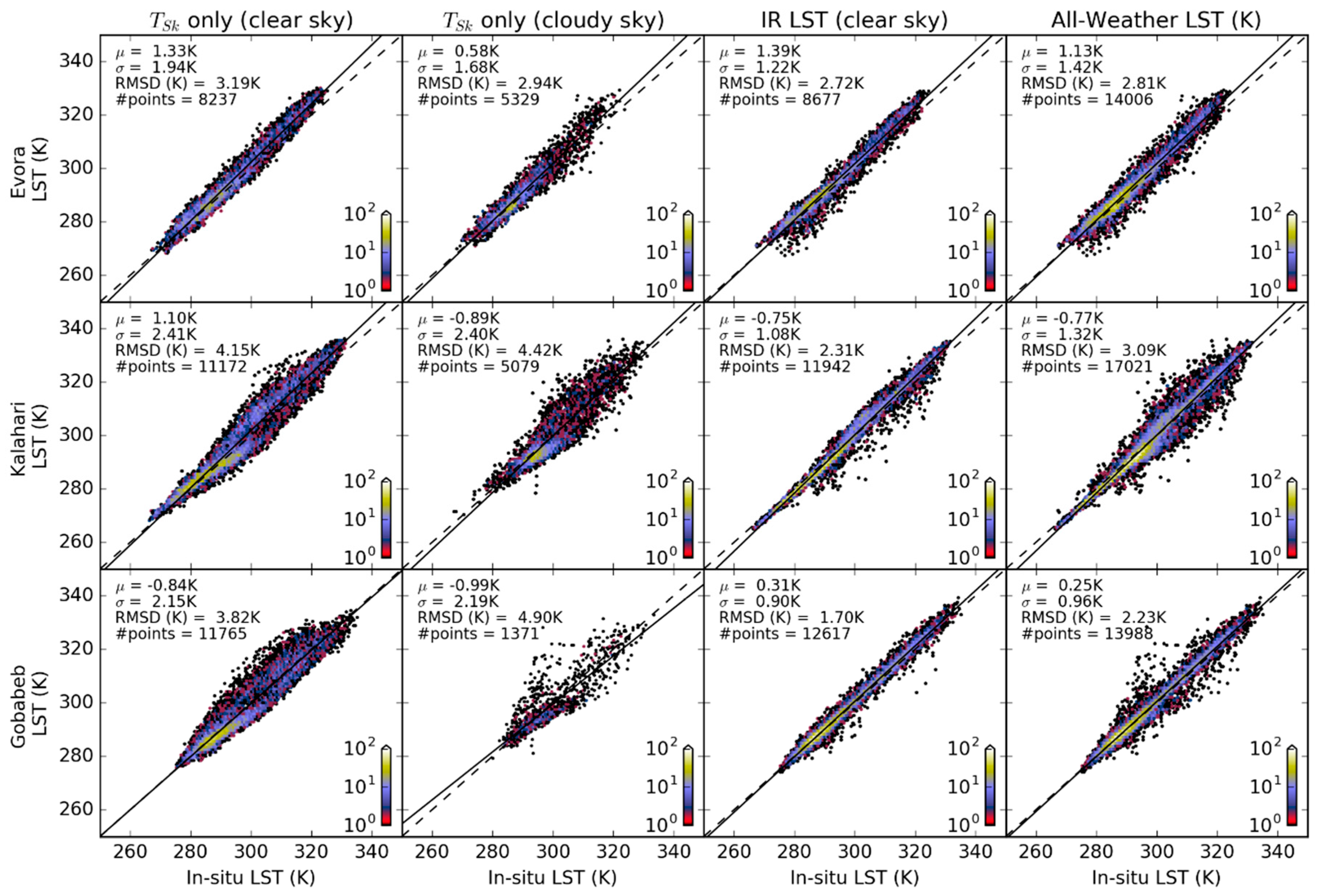
3.1. Infrared (IR) and Energy Balance (EB) Model Comparison in Clear Sky Situations
3.2. IR and EB Model In Situ Comparisons
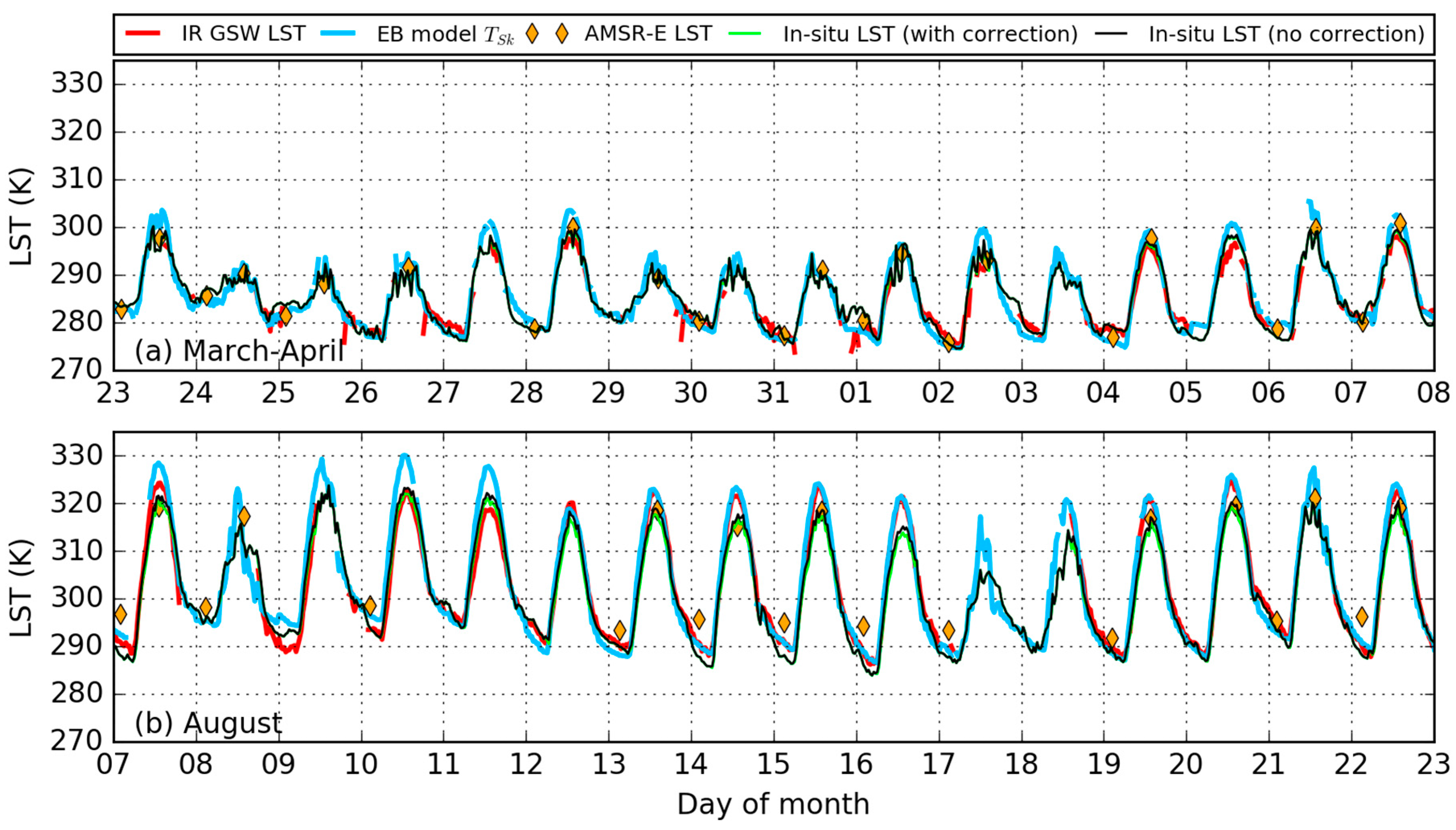
3.2.1. Time Series
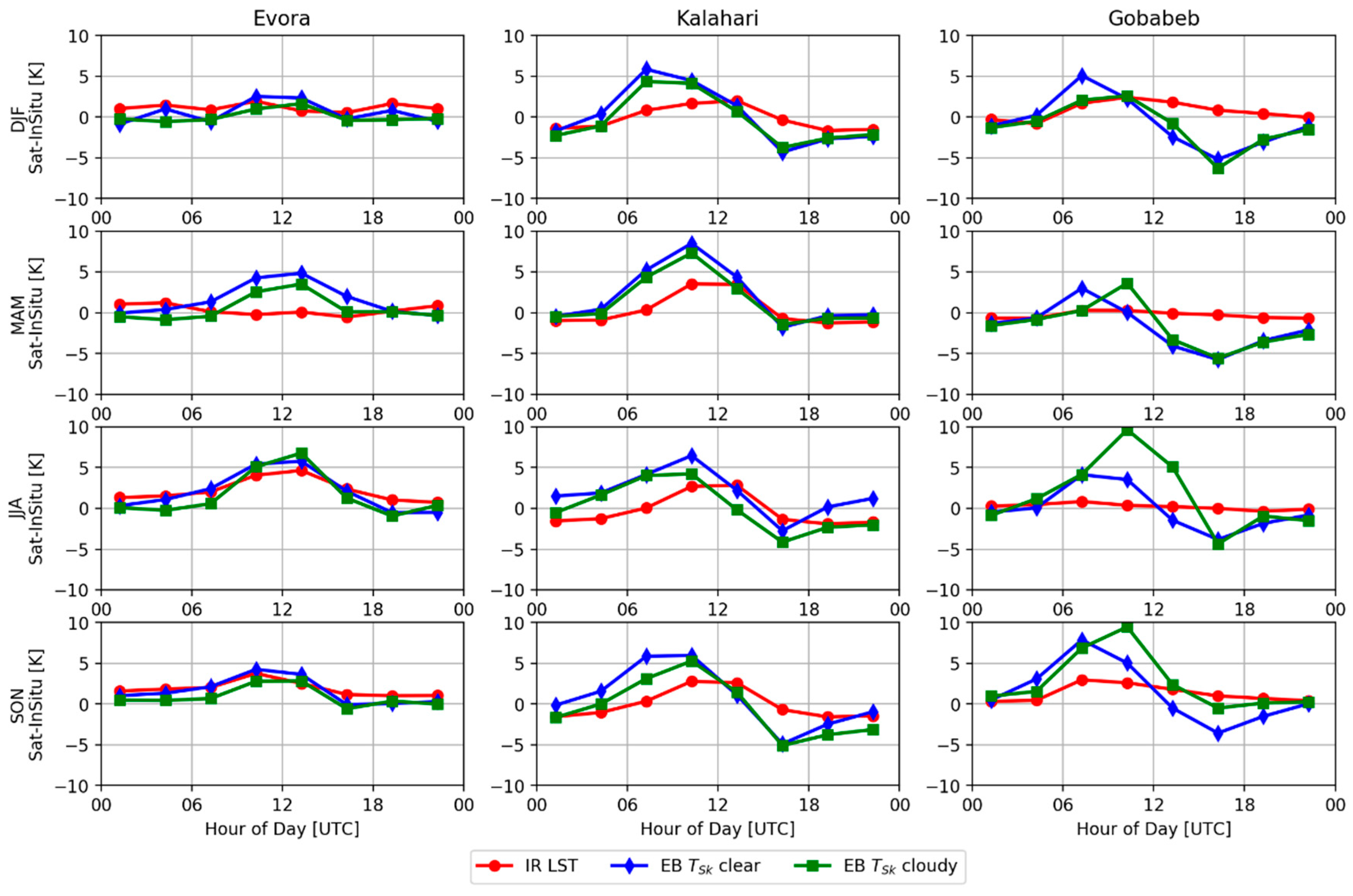
3.2.2. Median Diurnal Cycle of Error
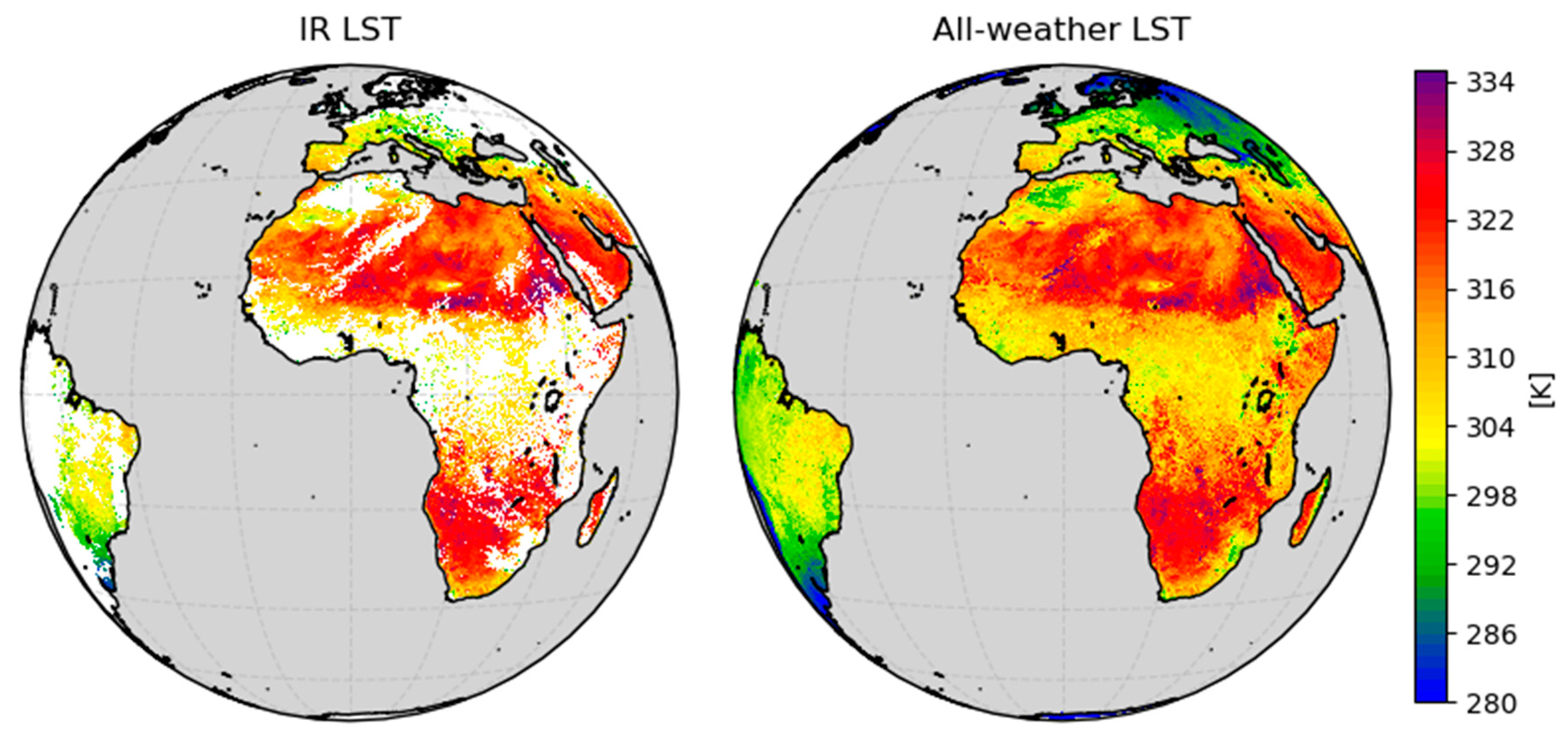
3.3. Comparison to AMSR-E
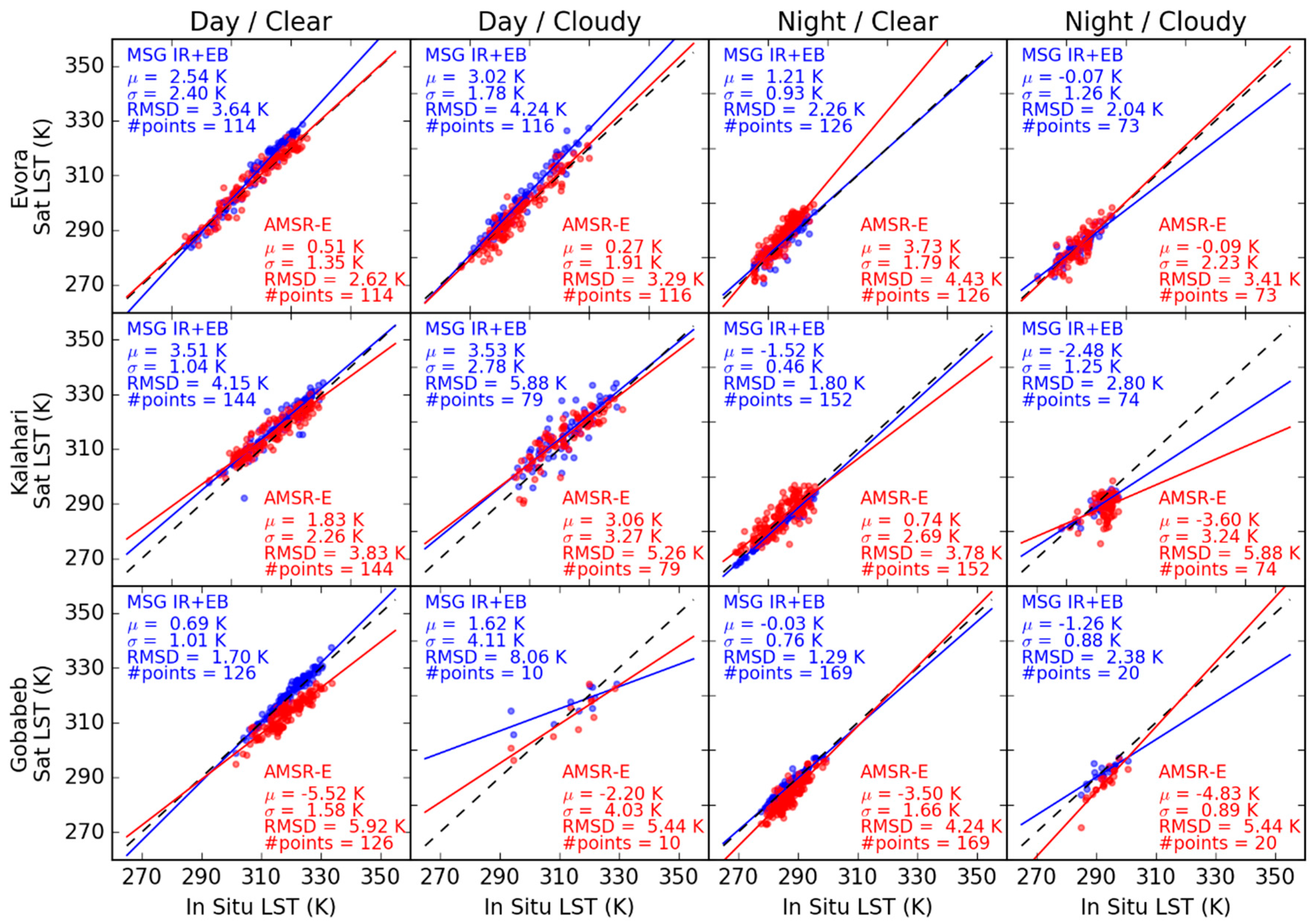
3.3.1. In Situ Comparisons
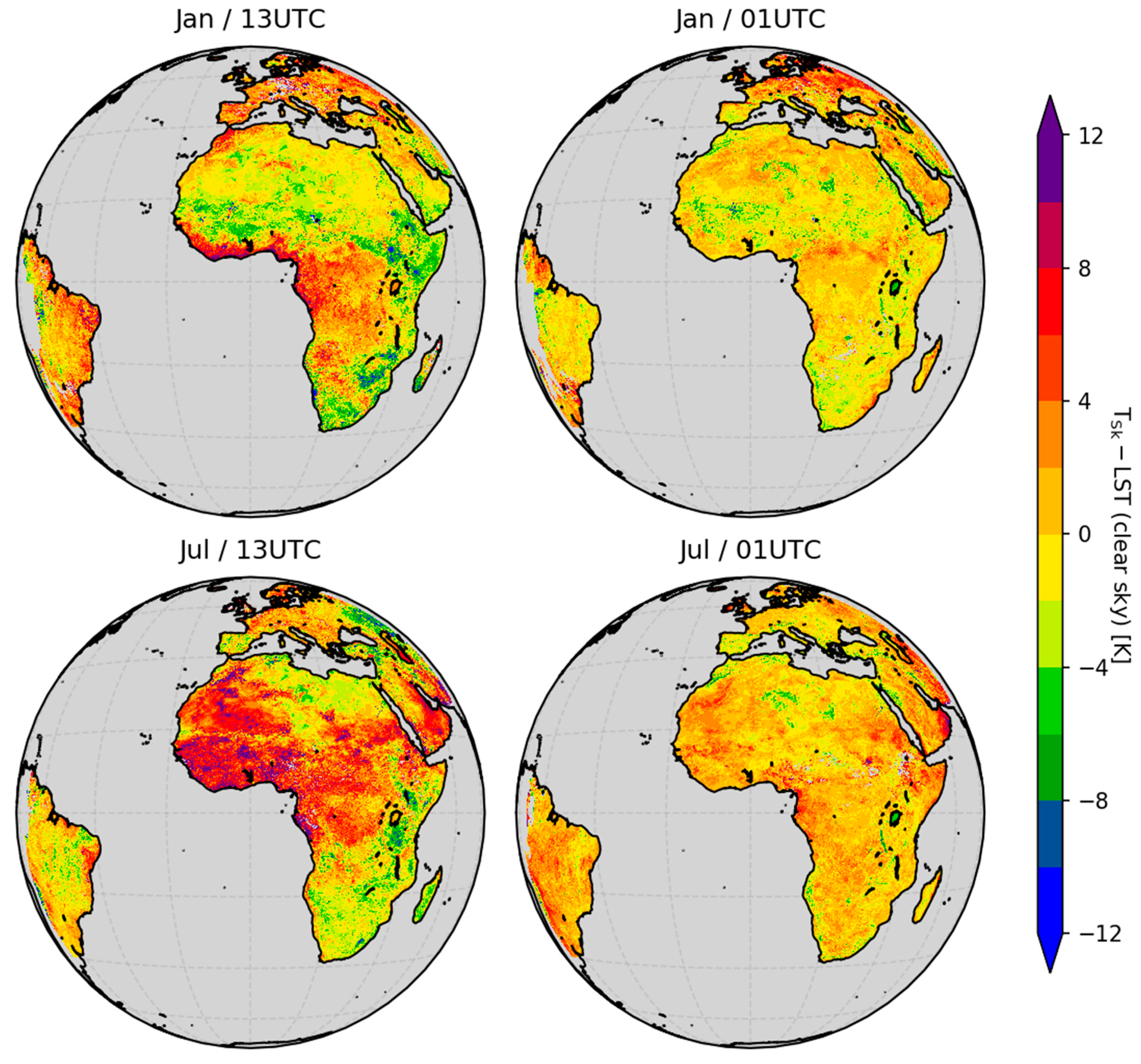
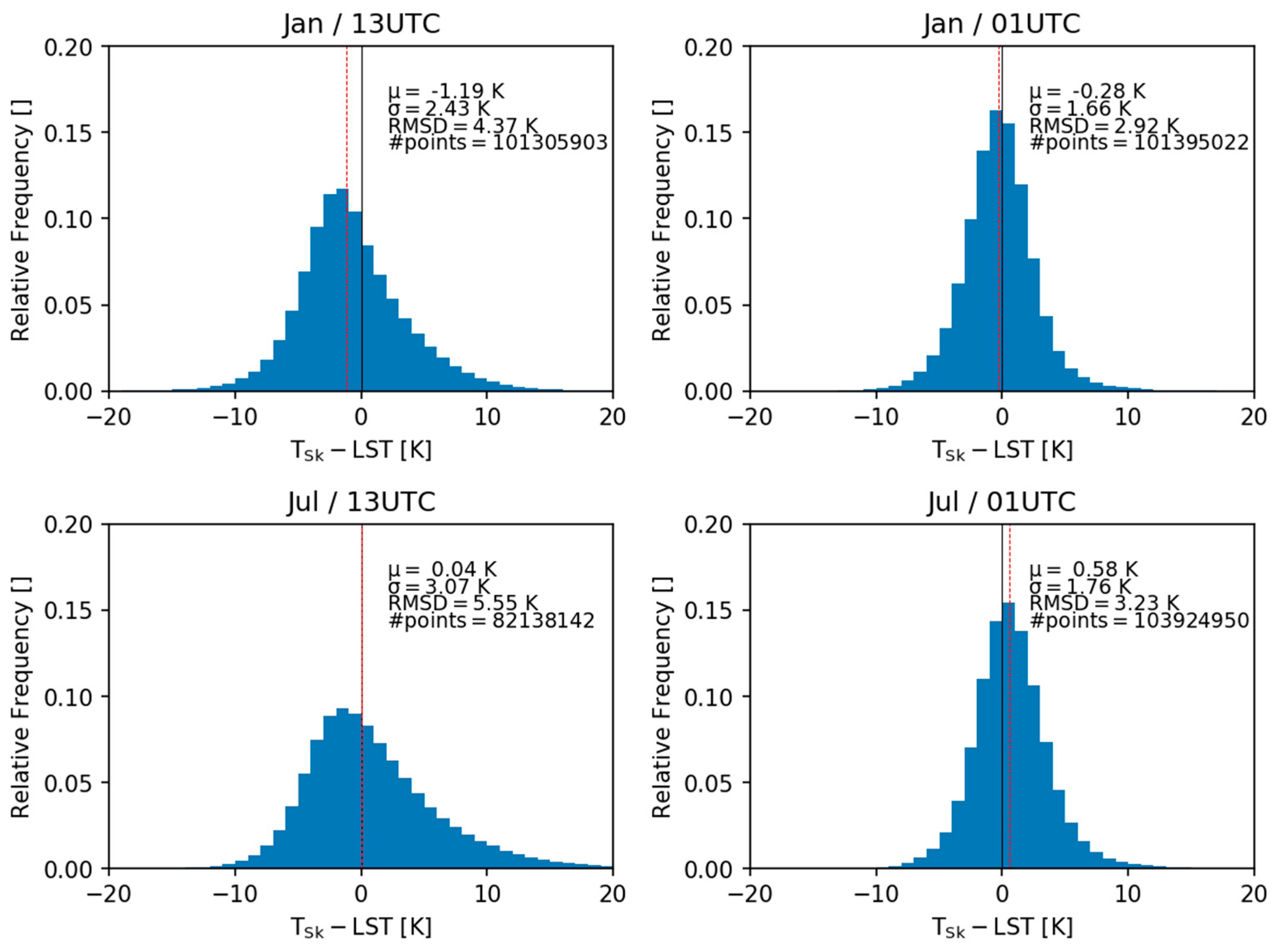
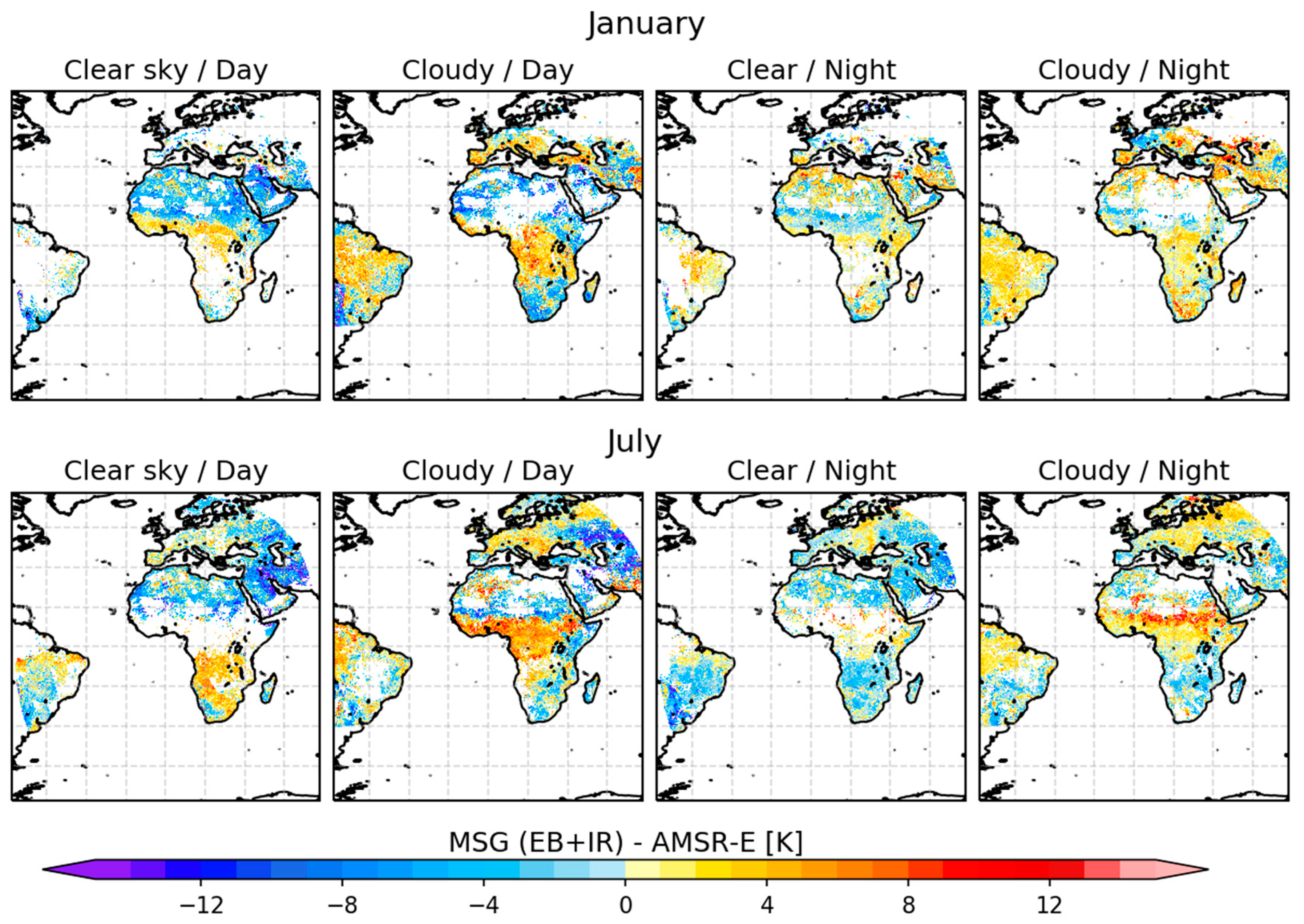
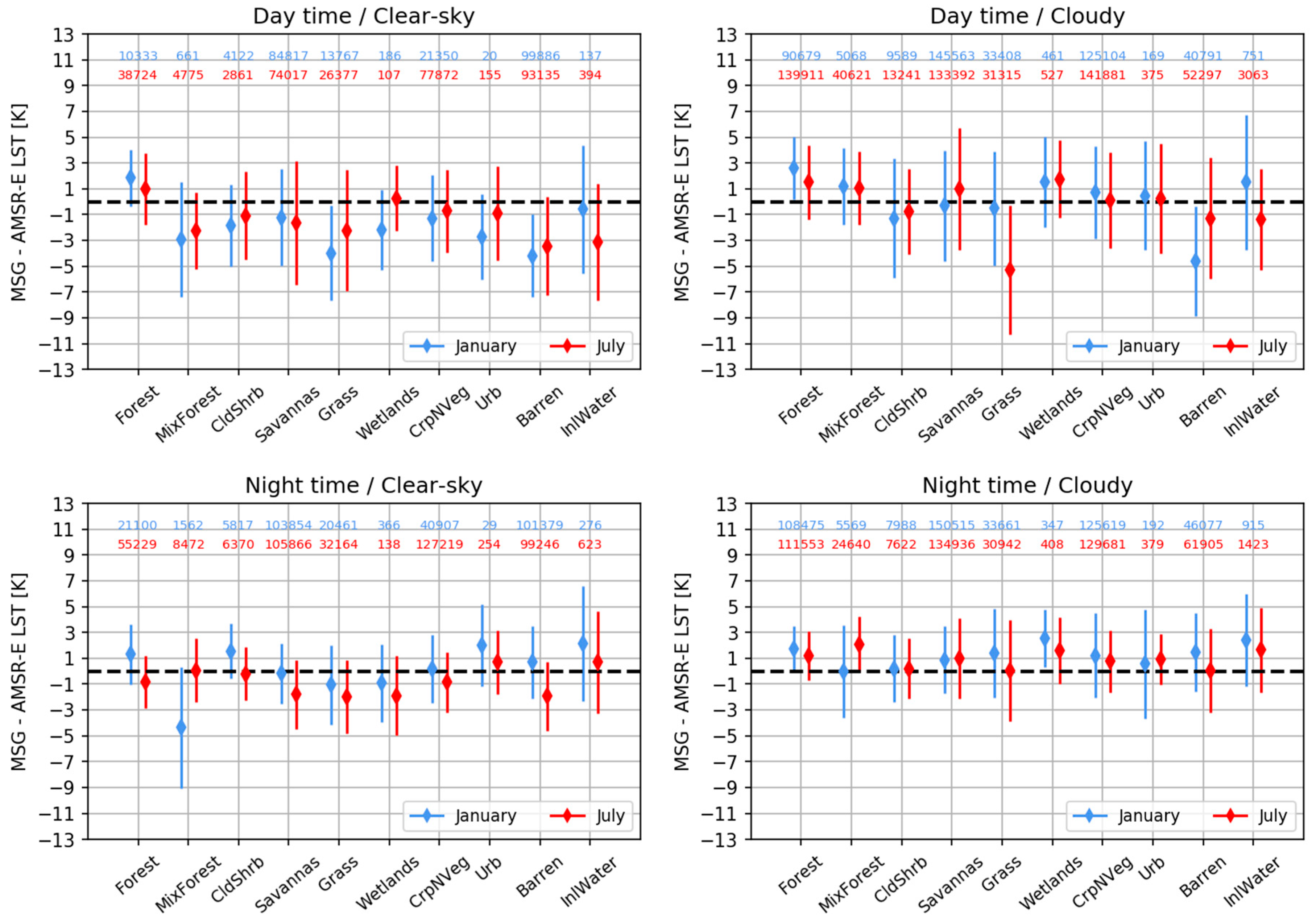
3.3.2. Spatial Comparisons
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Norman, J.M.; Becker, F. Terminology in thermal infrared remote sensing of natural surfaces. Agric. For. Meteorol. 1995, 77, 153–166. [Google Scholar] [CrossRef]
- Lakshmi, V. A simple surface temperature assimilation scheme for use in land surface models. Water Resour. Res. 2000, 36, 3687–3700. [Google Scholar] [CrossRef]
- Schmugge, T.J.; Becker, F. Remote Sensing Observations for the Monitoring of Land-Surface Fluxes and Water Budgets. In Land Surface Evaporation; Schmugge, T.J., André, J.C., Eds.; Springer: New York, NY, USA, 1991; pp. 337–347. ISBN 978-1-4612-3032-8. [Google Scholar]
- Caparrini, F.; Castelli, F.; Entekhabi, D. Variational estimation of soil and vegetation turbulent transfer and heat flux parameters from sequences of multisensor imagery. Water Resour. Res. 2004, 40, 1–15. [Google Scholar] [CrossRef]
- Ghilain, N.; Arboleda, A.; Batelaan, O.; Ardö, J.; Trigo, I.; Barrios, J.-M.; Gellens-Meulenberghs, F. A New Retrieval Algorithm for Soil Moisture Index from Thermal Infrared Sensor On-Board Geostationary Satellites over Europe and Africa and Its Validation. Remote Sens. 2019, 11, 1968. [Google Scholar] [CrossRef]
- Freitas, S.C.; Trigo, I.F.; Macedo, J.; Barroso, C.; Silva, R.; Perdigão, R. Land surface temperature from multiple geostationary satellites. Int. J. Remote Sens. 2013, 34, 3051–3068. [Google Scholar] [CrossRef]
- Bojinski, S.; Verstraete, M.; Peterson, T.C.; Richter, C.; Simmons, A.; Zemp, M. The concept of essential climate variables in support of climate research, applications, and policy. Bull. Am. Meteorol. Soc. 2014, 95, 1431–1443. [Google Scholar] [CrossRef]
- Good, E.J. An in situ-based analysis of the relationship between land surface “skin” and screen-level air temperatures. J. Geophys. Res. 2016, 121, 8801–8819. [Google Scholar] [CrossRef]
- Orth, R.; Dutra, E.; Trigo, I.F.; Balsamo, G. Advancing land surface model development with satellite-based Earth observations. Hydrol. Earth Syst. Sci. 2017, 21, 2483–2495. [Google Scholar] [CrossRef]
- Trigo, I.F.; Boussetta, S.; Viterbo, P.; Balsamo, G.; Beljaars, A.; Sandu, I. Comparison of model land skin temperature with remotely sensed estimates and assessment of surface-atmosphere coupling. J. Geophys. Res. Atmos. 2015, 120, 12096–12111. [Google Scholar] [CrossRef]
- Johannsen, F.; Ermida, S.; Martins, J.P.A.; Trigo, I.F.; Nogueira, M.; Dutra, E. Cold Bias of ERA5 Summertime Daily Maximum Land Surface Temperature over Iberian Peninsula. Remote Sens. 2019, 11, 2570. [Google Scholar] [CrossRef]
- Wang, A.; Barlage, M.; Zeng, X.; Draper, C.S. Comparison of land skin temperature from a land model, remote sensing, and in situ measurement. J. Geophys. Res. Atmos. 2014, 119, 3093–3106. [Google Scholar] [CrossRef]
- Trigo, I.F.; Viterbo, P. Clear-Sky Window Channel Radiances: A Comparison between Observations and the ECMWF Model. J. Appl. Meteorol. 2003, 42, 1463–1479. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Trigo, I.F.; Monteiro, I.T.; Olesen, F.; Kabsch, E. An assessment of remotely sensed land surface temperature. J. Geophys. Res. 2008, 113, 1–12. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A Generalized Split-Window Algorithm for Retrieving Land-Surface Temperature from Space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Göttsche, F.M.; Olesen, F.S.; Trigo, I.F.; Bork-Unkelbach, A.; Martin, M.A. Long term validation of land surface temperature retrieved from MSG/SEVIRI with continuous in-situ measurements in Africa. Remote Sens. 2016, 8, 410. [Google Scholar] [CrossRef]
- Ermida, S.L.; Trigo, I.F.; DaCamara, C.C.; Göttsche, F.M.; Olesen, F.S.; Hulley, G. Validation of remotely sensed surface temperature over an oak woodland landscape-The problem of viewing and illumination geometries. Remote Sens. Environ. 2014, 148, 16–27. [Google Scholar] [CrossRef]
- Freitas, S.C.; Trigo, I.F.; Bioucas-dias, J.M.; Göttsche, F. Quantifying the Uncertainty of Land Surface Temperature Retrievals from SEVIRI/Meteosat. IEEE Trans. Geosci. Remote Sens. 2009, 48, 523–534. [Google Scholar] [CrossRef]
- Göttsche, F.M.; Olesen, F.S.; Bork-Unkelbach, A. Validation of land surface temperature derived from MSG/SEVIRI with in situ measurements at Gobabeb, Namibia. Int. J. Remote Sens. 2013, 34, 3069–3083. [Google Scholar] [CrossRef]
- Duan, S.B.; Li, Z.L.; Leng, P. A framework for the retrieval of all-weather land surface temperature at a high spatial resolution from polar-orbiting thermal infrared and passive microwave data. Remote Sens. Environ. 2017. [Google Scholar] [CrossRef]
- Crosson, W.L.; Al-Hamdan, M.Z.; Hemmings, S.N.J.; Wade, G.M. A daily merged MODIS Aqua-Terra land surface temperature data set for the conterminous United States. Remote Sens. Environ. 2012. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C.; Zhao, H.; Lu, Z. Retrievals of all-weather daytime land surface temperature from FengYun-2D data. Opt. Express 2017, 25, 27210. [Google Scholar] [CrossRef] [PubMed]
- Ermida, S.L.; Trigo, I.F.; DaCamara, C.C.; Jiménez, C.; Prigent, C. Quantifying the Clear-Sky Bias of Satellite Land Surface Temperature Using Microwave-Based Estimates. J. Geophys. Res. Atmos. 2019, 124, 844–857. [Google Scholar] [CrossRef]
- Jimenez, C.; Prigent, C.; Ermida, S.L.; Moncet, J.-L. Inversion of AMSR-E observations for land surface temperature estimation: 1. Methodology and evaluation with station temperature. J. Geophys. Res. Atmos. 2017, 122, 3330–3347. [Google Scholar] [CrossRef]
- Ermida, S.L.; Jimenez, C.; Prigent, C.; Trigo, I.F.; Dacamara, C.C. Inversion of AMSR-E observations for land surface temperature estimation: 2. Global comparison with infrared satellite temperature. J. Geophys. Res. Atmos. 2017, 122, 3348–3360. [Google Scholar] [CrossRef]
- Gao, H.; Fu, R.; Dickinson, R.E.; Juárez, R.I.N. A practical method for retrieving land surface temperature from AMSR-E over the amazon forest. IEEE Trans. Geosci. Remote Sens. 2008. [Google Scholar] [CrossRef]
- Holmes, T.R.H.; De Jeu, R.A.M.; Owe, M.; Dolman, A.J. Land surface temperature from Ka band (37 GHz) passive microwave observations. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Jang, K.; Kang, S.; Kimball, J.S.; Hong, S.Y. Retrievals of all-weather daily air temperature using MODIS and AMSR-E data. Remote Sens. 2014. [Google Scholar] [CrossRef]
- Zhao, E.; Gao, C.; Jiang, X.; Liu, Z. Land surface temperature retrieval from AMSR-E passive microwave data. Opt. Express 2017, 25, A940–A952. [Google Scholar] [CrossRef]
- Njoku, E.G.; Li, L. Retrieval of land surface parameters using passive microwave measurements at 6–18 GHz. IEEE Trans. Geosci. Remote Sens. 1999. [Google Scholar] [CrossRef]
- Aires, F.; Prigent, C.; Rossow, W.B.; Rothstein, M. A new neural network approach including first guess for retrieval of atmospheric water vapor, cloud liquid water path, surface temperature, and emissivities over land from satellite microwave observations. J. Geophys. Res. Atmos. 2001, 106, 14887–14907. [Google Scholar] [CrossRef]
- Basist, A.; Grody, N.C.; Peterson, T.C.; Williams, C.N. Using the Special Sensor Microwave/Imager to Monitor Land Surface Temperatures, Wetness, and Snow Cover. J. Appl. Meteorol. 2002. [Google Scholar] [CrossRef]
- Fily, M.; Royer, A.; Goïta, K.; Prigent, C. A simple retrieval method for land surface temperature and fraction of water surface determination from satellite microwave brightness temperatures in sub-arctic areas. Remote Sens. Environ. 2003. [Google Scholar] [CrossRef]
- Prigent, C.; Jimenez, C.; Aires, F. Toward “all weather” long record, and real-time land surface temperature retrievals from microwave satellite observations. J. Geophys. Res. Atmos. 2016, 121, 5699–5717. [Google Scholar] [CrossRef]
- Weng, F.; Grody, N.C. Physical retrieval of land surface temperature using the special sensor microwave imager. J. Geophys. Res. Atmos. 1998, 103, 8839–8848. [Google Scholar] [CrossRef]
- Wen, J. Determination of land surface temperature and soil moisture from Tropical Rainfall Measuring Mission/Microwave Imager remote sensing data. J. Geophys. Res. 2003. [Google Scholar] [CrossRef]
- Galantowicz, J.F.; Moncet, J.L.; Liang, P.; Lipton, A.E.; Uymin, G.; Prigent, C.; Grassotti, C. Subsurface emission effects in AMSR-E measurements: Implications for land surface microwave emissivity retrieval. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Holmes, T.R.H.; Crow, W.T.; Hain, C. Spatial patterns in timing of the diurnal temperature cycle. Hydrol. Earth Syst. Sci. 2013, 17, 3695–3706. [Google Scholar] [CrossRef]
- Prigent, C.; Rossow, W.B.; Matthews, E.; Marticorena, B. Microwave radiometric signatures of different surface types in deserts. J. Geophys. Res. Atmos. 1999, 104, 12147–12158. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, X.; Zhan, W.; Göttsche, F.M.; Liu, S.; Olesen, F.S.; Hu, W.; Dai, F. A Thermal Sampling Depth Correction Method for Land Surface Temperature Estimation from Satellite Passive Microwave Observation Over Barren Land. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4743–4756. [Google Scholar] [CrossRef]
- Prigent, C.; Aires, F.; Rossow, W.B.; Robock, A. Sensitivity of satellite microwave and infrared observations to soil moisture at a global scale: Relationship of satellite observations to in situ soil moisture measurements. J. Geophys. Res. Atmos. 2005. [Google Scholar] [CrossRef]
- Cordisco, E.; Prigent, C.; Aires, F. Snow characterization at a global scale passive microwave satelite observations. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- André, C.; Ottlé, C.; Royer, A.; Maignan, F. Land surface temperature retrieval over circumpolar Arctic using SSM/I-SSMIS and MODIS data. Remote Sens. Environ. 2015. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Gottsche, F.-M.; Zhan, W.; Liu, S.; Cao, R. A Method Based on Temporal Component Decomposition for Estimating 1-km All-Weather Land Surface Temperature by Merging Satellite Thermal Infrared and Passive Microwave Observations. IEEE Trans. Geosci. Remote Sens. 2019, 1–22. [Google Scholar] [CrossRef]
- Jin, M.; Dickinson, R.E. A generalized algorithm for retrieving cloudy sky skin temperature from satellite thermal infrared radiances. J. Geophys. Res. Atmos. 2000. [Google Scholar] [CrossRef]
- Lu, L.; Venus, V.; Skidmore, A.; Wang, T.; Luo, G. Estimating land-surface temperature under clouds using MSG/SEVIRI observations. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 265–276. [Google Scholar] [CrossRef]
- Leng, P.; Li, Z.L.; Duan, S.B.; Tang, R.; Gao, M.F. A Method for Deriving All-Sky Evapotranspiration from the Synergistic Use of Remotely Sensed Images and Meteorological Data. J. Geophys. Res. Atmos. 2017. [Google Scholar] [CrossRef]
- Trigo, I.F.; Dacamara, C.C.; Viterbo, P.; Roujean, J.-L.; Olesen, F.; Barroso, C.; Camacho-de-Coca, F.; Carrer, D.; Freitas, S.C. The Satellite Application Facility for Land Surface Analysis. Int. J. Remote Sens. 2011, 32, 2725–2744. [Google Scholar] [CrossRef]
- Trigo, I.F.; Peres, L.F.; DaCamara, C.C.; Freitas, S.C. Thermal land surface emissivity retrieved from SEVIRI/Meteosat. IEEE Trans. Geosci. Remote Sens. 2008, 46, 307–315. [Google Scholar] [CrossRef]
- Geiger, B.; Carrer, D.; Franchistéguy, L.; Roujean, J.L.; Meurey, C. Land surface albedo derived on a daily basis from meteosat second generation observations. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3841–3856. [Google Scholar] [CrossRef]
- Geiger, B.; Meurey, C.; Lajas, D.; Franchistéguy, L.; Carrer, D.; Roujean, J.L. Near real-time provision of downwelling shortwave radiation estimates derived from satellite observations. Meteorol. Appl. 2008, 15, 411–420. [Google Scholar] [CrossRef]
- Roujean, J.-L.; Lacaze, R. Global mapping of vegetation parameters from POLDER multiangular measurements for studies of surface-atmosphere interactions: A pragmatic method and its validation. J. Geophys. Res. 2002, 107, 4150. [Google Scholar] [CrossRef]
- Roujean, J.L.; Breon, F.M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- García-Haro, F.J.; Sommer, S.; Kemper, T. A new tool for variable multiple endmember spectral mixture analysis (VMESMA). Int. J. Remote Sens. 2005, 26, 2135–2162. [Google Scholar] [CrossRef]
- Ghilain, N.; Arboleda, A.; Gellens-Meulenberghs, F. Evapotranspiration modelling at large scale using near-real time MSG SEVIRI derived data. Hydrol. Earth Syst. Sci. 2011, 15, 771–786. [Google Scholar] [CrossRef]
- De Bruin, H.A.R.; Trigo, I.F.; Bosveld, F.C.; Meirink, J.F. A Thermodynamically Based Model for Actual Evapotranspiration of an Extensive Grass Field Close to FAO Reference, Suitable for Remote Sensing Application. J. Hydrometeorol. 2016, 17, 1373–1382. [Google Scholar] [CrossRef]
- Amraoui, M.; DaCamara, C.C.; Pereira, J.M.C. Detection and monitoring of African vegetation fires using MSG-SEVIRI imagery. Remote Sens. Environ. 2010, 114, 1038–1052. [Google Scholar] [CrossRef]
- Wooster, M.J.; Roberts, G.; Freeborn, P.H.; Xu, W.; Govaerts, Y.; Beeby, R.; He, J.; Lattanzio, A.; Fisher, D.; Mullen, R. LSA SAF Meteosat FRP products-Part 1: Algorithms, product contents, and analysis. Atmos. Chem. Phys. 2015, 15, 13217–13239. [Google Scholar] [CrossRef]
- Roberts, G.; Wooster, M.J.; Xu, W.; Freeborn, P.H.; Morcrette, J.J.; Jones, L.; Benedetti, A.; Jiangping, H.; Fisher, D.; Kaiser, J.W. LSA SAF Meteosat FRP products-Part 2: Evaluation and demonstration for use in the Copernicus Atmosphere Monitoring Service (CAMS). Atmos. Chem. Phys. 2015, 15, 13241–13267. [Google Scholar] [CrossRef]
- Van den Hurk, B.J.J.M.; Viterbo, P.; Beljaars, A.C.M.; Betts, A.K. Offline Validation of the ERA40 Surface Scheme; Technical Memorandum: Shinfield Park, Reading, UK, 2000. [Google Scholar]
- Albergel, C.; Balsamo, G.; De Rosnay, P.; Muñoz-Sabater, J.; Boussetta, S. A bare ground evaporation revision in the ECMWF land-surface scheme: Evaluation of its impact using ground soil moisture and satellite microwave data. Hydrol. Earth Syst. Sci. 2012, 16, 3607–3620. [Google Scholar] [CrossRef]
- Balsamo, G.; Beljaars, A.; Scipal, K.; Viterbo, P.; van den Hurk, B.; Hirschi, M.; Betts, A.K. A Revised Hydrology for the ECMWF Model: Verification from Field Site to Terrestrial Water Storage and Impact in the Integrated Forecast System. J. Hydrometeorol. 2009, 10, 623–643. [Google Scholar] [CrossRef]
- Viterbo, P.; Beljaars, A.C.M. An improved land surface parameterization scheme in the ECMWF model and its validation. J. Clim. 1995, 8, 2716–2748. [Google Scholar] [CrossRef]
- Ghilain, N. Continental Scale Monitoring of Subdaily and Daily Evapotranspiration Enhanced by the Assimilation of Surface Soil Moisture Derived from Thermal Infrared Geostationary Data. In Satellite Soil Moisture Retrieval: Techniques and Applications; Elsevier Inc.: Amsterdam, The Netherlands, 2016; pp. 309–332. ISBN 9780128033890. [Google Scholar]
- Yu, Y.; Privette, J.L.; Pinheiro, A.C. Evaluation of Split-Window Land Surface Temperature Algorithms for Generating Climate Data Records. IEEE Trans. Geosci. Remote Sens. 2008, 46, 179–192. [Google Scholar] [CrossRef]
- Dash, P.; Göttsche, F.M.; Olesen, F.S.; Fischer, H. Land surface temperature and emissivity estimation from passive sensor data: Theory and practice-current trends. Int. J. Remote Sens. 2002, 23, 2563–2594. [Google Scholar] [CrossRef]
- Martins, J.P.; Trigo, I.; Bento, V.; da Camara, C. A Physically Constrained Calibration Database for Land Surface Temperature Using Infrared Retrieval Algorithms. Remote Sens. 2016, 8, 808. [Google Scholar] [CrossRef]
- Salisbury, J.W.; D’Aria, D.M. Emissivity of terrestrial materials in the 3–5 μm atmospheric window. Remote Sens. Environ. 1994. [Google Scholar] [CrossRef]
- Peres, L.F.; DaCamara, C.C. Land surface temperature and emissivity estimation based on the two-temperature method: Sensitivity analysis using simulated MSG/SEVIRI data. Remote Sens. Environ. 2004, 91, 377–389. [Google Scholar] [CrossRef]
- Ghilain, N.; Arboleda, A.; Sepulcre-Cantò, G.; Batelaan, O.; Ardö, J.; Gellens-Meulenberghs, F. Improving evapotranspiration in a land surface model using biophysical variables derived from MSG/SEVIRI satellite. Hydrol. Earth Syst. Sci. 2012, 16, 2567–2583. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Ireland, G.; Lamine, S.; Griffiths, H.M.; Ghilain, N.; Anagnostopoulos, V.; North, M.R.; Srivastava, P.K.; Georgopoulou, H. Operational evapotranspiration estimates from SEVIRI in support of sustainable water management. Int. J. Appl. Earth Obs. Geoinf. 2016. [Google Scholar] [CrossRef]
- Ghilain, N. Algorithm Theoretical Basis Document Meteosat Second Generation based products Instantaneous Evapotranspiration (MET v2), Daily Evapotranspiration (DMET v2), Surface Latent Heat Flux (LE), Surface Sensible Heat Flux (H); SAF/LAND/RMI/ATBD_ETv2HLE/1.1; Land Surface Analysis Satellite Application Facility: Lisbon, Portugal, 2016; Available online: http://lsa-saf.eumetsat.int/ (accessed on 13 December 2019).
- Faroux, S.; Kaptué Tchuenté, A.T.; Roujean, J.-L.; Masson, V.; Martin, E.; Le Moigne, P. ECOCLIMAP-II/Europe: A twofold database of ecosystems and surface parameters at 1 km resolution based on satellite information for use in land surface, meteorological and climate models. Geosci. Model. Dev. 2013, 6, 563–582. [Google Scholar] [CrossRef]
- Masson, V.; Champeaux, J.L.; Chauvin, F.; Meriguet, C.; Lacaze, R. A global database of land surface parameters at 1-km resolution in meteorological and climate models. J. Clim. 2003, 16, 1261–1282. [Google Scholar] [CrossRef]
- Carrer, D.; Lafont, S.; Roujean, J.-L.; Calvet, J.-C.; Meurey, C.; Le Moigne, P.; Trigo, I.F. Incoming Solar and Infrared Radiation Derived from METEOSAT: Impact on the Modeled Land Water and Energy Budget over France. J. Hydrometeorol. 2011. [Google Scholar] [CrossRef]
- Trigo, I.F.; Barroso, C.; Viterbo, P.; Freitas, S.C.; Monteiro, I.T. Estimation of downward long-wave radiation at the surface combining remotely sensed data and NWP data. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Lakshmi, V.; Jackson, T.J.; Zehrfuhs, D. Soil moisture-temperature relationships: Results from two field experiments. Hydrol. Process 2003, 17, 3041–3057. [Google Scholar] [CrossRef]
- Verstraeten, W.W.; Veroustraete, F.; Van Der Sande, C.J.; Grootaers, I.; Feyen, J. Soil moisture retrieval using thermal inertia, determined with visible and thermal spaceborne data, validated for European forests. Remote Sens. Environ. 2006, 101, 299–314. [Google Scholar] [CrossRef]
- Albergel, C.; de Rosnay, P.; Gruhier, C.; Muñoz-Sabater, J.; Hasenauer, S.; Isaksen, L.; Kerr, Y.; Wagner, W. Evaluation of remotely sensed and modelled soil moisture products using global ground-based in situ observations. Remote Sens. Environ. 2012, 118, 215–226. [Google Scholar] [CrossRef]
- Guillevic, P.; Göttsche, F.; Nickeson, J.; Hulley, G.; Ghent, D.; Yu, Y.; Trigo, I.; Hook, S.; Sobrino, J.A.; Remedios, J.; et al. Land Surface Temperature Product Validation Best Practice Protocol. Version 1.0. In Best Practice for Satellite-Derived Land Product Validation; Göttsche, F., Nickeson, J., Román, M., Eds.; Land Product Validation Subgroup (WGCV/CEOS); Internal Publication: Brussels, Belgium, 2017; p. 60. Available online: http://ceos.org/ourwork/lessons-learned-best-practices/ (accessed on 13 December 2019). [CrossRef]
- Göttsche, F.-M.; Hulley, G.C. Validation of six satellite-retrieved land surface emissivity products over two land cover types in a hyper-arid region. Remote Sens. Environ. 2012, 124, 149–158. [Google Scholar] [CrossRef]
- Masiello, G.; Serio, C.; Venafra, S.; Liuzzi, G.; Poutier, L.; Göttsche, F.-M.; Masiello, G.; Serio, C.; Venafra, S.; Liuzzi, G.; et al. Physical Retrieval of Land Surface Emissivity Spectra from Hyper-Spectral Infrared Observations and Validation with In Situ Measurements. Remote Sens. 2018, 10, 976. [Google Scholar] [CrossRef]
- Guillevic, P.C.; Bork-Unkelbach, A.; Gottsche, F.M.; Hulley, G.; Gastellu-Etchegorry, J.P.; Olesen, F.S.; Privette, J.L. Directional viewing effects on satellite land surface temperature products over sparse vegetation canopies-a multisensor analysis. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1464–1468. [Google Scholar] [CrossRef]
- Belward, A.S. The IGBP-DIS Global 1km Land Cover Data Set (DISCover)–Proposal and Implementation Plans; IGBP-DIS Working Paper: Toulouse, France, 1996. [Google Scholar]
- Ghent, D.J.; Corlett, G.K.; Göttsche, F.M.; Remedios, J.J. Global Land Surface Temperature from the Along-Track Scanning Radiometers. J. Geophys. Res. Atmos. 2017, 122, 12167–12193. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the collection-6 MODIS land-surface temperature/emissivity product. Remote Sens. Environ. 2014, 140, 36–45. [Google Scholar] [CrossRef]
- Zheng, W.; Wei, H.; Wang, Z.; Zeng, X.; Meng, J.; Ek, M.; Mitchell, K.; Derber, J. Improvement of daytime land surface skin temperature over arid regions in the NCEP GFS model and its impact on satellite data assimilation. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Ermida, S.L.; DaCamara, C.C.; Trigo, I.F.; Pires, A.C.; Ghent, D.; Remedios, J. Modelling directional effects on remotely sensed land surface temperature. Remote Sens. Environ. 2017, 190, 56–69. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, Y.; Yu, P.; Göttsche, F.M.; Trigo, I.F. Quality assessment of S-NPP VIIRS land surface temperature product. Remote Sens. 2015, 7, 12215–12241. [Google Scholar] [CrossRef]
- Martin, M.A.; Ghent, D.; Pires, A.C.; Göttsche, F.-M.; Cermak, J.; Remedios, J.J.; Martin, M.A.; Ghent, D.; Pires, A.C.; Göttsche, F.-M.; et al. Comprehensive In Situ Validation of Five Satellite Land Surface Temperature Data Sets over Multiple Stations and Years. Remote Sens. 2019, 11, 479. [Google Scholar] [CrossRef]
- Ramanathan, V.; Crutzen, P.J.; Kiehl, J.T.; Rosenfeld, D. Atmosphere: Aerosols, climate, and the hydrological cycle. Science 2001, 294, 2119–2124. [Google Scholar] [CrossRef]
- Thiery, W.; Martynov, A.; Darchambeau, F.; Descy, J.P.; Plisnier, P.D.; Sushama, L.; Van Lipzig, N.P.M. Understanding the performance of the FLake model over two African Great Lakes. Geosci. Model. Dev. 2014, 7, 317–337. [Google Scholar] [CrossRef]
- Duguay-Tetzlaff, A.; Stöckli, R.; Bojanowski, J. Product User Manual Land Surface Temperature (LST); (SUMET) Ed. 1. Satellite Application Facility for Climate Monitoring, EUMETSAT: Darmstadt, Germany, (SAF/CM/MeteoSwiss/PUM/MET/LST); 2017. [Google Scholar]
- Bulgin, C.E.; Merchant, C.J.; Ghent, D.; Klüser, L.; Popp, T.; Poulsen, C.; Sogacheva, L. Quantifying uncertainty in satellite-retrieved land surface temperature from cloud detection errors. Remote Sens. 2018, 10, 616. [Google Scholar] [CrossRef]
- Prigent, C.; Aires, F.; Rossow, W. Land surface skin temperatures from a combined analysis of microwave and infrared satellite observations for an all-weather evaluation of the differences between air and skin temperatures. J. Geophys. Res. 2003. [Google Scholar] [CrossRef]
- Favrichon, S.; Prigent, C.; Jimenez, C.; Aires, F. Detecting cloud contamination in passive microwave satellite measurements over land. Atmos. Meas. Tech. 2019, 12, 1531–1543. [Google Scholar] [CrossRef]
| Source (Product ID) | Original Resolution (spatial/temporal) | Comments | |
|---|---|---|---|
| LSA-SAF (LSA-311) | 3 km at nadir/30 min | Byproduct of LSA-311 | |
| IR LST | LSA-SAF (LSA-001) | 3 km at nadir/15 min | Clear sky only |
| IR+EB model LST | LSA-SAF (LSA-005) | 3 km at nadir/30 min | All-weather LST presented here |
| In situ LST | KIT | Point measurement/1 min) | Evora (Portugal); Kalahari and Gobabeb (Namibia) |
| AMSR-E LST | GlobTemperature (AMSRE_LST_2) | 12 km/Ascending and descending orbits | MW; All-weather LST |
| Accuracy (µ, K) | , K) | RMSD (K) | |
|---|---|---|---|
| EB(clear sky) | 0.4 | 2.2 | 3.8 |
| EB(cloudy sky) | −0.2 | 2.0 | 3.8 |
| IR LST | 0.2 | 1.0 | 2.2 |
| All-weather LST | 0.1 | 1.2 | 2.7 |
| Station | , K) | , K) | RMSD (K) | # Points | |||
|---|---|---|---|---|---|---|---|
| MSG/SEVIRI | AMSR-E | MSG/SEVIRI | AMSR-E | MSG/SEVIRI | AMSR-E | ||
| Evora | 1.5 | 1.1 | 1.6 | 2.3 | 3.3 | 3.5 | 429 |
| Kalahari | −0.4 | 0.9 | 2.4 | 2.8 | 3.7 | 4.5 | 449 |
| Gobabeb | 0.2 | −4.4 | 1.0 | 1.8 | 2.1 | 5.1 | 325 |
| Clear Sky | Cloudy | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy (K) | Precision (K) | RMSD (K) | # Points | Accuracy (K) | Precision (K) | RMSD (K) | # Points | |||
| January | Day | –2.6 | 3.2 | 5.3 | 235324 | Day | 0.5 | 3.2 | 5.2 | 451657 |
| Night | 0.2 | 2.0 | 3.6 | 295802 | Night | 1.3 | 2.0 | 3.9 | 479401 | |
| July | Day | –1.6 | 3.3 | 5.6 | 318424 | Day | 0.4 | 3.1 | 5.3 | 556763 |
| Night | –1.3 | 2.0 | 3.7 | 435619 | Night | 0.9 | 1.9 | 4.0 | 503576 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martins, J.P.A.; Trigo, I.F.; Ghilain, N.; Jimenez, C.; Göttsche, F.-M.; Ermida, S.L.; Olesen, F.-S.; Gellens-Meulenberghs, F.; Arboleda, A. An All-Weather Land Surface Temperature Product Based on MSG/SEVIRI Observations. Remote Sens. 2019, 11, 3044. https://doi.org/10.3390/rs11243044
Martins JPA, Trigo IF, Ghilain N, Jimenez C, Göttsche F-M, Ermida SL, Olesen F-S, Gellens-Meulenberghs F, Arboleda A. An All-Weather Land Surface Temperature Product Based on MSG/SEVIRI Observations. Remote Sensing. 2019; 11(24):3044. https://doi.org/10.3390/rs11243044
Chicago/Turabian StyleMartins, João P. A., Isabel F. Trigo, Nicolas Ghilain, Carlos Jimenez, Frank-M. Göttsche, Sofia L. Ermida, Folke-S. Olesen, Françoise Gellens-Meulenberghs, and Alirio Arboleda. 2019. "An All-Weather Land Surface Temperature Product Based on MSG/SEVIRI Observations" Remote Sensing 11, no. 24: 3044. https://doi.org/10.3390/rs11243044
APA StyleMartins, J. P. A., Trigo, I. F., Ghilain, N., Jimenez, C., Göttsche, F.-M., Ermida, S. L., Olesen, F.-S., Gellens-Meulenberghs, F., & Arboleda, A. (2019). An All-Weather Land Surface Temperature Product Based on MSG/SEVIRI Observations. Remote Sensing, 11(24), 3044. https://doi.org/10.3390/rs11243044