Thunderstorm Classification Functions Based on Instability Indices and GNSS IWV for the Sofia Plain
Abstract
1. Introduction
2. Datasets and Method
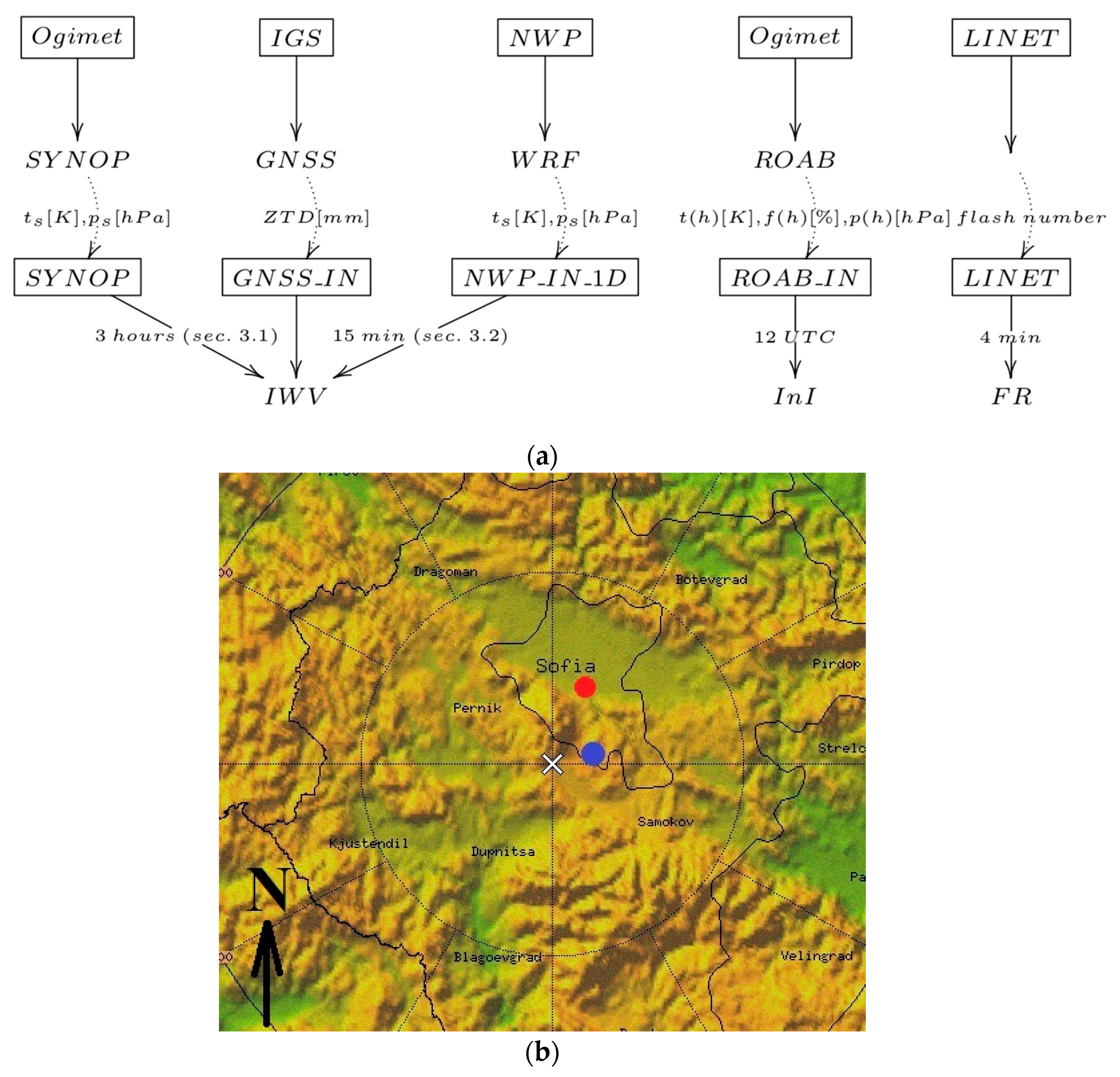
2.1. Observation Datasets
2.1.1. GNSS Tropospheric Products—SOFI Station
2.1.2. Surface, Upper-Air and Lightning Observations at Sofia
2.2. Statistical Analysis
3. Results
3.1. Classification Functions for Thunderstorm Forecasting
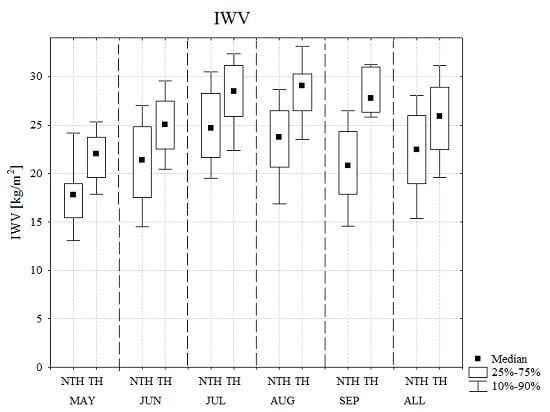
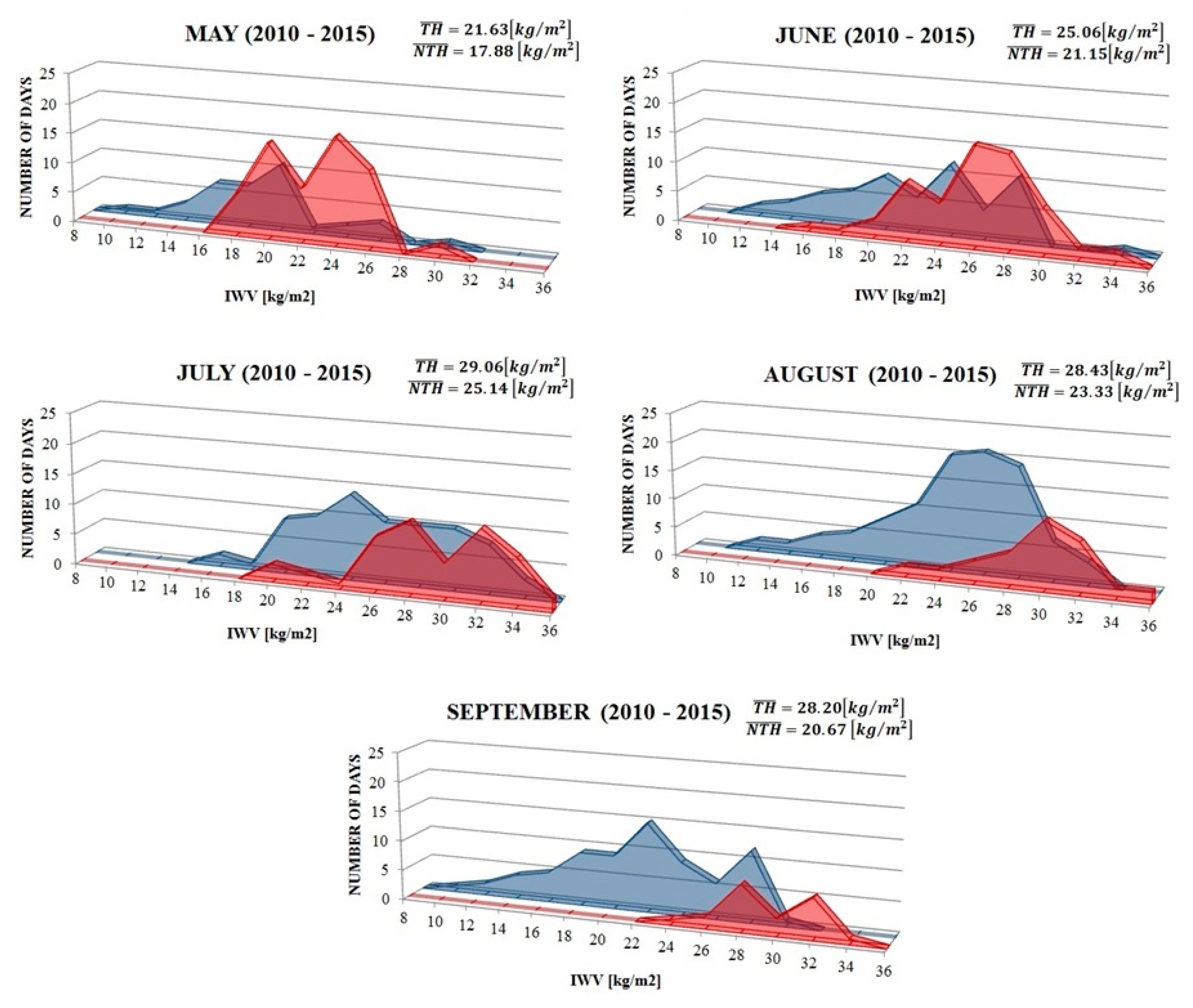
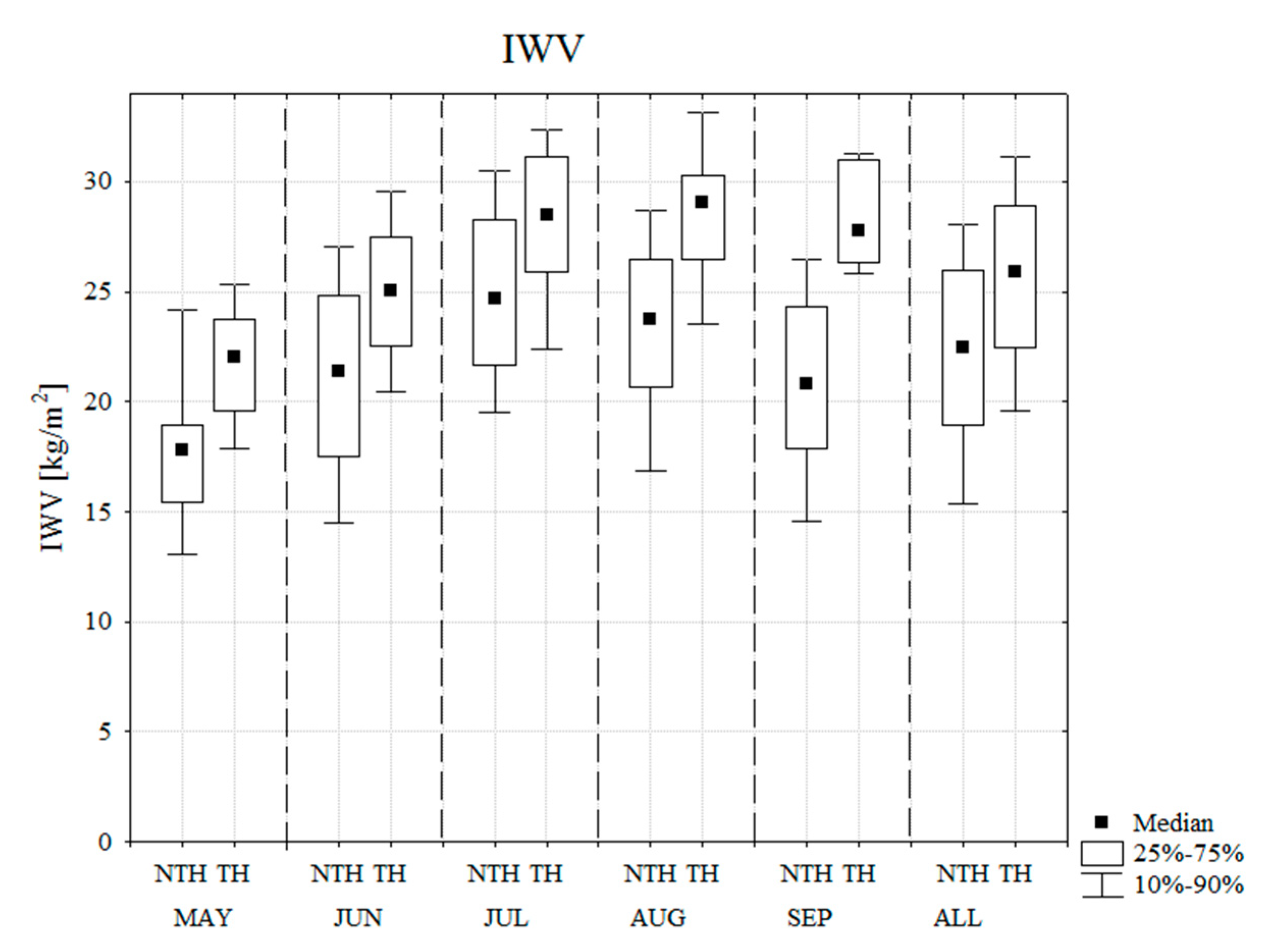
3.1.1. IWV Threshold for TH and NTH Days 2010–2015
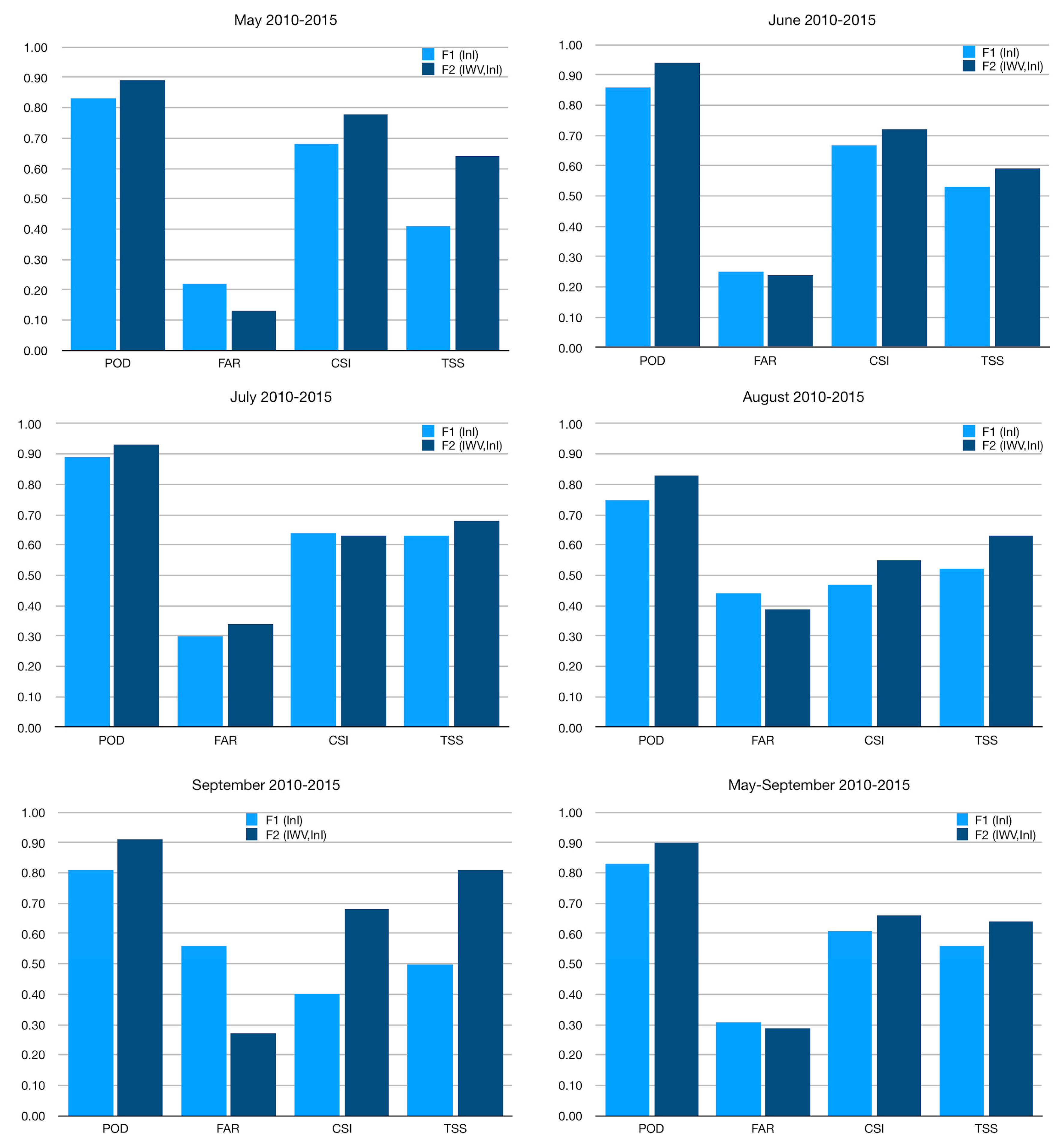
3.1.2. Classification Functions May–September 2010–2015
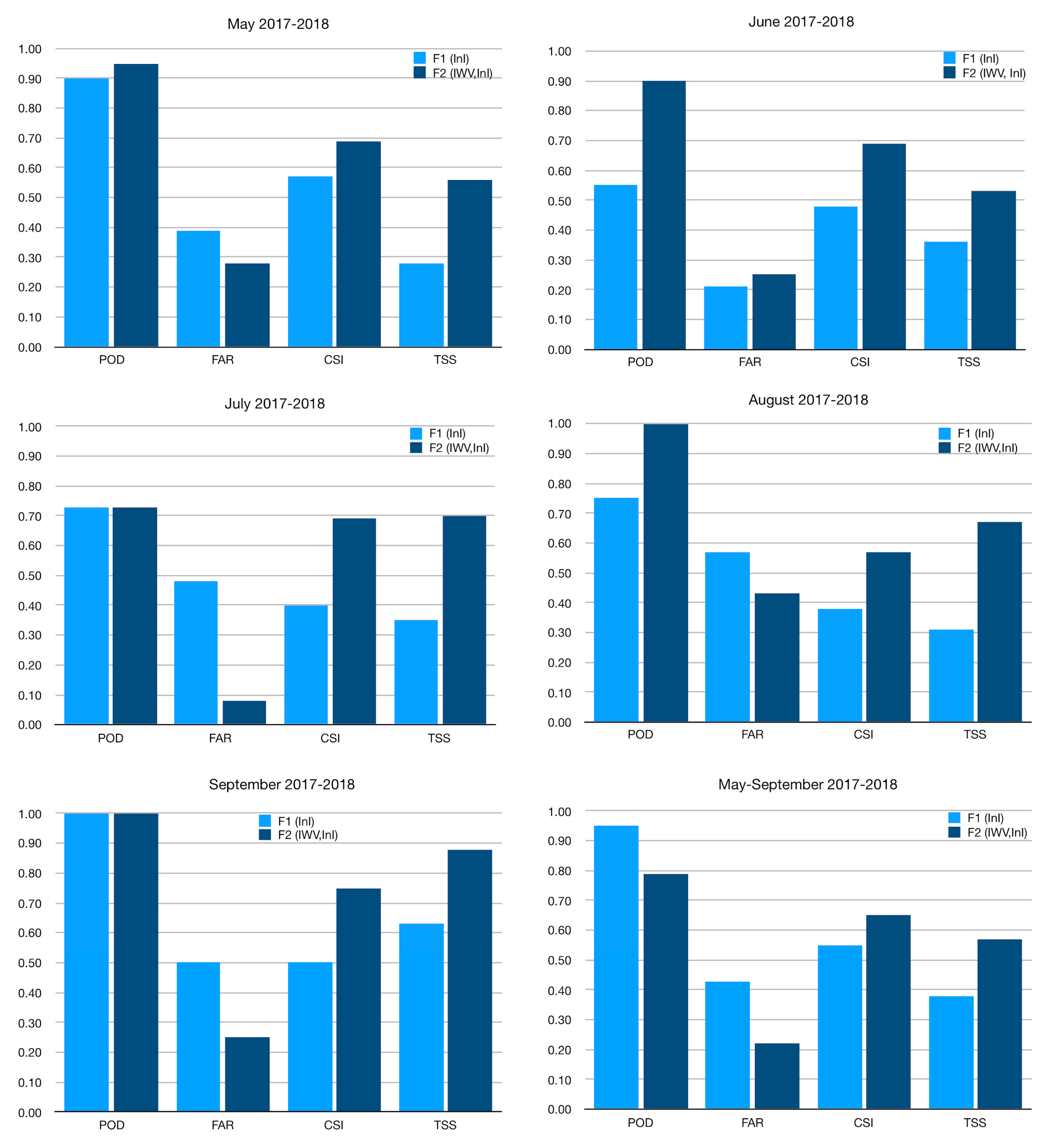
3.1.3. Verification of Classification Functions for May–September 2017–2018
3.2. Case Studies—Supercell & Multicell Thunderstorm
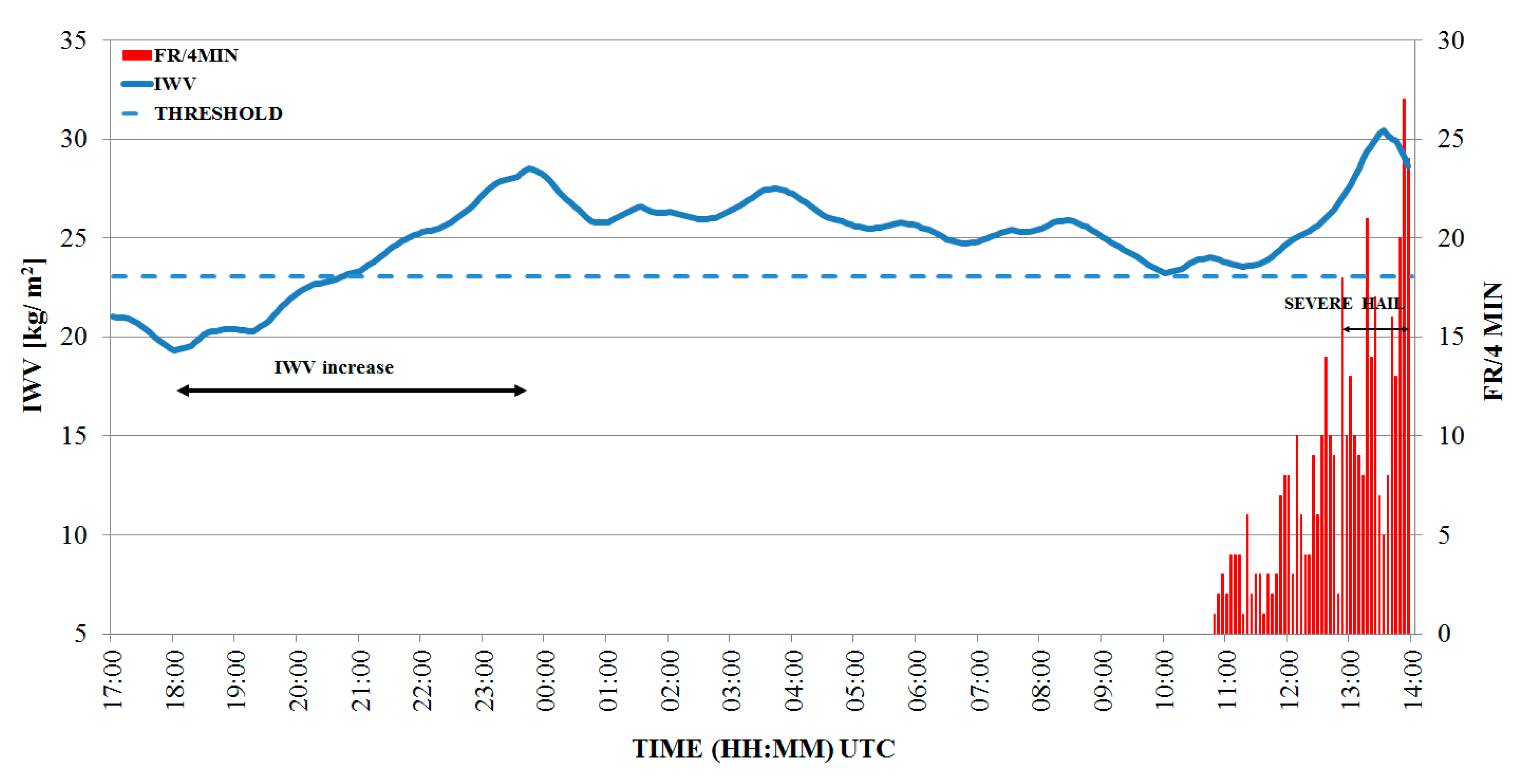
3.2.1. Multicell Thunderstorm—18 June 2014
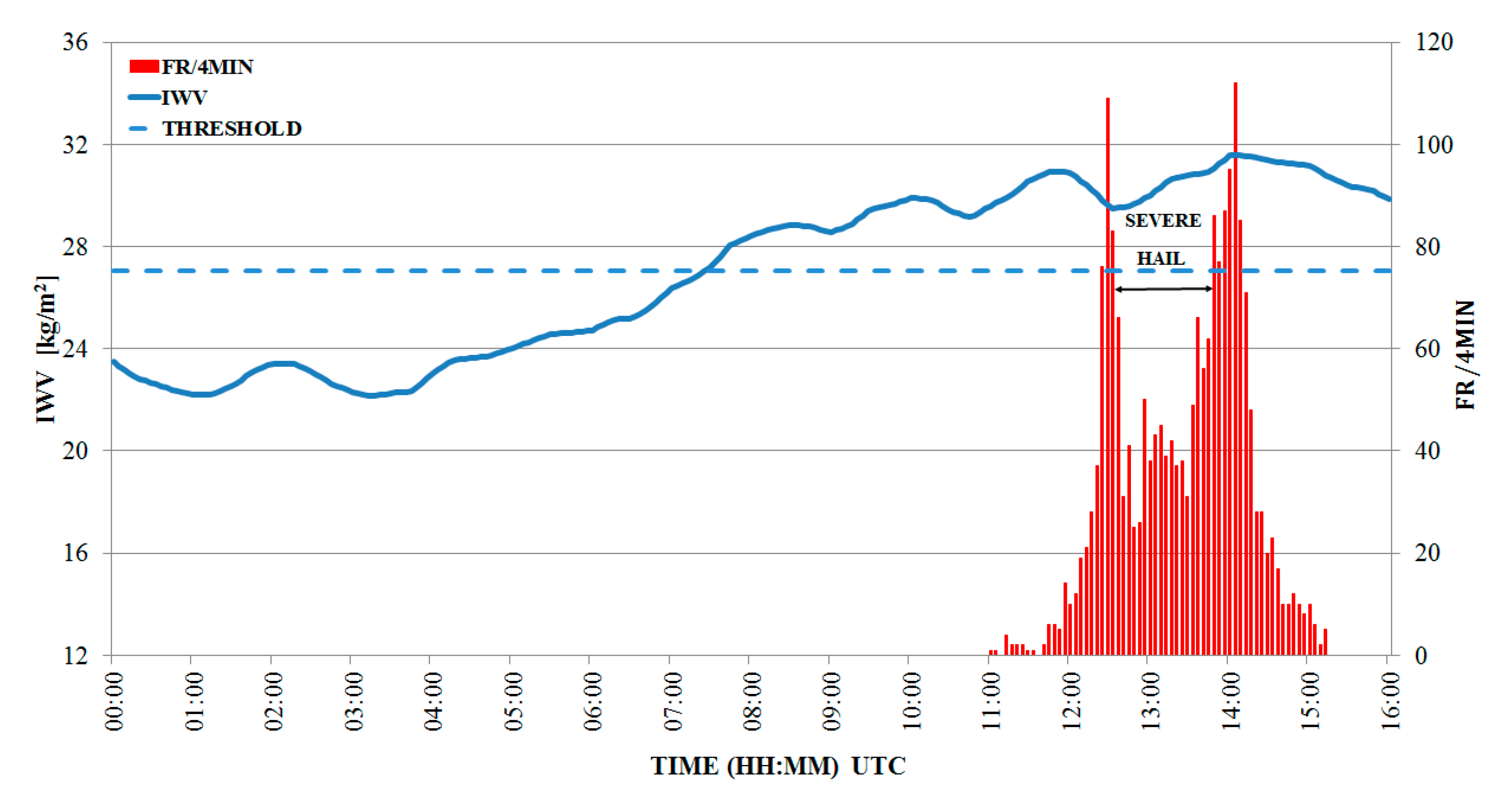
3.2.2. Supercell Thunderstorm—8 July 2014
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Taszarek, M.; Allen, J.; Púčik, T.; Groenemeijer, P.; Czernecki, B.; Kolendowicz, L.; Lagouvardos, K.; Kotroni, V.; Schulz, W. A climatology of thunderstorms across Europe from a synthesis of multiple data sources. J. Clim. 2019, 32, 1813–1837. [Google Scholar] [CrossRef]
- Bocheva, L.; Simeonov, P.; Marinova, T. Variations of thunderstorm activity in non mountainous regions of Bulgaria (1961–2010). BJMH 2013, 18, 38–47. [Google Scholar]
- Bocheva, L.; Dimitrova, T.; Penchev, R.; Gospodinov, I.; Simeonov, P. Severe convective supercell outbreak over western Bulgaria on July 8 2014. Idojaras 2018, 122, 177–203. [Google Scholar] [CrossRef]
- Dimitrova, T.; Mitzeva, R.; Savtchenko, A. Environmental conditions responsible for the type of precipitation in summer convective storms over Bulgaria. Atmos. Res. 2009, 93, 30–38. [Google Scholar] [CrossRef]
- Kunz, M. The skill of convective parameters and indices to predict isolated and severe thunderstorms. Nat. Hazards Earth Syst. Sci. 2007, 7, 327–342. [Google Scholar] [CrossRef]
- Jacovides, C.P.; Yonetani, T. An evaluation of stability indices for thunderstorm prediction in Greater Cyprus. Weather Forecas. 1990, 5, 559–569. [Google Scholar] [CrossRef]
- Ukkonen, P.; Manzato, A.; Mäkelä, A. Evaluation of thunderstorm predictors for Finland using reanalyses and neural networks. J. Appl. Meteorol. Climatol. 2017, 56, 2335–2352. [Google Scholar] [CrossRef]
- Huntrieser, H.; Schiesser, H.H.; Schmid, W.; Waldvogel, A. Comparison of Traditional and Newly Developed Thunderstorm Indices for Switzerland. Weather Forecast. 1997, 12, 108–125. [Google Scholar] [CrossRef]
- Markova, B.; Dimitrova, T.S.; Kadiyska, N.; Mitzeva, R. Stability indices and wind shear for forecasting severe storm type over Bulgaria. In Proceedings of the 9th European Conference on Severe Storms, Pula, Croatia, 18–22 September 2017. [Google Scholar]
- Guerova, G.; Jones, J.; Douša, J.; Dick, G.; Haan, S.D.; Pottiaux, E.; Bock, O.; Pacione, R.; Elgered, G.; Vedel, H.; et al. Review of the state of the art and future prospects of the ground-based GNSS meteorology in Europe. Atmos. Meas. Tech. 2016, 9, 5385–5406. [Google Scholar] [CrossRef]
- Benevides, P.; Catalao, J.; Miranda, P.M.A. On the inclusion of GPS precipitable water vapour in the nowcasting of rainfall. Nat. Hazards Earth Syst. Sci. 2015, 15, 2605–2616. [Google Scholar] [CrossRef]
- Benevides, P.; Catalao, J.; Nico, G. Neural Network Approach to Forecast Hourly Intense Rainfall Using GNSS Precipitable Water Vapor and Meteorological Sensors. Remote Sens. 2019, 11, 966. [Google Scholar] [CrossRef]
- Shoji, Y. Retrieval of water vapor inhomogeneity using the Japanese nationwide GPS array and its potential for prediction of convective precipitation. J. Meteorol. Soc. Jpn. 2013, 91, 43–62. [Google Scholar] [CrossRef][Green Version]
- Seto, Y.; Yokoyama, H.; Nakatani, T.; Ando, H.; Tsunematsu, N.; Shoji, Y.; Kusunoki, K.; Nakayama, M.; Saitoh, Y.; Takahashi, H. Relationships among Rainfall Distribution, Surface Wind, and Precipitable Water Vapor during Heavy Rainfall in Central Tokyo in Summer. J. Meteorol. Soc. Jpn. 2018, 96A, 35–49. [Google Scholar] [CrossRef]
- Sapucci, L.F.; Machado, L.A.; de Souza, E.M.; Campos, T.B. Global Positioning System precipitable water vapour (GPS-PWV) jumps before intense rain events: A potential application to nowcasting. Meteorol. Appl. 2019, 26, 49–63. [Google Scholar] [CrossRef]
- Huelsing, H.K.; Wang, J.; Mears, C.; Braun, J.J. Precipitable water characteristics during the 2013 Colorado flood using ground-based GPS measurements. Atmos. Meas. Tech. 2017, 10, 4055–4066. [Google Scholar] [CrossRef]
- Nykiel, G.; Figurski, M.; Baldysz, Z. Analysis of GNSS sensed precipitable water vapour and tropospheric gradients during the derecho event in Poland of 11th August 2017. J. Atmos. Sol. Terr. Phys. 2019, 193, 105082. [Google Scholar] [CrossRef]
- Brenot, H.; Neméghaire, J.; Delobbe, L.; Clerbaux, N.; De Meutter, P.; Deckmyn, A.; Delcloo, A.; Frappez, L.; Van Roozendael, M. Preliminary signs of the initiation of deep convection by GNSS. Atmos. Chem. Phys. 2013, 13, 5425–5449. [Google Scholar] [CrossRef]
- Douša, J.; Dick, G.; Kačmařík, M.; Brožková, R.; Zus, F.; Brenot, H.; Stoycheva, A.; Möller, G.; Kaplon, J. Benchmark campaign and case study episode in central Europe for development and assessment of advanced GNSS tropospheric models and products. Atmos. Meas. Tech. 2016, 9, 2989–3008. [Google Scholar] [CrossRef]
- Guerova, G.; Simeonov, T.S.; Yordanova, N. The Sofia University Atmospheric Data Archive (SUADA). Atmos. Meas. Tech. 2014, 7, 2683–2694. [Google Scholar] [CrossRef]
- Beutler, G.; Bock, H.; Dach, R.; Fridez, P.; Gäde, A.; Hugentobler, U.P.; Jäggi, A.; Meindl, M.; Mervart, L.; Prange, L.; et al. Bernese GPS software Version 5.0; Astronomical Institute, University of Bern: Bern, Switzerland, 2007. [Google Scholar]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Byram, S. IGS Final Troposphere Product Update. In Proceedings of the IGS Workshop 2017, Paris, France, 3–7 July 2017; Available online: http://www.igs.org/assets/pdf/W2017-PS04-03%20-%20Byram.pdf (accessed on 11 December 2019).
- Bohm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global mapping function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Davis, J.; Herring, T.; Shapiro, I.; Rogers, A.; Elgered, G. Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS Meteorology: Remote sensing of atmospheric water vapour using the Global Positioning System. J. Geophys. Res. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Thayer, G.D. An improved equation for the radio refractive index of air. Radio Sci. 1974, 9, 803–807. [Google Scholar] [CrossRef]
- Sissenwine, N.; Dubin, M.; Wexler, H. The US standard atmosphere, 1962. J. Geophys. Res. 1962, 67, 3627–3630. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J. A Description of the Advanced Research WRF Version 3. Available online: https://opensky.ucar.edu/islandora/object/technotes%3A500/datastream/PDF/view (accessed on 1 December 2019).
- Chen, F.; Mitchell, K.; Schaake, J.; Xue, Y.; Pan, H.-L.; Koren, V.; Duan, Q.Y.; Ek, M.; Betts, A. Modeling of land surface evaporation by four schemes and comparison with FIFE observations. J. Geophys. Res. 1996, 101, 7251–7268. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Lin, Y.; Colle, B.A. A new bulk microphysical scheme that includes riming intensity and temperature-dependent ice characteristics. Mon. Weather Rev. 2011, 139, 1013–1035. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Betz, H.-D.; Schmidt, K.; Oettinger, P.; Wirz, M. Lightning detection with 3-D discrimination of intracloud and cloud-to-ground discharges. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Betz, H.D.; Schmidt, K.; Laroche, P.; Blanchet, P.; Oettinger, W.P.; Defer, E.; Dziewit, Z.; Konarski, J. LINET-An international lightning detection network in Europe. Atmos. Res. 2009, 91, 564–573. [Google Scholar] [CrossRef]
- Miller, R.C. Notes on analysis and severe storm forecasting procedures of the Air Force Global Weather Central. AWS 1972, 200, 190. [Google Scholar]
- Showalter, A.K. A stability index for forecasting thunderstorms. Bull. Am. Meteorol. Soc. 1947, 34, 250–252. [Google Scholar] [CrossRef]
- Galway, J.G. The lifted index as a predictor of latent instability. Bull. Am. Meteorol. Soc. 1956, 43, 528–529. [Google Scholar] [CrossRef]
- George, J.J. Weather Forecasting for Aeronautics; Academic Press: Cambridge, MA, USA, 1960; p. 673. [Google Scholar]
- Glickman, T.S. (Ed.) Glossary of Meteorology, 2nd ed.; American Meteorological Society: Boston, MA, USA, 2000; p. 855. [Google Scholar]
- Weisman, M.L.; Klemp, J.B. The dependence of numerically simulated convective storms on vertical wind shear and buoyancy. Mon. Weather Rev. 1982, 110, 504–520. [Google Scholar] [CrossRef]
- Doswell III, C.A.; Schultz, D.M. On the use of indices and parameters in forecasting severe storms. E J. Sev. Storms Meteorol. 2006, 1, 1–22. [Google Scholar]
- StatSoft Inc. STATISTICA (Data Analysis Software System), 6th ed.; Tulsa, OK, USA, 2001; p. 150. Available online: www.statsoft.com (accessed on 11 December 2019).
- Donaldson, R.J.; Dyer, R.M.; Kraus, M.J. Objective evaluator of techniques for predicting severe weather events. Bull. Am. Meteorol. Soc. 1975, 56, 755. [Google Scholar]
- Hanssen, A.W.; Kuipers, W.J.A. On the Relationship Between the Frequency of Rain and Various Meteorological Parameters: (with Reference to the Problem Ob Objective Forecasting). Staatsdrukkerij-en Uitgeverijbedrijf 1965, 65, 2–15. [Google Scholar]
- Brenot, H.; Ducrocq, V.; Walpersdorf, A.; Champollion, C.; Caumont, O. GPS zenith delay sensitivity evaluated from high-resolution numerical weather prediction simulations of the 8–9 September 2002 flash flood over southeastern France. J. Geophys. Res. Atmos. 2006, 111, D15. [Google Scholar] [CrossRef]
- Viktor, E.; Reese, S.; Zimmerli, P. Hail losses under microscope—Comparing losses from three major hail events of the recent past. In Proceedings of the 8th ECSS, Wiener Neustadt, Austria, 14–18 September 2015; Available online: http://www.meetingorganizer.copernicus.org/ECSS2015/ECSS2015-19.pdf (accessed on 11 December 2019).
- Haralambous, H.; Oikonomou, C.; Pikridas, C.; Guerova, G.; Dimitrova, T.; Lagouvardos, K.; Kotroni, V.; Tymvios, F. BeRTISS project: Balkan-Mediterranean real-time severe weather service. In Proceedings of the Sixth International Conference on Remote Sensing and Geoinformation of the Environment, Paphos, Cyprus, 26–29 March 2018; Volume 10773, p. 1077313. [Google Scholar]
| Index Abbreviation Full Name | Formula | Reference |
|---|---|---|
| SWEAT Severe Weather Threat Index | 20(TT −49) + 12 D850 + 2 V850 + V500 + 125 (sin (500-850) + 0.2)) | [36] |
| SHI Showalter Index | T500 − Tlp(850hPa) | [37] |
| LI Lifted Index | Tlp(fcs surface) −T500 | [38] |
| K K Index | (T850 − T500) + D850 - (T700 − D700) | [39] |
| CAPE Convective Available Potential Energy | g | [40] |
| TT Total Totals Index | (T850 − T500) + (D850 − T500) | [36] |
| BRN Bulk Richardson Number | [41] |
| Month | IWV (kg/m2) | NTH Days (% of All NTH days) | TH Days (% of All TH days) |
|---|---|---|---|
| May | >20 | 19 | 65 |
| June | >24 | 28 | 68 |
| July | >28 | 28 | 51 |
| August | >28 | 11 | 64 |
| September | >26 | 18 | 86 |
| Month | IWV [kg/m2] | POD | FAR |
|---|---|---|---|
| May | 19.68 | 0.69 | 0.13 |
| June | 23.09 | 0.75 | 0.31 |
| July | 27.05 | 0.69 | 0.44 |
| August | 25.60 | 0.79 | 0.51 |
| September | 24.55 | 0.91 | 0.46 |
| May–September | 23.50 | 0.67 | 0.45 |
| Month | F1 (InI) | F2 (IWV,InI) |
|---|---|---|
| May | 0.15×K + 0.32×LI + 0.01×SWEAT − 5.355 | 0.54×IWV + 1.36×SHI + 0.74×TT + 0.07*K − 51.16 |
| June | 0.11×K + 0.57×TT + 0.97×SHI + 0.01×SWEAT − 33.35 | 0.16×IWV + 1.24×SHI + 0.08×K + 0.75×TT + 0.24×TLCL − 110.97 |
| July | 0.06×K + 0.80×TT + 0.79×SHI + 0.34×TLCL + 0.44×LI − 136.17 | 0.16×IWV + 0.45×SHI + 0.27×LI + 0.02×K + 0.58×TT + 0.16×TLCL − 78.34 |
| August | 1.43×SHI – 0.34×LI + 0.03×SWEAT – 0.01×K + 0.77×TT – 40.92 | 0.28×IWV + 0.99×TT + 1.72×SHI + 0.03×SWEAT – 59.33 |
| September | 0.03×SWEAT + 0.06×K + 1.35×SHI -0.59×LI +0.40×TT – 26.12 | 0.83×IWV + 1.48×SHI + 0.01×SWEAT – 0.06K + 0.64×TT - 52.54 |
| May–September | 0.63×TT + 0.05×K + 0.74×SHI + 0.21×TLCL + 0.01×SWEAT + 0.32×LI – 92.12 | 0. 24×IWV + 0.85×TT + 1.44SHI + 0.01×SWEAT + 0.11×TLCL + 0.02×K – 81.57 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerova, G.; Dimitrova, T.; Georgiev, S. Thunderstorm Classification Functions Based on Instability Indices and GNSS IWV for the Sofia Plain. Remote Sens. 2019, 11, 2988. https://doi.org/10.3390/rs11242988
Guerova G, Dimitrova T, Georgiev S. Thunderstorm Classification Functions Based on Instability Indices and GNSS IWV for the Sofia Plain. Remote Sensing. 2019; 11(24):2988. https://doi.org/10.3390/rs11242988
Chicago/Turabian StyleGuerova, Guergana, Tsvetelina Dimitrova, and Stefan Georgiev. 2019. "Thunderstorm Classification Functions Based on Instability Indices and GNSS IWV for the Sofia Plain" Remote Sensing 11, no. 24: 2988. https://doi.org/10.3390/rs11242988
APA StyleGuerova, G., Dimitrova, T., & Georgiev, S. (2019). Thunderstorm Classification Functions Based on Instability Indices and GNSS IWV for the Sofia Plain. Remote Sensing, 11(24), 2988. https://doi.org/10.3390/rs11242988