A Composite Method for Predicting Local Accuracies in Remotely Sensed Land-Cover Change Using Largely Non-Collocated Sample Data
Abstract
1. Introduction
2. Materials and Methods
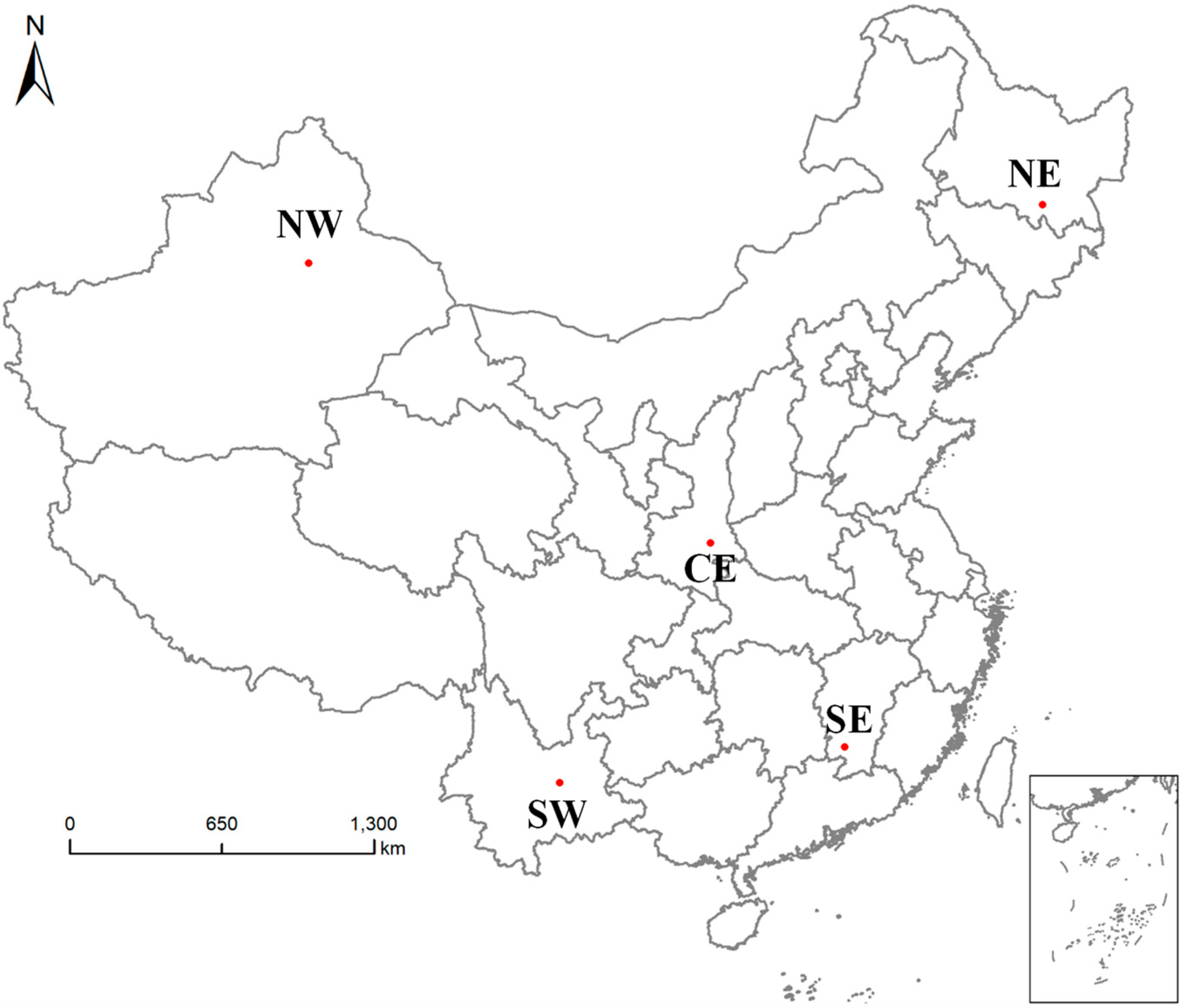
2.1. Study Area and Datasets
2.2. Methods
3. Results
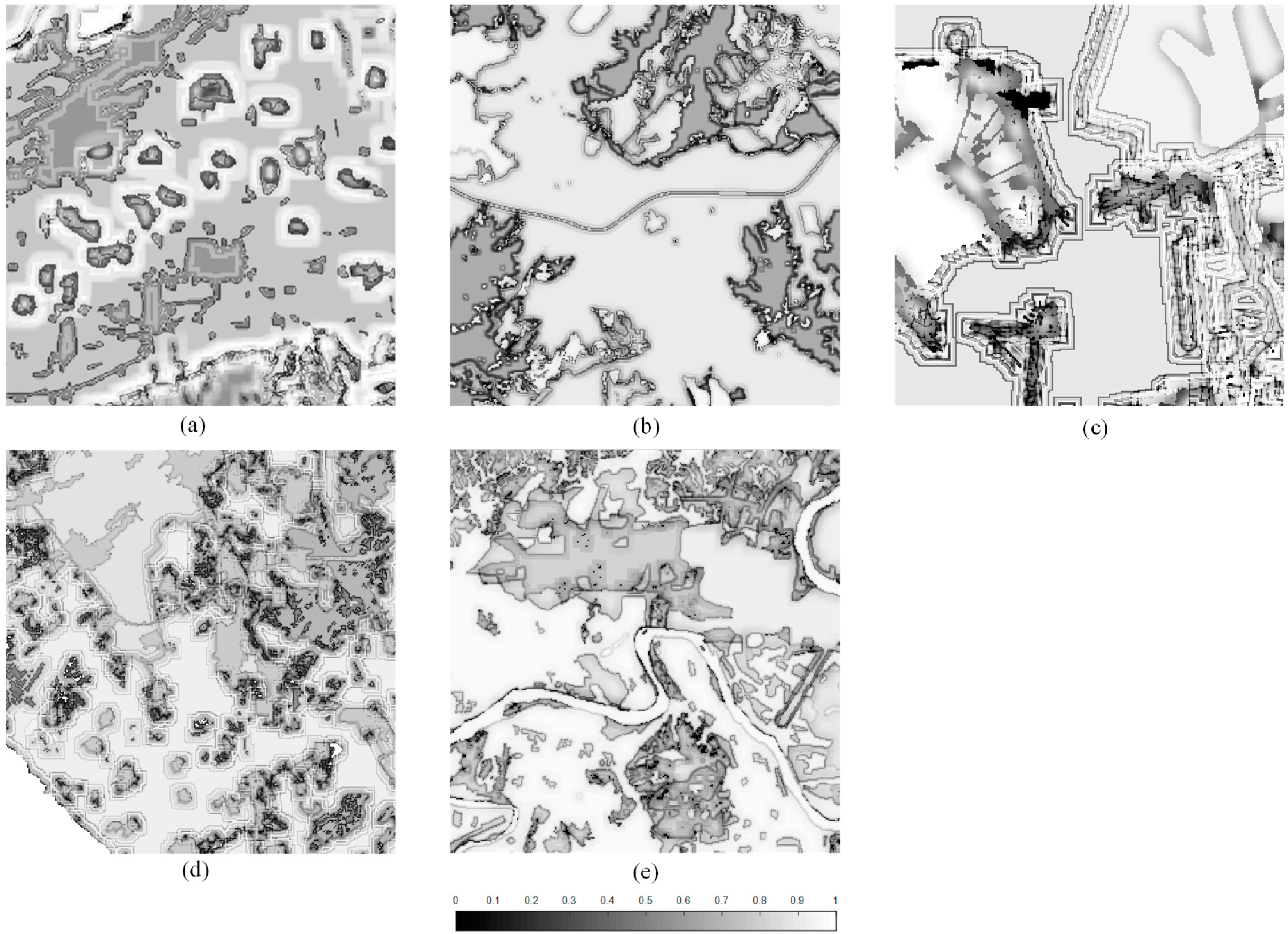
3.1. Model Fitting and Predictions
3.2. Performance Evaluations
4. Discussion
4.1. Fuzzy+Product versus PXCOV
4.2. Extensions of Fuzzy+Product to Multi-Temporal Change Analyses and Fuzzy/Fractional Classifications
4.3. Accuracy Characterization: from Local back to Global
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lambin, E.F.; Turner, B.L.; Geist, H.J.; Agbola, S.B.; Angelsen, A.; Bruce, J.W.; Folke, C. The causes of land-use and land-cover change: Moving beyond the myths. Glob. Environ. Chang. 2001, 11, 261–269. [Google Scholar] [CrossRef]
- See, L.; Schepaschenko, D.; Lesiv, M.; Mccallum, I.; Fritz, S.; Comber, A.; Maus, V. Building a hybrid land cover map with crowdsourcing and geographically weighted regression. ISPRS J. Photogramm. Remote Sens. 2015, 103, 48–56. [Google Scholar] [CrossRef]
- Friedl, M.A.; Sullamenashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X.M. MODIS collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Hansen, M.C.; Loveland, T.R. A review of large area monitoring of land cover change using Landsat data. Remote Sens. Environ. 2012, 122, 66–74. [Google Scholar] [CrossRef]
- Chen, J.; Chen, J.; Liao, A.; Cao, X.; Chen, L.; Chen, X.; He, C.; Han, G.; Peng, S.; Lu, M.; et al. Globel land cover mapping at 30m resolution: A POK-based operational approach. ISPRS J. Photogramm. Remote Sens. 2015, 103, 7–27. [Google Scholar] [CrossRef]
- Yang, L.; Jin, S.; Danielson, P.; Homer, C.; Gass, L.; Bender, S.M.; Fry, J. A new generation of the United States national land cover database: Requirements, research priorities, design, and implementation strategies. ISPRS J. Photogramm. Remote Sens. 2018, 146, 108–123. [Google Scholar] [CrossRef]
- Tsutsumida, N.; Comber, A.J. Measures of spatio-temporal accuracy for time series land cover data. Int. J. Appl. Earth Obs. Geoinf. 2015, 41, 46–55. [Google Scholar] [CrossRef]
- Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W. Disturbance-informed annual land cover classification maps of Canada’s forested ecosystems for a 29-year Landsat time series. Can. J. Remote Sens. 2018, 44, 67–87. [Google Scholar] [CrossRef]
- Hayes, D.J.; Cohen, W.B.; Sader, S.A.; Irwin, D.E. Estimating proportional change in forest cover as a continuous variable from multi-year MODIS data. Remote Sens. Environ. 2008, 112, 735–749. [Google Scholar] [CrossRef]
- Chi, Z.; Chen, Y.; Lu, D. Detecting fractional land-cover change in arid and semiarid urban landscapes with multitemporal Landsat Thematic mapper imagery. GISci. Remote Sens. 2015, 52, 700–722. [Google Scholar]
- Rigge, M.; Shi, H.; Homer, C.; Danielson, P.; Granneman, B. Long-term trajectories of fractional component change in the Northern Great Basin, USA. Ecosphere 2019, 10, e02762. [Google Scholar] [CrossRef]
- Congalton, R.G.; Gu, J.Y.; Yadav, K.; Thenkabail, P.; Ozdogan, M. Global land cover mapping: A review and uncertainty analysis. Remote Sens. 2014, 6, 12070–12093. [Google Scholar] [CrossRef]
- White, M.A.; Shaw, J.D.; Ramsey, R.D. Accuracy assessment of the vegetation continuous field tree cover product using 3954 ground plots in the southwestern USA. Int. J. Remote Sens. 2005, 26, 2699–2704. [Google Scholar] [CrossRef]
- Wickham, J.D.; Stehman, S.V.; Gass, L.; Dewitz, J.; Fry, J.A.; Wade, T.G. Accuracy assessment of NLCD 2006 land cover and impervious surface. Remote Sens. Environ. 2013, 130, 294–304. [Google Scholar] [CrossRef]
- Tsendbazar, N.E.; Bruin, S.D.; Fritz, S.; Herold, M. Spatial accuracy assessment and integration of global land cover datasets. Remote Sens. 2015, 7, 15804–15821. [Google Scholar] [CrossRef]
- Leyk, S.; Uhl, J.H.; Balk, D.; Jones, B. Assessing the accuracy of multi-temporal built-up land layers across rural-urban trajectories in the United States. Remote Sens. Environ. 2018, 204, 898–917. [Google Scholar] [CrossRef]
- Stehman, S.V.; Foody, G.M. Key issues in rigorous accuracy assessment of land cover products. Remote Sens. Environ. 2019, 231, 111199. [Google Scholar] [CrossRef]
- Comber, A.J. Geographically weighted methods for estimating local surfaces of overall, user and producer accuracies. Remote Sens. Lett. 2013, 4, 373–380. [Google Scholar] [CrossRef]
- Steele, B.M.; Winne, J.C.; Redmond, R.L. Estimation and mapping of misclassification probabilities for thematic land cover maps. Remote Sens. Environ. 1998, 66, 192–202. [Google Scholar] [CrossRef]
- Smith, J.H.; Stehman, S.V.; Wickham, J.D.; Yang, L. Effects of landscape characteristics on land-cover class accuracy. Remote Sens. Environ. 2003, 84, 342–349. [Google Scholar] [CrossRef]
- Van Oort, P.A.J.; Bregt, A.K.; de Bruin, S.; de Wit, A.J.W.; Stein, A. Spatial variability in classification accuracy of agricultural crops in the Dutch national land-cover database. Int. J. Geogr. Inf. Sci. 2004, 18, 611–626. [Google Scholar] [CrossRef]
- Foody, G.M. Local characterization of thematic classification accuracy through spatially constrained confusion matrices. Int. J. Remote Sens. 2005, 26, 1217–1228. [Google Scholar] [CrossRef]
- Burnicki, A.C. Modeling the probability of misclassification in a map of land cover change. Photogramm. Eng. Remote Sens. 2011, 77, 39–49. [Google Scholar] [CrossRef]
- Park, N.W.; Kyriakidis, P.; Hong, S.Y. Spatial estimation of classification accuracy using indicator Kriging with an image-derived ambiguity index. Remote Sens. 2016, 8, 320. [Google Scholar] [CrossRef]
- Khatami, R.; Mountrakis, G.; Stehman, S.V. Mapping per-pixel predicted accuracy of classified remote sensing images. Remote Sens. Environ. 2017, 191, 156–167. [Google Scholar] [CrossRef]
- Yang, Y.; Xiao, P.; Feng, X.; Li, H. Accuracy assessment of seven global land cover datasets over China. ISPRS J. Photogramm. Remote Sens. 2017, 125, 156–173. [Google Scholar] [CrossRef]
- Wickham, J.; Stehman, S.V.; Homer, C.G. Spatial patterns of the United States National Land Cover Dataset (NLCD) land-cover change thematic accuracy (2001–2011). Int. J. Remote Sens. 2018, 39, 1729–1743. [Google Scholar] [CrossRef]
- Comber, A.; Brunsdon, C.; Charlton, M.; Harris, P. Geographically weighted correspondence matrices for local error reporting and change analyses: Mapping the spatial distribution of errors and change. Remote Sens. Lett. 2017, 8, 234–243. [Google Scholar] [CrossRef]
- Khatami, R.; Mountrakis, G.; Stehman, S.V. Predicting individual pixel error in remote sensing soft classification. Remote Sens. Environ. 2017, 199, 401–414. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, W.; Zhang, W.; Wang, Y.; Liu, D.; Xiu, Y. An explorative study on estimating local accuracies in land-cover information using logistic regression and class-heterogeneity-stratified data. Remote Sens. 2018, 10, 21. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, W.; Mei, Y.; Yang, W. Geostatistical characterization of local accuracies in remotely sensed land cover change categorization with complexly configured reference samples. Remote Sens. Environ. 2019, 223, 63–81. [Google Scholar] [CrossRef]
- Bey, A.; Sánchezpaus Díaz, A.; Maniatis, D.; Marchi, G.; Mollicone, D.; Ricci, S.; Rezende, M. Collect earth: Land use and land cover assessment through augmented visual interpretation. Remote Sens. 2016, 8, 807. [Google Scholar] [CrossRef]
- Cohen, W.B.; Yang, Z.; Kennedy, R. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 2. TimeSync-tools for calibration and validation. Remote Sens. Environ. 2010, 114, 2911–2924. [Google Scholar] [CrossRef]
- Lark, R.M.; Bellamy, P.H.; Rawlins, B.G. Spatio-temporal variability of some metal concentrations in the soil of eastern England, and implications for soil monitoring. Geoderma 2006, 133, 363–379. [Google Scholar] [CrossRef]
- Fritz, S.; Mccallum, I.; Schill, C.; Perger, C.; See, L.; Schepaschenko, D.; Obersteiner, M. Geo-Wiki: An online platform for improving global land cover. Environ. Model. Softw. 2012, 31, 110–123. [Google Scholar] [CrossRef]
- Stehman, S.V.; Olofsson, P.; Woodcock, C.E.; Herold, M.; Friedl, M.A. A global land-cover validation data set, II: Augmenting a stratified sampling design to estimate accuracy by region and land-cover class. Int. J. Remote Sens. 2012, 33, 6975–6993. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Herold, M.; Stehman, S.V.; Woodcock, C.E.; Wulder, M.A. Good practices for estimating area and assessing accuracy of land change. Remote Sens. Environ. 2014, 148, 42–57. [Google Scholar] [CrossRef]
- Mcroberts, R.E.; Walters, B.F. Statistical inference for remote sensing-based estimates of net deforestation. Remote Sens. Environ. 2012, 124, 394–401. [Google Scholar] [CrossRef]
- Zhang, J.; Mei, Y. Integrating logistic regression and geostatistics for user-oriented and uncertainty-informed accuracy characterization in remotely-sensed land cover change information. ISPRS Int. J. Geo-Inf. 2016, 5, 113. [Google Scholar] [CrossRef]
- Overton, W.S.; Stehman, S.V. Desirable design characteristics for long-term monitoring of ecological variables. Environ. Ecol. Stat. 1996, 3, 349–361. [Google Scholar] [CrossRef]
- Steele, B.M. Combining multiple classifiers: An application using spatial and remotely sensed information for land cover type mapping. Remote Sens. Environ. 2000, 74, 545–556. [Google Scholar] [CrossRef]
- Pontius, R.G.; Cheuk, M.L. A generalized cross-tabulation matrix to compare soft-classified maps at multiple resolutions. Int. J. Geogr. Inf. Sci. 2006, 20, 1–30. [Google Scholar] [CrossRef]
- Binaghi, E.; Brivio, P.A.; Ghezzi, P.; Rampini, A. A fuzzy set-based accuracy assessment of soft classification. Pattern Recognit. Lett. 1999, 20, 935–948. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Ahlqvist, O. Extending post-classification change detection using semantic similarity metrics to overcome class heterogeneity: A study of 1992 and 2001 U.S. national land cover database changes. Remote Sens. Environ. 2008, 112, 1226–1241. [Google Scholar] [CrossRef]
- Smith, J.H.; Stehman, S.V.; Wickham, J.D. Impacts of patch size and land-cover heterogeneity on thematic image classification accuracy. Photogramm. Eng. Remote Sens. 2002, 68, 65–70. [Google Scholar]
- Liu, C.; White, M.; Newell, G. Measuring and comparing the accuracy of species distribution models with presence-absence data. Ecography 2011, 34, 232–243. [Google Scholar] [CrossRef]
- Robin, X.; Turck, N.; Hainard, A.; Tiberti, N.; Lisacek, F.; Sanchez, J.-C.; Müller, M. pROC: An open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinform. 2011, 12, 77. [Google Scholar] [CrossRef]
- DeLong, E.; DeLong, D.; Clarke-Pearson, D. Comparing the areas under two or more correlated receiver operating characteristic curves: A nonparametric approach. Biometrics 1988, 44, 837–845. [Google Scholar] [CrossRef]
- Hanley, J.A.; McNeil, B.J. A method of comparing the areas under receiver operating characteristic curves derived from the same cases. Radiology 1983, 148, 839–843. [Google Scholar] [CrossRef]
- Venkatraman, E.S. A permutation test to compare receiver operating characteristic curves. Biometrics 2000, 56, 1134–1138. [Google Scholar] [CrossRef] [PubMed]
- Venkatraman, E.S.; Begg, C.B. A distribution-free procedure for comparing receiver operating characteristic curves from a paired experiment. Biometrika 1996, 83, 835–848. [Google Scholar] [CrossRef]
- Dombi, J. A general class of fuzzy operators, the DeMorgan class of fuzzy operators and fuzziness measures induced by fuzzy operators. Fuzzy Sets Syst. 1982, 8, 149–163. [Google Scholar] [CrossRef]
- Fritz, S.; Lee, L. Comparison of land cover maps using fuzzy agreement. Int. J. Geogr. Inf. Sci. 2005, 19, 787–807. [Google Scholar] [CrossRef]
- Koch, J.; Jensen, K.H.; Stisen, S. Toward a true spatial model evaluation in distributed hydrological modeling: Kappa statistics, Fuzzy theory, and EOF analysis benchmarked by the human perception and evaluated against a modeling case study. Water Resour. Res. 2015, 51, 1225–1246. [Google Scholar] [CrossRef]
- Lowry, J.H.; Ramsey, R.D.; Stoner, L.L.; Kirby, J.; Schulz, K. An Ecological Framework for Evaluating Map Errors Using Fuzzy Sets. Photogramm. Eng. Remote Sens. 2008, 74, 1509–1519. [Google Scholar] [CrossRef]
- Hester, D.B.; Nelson, S.A.C.; Cakir, H.I.; Khorram, S.; Cheshire, H. High-resolution land cover change detection based on fuzzy uncertainty analysis and change reasoning. Int. J. Remote Sens. 2010, 31, 455–475. [Google Scholar] [CrossRef]
- McRoberts, R.E. Probability- and model-based approaches to inference for proportion forest using satellite imagery as ancillary data. Remote Sens. Environ. 2010, 114, 11017–11025. [Google Scholar] [CrossRef]
- Stahl, G.; Saarela, S.; Schnell, S.; Holm, S.; Breidenbach, J.; Healey, S.P.; Patterson, P.L.; Magnussen, S.; Naesset, E.; McRoberts, R.E.; et al. Use of models in large-area forest surveys: Comparing model-assisted, model-based and hybrid estimation. For. Ecosyst. 2016, 3, 5. [Google Scholar] [CrossRef]
- Naesset, E.; Orka, H.O.; Solberg, S.; Bollandsas, O.M.; Hansen, E.H.; Mauya, E.; Zahabu, E.; Malimbwi, R.; Chamuya, N.; Olsson, H.; et al. Mapping and estimating forest area and aboveground biomass in miombo woodlands in Tanzania using data from airborne laser scanning. Remote Sens. Environ. 2016, 175, 282–300. [Google Scholar] [CrossRef]
- Stahl, G.; Holm, S.; Timothy, G.; Gregoire, T.; Naesset, E.; Nelson, R. Model-based inference for biomass estimation in a LiDAR sample survey in Hedmark County, Norway. Can. J. For. Res. 2011, 41, 96–107. [Google Scholar] [CrossRef]
- Esteban, J.; McRoberts, R.E.; Fernandez-Landa, A.; Tome, J.L.; Naesset, E. Estimating Forest Volume and Biomass and Their Changes Using Random Forests and Remotely Sensed Data. Remote Sens. 2019, 11, 1944. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Stehman, S.V.; Woodcock, C.E. Making better use of accuracy data in land change studies: Estimating accuracy and area and quantifying uncertainty using stratified estimation. Remote Sens. Environ. 2013, 129, 122–131. [Google Scholar] [CrossRef]
- Stehman, S.V. Estimating area from an accuracy assessment error matrix. Remote Sens. Environ. 2013, 132, 202–211. [Google Scholar] [CrossRef]
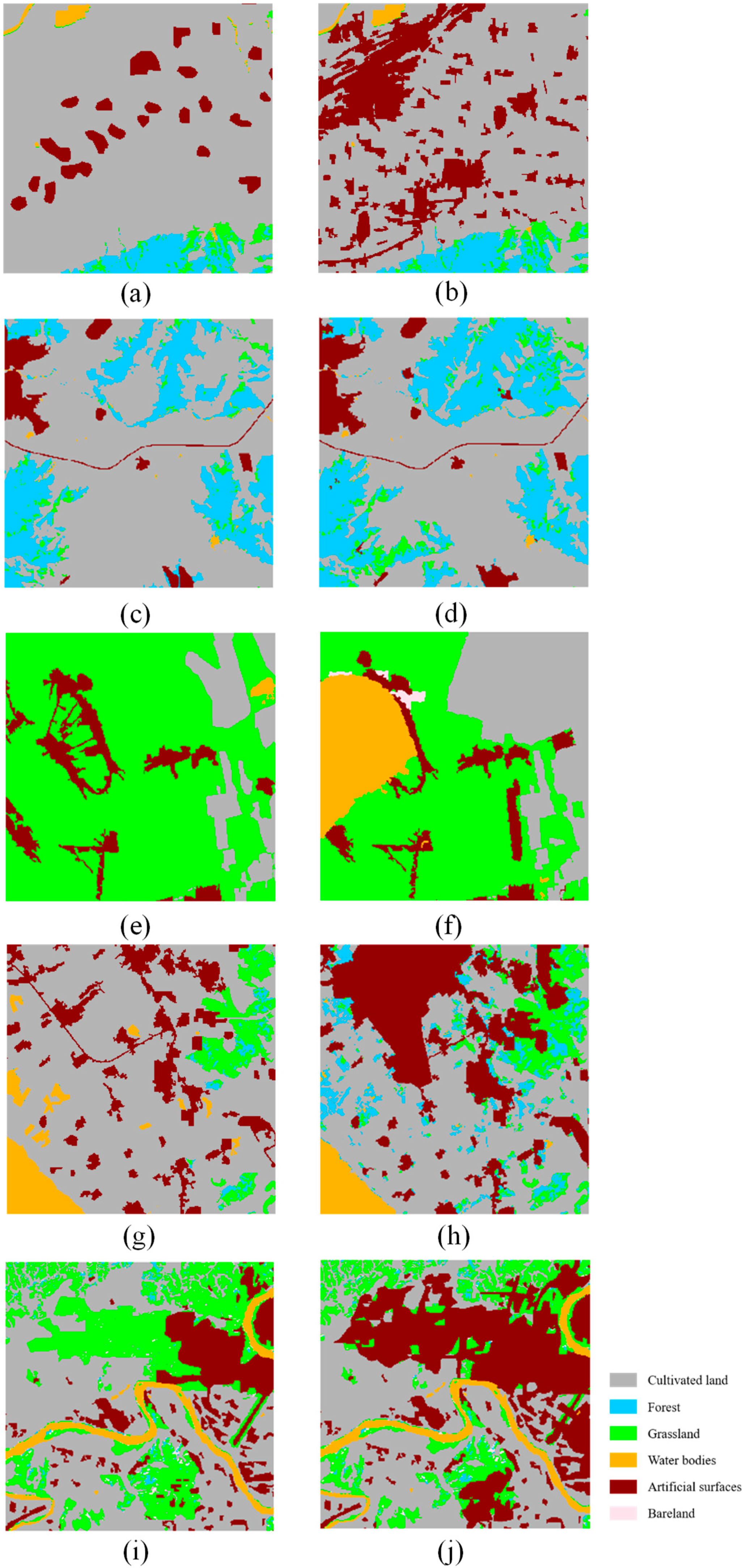


| Type | Definition |
|---|---|
| Cultivated land | Land used for agriculture, horticulture, and gardens, including paddy fields, irrigated and dry farmland, vegetable and fruit garden, etc. |
| Forest | Land covered by trees, vegetation covers over 30%, including deciduous and coniferous forests, and sparse woodland with cover 10–30%, etc. |
| Grassland | Land covered by natural grass with cover over 10%, etc. |
| Water bodies | Water bodies in land area, including river, lake, reservoir, fish pond, etc. |
| Artificial surfaces | Land modified by human activities, including all kinds of habitation, industrial and mining area, transportation facilities, interior urban green zones and water bodies, etc. |
| Bare land | Land with vegetation cover lower than 10%, including desert, sandy fields, Gobi, bare rocks, saline and alkaline land, etc. |
| Configurations | Numbers of Sample Pixels | |||
|---|---|---|---|---|
| Collocated | Non-Collocated | |||
| time 1 | time 2 | time 1 | time 2 | |
| 0 | 0 | 0 | 630 | 630 |
| 1 | 63 | 63 | 567 | 567 |
| 2 | 126 | 126 | 504 | 504 |
| 3 | 189 | 189 | 441 | 441 |
| 4 | 252 | 252 | 378 | 378 |
| Study Sites | Configurations | ||||
|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | |
| (a) | |||||
| CE | class + ent21 + con9 | class + dom19 + het19 + ent21 + hom7 | class + ent21 + con9 | class + ent21 + con9 | class + ent21 + con17 + hom3 |
| NE | class + con5 | class + con5 | class + het5 + ent19 | class + het5 + ent21 | class + het5 |
| NW | hom21 + class + ent21 | hom21 + class + ent21 | hom21 + class + ent21 | class + ent21 | class + ent21 |
| SW | class + hom3 | class + hom5 | class + dom3 | class + con5 + het5 + dom15 | class + het3 |
| SE | class + hom5 + dom9 | class + ent5 + dom17 + dom5 + dom9 + het9 + con5 | class + ent5 + dom19 + con7 + ent11 | class + ent5 + dom19 + con7 + ent11 | class + ent5 + het19 |
| (b) | |||||
| CE | con7 + class + dom13 + hom3 + dom3 + ent3 + het7 | con7 + class + dom13 | class + ent7 + het15 + ent21 + con15- + dom3 + ent3 + hom5 + con17 + ent11 + ent19 + het19 + het21 | con7 + class + het15 + ent21 + con15 + dom3 + ent3 + het19 + het21 + con19 + ent11 + het7 | con7 + class + dom19 + dom21 + dom3 + ent3 + hom13 |
| NE | con7 + class + hom3 + hom5 + hom17 | ent3 + dom5 + class | ent3 + dom7 + class | ent3 + class + con17 | ent3 + class + ent15 |
| NW | class + hom9 + con7 + dom21 + het19 + dom13 + con11 + dom9 + hom15 + het15 | class + hom9 + dom21 + het19 + dom13 | class + hom9 + dom21 + het19 + dom13 | class + hom9 + dom21 + het19 + dom13 | class + hom9 + dom21 + het19 + dom13 + het5 + hom21 + con13 + het13 |
| SW | con15 + class + con3 + dom7 + dom9 + dom11 | con15 + class + het3 + dom7 + dom9 + dom11 | con15 + class + het3 + dom7 + het9 + het11 | con13 + class + het3 + dom11 | con13 + class + het3 + dom11 + dom7 + dom9 |
| SE | ent3 + class + ent15 | ent3 + class + ent15 | ent3 + class + ent15 | ent3 + class + ent19 + het21 + dom21 | ent3 + class + ent21 + het21 + dom21 |
| Study Sites | Sample Configurations | |||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | ||
| CE | change | 0.00 | −0.48 | −0.18 | −0.10 | −0.14 |
| no-change | 0.83 | 1.00 | 1.00 | 0.51 | 0.78 | |
| NE | change | 0.00 | −0.04 | −0.02 | −0.02 | −0.03 |
| no-change | 1.00 | 1.00 | 1.00 | 1.00 | 0.70 | |
| NW | change | 0.00 | −0.21 | −0.10 | −0.11 | −0.06 |
| no-change | 1.00 | 1.00 | 1.00 | 0.92 | 0.80 | |
| SW | change | 0.00 | −0.05 | −0.07 | −0.08 | −0.01 |
| no-change | 1.00 | 0.79 | 0.94 | 1.00 | 0.86 | |
| SE | change | 0.00 | 0.06 | 0.08 | −0.01 | 0.00 |
| no-change | 0.45 | 1.00 | 1.00 | 0.77 | 0.77 | |
| Study Sites | Methods | Configurations | ||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | ||
| CE | I | 0.84 | 0.84 | 0.83 | 0.84 | 0.84 |
| II | 0.86 | 0.89 | 0.86 | 0.84 | 0.86 | |
| III | 0.77 | 0.74 | 0.76 | 0.78 | 0.76 | |
| IV | 0.78 | 0.78 | 0.79 | 0.80 | 0.79 | |
| NE | I | 0.72 | 0.70 | 0.70 | 0.72 | 0.72 |
| II | 0.73 | 0.71 | 0.72 | 0.72 | 0.72 | |
| III | 0.72 | 0.70 | 0.71 | 0.71 | 0.71 | |
| IV | 0.72 | 0.70 | 0.70 | 0.70 | 0.71 | |
| NW | I | 0.75 | 0.78 | 0.78 | 0.79 | 0.79 |
| II | 0.75 | 0.79 | 0.79 | 0.80 | 0.79 | |
| III | 0.73 | 0.76 | 0.77 | 0.78 | 0.78 | |
| IV | 0.75 | 0.78 | 0.79 | 0.80 | 0.79 | |
| SW | I | 0.80 | 0.81 | 0.81 | 0.81 | 0.81 |
| II | 0.81 | 0.81 | 0.81 | 0.82 | 0.81 | |
| III | 0.78 | 0.79 | 0.78 | 0.79 | 0.79 | |
| IV | 0.78 | 0.78 | 0.79 | 0.79 | 0.79 | |
| SE | I | 0.71 | 0.71 | 0.71 | 0.71 | 0.71 |
| II | 0.71 | 0.72 | 0.72 | 0.71 | 0.71 | |
| III | 0.70 | 0.69 | 0.70 | 0.69 | 0.70 | |
| IV | 0.70 | 0.70 | 0.70 | 0.69 | 0.70 | |
| Study Sites | Methods Pairs | Configurations | ||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | ||
| CE | I versus II | −0.02 | −0.05 | −0.03 | −0.00 | −0.02 |
| I versus III | 0.07 * | 0.09 * | 0.07 * | 0.06 * | 0.08 * | |
| I versus IV | 0.07 * | 0.05 * | 0.04 * | 0.04 * | 0.06 * | |
| NE | I versus II | −0.01 | −0.01 | −0.02 | −0.01 | −0.01 |
| I versus III | 0.00 | −0.01 | −0.00 | 0.01 * | 0.00 | |
| I versus IV | 0.00 | −0.00 | 0.01 | 0.01 * | 0.00 | |
| NW | I versus II | −0.01 | −0.01 | −0.01 | −0.01 | −0.00 |
| I versus III | 0.01 * | 0.01 * | 0.01 * | 0.01 * | 0.01 * | |
| I versus IV | −0.01 | −0.00 | −0.01 | −0.01 | −0.00 | |
| SW | I versus II | −0.01 | −0.01 | −0.01 | −0.01 | −0.00 |
| I versus III | 0.02 * | 0.02 * | 0.02 * | 0.02 * | 0.02 * | |
| I versus IV | 0.02 * | 0.02 * | 0.02 * | 0.02 * | 0.02 * | |
| SE | I versus II | 0.00 | −0.01 | −0.01 | −0.00 | −0.00 |
| I versus III | 0.01 * | 0.01 * | 0.02 * | 0.02 * | 0.01 * | |
| I versus IV | 0.01 * | 0.01 * | 0.01 * | 0.01 * | 0.01 * | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, Y.; Zhang, J.; Zhang, W.; Liu, F. A Composite Method for Predicting Local Accuracies in Remotely Sensed Land-Cover Change Using Largely Non-Collocated Sample Data. Remote Sens. 2019, 11, 2818. https://doi.org/10.3390/rs11232818
Mei Y, Zhang J, Zhang W, Liu F. A Composite Method for Predicting Local Accuracies in Remotely Sensed Land-Cover Change Using Largely Non-Collocated Sample Data. Remote Sensing. 2019; 11(23):2818. https://doi.org/10.3390/rs11232818
Chicago/Turabian StyleMei, Yingying, Jingxiong Zhang, Wangle Zhang, and Fengzhu Liu. 2019. "A Composite Method for Predicting Local Accuracies in Remotely Sensed Land-Cover Change Using Largely Non-Collocated Sample Data" Remote Sensing 11, no. 23: 2818. https://doi.org/10.3390/rs11232818
APA StyleMei, Y., Zhang, J., Zhang, W., & Liu, F. (2019). A Composite Method for Predicting Local Accuracies in Remotely Sensed Land-Cover Change Using Largely Non-Collocated Sample Data. Remote Sensing, 11(23), 2818. https://doi.org/10.3390/rs11232818







