Eco-Friendly Estimation of Heavy Metal Contents in Grapevine Foliage Using In-Field Hyperspectral Data and Multivariate Analysis
Abstract
1. Introduction
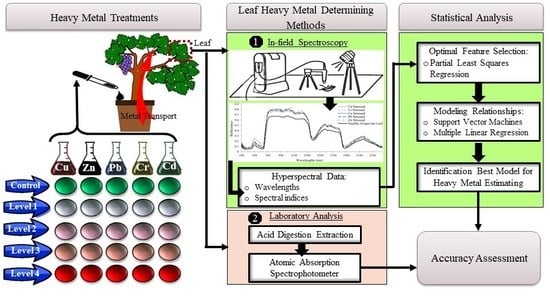
2. Materials and Methods
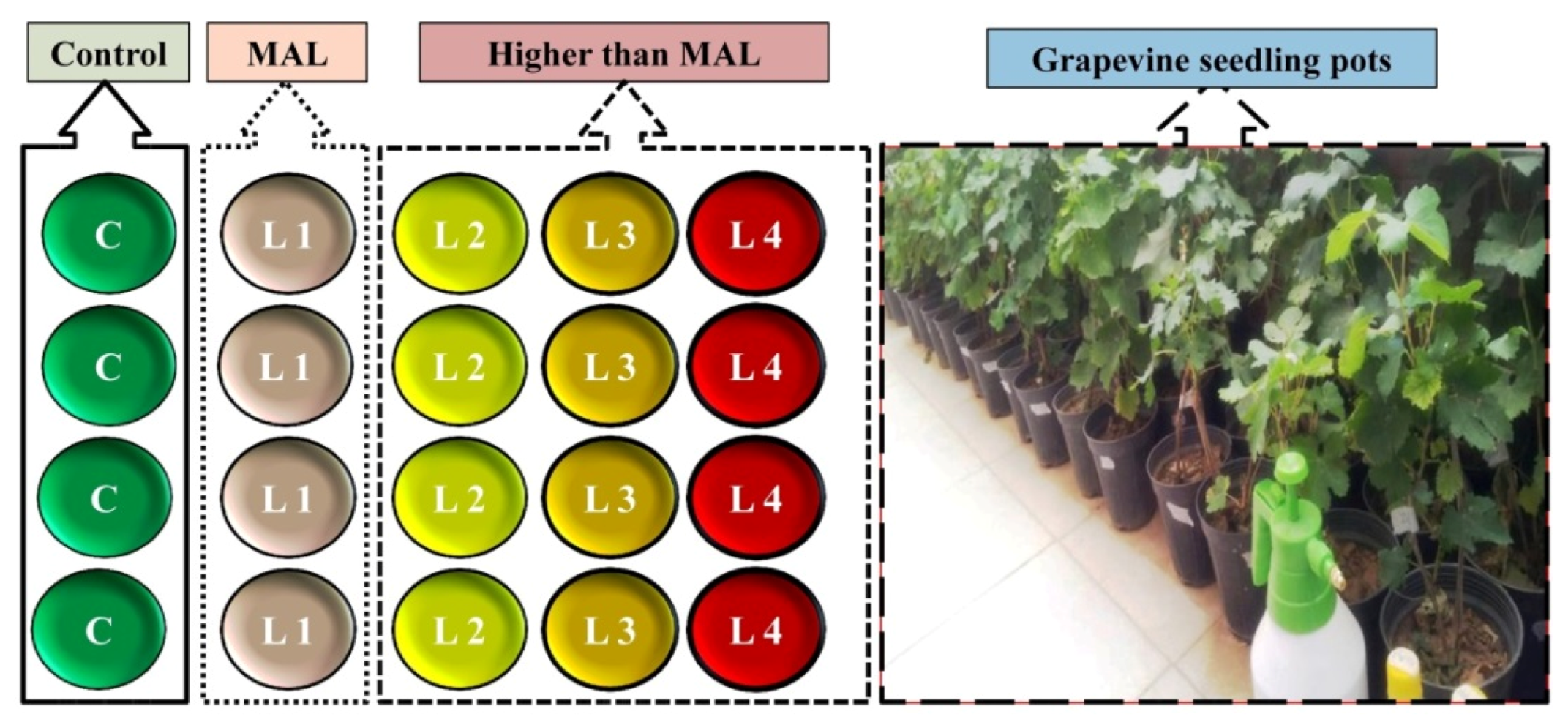
2.1. Pollutant Exposure Experiments
2.2. Spectra Acquisition
2.3. Heavy Metal Laboratory Analysis
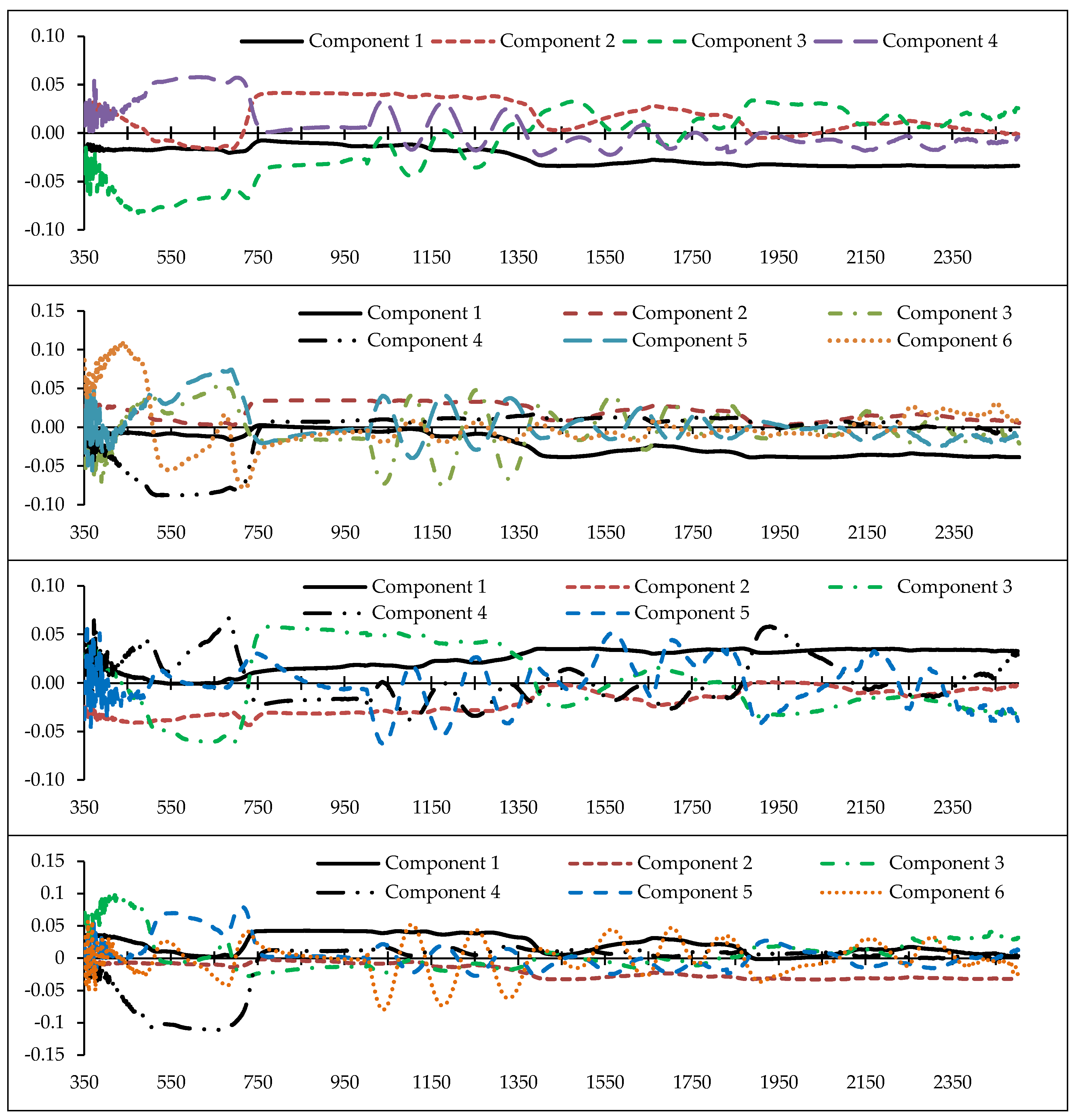
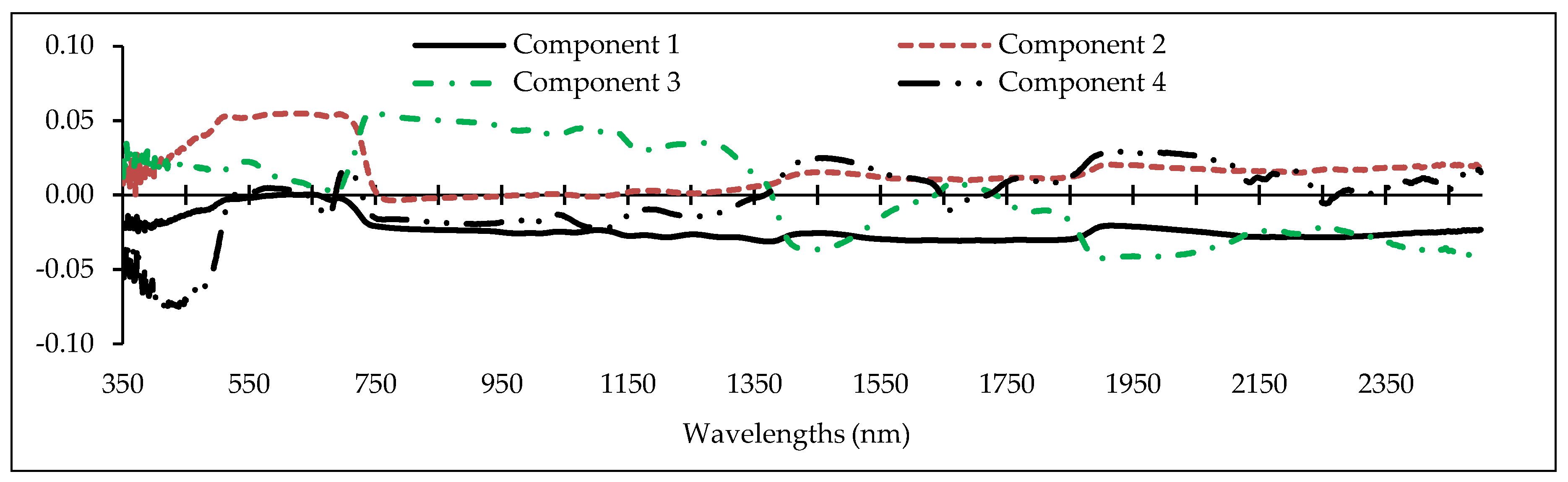
2.4. Feature Selection/Partial Least Squares (PLS)
2.5. Modelling the Relationship Between Spectral Data and Heavy Metal Contents
2.5.1. Support Vector Machine (SVM)
2.5.2. Multiple Linear Regressions (MLR)
3. Results and Discussion
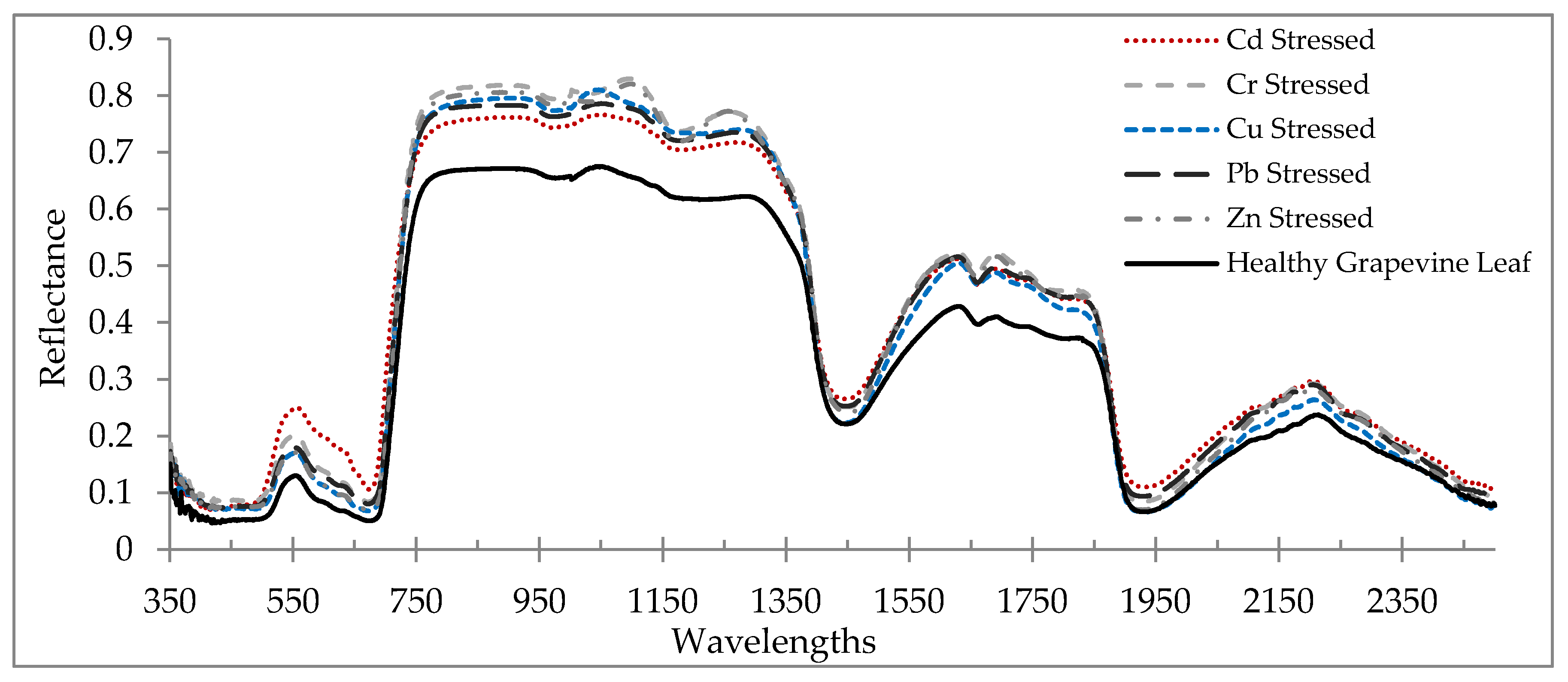
3.1. Reflectance Spectra of Healthy and Stressed Leaves
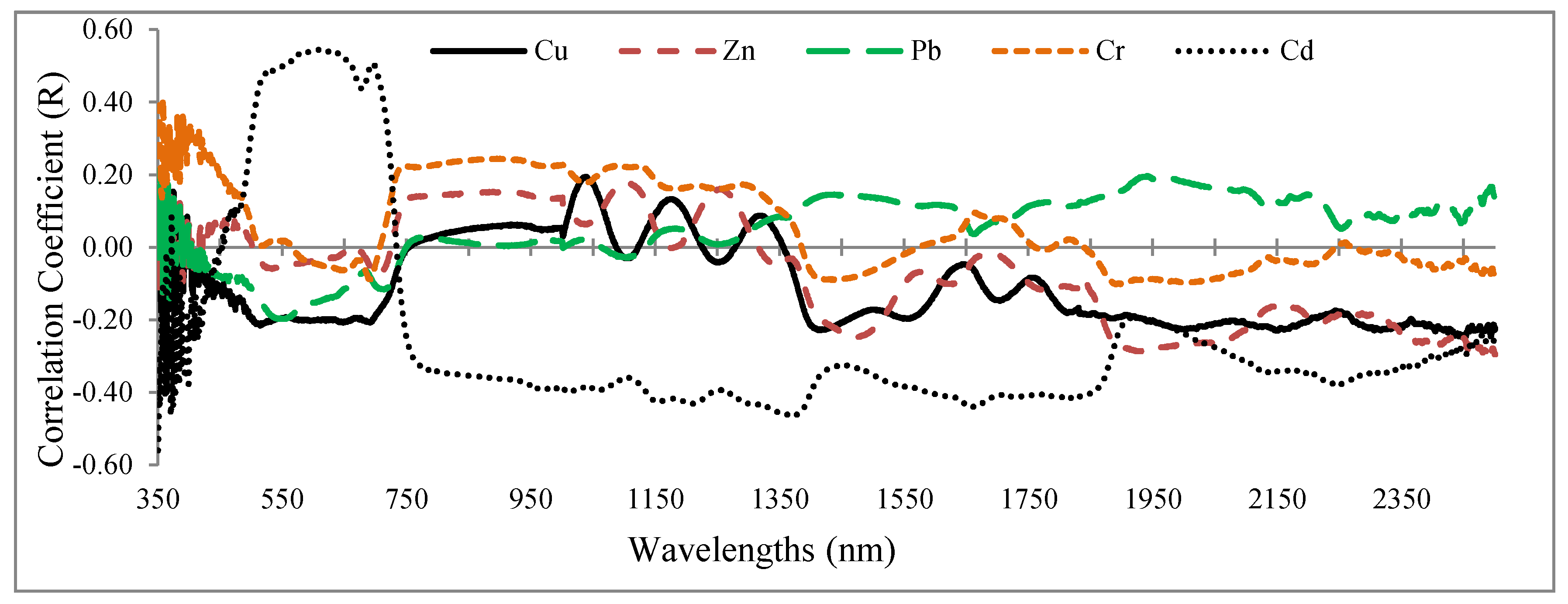
3.2. Correlation Coefficient
3.3. Optimal Feature Selection
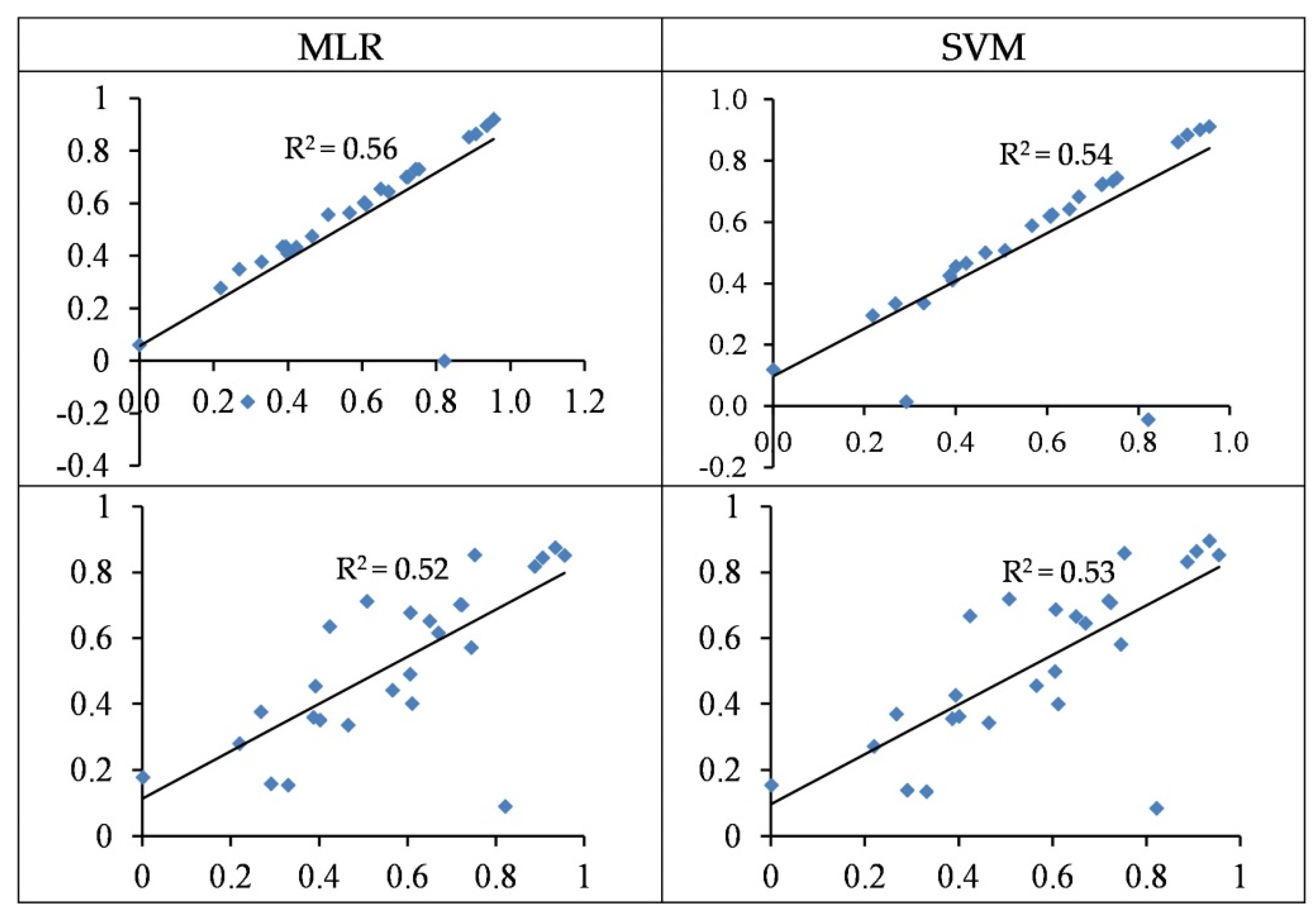
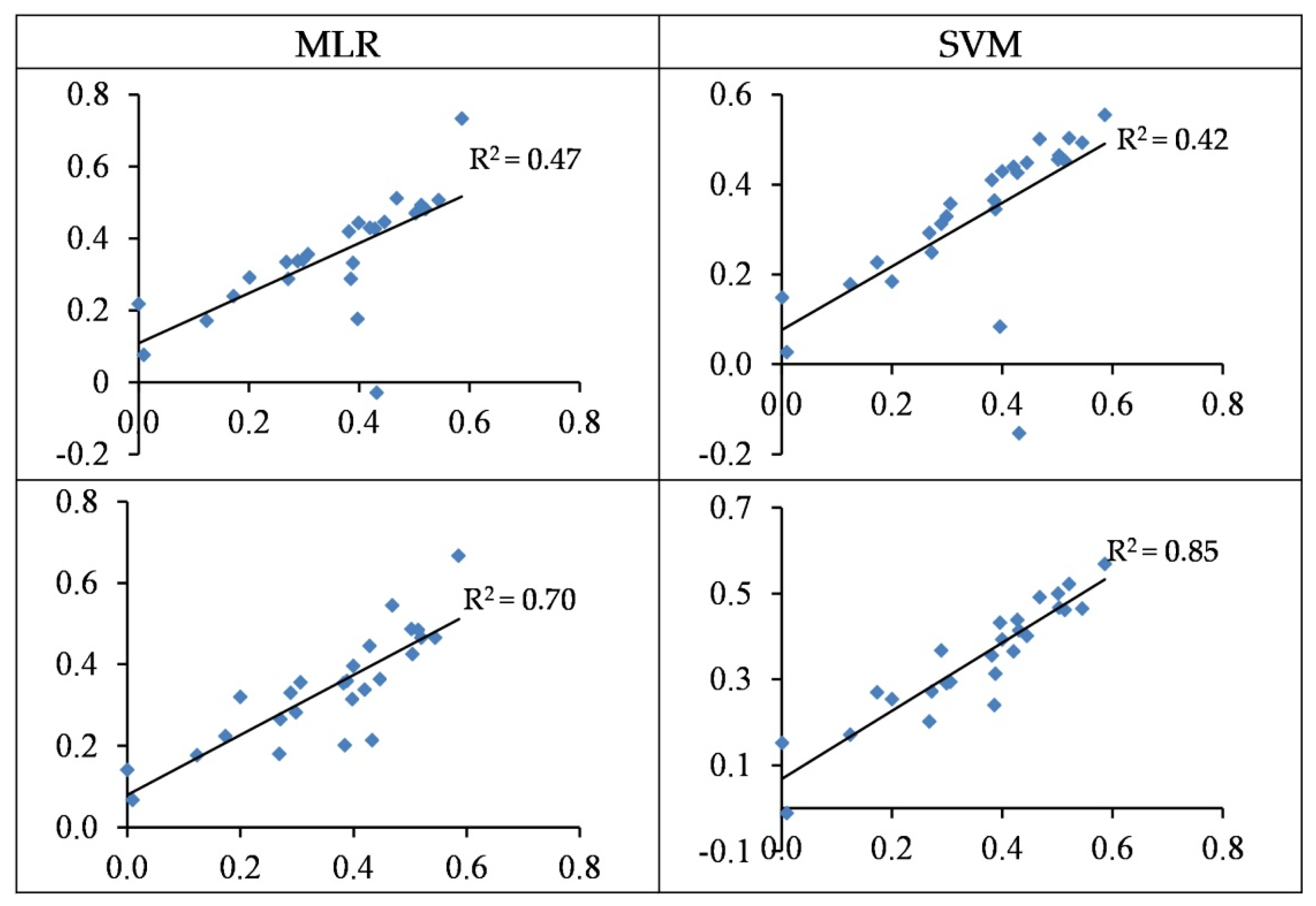
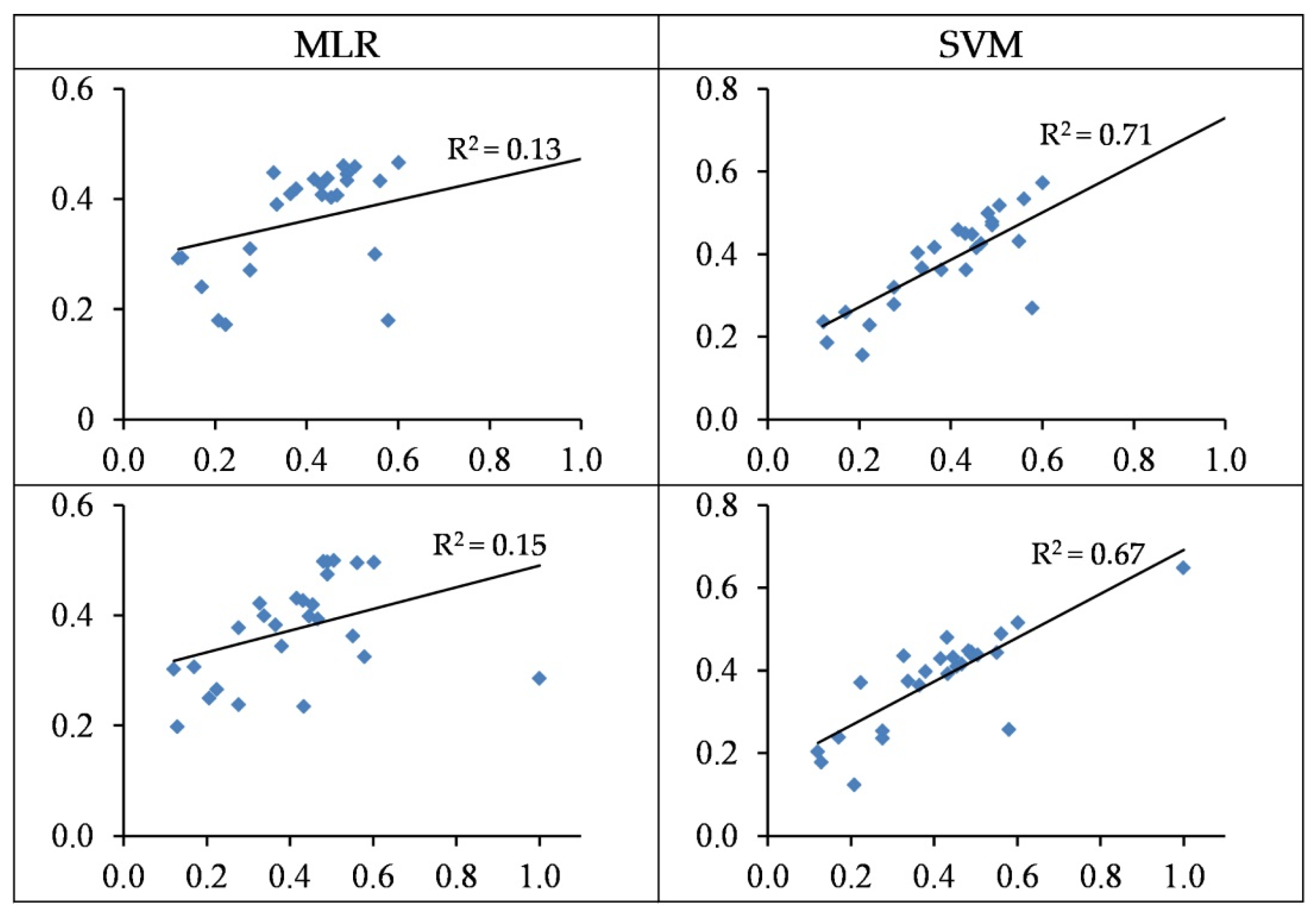
3.4. Modelling and Accuracy Assessment
3.4.1. Modelling of Cu Concentration
3.4.2. Modelling of Zn Concentration
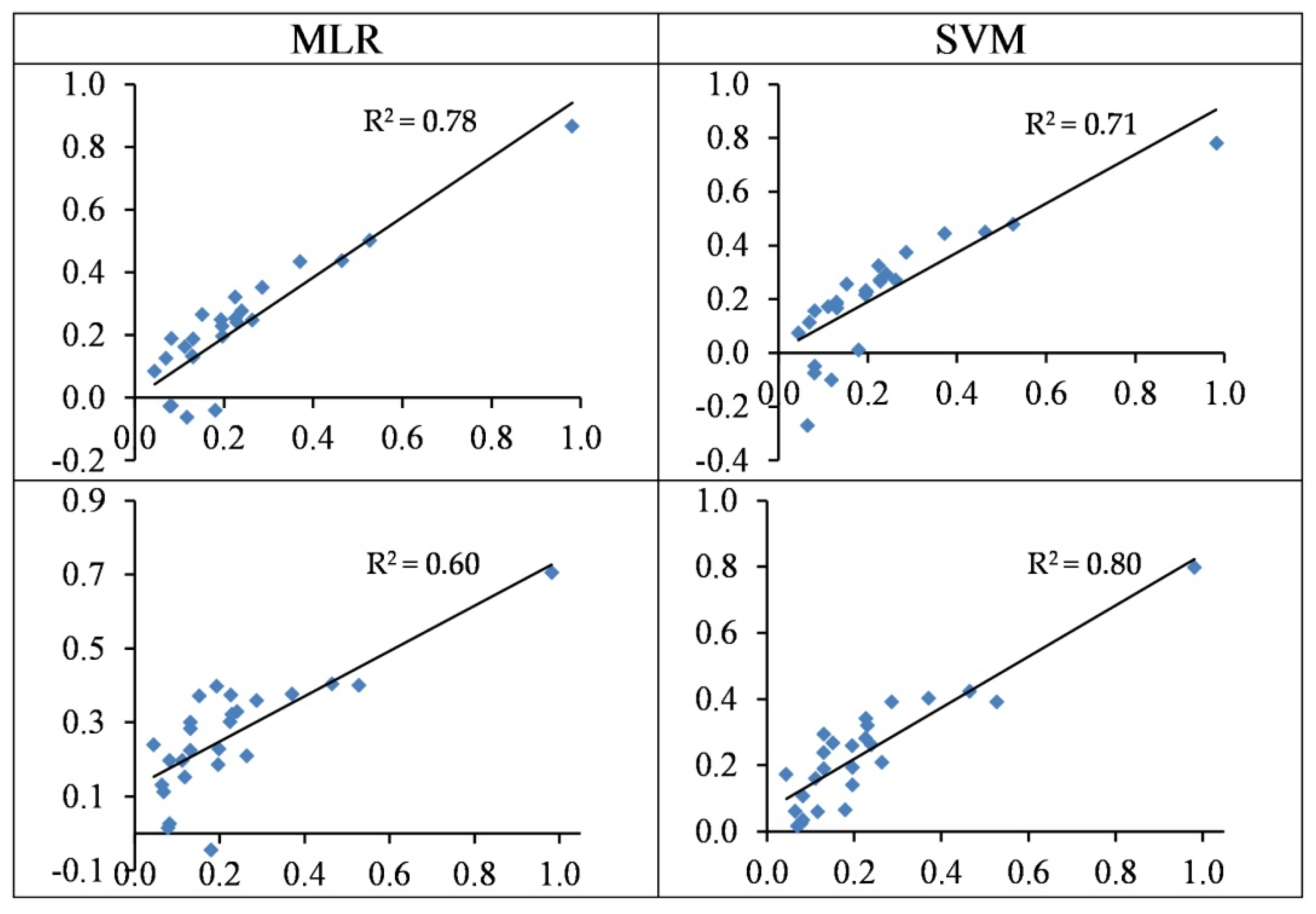
3.4.3. Modelling of Pb Concentration
3.4.4. Modelling of Cr Concentrations
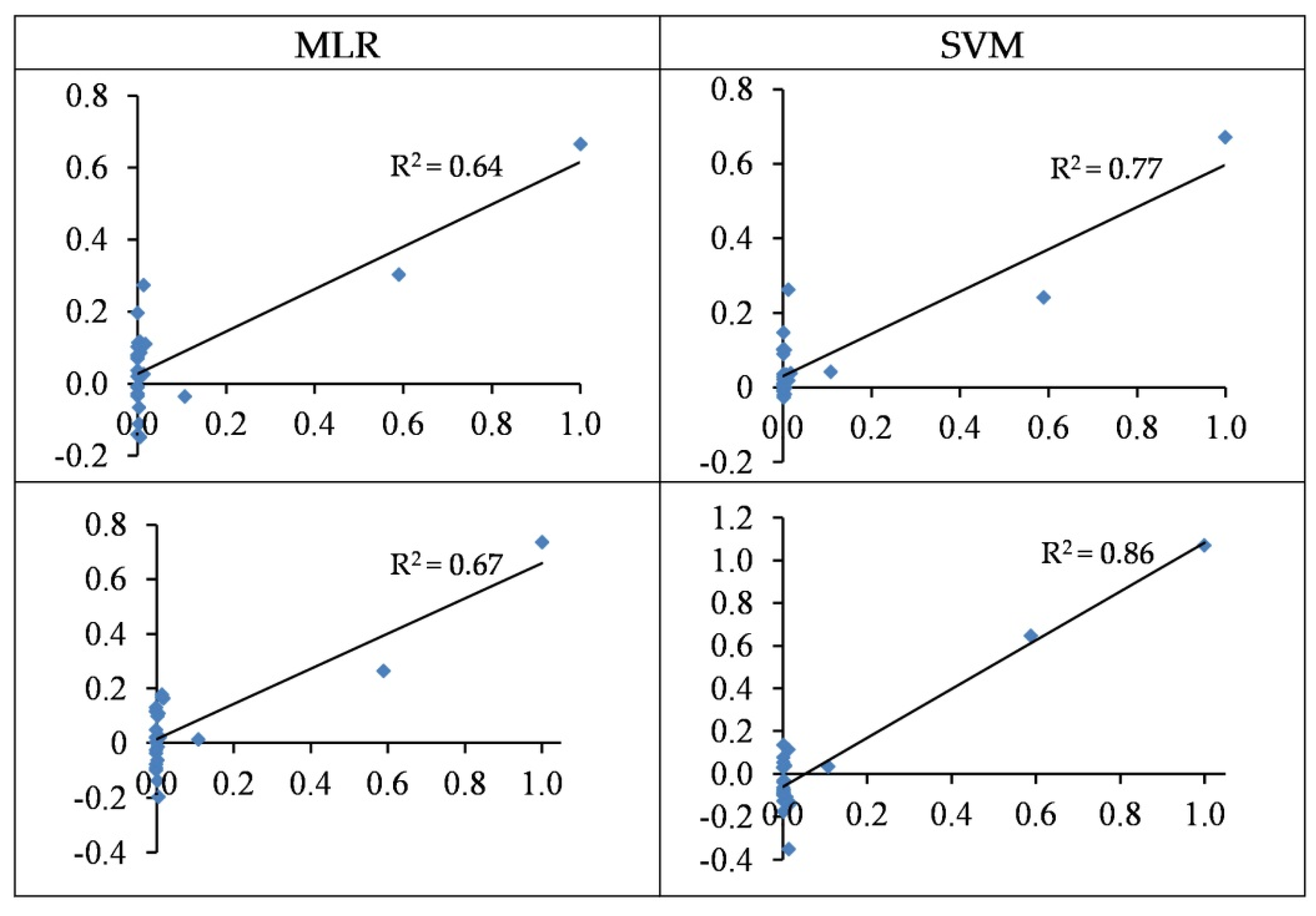
3.4.5. Modelling of Cd Concentrations
3.5. Summarizing Heavy Metal Modelling
4. Conclusions
- (i)
- The grapevine’s foliar spectral signatures (reflectance characteristics) altered when applying heavy metal stress due to their effects on the biochemical components and the leaves’ structure. Considerable changes are observed in the VIS, RDE, NIR, and MIR regions of the electromagnetic spectrum.
- (ii)
- Significant correlations are found between the heavy metal contents and the grapevine’s foliar spectral response, especially in VIS and RDE regions.
- (iii)
- From the reflectance data, 32 spectral indices were formulated using two or more bands. In PLS analysis, it was found that the Simple Ratio (SR), Cellulose Absorption Index (CAI), RATIO9752, and DWSI; R680, Water Index (WI), Lic1, MSI, and Photochemical Reflectance Index (PRI)2; Vogelman Index (VOG), MSI, SIPI, and R550; mNDVI705, Greenness Index (GI), RATIO975, and SIPI; and SIPI and DWSI are more responsive to heavy metal contents compared with the other indices. They are considered to be optimal indices to estimate Cu, Zn, Pb, Cr, and Cd concentrations, respectively.
- (iv)
- Also based on the PLS results, the wavelengths in the vicinity of 2431, 809, 489, and 616 nm; 2032, 883, 665, 564, 688, and 437 nm; 1865, 728, 692, 683, and 356 nm; 863, 2044, 415, 652, 713, and 1036 nm; and 1373, 631, 744, and 438 nm are optimal for estimating Cu, Zn, Pb, Cr, and Cd contents in the grapevine leaves, respectively. Accordingly, VIS and RDE emerged as the most sensitive regions for monitoring heavy metal contents in grapevine leaves.
- (v)
- In most cases, the SVM regression models yielded more accurate performances when estimating heavy metal contents as opposed to the MLR models. For the best SVM structures, the concentrations of Cu, Zn, Pb, Cr, and Cd are estimated with R2 values of 0.56, 0.85, 0.71, 0.80, and 0.86 in the testing set, respectively.
- (vi)
- As a general finding, spectral indices yielded more acceptable performance as opposed to wavelengths in forecasting heavy metal contents in the grapevine leaves.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, P.; Huang, F.; Liu, X. Assessment of heavy metal stress using hyperspectral data. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fox Worth, TX, USA, 23–28 July 2017; pp. 6178–6181. [Google Scholar]
- Wang, F.; Gao, J.; Zha, Y. Hyperspectral sensing of heavy metals in soil and vegetation: Feasibility and challenges. ISPRS J. Photogramm. Remote Sens. 2018, 136, 73–84. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; González-Dugo, V.; Berni, J.A. Fluorescence, temperature and narrow-band indices acquired from a UAV platform for water stress detection using a micro-hyperspectral imager and a thermal camera. Remote Sens. Environ. 2012, 117, 322–337. [Google Scholar] [CrossRef]
- Bock, C.; Poole, G.; Parker, P.; Gottwald, T. Plant disease severity estimated visually, by digital photography and image analysis, and by hyperspectral imaging. Crit. Rev. Plant Sci. 2010, 29, 59–107. [Google Scholar] [CrossRef]
- Golhani, K.; Balasundram, S.K.; Vadamalai, G.; Pradhan, B. A review of neural networks in plant disease detection using hyperspectral data. Inf. Process. Agric. 2018, 5, 354–371. [Google Scholar] [CrossRef]
- Thomas, S.; Kuska, M.T.; Bohnenkamp, D.; Brugger, A.; Alisaac, E.; Wahabzada, M.; Behmann, J.; Mahlein, A.-K. Benefits of hyperspectral imaging for plant disease detection and plant protection: A technical perspective. J. Plant Dis. Prot. 2018, 125, 5–20. [Google Scholar] [CrossRef]
- Clevers, J.G.; Kooistra, L.; Schaepman, M.E. Estimating canopy water content using hyperspectral remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 119–125. [Google Scholar] [CrossRef]
- Murphy, R.J.; Whelan, B.; Chlingaryan, A.; Sukkarieh, S. Quantifying leaf-scale variations in water absorption in lettuce from hyperspectral imagery: A laboratory study with implications for measuring leaf water content in the context of precision agriculture. Precis. Agric. 2019, 20, 767–787. [Google Scholar] [CrossRef]
- Ma, Y.; Fang, S.; Peng, Y.; Gong, Y.; Wang, D. Remote Estimation of Biomass in Winter Oilseed Rape (Brassica napus L.) Using Canopy Hyperspectral Data at Different Growth Stages. Appl. Sci. 2019, 9, 545. [Google Scholar] [CrossRef]
- Beeri, O.; Phillips, R.; Hendrickson, J.; Frank, A.B.; Kronberg, S. Estimating forage quantity and quality using aerial hyperspectral imagery for northern mixed-grass prairie. Remote Sens. Environ. 2007, 110, 216–225. [Google Scholar] [CrossRef]
- Ryu, C.; Suguri, M.; Umeda, M. Estimation of the quantity and quality of green tea using hyperspectral sensing. J. Jpn. Soc. Agric. Mach. 2010, 72, 46–53. [Google Scholar]
- Mirzaei, M.; Marofi, S.; Abbasi, M.; Solgi, E.; Karimi, R.; Verrelst, J. Scenario-based discrimination of common grapevine varieties using in-field hyperspectral data in the western of Iran. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 26–37. [Google Scholar] [CrossRef]
- Cho, M.A.; Sobhan, I.; Skidmore, A.K.; De Leeuw, J. Discriminating species using hyperspectral indices at leaf and canopy scales. Int. Arch. Spat. Inf. Sci. 2008, 369–376. [Google Scholar]
- Manevski, K.; Manakos, I.; Petropoulos, G.P.; Kalaitzidis, C. Discrimination of common Mediterranean plant species using field spectroradiometry. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 922–933. [Google Scholar] [CrossRef]
- Li, X.; Liu, X.; Liu, M.; Wang, C.; Xia, X. A hyperspectral index sensitive to subtle changes in the canopy chlorophyll content under arsenic stress. Int. J. Appl. Earth Obs. Geoinf. 2015, 36, 41–53. [Google Scholar] [CrossRef]
- Mirzaei, M.; Marofi, S.; Solgi, E.; Abbasi, M.; Karimi, R.; Bakhtyari, H.R.R. Ecological and health risks of soil and grape heavy metals in long-term fertilized vineyards (Chaharmahal and Bakhtiari province of Iran). Environ. Geochem. Health 2019, 1–17. [Google Scholar] [CrossRef]
- Sun, X.; Ma, T.; Yu, J.; Huang, W.; Fang, Y.; Zhan, J. Investigation of the copper contents in vineyard soil, grape must and wine and the relationship among them in the Huaizhuo Basin Region, China: A preliminary study. Food Chem. 2018, 241, 40–50. [Google Scholar] [CrossRef]
- Milićević, T.; Urošević, M.A.; Relić, D.; Vuković, G.; Škrivanj, S.; Popović, A. Bioavailability of potentially toxic elements in soil–grapevine (leaf, skin, pulp and seed) system and environmental and health risk assessment. Sci. Total Environ. 2018, 626, 528–545. [Google Scholar] [CrossRef]
- Wei, B.; Yang, L. A review of heavy metal contaminations in urban soils, urban road dusts and agricultural soils from China. Microchem. J. 2010, 94, 99–107. [Google Scholar] [CrossRef]
- Liang, Q.; Xue, Z.-J.; Wang, F.; Sun, Z.-M.; Yang, Z.-X.; Liu, S.-Q. Contamination and health risks from heavy metals in cultivated soil in Zhangjiakou City of Hebei Province, China. Environ. Monit. Assess. 2015, 187, 754. [Google Scholar] [CrossRef]
- Alagić, S.Č.; Tošić, S.B.; Dimitrijević, M.D.; Antonijević, M.M.; Nujkić, M.M. Assessment of the quality of polluted areas based on the content of heavy metals in different organs of the grapevine (Vitis vinifera) cv Tamjanika. Environ. Sci. Pollut. Res. 2015, 22, 7155–7175. [Google Scholar] [CrossRef]
- Guyot, G.; Baret, F.; Jacquemoud, S. Imaging spectroscopy for vegetation studies. Imaging Spectrosc. Fundam. Prospect. Appl. 1992, 2, 145–165. [Google Scholar]
- Slaton, M.R.; Raymond Hunt, E., Jr.; Smith, W.K. Estimating near-infrared leaf reflectance from leaf structural characteristics. Am. J. Bot. 2001, 88, 278–284. [Google Scholar] [CrossRef] [PubMed]
- Adam, E.; Mutanga, O. Spectral discrimination of papyrus vegetation (Cyperus papyrus L.) in swamp wetlands using field spectrometry. ISPRS J. Photogramm. Remote Sens. 2009, 64, 612–620. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Red edge shift and biochemical content in grass canopies. ISPRS J. Photogramm. Remote Sens. 2007, 62, 34–42. [Google Scholar] [CrossRef]
- Aneece, I.; Epstein, H. Identifying invasive plant species using field spectroscopy in the VNIR region in successional systems of north-central Virginia. Int. J. Remote Sens. 2017, 38, 100–122. [Google Scholar] [CrossRef]
- Damm, A.; Paul-Limoges, E.; Haghighi, E.; Simmer, C.; Morsdorf, F.; Schneider, F.D.; van der Tol, C.; Migliavacca, M.; Rascher, U. Remote sensing of plant-water relations: An overview and future perspectives. J. Plant Physiol. 2018, 227, 3–19. [Google Scholar] [CrossRef]
- Font, R.; Del Rıo, M.; Vélez, D.; Montoro, R.; De Haro, A. Use of near-infrared spectroscopy for determining the total arsenic content in prostrate amaranth. Sci. Total Environ. 2004, 327, 93–104. [Google Scholar] [CrossRef]
- Font, R.; Vélez, D.; Del Río-Celestino, M.; De Haro-Bailón, A.; Montoro, R. Screening inorganic arsenic in rice by visible and near-infrared spectroscopy. Microchim. Acta 2005, 151, 231–239. [Google Scholar] [CrossRef]
- Ping, W.; Liu, X.; Huang, F. Retrieval model for subtle variation of contamination stressed maize chlorophyll using hyperspectral data. Guang Pu Xue Yu Guang Pu Fen Xi = Guang Pu 2010, 30, 197–201. [Google Scholar]
- Asner, G.P.; Martin, R.E. Airborne spectranomics: Mapping canopy chemical and taxonomic diversity in tropical forests. Front. Ecol. Environ. 2009, 7, 269–276. [Google Scholar] [CrossRef]
- Harmon, R.S.; Remus, J.; McMillan, N.J.; McManus, C.; Collins, L.; Gottfried Jr, J.L.; DeLucia, F.C.; Miziolek, A.W. LIBS analysis of geomaterials: Geochemical fingerprinting for the rapid analysis and discrimination of minerals. Appl. Geochem. 2009, 24, 1125–1141. [Google Scholar] [CrossRef]
- Banerjee, B.P.; Raval, S.; Zhai, H.; Cullen, P.J. Health condition assessment for vegetation exposed to heavy metal pollution through airborne hyperspectral data. Environ. Monit. Assess. 2017, 189, 604. [Google Scholar] [CrossRef] [PubMed]
- Rosso, P.H.; Pushnik, J.C.; Lay, M.; Ustin, S.L. Reflectance properties and physiological responses of Salicornia virginica to heavy metal and petroleum contamination. Environ. Pollut. 2005, 137, 241–252. [Google Scholar] [CrossRef] [PubMed]
- Ni, C.; Zhang, D.; Song, P.; Zhao, S.; Yang, W. Hyperspectral Response of Dominant Plants in the Poyang Lake Wetlands to Heavy Metal Pollution. In Chinese Water Systems; Springer: Cham, Switzerland, 2019; pp. 99–112. [Google Scholar]
- Gu, Y.; Li, S.; Gao, W.; Wei, H. Hyperspectral estimation of the cadmium content in leaves of Brassica rapa chinesis based on the spectral parameters. Acta Ecol. Sin. 2015, 35, 4445–4453. [Google Scholar]
- Liu, M.; Liu, X.; Ding, W.; Wu, L. Monitoring stress levels on rice with heavy metal pollution from hyperspectral reflectance data using wavelet-fractal analysis. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 246–255. [Google Scholar] [CrossRef]
- Liu, M.; Liu, X.; Li, M.; Fang, M.; Chi, W. Neural-network model for estimating leaf chlorophyll concentration in rice under stress from heavy metals using four spectral indices. Biosyst. Eng. 2010, 106, 223–233. [Google Scholar] [CrossRef]
- Li, N.; Lue, J.; Altermann, W. Applications of spectral analysis to monitoring of heavy metal-induced contamination in vegetation. Spectrosc. Spectr. Anal. 2010, 30, 2508–2511. [Google Scholar]
- Mirzael, M.; Abbasi, M.; Marofi, S.; Solgi, E.; Karimi, R. Spectral Discrimination of Important Orchard Species Using Hyperspectral Indices and Artificial Intelligence Approaches. J. RS and GIS for Nat. Resour. 2018, 9, 76–92. [Google Scholar]
- ZHUANG, D.-F. Study on canopy spectral characteristics of paddy polluted by heavy metals. Spectrosc. Spectr. Anal. 2010, 30, 430–434. [Google Scholar]
- Lehmann, J.; Große-Stoltenberg, A.; Römer, M.; Oldeland, J. Field spectroscopy in the VNIR-SWIR region to discriminate between Mediterranean native plants and exotic-invasive shrubs based on leaf tannin content. Remote Sens. 2015, 7, 1225–1241. [Google Scholar] [CrossRef]
- Diago, M.P.; Fernandes, A.M.; Millan, B.; Tardáguila, J.; Melo-Pinto, P. Identification of grapevine varieties using leaf spectroscopy and partial least squares. Comput. Electron. Agric. 2013, 99, 7–13. [Google Scholar] [CrossRef]
- Li, Y.M. Spectrum Variation of Vegetation in Yanzhou Coal Mine Area and Heavy Metal Stress Characteristics; Handong University of Science and Technology: Qingdao, China, 2011. [Google Scholar]
- Kooistra, L.; Leuven, R.; Wehrens, R.; Nienhuis, P.; Buydens, L. A comparison of methods to relate grass reflectance to soil metal contamination. Int. J. Remote Sens. 2003, 24, 4995–5010. [Google Scholar] [CrossRef]
- Prospere, K.; McLaren, K.; Wilson, B. Plant species discrimination in a tropical wetland using in situ hyperspectral data. Remote Sens. 2014, 6, 8494–8523. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Guillén-Climent, M.L.; Hernández-Clemente, R.; Catalina, A.; González, M.; Martín, P. Estimating leaf carotenoid content in vineyards using high resolution hyperspectral imagery acquired from an unmanned aerial vehicle (UAV). Agric. For. Meteorol. 2013, 171, 281–294. [Google Scholar] [CrossRef]
- Gutiérrez, S.; Tardaguila, J.; Fernández-Novales, J.; Diago, M.P. Support vector machine and artificial neural network models for the classification of grapevine varieties using a portable NIR spectrophotometer. PLoS ONE 2015, 10, e0143197. [Google Scholar] [CrossRef]
- Kumar, L.; Schmidt, K.; Dury, S.; Skidmore, A. Review of hyperspectral remote sensing and vegetation science. Imaging Spectrom. Basic Princ. Prospect. Appl. 2001, 111–155. [Google Scholar]
- Devadas, R.; Lamb, D.; Simpfendorfer, S.; Backhouse, D. Evaluating ten spectral vegetation indices for identifying rust infection in individual wheat leaves. Precis. Agric. 2009, 10, 459–470. [Google Scholar] [CrossRef]
- Li, M.; Luo, Y.; Su, Z. Heavy metal concentrations in soils and plant accumulation in a restored manganese mineland in Guangxi, South China. Environ. Pollut. 2007, 147, 168–175. [Google Scholar] [CrossRef]
- Orisakwe, O.E.; Nduka, J.K.; Amadi, C.N.; Dike, D.O.; Bede, O. Heavy metals health risk assessment for population via consumption of food crops and fruits in Owerri, South Eastern, Nigeria. Chem. Cent. J. 2012, 6, 77. [Google Scholar] [CrossRef]
- Mirzaei, M.; Jafari, A.; Gholamalifard, M.; Azadi, H.; Shooshtari, S.J.; Moghaddam, S.M.; Gebrehiwot, K.; Witlox, F. Mitigating environmental risks: Modeling the interaction of water quality parameters and land use cover. LUse Policy 2019. [Google Scholar] [CrossRef]
- Xu, H.-R.; Yu, P.; Fu, X.-P.; Ying, Y.-B. On-site variety discrimination of tomato plant using visible-near infrared reflectance spectroscopy. J. Zhejiang Univ. Sci. B 2009, 10, 126–132. [Google Scholar] [CrossRef] [PubMed]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Chauchard, F.; Cogdill, R.; Roussel, S.; Roger, J.; Bellon-Maurel, V. Application of LS-SVM to non-linear phenomena in NIR spectroscopy: Development of a robust and portable sensor for acidity prediction in grapes. Chemom. Intell. Lab. Syst. 2004, 71, 141–150. [Google Scholar] [CrossRef]
- Ferreira, M.P.; Zortea, M.; Zanotta, D.C.; Shimabukuro, Y.E.; de Souza Filho, C.R. Mapping tree species in tropical seasonal semi-deciduous forests with hyperspectral and multispectral data. Remote Sens. Environ. 2016, 179, 66–78. [Google Scholar] [CrossRef]
- Laurin, G.V.; Puletti, N.; Hawthorne, W.; Liesenberg, V.; Corona, P.; Papale, D.; Chen, Q.; Valentini, R. Discrimination of tropical forest types, dominant species, and mapping of functional guilds by hyperspectral and simulated multispectral Sentinel-2 data. Remote Sens. Environ. 2016, 176, 163–176. [Google Scholar] [CrossRef]
- Stitson, M.; Weston, J.; Gammerman, A.; Vovk, V.; Vapnik, V. Theory of support vector machines. Univ. London 1996, 117, 188–191. [Google Scholar]
- Hipni, A.; El-shafie, A.; Najah, A.; Karim, O.A.; Hussain, A.; Mukhlisin, M. Daily forecasting of dam water levels: Comparing a support vector machine (SVM) model with adaptive neuro fuzzy inference system (ANFIS). Water Resour. Manag. 2013, 27, 3803–3823. [Google Scholar] [CrossRef]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Midi, H.; Bagheri, A. Robust multicollinearity diagnostic measure in collinear data set. In Proceedings of the 4th International Conference on Applied Mathematics, Simulation, Modeling, Corfu Island, Greece, 22–25 July 2010; pp. 138–142. [Google Scholar]
- Hair, J.F., Jr. Multivariate Data Analysis; Anderson Seventh Edition; Joseph, F., Hair William, C., Jr., Black Barry, J., Babin Rolph, E., Eds.; Pearson: London, UK.
- Penuelas, J.; Gamon, J.A.; Griffin, K.L.; Field, C.B. Assessing community type, plant biomass, pigment composition, and photosynthetic efficiency of aquatic vegetation from spectral reflectance. Remote Sens. Environ. 1993, 46, 110–118. [Google Scholar] [CrossRef]
- Boyer, M.; Miller, J.; Belanger, M.; Hare, E.; Wu, J. Senescence and spectral reflectance in leaves of northern pin oak (Quercus palustris Muenchh.). Remote Sens. Environ. 1988, 25, 71–87. [Google Scholar] [CrossRef]
- Vogelmann, T.C. Plant tissue optics. Ann. Rev. Plant Biol. 1993, 44, 231–251. [Google Scholar] [CrossRef]
- Strever, A.A.E. Non-Destructive Assessment of Leaf Composition as Related to Growth of the Grapevine (Vitis vinifera L. cv. Shiraz); Stellenbosch University: Stellenbosch, South Africa, 2012. [Google Scholar]
- Adam, E.; Mutanga, O.; Rugege, D. Multispectral and hyperspectral remote sensing for identification and mapping of wetland vegetation: A review. Wetl. Ecol. Manag. 2010, 18, 281–296. [Google Scholar] [CrossRef]
- Penuelas, J.; Baret, F.; Filella, I. Semi-empirical indices to assess carotenoids/chlorophyll a ratio from leaf spectral reflectance. Photosynthetica 1995, 31, 221–230. [Google Scholar]
- Malar, S.; Vikram, S.S.; Favas, P.J.; Perumal, V. Lead heavy metal toxicity induced changes on growth and antioxidative enzymes level in water hyacinths [Eichhornia crassipes (Mart.)]. Bot. Stud. 2016, 55, 54. [Google Scholar] [CrossRef] [PubMed]
- Chaoui, A.; El Ferjani, E. Effects of cadmium and copper on antioxidant capacities, lignification and auxin degradation in leaves of pea (Pisum sativum L.) seedlings. C. R. Biol. 2005, 328, 23–31. [Google Scholar] [CrossRef] [PubMed]
- Mishra, S.; Srivastava, S.; Tripathi, R.; Govindarajan, R.; Kuriakose, S.; Prasad, M. Phytochelatin synthesis and response of antioxidants during cadmium stress in Bacopa monnieri L. Plant Physiol. Biochem. 2006, 44, 25–37. [Google Scholar] [CrossRef] [PubMed]
- Rai, V.; Khatoon, S.; Bisht, S.; Mehrotra, S. Effect of cadmium on growth, ultramorphology of leaf and secondary metabolites of Phyllanthus amarus Schum. and Thonn. Chemosphere 2005, 61, 1644–1650. [Google Scholar] [CrossRef] [PubMed]
- Tirillini, B.; Ricci, A.; Pintore, G.; Chessa, M.; Sighinolfi, S. Induction of hypericins in Hypericum perforatum in response to chromium. Fitoterapia 2006, 77, 164–170. [Google Scholar] [CrossRef]
- Gutiérrez, S.; Tardaguila, J.; Fernández-Novales, J.; Diago, M. Data mining and NIR spectroscopy in viticulture: Applications for plant phenotyping under field conditions. Sensors 2016, 16, 236. [Google Scholar] [CrossRef]
- Yadav, S. Heavy metals toxicity in plants: An overview on the role of glutathione and phytochelatins in heavy metal stress tolerance of plants. S. Afr. J. Bot. 2010, 76, 167–179. [Google Scholar] [CrossRef]
| Indices | Equation | Indices | Equation |
|---|---|---|---|
| Cellulose Absorption Index, CAI | 0.5(R2000 + R2200) − R2100 | Gitelson and Merzlyak Chlorophyll, GM1 and 2 | GM1 = (R750)/(R550) |
| Moisture Stress Index, MSI | (R1600)/(R820) | GM2 = (R750)/(R700) | |
| Normalized Difference Water Index, NDWI | (R860 - R1240)/(R860 + R1240) | Lichtenthaler Indices, Lic1 to 3 | Lic1 = (R800 − R680)/(R800 + R680) |
| Disease Water Stress Index, DWSI | (R802 + R547)/(R1657 + R682) | Lic2 = (R440)/(R690) | |
| Band ratio at 975 nm, RATIO975 | 2 × R960 − 990/(R920 – 940 + R1090 − 1110) | Lic3 = (R440)/(R740) | |
| Band ratio at 1200 nm, RATIO975-2 | 2 × R1180 − 1220/(R1090 − 1110 + R1265 − 1285) | Simple Ratio Pigment Index, SRPI | (R430)/(R680) |
| Leaf Chlorophyll Index, LCI | (R850 − R710)/(R850 + R680) | Normalized Phaepophytiniz Index, NPQI | (R415 − R435)/(R415 + R435) |
| DattA | (R780 − R710)/(R780 − R680) | Normalized Pigment Chlorophyll Ratio Index, NPCI | (R680 − R430)/(R680 + R430) |
| Modified Red Edge Normalized Difference VegetationIndex, mNDVI705 | (R750 + R705)/(R750 + R705 − 2 × R445) | Greenness Index, GI | (R554)/(R677) |
| Chlorophyll Index, SGB | (R750 − R445)/(R705 − R445) | Water Index at 1180nm, WI1180 | (R900)/(R1180) |
| Structure Intensive Pigment Index, SIPI | (R445 − R800)/(R680 − R800) | Normalized Difference Vegetation Index, NDVI | (R831 − R667)/(R831 + R667) |
| Simple Ratio, SR | (R774)/(R677) | Carter Index, CI | (R760/R695) |
| Reflectance at 550 nm, R550 | (R550) | Vogelman Index, VOG | (R740/R720) |
| Reflectance at 680 nm, R680 | (R680) | Carotenoid Reflectance Index, CRI | R800(1/R520 − 1/R550) |
| Water Index, WI | (R900)/(R970) | Photochemical Reflectance Index, PRI | PRI1 = (R531 − R570)/(R531 + R570)PRI2 = 1.5(R830 − R660)/(R830 − R660 + 0.5)PRI3 = (R539 − R570)/(R539 + R570) |
| Heavy Metal | No. of Optimal Components | Cumulative Variance (%) | Optimal Indices in Components |
|---|---|---|---|
| Cu | 4 | 82 | SR, CAI, RATIO9752, and DWSI |
| Zn | 5 | 84 | R680, WI, Lic1, MSI, and PRI2 |
| Pb | 4 | 88 | VOG, MSI, SIPI, and R550 |
| Cr | 4 | 92 | mNDVI705, GI, RATIO975, and SIPI |
| Cd | 2 | 81 | SIPI and DWSI |
| Hyperspectral Data Type | Heavy Metal | Model Structure | Train | Test | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Kernel Function | No. of Vectors | Coefficient | Degree | Gamma | R2 | RMSE * | R2 | RMSE * | ||
| Wavelengths | Cu | RBF | 13 | - | - | 0.25 | 0.97 | 7.46 | 0.54 | 25.06 |
| Zn | Linear | 25 | - | - | - | 0.67 | 22.50 | 0.42 | 29.65 | |
| Pb | RBF | 21 | - | - | 0.20 | 0.89 | 22.28 | 0.71 | 24.09 | |
| Cr | Linear | 30 | - | - | - | 0.84 | 5.61 | 0.71 | 7.82 | |
| Cd | RBF | 34 | - | - | 0.25 | 0.78 | 98.16 | 0.77 | 103.09 | |
| Spectral Indices | Cu | Linear | 32 | - | - | - | 0.88 | 13.01 | 0.50 | 25.46 |
| Zn | RBF | 23 | - | - | 0.8 | 0.92 | 13.42 | 0.85 | 15.94 | |
| Pb | RBF | 24 | - | - | 0.4 | 0.85 | 22.49 | 0.67 | 24.51 | |
| Cr | RBF | 43 | - | - | 0.32 | 0.80 | 7.27 | 0.79 | 6.11 | |
| Cd | Polynomial | 19 | 1 | 11 | 0.7 | 0.88 | 91.94 | 0.86 | 102.85 | |
| Hyperspectral Data Type | Heavy Metal | Predictor Variable VIF | Sig. of Regression Confident | Durbin–Watson | Model Structure | Train | Test | ||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE * | R2 | RMSE | ||||||
| Wavelengths | Cu | All < 10 | <0.05 | 2.17 | CCu = −1.27 − (0.28 × R2431) + (4.08 × R809) − (5.32 × R489) −(8.73 × R616) | 0.94 | 9.35 | 0.56 | 25.60 |
| Zn | All < 10 | <0.05 | 2.18 | CZn = −1.11 − (5.77 × R2032) − (1.83 × R665) + (2.38 × R564) + (13.85 × R688) − (7.7 × R437) | 0.73 | 20.46 | 0.47 | 399.13 | |
| Pb | Some cases >10 | >0.05 | 1.39 | CPb = 0.46 − (5.1 × R692) + (6.24 × R683) | 0.32 | 25.29 | 0.13 | 27.28 | |
| Cr | All < 10 | <0.05 | 1.59 | CCr = 0.61 + (18.08 × R415) − (1.41 × R2044) − (4.01 × R652) −(1.99 × R1036) + (1.11 × R713) | 0.84 | 5.58 | 0.78 | 6.79 | |
| Cd | All < 10 | <0.05 | 1.38 | CCd = 0.98 + (2.76 × R1373) + (3.15 × R631) + (1.04 × R744) −(5.09 × R438) | 0.63 | 132.79 | 0.64 | 117.26 | |
| Spectral Indices | Cu | All < 10 | <0.05 | 1.74 | CCu = −2.95 + (3.38 × SR) − (0.01 × CAI) + (6.76 × RATIO9752) − (0.77 × DWSI) | 0.89 | 12.63 | 0.52 | 25.33 |
| Zn | Some cases >10 | <0.05 | 1.81 | CZn = −2.26 − (11.34 × R680) + (41.89 × WI) + (20.68 × Lic1) −(3.63 × MSI) − (4.14 × PRI2) | 0.87 | 15.73 | 0.70 | 20.38 | |
| Pb | All < 10 | <0.05 | 1.55 | CPb = 2.53 − (1.33 × VOG) + (1.93 × MSI) + (0.85 × SIPI) | 0.50 | 24.45 | 0.15 | 27.03 | |
| Cr | All < 10 | <0.05 | 1.06 | CCr = −4.97 + (5.23 × mNDVI705) + (0.17 × GI) − (1.28 × RATIO975) | 0.59 | 8.48 | 0.60 | 8.78 | |
| Cd | All < 10 | <0.05 | 1.27 | CCd = −6.66 + (4.70 × SIPI) + (1.13 × DWSI) | 0.66 | 121.77 | 0.67 | 112.17 | |
| Metal | Reference | Plant/Species | Approach | Optimal Spectral Indices/Wavelengths | R2 |
|---|---|---|---|---|---|
| Cu | Present study | Grape | MLR | R616, R489, R809, R2431 | 0.56 |
| Li [44] | Vegetation | MLR | 0.60 | ||
| Zhuang [41] | Paddy/Rice | MLR | 0.76 | ||
| Ping et al. [30] | Maize | MLR | NI15, NI11 | 0.69 | |
| Zn | Present study | Grape | SVM | R680 WI, Lic1, MSI, PRI2 | 0.85 |
| Li [44] | Vegetation | MLR | 0.48 | ||
| Zhuang [41] | Paddy/Rice | MLR | 661.96×R2210-136.26 | 0.34 | |
| Kooistra et al. [45] | Grass | MLR | MSAVI2 | 0.64 | |
| Liu et al. [37] | Rice | ANN | 0.95 | ||
| Pb | Present study | Grape | SVM | R1865, R728 R692, R683, R356 | 0.71 |
| Li [44] | Vegetation | MLR | 0.77 | ||
| Zhuang [41] | Paddy/Rice | MLR | 0.70 | ||
| Ping et al. [30] | Maize | MLR | NI15, NI17 | 0.87 | |
| Cr | Present study | Grape | SVM | mNDVI705, GI, RATIO975, SIPI | 0.80 |
| Ping et al. [30] | Maize | MLR | NI5, R553 | 0.49 | |
| Li et al. [39] | Vegetation | MLR | R688, R672, R874, R677, R678, R679, R 680, R566 | 0.81 | |
| Cd | Present study | Grape | SVM | SIPI, DWSI | 0.86 |
| Ping et al. [30] | Maize | MLR | NI11, NI17 | 0.63 | |
| Liu et al. [37] | Rice | MLR | 0.70 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirzaei, M.; Verrelst, J.; Marofi, S.; Abbasi, M.; Azadi, H. Eco-Friendly Estimation of Heavy Metal Contents in Grapevine Foliage Using In-Field Hyperspectral Data and Multivariate Analysis. Remote Sens. 2019, 11, 2731. https://doi.org/10.3390/rs11232731
Mirzaei M, Verrelst J, Marofi S, Abbasi M, Azadi H. Eco-Friendly Estimation of Heavy Metal Contents in Grapevine Foliage Using In-Field Hyperspectral Data and Multivariate Analysis. Remote Sensing. 2019; 11(23):2731. https://doi.org/10.3390/rs11232731
Chicago/Turabian StyleMirzaei, Mohsen, Jochem Verrelst, Safar Marofi, Mozhgan Abbasi, and Hossein Azadi. 2019. "Eco-Friendly Estimation of Heavy Metal Contents in Grapevine Foliage Using In-Field Hyperspectral Data and Multivariate Analysis" Remote Sensing 11, no. 23: 2731. https://doi.org/10.3390/rs11232731
APA StyleMirzaei, M., Verrelst, J., Marofi, S., Abbasi, M., & Azadi, H. (2019). Eco-Friendly Estimation of Heavy Metal Contents in Grapevine Foliage Using In-Field Hyperspectral Data and Multivariate Analysis. Remote Sensing, 11(23), 2731. https://doi.org/10.3390/rs11232731