Spatial Upscaling of Tree-Ring-Based Forest Response to Drought with Satellite Data
Abstract
1. Introduction
2. Materials and Methods
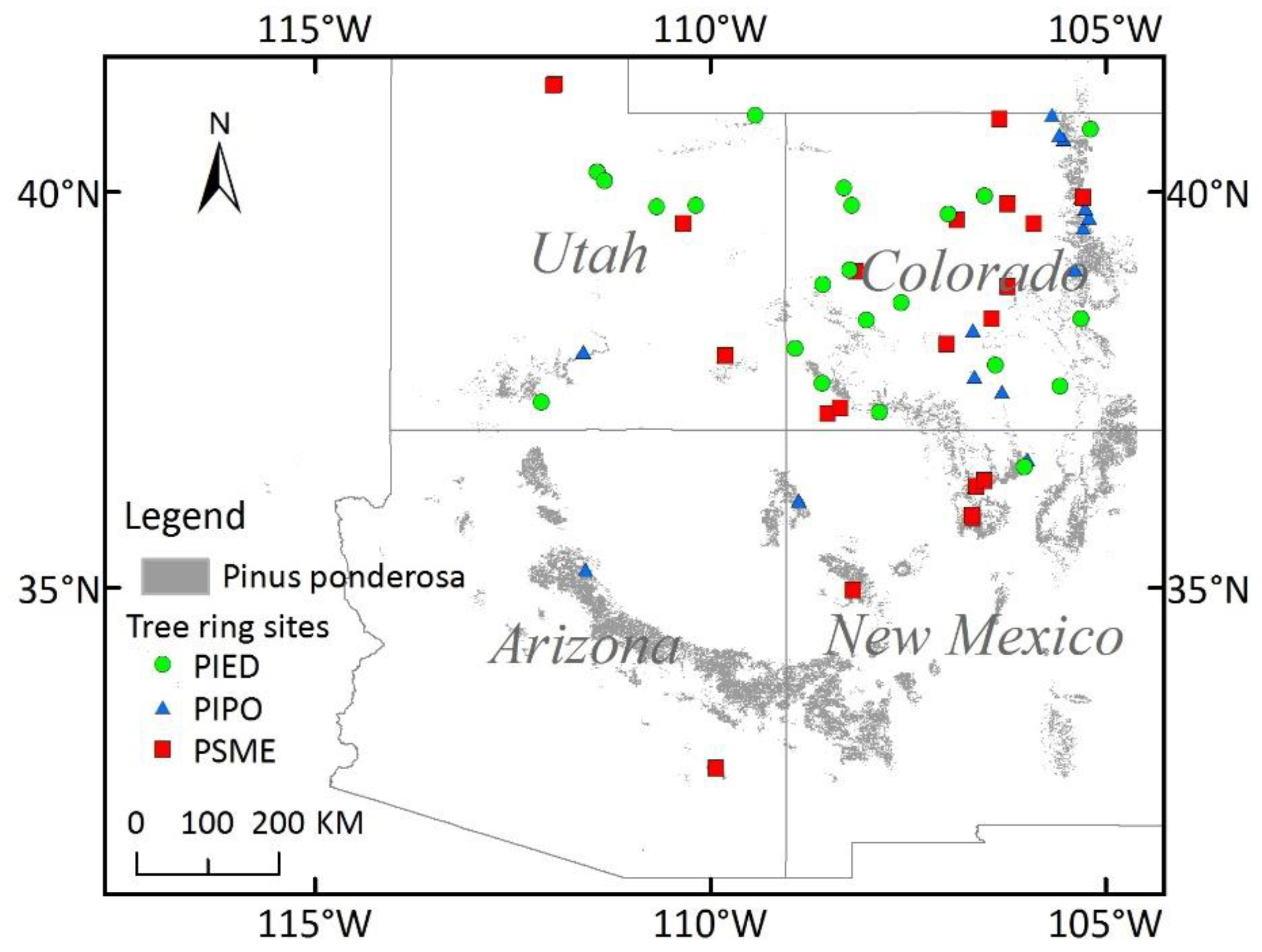
2.1. Study Region
2.2. Tree Ring Data
2.3. Satellite Data
2.4. Climate Data
2.5. Time-Scale Test and Empirical Model
2.5.1. Quality Assessment of NDVI Data
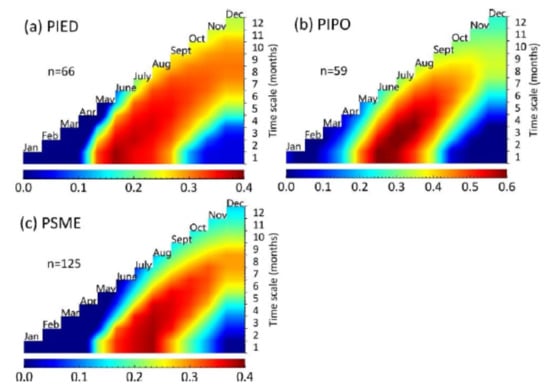
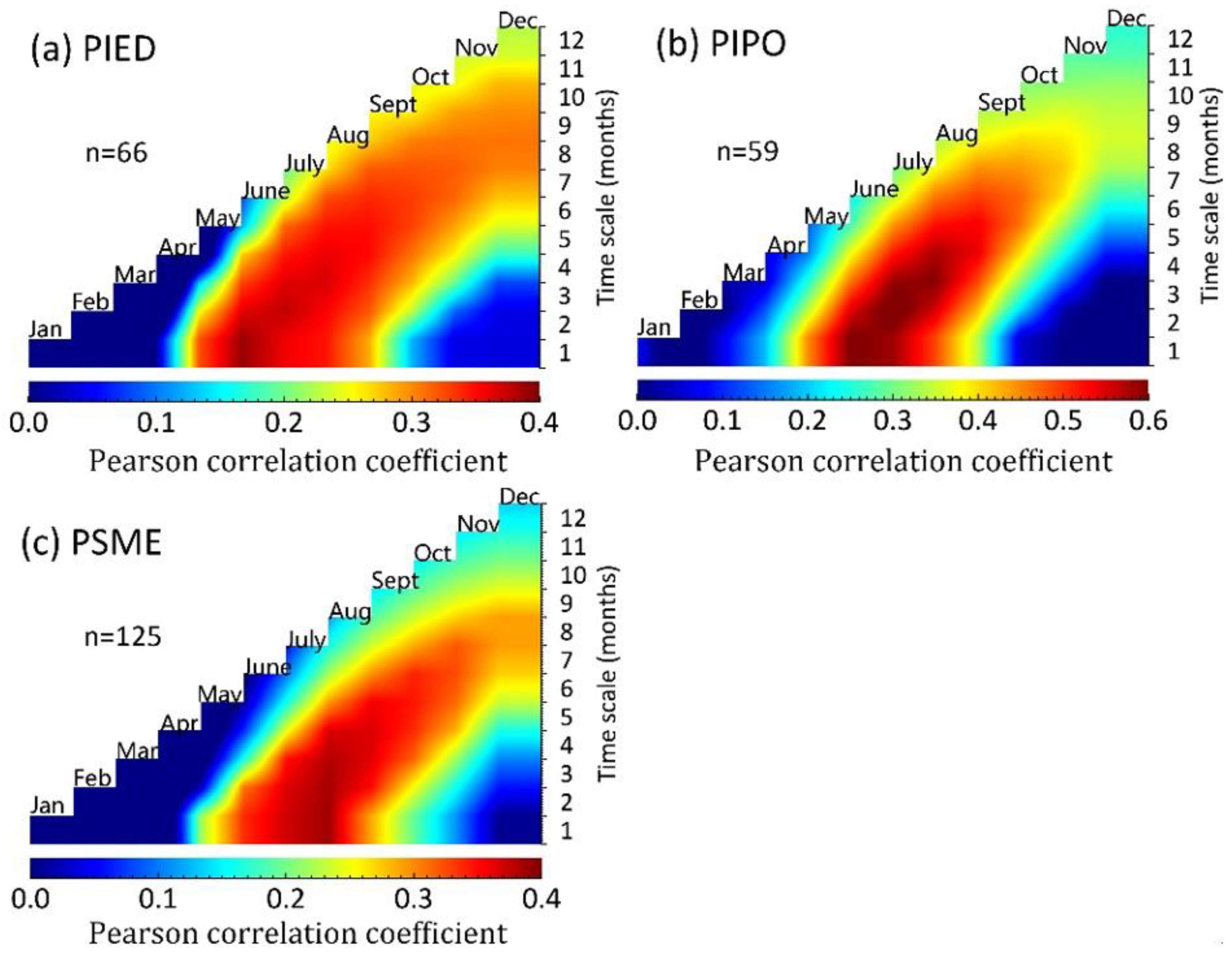
2.5.2. Optimum Time Windows
2.5.3. Empirical Model
2.6. Temporal Trend Analysis at Regional Scale
3. Results and Discussion
3.1. Quality Control of NDVI Data
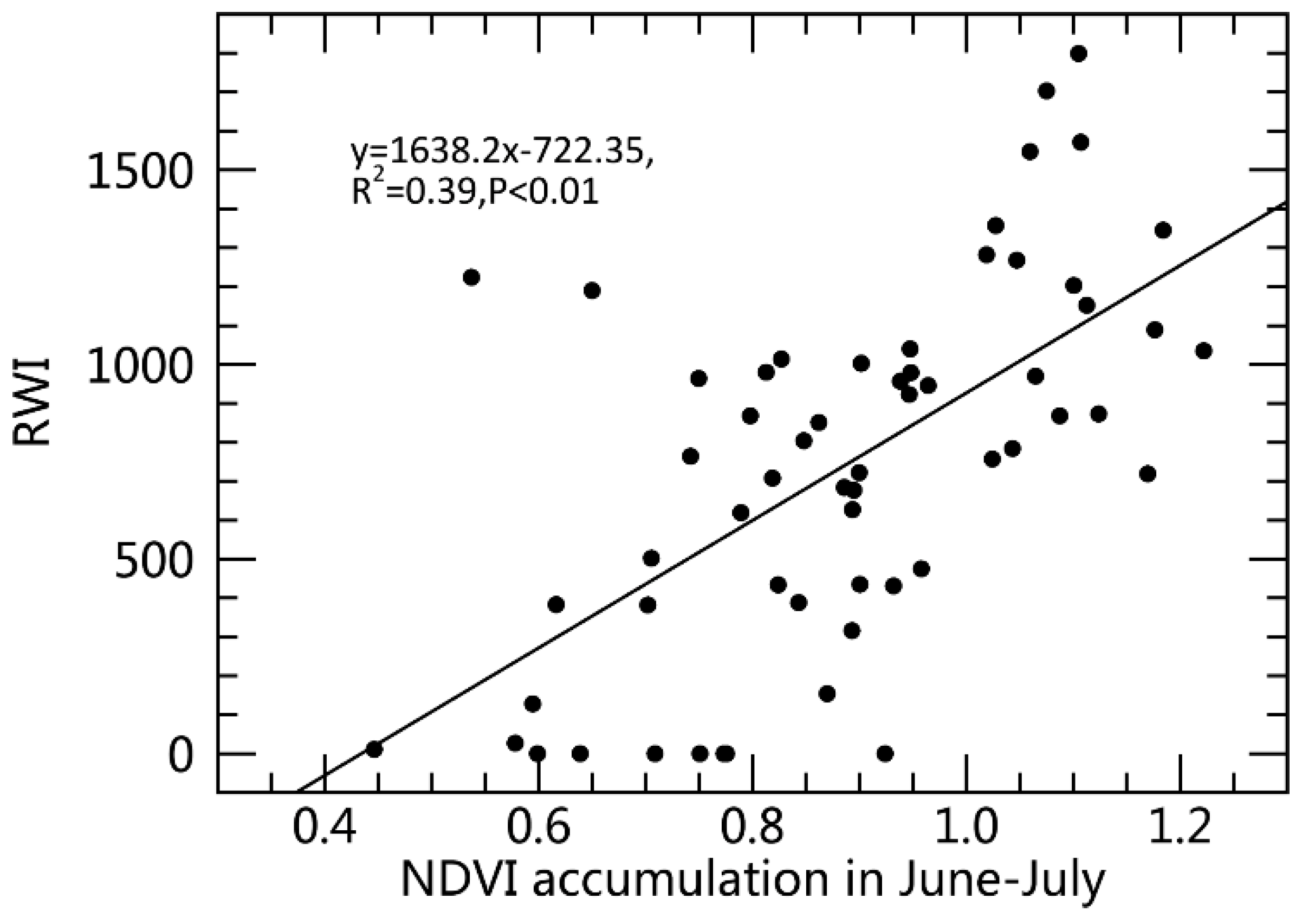
3.2. Relationship between RWI and NDVI
3.3. Analyses of RWI over Space and Time
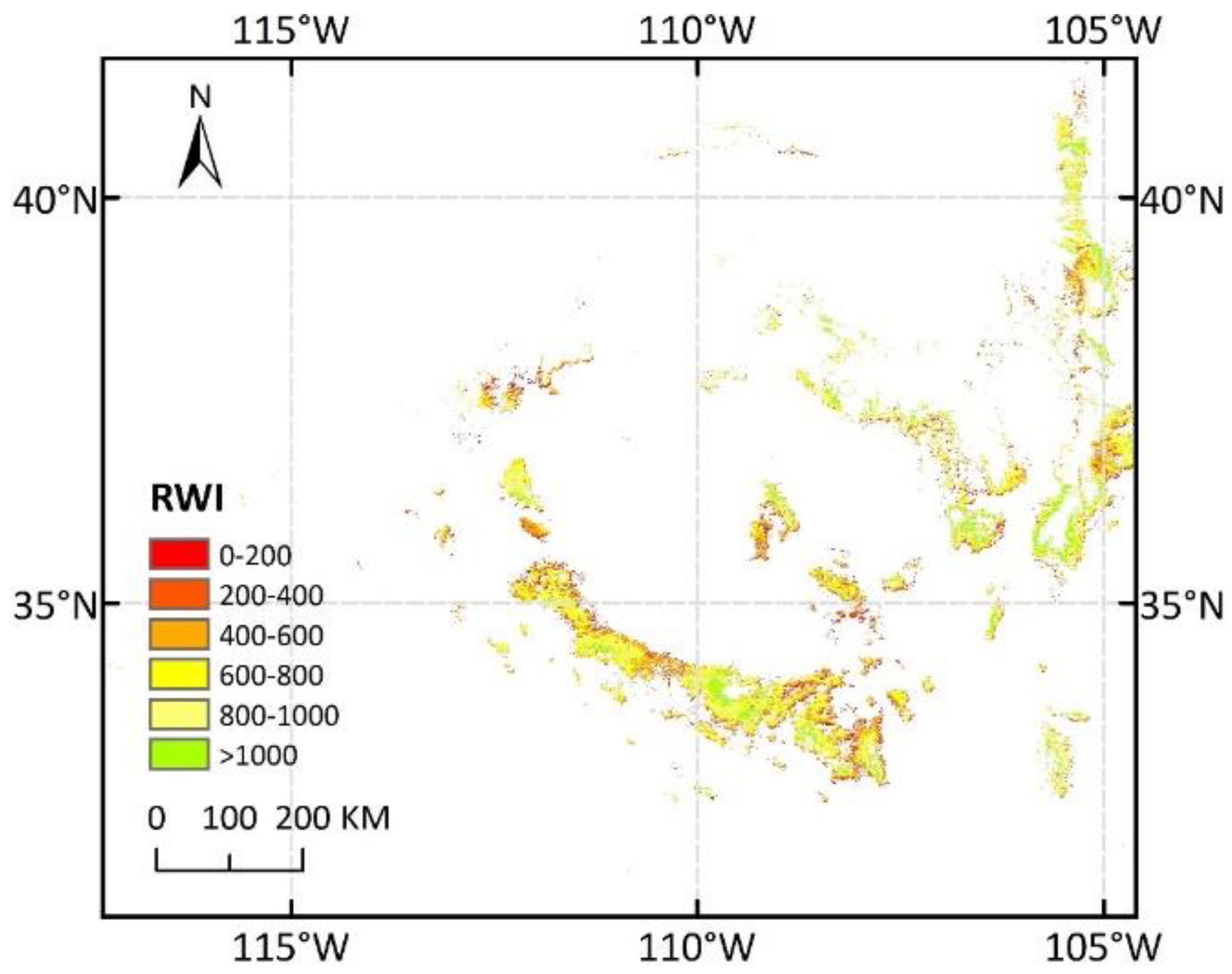
3.3.1. RWI Upscaling
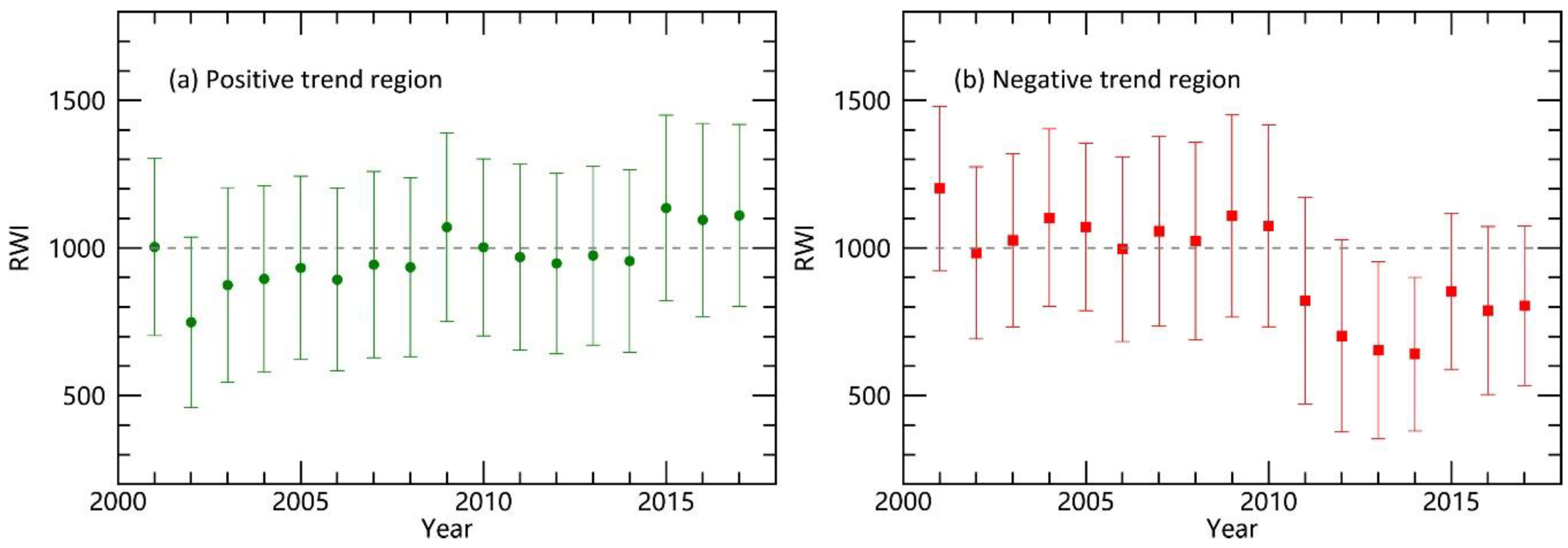
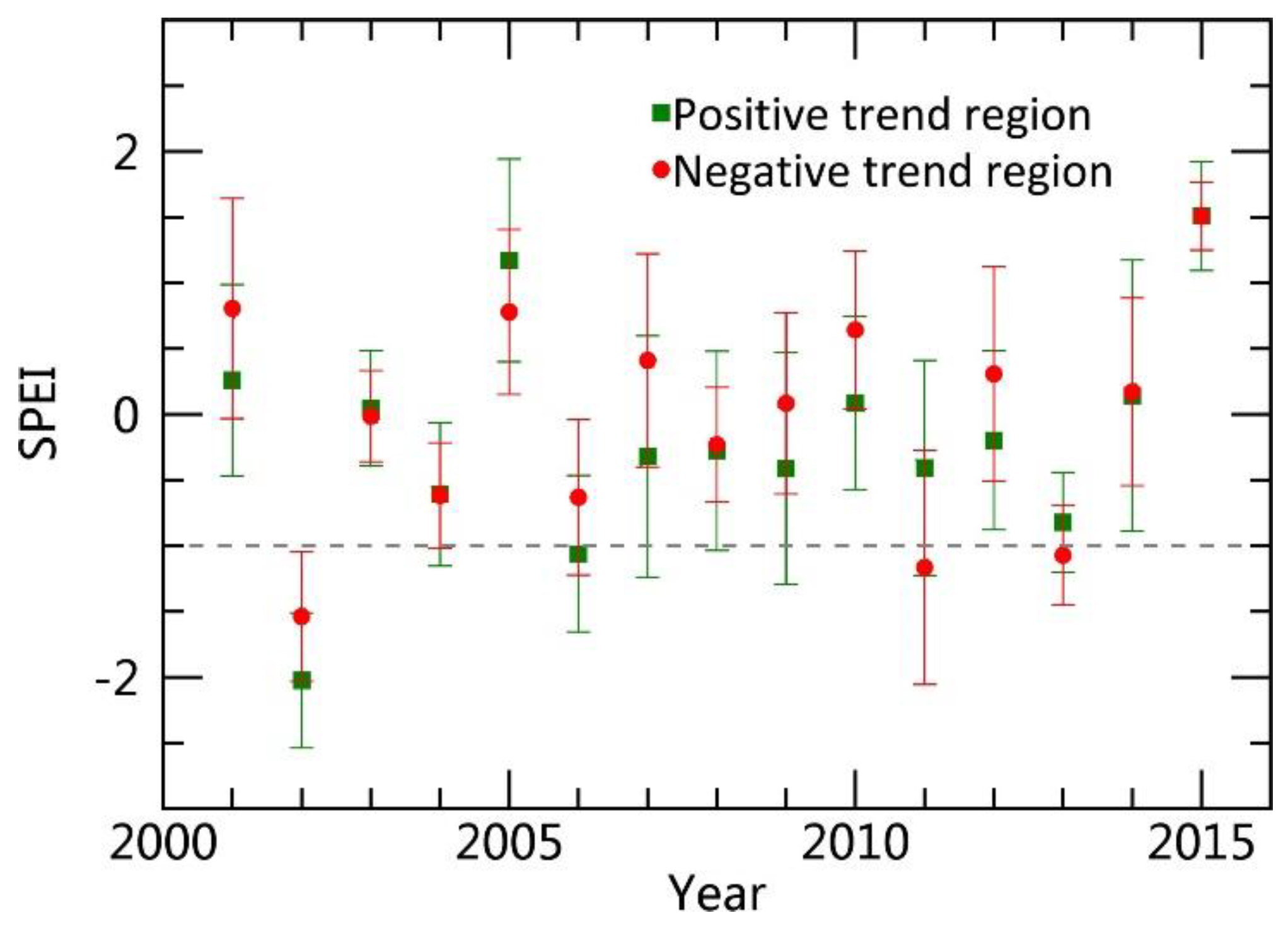
3.3.2. Regional RWI Change over Time and Response to Drought
3.4. Uncertainty
4. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cook, B.I.; Smerdon, J.E.; Seager, R.; Coats, S. Global warming and 21st century drying. Clim. Dyn. 2014, 43, 2607–2627. [Google Scholar] [CrossRef]
- Yi, C.; Pendall, E.; Ciais, P. Focus on extreme events and the carbon cycle. Environ. Res. Lett. 2015, 10, 070201. [Google Scholar] [CrossRef]
- Ciais, P.; Reichstein, M.; Viovy, N.; Granier, A.; Ogée, J.; Allard, V.; Aubinet, M.; Buchmann, N.; Bernhofer, C.; Carrara, A. Europe-wide reduction in primary productivity caused by the heat and drought in 2003. Nature 2005, 437, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.T. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef]
- Gao, S.; Liu, R.; Zhou, T.; Fang, W.; Yi, C.; Lu, R.; Zhao, X.; Luo, H. Dynamic responses of tree-ring growth to multiple dimensions of drought. Glob. Chang. Biol. 2018. [Google Scholar] [CrossRef] [PubMed]
- Babst, F.; Bouriaud, O.; Poulter, B.; Trouet, V.; Frank, D.C. Twentieth century redistribution in climatic drivers of global tree growth. Sci. Adv. 2019, 5, eaat4313. [Google Scholar] [CrossRef]
- Huang, K.; Yi, C.; Wu, D.; Zhou, T.; Zhao, X.; Blanford, W.J.; Wei, S.; Wu, H.; Ling, D.; Li, Z. Tipping point of a conifer forest ecosystem under severe drought. Environ. Res. Lett. 2015, 10, 024011. [Google Scholar] [CrossRef]
- Assal, T.J.; Anderson, P.J.; Sibold, J. Spatial and temporal trends of drought effects in a heterogeneous semi-arid forest ecosystem. For. Ecol. Manag. 2016, 365, 137–151. [Google Scholar] [CrossRef]
- Wei, S.; Yi, C.; Wei, F.; Hendrey, G. A global study of GPP focusing on light-use efficiency in a random forest regression model. Ecosphere 2017, 8, e01724. [Google Scholar] [CrossRef]
- Xu, P.; Zhou, T.; Yi, C.; Fang, W.; Hendrey, G.; Zhao, X. Forest drought resistance distinguished by canopy height. Environ. Res. Lett. 2018, 13, 075003. [Google Scholar] [CrossRef]
- Bhuyan, U.; Zang, C.; Vicente-Serrano, S.M.; Menzel, A. Exploring Relationships among Tree-Ring Growth, Climate Variability, and Seasonal Leaf Activity on Varying Timescales and Spatial Resolutions. Remote Sens. 2017, 9, 526. [Google Scholar] [CrossRef]
- Andujar, E.; Krakauer, N.Y.; Yi, C.; Kogan, F. Ecosystem Drought Response Timescales from Thermal Emission versus Shortwave Remote Sensing. Adv. Meteorol. 2017, 3, 1–10. [Google Scholar] [CrossRef]
- Wang, J.; Rich, P.M.; Price, K.P.; Kettle, W.D. Relations between NDVI and tree productivity in the central great plains. Int. J. Remote Sens. 2004, 16, 12. [Google Scholar] [CrossRef]
- Bunn, A.G.; Hughes, M.K.; Kirdyanov, A.V.; Losleben, M.; Shishov, V.V.; Berner, L.T.; Oltchev, A.; Vaganov, E.A. Comparing forest measurements from tree rings and a space-based index of vegetation activity in Siberia. Environ. Res. Lett. 2013, 8, 035034. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Camarero, J.J.; Olano, J.M.; Martín-Hernández, N.; Peña-Gallardo, M.; Tomás-Burguera, M.; Gazol, A.; Azorin-Molina, C.; Bhuyan, U.; Kenawy, A.E. Diverse relationships between forest growth and the Normalized Difference Vegetation Index at a global scale. Remote Sens. Environ. 2016, 187, 14–29. [Google Scholar] [CrossRef]
- Speer, J.H. Fundamentals of Tree-Ring Research; University of Arizona Press: Tucson, AZ, USA, 2010. [Google Scholar]
- Babst, F.; Carrer, M.; Poulter, B.; Urbinati, C.; Neuwirth, B.; Frank, D. 500 years of regional forest growth variability and links to climatic extreme events in Europe. Environ. Res. Lett. 2012, 7, 045705. [Google Scholar] [CrossRef]
- Brehaut, L.; Danby, R.K. Inconsistent relationships between annual tree ring-widths and satellite-measured NDVI in a mountainous subarctic environment. Ecol. Indic. 2018, 91, 698–711. [Google Scholar] [CrossRef]
- Graumlich, L.J.; Brubaker, L.B.; Grier, C.C. Long-Term Trends in Forest Net Primary Productivity: Cascade Mountains, Washington. Ecology 1989, 70, 405–410. [Google Scholar] [CrossRef]
- Hasenauer, H.; Nemani, R.R.; Schadauer, K.; Running, S.W. Forest growth response to changing climate between 1961 and 1990 in Austria. For. Ecol. Manag. 1999, 122, 209–219. [Google Scholar] [CrossRef]
- Flurin, B.; Olivier, B.; Dario, P.; Bert, G.; Janssens, I.A.; Eero, N.; Andreas, I.; Jian, W.; Christian, B.; Barbara, K.S. Above-ground woody carbon sequestration measured from tree rings is coherent with net ecosystem productivity at five eddy-covariance sites. New Phytol. 2014, 201, 1289–1303. [Google Scholar]
- Xu, K.; Wang, X.; Liang, P.; An, H.; Sun, H.; Han, W.; Li, Q. Tree-ring widths are good proxies of annual variation in forest productivity in temperate forests. Sci. Rep. 2017, 7, 1945. [Google Scholar] [CrossRef] [PubMed]
- Kaufmann, R.K.; D’Arrigo, R.D.; Laskowski, C.; Myneni, R.B.; Davi, N.K. The effect of growing season and summer greenness on northern forests. Geophys. Res. Lett. 2004, 31, 111–142. [Google Scholar] [CrossRef]
- Berner, L.T.; Beck, P.S.A.; Bunn, A.; Lloyd, A.; Goetz, S.J. High-latitude tree growth and satellite vegetation indices: Correlations and trends in Russia and Canada (1982–2008). J. Geophys. Res. Biogeosci. 2015, 116, 321–342. [Google Scholar] [CrossRef]
- Seiler, R.; Kirchner, J.W.; Krusic, P.J.; Tognetti, R.; Houliã, N.; Andronico, D.; Cullotta, S.; Egli, M.; D’Arrigo, R.; Cherubini, P. Insensitivity of Tree-Ring Growth to Temperature and Precipitation Sharpens the Puzzle of Enhanced Pre-Eruption NDVI on Mt. Etna (Italy). PLoS ONE 2017, 12, e0169297. [Google Scholar] [CrossRef] [PubMed]
- Carreiras, J.M.B.; Pereira, J.M.C.; Pereira, J.S. Estimation of tree canopy cover in evergreen oak woodlands using remote sensing. For. Ecol. Manag. 2006, 223, 45–53. [Google Scholar] [CrossRef]
- Beck, P.S.A.; Goetz, S.J. Satellite observations of high northern latitude vegetation productivity changes between 1982 and 2008: Ecological variability and regional differences. Environ. Res. Lett. 2011, 6, 45501. [Google Scholar] [CrossRef]
- Bunn, A.G.; Goetz, S.J. Trends in Satellite-Observed Circumpolar Photosynthetic Activity from 1982 to 2003: The Influence of Seasonality, Cover Type, and Vegetation Density. Earth Interact. 2006, 10, 1723–1731. [Google Scholar] [CrossRef]
- Xing, W.Z.; Liu, C.; Alfredo, H. From AVHRR-NDVI to MODIS-EVI: Advances in vegetation index research. Acta Ecol. Sin. 2003, 23, 979–987. [Google Scholar]
- Brown, M.E.; Pinzon, J.E.; Didan, K.; Morisette, J.T.; Tucker, C.J. Evaluation of the consistency of long-term NDVI time series derived from AVHRR, SPOT-vegetation, SeaWiFS, MODIS, and Landsat ETM+ sensors. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1787–1793. [Google Scholar] [CrossRef]
- Hope, A.; Fouad, G.; Granovskaya, Y. Evaluating drought response of Southern Cape Indigenous Forests, South Africa, using MODIS data. Int. J. Remote Sens. 2014, 35, 4852–4864. [Google Scholar] [CrossRef]
- Xu, P.; Zhou, T.; Zhao, X.; Luo, H.; Gao, S.; Li, Z.; Cao, L. Diverse responses of different structured forest to drought in southwest china through remotely sensed data. Int. J. Appl. Earth Obs. Geoinf. 2018, 69, 217–225. [Google Scholar] [CrossRef]
- Breshears, D.D.; Cobb, N.S.; Rich, P.M.; Price, K.P.; Allen, C.D.; Balice, R.G.; Romme, W.H.; Kastens, J.H.; Floyd, M.L.; Belnap, J. Regional vegetation die-off in response to global-change-type drought. Proc. Natl. Acad. Sci. USA 2005, 102, 15144–15148. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Zhao, X.; Liang, S.; Zhou, T.; Huang, K.; Tang, B.; Zhao, W. Time-lag effects of global vegetation responses to climate change. Glob. Chang. Biol. 2015, 21, 3520–3531. [Google Scholar] [CrossRef] [PubMed]
- Matsushita, B.; Yang, W.; Chen, J.; Onda, Y.; Qiu, G. Sensitivity of the Enhanced Vegetation Index (EVI) and Normalized Difference Vegetation Index (NDVI) to Topographic Effects: A Case Study in High-Density Cypress Forest. Sensors 2007, 7, 2636–2651. [Google Scholar] [CrossRef] [PubMed]
- Luo, H.; Zhou, T.; Wu, H.; Zhao, X.; Wang, Q.; Gao, S.; Li, Z. Contrasting Responses of Planted and Natural Forests to Drought Intensity in Yunnan, China. Remote Sens. 2016, 8, 635. [Google Scholar] [CrossRef]
- Gazol, A.; Camarero, J.J.; Vicente-Serrano, S.M.; Sánchez-Salguero, R.; Gutiérrez, E.; De, L.M.; Sangüesa-Barreda, G.; Novak, K.; Rozas, V.; Tíscar, P.A. Forest resilience to drought varies across biomes. Glob. Chang. Biol. 2018, 24, 2143. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Wang, X.; Silander, J.A., Jr. Deciduous forest responses to temperature, precipitation, and drought imply complex climate change impacts. Proc. Natl. Acad. Sci. USA 2015, 112, 13585–13590. [Google Scholar] [CrossRef]
- PenUelas, J.; Filella, I. Phenology. Responses to a warming world. Science 2001, 294, 793–795. [Google Scholar] [CrossRef]
- Yi, C.; Mu, G.; Hendrey, G.; Vicente-Serrano, S.M.; Fang, W.; Zhou, T.; Shan, G.; Xu, P. Bifurcated Response of a Regional Forest to Drought. Expert Opin. Environ. Biol. 2018, 7, 2. [Google Scholar] [CrossRef]
- Vicenteserrano, S.M.; Beguería, S.; Lópezmoreno, J.I.; Angulo, M.; Elkenawy, A. A new global 0.5° gridded dataset (1901–2006) of a multiscalar drought index: Comparison with current drought index datasets based on the Palmer drought severity index. J. Hydrometeorol. 2010, 11, 1033–1043. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Gouveia, C.; Camarero, J.J.; Beguería, S.; Trigo, R.; López-Moreno, J.I.; Azorín-Molina, C.; Pasho, E.; Lorenzo-Lacruz, J.; Revuelto, J. Response of vegetation to drought time-scales across global land biomes. Proc. Natl. Acad. Sci. USA 2013, 110, 52–57. [Google Scholar] [CrossRef] [PubMed]
- Kolb, T.E. A new drought tipping point for conifer mortality. Environ. Res. Lett. 2015, 10, 031002. [Google Scholar] [CrossRef]
- McManus, K.M.; Morton, D.C.; Masek, J.G.; Wang, D.; Sexton, J.O.; Nagol, J.R.; Ropars, P.; Boudreau, S. Satellite-based evidence for shrub and graminoid tundra expansion in northern Q uebec from 1986 to 2010. Glob. Chang. Biol. 2012, 18, 2313–2323. [Google Scholar] [CrossRef]
- Vogelmann, J.E.; Tolk, B.; Zhu, Z. Monitoring forest changes in the southwestern United States using multitemporal Landsat data. Remote Sens. Environ. 2009, 113, 1739–1748. [Google Scholar] [CrossRef]
- Czerwinski, C.J.; King, D.J.; Mitchell, S.W. Mapping forest growth and decline in a temperate mixed forest using temporal trend analysis of Landsat imagery, 1987–2010. Remote Sens. Environ. 2014, 141, 188–200. [Google Scholar] [CrossRef]
- Hanson, P.J.; Weltzin, J.F. Drought disturbance from climate change: Response of United States forests. Sci. Total Environ. 2000, 262, 205–220. [Google Scholar] [CrossRef]
- Weiss, J.L.; Gutzler, D.S.; Coonrod, J.E.A.; Dahm, C.N. Seasonal and inter-annual relationships between vegetation and climate in central New Mexico, USA. J. Arid Environ. 2004, 57, 507–534. [Google Scholar] [CrossRef]
- Kaufmann, R.K.; D’Arrigo, R.D.; Paletta, L.F.; Tian, H.Q.; Jolly, W.M.; Myneni, R.B. Identifying Climatic Controls on Ring Width: The Timing of Correlations between Tree Rings and NDVI. Earth Interact. 2008, 12, 1. [Google Scholar] [CrossRef]
- Hicke, J.A.; Meddens, A.J.H.; Kolden, C.A. Recent tree mortality in the Western United States from bark beetles and forest fires. For. Sci. 2016, 62, 141–153. [Google Scholar] [CrossRef]
- Anderson-Teixeira, K.J.; Miller, A.D.; Mohan, J.E.; Hudiburg, T.W.; Duval, B.D.; Delucia, E.H. Altered dynamics of forest recovery under a changing climate. Glob. Chang. Biol. 2013, 19, 2001–2021. [Google Scholar] [CrossRef]
- Xu, P.; Zhou, T.; Yi, C.; Luo, H.; Zhao, X.; Fang, W.; Gao, S.; Liu, X. Impacts of Water Stress on Forest Recovery and Its Interaction with Canopy Height. Int. J. Environ. Res. Public Health 2018, 15, 1257. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Moran, M.S.; Zhao, X.; Liu, S.; Zhou, T.; Ponce-Campos, G.E.; Liu, F. Impact of prolonged drought on rainfall use efficiency using MODIS data across China in the early 21st century. Remote Sens. Environ. 2014, 150, 188–197. [Google Scholar] [CrossRef]
- Xiao, J. Satellite evidence for significant biophysical consequences of the “Grain for Green” Program on the Loess Plateau in China. J. Geophys. Res. Biogeosci. 2014, 119, 2261–2275. [Google Scholar] [CrossRef]
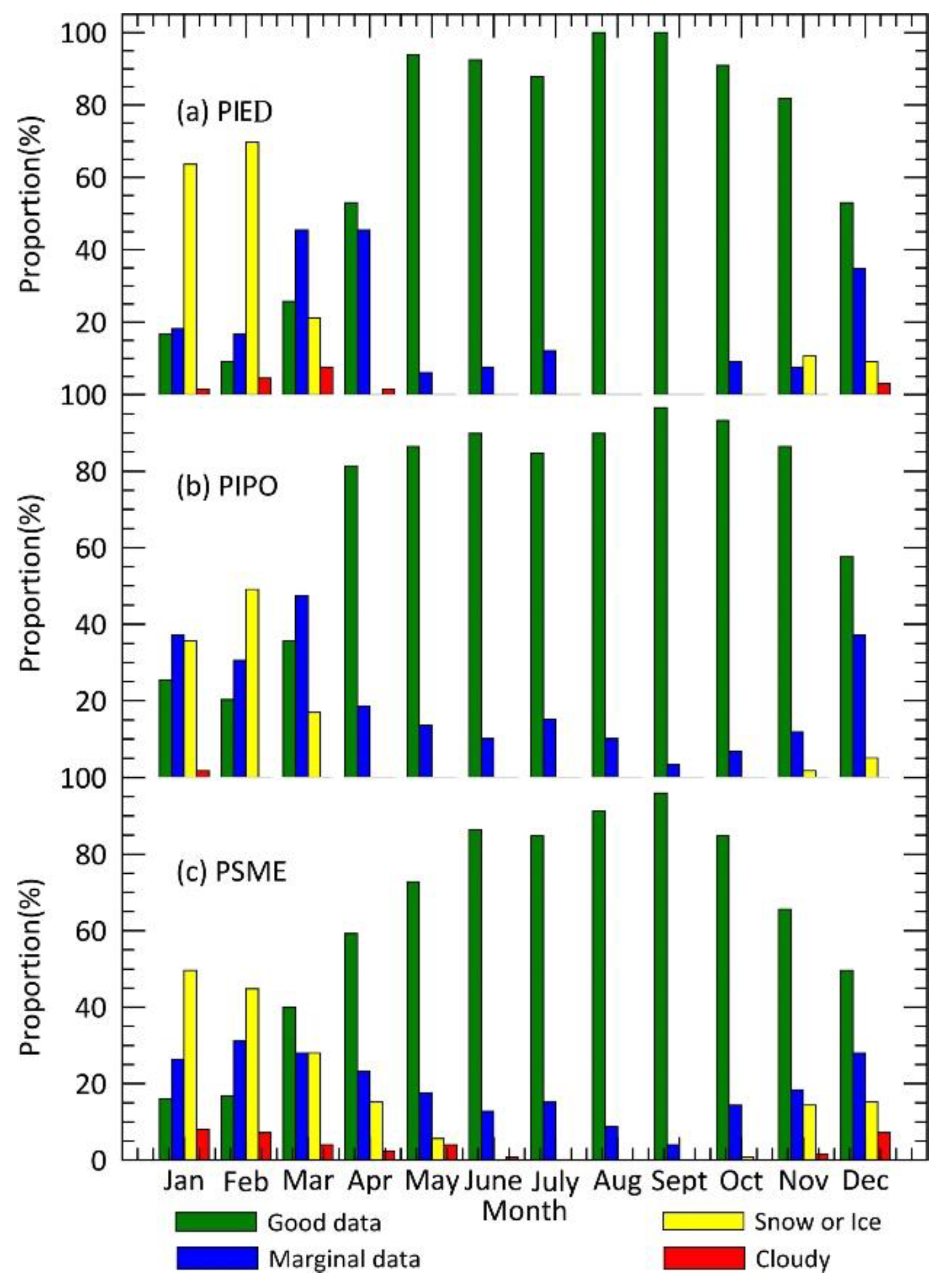
| Rank Key | Summary Quality Assurance | Description |
|---|---|---|
| −1 | Fill/no data | Not processed |
| 0 | Good data | Use with confidence |
| 1 | Marginal data | Useful, but look at other QA information |
| 2 | Snow/ice | Target covered with snow/ice |
| 3 | Cloudy | Target not visible, covered with cloud |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, P.; Fang, W.; Zhou, T.; Zhao, X.; Luo, H.; Hendrey, G.; Yi, C. Spatial Upscaling of Tree-Ring-Based Forest Response to Drought with Satellite Data. Remote Sens. 2019, 11, 2344. https://doi.org/10.3390/rs11202344
Xu P, Fang W, Zhou T, Zhao X, Luo H, Hendrey G, Yi C. Spatial Upscaling of Tree-Ring-Based Forest Response to Drought with Satellite Data. Remote Sensing. 2019; 11(20):2344. https://doi.org/10.3390/rs11202344
Chicago/Turabian StyleXu, Peipei, Wei Fang, Tao Zhou, Xiang Zhao, Hui Luo, George Hendrey, and Chuixiang Yi. 2019. "Spatial Upscaling of Tree-Ring-Based Forest Response to Drought with Satellite Data" Remote Sensing 11, no. 20: 2344. https://doi.org/10.3390/rs11202344
APA StyleXu, P., Fang, W., Zhou, T., Zhao, X., Luo, H., Hendrey, G., & Yi, C. (2019). Spatial Upscaling of Tree-Ring-Based Forest Response to Drought with Satellite Data. Remote Sensing, 11(20), 2344. https://doi.org/10.3390/rs11202344