Effects of Spatiotemporal Filtering on the Periodic Signals and Noise in the GPS Position Time Series of the Crustal Movement Observation Network of China
Abstract
1. Introduction
2. Materials and Methods
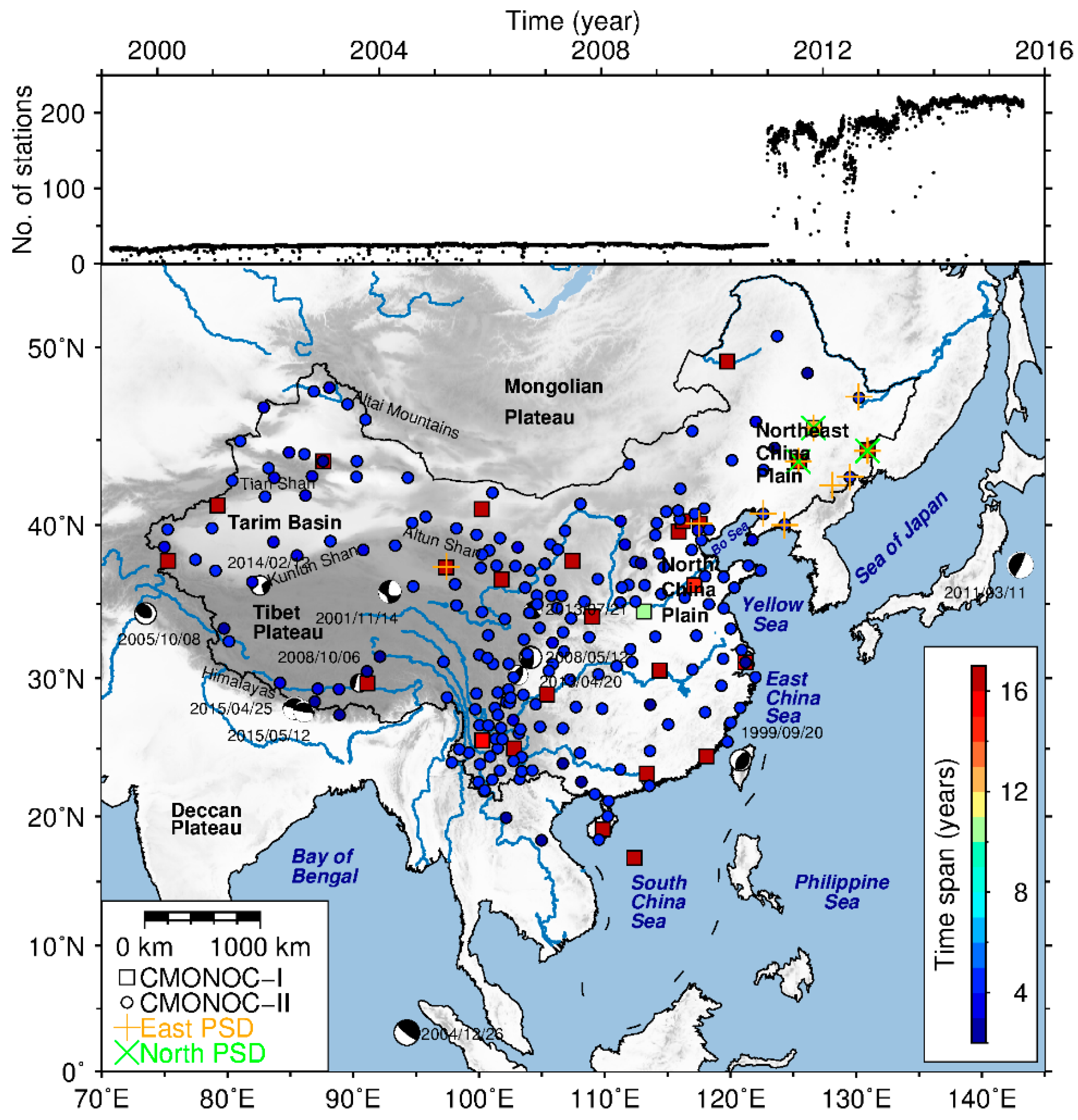
2.1. GPS Data Processing
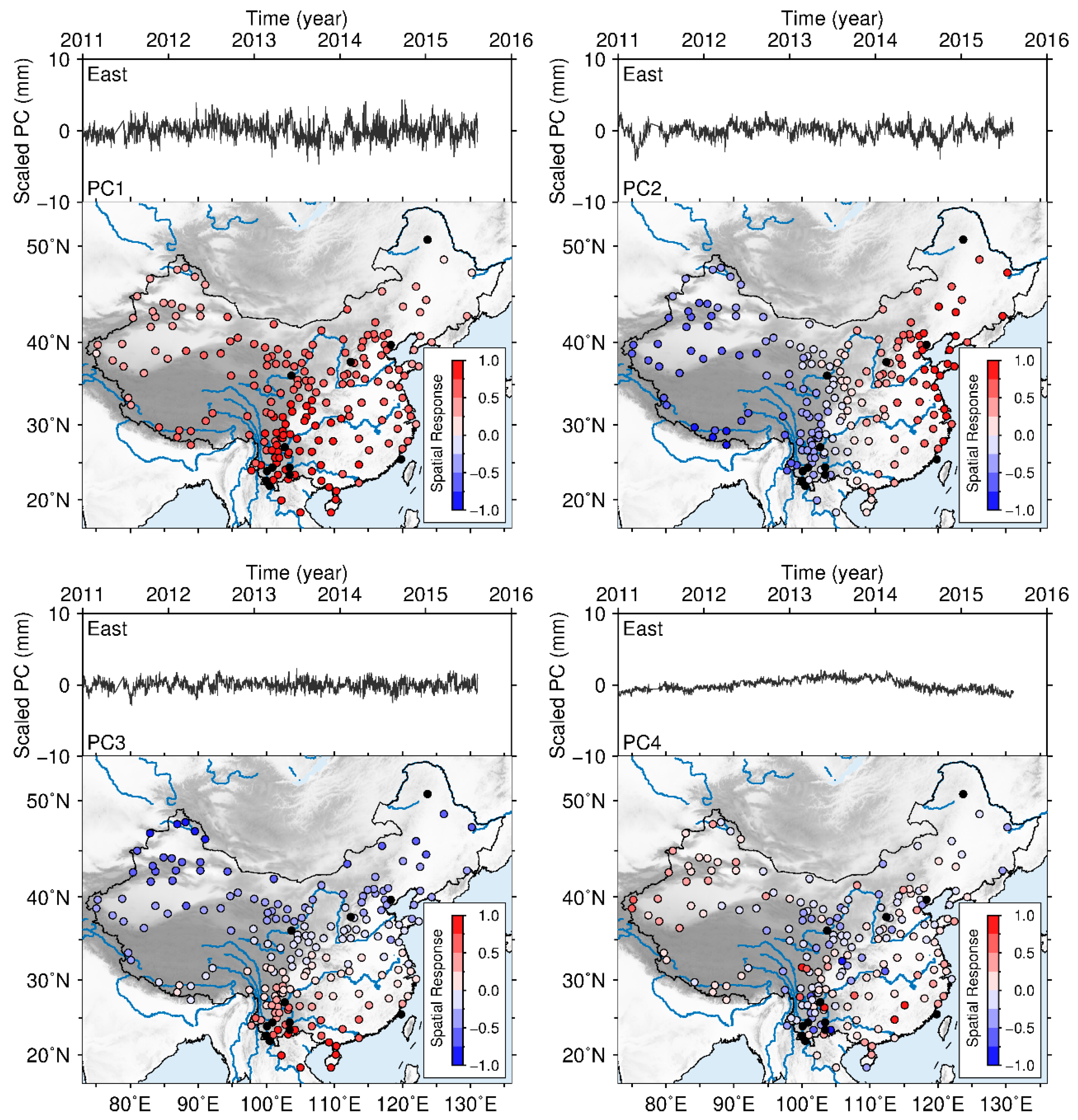
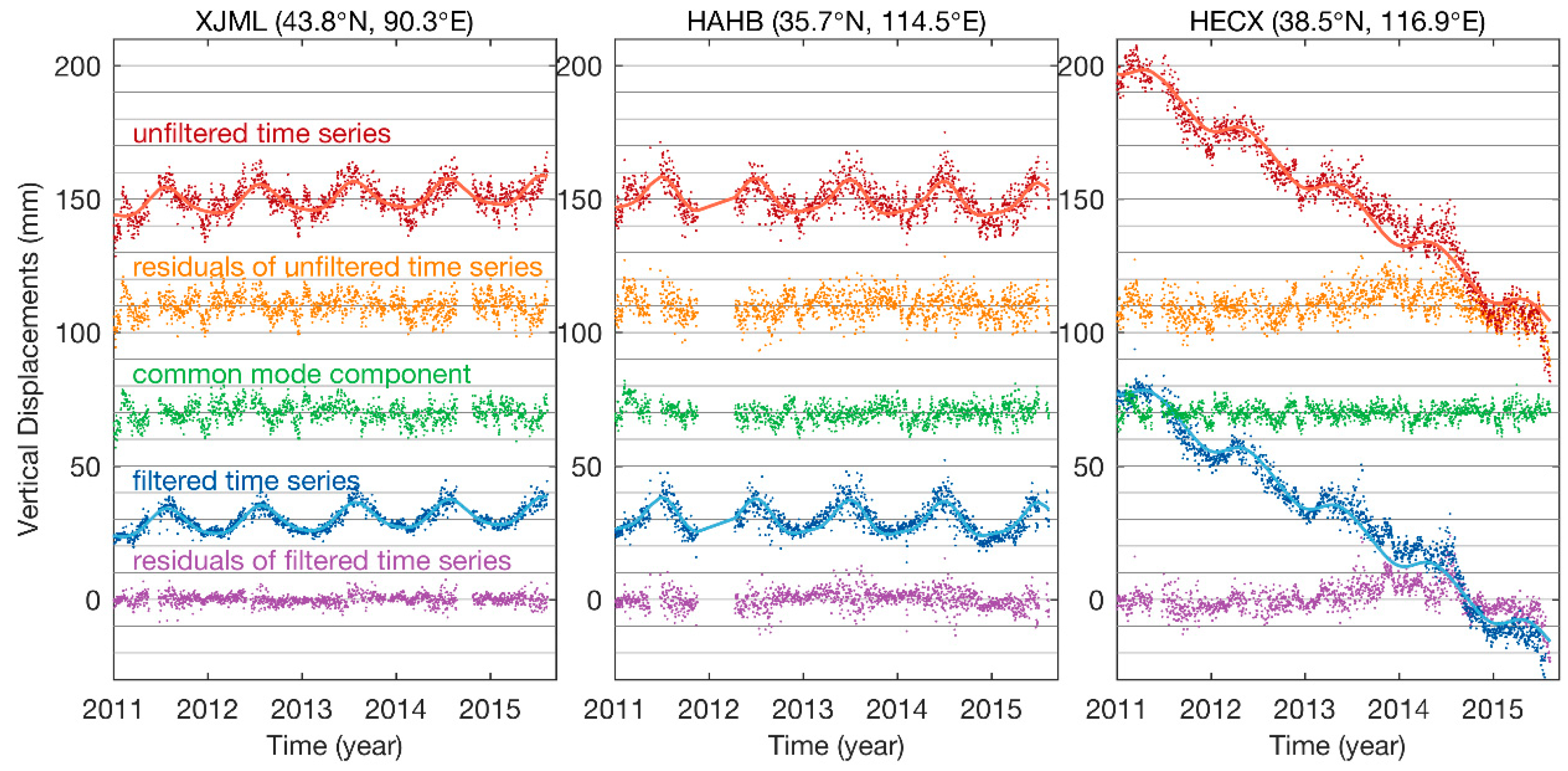
2.2. Regional Filtering of CMC
- Obtain the residual position time series of all stations according to Equation (1) with trend, offsets, seasonal, and post-seismic terms removed and construct a residual data matrix , in which and are the number of epochs and stations, respectively.
- Calculate the covariance matrix .
- Decompose the symmetric matrix as and sort the eigenvectors to rank the eigenvalues in descending order.
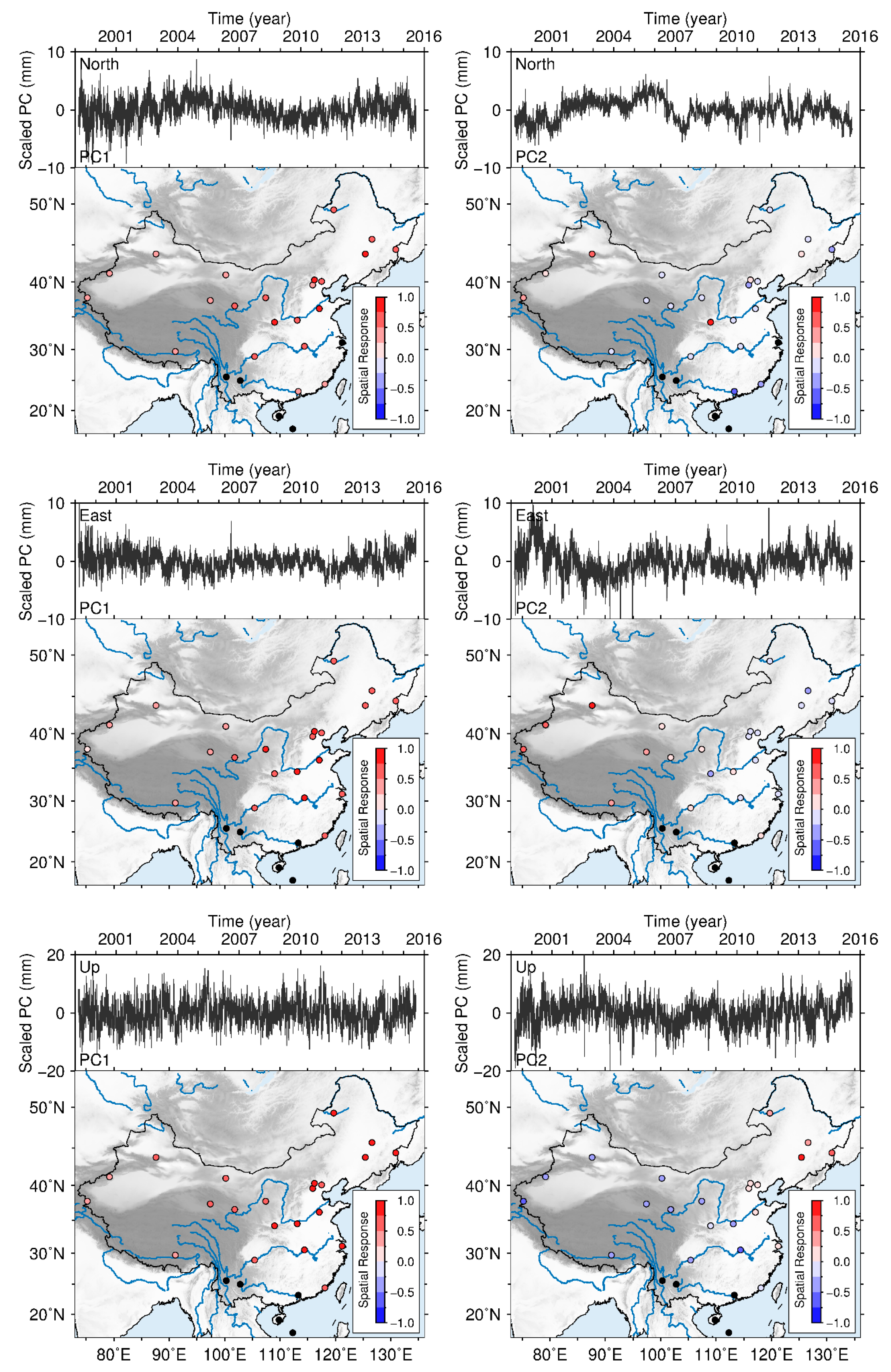
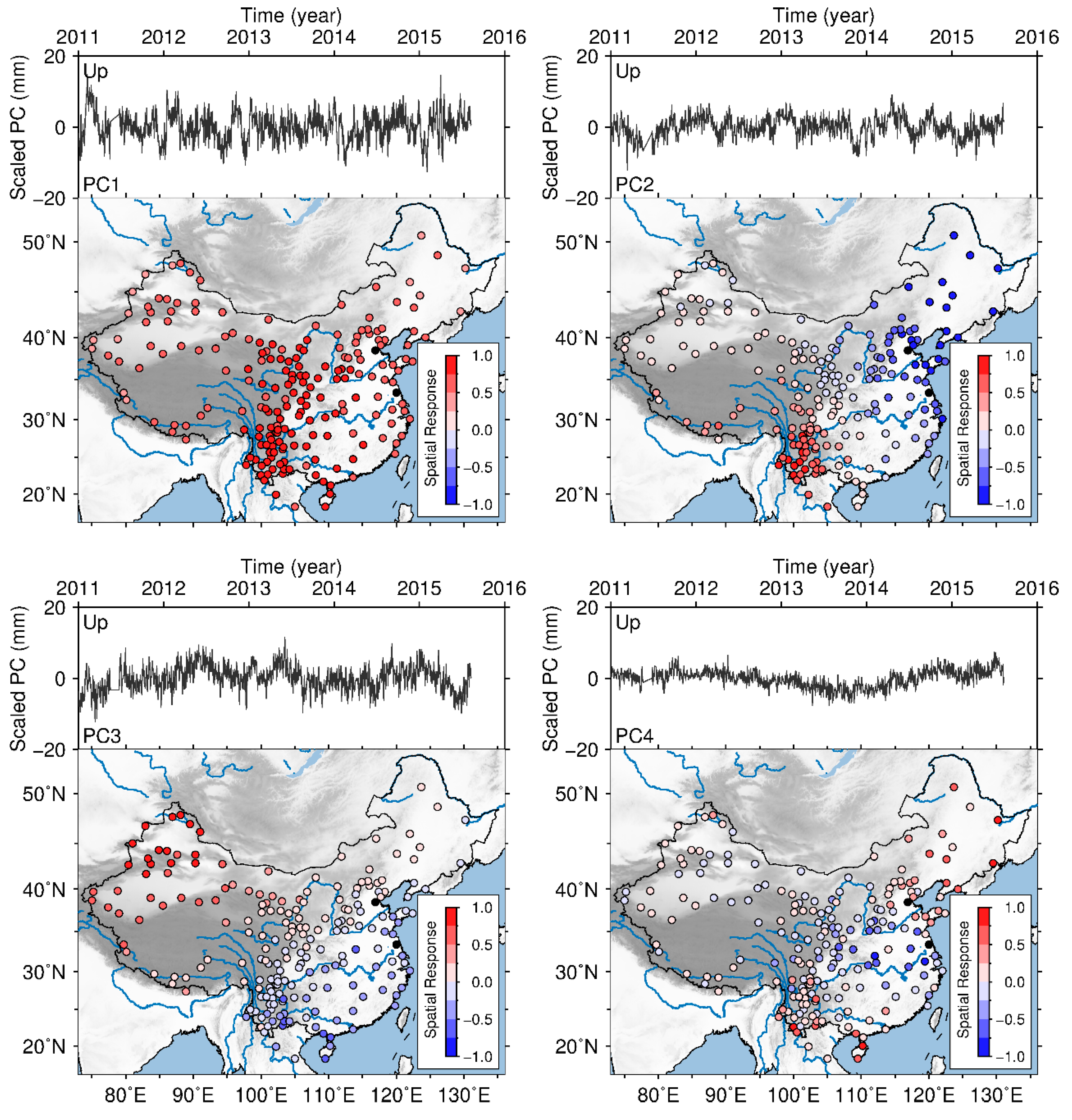
- Consider a linear transformation , thus we have . The columns of and rows of are termed as principle components (PC) and spatial responses (SR), respectively. The th PC and SR are termed as “mode ” together.
- Normalize each SR and scaling the corresponding PC by and , in which is the component with the maximum absolute value in this SR.
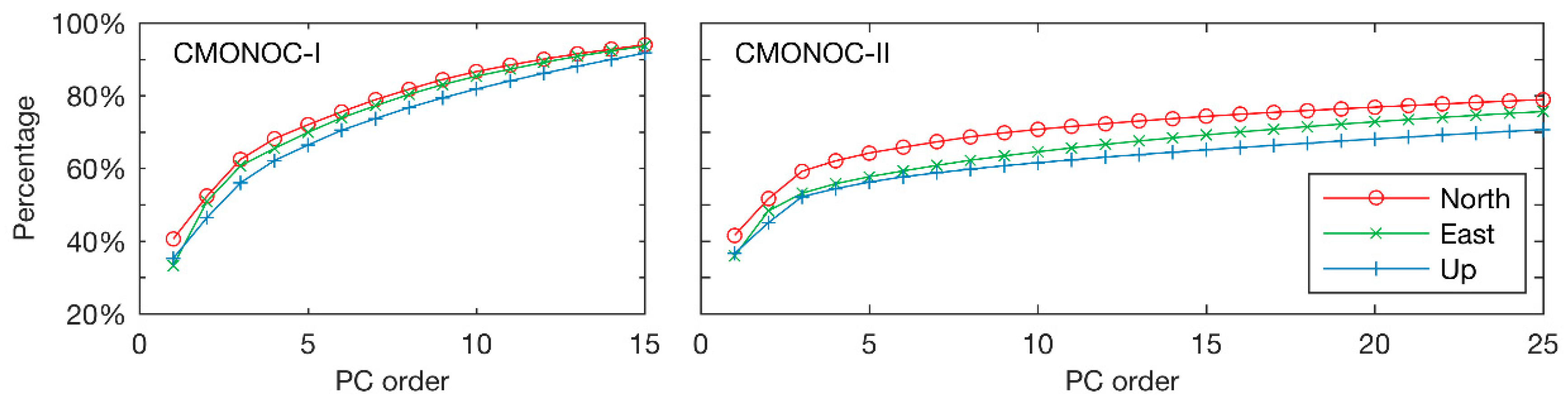
- Select the significant PCs to calculate the CMC. . The columns of are the first PCs that are considered to be significant and rows of are the corresponding SR.
3. Results
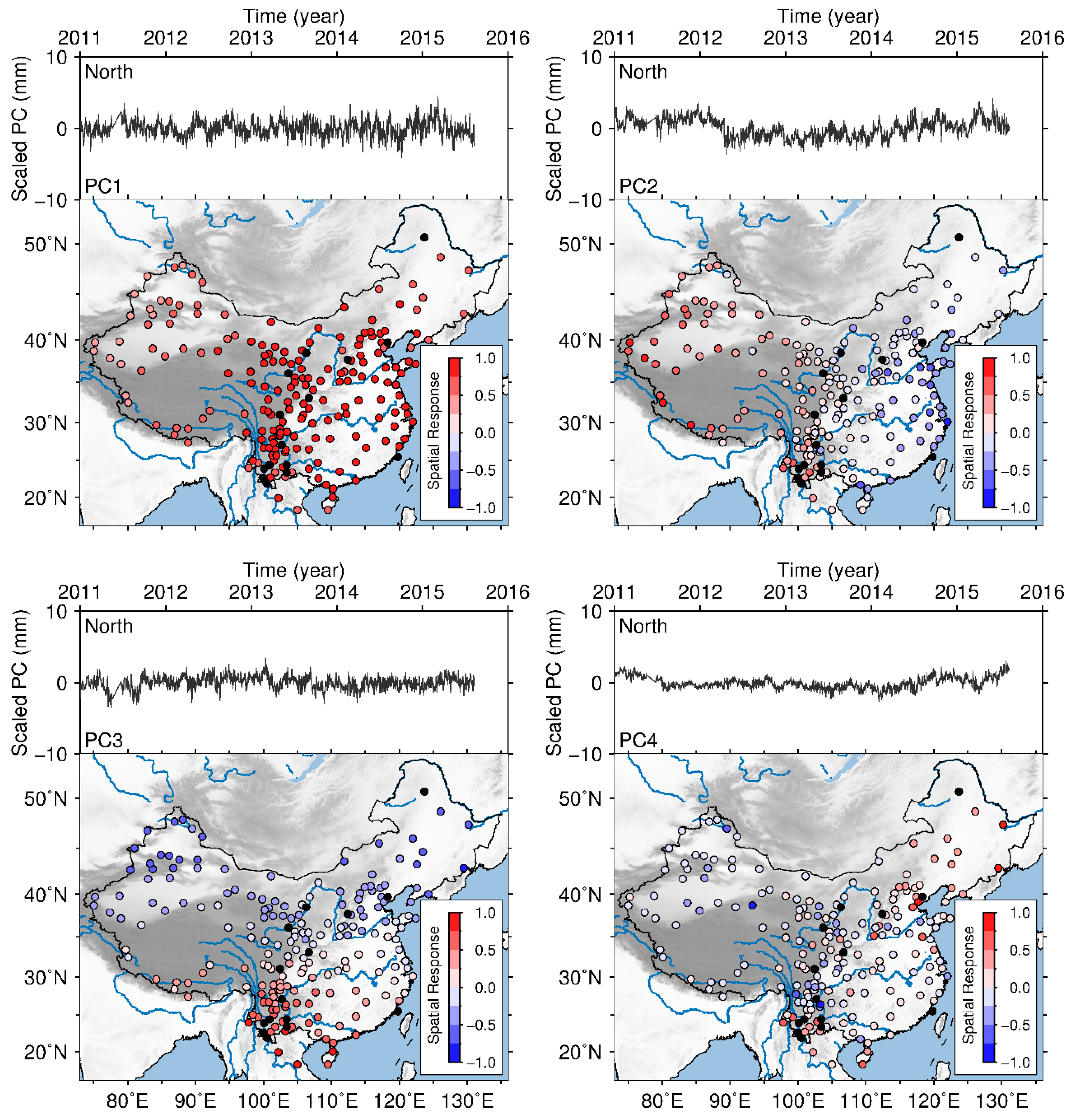
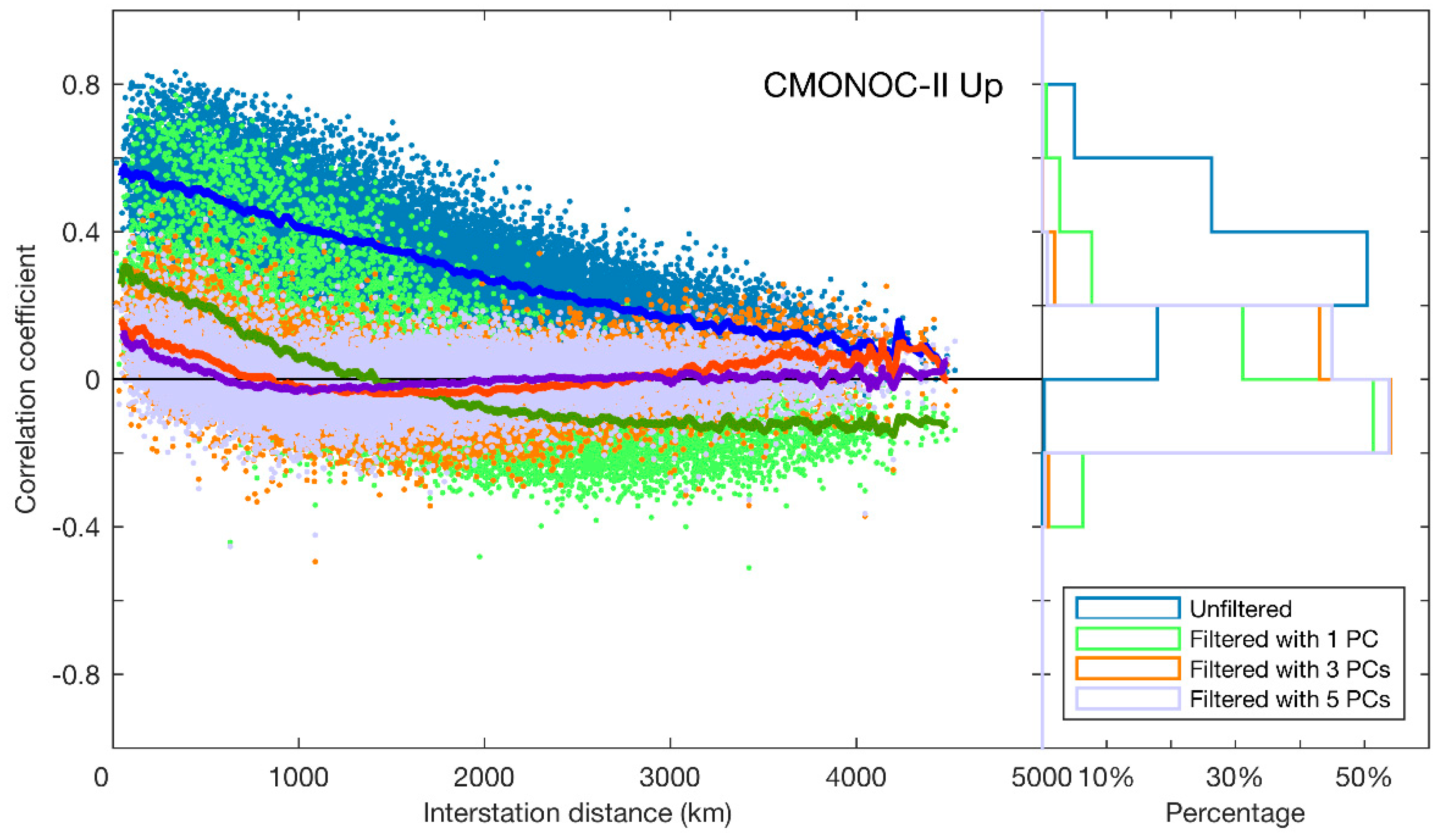
3.1. Spatial Correlation
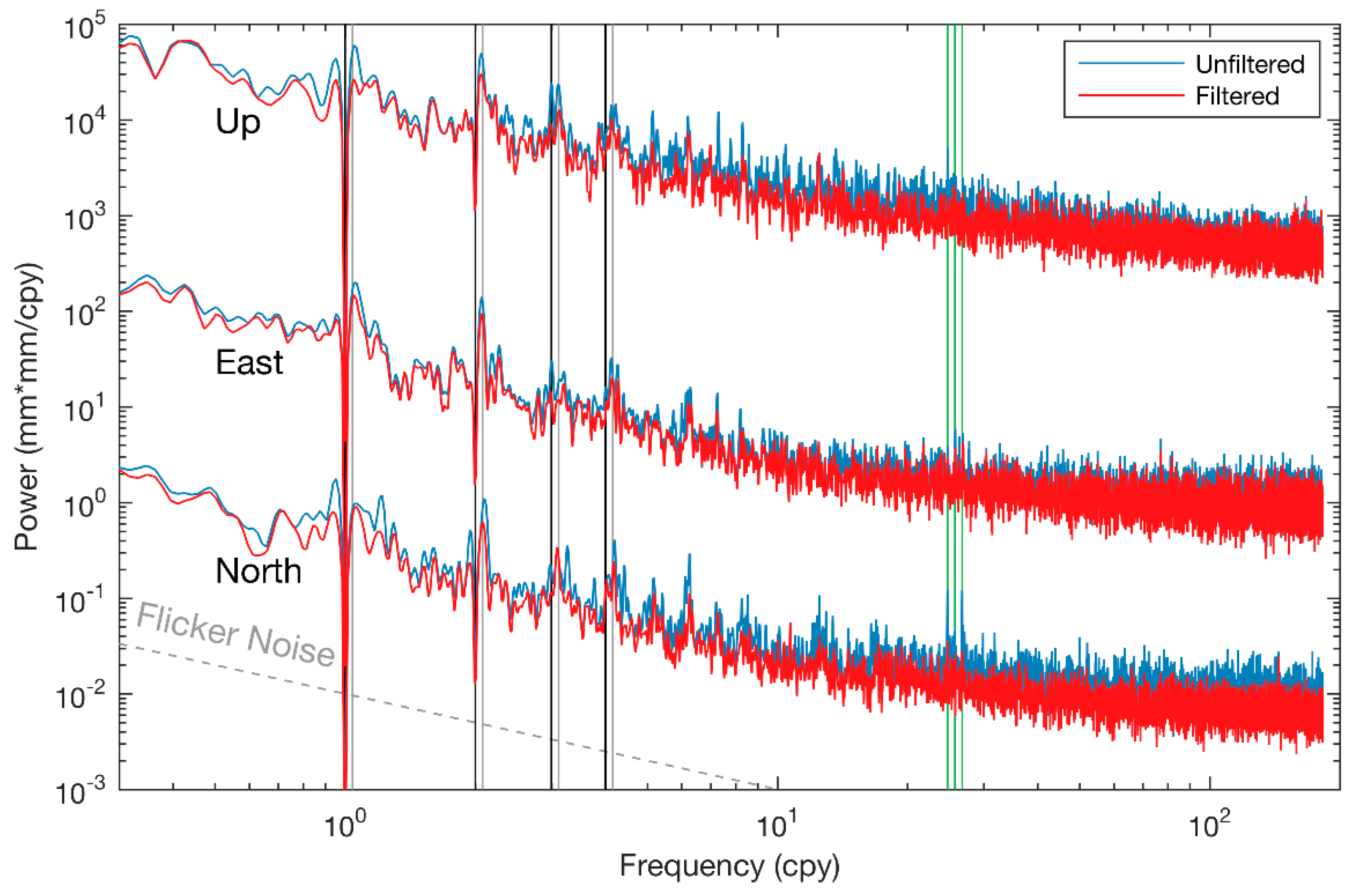
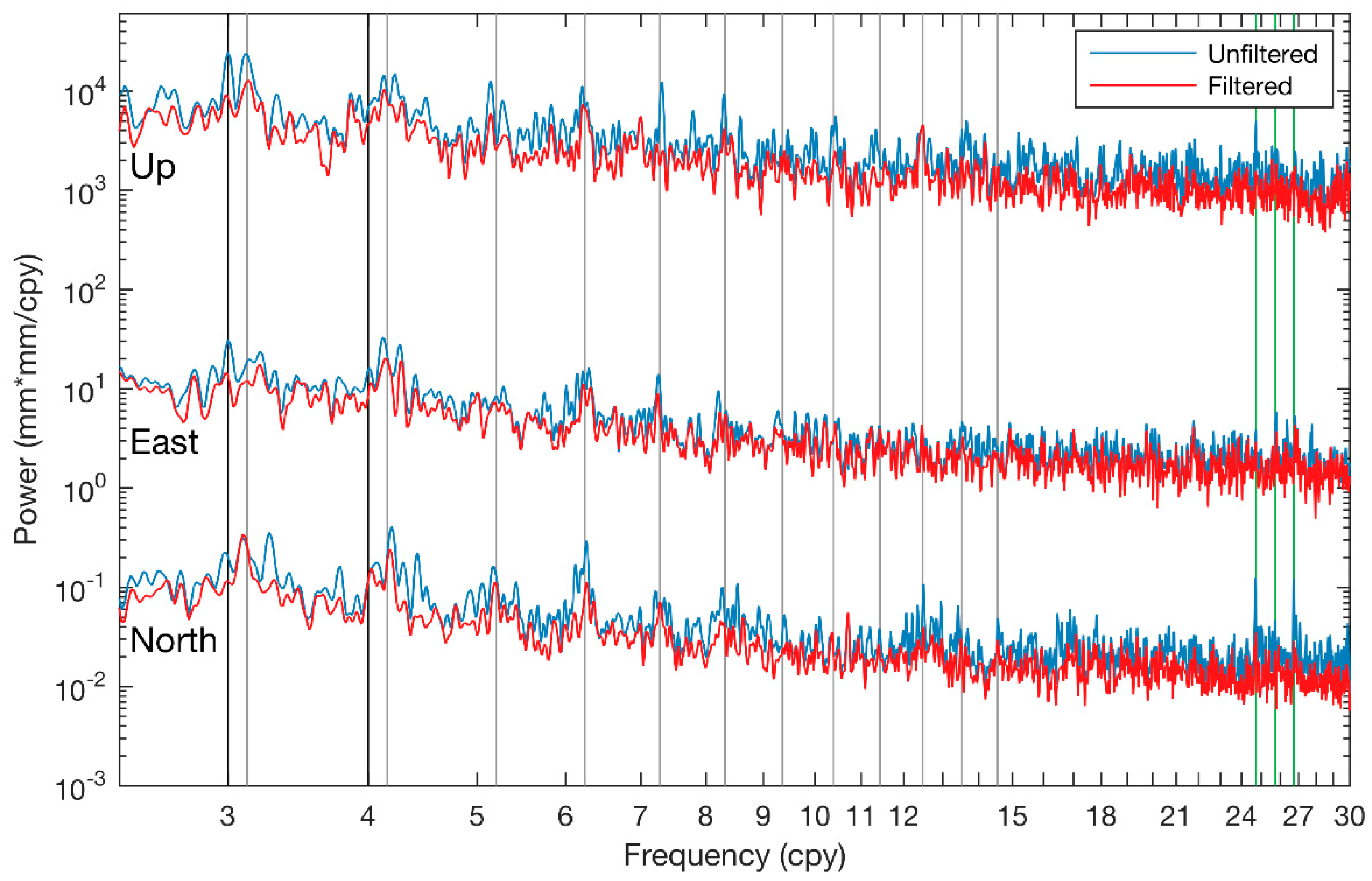
3.2. Periodic Signal
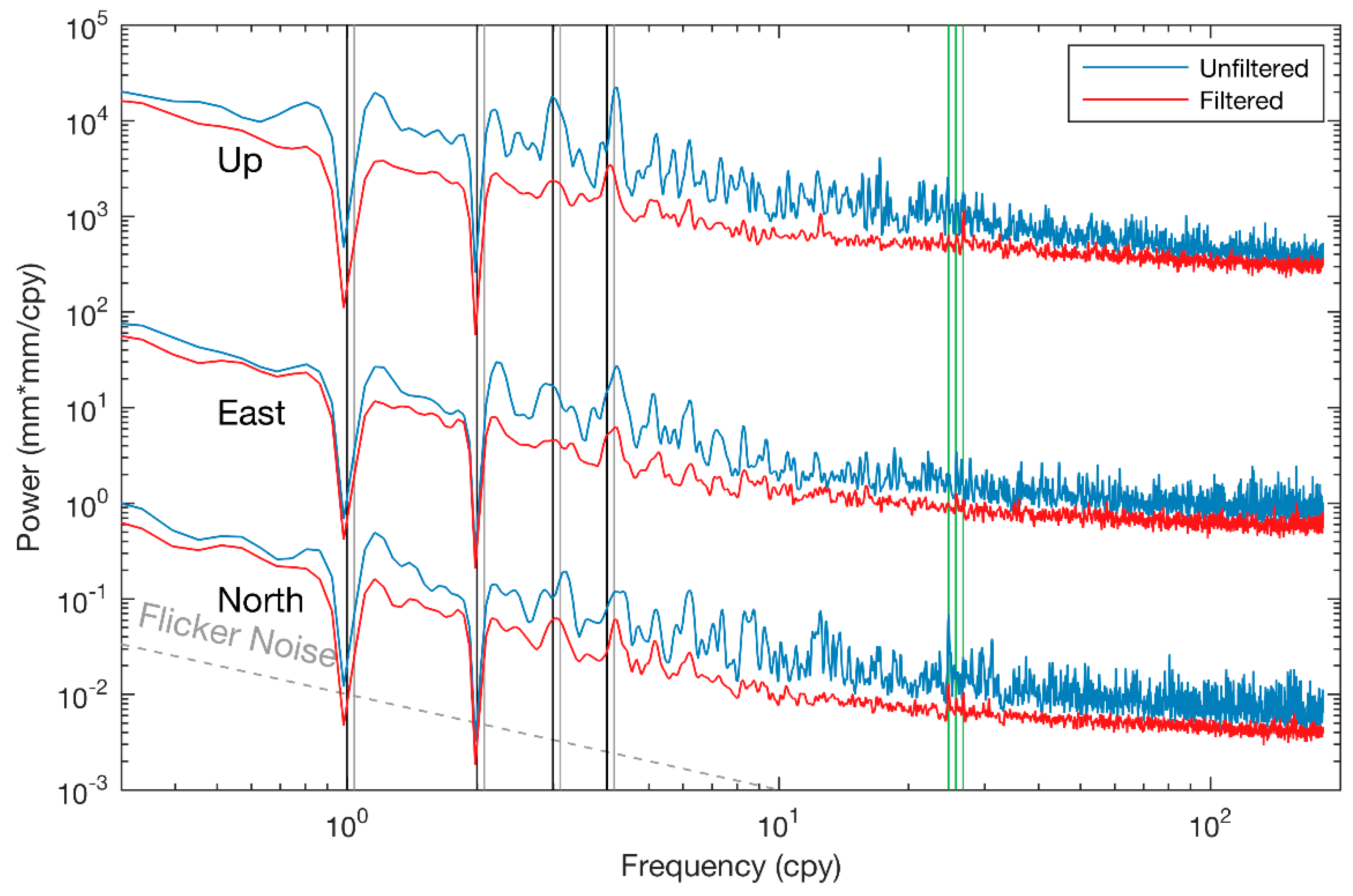
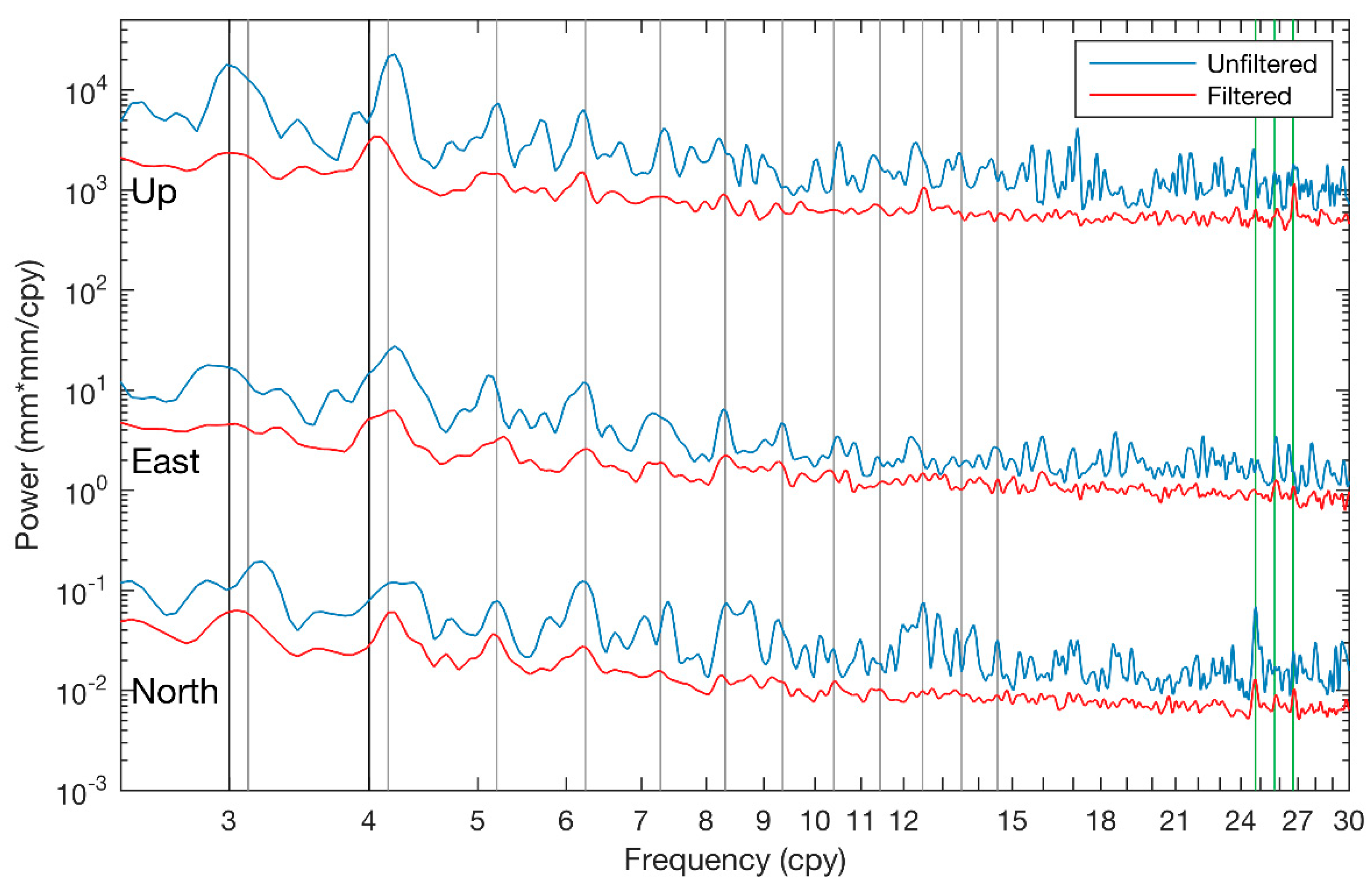
3.3. Noise Characteristics
4. Discussion
4.1. Characteristics of the Draconitic Harmonics
4.2. Changes of the Noise Characteristics Due to CMC Filtering
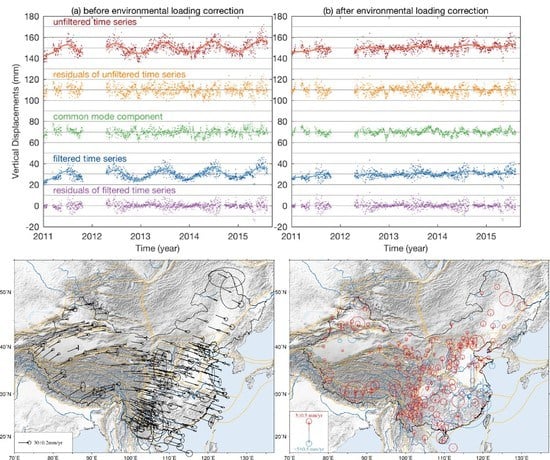
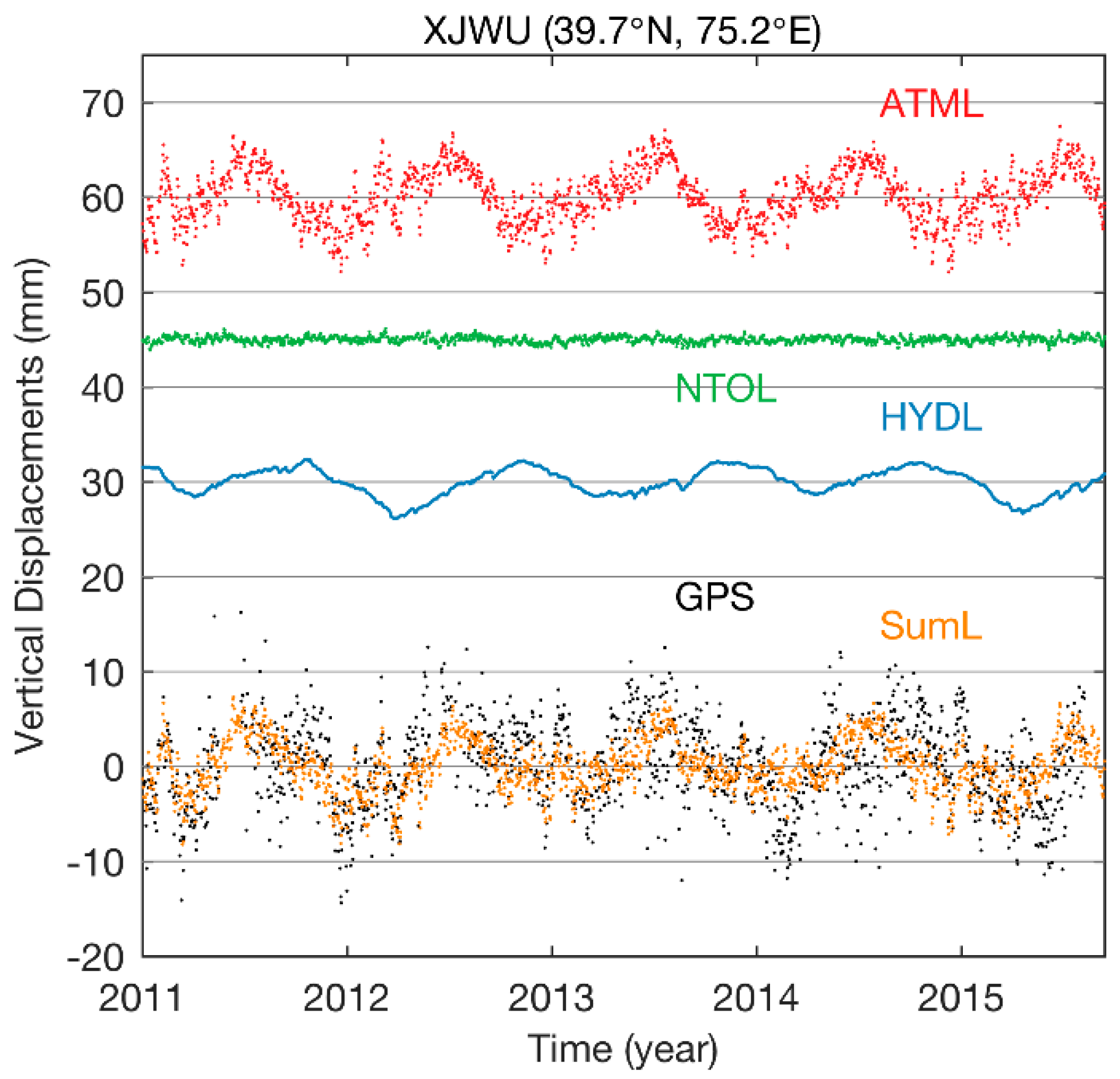
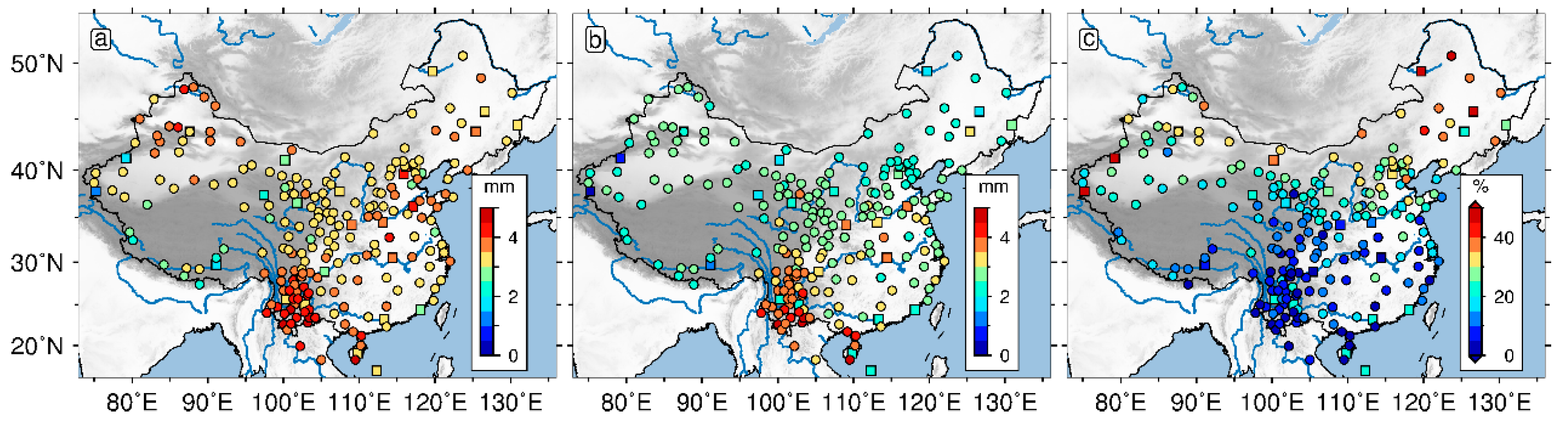
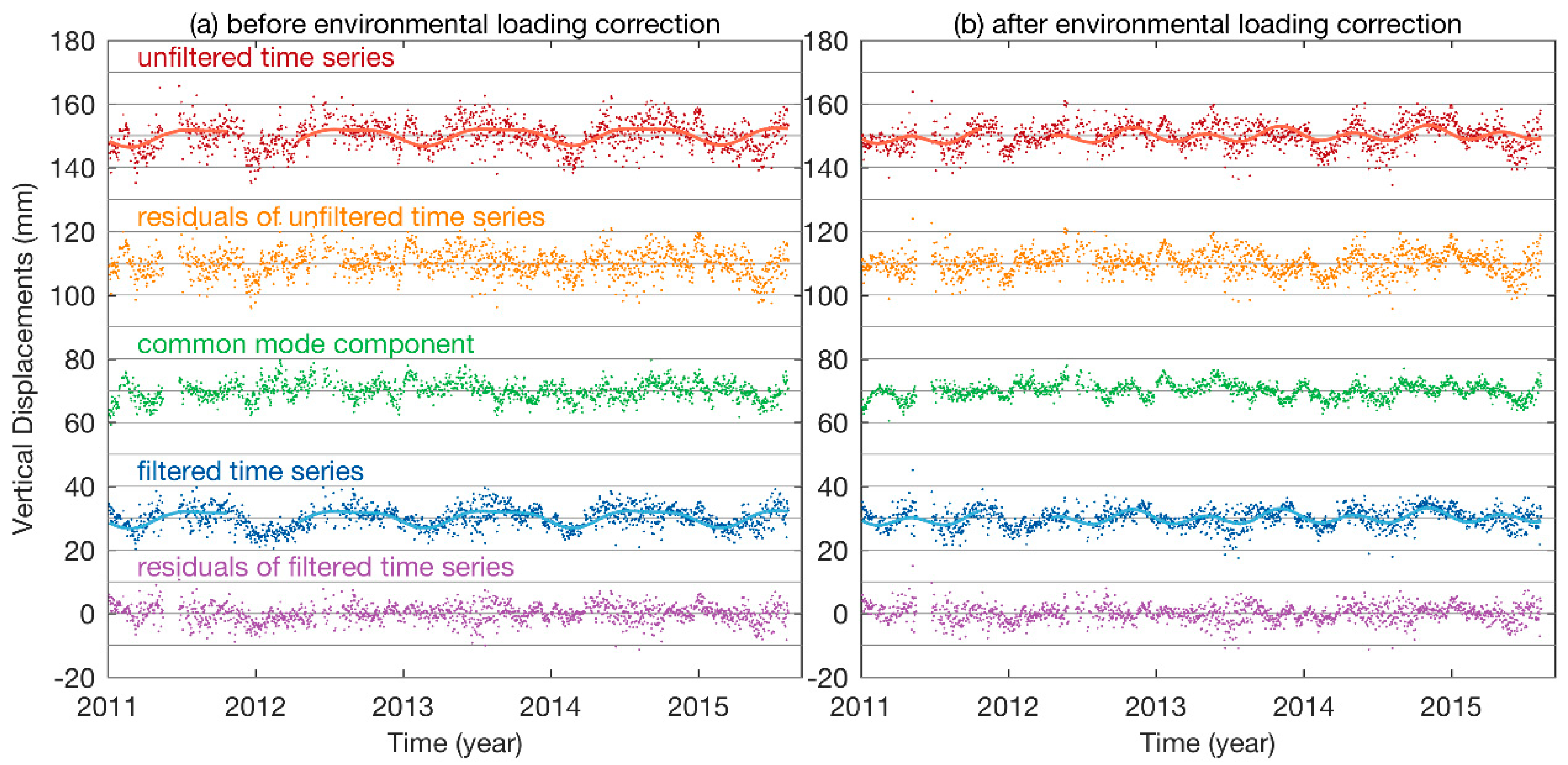
4.3. Environmental Loading Effects on the CMC
5. Conclusions
- The stacked power spectra of the CMC-filtered CMONOC residual time series show that peaks are reduced significantly at frequencies of tri-annual, draconitic harmonics up to 14th, and 24.75, 25.74, and 26.74 cpy, indicating that the CMC of the CMONOC network contains draconitic harmonics and some other periodic signals. These results support the view that the draconitic signal is spatially correlated. However, the possibility that the draconitic signal is caused by site-specific effects cannot be ruled out because of the weakened, but still visible, peaks at the frequencies of the draconitic harmonics.
- For the unfiltered time series, the velocity uncertainties of the CMONOC stations estimated with an assumption of the PLN + WN model generally vary up to 0.8 mm/year and up to 2.4 mm/year for the horizontal and vertical components, respectively. After CMC filtering, the average white noise amplitudes are slightly reduced in horizontal but enlarged in vertical for both the CMONOC-I (≈16.5 years) and CMONOC-II (≈4.6 years) stations. Nevertheless, the average power-law noise amplitudes are significantly suppressed by CMC filtering. Therefore, the velocity uncertainty estimates of north, east and up components for both the CMONOC-I and CMONOC-II stations are reduced. Compared with CMONOC-I, the CMONOC-II stations obtain greater reduction ratios in velocity uncertainty estimates with average values of 33%, 38%, and 54% for the north, east, and up components, respectively. These results indicate that CMC filtering can suppress the colored noise amplitudes and improve the precision of velocity estimates.
- After environmental loading correction, vertical CMC are reduced at 224 of the 231 CMONOC stations. In addition, 170 of them are with an RMS reduction ratio of CMC larger than 10%, confirming that environmental loading is one of the sources of CMC for the CMONOC height time series.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Time (Greenwich Mean Time) | Epicenter | Magnitude (Mw) | ||
|---|---|---|---|---|
| Longitude (°) | Latitude (°) | Region | ||
| 20 September 1999 | 120.8 | 24.2 | Nantou, Taiwan, China | 7.6 |
| 14 November 2001 | 92.9 | 35.8 | Kokoxili, Qinghai, China | 7.8 |
| 26 December 2004 | 94.3 | 3.1 | Indian Ocean | 9.0 |
| 8 October 2005 | 73.5 | 34.4 | Pakistan | 7.6 |
| 12 May 2008 | 104.1 | 31.4 | Wenchuan, Sichuan, China | 7.9 |
| 6 October 2008 | 90.5 | 29.7 | Dangxiong, Xizang, China | 6.3 |
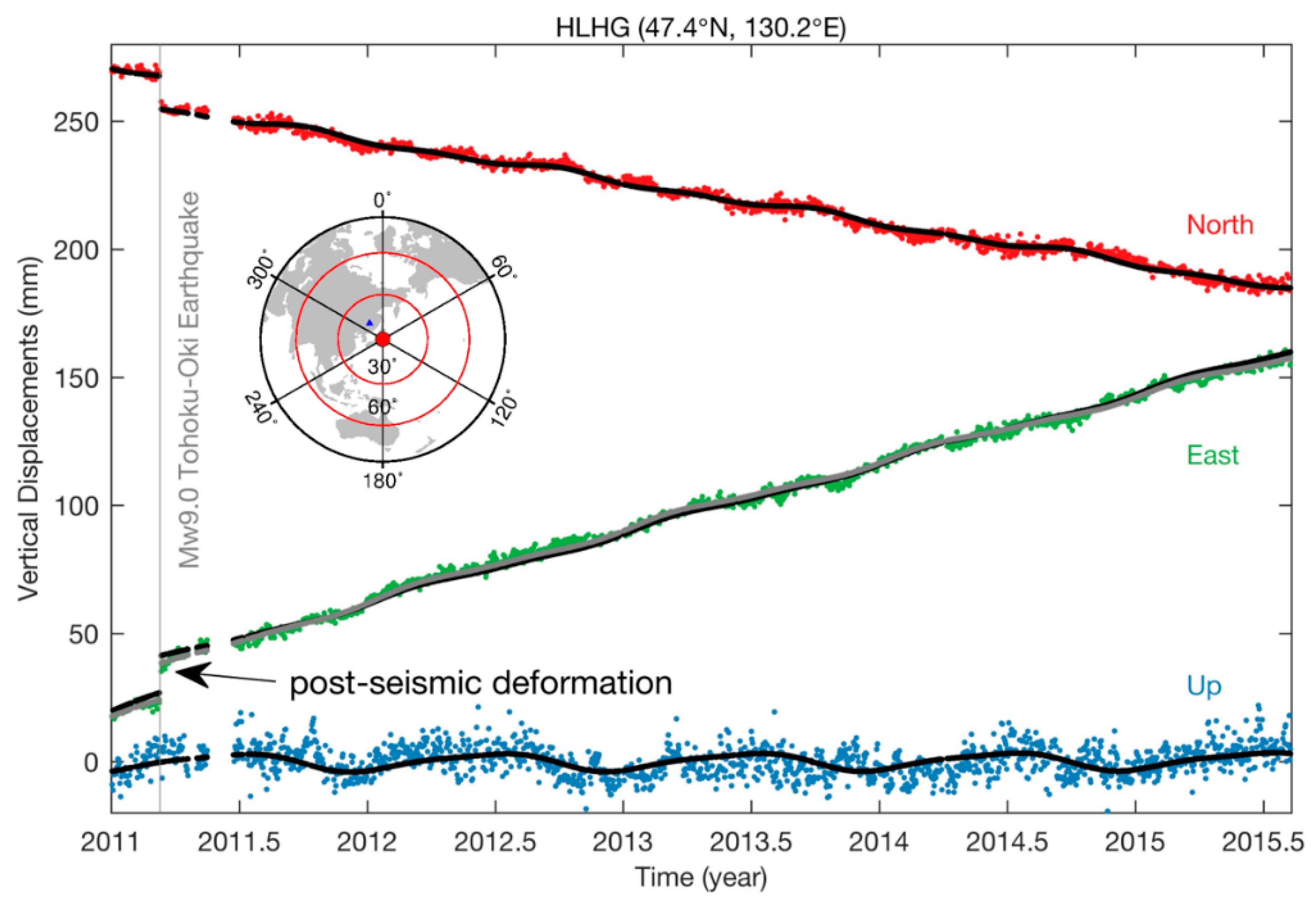
| 11 March 2011 | 143.1 | 37.5 | Tohoku-Oki, Japan | 9.1 |
| 20 April 2013 | 103.1 | 30.2 | Lushan, Sichuan, China | 6.6 |
| 21 July 2013 | 104.3 | 34.6 | Minxian, Gansu, China | 6.0 |
| 12 February 2014 | 82.6 | 36.2 | Yutian, Xinjiang, China | 6.9 |
| 25 April 2015 | 85.3 | 27.9 | Nepal | 7.9 |
| 12 May 2015 | 86.1 | 27.7 | Nepal | 7.2 |
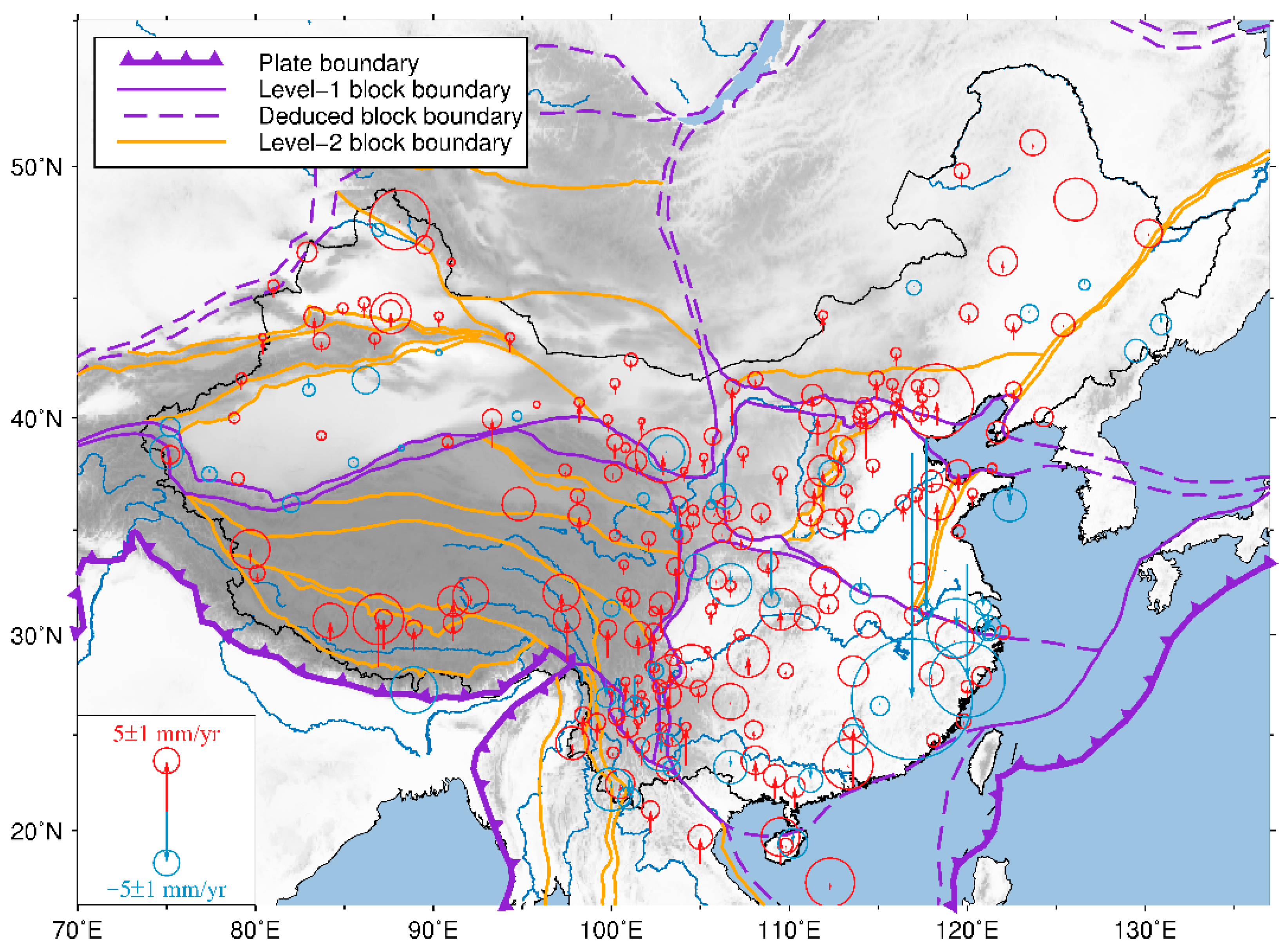
| Station | Lat. (°) | Lon. (°) | Velocity (mm/year) | Velocity Uncertainty (mm/year) | ||||
|---|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | |||
| AHAQ | 117.0 | 30.6 | −11.17 | 33.03 | 0.72 | 0.06 | 0.07 | 0.36 |
| AHBB | 117.3 | 32.9 | −10.78 | 32.79 | 0.18 | 0.10 | 0.06 | 0.40 |
| BJFS | 115.9 | 39.6 | −10.69 | 30.20 | 1.83 | 0.24 | 0.18 | 0.16 |
| BJGB | 117.2 | 40.7 | −10.48 | 29.78 | 1.57 | 0.05 | 0.05 | 0.23 |
| BJSH | 116.2 | 40.3 | −11.28 | 29.55 | 0.82 | 0.09 | 0.07 | 0.15 |
| BJYQ | 116.0 | 40.4 | −10.59 | 30.66 | 1.14 | 0.09 | 0.06 | 0.19 |
| CHUN | 125.4 | 43.8 | −11.77 | 25.89 | 0.27 | 0.12 | 0.14 | 0.45 |
| CQCS | 107.2 | 29.9 | −9.15 | 34.68 | 0.27 | 0.09 | 0.17 | 0.19 |
| DLHA | 97.4 | 37.4 | 1.03 | 37.23 | 0.70 | 0.15 | 0.32 | 0.23 |
| DXIN | 100.2 | 41.0 | −4.58 | 30.72 | 1.15 | 0.13 | 0.10 | 0.18 |
| FJPT | 119.8 | 25.5 | −11.71 | 31.22 | 0.40 | 0.30 | 0.47 | 0.28 |
| FJWY | 118.0 | 27.6 | −11.50 | 33.03 | 0.93 | 0.16 | 0.14 | 0.47 |
| FJXP | 120.0 | 26.9 | −11.46 | 32.96 | 1.06 | 0.08 | 0.15 | 0.23 |
| GDSG | 113.6 | 24.8 | −10.59 | 33.60 | −0.06 | 0.11 | 0.44 | 0.57 |
| GDZH | 113.6 | 22.3 | −11.18 | 33.68 | 5.75 | 0.07 | 0.09 | 0.40 |
| GDZJ | 110.3 | 21.2 | −10.50 | 33.67 | 2.06 | 0.20 | 0.23 | 0.40 |
| GSAX | 95.8 | 40.5 | −0.24 | 31.27 | 0.21 | 0.12 | 0.09 | 0.13 |
| GSDH | 94.7 | 40.1 | 0.48 | 30.81 | −0.01 | 0.17 | 0.26 | 0.19 |
| GSDX | 104.6 | 35.6 | −6.69 | 36.40 | 0.68 | 0.06 | 0.04 | 0.19 |
| GSGL | 102.9 | 37.5 | −4.78 | 34.37 | 1.96 | 0.45 | 0.48 | 1.07 |
| GSGT | 99.8 | 39.4 | −3.38 | 31.61 | 1.24 | 0.09 | 0.08 | 0.18 |
| GSJN | 105.8 | 35.5 | −8.49 | 34.68 | 0.67 | 0.18 | 0.08 | 0.44 |
| GSJT | 104.1 | 37.2 | −5.29 | 34.75 | 1.09 | 0.08 | 0.25 | 0.13 |
| GSJY | 98.2 | 39.8 | −1.93 | 31.51 | 2.02 | 0.17 | 0.16 | 0.19 |
| GSLX | 104.6 | 35.0 | −7.01 | 35.52 | 0.91 | 0.10 | 0.11 | 0.26 |
| GSLZ | 103.7 | 36.1 | −0.75 | 40.94 | −2.66 | 1.75 | 0.75 | 0.23 |
| GSMA | 102.1 | 34.0 | −4.25 | 41.41 | 1.31 | 0.35 | 0.13 | 0.27 |
| GSML | 100.8 | 38.4 | −2.92 | 33.02 | 0.68 | 0.11 | 0.12 | 0.19 |
| GSMQ | 103.1 | 38.6 | −5.50 | 32.48 | −0.30 | 0.37 | 0.06 | 0.71 |
| GSMX | 104.0 | 34.4 | −5.92 | 38.08 | 0.83 | 0.12 | 0.14 | 0.36 |
| GSPL | 106.6 | 35.5 | −8.95 | 35.06 | 1.04 | 0.05 | 0.61 | 0.48 |
| GSQS | 106.2 | 34.7 | −7.71 | 33.77 | 0.34 | 0.22 | 0.20 | 0.37 |
| GSWD | 104.8 | 33.4 | −8.15 | 36.17 | −0.24 | 0.39 | 0.31 | 0.50 |
| GUAN | 113.3 | 23.2 | −11.03 | 32.64 | 0.55 | 0.20 | 0.32 | 0.97 |
| GXBH | 109.2 | 21.7 | −8.41 | 33.30 | 2.20 | 0.31 | 0.14 | 0.45 |
| GXBS | 106.7 | 23.9 | −9.07 | 34.60 | −1.07 | 0.16 | 0.12 | 0.65 |
| GXHC | 108.0 | 24.7 | −9.30 | 34.54 | 1.07 | 0.08 | 0.11 | 0.36 |
| GXNN | 108.1 | 22.6 | −9.22 | 33.85 | 2.07 | 0.14 | 0.09 | 0.55 |
| GXWZ | 111.2 | 23.5 | −9.43 | 34.24 | −1.57 | 0.16 | 0.16 | 0.47 |
| GZFG | 107.7 | 28.0 | −9.42 | 33.32 | 1.89 | 0.37 | 0.60 | 0.82 |
| GZGY | 106.7 | 26.5 | −9.01 | 34.94 | 0.37 | 0.05 | 0.20 | 0.70 |
| GZSC | 104.9 | 26.6 | −8.73 | 34.68 | 1.46 | 0.08 | 0.10 | 0.31 |
| HAHB | 114.5 | 35.7 | −10.81 | 32.43 | −0.54 | 0.06 | 0.09 | 0.42 |
| HAJY | 112.4 | 35.2 | −10.35 | 33.14 | 0.19 | 0.15 | 0.09 | 0.56 |
| HAQS | 114.0 | 32.8 | −10.61 | 34.24 | −1.64 | 0.04 | 0.08 | 0.40 |
| HBES | 109.5 | 30.3 | −9.99 | 34.10 | 1.94 | 0.19 | 0.11 | 0.81 |
| HBJM | 112.2 | 31.1 | −10.73 | 34.77 | 0.83 | 0.19 | 0.34 | 0.38 |
| HBXF | 112.0 | 32.0 | −10.48 | 33.69 | 1.20 | 0.10 | 0.06 | 0.58 |
| HBZG | 111.0 | 30.8 | −9.26 | 34.57 | 0.10 | 0.47 | 0.44 | 0.49 |
| HECC | 115.8 | 40.9 | −10.64 | 29.85 | 1.28 | 0.10 | 0.05 | 0.21 |
| HECD | 117.9 | 41.0 | −9.85 | 29.81 | 0.71 | 0.08 | 0.12 | 0.36 |
| HECX | 116.9 | 38.5 | −9.74 | 30.82 | −24.12 | 0.43 | 0.38 | 2.34 |
| HELQ | 114.3 | 38.2 | −10.48 | 32.11 | 4.24 | 0.08 | 0.14 | 0.49 |
| HELY | 114.7 | 37.4 | −10.37 | 33.23 | 1.17 | 0.20 | 0.14 | 0.25 |
| HETS | 118.3 | 39.7 | −6.33 | 27.70 | 2.39 | 0.77 | 0.89 | 1.43 |
| HEYY | 114.2 | 40.1 | −10.90 | 32.47 | 1.01 | 0.12 | 0.39 | 0.31 |
| HEZJ | 114.9 | 40.8 | −9.91 | 30.08 | 2.05 | 0.34 | 0.19 | 0.29 |
| HIHK | 110.2 | 20.0 | −10.43 | 33.02 | −1.25 | 0.37 | 0.13 | 0.57 |
| HISY | 109.5 | 18.2 | −8.15 | 34.07 | 2.68 | 0.26 | 0.63 | 0.75 |
| HLAR | 119.7 | 49.3 | −11.32 | 25.79 | 1.44 | 0.10 | 0.09 | 0.30 |
| HLHG | 130.2 | 47.4 | −15.90 | 24.38 | 0.29 | 0.78 | 1.45 | 0.54 |
| HLWD | 126.1 | 48.7 | −12.24 | 25.21 | 0.25 | 0.44 | 0.41 | 0.83 |
| HNLY | 113.6 | 28.2 | −10.35 | 33.72 | 0.03 | 0.08 | 0.08 | 0.59 |
| HNMY | 109.8 | 27.9 | −9.71 | 34.51 | 0.68 | 0.06 | 0.20 | 0.29 |
| HRBN | 126.6 | 45.7 | −11.76 | 24.98 | −0.45 | 0.16 | 0.18 | 0.21 |
| JIXN | 117.5 | 40.1 | −10.12 | 28.17 | 1.74 | 0.12 | 0.06 | 0.17 |
| JLCL | 123.5 | 44.6 | −11.62 | 28.38 | −0.55 | 0.26 | 0.23 | 0.35 |
| JLYJ | 129.5 | 42.9 | −16.81 | 26.47 | −0.11 | 0.32 | 0.70 | 0.44 |
| JSLS | 119.4 | 31.3 | −11.39 | 33.56 | −1.92 | 0.27 | 0.12 | 1.14 |
| JSLY | 119.5 | 34.7 | −12.05 | 32.06 | 0.47 | 0.06 | 0.08 | 0.26 |
| JSNT | 120.9 | 32.0 | −11.78 | 32.83 | −1.33 | 0.10 | 0.13 | 0.31 |
| JSYC | 120.0 | 33.4 | −9.76 | 32.46 | −11.28 | 0.44 | 0.27 | 1.46 |
| JXJA | 115.1 | 26.7 | −11.13 | 33.93 | −0.44 | 0.06 | 0.31 | 0.37 |
| KMIN | 102.8 | 25.0 | −16.73 | 33.53 | −1.67 | 0.39 | 0.97 | 0.75 |
| LALB | 102.2 | 19.9 | −6.25 | 31.40 | 2.23 | 0.40 | 0.28 | 0.34 |
| LALX | 105.0 | 18.2 | −8.74 | 31.52 | 2.68 | 0.40 | 0.44 | 0.47 |
| LHAS | 91.1 | 29.7 | 15.50 | 46.66 | 1.79 | 0.12 | 0.15 | 0.38 |
| LNDD | 124.3 | 40.0 | −10.68 | 26.09 | 0.13 | 0.27 | 1.12 | 0.37 |
| LNJZ | 121.7 | 39.1 | −12.03 | 29.42 | 0.63 | 0.29 | 0.11 | 0.42 |
| LNYK | 122.6 | 40.7 | −11.64 | 27.76 | 1.20 | 0.12 | 0.26 | 0.31 |
| LUZH | 105.4 | 28.9 | −9.56 | 34.65 | 0.73 | 0.10 | 0.19 | 0.12 |
| NMAG | 122.6 | 43.3 | −11.00 | 28.74 | 1.67 | 0.10 | 0.15 | 0.33 |
| NMAL | 120.1 | 43.9 | −10.92 | 28.74 | 1.20 | 0.12 | 0.10 | 0.36 |
| NMAY | 101.7 | 39.2 | −5.25 | 31.82 | 1.51 | 0.23 | 0.05 | 0.12 |
| NMAZ | 105.7 | 38.8 | −6.63 | 31.84 | 0.92 | 0.26 | 0.21 | 0.33 |
| NMDW | 117.0 | 45.5 | −10.53 | 28.40 | −0.24 | 0.12 | 0.08 | 0.29 |
| NMEJ | 101.1 | 42.0 | −4.50 | 31.41 | 1.12 | 0.23 | 0.03 | 0.26 |
| NMEL | 111.9 | 43.6 | −9.61 | 29.52 | 1.70 | 0.17 | 0.30 | 0.17 |
| NMER | 123.7 | 50.6 | −11.28 | 25.12 | 0.71 | 1.92 | 1.37 | 0.50 |
| NMTK | 111.3 | 40.3 | −10.57 | 31.58 | 1.61 | 0.18 | 0.40 | 0.41 |
| NMWH | 106.8 | 39.7 | −9.62 | 32.42 | 3.75 | 0.12 | 0.19 | 0.29 |
| NMWJ | 108.1 | 41.3 | −9.43 | 30.09 | 0.86 | 0.12 | 0.27 | 0.29 |
| NMWL | 122.0 | 46.0 | −10.96 | 27.57 | 1.12 | 0.17 | 0.17 | 0.56 |
| NMZL | 116.0 | 42.2 | −10.20 | 29.60 | 1.33 | 0.28 | 0.03 | 0.20 |
| NXHY | 105.6 | 36.6 | −6.55 | 34.59 | −0.93 | 0.10 | 0.15 | 0.18 |
| NXYC | 106.3 | 38.5 | −7.34 | 32.04 | −4.25 | 0.68 | 0.62 | 0.49 |
| NXZW | 105.2 | 37.6 | −5.62 | 33.25 | 1.52 | 0.05 | 0.13 | 0.16 |
| QHBM | 100.7 | 32.9 | −4.94 | 44.90 | 1.02 | 0.07 | 0.05 | 0.18 |
| QHDL | 98.1 | 36.3 | 2.53 | 38.02 | 0.58 | 0.08 | 0.11 | 0.27 |
| QHGC | 100.1 | 37.3 | −2.10 | 37.58 | 0.63 | 0.14 | 0.07 | 0.34 |
| QHGE | 94.8 | 36.1 | 4.53 | 37.16 | 0.20 | 0.14 | 0.13 | 0.65 |
| QHLH | 93.3 | 38.7 | 3.12 | 34.62 | 2.86 | 0.50 | 0.15 | 0.38 |
| QHMD | 98.2 | 34.9 | 0.50 | 45.52 | 1.62 | 0.07 | 0.09 | 0.42 |
| QHME | 101.4 | 37.5 | −3.12 | 37.09 | 1.35 | 0.10 | 0.14 | 0.40 |
| QHMQ | 100.2 | 34.5 | −1.12 | 42.30 | 0.51 | 0.17 | 0.05 | 0.22 |
| QHMY | 90.8 | 38.5 | 7.16 | 35.51 | 1.06 | 0.14 | 0.07 | 0.22 |
| QHQL | 100.2 | 38.2 | −3.13 | 34.70 | 1.67 | 0.15 | 0.34 | 0.30 |
| QION | 109.8 | 19.0 | −10.93 | 31.64 | 0.39 | 0.20 | 0.15 | 0.28 |
| SCBZ | 106.7 | 31.8 | −9.13 | 34.33 | 1.21 | 0.04 | 0.06 | 0.20 |
| SCDF | 101.1 | 31.0 | −12.25 | 43.38 | 1.60 | 0.09 | 0.48 | 0.33 |
| SCGY | 105.9 | 32.4 | −8.33 | 34.56 | 0.58 | 0.19 | 0.79 | 0.38 |
| SCGZ | 100.0 | 31.6 | −9.30 | 47.06 | −0.60 | 0.11 | 0.42 | 0.33 |
| SCJL | 101.5 | 29.0 | −17.82 | 39.77 | 2.03 | 0.10 | 0.06 | 0.52 |
| SCJU | 104.5 | 28.2 | −7.61 | 34.73 | 0.51 | 0.17 | 0.27 | 0.84 |
| SCLH | 100.7 | 31.4 | −11.09 | 46.19 | 1.16 | 0.06 | 0.19 | 0.28 |
| SCMB | 103.5 | 28.8 | −8.99 | 35.25 | 0.22 | 0.13 | 0.21 | 0.32 |
| SCML | 101.3 | 27.9 | −19.49 | 48.87 | −2.91 | 0.07 | 0.24 | 0.39 |
| SCMN | 102.2 | 28.3 | −16.29 | 39.10 | 0.32 | 0.05 | 0.09 | 0.20 |
| SCMX | 103.8 | 31.7 | −6.48 | 45.06 | 9.28 | 0.24 | 0.31 | 0.34 |
| SCNC | 105.9 | 31.0 | −9.58 | 34.82 | 1.28 | 0.10 | 0.19 | 0.12 |
| SCNN | 102.7 | 27.1 | −16.34 | 37.93 | 0.67 | 0.61 | 0.36 | 0.27 |
| SCPZ | 101.7 | 26.5 | −17.80 | 36.01 | 1.06 | 0.09 | 0.08 | 0.15 |
| SCSM | 102.4 | 29.2 | −12.19 | 38.08 | 1.86 | 0.05 | 0.06 | 0.34 |
| SCSN | 105.6 | 30.5 | −8.83 | 34.30 | 1.50 | 0.04 | 0.11 | 0.21 |
| SCSP | 103.6 | 32.6 | −10.03 | 41.08 | 1.43 | 0.14 | 0.15 | 0.34 |
| SCTQ | 102.8 | 30.1 | −9.66 | 35.94 | 2.92 | 0.18 | 0.29 | 0.45 |
| SCXC | 99.8 | 28.9 | −16.99 | 41.52 | 2.82 | 0.05 | 0.12 | 0.34 |
| SCXD | 102.4 | 28.3 | −14.15 | 38.71 | 0.17 | 0.04 | 0.09 | 0.19 |
| SCXJ | 102.4 | 31.0 | −6.05 | 40.86 | 0.30 | 0.35 | 0.24 | 0.19 |
| SCYX | 102.5 | 28.7 | −13.09 | 38.12 | −0.91 | 0.13 | 0.16 | 0.30 |
| SCYY | 101.5 | 27.4 | −17.60 | 38.62 | 0.80 | 0.10 | 0.10 | 0.16 |
| SDCY | 119.5 | 36.8 | −11.46 | 31.38 | 1.84 | 0.11 | 0.07 | 0.47 |
| SDJX | 116.4 | 35.4 | −11.06 | 32.74 | 1.82 | 0.13 | 0.08 | 0.30 |
| SDLY | 118.3 | 35.0 | −12.42 | 31.71 | 2.72 | 0.94 | 0.28 | 0.70 |
| SDQD | 120.3 | 36.1 | −11.34 | 31.78 | 1.24 | 0.05 | 0.05 | 0.19 |
| SDRC | 122.4 | 37.2 | −11.38 | 31.25 | −2.27 | 0.10 | 0.14 | 0.65 |
| SDYT | 121.4 | 37.5 | −10.96 | 30.29 | 0.68 | 0.17 | 0.07 | 0.18 |
| SDZB | 118.0 | 36.8 | −11.28 | 32.24 | 0.92 | 0.27 | 0.17 | 0.42 |
| SHA2 | 121.2 | 31.1 | −11.77 | 31.93 | −1.55 | 0.15 | 0.17 | 0.48 |
| SHAO | 121.2 | 31.1 | −13.32 | 32.16 | −1.91 | 0.25 | 0.24 | 0.27 |
| SNAK | 108.8 | 32.8 | −9.81 | 34.62 | 1.45 | 0.25 | 0.28 | 0.40 |
| SNMX | 106.7 | 33.1 | −10.57 | 35.06 | −1.39 | 0.68 | 0.28 | 0.82 |
| SNTB | 107.3 | 34.1 | −9.60 | 35.28 | 1.06 | 0.06 | 0.10 | 0.43 |
| SNXY | 108.4 | 35.2 | −9.27 | 34.18 | 1.28 | 0.06 | 0.06 | 0.37 |
| SNYA | 109.5 | 36.6 | −10.47 | 32.08 | 2.16 | 0.12 | 0.59 | 0.27 |
| SUIY | 130.9 | 44.4 | −12.49 | 24.52 | −1.14 | 0.11 | 0.18 | 0.40 |
| SXCZ | 113.2 | 36.2 | −9.58 | 30.04 | 1.34 | 0.25 | 0.29 | 0.23 |
| SXGX | 111.9 | 36.3 | −9.69 | 32.54 | 3.02 | 0.36 | 0.10 | 0.61 |
| SXKL | 111.6 | 38.8 | −8.84 | 32.73 | 2.97 | 0.12 | 0.06 | 0.71 |
| SXLF | 111.4 | 36.1 | −10.14 | 33.63 | 1.77 | 0.08 | 0.09 | 0.39 |
| SXLQ | 114.0 | 39.4 | −10.32 | 32.39 | 1.87 | 0.05 | 0.05 | 0.25 |
| SXTY | 112.4 | 37.7 | −9.21 | 33.87 | −0.28 | 0.47 | 0.58 | 0.51 |
| SXXX | 111.2 | 35.1 | −8.69 | 33.03 | 1.38 | 0.44 | 0.14 | 0.47 |
| SXYC | 112.9 | 37.6 | −10.62 | 32.55 | 2.26 | 0.09 | 0.09 | 0.55 |
| TAIN | 117.1 | 36.2 | −11.73 | 30.76 | 0.92 | 0.10 | 0.05 | 0.27 |
| TASH | 75.2 | 37.8 | 23.46 | 25.44 | 1.34 | 0.15 | 0.15 | 0.35 |
| TJBD | 117.4 | 39.7 | −11.65 | 30.62 | 1.11 | 0.20 | 0.04 | 0.29 |
| TJBH | 117.7 | 39.1 | −11.92 | 31.96 | −16.82 | 0.49 | 0.24 | 0.28 |
| URU2 | 87.6 | 43.8 | 5.17 | 30.83 | 1.41 | 0.18 | 0.23 | 0.79 |
| URUM | 87.6 | 43.8 | 6.89 | 32.52 | 1.63 | 0.34 | 0.36 | 0.43 |
| WUHN | 114.4 | 30.5 | −10.73 | 32.28 | 0.03 | 0.28 | 0.20 | 0.51 |
| WUSH | 79.2 | 41.2 | 15.17 | 30.30 | 1.16 | 0.12 | 0.17 | 0.21 |
| XIAA | 109.0 | 34.2 | −6.77 | 30.06 | −5.10 | 0.30 | 0.47 | 0.31 |
| XIAG | 100.3 | 25.6 | −16.68 | 29.96 | 0.67 | 0.14 | 0.25 | 0.33 |
| XIAM | 118.1 | 24.4 | −12.82 | 32.57 | 0.61 | 0.14 | 0.12 | 0.26 |
| XJAL | 88.1 | 47.9 | 3.72 | 28.83 | 0.31 | 0.37 | 0.30 | 1.16 |
| XJBC | 78.8 | 39.8 | 17.37 | 29.21 | 0.49 | 0.11 | 0.10 | 0.21 |
| XJBE | 86.9 | 47.7 | 3.34 | 29.20 | −0.14 | 0.09 | 0.12 | 0.25 |
| XJBL | 75.0 | 38.7 | 21.97 | 24.10 | −0.41 | 0.25 | 0.35 | 0.65 |
| XJBY | 83.7 | 42.8 | 7.75 | 31.59 | 1.08 | 0.15 | 0.26 | 0.33 |
| XJDS | 84.9 | 44.3 | 6.68 | 31.88 | 0.72 | 0.08 | 0.09 | 0.20 |
| XJFY | 89.5 | 47.0 | 3.15 | 29.58 | 0.20 | 0.24 | 0.10 | 0.35 |
| XJHT | 79.0 | 37.2 | 18.38 | 26.28 | 0.31 | 0.22 | 0.12 | 0.24 |
| XJJJ | 94.3 | 42.8 | 0.54 | 32.55 | 1.45 | 0.07 | 0.05 | 0.17 |
| XJKC | 83.0 | 41.7 | 10.92 | 32.23 | −1.12 | 0.09 | 0.10 | 0.24 |
| XJKE | 86.2 | 41.8 | 8.06 | 31.22 | −0.40 | 0.17 | 0.28 | 0.53 |
| XJML | 90.3 | 43.8 | 3.39 | 32.19 | 1.13 | 0.08 | 0.14 | 0.16 |
| XJQH | 91.0 | 46.2 | 2.54 | 31.35 | 0.51 | 0.11 | 0.13 | 0.15 |
| XJQM | 85.5 | 38.1 | 8.63 | 28.83 | −0.10 | 0.32 | 0.19 | 0.20 |
| XJRQ | 88.2 | 39.0 | 6.62 | 29.97 | −0.67 | 0.06 | 0.04 | 0.11 |
| XJSH | 86.1 | 44.2 | 5.00 | 31.66 | 1.49 | 0.07 | 0.07 | 0.22 |
| XJSS | 90.3 | 42.9 | 3.84 | 32.27 | −0.27 | 0.07 | 0.06 | 0.12 |
| XJTC | 82.9 | 46.8 | 2.38 | 28.37 | 0.00 | 0.15 | 0.21 | 0.39 |
| XJTZ | 83.7 | 39.0 | 11.41 | 29.25 | 0.54 | 0.31 | 0.04 | 0.18 |
| XJWL | 86.7 | 42.9 | 6.84 | 32.33 | 1.10 | 0.17 | 0.05 | 0.21 |
| XJWQ | 81.0 | 45.0 | 4.22 | 29.32 | 1.22 | 0.14 | 0.06 | 0.22 |
| XJWU | 75.2 | 39.7 | 14.86 | 28.82 | −0.20 | 0.18 | 0.26 | 0.37 |
| XJXY | 83.3 | 43.4 | 7.17 | 30.65 | 1.99 | 0.05 | 0.05 | 0.40 |
| XJYC | 77.4 | 37.9 | 20.92 | 27.25 | −0.80 | 0.18 | 0.11 | 0.29 |
| XJYT | 82.0 | 36.4 | 13.85 | 25.58 | −0.42 | 0.30 | 0.20 | 0.34 |
| XJZS | 80.4 | 42.7 | 7.99 | 31.48 | 1.70 | 0.09 | 0.16 | 0.14 |
| XNIN | 101.8 | 36.6 | −3.76 | 37.88 | −0.36 | 0.17 | 0.13 | 0.23 |
| XZAR | 87.2 | 29.3 | 21.06 | 40.03 | 3.06 | 0.19 | 0.39 | 0.33 |
| XZCD | 97.2 | 31.1 | −4.74 | 50.20 | 1.93 | 0.11 | 0.15 | 0.71 |
| XZCY | 97.5 | 28.7 | −9.34 | 42.22 | 4.20 | 0.17 | 0.18 | 0.52 |
| XZDX | 91.1 | 30.5 | 13.77 | 47.03 | 2.31 | 0.29 | 0.10 | 0.59 |
| XZGE | 80.1 | 32.5 | 17.96 | 30.82 | 0.99 | 0.08 | 0.10 | 0.30 |
| XZNQ | 92.1 | 31.5 | 9.10 | 50.73 | 0.86 | 0.29 | 0.18 | 0.70 |
| XZRK | 88.9 | 29.2 | 21.54 | 42.39 | 2.27 | 0.18 | 0.16 | 0.32 |
| XZRT | 79.7 | 33.4 | 17.72 | 30.21 | 1.48 | 0.28 | 0.21 | 0.76 |
| XZYD | 88.9 | 27.4 | 29.84 | 39.90 | −0.26 | 0.56 | 0.34 | 0.90 |
| XZZB | 84.2 | 29.7 | 22.35 | 36.60 | 2.00 | 0.60 | 0.26 | 0.68 |
| XZZF | 86.9 | 28.4 | 24.02 | 40.01 | 4.74 | 0.31 | 0.22 | 0.98 |
| YANC | 107.4 | 37.8 | −9.43 | 31.99 | 1.60 | 0.11 | 0.09 | 0.21 |
| YNCX | 101.5 | 25.0 | −16.38 | 31.63 | 1.40 | 0.06 | 0.08 | 0.16 |
| YNDC | 103.2 | 26.1 | −12.33 | 34.99 | 1.82 | 0.12 | 0.09 | 0.50 |
| YNHZ | 103.3 | 26.4 | −11.45 | 34.91 | 3.49 | 0.29 | 0.21 | 0.64 |
| YNJD | 100.9 | 24.4 | −16.11 | 29.06 | 1.91 | 0.54 | 0.49 | 0.43 |
| YNJP | 103.2 | 22.8 | −8.42 | 34.33 | 0.87 | 0.35 | 0.15 | 0.46 |
| YNLA | 100.0 | 22.6 | −9.92 | 28.61 | −0.78 | 0.41 | 0.70 | 0.83 |
| YNLC | 100.1 | 23.9 | −13.21 | 29.85 | 0.34 | 0.17 | 0.71 | 0.22 |
| YNLJ | 100.0 | 26.7 | −18.19 | 32.54 | 1.16 | 0.07 | 0.06 | 0.13 |
| YNMH | 100.5 | 21.9 | −9.93 | 28.26 | 1.05 | 0.76 | 1.01 | 0.57 |
| YNMJ | 101.7 | 23.4 | −14.35 | 31.01 | 1.98 | 0.39 | 0.25 | 0.30 |
| YNML | 103.4 | 24.4 | −9.85 | 35.53 | 1.15 | 2.33 | 0.76 | 0.44 |
| YNMZ | 103.4 | 23.4 | −9.13 | 33.72 | −0.25 | 0.34 | 0.27 | 0.32 |
| YNRL | 97.8 | 24.0 | −7.87 | 23.50 | 1.10 | 0.26 | 0.30 | 0.64 |
| YNSD | 99.2 | 24.7 | −13.70 | 26.88 | 1.85 | 0.09 | 0.08 | 0.33 |
| YNSM | 101.0 | 22.7 | −13.65 | 29.20 | −1.84 | 2.73 | 1.00 | 0.43 |
| YNTC | 98.4 | 25.0 | −10.34 | 24.65 | 1.95 | 0.09 | 0.43 | 0.31 |
| YNTH | 102.8 | 24.1 | −13.11 | 33.04 | 2.40 | 0.13 | 0.19 | 0.21 |
| YNWS | 104.2 | 23.4 | −10.57 | 32.14 | 3.82 | 0.87 | 0.89 | 0.18 |
| YNYA | 101.3 | 25.7 | −16.45 | 33.30 | 2.15 | 0.04 | 0.10 | 0.15 |
| YNYM | 101.9 | 25.7 | −16.97 | 33.83 | 1.72 | 0.27 | 0.13 | 0.18 |
| YNYS | 100.8 | 26.7 | −16.97 | 35.98 | 1.95 | 0.08 | 0.17 | 0.17 |
| YNZD | 99.7 | 27.8 | −20.66 | 34.02 | −1.76 | 0.13 | 0.18 | 0.38 |
| YONG | 112.3 | 16.8 | −10.80 | 29.73 | 0.76 | 0.40 | 0.40 | 0.95 |
| ZHNZ | 113.1 | 34.5 | −11.40 | 32.76 | 2.42 | 0.06 | 0.13 | 0.33 |
| ZJJD | 119.3 | 29.5 | −11.71 | 33.07 | 0.56 | 0.07 | 0.10 | 0.75 |
| ZJWZ | 120.8 | 27.9 | −11.67 | 32.37 | 0.10 | 0.07 | 0.13 | 0.38 |
| ZJZS | 122.0 | 30.1 | −11.29 | 32.32 | 0.05 | 0.11 | 0.11 | 0.27 |
References
- Kreemer, C.; Blewitt, G.; Klein, E.C. A Geodetic Plate Motion and Global Strain Rate Model. Geochem. Geophys. Geosyst. 2014, 15, 3849–3889. [Google Scholar] [CrossRef]
- Zhang, P.; Shen, Z.; Wang, M.; Gan, W.; Bürgmann, R.; Molnar, P.; Wang, Q.; Niu, Z.; Sun, J.; Wu, J.; et al. Continuous deformation of the Tibetan Plateau from global positioning system data. Geology 2004, 32, 809–812. [Google Scholar] [CrossRef]
- Liang, S.; Gan, W.; Shen, C.; Xiao, G.; Liu, J.; Chen, W.; Ding, X.; Zhou, D. Three-dimensional velocity field of present-day crustal motion of the Tibetan Plateau derived from GPS measurements. J. Geophys. Res. Solid Earth 2013, 118, JB010503. [Google Scholar] [CrossRef]
- Liu, R.; Zou, R.; Li, J.; Zhang, C.; Zhao, B.; Zhang, Y. Vertical Displacements Driven by Groundwater Storage Changes in the North China Plain Detected by GPS Observations. Remote Sens. 2018, 10, 259. [Google Scholar] [CrossRef]
- Wang, M.; Shen, Z.-K.; Dong, D.-N. Effects of non-tectonic crustal deformation on continuous GPS position time series and correction to them. Diqiu Wuli Xuebao Chin. J. Geophys. 2005, 48, 1045–1052. [Google Scholar]
- Zhu, Z.; Zhou, X.; Deng, L.; Wang, K.; Zhou, B. Quantitative analysis of geophysical sources of common mode component in CMONOC GPS coordinate time series. Adv. Space Res. 2017, 60, 2896–2909. [Google Scholar] [CrossRef]
- Yuan, P.; Li, Z.; Jiang, W.; Ma, Y.; Chen, W.; Sneeuw, N. Influences of Environmental Loading Corrections on the Nonlinear Variations and Velocity Uncertainties for the Reprocessed Global Positioning System Height Time Series of the Crustal Movement Observation Network of China. Remote Sens. 2018, 10, 958. [Google Scholar] [CrossRef]
- Jiang, W.; Yuan, P.; Chen, H.; Cai, J.; Li, Z.; Chao, N.; Sneeuw, N. Annual variations of monsoon and drought detected by GPS: A case study in Yunnan, China. Sci. Rep. 2017, 7, 5874. [Google Scholar] [CrossRef] [PubMed]
- Blewitt, G.; Lavallee, D. Effect of annual signals on geodetic velocity. J. Geophys. Res. Solid Earth 2002, 107, B7. [Google Scholar] [CrossRef]
- Ray, J.; Altamimi, Z.; Collilieux, X.; van Dam, T. Anomalous harmonics in the spectra of GPS position estimates. GPS Solut. 2007, 12, 55–64. [Google Scholar] [CrossRef]
- Penna, N.T.; King, M.A.; Stewart, M.P. GPS height time series: Short-period origins of spurious long-period signals. J. Geophys. Res. 2007, 112, B02402. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.R.; Mohammadloo, T.H.; Argus, D.F. Multivariate analysis of GPS position time series of JPL second reprocessing campaign. J. Geodesy 2017, 91, 685–704. [Google Scholar] [CrossRef]
- Tregoning, P.; Watson, C. Atmospheric effects and spurious signals in GPS analyses. J. Geophys. Res. 2009, 114, B09403. [Google Scholar] [CrossRef]
- Rodriguez-Solano, C.J.; Hugentobler, U.; Steigenberger, P.; Lutz, S. Impact of Earth radiation pressure on GPS position estimates. J. Geodesy 2012, 86, 309–317. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, W.; Ding, W.; Deng, L.; Peng, L. Estimates of Minor Ocean Tide Loading Displacement and Its Impact on Continuous GPS Coordinate Time Series. Sensors 2014, 14, 5552–5572. [Google Scholar] [CrossRef] [PubMed]
- King, M.A.; Watson, C.S. Long GPS coordinate time series: Multipath and geometry effects. J. Geophys. Res. 2010, 115, B04403. [Google Scholar] [CrossRef]
- Abraha, K.E.; Teferle, F.N.; Hunegnaw, A.; Dach, R. GNSS related periodic signals in coordinate time-series from Precise Point Positioning. Geophys. J. Int. 2017, 208, 1449–1464. [Google Scholar] [CrossRef]
- Zhang, J.; Bock, Y.; Johnson, H.; Fang, P.; Williams, S.; Genrich, J.; Wdowinski, S.; Behr, J. Southern California permanent GPS geodetic array: Error analysis of daily position estimates and site velocities. J. Geophys. Res. 1997, 102, 18035–18055. [Google Scholar] [CrossRef]
- Mao, A.; Harrison, C.G.A.; Dixon, T.H. Noise in GPS coordinate time series. J. Geophys. Res. 1999, 104, 2797–2816. [Google Scholar] [CrossRef]
- Williams, S.D.P.; Bock, Y.; Fang, P.; Jamason, P.; Nikolaidis, R.M.; Prawirodirdjo, L.; Miller, M.; Johnson, D.J. Error analysis of continuous GPS position time series. J. Geophys. Res. 2004, 109, B03412. [Google Scholar] [CrossRef]
- Langbein, J. Estimating rate uncertainty with maximum likelihood: Differences between power-law and flicker-random-walk models. J. Geodesy 2012, 86, 775–783. [Google Scholar] [CrossRef]
- Bos, M.S.; Fernandes, R.M.S.; Williams, S.D.P.; Bastos, L. Fast error analysis of continuous GNSS observations with missing data. J. Geodesy 2012, 87, 351–360. [Google Scholar] [CrossRef]
- Wdowinski, S.; Bock, Y.; Zhang, J.; Fang, P.; Genrich, J. Southern California permanent GPS geodetic array: Spatial filtering of daily positions for estimating coseismic and postseismic displacements induced by the 1992 Landers earthquake. J. Geophys. Res. Solid Earth 1997, 102, 18057–18070. [Google Scholar] [CrossRef]
- Johansson, J.M.; Davis, J.L.; Scherneck, H.-G.; Milne, G.A.; Vermeer, M.; Mitrovica, J.X.; Bennett, R.A.; Jonsson, B.; Elgered, G.; Elósegui, P.; et al. Continuous GPS measurements of postglacial adjustment in Fennoscandia 1. Geodetic results. J. Geophys. Res. 2002, 107, ETG 3. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Webb, F.; Prawirodirdjo, L.; Kedar, S.; Jamason, P. Spatiotemporal filtering using principal component analysis and Karhunen-Loeve expansion approaches for regional GPS network analysis. J. Geophys. Res. 2006, 111, B03405. [Google Scholar] [CrossRef]
- Nikolaidis, R. Observation of Geodetic and Seismic Deformation with the Global Positioning System. Ph.D. Thesis, University of California, San Diego, CA, USA, 2002. [Google Scholar]
- Smith, K.D.; von Seggern, D.; Blewitt, G.; Preston, L.; Anderson, J.G.; Wernicke, B.P.; Davis, J.L. Evidence for Deep Magma Injection Beneath Lake Tahoe, Nevada-California. Science 2004, 305, 1277–1280. [Google Scholar] [CrossRef] [PubMed]
- Wdowinski, S.; Bock, Y.; Baer, G.; Prawirodirdjo, L.; Bechor, N.; Naaman, S.; Knafo, R.; Forrai, Y.; Melzer, Y. GPS measurements of current crustal movements along the Dead Sea Fault. J. Geophys. Res. Solid Earth 2004, 109, B05403. [Google Scholar] [CrossRef]
- Márquez-Azúa, B.; DeMets, C. Crustal velocity field of Mexico from continuous GPS measurements, 1993 to June 2001: Implications for the neotectonics of Mexico. J. Geophys. Res. 2003, 108, 2450. [Google Scholar] [CrossRef]
- Tian, Y.; Shen, Z.-K. Extracting the regional common-mode component of GPS station position time series from dense continuous network. J. Geophys. Res. Solid Earth 2016, 121, JB012253. [Google Scholar] [CrossRef]
- Serpelloni, E.; Faccenna, C.; Spada, G.; Dong, D.; Williams, S.D.P. Vertical GPS ground motion rates in the Euro-Mediterranean region: New evidence of velocity gradients at different spatial scales along the Nubia-Eurasia plate boundary. J. Geophys. Res. Solid Earth 2013, 118, JB010102. [Google Scholar] [CrossRef]
- Shen, Y.; Li, W.; Xu, G.; Li, B. Spatiotemporal filtering of regional GNSS network’s position time series with missing data using principle component analysis. J. Geodesy 2014, 88, 1–12. [Google Scholar] [CrossRef]
- Ming, F.; Yang, Y.; Zeng, A.; Zhao, B. Spatiotemporal filtering for regional GPS network in China using independent component analysis. J. Geodesy 2017, 91, 419–440. [Google Scholar] [CrossRef]
- Teferle, F.N.; Williams, S.D.P.; Kierulf, H.P.; Bingley, R.M.; Plag, H.-P. A continuous GPS coordinate time series analysis strategy for high-accuracy vertical land movements. Phys. Chem Earth Parts A/B/C 2008, 33, 205–216. [Google Scholar] [CrossRef]
- Bogusz, J.; Klos, A. On the significance of periodic signals in noise analysis of GPS station coordinates time series. GPS Solut. 2016, 20, 655–664. [Google Scholar] [CrossRef]
- Klos, A.; Olivares, G.; Teferle, F.N.; Hunegnaw, A.; Bogusz, J. On the combined effect of periodic signals and colored noise on velocity uncertainties. GPS Solut. 2018, 22, 1. [Google Scholar] [CrossRef]
- Teferle, F.N.; Bingley, R.M.; Orliac, E.J.; Williams, S.D.P.; Woodworth, P.L.; McLaughlin, D.; Baker, T.F.; Shennan, I.; Milne, G.A.; Bradley, S.L.; et al. Crustal motions in Great Britain: Evidence from continuous GPS, absolute gravity and Holocene sea level data. Geophys. J. Int. 2009, 178, 23–46. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, P.-Z.; Freymueller, J.T.; Bilham, R.; Larson, K.M.; Lai, X.; You, X.; Niu, Z.; Wu, J.; Li, Y.; et al. Present-Day Crustal Deformation in China Constrained by Global Positioning System Measurements. Science 2001, 294, 574–577. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Shi, C.; Xu, C.; Jiang, W. Present day crustal movement speed field of China continent block using local repeated GPS network. Geomat. Inf. Sci. Wuhan Univ. 2001, 26, 189–195. [Google Scholar]
- Shen, Z.-K.; Lü, J.; Wang, M.; Bürgmann, R. Contemporary crustal deformation around the southeast borderland of the Tibetan Plateau. J. Geophys. Res. 2005, 110, B11409. [Google Scholar] [CrossRef]
- Zhao, B.; Huang, Y.; Zhang, C.; Wang, W.; Tan, K.; Du, R. Crustal deformation on the Chinese mainland during 1998–2014 based on GPS data. Geodesy Geodyn. 2015, 6, 7–15. [Google Scholar] [CrossRef]
- Wang, W.; Qiao, X.; Yang, S.; Wang, D. Present-day velocity field and block kinematics of Tibetan Plateau from GPS measurements. Geophys. J. Int. 2017, 208, 1088–1102. [Google Scholar] [CrossRef]
- Zheng, G.; Wang, H.; Wright, T.J.; Lou, Y.; Zhang, R.; Zhang, W.; Shi, C.; Huang, J.; Wei, N. Crustal Deformation in the India-Eurasia Collision Zone From 25 Years of GPS Measurements. J. Geophys. Res. Solid Earth 2017, 122, 9290–9312. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; McClusky, S.C. Introduction to GAMIT/GLOBK; Massachusetts Institute of Technology: Cambridge, MA, USA, 2013. [Google Scholar]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. Solid Earth 2006, 111, B02406. [Google Scholar] [CrossRef]
- Simmons, A.J.; Gibson, J. The ERA-40 Project Plan; European Centre for Medium-Range Weather Forecasts: Reading, UK, 2000. [Google Scholar]
- Finlay, C.C.; Maus, S.; Beggan, C.D.; Bondar, T.N.; Chambodut, A.; Chernova, T.A.; Chulliat, A.; Golovkov, V.P.; Hamilton, B.; Hamoudi, M.; et al. International Geomagnetic Reference Field: The eleventh generation. Geophys. J. Int. 2010, 183, 1216–1230. [Google Scholar] [CrossRef]
- Schaer, S. Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System; Institut für Geodäsie und Photogrammetrie, Technische Hochschule Zürich: Zürich, Switzerland, 1999; Volume 59. [Google Scholar]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Rebischung, P. IGSMAIL-6663. IGb08: An Update on IGS08. 2012. Available online: https://lists.igs.org/pipermail/igsmail/2012/000497.html (accessed on 11 September 2018).
- Dziewonski, A.; Chou, T.-A.; Woodhouse, J. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J. Geophys. Res. Solid Earth 1981, 86, 2825–2852. [Google Scholar] [CrossRef]
- Ekström, G.; Nettles, M.; Dziewoński, A. The global CMT project 2004–2010: Centroid-moment tensors for 13,017 earthquakes. Phys. Earth Planet. Inter. 2012, 200, 1–9. [Google Scholar] [CrossRef]
- Bevis, M.; Brown, A. Trajectory models and reference frames for crustal motion geodesy. J. Geodesy 2014, 88, 283–311. [Google Scholar] [CrossRef]
- Ozawa, S.; Nishimura, T.; Suito, H.; Kobayashi, T.; Tobita, M.; Imakiire, T. Coseismic and postseismic slip of the 2011 magnitude-9 Tohoku-Oki earthquake. Nature 2011, 475, 373–376. [Google Scholar] [CrossRef] [PubMed]
- Lasserre, C.; Peltzer, G.; Crampé, F.; Klinger, Y.; der Woerd, J.V.; Tapponnier, P. Coseismic deformation of the 2001 Mw = 7.8 Kokoxili earthquake in Tibet, measured by synthetic aperture radar interferometry. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Langbein, J.; Bock, Y. High-rate real-time GPS network at Parkfield: Utility for detecting fault slip and seismic displacements. Geophys. Res. Lett. 2004, 31, L15S20. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, B.; Wang, Q.; Yang, S. Noise analysis of continuous GPS coordinate time series for CMONOC. Adv. Space Res. 2012, 49, 943–956. [Google Scholar] [CrossRef]
- Lomb, N.R. Least-squares frequency analysis of unequally spaced data. Astrophys. Space Sci. 1976, 39, 447–462. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in astronomical time series analysis. II—Statistical aspects of spectral analysis of unevenly spaced data. Astrophys. J. 1982, 263, 835–853. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in Fortran 77: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 1992; ISBN 978-0-521-43064-7. [Google Scholar]
- Godin, G. The Analysis of Tides, 1st ed.; University of Toronto Press: Toronto, ON, Canada; Buffalo, NY, USA, 1972; ISBN 978-0-8020-1747-5. [Google Scholar]
- Penna, N.T.; Stewart, M.P. Aliased tidal signatures in continuous GPS height time series. Geophys. Res. Lett. 2003, 30, 2184. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.R. On the nature of GPS draconitic year periodic pattern in multivariate position time series. J. Geophys. Res. Solid Earth 2013, 118, 2500–2511. [Google Scholar] [CrossRef]
- Klos, A.; Bogusz, J.; Figurski, M.; Gruszczynski, M. Error analysis for European IGS stations. Stud. Geophys. Geod. 2016, 60, 17–34. [Google Scholar] [CrossRef]
- Zhang, P.; Deng, Q.; Zhang, G.; Ma, J.; Gan, W.; Min, W.; Mao, F.; Wang, Q. Active tectonic blocks and strong earthquakes in the continent of China. Sci. China Ser. D Earth Sci. 2003, 46, 13–24. [Google Scholar] [CrossRef]
- Dill, R.; Dobslaw, H. Numerical simulations of global-scale high-resolution hydrological crustal deformations. J. Geophys. Res. Solid Earth 2013, 118, 5008–5017. [Google Scholar] [CrossRef]

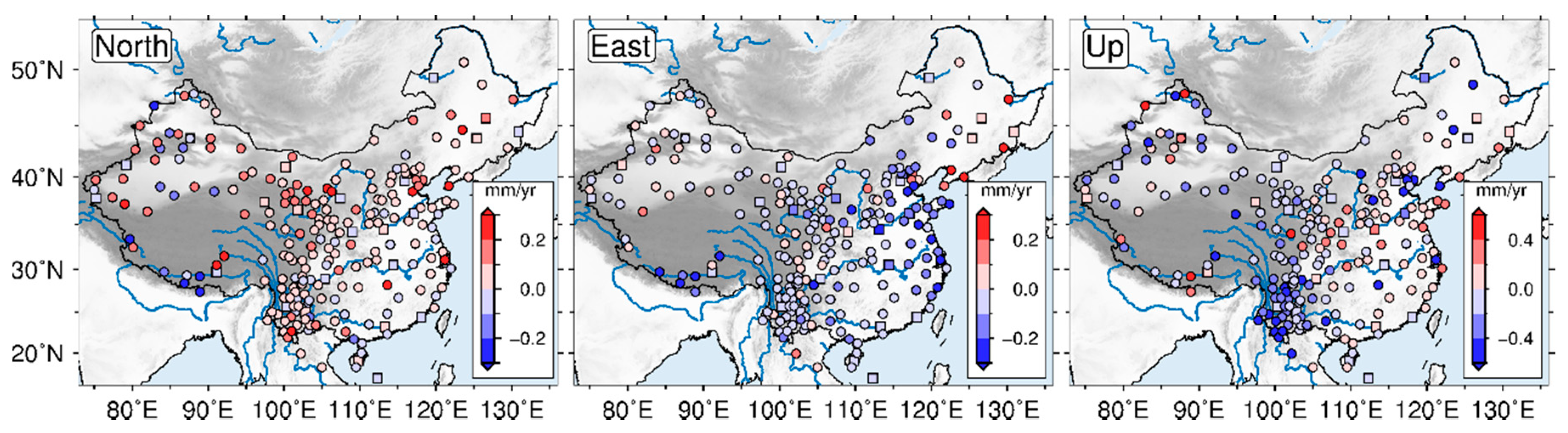

| Unfiltered Time Series | Filtered Time Series | |||||
|---|---|---|---|---|---|---|
| N | E | U | N | E | U | |
| (mm) | 1.0 ± 0.3 | 1.1 ± 0.5 | 2.0 ± 2.0 | 0.9 ± 0.3 | 1.0 ± 0.5 | 2.7 ± 1.7 |
| (mm/year−κ/4) | 4.2 ± 0.9 | 4.1 ± 1.1 | 14.9 ± 3.1 | 3.1 ± 1.2 | 3.4 ± 1.5 | 11.1 ± 4.2 |
| −1.2 ± 0.1 | −1.3 ± 0.2 | −0.9 ± 0.1 | −1.3 ± 0.2 | −1.3 ± 0.2 | −1.0 ± 0.2 | |
| (mm/year) | 0.2 ± 0.1 | 0.2 ± 0.1 | 0.4 ± 0.2 | 0.2 ± 0.1 | 0.2 ± 0.2 | 0.3 ± 0.2 |
| RMS (mm) | 2.4 ± 1.2 | 2.6 ± 1.3 | 6.6 ± 2.3 | 2.1 ± 1.3 | 2.3 ± 1.6 | 5.7 ± 2.7 |
| Unfiltered Time Series | Filtered Time Series | |||||
|---|---|---|---|---|---|---|
| N | E | U | N | E | U | |
| (mm) | 0.7 ± 0.3 | 0.9 ± 0.4 | 1.3 ± 1.4 | 0.6 ± 0.3 | 0.7 ± 0.4 | 1.9 ± 1.2 |
| (mm/year−κ/4) | 3.4 ± 0.7 | 3.3 ± 0.8 | 12.5 ± 1.6 | 1.9 ± 0.9 | 1.9 ± 1.0 | 6.1 ± 2.0 |
| −0.9 ± 0.2 | −1.0 ± 0.2 | −0.9 ± 0.1 | −1.0 ± 0.4 | −1.0 ± 0.4 | −0.7 ± 0.3 | |
| (mm/year) | 0.3 ± 0.2 | 0.3 ± 0.2 | 0.9 ± 0.3 | 0.2 ± 0.3 | 0.2 ± 0.2 | 0.4 ± 0.3 |
| RMS (mm) | 1.5 ± 0.4 | 1.6 ± 0.5 | 5.0 ± 0.9 | 1.1 ± 0.6 | 1.1 ± 0.6 | 3.6 ± 1.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, P.; Jiang, W.; Wang, K.; Sneeuw, N. Effects of Spatiotemporal Filtering on the Periodic Signals and Noise in the GPS Position Time Series of the Crustal Movement Observation Network of China. Remote Sens. 2018, 10, 1472. https://doi.org/10.3390/rs10091472
Yuan P, Jiang W, Wang K, Sneeuw N. Effects of Spatiotemporal Filtering on the Periodic Signals and Noise in the GPS Position Time Series of the Crustal Movement Observation Network of China. Remote Sensing. 2018; 10(9):1472. https://doi.org/10.3390/rs10091472
Chicago/Turabian StyleYuan, Peng, Weiping Jiang, Kaihua Wang, and Nico Sneeuw. 2018. "Effects of Spatiotemporal Filtering on the Periodic Signals and Noise in the GPS Position Time Series of the Crustal Movement Observation Network of China" Remote Sensing 10, no. 9: 1472. https://doi.org/10.3390/rs10091472
APA StyleYuan, P., Jiang, W., Wang, K., & Sneeuw, N. (2018). Effects of Spatiotemporal Filtering on the Periodic Signals and Noise in the GPS Position Time Series of the Crustal Movement Observation Network of China. Remote Sensing, 10(9), 1472. https://doi.org/10.3390/rs10091472