Drought and Flood Monitoring of the Liao River Basin in Northeast China Using Extended GRACE Data
Abstract
1. Introduction
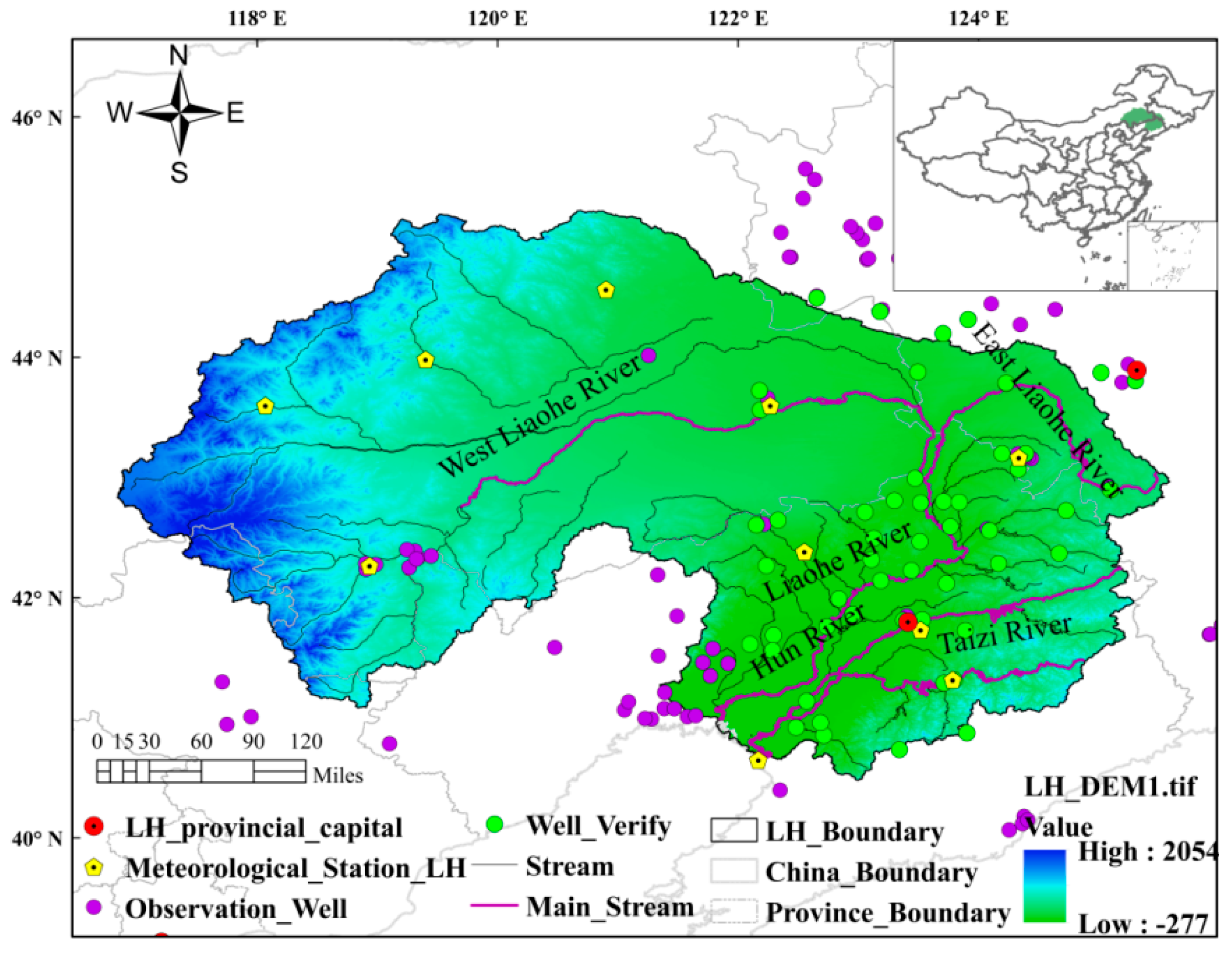
2. Study Area
3. Materials and Methods
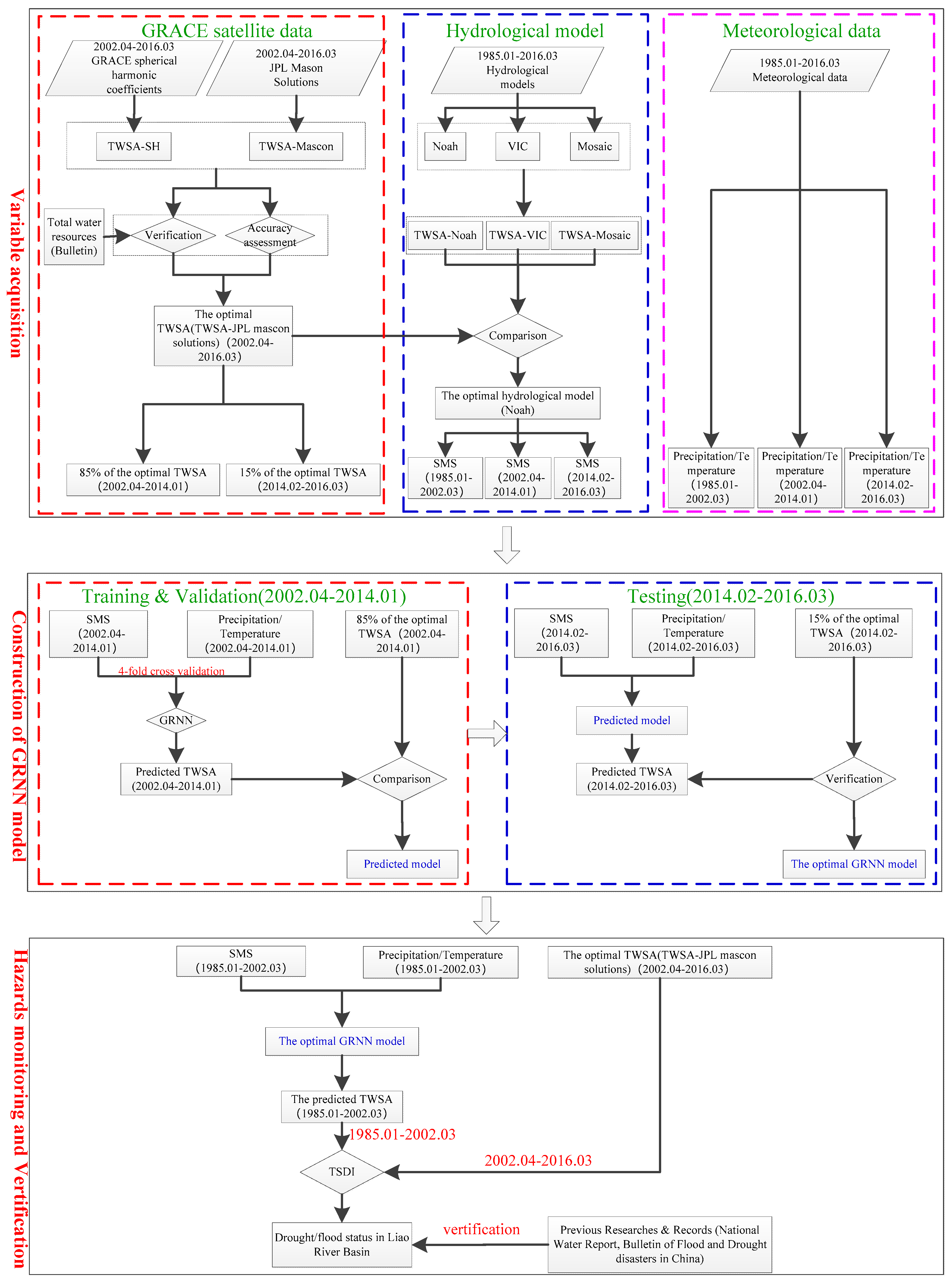
3.1. Data and Processing
3.1.1. GRACE Data
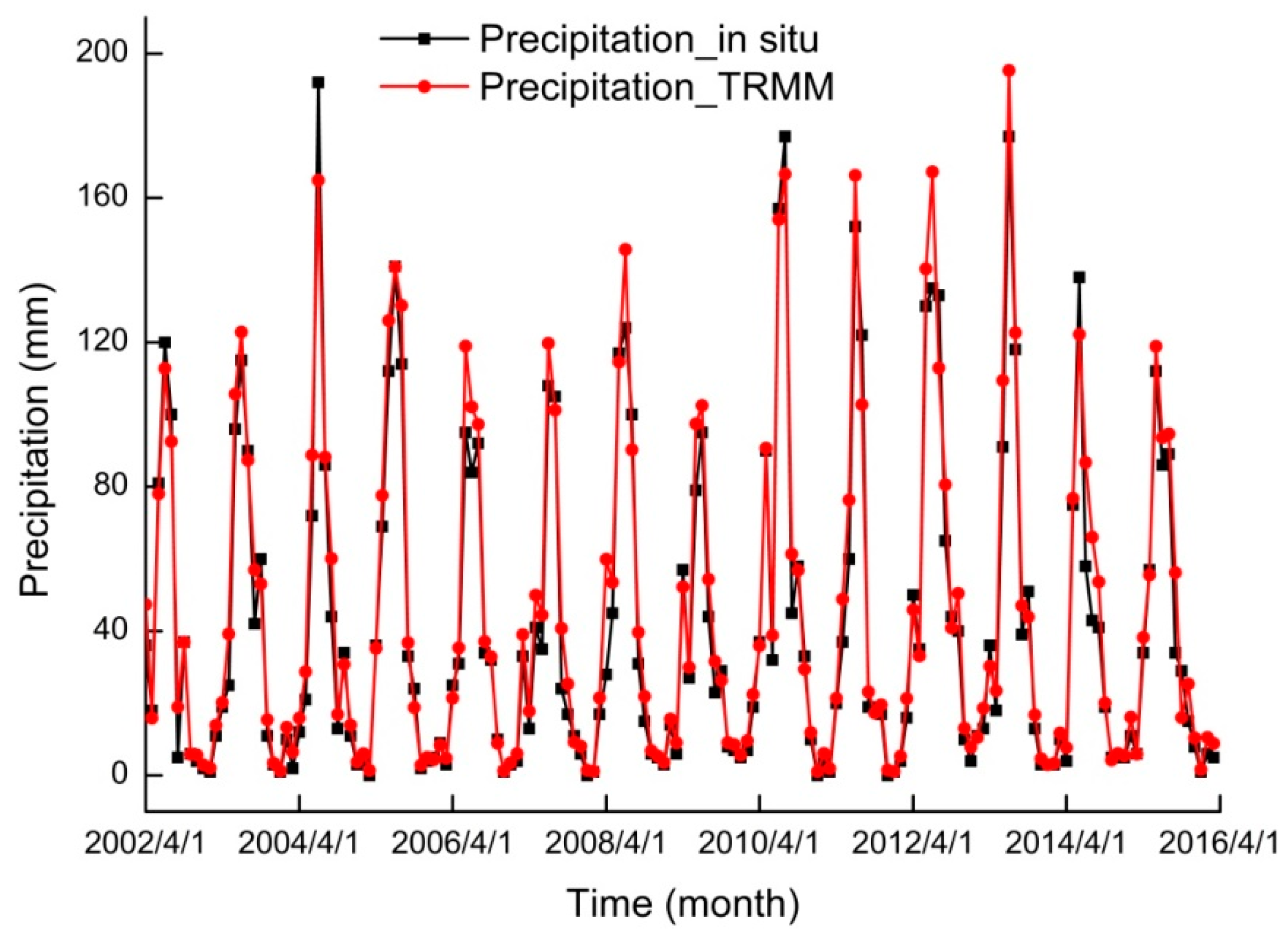
3.1.2. Hydro-Meteorological Data
3.1.3. Hydrological Model Data
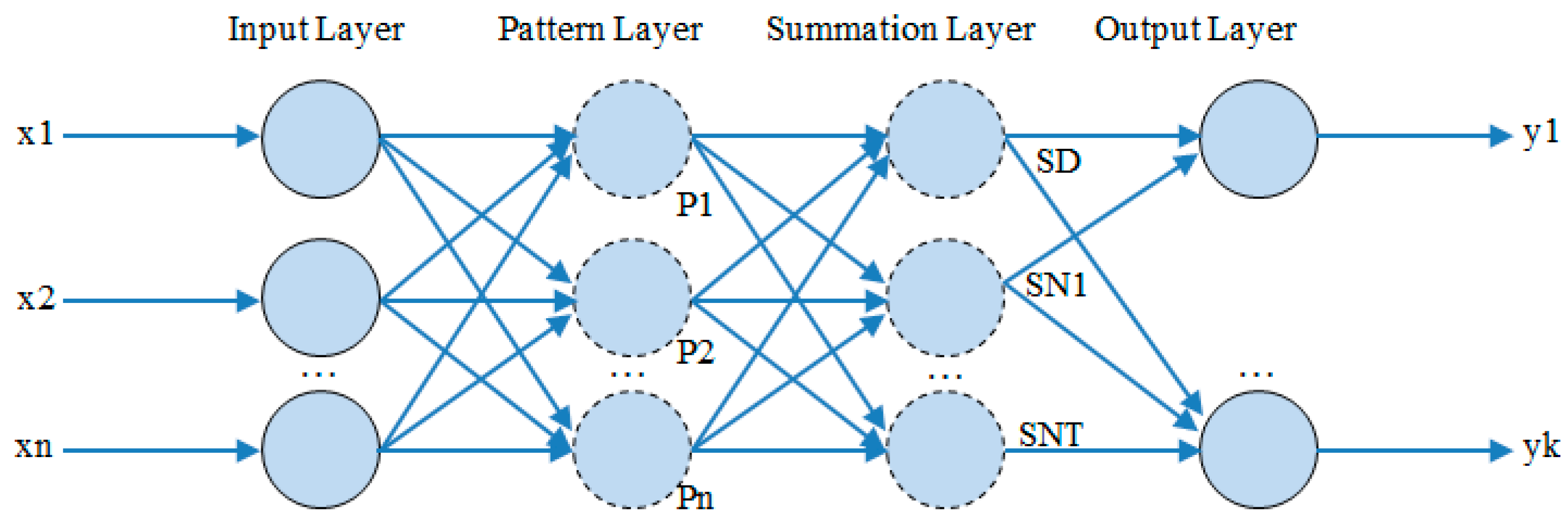
3.2. GRNN Model
3.3. Total Storage Deficit Index (TSDI)
4. Results
4.1. Evaluation of the GRACE TWSAs
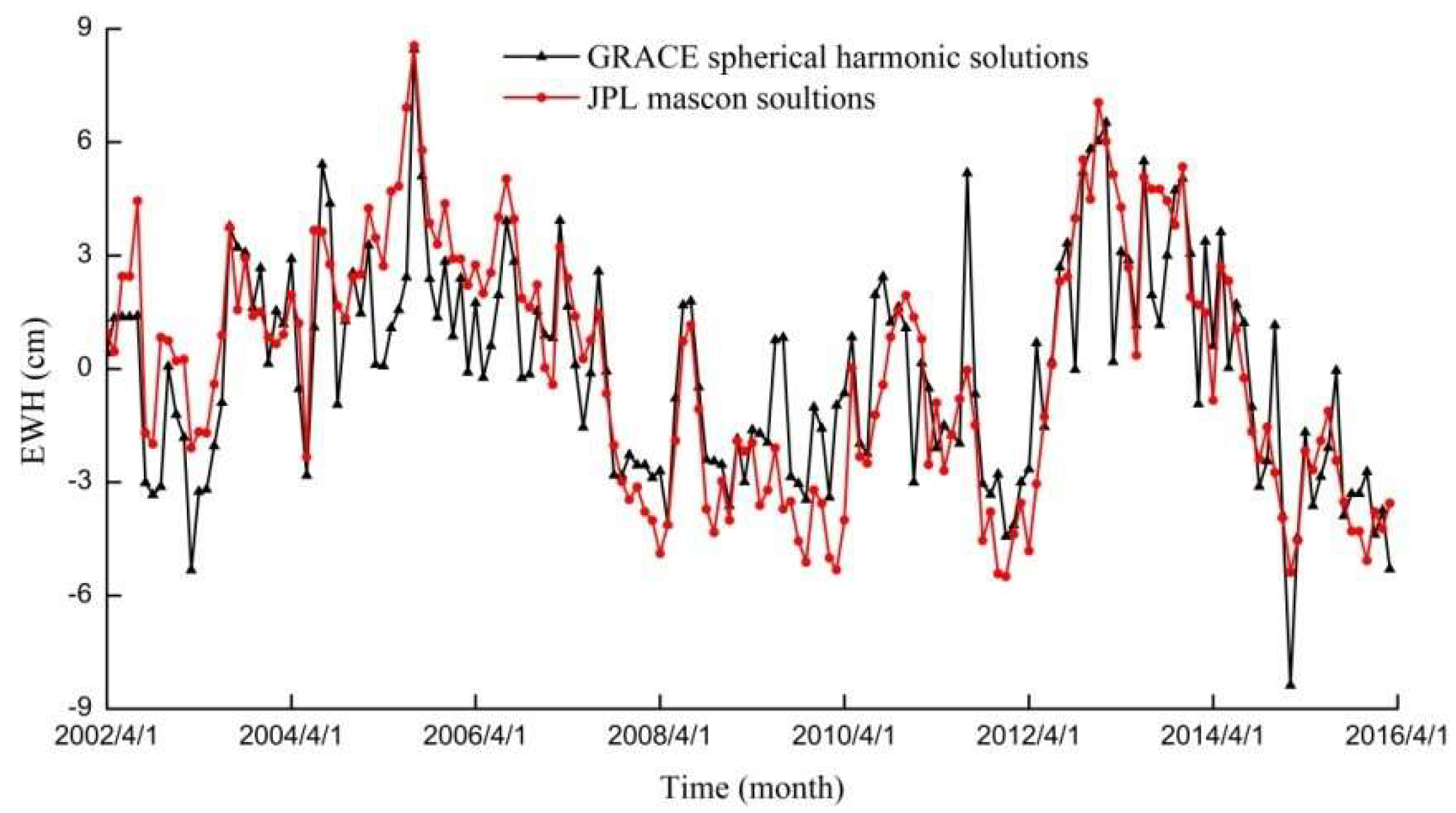
4.1.1. Comparison between GRACE Spherical Harmonic Solutions and JPL Mascon Solutions
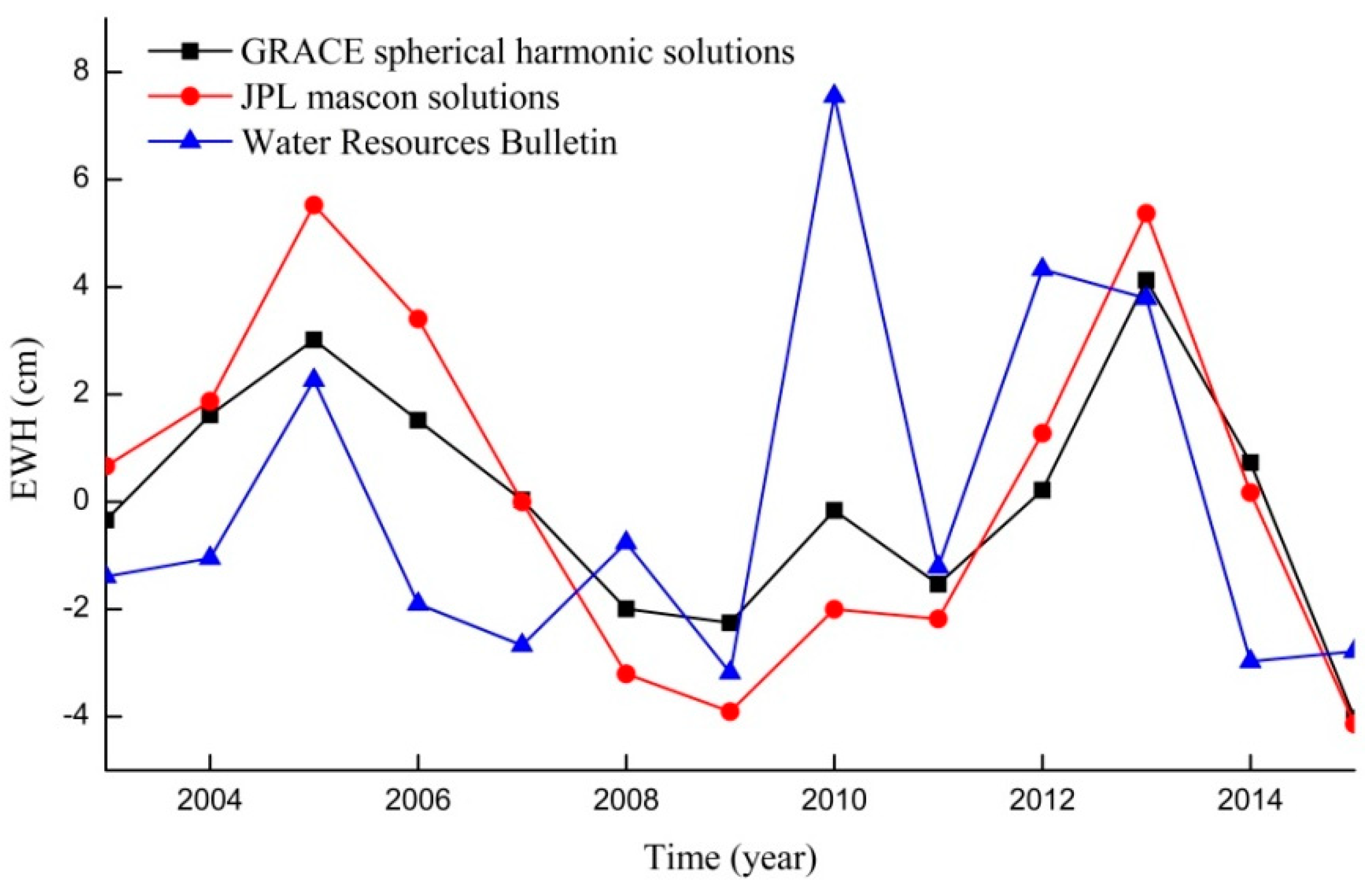
4.1.2. Comparison between the Two Solutions and the Statistical Bulletin Data
4.1.3. Error Estimation
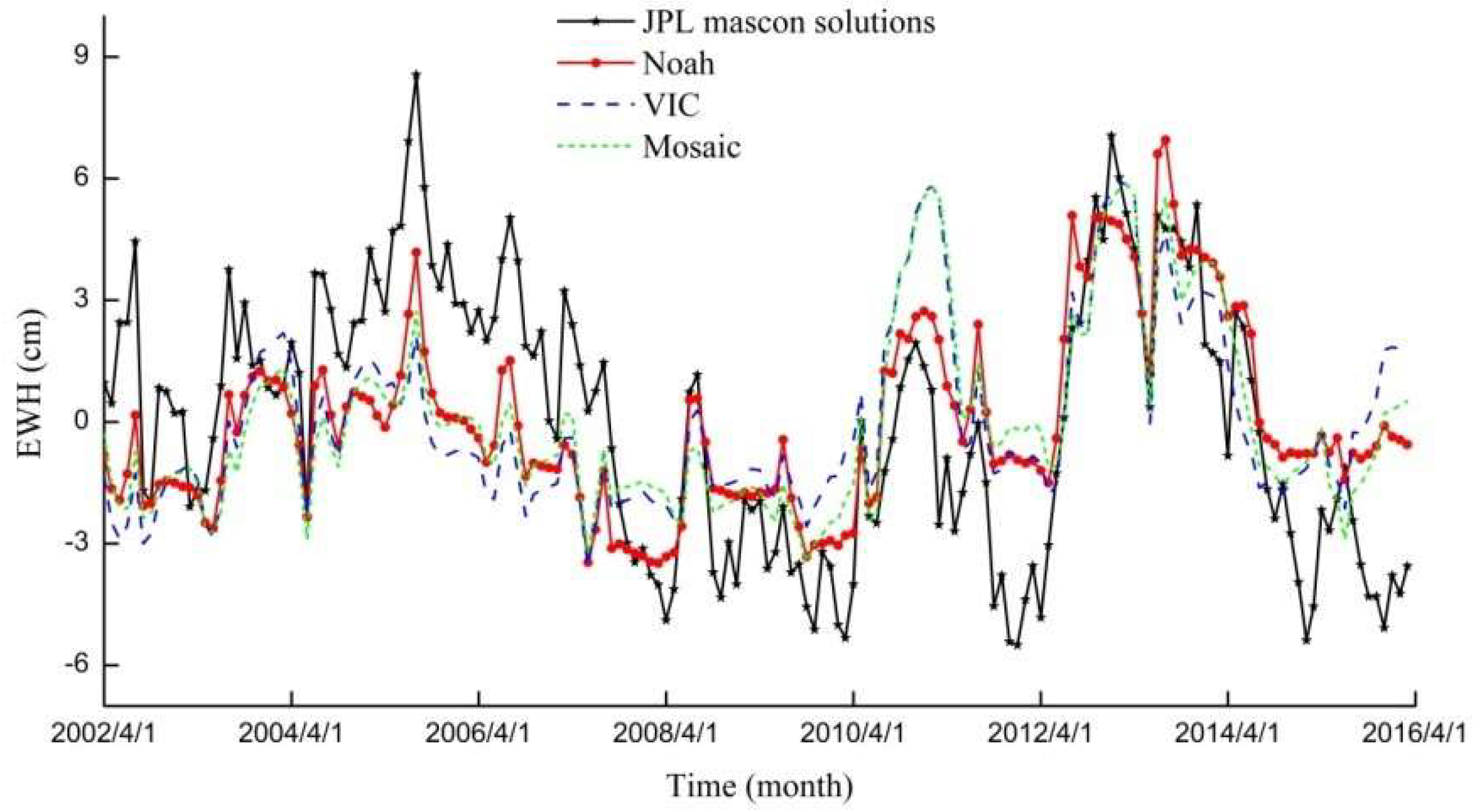
4.2. Selection of the Optimal Hydrological Model
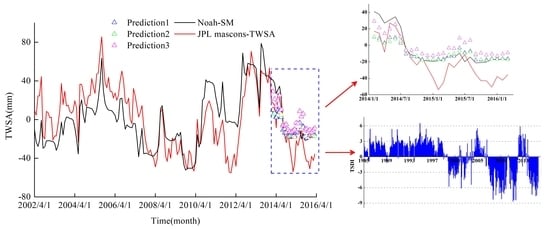
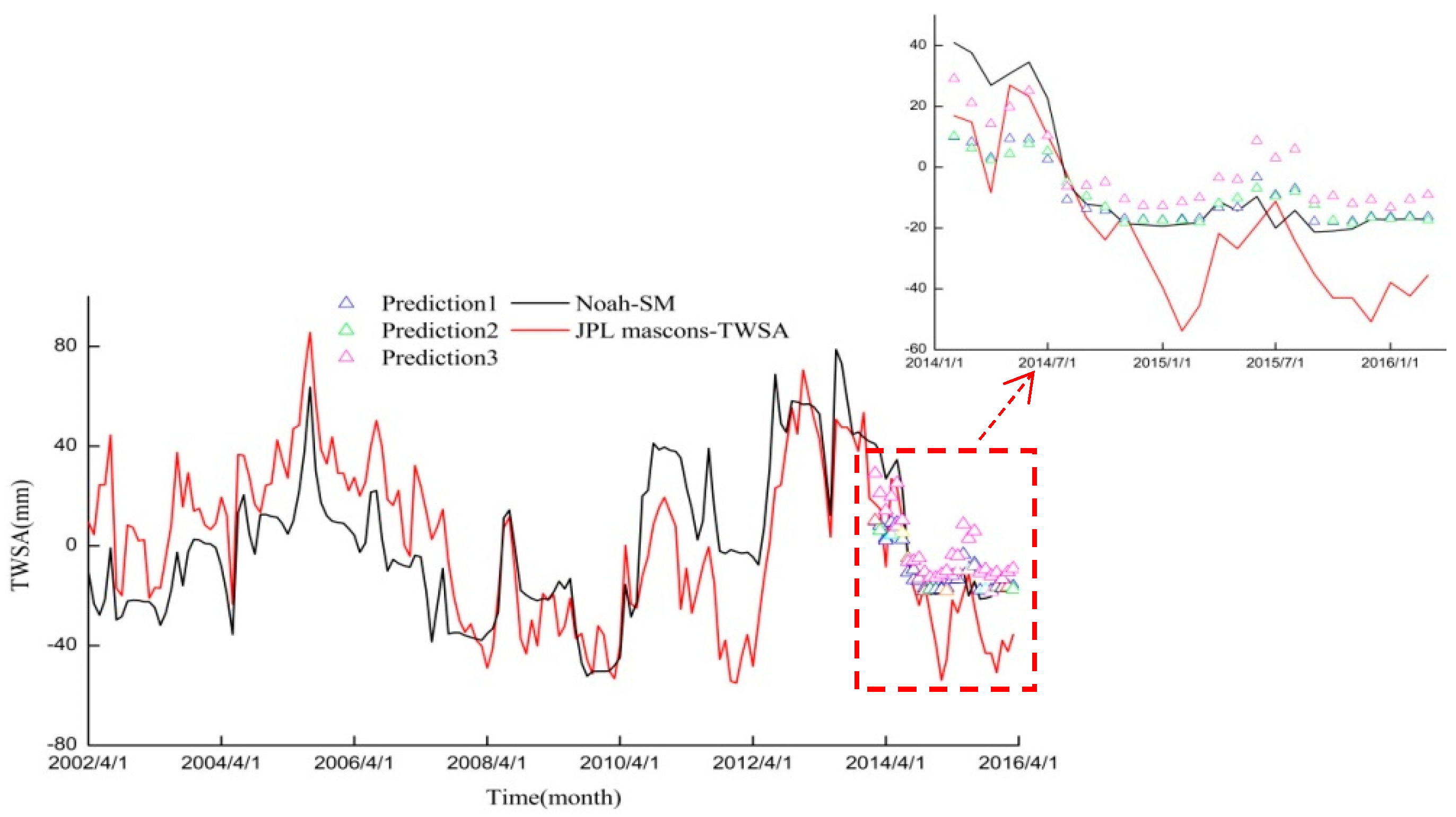
4.3. Evaluation of the TWSAs Predicted by the GRNN Models
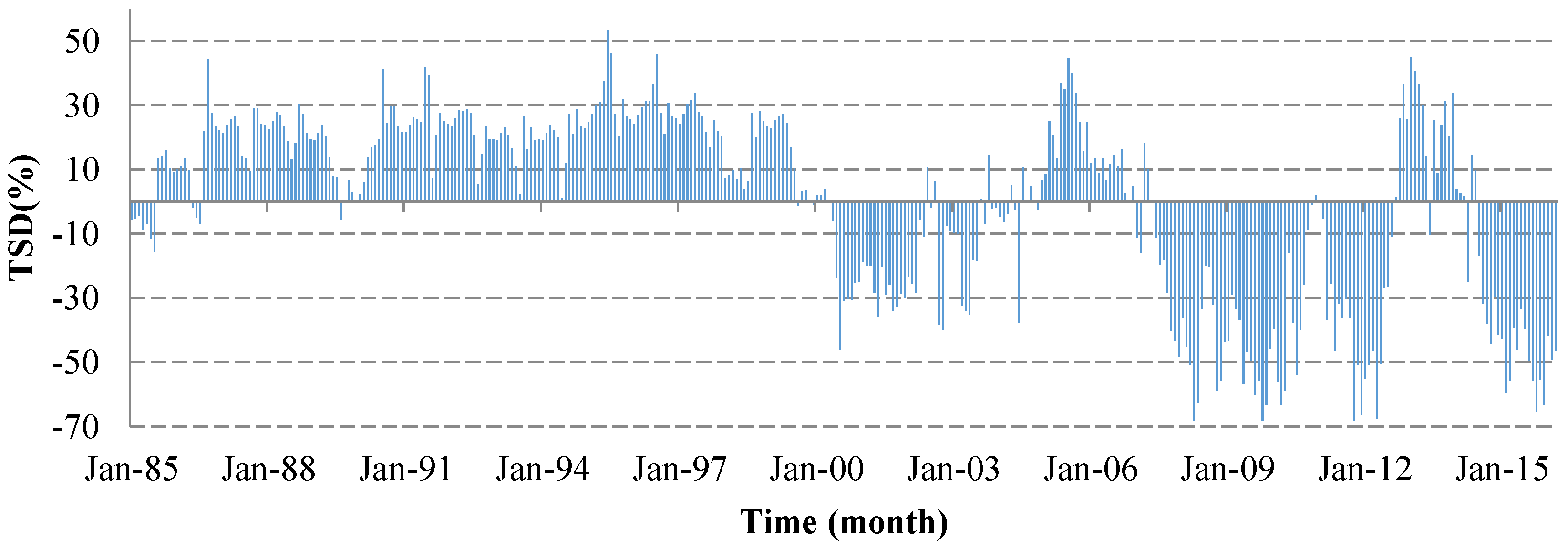
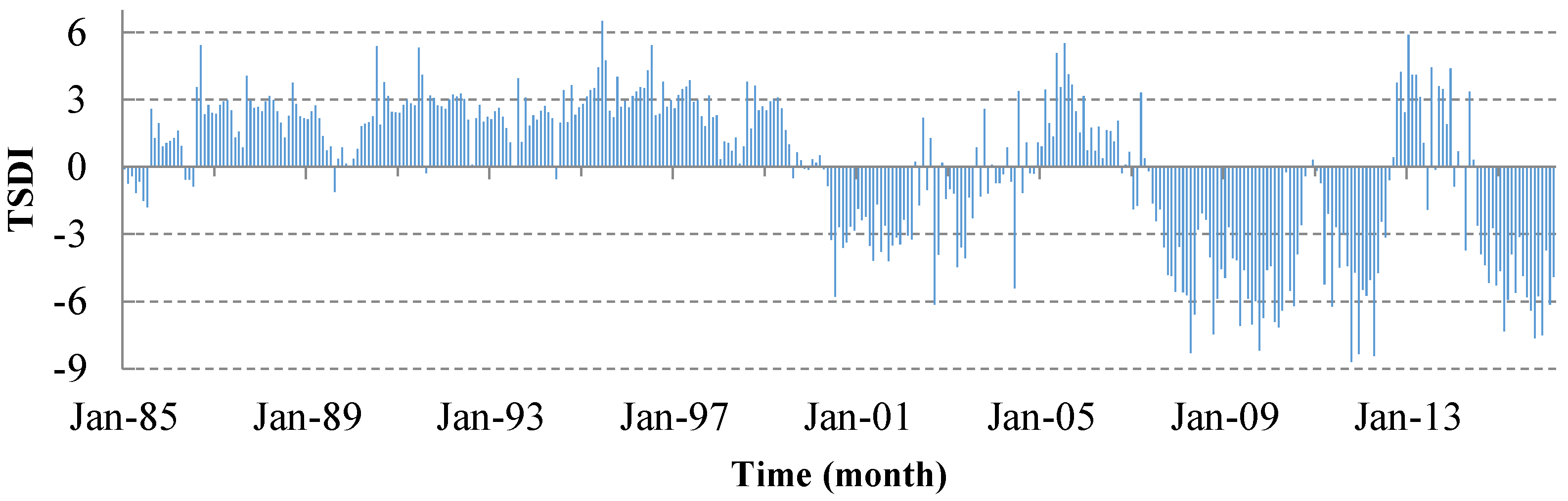
4.4. Drought/Flood Status of the Liao River Basin Monitored by the TSDI
5. Discussion
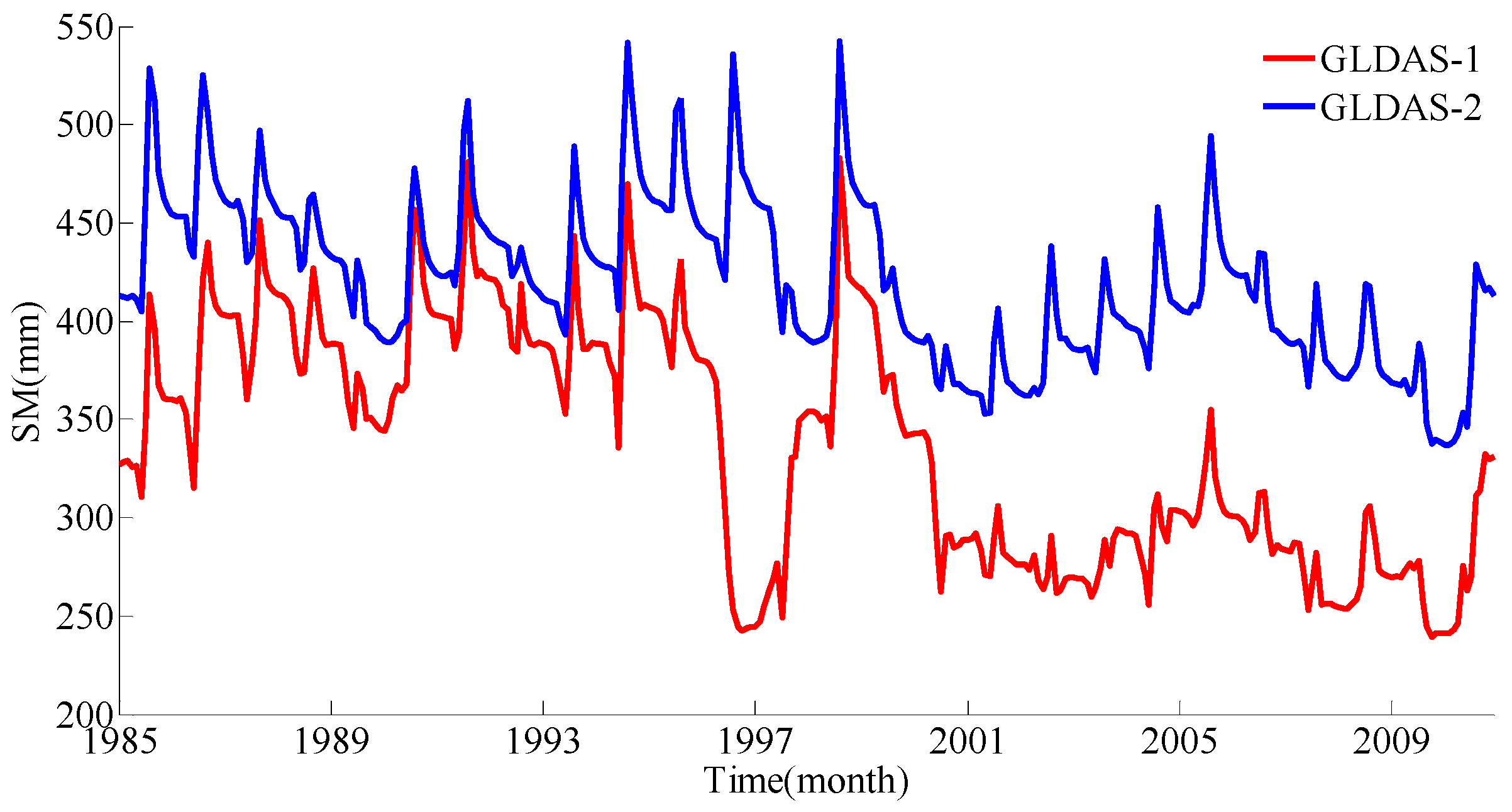
5.1. Noah-Based SM versus JPL Mascon-Based TWSA
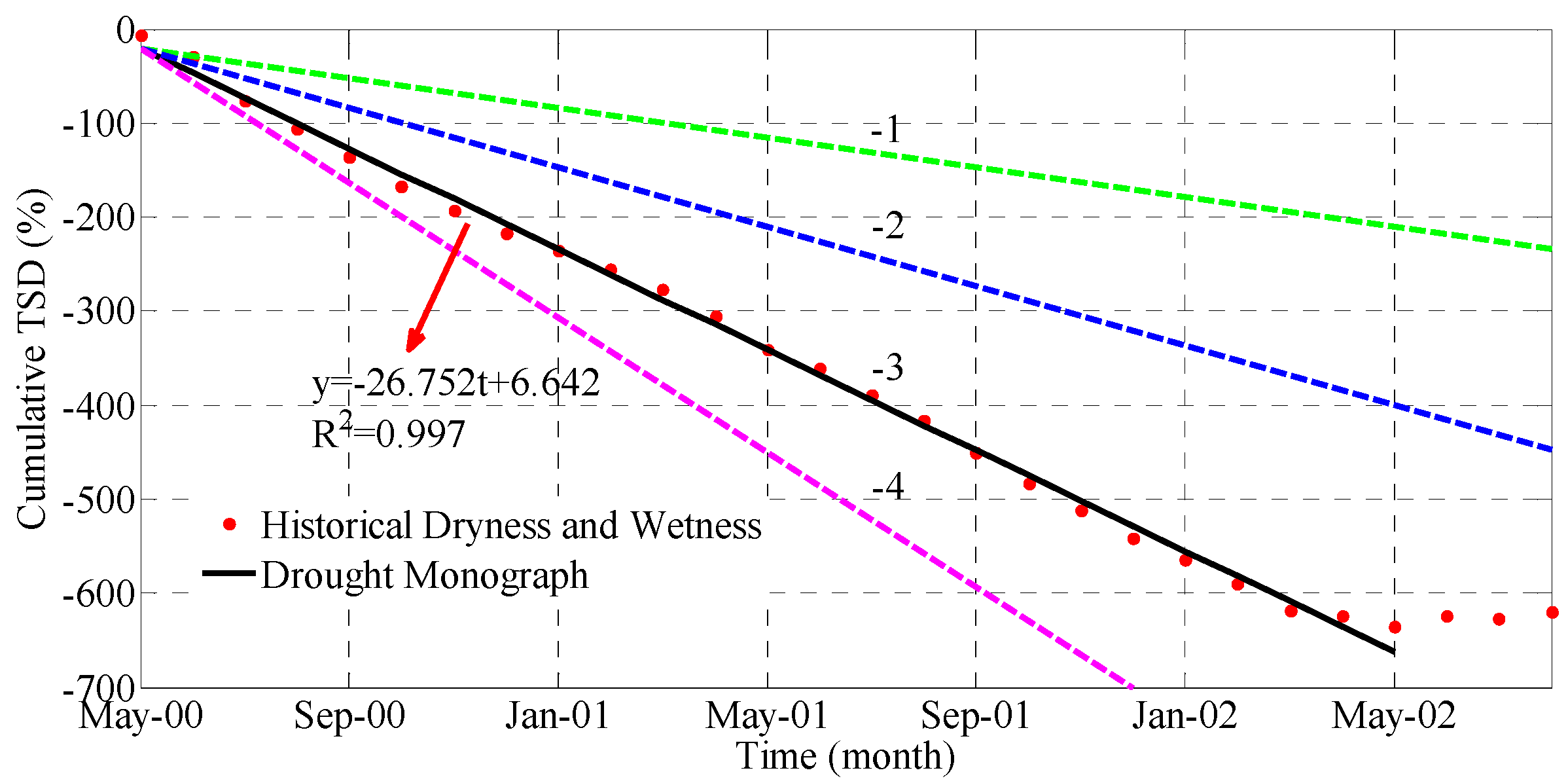
5.2. Analysis of TSDI Results
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Li, Z.Y.; Li, X.; Tang, J.; Liu, C.; Wang, X.J. Study on the Response of Land Use/Land Cover to Climate Change in Liao River Basin of Jilin Province. Res. Soil Water Conserv. 2014, 21, 104–110. [Google Scholar]
- Wang, C.H. Analysis of “05.08” storm flood of Liaohe basin. Water Resour. Plan. Des. 2006, 5, 22–26. [Google Scholar] [CrossRef]
- Wang, D.W.; Wang, C.; Fu, H.T.; Liang, F.G. Analysis of “2005.08” Storm Flood in Liao River Basin. J. China Hydrol. 2006, 1, 76–79. [Google Scholar] [CrossRef]
- Sun, F.H.; Li, L.G.; Liang, H.; Yuan, J.; Lu, S. Climate change characteristics and its impacts on water resources in the Liaohe river basin from 1961 to 2009. J. Meteorol. Environ. 2012, 28, 8–13. [Google Scholar]
- Cui, W.; Mao, Y.F.; Geng, Y.B.; Wang, J.Z. Analysis of flood and waterlogging disaster at the middle—Lower area of Liao river basin. Water Resour. Hydropower Northeast China 2009, 27, 36, 70. [Google Scholar] [CrossRef]
- Cao, L.G. Impact of Climate Change on Runoff in Liao River Basin; Chinese Academy of Meteorological Science: Beijing, China, 2013. [Google Scholar]
- Han, D.M.; Yang, G.Y.; Yan, D.H.; Fang, H.Y. Spatial temporal Feature Analysis of Drought and Flood in Northeast China in Recent 50 years. Water Resour. Power 2014, 6, 5–8. [Google Scholar]
- Feng, W.; Shum, C.K.; Zhong, M.; Pan, Y. Groundwater Storage Changes in China from Satellite Gravity: An Overview. Remote Sens. 2018, 10, 674. [Google Scholar] [CrossRef]
- Zhong, Y.L.; Zhong, M.; Feng, W.; Zhang, Z.Z.; Shen, Y.C.; Wu, D.C. Groundwater Depletion in the West Liaohe River Basin, China and Its Implications Revealed by GRACE and In Situ Measurements. Remote Sens. 2018, 10, 493. [Google Scholar] [CrossRef]
- Abelen, S.; Seitz, F.; Abarcadelrio, R.; Güntner, A. Droughts and Floods in the La Plata Basin in Soil Moisture Data and GRACE. Remote Sens. 2015, 7, 7324–7349. [Google Scholar] [CrossRef]
- Awange, J.L.; Schumacher, K.; Forootan, M.E.; Heck, B. Exploring hydro-meteorological drought patterns over the Greater Horn of Africa (1979–2014) using remote sensing and reanalysis products. Adv. Water Resour. 2016, 94, 45–59. [Google Scholar] [CrossRef]
- Agboma, C.O.; Yirdaw, S.Z.; Snelgrove, K.R. Intercomparison of the total storage deficit index (TSDI) over two Canadian Prairie catchments. J. Hydrol. 2009, 374, 351–359. [Google Scholar] [CrossRef]
- Long, D.; Shen, Y.J.; Sun, A.; Hong, Y.; Longuevergne, L.; Yang, Y.T.; Li, B.; Chen, L. Drought and flood monitoring for a large karst plateau in Southwest China using extended GRACE data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Thomas, A.C.; Reager, J.T.; Famiglietti, J.S.; Rodell, M. A GRACE-based water storage deficit approach for hydrological drought characterization. Geophys. Res. Lett. 2014, 41, 1537–1545. [Google Scholar] [CrossRef]
- Yirdaw, S.Z.; Snelgrove, K.R.; Agboma, C.O. GRACE satellite observations of terrestrial moisture changes for drought characterization in the Canadian prairie. J. Hydrol. 2008, 356, 84–92. [Google Scholar] [CrossRef]
- Yi, H.; Wen, L.X. Satellite gravity measurement monitoring terrestrial water storage change and drought in the continental United States. Sci. Rep. 2016, 6, 19909. [Google Scholar] [CrossRef] [PubMed]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Xu, H.Z. Satellite Gravity Missions-New Hotpoint in Geodesy. Sci. Surv. Map. 2001, 26, 1–3. [Google Scholar] [CrossRef]
- Hu, X.G.; Chen, J.L.; Zhou, Y.H.; Huang, C.; Liao, X.H. Seasonal variation of water distribution in Yangtze River basin from spatial gravity survey of GRACE. Sci. China Ser. D Earth Sci. 2006, 36, 225–232. [Google Scholar] [CrossRef]
- Long, D.; Chen, X.; Scanlon, B.R.; Wada, Y.; Hong, Y.; Singh, V.P.; Chen, Y.; Wang, C.; Han, Z.; Yang, W. Have GRACE satellites overestimated groundwater depletion in the Northwest India Aquifer? Sci. Rep. 2016, 6, 24398. [Google Scholar] [CrossRef] [PubMed]
- Klees, R.; Zapreeva, E.A.; Winsemius, H.C.; Hhg, S. The bias in grace estimates of continental water storage variations. Hydrol. Earth Syst. Sci. 2007, 11, 1227–1241. [Google Scholar] [CrossRef]
- Longuevergne, L.; Scanlon, B.R.; Wilson, C.R. GRACE Hydrological estimates for small basins: Evaluating processing approaches on the High Plains Aquifer, USA. Water Resour. Res. 2012, 46, 6291–6297. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48, 4531. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Global analysis of approaches for deriving total water storage changes from GRACE satellites. Water Resour. Res. 2015, 51, 2574–2594. [Google Scholar] [CrossRef]
- Long, D.; Yang, Y.; Wada, Y.; Hong, Y.; Liang, W.; Chen, Y.N.; Yong, B.; Hou, A.; Wei, J.F.; Chen, L. Deriving scaling factors using a global hydrological model to restore GRACE total water storage changes for China’s Yangtze River Basin. Remote Sens. Environ. 2015, 168, 177–193. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Zhang, Z.; Ni, S. Long-term groundwater variations in Northwest India from satellite gravity measurements. Glob. Planet. Chang. 2014, 116, 130–138. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Multi-sensor analysis of water storage variations of the Caspian Sea. Geophys. Res. Lett. 2007, 34, 245–250. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.; Boening, C.; Landerer, F.W. Improved methods for observing earth’s time variable mass distribution with grace using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Chen, X.; Long, D.; Hong, Y.; Zeng, C.; Yan, D.H. Improved modeling of snow and glacier melting by a progressive two-stage calibration strategy with GRACE and multisource data: How snow and glacier meltwater contributes to the runoff of the Upper Brahmaputra River basin? Water Resour. Res. 2017, 53, 2431–2466. [Google Scholar] [CrossRef]
- Long, D.; Pan, Y.; Zhou, J.; Chen, Y.; Hou, X.; Hong, Y.; Scanlon, B.R.; Longuevergne, L. Global analysis of spatiotemporal variability in merged total water storage changes using multiple GRACE products and global hydrological models. Remote Sens. Environ. 2017, 192, 198–216. [Google Scholar] [CrossRef]
- Cao, Y.P.; Nan, Z.; Cheng, G. GRACE Satellite Observations of Terrestrial Water Storage Changes for Drought Characterization in the Arid Land of Northwestern China. Remote Sens. 2015, 7, 1021–1047. [Google Scholar] [CrossRef]
- Bates, P.; Horritt, M.; Smith, C.; Mason, D. Integrating remote sensing observations of flood hydrology and hydraulic modelling. Hydrol. Process. 1997, 11, 1777–1795. [Google Scholar] [CrossRef]
- Houser, P.R.; Shuttleworth, W.J.; Famiglietti, J.S.; Gupta, H.V.; Syed, K.H.; Goodrich, D.C. Integration of soil moisture remote sensing and hydrologic modeling using data assimilation. Water Resour. Res. 1998, 34, 3405–3420. [Google Scholar] [CrossRef]
- Tarantino, E.; Novelli, A.; Laterza, M.; Gioia, A. Testing high spatial resolution WorldView-2 imagery for retrieving the leaf area index. In Proceedings of the SPIE 9535, Third International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2015), Paphos, Cyprus, 16–19 March 2015. 95351N. [Google Scholar] [CrossRef]
- Pan, M.; Sahoo, A.K.; Troy, T.J.; Vinukollu, R.K.; Sheffield, J.; Wood, E.F. Multi-source estimation of long-term terrestrial water budget for major global river basins. J. Clim. 2012, 25, 3191–3206. [Google Scholar] [CrossRef]
- Sun, A.Y. Predicting groundwater level changes using GRACE data. Water Resour. Res. 2013, 49, 5900–5912. [Google Scholar] [CrossRef]
- Guo, F. Harmful red tide warning based on general regression neural network. Informationization 2009, 28, 015. [Google Scholar]
- Li, W.; Luo, Y.; Zhu, Q.; Liu, J.; Le, J. Applications of AR*-GRNN model for financial time series forecasting. Neural Comput. Appl. 2008, 17, 441–448. [Google Scholar] [CrossRef]
- Wang, X.C.; Shi, F.; Yu, L.; Li, Y. 43 Case Studies of MATLAB Neural Network; Beijing University Press: Beijing, China, 2013. [Google Scholar]
- Liu, Q.H. Application of drought index in Liaohe Basin. Jilin Water Resour. 2016, 9, 31–35. [Google Scholar] [CrossRef]
- Sheng, Y.; Zhou, H.W.; Wang, J.; Tan, G.R.; Wang, Q. Response of Water Resources to Climate Change in Liaohe River Basin. J. Anhui Agric. Sci. 2011, 29, 140. [Google Scholar] [CrossRef]
- Sun, F.H.; Li, L.G.; Yuan, J.; Dai, P. Research status analysis of impact of climate change on water resource in Liaohe river basin. J. Meteorol. Environ. 2015, 31, 147–152. [Google Scholar] [CrossRef]
- Wei, S. Change of NDVI and the Response to Climate in the Liaohe Basin; Nanjing University of Information Science & Technology: Nanjing, China, 2012. [Google Scholar]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. Atmos. 2008, 113, 194–205. [Google Scholar] [CrossRef]
- Cheng, M.K.; Tapley, B.D. Variations in the Earth’s oblateness during the past 28 years. J. Geophys. Res. Solid Earth 2004, 109, 1404–1406. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Methods for inferring regional surface-mass anomalies from Gravity Recovery and Climate Experiment (GRACE) measurements of time-variable gravity. J. Geophys. Res. 2002, 107, 389–392. [Google Scholar] [CrossRef]
- Ferreira, V.G.; Andam-Akorful, S.A.; Xiu-Feng, H.E.; Xiao, R.Y. Estimating water storage changes and sink terms in Volta Basin from satellite missions. Water Sci. Eng. 2014, 7, 5–16. [Google Scholar] [CrossRef]
- Zhang, X.L. Shock Overpressure Outlier Processing Based on Grubbs Criteria. J. Sichuan Ordnance 2017, 38, 37–39. [Google Scholar] [CrossRef]
- Rodell, M.; House, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Ren, Y.Q.; Pan, Y.; Gong, H.L. Haihe Basin Groundwater Reserves Space Trend Analysis. J. Cap. Normal Univ. 2014, 35, 89–98. [Google Scholar] [CrossRef]
- Feng, W.; Zhong, M.; Lemoine, J.M.; Biancale, R.; Hsu, H.T.; Xia, J. Evaluation of groundwater depletion in North China using the Gravity Recovery and Climate Experiment (GRACE) data and ground-based measurements. Water Resour. Res. 2013, 49, 2110–2118. [Google Scholar] [CrossRef]
- Zhou, S.L.; Zhou, F. GRNN model for prediction of port cargo throughput based on time series. J. Shanghai Marit. Univ. 2011, 32, 70–73. [Google Scholar] [CrossRef]
- Palmer, W. Meteorological Drought. U.S. Weather Bureau, Research Paper. 1965, Volume 45. Available online: http://ci.nii.ac.jp/naid/10019234031/en/ (accessed on 18 May 2017).
- Narasimhan, B.; Srinivasan, R. Development and evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for agricultural drought monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. J. Hydrol. 1993, 179, 17–22. [Google Scholar]
- Water Resources Bulletin of Song Liao River Basin. Song Liao Water Resources Commission of the Ministry of Water Resources; Songliao Water Resources Commission: Changchun, China, 2002–2016.
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Yang, Z.L.; Niu, G.Y. 2005 drought event in the Amazon River basin as measured by grace and estimated by climate models. J. Geophys. Res. Solid Earth 2009, 114, B05404. [Google Scholar] [CrossRef]
- README Document for NASA GLDAS Version 2 Data Products. Available online: https://hydro1.gesdisc.eosdis.nasa.gov/data/GLDAS/README_GLDAS2.pdf (accessed on 18 May 2017).
- Jiang, H.W.; Guo, T.T.; Bao, Y.; Su, G.L.; Liao, J.J. Spatiotemporal Distribution of Drought and Flood Disasters over the Last 50 Years of Liaoning Province. Res. Soil Water Conserv. 2012, 19, 000029. [Google Scholar]
- Wu, Q.; Zhao, C.Y.; Wang, D.J.; Li, Q.; Wu, J.Y.; Lin, R. Spatial and temporal characteristics of meteorological drought in Liaoning Province from 1951 to 2014. J. Arid Land Resour. Environ. 2016, 30, 151–157. [Google Scholar] [CrossRef]
- Wang, Z.W.; Zhai, P.M.; Wu, Y.L. Analysis on Drought Variation over 10 Hydrological Regions in China during 1951–2005. Plateau Meteorol. 2007, 26, 874–880. [Google Scholar]
- Zou, X.K.; Ren, G.Y.; Zhang, Q. Droughts Variations in China Based on a Compound index of Meteorological Drought. Clim. Environ. Res. 2010, 15, 371–378. [Google Scholar]
- Reichle, R.H.; Koster, R.D. Bias reduction in short records of satellite soil moisture. Geophys. Res. Lett. 2004, 31, L19501. [Google Scholar] [CrossRef]
- Tu, G.; Li, S.F.; Sun, L.; Yao, Y.X. Temporal Variation of Observed Runoff in Songhua River and Liaohe River Basins and Its Relationship with Precipitation. Prog. Inquis. Mutat. Clim. 2012, 8, 456–461. [Google Scholar] [CrossRef]
- Zhang, D.E.; Liu, C.Z. Replenishment of the Atlas of the drought and flood distribution in China for the past 500 years (1980–1992). Meteorol. Mon. 1993, 41–45. [Google Scholar] [CrossRef]
- Zhao, W.G.; Feng, L.L. Analysis on Flood Characteristics of Wangben hydrological station in East Liaohe River. Jilin Agriculture 2011, 9, 213. [Google Scholar]
- Xu, W.L.; Jia, X.X.; Zhou, L.; Liang, G.H. Analysis of Water Resources Situation in Liaohe River Valley. Shanxi Sci. Technol. 2010, 25, 15–16. [Google Scholar] [CrossRef]
| TSDI Category | TSDI | TSDI Category | TSDI |
|---|---|---|---|
| Extreme wetness | Mild drought | (−2,−1) | |
| Severe wetness | (3,4) | Moderate drought | (−3,−2) |
| Moderate wetness | (2,3) | Severe drought | (−4,−3) |
| Mild wetness | (1,2) | Extreme drought | |
| Normal | (−1,1) |
| Variables | r | RMSE (cm) | |
|---|---|---|---|
| 2003–2009 | Bulletin vs. SH | 0.64 | 2.08 |
| Bulletin vs. mascon | 0.65 | 3.05 | |
| 2011–2015 | Bulletin vs. SH | 0.64 | 2.54 |
| Bulletin vs. mascon | 0.76 | 2.21 | |
| Variable | r |
|---|---|
| Noah vs. JPL mascon solutions | 0.69 |
| VIC vs. JPL mascon solutions | 0.47 |
| Mosaic vs. JPL mascon solutions | 0.56 |
| Prediction | Model | r (TWSA-GRNN vs. TWSA-JPL Mascon) | RMSE (mm) | F-Test (α = 0.05) |
|---|---|---|---|---|
| 1 | SMS | 0.90 | 18 | 5.51 |
| Precipitation | ||||
| 2 | SMS | 0.91 | 22 | 4.03 |
| Temperature | ||||
| 3 | SMS | 0.87 | 24 | 3.16 |
| Precipitation | ||||
| Temperature |
| ID | Time Span | Duration/Month | Cumulative TSDI Slope | Disaster Level |
|---|---|---|---|---|
| 1 | 1985.08–1985.10 | 3 | 1.62 | Mild wetness |
| 2 | 1985.12–1986.03 | 4 | 1.35 | Mild wetness |
| 3 | 1986.08–1987.07 | 12 | 2.62 | Moderate wetness |
| 4 | 1987.09–1989.05 | 21 | 2.50 | Moderate wetness |
| 5 | 1990.03–1991.07 | 17 | 2.96 | Moderate wetness |
| 6 | 1991.09–1992.07 | 11 | 2.93 | Moderate wetness |
| 7 | 1992.09–1993.06 | 10 | 2.21 | Moderate wetness |
| 8 | 1993.08–1994.05 | 10 | 2.31 | Moderate wetness |
| 9 | 1994.07–1997.12 | 42 | 3.32 | Severe wetness |
| 10 | 1998.08–1999.07 | 12 | 2.65 | Moderate wetness |
| 11 | 2000.06–2002.03 | 22 | −3.03 | Severe drought |
| 12 | 2003.02–2003.07 | 6 | −3.14 | Severe drought |
| 13 | 2005.02–2005.12 | 11 | 3.52 | Severe wetness |
| 14 | 2006.06–2006.09 | 4 | 1.55 | Mild wetness |
| 15 | 2007.06–2010.04 | 35 | −5.08 | Extreme drought |
| 16 | 2010.06–2010.09 | 4 | −4.20 | Extreme drought |
| 17 | 2011.03–2012.07 | 17 | −5.41 | Extreme drought |
| 18 | 2012.10–2013.05 | 8 | 3.80 | Severe wetness |
| 19 | 2013.09–2013.12 | 4 | 3.12 | Severe wetness |
| 20 | 2014.07–2016.03 | 21 | −5.33 | Extreme drought |
| Disaster Classification | Time | References |
|---|---|---|
| Drought | 1997 −−, 1999 −−−, 2000 −−−−, | Cao (2013) [6]; Sun et al. (2012, 2015) [4,43]; Cui et al. (2009) [5]; Tu et al. (2012) [66]; Zhang et al. (1993) [67]; Zhao et al. (2011) [68]; Xu et al. (2010) [69] |
| Flood | 1985 +++, 1986 ++++, 1987 ++++, 1988 ++, 1989 ++, 1991 +, 1992 +, 1994 +++, 1995 +++, 1998 ++, |
| Disaster Classification | Time | References |
|---|---|---|
| Drought | 2001, 2002, 2007, 2008, 2009, 2014, 2015 | National Water Report (2000–2016); Bulletin of Flood and Drought Disasters in China (2006–2016) |
| Flood | 2005, 2006, 2010, 2011,2012, 2013 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Jiang, J.; Li, H. Drought and Flood Monitoring of the Liao River Basin in Northeast China Using Extended GRACE Data. Remote Sens. 2018, 10, 1168. https://doi.org/10.3390/rs10081168
Chen X, Jiang J, Li H. Drought and Flood Monitoring of the Liao River Basin in Northeast China Using Extended GRACE Data. Remote Sensing. 2018; 10(8):1168. https://doi.org/10.3390/rs10081168
Chicago/Turabian StyleChen, Xuhui, Jinbao Jiang, and Hui Li. 2018. "Drought and Flood Monitoring of the Liao River Basin in Northeast China Using Extended GRACE Data" Remote Sensing 10, no. 8: 1168. https://doi.org/10.3390/rs10081168
APA StyleChen, X., Jiang, J., & Li, H. (2018). Drought and Flood Monitoring of the Liao River Basin in Northeast China Using Extended GRACE Data. Remote Sensing, 10(8), 1168. https://doi.org/10.3390/rs10081168