Dual-Polarized L-Band SAR Imagery for Temporal Monitoring of Marine Oil Slick Concentration
Abstract
1. Introduction
2. Radar Backscattering from the Ocean Surface
2.1. Bragg Scattering Theory
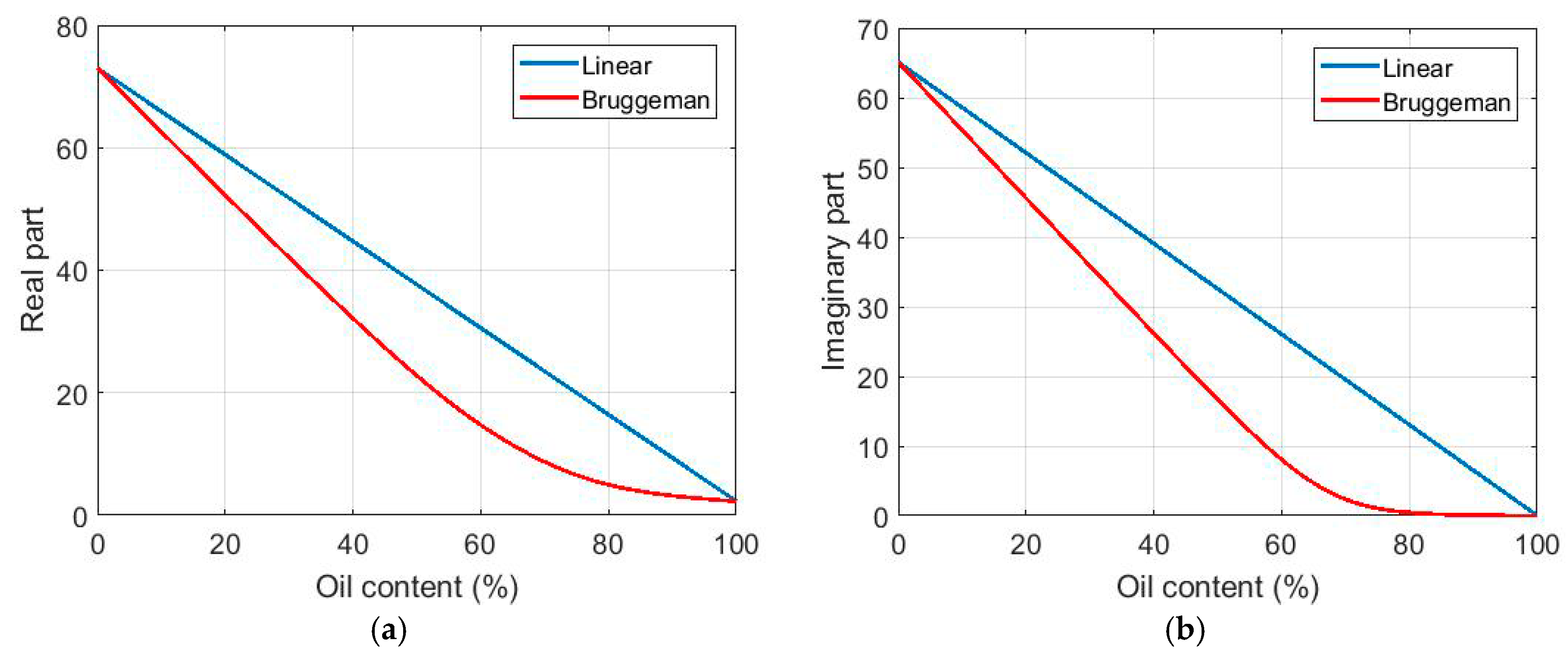
2.2. Impact of Oil on the Sea Surface
3. Airborne Campaign of Acquisition over Controlled Releases of Mineral Oil at Sea
3.1. NOFO’2015 Oil-on-Water Exercise
3.2. Airborne SAR Acquisitions
4. Estimation of Oil Concentration in an Oil-in-Water Slick Emulsion
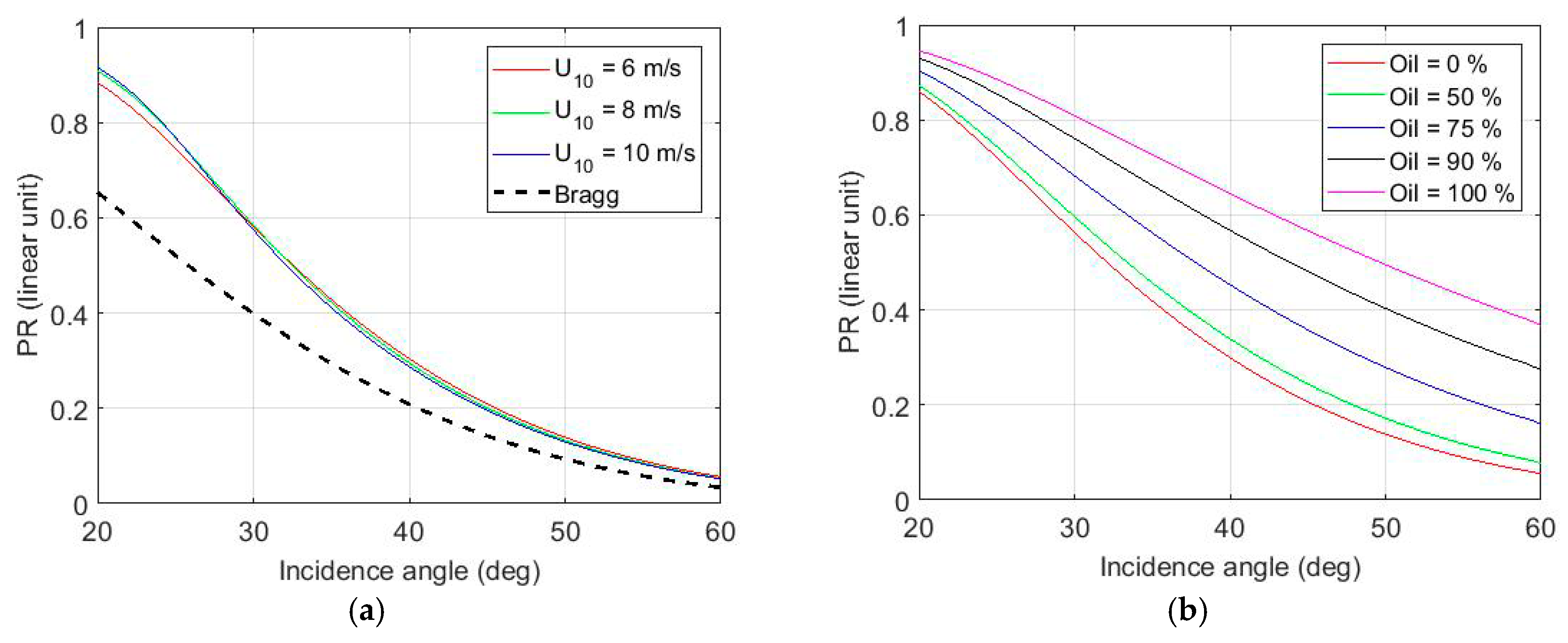
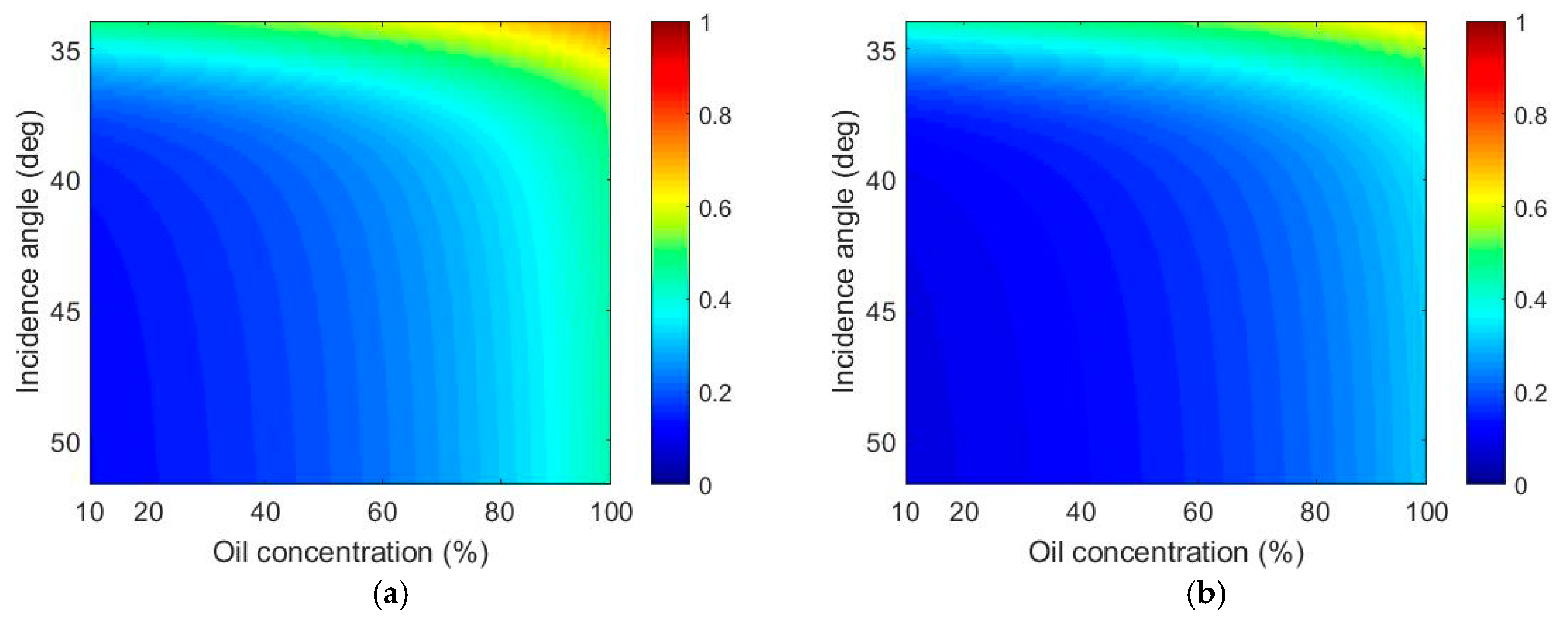
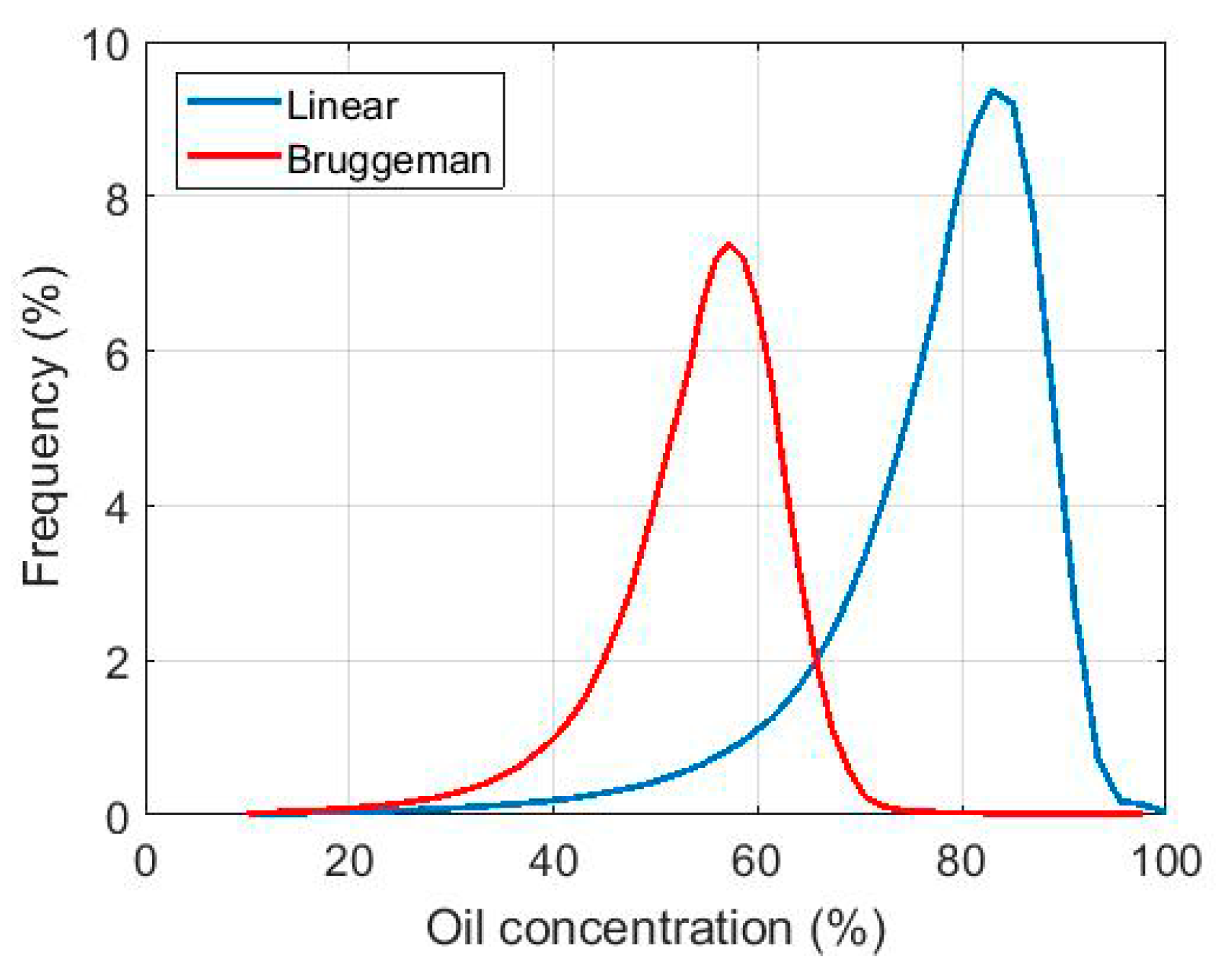
4.1. The Universal Weighted Curvature Approximation Scattering Model
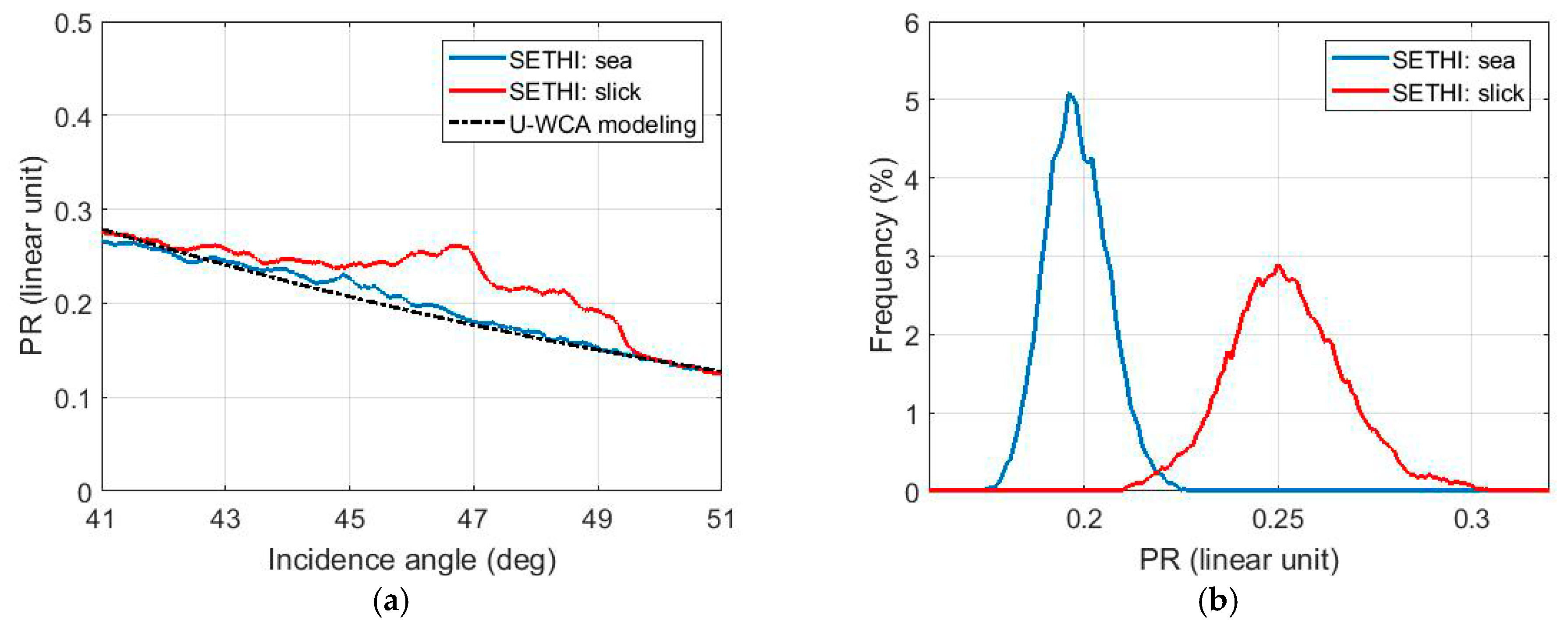
4.2. Comparison with L-Band Remote Sensing Data
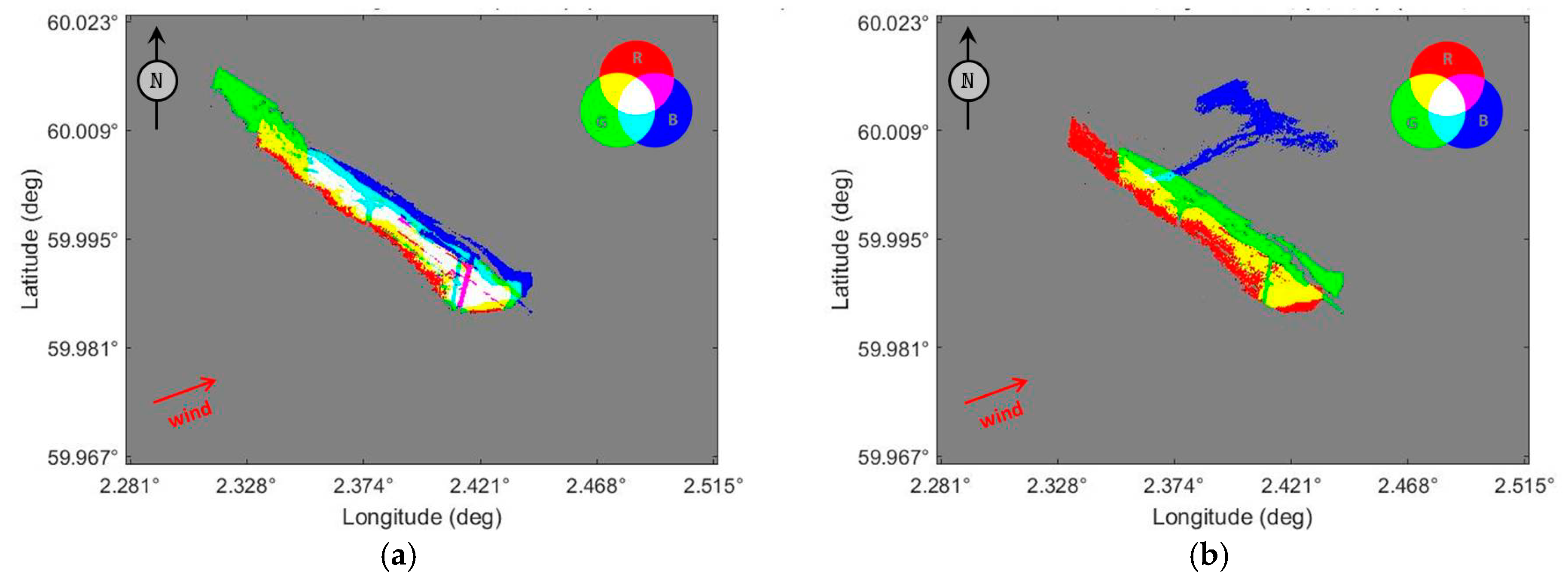
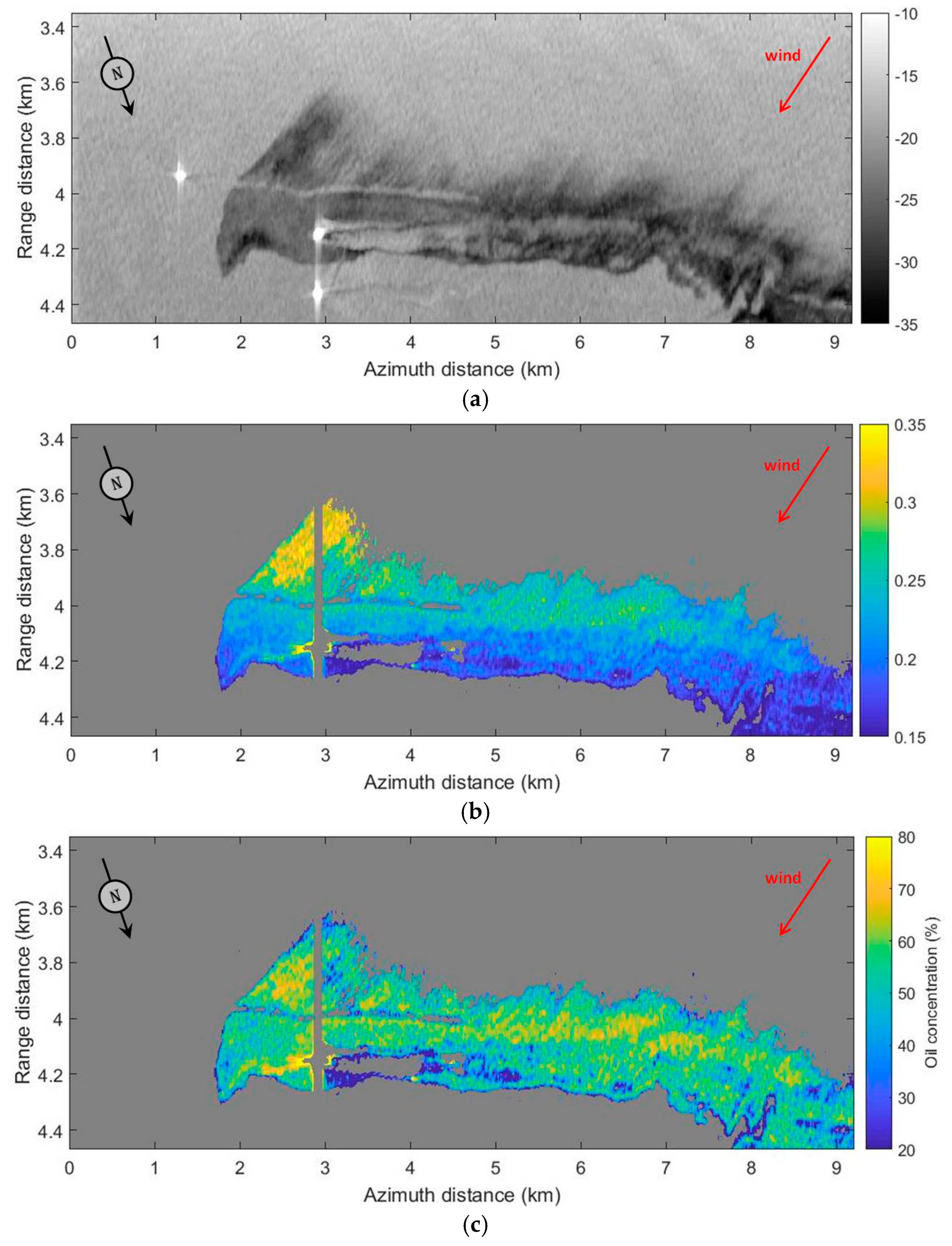
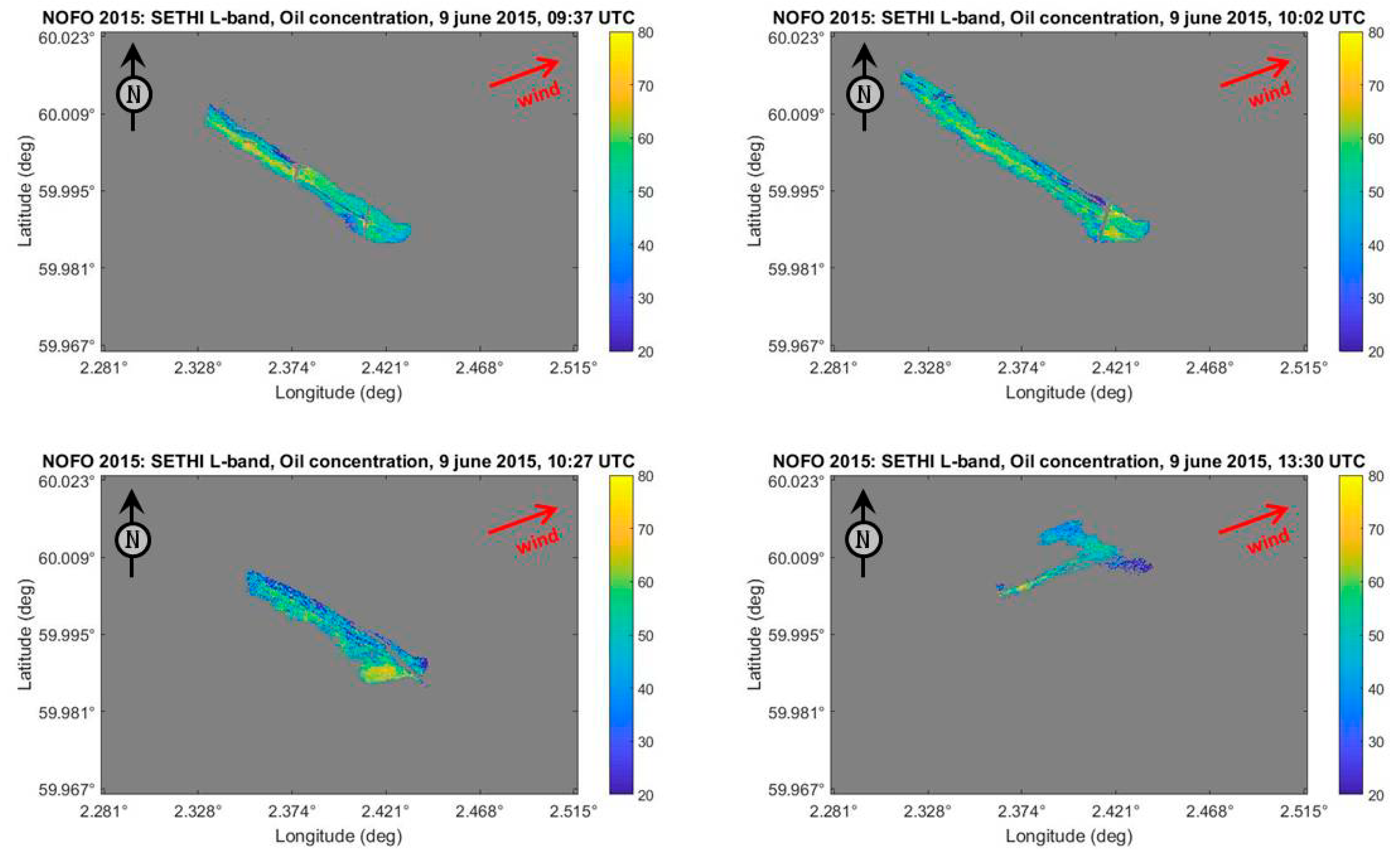
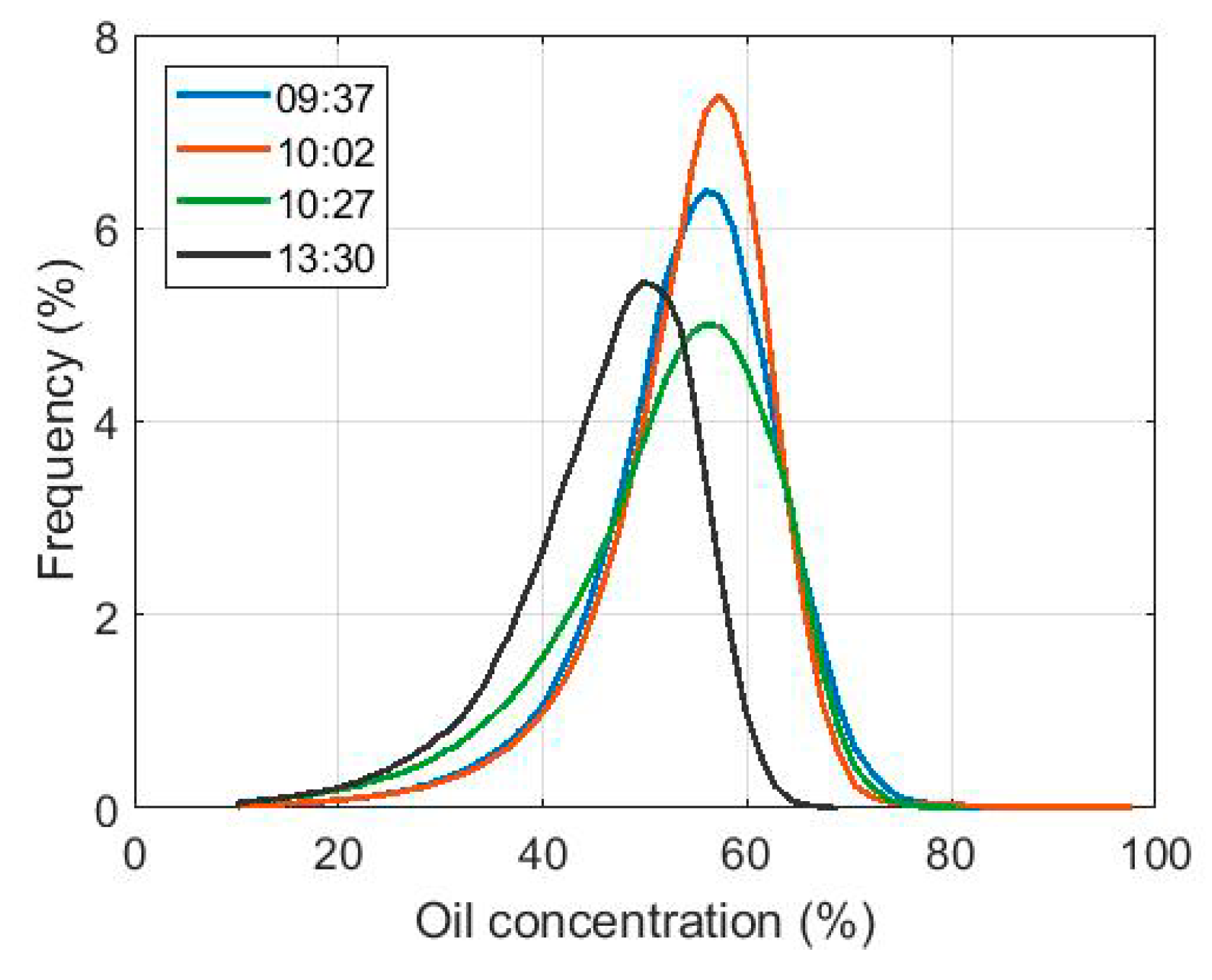
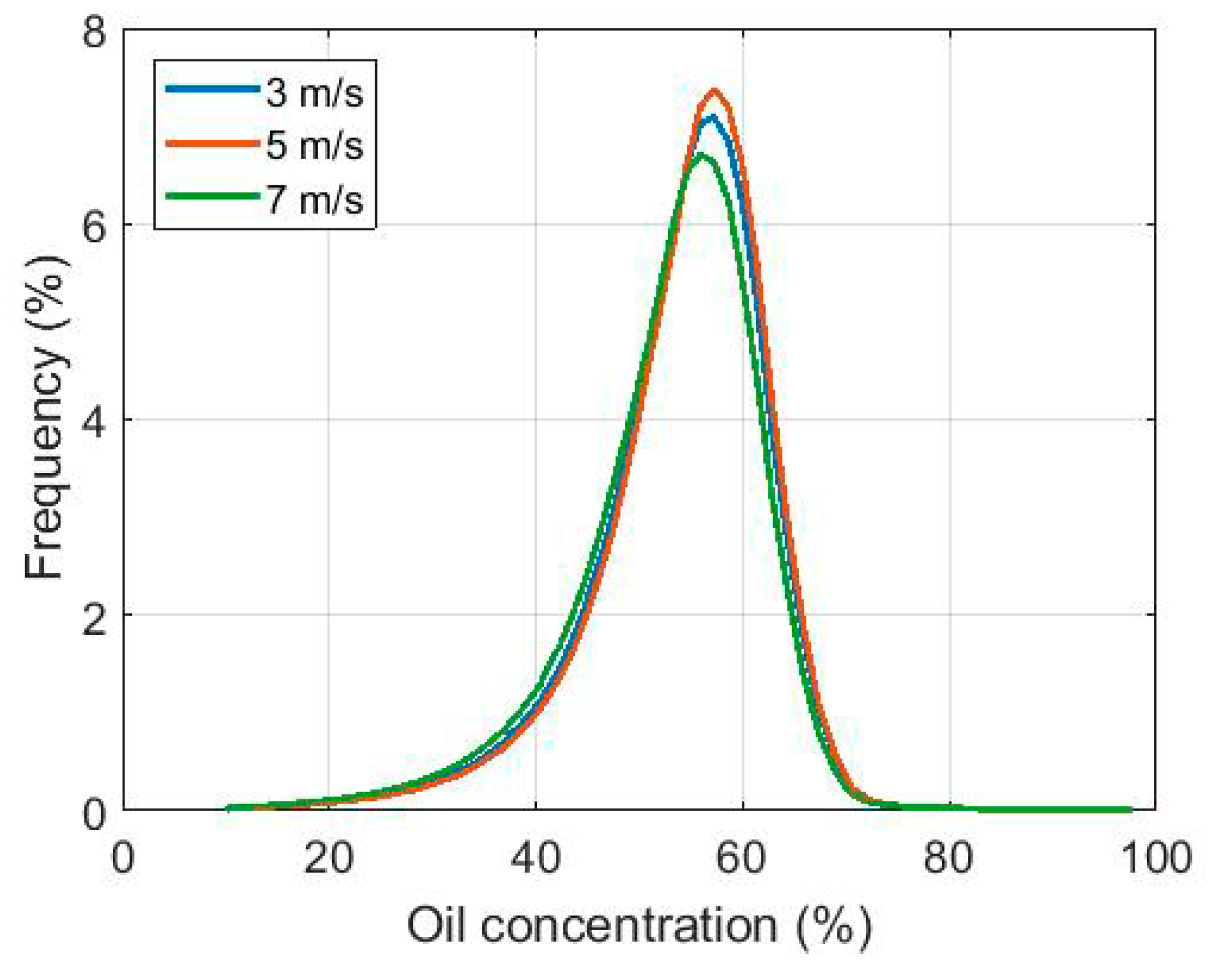
5. Quantifying the Concentration of Oil within a Marine Slick with Real Airborne SAR Data
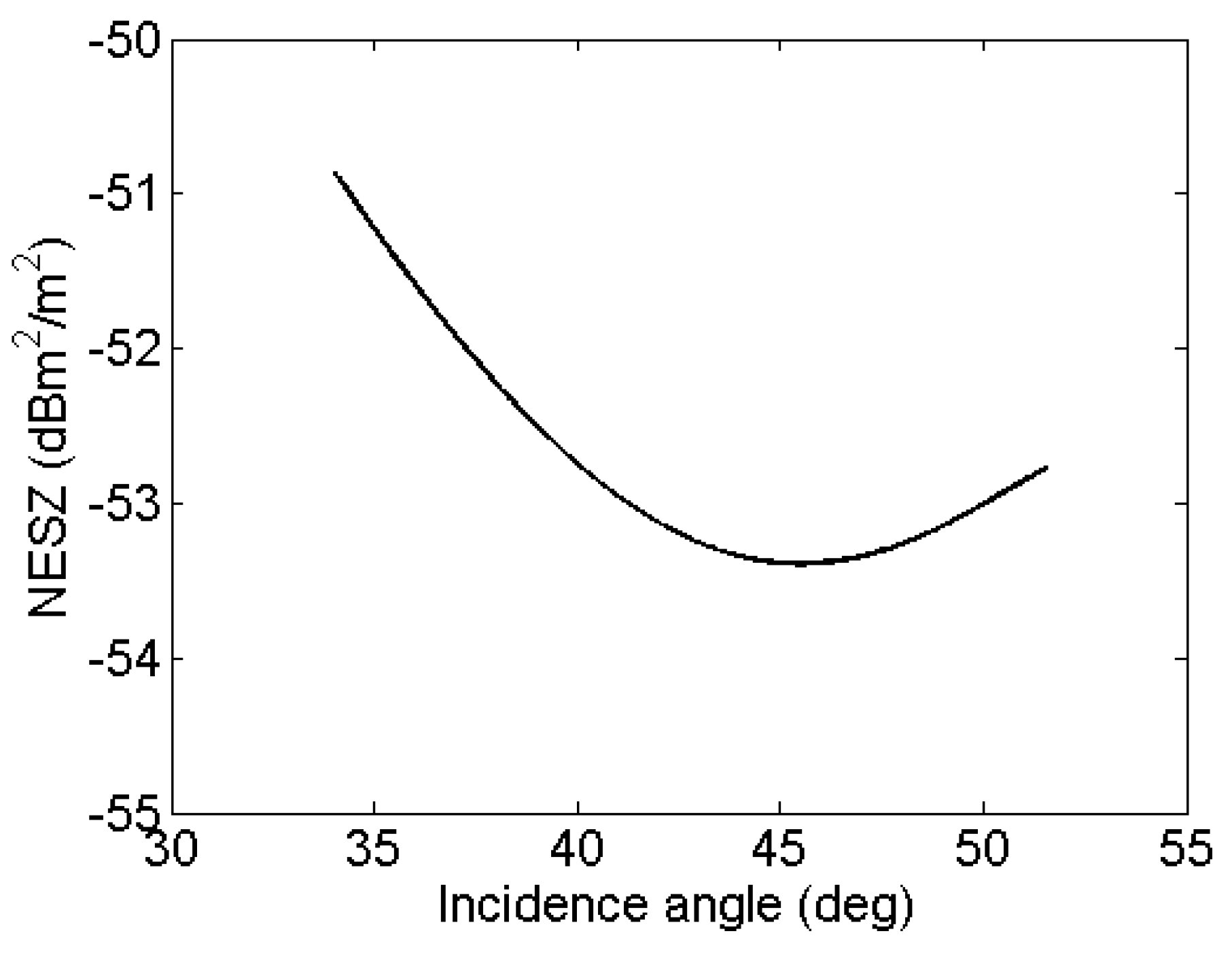
6. Confidence in Oil Concentration Estimate
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fingas, M.; Brown, C. Review of oil spill remote sensing. Mar. Pollut. Bull. 2014, 83, 9–23. [Google Scholar] [CrossRef] [PubMed]
- Brekke, C.; Solberg, A. Oil spill detection by satellite remote sensing. Remote Sens. Environ. 2005, 95, 1–13. [Google Scholar] [CrossRef]
- Gade, M.; Alpers, W. Using ERS-2 SAR images for routine observation of marine pollution in European coastal waters. Sci. Total Environ. 1999, 237–238, 441–448. [Google Scholar] [CrossRef]
- Girard-Ardhuin, F.; Mercier, G.; Collard, F.; Garello, R. Operational oil-slick characterization by SAR imagery and synergistic data. IEEE J. Ocean. Eng. 2005, 30, 487–495. [Google Scholar] [CrossRef]
- Leifer, I.; Lehr, W.J.; Simecek-Beatty, D.; Bradley, E.; Clark, R.; Dennison, P.; Hu, Y.; Matheson, S.; Jones, C.E.; Holt, B.; et al. State of the art satellite and airborne marine oil spill remote sensing: Application to the BP Deepwater Horizon oil spill. Remote Sens. Environ. 2012, 124, 185–209. [Google Scholar] [CrossRef]
- Valenzuela, G.R. Theories for the interaction of electromagnetic and oceanic waves—A review. Bound.-Layer Meteorol. 1978, 13, 61–85. [Google Scholar] [CrossRef]
- Alpers, W.; Holt, B.; Zeng, K. Oil spill detection by imaging radars: Challenges and pitfalls. Remote Sens. Environ. 2017, 201, 133–147. [Google Scholar] [CrossRef]
- Wismann, V.; Gade, M.; Alpers, W.; Huhnerfuss, H. Radar signatures of marine mineral oil spills measured by an airborne multi-frequency radar. Int. J. Remote Sens. 1998, 19, 3607–3623. [Google Scholar] [CrossRef]
- Gade, M.; Alpers, W.; Hühnerfuss, H.; Masuko, H.; Kobayashi, T. Imaging of biogenic and anthropogenic ocean surface films by the multifrequency/multipolarization SIR-C/X-SAR. J. Geophys. Res. 1998, 103, 18851–18866. [Google Scholar] [CrossRef]
- Angelliaume, S.; Minchew, B.; Chataing, S.; Martineau, P.; Miegebielle, V. Multifrequency Radar Imagery and Characterization of Hazardous and Noxious Substances at Sea. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3051–3066. [Google Scholar] [CrossRef]
- Minchew, B. Determining the mixing of oil and seawater using polarimetric synthetic aperture radar. Geophys. Res. Lett. 2012, 39, L16607. [Google Scholar] [CrossRef]
- Angelliaume, S.; Dubois-Fernandez, P.C.; Jones, C.E.; Holt, B.; Minchew, B.; Amri, E.; Miegebielle, V. SAR Imagery for Detecting Sea Surface Slicks: Performance Assessment of Polarization-Dependent Parameters. IEEE Trans. Geosci. Remote Sens. 2018, PP, 1–21. [Google Scholar] [CrossRef]
- Minchew, B.; Jones, C.E.; Holt, B. Polarimetric Analysis of Backscatter from the Deepwater Horizon Oil Spill Using L-Band Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3812–3830. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Chapron, B.; Myasoedov, A.G.; Collard, F.; Johannessen, J.A. On Dual Co-Polarized SAR Measurements of the Ocean Surface. IEEE Geosci. Remote Sens. Lett. 2013, 10, 761–765. [Google Scholar] [CrossRef]
- Plant, W.J.; Irisov, V. A joint active/passive physical model of sea surface microwave signatures. J. Geophys. Res. Oceans 2017, 122, 3219–3239. [Google Scholar] [CrossRef]
- Makhoul, E.; López-Martínez, C.; Broquetas, A. Exploiting Polarimetric TerraSAR-X Data for Sea Clutter Characterization. IEEE Trans. Geosci. Remote Sens. 2016, 54, 358–372. [Google Scholar] [CrossRef]
- Ivonin, D.V.; Skrunes, S.; Brekke, C.; Ivanov, A.Y. Interpreting sea surface slicks on the basis of the normalized radar cross-section model using RADARSAT-2 copolarization dual-channel SAR images. Geophys. Res. Lett. 2016, 43, 2748–2757. [Google Scholar] [CrossRef]
- Quilfen, Y.; Chapron, B.; Bentamy, A.; Gourrion, J.; Elfouhaily, T.M.; Vandemark, D. Global ERS 1 and 2 and NSCAT observations: Upwind/crosswind and upwind/downwind measurements. J. Geophys. Res. Oceans 1999, 104, 11459–11469. [Google Scholar] [CrossRef]
- Horstmann, J.; Koch, W.; Lehner, S.; Tonboe, R. Wind retrieval over the ocean using synthetic aperture radar with C-band HH polarization. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2122–2131. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Hauser, D.; Caudal, G.; Chapron, B. A semiempirical model of the normalized radar cross section of the sea surface, 2, Radar modulation transfer function. J. Geophys. Res. 2003, 108, 2156–2202. [Google Scholar] [CrossRef]
- Boisot, O.; Angelliaume, S.; Guerin, C.-A. Marine Oil Slicks Quantification from L-band dual-polarization SAR imagery. IEEE Trans. Geosci. Remote Sens. Submitted.
- Guerin, C.-A.; Soriano, G.; Chapron, B. The weighted curvature approximation in scattering from sea surfaces. Waves Random Complex Media 2010, 20, 364–384. [Google Scholar] [CrossRef]
- Angelliaume, S.; Ceamanos, X.; Viallefont-Robinet, F.; Baqué, R.; Déliot, P.; Miegebielle, V. Hyperspectral and Radar Airborne Imagery over Controlled Release of Oil at Sea. Sensors 2017, 17, 1772. [Google Scholar] [CrossRef] [PubMed]
- Zebker, H.A.; van Zyl, J.; Held, D.N. Imaging radar polarimetry from wave synthesis. J. Geophys. Res. 1987, 92, 683–701. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, W.J. The complex dielectric constant of pure and sea water from microwave satellite observations. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1836–1849. [Google Scholar] [CrossRef]
- Folgerø, K. Bilinear calibration of coaxial transmission/reflection cells for permittivity measurement of low-loss liquids. Meas. Sci. Technol. 1996, 7, 1260–1269. [Google Scholar] [CrossRef]
- Friisø, T.; Schildberg, Y.; Rambeau, O.; Tjomsland, T.; Førdedal, H.; Sjøblom, J. Complex premittivity of crude oils and solutions of heavy crude oil fractions. J. Dispers. Sci. Technol. 1998, 19, 93–126. [Google Scholar] [CrossRef]
- Sihvola, A. Electromagnetic Mixing Formulas and Applications; IEE Electromagnetic Waves Series; Institution of Engineering and Technology: London, UK, 1999. [Google Scholar]
- MOS Sweeper. Available online: http://www.egersundgroup.no/oilspill/mos-sweeper (accessed on 20 April 2018).
- DESMI Boom. Available online: https://www.desmi.com/news-(3)/nofo-accelerates-spill-recovery-with-desmi-speed-sweep.aspx#1 (accessed on 20 April 2018).
- Hansen, M.W.; Kudryavtsev, V.; Chapron, B.; Brekke, C.; Johannessen, J.A. Wave Breaking in Slicks: Impacts on C-Band Quad-Polarized SAR Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4929–4940. [Google Scholar] [CrossRef]
- Elfouhaily, T.; Guérin, C.-A. A critical survey of approximate scattering wave theories from random rough surfaces. Waves Random Media 2004, 14, R1–R40. [Google Scholar] [CrossRef]
- Soriano, G.; Guérin, C.-A. A cutoff invariant two-scale model in electromagnetic scattering from sea surfaces. IEEE Geosci. Remote Sens. Lett. 2008, 5, 199–203. [Google Scholar] [CrossRef]
- Voronovich, A.G. Small-slope approximation in wave scattering from rough surfaces. J. Exp. Theor. Phys. 1985, 62, 65–70. [Google Scholar]
- Hasselmann, K.; Raney, R.K.; Plant, W.J.; Alpers, W.; Shuchman, R.A.; Lyzenga, D.R.; Rufenach, C.L.; Tucker, M.J. Theory of synthetic aperture radar ocean imaging: A MARSEN view. J. Geophys. Res. 1985, 90, 4659–4686. [Google Scholar] [CrossRef]
- Elfouhaily, T.; Chapron, B.; Katsaros, K.; Vandemark, D. A unified directional spectrum for long and short wind-driven waves. J. Geophys. Res. 1997, 102, 15781–15796. [Google Scholar] [CrossRef]
- Fingas, M.; Fieldhouse, B. Studies on water-in-oil products from crude oils and petroleum products. Mar. Pollut. Bull. 2012, 64, 272–283. [Google Scholar] [CrossRef] [PubMed]




| Surface | L-band [1.3 GHz] | C-band [5.0 GHz] | X-band [10 GHz] |
|---|---|---|---|
| Seawater (15 °C 35 PSU) | 73.0 + 65.1i | 66.8 + 35.7i | 52.9 + 39.0i |
| Mineral oil | 2.3 + 0.01i | 2.3 + 0.01i | 2.3 + 0.01i |
| Date | Time (UTC) | Experiment | Wind Speed at 10 m (m·s−1) | Wind Direction (from-deg) | Significant Wave Height (m) |
|---|---|---|---|---|---|
| 9 June 2015 | 06:00 | MOS Sweeper | 5 | 250 | 1 |
| 09:00 | 5 | 250 | 1 | ||
| 12:00 | DESMI Boom | 7 | 250 | 1 | |
| 15:00 | 7 | 250 | 1 |
| Date | Run Number | Time of Imaging (UTC) | Cleanup Exercise | Flight Heading (deg) |
|---|---|---|---|---|
| 9 June 2015 | 1 | 09:37 | MOS Sweeper | 105 |
| 2 | 10:02 | MOS Sweeper | 290 | |
| 3 | 10:27 | MOS Sweeper | 105 | |
| 4 | 13:30 | DESMI Boom | 250 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Angelliaume, S.; Boisot, O.; Guérin, C.-A. Dual-Polarized L-Band SAR Imagery for Temporal Monitoring of Marine Oil Slick Concentration. Remote Sens. 2018, 10, 1012. https://doi.org/10.3390/rs10071012
Angelliaume S, Boisot O, Guérin C-A. Dual-Polarized L-Band SAR Imagery for Temporal Monitoring of Marine Oil Slick Concentration. Remote Sensing. 2018; 10(7):1012. https://doi.org/10.3390/rs10071012
Chicago/Turabian StyleAngelliaume, Sébastien, Olivier Boisot, and Charles-Antoine Guérin. 2018. "Dual-Polarized L-Band SAR Imagery for Temporal Monitoring of Marine Oil Slick Concentration" Remote Sensing 10, no. 7: 1012. https://doi.org/10.3390/rs10071012
APA StyleAngelliaume, S., Boisot, O., & Guérin, C.-A. (2018). Dual-Polarized L-Band SAR Imagery for Temporal Monitoring of Marine Oil Slick Concentration. Remote Sensing, 10(7), 1012. https://doi.org/10.3390/rs10071012







