Using Google Earth Engine to Map Complex Shade-Grown Coffee Landscapes in Northern Nicaragua
Abstract
1. Introduction
- (1)
- Developing an open-access and multi-temporal approach to classifying both shade coffee and overall land cover with high accuracy in northern Nicaragua.
- (2)
- Assessing the relative value of various spectral and ancillary data combinations in enabling shade coffee and overall land-cover classification accuracy in this context.
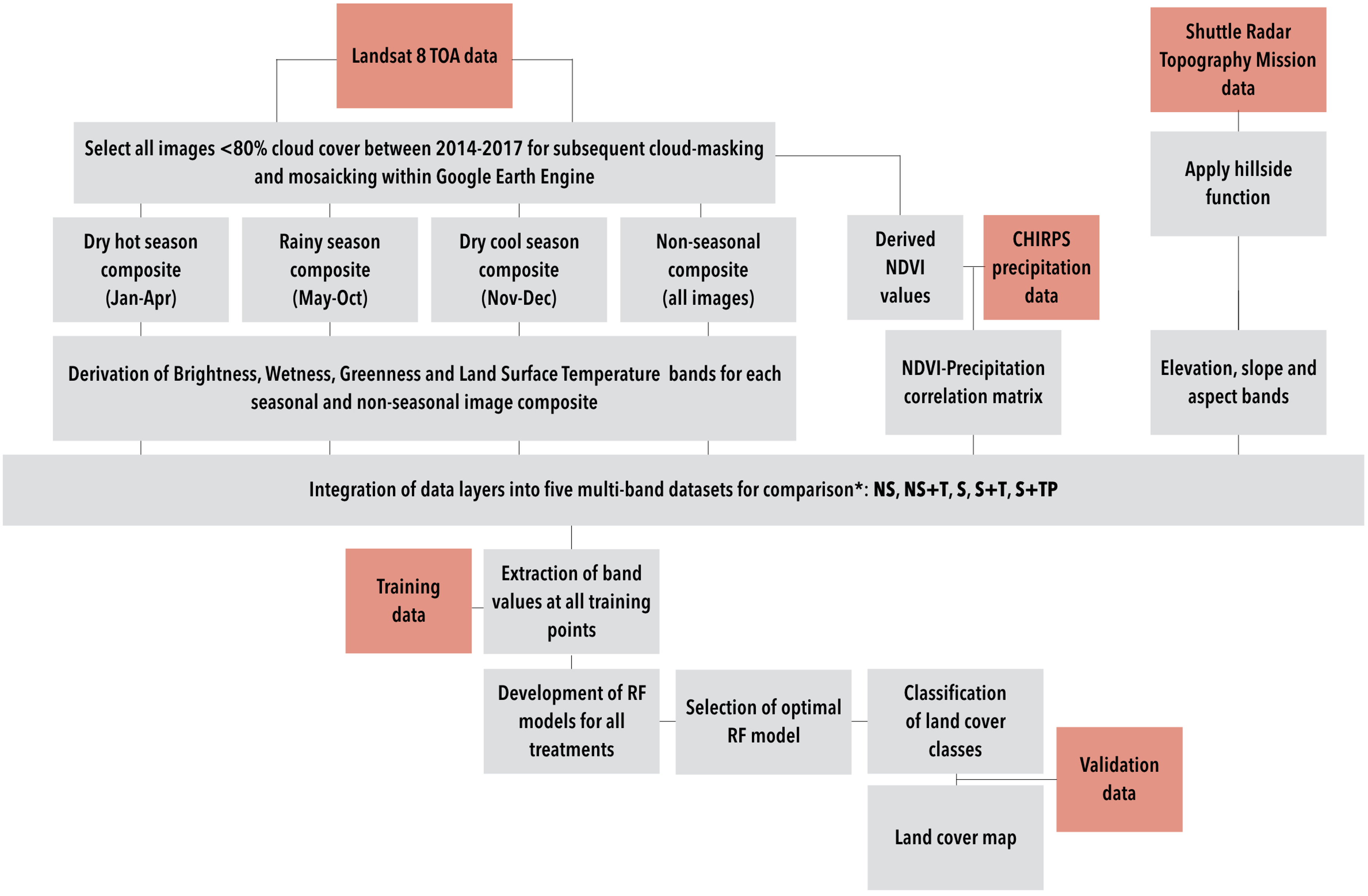
2. Materials and Methods
2.1. Study Area
2.2. Land-Cover Classification Categories
2.3. Landsat Imagery
2.4. Development of Multi-Seasonal and Non-Seasonal Image Composites
2.5. Kauth–Thomas Linear Transformation
2.6. Land Surface Temperature, Topography, and Precipitation
2.7. Training and Validation Data
2.8. Classification with Random Forest
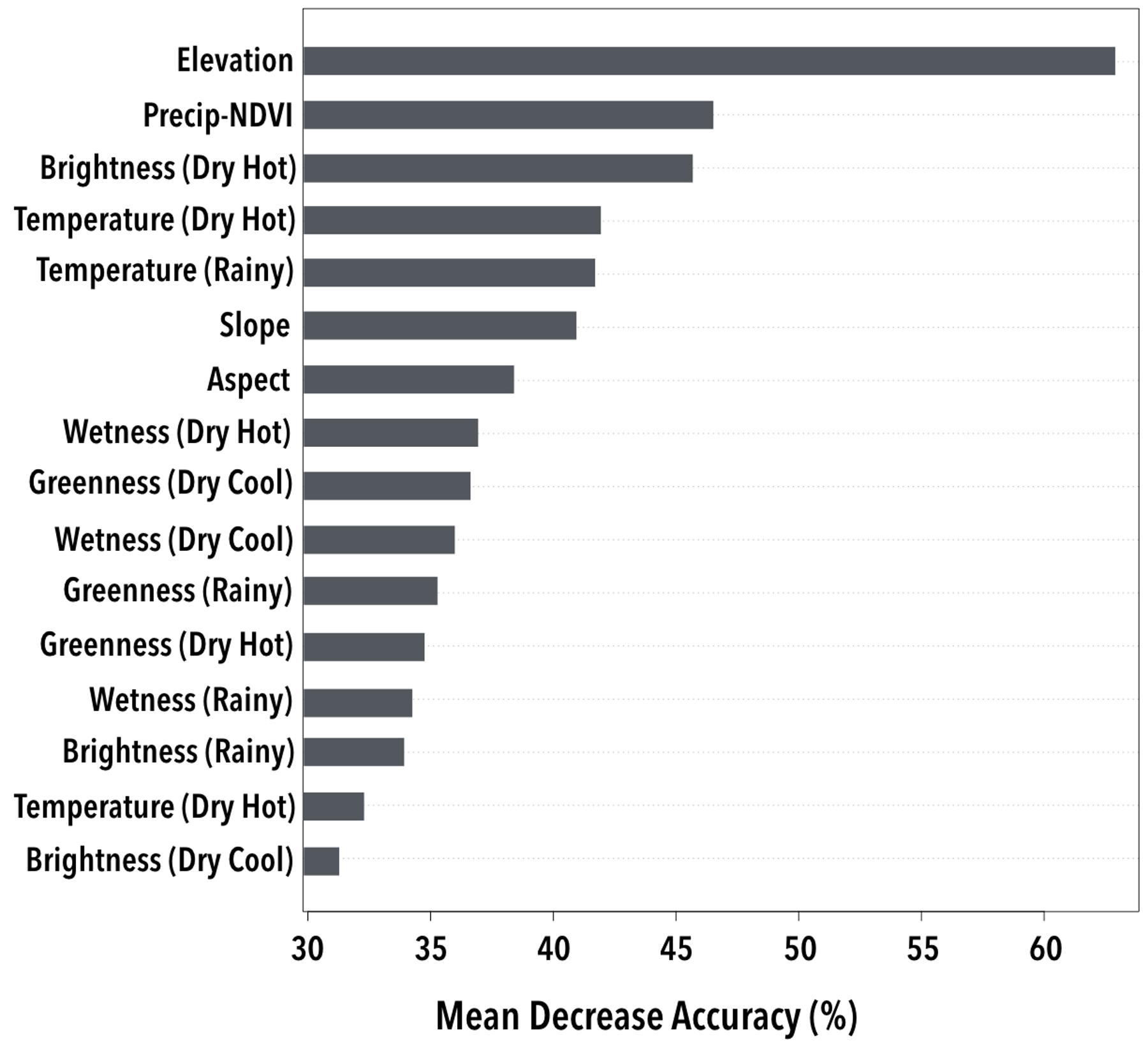
2.9. Accuracy and Variable Importance Assessments
3. Results
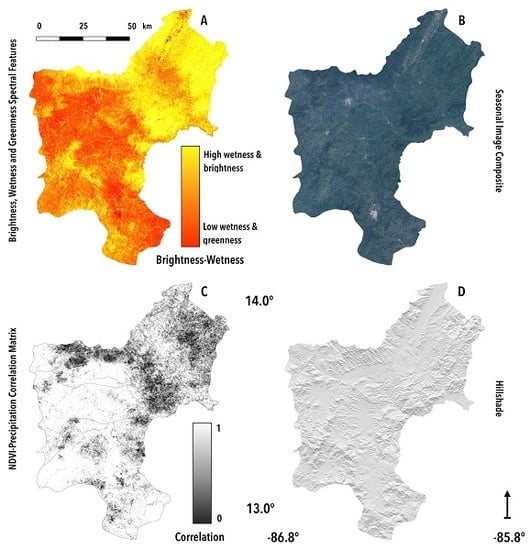
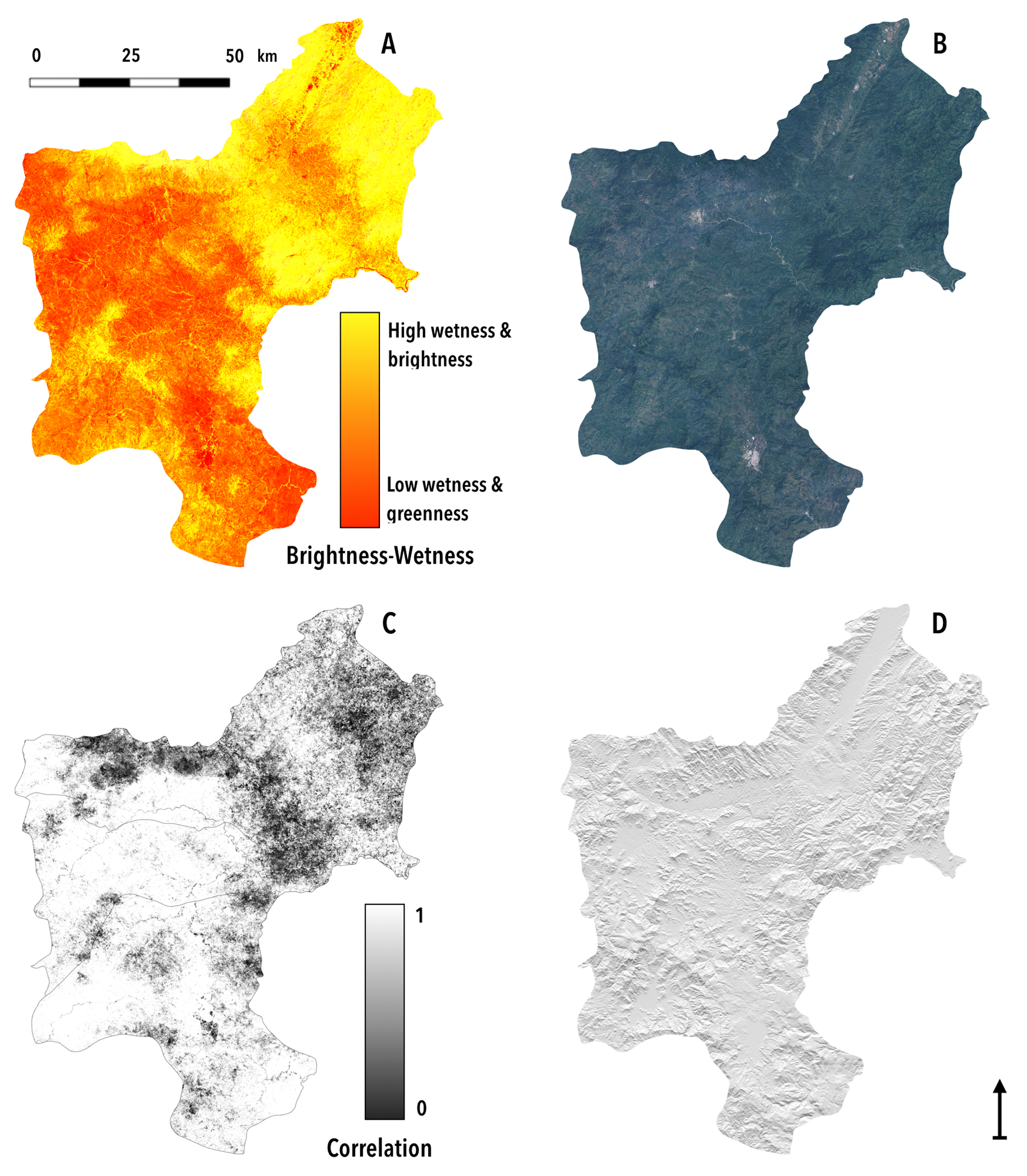
The Distribution of Shade-Grown Coffee in Northern Nicaragua
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Perfecto, I.; Rice, R.A.; Greenberg, R.; Van der Voort, M.E. Shade coffee: A disappearing refuge for biodiversity. BioScience 1996, 46, 598–608. [Google Scholar] [CrossRef]
- Moguel, P.; Toledo, V.M. Biodiversity conservation in traditional coffee systems of Mexico. Conserv. Biol. 1999, 13, 11–21. [Google Scholar] [CrossRef]
- Jha, S.; Bacon, C.M.; Philpott, S.M.; Ernesto Méndez, V.; Läderach, P.; Rice, R.A. Shade coffee: Update on a disappearing refuge for biodiversity. BioScience 2014, 64, 416–428. [Google Scholar] [CrossRef]
- Getachew, T.; Zavaleta, E.; Shennan, C. Coffee landscapes as refugia for native woody biodiversity as forest loss continues in southwest Ethiopia. Biol. Conserv. 2014, 169, 384–391. [Google Scholar]
- Cerdán, C.R.; Rebolledo, M.C.; Soto, G.; Rapidel, B.; Sinclair, F.L. Local knowledge of impacts of tree cover on ecosystem services in smallholder coffee production systems. Agric. Syst. 2012, 110, 119–130. [Google Scholar] [CrossRef]
- Tscharntke, T.; Clough, Y.; Bhagwat, S.A.; Buchori, D.; Faust, H.; Hertel, D.; Hölscher, D.; Juhrbandt, J.; Kessler, M.; Perfecto, I.; et al. Multifunctional shade-tree management in tropical agroforestry landscapes: A review. J. Appl. Ecol. 2011, 48, 619–629. [Google Scholar] [CrossRef]
- Philpott, S.M.; Arendt, W.J.; Armbrecht, I.; Bichier, P.; Diestch, T.V.; Gordon, C.; Greenberg, R.; Perfecto, I.; Reynoso-Santos, R.; Soto-Pinto, L.; et al. Biodiversity loss in Latin American coffee landscapes: Review of the evidence on ants, birds, and trees. Conserv. Biol. 2008, 22, 1093–1105. [Google Scholar] [CrossRef] [PubMed]
- Imbach, P.; Fung, E.; Hannah, L.; Navarro-Racines, C.E.; Roubik, D.W.; Ricketts, T.H.; Harvey, C.A.; Donatti, C.I.; Läderach, P.; Locatelli, B.; et al. Coupling of pollination services and coffee suitability under climate change. Proc. Natl. Acad. Sci. USA 2017, 114, 10438–10442. [Google Scholar] [CrossRef] [PubMed]
- Perfecto, I.; Vandermeer, J.; Mas, A.; Pinto, L.S. Biodiversity, yield, and shade coffee certification. Ecol. Econ. 2005, 54, 435–446. [Google Scholar] [CrossRef]
- Langford, M.; Bell, W. Land cover mapping in a tropical hillsides environment: A case study in the Cauca region of Colombia. Int. J. Remote Sens. 1997, 18, 1289–1306. [Google Scholar] [CrossRef]
- Cordero-Sancho, S.; Sader, S.A. Spectral analysis and classification accuracy of coffee crops using Landsat and a topographic-environmental model. Int. J. Remote Sens. 2007, 28, 1577–1593. [Google Scholar] [CrossRef]
- Gomez, C.; Mangeas, M.; Petit, M.; Corbane, C.; Hamon, P.; Hamon, S.; De Kochko, A.; Le Pierres, D.; Poncet, V.; Despinoy, M. Use of high-resolution satellite imagery in an integrated model to predict the distribution of shade coffee tree hybrid zones. Remote Sens. Environ. 2010, 114, 2731–2744. [Google Scholar] [CrossRef]
- Ortega-Huerta, M.A.; Komar, O.; Price, K.P.; Ventura, H.J. Mapping coffee plantations with Landsat imagery: An example from El Salvador. Int. J. Remote Sens. 2012, 33, 220–242. [Google Scholar] [CrossRef]
- Carvalho, L.M.T.; Clevers, J.G.P.W.; Skidmore, A.K.; de Jong, S.M. Selection of imagery data and classifiers for mapping Brazilian semi-deciduous Atlantic forests. Int. J. Appl. Earth Obs. Geoinf. 2004, 5, 173–186. [Google Scholar] [CrossRef]
- Moreira, M.A.; Adami, M.; Rudorff, B.F.T. Análise espectral e temporal dacultura do café em imagens Landsat. Pesquisa Agropecuária Brasileira 2004, 39, 223–231. [Google Scholar] [CrossRef]
- Moreira, M.A.; Rudorff, B.F.T.; Barros, M.A.; De Faria, V.G.C.; Adami, M. Geotechnologies to map coffee fields in the states of Minas Gerais and Sao Paulo. Eng. Agric. 2010, 30, 1123–1135. [Google Scholar]
- Chemura, A.; Mutanga, O.; Dube, T. Integrating age in the detection and mapping of incongruous patches in coffee (Coffea arabica) plantations using multi-temporal Landsat 8 NDVI anomalies. Int. J. Appl. Earth Obs. Geoinf. 2017, 57, 1–13. [Google Scholar] [CrossRef]
- Mukashema, A.; Veldkamp, A.; Vrieling, A. Automated high resolution mapping of coffee in Rwanda using an expert Bayesian network. Int. J. Appl. Earth Obs. Geoinf. 2014, 33, 331–340. [Google Scholar] [CrossRef]
- Hansen, M.C.; Loveland, T.R. A review of large area monitoring of land cover change using Landsat data. Remote Sens. Environ. 2012, 122, 66–74. [Google Scholar] [CrossRef]
- Luvall, J.C.; Lieberman, D.; Lieberman, M.; Hartshorn, G.S.; Peralta, R. Estimation of tropical forest canopy temperatures, thermal response numbers, and evapotranspiration using aircraft-based thermal sensor. Photogramm. Eng. Remote Sens. 1990, 56, 1393–1401. [Google Scholar]
- Zhu, X.; Liu, D. Accurate mapping of forest types using dense seasonal Landsat time series. ISPRS J. Photogramm. Remote Sens. 2014, 96, 1–11. [Google Scholar] [CrossRef]
- Gao, T.; Zhu, J.; Zheng, X.; Shang, G.; Huang, L.; Wu, S. Mapping spatial distribution of larch plantations from multi-seasonal Landsat-8 OLI imagery and multi-scale textures using random forests. Remote Sens. 2015, 7, 1702–1720. [Google Scholar] [CrossRef]
- Xiong, J.; Thenkabail, P.S.; Tilton, J.C.; Gumma, M.K.; Teluguntla, P.; Oliphant, A.; Congalton, R.G.; Yadav, K.; Gorelick, N. Nominal 30-m cropland extent map of continental Africa by integrating pixel-based and object-based algorithms using Sentinel-2 and Landsat-8 data on Google Earth Engine. Remote Sens. 2016, 9, 1065. [Google Scholar] [CrossRef]
- Chrysafis, I.; Mallinis, G.; Gitas, I.; Tsakiri-Strati, M. Estimating Mediterranean forest parameters using multi seasonal Landsat 8 OLI imagery and an ensemble learning method. Remote Sens. Environ. 2017, 199, 154–166. [Google Scholar] [CrossRef]
- Aguilar, R.; Zurita-Milla, R.; Izquierdo-Verdiguier, E.; de By, R.A. A cloud-based multi-temporal ensemble classifier to map smallholder farming systems. Remote Sens. 2018, 10, 729. [Google Scholar]
- Misra, G.; Kumar, A.; Patel, N.R.; Zurita-Milla, R. Mapping a Specific Crop-A Temporal Approach for Sugarcane Ratoon. J. Indian Soc. Remote Sens. 2014, 42, 325–334. [Google Scholar] [CrossRef]
- Hu, Q.; Wu, W.; Song, Q.; Lu, M.; Chen, D.; Yu, Q.; Tang, H. How do temporal and spectral features matterin crop classification in Heilongjiang Province, China? J. Integr. Agric. 2017, 16, 324–336. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Chica-Olmo, M. Land cover change analysis of a Mediterranean area in Spain using different sources of data: Multi-seasonal Landsat images, land surface temperature, digital terrain models and texture. Appl. Geogr. 2012, 35, 208–218. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.R.; Chica-Olmo, M.; Abarca-Hernandez, F.; Atkinson, P.M.; Jeganathan, C. Random forest classification of Mediterranean land cover using multi-seasonal imagery and multi-season texture. Remote Sens. Environ. 2012, 121, 93–107. [Google Scholar] [CrossRef]
- Wulder, M.A.; Masek, J.G.; Cohen, W.B.; Loveland, T.R.; Woodcock, C.E. Opening the archive: How free data has enabled the science and monitoring promise of Landsat. Remote Sens. Environ. 2012, 122, 2–10. [Google Scholar] [CrossRef]
- Crawford, C.J.; Manson, S.M.; Bauer, M.E.; Hall, D.K. Multitemporal snow cover mapping in mountainous terrain for Landsat climate data record development. Remote Sens. Environ. 2013, 135, 224–233. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-resolution global maps of 21st century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Kelley, L.C.; Evans, S.G.; Potts, M.D. Richer histories for more relevant policies: 42 years of tree cover loss and gain in Southeast Sulawesi, Indonesia. Glob. Chang. Biol. 2016. [Google Scholar] [CrossRef] [PubMed]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Gaertner, J.; Genovese, V.B.; Potter, C.; Sewake, K.; Manoukis, N.C. Vegetation classification of Coffea on Hawaii Island using WorldView-2 satellite imagery. J. Appl. Remote Sens. 2017, 11, 046005. [Google Scholar] [CrossRef]
- Cooley, S.W.; Smith, L.C.; Stepan, L.; Mascaro, J. Tracking Dynamic Northern Surface Water Changes with High-Frequency Planet CubeSat Imagery. Remote Sens. 2017, 9, 1306. [Google Scholar] [CrossRef]
- Perfecto, I.; Vandermeer, J.; Wright, A. Nature’s Matrix: Linking Agriculture, Conservation and Food Sovereignty, 1st ed.; Earthscan: London, UK, 2009. [Google Scholar]
- Cerda, F.; Flores, N.; Toval Hernández, K.I. Diversidad y Usos de la Fauna Silvestre en el Parque Ecológico Municipal Cerro Canta Gallo, Telpaneca, Condega, Nicaragua. Ph.D. Thesis, Universidad Nacional Agraria, Managua, Nicaragua, 2009. [Google Scholar]
- Kauth, R.J.; Thomas, G.S. The Tasseled Cap—A graphic description of the spectral-temporal development of agricultural crops as seen by Landsat. In Proceedings of the Symposium on Machine Processing of Remotely Sensed Data, Purdue University, West Lafayette, IN, USA, 29 June–1 July 1976; pp. 4b41–4b51. [Google Scholar]
- Huang, C.; Wylie, B.; Yang, L.; Homer, C.; Zylstra, G. Derivation of a tasselled cap transformation based on Landsat 7 at-satellite reflectance. Int. J. Remote Sens. 2002, 23, 1741–1748. [Google Scholar] [CrossRef]
- Yarbrough, L.D.; Easson, G.; Kuszmaul, J.S. Proposed workflow for improved Kauth–Thomas transform derivations. Remote Sens. Environ. 2012, 124, 810–818. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Taylor, B.W. An outline of the vegetation of Nicaragua. J. Ecol. 1963, 51, 27–54. [Google Scholar] [CrossRef]
- INIFOM Municipios Instituto Nicaragüense de Fomento Municipal. Available online: http://www.inifom.gob.ni/municipios/municipios.html (accessed on 10 July 2015).
- Gourdji, S.; Laderach, P.; Martinez Valle, A.; Zelaya Martinez, C.; Lobell, D. Historical climate trends, deforestation, and maize and bean yields in Nicaragua. Agric. For. Meteorol. 2015, 200, 270–281. [Google Scholar] [CrossRef]
- USGS (United States Geological Survey). Landsat Collection 1 Level 1 Product Definition. Version 1.0. United States Geological Survey, Department of Interior 2017, Version 1.0. Available online: https://landsat.usgs.gov/sites/default/files/documents/LSDS-1656_Landsat_Level-1_Product_Collection_Definition.pdf (accessed on 1 May 2018).
- Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar] [CrossRef]
- Chander, G.; Markham, B.L.; Barsi, J.A. Revised Landsat-5 thematic mapper radiometric calibration. IEEE Geosci. Remote Sens. Lett. 2007, 4, 490–494. [Google Scholar] [CrossRef]
- Song, C.; Woodcock, C.E.; Seto, K.C.; Lenney, M.P.; Macomber, S.A. Classification and change detection using Landsat TM data: When and how to correct atmospheric effects? Remote Sens. Environ. 2001, 75, 230–244. [Google Scholar] [CrossRef]
- Baig, M.H.A.; Zhang, L.; Shuai, T.; Tong, Q. Derivation of a tasselled cap transformation based on Landsat 8 at-satellite reflectance. Remote Sens. Lett. 2014, 5, 423–431. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, G.; Huang, C.; Xie, C. Comparison of tasselled cap transformations based on the selective bands of Landsat 8 OLI TOA reflectance images. Int. J. Remote Sens. 2015, 36, 417–441. [Google Scholar] [CrossRef]
- Tasseled Cap Transformation of Landsat 8 Surface Reflectance. Available online: https://groups.google.com/forum/?utm_source=digest&utm_medium=email#!searchin/google-earth-engine-developers/TOA$20cap$20transformation$20$20%7Csort:date/google-earth-engine-developers/sj_IY7ZXipw/MZ8QsKK2BwAJ (accessed on 28 March 2018).
- Dong, J.; Xiao, X.; Menarguez, M.A.; Zhang, G.; Qin, Y.; Thau, D.; Biradar, C.; Moore, B., III. Mapping paddy rice planting area in northeastern Asia with Landsat 8 images, phenology-based algorithm and Google Earth Engine. Remote Sens. Environ. 2016, 185, 142–154. [Google Scholar] [CrossRef] [PubMed]
- Orengo, H.A.; Petrie, C.A. Large-scale, multi-temporal remote sensing of paleo-river networks: A case study from Northwest India and its implications for the Indus Civilisation. Remote Sens. 2017, 9, 735. [Google Scholar] [CrossRef]
- Landsat Composite Methods and Earth Engine Algorithms. Available online: https://docs.google.com/document/d/14fNqbm8-oguRylapdhmif-tLckYI-87RbKiPfckc5N0/edit#heading=h.c855pzu7ubf3 (accessed on 30 May 2018).
- Hansen, M.C.; Stehman, S.V.; Potapov, P.V.; Loveland, T.R.; Townshend, J.R.G.; DeFries, R.S.; Pittman, K.W.; Arunarwati, B.; Stolle, F.; Steininger, M.K.; et al. Humid tropical forest clearing from 2000 to 2005 quantified by using multitemporal and multiresolution remotely sensed data. Proc. Natl. Acad. Sci. USA 2008, 105, 9439–9444. [Google Scholar] [CrossRef] [PubMed]
- Potapov, P.V.; Turubanova, S.A.; Hansen, M.C.; Adusei, B.; Broich, M.; Altstatt, A.; Mane, L.; Justice, C.O. Quantifying forest cover loss in Democratic Republic of the Congo, 2000–2010, with Landsat ETM + data. Remote Sens. Environ. 2012, 122, 106–116. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.R.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier to land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Crist, E.P.; Cicone, R.C. A physically-based transformation of Thematic Mapper data—The TM Tasseled Cap. IEEE Trans. Geosci. Remote Sens. 1984, 3, 256–263. [Google Scholar] [CrossRef]
- Lobser, S.E.; Cohen, W.B. MODIS Tasselled Cap: Land Cover Characteristics Expressed through Transformed MODIS Data. Int. J. Remote Sens. 2007, 28, 5079–5101. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Time Series Analysis. Available online: http://earthenginesummit2016.earthoutreach.org/training-materials (accessed on 28 March 2018).
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Zhao, K.; Zheng, X.; Jiang, T. Temporal dynamics of spatial heterogeneity over cropland quantified by time-series NDVI, near infrared and red reflectance of Landsat 8 OLI imagery. Int. J. Appl. Earth Obs. Geoinf. 2014, 30, 139–145. [Google Scholar] [CrossRef]
- Glenn, E.P.; Huete, A.R.; Nagler, P.L.; Nelson, S.G. Relationship between remotely-sensed vegetation indices, canopy attributes and plant physiological processes: What vegetation indices can and cannot tell us about the landscape. Sensors 2008, 8, 2136–2160. [Google Scholar] [CrossRef] [PubMed]
- Dalponte, M.; Orka, H.O.; Gobakken, T.; Gianelle, D.; Naesset, E. Tree species classification in boreal forests with hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2632–2645. [Google Scholar] [CrossRef]
- Jin, H.; Stehman, S.V.; Mountrakis, G. Assessing the impact of training sample selection on accuracy of an urban classification: A case study in Denver, Colorado. Int. J. Remote Sens. 2014, 35, 2067–2081. [Google Scholar]
- Hua, J.P.; XIong, Z.C.; Lowey, J.; Suh, E.; Dougherty, E.R. Optimal number of features as a function of sample size for various classification rules. Bioinformatics 2005, 8, 1509–1515. [Google Scholar] [CrossRef] [PubMed]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Google Earth Engine API. Available online: https://developers.google.com/earth-engine/api_docs (accessed on 28 May 2018).
- Guo, L.; Chehata, N.; Mallet, C.; Boukir, S. Relevance of airborne lidar and multispectral image data for urban scene classification using Random Forests. ISPRS J. Photogramm. Remote Sens. 2011, 66, 56–66. [Google Scholar] [CrossRef]
- Lee, J.S.H.; Wich, S.; Widayati, A.; Koh, L.P. Detecting industrial oil palm plantations on Landsat images with Google Earth Engine. Remote Sens. Appl.: Soc. Environ. 2016, 4, 219–224. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Sexton, J.O.; Song, X.P.; Feng, M.; Noojipady, P.; Anand, A.; Huang, C.; Kim, D.H.; Collins, K.M.; Channan, S.; DiMiceli, C.; et al. Global, 30-m resolution continuous fields of tree cover: Landsat-based rescaling of MODIS Vegetation Continuous Fields with lidar-based estimates of error. Int. J. Digit. Earth 2013. [Google Scholar] [CrossRef]
- Läderach, P.; Ramirez–Villegas, J.; Navarro-Racines, C.; Zelaya, C.; Martinez–Valle, A.; Jarvis, A. Climate change adaptation of coffee production in space and time. Clim. Chang. 2017, 141, 47–62. [Google Scholar] [CrossRef]
- Maurer, E.P.; Roby, N.; Stewart-Frey, I.T.; Bacon, C.M. Projected twenty-first-century changes in the Central American mid-summer drought using statistically downscaled climate projections. Reg. Environ. Chang. 2017, 17, 2421–2432. [Google Scholar] [CrossRef]
- Millard, K.; Richardson, M. On the importance of training data sample selection in random forest image classification: A case study in peatland ecosystem mapping. Remote Sens. 2015, 7, 8489–8515. [Google Scholar] [CrossRef]
- Bandeira, F.P.; Martorell, C.; Meave, J.A.; Caballero, J. The role of rustic coffee plantations in the conservation of wild tree diversity in the Chinantec region of Mexico. Biodivers. Conserv. 2005, 14, 1225–1240. [Google Scholar] [CrossRef]
- Soto-Pinto, L.; Romero-Alvarado, Y.; Caballero-Nieto, J.; Segura Warnholtz, G. Woody plant diversity and structure of shade-grown-coffee plantations in Northern Chiapas, Mexico. Rev. Biol. Trop. 2001, 49, 977–987. [Google Scholar] [PubMed]
- Soto-Pinto, L.; Villalvazo-López, V.; Jiménez-Ferrer, G.; Ramírez-Marcial, N.; Montoya, G.; Sinclair, F.L. The role of local knowledge in determining shade composition of multistrata coffee systems in Chiapas, Mexico. Biodivers. Conserv. 2007, 16, 419–436. [Google Scholar] [CrossRef]
| Dataset | Use | Resolution | Source |
|---|---|---|---|
| Landsat 8 TOA Reflectance | Spectral indices; land surface temperature data; NDVI trajectories | Spatial: 30 m Date range: 2014–2017 | USGS/NASA |
| CHIRPS Precipitation Data | Construction of NDVI-precipitation correlation matrix | Spatial: 0.05° Date range: 2014–2017 | Funk et al. (2014) |
| Shuttle Radar Topography Mission | Digital Elevation Raster | Spatial: 30 m | STRM, NASA |
| Tree Canopy Coverage | Data validation | Spatial: 30 m Date range: 2010 | Sexton et al. (2013) |
| Class | Description |
|---|---|
| “Milpa” (1) | Open area seasonally covered by rotational corn and bean crops (first cycle: May–August, second cycle: September–November) |
| Multi-Use Pasture (2) | Open area predominantly covered by grass species though some woody tree species, including Pinus species, are occasionally present (<30% cover) |
| Pine Stands (3) | Forested area predominantly covered by Pinus species (>30% cover) |
| Pine-Oak Forests (4) | Forested area predominantly covered by mixed Pinus species and Querus species (>30% cover) |
| Semi-Humid Broadleaf Forests (5) | Forested area (>30% cover) typically found at higher elevations; can consist of as much as 75% facultative deciduous species |
| Deciduous Dry Forest (6) | Forested area (>30% cover) typically found at lower elevations; consists of 75–100% deciduous species |
| Shade Coffee (7) | Agroforested area (>30% tree cover) predominantly covered by coffee production, and diverse deciduous and evergreen shade trees |
| Built (8) | Urban area, roads, other constructed settlement areas |
| Water (9) | Water bodies |
| Wet Rice (10) | Irrigated rice fields |
| Dataset | Bands | Data Layers |
|---|---|---|
| NS | 4 | Non-seasonal brightness, greenness, wetness, and land surface temperature data |
| NS+T | 7 | NS dataset; elevation, slope, and aspect data |
| S | 12 | All seasonal (dry hot, rainy, and dry cool) brightness, greenness, wetness, and land surface temperature data |
| S+T | 15 | S dataset; elevation, slope, and aspect data |
| S+TP | 16 | S+T dataset; precipitation-NDVI correlation matrix |
| S+TP | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Total | UA | PA |
| 1 | 34 | 2 | 0 | 0 | 0 | 1 | 2 | 2 | 0 | 0 | 41 | 82.9 | 85.0 |
| 2 | 0 | 33 | 0 | 1 | 0 | 1 | 0 | 2 | 0 | 0 | 37 | 89.1 | 82.5 |
| 3 | 1 | 2 | 40 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 44 | 90.9 | 100 |
| 4 | 0 | 0 | 0 | 38 | 0 | 0 | 1 | 0 | 0 | 0 | 39 | 97.4 | 95.0 |
| 5 | 0 | 1 | 0 | 0 | 37 | 0 | 4 | 0 | 0 | 0 | 42 | 88.1 | 92.5 |
| 6 | 3 | 2 | 0 | 0 | 0 | 38 | 0 | 2 | 0 | 0 | 45 | 84.4 | 95.0 |
| 7 | 1 | 0 | 0 | 1 | 3 | 0 | 32 | 2 | 0 | 0 | 39 | 82.1 | 80.0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 31 | 1 | 0 | 32 | 96.9 | 77.5 |
| 9 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 38 | 0 | 39 | 97.4 | 97.4 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 40 | 41 | 97.6 | 100 |
| Total | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 39 | 40 | 361/399 | OA: 90.5% | |
| Kappa: 0.89 | |||||||||||||
| Dataset | NS | NS+T | S | S+T | S+TP |
|---|---|---|---|---|---|
| Number of variables | 4 | 7 | 12 | 15 | 16 |
| mtry | 3 | 3 | 7 | 3 | 3 |
| Overall Accuracy (%) | 65.6% | 85.7% | 81.7% | 89.5% | 90.5% |
| Kappa Index | 0.62 | 0.84 | 0.80 | 0.88 | 0.89 |
| ID | Class | NS | NS+T | S | S+T | S+TP |
|---|---|---|---|---|---|---|
| 1 | “Milpa” | 34.1 (37.5) | 81.6 (77.5) | 59.5 (62.5) | 92.1 (87.5) | 82.9 (85.0) |
| 2 | Multi-Use Pasture | 68.6 (60.0) | 75.6 (77.5) | 79.4 (67.5) | 75.6 (77.5) | 89.1 (82.5) |
| 3 | Pine Stands | 76.0 (95.0) | 95.2 (100) | 88.9 (100) | 95.2 (100) | 90.9 (100) |
| 4 | Pine-Oak Forests | 65.6 (52.5) | 94.7 (90.0) | 86.8 (82.5) | 100 (95.0) | 97.4 (95.0) |
| 5 | Broadleaf Forest | 75.0 (82.5) | 81.8 (90.0) | 83.3 (87.5) | 86.4 (95.0) | 88.1 (92.5) |
| 6 | Deciduous Forest | 52.8 (70.0) | 80.9 (95.0) | 80.4 (92.5) | 83.0 (97.5) | 84.4 (95.0) |
| 7 | Shade Coffee | 77.1 (67.5) | 81.2 (75.0) | 73.7 (70.0) | 86.5 (80.0) | 82.1 (80.0) |
| 8 | Built/Constructed | 68.8 (55.0) | 78.1 (62.5) | 78.8 (65.0) | 84.4 (67.5) | 96.9 (77.5) |
| 9 | Wet Rice | 94.6 (89.7) | 97.4 (94.5) | 97.4 (94.9) | 97.4 (94.9) | 97.4 (97.4) |
| 10 | Water | 51.4 (47.5) | 90.5 (95.0) | 88.4 (95.0) | 95.2 (100) | 97.6 (100) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kelley, L.C.; Pitcher, L.; Bacon, C. Using Google Earth Engine to Map Complex Shade-Grown Coffee Landscapes in Northern Nicaragua. Remote Sens. 2018, 10, 952. https://doi.org/10.3390/rs10060952
Kelley LC, Pitcher L, Bacon C. Using Google Earth Engine to Map Complex Shade-Grown Coffee Landscapes in Northern Nicaragua. Remote Sensing. 2018; 10(6):952. https://doi.org/10.3390/rs10060952
Chicago/Turabian StyleKelley, Lisa C., Lincoln Pitcher, and Chris Bacon. 2018. "Using Google Earth Engine to Map Complex Shade-Grown Coffee Landscapes in Northern Nicaragua" Remote Sensing 10, no. 6: 952. https://doi.org/10.3390/rs10060952
APA StyleKelley, L. C., Pitcher, L., & Bacon, C. (2018). Using Google Earth Engine to Map Complex Shade-Grown Coffee Landscapes in Northern Nicaragua. Remote Sensing, 10(6), 952. https://doi.org/10.3390/rs10060952