East Africa Rainfall Trends and Variability 1983–2015 Using Three Long-Term Satellite Products
Abstract
1. Introduction
2. Data and Methodologies
2.1. Satellite Rainfall Products
- CPC Africa Rainfall Climatology version 2.0 (ARC2) is a daily climatological dataset centered over Africa (40S–40N and 20W–55E) with a spatial resolution of 0.1° starting from 1983 and updated in near-real time [25]. The dataset guarantees an historical consistency through the use of a single retrieval algorithm based on the use of calibrated three-hourly IR satellite imagery with quality-controlled gauge observations from the Global Telecommunication System (GTS), and is particularly suited for studies of extreme events, wet and dry spells, and rainfall frequency. The algorithm is based on the use of the Geostationary Operational Environmental Satellite (GOES) Precipitation Index (GPI), whose rainfall estimates are combined in a two-step merging methodology with the GTS rain gauge measurements.
- TAMSAT African Rainfall Climatology And Time series (TARCAT), version 2, contains rainfall estimation over Africa at a spatial resolution of 0.0375°, and provides daily estimates since 1983 [26,27,28]. The main input data are the IR brightness temperatures from Meteosat platforms. The number of hours for which a given satellite pixel is associated with a temperature lower than a specific threshold value over a 10-day period, i.e., the cold cloud duration (CCD), is the basis of this algorithm, and is linearly related to precipitation over the same time period. The threshold temperature and the linear relationship coefficients are estimated for a given region and time of the year (month) by means of the analysis of historic rain gauge data relative to that region and time of the year. This calibration methodology based on a historical rain gauge dataset, rather than on simultaneous rain gauge observations, makes TARCAT useful for climate-related risk assessment, even in regions with insufficient gauge coverage.
- Climate Hazards Group InfraRed Precipitation with Stations (CHIRPS) version 2.0 starts from 1981 to near present with a quasi-global land coverage (50S–50N) and a 0.05° spatial resolution; it was designed for studies on hydrologic impacts and trend analysis [29]. The algorithm dwells on pentadal CCDs obtained with a fixed IR brightness temperature threshold (235 K) to identify precipitating cloud systems. The CCD’s calibration method makes use of the Tropical Rainfall Measuring Mission (TRMM) Multi-satellite Precipitation Analysis (TMPA 3B42 v7). These IR rainfall estimates are converted to percent anomalies, and subsequently multiplied by the high-resolution climatology CHPclim to produce unbiased precipitation fields. Finally, rain gauge data are combined with the previous precipitation estimates to obtain rain gauge adjusted estimates. The number of gauges is higher than for ARC2 since additional gauges from National Meteorological Agencies are included.
2.2. Analysis Methodologies
2.2.1. Time Series Homogenization
2.2.2. CCL/CLIVAR/JCOMM ETCCDI Rainfall Indices
2.2.3. Trend Analysis
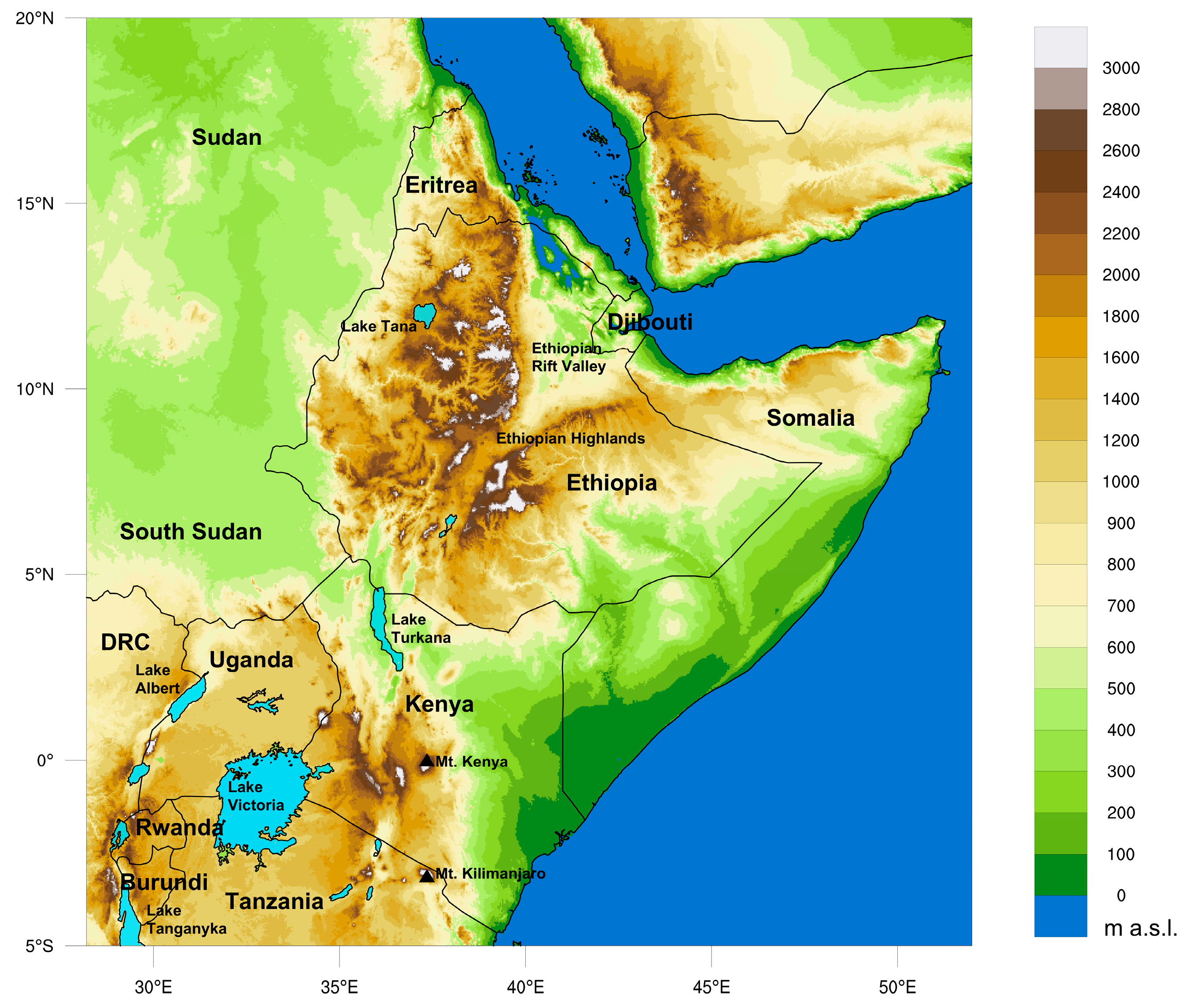
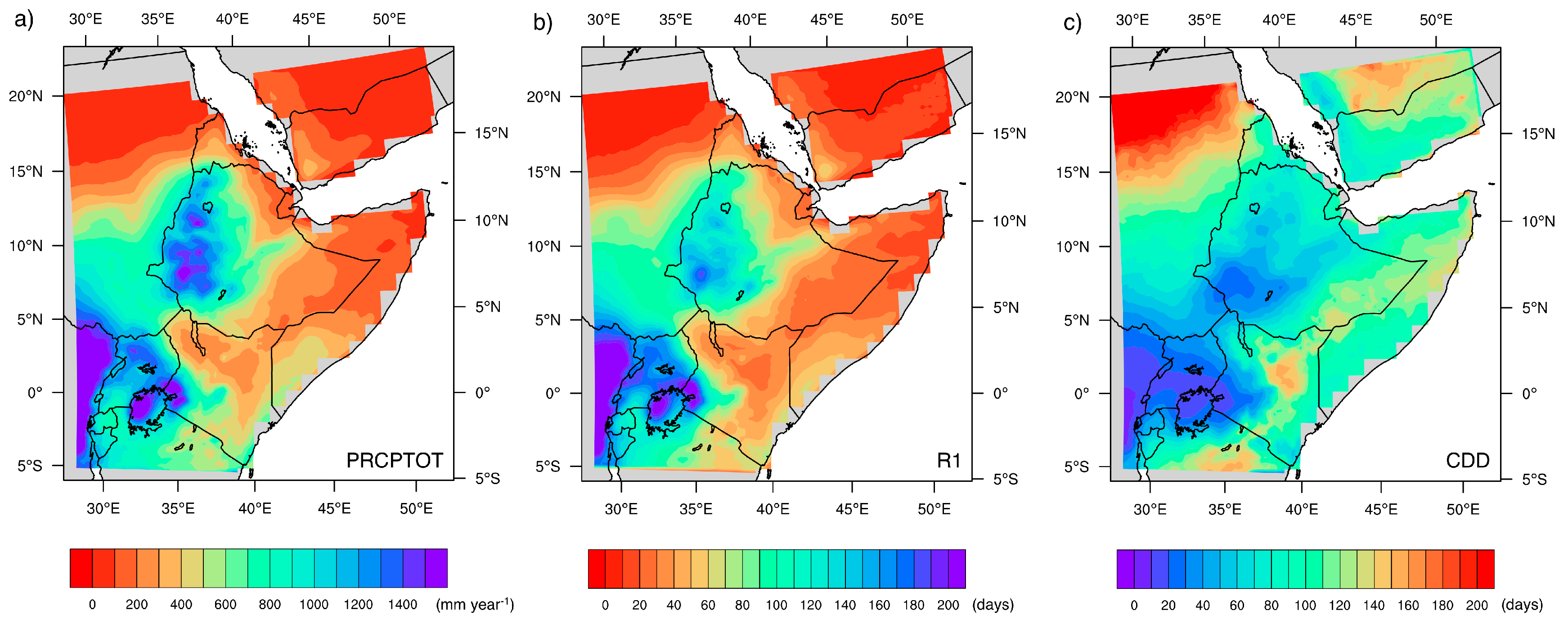
3. East Africa Annual and Seasonal Rainfall Climatology
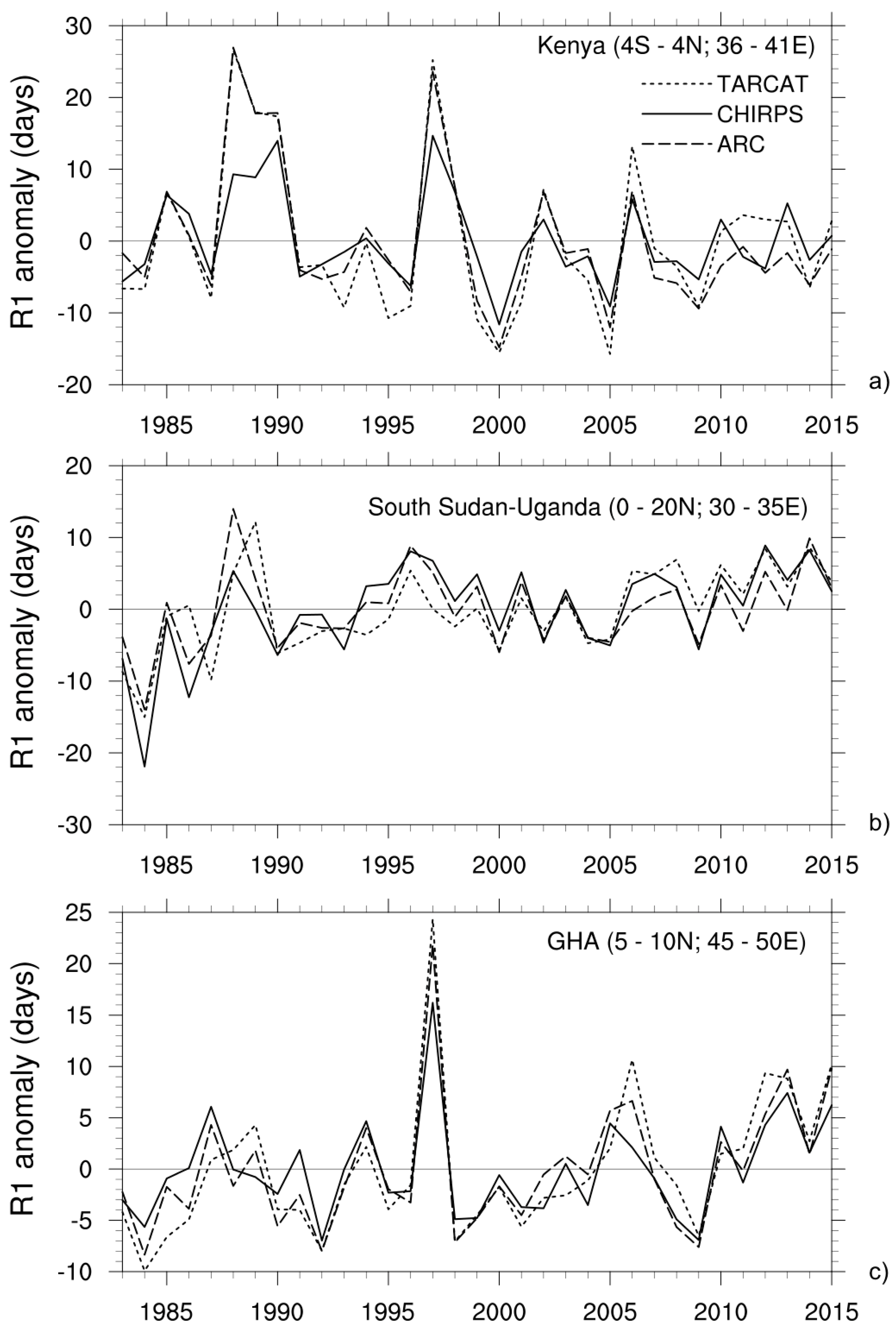
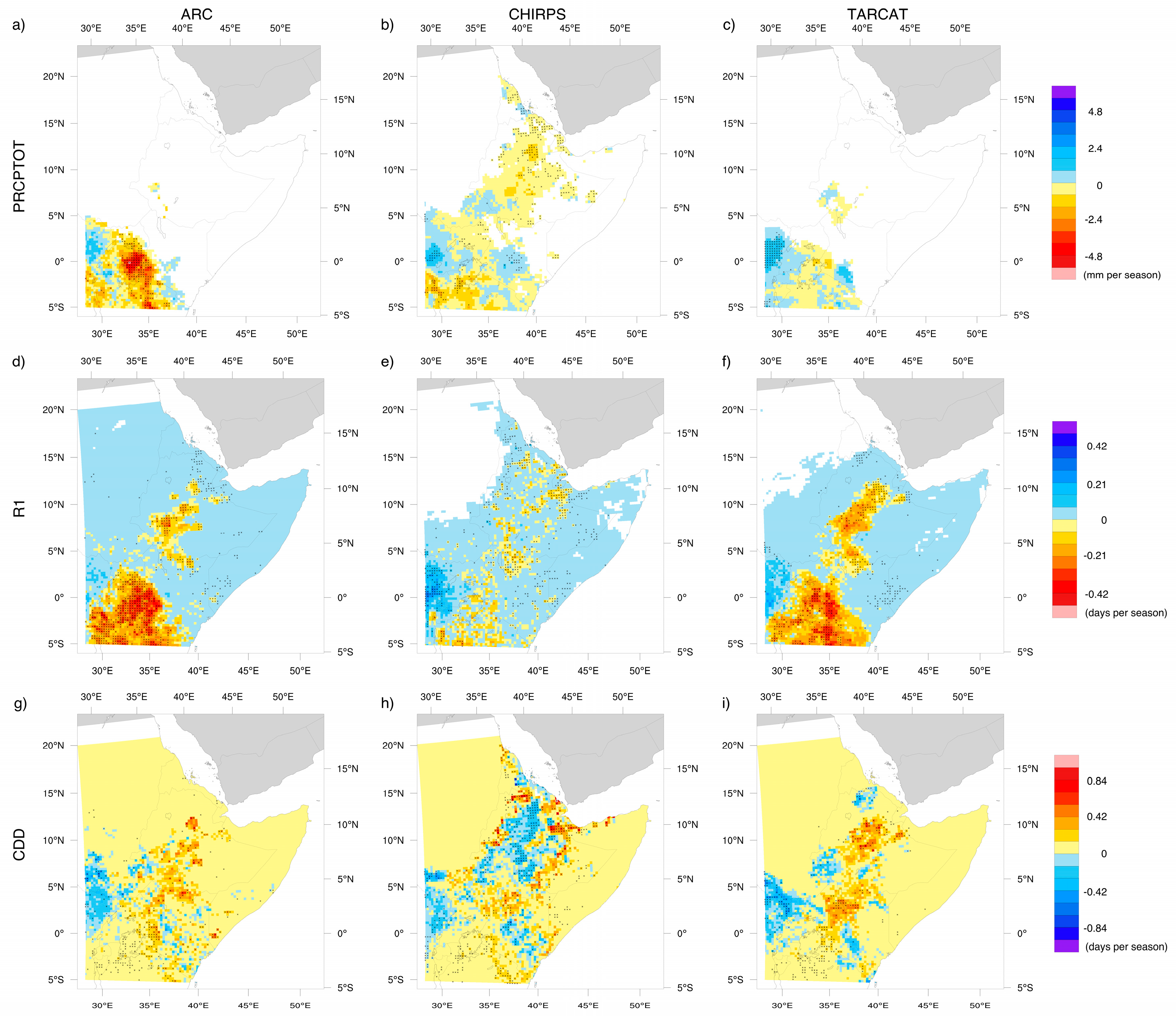
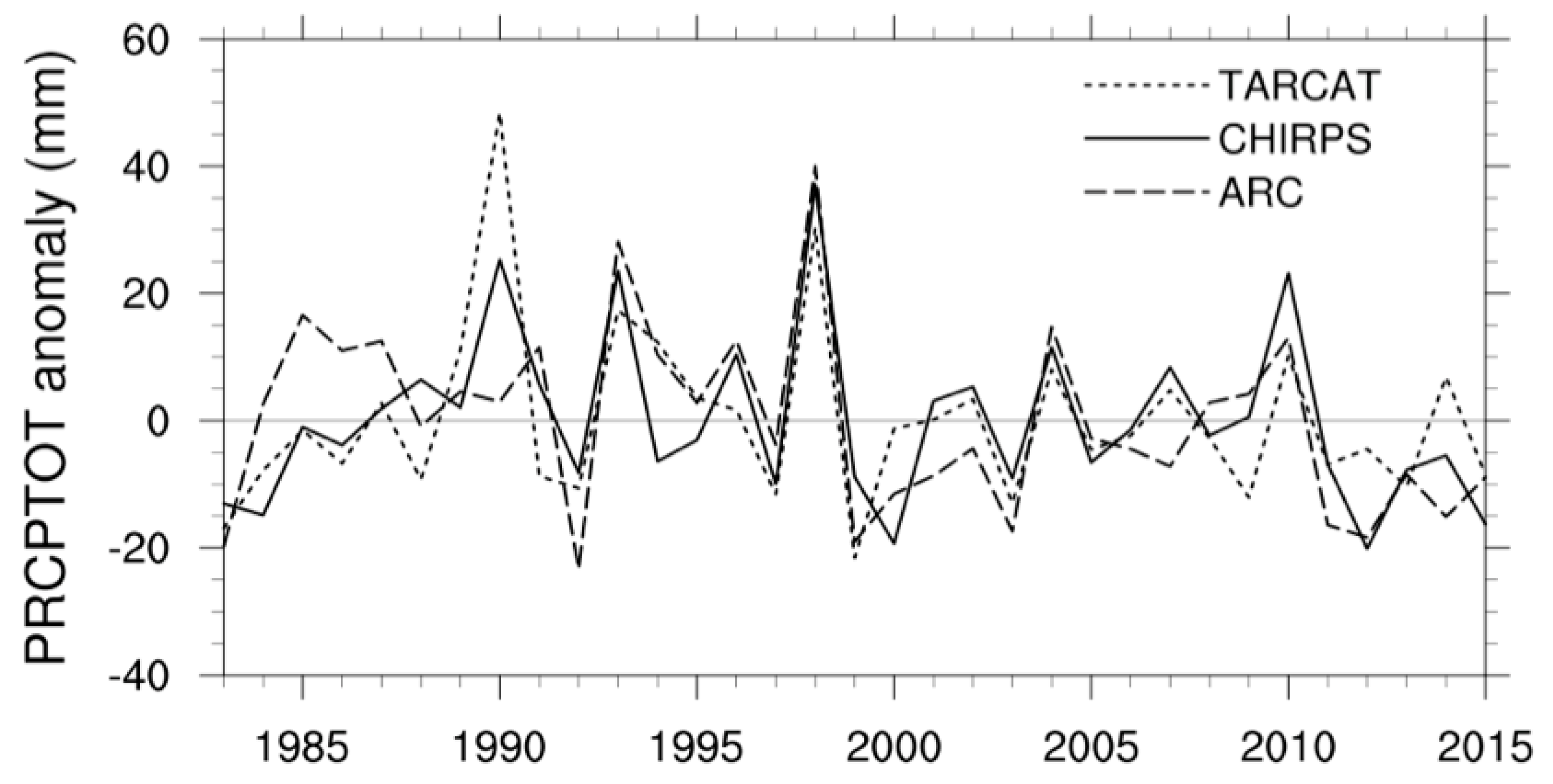
4. Trend Analysis Results
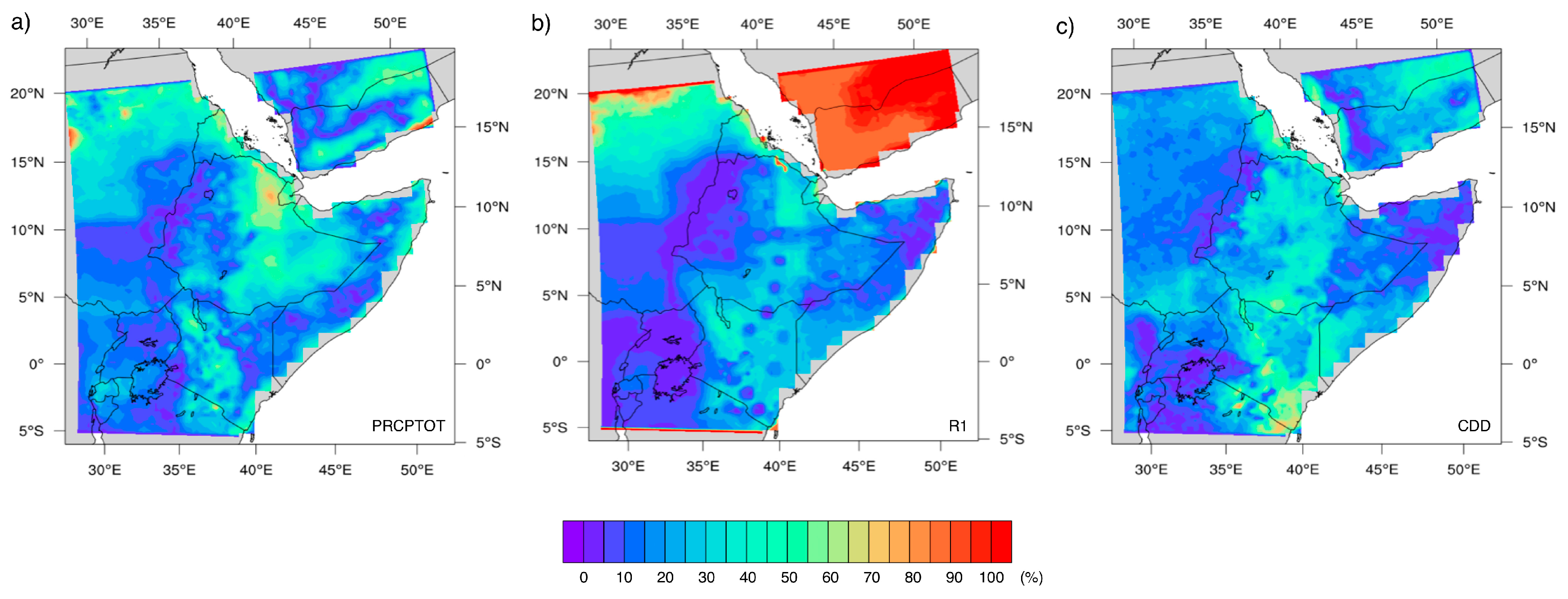
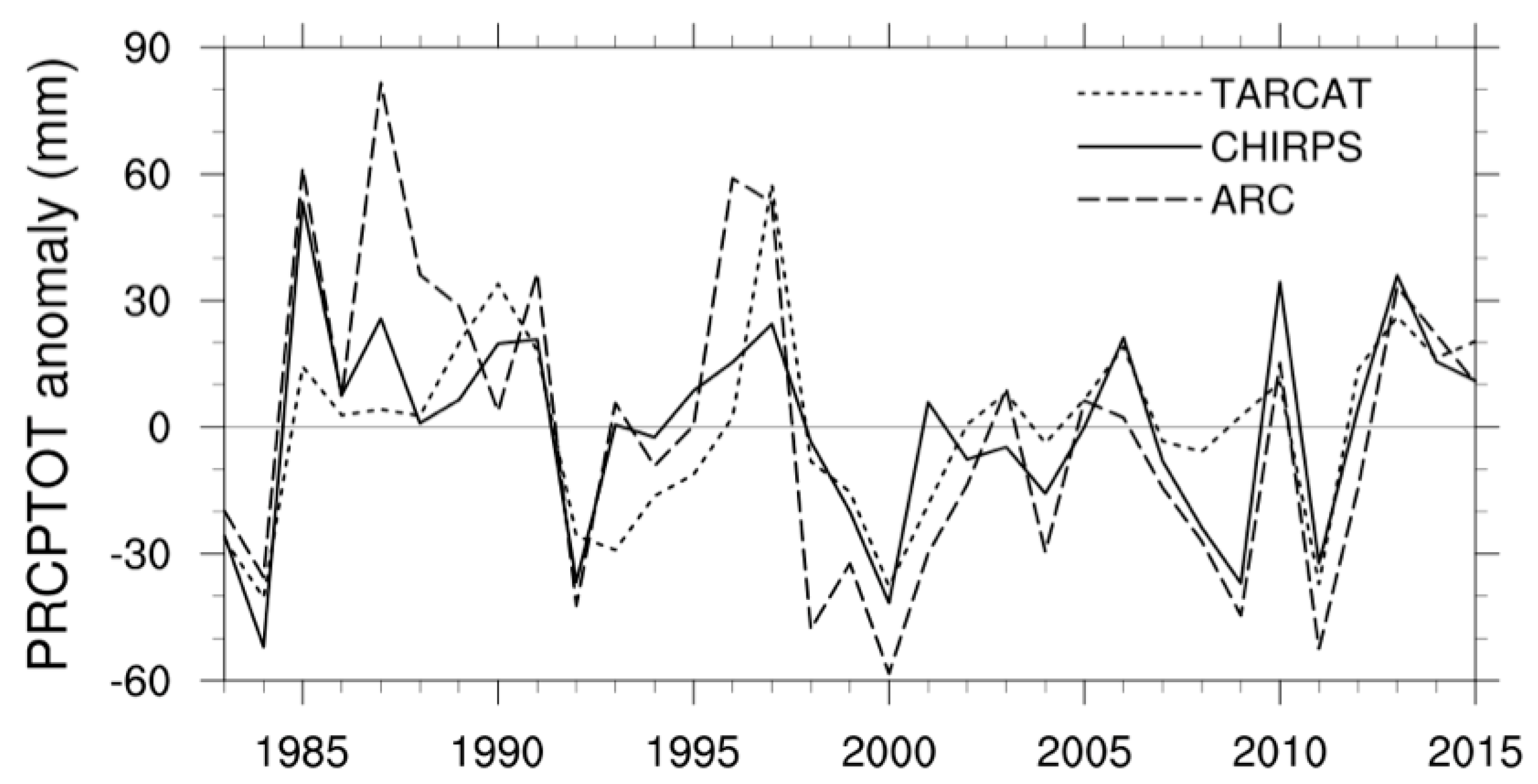
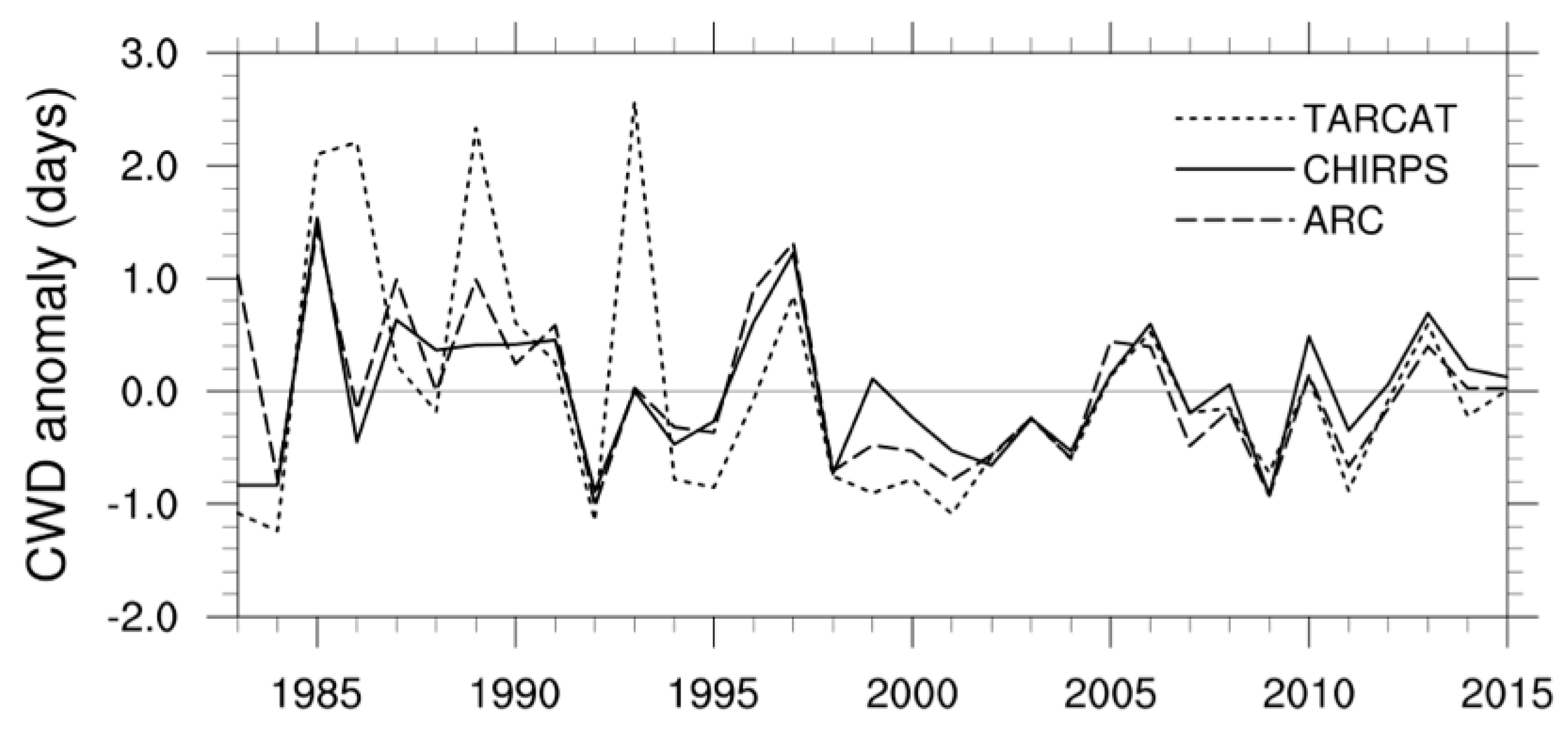
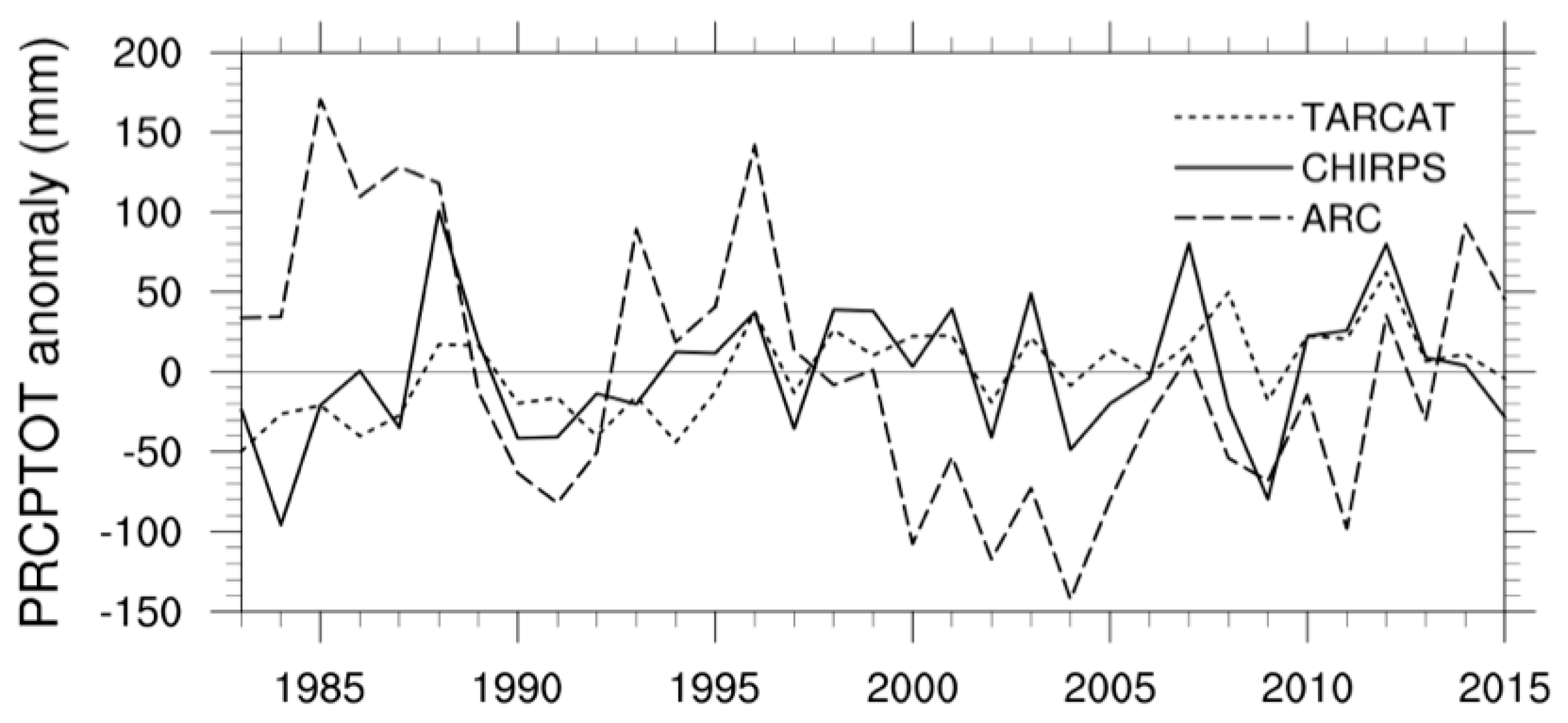
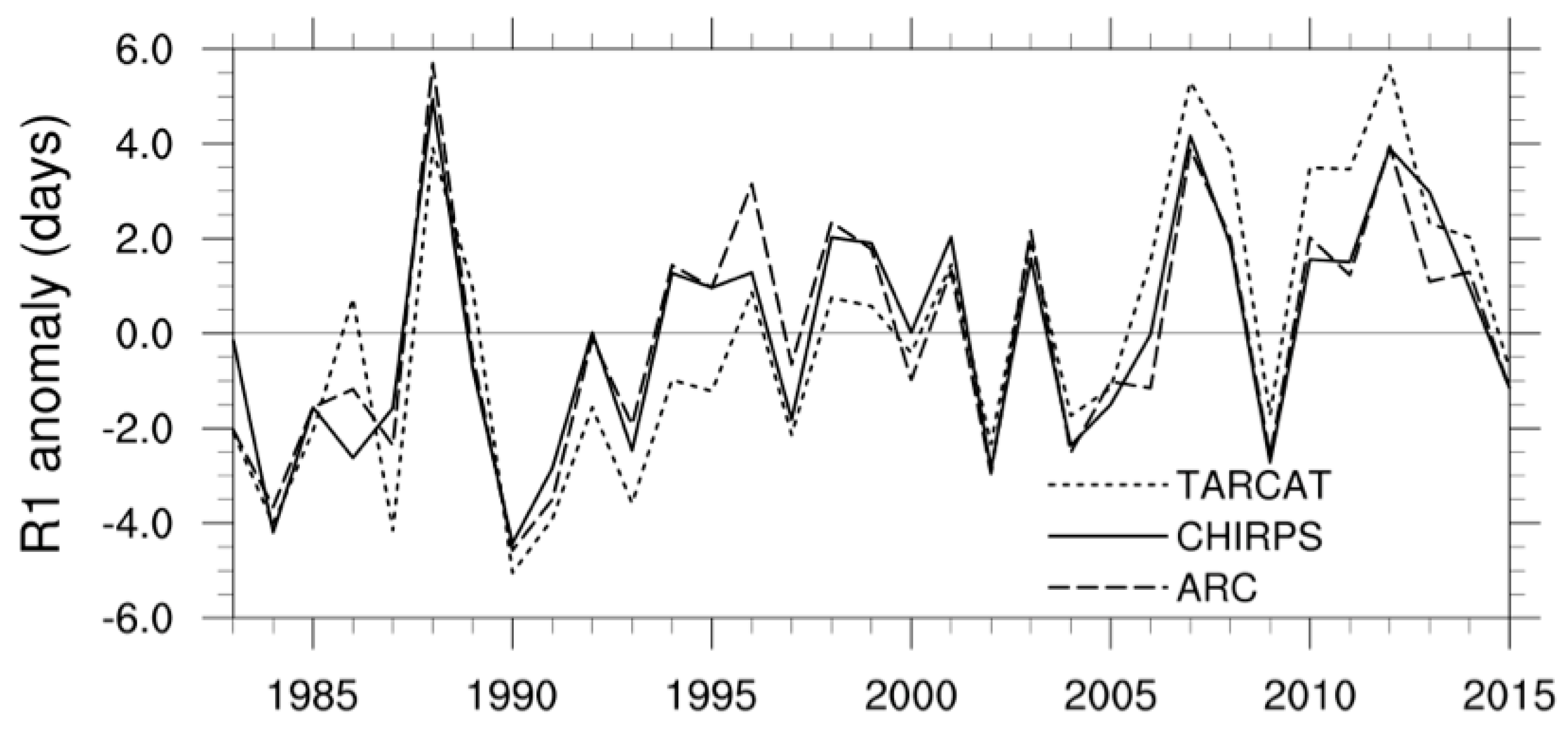
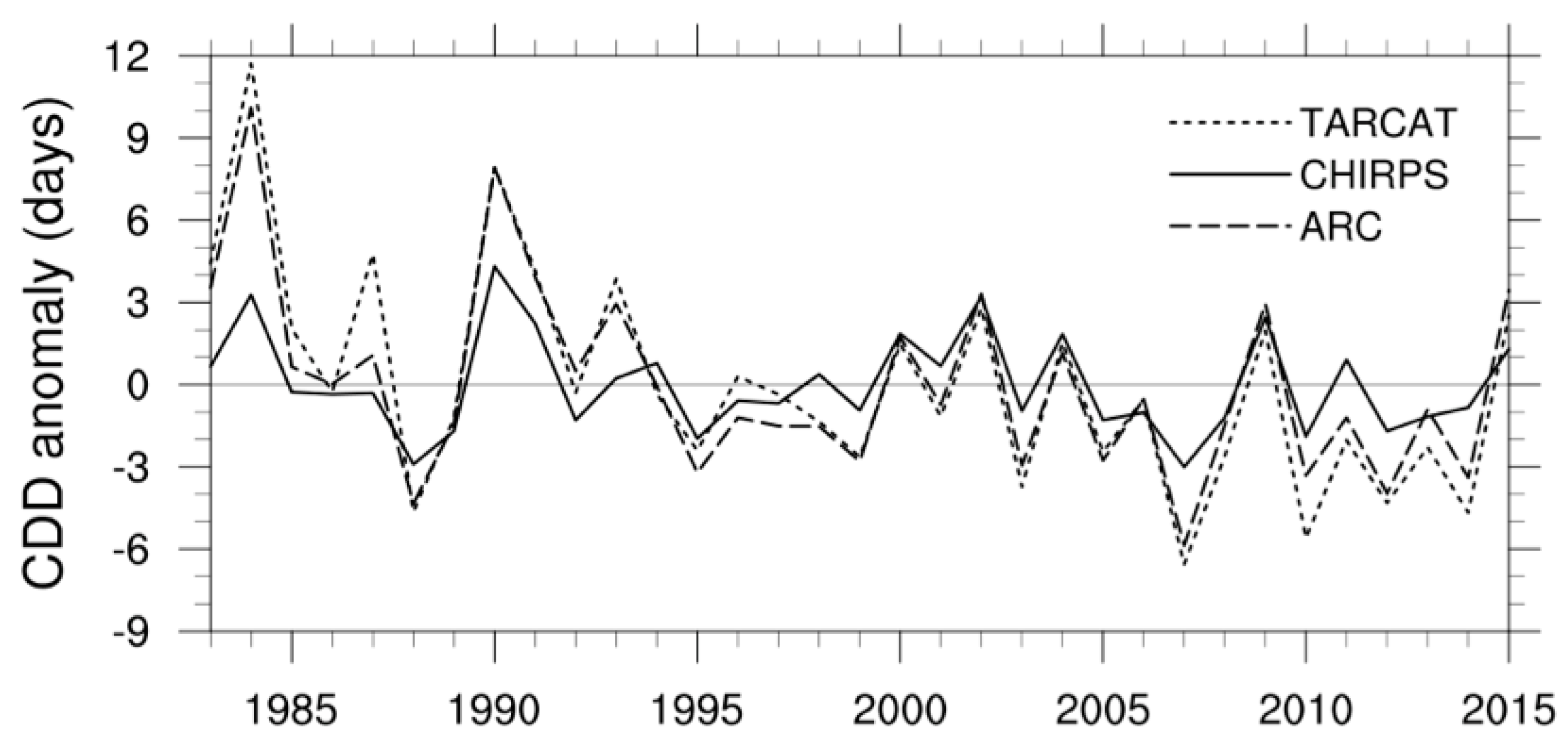
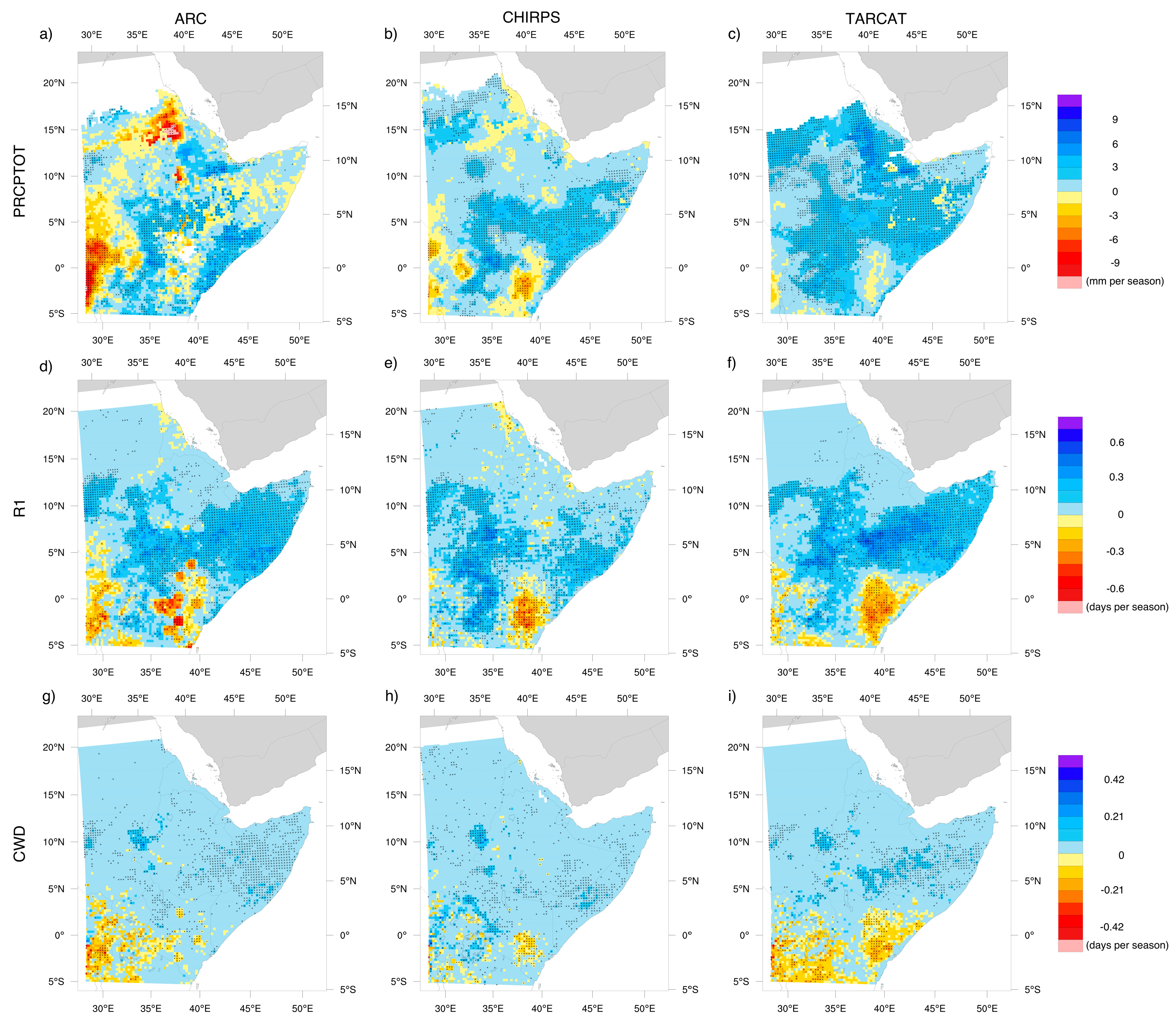
4.1. Trend Analysis of Annual Rainfall Indices
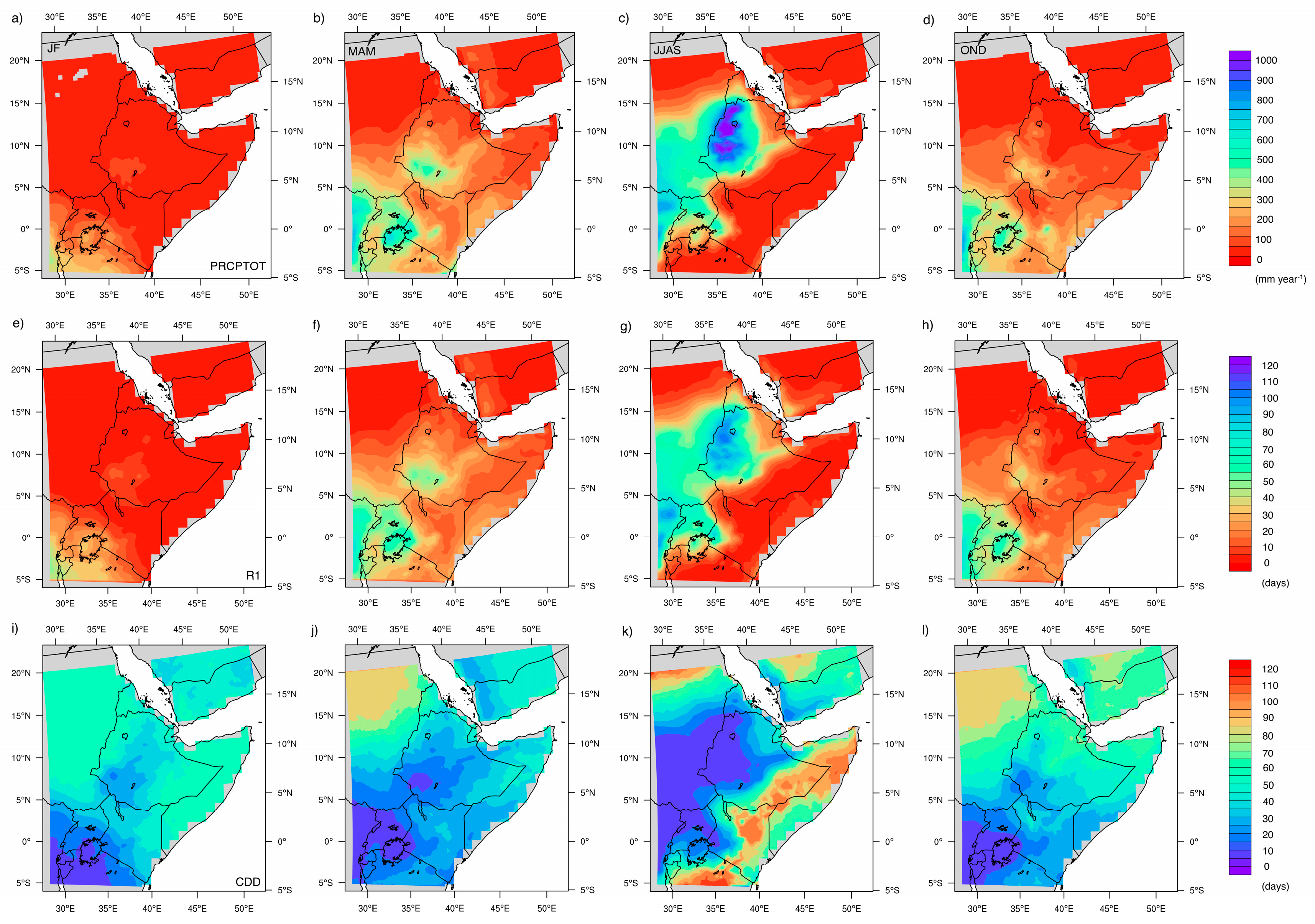
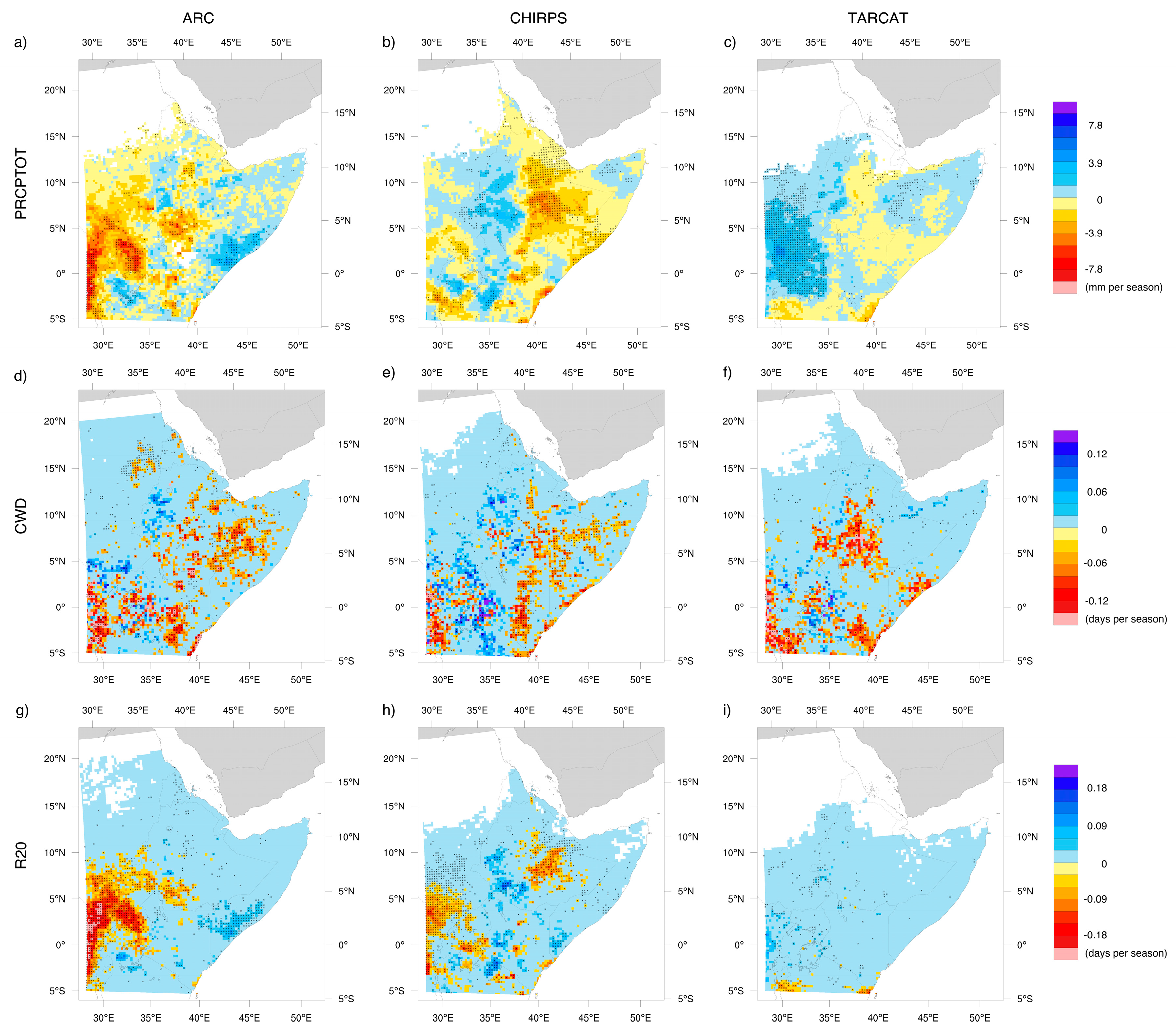
4.2. Trend Analysis of Seasonal Rainfall Indices
4.2.1. January–February (JF) Season
4.2.2. March–April–May (MAM) Season
4.2.3. June–July–August–September (JJAS) Season
4.2.4. October–November–December (OND) Season
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| ARC2 | Africa Rainfall Climatology v.2 |
| CCD | Cold Cloud Duration |
| CDD | Consecutive Dry Days index |
| CDR | Climate Data Record |
| CHG | Climate Hazards Group of University of California, Santa Barbara |
| CHIRP | CHG InfraRed Precipitation |
| CHIRPS | CHG InfraRed Precipitation with Stations |
| CHPclim | CHG Precipitation Climatology |
| CMAP | CPC Merged Analysis of Precipitation |
| CMIP5 | Coupled Model Intercomparison Project Phase 5 |
| CPC | Climate Prediction Center |
| CRU | Climate Research Unit |
| CWD | Consecutive Wet Days index |
| DRC | Democratic Republic of Congo |
| EA | East Africa |
| ECV | Essential Climate Variable |
| EM-DAT | Emergency Events Database |
| ETCCDI | Expert Team on Climate Change Detection and Indices |
| GHA | Greater Horn of Africa |
| GOES | Geostationary Operational Environmental Satellite |
| GPCC | Global Precipitation Climatology Center |
| GPCP | Global Precipitation Climatology Project |
| GPI | GOES Precipitation Index |
| GTS | Global Telecommunication System |
| IOD | Indian Ocean Dipole |
| IR | Infrared |
| JF | January–February |
| JJAS | June–July–August–September |
| MAM | March–April–May |
| NCAR | National Center for Atmospheric Research |
| NCL | NCAR Command Language |
| OND | October–November–December |
| PRCPTOT | Total precipitation index |
| R1 | Number of precipitating days index |
| R20 | Number of days with precipitation exceeding 20 mm day−1 index |
| SDII | Simple Daily Intensity Index |
| SNHT | Standard Normal Homogeneity Test |
| SST | Sea Surface Temperature |
| TAMSAT | Tropical Applications of Meteorology using SATellite |
| TARCAT | TAMSAT African Rainfall Climatology And Time series |
| TMPA | TRMM Multi-satellite Precipitation Analysis |
| TRMM | Tropical Rainfall Measuring Mission |
| UN-OCHA | United Nation Office for the Coordination of Humanitarian Affairs |
References
- FAO. The Impact of Disasters on Agriculture and Food Security; FAO: Rome, Italy, 2015; 54p, ISBN 978-92-5-108962-0. Available online: http://www.fao.org/publications/card/en/c/fa17f187-9b92-439f-9952-1d6c13d14782/ (accessed on 13 March 2018).
- Nicholson, S.E. An analysis of recent rainfall conditions in eastern Africa. Int. J. Climatol. 2016, 36, 526–532. [Google Scholar] [CrossRef]
- Webb, P.; von Braun, J. Drought and Food Shortages in Ethiopia: A Preliminary Review of Effects and Policy Implications; International Food Policy Research Institute: Washington, DC, USA, 1990; 169p. Available online: http://pdf.usaid.gov/pdf_docs/PNABI218.pdf (accessed on 19 March 2018).
- Lyon, B. Seasonal drought in the Greater Horn of Africa and its recent increase during the March-May long rains. J. Clim. 2014, 27, 7953–7975. [Google Scholar] [CrossRef]
- Masih, I.; Maskey, S.; Mussá, F.E.F.; Trambauer, P. A review of droughts on the African continent—A geospatial and long-term perspective. Hydrol. Earth Syst. Sci. 2014, 18, 3635–3649. [Google Scholar] [CrossRef]
- Liebmann, B.; Hoerling, M.P.; Funk, C.; Bladé, I.; Dole, R.M.; Allured, D.; Quan, X.; Pegion, P.; Eischeid, J.K. Understanding recent eastern Horn of Africa rainfall variability and change. J. Clim. 2014, 27, 8630–8645. [Google Scholar] [CrossRef]
- Kijazi, A.; Reason, C.J.C. Analysis of the 2006 floods over northern Tanzania. Int. J. Climatol. 2009, 29, 955–970. [Google Scholar] [CrossRef]
- Bayissa, Y.; Maskey, S.; Tadesse, T.; van Andel, S.J.; Moges, S.; van Griensven, A.; Solomatine, D. Comparison of the performance of six drought índices in characterizing historical drought for the Upper Blue Nile Basin, Ethiopia. Geosciences 2018, 8, 81. [Google Scholar] [CrossRef]
- Gitau, W.; Camberlin, P.; Ogallo, L.; Bosire, E. Trends of intraseasonal descriptors of wet and dry spells over equatorial eastern Africa. Int. J. Climatol. 2018, 38, 1189–1200. [Google Scholar] [CrossRef]
- Prudhomme, C.; Giuntoli, I.; Robinson, E.L.; Clark, D.B.; Arnell, N.W.; Dankers, R.; Fekete, B.M.; Franssen, W.; Gerten, D.; Gosling, S.N.; et al. Hydrological droughts in the 21st century, hotspots and uncertainties from a global multimodel ensemble experiment. Proc. Natl. Acad. Sci. USA 2014, 111, 3262–3267. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, U.; Nejadhashemi, A.P.; Woznicki, S.A. Climate change and eastern Africa: A review of impact on major crops. Food Energy Secur. 2015, 4, 110–132. [Google Scholar] [CrossRef]
- Cattani, E.; Merino, A.; Levizzani, V. Evaluation of monthly satellite-derived precipitation products over East Africa. J. Hydrometeorol. 2016, 17, 2555–2573. [Google Scholar] [CrossRef]
- Yang, W.; Seager, R.; Cane, M.A. The annual cycle of East African precipitation. J. Clim. 2015, 28, 2385–2404. [Google Scholar] [CrossRef]
- Seleshi, Y.; Zanke, U. Recent changes in rainfall and rainy days in Ethiopia. Int. J. Climatol. 2004, 24, 973–983. [Google Scholar] [CrossRef]
- Cheung, W.H.; Senay, G.B.; Singh, A. Trends and spatial distribution of annual and seasonal rainfall in Ethiopia. Int. J. Climatol. 2008, 28, 1723–1734. [Google Scholar] [CrossRef]
- Jury, M.R.; Funk, C. Climatic trends over Ethiopia: Regional signals and drivers. Int. J. Climatol. 2013, 33, 1924–1935. [Google Scholar] [CrossRef]
- Maidment, R.; Allan, R.P.; Black, E. Recent observed and simulated changes in precipitation over Africa. Geophys. Res. Lett. 2015, 42, 8155–8164. [Google Scholar] [CrossRef]
- Lyon, B.; DeWitt, D.G. A recent and abrupt decline in the East African long rains. Geophys. Res. Lett. 2012, 39, L02702. [Google Scholar] [CrossRef]
- Diem, J.E.; Ryan, S.J.; Hartter, J.; Palace, M.W. Satellite-based rainfall data reveal a recent drying trend in central equatorial Africa. Clim. Chang. 2014, 126, 263–272. [Google Scholar] [CrossRef]
- Yang, W.; Seager, R.; Cane, M.A. The East African long rains in observations and models. J. Clim. 2014, 27, 7185–7202. [Google Scholar] [CrossRef]
- Verdin, J.; Funk, C.; Senay, G.; Choularton, R. Climate science and famine early warning. Philos. Trans. R. Soc. B 2005, 360, 2155–2168. [Google Scholar] [CrossRef] [PubMed]
- Williams, A.P.; Funk, C. A westward extension of the warm pool leads to a westward extension of the Walker circulation, drying eastern Africa. Clim. Dyn. 2011, 37, 2147–2435. [Google Scholar] [CrossRef]
- Bojinski, S.; Verstraete, M.; Peterson, T.C.; Richter, C.; Simmons, A.; Zemp, M. The concept of Essential Climate Variables in support of climate research, applications, and policy. Bull. Am. Meteorol. Soc. 2014, 95, 1431–1443. [Google Scholar] [CrossRef]
- Wenhaji Ndomeni, C.; Cattani, E.; Merino, A.; Levizzani, V. An observational study of the variability of East African rainfall with respect to sea surface temperature and soil moisture. Q. J. R. Meteorol. Soc. 2018. [Google Scholar] [CrossRef]
- Novella, N.S.; Thiaw, W.M. African rainfall climatology version 2 for Famine Early Warning Systems. J. Appl. Meteorol. Climatol. 2013, 52, 588–606. [Google Scholar] [CrossRef]
- Maidment, R.; Grimes, D.; Allan, R.P.; Tarnavsky, E.; Stringer, M.; Hewison, T.; Roebeling, R.; Black, E. The 30 year TAMSAT African Rainfall Climatology and Time series (TARCAT) data set. J. Geophys. Res. 2014, 119, 10619–10644. [Google Scholar] [CrossRef]
- Maidment, R.; Grimes, D.; Black, E.; Tarnavsky, E.; Young, M.; Greatrex, H.; Allan, R.P.; Stein, T.; Nkonde, E.; Senkunda, S.; et al. A new, long-term daily satellite-based rainfall dataset for operational monitoring in Africa. Sci. Data 2017, 4, 170063. [Google Scholar] [CrossRef] [PubMed]
- Tarnavsky, E.; Grimes, D.; Maidment, R.; Black, E.; Allan, R.; Stringer, M.; Chadwick, R.; Kayitakire, F. Extension of the TAMSAT satellite-based rainfall monitoring over Africa and from 1983 to present. J. Appl. Meteorol. Climatol. 2014, 53, 2805–2822. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Brunetti, M.; Maugeri, M.; Monti, F.; Nanni, T. Temperature and precipitation variability in Italy in the last two centuries from homogenised instrumental time series. Int. J. Climatol. 2006, 26, 345–381. [Google Scholar] [CrossRef]
- Longobardi, A.; Villani, P. Trend analysis of annual and seasonal rainfall time series in the Mediterranean area. Int. J. Climatol. 2010, 30, 1538–1546. [Google Scholar] [CrossRef]
- Otte, I.; Detsch, F.; Mwangomo, E.; Hemp, A. Multidecadal trends and interannual variability of rainfall as observed from five lowland stations at Mt. Kilimanjaro, Tanzania. J. Hydrometeorol. 2017, 18, 349–361. [Google Scholar] [CrossRef]
- Dinku, T.; Funk, C.; Peterson, P.; Maidment, R.; Tadesse, T.; Gadain, H.; Ceccato, P. Validation of the CHIRPS satellite rainfall estimates over eastern of Africa. Q. J. R. Meteorol. Soc. 2018. [Google Scholar] [CrossRef]
- Gujarro, J.A. Automatización de la homogeneización de series climáticas: Nuevas funciones del paquete Climatol 3.0. In Clima, Sociedad, Riesgos y Ordenación del Territorio; Olcina, J., Rico, A.M., Moltó, E., Eds.; Universidad de Alicante: Alicante, Spain; Asociación Española de Climatología: Zaragoza, Spain, 2016; pp. 153–160. ISBN 978-84-16724-19-2. [Google Scholar]
- Alexandersson, H. A homogeneity test applied to precipitation data. Int. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Vicente-Serrano, S.M.; Angulo-Martínez, M.; Beguería, S.; Kenawy, A. Trends in daily precipitation on the northeastern Iberian Peninsula, 1955–2006. Int. J. Climatol. 2010, 30, 1026–1041. [Google Scholar] [CrossRef]
- Rodrigo, F.S.; Trigo, R.M. Trends in daily rainfall in the Iberian Peninsula from 1951 to 2002. Int. J. Climatol. 2007, 27, 513–529. [Google Scholar] [CrossRef]
- Karl, T.R.; Nicholls, N.; Ghazi, A. CLIVAR/GCOS/WMO workshop on indices and indicators for climate extremes: Workshop summary. Clim. Chang. 1999, 42, 3–7. [Google Scholar] [CrossRef]
- Peterson, T.C.; Folland, C.; Gruza, G.; Hogg, W.; Mokssit, A.; Plummer, N. Report on the Activities of the Working Group on Climate Change Detection and Related Rapporteurs 1998–2001; WMO, Report WCDMP-47, WMO-TD 1071; WMO: Geneva, Switzerland, 2001; 143p, Available online: http://etccdi.pacificclimate.org/docs/wgccd.2001.pdf (accessed on 13 March 2018).
- Frich, P.; Alexander, L.V.; Della-Marta, P.; Gleason, B.; Haylock, M.; Klein Tank, A.M.G.; Peterson, T. Observed coherent changes in climatic extremes during the second half of the twentieth century. Clim. Res. 2002, 19, 193–212. [Google Scholar] [CrossRef]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Klein Tank, A.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. WIREs Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Klein Tank, A.M.G.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. 2006, 111, D05109. [Google Scholar] [CrossRef]
- Aguilar, E.; Peterson, T.C.; Ramírez Obando, P.; Frutos, R.; Retana, J.A.; Solera, M.; Soley, J.; González García, I.; Araujo, R.M.; Rosa Santos, A.; et al. Changes in precipitation and temperature extremes in Central America and northern South America, 1961–2003. J. Geophys. Res. 2005, 110, D23107. [Google Scholar] [CrossRef]
- Zolina, O.; Simmer, C.; Kapala, A.; Bachner, S.; Gulev, S.; Maechel, H. Seasonally dependent changes of precipitation extremes over Germany since 1950 from a very dense observational network. J. Geophys. Res. 2008, 113, D06110. [Google Scholar] [CrossRef]
- Mann, H.B. Non-parametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Charles Griffin: London, UK, 1975; ISBN 978-0195208375. [Google Scholar]
- Santos, M.; Fragoso, M. Precipitation variability in Northern Portugal: Data homogeneity assessment and trends in extreme precipitation indices. Atmos. Res. 2013, 131, 34–45. [Google Scholar] [CrossRef]
- Merino, A.; Fernández-Vaquero, M.; López, L.; Fernández-González, S.; Hermida, L.; Sánchez, J.L.; García-Ortega, E.; Gascón, E. Large-scale patterns of daily precipitation extremes on the Iberian Peninsula. Int. J. Climatol. 2016, 36, 3873–3891. [Google Scholar] [CrossRef]
- Tian, J.; Liu, J.; Wang, J.; Li, C.; Nie, H.; Yu, F. Trend analysis of temperature and precipitation extremes in major grain producing area of China. Int. J. Climatol. 2016, 37, 672–687. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Dinku, T.; Ceccato, P.; Connor, S.J. Challenges of satellite rainfall estimation over mountainous and arid parts of east Africa. Int. J. Remote Sens. 2011, 32, 5965–5979. [Google Scholar] [CrossRef]
- Dinku, T.; Block, P.; Sharoff, J.; Hailemariam, K.; Osgood, D.; del Corral, J.; Cousin, R.; Thomson, M.C. Bridging critical gaps in climate services and applications in Africa. Earth Perspect. 2014, 1, 1–15. [Google Scholar] [CrossRef]
- Funk, C. A Climate Trend Analysis of Kenya-August 2010. U.S. Geological Survey Fact Sheet 2010-3074. 2010; 4p. Available online: https://pubs.usgs.gov/fs/2010/3074/ (accessed on 13 March 2018).
- Tierney, J.E.; Ummenhofer, C.C.; deMenocal, P.B. Past and future rainfall in the Horn of Africa. Sci. Adv. 2015, 1, e1500682. [Google Scholar] [CrossRef] [PubMed]
- Williams, A.P.; Funk, C.; Michaelsen, J.; Rauscher, S.A.; Robertson, I.; Wils, T.H.G.; Koprowski, M.; Eshetu, Z.; Loader, N.J. Recent summer precipitation trends in the Greater Horn of Africa and the emerging role of Indian Ocean sea surface temperature. Clim. Dyn. 2012, 39, 2307–2328. [Google Scholar] [CrossRef]
- Brown, M.E.; Funk, C.; Pedreros, D.; Korecha, D.; Lemma, M.; Rowland, J.; Williams, E.; Verdin, J. A climate trend analysis of Ethiopia: Examining subseasonal climate impacts on crops and pasture conditions. Clim. Chang. 2017, 142, 169–182. [Google Scholar] [CrossRef]
- Nicholson, S.E. Climate and climatic variability of rainfall over eastern Africa. Rev. Geophys. 2017, 55, 590–635. [Google Scholar] [CrossRef]
- Nicholson, S.E. Long-term variability of the East African ‘short rains’ and its links to large-scale factors. Int. J. Climatol. 2015, 35, 3979–3990. [Google Scholar] [CrossRef]

| ID | Definition | Units |
|---|---|---|
| R1 1 | Number of precipitating days (rain rate, RR ≥ 1 mm) | days |
| SDII | Simple daily intensity index Ratio of total precipitation (annual/seasonal) to the number of precipitating days (RR ≥ 1 mm) | mm day−1 |
| R20 | Number of very heavy precipitating days (RR ≥ 20 mm) | days |
| CDD | Maximum number of consecutive dry days (RR < 1 mm) | days |
| CWD | Maximum number of consecutive precipitating days | days |
| PRCPTOT | Total precipitation from days with RR ≥ 1 mm | mm |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cattani, E.; Merino, A.; Guijarro, J.A.; Levizzani, V. East Africa Rainfall Trends and Variability 1983–2015 Using Three Long-Term Satellite Products. Remote Sens. 2018, 10, 931. https://doi.org/10.3390/rs10060931
Cattani E, Merino A, Guijarro JA, Levizzani V. East Africa Rainfall Trends and Variability 1983–2015 Using Three Long-Term Satellite Products. Remote Sensing. 2018; 10(6):931. https://doi.org/10.3390/rs10060931
Chicago/Turabian StyleCattani, Elsa, Andrés Merino, José A. Guijarro, and Vincenzo Levizzani. 2018. "East Africa Rainfall Trends and Variability 1983–2015 Using Three Long-Term Satellite Products" Remote Sensing 10, no. 6: 931. https://doi.org/10.3390/rs10060931
APA StyleCattani, E., Merino, A., Guijarro, J. A., & Levizzani, V. (2018). East Africa Rainfall Trends and Variability 1983–2015 Using Three Long-Term Satellite Products. Remote Sensing, 10(6), 931. https://doi.org/10.3390/rs10060931







