Realistic Forest Stand Reconstruction from Terrestrial LiDAR for Radiative Transfer Modelling
Abstract
1. Introduction
2. Materials and Methods
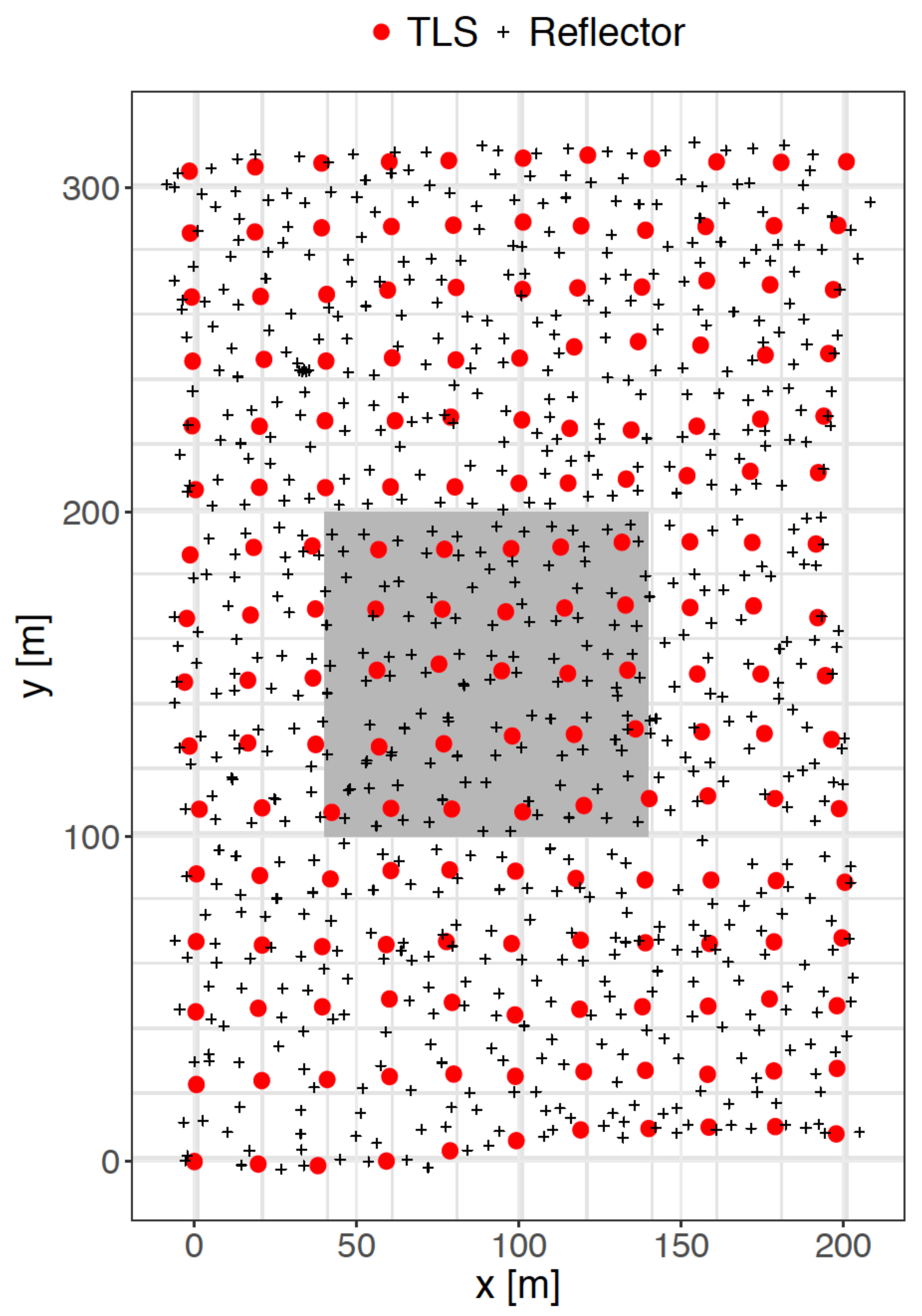
2.1. Study Area and Data Collection
2.2. Forest Stand Reconstruction
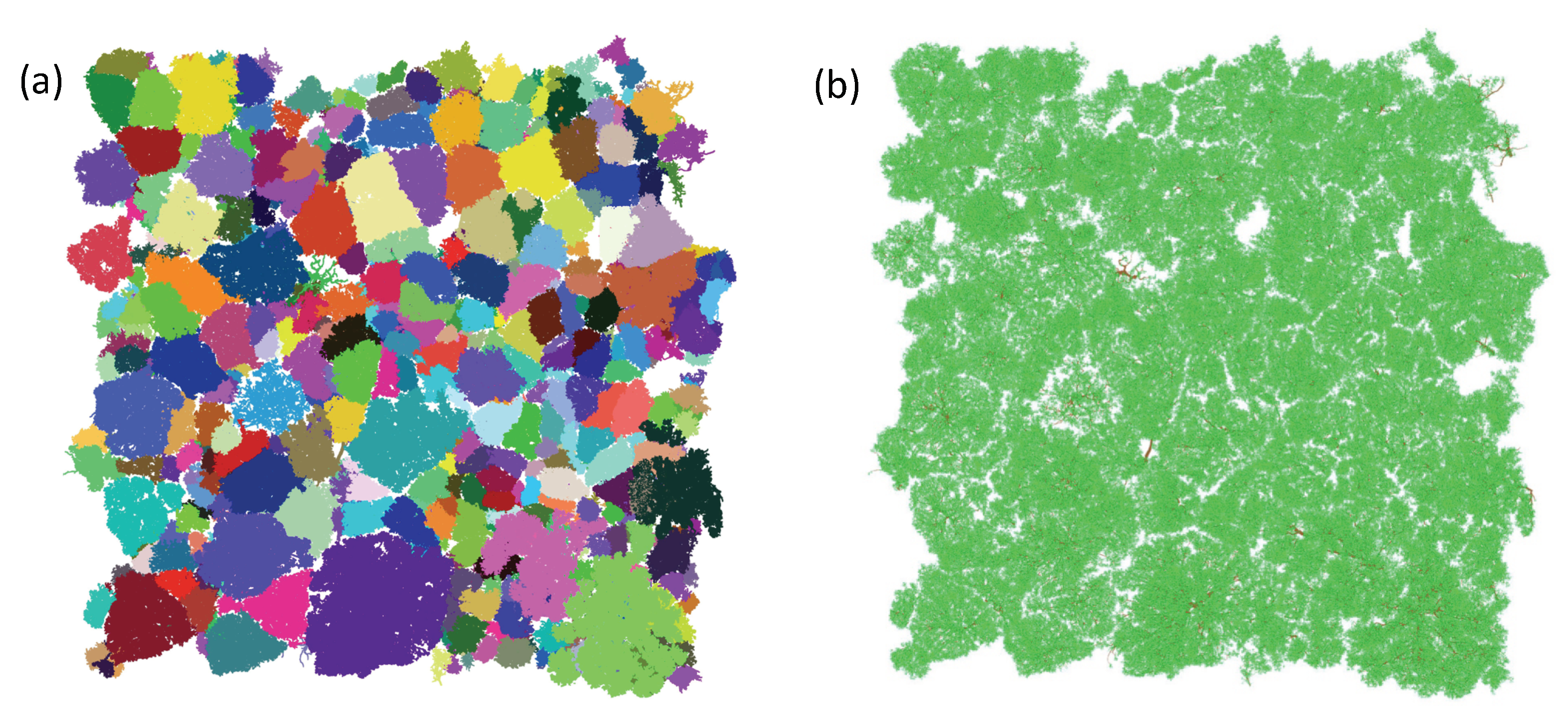
2.2.1. Tree Extraction
- Filtering. Spurious points were detected and removed. We used the deviation of the recorded waveform with the stored reference waveforms’ shapes to define the quality of a point in the point cloud [28].
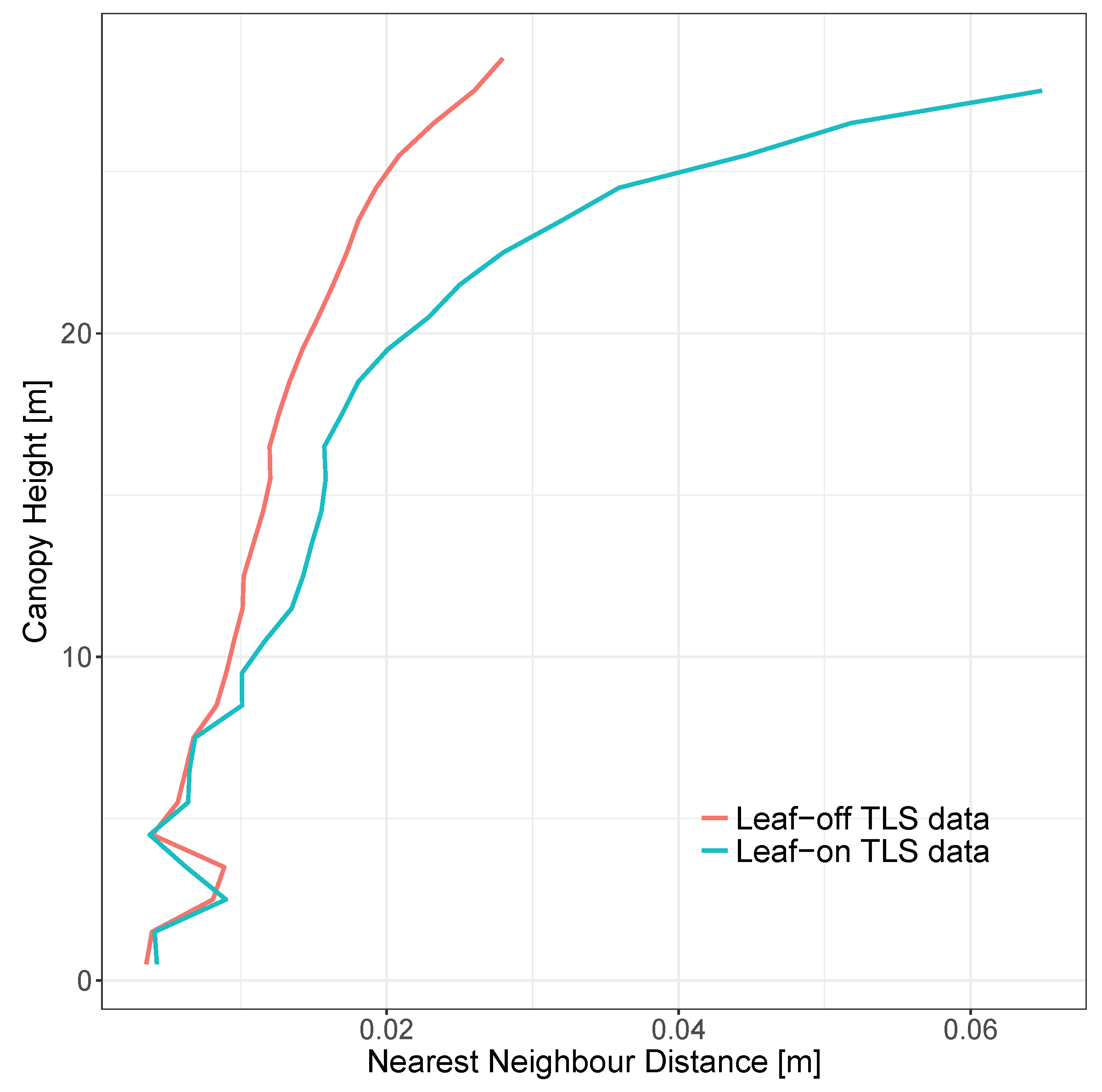
- Downsampling. Many processing steps are susceptible to the variation in nearest neighbour distance. It is therefore recommended [25] to downsample the point cloud via voxel grid aggregation. We downsampled the original point cloud to 0.026 m resolution. This resolution was decided based on the analysis of the 4 nearest neighbours for each point and the consideration of the beam exit diameter, beam divergence and approximate path length through the canopy.
- Stem Identification & Stem Segmentation. We identified individual stems through segmentation of a height slice above the ground plane. This required the following steps: (a) A DTM was constructed across the larger-area point cloud, from which a slice in the point cloud, in the z-axis, was generated. We used a 2 m slice between 1 and 3 m above the terrain (1 m DTM); (b) This slice was organised into sets of point clouds representing common underlying surfaces via Euclidean clustering and region-based segmentation and (c) each set was considered a stem based on the residual error of multiple RANSAC cylinder fits, and the angle between the vector of the cylinder centreline and the vector perpendicular to the underlying DTM tile plane.
- Crown Isolation. Sequential identification of point clusters defined by point density in height slices along the length of the tree to remove unrelated vegetation and noise from these clouds.
- Visual Inspection. Quality control and, if necessary, removing or adding crown material. This will happen most likely in trees with overlapping crowns and in smaller understorey shrubs.
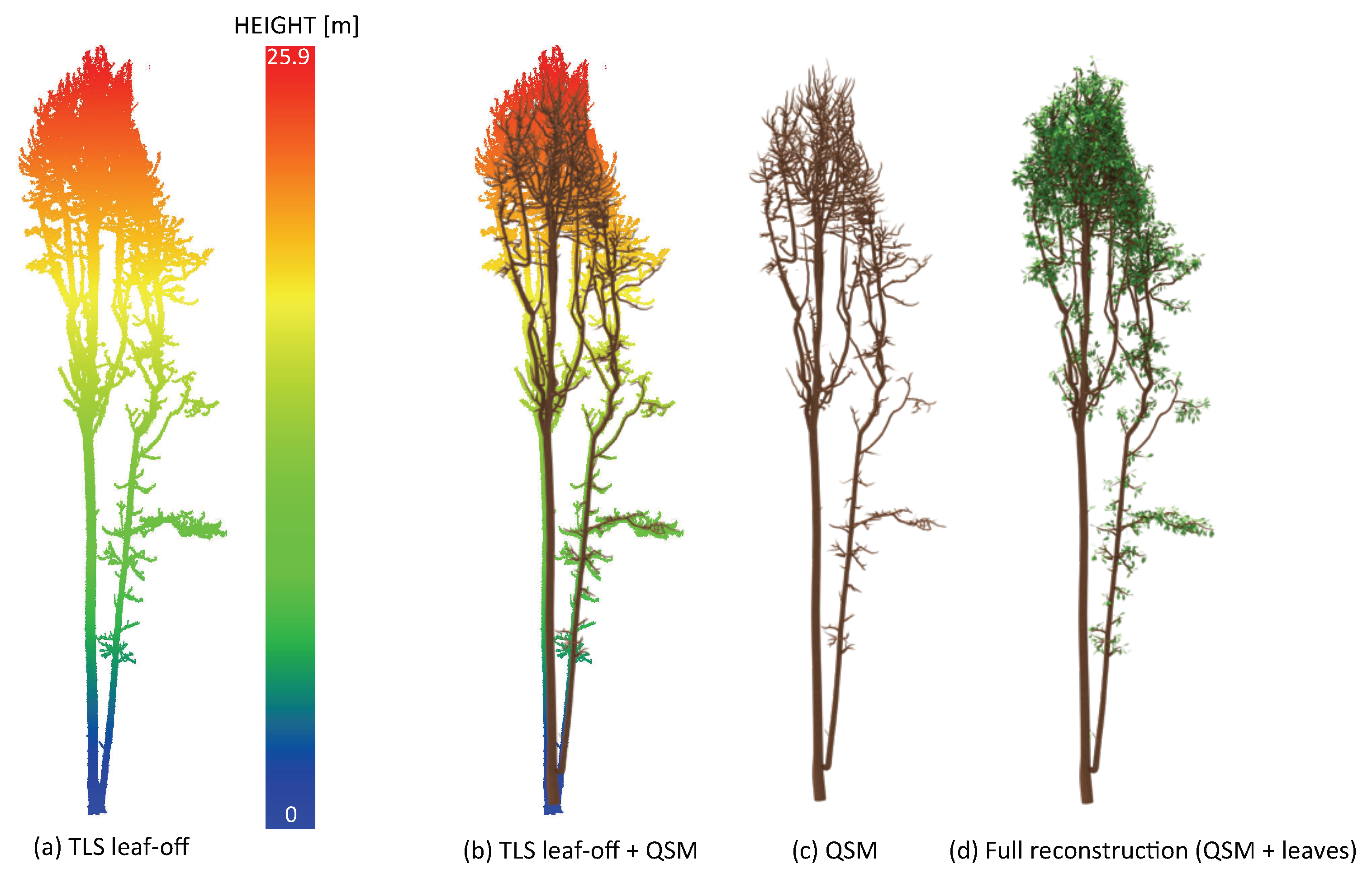
2.2.2. Tree Structure Modelling
- The single tree point cloud was reconstructed 10 times over the desired d-range of 0.02 m to 0.11 m at an increment of 0.005 m.
- For each of the 10 QSMs for each d value, 4 trunk cylinders at 7.5%, 10%, 12.5% and 15% of the trunk length were extracted from the QSMs. The coordinates of these four cylinders drive a pass-through filter to extract the point cloud slice from which the QSM was formed.
- The trunk diameters were estimated using least squares circle fitting on the point cloud slices and the diameters compared with the cylinders as a percentage change to quantify model conformity to the cloud. A single value (trunk) is calculated by averaging the four diameter comparisons for each of the 10 models.
- For each d value the mean and standard deviation were generated from the 10 models. The coefficients of variation (CVs) are calculated as standard deviation/mean.
- If no optimised d is identified in step five, the method falls back onto the d with the lowest CV.
2.2.3. Leaf Addition
- Leaf shape: tetragon (see Figure 2).
- Target leaf area.
- Leaf area density distribution (LADD): the probability of a cylinder to have leaves depended on its relative height along the tree, the cylinders position along the respective branch and the order of that branch. Height-dependent leaf area probability was interpolated linearly from 0.2 at ground level to 1.0 at tree top. Leaves are allowed to occupy the last 5% of the stem, with that percentage rising with the branch order, reaching 60% for branch orders four and up. For more details see the definition of LADD 2 in Åkerblom et al. [18].
- Leaf size distribution (LSD): a uniform distribution where the length of the tetragon is sampled between 25 cm and 30 cm. This length was selected as a trade-off between the number of objects (i.e., leaves) and RAM requirements.
- Leaf orientation distribution (LOD): an initial leaf normal is generated depending on the generated petiole directions. If the initial normal is less than 20 different compared to a reference vector pointing straight up, then the final normal points straight up. Otherwise the initial normal is rotated 20 towards the reference vector and used as the final normal, resulting in most leaves facing upwards but with some random variation. For more details see the definition of the default leaf orientation distribution in Åkerblom et al. [18].
2.2.4. Radiometric Properties
2.3. Radiative Transfer Modelling
3. Results and Discussion
3.1. Forest Stand Reconstruction
3.2. Radiative Transfer Modelling
3.3. Framework and Model Evaluation
4. Conclusions
5. Data Availability
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

References
- Fang, H.; Wei, S.; Liang, S. Validation of MODIS and CYCLOPES LAI products using global field measurement data. Remote Sens. Environ. 2012, 119, 43–54. [Google Scholar] [CrossRef]
- Calders, K.; Origo, N.; Disney, M.; Nightingale, J.; Woodgate, W.; Armston, J.; Lewis, P. Variability and bias in active and passive ground-based measurements of effective plant, wood and leaf area index. Agric. For. Meteorol. 2018, 252, 231–240. [Google Scholar] [CrossRef]
- Widlowski, J.L.; Mio, C.; Disney, M.; Adams, J.; Andredakis, I.; Atzberger, C.; Brennan, J.; Busetto, L.; Chelle, M.; Ceccherini, G.; et al. The fourth phase of the radiative transfer model intercomparison (RAMI) exercise: Actual canopy scenarios and conformity testing. Remote Sens. Environ. 2015, 169, 418–437. [Google Scholar] [CrossRef]
- Disney, M.; Lewis, P.; Gomez-Dans, J.; Roy, D.; Wooster, M.J.; Lajas, D. 3D radiative transfer modelling of fire impacts on a two-layer savanna system. Remote Sens. Environ. 2011, 115, 1866–1881. [Google Scholar] [CrossRef]
- Calders, K.; Lewis, P.; Disney, M.; Verbesselt, J.; Herold, M. Investigating assumptions of crown archetypes for modelling LiDAR returns. Remote Sens. Environ. 2013, 134, 39–49. [Google Scholar] [CrossRef]
- Schneider, F.D.; Leiterer, R.; Morsdorf, F.; Gastellu-Etchegorry, J.P.; Lauret, N.; Pfeifer, N.; Schaepman, M.E. Simulating imaging spectrometer data: 3D forest modeling based on LiDAR and in situ data. Remote Sens. Environ. 2014, 152, 235–250. [Google Scholar] [CrossRef]
- Widlowski, J.L.; Côté, J.F.; Béland, M. Abstract tree crowns in 3D radiative transfer models: Impact on simulated open-canopy reflectances. Remote Sens. Environ. 2014, 142, 155–175. [Google Scholar] [CrossRef]
- Lintermann, B.; Deussen, O. Interactive modelling of plants. IEEE Comput. Graph. 1999, 19, 2–11. [Google Scholar] [CrossRef]
- Weber, J.; Penn, J. Creation and rendering of realistic trees. In Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 6–11 August 1995; pp. 119–128. [Google Scholar]
- Armston, J.; Newnham, G.; Strahler, A.H.; Schaaf, C.; Danson, M.; Gaulton, R.; Zhang, Z.; Disney, M.; Sparrow, B.; Phinn, S.R.; et al. Intercomparison of Terrestrial Laser Scanning Instruments for Assessing Forested Ecosystems: A Brisbane Field Experiment. In Proceedings of the AGU Fall Meeting, San Fransico, CA, USA, 3–19 December 2013. [Google Scholar]
- Woodgate, W.; Disney, M.; Armston, J.D.; Jones, S.D.; Suarez, L.; Hill, M.J.; Wilkes, P.; Soto-Berelov, M.; Haywood, A.; Mellor, A. An improved theoretical model of canopy gap probability for Leaf Area Index estimation in woody ecosystems. For. Ecol. Manag. 2015, 358, 303–320. [Google Scholar] [CrossRef]
- Newnham, G.; Armston, J.; Calders, K.; Disney, M.; Lovell, J.; Schaaf, C.; Strahler, A.; Danson, F. Terrestrial Laser Scanning For Plot Scale Forest Measurement. Curr. For. Rep. 2015, 1, 239–251. [Google Scholar] [CrossRef]
- Raumonen, P.; Kaasalainen, M.; Markku, A.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast automatic precision tree models from terrestrial laser scanner data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef]
- Hackenberg, J.; Spiecker, H.; Calders, K.; Disney, M.; Raumonen, P. SimpleTree—An Efficient Open Source Tool to Build Tree Models from TLS Clouds. Forests 2015, 6, 4245–4294. [Google Scholar] [CrossRef]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Avitabile, V.; Disney, M.; Armston, J.; et al. Nondestructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- Côté, J.F.; Widlowski, J.L.; Fournier, R.A.; Verstraete, M.M. The structural and radiative consistency of three-dimensional tree reconstructions from terrestrial lidar. Remote Sens. Environ. 2009, 113, 1067–1081. [Google Scholar] [CrossRef]
- Côté, J.F.; Fournier, R.A.; Egli, R. An architectural model of trees to estimate forest structural attributes using terrestrial LiDAR. Environ. Modell. Softw. 2011, 26, 761–777. [Google Scholar] [CrossRef]
- Åkerblom, M.; Raumonen, P.; Casella, E.; Disney, M.; Danson, F.; Gaulton, R.; Schofield, L.A.; Kaasalainen, M. Non-Intersecting leaf insertion algorithm for tree structure models. Interface Focus 2018, 8, 20170045. [Google Scholar] [CrossRef] [PubMed]
- Côté, J.F.; Fournier, R.A.; Frazer, G.W.; Niemann, K.O. A fine-scale architectural model of trees to enhance LiDAR-derived measurements of forest canopy structure. Agric. For. Meteorol. 2012, 166–167, 72–85. [Google Scholar] [CrossRef]
- Butt, N.; Campbell, G.; Malhi, Y.; Morecroft, M.; Fenn, K.; Thomas, M. Initial Results from Establishment of a Long-Term Broadleaf Monitoring Plot at Wytham Woods; University of Oxford: Oxford, UK, 2009. [Google Scholar]
- Lovell, J.L.; Jupp, D.L.B.; Culvenor, D.S.; Coops, N.C. Using airborne and ground-based ranging lidar to measure canopy structure in Australian forests. Can. J. Remote Sens. 2003, 29, 607–622. [Google Scholar] [CrossRef]
- Calders, K.; Armston, J.; Newnham, G.; Herold, M.; Goodwin, N. Implications of sensor configuration and topography on vertical plant profiles derived from terrestrial LiDAR. Agric. For. Meteorol. 2014, 194, 104–117. [Google Scholar] [CrossRef]
- Calders, K.; Burt, A.; Origo, N.; Disney, M.; Nightingale, J.; Raumonen, P.; Lewis, P. Large-area virtual forests from terrestrial laser scanning data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 1765–1767. [Google Scholar]
- Wilkes, P.; Lau, A.; Disney, M.; Calders, K.; Burt, A.; de Tanago, J.G.; Bartholomeus, H.; Brede, B.; Herold, M. Data acquisition considerations for Terrestrial Laser Scanning of forest plots. Remote Sens. Environ. 2017, 196, 140–153. [Google Scholar] [CrossRef]
- Burt, A.; Disney, M.; Calders, K. Extracting individual trees from lidar point clouds using treeseg. Methods Ecol. Evol. 2018. in review. [Google Scholar]
- Burt, A. New 3D Measurements of Forest Structure. Ph.D. Thesis, University College London, London, UK, 2017. [Google Scholar]
- Rusu, R.B.; Cousins, S. 3D is here: Point Cloud Library (PCL). In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011. [Google Scholar]
- Calders, K.; Disney, M.I.; Armston, J.; Burt, A.; Brede, B.; Origo, N.; Muir, J.; Nightingale, J. Evaluation of the Range Accuracy and the Radiometric Calibration of Multiple Terrestrial Laser Scanning Instruments for Data Interoperability. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2716–2724. [Google Scholar] [CrossRef]
- Juchheim, J.; Annighöfer, P.; Ammer, C.; Calders, K.; Raumonen, P.; Seidel, D. How management intensity and neighborhood composition affect the structure of beech (Fagus sylvatica L.) trees. Trees 2017, 31, 1723–1735. [Google Scholar] [CrossRef]
- Åkerblom, M.; Raumonen, P.; Kaasalainen, M.; Casella, E. Analysis of Geometric Primitives in Quantitative Structure Models of Tree Stems. Remote Sens. 2015, 7, 4581–4603. [Google Scholar]
- Calders, K.; Newnham, G.; Herold, M.; Murphy, S.; Culvenor, D.; Raumonen, P.; Burt, A.; Armston, J.; Avitabile, V.; Disney, M. Estimating above ground biomass from terrestrial laser scanning in Australian Eucalypt Open Forest. In Proceedings of the 2013 SilviLaser, Beijing, China, 9–11 October 2013; pp. 90–97. [Google Scholar]
- Calders, K.; Burt, A.; Newnham, G.; Disney, M.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Armston, J.; Avitabile, V.; et al. Reducing uncertainties in above-ground biomass estimates using terrestrial laser scanning. In Proceedings of the 2015 SilviLaser, La Grande Motte, France, 28–30 September 2015; pp. 197–199. [Google Scholar]
- Disney, M.; Boni Vicari, M.; Burt, A.; Calders, K.; Lewis, S.L.; Raumonen, P.; Wilkes, P. Weighing trees with lasers: advances, challenges and opportunities. Interface Focus 2018, 8, 20170048. [Google Scholar] [CrossRef] [PubMed]
- Jupp, D.L.B.; Culvenor, D.S.; Lovell, J.L.; Newnham, G.J.; Strahler, A.H.; Woodcock, C.E. Estimating forest LAI profiles and structural parameters using a ground-based laser called Echidna®. Tree Physiol. 2009, 29, 171–181. [Google Scholar] [CrossRef] [PubMed]
- Calders, K.; Schenkels, T.; Bartholomeus, H.; Armston, J.; Verbesselt, J.; Herold, M. Monitoring spring phenology with high temporal resolution terrestrial LiDAR measurements. Agric. For. Meteorol. 2015, 203, 158–168. [Google Scholar] [CrossRef]
- Ryu, Y.; Nilson, T.; Kobayashi, H.; Sonnentag, O.; Law, B.E.; Baldocchi, D.D. On the correct estimation of effective leaf area index: Does it reveal information on clumping effects? Agric. For. Meteorol. 2010, 150, 463–472. [Google Scholar] [CrossRef]
- Lewis, P. Three-dimensional plant modelling for remote sensing simulation studies using the Botanical Plant Modelling System. Agron. Agric. Environ. 1999, 19, 185–210. [Google Scholar] [CrossRef]
- Pinty, B.; Widlowski, J.L.; Taberner, M.; Gobron, N.; Verstraete, M.M.; Disney, M.; Gascon, F.; Gastellu, J.P.; Jiang, L.; Kuusk, A.; et al. Radiation Transfer Model Intercomparison (RAMI) exercise: Results from the second phase. J. Geophys. Res. 2004, 109, D06210. [Google Scholar] [CrossRef]
- Widlowski, J.L.; Taberner, M.; Pinty, B.; Bruniquel-Pinel, D.; Disney, M.; Fernandes, R.; Gastellu-Etchegorry, J.P.; Gobron, N.; Kuusk, A.; Lavergne, T.; et al. Third Radiation transfer Model Intercomparison (RAMI) exercise: Documenting progress in canopy reflectance models. J. Geophys. Res. 2007, 112, D09111. [Google Scholar] [CrossRef]
- Disney, M.I.; Kalogirou, V.; Lewis, P.; Prieto-Blanco, A.; Hancock, S.; Pfeifer, M. Simulating the impact of discrete-return lidar system and survey characteristics over young conifer and broadleaf forests. Remote Sens. Environ. 2010, 114, 1546–1560. [Google Scholar] [CrossRef]
- Darrodi, M.M.; Finlayson, G.; Goodman, T.; Mackiewicz, M. Reference data set for camera spectral sensitivity estimation. J. Opt. Soc. Am. A 2015, 32, 381–391. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez de Tanago, J.; Lau, A.; Bartholomeus, H.; Herold, M.; Avitabile, V.; Raumonen, P.; Martius, C.; Goodman, R.C.; Disney, M.; Manuri, S.; et al. Estimation of above-ground biomass of large tropical trees with terrestrial LiDAR. Methods Ecol. Evol. 2018, 9, 223–234. [Google Scholar] [CrossRef]
- Kükenbrink, D.; Schneider, F.D.; Leiterer, R.; Schaepman, M.E.; Morsdorf, F. Quantification of hidden canopy volume of airborne laser scanning data using a voxel traversal algorithm. Remote Sens. Environ. 2017, 194, 424–436. [Google Scholar] [CrossRef]




| Processing Step | Automation | Reference | Link |
|---|---|---|---|
| (1) Tree Extraction | Semi-Automated | [25], Burt [26] | github.com/apburt/treeseg |
| (2) Tree structure Modelling | Automated | Raumonen et al. [13], Calders et al. [15] | github.com/InverseTampere/TreeQSM |
| (3) Leaf Addition | Automated | Åkerblom et al. [18] | github.com/InverseTampere/qsm-fanni-matlab |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calders, K.; Origo, N.; Burt, A.; Disney, M.; Nightingale, J.; Raumonen, P.; Åkerblom, M.; Malhi, Y.; Lewis, P. Realistic Forest Stand Reconstruction from Terrestrial LiDAR for Radiative Transfer Modelling. Remote Sens. 2018, 10, 933. https://doi.org/10.3390/rs10060933
Calders K, Origo N, Burt A, Disney M, Nightingale J, Raumonen P, Åkerblom M, Malhi Y, Lewis P. Realistic Forest Stand Reconstruction from Terrestrial LiDAR for Radiative Transfer Modelling. Remote Sensing. 2018; 10(6):933. https://doi.org/10.3390/rs10060933
Chicago/Turabian StyleCalders, Kim, Niall Origo, Andrew Burt, Mathias Disney, Joanne Nightingale, Pasi Raumonen, Markku Åkerblom, Yadvinder Malhi, and Philip Lewis. 2018. "Realistic Forest Stand Reconstruction from Terrestrial LiDAR for Radiative Transfer Modelling" Remote Sensing 10, no. 6: 933. https://doi.org/10.3390/rs10060933
APA StyleCalders, K., Origo, N., Burt, A., Disney, M., Nightingale, J., Raumonen, P., Åkerblom, M., Malhi, Y., & Lewis, P. (2018). Realistic Forest Stand Reconstruction from Terrestrial LiDAR for Radiative Transfer Modelling. Remote Sensing, 10(6), 933. https://doi.org/10.3390/rs10060933







