Monitoring Groundwater Storage Changes Using the Gravity Recovery and Climate Experiment (GRACE) Satellite Mission: A Review
Abstract
1. Introduction
2. The GRACE Mission
2.1. Orbit and On-Board Instruments
- the K-band ranging (KBR) system, which provides distance measurements between the two satellites, with an accuracy of 10 μm, using the phases of carrier electromagnetic waves in the K and the Ka bands, at frequencies of 26 and 32 GHz;
- the Ultra-Stable Oscillator (USO), which generates electromagnetic waves in the K-band for the KBR system at the desired frequency;
- the SuperSTAR accelerometers (ACC) accurately measures the non-conservative forces applied to each satellite along three axes;
- the Stellar Camera ASSEMBLY (SCA) determines the orientation of the satellite relatively to the position of fixed stars; and,
- The Black-Jack GPS receivers and Instrument Processing Unit provides the three components of the position and velocity of each of the satellites.
2.2. Data from the GRACE Mission
- the Center for Space Research (CSR) in Austin, Texas, United States,
- the GeoForschungs Zentrum (GFZ) in Potsdam, Germany, and
- the Jet Propulsion Laboratory (JPL) in Pasadena, California, United States.
2.3. Accuracy and Spatial Resolution of GRACE-Based Products over Land
3. Estimating Groundwater Storage Using the GRACE Data: Different Approaches
3.1. The Direct Approach
3.1.1. Regions Where TWS Is Limited to Soil Water Storage
3.1.2. More Complex Environments
3.2. Calibration and/or Assimilation into Hydological Models
4. Error Budget and Validation of the GRACE-Based Groundwater Storage
4.1. Error Budget of the GRACE-Based Groundwater Storage
4.2. Validation of the GRACE-Based Groundwater Storage Variations
5. Results
5.1. Groundwater Depletion
5.2. Determining Groundwater Related Parameters Using GRACE-Based TWS
6. Discussion
6.1. Sources of Errors in the GRACE Solutions
6.2. Impacts of the Non Inclusion of Hydrological Water Compartments and Fluxes
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef] [PubMed]
- Zektser, I.S.; Loaiciga, H.A. Groundwater fluxes in the global hydrologic cycle: Past, present and future. J. Hydrol. 1993, 144, 405–427. [Google Scholar] [CrossRef]
- Jackson, R.B.; Carpenter, S.R.; Dahm, C.N.; McKnight, D.M.; Naiman, R.J.; Postel, S.L.; Running, S.W. Water in a changing world. Ecol. Appl. 2001, 11, 1027–1045. [Google Scholar] [CrossRef]
- Sophocleous, M. Interactions between groundwater and surface water: The state of the science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Griebler, C.; Avramov, M. Groundwater ecosystem services: A review. Freshw. Sci. 2015, 34, 355–367. [Google Scholar] [CrossRef]
- Giordano, M. Global Groundwater? Issues and Solutions. Annu. Rev. Environ. Resour. 2009, 34, 153–178. [Google Scholar] [CrossRef]
- Siebert, S.; Burke, J.; Faures, J.M.; Frenken, K.; Hoogeveen, J.; Döll, P.; Portmann, F.T. Groundwater use for irrigation—A global inventory. Hydrol. Earth Syst. Sci. 2010, 14, 1863–1880. [Google Scholar] [CrossRef]
- Konikow, L.F.; Kendy, E. Groundwater depletion: A global problem. Hydrogeol. J. 2005, 13, 317–320. [Google Scholar] [CrossRef]
- Gleeson, T.; Wada, Y.; Bierkens, M.F.P.; van Beek, L.P.H. Water balance of global aquifers revealed by groundwater footprint. Nature 2012, 488, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Wada, Y.; van Beek, L.P.H.; Sperna Weiland, F.C.; Chao, B.F.; Wu, Y.-H.; Bierkens, M.F.P. Past and future contribution of global groundwater depletion to sea-level rise. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Konikow, L.F. Contribution of global groundwater depletion since 1900 to sea-level rise. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Famiglietti, J.S. The global groundwater crisis. Nat. Clim. Chang. 2014, 4, 945–948. [Google Scholar] [CrossRef]
- Konikow, L.F. Long-Term Groundwater Depletion in the United States. Groundwater 2015, 53, 2–9. [Google Scholar] [CrossRef] [PubMed]
- Zektser, I.S.; Everett, L.G. Groundwater Resources of the World: And Their Use; UNESCO: Paris, France, 2004; Volume 6, ISBN 9292200070. [Google Scholar]
- Shah, T. 10_Groundwater: A global assessment of scale and significance. In Water for Food, Water for Life: A Comprehensive Assessment of Water Management in Agriculture; Routledge: London, UK, 2007; pp. 395–423. [Google Scholar]
- Döll, P. Vulnerability to the impact of climate change on renewable groundwater resources: A global-scale assessment. Environ. Res. Lett. 2009, 4, 035006. [Google Scholar] [CrossRef]
- Gleeson, T.; VanderSteen, J.; Sophocleous, M.A.; Taniguchi, M.; Alley, W.M.; Allen, D.M.; Zhou, Y. Groundwater sustainability strategies. Nat. Geosci. 2010, 3, 378–379. [Google Scholar] [CrossRef]
- Green, T.R.; Taniguchi, M.; Kooi, H.; Gurdak, J.J.; Allen, D.M.; Hiscock, K.M.; Treidel, H.; Aureli, A. Beneath the surface of global change: Impacts of climate change on groundwater. J. Hydrol. 2011, 405, 532–560. [Google Scholar] [CrossRef]
- Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S.; Edmunds, M.; et al. Ground water and climate change. Nat. Clim. Chang. 2013, 3, 322–329. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Wouters, B.; Bonin, J.A.; Chambers, D.P.; Riva, R.E.M.; Sasgen, I.; Wahr, J. GRACE, time-varying gravity, Earth system dynamics and climate change. Rep. Prog. Phys. 2014, 77, 116801. [Google Scholar] [CrossRef] [PubMed]
- Frappart, F.; Ramillien, G.; Seoane, L. Monitoring water mass redistributions on land and polar ice sheets using the grace gravimetry from space mission. In Land Surface Remote Sensing in Continental Hydrology; Elsevier: Amsterdam, The Netherlands, 2016; pp. 255–279. ISBN 978-0-08-101181-2. [Google Scholar]
- Andersen, O.B.; Seneviratne, S.I.; Hinderer, J.; Viterbo, P. GRACE-derived terrestrial water storage depletion associated with the 2003 European heat wave. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Yang, Z.L.; Niu, G.Y. 2005 drought event in the Amazon River basin as measured by GRACE and estimated by climate models. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Long, D.; Shen, Y.; Sun, A.; Hong, Y.; Longuevergne, L.; Yang, Y.; Li, B.; Chen, L. Drought and flood monitoring for a large karst plateau in Southwest China using extended GRACE data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Frappart, F.; Ramillien, G.; Famiglietti, J.S. Water balance of the Arctic drainage system using GRACE gravimetry products. Int. J. Remote Sens. 2011, 32, 431–453. [Google Scholar] [CrossRef]
- Syed, T.H.; Famiglietti, J.S.; Rodell, M.; Chen, J.; Wilson, C.R. Analysis of terrestrial water storage changes from GRACE and GLDAS. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Syed, T.H.; Famiglietti, J.S.; Chambers, D.P. GRACE-Based Estimates of Terrestrial Freshwater Discharge from Basin to Continental Scales. J. Hydrometeorol. 2009, 10, 22–40. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S.; Chen, J.; Seneviratne, S.I.; Viterbo, P.; Holl, S.; Wilson, C.R. Basin scale estimates of evapotranspiration using GRACE and other observations. Geophys. Res. Lett. 2004, 31, L20504. [Google Scholar] [CrossRef]
- Ramillien, G.; Frappart, F.; Güntner, A.; Ngo-Duc, T.; Cazenave, A.; Laval, K. Time variations of the regional evapotranspiration rate from Gravity Recovery and Climate Experiment (GRACE) satellite gravimetry. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S. The potential for satellite-based monitoring of groundwater storage changes using GRACE: The High Plains aquifer, Central US. J. Hydrol. 2002, 263, 245–256. [Google Scholar] [CrossRef]
- Schmidt, R.; Flechtner, F.; Meyer, U.; Neumayer, K.-H.; Dahle, C.; König, R.; Kusche, J. Hydrological Signals Observed by the GRACE Satellites. Surv. Geophys. 2008, 29, 319–334. [Google Scholar] [CrossRef]
- NASA JPL Space images. Available online: https://www.jpl.nasa.gov/spaceimages/images/largesize/PIA04235_hires.jpg (accessed on 10 November 2017).
- Wolff, M. Direct measurements of the Earth’s gravitational potential using a satellite pair. J. Geophys. Res. 1969, 74, 5295–5300. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Integrated System Data Center. Available online: http://isdc.gfz-potsdam.de (accessed on 10 November 2017).
- Physical Oceanography Distributive Active Data Center. Available online: http://podaac.jpl.nasa.gov/GRACE (accessed on 10 November 2017).
- Tapley, B.D.; Reigber, C. The GRACE mission: Status and Early Results. In Proceedings of the Grace Science Team Meeting, Austin, TX, USA, 8–10 October 2003; pp. 41–63. [Google Scholar]
- Reigber, C.; Schmidt, R.; Flechtner, F.; König, R.; Meyer, U.; Neumayer, K.H.; Schwintzer, P.; Zhu, S.Y. An Earth gravity field model complete to degree and order 150 from GRACE: EIGEN-GRACE02S. J. Geodyn. 2005, 39, 1–10. [Google Scholar] [CrossRef]
- Tapley, B.; Ries, J.; Bettadpur, S.; Chambers, D.; Cheng, M.; Condi, F.; Gunter, B.; Kang, Z.; Nagel, P.; Pastor, R.; et al. GGM02—An improved Earth gravity field model from GRACE. J. Geod. 2005, 79, 467–478. [Google Scholar] [CrossRef]
- Ramillien, G.; Frappart, F.; Seoane, L. Space Gravimetry Using GRACE Satellite Mission: Basic Concepts. In Microwave Remote Sensing of Land Surfaces: Techniques and Methods; Elsevier: Amsterdam, The Netherlands, 2016; pp. 285–302. ISBN 978-0-08-101768-5. [Google Scholar]
- Rodell, M.; Famiglietti, J.S. Detectability of variations in continental water storage from satellite observations of the time dependent gravity field. Water Resour. Res. 1999, 35, 2705–2723. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J.; Milly, P.C.D. Estimated accuracies of regional water storage variations inferred from the Gravity Recovery and Climate Experiment (GRACE). Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Geruo, A.; Wahr, J.; Zhong, S. Computations of the viscoelastic response of a 3-D compressible earth to surface loading: An application to glacial isostatic adjustment in Antarctica and Canada. Geophys. J. Int. 2013, 192, 557–572. [Google Scholar] [CrossRef]
- Sella, G.F.; Stein, S.; Dixon, T.H.; Craymer, M.; James, T.S.; Mazzotti, S.; Dokka, R.K. Observation of glacial isostatic adjustment in “stable” North America with GPS. Geophys. Res. Lett. 2007, 34, L02306. [Google Scholar] [CrossRef]
- Milne, G.A.; Davis, J.L.; Mitrovica, J.X.; Scherneck, H.G.; Johansson, J.M.; Vermeer, M.; Koivula, H. Space-geodetic constraints on glacial isostatic adjustment in Fennoscandia. Science 2001, 291, 2381–2385. [Google Scholar] [CrossRef] [PubMed]
- Yeh, P.J.-F.; Swenson, S.C.; Famiglietti, J.S.; Rodell, M. Remote sensing of groundwater storage changes in Illinois using the Gravity Recovery and Climate Experiment (GRACE). Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Strassberg, G.; Scanlon, B.R.; Chambers, D. Evaluation of groundwater storage monitoring with the GRACE satellite: Case study of the High Plains aquifer, central United States. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Swenson, S.; Famiglietti, J.; Basara, J.; Wahr, J. Estimating profile soil moisture and groundwater variations using GRACE and Oklahoma Mesonet soil moisture data. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Döll, P.; Kaspar, F.; Lehner, B. A global hydrological model for deriving water availability indicators: Model tuning and validation. J. Hydrol. 2003, 270, 105–134. [Google Scholar] [CrossRef]
- Van Dijk, A.I.J.M. The Australian Water Resources Assessment System, Technical report 3, Landscape Model (version 0.5) Technical Description; CSIRO: Canberra, ACT, Australia, 2010. [Google Scholar]
- Strassberg, G.; Scanlon, B.R.; Rodell, M. Comparison of seasonal terrestrial water storage variations from GRACE with groundwater-level measurements from the High Plains Aquifer (USA). Geophys. Res. Lett. 2007, 34, L14402. [Google Scholar] [CrossRef]
- Munier, S.; Becker, M.; Maisongrande, P.; Cazenave, A. Using grace to detect groundwater storage variations: the cases of canning basin and guarani aquifer system. Int. Water Technol. J. 2012, 2, 2–13. [Google Scholar]
- Khaki, M.; Forootan, E.; Kuhn, M.; Awange, J.; van Dijk, A.I.J.M.; Schumacher, M.; Sharifi, M.A. Determining water storage depletion within Iran by assimilating GRACE data into the W3RA hydrological model. Adv. Water Resour. 2018, 114, 1–18. [Google Scholar] [CrossRef]
- Leblanc, M.J.; Tregoning, P.; Ramillien, G.; Tweed, S.O.; Fakes, A. Basin-scale, integrated observations of the early 21st century multiyear drought in southeast Australia. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Shamsudduha, M.; Taylor, R.G.; Longuevergne, L. Monitoring groundwater storage changes in the highly seasonal humid tropics: Validation of GRACE measurements in the Bengal Basin. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Lo, M.; Ho, S.L.; Bethune, J.; Anderson, K.J.; Syed, T.H.; Swenson, S.C.; de Linage, C.R.; Rodell, M. Satellites measure recent rates of groundwater depletion in California’s Central Valley. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Huang, J.; Halpenny, J.; van der Wal, W.; Klatt, C.; James, T.S.; Rivera, A. Detectability of groundwater storage change within the Great Lakes Water Basin using GRACE. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Tiwari, V.M.; Wahr, J.; Swenson, S. Dwindling groundwater resources in northern India, from satellite gravity observations. Geophys. Res. Lett. 2009, 36, L18401. [Google Scholar] [CrossRef]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed]
- Werth, S.; White, D.; Bliss, D.W. GRACE Detected Rise of Groundwater in the Sahelian Niger River Basin. J. Geophys. Res. Solid Earth 2017. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Scanlon, B.; Güntner, A. Long-term groundwater storage change in Victoria, Australia from satellite gravity and in situ observations. Glob. Planet. Chang. 2016, 139, 56–65. [Google Scholar] [CrossRef]
- Becker, M.; LLovel, W.; Cazenave, A.; Güntner, A.; Crétaux, J.-F. Recent hydrological behavior of the East African great lakes region inferred from GRACE, satellite altimetry and rainfall observations. Comptes Rendus Geosci. 2010, 342, 223–233. [Google Scholar] [CrossRef]
- Ramillien, G.; Frappart, F.; Seoane, L. Application of the regional water mass variations from GRACE satellite gravimetry to large-scale water management in Africa. Remote Sens. 2014, 6, 7379–7405. [Google Scholar] [CrossRef]
- Voss, K.A.; Famiglietti, J.S.; Lo, M.; de Linage, C.; Rodell, M.; Swenson, S.C. Groundwater depletion in the Middle East from GRACE with implications for transboundary water management in the Tigris-Euphrates-Western Iran region. Water Resour. Res. 2013, 49, 904–914. [Google Scholar] [CrossRef] [PubMed]
- Longuevergne, L.; Wilson, C.R.; Scanlon, B.R.; Crétaux, J.F. GRACE water storage estimates for the Middle East and other regions with significant reservoir and lake storage. Hydrol. Earth Syst. Sci. 2013, 17, 4817–4830. [Google Scholar] [CrossRef]
- Frappart, F.; Papa, F.; Güntner, A.; Werth, S.; Santos da Silva, J.; Tomasella, J.; Seyler, F.; Prigent, C.; Rossow, W.B.; Calmant, S.; et al. Satellite-based estimates of groundwater storage variations in large drainage basins with extensive floodplains. Remote Sens. Environ. 2011, 115, 1588–1594. [Google Scholar] [CrossRef]
- Frappart, F.; Papa, F.; Güntner, A.; Werth, S.; Ramillien, G.; Prigent, C.; Rossow, W.B.; Bonnet, M.-P. Interannual variations of the terrestrial water storage in the lower ob’ basin from a multisatellite approach. Hydrol. Earth Syst. Sci. 2010, 14, 2443–2453. [Google Scholar] [CrossRef]
- Ramillien, G.; Frappart, F.; Cazenave, A.; Güntner, A. Time variations of land water storage from an inversion of 2 years of GRACE geoids. Earth Planet. Sci. Lett. 2005, 235, 283–301. [Google Scholar] [CrossRef]
- Frappart, F.; Ramillien, G.; Biancamaria, S.; Mognard, N.M.; Cazenave, A. Evolution of high-latitude snow mass derived from the GRACE gravimetry mission (2002–2004). Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Sun, A.Y.; Green, R.; Swenson, S.; Rodell, M. Toward calibration of regional groundwater models using GRACE data. J. Hydrol. 2012, 422–423, 1–9. [Google Scholar] [CrossRef]
- Haddad, O.B.; Tabari, M.M.R.; Fallah-Mehdipour, E.; Mariño, M.A. Groundwater Model Calibration by Meta-Heuristic Algorithms. Water Resour. Manag. 2013, 27, 2515–2529. [Google Scholar] [CrossRef]
- Hu, L.; Jiao, J.J. Calibration of a large-scale groundwater flow model using GRACE data: A case study in the Qaidam Basin, China. Hydrogeol. J. 2015, 23, 1305–1317. [Google Scholar] [CrossRef]
- Werth, S.; Güntner, A. Calibration analysis for water storage variability of the global hydrological model WGHM. Hydrol. Earth Syst. Sci. 2010, 14, 59–78. [Google Scholar] [CrossRef]
- Eicker, A.; Schumacher, M.; Kusche, J.; Döll, P.; Schmied, H.M. Calibration/Data Assimilation Approach for Integrating GRACE Data into the WaterGAP Global Hydrology Model (WGHM) Using an Ensemble Kalman Filter: First Results. Surv. Geophys. 2014, 35, 1285–1309. [Google Scholar] [CrossRef]
- Bonan, G.B.; Oleson, K.W.; Vertenstein, M.; Levis, S.; Zeng, X.; Dai, Y.; Dickinson, R.E.; Yang, Z.L. The land surface climatology of the community land model coupled to the NCAR community climate model. J. Clim. 2002, 15, 3123–3149. [Google Scholar] [CrossRef]
- Yeh, P.J.F.; Eltahir, E.A.B. Representation of water table dynamics in a land surface scheme. Part I: Model development. J. Clim. 2005, 18, 1861–1880. [Google Scholar] [CrossRef]
- Lo, M.-H.; Famiglietti, J.S.; Yeh, P.J.-F.; Syed, T.H. Improving parameter estimation and water table depth simulation in a land surface model using GRACE water storage and estimated base flow data. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Koster, R.D.; Suarez, M.J.; Ducharne, A.; Stieglitz, M.; Kumar, P. A catchment-based approach to modeling land surface processes in a general circulation model: 1. Model structure. J. Geophys. Res. Atmos. 2000, 105, 24809–24822. [Google Scholar] [CrossRef]
- Zaitchik, B.F.; Rodell, M.; Reichle, R.H.; Zaitchik, B.F.; Rodell, M.; Reichle, R.H. Assimilation of GRACE Terrestrial Water Storage Data into a Land Surface Model: Results for the Mississippi River Basin. J. Hydrometeorol. 2008, 9, 535–548. [Google Scholar] [CrossRef]
- Li, B.; Rodell, M.; Zaitchik, B.F.; Reichle, R.H.; Koster, R.D.; van Dam, T.M. Assimilation of GRACE terrestrial water storage into a land surface model: Evaluation and potential value for drought monitoring in western and central Europe. J. Hydrol. 2012, 446–447, 103–115. [Google Scholar] [CrossRef]
- Schumacher, M.; Kusche, J.; Döll, P. A systematic impact assessment of GRACE error correlation on data assimilation in hydrological models. J. Geod. 2016, 90, 537–559. [Google Scholar] [CrossRef]
- Khaki, M.; Schumacher, M.; Forootan, E.; Kuhn, M.; Awange, J.L.; van Dijk, A.I.J.M. Accounting for spatial correlation errors in the assimilation of GRACE into hydrological models through localization. Adv. Water Resour. 2017, 108, 99–112. [Google Scholar] [CrossRef]
- Khaki, M.; Ait-El-Fquih, B.; Hoteit, I.; Forootan, E.; Awange, J.; Kuhn, M. A two-update ensemble Kalman filter for land hydrological data assimilation with an uncertain constraint. J. Hydrol. 2017, 555, 447–462. [Google Scholar] [CrossRef]
- Tian, S.; Tregoning, P.; Renzullo, L.J.; van Dijk, A.I.J.M.; Walker, J.P.; Pauwels, V.R.N.; Allgeyer, S. Improved water balance component estimates through joint assimilation of GRACE water storage and SMOS soil moisture retrievals. Water Resour. Res. 2017, 53, 1820–1840. [Google Scholar] [CrossRef]
- Khaki, M.; Forootan, E.; Kuhn, M.; Awange, J.; Papa, F.; Shum, C.K. A study of Bangladesh’s sub-surface water storages using satellite products and data assimilation scheme. Sci. Total Environ. 2018, 625, 963–977. [Google Scholar] [CrossRef] [PubMed]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33, L08402. [Google Scholar] [CrossRef]
- GRACE Tellus. Available online: https://grace.jpl.nasa.gov/ (accessed on 26 February 2018).
- Scanlon, B.R.; Longuevergne, L.; Long, D. Ground referencing GRACE satellite estimates of groundwater storage changes in the California Central Valley, USA. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Feng, W.; Zhong, M.; Lemoine, J.-M.; Biancale, R.; Hsu, H.-T.; Xia, J. Evaluation of groundwater depletion in North China using the Gravity Recovery and Climate Experiment (GRACE) data and ground-based measurements. Water Resour. Res. 2013, 49, 2110–2118. [Google Scholar] [CrossRef]
- Castle, S.L.; Thomas, B.F.; Reager, J.T.; Rodell, M.; Swenson, S.C.; Famiglietti, J.S. Groundwater depletion during drought threatens future water security of the Colorado River Basin. Geophys. Res. Lett. 2014, 41, 5904–5911. [Google Scholar] [CrossRef] [PubMed]
- Swenson, S.; Yeh, P.J.-F.; Wahr, J.; Famiglietti, J. A comparison of terrestrial water storage variations from GRACE with in situ measurements from Illinois. Geophys. Res. Lett. 2006, 33, L16401. [Google Scholar] [CrossRef]
- Ek, M.B.; Mitchell, K.E.; Lin, Y.; Rogers, E.; Grunmann, P.; Koren, V.; Gayno, G.; Tarpley, J.D. Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model. J. Geophys. Res. 2003, 108, 8851. [Google Scholar] [CrossRef]
- Chinnasamy, P.; Hubbart, J.A.; Agoramoorthy, G.; Chinnasamy, P.; Hubbart, J.A.; Agoramoorthy, G. Using Remote Sensing Data to Improve Groundwater Supply Estimations in Gujarat, India. Earth Interact. 2013, 17, 1–17. [Google Scholar] [CrossRef]
- Fan, Y.; van den Dool, H. Climate Prediction Center global monthly soil moisture data set at 0.5° resolution for 1948 to present. J. Geophys. Res. 2004, 109, D10102. [Google Scholar] [CrossRef]
- Huang, Z.; Pan, Y.; Gong, H.; Yeh, P.J.-F.; Li, X.; Zhou, D.; Zhao, W. Subregional-scale groundwater depletion detected by GRACE for both shallow and deep aquifers in North China Plain. Geophys. Res. Lett. 2015, 42, 1791–1799. [Google Scholar] [CrossRef]
- Frappart, F.; Ramillien, G.; Leblanc, M.; Tweed, S.O.; Bonnet, M.-P.; Maisongrande, P. An independent component analysis filtering approach for estimating continental hydrology in the GRACE gravity data. Remote Sens. Environ. 2011, 115, 187–204. [Google Scholar] [CrossRef]
- Frappart, F.; Papa, F.; Famiglietti, J.S.; Prigent, C.; Rossow, W.B.; Seyler, F. Interannual variations of river water storage from a multiple satellite approach: A case study for the Rio Negro River basin. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Shmakin, A.B. Global Modeling of Land Water and Energy Balances. Part I: The Land Dynamics (LaD) Model. J. Hydrometeorol. 2002, 3, 283–299. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Faunt, C.C.; Longuevergne, L.; Reedy, R.C.; Alley, W.M.; McGuire, V.L.; McMahon, P.B. Groundwater depletion and sustainability of irrigation in the US High Plains and Central Valley. Proc. Natl. Acad. Sci. USA 2012, 109, 9320–9325. [Google Scholar] [CrossRef] [PubMed]
- Forootan, E.; Rietbroek, R.; Kusche, J.; Sharifi, M.A.; Awange, J.L.; Schmidt, M.; Omondi, P.; Famiglietti, J. Separation of large scale water storage patterns over Iran using GRACE, altimetry and hydrological data. Remote Sens. Environ. 2014, 140, 580–595. [Google Scholar] [CrossRef]
- Gonçalvès, J.; Petersen, J.; Deschamps, P.; Hamelin, B.; Baba-Sy, O. Quantifying the modern recharge of the “fossil” Sahara aquifers. Geophys. Res. Lett. 2013, 40, 2673–2678. [Google Scholar] [CrossRef]
- Ahmed, M.; Sultan, M.; Wahr, J.; Yan, E. The use of GRACE data to monitor natural and anthropogenic induced variations in water availability across Africa. Earth-Science Rev. 2014, 136, 289–300. [Google Scholar] [CrossRef]
- Richey, A.S.; Thomas, B.F.; Lo, M.H.; Famiglietti, J.S.; Swenson, S.; Rodell, M. Uncertainty in global groundwater storage estimates in a Total Groundwater Stress framework. Water Resour. Res. 2015, 51, 5198–5216. [Google Scholar] [CrossRef] [PubMed]
- Joodaki, G.; Wahr, J.; Swenson, S. Estimating the human contribution to groundwater depletion in the Middle East, from GRACE data, land surface models, and well observations. Water Resour. Res. 2014, 50, 2679–2692. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Zhang, Z.; Ni, S. Long-term groundwater variations in Northwest India from satellite gravity measurements. Glob. Planet. Chang. 2014, 116, 130–138. [Google Scholar] [CrossRef]
- Shen, H.; Leblanc, M.; Tweed, S.; Liu, W. Groundwater depletion in the Hai River Basin, China, from in situ and GRACE observations. Hydrol. Sci. J. 2015, 60, 671–687. [Google Scholar] [CrossRef]
- Breña-Naranjo, J.A.; Kendall, A.D.; Hyndman, D.W. Improved methods for satellite-based groundwater storage estimates: A decade of monitoring the high plains aquifer from space and ground observations. Geophys. Res. Lett. 2014, 41, 6167–6173. [Google Scholar] [CrossRef]
- Sun, A.Y.; Green, R.; Rodell, M.; Swenson, S. Inferring aquifer storage parameters using satellite and in situ measurements: Estimation under uncertainty. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Sun, A.Y. Predicting groundwater level changes using GRACE data. Water Resour. Res. 2013, 49, 5900–5912. [Google Scholar] [CrossRef]
- Thomas, B.F.; Famiglietti, J.S.; Landerer, F.W.; Wiese, D.N.; Molotch, N.P.; Argus, D.F. GRACE Groundwater Drought Index: Evaluation of California Central Valley groundwater drought. Remote Sens. Environ. 2017, 198, 384–392. [Google Scholar] [CrossRef]
- Richey, A.S.; Thomas, B.F.; Lo, M.-H.; Reager, J.T.; Famiglietti, J.S.; Voss, K.; Swenson, S.; Rodell, M. Quantifying renewable groundwater stress with GRACE. Water Resour. Res. 2015, 51, 5217–5238. [Google Scholar] [CrossRef] [PubMed]
- Han, S.-C.; Jekeli, C.; Shum, C.K. Time-variable aliasing effects of ocean tides, atmosphere, and continental water mass on monthly mean GRACE gravity field. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Thompson, P.F.; Bettadpur, S.V.; Tapley, B.D. Impact of short period, non-tidal, temporal mass variability on GRACE gravity estimates. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Ray, R.D.; Luthcke, S.B. Tide model errors and GRACE gravimetry: Towards a more realistic assessment. Geophys. J. Int. 2006, 167, 1055–1059. [Google Scholar] [CrossRef]
- Forootan, E.; Didova, O.; Schumacher, M.; Kusche, J.; Elsaka, B. Comparisons of atmospheric mass variations derived from ECMWF reanalysis and operational fields, over 2003–2011. J. Geod. 2014, 88, 503–514. [Google Scholar] [CrossRef]
- Seo, K.W.; Wilson, C.R.; Chen, J.; Waliser, D.E. GRACE’s spatial aliasing error. Geophys. J. Int. 2008, 172, 41–48. [Google Scholar] [CrossRef]
- Frappart, F.; Ramillien, G.; Maisongrande, P.; Bonnet, M.-P. Denoising satellite gravity signals by independent component analysis. IEEE Geosci. Remote Sens. Lett. 2010, 7, 421–425. [Google Scholar] [CrossRef]
- Freeden, W.; Schreiner, M. Spherical Functions of Mathematical Geosciences; Springer: New York, NY, USA, 2009; ISBN 978-3-54-085112-7. [Google Scholar]
- Ramillien, G.; Lombard, A.; Cazenave, A.; Ivins, E.R.; Llubes, M.; Remy, F.; Biancale, R. Interannual variations of the mass balance of the Antarctica and Greenland ice sheets from GRACE. Glob. Planet. Chang. 2006, 53, 198–208. [Google Scholar] [CrossRef]
- Klees, R.; Zapreeva, E.A.; Winsemius, H.C.; Savenije, H.H.G. The bias in GRACE estimates of continental water storage variations. Hydrol. Earth Syst. Sci. 2007, 11, 1227–1241. [Google Scholar] [CrossRef]
- Longuevergne, L.; Scanlon, B.R.; Wilson, C.R. GRACE Hydrological estimates for small basins: Evaluating processing approaches on the High Plains Aquifer, USA. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Multi-sensor analysis of water storage variations of the Caspian Sea. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Long, D.; Chen, X.; Scanlon, B.R.; Wada, Y.; Hong, Y.; Singh, V.P.; Chen, Y.; Wang, C.; Han, Z.; Yang, W. Have GRACE satellites overestimated groundwater depletion in the Northwest India Aquifer? Sci. Rep. 2016, 6, 24398. [Google Scholar] [CrossRef] [PubMed]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
- Ramillien, G.L.; Seoane, L.; Frappart, F.; Biancale, R.; Gratton, S.; Vasseur, X.; Bourgogne, S. Constrained Regional Recovery of Continental Water Mass Time-variations from GRACE-based Geopotential Anomalies over South America. Surv. Geophys. 2012, 33, 887–905. [Google Scholar] [CrossRef]
- Seoane, L.; Ramillien, G.; Frappart, F.; Leblanc, M. Regional GRACE-based estimates of water mass variations over Australia: Validation and interpretation. Hydrol. Earth Syst. Sci. 2013, 17, 4925–4939. [Google Scholar] [CrossRef]
- Frappart, F.; Seoane, L.; Ramillien, G. Validation of GRACE-derived terrestrial water storage from a regional approach over South America. Remote Sens. Environ. 2013, 137, 69–83. [Google Scholar] [CrossRef]
- Frappart, F.; Papa, F.; Santos Da Silva, J.; Ramillien, G.; Prigent, C.; Seyler, F.; Calmant, S. Surface freshwater storage and dynamics in the Amazon basin during the 2005 exceptional drought. Environ. Res. Lett. 2012, 7, 044010. [Google Scholar] [CrossRef]
- Papa, F.; Frappart, F.; Güntner, A.; Prigent, C.; Aires, F.; Getirana, A.C.V.; Maurer, R. Surface freshwater storage and variability in the Amazon basin from multi-satellite observations, 1993–2007. J. Geophys. Res. Atmos. 2013, 118, 11951–11965. [Google Scholar] [CrossRef]
- Frappart, F.; Papa, F.; Malbeteau, Y.; León, J.G.; Ramillien, G.; Prigent, C.; Seoane, L.; Seyler, F.; Calmant, S. Surface freshwater storage variations in the orinoco floodplains using multi-satellite observations. Remote Sens. 2015, 7, 89–110. [Google Scholar] [CrossRef]
- Papa, F.; Frappart, F.; Malbeteau, Y.; Shamsudduha, M.; Vuruputur, V.; Sekhar, M.; Ramillien, G.; Prigent, C.; Aires, F.; Pandey, R.K.; et al. Satellite-derived surface and sub-surface water storage in the Ganges-Brahmaputra River Basin. J. Hydrol. Reg. Stud. 2015, 4, 15–35. [Google Scholar] [CrossRef]
- Salameh, E.; Frappart, F.; Papa, F.; Güntner, A.; Venugopal, V.; Getirana, A.; Prigent, C.; Aires, F.; Labat, D.; Laignel, B. Fifteen years (1993–2007) of surface freshwater storage variability in the ganges-brahmaputra river basin using multi-satellite observations. Water 2017, 9, 245. [Google Scholar] [CrossRef]
- Biancamaria, S.; Lettenmaier, D.P.; Pavelsky, T.M. The SWOT Mission and Its Capabilities for Land Hydrology. Surv. Geophys. 2016, 37, 307–337. [Google Scholar] [CrossRef]
- Kurtenbach, E.; Eicker, A.; Mayer-Gürr, T.; Holschneider, M.; Hayn, M.; Fuhrmann, M.; Kusche, J. Improved daily GRACE gravity field solutions using a Kalman smoother. J. Geodyn. 2012, 59–60, 39–48. [Google Scholar] [CrossRef]
- Ramillien, G.L.; Frappart, F.; Gratton, S.; Vasseur, X. Sequential estimation of surface water mass changes from daily satellite gravimetry data. J. Geod. 2015, 89, 259–282. [Google Scholar] [CrossRef]
- Alley, W.M.; Konikow, L.F. Bringing GRACE Down to Earth. Groundwater 2015, 53, 826–829. [Google Scholar] [CrossRef] [PubMed]
- Castellazzi, P.; Martel, R.; Galloway, D.L.; Longuevergne, L.; Rivera, A. Assessing Groundwater Depletion and Dynamics Using GRACE and InSAR: Potential and Limitations. Groundwater 2016, 54, 768–780. [Google Scholar] [CrossRef] [PubMed]

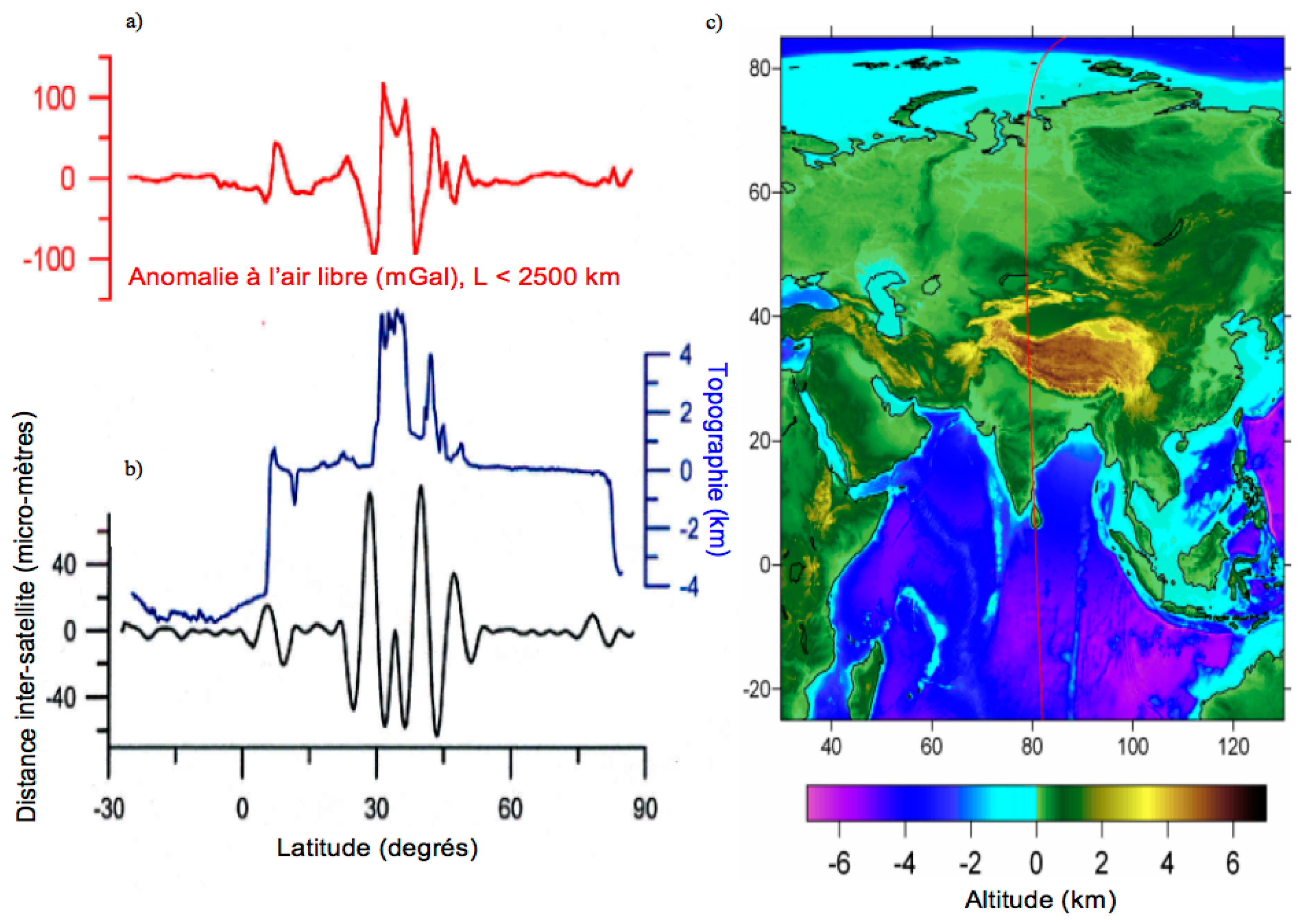
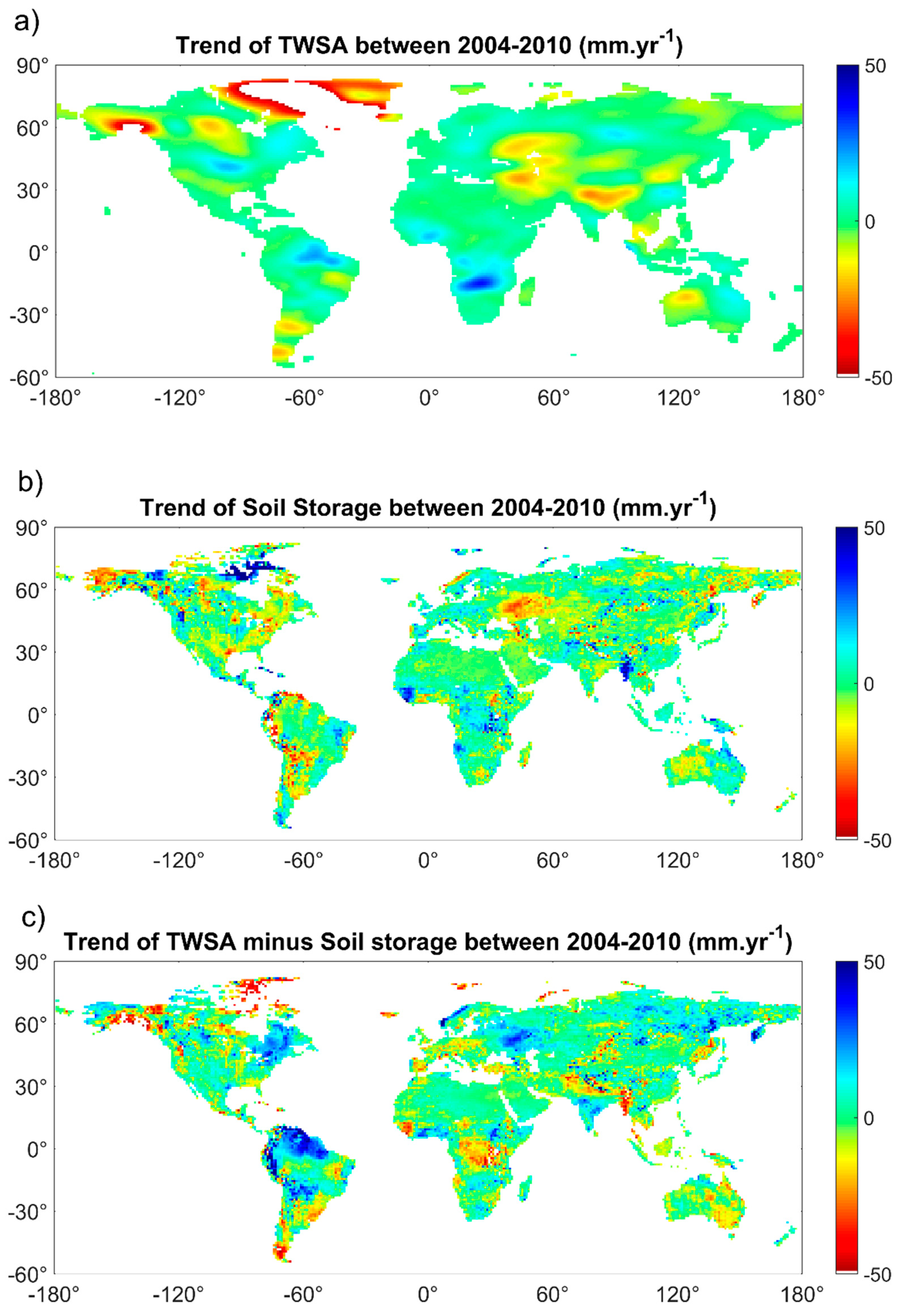
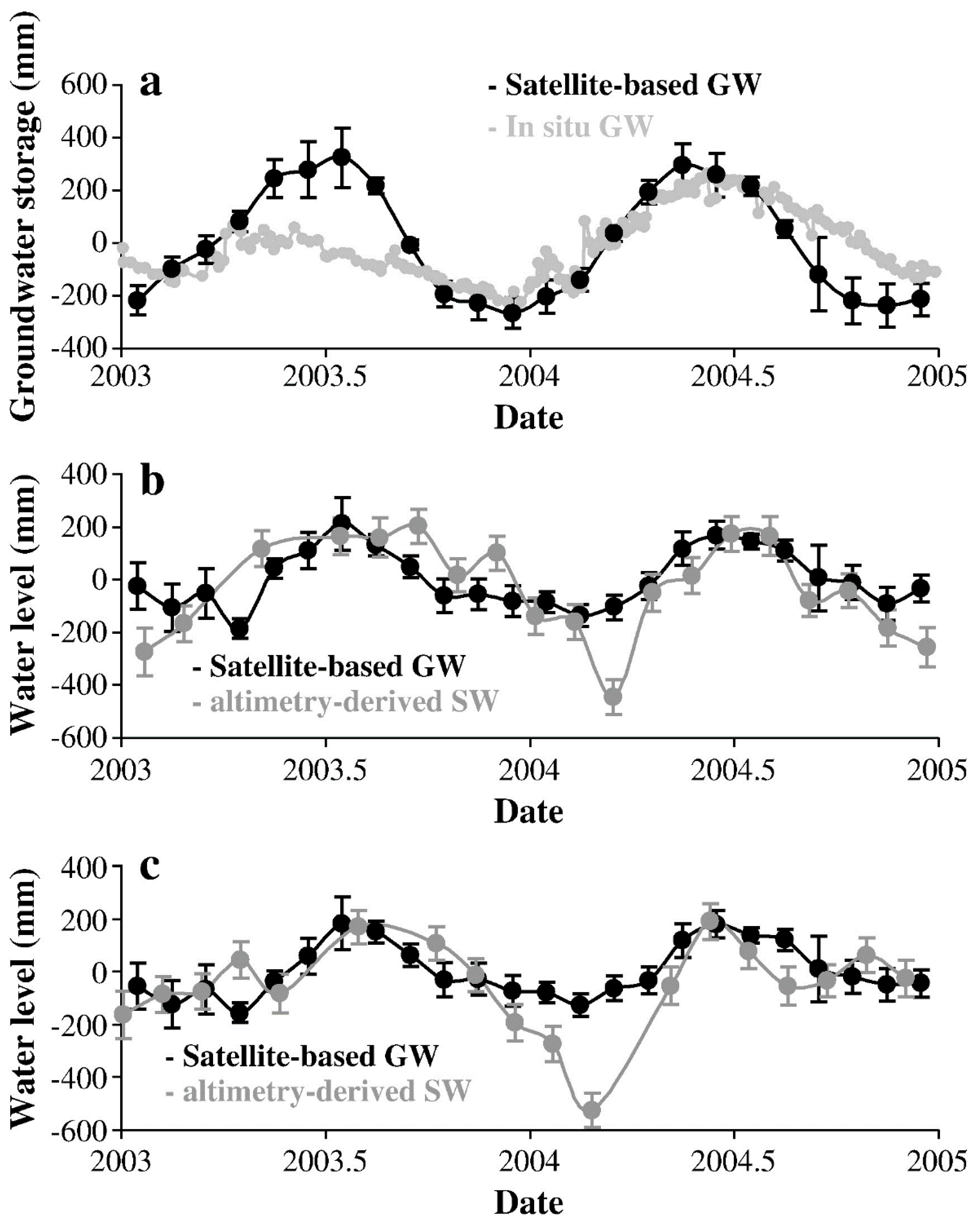
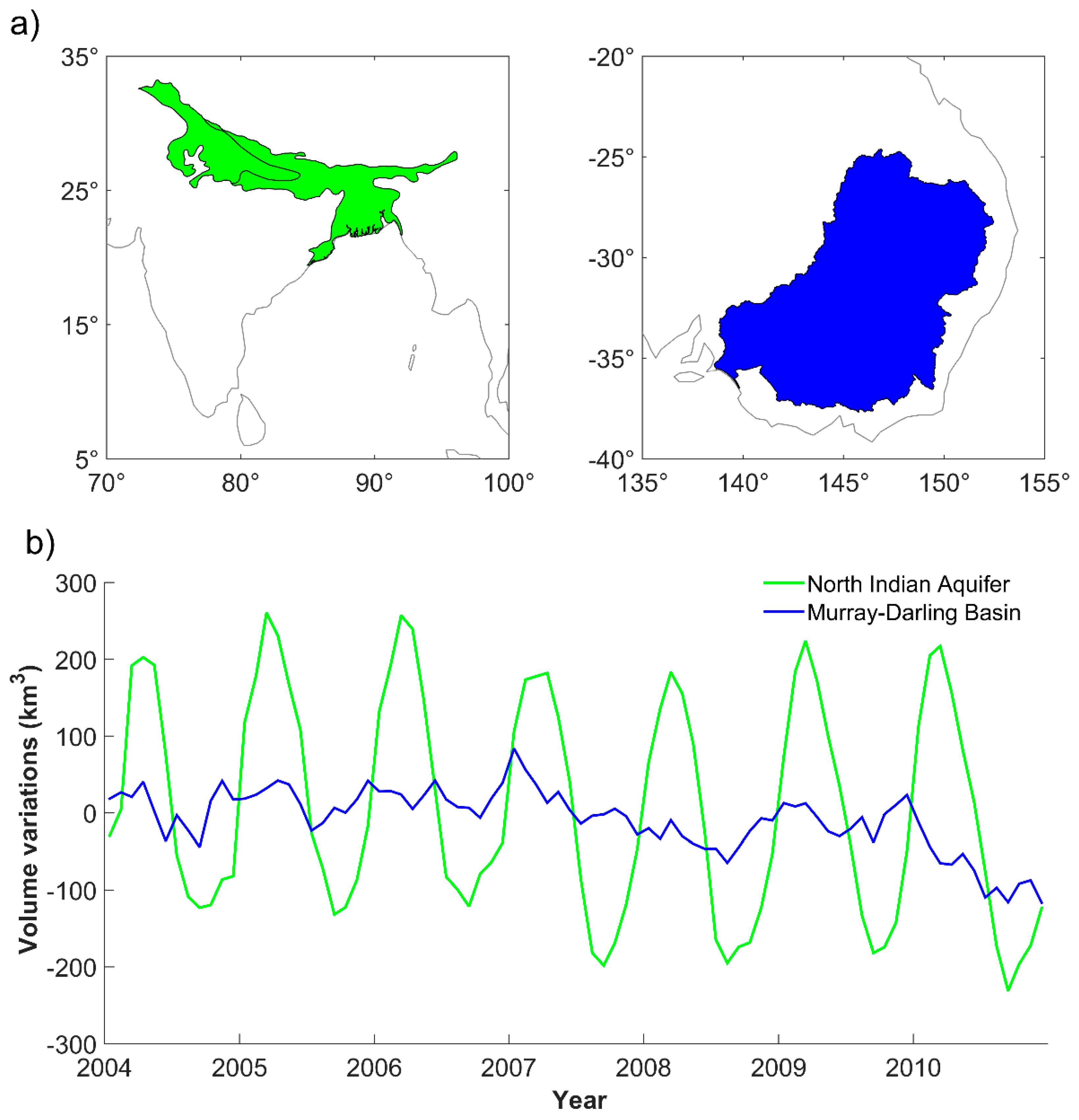
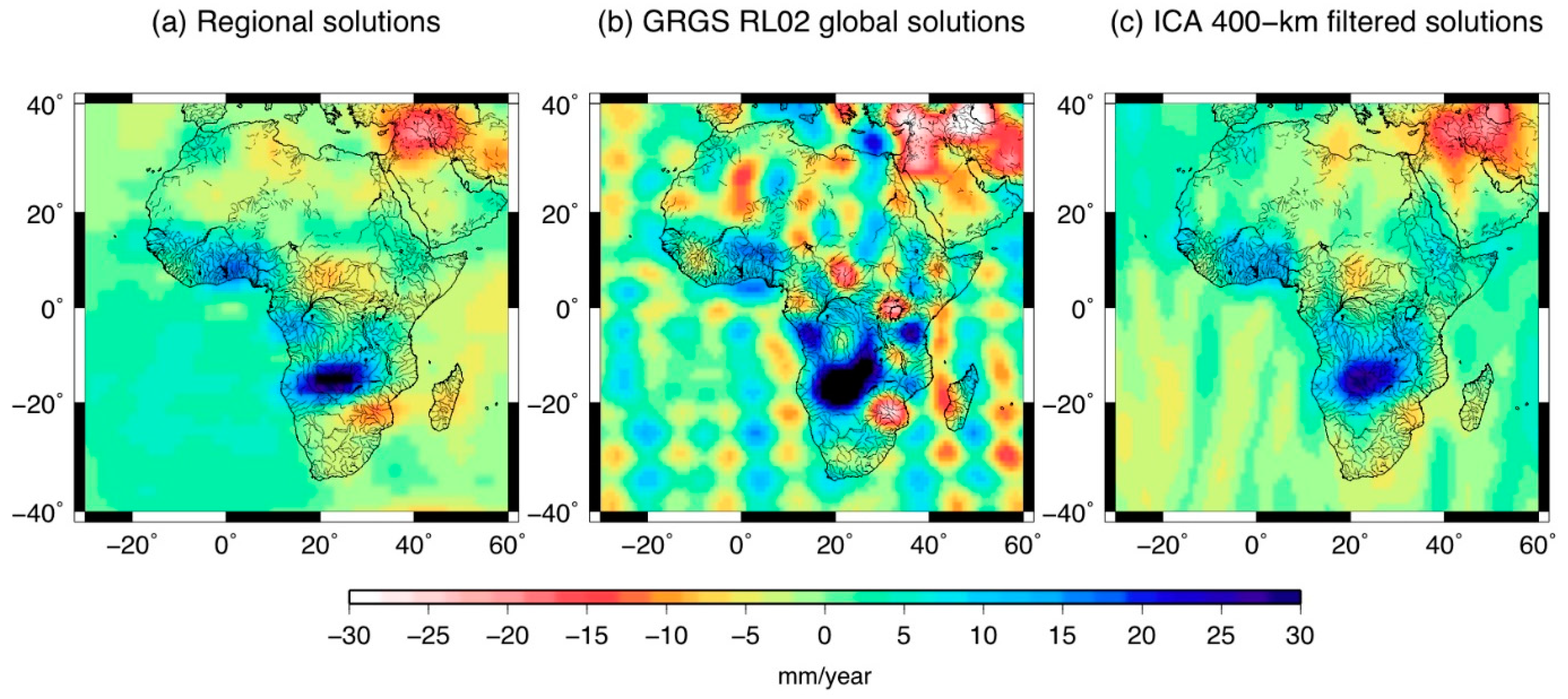
| Region | Area 106 km2 | Countries | Estimated Depletion Rate | GRACE Product and Release | SM Product | SW Product | Snow Product | Period (MM/YYYY–MM/YYYY) | Ref | |
|---|---|---|---|---|---|---|---|---|---|---|
| mm·year−1 | km3·year−1 | |||||||||
| Northwestern Sahara Aquifer System | 1 | Algeria, Lybia, Tunisia | −0.54 ± 1.40 | −0.54 ± 1.40 | NA | GLDAS | None | None | 01/2003–12/2007 | [105] |
| −0.81 ± 0.16 | −0.81 ± 0.16 | CSR 05 | None | None | None | 01/2003–09/2012 | [106] | |||
| −4.48 | −4.48 | Regional | None | None | None | 06/2003–12/2012 | [67] | |||
| 2.69 ± 0.8 | −2.69 ± 0.8 | CSR 05 | GLDAS | CLM 0.4 | None | 01/2003–12/2013 | [107] | |||
| Nubian Sandstone Aquifer System | 2.2 | Chad, Egypt, Lybia, Sudan | −3.72 ± 0.27 | −8.18 ± 0.59 | CSR 05 | None | None | None | 01/2003–09/2012 | [106] |
| −2.76 ± 0.86 | −6.08 ± 1.9 | CSR 05 | GLDAS | CLM 0.4 | None | 01/2003–12/2013 | [107] | |||
| Tigris and Euphrates River Basin | 0.75 | Turkey, Syria, Iraq, Iran | −27.2 ± 0.6 | −20.4 ± 0.45 | CSR 05 | GLDAS | Altimetry | None | 01/2003–12/2009 | [68] |
| Middle East | NA | Irak, Iran, Saudi Arabia, Turkey | NA | −43 ± 3 | CSR 05 | CLM 4.5 | CLM 4.5 + Altimetry | None | 02/2003–12/2012 | [108] |
| Northwest India | 0.56 | India | −40 ± 10 | −17.7 ± 4.5 | CSR 04 | GLDAS | None | GLDAS | 08/2002–10/2008 | [63] |
| −47.7 ± 12 | −20.4 ± 7.1 | CSR 05 | GLDAS | None | GLDAS | 01/2003–12/2012 | [109] | |||
| Norhern India | 2.7 | India | −20 ± 3 | −54 ± 9 | CSR 04 | CLM | CLM | GLDAS | 04/2002–06/2008 | [62] |
| North China | 0.37 | China | −22 ± 3 | −8.3 ± 1.1 | CSR 05 | GLDAS | None | None | 01/2003–12/2010 | [93] |
| Hai River | China | −17.0 ± 4.3 | −5.5 ± 1.4 | GRGS 2 | In situ | In situ | None | 01/2003–12/2012 | [110] | |
| −8.3 ± 4.5 | −2.7 ± 5.5 | CSR 05 | ||||||||
| Piedmont Plain | 0.054 | China | −46.5 ± 6.8 | −2.5 ± 0.4 | CSR 05 | GLDAS | None | None | 01/2003–07/2013 | [99] |
| East Central Plain | 0.086 | China | −16.9 ± 1.9 | −1.5 ± 0.2 | CSR 05 | GLDAS | None | None | 01/2003–07/2013 | [99] |
| Canning | 0.43 | Australia | −25.6 | −11 | GRGS 2 | NOAH | None | None | 01/2003–12/2009 | [56] |
| Murray Darling Basin | 1 | Australia | −17 ± 7 | 17 ± 7 | GRGS 1 | NOAH | In situ | None | 01/2003–12/2007 | [58] |
| −17.2 ± 4.7 | 17.2 ± 4.7 | CSR 05 | WGHM | WGHM | None | 01/2003–12/2012 | [65] | |||
| High Plains Aquifer | 0.45 | USA | −25.1 ± 2.1 | −11.4 ± 0.4 | CSR 05 | NOAH | In situ | None | 03/2003–02/2013 | [111] |
| Sacramento and San Joaquin River Basins | 0.154 | USA | −20.4 ± 3.9 | −3.1 ± 0.6 | CSR 04 | GLDAS | In situ | NORHSC | 10/2002–03/2010 | [60] |
| −55.9 ± 5.3 | −8.6 ± 0.8 | GRGS 2 | GLDAS | In situ | SNODAS | 04/2006–03/2010 | [92] | |||
| −44.9 ± 8.5 | −6.9 ± 1.3 | CSR 04 | GLDAS | In situ | SNODAS | 04/2006–03/2010 | [92] | |||
| Colorado River Basin | 0.64 | USA | 8.75 ± 0.63 | −5.6 ± 0.4 | CSR 05 | GLDAS | In situ | SNODAS | 12/2004–11/2013 | [94] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frappart, F.; Ramillien, G. Monitoring Groundwater Storage Changes Using the Gravity Recovery and Climate Experiment (GRACE) Satellite Mission: A Review. Remote Sens. 2018, 10, 829. https://doi.org/10.3390/rs10060829
Frappart F, Ramillien G. Monitoring Groundwater Storage Changes Using the Gravity Recovery and Climate Experiment (GRACE) Satellite Mission: A Review. Remote Sensing. 2018; 10(6):829. https://doi.org/10.3390/rs10060829
Chicago/Turabian StyleFrappart, Frédéric, and Guillaume Ramillien. 2018. "Monitoring Groundwater Storage Changes Using the Gravity Recovery and Climate Experiment (GRACE) Satellite Mission: A Review" Remote Sensing 10, no. 6: 829. https://doi.org/10.3390/rs10060829
APA StyleFrappart, F., & Ramillien, G. (2018). Monitoring Groundwater Storage Changes Using the Gravity Recovery and Climate Experiment (GRACE) Satellite Mission: A Review. Remote Sensing, 10(6), 829. https://doi.org/10.3390/rs10060829






