Suspended Sediment Concentration Estimation from Landsat Imagery along the Lower Missouri and Middle Mississippi Rivers Using an Extreme Learning Machine
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Methods
2.2.1. Suspended Sediment Data
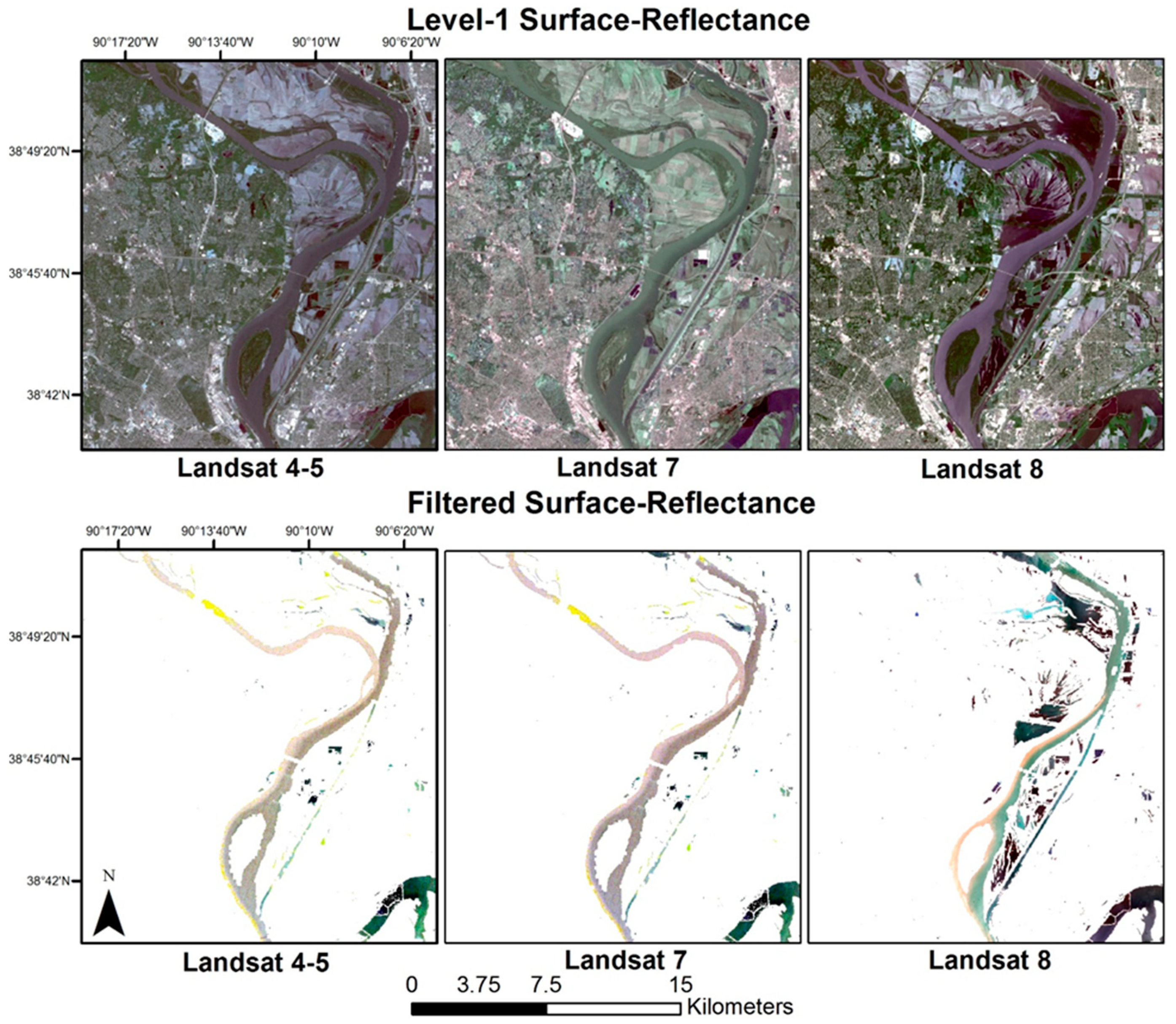
2.2.2. Landsat Imagery
2.2.3. Suspended Sediment Modeling
2.2.4. Feature Fusion
2.2.5. Regression Modeling
2.2.6. Quantitative Evaluation
3. Results
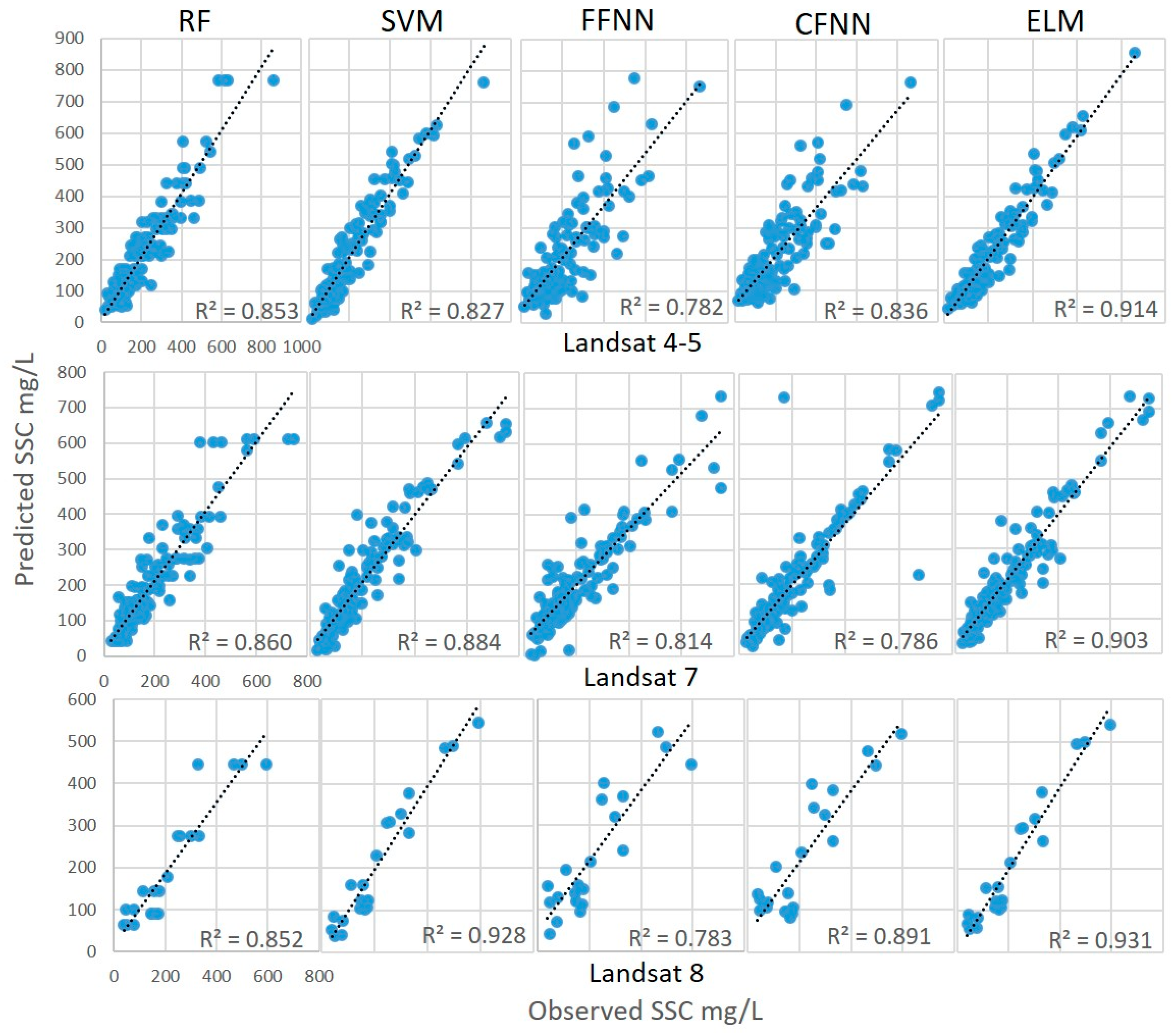
3.1. Suspended Sediment Modeling
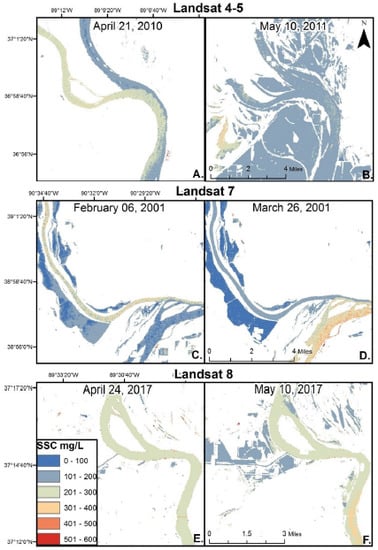
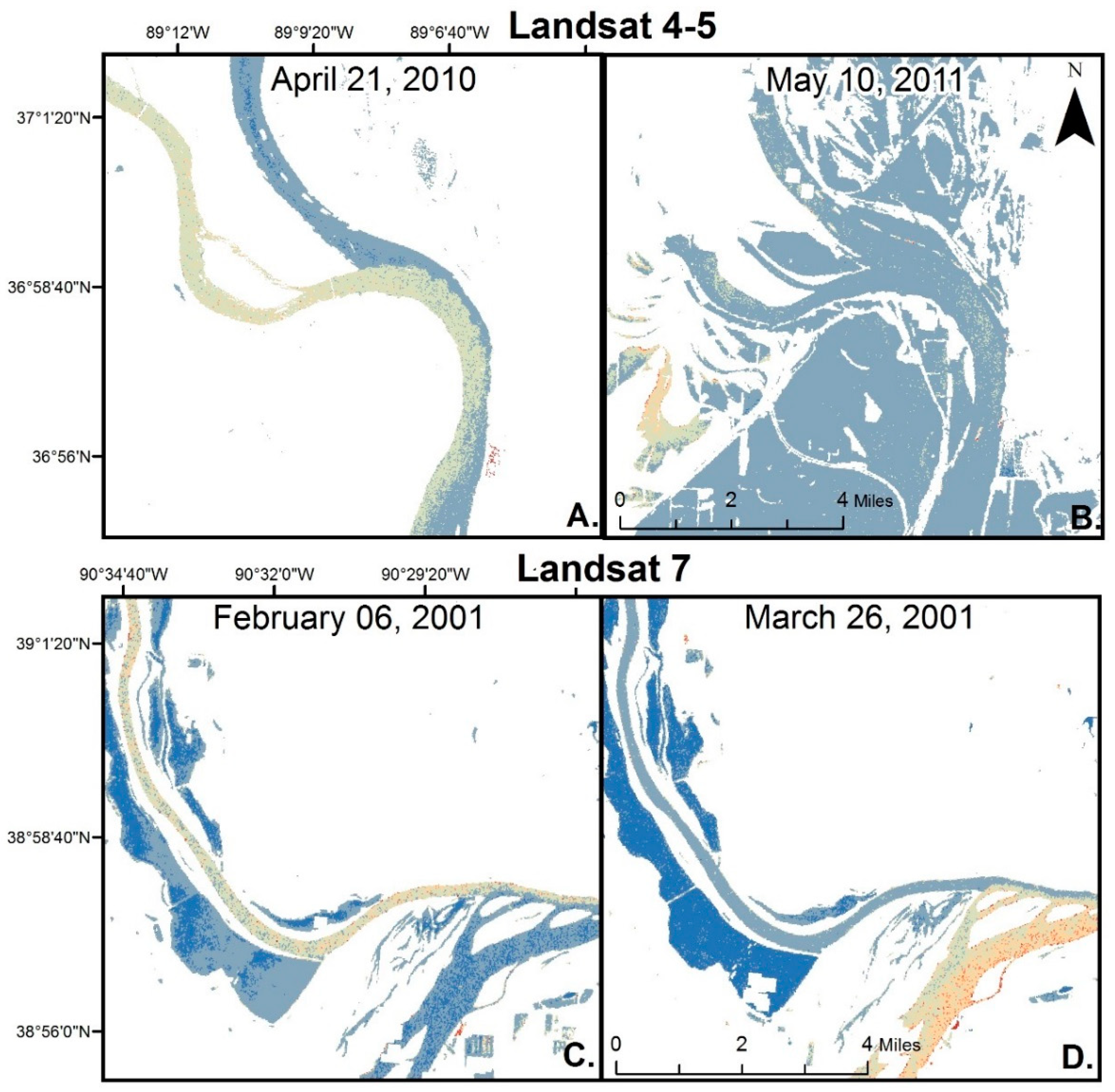
3.2. Suspended Sediment Mapping
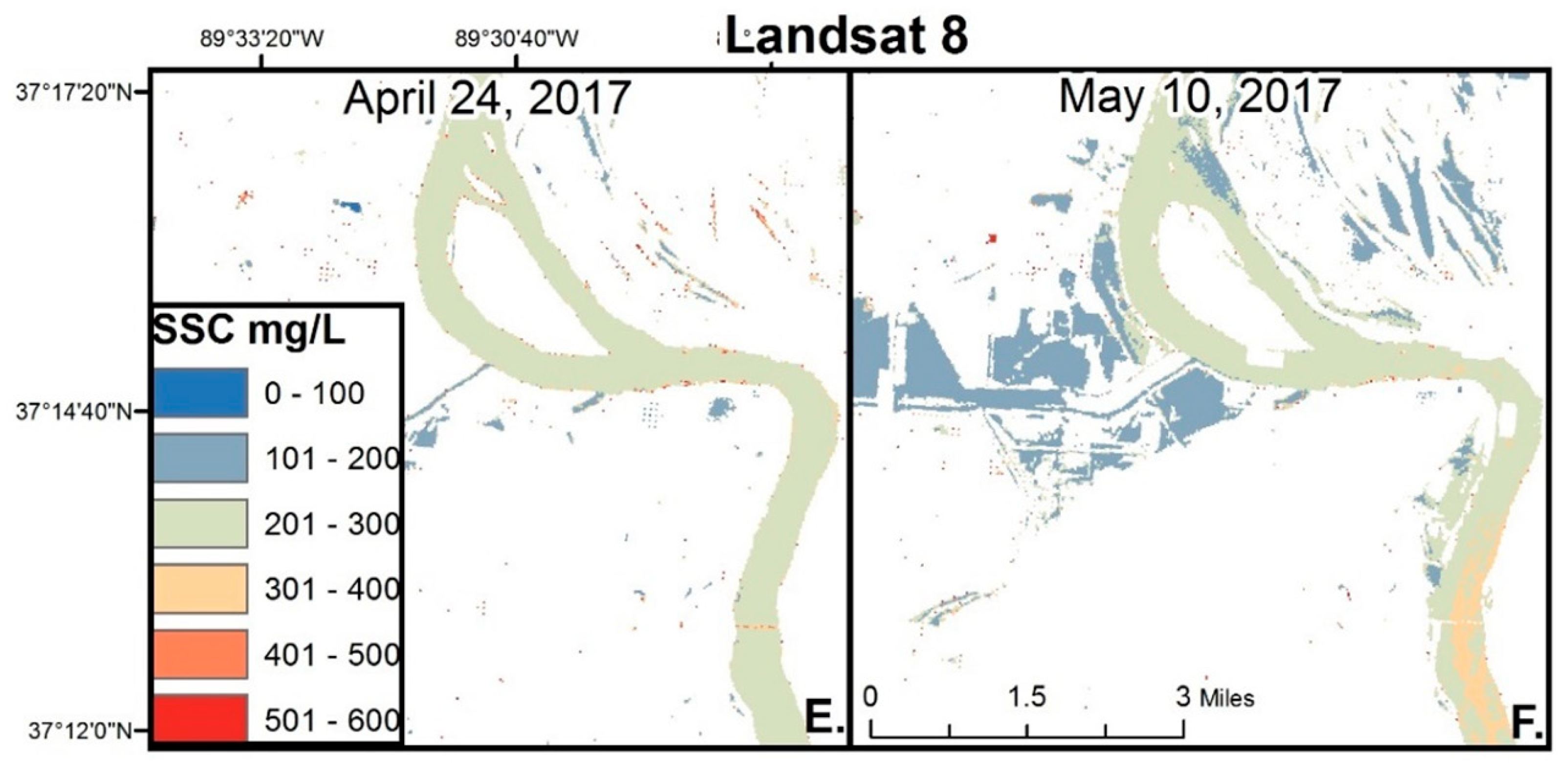
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Asselman, N.E. Suspended sediment dynamics in a large drainage basin: The River Rhine. Hydrol. Process. 1999, 13, 1437–1450. [Google Scholar] [CrossRef]
- Chapra, S.C. Surface Water Quality Modeling. Available online: https://bit.ly/2xcz9Iz (accessed on 17 September 2018).
- Welch, H.L.; Coupe, R.H.; Aulenbach, B.T. Concentrations and Transport of Suspended Sediment, Nutrients, and Pesticides in the Lower Mississippi-Atchafalaya River Subbasin during the 2011 Mississippi River Flood, April through July. Available online: https://pubs.er.usgs.gov/publication/sir20145100 (accessed on 17 September 2018).
- Kondolf, G.M.; Rubin, Z.K.; Minear, J.T. Dams on the mekong: Cumulative sediment starvation. Water Resour. Res. 2014, 50, 5158–5169. [Google Scholar] [CrossRef]
- Meade, R.H.; Moody, J.A. Causes for the decline of suspened-sediment discharge in the Mississippi River system, 1950–2007. Hydrol. Process. 2010, 24, 35–49. [Google Scholar]
- Edwards, T.K.; Glysson, G.D. Field Methods for Measurement of Fluvial Sediment. Available online: https://pubs.er.usgs.gov/publication/ofr86531 (accessed on 17 September 2018).
- Meade, R.H. Setting: Geology, Hydrology, Sediments, and Engineering of the Mississippi River. Available online: https://pubs.usgs.gov/circ/circ1133/geosetting.html (accessed on 17 September 2018).
- Ritchie, J.C.; Schiebe, F.R.; McHenry, J.R. Remote sensing of suspended sediment in surface water. Photogramm. Eng. Remote Sens. 1976, 42, 1539–1545. [Google Scholar]
- Feng, L.; Hu, C.; Chen, X.; Tian, L.; Chen, L. Human induced turbidity changes in Poyang Lake between 2000 and 2010: Observations from MODIS. J. Geophys. Res. 2012, 117, 1–19. [Google Scholar] [CrossRef]
- Petus, C.; Chust, G.; Gohin, F.; Doxaran, D.; Froidefond, J.M.; Sagarminaga, Y. Estimating turbidity and total suspended matter in the Adour riverplume (south bay of biscay) using MODIS 250-m imagery. Cont. Shelf Res. 2010, 30, 379–392. [Google Scholar] [CrossRef]
- Ritchie, J.C.; Zimba, P.V.; Everitt, J.H. Remote sensing techniques to assess water quality. Photogramm. Eng. Remote Sens. 2003, 69, 695–704. [Google Scholar] [CrossRef]
- Shen, F.; Verhoef, W.; Zhou, Y.; Salama, M.S.; Liu, X. Satellite estimates of wide-range suspended sediment concentrations in Changjiang (Yangtze) Estuary using MERIS data. Estuaries Coasts 2010, 33, 1420–1429. [Google Scholar] [CrossRef]
- Son, S.; Wang, M. Water properties in Chesapeake Bay from MODIS-Aqua measurements. Remote Sens. Environ. 2012, 123, 163–174. [Google Scholar] [CrossRef]
- Montanher, O.C.; Novo, E.M.L.M.; Barbosa, C.C.F.; Renno, C.D.; Silva, T.S. Empirical models for estimating the suspended sediment concentration in Amazonian white water rivers using Landsat 5/TM. Int. J. Appl. Earth Obs. Geoinf. 2014, 29, 66–77. [Google Scholar] [CrossRef]
- Pereira, L.S.F.; Andes, L.C.; Cox, A.L.; Ghulam, A. Measuring suspended-sediment concentration and turbidity in the middle Mississippi and lower Missouri Rivers using Landsat data. J. Am. Water Resour. Assoc. 2018, 54, 440–450. [Google Scholar] [CrossRef]
- Wang, J.J.; Lu, X.X.; Liew, S.C.; Zhou, Y. Retrieval of suspended sediment concentrations in large turbid rivers using Landsat ETM+: An example from the Yangtze River, China. Earth Surf. Process. Landf. 2009, 34, 1082–1092. [Google Scholar] [CrossRef]
- Wu, G.; Cui, L.; Liu, L.; Chen, F.; Fei, T.; Liu, Y. Statistical model development and estimation of suspended particulate matter concentrations with Landsat 8 OLI images of Dongting Lake, China. Int. J. Remote Sens. 2015, 36, 343–360. [Google Scholar] [CrossRef]
- Zhang, M.; Dong, Q.; Cui, T.; Xue, C.; Zhang, S. Suspended sediment monitoring and assessment for Yellow River Estuary from Landsat TM and ETM+ imagery. Remote Sens. Environ. 2014, 146, 136–147. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, Y.; Guo, Y.; Xu, Y.; Liu, G.; Du, C. Landsat-based long-term monitoring of total suspended matter concentration pattern change in the wet season for Dongting Lake, China. Remote Sens. 2015, 7, 13975–13999. [Google Scholar] [CrossRef]
- Bukata, R.P.; Jerome, J.H.; Kondratyev, A.S.; Pozdnyakov, D.V. Optical Properties and Remote Sensing of Inland and Coastal Waters. Available online: https://bit.ly/2OsMMd3 (accessed on 17 September 2018).
- Umar, M.; Rhoads, B.L.; Greenburg, J.A. Use of multispectral satellite remote sensing to assess mixing of suspended sediment downstream of large river confluences. J. Hydrol. 2018, 556, 325–338. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Pullianen, J.T.; Koponen, S.S.; Hallikainen, M.T. Application of an empirical neural network to surface water quality estimation in the Gulf of Finland using combined optical data and microwave data. Remote Sens. Environ. 2002, 81, 327–336. [Google Scholar] [CrossRef]
- Hassoun, M.H. Fundamentals of Artificial Neural Networks. Available online: https://amzn.to/2Ni38IV (accessed on 17 September 2018).
- Sudheer, K.P.; Chaubey, I.; Garg, V. Lake water quality assessment from Landsat thematic mapper data using neural network: An approach to optimal band combination selection. J. Am. Water Resour. Assoc. 2006, 42, 1683–1695. [Google Scholar] [CrossRef]
- Mas, J.F.; Flores, J.J. The application of artificial neural networks to the analysis of remotely sensed data. Int. J. Remote Sens. 2008, 29, 617–663. [Google Scholar] [CrossRef]
- Chebud, Y.; Naja, G.M.; Rivero, R.G.; Melesse, A.M. Water quality monitoring using remote sensing and an artificial neural network. Water Air Soil Pollut. 2012, 223, 4875–4887. [Google Scholar] [CrossRef]
- Heimann, D.C.; Sprague, L.A.; Blevins, D.W. Trends in Suspended-Sediment Loads and Concentrations in the Mississippi River Basin. Available online: https://pubs.usgs.gov/sir/2011/5200/pdf/sir2011-5200.pdf (accessed on 17 September 2018).
- Koltun, G.F.; Eberle, M.; Gray, J.R.; Glysson, G.D. USGS Geological Survey Techniques and Methods. Available online: https://pubs.usgs.gov/tm/tm7c5/pdf/TM-7-C5.pdf (accessed on 17 September 2018).
- United States Geological Survey. Landsat Thematic Mapper (TM) Level 1 (L1) Data Format Control Book (DFCB). Available online: https://landsat.usgs.gov/sites/default/files/documents/LSDS-284.pdf (accessed on 17 September 2018).
- United States Geological Survey. Landsat 8 (L8) Level 1(L1) Data Format Control Book. Available online: https://bit.ly/2xiVxzV (accessed on 17 September 2018).
- United States Geological Survey. Landsat 4-7 Climate Data Record (CDR) Surface Reflectance. Available online: https://on.doi.gov/2xvg5oa (accessed on 17 September 2018).
- Dekker, A.G.; Vos, R.J.; Peters, S.W.M. Analytical algorithms for lake water TSM estimation for retrospective analyses of TM and SPOT sensor data. Int. J. Remote Sens. 2002, 23, 15–35. [Google Scholar] [CrossRef]
- Doxoran, D.; Froidefond, J.M.; Castaing, P. Remote-sensing reflectance of turbid sediment-dominated waters reduction of sediment type variations and changing illumination conditions effects by use of reflectance ratios. Appl. Opt. 2003, 42, 2623–2634. [Google Scholar] [CrossRef]
- Joshi, I.D.; D’Sa, E.J.; Osborn, C.L.; Bianchi, T.S. Turbidity in Apalachicola Bay, Florida from Landsat 5 TM and field data: Seasonal patterns and response to extreme events. Remote Sens. 2017, 9, 367. [Google Scholar] [CrossRef]
- Lathrop, R.G.; Lillesand, T.M. Monitoring water-quality and river plume transport in Green Bay, Lake-Michigan with SPOT-1 imagery. Photogramm. Eng. Remote Sens. 1989, 55, 349–354. [Google Scholar]
- Onderka, M.; Pekárová, P. Retrieval of suspended particulate matter concentrations in the Danube River from Landsat ETM data. Sci. Total Environ. 2008, 397, 238–243. [Google Scholar] [CrossRef] [PubMed]
- Svab, E.; Tyler, A.N.; Preston, T.; Presing, M.; Balogh, K.V. Characterizing the spectral reflectance of algae in lake waters with high suspended sediment concentrations. Int. J. Remote Sens. 2005, 26, 919–928. [Google Scholar] [CrossRef]
- Sun, Q.S.; Zeng, S.G.; Liu, Y.; Heng, P.A.; Xia, D.S. A new method of feature fusion and its application in image recognition. Pattern Recognit. 2005, 38, 2437–2448. [Google Scholar] [CrossRef]
- Haghighat, M.; Abdel-Mottaleb, M.; Alhalabi, W. Fully automatic face normalization and single sample face recognition in unconstrained environments. Expert Syst. Appl. 2015, 47, 23–34. [Google Scholar] [CrossRef]
- Peterson, K.T. Machine Learning Based Ensemble Prediction of Water Quality Variables Using Feature-Level and Decision-Level Fusion; Remote Sensing Saint Louis University: St. Louis, MO, USA, 2018. [Google Scholar]
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Lin, Y.; Yu, J.; Cai, J.; Sneeuw, N.; Li, F. Spatio-temporal analysis of wetland changes using a kernel extreme learning machine approach. Remote Sens. 2018, 10, 1129. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Ghulam, A.; Sidike, P.; Hartling, S.; Maimaitiyiming, M.; Peterson, K.T.; Shavers, E.; Fishman, J.; Peterson, J.; Kadam, S.; et al. Unmanned aerial system (UAS)-based phenotyping of soybean using multi-sensor data fusion and extreme learning machine. ISPRS J. Photogramm. Remote Sens. 2017, 134, 43–58. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and 641 applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond. Available online: https://dl.acm.org/citation.cfm?id=559923 (accessed on 17 September 2018).
- Liaw, A.; Wiener, M. Classification and regression by randomforest. R News 2002, 2, 18–22. [Google Scholar]
- Fan, R.E.; Chen, P.H.; Lin, C.J. Working set selection using second order information for training support vector machines. J. Mach. Learn. Res. 2005, 6, 1889–1918. [Google Scholar]
- Alexander, J.S.; Jacobson, R.B.; Rus, D.L. Sediment Transport and Deposition in the Lower Missouri River during the 2011 Flood. Available online: https://pubs.usgs.gov/pp/1798f/ (accessed on 17 September 2018).
- Heimann, D.C.; Holmes, R.R.J.; Harris, T.E. Flooding in the Southern Midwestern United States, April–May 2017: U.S. Geological Survey Open-File Report. Available online: https://bit.ly/2OrL5g5 (accessed on 17 September 2018).
- Gray, J.R.; Gartner, J.W. Technological advances in suspended-sediment surrograte monitoring. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Wall, G.R.; Nystrom, E.; Litten, S. Use of ADCP to Compute Suspended Sediment Discharge in the Tidal Hudson River, NY. Available online: https://bit.ly/2OtSgV5 (accessed on 17 September 2018).
- Long, C.M.; Pavelsky, T.M. Remote sensing of suspended sediment concentration and hydrologic connectivity in a complex wetland environment. Remote Sens. Environ. 2013, 129, 197–209. [Google Scholar] [CrossRef]
- Feng, L.; Hu, C.; Chen, X.; Song, Q. Influence of the Three Gorges Dam on total suspended matters in the Yangtze Estuary and its adjacent coastal waters: Observations from MODIS. Remote Sens. Environ. 2014, 140, 779–788. [Google Scholar] [CrossRef]
- Han, B.; Loisel, H.; Vantrepotte, V.; Mériaux, X.; Bryère, P.; Ouillon, S.; Dessailly, D.; Xing, Q.; Zhu, J. Development of a semi-analytical algorithm for the retrieval of suspended particulate matter from remote sensing over clear to very turbid waters. Remote Sens. 2016, 8, 211. [Google Scholar] [CrossRef]
- Jensen, J.R. Remote Sensing of the Environment: An Earth Resource Perspective (Second Edition). Available online: https://amzn.to/2OrZx7W (accessed on 17 September 2018).

| USGS Station ID | Station Name | Period of Record | Drainage Area (km2) |
|---|---|---|---|
| 07020500 | Chester, IL | 1 October 1982–30 September 2017 | 1,140,381.16 |
| 05586300 | Florence, IL | 13 February 1980–29 September 2014 | 43,243.07 |
| 06934500 | Hermann, MO | 24 February 2006–11 March 2018 | 43,243.07 |
| 06935965 | St. Charles, MO | 1 October 2005–30 September 2008 | 843,296.26 |
| 06818000 | St. Joseph, MO | 1 March 2006–2 April 2018 | 686,385.22 |
| 07022000 | Thebes, IL | 1 October 1982–30 September 2017 | 1,147,784.14 |
| USGS Station ID | Station Name | Period of Record | Samples (n) | SSC mg/L | ||
|---|---|---|---|---|---|---|
| Min | Max | Mean | ||||
| 07020500 | Chester, IL | 12 January 1983–20 September 2016 | 187 | 39.0 | 863.0 | 236.1 |
| 05586300 | Florence, IL | 3 January 1983–22 September 2014 | 266 | 17.8 | 860.0 | 140.7 |
| 06934500 | Hermann, MO | 8 March 2009–12 July 2017 | 82 | 46.8 | 1200.0 | 288.0 |
| 06935965 | St. Charles, MO | 15 October 2005–12 August 2008 | 27 | 116.0 | 667.0 | 233.7 |
| 06818000 | St. Joseph, MO | 4 October 2008–25 July 2017 | 86 | 150.0 | 1100.0 | 359.4 |
| 07022000 | Thebes, IL | 3 September 1984–20 September 2016 | 288 | 40.9 | 961.0 | 218.8 |
| Band Ratio | R2 | ||
|---|---|---|---|
| Landsat 4–5 | Landsat 7 | Landsat 8 | |
| (Green + Red)/2 | 0.297 | 0.345 | 0.401 |
| Green/Red | 0.474 | 0.455 | 0.478 |
| Red/Green | 0.513 | 0.503 | 0.552 |
| NIR/Green | 0.445 | 0.448 | 0.640 |
| Red/Green + NIR | 0.484 | 0.505 | 0.720 |
| Red | 0.413 | 0.349 | 0.497 |
| NIR | 0.459 | 0.407 | 0.714 |
| Regression Model Results | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Landsat 4–5 | Landsat 7 | Landsat 8 | ||||||||||
| Training | Testing | Training | Testing | Training | Testing | |||||||
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| RF | 0.942 | 37.6 | 0.853 | 56.7 | 0.942 | 41.2 | 0.860 | 57.6 | 0.911 | 57.0 | 0.852 | 58.0 |
| SVM | 0.856 | 58.2 | 0.827 | 59.5 | 0.890 | 52.6 | 0.884 | 56.8 | 0.962 | 37.1 | 0.928 | 40.4 |
| FFNN | 0.855 | 75.4 | 0.782 | 88.8 | 0.868 | 82.1 | 0.814 | 93.1 | 0.909 | 71.6 | 0.783 | 71.7 |
| CFNN | 0.855 | 81.1 | 0.836 | 82.7 | 0.903 | 73.5 | 0.786 | 102.3 | 0.933 | 68.9 | 0.891 | 69.7 |
| ELM | 0.916 | 43.3 | 0.914 | 45.2 | 0.910 | 48.1 | 0.903 | 51.4 | 0.968 | 34.2 | 0.931 | 39.7 |
| Sensor | Location | Image Date | Discharge (m3) | USGS Station Location |
|---|---|---|---|---|
| Landsat 4–5 | Mississippi River near Cairo, IL | 21 April 2010 | 10,279 | Mississippi River at Thebes, IL |
| 10 May 2011 | 16,225 | |||
| Landsat 7 | Mississippi River, North of St. Louis, MO | 6 February 2001 | 2673 | Mississippi River at Grafton, IL |
| 26 March 2001 | 6456 | |||
| Landsat 8 | Mississippi River near Cape Girardeau, MO | 24 April 2017 | 10,364 | Mississippi River at Thebes, IL |
| 10 May 2017 | 21,776 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peterson, K.T.; Sagan, V.; Sidike, P.; Cox, A.L.; Martinez, M. Suspended Sediment Concentration Estimation from Landsat Imagery along the Lower Missouri and Middle Mississippi Rivers Using an Extreme Learning Machine. Remote Sens. 2018, 10, 1503. https://doi.org/10.3390/rs10101503
Peterson KT, Sagan V, Sidike P, Cox AL, Martinez M. Suspended Sediment Concentration Estimation from Landsat Imagery along the Lower Missouri and Middle Mississippi Rivers Using an Extreme Learning Machine. Remote Sensing. 2018; 10(10):1503. https://doi.org/10.3390/rs10101503
Chicago/Turabian StylePeterson, Kyle T., Vasit Sagan, Paheding Sidike, Amanda L. Cox, and Megan Martinez. 2018. "Suspended Sediment Concentration Estimation from Landsat Imagery along the Lower Missouri and Middle Mississippi Rivers Using an Extreme Learning Machine" Remote Sensing 10, no. 10: 1503. https://doi.org/10.3390/rs10101503
APA StylePeterson, K. T., Sagan, V., Sidike, P., Cox, A. L., & Martinez, M. (2018). Suspended Sediment Concentration Estimation from Landsat Imagery along the Lower Missouri and Middle Mississippi Rivers Using an Extreme Learning Machine. Remote Sensing, 10(10), 1503. https://doi.org/10.3390/rs10101503