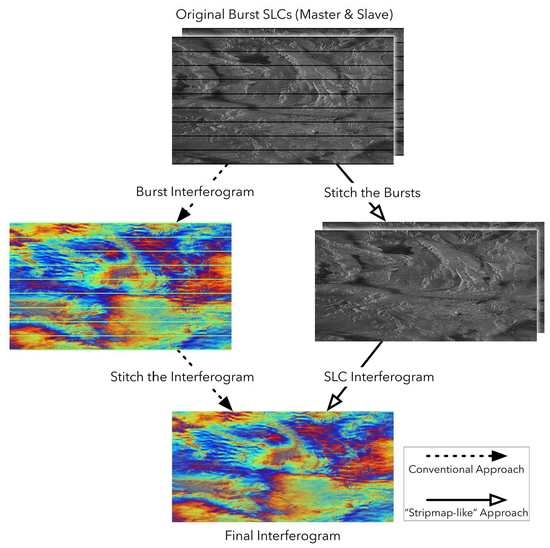
A Common “Stripmap-Like” Interferometric Processing Chain for TOPS and ScanSAR Wide Swath Mode
Abstract
:1. Introduction
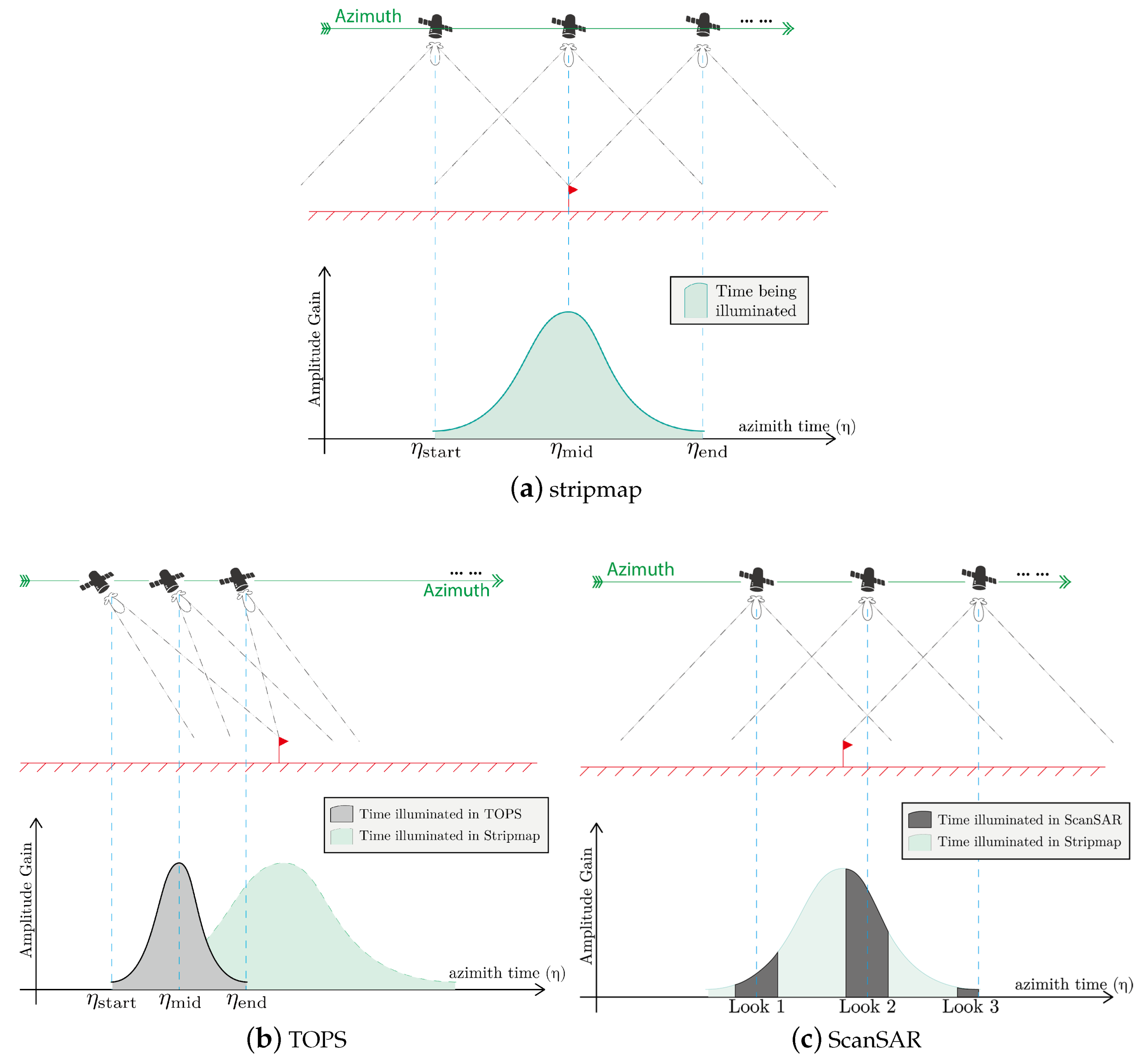
1.1. An Introduction to ScanSAR and TOPS
1.2. A “Stripmap-like” Processing Chain for TOPS and ScanSAR
- Designing the user-friendly “stripmap-like” interface for processing the wide swath mode. As mentioned above, this interface, including the processing steps and all outcomes, will be identical to processing a stripmap;
- Designing the common processing chain for ScanSAR and TOPS. Although ScanSAR and TOPS work differently in terms of imaging, a common processing chain is feasible because the two systems share a large portion of similarities and their impulse response functions (IRFs) are almost identical. Hence, the processing flow could be commonly used for both systems;
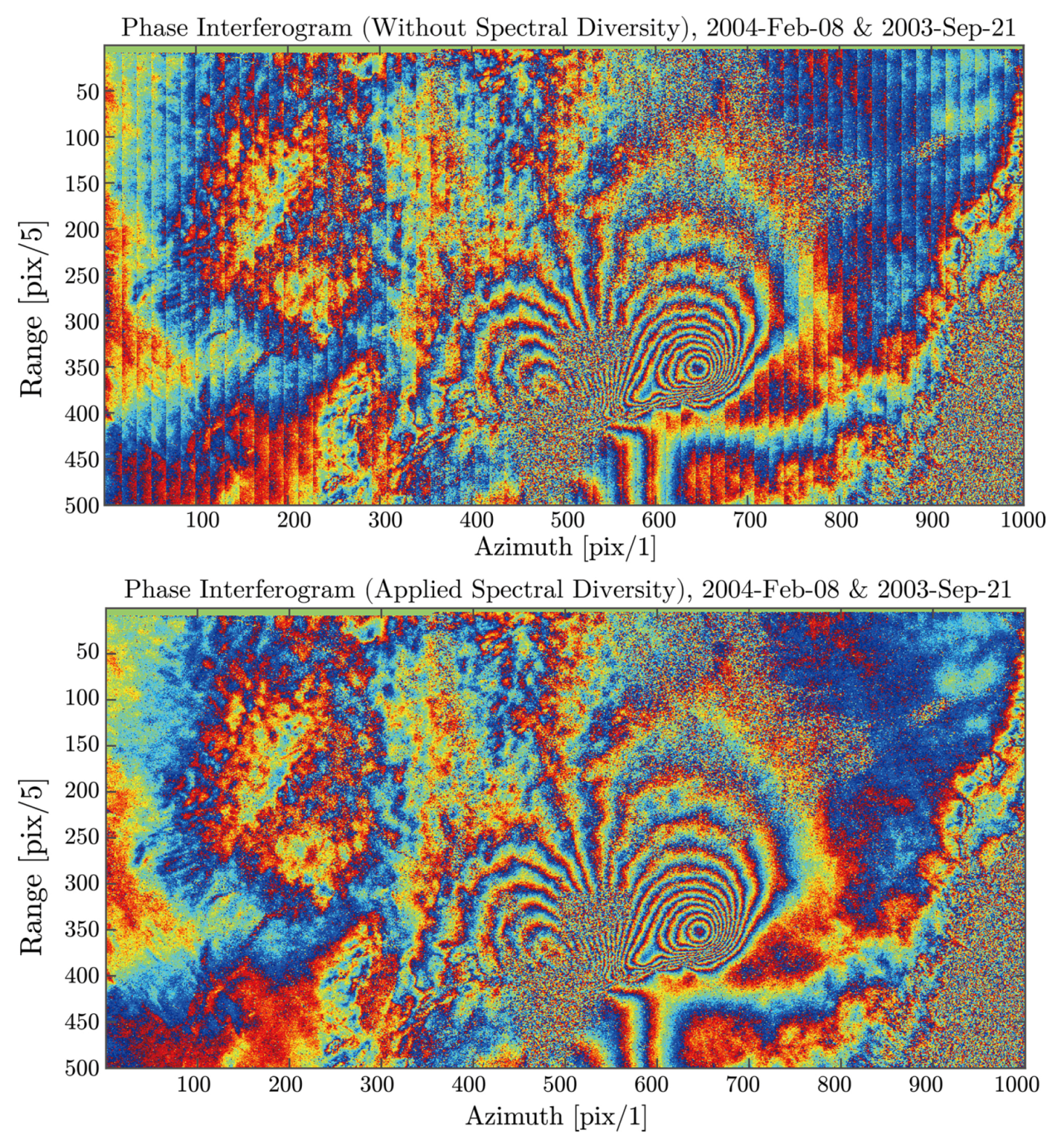
- In addition, we propose a simple method for correcting the miscoregistration residual that is estimated during the ESD step. This method does not require a resampling of the slave SLC using the conventional interpolation methods, but only requires a modulation in the frequency domain. This method will be more efficient because it only requires a point-wise multiplication in the time domain.
2. Burst Nature and Impulse Response Function of Wide Swath Mode
2.1. Bursts Nature and Impulse Response Function of Sentinel TOPS
- This equation is the most important point in this article. Everything hereinafter is based on this equation: stitching, deramping, coregistration, etc. This equation is what makes TOPS different from the stripmap mode. However, the equation is really very simple, elegant and the only difference between TOPS and stripmap [37] is the last term in the equation, the quadratic phase term . The intuitive understanding of this term is the extra doppler introduced by the steering of the antenna along the azimuth.
- This extra quadratic phase term is also a legitimate measurement of the slant-range distance to the point target and it provides the real distance for the zero doppler geometry [16]. Therefore, this term needs to be preserved and can not be discarded if we want to do interferometry.
- This quadratic phase term is azimuth dependent and is responsible for the high coregistration accuracy requirement along the azimuth direction. For example, in the presence of a miscoregistration time of in the azimuth direction, the interferometric phase error would become and varies with azimuth time . A special coregistration method, enhanced spectral diversity (ESD), is required for perfect spectral alignment. In addition, this quadratic phase term exceeds the PRF. By Nyquist sampling theorem, when the bandwidth exceeds sampling rate (in complex domain), an alias occurs when resampling. To work around, the quadratic term and baseband term needs to be resampled separately. This is well known as the deramping and reramping process.
2.2. Bursts Nature and Impulse Response Function of ScanSAR
2.3. Similarities between TOPS and ScanSAR
3. The Interferometric Processing Flow
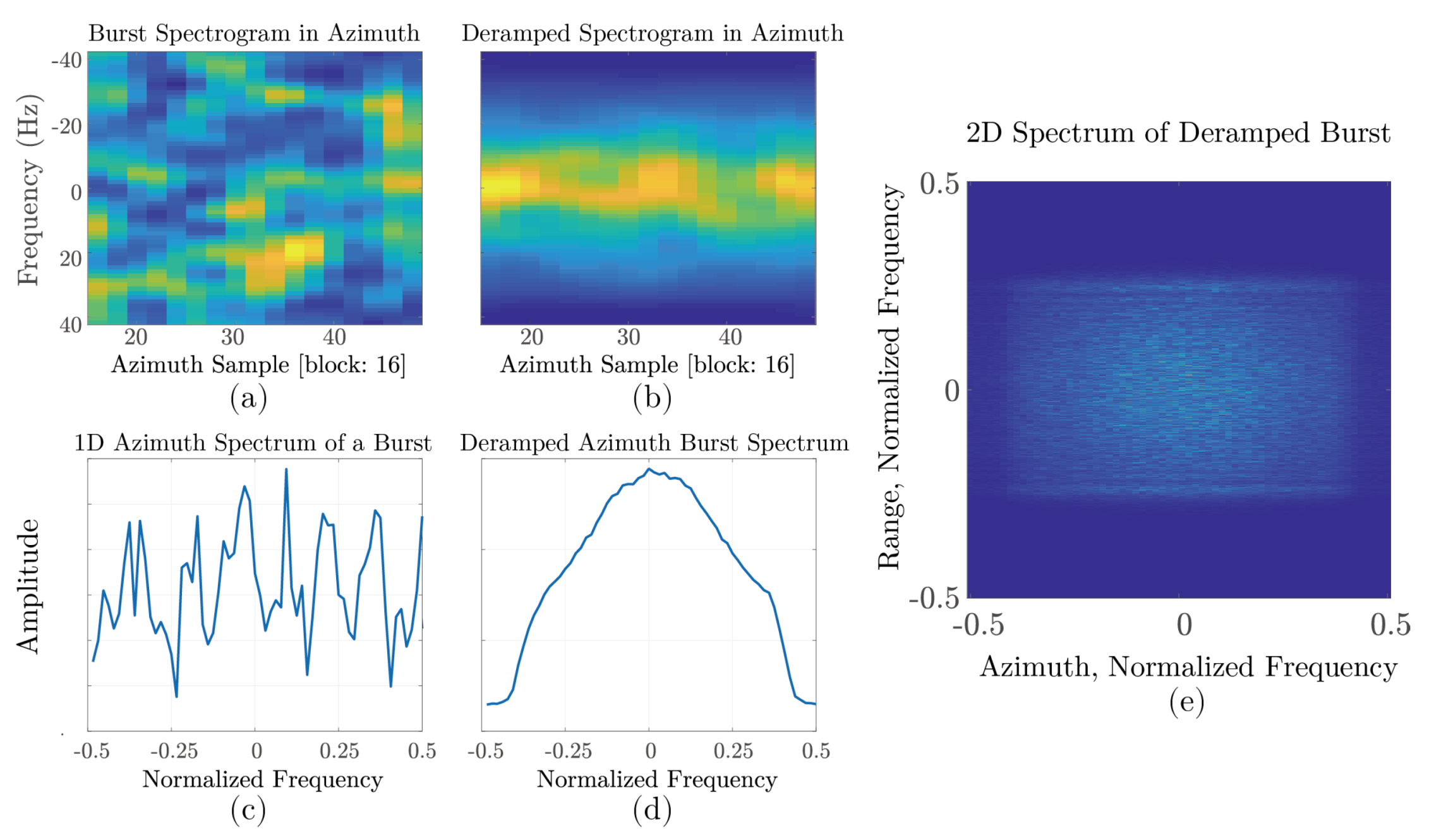
3.1. Stitching Bursts
3.1.1. TOPS
3.1.2. ScanSAR
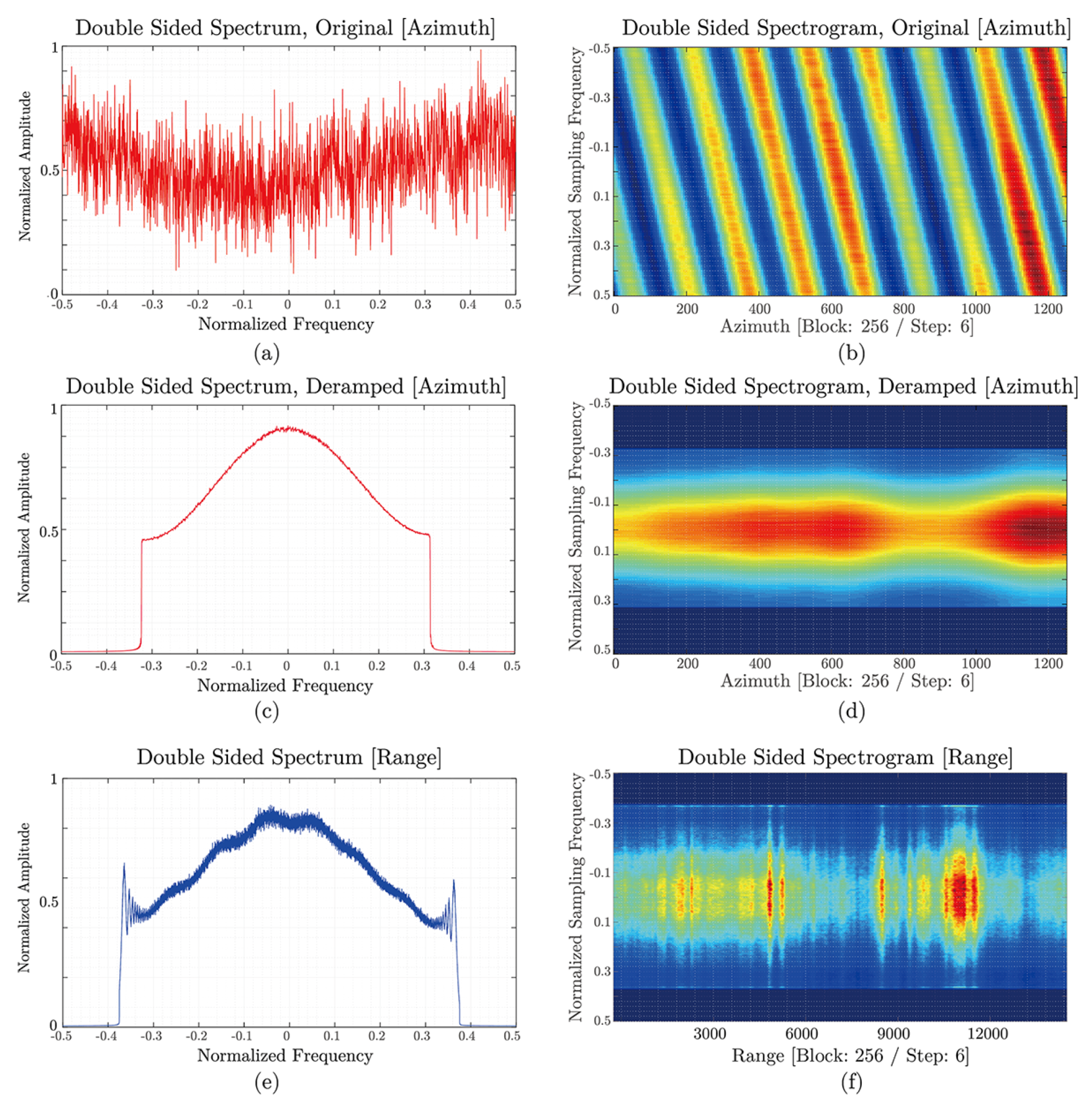
3.2. Deramp
3.2.1. TOPS
- TOPS is zero doppler steered, and is very close to zero. For the resampling process, it is not necessary to demodulate azimuth frequency to baseband, since the PRF (486 Hz) of TOPS system left enough margin in azimuth bandwidth (313 Hz). However, when one is using S1A or S1B data from their commissioning phase (S1A is before September 2014, S1B is before September 2016), it has been reported that the doppler centroid frequency could exceed 100 Hz [13,40]. In such cases, it is advised to also demodulate to baseband before the resampling process.
- Figure 9e,f shows that the range spectrum is baseband. This means that no extra care needs to be taken during the resampling process on the range direction.
3.2.2. ScanSAR
3.3. Initial Coregistration and Reramping
- The accuracy of the geometrical method does not depend on the size of the processing area. Thus, one can apply this coregistration method to each individual burst. On the other side, if one uses the cross-correlation-and-linear-transformation method in the coregistration step, then coregistering the stitched SLC image will have a better accuracy than applying the coregistration with respect to each individual bursts because the coregistration accuracy in general increases with the image size. Stitching the bursts together will give us a bigger image and thus a better coregistration accuracy than performing the coregistration burst by burst.
3.4. Enhanced Spectral Diversity and a Quick Implementation of Correcting the Coregistration Error
3.4.1. TOPS
3.4.2. ScanSAR
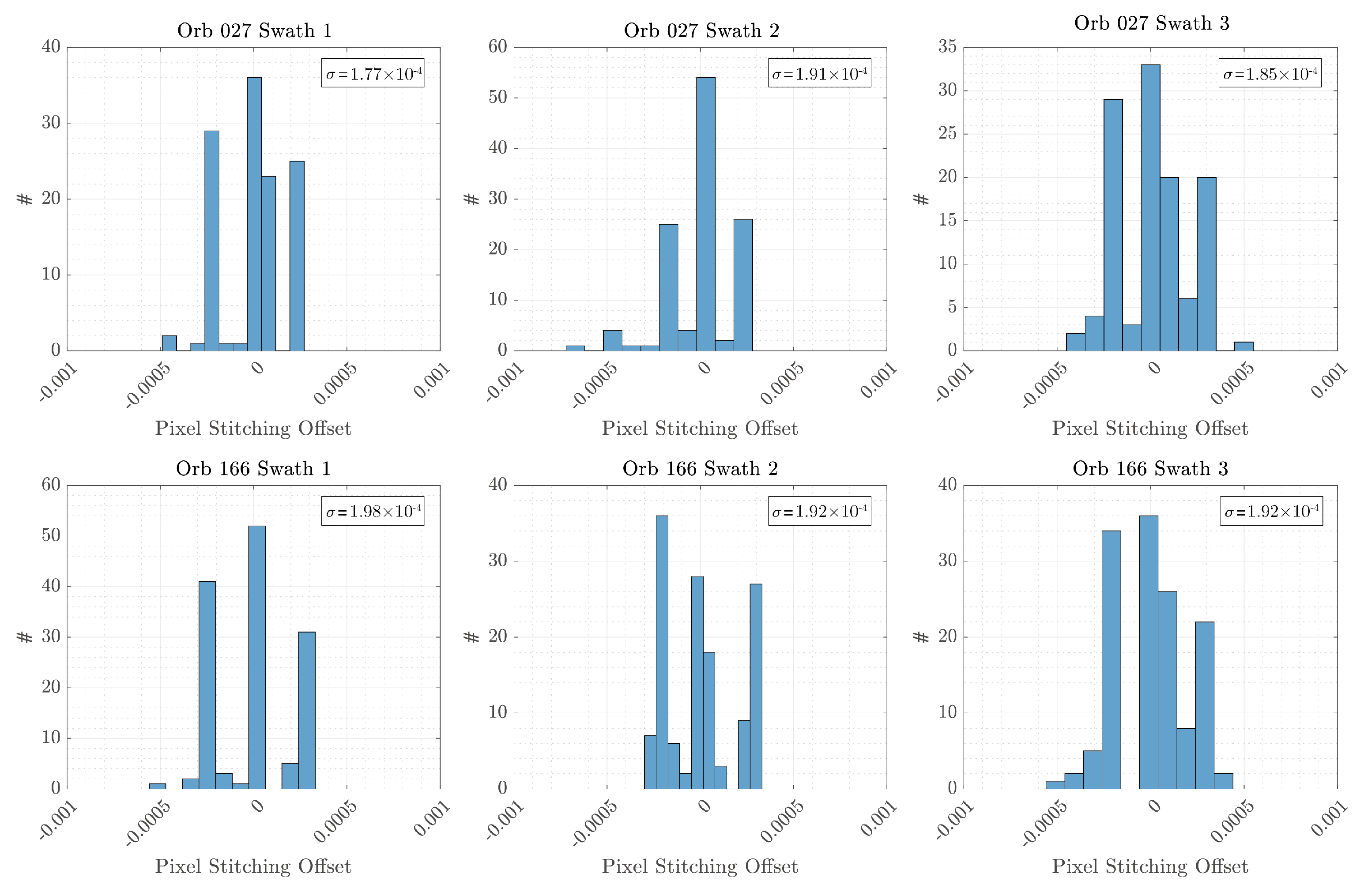
4. Comparison between the Conventional Method and Proposed Method with Real Data
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. TOPS Interferogram Examples
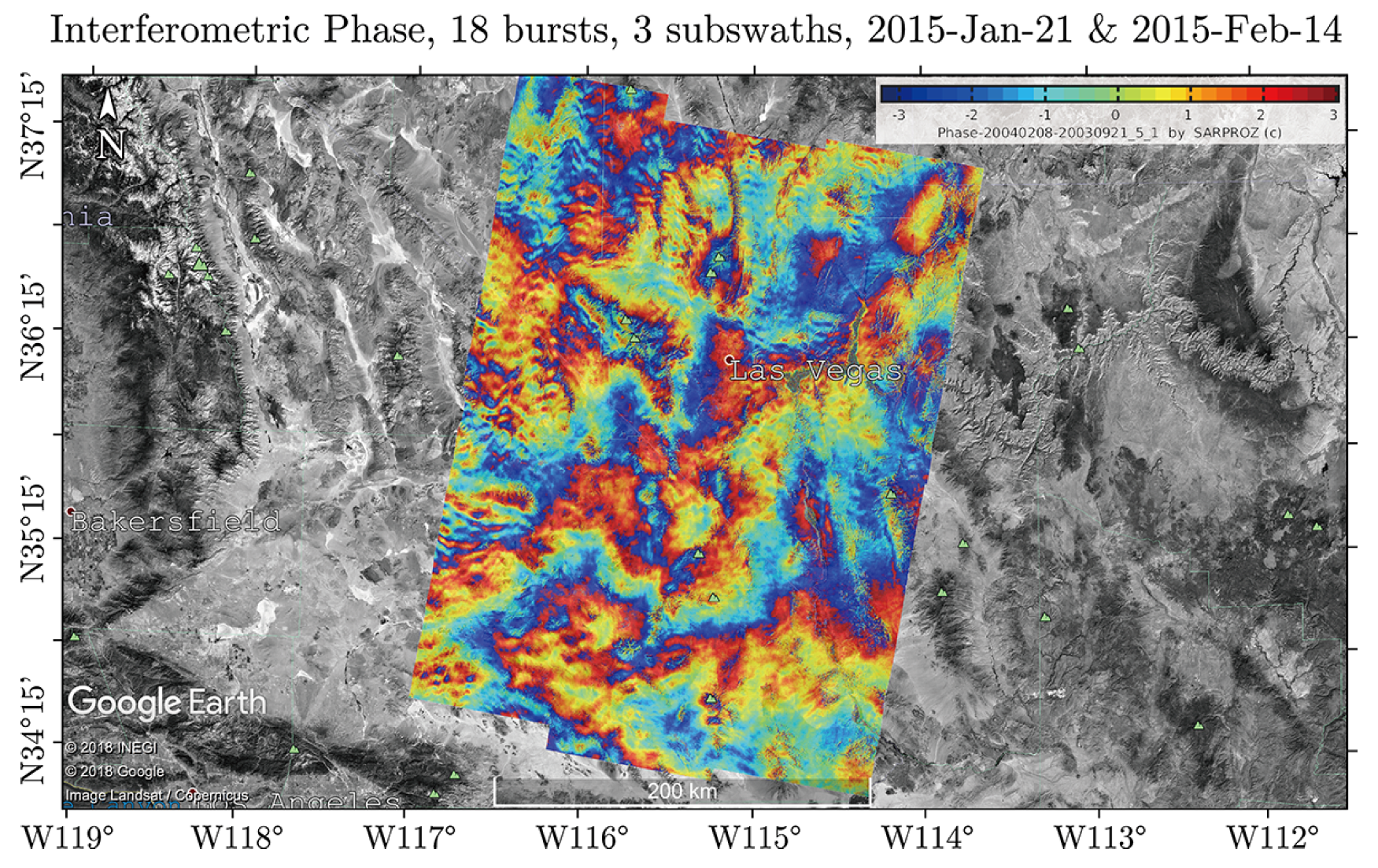

Appendix B. ScanSAR Interferogram Example

References
- Cumming, I.G.; Wong, F.H. Chapter 4: Synthetic Aperture Concepts. In Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Norwood, MA, USA, 2005; p. 136. [Google Scholar]
- Tomiyasu, K. Conceptual performance of a satellite borne, wide swath synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 1981, GE-19, 108–116. [Google Scholar] [CrossRef]
- Moore, R.K.; Claassen, J.P.; Lin, Y.H. Scanning spaceborne synthetic aperture radar with integrated radiometer. IEEE Trans. Aerosp. Electron. Syst. 1981, AES-17, 410–421. [Google Scholar] [CrossRef]
- Guarnieri, A.M.; Prati, C. ScanSAR focusing and interferometry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1029–1038. [Google Scholar] [CrossRef]
- Holzner, J.; Bamler, R. Burst-mode and ScanSAR interferometry. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1917–1934. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Guccione, P. Interferometry with ENVISAT wide swath ScanSAR data. IEEE Geosci. Remote Sens. Lett. 2006, 3, 377–381. [Google Scholar] [CrossRef]
- Miranda, N.; Meadows, P. ASAR Wide Swath Burst Synchronization Data Update; Techreport; ESA: Paris, France, 2013. [Google Scholar]
- Ferretti, A.; Monti Guarnieri, A.; Prati, C.; Rocca, F. InSAR processing: a practical approach. In InSAR Principles: Guidelines for SAR Interferometry Processing and Interpretation; ESA: Paris, France, 2007. [Google Scholar]
- De Zan, F.; Guarnieri, A.M.M. TOPSAR: Terrain observation by progressive scans. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2352–2360. [Google Scholar] [CrossRef]
- Meta, A.; Mittermayer, J.; Prats, P.; Scheiber, R.; Steinbrecher, U. TOPS imaging with TerraSAR-X: Mode design and performance analysis. IEEE Trans. Geosci. Remote Sens. 2010, 48, 759–769. [Google Scholar] [CrossRef] [Green Version]
- Wollstadt, S.; Prats, P.; Bachmann, M.; Mittermayer, J.; Scheiber, R. Scalloping correction in TOPS imaging mode SAR data. IEEE Geosci. Remote Sens. Lett. 2012, 9, 614–618. [Google Scholar] [CrossRef]
- Miranda, N.; Meadows, P.; Hajduch, G.; Pilgrim, A.; Piantanida, R.; Giudici, D.; Small, D.; Schubert, A.; Husson, R.; Vincent, P.; et al. The Sentinel-1A instrument and operational product performance status. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 2824–2827. [Google Scholar] [CrossRef]
- Prats-Iraola, P.; Scheiber, R.; Marotti, L.; Wollstadt, S.; Reigber, A. TOPS interferometry with TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3179–3188. [Google Scholar] [CrossRef] [Green Version]
- Scheiber, R.; Jäger, M.; Prats-Iraola, P.; De Zan, F.; Geudtner, D. Speckle tracking and interferometric processing of TerraSAR-X TOPS data for mapping nonstationary scenarios. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1709–1720. [Google Scholar] [CrossRef]
- De Zan, F.; Prats-Iraola, P.; Scheiber, R.; Rucci, A. Interferometry with TOPS: Coregistration and azimuth shifts. In Proceedings of the 10th European Conference on Synthetic Aperture Radar (EUSAR 2014), Berlin, Germany, 3–5 June 2014; pp. 1–4. [Google Scholar]
- Potin, P.; Rosich, B.; Grimont, P.; Miranda, N.; Shurmer, I.; O’Connell, A.; Torres, R.; Krassenburg, M. Sentinel-1 mission status. In Proceedings of the EUSAR 2016: 11th European Conference on Synthetic Aperture Radar, Fort Worth, TX, USA, 23–28 July 2017; pp. 1–6. [Google Scholar]
- Yagüe-Martínez, N.; Prats-Iraola, P.; González, F.R.; Brcic, R.; Shau, R.; Geudtner, D.; Eineder, M.; Bamler, R. Interferometric Processing of Sentinel-1 TOPS Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2220–2234. [Google Scholar] [CrossRef]
- Wright, T.J.; Biggs, J.; Crippa, P.; Ebmeier, S.K.; Elliott, J.; Gonzalez, P.; Hooper, A.; Larsen, Y.; Li, Z.; Marinkovic, P.; et al. Towards Routine Monitoring of Tectonic and Volcanic Deformation with Sentinel-1. In Proceedings of the ESA FRINGE Workshop, Frascati, Italy, 23–27 March 2015. [Google Scholar]
- Geudtner, D.; Torres, R.; Snoeij, P.; Davidson, M. Sentinel-1 System Overview. In Proceedings of the ESA FRINGE Workshop, Frascati, Italy, 19–23 September 2011; pp. 1–6. [Google Scholar]
- Holzner, J. Signal Theory and Processing for Burst-Mode and ScanSAR Interferometry. Ph.D. Thesis, The University of Edinburgh, Edinburgh, UK, 2003. [Google Scholar]
- Liang, C. Interferometric Processing of Multi-Mode Synthetic Aperture Radar Data and the Applications. Ph.D. Thesis, Peking University, Beijing, China, 2014. [Google Scholar]
- Veci, L. Sentinel-1 Toolbox: TOPS Interferometry Tutorial; Techreport; ESA: Paris, France, 2016. [Google Scholar]
- Sansosti, E.; Berardino, P.; Manunta, M.; Serafino, F.; Fornaro, G. Geometrical SAR image registration. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2861–2870. [Google Scholar] [CrossRef]
- Wegnüller, U.; Werner, C.; Strozzi, T.; Wiesmann, A.; Frey, O.; Santoro, M. Sentinel-1 Support in the GAMMA Software. Procedia Comput. Sci. 2016, 100, 1305–1312. [Google Scholar] [CrossRef]
- Wang, K.; Xu, X.; Fialko, Y. Improving Burst Alignment in TOPS Interferometry with Bivariate Enhanced Spectral Diversity. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2423–2427. [Google Scholar] [CrossRef]
- Grandin, R. Interferometric processing of SLC Sentinel-1 TOPS data. In Proceedings of the ESA FRINGE Workshop, Frascati, Italy, 23–27 March 2015. [Google Scholar]
- Bamler, R.; Eineder, M. ScanSAR processing using standard high precision SAR algorithms. IEEE Trans. Geosci. Remote Sens. 1996, 34, 212–218. [Google Scholar] [CrossRef]
- Liang, C.; Fielding, E.J. Interferometry with ALOS-2 full-aperture ScanSAR data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2739–2750. [Google Scholar] [CrossRef]
- Sack, M.; Ito, M.R.; Cumming, I.G. Application of efficient linear FM matched filtering algorithms to synthetic aperture radar processing. In IEE Proceedings F (Communications, Radar and Signal Processing); Institution of Engineering and Technology (IET): Stevenage, UK, 1985; Volume 132, pp. 45–57. [Google Scholar]
- Moreira, A.; Mittermayer, J.; Scheiber, R. Extended chirp scaling algorithm for air-and spaceborne SAR data processing in stripmap and ScanSAR imaging modes. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1123–1136. [Google Scholar] [CrossRef]
- Ortiz, A.B. ScanSAR-to-Stripmap Interferometric Observations of Hawaii. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2007. [Google Scholar]
- Kult, A.; Barstow, R.; Ramsbottom, D.; Peake, G.; Wong, T. Volume 8: ASAR Products Specifications; Techreport; ESA & MDA: Paris, France, 2016. [Google Scholar]
- Ortiz, A.B.; Zebker, H. ScanSAR-to-stripmap mode interferometry processing using ENVISAT/ASAR data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3468–3480. [Google Scholar] [CrossRef]
- Miranda, N. Definition of the TOPS SLC Deramping Function for Products Generated by the S-1 IPF; Techreport COPE-GSEG-EOPG-TN-14-0025; ESA: Paris, France, 2015. [Google Scholar]
- Piantanida, R.; Hajduch, G.; Poullaouec, J. Sentinel-1 Level 1 Detailed Algorithm Definition; Techreport SEN-TN-52-7445; ESA: Paris, France, 2016. [Google Scholar]
- Cumming, I.G.; Wong, F.H. Chapter 6: The Range Doppler Algorithin. In Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Norwood, MA, USA, 2005; p. 245. [Google Scholar]
- Cumming, I.G.; Wong, F.H. Chapter 10: Processing ScanSAR Data. In Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Norwood, MA, USA, 2005; p. 432. [Google Scholar]
- Manunta, M.; Berardino, P.; Bonano, M.; De Luca, C.; Elefante, S.; Fusco, A.; Lanari, R.; Manzo, M.; Pepe, A.; Sansosti, E.; et al. An Efficient Sentinel-1 TOPS SBAS-DInSAR Processing Chain. In Proceedings of the ESA FRINGE Workshop, Frascati, Italy, 23–27 March 2015. [Google Scholar]
- Schwerdt, M.; Schmidt, K.; Tous Ramon, N.; Klenk, P.; Yague-Martinez, N.; Prats-Iraola, P.; Zink, M.; Geudtner, D. Independent system calibration of Sentinel-1B. Remote Sens. 2017, 9, 511. [Google Scholar] [CrossRef]
- Mancon, S.; Monti Guarnieri, A.; Tebaldini, S. Sentinel-1 precise orbit calibration and validation. In Proceedings of the ESA FRINGE Workshop, Frascati, Italy, 23–27 March 2015. [Google Scholar]
- Qin, Y.; Perissin, D.; Bai, J. Investigations on the Coregistration of Sentinel-1 TOPS with the Conventional Cross-Correlation Technique. Remote Sens. 2018, 10, 1405. [Google Scholar] [CrossRef]
- Scheiber, R.; Moreira, A. Coregistration of interferometric SAR images using spectral diversity. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2179–2191. [Google Scholar] [CrossRef]
- Qin, Y. Yuxiao’s Tutorials. Available online: https://www.sarproz.com/yuxiaos-tutorials/ (accessed on 1 September 2018).
- Bakon, M.; Marchamalo, M.; Qin, Y.; García-Sánchez, A.J.; Alvarez, S.; Perissin, D.; Papco, J.; Martínez, R. Madrid as Seen from Sentinel-1: Preliminary Results. Procedia Comput. Sci. 2016, 100, 1155–1162. [Google Scholar] [CrossRef]
- Canaslan Comut, F.; Ustun, A.; Lazecky, M.; Perissin, D. Capability of Detecting Rapid Subsidence with COSMO SKYMED and Sentinel-1 Dataset over Konya City. In Proceedings of the Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016; ESA Special Publication: Paris, France, 2016; Volume 740, p. 295. [Google Scholar]
- Milillo, P.; Bürgmann, R.; Lundgren, P.; Salzer, J.; Perissin, D.; Fielding, E.; Biondi, F.; Milillo, G. Space Geodetic Monitoring of Engineered Structures: The Ongoing Destabilization of the Mosul Dam, Iraq. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Lazecky, M.; Comut, F.C.; Bakon, M.; Qin, Y.; Perissin, D.; Hatton, E.; Spaans, K.; Mendez, P.J.G.; Guimaraes, P.; de Sousa, J.J.M.; et al. Concept of an Effective Sentinel-1 Satellite SAR Interferometry System. Procedia Comput. Sci. 2016, 100, 14–18. [Google Scholar] [CrossRef]
- Lazecky, M.; Canaslan Comut, F.; Qin, Y.; Perissin, D. Sentinel-1 Interferometry System in the High-Performance Computing Environment. In The Rise of Big Spatial Data; Ivan, I., Singleton, A., Horák, J., Inspektor, T., Eds.; Springer: Cham, Germany, 2017; pp. 131–139. [Google Scholar] [CrossRef]
- Mi, S.J.; Li, Y.T.; Wang, F.; Li, L.; Ge, Y.; Luo, L.; Zhang, C.L.; Chen, J.B. A Research on Monitoring Surface Deformation and Relationships with Surface Parameters in Qinghai Tibetan Plateau Permafrost. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Wuhan, China, 18–22 September 2017; pp. 629–633. [Google Scholar] [CrossRef]
- Maghsoudi, Y.; van der Meer, F.; Hecker, C.; Perissin, D.; Saepuloh, A. Using PS-InSAR to detect surface deformation in geothermal areas of West Java in Indonesia. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 386–396. [Google Scholar] [CrossRef]
- Wiesmann, A.; Werner, C.; Santoro, M.; Wegmuller, U.; Strozzi, T. ScanSAR interferometry for land use applications and terrain deformation. In Proceedings of the IEEE International Conference on Geoscience and Remote Sensing Symposium, Denver, CO, USA, 31 July–4 August 2006; pp. 3103–3106. [Google Scholar] [CrossRef]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Y.; Perissin, D.; Bai, J. A Common “Stripmap-Like” Interferometric Processing Chain for TOPS and ScanSAR Wide Swath Mode. Remote Sens. 2018, 10, 1504. https://doi.org/10.3390/rs10101504
Qin Y, Perissin D, Bai J. A Common “Stripmap-Like” Interferometric Processing Chain for TOPS and ScanSAR Wide Swath Mode. Remote Sensing. 2018; 10(10):1504. https://doi.org/10.3390/rs10101504
Chicago/Turabian StyleQin, Yuxiao, Daniele Perissin, and Jing Bai. 2018. "A Common “Stripmap-Like” Interferometric Processing Chain for TOPS and ScanSAR Wide Swath Mode" Remote Sensing 10, no. 10: 1504. https://doi.org/10.3390/rs10101504
APA StyleQin, Y., Perissin, D., & Bai, J. (2018). A Common “Stripmap-Like” Interferometric Processing Chain for TOPS and ScanSAR Wide Swath Mode. Remote Sensing, 10(10), 1504. https://doi.org/10.3390/rs10101504