Estimating Energy Consumption of Transport Modes in China Using DEA
Abstract
:1. Introduction
2. Methodology and Data
2.1. Data Envelopment Analysis
2.2. Extended DEA Model
- (1)
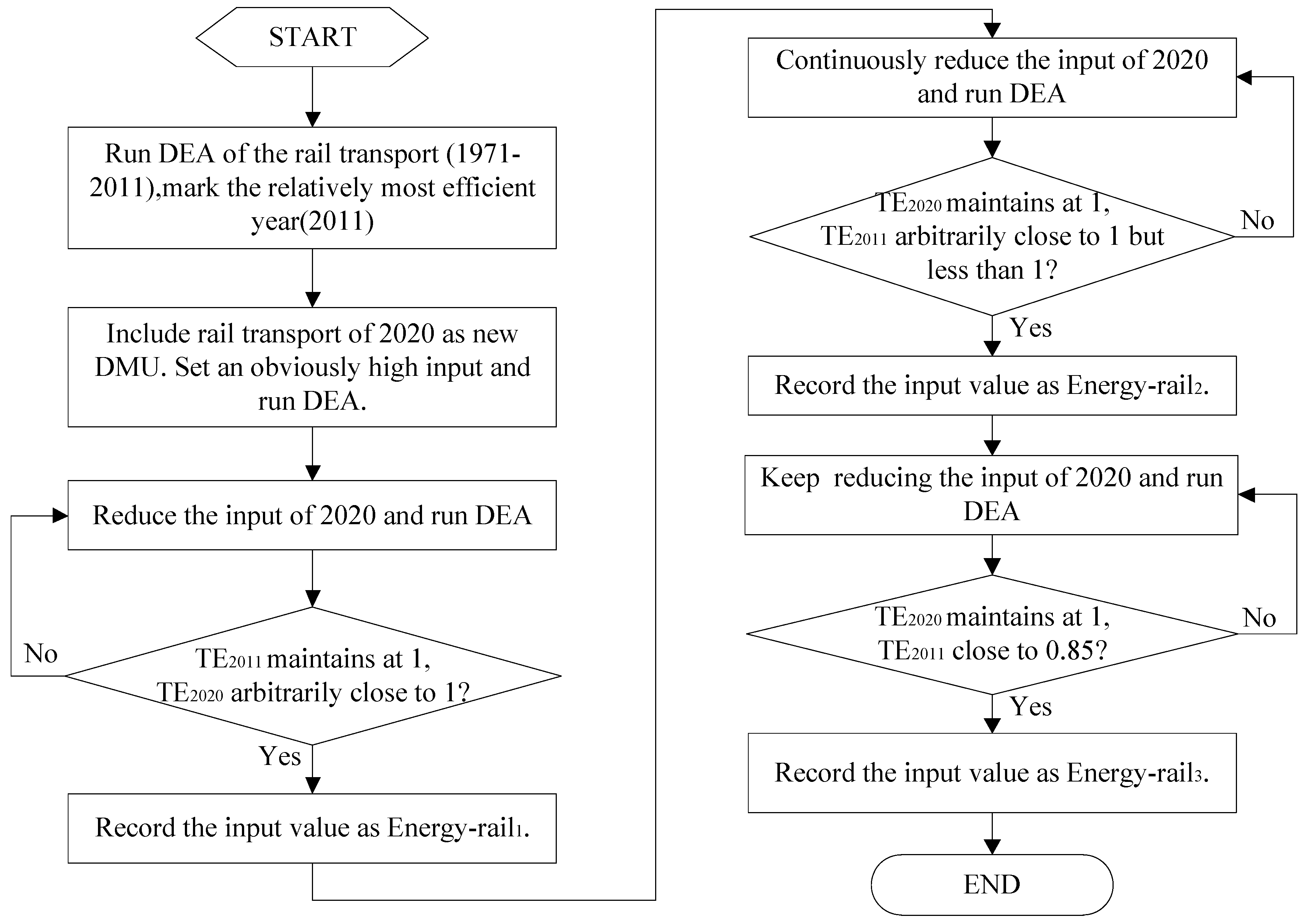
- Run DEA for rail transport (1971 to 2011) and record the efficiency score of each year. Record the most efficient year (efficiency score equal to 1), e.g., 2011.
- (2)
- Include rail transport in 2020 as a new DMU. The outputs (TKM and PKM) of the new DMU can be obtained in the data sector of this paper. Set an obviously high rail energy consumption amount in 2020 as the input and run the DEA model. The new DMU is absolutely DEA-inefficient.
- (3)
- Reduce the rail energy consumption amount in 2020 until the efficiency score for 2011 (TE2011) is maintained at 1 and the efficiency score for 2020 (TE2020) increases arbitrarily close to 1. Record this value of energy consumption as Energy-rail1.
- (4)
- Reduce the rail energy consumption amount in 2020 continuously until TE2020 is maintained at 1 and TE2011 is arbitrarily close to 1, but less than 1. Record this energy consumption value as Energy-rail2.
- (5)
- Consider efficiency improvements over time and assign a proper proportion of efficiency increases. For example, assign a 15% higher energy efficiency for 2020 relative to 2011. Then, continue reducing the rail energy consumption amount for 2020 until TE2020 remains at 1 and TE2011 is close to 0.85. Record this energy consumption value as Energy-rail3.
2.3. Data
| Year | PKM (billion passengers-km) | TKM (billion tons-km) | ||||||
|---|---|---|---|---|---|---|---|---|
| Rail | Road | Aviation | Water | Rail | Road | Aviation | Water | |
| 2011 | 961.2 | 1676.0 | 453.7 | 7.5 | 2946.6 | 5137.5 | 17.4 | 7542.4 |
| (31.0%) | (54.1%) | (14.6%) | (0.2%) | (18.5%) | (32.2%) | (0.1%) | (47.3%) | |
| 2020 | 1322.5 | 2677.9 | 985.4 | 7.5 | 4211.1 | 9251.0 | 38.5 | 11,169.0 |
| (26.5%) | (53.6%) | (19.7%) | (0.1%) | (16.5%) | (36.3%) | (0.2%) | (43.8%) | |
3. Results and Discussion
3.1. Energy Efficiency Assessments for Different Transport Modes
| Year | Energy Efficiency | Year | Energy Efficiency | |||||
|---|---|---|---|---|---|---|---|---|
| Rail | Road | Aviation | Rail | Road | Aviation | Water | ||
| 1971 | 0.198 | 0.072 | - | 1992 | 0.464 | 0.154 | 0.397 | 0.921 |
| 1972 | 0.200 | 0.069 | - | 1993 | 0.514 | 0.150 | 0.473 | 0.801 |
| 1973 | 0.207 | 0.065 | - | 1994 | 0.629 | 0.183 | 0.485 | 0.882 |
| 1974 | 0.202 | 0.057 | - | 1995 | 0.702 | 0.184 | 0.454 | 0.787 |
| 1975 | 0.184 | 0.056 | - | 1996 | 0.582 | 0.161 | 0.393 | 0.346 |
| 1976 | 0.171 | 0.060 | - | 1997 | 0.651 | 0.194 | 0.305 | 0.626 |
| 1977 | 0.171 | 0.062 | - | 1998 | 0.610 | 0.205 | 0.335 | 0.766 |
| 1978 | 0.181 | 0.065 | - | 1999 | 0.689 | 0.209 | 0.261 | 0.515 |
| 1979 | 0.190 | 0.070 | - | 2000 | 0.636 | 0.146 | 0.292 | 0.455 |
| 1980 | 0.216 | 0.087 | - | 2001 | 0.666 | 0.153 | 0.338 | 0.489 |
| 1981 | 0.205 | 0.106 | - | 2002 | 0.682 | 0.156 | 0.293 | 0.510 |
| 1982 | 0.211 | 0.116 | 0.727 | 2003 | 0.615 | 0.139 | 0.279 | 0.466 |
| 1983 | 0.230 | 0.119 | 0.540 | 2004 | 0.668 | 0.134 | 0.337 | 0.694 |
| 1984 | 0.246 | 0.131 | 0.606 | 2005 | 0.680 | 0.128 | 0.404 | 0.761 |
| 1985 | 0.285 | 0.164 | 0.702 | 2006 | 0.736 | 0.125 | 0.468 | 0.747 |
| 1986 | 0.308 | 0.175 | 0.759 | 2007 | 0.787 | 0.132 | 0.467 | 0.746 |
| 1987 | 0.342 | 0.177 | 0.847 | 2008 | 0.834 | 0.130 | 0.437 | 0.802 |
| 1988 | 0.371 | 0.185 | 0.877 | 2009 | 0.877 | 0.134 | 0.464 | 0.844 |
| 1989 | 0.361 | 0.185 | 0.679 | 2010 | 0.943 | 0.125 | 0.456 | 0.947 |
| 1990 | 0.364 | 0.167 | 0.512 | 2011 | 1.000 | 0.126 | 0.520 | 1.000 |
| 1991 | 0.406 | 0.157 | 0.375 | - | - | - | - | - |
3.2. Estimation of Future Energy Consumption of Transport in China
| Year | Energy Efficiency | Year | Energy Efficiency | |||||
|---|---|---|---|---|---|---|---|---|
| Rail | Road | Aviation | Rail | Road | Aviation | Water | ||
| 1971 | 0.240 | 0.343 | - | 1992 | 0.503 | 0.795 | 0.453 | 1.000 * |
| 1972 | 0.237 | 0.332 | - | 1993 | 0.544 | 0.756 | 0.556 | 0.867 |
| 1973 | 0.243 | 0.312 | - | 1994 | 0.665 | 0.913 | 0.554 | 0.941 |
| 1974 | 0.229 | 0.275 | - | 1995 | 0.761 | 0.910 | 0.518 | 0.830 |
| 1975 | 0.215 | 0.269 | - | 1996 | 0.647 | 0.796 | 0.447 | 0.363 |
| 1976 | 0.193 | 0.287 | - | 1997 | 0.708 | 0.936 | 0.388 | 0.654 |
| 1977 | 0.200 | 0.295 | - | 1998 | 0.633 | 0.983 | 0.474 | 0.791 |
| 1978 | 0.219 | 0.311 | - | 1999 | 0.695 | 1.000 * | 0.435 | 0.528 |
| 1979 | 0.225 | 0.336 | - | 2000 | 0.636 | 0.701 | 0.511 | 0.464 |
| 1980 | 0.246 | 0.417 | - | 2001 | 0.667 | 0.732 | 0.457 | 0.496 |
| 1981 | 0.228 | 0.507 | - | 2002 | 0.690 | 0.750 | 0.403 | 0.516 |
| 1982 | 0.234 | 0.555 | 0.828 | 2003 | 0.660 | 0.666 | 0.432 | 0.470 |
| 1983 | 0.251 | 0.570 | 0.711 | 2004 | 0.698 | 0.641 | 0.459 | 0.696 |
| 1984 | 0.262 | 0.626 | 0.763 | 2005 | 0.714 | 0.616 | 0.527 | 0.763 |
| 1985 | 0.298 | 0.828 | 0.862 | 2006 | 0.763 | 0.604 | 0.630 | 0.749 |
| 1986 | 0.322 | 0.878 | 0.865 | 2007 | 0.814 | 0.644 | 0.658 | 0.747 |
| 1987 | 0.355 | 0.927 | 1.000 * | 2008 | 0.854 | 0.946 | 0.613 | 0.803 |
| 1988 | 0.371 | 0.983 | 1.000 * | 2009 | 0.895 | 1.000 * | 0.587 | 0.845 |
| 1989 | 0.379 | 0.983 | 0.848 | 2010 | 0.955 | 0.959 | 0.682 | 0.947 |
| 1990 | 0.411 | 0.887 | 0.615 | 2011 | 1.000 * | 1.000 * | 0.674 | 1.000 * |
| 1991 | 0.450 | 0.815 | 0.428 | - | - | - | - | - |
| Year | Rail | Road | Aviation | Water |
|---|---|---|---|---|
| 2011 | 17,497 | 242,017 | 15,878 | 24,009 |
| 2020-Round 1 | 25,047 (4.1%) | 436,025 (6.8%) | 23,703 (4.6%) | 35,574 (4.5%) |
| 2020-Round 2 | 24,043 (3.6%) | 413,832 (6.1%) | 20,432 (2.8%) | 35,412 (4.4%) |
| Annual growth rate | Rail | Road | Aviation | Water | Total (pipeline and non-specified excluded) |
|---|---|---|---|---|---|
| PKM | 3.6 | 5.3 | 9.0 | 0.0 | 5.4 |
| TKM | 4.0 | 6.8 | 9.2 | 4.5 | 5.0 |
| Energy Consumption | 3.6 | 6.1 | 2.8 | 4.4 | 5.7 |
| Year | Rail | Road | Aviation | Water |
|---|---|---|---|---|
| 2011 | 17,497 | 242,017 | 15,878 | 24,009 |
| 2020-Round 3 | 20,460 (1.8%) | 368,706 (4.8%) | 20,432 (2.8%) | 29,983 (2.5%) |
| Ref. | Model | Future transport energy consumption (mtce) | |
|---|---|---|---|
| International Energy Agency, 2007 [48] | Reference scenario analysis | 425.22 | |
| Energy Research Institute, 2006 [50] | Partial least square regression | Baseline scenario | 460 |
| Policy scenario | 416 | ||
| Zhang et al., 2009 [51] | Partial least square regression | Scenario 1 | 468.26 |
| Scenario 2 | 433.13 | ||
| Liu et al., 2013 [52] | TransportPLAN | Reference case | 601 (17,605 PJ) |
| Combined case | 522 (15,306 PJ) | ||
| This study | Extended DEA model | 443.13 | |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- International Enegy Agency. Statistic, Statistic Search. Available online: http://www.iea.org/statistics/statisticssearch/ (accessed on 4 January 2015).
- Department of Energy Statistics, National Bureau Statistics, People’s Republic of China. China Energy Statistical Yearbook 2013; China Statistics Press: Beijing, China, 2014. (In Chinese)
- Intergovernmental Panel on Climate Change. Summary for Policy Makers. Available online: http://www.climatechange2013.org/images/report/WG1AR5_SPM_FINAL.pdf (accesses on 4 January 2015).
- International Enegy Agency. CO2 Emissions From Fuel Combustion Highlights. Available online: http://www.iea.org/publications/freepublications/publication/CO2EmissionsFromFuelCombustionHighlights2014.pdf (accessed on 4 January 2015).
- Ramanathan, R. A holistic approach to compare energy efficiencies of different transport modes. Energy Policy. 2000, 28, 743–747. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Mukherjee, K. Energy use efficiency in U.S. manufacturing: A nonparametric analysis. Energy Econ. 2008, 30, 76–96. [Google Scholar] [CrossRef]
- Honma, S; Hu, J. Total-factor energy efficiency of regions in Japan. Energy Policy 2008, 36, 821–833. [Google Scholar]
- Sueyoshi, T.; Goto, M. DEA approach for unified efficiency measurement: Assessment of Japanese fossil fuel power generation. Energy Econ. 2011, 33, 292–303. [Google Scholar] [CrossRef]
- Goto, M.; Otsuka, A.; Sueyoshi, T. DEA (Data Envelopment Analysis) assessment of operational and environmental efficiencies on Japanese regional industries. Energy 2014, 66, 535–549. [Google Scholar] [CrossRef]
- Hu, J.; Lio, M.; Yeh, F.; Lin, C. Environment-adjusted regional energy efficiency in Taiwan. Appl. Energy. 2011, 88, 2893–2899. [Google Scholar] [CrossRef]
- Fang, C.; Hu, J.; Lou, T. Environment-adjusted total-factor energy efficiency of Taiwan’s service sectors. Energy Policy 2013, 63, 1160–1168. [Google Scholar] [CrossRef]
- Blomberg, J.; Henriksson, E.; Lundmark, R. Energy efficiency and policy in Swedish pulp and paper mills: A data envelopment analysis approach. Energy Policy 2012, 42, 569–579. [Google Scholar] [CrossRef]
- Voltes-Dorta, A.; Perdiguero, J.; Jiménez, J.L. Are car manufacturers on the way to reduce CO2 emissions? A DEA approach. Energy Econ. 2013, 38, 77–86. [Google Scholar] [CrossRef]
- Blancard, S.; Martin, E. Energy efficiency measurement in agriculture with imprecise energy content information. Energy Policy 2014, 66, 198–208. [Google Scholar] [CrossRef]
- Mukherjee, K. Measuring energy efficiency in the context of an emerging economy: The case of indian manufacturing. Eur. J. Oper. Res. 2010, 201, 933–941. [Google Scholar] [CrossRef]
- Mandal, S.K. Do undesirable output and environmental regulation matter in energy efficiency analysis? Evidence from Indian Cement Industry. Energy Policy 2010, 38, 6076–6083. [Google Scholar] [CrossRef]
- Ramanathan, R. Estimating Energy Consumption of Transport Modes in India Using DEA and Application to Energy and Environmental Policy. J. Op. Res. Soc. 2005, 56, 732–737. [Google Scholar] [CrossRef]
- Khoshnevisan, B.; Rafiee, S.; Omid, M.; Mousazadeh, H. Reduction of CO2 emission by improving energy use efficiency of greenhouse cucumber production using DEA approach. Energy 2013, 55, 676–682. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.W. Linear programming models for measuring economy-wide energy efficiency performance. Energy Policy 2008, 36, 2911–2916. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, X.; Yuan, J.; Gao, X. Total-factor energy efficiency in developing countries. Energy Policy 2011, 39, 644–650. [Google Scholar] [CrossRef]
- Song, M.; Zhang, L.; Liu, W.; Fisher, R. Bootstrap-DEA analysis of BRICS’ energy efficiency based on small sample data. Appl. Energy. 2013, 112, 1049–1055. [Google Scholar] [CrossRef]
- Vlontzos, G.; Niavis, S.; Manos, B. A DEA approach for estimating the agricultural energy and environmental efficiency of EU countries. Renew. Sustain. Energy Rev. 2014, 40, 91–96. [Google Scholar] [CrossRef]
- Meng, F.Y.; Zhou, P.; Zhou, D.Q.; Bai, Y. Inefficiency and Congestion Assessment of Mix Energy Consumption in 16 APEC Countries by using DEA Window Analysis. Energy Procedia 2014, 61, 2518–2523. [Google Scholar] [CrossRef]
- Hu, J.; Wang, S. Total-factor energy efficiency of regions in China. Energy Policy. 2006, 34, 3206–3217. [Google Scholar] [CrossRef]
- Wei, C.; Shen, M.H. Energy efficiency and its influencing factors: An empirical analysis based on DEA. Manag. World 2007, 8, 66–76. (In Chinese) [Google Scholar]
- Shu, T.; Zhong, X.; Zhang, S. TFP Electricity Consumption Efficiency and Influencing Factor Analysis Based on DEA Method. Energy Procedia 2011, 12, 91–97. [Google Scholar]
- Wang, Z.; Zeng, H.; Wei, Y.; Zhang, Y. Regional total factor energy efficiency: An empirical analysis of industrial sector in China. Appl. Energy 2012, 97, 115–123. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, C.; Zhang, B. An empirical analysis of China’s energy efficiency from both static and dynamic perspectives. Energy 2014, 74, 322–330. [Google Scholar] [CrossRef]
- Yeh, T.; Chen, T.; Lai, P. A comparative study of energy utilization efficiency between Taiwan and China. Energy Policy 2010, 38, 2386–2394. [Google Scholar] [CrossRef]
- Shi, G.; Bi, J.; Wang, J. Chinese regional industrial energy efficiency evaluation based on a DEA model of fixing non-energy inputs. Energy Policy 2010, 38, 6172–6179. [Google Scholar] [CrossRef]
- Lin, W.; Yang, J.; Chen, B. Temporal and spatial analysis of intergrated energy and environment efficiency in China based on a green GDP index. Energies 2011, 4, 1367–1390. [Google Scholar] [CrossRef]
- Yang, L.; Wang, K. Regional differences of environmental efficiency of China’s energy utilization and environmental regulation cost based on provincial panel data and DEA method. Math. Computer Model. 2013, 58, 1074–1083. [Google Scholar] [CrossRef]
- Bian, Y.; He, P.; Xu, H. Estimation of potential energy saving and carbon dioxide emission reduction in China based on an extended non-radial DEA approach. Energy Policy 2013, 63, 962–971. [Google Scholar] [CrossRef]
- Bi, G.; Song, W.; Zhou, P.; Liang, L. Does environmental regulation affect energy efficiency in China’s thermal power generation? Empirical evidence from a slacks-based DEA model. Energy Policy 2014, 66, 537–546. [Google Scholar] [CrossRef]
- Song, M.; Yang, L.; Wu, J.; Lv, W. Energy saving in China: Analysis on the energy efficiency via bootstrap-DEA approach. Energy Policy 2013, 57, 1–6. [Google Scholar] [CrossRef]
- Wang, K.; Lu, B.; Wei, Y. China’s regional energy and environmental efficiency: A Range-Adjusted Measure based analysis. Appl. Energy 2013, 112, 1403–1415. [Google Scholar] [CrossRef]
- Chang, Y.; Zhang, N.; Danao, D.; Zhang, N. Environmental efficiency analysis of transportation system in China: A non-radial DEA approach. Energy Policy 2013, 58, 277–283. [Google Scholar] [CrossRef]
- Zhou, G.; Chung, W.; Zhang, Y. Measuring energy efficiency performance of China’s transport sector: A data envelopment analysis approach. Expert Syst. Appl. 2014, 41, 709–722. [Google Scholar] [CrossRef]
- Cui, Q.; Li, Y. The evaluation of transportation energy efficiency: An application of three-stage virtual frontier DEA. Transp. Res. Part D 2014, 29, 1–11. [Google Scholar] [CrossRef]
- Burley, H. Productive efficiency in U.S. manufacturing: A linear programming approach. Rev. Econ. Stat. 1980, 62, 619–622. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Fare, R.; Grosskopf, S.; Norris, M.; Zhang, Z. Productivity growth, technical progress, and efficiency changes in industrialized countries. Am. Econ. Rev. 1994, 84, 66–83. [Google Scholar]
- Lovell, C.A.K.; Grosskopf, S.; Ley, E. Linear programming approaches to the measurement and analysis of productive efficiency. Top 1994, 2, 175–248. [Google Scholar] [CrossRef]
- International Energy Agency. World Energy Statistics and Balances (2013 edition). Available online: http://data.iea.org/ieastore/product.asp?dept_id=101&pf_id=205 (accessed on 7 December 2013).
- National Bureau of Statistics of China. Available online: http://data.stats.gov.cn/workspace/index?m=hgnd (accesses on 4 January 2015). (In Chinese)
- Energy Research Institute (ERI), National Development and Reform Commission, People’s Republic of China. China’s Low Carbon Development Pathways by 2050; ERI: Beijing, China, 2009. (In Chinese)
- International Energy Agency. World Energy Outlook 2007—Special Report—Focus on China and India. Available online: http://www.iea.org/publications/freepublications/publication/weo-2007---special-report---focus-on-china-and-india.html (accessed on 19 March 2015).
- Wang, Y.; Li, K.; Xu, X.; Zhang, Y. Transport energy consumption and saving in China. Renew. Sustain. Energy Rev. 2014, 29, 641–655. [Google Scholar] [CrossRef]
- Energy Research Institute, National Devlopment and Reform Commission. Scenarios Analysis of China’s Energy Demand for 2050, Technical Report; ERI: Beijing, China, 2006. (In Chinese) [Google Scholar]
- Zhang, M.; Mu, H.; Li, G.; Ning, Y. Forecasting the transport energy demand based on PLSR method in China. Energy 2009, 34, 1396–1400. [Google Scholar] [CrossRef]
- Liu, W.; Lund, H.; Mathiesen, B. Modelling the transport system in China and evaluating the current strategies towards the sustainable transport development. Energy Policy 2013, 58, 347–357. [Google Scholar] [CrossRef]
- The General Office of State Council. Energy Strategy Action Plan 2014 to 2020. Available online: http://www.gov.cn/zhengce/content/2014-11/19/content_9222.htm (accessed on 19 March 2015). (In Chinese)
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, W.; Chen, B.; Xie, L.; Pan, H. Estimating Energy Consumption of Transport Modes in China Using DEA. Sustainability 2015, 7, 4225-4239. https://doi.org/10.3390/su7044225
Lin W, Chen B, Xie L, Pan H. Estimating Energy Consumption of Transport Modes in China Using DEA. Sustainability. 2015; 7(4):4225-4239. https://doi.org/10.3390/su7044225
Chicago/Turabian StyleLin, Weibin, Bin Chen, Lina Xie, and Haoran Pan. 2015. "Estimating Energy Consumption of Transport Modes in China Using DEA" Sustainability 7, no. 4: 4225-4239. https://doi.org/10.3390/su7044225
APA StyleLin, W., Chen, B., Xie, L., & Pan, H. (2015). Estimating Energy Consumption of Transport Modes in China Using DEA. Sustainability, 7(4), 4225-4239. https://doi.org/10.3390/su7044225






