Optimal Planning and Techno-Economic Analysis of P2G-Multi-Energy Systems
Abstract
1. Introduction
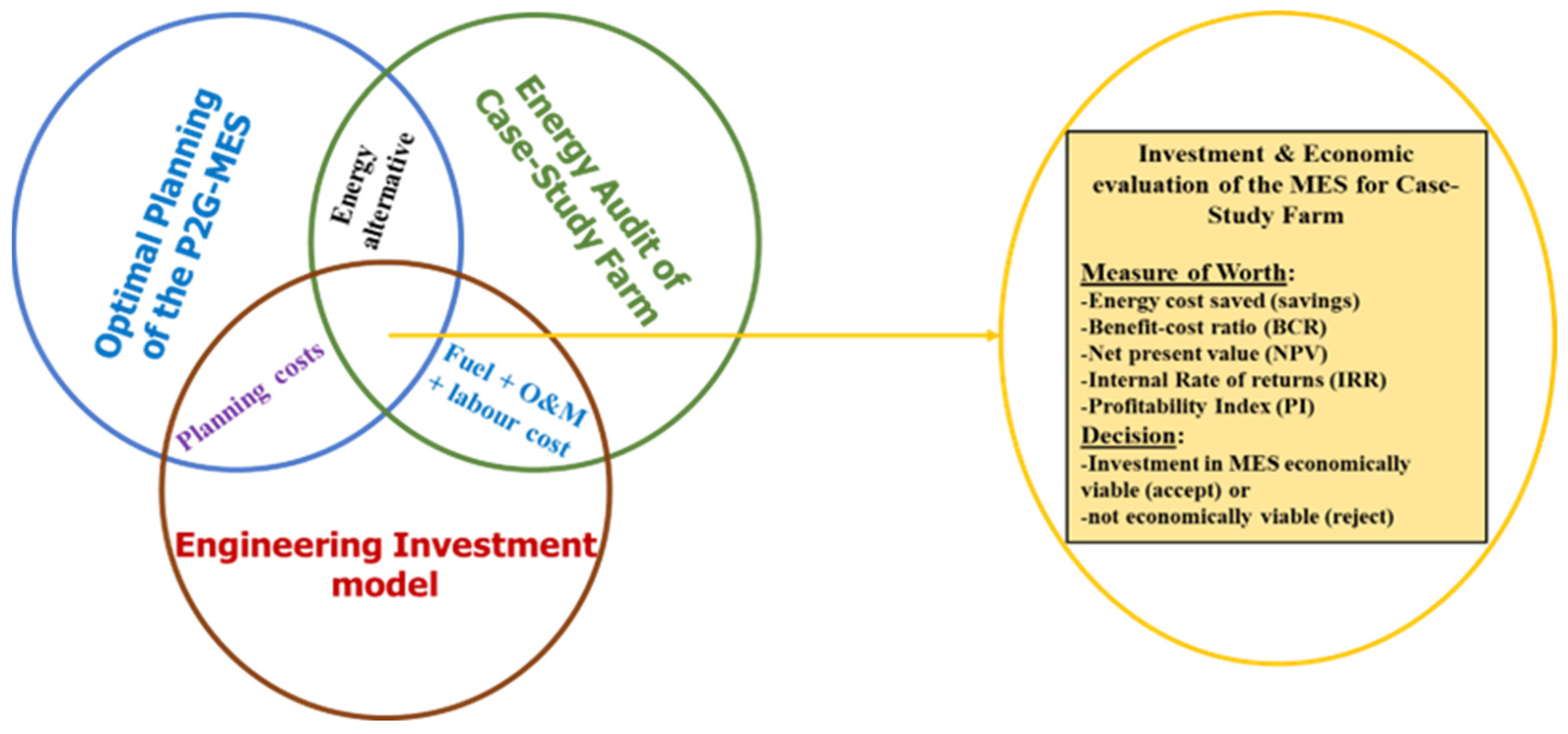
- Developing an optimization planning model and technical constraints to evaluate both the economic and technical viability of the referenced MES.
- Formulating an investment model linking optimal planning cost and the cost of fuel utilized by the case study farm. It also supports sensitivity analysis on fuel price volatility and discount rate, which is critical for long-term investment decisions in energy-intensive agricultural applications.
- Investigating the influence of P2G and DRPs in four scenarios to comprehend their effects on the sizing of components in the P2G-integrated MES and the associated planning costs. This enables incorporating sustainable energy solutions, lowering emissions (P2G), and better managing energy usage (DRPs).
- Evaluating measures of indices to ascertain the economic feasibility of investing in MESs and transitioning the energy supply of a farmstead to the specified MES. An investment model is then used to evaluate the economic viability of adopting the MES in the case study farm. This will enable stakeholders to benchmark MES investment outcomes against traditional energy supply models and support the business case for MES integration.
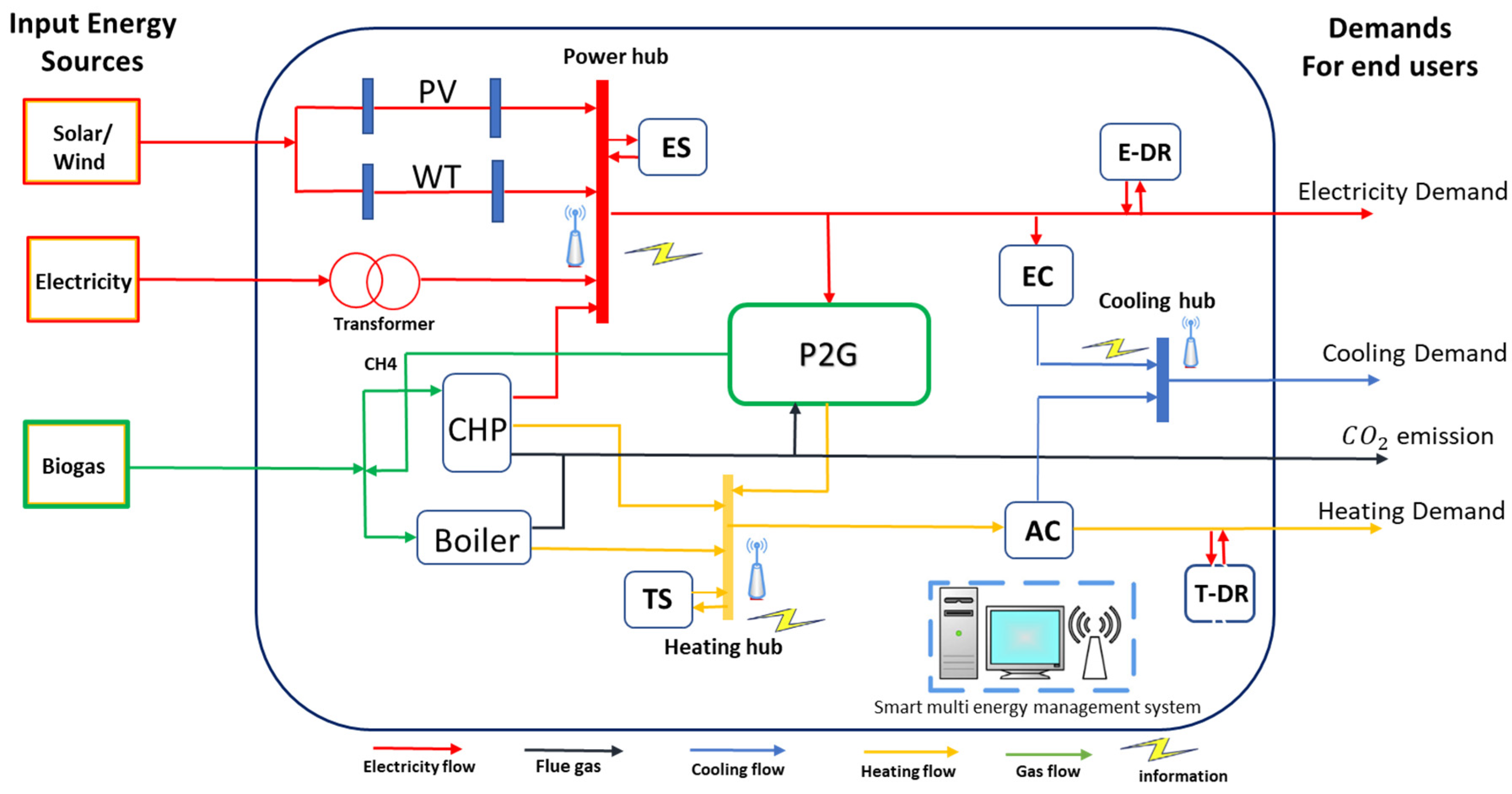
2. P2G-Multi-Energy Systems
2.1. MES and Operational Concept
2.2. P2G Operational Concept
2.3. The Proposed Optimal Planning and Research Framework
3. MES Planning Optimization Model
3.1. Objective Function
- Index are set of major components associated with variable ;
- Index are set of minor components that are not associated with the decision variable ;
- = needed capacity of component k;
- = capital cost of the MES components;
- = replacement cost of components k and m;
- = maintenance cost of components k and m;
- = single payment present worth of the respective MES component;
- = real interest rate;
- = economics of components k and m;
- = replacement number of components k and m;
- PWA = present worth annual payment.where
- set of storage operations components within the MES architecture
- demand response program with shedding and shifting power;
- , = price of electricity at time slot t and that of biogas network, respectively;
- , = purchased electricity and biogas power from network at time slot t, respectively;
- and = cost coefficients associated with storage and demand response operations;
- = charged and discharge energies of storage devices at time slot t, respectively;
- = shifting down and shifting up energies at time slot t, respectively.
3.2. Wind and Solar Power Models
3.3. Constraints
3.3.1. Energy Balance Constraints
- , , , and are the numbers of electricity generation, heating, cooling, and gas devices, respectively.
- L is the index of loads.
- , , , and are the numbers of electrical, heating, cooling, and gas loads, respectively.
- represents the output electrical power of device k, which includes the energy converter, renewable generation, and electricity storage device at time slot t.
- denotes the power of electrical loads at time t, and likewise for heating, cooling, and gas balance.
3.3.2. Energy Networks Constraints
3.3.3. Energy Converter Constraints
3.3.4. MES Component Constraints
3.3.5. Operational Constraints of Energy Storage Devices
3.3.6. P2G Constraints
3.3.7. Energy Demand Response Constraints
3.3.8. ENS Constraints
4. The Case Study Farm and Investment Model
5. Results and Discussion
5.1. Input Data
5.2. Results and Comparison of MES Operational Scenarios
5.3. Results and Analysis on the Farm Energy Audit and Investment Analysis
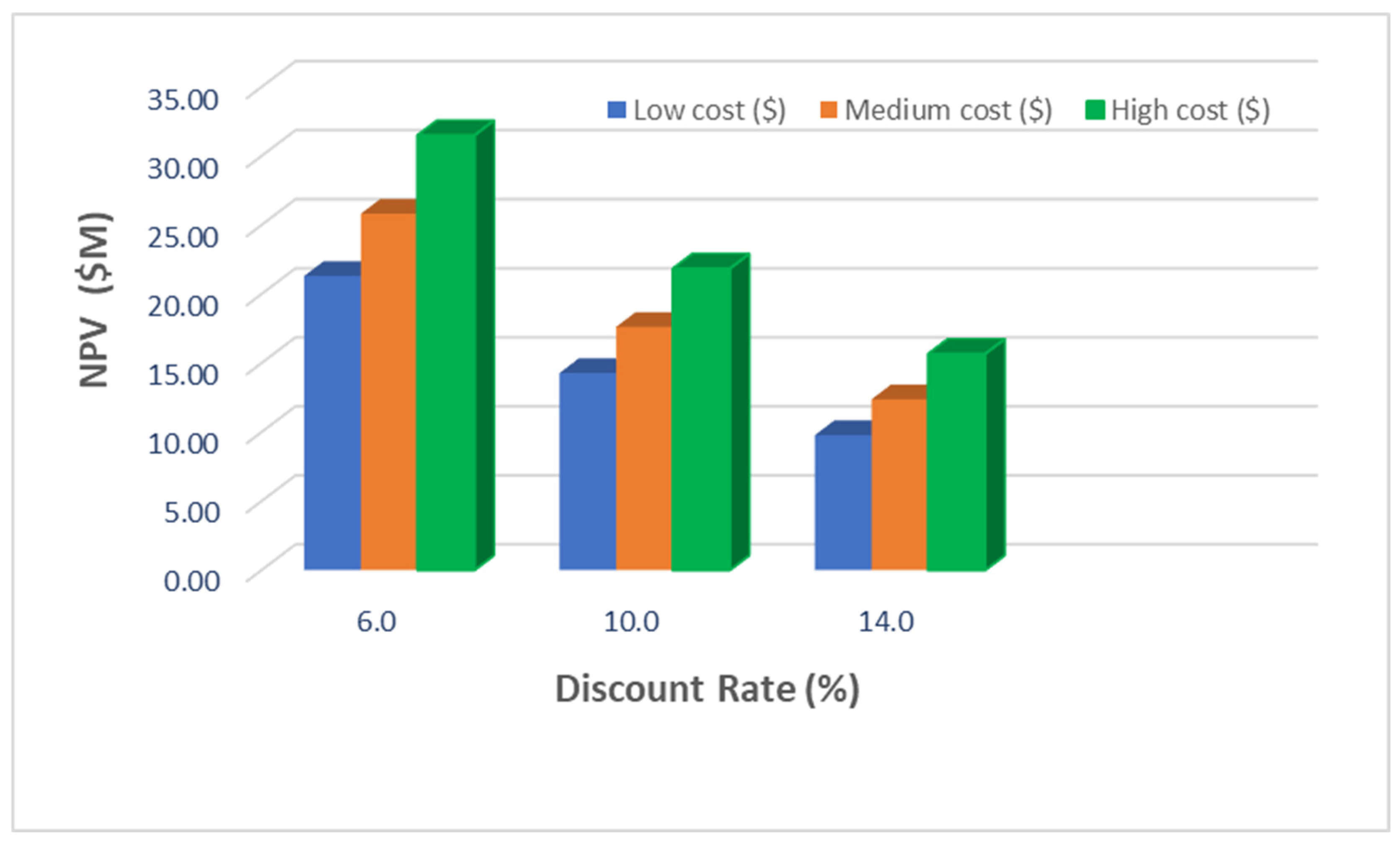
5.4. Sensitivity Analysis on the Discount Rate and Fuel Price
6. Conclusions and Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| t | Index of time |
| k | Index of device associated with optimized capacity |
| m | Index of device not associated with optimized capacity |
| s | Index of storage operations components of MES |
| d | Index of demand response operations of MES |
| e | Index of electricity |
| i, j | Index of energy type |
| f | Index of fuel types |
| em | Index of emission type |
| AMI | Advanced Metering Infrastructure |
| CON | Converter |
| MES | Multi-Energy System |
| P2G-EH | Power-to-Gas Energy Hub |
| PV | Photovoltaic |
| WT | Wind Turbine |
| B | Boiler |
| CHP | Combined Heat and Cooling |
| AC | Absorption Chiller |
| EC | Electric Chiller |
| T | Transformer |
| P2G | Power-to-Gas |
| TES | Therma Storage |
| ES | Electricity Storage |
| DRP | Demand Response Program |
| E-DR | Electricity Demand Response |
| T-DR | Thermal Demand Response |
| CCS | Carbon Captur and Storage |
| IES | Integrated Energy System |
| MILP | Mixed-Integer Linear Programming |
| BCR | Benefit–Cost Ratio |
| IRR | Internal Rate of Return |
| Profitability Index | |
| NPV | Net Present Value |
| PWA | Present worth annual payment |
| PEM | Proton Exchange Membrane |
| AWE | Alkaline Water Electrolysis |
| SOE | Solid Oxide Electrolysis |
| O2 | Oxygen |
| Carbon (iv) oxide | |
| Nitrogen (iv) oxide | |
| Sulphur (iv) oxide | |
| OF | Objective function |
Appendix A
| Parameter | Value | Parameter | Value | Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|---|---|---|---|
| 1.432 | 0.454 | 21.8 | 1.596 | 0.008 | |||||
| 0.440 | 1.755 | 0.011 | 0.62 | 0.01 | |||||
| 0.1 | 0.1 | 0.1 | 0.1 | 50 | |||||
| 50 | 800 | 0.12 | 0.14 | 0.0179 | |||||
| 0.9 | 0.157 | 0.9 | 0.75 | 0.85 | |||||
| 0.3 | 0.45 | 0.9 | 0.9 | 0.9 | |||||
| 0.9 | 0.96 | 0.70 | 0.96 | 0.01 | |||||
| 0.03 | 0.07 | 0.7 | 3.5 | 1 | |||||
| 3 | 1 | 2 | 1 | 1 | |||||
| 1 | 2 | 2 | 1 | 1 | |||||
| 1 | 1 | 550 | 2000 | 950 | |||||
| 800 | 1000 | 900 | 500 | 2500 | |||||
| 850 | 270 | 680 | 1300 | 400 | |||||
| 400 | 2500 | 598 | 700 | 400 | |||||
| 1000 | 300 | 600 | 700 | 4000 | |||||
| 0.16 | 0.012 | 10 | 68 | 0.13 | |||||
| 3 | 0.01 | 10 | 0.012 | 0.012 | |||||
| 0.03 | 50 | 1000 | 15 | 15 | |||||
| 20 | 20 | 20 | 15 | 20 | |||||
| 15 | 10 | 20 | 20 | 20 | |||||
| 600 | 400 | 1000 | 2000 | 900 | |||||
| 500 | 400 | 4200 | 700 | 800 | |||||
| 35.8 | 120 | 0.1 | 0.9 | 0.02 | |||||
| 0.1 | 0.9 | 0.02 | 0.25 | 900 | |||||
| 0.25 | 4.2 | 0.99 | 0.014 | 2 | |||||
| 0.3 | 5 | 20 | 3 | 2 | |||||
| 4 | 22 | 10 |
| Time | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| t1 | 908.2 | 47.7 | 18.5 | 23.3 | 34.8 | 60.6 | 120.0 | 835.3 | ||
| t2 | 908.2 | 47.7 | 6.7 | 11.3 | 46.4 | 46.9 | 120.0 | 405.3 | ||
| t3 | 908.2 | 47.7 | 6.9 | 11.5 | 58.0 | 50.3 | 120.0 | 412.5 | ||
| t4 | 908.2 | 47.7 | 4.5 | 69.6 | 42.1 | 120.0 | 160.1 | |||
| t5 | 908.2 | 47.7 | 0.6 | 5.1 | 70.8 | 40.1 | 120.0 | 181.8 | ||
| t6 | 908.2 | 47.7 | 3.7 | 8.3 | 81.3 | 40.1 | 120.0 | 296.9 | ||
| t7 | 908.2 | 47.7 | 6.2 | 10.8 | 229.8 | 41.8 | 120.0 | 388.2 | ||
| t8 | 955.4 | 47.7 | 18.3 | 23.2 | 371.4 | 59.9 | 120.0 | 831.3 | ||
| t9 | 908.2 | 47.7 | 14.8 | 19.6 | 499.1 | 60.3 | 120.0 | 701.3 | ||
| t10 | 908.2 | 47.7 | 0.0 | 4.5 | 603.6 | 50.0 | 120.0 | 162.1 | ||
| t11 | 908.2 | 47.7 | 18.1 | 23.0 | 673.3 | 59.9 | 120.0 | 823.3 | ||
| t12 | 953.2 | 47.7 | 20.2 | 25.1 | 754.5 | 70.2 | 120.0 | 899.2 | ||
| t13 | 1008.7 | 47.7 | 16.4 | 21.2 | 719.7 | 70.5 | 120.0 | 759.4 | ||
| t14 | 1060.8 | 47.7 | 16.3 | 21.2 | 603.6 | 69.9 | 120.0 | 757.4 | ||
| t15 | 1094.3 | 64.8 | 1.1 | 21.6 | 499.1 | 120.0 | 773.9 | |||
| t16 | 1094.3 | 63.7 | 20.4 | 371.4 | 22.2 | 120.0 | 732.0 | |||
| t17 | 1094.3 | 63.9 | 20.7 | 229.8 | 57.6 | 120.0 | 740.0 | |||
| t18 | 1094.3 | 65.1 | 342.0 | 21.9 | 58.0 | 85.6 | 120.0 | 783.9 | ||
| t19 | 1094.3 | 65.0 | 1000.0 | 21.8 | 46.4 | 120.2 | 120.0 | 779.9 | ||
| t20 | 1094.3 | 65.0 | 876.3 | 21.8 | 34.8 | 120.2 | 120.0 | 781.9 | ||
| t21 | 1094.3 | 2.1 | 65.1 | 767.1 | 24.0 | 23.2 | 120.2 | 120.0 | 860.6 | |
| t22 | 1094.3 | 2.1 | 65.1 | 575.1 | 24.0 | 22.1 | 112.0 | 120.0 | 860.6 | |
| t23 | 1094.3 | 65.1 | 81.0 | 21.9 | 17.4 | 77.5 | 120.0 | 783.9 | ||
| t24 | 1094.3 | 65.0 | 45.3 | 21.8 | 11.6 | 47.2 | 120.0 | 781.9 |
| Time | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| t1 | 1031.4 | 210.5 | 352.6 | 34.8 | 0.6 | 60.6 | |||
| t2 | 928.9 | 560.3 | 46.4 | 28.1 | 46.9 | ||||
| t3 | 929.2 | 560.3 | 58.0 | 20.3 | 50.3 | ||||
| t4 | 856.0 | 560.3 | 69.6 | 20.1 | 42.1 | ||||
| t5 | 856.0 | 544.6 | 15.9 | 70.8 | 18.5 | 40.1 | |||
| t6 | 866.4 | 485.3 | 75.7 | 81.3 | 15.4 | 40.1 | |||
| t7 | 889.9 | 477.4 | 83.7 | 229.8 | 15.0 | 41.8 | |||
| t8 | 1031.4 | 392.2 | 169.5 | 371.4 | 4.9 | 59.9 | |||
| t9 | 1013.0 | 560.3 | 499.1 | 20.5 | 60.3 | ||||
| t10 | 856.6 | 560.3 | 603.6 | 20.3 | 50.0 | ||||
| t11 | 1031.4 | 524.4 | 36.2 | 673.3 | 4.9 | 59.9 | |||
| t12 | 1031.4 | 343.0 | 219.2 | 754.5 | 9.1 | 70.2 | |||
| t13 | 1031.4 | 305.6 | 256.8 | 719.7 | 4.9 | 70.5 | |||
| t14 | 1031.4 | 158.4 | 405.2 | 603.6 | 20.3 | 69.9 | |||
| t15 | 1031.4 | 28.7 | 536.0 | 0.6 | 499.1 | 13.8 | |||
| t16 | 1031.4 | 28.7 | 536.0 | 371.4 | 15.0 | 11.2 | |||
| t17 | 1031.4 | 28.7 | 536.0 | 229.8 | 15.8 | 48.4 | |||
| t18 | 1031.4 | 35.2 | 529.4 | 346.8 | 58.0 | 20.3 | 85.6 | ||
| t19 | 1031.4 | 28.7 | 536.0 | 1000.0 | 46.4 | 19.9 | 120.2 | ||
| t20 | 1031.4 | 31.9 | 532.7 | 878.7 | 34.8 | 20.1 | 120.2 | ||
| t21 | 1031.4 | 161.4 | 402.2 | 863.7 | 23.2 | 28.1 | 120.2 | ||
| t22 | 1031.4 | 161.4 | 402.2 | 671.7 | 22.1 | 28.1 | 112.0 | ||
| t23 | 1031.4 | 35.2 | 529.4 | 85.7 | 17.4 | 20.3 | 77.5 | ||
| t24 | 1031.4 | 31.9 | 532.7 | 15.5 | 11.6 | 20.1 | 67.4 |
| Time | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| t1 | 945.5 | 568.5 | 73.8 | 160 | 34.8 | 160.0 | 376.7 | |||
| t2 | 784.7 | 631.4 | 6.6 | 46.4 | 160.0 | 239.4 | ||||
| t3 | 784.7 | 631.4 | 6.4 | 58.0 | 160.0 | 232.9 | ||||
| t4 | 784.7 | 631.4 | 0.4 | 69.6 | 160.0 | 13.3 | ||||
| t5 | 784.7 | 631.4 | 1.2 | 70.8 | 160.0 | 43.1 | ||||
| t6 | 784.7 | 631.4 | 4.3 | 81.3 | 160.0 | 158.2 | ||||
| t7 | 793.6 | 631.4 | 5.8 | 229.8 | 160.0 | 211.9 | ||||
| t8 | 911.9 | 631.4 | 9.2 | 371.4 | 160.0 | 337.7 | ||||
| t9 | 847.4 | 631.4 | 7.3 | 499.1 | 160.0 | 265.8 | ||||
| t10 | 784.7 | 631.4 | 603.6 | 20.2 | 160.0 | |||||
| t11 | 842.7 | 631.4 | 11.1 | 673.3 | 160.0 | 405.6 | ||||
| t12 | 897.8 | 631.4 | 11.1 | 754.5 | 160.0 | 405.6 | ||||
| t13 | 945.5 | 617.7 | 21.4 | 719.7 | 160.0 | 273.5 | ||||
| t14 | 945.5 | 518.9 | 122.4 | 603.6 | 160.0 | 326.3 | ||||
| t15 | 945.5 | 256.2 | 390.9 | 499.1 | 160.0 | 462.2 | ||||
| t16 | 945.5 | 209.7 | 437.4 | 371.4 | 160.0 | 446.1 | ||||
| t17 | 945.5 | 133.3 | 515.8 | 229.8 | 160.0 | 496.5 | ||||
| t18 | 1494.2 | 631.4 | 7.2 | 58.0 | 160.0 | 263.8 | ||||
| t19 | 945.5 | 653.8 | 1000.0 | 46.4 | 19.8 | 160.0 | 630.2 | |||
| t20 | 945.5 | 653.3 | 877.8 | 34.8 | 160.0 | 612.5 | ||||
| t21 | 945.5 | 1.1 | 653.8 | 769.5 | 23.2 | 20.0 | 160.0 | 671.8 | ||
| t22 | 945.5 | 1.1 | 653.8 | 564.5 | 22.1 | 20.0 | 160.0 | 671.8 | ||
| t23 | 1294.4 | 631.4 | 7.2 | 17.4 | 160.0 | 263.8 | ||||
| t24 | 945.5 | 94.1 | 557.0 | 11.6 | 160.0 | 560.2 |
| Time | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t1 | 953.0 | 43.2 | 19.0 | 23.4 | 34.8 | 160.0 | 838.9 | |||||
| t2 | 908.9 | 43.2 | 7.1 | 11.3 | 46.4 | 46.9 | 160.0 | 405.1 | ||||
| t3 | 908.9 | 43.2 | 7.3 | 11.5 | 58.0 | 50.3 | 160.0 | 412.3 | ||||
| t4 | 908.9 | 43.2 | . | 4.0 | 69.6 | 20.1 | 42.1 | 160.0 | 143.9 | |||
| t5 | 908.9 | 43.2 | 1.0 | 5.1 | 70.8 | 40.1 | 160.0 | 181.6 | ||||
| t6 | 908.9 | 43.2 | 4.1 | 8.3 | 81.3 | 40.1 | 160.0 | 296.6 | ||||
| t7 | 908.9 | 43.2 | 6.6 | 10.8 | 229.8 | 41.8 | 160.0 | 388.0 | ||||
| t8 | 953.7 | 43.2 | 18.9 | 23.3 | 371.4 | 58.8 | 160.0 | 834.9 | ||||
| t9 | 908.9 | 43.2 | 15.2 | 19.6 | 499.1 | 60.3 | 160.0 | 701.1 | ||||
| t10 | 908.9 | 43.2 | 4.1 | 603.6 | 19.8 | 50.0 | 160.0 | 146.1 | ||||
| t11 | 908.9 | 43.2 | 18.5 | 23.0 | 673.3 | 59.9 | 160.0 | 823.1 | ||||
| t12 | 964.6 | 43.2 | 19.6 | 24.1 | 754.5 | 70.2 | 160.0 | 862.0 | ||||
| t13 | 1008.3 | 43.2 | 16.9 | 21.3 | 719.7 | 70.5 | 160.0 | 763.0 | ||||
| t14 | 980.4 | 43.2 | 16.8 | 21.3 | 603.6 | 0.8 | 160.0 | 761.0 | ||||
| t15 | 1095.2 | 60.8 | 21.6 | 499.1 | 1.6 | 160.0 | 775.1 | |||||
| t16 | 1095.2 | 59.6 | 20.5 | 371.4 | 23.2 | 160.0 | 733.1 | |||||
| t17 | 1095.2 | 59.9 | 20.7 | 229.8 | 58.5 | 160.0 | 741.1 | |||||
| t18 | 1468.9 | 43.2 | 16.8 | 21.3 | 58.0 | 0.8 | 160.0 | 761.0 | ||||
| t19 | 1095.2 | 61.5 | 1000.0 | 22.4 | 46.4 | 19.9 | 120.2 | 160.0 | 800.8 | |||
| t20 | 1095.2 | 61.6 | 876.3 | 22.4 | 34.8 | 20.0 | 120.2 | 160.0 | 802.8 | |||
| t21 | 1095.2 | 1.6 | 61.6 | 768.3 | 24.1 | 23.2 | 120.2 | 160.0 | 862.0 | |||
| t22 | 1095.2 | 1.6 | 61.6 | 576.3 | 24.1 | 22.1 | 112.0 | 160.0 | 862.0 | |||
| t23 | 1095.2 | 43.2 | 61.1 | 82.5 | 21.9 | 17.4 | 77.5 | 160.0 | 785.0 | |||
| t24 | 1208.0 | 43.2 | 16.8 | 21.2 | 11.6 | 0.8 | 160.0 | 759.0 |
| Costs ($) | Year 1 | Year 2…20 | Discount Rate (%) | |
|---|---|---|---|---|
| Low cost | 2,378,000 | 2,378,000 | ||
| Farm total cost | 2,379,110.06 | 2,379,110.06 | ||
| Present worth | 27,288,154.48 | |||
| MES total cost | 2,369,681.31 | 345,013.93 | ||
| Present Worth | 5,981,942.66 | |||
| Net Benefit | 9428.75 | 2,034,096.13 | ||
| Investment Indices: NPV = 21,306,212.82, IRR = Above 60%, BCR = 4.6, PI = 11.52 | ||||
| Low cost | 2,378,000 | 2,378,000 | ||
| Farm total cost | 2,379,110.06 | 2,379,110.06 | ||
| Present worth | 20,254,791.41 | |||
| MES total cost | 2,489,514.1 | 464,846.72 | ||
| Present Worth | 5,982,186.42 | |||
| Net Benefit | −110,404.04 | 1,914,263.34 | ||
| Investment Indices: NPV = 14,272,605.99, IRR = Above 60%, BCR = 3.4, PI = 8.01 | ||||
| Low cost | 2,378,000 | 2,378,000 | ||
| Farm total cost | 2,379,110.06 | 2,379,110.06 | ||
| Present worth | 15,757,083.84 | |||
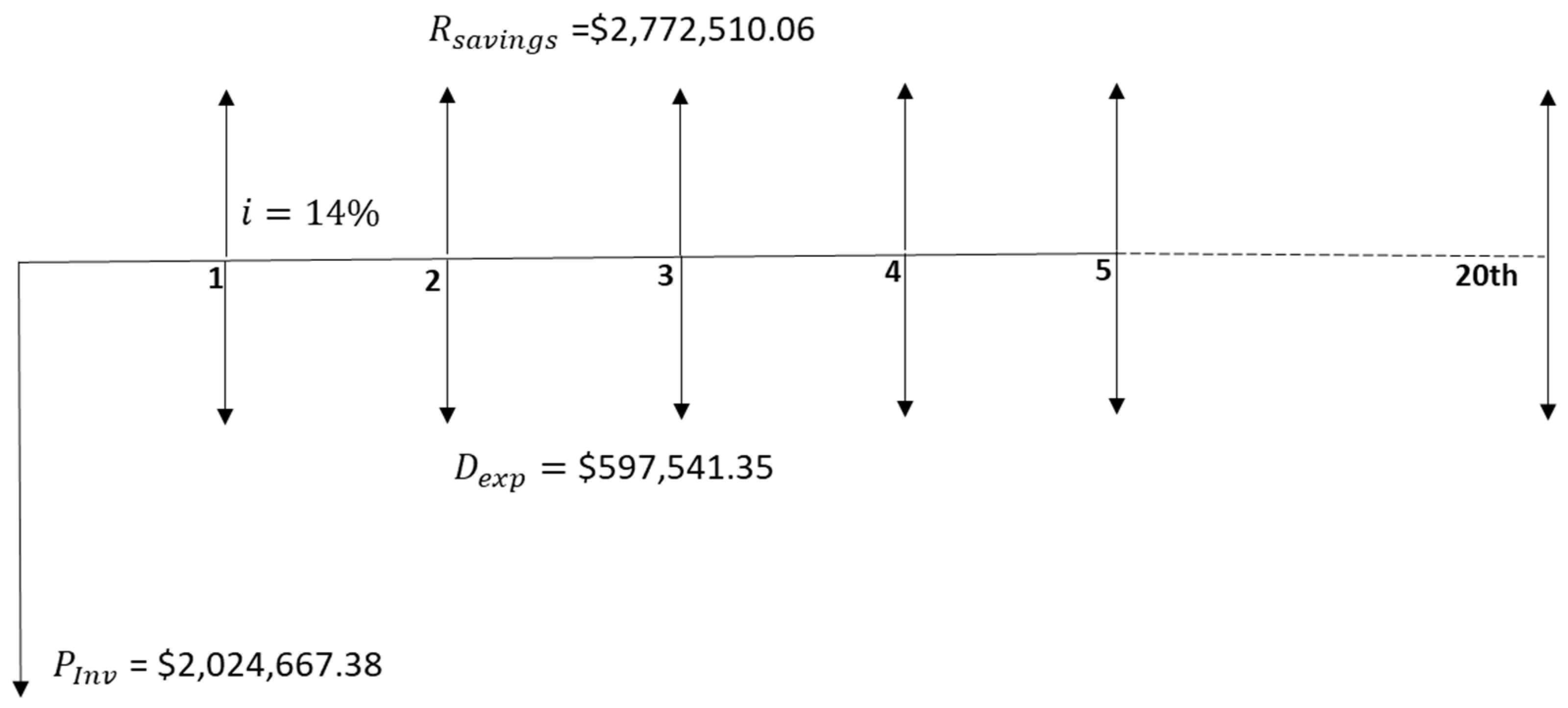
| MES total cost | 2,622,208.73 | 597,541.35 | ||
| Present Worth | 5,982,243.50 | |||
| Net Benefit | −243,098.67 | 1,781,568.71 | ||
| Investment Indices: NPV = 9,774,840.34, IRR = Above 60%, BCR = 2.6, PI = 5.83 | ||||
| Medium cost | 2,771,400 | 2,771,400 | ||
| Farm toral cost | 2,772,510.06 | 2,772,510.06 | ||
| Present Worth | 31,800,413.14 | |||
| MES total cost | 2,369,681.31 | 345,013.93 | ||
| Present Worth | 5,981,942.66 | |||
| Net Benefit | 402,828.75 | 2,427,496.13 | ||
| Investment Indices: NPV = 25,818,470.48, IRR = Above 60%, BCR = 5.3, PI = 13.7 | ||||
| Medium cost | 2,771,400 | 2,771,400 | ||
| Farm total cost | 2,772,510.06 | 2,772,510.06 | ||
| Present Worth | 23,604,041.65 | |||
| MES total cost | 2,489,514.1 | 464,846.72 | ||
| Present Worth | 5,982,186.42 | |||
| Net Benefit | 282,995.96 | 2,307,663.34 | ||
| Investment Indices: NPV = 17,621,855.23, IRR = Above 60%, BCR = 3.95, PI = 9.7 | ||||
| Medium cost | 2,771,400 | 2,771,400 | ||
| Farm total cost | 2,772,510.06 | 2,772,510.06 | ||
| Present Worth | 18,355,259.34 | |||
| MES total cost | 2,622,208.73 | 597,541.35 | ||
| Present Worth | 5,982,243.50 | |||
| Net Benefit | 150,301.33 | 2,174,968.71 | ||
| Investment Indices: NPV = 12,373,016.84, IRR = Above 60%, BCR = 2.3, PI = 7.12 | ||||
| High cost | 3,266,000 | 3,266,000 | ||
| Farm total cost | 3,267,110.06 | 3,267,110.06 | ||
| Present Worth | 37,473,425.68 | |||
| MES total cost | 2,369,681.31 | 345,013.93 | ||
| Present Worth | 5,981,942.66 | |||
| Net Benefit | 897,428.73 | 2,922,096.13 | ||
| Investment Indices: NPV = 31,491,483.02, IRR = Above 60%, BCR = 6.3, PI = 17.5 | ||||
| High cost | 3,266,000 | 3,266,000 | ||
| Farm total cost | 2,369,681.31 | 2,369,681.31 | ||
| Present Worth | 27,8148,68.21 | |||
| MES total cost | 2,489,514.1 | 464,846.72 | ||
| Present Worth | 5,982,186.42 | |||
| Net Benefit | 777,595.96 | 2,802,263.34 | ||
| Investment Indices: NPV = 21,832,682.79, IRR = Above 60%, BCR = 4.6, PI = 11.8 | ||||
| High cost | 3,266,000 | 3,266,000 | ||
| Farm total cost | 2,369,681.31 | 2,369,681.31 | ||
| Present Worth | 21,638,396.64 | |||
| MES total cost | 2,622,208.73 | 597,541.35 | ||
| Present Worth | 5,982,243.50 | |||
| Net Benefit | 644,901.33 | 2,669,568.71 | ||
| Investment Indices: NPV = 15,656,153.14, IRR = Above 60%, BCR = 3.6, PI = 8.7 | ||||
References
- Mancarella, P. MES (multi-energy systems): An overview of concepts and evaluation models. Energy 2014, 65, 1–17. [Google Scholar] [CrossRef]
- Mancarella, P.; Andersson, G.; Peças-Lopes, J.A.; Bell, K.R.W. Modelling of integrated multi-energy systems: Drivers, requirements, and opportunities. In Proceedings of the 2016 Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016; pp. 1–22. [Google Scholar]
- Ademollo, A.; Carcasci, C.; Ilo, A. Behavior of the Electricity and Gas Grids When Injecting Synthetic Natural Gas Produced with Electricity Surplus of Rooftop PVs. Sustainability 2024, 16, 9747. [Google Scholar] [CrossRef]
- Shobayo, L.O.; Dao, C.D. Smart Integration of Renewable Energy Sources Employing Setpoint Frequency Control—An Analysis on the Grid Cost of Balancing. Sustainability 2024, 16, 9906. [Google Scholar] [CrossRef]
- Alabi, T.M.; Agbajor, F.D.; Yang, Z.; Lu, L.; Ogungbile, A.J. Strategic potential of multi-energy system towards carbon neutrality: A forward-looking overview. Energy Built Environ. 2023, 4, 689–708. [Google Scholar] [CrossRef]
- Ma, T.; Wu, J.; Hao, L.; Lee, W.-J.; Yan, H.; Li, D. The optimal structure planning and energy management strategies of smart multi energy systems. Energy 2018, 160, 122–141. [Google Scholar] [CrossRef]
- Onen, P.S.; Mokryani, G.; Zubo, R.H.A. Planning of Multi-Vector Energy Systems with High Penetration of Renewable Energy Source: A Comprehensive Review. Energies 2022, 15, 5717. [Google Scholar] [CrossRef]
- Wang, J.; Hu, Z.; Xie, S. Expansion planning model of multi-energy system with the integration of active distribution network. Appl. Energy 2019, 253, 113517. [Google Scholar] [CrossRef]
- Cao, J.; Crozier, C.; McCulloch, M.; Fan, Z. Optimal Design and Operation of a Low Carbon Community Based Multi-Energy Systems Considering EV Integration. IEEE Trans. Sustain. Energy 2019, 10, 1217–1226. [Google Scholar] [CrossRef]
- Son, Y.-G.; Oh, B.-C.; Acquah, M.A.; Fan, R.; Kim, D.-M.; Kim, S.-Y. Multi Energy System With an Associated Energy Hub: A Review. IEEE Access 2021, 9, 127753–127766. [Google Scholar] [CrossRef]
- Sokolnikova, P.; Lombardi, P.; Arendarski, B.; Suslov, K.; Pantaleo, A.M.; Kranhold, M.; Komarnicki, P. Net-zero multi-energy systems for Siberian rural communities: A methodology to size thermal and electric storage units. Renew. Energy 2020, 155, 979–989. [Google Scholar] [CrossRef]
- Geidl, M.; Koeppel, G.; Favre-Perrod, P.; Klockl, B.; Andersson, G.; Frohlich, K. Energy hubs for the future. IEEE Power Energy Mag. 2007, 5, 24–30. [Google Scholar] [CrossRef]
- Pazouki, S.; Haghifam, M.-R. Optimal planning and scheduling of energy hub in presence of wind, storage and demand response under uncertainty. Int. J. Electr. Power Energy Syst. 2016, 80, 219–239. [Google Scholar] [CrossRef]
- Noorollahi, Y.; Golshanfard, A.; Hashemi-Dezaki, H. A scenario-based approach for optimal operation of energy hub under different schemes and structures. Energy 2022, 251, 123740. [Google Scholar] [CrossRef]
- Chen, X.; Cao, W.; Xing, L. GA Optimization Method for a Multi-Vector Energy System Incorporating Wind, Hydrogen, and Fuel Cells for Rural Village Applications. Appl. Sci. 2019, 9, 3554. [Google Scholar] [CrossRef]
- Eladl, A.A.; El-Afifi, M.I.; El-Saadawi, M.M.; Sedhom, B.E. A review on energy hubs: Models, methods, classification, applications, and future trends. Alex. Eng. J. 2023, 68, 315–342. [Google Scholar] [CrossRef]
- Mazza, A.; Bompard, E.; Chicco, G. Applications of power to gas technologies in emerging electrical systems. Renew. Sustain. Energy Rev. 2018, 92, 794–806. [Google Scholar] [CrossRef]
- Qin, G.; Yan, Q.; Kammen, D.M.; Shi, C.; Xu, C. Robust optimal dispatching of integrated electricity and gas system considering refined power-to-gas model under the dual carbon target. J. Clean. Prod. 2022, 371, 133451. [Google Scholar] [CrossRef]
- Onen, P.S.; Zubo, R.H.A.; Mokryani, G.; Abd-Alhameed, R. A Bi-Level Bidding Strategy Model for Gas-Fired units, Power-to-Gas facility and Renewable Power in a coordinated Energy Market Considering Demand Response Programs. 2023. Available online: https://ssrn.com/abstract=4602639 (accessed on 18 January 2025).
- Jiang, J.; Zhang, L.; Wen, X.; Valipour, E.; Nojavan, S. Risk-based performance of power-to-gas storage technology integrated with energy hub system regarding downside risk constrained approach. Int. J. Hydrogen Energy 2022, 47, 39429–39442. [Google Scholar] [CrossRef]
- Habibifar, R.; Khoshjahan, M.; Ghasemi, M.A. Optimal Scheduling of Multi-Carrier Energy System Based on Energy Hub Concept Considering Power-to-Gas Storage. In Proceedings of the 2020 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 17–20 February 2020; pp. 1–5. [Google Scholar]
- Eladl, A.A.; El-Afifi, M.I.; Saeed, M.A.; El-Saadawi, M.M. Optimal operation of energy hubs integrated with renewable energy sources and storage devices considering CO2 emissions. Int. J. Electr. Power Energy Syst. 2020, 117, 105719. [Google Scholar] [CrossRef]
- Sun, H.; Sun, X.; Kou, L.; Ke, W. Low-Carbon Economic Operation Optimization of Park-Level Integrated Energy Systems with Flexible Loads and P2G under the Carbon Trading Mechanism. Sustainability 2023, 15, 15203. [Google Scholar] [CrossRef]
- Zhang, S.; Pan, G.; Li, B.; Gu, W.; Fu, J.; Sun, Y. Multi-Timescale Security Evaluation and Regulation of Integrated Electricity and Heating System. IEEE Trans. Smart Grid 2025, 16, 1088–1099. [Google Scholar] [CrossRef]
- Yang, C.; Dong, X.; Wang, G.; Lv, D.; Gu, R.; Lei, Y. Low-carbon economic dispatch of integrated energy system with CCS-P2G-CHP. Energy Rep. 2024, 12, 42–51. [Google Scholar] [CrossRef]
- Alizad, E.; Rastegar, H.; Hasanzad, F. Dynamic planning of Power-to-Gas integrated energy hub considering demand response programs and future market conditions. Int. J. Electr. Power Energy Syst. 2022, 143, 108503. [Google Scholar] [CrossRef]
- Thommessen, C.; Otto, M.; Nigbur, F.; Roes, J.; Heinzel, A. Techno-economic system analysis of an offshore energy hub with an outlook on electrofuel applications. Smart Energy 2021, 3, 100027. [Google Scholar] [CrossRef]
- Xia, Q.; Zou, Y.; Wang, Q. Optimal Capacity Planning of Green Electricity-Based Industrial Electricity-Hydrogen Multi-Energy System Considering Variable Unit Cost Sequence. Sustainability 2024, 16, 3684. [Google Scholar] [CrossRef]
- Chambon, C.L.; Karia, T.; Sandwell, P.; Hallett, J.P. Techno-economic assessment of biomass gasification-based mini-grids for productive energy applications: The case of rural India. Renew. Energy 2020, 154, 432–444. [Google Scholar] [CrossRef]
- Di Micco, S.; Romano, F.; Jannelli, E.; Perna, A.; Minutillo, M. Techno-economic analysis of a multi-energy system for the co-production of green hydrogen, renewable electricity and heat. Int. J. Hydrogen Energy 2023, 48, 31457–31467. [Google Scholar] [CrossRef]
- Oyaniran, T. Current State of Nigeria Agriculture and Agribusiness Sector; AfCFTA: Accra, Ghana, 2020. [Google Scholar]
- He, L.; Lu, Z.; Zhang, J.; Geng, L.; Zhao, H.; Li, X. Low-carbon economic dispatch for electricity and natural gas systems considering carbon capture systems and power-to-gas. Appl. Energy 2018, 224, 357–370. [Google Scholar] [CrossRef]
- Kenarsari, S.D.; Yang, D.; Jiang, G.; Zhang, S.; Wang, J.; Russell, A.G.; Wei, Q.; Fan, M. Review of recent advances in carbon dioxide separation and capture. RSC Adv. 2013, 3, 22739–22773. [Google Scholar] [CrossRef]
- Majidi, M.; Nojavan, S.; Zare, K. A cost-emission framework for hub energy system under demand response program. Energy 2017, 134, 157–166. [Google Scholar] [CrossRef]
- Futo, S. Challenges and Prospects of Grasscutter Farming in Selected Areas of Rivers State, Nigeria. Int. J. Agric. Rural. Dev. 2016, 19, 2600–2610. [Google Scholar]
- Mtamabari, T.; Ebigennibo, S. Economics of Methane Production from Animal Dung Using 681.3 M3 Fixed-Domes Digester for Farm Application. Afr. J. Eng. Environ. Res. 2021, 9, 146–162. [Google Scholar]
- Nigeria Central Bank. Nigeria Interest Rate. Available online: https://tradingeconomics.com/nigeria/interest-rate (accessed on 25 May 2025).
- GAMS. GAMS The Modelling Language. Available online: https://www.gams.com/products/gams/gams-language/ (accessed on 28 April 2025).

| Time (h) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lh | 281 | 281 | 203 | 201 | 185 | 154 | 150 | 277 | 205 | 203 | 346 | 346 | 205 | 203 | 193 | 150 | 158 | 203 | 199 | 201 | 281 | 281 | 203 | 201 |
| Le | 606 | 469 | 503 | 421 | 401 | 401 | 418 | 599 | 603 | 500 | 599 | 702 | 705 | 699 | 798 | 805 | 801 | 856 | 1202 | 1202 | 1202 | 1120 | 775 | 733 |
| Lc | 1428 | 1266 | 1232 | 1365 | 1478 | 1633 | 2118 | 2308 | 2491 | 2744 | 3061 | 3124 | 3145 | 2963 | 2710 | 2352 | 2043 | 2170 | 2494 | 2185 | 1918 | 1750 | 1722 | 1666 |
| λ | 6.18 | 6.88 | 6.18 | 6.81 | 7.27 | 8.6 | 7.74 | 6.03 | 7.27 | 8.83 | 10.9 | 12.1 | 11.6 | 11.8 | 10.9 | 14.5 | 16.8 | 14.7 | 19.2 | 20 | 20.5 | 16.9 | 14.3 | 13.7 |
| Lwd | 13.7 | 13.3 | 12.3 | 10.9 | 10.4 | 9.94 | 8.46 | 7.97 | 7.52 | 7.64 | 7.77 | 7.44 | 7.36 | 6.95 | 6.7 | 6.91 | 5.19 | 9.53 | 8.18 | 8.3 | 9.16 | 10.6 | 12.8 | 13.9 |
| Irad | 5 | 10 | 10 | 11 | 13 | 50 | 195 | 305 | 410 | 520 | 550 | 650 | 610 | 520 | 410 | 305 | 196 | 50 | 13 | 12 | 11 | 10 | 10 | 5 |
| Fuel Source | Unit | Qty/Month | Unit Price ($) | Cost/Month ($) |
|---|---|---|---|---|
| Coal | kg | 50,000 | 0.74 | 37,000 |
| Fuelwood | kg | 35,000 | 0.45 | 13,000 |
| Diesel | L | 60,000 | 1.07 | 64,000 |
| PMS | L | 60,000 | 0.79 | 47,400 |
| Kerosene | L | 45,000 | 1.53 | 68,850 |
| Biogas | m3 | 51,417.6 | 0.25 | 12,854.4 |
| Scenario No. | P2G | E-DRP | T-DRP |
|---|---|---|---|
| 1 | √ | √ | - |
| 2 | - | √ | √ |
| 3 | √ | - | √ |
| 4 | √ | √ | √ |
| Planning Costs ($) | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 |
|---|---|---|---|---|
| 1,917,233.82 | 2,763,692.10 | 3,394,997.75 | 2,024,667.38 | |
| 4,051,280.63 | 4,452,858.06 | 3,667,833.52 | 3,753,502.67 | |
| 224,909.67 | 2,911,419.54 | 3,280,732.26 | 203,986.86 | |
| 0.00 | 0.00 | 0.00 | 0.00 | |
| 6,193,424.12 | 10,127,970.00 | 10,343,564.00 | 5,982,156.91 |
| Selected Components | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 |
|---|---|---|---|---|
| WT | - | - | - | - |
| CHP | 29.2933 | 241.18 | 294 | 27.7 |
| B | 40.5149 | 476.293 | 536.7 | 36.74 |
| T | 900 | 900 | 900 | 900 |
| EC | - | - | - | - |
| AC | 420 | 185.1571 | 420 | 420 |
| TES | - | - | - | - |
| EES | - | - | - | - |
| PV | - | - | - | - |
| P2G | 25.43 | - | 18.76 | 24.0787 |
| Fuel | Heat Values (MJ/kg or m3) | Energy/Month (MJ) | Cost/Month ($) | Cost/Year ($M) |
|---|---|---|---|---|
| Coal | 25–35 | 1,750,000 | 37,000 | 0.444 |
| Fuelwood | 18.60 | 651,000 | 13,000 | 0.156 |
| Diesel | 46.00 | 2,760,000 | 64,000 | 0.768 |
| PMS | 46.80 | 2,808,000 | 47,400 | 0.5688 |
| Kerosene | 46.26 | 2,081,700 | 68,850 | 0.8262 |
| Biogas | 35.8 | 1,840,750 | 12,854.4 | 0.1543 |
| Total | 11,891,540 | 243,104 | 2.92 | |
| Type of Cost | Year 1 | Years 2–20 (Per Year) | |
|---|---|---|---|
| Farm Annual Costs | Fuel | 2,771,400 | 2,771,400 |
| Labour | 560.06 | 560.06 | |
| O&M | 550 | 550 | |
| Total Annual | 2,772,510.06 | 2,772,510.06 | |
| Present Worth | 18,355,259.34 | - | |
| MES Costs | Investment | 2,024,667.38 | - |
| Operations | 566,741.37 | 566,741.37 | |
| Emissions | 30,799.98 | 30,799.98 | |
| Total Annual | 2,622,208.73 | 597,541.35 | |
| Present Worth | 5,982,243.50 | - | |
| Net Benefit | 150,301.33 | 2,174,968.71 | |
| Investment Indices | Values | Indication |
|---|---|---|
| NPC/NPV | USD 12.37 million | viable |
| BCR | 2.3 | viable |
| IRR | Above 60% | acceptable |
| PI | 7.12 | viable |
| Fuel Source | Quantity/ Month | Unit Price ($) Low | Unit Price ($) Medium | Unit Price ($) High |
|---|---|---|---|---|
| Coal | 50,000 kg | 0.78 | 0.74 | 0.85 |
| Fuelwood | 35,000 kg | 0.50 | 0.45 | 0.55 |
| Diesel | 60,000 L | 0.85 | 1.07 | 1.25 |
| PMS | 60,000 L | 0.58 | 0.79 | 1.02 |
| Kerosene | 45,000 L | 1.26 | 1.53 | 1.65 |
| Biogas | 51,417.6 m3 | 0.25 | 0.25 | 0.25 |
| Fuel | Heat Values (MJ/kg or m3) | Energy/Month (MJ) | Cost/Year Low ($M) | Cost/Year Medium ($M) | Cost/Year High ($M) |
|---|---|---|---|---|---|
| Coal | 25-35 | 1,750,000 | 0.468 | 0.444 | 0.510 |
| Fuelwood | 18.60 | 651,000 | 0.210 | 0.162 | 0.231 |
| Diesel | 46.00 | 2,760,000 | 0.612 | 0.7704 | 0.9 |
| PMS | 46.80 | 2,808,000 | 0.408 | 0.5688 | 0.734 |
| Kerosene | 46.26 | 2,081,700 | 0.680 | 0.8262 | 0.891 |
| Biogas | 35.8 | 1,840,750 | 0.1543 | 0.1543 | 0.1543 |
| Total | 11,891,540 | 2.53 | 2.92 | 3.42 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torbira, M.; Dao, C.D.; Badawy, A.D.; Campean, F. Optimal Planning and Techno-Economic Analysis of P2G-Multi-Energy Systems. Sustainability 2025, 17, 5759. https://doi.org/10.3390/su17135759
Torbira M, Dao CD, Badawy AD, Campean F. Optimal Planning and Techno-Economic Analysis of P2G-Multi-Energy Systems. Sustainability. 2025; 17(13):5759. https://doi.org/10.3390/su17135759
Chicago/Turabian StyleTorbira, Mtamabari, Cuong Duc Dao, Ahmed Darwish Badawy, and Felician Campean. 2025. "Optimal Planning and Techno-Economic Analysis of P2G-Multi-Energy Systems" Sustainability 17, no. 13: 5759. https://doi.org/10.3390/su17135759
APA StyleTorbira, M., Dao, C. D., Badawy, A. D., & Campean, F. (2025). Optimal Planning and Techno-Economic Analysis of P2G-Multi-Energy Systems. Sustainability, 17(13), 5759. https://doi.org/10.3390/su17135759







