Abstract
Solar Photovoltaic (PV) systems typically convert solar irradiance into electricity, thereby helping to reduce the need for fossil fuels and the amount of greenhouse gases released. They provide a reliable and continuous renewable source of energy. However, PV systems are continuously exposed to diverse and changing environmental conditions, such as temperature, humidity, dust, and rain. Exposure to such conditions creates electrical and visible faults in the PV systems. These faults may reduce the PV system’s performance, reliability, and lifetime. In this regard, this paper aims to propose a framework/methodology for reliability modeling and assessment of large-scale grid-connected PV systems using a Fault Tree Analysis (FTA) approach. Specifically, an exhaustive literature survey is carried out to acquire the failure rates of different components/faults existing on the DC side of the PV system. Then, the Fussel-Vesely (F-V) importance measure is employed to identify critical faults and their criticality ranking. Results showed that solder bond failure, broken cell, broken interconnect (finger interruption), rack structure, grounding/lightning protection system, delamination, discoloration, and partial shading are the most critical faults which severely degrade the performance of the PV systems. The recommendations and scope for further study are provided to optimize operations and maintenance costs.
1. Introduction
In recent years, the market for Photovoltaic (PV) solar power plants has expanded dramatically and is currently playing a crucial role in limiting the usage of traditional limited sources of energy (e.g., natural gas, oil, coal, or nuclear energy, etc.) and thereby limiting the emission of greenhouse gases and air pollution. As per the report published by the International Renewable Energy Agency (IEA) [1], the total cumulative installed capacity at the global level for PV in 2021 reached up to 942 GW. Some of the major solar power parks are Golmud Desert Solar Park, with an installed capacity of 2.8 GW making it the world’s largest solar park, located in Qinghai Province of China, followed by Bhadla Solar Park, Rajasthan, India (2.7 GW), Longyangxia, Eastern Qinghai, China (2.4 GW), Benban, Solar Park, Egypt (1.3 GW), NP Kunta Solar Park, Andhra Pradesh, India (1.2 GW), Sheikh Mohammed Bin Rashid Al Maktoum Solar Park, UAE emirate of Dubai (1.03 GW), etc. [2]. It is expected to reach up to 1500 GW by 2030 [3].
PV panels or modules and Balance Of System (BOS) components are the two main parts that make up a PV system. The BOS element includes connectors, AC and DC wiring, fuses, Miniature Circuit Breakers (MCBs), overcurrent protection devices, inverters, Maximum Power Point Tracker (MPPT) controllers, and storage devices (depicted in Figure 1). The parallel strings of PV modules constitute a solar PV array, each containing a series of PV modules. It converts solar energy into electric energy. A blocking diode allows a unidirectional current flow from the PV panel to the inverter. The DC MCB separates the PV array from the rest of the system. The fuse protects the rest of the system against overcurrent produced by the PV array. A Surge Protection Device (SPD) protects against electrical spikes or surges. These surges may get produced into the system or from lighting. They are connected to both sides of the inverter to handle DC and AC spikes. The DC electricity produced by a PV array is converted into AC via an inverter. The MPPT controller maximizes the energy available from solar module arrays at any time during its operation. An earth plate is provided to each PV module to handle leakage or short circuit current.
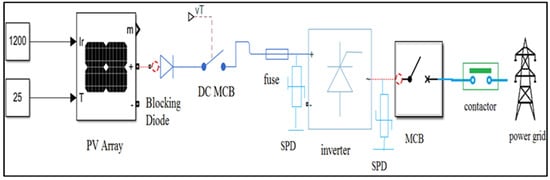
Figure 1.
Single line diagram of a solar PV system.
PV power plants are generally designed for 20–25 years to generate the maximum possible electric energy at a minimum cost. However, PV systems are continuously exposed to diverse and changing environmental conditions and loads, such as temperature, humidity, dust, rain, etc. Such conditions may cause various faults, such as delamination, hot spots, cell cracks [4], glass soiling, discoloration, frame defects, junction box defects, and corrosion [5,6,7]. In general, the rate of degradation in silicon PV module power ratings due to aging is 0.8% each year [8,9]. It is observed that the occurrence of different faults in the PV system may reduce the power output by up to 19% of its capacity. Hence the overall effect of the presence of fault would be lowered power generation, reduced reliability and lifetime, and increased operation and maintenance cost of the PV system. If such faults persist for a longer duration, it may create a catastrophic effect resulting in system burnout. Therefore, there is a need to conduct a reliability analysis of the solar PV system for system planning, long-term operation, facilitating risk assessment, and limiting revenue losses. Analysis of the reliability and durability of PV systems has been the point of interest for various stakeholders, e.g., government, manufacturers, investors, and suppliers.
Due to the complexity of PV systems and their exposure to variable loading conditions, it is a critical task to develop a reliability assessment model capable of accurately predicting the behavior of the PV system. The changing environmental parameters, such as variable solar irradiance, high uncertainty, and variability of system components, affect the performance of PV plants and degrade their output. The Markov process method [10], Monte-Carlo simulation [11], State Enumeration [12], Fault Tree Analysis (FTA) [13,14], Failure Mode and Effect Analysis (FMEA) [15], and Reliability Block Diagram (RBD) [16] are different techniques available for reliability analysis of PV plants.
In this paper, the FTA is used for solar PV system reliability assessment. FTA basically comprises cause and effect analysis which provides information about how the failures are propagated into the system and how failure in the components leads to the complete or partial failure of the system. The major benefits of FTA are the deductive identification of failures, the emphasis on the critical elements of the system related to system failure, the creation of a graphical aid for system analysis and management, the focus on a single fault at a time, and the exposure of system behavior and possible interactions. A micro-level analysis that considers all possible failure modes of the PV module is used to develop an accurate model instead of assuming PV module failure as a basic event. This is one of this paper’s distinct contributions to the reliability analysis of PV systems reported until today.
A hybrid FTA approach is proposed and used for solar PV systems’ reliability and criticality analysis. The proposed methodology uses the data from the literature, manufacturers, researchers, service providers, plant installers, etc., for designing the generalized Fault Tree (FT) diagram that can be used for the analysis of different solar PV systems/plants. The Fussel-Vesely (F-V) importance measure is integrated with the FTA to accurately identify the micro-level faults and degradation of the plant’s performance. In addition to calculating the top event’s reliability, the key faults at the fundamental and intermediate levels and their failure probability are determined.
The remainder of this paper is structured as follows: Section 2 contains the literature review of the topic at hand. In Section 3, the suggested FTA methodology is presented, whereas in Section 4, the results of reliability and FTA study of a solar PV plant are provided and analyzed. Finally, Section 5 concludes the paper and highlights potential future works.
2. Literature Survey
This section presents a literature survey on reliability modeling, analysis, and predictions of a solar PV system. It primarily focuses on three key aspects:
- Different methodologies used for data collection (Section 2.1);
- Methods/techniques used for system reliability modeling and analysis (Section 2.2); and
- Approaches used for estimating best-fit (most suitable) probability distributions for the given data set (time to failure data). The given data set is the failure rate of basic events or failure modes (Section 2.3).
2.1. Methodologies Used for Data Collection
The accuracy of reliability modeling and predictions largely depend on the availability of sufficient data and the quality of the collected data. The required data can be collected from four different sources: (1) field visits, (2) experiments/tests, (3) literature, and (4) expert opinions/judgments. Table 1 summarizes the data collection methodologies used for the analysis of solar PV systems by different researchers between 1982 and 2021. It is observed that most of the data have been taken from the published literature. The failure rates of various subsystems, components, or basic events from the literature were used by [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. Furthermore, few researchers used data collected from more than one source.
The field failure data was used to analyze the reliability and availability of PV plants of various capacities, as shown in [27,31,32,38,39,40,41,42,43,44,45]. Failure data of panel and inverter was collected by Sacramento Municipal Utility District (SMUD), USA, for four years and published in 1997 [39]. International Energy Agency (IEA) investigated the performance of 368 grid-connected PV systems under the PV Power System (PVPS) program [40]. Reliability and availability analysis of PV modules, power conditioners, monitoring systems, and BoS was carried out in Japan under a field test project [41]. Rajput et al. [38] performed FMEA of PV systems by using test data and field trails. Highly Accelerated Stress Screening (HASS) was used by Fara and Craciunescu in 2020 [33] to create and identify defects in a short time. Perveen et al. [34] developed a fuzzy-based hybrid approach for reliability analysis in which they used the data from the literature and the expert judgments for the failures/faults whose failure data is unavailable.

Table 1.
Data collection methodologies used for a PV system.
Table 1.
Data collection methodologies used for a PV system.
| Sr. No. | Author(s) and Reference(s) | Data Collection Methodologies | |||
|---|---|---|---|---|---|
| Field Data | Test Data | Literature | Expert Judgments | ||
| 1 | Stember et al. [46] | √ | |||
| 2 | Mishra and Joshi [20] | √ | |||
| 3 | Maish et al. [39] | √ | |||
| 4 | Jahn and Nasse [40] | √ | |||
| 5 | Oozeki et al. [41] | √ | |||
| 6 | Huffman et al. [47] | √ | |||
| 7 | Collins et al. [42] | √ | √ | ||
| 8 | Zini et al. [35] | √ | |||
| 9 | Golnas [43] | √ | |||
| 10 | Theristies and Papazoglou [21] | √ | |||
| 11 | Hu et al. [22] | √ | |||
| 12 | Charki et al. [36] | √ | |||
| 13 | Ghaedi et al. [24] | √ | |||
| 14 | Ahadi et al. [25] | √ | |||
| 15 | Ahadi et al. [27] | √ | √ | ||
| 16 | Colli [26] | √ | |||
| 17 | Sulaeman et al. [28] | √ | |||
| 18 | Cai et al. [48] | √ | |||
| 19 | Sulaeman et al. [31] | √ | √ | ||
| 20 | Nemes et al. [36] | √ | |||
| 21 | El- Metwally et al. [37] | √ | |||
| 22 | Gupta et al. [17] | √ | |||
| 23 | Perveen et al. [34] | √ | √ | ||
| 24 | Baschel et al. [32] | √ | √ | ||
| 25 | Chiacchio et al. [18] | √ | |||
| 26 | Sayed et al. [19] | √ | |||
| 27 | Rajput et al. [15] | √ | |||
| 28 | Sayed et al. [29] | √ | |||
| 29 | Aguisti et al. [44] | √ | |||
| 30 | Rajput et al. [38] | √ | √ | ||
| 31 | Fara and Craciunescu [33] | √ | |||
| 32 | Qadeer and Ikram [16] | √ | |||
| 33 | Yian Liu [45] | √ | |||
| 34 | Ong et al. [30] | √ | |||
| 35 | Simon et al. [49] | √ | |||
| 36 | Spertino et al. [50] | √ | |||
| 37 | Li et al. [51] | √ | |||
| 38 | Luo et al. [52] | √ | |||
| 39 | Yinan Liu [45] | √ | |||
| 40 | Ostovar et al. [53] | √ | |||
| 15 | 5 | 24 | 2 | ||
Table 1 depicts that many researchers used failure rates from the literature to carry out reliability analysis. Few researchers tried to develop the reliability model with field failure data, and very little attention was paid to test data/accelerated testing based on failure data generation. For an accurate study, however, the failure rate of all basic events and components must be known, which may not be published or unavailable in the public domain. The results obtained from the reliability analysis carried out using literature data must be supported by field failure data, reliability test results, or expert opinion.
2.2. Methods/Techniques Used for System Reliability Modeling and Analysis
FTA, FMEA, RBD, Fuzzy FTA, Markov chains/models, control charts, Monte Carlo simulation, Petri networks, state enumeration method, dynamic Bayesian networks, discrete convolution, and logic gate representation are the methods used for system reliability modeling and analysis, as summarized in Table 2. For instance, the FTA technique was extensively used by [25,27,30,32,35,46,51,54]. The RBD method was used for the analysis of critical components of large-scale grid-connected solar PV systems by [16,19,29,33,42,47]. A Binary Decision Diagram (BDD) to carry out qualitative and quantitative analysis in combination with fault tree analysis was proposed by Hu et al., 2013 [22]. Colli, 2015 [26] performed FMEA of system components and subcomponents. Reliability, maintainability, and life cycle cost analysis of monocrystalline silicon PV systems of different capacities were carried out using field failure data and data available in the literature [15,38]. The control chart method was used to perform a Reliability, Availability, and Maintainability (RAM) analysis on a 12.5 kW PV system [44]. Dynamic reliability analysis based on Stochastic Hybrid FTA (SHyFTA) was proposed by Chiacchio et al., 2018 [18]. Reliability assessment of solar PV systems has been conducted using Fuzzy FTA (FFTA) approach for the basic events whose failure rate data is ambiguous in nature [34].

Table 2.
Methods used for system reliability evaluation.
It is observed that limited data sets on failure rates/failure modes, etc., are available in the literature with inconsistency. There is a need to collect location/region-specific failure data using field trials, expert judgments, and experiences. A framework needs to be developed for data collection and system reliability modeling. Though many researchers used a particular technique for reliability analysis, multiple methods provide a well-round approach that supports a PV system with optimal reliability, availability, maintainability, and safety.
From Table 2, it is evident before the year 2000, i.e., in the initial phase of PV installations, the reliability of solar PV plants was expressed with failure data of limited but major subassemblies. After the availability of failure rates of various subassemblies, failure modes, and components, more robust techniques were used, such as FTA and RBD, which are suitable for such kind of complex and large systems. To improve the accuracy of results, techniques such as FTA were integrated with Fuzzy logic, BDD, and stochastic hybrid approach. The FTA is found to be one of the effective methods for obtaining critical faults, and the accuracy of this method can be improved with the hybrid approach. Therefore, there is a need to develop a hybrid FTA approach for the reliability and criticality analysis of solar PV systems.
2.3. Methodologies Used for Data Collection, Sorting, and Estimating Best-Fit Probability Distributions
Probability distributions, such as Weibull, exponential, lognormal, normal, arithmetic, and Gamma are used to model field failure data. Most papers assume that component failure rates are constant and that an exponential distribution is used for modelling, as shown in Table 3. A more focus can be provided on Weibull analysis which is used to predict failure and reliability based on the assessment of trends in the data. The Weibull was popularly used when failure rates vary [18,19,33], whereas lognormal distribution was used by [19,42]. A framework for failure data pre-processing and estimating best-fit probability distribution for the given data set needs to be developed.

Table 3.
Probability distribution used in literature for reliability calculation.
The accuracy of the developed models is largely dependent on the quality of the data. Thus, it is required to use certain pre-processing operations/methods to collect, classify, and sort the failure data, especially in the case of a large amount of data collected from various sources. Sometimes, the data needs to be edited (omission and correction) to detect and remove errors, if any, to ensure accuracy, consistency, and uniformity in the data. Classification operation is applied to arrange the raw data in groups, such as failure rates related to subassemblies or subsystems. A suitable measure of central tendency needs to be considered to obtain the most representative figure for the entire pool of failure data. The median value of failure data was considered by a few researchers [19,29] to handle extreme lower and upper limits. It also helps to overcome certain unexpected or uncertain values. Data is sorted in ascending order before the application of the measure of central tendency (median). Accelerated life testing is also one of the statistical tools used for reliability and performance analysis which requires more future work.
From the study of literature on reliability analysis of PV systems, the following remarks are drawn. Most of the reliability studies on solar PV systems are carried out using the failure data published in the literature. It is evident that exponential probability distribution is a widely used distribution that assumes that failure rates of components remain constant throughout time duration. It is required to develop a framework for the analysis of such data to minimize the effect of variation in the data and increase the accuracy of the prediction. To carry out a reliability assessment of solar PV systems, the selection of the most suitable mathematical model/method, collection/measurement of failure rates of various subassemblies/components/failure modes along with a selection of probability functions are important factors. FTA is found to be a more suitable approach for reliability modeling and identifying critical faults of the solar PV system.
3. Methodology
A detailed framework/flowchart of the proposed methodology for reliability data modeling and assessment of solar PV system using the FTA approach is shown in Figure 2. The methodology is organized as follows:
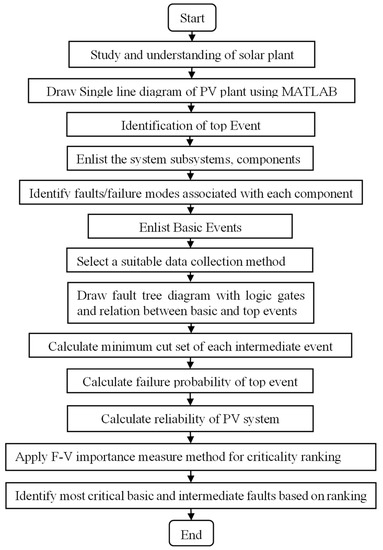
Figure 2.
A proposed framework of reliability modeling and assessment of solar PV system.
- A process to identify various subsystems, components, and failure modes of a solar PV system (Section 3.1);
- How to construct a fault tree diagram for a given system (Section 3.2);
- Data collection strategy (Section 3.3);
- Steps to calculate the minimum cut set of each basic and intermediate events (Section 3.4), and finally;
- Criticality ranking of intermittent and basic events (Section 3.5).
3.1. Identification of Subsystems, Components, and Faults Related to Components
The first step is to comprehend the configuration of the solar PV system and categorize it into various subsystems, assemblies, and components of each subsystem. The faults/failure modes of each component are then identified. This data is collected from the literature, plant installation firm, and service engineers. A sheet is prepared for the collection and organization of the data, as shown in Table 4. Information such as the potential effects energy output, i.e., no output or degraded output, technical damage, financial damage, and human safety damage, are also collected. The exhaustive list comprises rare/uncommon events, incomplete events, the relation and interdependencies between the components.

Table 4.
Sample part list and related faults.
3.2. Construction of Fault Tree Diagram of Solar PV System
A Fault Tree (FT) will be constructed for all faults related with the PV systems DC side and published in the literature. FT will help in identifying how the failure of an individual component leads to system failure [59]. FTA simply analyses the causes and effects of a system failure and traces it to one or more levels [60]. FT helps to understand the interdependence between components of a system. The steps involved in the construction of FT of a solar PV system are as below:
- Identification of top event. The top occurrence/event in this study is “No output or reduced power output”.
- Using a top-down approach, it is necessary to determine the basic events and intermediate ones that led to the top event. The dominating external events, such as weather conditions and radiation levels, are considered while constructing the FT diagram.
- Create a FT diagram with logic gates and symbols (as depicted in Table 5) that can be represented by a Boolean equation. The OR gate connects all basic and intermediate events. A rectangle represents the top event.
 Table 5. Logic gates and symbols used in FTA.
Table 5. Logic gates and symbols used in FTA.
3.3. Data Collection
Data required for the calculation of failure rate or failure probability can be collected through field data, literature, and expert opinion. In this paper, the data on time to failure and probability of failure will be collected from the published literature and maintained as per Table 6. The collected data may have a lot of variation as they might have been collected from different system configurations, geographical locations, countries, and weather conditions. Therefore, the data will be normalized for the same units, and parameters such as mean, median, mode, a minimum and maximum value of failure rates will be estimated for further analysis.

Table 6.
Failure data collected from the literature.
Exponential probability distribution will be used for modeling and analysis of various faults. We shall compute the probability that events will occur using Equation (1):
where is failure probability at time , is the failure rate, and is mission time in hours.
3.4. Calculate the Minimum Cut Set of Each Basic Event
The FT must be transformed into a Boolean equation and then a probability equation in order to determine the overall likelihood of a top event. OR gates are used to connect all basic events and intermediate events. Hence, each fault generated propagates and causes the top event. OR gates are used to connect each basic event and each intermediate event. To carry out qualitative analysis, three prominent techniques are available: (1) Minimum Cut Set (MCS), (2) minimum path set, and (3) common cause failures. In the proposed methodology of this work, the MCS technique is used by considering the complex nature of the system. Minimum path set and common cause failure techniques are suitable when the system has few components or subassemblies. Further, to find or carry out cut set analysis, multiple methods are available in the literature [59]: the classical approach based on the manipulation of Boolean expression of FT, Binary Decision Diagrams (BDD), Minimum Cut Vote (MCV), and Monte Carlo method.
To perform this task, two popular methods were used in the literature [62]: Monte-Carlo simulation and analytical methods. In this research, MCS is used over Monte-Carlo to reduce computation complexity. MCSs represents the intersection or combination of fundamental events and display the shortest route to the top event [63]. They provide information about the vulnerability of a system. A cut set is a collection of elements or occurrences that together lead to a system failure. The overall reliability of the system can be increased by lowering the failure probability of these cut sets.
Calculation of Reliability of a Solar PV System
In a solar PV system’s FT, basic events are connected in sequence via an OR gate. From the basic theory of probability, the reliability of the system will be determined by Equations (2) and (3).
where is the occurrence of the probability of a basic event . However, ; ; ….; , where represents the reliability or probability of event 1, represents the reliability or probability of event 2, represents the reliability or probability of event 3, and so on.
Thus, the system’s reliability can be evaluated using Equation (4).
where is the occurrence of the probability of the ith MCS, given in Equation (5).
3.5. Criticality Ranking of MCSs of Basic Events
The Fusell-Vesely (F-V) importance measure is used to rank the criticality of minimum cut sets. Basic events can be ranked as per the F-V measure. Initially, the failure probability of each MCSs is calculated by taking a union of respective basic events failure probability followed by F-V importance measure calculation as given by Equation (6):
In this equation is the importance measure of ith MCS. is the likelihood or probability of ith MCS and is the likelihood or probability of a Top Event (TE) for all MCSs. The MCSs or basic events can be ranked as highly critical, medium, and low based on the F-V measure ranking range, as shown in Table 7.

Table 7.
Ranking range.
4. Reliability Analysis of Solar PV System
The FTA approach is used in this section to perform a reliability analysis on the solar PV system. The required data on faults/failures and fault failure rates are gathered from the published literature. To identify critical faults, the developed FT is subjected to qualitative and quantitative analysis.
4.1. FT Diagram of Solar PV System under Study
The primary goal of solar PV system maintenance is to keep the system in good working order so that it can produce maximum power output continuously over its design life. This research also focuses on the DC side of the plant. Therefore, the top event is considered as “No output or degraded output at Surge Protection Devices (SPDs)”. The intermediate and basic events that cause the top event to occur are identified [64] and connected to the top event using logic gates based on fault propagation. Because the occurrence of a single basic event causes the top event to occur, all basic events are connected to the top event using an OR gate. Figure 3 depicts an FT diagram of a solar PV system with 31 basic events and 14 intermediate events.
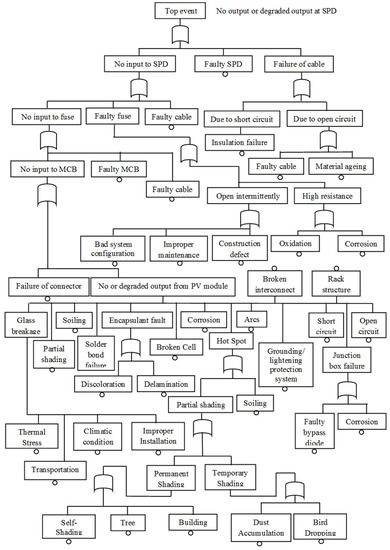
Figure 3.
FT diagram of a solar PV system.
4.2. Qualitative FTA of a Solar PV System
The qualitative analysis includes the identification of the relationship between basic events with a corresponding intermediate event and intermediate events with a top event. The qualitative analysis of the solar PV system reveals the connection between basic and intermediate events and a top event. It has been discovered that basic events are related to intermediate events via an OR gate, and all intermediate events are related to the top event via an OR gate. MCSs are also obtained, which are all the combinations of basic events that, when occurring simultaneously, resulting in the occurrence of the top event. Because the occurrence of any of the basic events leads to the occurrence of the top event, they are all MCSs.
The developed FT diagram is transformed into an equivalent RBD for analysis purposes. All of the basic events are linked to the top event, either directly or indirectly, by a ‘OR’ gate, and the occurrence of a single event causes the top event to occur. As a result, shown in Figure 4, all of the basic events are connected in series.
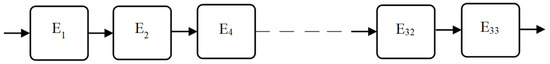
Figure 4.
RBD for solar PV system.
In the case of series configuration, all events are regarded as critical. The reliability of solar PV () systems can be estimated using the probability of non-occurrence of events/faults as follows: E1 = indicates that the event 1 does not occur; E2 = indicates that the event 2 does not occur; …; E33 = indicates that the event 33 does not occur.
Using the principles of probability, the solar PV system’s reliability (probability of survival) () is estimated as follows:
However,
where is the likelihood or probability that event 1 will not happen, is the likelihood or probability that event 2 will not happen, is the likelihood or probability that event 3 will not happen, and so on.
Equation (10) is SPV’s governing reliability model. In this case, all of the SPV system’s events are assumed to be independent (i.e., the occurrence or non-occurrence of one event component does not affect the occurrence or non-occurrence of the other event). In other words, all 33 events must not occur for the system to function. Furthermore, if the probability of occurrence () values for all 33 events are known, the solar PV system reliability () is calculated as follows:
Estimating the reliability model for the first-level intermediate events is as follows:
Table 8 lists the notation used to describe the reliability of intermediate events. Equation (12) to (25) can be utilized to evaluate the reliability of intermediate events or the probability that intermediate events will not occur.

Table 8.
Notation used for reliability of intermediate events.
4.3. Quantitative Reliability Analysis of Solar PV System
The failure rates/occurrence rates of individual components of various large-scale PV systems described in the literature are taken into account to determine the overall system’s reliability. The analysis of reliability is conducted over a one-year period with 8.5 h of operation every day. Failure rates are transformed evenly to an hourly rate of failures. Various layouts and configurations are considered while obtaining the data. Table 9 shows the average, median, mode, lowest, and highest failure rates of data available in the literature. Here, the median value is used to calculate the failure probability as the median value reduces the uncertainties in the predictions.

Table 9.
Failure rates of various components, subassemblies, and failure modes of solar PV system.
Table 9 summarizes the mean failure rates, median failure rates, lowest failure rates, and highest failure rates of components/basic events of the solar PV system used to estimate failure probability (10−6 failures per hour). In total, 33 basic events are identified during FTA, but literature data is available for 27 events. It is observed that the statistical uncertainty of the data obtained for each basic event/failure mode is reduced when the median values, rather than average values or modes, are used. Hence in this work median value is considered for further analysis.
The probability of occurrence (failure probability) of 27 basic events whose data is available is calculated using Equation (1) and mentioned in Table 10. For instance, the failure probability of faulty SPD equals to =.

Table 10.
Failure probability and reliability of basic events.
In this study, is mission time used to calculate the BEs failure probability for one year. Let us consider sun is available 8.5 h per day during the year. As a result, the mission time is 3102.5 sec., i.e., .
Here, the failure data of events such as transportation, self-shading, tree, building, dust accumulation, and bird dropping is not found in the literature/ambiguous in nature; hence not considered for analysis. The reliability of these events is assumed as one to nullify their effect. Similarly, the reliability of a basic event is calculated by using the following Equation (26):
The ranking of the components has a significant impact on monitoring, maintenance, and future reliability upgrade efforts. Table 11 lists the critical ranking of basic events of the system as per values of the F-V importance measure. For instance, the F-V measure of basic event faulty SPD can be calculated using Equation (27):
where is a probability of the basic event and is a probability of the top event.

Table 11.
Criticality ranking of basic events using F-V importance measure.
The reliability of the top event is calculated by converting the FT diagram of a system into a Boolean expression or logic representation. There are 27 MCSs for the 27 basic events. According to probability theorists, the union of the MCSs represents the failure probability of the top event.
The failure probability of a top event () is 0.552. Thus, the Importance Measure (IM) of the faulty SPD can be computed as:
Once the F-V importance measure of all basic events is calculated, the criticality ranking is provided as the descending value of the F-V measure.
As per the criticality ranking range mentioned in Table 7, solder bond failure, broken cell, broken interconnect, rack structure, grounding/lightening protection system, delamination, discoloration, and partial shading are highly critical faults or events with F-V importance measure , , , , , , and , respectively, while basic events with criticality ranking between 9 and 18 are medium critical faults, the remaining basic events appear in the low criticality range. The failure of connectors, thermal stress, climatic conditions, bad system configuration, construction defect, and oxidation have a comparatively lower impact on system reliability.
After allocation of criticality ranking to basic events, in order to provide critical rank to intermediate events, calculate their reliability. The reliability of 14 intermediate events (sub-systems) is estimated using Equations (12)–(25) and summarized in Table 12. Subsequently, the failure probability of intermediate events is calculated and entered into Table 12.

Table 12.
Failure probability and reliability of intermediate events (sub-systems).
Now, calculate F-V importance measure of intermediate events. Table 13 lists the critical ranking of intermediate events of the system as per values of the F-V importance measure. For instance, the F-V measure of Encapsulation fault can be calculated as:
where is a probability of the intermediate event and is a probability of the top event. The probability of the top event is 0.552, which is calculated from Equation (29).

Table 13.
F-V Importance measure and criticality ranking of all intermediate events.
After the calculation of the IM factor of each intermediate event, criticality ranking will be provided under highly critical, medium, and low critical faults. Intermediate faults having criticality ranking 1 to 5 are the most critical, 6–7 are considered medium critical, and 8–14 are considered as low critical. From Table 13, no input to SPD, no input to fuse, fault in miniature circuit breaker, fault in PV module, and encapsulation fault are highly critical intermediate events with IM values 0.7934, 0.7932, 0.7921, 0.7921, 0.1032, respectively. At the same time, hot spot and junction box failure are medium critical events. An appropriate maintenance strategy could be developed to address all of the critical and essential intermediate events based on the ranking.
The overall PV system’s reliability is estimated using Equation (10), which is modified and calculated for 27 basic events as follows (Equation (33)):
A solar PV system’s reliability is 0.5601.
The solar PV system’s reliability, though, is lower than that of basic and intermediate events. As a result, it may be said that in a series configuration, the system reliability is lower than that of the least reliable component:
Therefore, it may be concluded that all components, especially if the system has a lot of components, should have high reliability.
4.4. Comparison of the Results Obtained by the Proposed Methodology with the Published Results
The criticality ranking for the intermediate events and the basic events obtained by the proposed methodology are presented in Table 14 and Table 15, respectively. It is observed from this comparative study that the proposed methodology provides a number and detailed faults associated with the solar PV system. Furthermore, the trends of the results obtained from the proposed methodology and the published results match. It can be concluded that the proposed methodology provides a detailed FTA and reliability analysis of solar PV systems with significant accuracy.

Table 14.
Comparison of criticality ranking of intermediate events obtained using the proposed methodology and published literature.

Table 15.
Comparison of criticality ranking of basic events obtained using proposed methodology and the published literature.
5. Conclusions and Future Works
A comprehensive and microlevel framework for failure data analysis and reliability model development using the Fault Tree Analysis (FTA) approach is developed in this paper. The Fault Tree (FT) for the DC side of a solar photovoltaic (PV) system is constructed using the data published in the literature. The system reliability model is developed using the median failure rates of 33 components/ faults. The median failure rates are estimated and used for system reliability modeling to overcome uncertainties that arises through extreme values and increase the accuracy of the model.
The results of the FTA show that the reliability/probability of non-occurrence of the top event, i.e., ‘No output or degraded output at Surge Protection Device (SPD)’ is 0.5601 per year. The solder bond failure, broken cell, broken interconnect, rack structure, grounding/lightening protection system, delamination, discoloration, and partial shading are the critical faults with a failure probability of 14.87%, 11.15%, 8.46%, 7.29%, 4.90%, 3.18%, 2.60%, and 0.88%, respectively. No input to SPD, no input to fuse, fault in miniature circuit breaker, and fault in a PV module are the critical intermediate events with a failure probability of 43.79%, 43.78%, 43.72%, 43.72%, and 5.69%, respectively. These findings will aid in the prediction and selection of the excellent spot in dynamic situations by the designer and operator of solar PV systems. It is recommended to develop an automatic fault detection and monitoring system for such critical faults. Special attention needs to be given to critical faults during preventive maintenance schedules, or a proper maintenance schedule needs to be prepared.
As for future work, the performance of the reliability model can be improved by considering the data collected from the field and integrating them with judgments collected from the experts in the field. A developed data analysis framework can be improved by incorporating a field failure data analysis approach and analyzing expert judgments using the fuzzy logic approach. The improved approach should be capable of developing an accurate model even in case of availability of limited or insufficient data. Automatic fault detection and diagnosis systems can be developed to address the identified critical faults, which significantly reduces output power and creates a huge economic loss. Hence, economic analysis of the PV system can be conducted.
Author Contributions
Conceptualization, P.R.S., S.B., R.B.P. and S.A.-D.; methodology, P.R.S., S.B., R.B.P. and S.A.-D.; software, P.R.S., S.B., R.B.P. and S.A.-D.; validation, P.R.S., S.B., R.B.P. and S.A.-D.; formal analysis, P.R.S., S.B., R.B.P. and S.A.-D.; investigation, P.R.S., S.B., R.B.P. and S.A.-D.; resources, P.R.S., S.B., R.B.P. and S.A.-D.; data curation, P.R.S., S.B., R.B.P. and S.A.-D.; writing—original draft preparation, P.R.S., S.B., R.B.P. and S.A.-D.; writing—review and editing, P.R.S., S.B., R.B.P. and S.A.-D.; visualization, P.R.S., S.B., R.B.P. and S.A.-D.; supervision, P.R.S., S.B., R.B.P. and S.A.-D.; project administration, P.R.S., S.B., R.B.P. and S.A.-D.; funding acquisition, R.B.P. and S.A.-D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in the literature and will be available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature & Abbreviations
| Failure probability | |
| Failure rate | |
| Mission time | |
| Importance measure of ith minimum cut set | |
| Probability of a top event | |
| Reliability of solar PV | |
| AC | Alternating Current |
| BDD | Binary Decision Diagram |
| BOS | Balance Of System |
| DBN | Dynamic Bayesian Network |
| DC | Direct Current |
| EVA | Ethylene Vinyl Acetate |
| FFTA | Fuzzy Fault Tree Analysis |
| FMEA | Failure Mode and Effect Analysis |
| FMECA | Failure Mode, Effects, and Criticality Analysis |
| FTA | Fault Tree Analysis |
| FT | Fault Tree |
| F-V | Fussel Vesely |
| GW | Gigawatt |
| HASS | Highly Accelerated Stress Screening |
| IEA | International Energy Agency |
| IM | Importance Measure |
| MCB | Miniature Circuit Breaker |
| MCS | Minimum Cut Set |
| MPPT | Maximum Power Point Tracking |
| MTTF | Mean Time To Failure |
| PV | Photovoltaic |
| PR | Performance Ratio |
| RAM | Reliability, Availability, Maintainability |
| RBD | Reliability Block Diagram |
| SHyFTA | Stochastic hybrid FTA |
| SMUD | Municipal Utility District |
| SPD | Surge Protection Device |
| TE | Top Event |
References
- IEA-Photovoltaic Power Systems Programme. Snapshot of Global PV Markets 2022; IEA: Paris, France, 2022. [Google Scholar]
- Wolfe, P. pv Magazine Group GmbH & Co. KG. 2021. Available online: https://www.pv-magazine.com/2021/09/23/the-worlds-largest-solar-parks/ (accessed on 1 January 2023).
- GlobalData. Global Solar Photovoltaic Capacity Expected to Exceed 1500GW by 2030, Says GlobalData. Available online: https://pes.eu.com/wind/global-solar-photovoltaic-capacity-expected-to-exceed-1500gw-by-2030-says-globaldata/ (accessed on 1 January 2023).
- Dhimish, M.; Ahmad, A.; Tyrrell, A.M. Inequalities in Photovoltaics Modules Reliability: From Packaging to PV Installation Site. Renew. Energy 2022, 192, 805–814. [Google Scholar] [CrossRef]
- Cristaldi, L.; Faifer, M.; Lazzaroni, M.; Khalil, M.M.A.F.; Catelani, M.; Ciani, L. Failure Modes Analysis and Diagnostic Architecture for Photovoltaic Plants. In Proceedings of the 13 th IMEKO TC10 Workshop on Technical Diagnostics Advanced Measurement Tools in Technical Diagnostics for Systems’ Reliability and Safety, Warsaw, Poland, 26–27 June 2014; pp. 186–191. [Google Scholar]
- Atsu, D.; Seres, I.; Aghaei, M.; Farkas, I. Analysis of Long-Term Performance and Reliability of PV Modules under Tropical Climatic Conditions in Sub-Saharan. Renew. Energy 2020, 162, 285–295. [Google Scholar] [CrossRef]
- Singh, R.; Sharma, M.; Yadav, K. Degradation and Reliability Analysis of Photovoltaic Modules after Operating for 12 Years: A Case Study with Comparisons. Renew. Energy 2022, 196, 1170–1186. [Google Scholar] [CrossRef]
- Aboagye, B.; Gyamfi, S.; Ofosu, E.A.; Djordjevic, S. Degradation Analysis of Installed Solar Photovoltaic (PV) Modules under Outdoor Conditions in Ghana. Energy Rep. 2021, 7, 6921–6931. [Google Scholar] [CrossRef]
- Quansah, D.A.; Adaramola, M.S. Comparative Study of Performance Degradation in Poly- and Mono-Crystalline-Si Solar PV Modules Deployed in Different Applications. Int. J. Hydrogen Energy 2018, 43, 3092–3109. [Google Scholar] [CrossRef]
- Cui, C.; Li, Z.; Zhang, J. Building a Prediction Model of Solar Power Generation Based on Improved Grey Markov Chain. Int. J. Glob. Energy Issues 2022, 44, 139–149. [Google Scholar] [CrossRef]
- Manohar, P.; Atla, C.R. Development of Predictive Reliability Model of Solar Photovoltaic System Using Stochastic Diffusion Process for Distribution System. IEEE J. Emerg. Sel. Top. Circuits Syst. 2022, 12, 279–289. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, K.; Tian, G.; Xu, G.; Zhao, H. Reliability Assessment of Power Generation System Using an Optimized State Enumeration Method. Recent Patents Eng. 2021, 16, 89–96. [Google Scholar] [CrossRef]
- Stember, L.H. Reliability Considerations in the Design of Solar Photovoltaic Power Systems. Sol. Cells 1981, 3, 269–285. [Google Scholar] [CrossRef]
- Nageh, M.; Abdullah, M.P.; Yousef, B. Reliability Evaluation and Cost Analysis for Optimized Large Scale Solar PV System. In Proceedings of the 2021 IEEE Industrial Electronics and Applications Conference (IEACon), Penang, Malaysia, 22–23 November 2021; pp. 195–200. [Google Scholar]
- Rajput, P.; Malvoni, M.; Kumar, N.M.; Sastry, O.S.; Tiwari, G.N. Risk Priority Number for Understanding the Severity of Photovoltaic Failure Modes and Their Impacts on Performance Degradation. Case Stud. Therm. Eng. 2019, 16, 100563. [Google Scholar] [CrossRef]
- Qadeer, A.; Huawei, L.; Ikram, M.T. Research on Reliability of Grid Connected Photovoltaic Renewable Generation System. IOP Conf. Ser. Earth Environ. Sci. 2021, 804, 032058. [Google Scholar] [CrossRef]
- Gupta, N.; Garg, R.; Kumar, P. Sensitivity and Reliability Models of a PV System Connected to Grid. Renew. Sustain. Energy Rev. 2017, 69, 188–196. [Google Scholar] [CrossRef]
- Chiacchio, F.; Famoso, F.; D’Urso, D.; Brusca, S.; Aizpurua, J.I.; Cedola, L. Dynamic Performance Evaluation of Photovoltaic Power Plant by Stochastic Hybrid Fault Tree Automaton Model. Energies 2018, 11, 306. [Google Scholar] [CrossRef]
- Sayed, A.; El-Shimy, M.; El-Metwally, M.; Elshahed, M. Reliability, Availability and Maintainability Analysis for Grid-Connected Solar Photovoltaic Systems. Energies 2019, 12, 1213. [Google Scholar] [CrossRef]
- Mishra, P.; Joshi, J. Reliability Estimation for Components of Photovoltaic Sysyems. Energy Stud. 1995, 37, 1371–1382. [Google Scholar]
- Theristis, M.; Papazoglou, I.A. Markovian Reliability Analysis of Standalone Photovoltaic Systems Incorporating Repairs. IEEE J. Photovolt. 2014, 4, 414–422. [Google Scholar] [CrossRef]
- Hu, R.; Mi, J.; Hu, T.; Fu, M.; Yang, P. Reliability Research for PV System Using BDD-Based Fault Tree Analysis. In Proceedings of the 2013 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE), Chengdu, China, 15–18 July 2013; pp. 359–363. [Google Scholar] [CrossRef]
- Charki, A.; Bigaud, D. Availability Estimation of a Photovoltaic System. In Proceedings of the 2013 Proceedings Annual Reliability and Maintainability Symposium (RAMS), Orlando, FL, USA, 28–31 January 2013; pp. 4–8. [Google Scholar] [CrossRef]
- Ghaedi, A.; Abbaspour, A.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M.; Othman, M. Reliability Evaluation of a Composite Power System Containing Wind and Solar Generation. In Proceedings of the 2013 IEEE 7th International Power Engineering and Optimization Conference (PEOCO), Langkawi, Malaysia, 3–4 June 2013; pp. 483–488. [Google Scholar] [CrossRef]
- Ahadi, A.; Ghadimi, N.; Mirabbasi, D. Reliability Assessment for Components of Large Scale Photovoltaic Systems. J. Power Sources 2014, 264, 211–219. [Google Scholar] [CrossRef]
- Colli, A. Failure Mode and Effect Analysis for Photovoltaic Systems. Renew. Sustain. Energy Rev. 2015, 50, 804–809. [Google Scholar] [CrossRef]
- Ahadi, A.; Hayati, H.; Miryousefi Aval, S.M. Reliability Evaluation of Future Photovoltaic Systems with Smart Operation Strategy. Front. Energy 2016, 10, 125–135. [Google Scholar] [CrossRef]
- Sulaeman, S.; Member, S.; Benidris, M. Modeling the Output Power of PV Farms for Power. In Proceedings of the 2015 North American Power Symposium (NAPS), Charlotte, NC, USA, 4–6 October 2015. [Google Scholar]
- Sayed, A.; EL-Shimy, M.; El-Metwally, M.; Elshahed, M. Impact of Subsystems on the Overall System Availability for the Large Scale Grid-Connected Photovoltaic Systems. Reliab. Eng. Syst. Saf. 2020, 196, 106742. [Google Scholar] [CrossRef]
- Mohd Nizam Ong, N.A.F.; Sadiq, M.A.; Md Said, M.S.; Jomaas, G.; Mohd Tohir, M.Z.; Kristensen, J.S. Fault Tree Analysis of Fires on Rooftops with Photovoltaic Systems. J. Build. Eng. 2022, 46, 103752. [Google Scholar] [CrossRef]
- Sulaeman, S.; Benidris, M.; Mitra, J. Modeling and Assessment of PV Solar Plants for Composite System Reliability Considering Radiation Variability and Component Availability. In Proceedings of the 2016 Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016. [Google Scholar] [CrossRef]
- Baschel, S.; Koubli, E.; Roy, J.; Gottschalg, R. Impact of Component Reliability on Large Scale Photovoltaic Systems’ Performance. Energies 2018, 11, 1579. [Google Scholar] [CrossRef]
- Fara, L.; Craciunescu, D. Reliability Analysis of Photovoltaic Systems for Specific Applications. Reliab. Ecol. Asp. Photovolt. Modul. 2020, 1–14. [Google Scholar] [CrossRef]
- Perveen, S.; Ashfaq, H.; Asjad, M. Reliability Assessment of Solar Photovoltaic Systems Based on Fuzzy Fault Tree Analysis. Life Cycle Reliab. Saf. Eng. 2019, 8, 129–139. [Google Scholar] [CrossRef]
- Zini, G.; Mangeant, C.; Merten, J. Reliability of Large-Scale Grid-Connected Photovoltaic Systems. Renew. Energy 2011, 36, 2334–2340. [Google Scholar] [CrossRef]
- Nemes, C.; Munteanu, F.; Rotariu, M.; Astanei, D. Availability Assessment for Grid-Connected Photovoltaic Systems with Energy Storage. In Proceedings of the 2016 International Conference and Exposition on Electrical and Power Engineering (EPE), Iasi, Romania, 20–22 October 2016; pp. 908–911. [Google Scholar] [CrossRef]
- El-Metwally, M.; Elshahed, M.; El-Shimy, M.; Sayad, A. Detailed Analyses of the Failure and Repair Rates of Wind and Solar-PV Systems for RAM Assessment Military Technical College Kobry El-Kobbah, Cairo, Egypt 11 Th International Conference on Electrical Engineering ICEENG 2018 Detailed Analyses of the Fail. In Proceedings of the International Conference on Electrical Engineering ICEENG 2018, Cairo, Egypt, 3–5 April 2018; pp. 3–5. [Google Scholar]
- Rajput, P.; Malvoni, M.; Sastry, O.S.; Tiwari, G.N. Failure Mode and Effect Analysis of Monocrystalline Silicon Photovoltaic Modules after 24 Years Outdoor Exposure in Semi-Arid Climate. AIP Conf. Proc. 2020, 2276, 020004. [Google Scholar] [CrossRef]
- Maish, A.B.; Atcitty, C.; Hester, S.; Greenberg, D.; Osborn, D.; Collier, D.; Brine, M. Photovoltaic System Reliability. Conf. Rec. IEEE Photovolt. Spec. Conf. 1997, 3, 1049–1054. [Google Scholar] [CrossRef]
- Jahn, U.; Nasse, W. Operational Performance of Grid-Connected PV Systems on Buildings in Germany. Prog. Photovoltaics Res. Appl. 2004, 12, 441–448. [Google Scholar] [CrossRef]
- Oozeki, T.; Yamada, T.; Kato, K.; Yamamoto, T. An Analysis of Reliability for Photovoltaic Systems on the Field Test Project for Photovoltaic in Japan. In Proceedings of ISES World Congress 2007 (Vol. I–Vol. V) Solar Energy and Human Settlement; Springer: Berlin/Heidelberg, Germany, 2007; Volume 3, pp. 1628–1632. [Google Scholar] [CrossRef]
- Collins, E.; Miller, S.; Stein, J.; Sorensen, R.; Granata, J.; Auintana, M. A Reliability and Availability Sensitivity Study of a Large Photovoltaic System. In Proceedings of the 25th European Photovoltaic Solar Energy Conference and Exhibition/5th World Conference on Photovoltaic Energy Conversion, Valencia, Spain, 6–10 September 2010; pp. 4463–4469. [Google Scholar]
- Golnas, A. PV System Reliability: An Operator’s Perspective. IEEE J. Photovoltaics 2013, 3, 416–421. [Google Scholar] [CrossRef]
- Causia Aguisti, F.; Musyafa’, A.; Khamim Asy’ari, M. Analysis of RAM (Reliability, Availability, Maintainability) Production of Electric Voltage from 48 v PV (Photovoltaic) at Pantai Baru Pandansimo, Indonesia. E3S Web Conf. 2020, 190, 00010. [Google Scholar] [CrossRef]
- Liu, Y. Reliability Analysis of Photovoltaic Module Based on Measured Data. IOP Conf. Ser.: Earth Environ. Sci. 2021, 793, 012019. [Google Scholar] [CrossRef]
- Stember, L.H.; Huss, W.R.; Bridgman, M.S. A Methodology for Photovoltaic System Reliability & Economic Analysis. IEEE Trans. Reliab. 1982, R-31, 296–303. [Google Scholar] [CrossRef]
- Huffman, D.L.; Antelme, F. Availability Analysis of a Solar Power System with Graceful Degradation. Proc. Annu. Reliab. Maintainab. Symp. 2009, 348–352. [Google Scholar] [CrossRef]
- Cai, B.; Liu, Y.; Ma, Y.; Huang, L.; Liu, Z. A Framework for the Reliability Evaluation of Grid-Connected Photovoltaic Systems in the Presence of Intermittent Faults. Energy 2015, 93, 1308–1320. [Google Scholar] [CrossRef]
- Simon, D.F.; Teixeira, M.; da Costa, J.P. Availability Estimation in Photovoltaic Generation Systems Using Timed Petri Net Simulation Models. Int. J. Electr. Power Energy Syst. 2022, 137, 106897. [Google Scholar] [CrossRef]
- Spertino, F.; Amato, A.; Casali, G.; Ciocia, A.; Malgaroli, G. Reliability Analysis and Repair Activity for the Components of 350 Kw Inverters in a Large Scale Grid-Connected Photovoltaic System. Electronics 2021, 10, 564. [Google Scholar] [CrossRef]
- Li, T.; Tao, S.; Zhang, R.; Liu, Z.; Ma, L.; Sun, J.; Sun, Y. Reliability Evaluation of Photovoltaic System Considering Inverter Thermal Characteristics. Electronics 2021, 10, 1763. [Google Scholar] [CrossRef]
- Luo, W.; Khoo, Y.S.; Hacke, P.; Jordan, D.; Zhao, L.; Ramakrishna, S.; Aberle, A.G.; Reindl, T. Analysis of the Long-Term Performance Degradation of Crystalline Silicon Photovoltaic Modules in Tropical Climates. IEEE J. Photovolt. 2019, 9, 266–271. [Google Scholar] [CrossRef]
- Ostovar, S.; Esmaeili-Nezhad, A.; Moeini-Aghtaie, M.; Fotuhi-Firuzabad, M. Reliability Assessment of Distribution System with the Integration of Photovoltaic and Energy Storage Systems. Sustain. Energy Grids Netw. 2021, 28, 100554. [Google Scholar] [CrossRef]
- Hamdy, M.A.; Beshir, M.E.; Elmasry, S.E. Reliability Analysis of Photovoltaic Systems. Appl. Energy 1989, 33, 253–263. [Google Scholar] [CrossRef]
- Cristaldi, L.; Khalil, M.; Soulatiantork, P. A Root Cause Analysis and a Risk Evaluation of PV Balance of Systems Failures. Acta IMEKO 2017, 6, 113–120. [Google Scholar] [CrossRef]
- Yan, W.; Liu, W.; Kong, W. Reliability Evaluation of PV Modules Based on Exponential Dispersion Process. Energy Rep. 2021, 7, 3023–3032. [Google Scholar] [CrossRef]
- Xiao, H.; Lin, C.; Kou, G.; Peng, R. Reliability Modeling and Configuration Optimization of a Photovoltaic Based Electric Power Generation System. Reliab. Eng. Syst. Saf. 2022, 220, 108285. [Google Scholar] [CrossRef]
- Hefaidh, H.; Mébarek, D.; Belkhir, N.; Driss, Z. Reliability Degradation Prediction of Photovoltaic Modules Based on Dependability Methods. Int. J. Qual. Reliab. Manag. 2021, 40, 478–495. [Google Scholar] [CrossRef]
- Ruijters, E.; Stoelinga, M. Fault Tree Analysis: A Survey of the State-of-the-Art in Modeling, Analysis and Tools. Comput. Sci. Rev. 2015, 15, 29–62. [Google Scholar] [CrossRef]
- Gupta, S.; Bhattacharya, J. Reliability Analysis of a Conveyor System Using Hybrid Data. Qual. Reliab. Eng. Int. 2007, 23, 867–882. [Google Scholar] [CrossRef]
- Cristaldi, L.; Khalil, M.; Faifer, M.; Soulatiantork, P. Markov Process Reliability Model for Photovoltaic Module Encapsulation Failures. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications (ICRERA), Palermo, Italy, 22–25 November 2015; 5, pp. 203–208. [Google Scholar] [CrossRef]
- Ferdous, R.; Khan, F.I.; Veitch, B.; Amyotte, P.R. Methodology for Computer-Aided Fault Tree Analysis. Process Saf. Environ. Prot. 2007, 85, 70–80. [Google Scholar] [CrossRef]
- Lavasani, S.M.; Zendegani, A.; Celik, M. An Extension to Fuzzy Fault Tree Analysis (FFTA) Application in Petrochemical Process Industry. Process Saf. Environ. Prot. 2015, 93, 75–88. [Google Scholar] [CrossRef]
- Prasanna, R.; Karthik, C.; Chowdhury, S.; Khan, B. Comprehensive Review on Modelling, Estimation, and Types of Faults in Solar Photovoltaic System. Int. J. Photoenergy 2022, 2022, 3053317. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).