Abstract
This study explores the influence of an inclined magnetic field and variable viscosity on the entropy generation in steady flow of a couple stress fluid in an inclined channel. The walls of the channel are stationary and non-isothermal. The fluid flow is driven due to pressure gradient and gravitational force. Reynold’s model for temperature-dependent viscosity was used. The dimensionless, non-linear coupled equations of momentum and energy was solved, and we obtained an analytical solution for the velocity and temperature fields. The entropy generation and Bejan number were evaluated. The variation of pertinent parameters on flow quantities was discussed graphically. The rate of volume flow, skin friction coefficient, and Nusselt number at the surfaces of the channel were calculated and their variations were discussed through surface graphs. From the results, it is noticed that the entropy generation rate can be minimized by increasing the magnetic field and the temperature difference parameters. The findings of the current study in some special cases are in precise agreement with the previous investigation.
1. Introduction
In the last few years, heat transfer in magnetohydrodynamic (MHD) flows is becoming an interesting topic of fluid dynamics due to its important applications. For example, such flows are characteristic of the engineering and industrial fields, such as metallurgical manufacturing, several materials processing methods [1,2], MHD energy production, chemical manufacturing, and synthesis of magnetic liquids [3,4,5]. Newtonian or non-Newtonian fluids can be used. One of the non-Newtonian fluids is the couple stress fluid, which was introduced by Stokes in 1966 [6]. Numerous studies have been conducted with a couple stress fluid using various geometries. Furthermore, entropy analysis may be used to assess the thermodynamic irreversibility of any fluid flow. A measurement of the intensity of irreversibility connected to actual processes is provided by entropy production. The minimization of the entropy production rate is needed to optimize the performance of thermal appliances such as heat exchangers, heat pump system, and refrigerators [7]. To evaluate the origins of irreversibility in components and systems, several studies have been published.
Ahmed et al. [8] carried out a theoretical study of electrically conducting couple stress fluid by an oscillatory viscous flow with heat transfer being affected by convection and MHD, which has significant applications in manufacturing electro-conductive polymers and liquids. Srinivas et al. [9] used an asymmetrically parallel plate to examine the entropy production rate on a couple stress fluid flow by the simultaneous result of the varying thermal conductivity and viscosity. Ajaz [10] discussed the influence of peristaltic flow with heat and mass transfer in a couple stress fluid when an inclined magnetic field is applied. Pei-Ying et al. [11] examined the velocity and temperature distributions by taking the collective results of variable thermal conductivity and viscosity in the appearance of hafnium nanoparticles with thermal radiation effect and a magnetic field. Ajala et al. [12] studied the effect of variable viscosity and thermal radiation on the 2-D flow of boundary layer with heat transfer in the existing magnetic field. Falade et al. [13] analyzed the minimizing of the entropy production rate under the result of temperature-dependent viscosity and couple stress fluid due to the heated channel. Ramesh [14] and Swarnalathamma et al. [15] scrutinized the consequence of heat transfer on the peristaltic flow of a couple stress fluid with MHD and a porous medium and studied the impacts of the emerging parameters on the peristaltic pumping rate, frictional forces, velocity, temperature, pressure gradient, and concentration fields. Divya et al. [16] presented the combined impact of temperature-dependent viscosity and thermal conductivity on the MHD peristaltic flow of the Bingham fluid in a porous medium with heat transfer and studied the effects on temperature, heat transfer coefficient, and pumping rate. Hayat et al. [17] examined the significant impacts of heat transfer on the fields of temperature, velocity, and concentration by the peristaltic flow of the Williamson fluid under the case of convection and magnetic field. Abbasi et al. [18,19] explored the heat transfer effect on non-Newtonian fluids using peristaltic flow with the conditions of Joule heating and viscous dissipation in an inclined magnetic field. The former has variable viscosity and a porous medium and latter took two types of non-Newtonian fluid. Both studied the impacts of embedded variables on pressure gradient, velocity, temperature, and size of a trapped bolus. Sathish et al. [20] explored the consequence of heat transfer on the squeezing flow of the Casson fluid accompanied by an aligned magnetic field and studied the results of several emerging parameters on velocity and temperature fields. Samuel et al. [21,22] presented the entropy production in a couple stress fluid flow with heat transfer to an inclined plate. The former is affected by porosity, whereas the latter is affected by a magnetic field; the variations in thermophysical parameters for velocity, temperature, entropy production, and Bejan number were examined. Ganji et al. [23] examined the entropy production on the Hagen–Poiseuille flow of viscous fluid within a circular pipe due to the variable viscosity and heat transfer. Numerous studies have been conducted on non-Newtonian fluids with heat and mass transfer under different effects and flows, in a porous medium and a magnetic field [24,25,26,27]. These studies have examined the impacts of pertinent parameters on concentration, velocity, volumetric flux and temperature fields. Manjunatha et al. [28] explored the heat transfer enhancement of the hybrid nanofluid due to natural convection and variable viscosity accompanied by a magnetic field. They examined the impacts on boundary layer thickness, velocity, and temperature fields in both hybrid and regular nanofluids and found that in the heat transfer process, the hybrid nanofluid flow is more effective than the regular nanofluid flow. Roja et al. [29] conducted a theoretical analysis of the nature of velocity and temperature profiles under the Hall and Ion impacts on a couple stress nanofluid flow subjected to heat generation, thermal radiations, and hydraulic slip. Hayat et al. [30] presented the third-grade fluid flow subjected to heat source, heat sink, and variable thermal conductivity, influenced by heat transfer and magnetic field, Sajjad et al. [31] discussed the significance of heat transfer on viscous fluid flow with MHD in a non-Darcy porous medium and analyzed velocity and temperature distributions graphically considered heat generation/absorption, variable porosity, permeability, and thermal conductivity. Makinde [32] analytically studied volumetric entropy generation and the Bejan number with variable viscosity. Makinde et al. [33] conducted a numerical investigation on heat and mass transfer in nanofluids in the Poiseuille–Couette flow with Hall effects and variable viscosity due to MHD. Disu et al. [34] studied the heat transfer impact of the free convection flow on radiative MHD viscous fluid with effects of heat source and variable viscosity via a porous medium using the differential transform method (DTM). Makinde et al. [35] used a numerical method to examine the impacts of MHD and heat transport on the chemically reacting convective flow of a conducting fluid with variable viscosity and porous medium and studied the significant results on the concentration, velocity, and temperature distributions. Finally, it is worth mentioning here that many other researchers have investigated the role of the nanofluids and the hybrid nanofluids on the heat transfer enhancement in different geometries along with the impact of different physical parameters [36,37,38,39,40,41,42,43,44,45,46,47,48].
The current work focuses on the minimization of entropy generation in a couple stress fluid accompanied by temperature-dependent viscosity and an aligned magnetic field in an inclined channel. In view of the above literature, no attempt has been made to investigate the heat transfer for the aforementioned characteristics. To attain the aim of this study, the regular perturbation technique was used to solve the governing equations for the velocity and temperature distributions. The problem discussed, graphically exhibits the variation of emerging parameters.
2. Outline of the Problem
Take into consideration a couple stress fluid flowing steadily along an infinitely long inclined channel that is inclined at an angle from the surface where irreversible heat transfer occurs. The channel has a height of with stable walls on either side. A uniformly inclined intensity magnetic field is provided at an angle to the direction of the fluid flow. The fluid runs through the force of gravity and pressure gradient. At the lower and upper walls, the temperatures were obtained as and respectively, where . According to Figure 1, the Cartesian coordinate system has been set up so that the x-axis runs parallel to the direction of the fluid flow and the y-axis runs perpendicular to it.
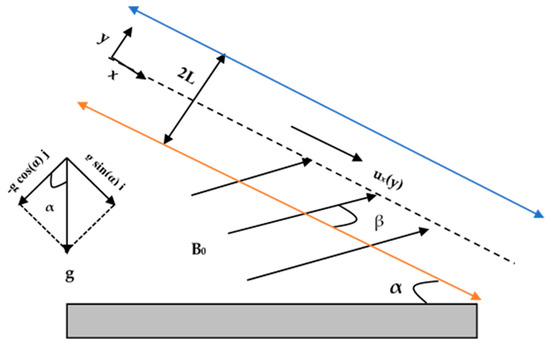
Figure 1.
Flow model of the problem.
The fields of velocity and temperature are provided as [9,13]:
Using the above scheme, we observed that the equation of continuity has been satisfied and the equation of momentum and energy becomes
The boundary conditions are
where
The temperature-dependent viscosity by Reynold’s model [32,34,49,50,51] is given by
The following introduces the non-dimensional parameters:
where is the pressure gradient parameter, i.e., , and is the gravitational parameter, i.e., . The non-dimensional form of Equations (2) and (3) become (eliminate asterisks)
and the boundary condition (4) becomes
3. Method of Solution
3.1. Derived Equations
The full extended derived long equations are listed in the Appendix A. First we derive the velocity and temperature and then we use the results to obtain the entropy generation rate. The non-dimensional form of Equation (5) is
Using Taylor’s series expansion [37], Equation (10) can be linearized as
Substitute Equation (11) in Equations (7) and (8) are transformed in the following form
where . To solve the above non-linear coupled equations, the perturbation method was used. Assuming that viscosity parameter is a perturbation parameter where , then the velocity and temperature distributions are of the following form
Substituting Equation (14) in Equations (9), (12), and (13) and splitting each approximate order gives:
3.1.1. Zeroth Order Equations
3.1.2. First Order Equations
Solving the equations for the zeroth order and first order with their corresponding boundary conditions, where and , has been given in the Appendix A.
Volume flux, Skin friction and Nusselt number on the walls:
The volume flux is
The non-dimensional form of skin friction and the Nusselt number at both the plates are given by
3.1.3. Rate of Entropy Generation Analysis
Heat transfer to fluid flow with variable viscosity is irreversible. As a result of the exchange of energy and momentum among the fluid particles in the channel, entropy generation becomes continuous. The total entropy generation within the fluid can be expressed as [13]
The non-dimensional form of equation (23) is
The entropy generation has been divided in two parts
where signifies the heat transfer irreversibility and signifies the irreversibility due to fluid friction or viscous dissipation. The Bejan number is defined as the irreversibility distribution ratio and is mathematically expressed as
Clearly, heat transfer irreversibility dominates when , and viscous dissipation irreversibility dominates when .
3.2. Deductions
3.2.1. In the Absence of Couple Stress Fluid
The non-dimensional forms of Equations (7), (8), and (24) become
and the boundary condition in Equation (9) becomes
The following are the obtained expressions of velocity and temperature distributions
3.2.2. In the absence of Magnetic field (M = 0)
The non-dimensional forms of Equations (7), (8), and (24) become
and the boundary condition in Equation (9) becomes
The velocity and temperature solutions are acquired as
3.2.3. In the Absence of Couple Stress Fluid and Magnetic Field
The non-dimensional forms of Equations (7), (8), and (24) become
and the boundary condition in Equation (9) becomes
The velocity and temperature solutions are acquired as
3.3. Validation
The present study with and by using the transformation , exactly validates the results of O D Makinde [32]. The non-dimensional forms of Equations (39)–(41) coincide with Equations (8), (10), and (23), and also using the transformation coincides with the boundary conditions of O D Makinde [32].
4. Results and Discussion
This study represents the MHD analysis of heat transfer in couple stress fluid flow with temperature-dependent viscosity in an inclined channel, and discusses the effects of pressure gradient force, the Hartmann number, the viscosity parameter, the Brinkman number, the couple stress parameter, and the angle of inclinations on velocity, temperature, rate of entropy generation, and the Bejan number distributions graphically. Figure 2a–d represent the variation of the Brinkman number . Figure 2a,b clearly depicts that velocity and temperature fields increase as increases because is the ratio of heat generation by viscous dissipation to the heat transported by molecular conduction. The higher the value of , the larger the heat generation caused by viscous dissipation, and hence, the velocity and temperature rise. Figure 2c shows that the rate of entropy increases as increases because is a source of heat production within the moving fluid particles. Figure 2d represents the Bejan number decreasing as increases. Figure 3a–d shows the variation of the Hartmann number .
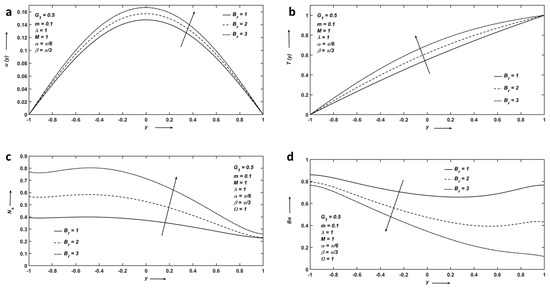
Figure 2.
(a) Velocity; (b) Temperature; (c) Entropy; and (d) Bejan number profiles affected by Brinkman number.
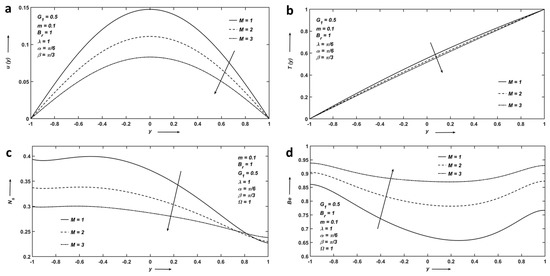
Figure 3.
(a) Velocity; (b) Temperature; (c) Entropy; and (d) Bejan number profiles affected by Hartmann number.
Figure 3a,b represents that velocity and temperature distributions decrease as increases. This is because the Hartmann number is the ratio between the Lorentz force and the viscous force. The higher the value of , the larger the Lorentz force, and the Lorentz force is the retardation force, which works against the fluid flow, and hence, shrink the velocity and temperature distributions. Figure 3c shows the influence of on the rate of entropy generation. decreases as increases because the fluid’s particles collectively slow the flow efficiency and reduce entropy. Figure 3d shows that increases as increases. This is because as increases, viscous force decreases, which will decrease the irreversibility due to fluid friction, and hence, increases.
Figure 4a–d represents the variation of the couple stress parameter . Figure 4a depicts that increasing reduces the rotating motion of fluid particles, giving sufficient strength to overcome the frictional resistance inside the fluid, and hence, velocity increases. Figure 4b portrays that as increases, the temperature is enhanced because of the viscous heating of the fluid particles within the flow channel. Figure 4c illustrates the rate of entropy. Figure 4d illustrates that when increases, the temperature increases; the heat irreversibility due to fluid friction, and hence , decrease.
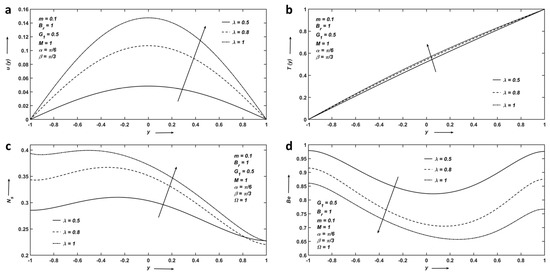
Figure 4.
(a) Velocity; (b) Temperature; (c) Entropy; and (d) Bejan number profiles affected by couple stress parameter.
Figure 5a–d represents the variation of the viscosity parameter . Figure 5a shows that with an increase in , a velocity profile reaches its maximum at the centerline of the channel and decreases at the vicinity of both plates. Figure 5b portrays that the higher the value of , the larger the viscous dissipation, and hence, the temperature increases. Figure 5c shows that entropy enhances as increases around the centerline. It can be seen that fluid friction predominates close to the upper surface of the channel, whereas irreversible heat transfer prevails around the centerline. The influence on is displayed in Figure 5d.
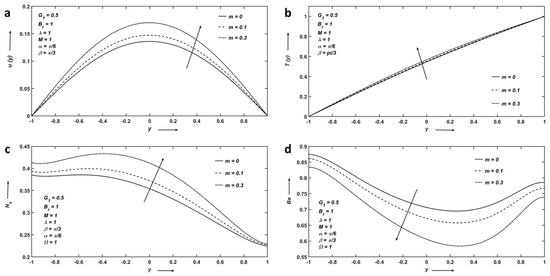
Figure 5.
(a) Velocity; (b) Temperature; (c) Entropy; and (d) Bejan number profiles affected by viscosity parameter.
Figure 6a–d exhibits the variation in flow quantities by varying the angle of inclined channel . In Figure 6a-6b, it is evident that velocity and temperature profiles are enhanced with the increment of because the channel will be vertical with the increase in , due to which fluid-driven force rises. Additionally, this increases the entropy, displayed in Figure 6c. If the channel is vertical, the velocity and temperature reach a maximum at the centerline of the channel. Figure 6d shows that decreases because the higher the value of the greater the fluid-driven force, which will increase the irreversibility due to fluid friction, and hence, decreases.
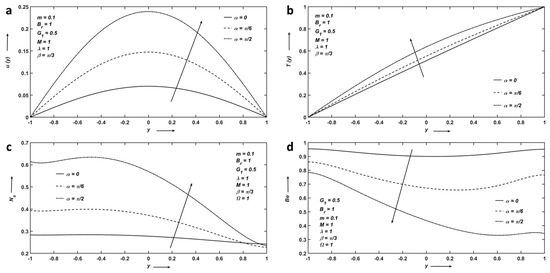
Figure 6.
(a) Velocity; (b) Temperature; (c) Entropy; and (d) Bejan number profiles affected by angle of inclined channel.
Figure 7a–d represents the variation of pressure gradient parameter . Clearly, the velocity and temperature distributions increase as increases. Figure 7c exhibits that as increases, entropy increases because the fluid friction irreversibility dominates and then declines gently around the upper surface of the channel. In Figure 6d, declines because the higher the value of the stronger the fluid driving force, which increases the irreversibility due to fluid friction, and therefore, drops.
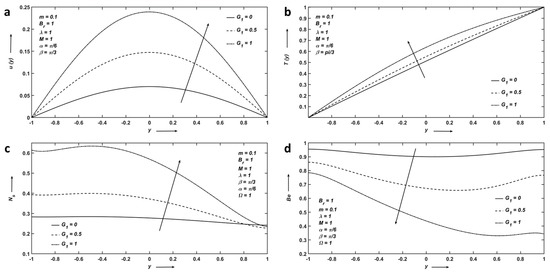
Figure 7.
(a) Velocity; (b) Temperature; (c) Entropy; and (d) Bejan number profiles affected by pressure gradient parameter.
Figure 8a–d depicts the impact of the angle of inclined magnetic field . Velocity and temperature decrease because increasing an angle of the applied magnetic field, enhances the intensity of the Lorentz force such that it slows down the fluid flow. Figure 8c shows that decreases as increases because the fluid’s particles collectively slow the flow efficiency and reduce entropy. The influence on is displayed in Figure 8d.
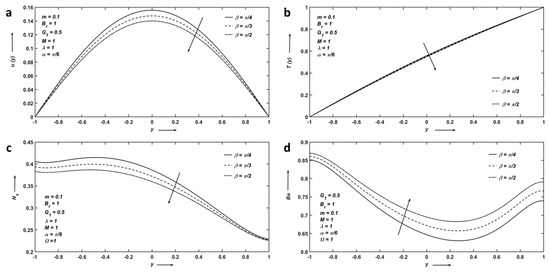
Figure 8.
(a) Velocity; (b) Temperature; (c) Entropy; and (d) Bejan number profiles affected by angle of inclined magnetic field.
Figure 9a–b exhibits the variation of the temperature difference parameter. Figure 9a depicts that entropy decreases as increases because fluid friction irreversibility dominates, which reduces the flow rate, and hence, entropy decelerates. Figure 9b shows that the Bejan number increases due to a reduction in the effect of fluid friction irreversibility.
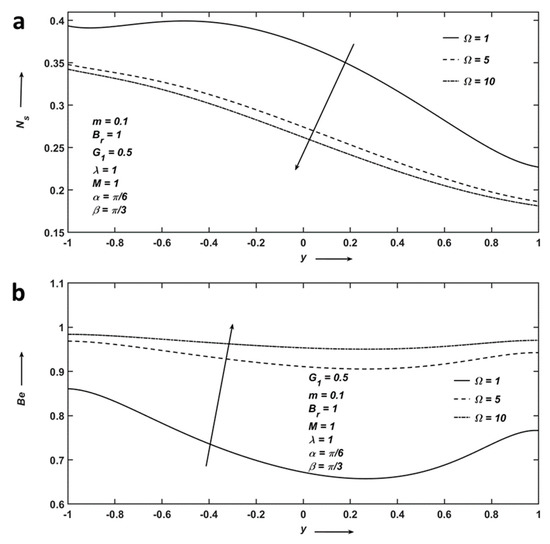
Figure 9.
(a) Entropy and (b) Bejan number profiles affected by temperature difference parameter.
Table 1 summarizes that the results of the present study for M = λ = 0 can be compared with the existing results of O D Makinde. The present results of velocity and temperature are found to be consistent with the previous study regarding all considered values of the Brinkman number. The table shows the comparison values for and at y = 0.5, and both distributions increase by varying the values of Br because the greater the value of Br the higher the heat production produced by viscous dissipation, and therefore, the increase in velocity and temperature.

Table 1.
Comparison of and by considering and .
Our present results were plotted along with the data obtained from the O D Makinde study [32] in Figure 10 and Figure 11. Figure 10 and Figure 11 represent the comparison between the present study and the deduction part, where the channel is horizontal and both the magnetic field and couple stress are absent, i.e., using the transformation . The results of the velocity and temperature profiles for varying Brinkman number and pressure gradient parameter coincide exactly with the already published investigation by O D Makinde [32].
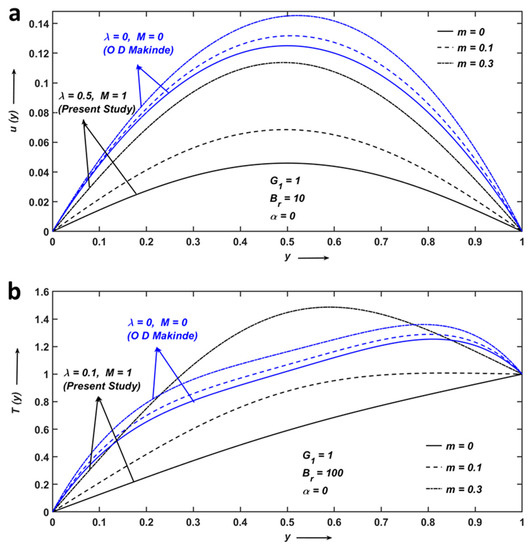
Figure 10.
Comparison between present study and O D Makinde [32] for (a) velocity and (b) temperature profiles on the non-dimensional viscosity parameter m.
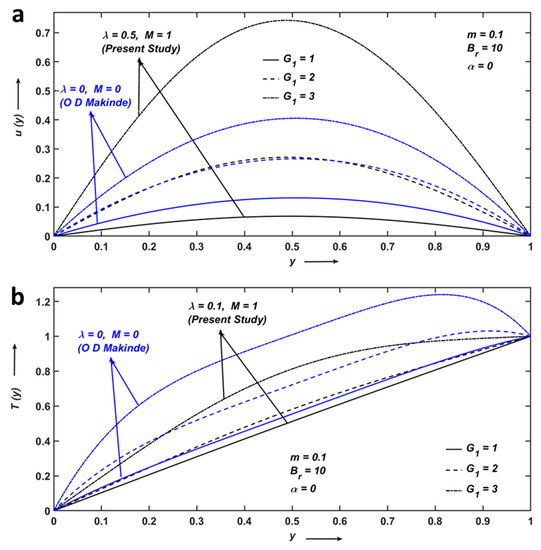
Figure 11.
Comparison between present study and O D Makinde [32] for (a) velocity and (b) temperature profiles on pressure gradient parameter G1.
Figure 12 shows that the rate of the volume flow increases as and increase because heat generation by viscous dissipation increases, which yields an enhancement of the volume flow. In Figure 13a–b we observe that when both and simultaneously increase and when one of the parameters varies while the other remains constant, then the velocity is enhanced, which increases the friction between the surface and the fluid flow, and hence, skin friction at both the surfaces of the channel increases. Figure 14a–b depicts that when both and simultaneously increase, and when one of the parameters varies while the other is constant, then the Nusselt number at both the surfaces of the channel increases because the temperature gradient rises, and thus, heat transfer irreversibility due to convection is more dominant.
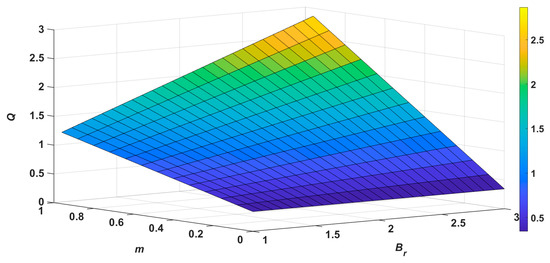
Figure 12.
Surface graph for volume flux.
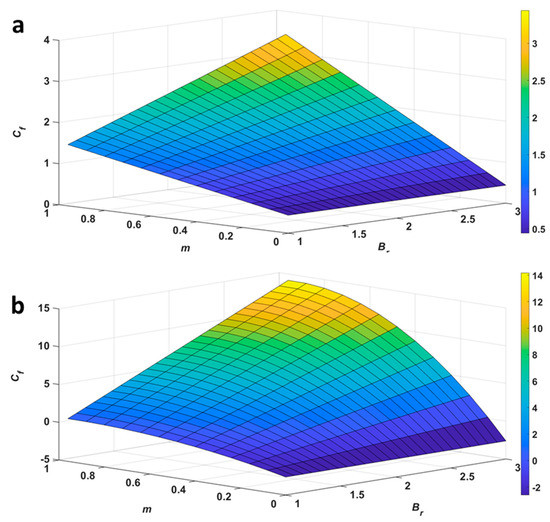
Figure 13.
Surface graph for skin friction at the (a) lower and (b) upper wall of the channel.
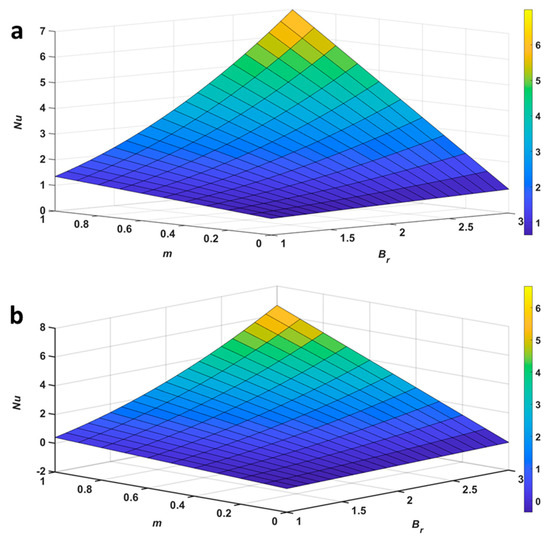
Figure 14.
Surface graph for Nusselt number at the (a) lower and (b) upper plate of the channel.
5. Conclusions
In this study, the heat transfer impacts have been analyzed in the steady flow of a couple stress fluid with MHD actions, and the temperature-dependent viscosity has also been analyzed through an inclined channel, and the applied magnetic field was taken as inclined. Graphical explanations were provided for the effects of the parameters on the MHD heat transfer. The following are the primary conclusions of this analysis:
- Velocity and temperature distributions increase as the viscosity variation parameter, couple stress parameter, pressure gradient parameter, Brinkman number, and angle of inclined channel expand.
- By enhancing the Hartmann number and angle of the inclined magnetic field parameter, velocity, and temperature distributions decline.
- The entropy production increases as the viscosity variation parameter, couple stress parameter, pressure gradient parameter, Brinkman number, and the angle of an inclined channel are enhanced.
- The entropy production decreases as the Hartmann number, temperature difference parameter, and angle of inclined magnetic field parameter increase.
- The Bejan number decreases as the viscosity variation parameter, couple stress parameter, pressure gradient parameter, Brinkman number, and angle of the inclined channel increase.
- The Hartmann number, angle of inclined magnetic field parameter, and temperature difference parameter increase the Bejan number.
Author Contributions
Conceptualization, W.A.-K. and S.S.K.R.; methodology, G.S., B.N.H., S.S.K.R., S.V.K.V. and W.A.-K.; software, S.S.K.R. and S.V.K.V.; validation, S.S.K.R. and W.A.-K.; formal analysis, B.N.H. and G.S.; resources, N.M.; data curation, S.V.K.V.; writing—original draft preparation, G.S.; writing—review and editing, H.M., K.B., B.N.H., H.M. and W.A.-K.; supervision, S.S.K.R.; project administration, N.M.; funding acquisition, G.S. and H.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The manuscript has no associated data.
Acknowledgments
One of the authors (Geetika Saini) would like to show her sincere thanks to CSIR-UGC for the financial support under the grant No.—09/1313(0001)/2020-EMR-I.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| width of the channel | |
| Brinkman number | |
| dimensional fluid velocity | |
| gravitational force | |
| non-dimensional fluid velocity | |
| Reference velocity | |
| dynamic pressure | |
| non-dimensional entropy | |
| dimensional temperature | |
| Hartmann number | |
| Dimensional Entropy generation | |
| non-dimensional temperature | |
| non-dimensional viscosity parameter | |
| Bejan number | |
| dimensional couple stress parameter | |
| Thermal conductivity | |
| electrical conductivity | |
| dimensional viscosity | |
| constant density | |
| non-dimensional couple stress parameter | |
| Reference viscosity | |
| Temperature difference parameter | |
| angle of inclination of channel | |
| angle of inclined magnetic field |
Appendix A
References
- Seddeek, M.A. Heat and mass transfer on a stretching sheet with a magnetic field in a visco-elastic fluid flow through a porous medium with heat source or sink. Comput. Mater. Sci. 2007, 38, 781–787. [Google Scholar] [CrossRef]
- Mansour, M.; El-Hakiem, M.; El Kabeir, S. Heat and mass transfer in magnetohydrodynamic flow of micropolar fluid on a circular cylinder with uniform heat and mass flux. J. Magn. Magn. Mater. 2000, 220, 259–270. [Google Scholar] [CrossRef]
- Bég, O.A.; Bakier, A.; Prasad, V.; Zueco, J.; Ghosh, S. Nonsimilar, laminar, steady, electrically-conducting forced convection liquid metal boundary layer flow with induced magnetic field effects. Int. J. Therm. Sci. 2009, 48, 1596–1606. [Google Scholar] [CrossRef]
- Tashtoush, B. Magnetic and buoyancy effects on melting from a vertical plate embedded in saturated porous media. Energy Convers. Manag. 2005, 46, 2566–2577. [Google Scholar] [CrossRef]
- El-Amin, M. Magnetohydrodynamic free convection and mass transfer flow in micropolar fluid with constant suction. J. Magn. Magn. Mater. 2001, 234, 567–574. [Google Scholar] [CrossRef]
- Stokes, V.K. Couple Stresses in Fluids. Phys. Fluids 1966, 9, 1709. [Google Scholar] [CrossRef]
- Cheng, X.-T.; Liang, X.-G. Role of entropy generation minimization in thermal optimization. Chin. Phys. B 2017, 26, 120505. [Google Scholar] [CrossRef]
- Ahmed, S.; Bég, O.A.; Ghosh, S. A couple stress fluid modeling on free convection oscillatory hydromagnetic flow in an inclined rotating channel. Ain Shams Eng. J. 2014, 5, 1249–1265. [Google Scholar] [CrossRef]
- Jangili, S.; Adesanya, S.O.; Ogunseye, H.A.; Lebelo, R. Couple stress fluid flow with variable properties: A second law analysis. Math. Methods Appl. Sci. 2019, 42, 85–98. [Google Scholar] [CrossRef]
- Dar, A.A.; Elangovan, K. Influence of an inclined magnetic field on heat and mass transfer of the peristaltic flow of a couple stress fluid in an inclined channel. World J. Eng. 2017, 14, 7–18. [Google Scholar] [CrossRef]
- Xiong, P.-Y.; Nazeer, M.; Hussain, F.; Khan, M.I.; Saleem, A.; Qayyum, S.; Chu, Y.-M. Two-phase flow of couple stress fluid thermally effected slip boundary conditions: Numerical analysis with variable liquids properties. Alex. Eng. J. 2021, 61, 3821–3830. [Google Scholar] [CrossRef]
- Ajala, O.A.; Aselebe, L.O.; Abimbade, S.F.; Ogunsola, A.W. Effects of magnetic Fields on the Boundary Layer Flow of Heat Transfer with variable Viscosity in the presence of Thermal Radiation. Int. J. Sci. Res. Publ. 2019, 9, 13–19. [Google Scholar] [CrossRef]
- Falade, J.; Adesanya, S.; Ukaegbu, J.; Osinowo, M. Entropy generation analysis for variable viscous couple stress fluid flow through a channel with non-uniform wall temperature. Alex. Eng. J. 2016, 55, 69–75. [Google Scholar] [CrossRef]
- Ramesh, K. Influence of heat and mass transfer on peristaltic flow of a couple stress fluid through porous medium in the presence of inclined magnetic field in an inclined asymmetric channel. J. Mol. Liq. 2016, 219, 256–271. [Google Scholar] [CrossRef]
- Swarnalathamma, B.V.; Krishna, M.V. Peristaltic hemodynamic flow of couple stress fluid through a porous medium under the influence of magnetic field with slip effect. AIP Conf. Proc. 2016, 1728, 020603. [Google Scholar] [CrossRef]
- Divya, B.B.; Manjunatha, G.; Rajashekhar, C.; Vaidya, H.; Prasad, K.V. Effects of Inclined Magnetic Field and Porous Medium on Peristaltic Flow of a Bingham Fluid with Heat Transfer. J. Appl. Comput. Mech. 2021, 7, 1892–1906. [Google Scholar] [CrossRef]
- Hayat, T.; Bibi, S.; Rafiq, M.; Alsaedi, A.; Abbasi, F. Effect of an inclined magnetic field on peristaltic flow of Williamson fluid in an inclined channel with convective conditions. J. Magn. Magn. Mater. 2016, 401, 733–745. [Google Scholar] [CrossRef]
- Abbasi, F.M.; Hayat, T.; Ahmad, B. Hydromagnetic Peristaltic Transport of Variable Viscosity Fluid with Heat Transfer and Porous Medium. Appl. Math. Inf. Sci. 2016, 10, 2173–2181. [Google Scholar] [CrossRef]
- Abbasi, F.; Hayat, T.; Alsaedi, A. Effects of inclined magnetic field and Joule heating in mixed convective peristaltic transport of non-Newtonian fluids. Bull. Pol. Acad. Sci. Tech. Sci. 2015, 63, 501–514. [Google Scholar] [CrossRef]
- Effect of Aligned Magnetic Field on MHD Squeezing Flow of Casson Fluid between Parallel Plates | Scientific.Net. Available online: https://www.scientific.net/DDF.384.1 (accessed on 4 December 2022).
- Adesanya, S.O.; Onanaye, A.; Adeyemi, O.; Rahimi-Gorji, M.; Alarifi, I.M. Evaluation of heat irreversibility in couple stress falling liquid films along heated inclined substrate. J. Clean. Prod. 2019, 239, 117608. [Google Scholar] [CrossRef]
- Adesanya, S.O.; Dairo, O.; Yusuf, T.; Onanaye, A.; Arekete, S. Thermodynamics analysis for a heated gravity-driven hydromagnetic couple stress film with viscous dissipation effects. Phys. A Stat. Mech. Appl. 2020, 540, 123150. [Google Scholar] [CrossRef]
- Ganji, D.D.; Nezhad, H.R.A.; Hasanpour, A. Effect of variable viscosity and viscous dissipation on the Hagen-Poiseuille flow and entropy generation. Numer. Methods Partial. Differ. Equations 2011, 27, 529–540. [Google Scholar] [CrossRef]
- Ahmed, N. Heat and Mass Transfer in MHD Poiseuille Flow with Porous Walls. J. Eng. Phys. Thermophys. 2019, 92, 122–131. [Google Scholar] [CrossRef]
- Mopuri, O.; Kodi, R.; Ganteda, C.; Srikakulapu, R.; Lorenzini, G. MHD Heat and Mass Transfer Steady Flow of a Convective Fluid through a Porous Plate in The Presence of Diffusion Thermo and Aligned Magnetic Field. J. Adv. Res. Fluid Mech. Therm. Sci. 2022, 89, 62–76. [Google Scholar] [CrossRef]
- Krishna, M.V.; Anand, P.V.S.; Chamkha, A.J. Heat and mass transfer on free convective flow of amicropolar fluid through a porous surface with inclined magnetic field and hall effects. Spec. Top. Amp Rev. Porous Media Int. J. 2019, 10, 203–223. [Google Scholar] [CrossRef]
- Dada, M.; Salawu, S. Analysis of Heat and Mass Transfer of an Inclined Magnetic Field Pressure-driven Flow Past a Permeable Plate. Appl. Appl. Math. Int. J. AAM 2017, 12, 12. Available online: https://digitalcommons.pvamu.edu/aam/vol12/iss1/12 (accessed on 20 December 2022).
- Manjunatha, S.; Kuttan, B.A.; Jayanthi, S.; Chamkha, A.; Gireesha, B. Heat transfer enhancement in the boundary layer flow of hybrid nanofluids due to variable viscosity and natural convection. Heliyon 2019, 5, e01469. [Google Scholar] [CrossRef]
- Roja, A.; Gireesha, B.J. Impact of Hall and Ion effects on MHD couple stress nanofluid flow through an inclined channel subjected to convective, hydraulic slip, heat generation, and thermal radiation. Heat Transf. 2020, 49, 3314–3333. [Google Scholar] [CrossRef]
- Hayat, T.; Shafiq, A.; Alsaedi, A.; Asghar, S. Effect of inclined magnetic field in flow of third grade fluid with variable thermal conductivity. AIP Adv. 2015, 5, 087108. [Google Scholar] [CrossRef]
- Saif, R.S.; Muhammad, T.; Sadia, H. Significance of inclined magnetic field in Darcy—Forchheimer flow with variable porosity and thermal conductivity. Phys. A Stat. Mech. Appl. 2020, 551, 124067. [Google Scholar] [CrossRef]
- Makinde, O.D. Entropy-generation analysis for variable-viscosity channel flow with non-uniform wall temperature. Appl. Energy 2008, 85, 384–393. [Google Scholar] [CrossRef]
- Makinde, O.; Iskander, T.; Mabood, F.; Khan, W.; Tshehla, M. MHD Couette-Poiseuille flow of variable viscosity nanofluids in a rotating permeable channel with Hall effects. J. Mol. Liq. 2016, 221, 778–787. [Google Scholar] [CrossRef]
- Disu, A.; Dada, M. Reynold’s model viscosity on radiative MHD flow in a porous medium between two vertical wavy walls. J. Taibah Univ. Sci. 2017, 11, 548–565. [Google Scholar] [CrossRef]
- Makinde, O.; Khan, W.; Culham, J. MHD variable viscosity reacting flow over a convectively heated plate in a porous medium with thermophoresis and radiative heat transfer. Int. J. Heat Mass Transf. 2016, 93, 595–604. [Google Scholar] [CrossRef]
- Venkateswarlu, A.; Murshid, N.; Mulki, H.; Abu-samha, M.; Suneetha, S.; Babu, M.J.; Raju, C.S.K.; Homod, R.Z.; Al-Kouz, W. A Sig-nificant Role of Activation Energy and Fourier Flux on the Quadratically Radiated Sphere in Low and High Conductivity of Hybrid Nanoparticles. Symmetry 2022, 14, 2335. [Google Scholar] [CrossRef]
- Murshid, N.; Mulki, H.; Abu-Samha, M.; Owhaib, W.; Raju, S.S.K.; Raju, C.S.; JayachandraBabu, M.; Homod, R.Z.; Al-Kouz, W. Entropy Gen-eration and Statistical Analysis of MHD Hybrid Nanofluid Unsteady Squeezing Flow between Two Parallel Rotating Plates with Activation Energy. Nanomaterials 2022, 12, 2381. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Nazari, M.A.; Mahariq, I.; Assad, M.E.H.; Ali, M.E.; Almuzaiqer, R.; Nuhait, A.; Murshid, N. Ther-mophysical properties of hybrid nanofluids and the proposed models: An updated comprehensive study. Nanomaterials 2021, 11, 3084. [Google Scholar] [CrossRef]
- Sohail, M.; Nazir, U.; Chu, Y.M.; Al-Kouz, W.; Thounthong, P. Bioconvection phenomenon for the boundary layer flow of magnetohydrodynamic Carreau liquid over a heated disk. Sci. Iran. 2021, 28, 1896–1907. [Google Scholar]
- Rana, P.; Al-Kouz, W.; Mahanthesh, B.; Mackolil, J. Heat transfer of TiO2−EG nanoliquid with active and pas-sive control of nanoparticles subject to nonlinear Boussinesq approximation. Int. Commun. Heat Mass Transf. 2021, 126, 105443. [Google Scholar] [CrossRef]
- Al-Kouz, W.; Abderrahmane, A.; Shamshuddin, M.D.; Younis, O.; Mohammed, S.; Bég, O.A.; Toghraie, D. Heat transfer and entropy generation analysis of water-Fe3O4/CNT hybrid magnetic nanofluid flow in a trapezoidal wavy enclosure containing porous media with the Galerkin finite element method. Eur. Phys. J. Plus 2021, 136, 1184. [Google Scholar] [CrossRef]
- Mahesh, A.; Varma, S.V.K.; Raju, C.S.K.; Babu, M.J.; Vajravelu, K.; Al-Kouz, W. Significance of non-Fourier heat flux and radiation on PEG–water based hybrid nanofluid flow among revolving disks with chemical reaction and en-tropy generation optimization. Int. Commun. Heat Mass Transf. 2021, 127, 105572. [Google Scholar] [CrossRef]
- Al-Kouz, W.; Al-Waked, R.; Sari, M.E.; Owhaib, W.; Atieh, A. Numerical study of heat transfer enhancement in the entrance region for low-pressure gaseous laminar pipe flows using Al2O3–air nanofluid. Adv. Mech. En Gineering 2018, 10, 1687814018784410. [Google Scholar] [CrossRef]
- Rana, P.; Mahanthesh, B.; Mackolil, J.; Al-Kouz, W. Nanofluid flow past a vertical plate with nanoparticle aggregation kinematics, thermal slip and significant buoyancy force effects using modified Buongiorno model. Waves Random Complex Media 2021, 1–25. [Google Scholar] [CrossRef]
- Ferhi, M.; Djebali, R.; Al-Kouz, W.; Abboudi, S.; Chamkha, A.J. MHD conjugate heat transfer and entropy generation analysis of MWCNT/water nanofluid in a partially heated divided medium. Heat Transf. 2021, 50, 126–144. [Google Scholar] [CrossRef]
- Algehyne, E.A.; Alrihieli, H.F.; Bilal, M.; Saeed, A.; Weera, W. Numerical Approach toward Ternary Hybrid Nanofluid Flow Using Variable Diffusion and Non-Fourier’s Concept. ACS Omega 2022, 7, 29380–29390. [Google Scholar] [CrossRef] [PubMed]
- Rehman, A.; Saeed, A.; Bilal, M. Analytical study of three-dimensional MHD hybrid nanofluid flow along with thermal characteristics and radiative solar energy. Waves Random Complex Media 2022, 1–15. [Google Scholar] [CrossRef]
- Bilal, M.; Alduais, F.S.; Alrabaiah, H.; Saeed, A. Numerical evaluation of Darcy Forchhemier hybrid nanofluid flow under the consequences of activation energy and second-order chemical reaction over a slender stretching sheet. Waves Random Complex Media 2022, 1–16. [Google Scholar] [CrossRef]
- Farooq, M.; Rahim, M.; Islam, S.; Siddiqui, A.M. Steady Poiseuille flow and heat transfer of couple stress fluids between two parallel inclined plates with variable viscosity. J. Assoc. Arab. Univ. Basic Appl. Sci. 2013, 14, 9–18. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Abbas, T. Two-Phase Couette Flow of Couple Stress Fluid with Temperature Dependent Viscosity Thermally Affected by Magnetized Moving Surface. Symmetry 2019, 11, 647. [Google Scholar] [CrossRef]
- Dar, A.A. Effect of Thermal Radiation, Temperature Jump and Inclined Magnetic Field on the Peristaltic Transport of Blood Flow in an Asymmetric Channel with Variable Viscosity and Heat Absorption/Generation. Iran. J. Sci. Technol. Trans. Mech. Eng. 2021, 45, 487–501. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).