Catalyzing Cooling Tower Efficiency: A Novel Energy Performance Indicator and Functional Unit including Climate and Cooling Demand Normalization
Abstract
:1. Introduction
1.1. Previous Literature and Indicators
| Efficiency Indicator | Cost Definition (Effort) | Benefit Definition (Use) | Reference | |
|---|---|---|---|---|
| Energy Management | Energy Efficiency | input of energy | output of performance, service, goods, commodities, or energy | ISO 50001 [8] (p. 7) |
| Best Available Techniques | Specific Direct Energy Consumption | energy consumed by all energy-consuming equipment | dissipated MWth | [18] (p. 4) |
| Efficiency of Buildings | Specific Electricity Consumption | electricity consumption (kWhel) | thermal load (MWth) 2219 operation hours [h] | DIN V 18599-7 [19] (p. 64) |
| EER | Energy Efficiency Ratio | ‘effective power input […] to the device’ (W) | ‘total cooling capacity’, ‘at any given set of rating conditions’ (W) | ISO 13253 [21] |
| LCA Eco-Efficiency | Environmental Impacts Per Functional Unit | environmental impacts | functional unit: ‘1 kWh of electricity produced by the plant, […] referred to the operating period of 1 year’ | ISO 14040 [23] ISO 14044 [31], [32] (p. 1079) |
| environmental impacts | ‘provision of 1-megawatt heat rejection (cooling) capacity (MWth) for a period of 1 year’ | [33] (p. 50) | ||
| environmental impacts | ‘cooling of 1 kg water from 35 to 28 °C in Germany for the overall usage time’ | [34] (p. 140) | ||
| environmental impacts | ‘cooling throughout 2019 with 2,450,000 m3 of circulating water cooled from 21.21 to 14.87 °C […] in Stuttgart-Vaihingen’ | [35] (p. 3) | ||
| Exergy Analysis | Exergy Efficiency | = exergy output / exergy input = 1 − exergy destruction / exergy input | [24] (p. 190), [27] (p. 504) | |
| = change in product exergy / change in supply exergy | [24] (p. 191) | |||
| = (air exergy output + input) / (water exergy input − output) | [26] (p. 2797) | |||
1.2. Objectives of This Work
2. Materials and Methods
2.1. Efficiency Evaluation
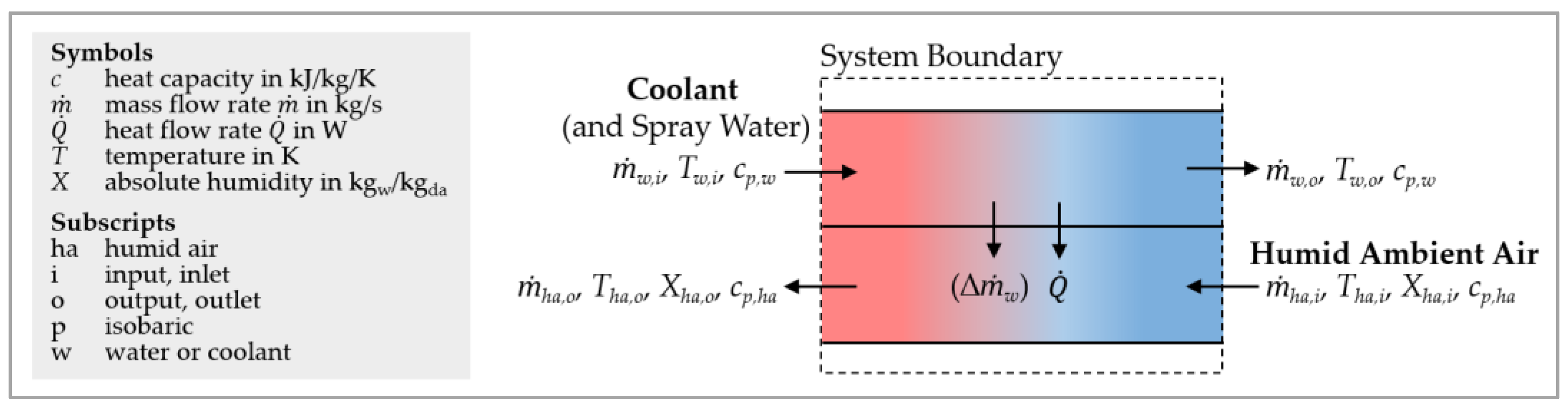
2.1.1. The Quantified Benefit of Cooling Towers
- The cooling tower operates at pure counterflow.
- The air outlet temperature equals the coolant inlet temperature: .
- The cooling tower uses evaporative cooling.
- The outlet air is 100% saturated: .
- Nevertheless, the ambient wet-bulb temperature (WBT) must be less than the required cooling temperature, .
2.1.2. The Effectiveness Indicator
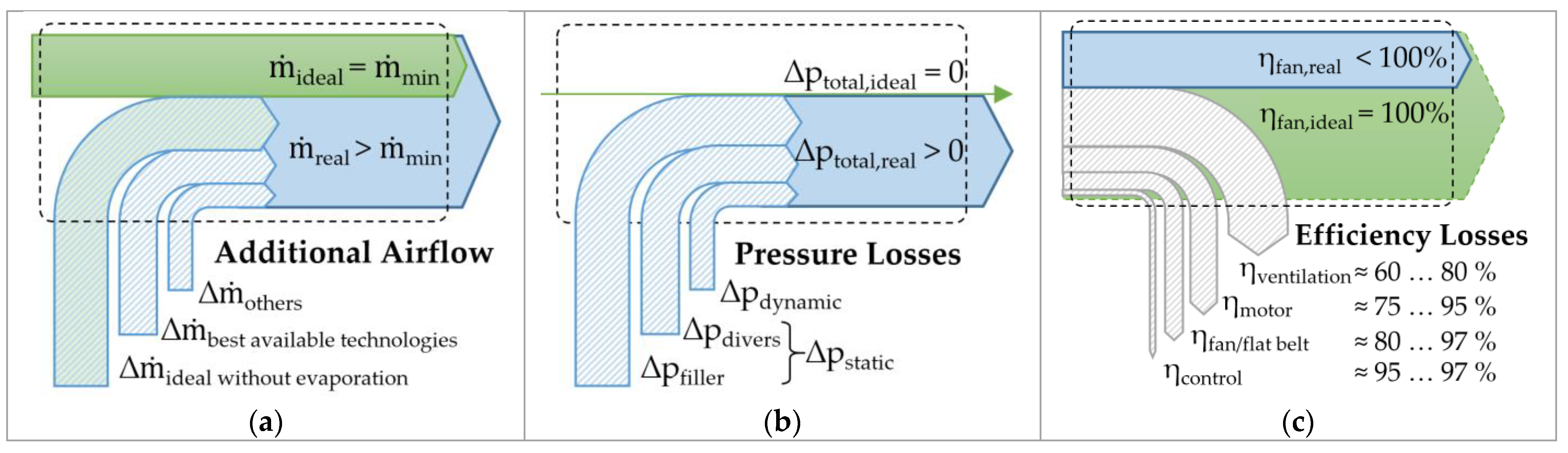
2.1.3. The Airflow Performance Indicator (AirPI)
2.2. System and Data
- Dry cooling towers;
- Wet cooling towers with open circuits (direct);
- Wet cooling towers with closed circuits (indirect);
- Hybrid cooling towers with direct wetting;
- Hybrid cooling towers with spraying devices;
- Hybrid cooling towers with wetting mats.
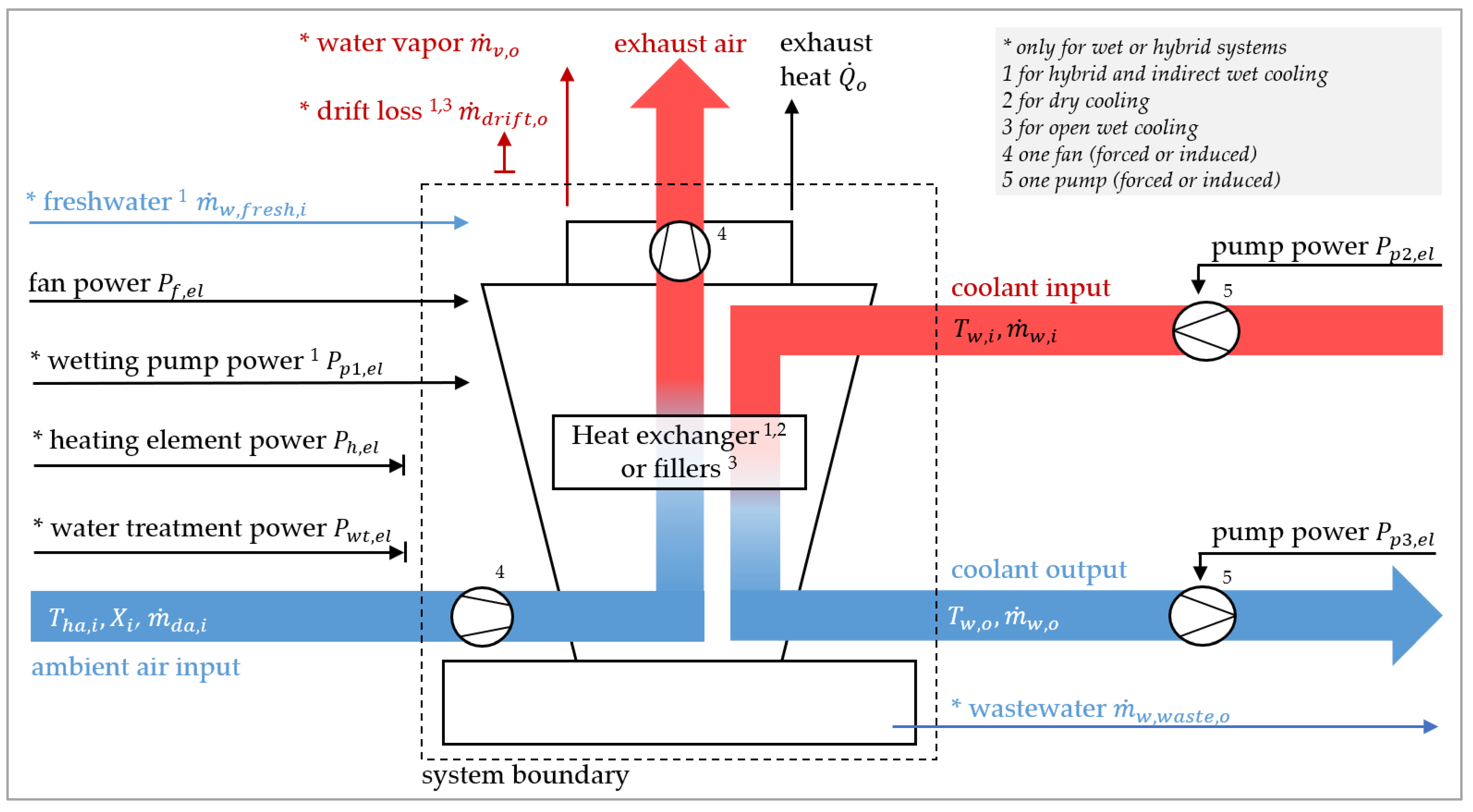
2.2.1. System Definition
2.2.2. Dataset of Cooling Tower Models
2.2.3. Case Study Data
3. Results and Discussion
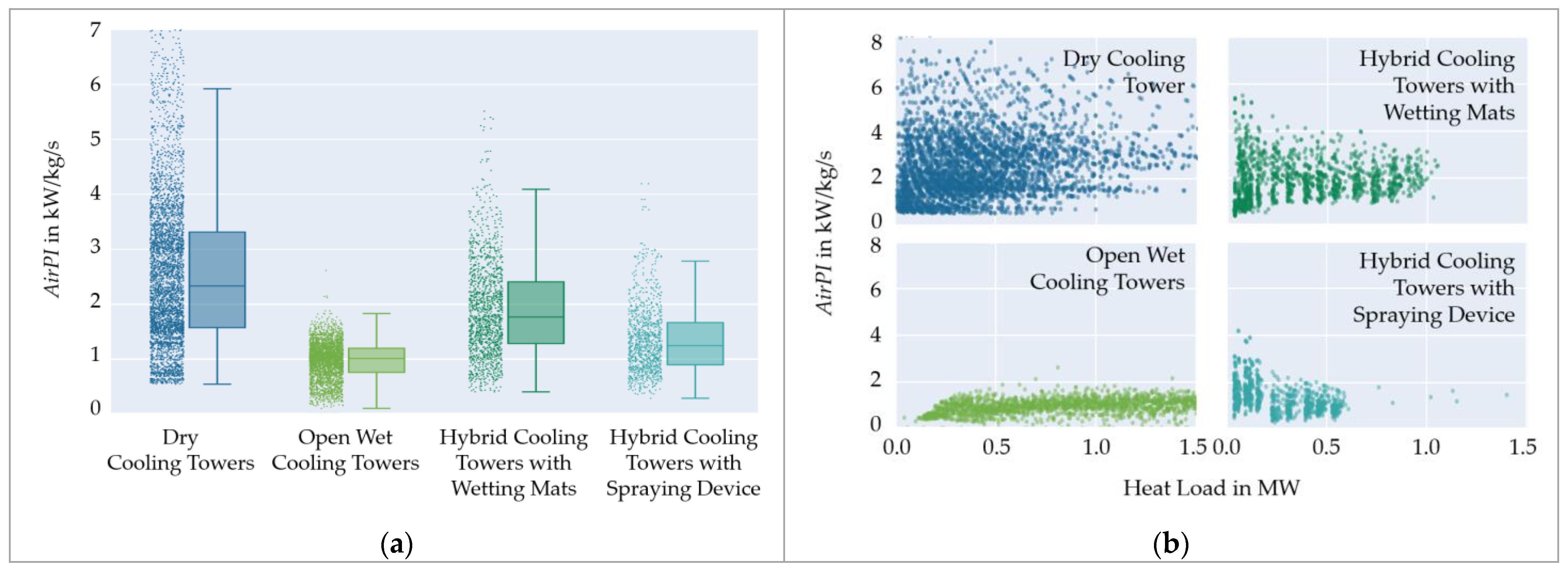
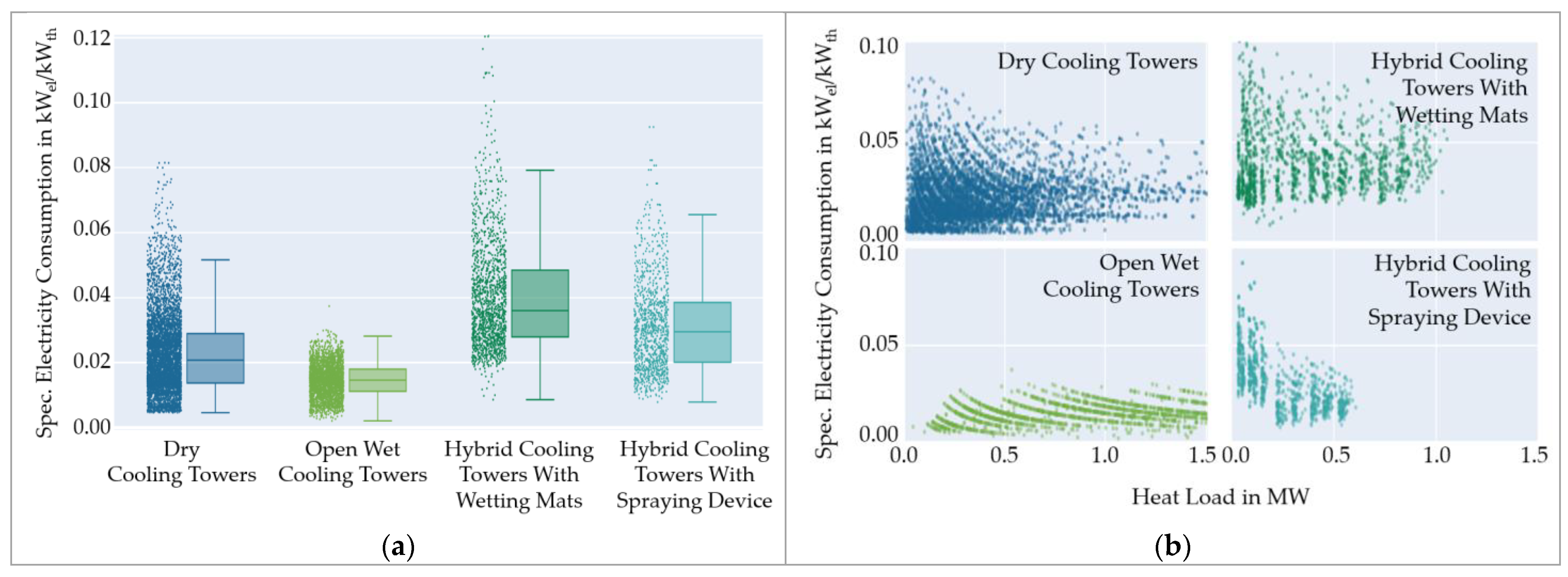
3.1. Efficiency Evaluation of Different Cooling Tower Models
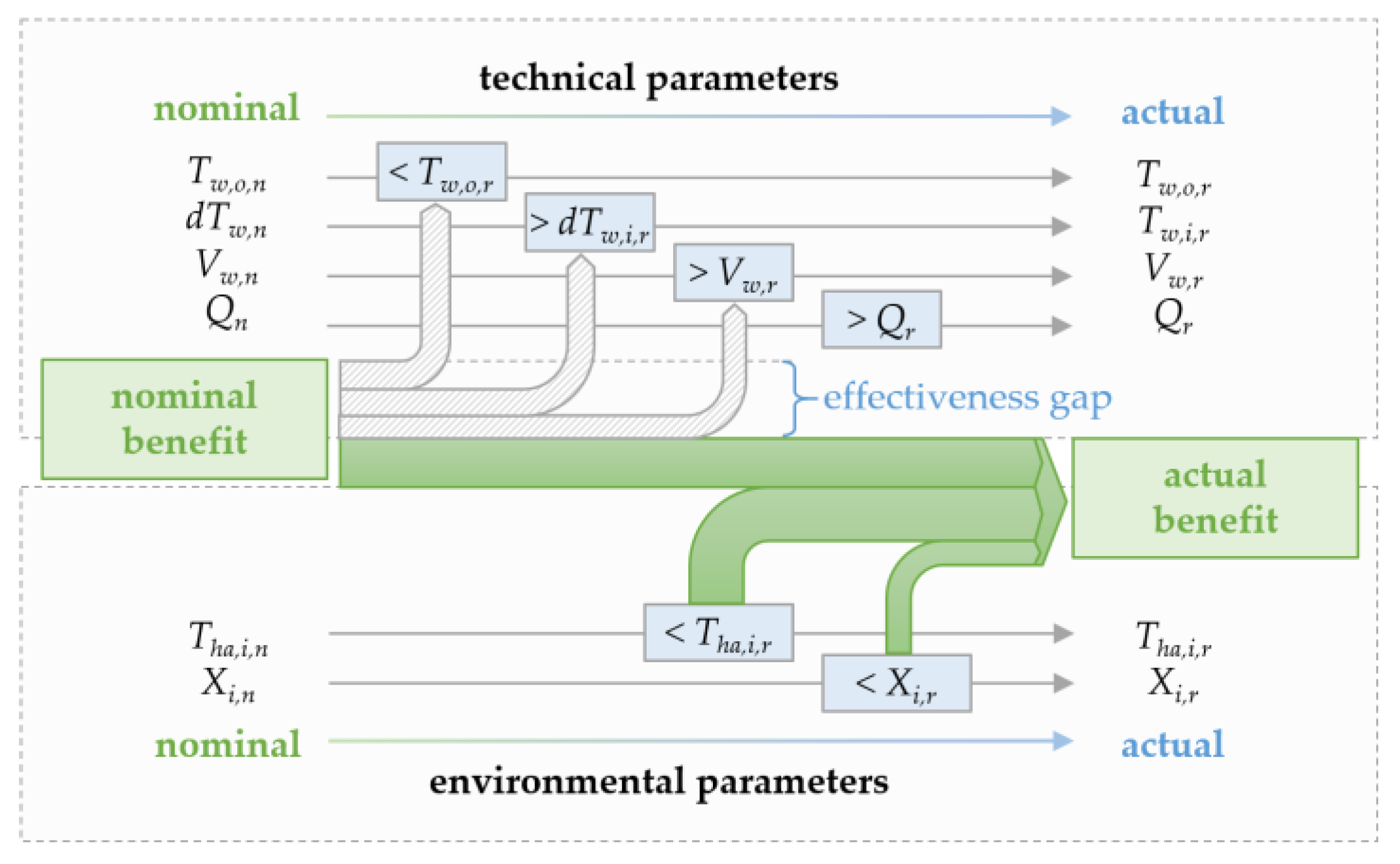
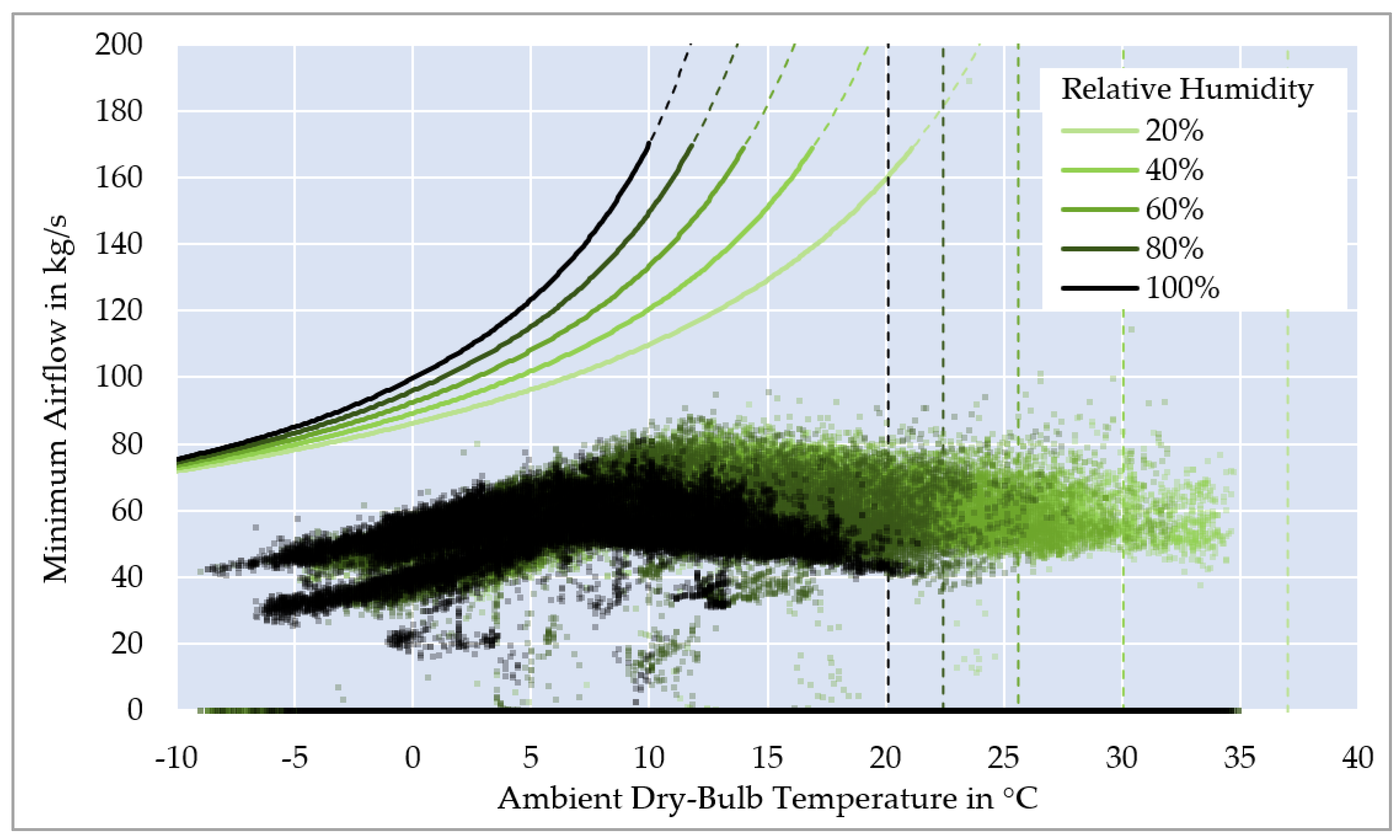
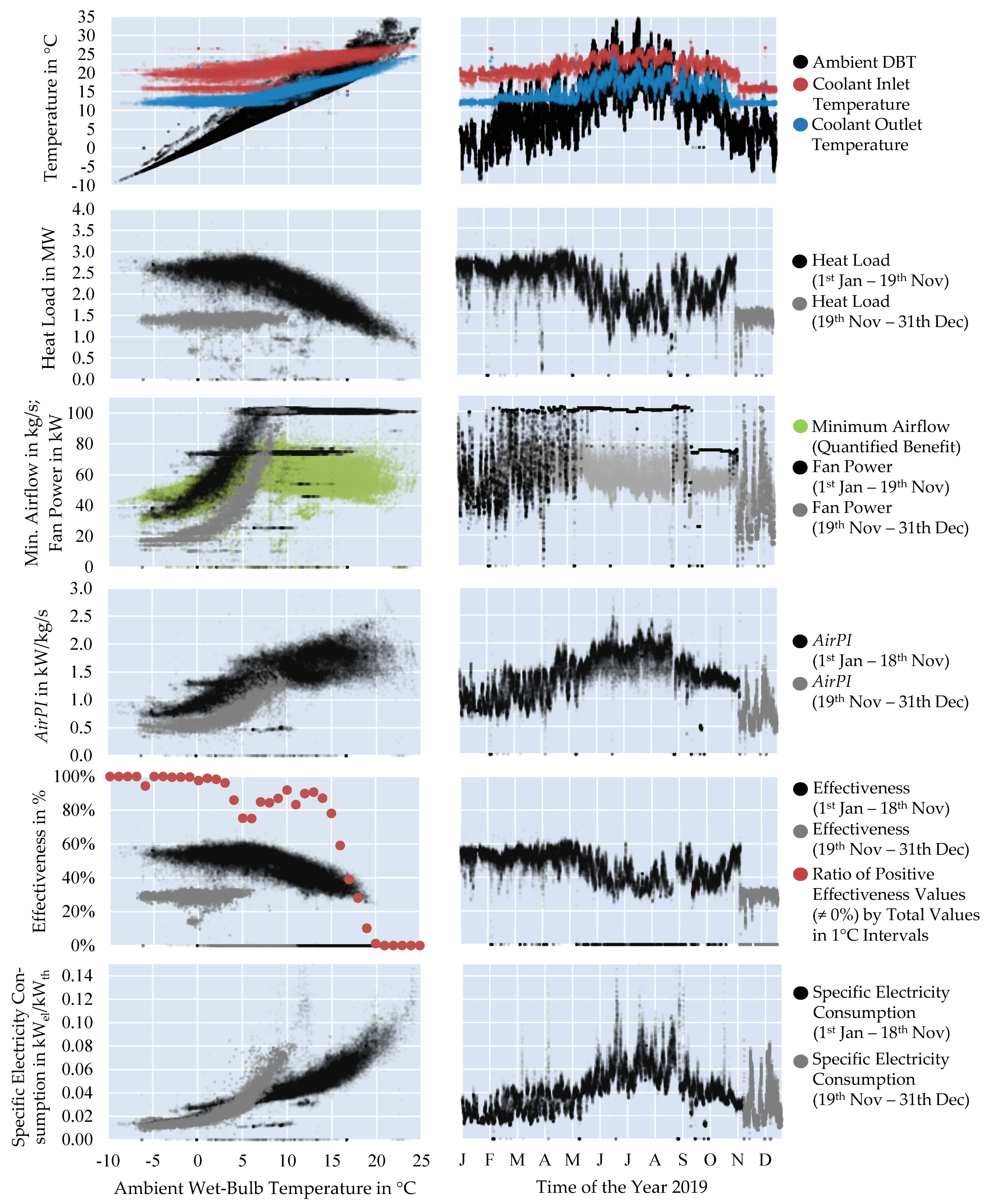
3.2. Efficiency Evaluation across Varying Environmental Conditions
3.3. Discussion on Indicator Feasibility
3.4. Implications for the SDGs
4. Conclusions
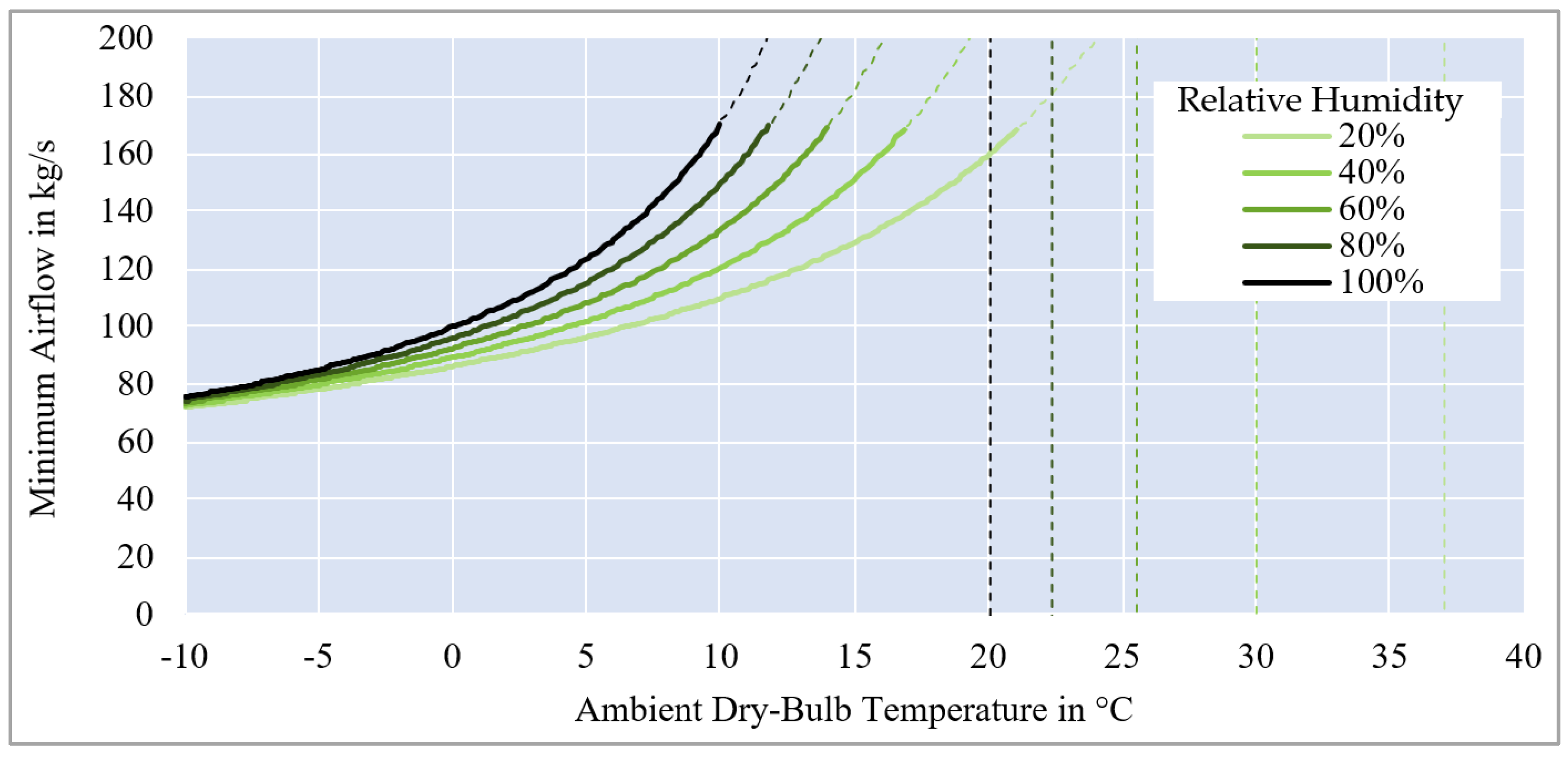
- Regarding the model dataset, the AirPI quantitatively confirms that wet cooling towers are more energy-efficient than dry cooling towers: dry cooling towers consume 2.3 kW/kg/s at the median, whereas wet cooling has a median of 1.0 kW/kg/s and hybrid cooling with wetting mats or spraying devices 1.3 and 1.8 kW/kg/s, respectively.
- Furthermore, the minimum airflow underscores the energy-saving potential of evaporative cooling. Regarding the median of dry cooling towers, approximately 7.8 times more airflow is theoretically needed if evaporative cooling is not implemented, directly correlating to the required fan power.
- The case study demonstrates that the indicator serves to determine the efficiency of cooling towers in operation instantaneously or integrated over time, for example, as seasonal AirPI. However, the operation differs significantly from the nominal heat transfer. Thus, we recommend assessing the effectiveness simultaneously. The effectiveness, quantified as the ratio between minimum airflow of actual to nominal benefit, highlights the necessity of additional cooling devices.
- Thanks to the normalization of outside conditions, the case study results are comparable to the dataset of 6575 cooling tower models in nominal operating points. The investigated wet cooling system turns out to be more efficient than the median of the manufacturer’s nominal data of wet cooling towers. However, at high ambient temperatures, the efficiency decreases, and the effectiveness is low. Further investigations must include the entire cooling and chilling system.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviations | |
| COP | coefficient of performance |
| DBT | dry-bulb temperature |
| EER | energy efficiency ratio |
| EnPI | energy performance indicator |
| HLRS | High-Performance Computing Centre of the University of Stuttgart |
| IQR | interquartile range |
| LCA | life cycle assessment |
| SDG | sustainable development goal |
| WBT | wet-bulb temperature |
| Symbols | |
| AirPI | airflow performance indicator |
| c | heat capacity in kJ/kg/K |
| EnPI | energy performance indicator |
| H | enthalpy in J; enthalpy flow rate in W |
| h | enthalpy per mass in J/kg (enthalpy of humid air refers to the mass of dry air) |
| m | mass in kg; mass flow rate in kg/s |
| P | power in W |
| p | pressure in Pa |
| Q | heat in J; heat flow rate in W |
| T | temperature in K |
| V | volume in m³; volume flow rate in m³/s |
| X | absolute humidity in kgw/kgda |
| ϑ | temperature in °C |
| φ | relative humidity in % |
| η | efficiency in % |
| … flow rate […/s] | |
| Subscripts | |
| ‘’ | saturated |
| 0.25 | 25% quartile |
| 0.75 | 75% quartile |
| a | air |
| ct | cooling tower |
| da | dry air |
| el | related to electricity |
| h | heating element |
| ha | humid air |
| i | input, inlet |
| min | minimum |
| n | nominal |
| o | output, outlet |
| p | pump or isobaric |
| r | real, actual |
| th | thermal |
| v | vapor |
| w | water or coolant |
| wt | water treatment |
Appendix A
| Type | Description |
|---|---|
| dry cooling towers | conductive heat transfer to dissipate heat to the surrounding air with a heat exchanger and forced ventilation |
| wet cooling towers with open circuit | heat dissipation by evaporation as the coolant trickles down fillers in direct contact with the ambient air |
| wet cooling towers with closed circuit | evaporative heat transfer but with a coolant-air heat exchanger and a separate circulating coolant system where the coolant trickles down to facilitate evaporation |
| hybrid cooling towers with direct wetting | hybrid cooling is a combination of dry and indirect wet cooling methods with seasonal shift, while directly wetted hybrid cooling towers involves a wetting circuit comprising an auxiliary water pump, water trickling down the heat exchanger, and a water collection tank |
| hybrid cooling towers with spraying device | the spraying system saturates the ambient air to enhance subsequent cooling in the heat exchanger |
| hybrid cooling towers with wetting mats | wetting-mat systems facilitate the water distribution by additional water trickling down the mats, enabling evaporation into the ambient air that subsequently passes the heat exchanger |
References
- United Nations. A/RES/70/1: Transforming Our World: The 2030 Agenda for Sustainable Development: Resolution adopted by the General Assembly on 25 September 2015; United Nations: San Francisco, CA, USA, 2015. [Google Scholar]
- Scoccimarro, E.; Cattaneo, O.; Gualdi, S.; Mattion, F.; Bizeul, A.; Risquez, A.M.; Quadrelli, R. Country-level energy demand for cooling has increased over the past two decades. Commun. Earth Environ. 2023, 4, 208. [Google Scholar] [CrossRef]
- IEA. Space Cooling. International Energy Agency, Paris, License: CC BY 4.0. Available online: https://www.iea.org/data-and-statistics/charts/final-energy-consumption-for-space-cooling-by-region-and-number-of-space-cooling-equipment-units-in-operation-in-the-net-zero-scenario-2000-2030 (accessed on 26 October 2023).
- Cannistraro, G.; Cannistraro, M.; Cannistraro, A.; Galvagno, A.; Trovato, G. Reducing the demand of energy cooling in the CED, “Centers of Processing Data”, with use of free-cooling systems. Int. J. Heat Technol. 2016, 34, 498–502. [Google Scholar] [CrossRef]
- Turek, D.; Radgen, P. Optimized data center site selection—Mesoclimatic effects on data center energy consumption and costs. Energy Effic. 2021, 14, 33. [Google Scholar] [CrossRef]
- Zhang, Q.; Meng, Z.; Hong, X.; Zhan, Y.; Liu, J.; Dong, J.; Bai, T.; Niu, J.; Deen, M.J. A survey on data center cooling systems: Technology, power consumption modeling and control strategy optimization. J. Syst. Archit. 2021, 119, 102253. [Google Scholar] [CrossRef]
- Deroubaix, A.; Labuhn, I.; Camredon, M.; Gaubert, B.; Monerie, P.-A.; Popp, M.; Ramarohetra, J.; Ruprich-Robert, Y.; Silvers, L.G.; Siour, G. Large uncertainties in trends of energy demand for heating and cooling under climate change. Nat. Commun. 2021, 12, 5197. [Google Scholar] [CrossRef] [PubMed]
- ISO 50001:2018; Energy Management Systems—Requirements with Guidance for Use. International Organization for Standardization (ISO): Geneva, Switzerland, 2018.
- Gonzalez Hernandez, A.; Paoli, L.; Cullen, J.M. How resource-efficient is the global steel industry? Resour. Conserv. Recycl. 2018, 133, 132–145. [Google Scholar] [CrossRef]
- Hashemi, Z.; Zamanifard, A.; Gholampour, M.; Liaw, J.-S.; Wang, C.-C. Recent Progress in Fill Media Technology for Wet Cooling Towers. Processes 2023, 11, 2578. [Google Scholar] [CrossRef]
- Kloppers, J.C.; Kröger, D.G. Cooling Tower Performance Evaluation: Merkel, Poppe, and e-NTU Methods of Analysis. J. Eng. Gas Turbines Power 2005, 127, 1–7. [Google Scholar] [CrossRef]
- El-Dessouky, H.T.A.; Al-Haddad, A.; Al-Juwayhel, F. A Modified Analysis of Counter Flow Wet Cooling Towers. J. Heat Transf. 1997, 119, 617–626. [Google Scholar] [CrossRef]
- Zargar, A.; Kodkani, A.; Peris, A.; Clare, E.; Cook, J.; Karupothula, P.; Vickers, B.; Flynn, M.R.; Secanell, M. Numerical analysis of a counter-flow wet cooling tower and its plume. Int. J. Thermofluids 2022, 14, 100139. [Google Scholar] [CrossRef]
- Merkel, F. Verdunstungskühlung; VDI-Verlag: Berlin, Germany, 1925. [Google Scholar]
- Jaber, H.; Webb, R.L. Design of Cooling Towers by the Effectiveness-NTU Method. J. Heat Transfer 1989, 111, 837–843. [Google Scholar] [CrossRef]
- Poppe, M.; Rögener, H. Berechnung von Rückkühlwerken. In VDI-Wärmeatlas, 10th ed.; Verein Deutscher Ingenieure, V.D. (VDI), Ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1228–1242. [Google Scholar] [CrossRef]
- Poppe, M. Wärme- und Stoffübertragung bei der Verdunstungskühlung im Gegen- und Kreuzstrom: Mitteilung aus dem Institut für Thermodynamik der Technischen Universität Hannover; VDI-Verlag: Düsseldorf, Germany, 1973; ISBN 3-18-85-0560-1. [Google Scholar]
- European Commission. Reference Document on the Application of Best Available Techniques to Industrial Cooling Systems: Integrated Pollution Prevention and Control (IPPC). 2001. Available online: https://eippcb.jrc.ec.europa.eu/sites/default/files/2019-11/cvs_bref_1201.pdf (accessed on 14 July 2022).
- DIN 18599-7:2018; Energy Efficiency of Buildings—Calculation of the Net, Final and Primary Energy Demand for Heating, Cooling, Ventilation, Domestic Hot Water and Lighting—Part 7: Final Energy Demand of Air-Handling and Air-Conditioning Systems for Non-Residential Buildings. Deutsches Institut für Normung e. V. (DIN): Beuth Verlag GmbH: Berlin, Germany, 2018.
- ISO 16818:2008; Building Environment Design—Energy Efficiency—Terminology. International Organization for Standardization (ISO): Geneva, Switzerland, 2008.
- ISO 13253:2017; Ducted Air-Conditioners and Air-to-Air Heat Pumps—Testing and Rating for Performance. International Organization for Standardization (ISO): Geneva, Switzerland, 2017.
- ISO 13612-2:2014; Heating and Cooling Systems in Buildings—Method for Calculation of the System Performance and System Design for Heat Pump Systems: Part 2: Energy Calculation. International Organization for Standardization (ISO): Geneva, Switzerland, 2014.
- ISO 14040:2021; Environmental Management—Life Cycle Assessment—Principles and Framework. Deutsches Institut für Normung e. V. (DIN) ISO: Beuth Verlag GmbH: Berlin, Germany, 2021.
- Qureshi, B.A.; Zubair, S.M. Second-law-based performance evaluation of cooling towers and evaporative heat exchangers. Int. J. Therm. Sci. 2007, 46, 188–198. [Google Scholar] [CrossRef]
- Madlool, N.A.; Saidur, R.; Rahim, N.A.; Islam, M.R.; Hossian, M.S. An exergy analysis for cement industries: An overview. Renew. Sustain. Energy Rev. 2012, 16, 921–932. [Google Scholar] [CrossRef]
- Muangnoi, T.; Asvapoositkul, W.; Wongwises, S. Effects of inlet relative humidity and inlet temperature on the performance of counterflow wet cooling tower based on exergy analysis. Energy Convers. Manag. 2008, 49, 2795–2800. [Google Scholar] [CrossRef]
- Ataei, A.; Panjeshahi, M.H.; Gharaie, M. Performance Evaluation of Counter-flow Wet Cooling Towers Using Exergetic Analysis. Trans. Can. Soc. Mech. Eng. 2008, 32, 499–512. [Google Scholar] [CrossRef]
- Bejan, A. Advanced Engineering Thermodynamics, 4th ed.; Wiley: Newark, NJ, USA, 2016; ISBN 9781119052098. [Google Scholar]
- Volta, D.; Weber, S.A. The Physical Optimum as an Ideal Reference Value for Balancing Thermodynamic Processes Integrating the Exergetic Evaluation by the Example of Heat Supply. Energies 2021, 14, 4426. [Google Scholar] [CrossRef]
- Volta, D. Das Physikalische Optimum als Basis von Systematiken zur Steigerung der Energie- und Stoffeffizienz von Produktionsprozessen. Dissertation; Technische Universität Clausthal: Clausthal, Germany, 2014. [Google Scholar]
- ISO 14044:2006; Environmental Management—Life Cycle Assessment—Requirements and Guidelines. International Organization for Standardization (ISO): Geneva, Switzerland, 2006.
- Asdrubali, F.; Baldinelli, G.; Scrucca, F. Comparative life cycle assessment of an innovative CSP air-cooled system and conventional condensers. Int. J. Life Cycle Assess. 2015, 20, 1076–1088. [Google Scholar] [CrossRef]
- Schlei-Peters, I.; Wichmann, M.G.; Matthes, I.-G.; Gundlach, F.-W.; Spengler, T.S. Integrated material flow analysis and process modeling to increase energy and water efficiency of industrial cooling water systems. J. Ind. Ecol. 2017, 22, 41–54. [Google Scholar] [CrossRef]
- Schulze, C.; Thiede, S.; Herrmann, C. Life cycle assessment of industrial cooling towers. In Progress in Life Cycle Assessment; Schebek, L., Herrmann, C., Cerdas, F., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 135–146. ISBN 978-3-319-92237-9. [Google Scholar]
- Wenzel, P.M.; Radgen, P. Extending effectiveness to efficiency: Comparing energy and environmental assessment methods for a wet cooling tower. J. Ind. Ecol. 2023, 27, 693–706. [Google Scholar] [CrossRef]
- Eggers, N.; Birth, T.; Sankol, B.; Kerpen, L.; Hurtado, A. A Literature Review on Existing Methods and Indicators for Evaluating the Efficiency of Power-to-X Processes. Clean Technol. 2023, 5, 167–189. [Google Scholar] [CrossRef]
- Wenzel, P.M.; Radgen, P. Multi-Criteria Comparison of Energy and Environmental Assessment Approaches for the Example of Cooling Towers. Appl. Syst. Innov. 2022, 5, 89. [Google Scholar] [CrossRef]
- Menghi, R.; Papetti, A.; Germani, M.; Marconi, M. Energy efficiency of manufacturing systems: A review of energy assessment methods and tools. J. Clean. Prod. 2019, 240, 118276. [Google Scholar] [CrossRef]
- Wenzel, P.M.; Mühlen, M.; Radgen, P. Free Cooling for Saving Energy: Technical Market Analysis of Dry, Wet, and Hybrid Cooling Based on Manufacturer Data. Energies 2023, 16, 3661. [Google Scholar] [CrossRef]
- ISO 50006:2014; Energiemanagementsysteme—Messung der energiebezogenen Leistung unter Nutzung von energetischen Ausgangsbasen (EnB) und Energieleistungskennzahlen (EnPI)—Allgemeine Grundsätze und Leitlinien. Deutsches Institut für Normung e. V. (DIN) ISO: Beuth Verlag GmbH: Berlin, Germany, 2017.
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and Pseudo-pure Fluid Thermophysical Property Evaluation and the Open-Source Thermophysical Property Library CoolProp. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef] [PubMed]
- Erens, P.J. N4 Cooling Towers. In VDI Heat Atlas, 2nd ed.; Verein Deutscher Ingenieure (VDI), Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1485–1501. ISBN 978-3-540-77876-9. [Google Scholar]
- VDI 2047-3:2018; Open Recooler Systems. Securing Hygienically Sound Operation of Evaporative Cooling Systems: Cooling Towers with a Cooling Power Greater than 200 MW (VDI Cooling Tower Code of Practice). Verein Deutscher Ingenieure (VDI): Beuth Verlag GmbH: Düsseldorf, Germany, 2018.
- Brodbeck, M.; Lorenz, B.; Fischer, T.; Conrad, N.; Wöckener, I. HLRS Umwelterklärung 2019, Stuttgart. 2020. Available online: https://www.hlrs.de/fileadmin/about/social_responsibility/Sustainability/HLRS_Umwelterklaerung-2019.pdf (accessed on 26 October 2023).
- Bayer, N.; Kerskes, H.; Stergiaropoulos, K. Transient numerical simulation for optimization of a water-cooled high-performance computing center with dynamic cooling circuit temperatures—Work-in-progress. In EnviroInfo 2022, Short-/Work in Progress-Papers: September 26–28, 2022, Hamburg, Germany; Wohlgemuth, V., Naumann, S., Arndt, H.-K., Behrens, G., Höb, M., Eds.; Gesellschaft für Informatik e.V. (GI): Bonn, Germany, 2022; ISBN 978-3-88579-722-7. [Google Scholar]
- Spindler, K.; Bedenik, S.; Heidemann, W. Untersuchung zur Optimierung der Kühlwasserversorgung des HLRS Hinsichtlich Energie- und Kosteneffizienz: Phase 1: Analyse des Klimatisierungskonzeptes des HLRS, Stuttgart; Institut für Thermodynamik und Wärmetechnik: Stuttgart, Germany, 2016. [Google Scholar]
- Blesl, M.; Kessler, A. Energy Efficiency in Industry; Springer: Berlin/Heidelberg, Germany, 2021; ISBN 978-3-662-63922-1. [Google Scholar]
- Grundmann, R.; Schönholtz, F.; Eidam, H.; Rahn, B. Grundlagen der Ventilatorentechnik. 2013. Available online: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&cad=rja&uact=8&ved=2ahUKEwi6ktjlnvWAAxV1XvEDHbs7AVIQFnoECBMQAQ&url=https%3A%2F%2Fwww.trox.de%2Fdownloads%2F9e22d16d3953f93c%2F07fachartikel_grundlagen_der_ventilatorentechnik.pdf&usg=AOvVaw1A78W8Bd9nCenm3zQeecwQ&opi=89978449 (accessed on 24 August 2023).
- Kaup, C. Energieeffizienz Zentraler Raumlufttechnsicher Anlagen. BHKS-Alm. Bundesindustrieverband Tech. Gebäudeausrüstung E.V. 2010, 52–59. Available online: https://www.umwelt-campus.de/fileadmin/Umwelt-Campus/User/CKaup/BHKS_Almanach.pdf (accessed on 1 October 2023).
- Mietzker, T. Systemwirkungsgrad von Ventilatoren. Available online: https://cci-dialog.de/lexikon_ventilator_systemwirkungsgrad/ (accessed on 13 March 2023).


| Parameter | Unit | Nominal Values | Actual Values (Min–Max; Avg) |
|---|---|---|---|
| coolant inlet temperature | K | 20 | 7.9–29.2; 21.2 |
| coolant outlet temperature | K | 10 | 8.0–28.1; 14.9 |
| coolant volume flow rate | m³/h | 412.8 | 0–413.9; 279.6 |
| cooling capacity | kWth | 4 800 | 0–3 672; 2 042 |
| Ref: [46] (p. 4) | Ref: [45] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wenzel, P.M.; Fensterle, E.; Radgen, P. Catalyzing Cooling Tower Efficiency: A Novel Energy Performance Indicator and Functional Unit including Climate and Cooling Demand Normalization. Sustainability 2023, 15, 15454. https://doi.org/10.3390/su152115454
Wenzel PM, Fensterle E, Radgen P. Catalyzing Cooling Tower Efficiency: A Novel Energy Performance Indicator and Functional Unit including Climate and Cooling Demand Normalization. Sustainability. 2023; 15(21):15454. https://doi.org/10.3390/su152115454
Chicago/Turabian StyleWenzel, Paula M., Eva Fensterle, and Peter Radgen. 2023. "Catalyzing Cooling Tower Efficiency: A Novel Energy Performance Indicator and Functional Unit including Climate and Cooling Demand Normalization" Sustainability 15, no. 21: 15454. https://doi.org/10.3390/su152115454
APA StyleWenzel, P. M., Fensterle, E., & Radgen, P. (2023). Catalyzing Cooling Tower Efficiency: A Novel Energy Performance Indicator and Functional Unit including Climate and Cooling Demand Normalization. Sustainability, 15(21), 15454. https://doi.org/10.3390/su152115454






