Dynamic Incentive Contract of Government for Port Enterprises to Reduce Emissions in the Blockchain Era: Considering Carbon Trading Policy
Abstract
1. Introduction
2. Literature Review
2.1. Blockchain Technology in the Shipping Industry
2.2. Port Emission Reduction and Government Subsidy
2.3. Incentive Contract Design
2.4. Research Gap
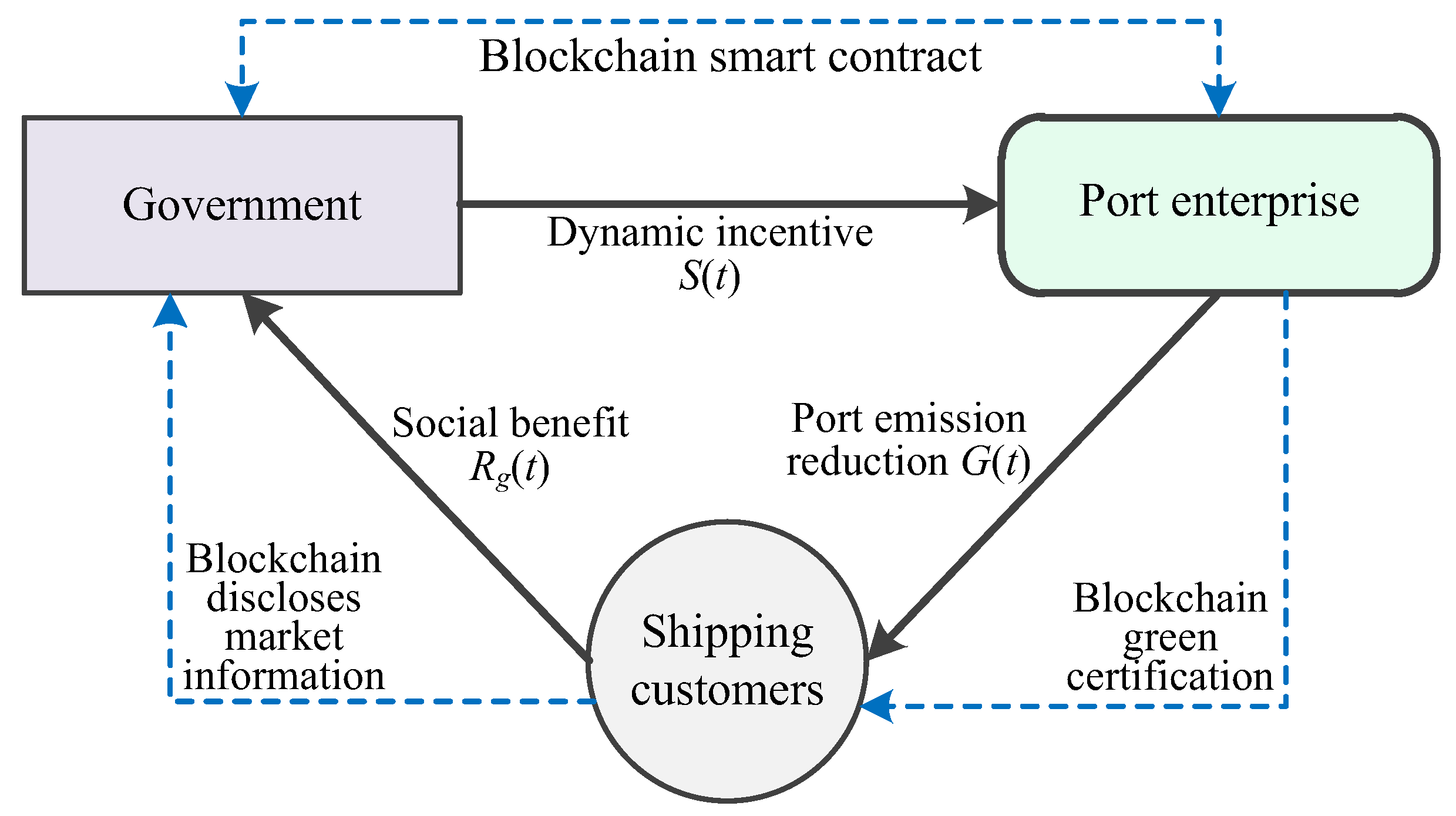
3. Problem Formulation and Assumptions
- We assume that the investment level of the port enterprise in emission reduction in the t period is I(t), which indicates the investment in energy-saving and emission reducing technologies such as “oil-to-electricity” shore-side power and LNG terminals by port enterprises to build green ports, and assume that the carbon emission reductions (CERs) of the port in period t is:where β > 0 refers to the impact factor of the port’s ERI level I(t) on the port’s CERs; s > 0 indicates the attenuation rate of the port’s CERs, which indicates that the emission reduction effect caused by port ERI before time t becomes worse (e.g., due to backward emission reduction technology, aging of shore power equipment, etc.), which makes it that there is a attenuation term in the cumulative emission reduction G(t) at time t; and v represents the exogenous uncertainty with the mean value of 0 and the variance of δ2, which reflects the uncertainty of port emission reduction market.
- Referring to existing relevant literature (e.g., Hong and Guo [55], Chai et al. [56]), we assume that the social benefit brought by the port enterprise to the government through efforts to improve carbon emission reductions in the period t is Rg(t) = h⋅G(t), and h is the monetary expression of the social benefit generated by unit port emission reduction. In addition, based on the dynamic changes of the port’s CERs, we propose a linear dynamic incentive contract for the government to implement subsidy to the port enterprise in the t period is:where s0(t) and s1(t), respectively, refer to the fixed subsidy and unit subsidy paid by the government to the port enterprise. In addition, we assume that the government will incur a contract execution cost c (such as information cost and supervision cost) in determining contract terms, fulfilling contracts, and resolving disputes during the t period.S(t) = s0(t) + s1(t) ⋅ G(t)
- As port emission reduction helps to attract green customers and promote shipping demand, it is assumed that the shipping customer demand caused by the port enterprise’s CERs in the t period is D(t) = γ⋅G(t). γ > 0 is the impact of port emission reduction on shipping customer demand, which depends on shipping customers’ awareness of green environmental protection. In addition, we also assume that the revenue of the port enterprise consists of two parts: one part is the revenue Rp(t) = ξ ⋅D(t), and ξ > 0 is the service price of the port. The other part is the revenue W(g0, S(t)) = g0⋅S(t) brought to the port enterprise by the government’s dynamic incentive contract S(t), and 0 < g0 < 1 is the execution efficiency of the contract, which reflects the sensitivity of port enterprise to the government contract.
- Considering that both the government and port enterprise are risk averse to their revenues [57], we define the degree of risk aversion θ using the Arrow–Pratt absolute risk aversion measure, and assume that the government’s risk avoidance cost for social benefit Rg(t) is CRg(t) = θ⋅Var(Rg(t))/2 = θ⋅h2δ2/2, and the port enterprise’s risk avoidance cost for its revenue is CRp(t) = θ⋅Var(Rp(t) + W(t))/2 = θ⋅(g0⋅s1(t) + γξ)2δ2/2.
- Suppose that the investment cost function of emission reduction for the port enterprise is η⋅I2(t)/2 (such as the cost of equipment purchase, human input, technological innovation, and shore power maintenance), where η > 0 is the corresponding cost coefficient. The setting of the cost function meets the general convexity assumption in economics, and the economic implication behind it is that the investment cost of port emission reduction meets the law of marginal cost increase. In addition, we assume that the revenue of the port enterprise without emission reduction investment while maintaining the traditional operation mode is Φ, which reflects the opportunity cost of the port enterprise’s green transformation investment in shore power and other emission reduction technologies. In addition, it is assumed that the government will provide dynamic incentives to the port enterprise’s emission reduction within time t ∈ [0, +∞), ρ is used to express the discount rate of the port service market.
- (1)
- According to the value of blockchain smart contracts, it is assumed that the execution efficiency of government dynamic incentive contracts under blockchain technology is g1 and meets 0 < g0 < g1 < 1. At the same time, without losing generality, let the contract execution cost c = 0.
- (2)
- According to the value of blockchain green certification, this paper introduces the green trust coefficient r of customers on the port’s ERI level, which is reflected in the accumulation of the port enterprise’s effort to reduce emissions. Therefore, it is assumed that the port’s CERs in the t period under blockchain technology is:where the green trust coefficient 0 < r < 1 reflects the impact of blockchain green certification on port emission reduction, and v* represents the uncertainty of the port emission reduction market under blockchain technology, which is different from v in Equation (1) (explained in (3) below).
- (3)
- According to the value of blockchain disclosure of market information on green energy efficiency and emission reduction in ports, this paper introduces the disclosure degree ω of blockchain for port emission reduction uncertain information [58]. We assume that the random disturbance factor of port emission reduction under blockchain technology is v* (see Equation (3)) with mean 0 and variance (1 − ω) ⋅ δ2, where 0 < ω < 1 denotes the degree of information disclosure. It reduces the variance of random disturbance factor without blockchain, and reduces the uncertainty of the port emission reduction market.
4. Models
4.1. No Blockchain (Case N)
4.2. Blockchain Adoption (Case B)
4.3. Blockchain Adoption When Considering Carbon Trading Policy (Case TB)
5. Model Analysis
5.1. Government’s Dynamic Incentive Strategy for Port Emission Reduction
- (i)
- When t < tthN, then , , , ;
- (ii)
- When t ≥ tthN, then , , , ;
- (i)
- When t < tthB, then , ,, ;
- (ii)
- When t ≥ tthB, then,,,;
- (i)
- When t < tthTB, then ,,,;
- (ii)
- When t ≥ tthTB, then,,,;
5.2. Parameter Analysis
- (i)
- ,,;
- (ii)
- ,,;
- (iii)
- ,,;
- (iv)
- ,,;
- (i)
- ,,;
- (ii)
- ,,;
- (iii)
- ,,,,,;
- (iv)
- ,,;
- (i)
- ,,;
- (ii)
- ,,;
- (iii)
- ,,;
5.3. Effects of Blockchain Technology and Carbon Trading Policy
- (i)
- ;
- (ii)
- sB*> sN*;
- (iii)
- ;
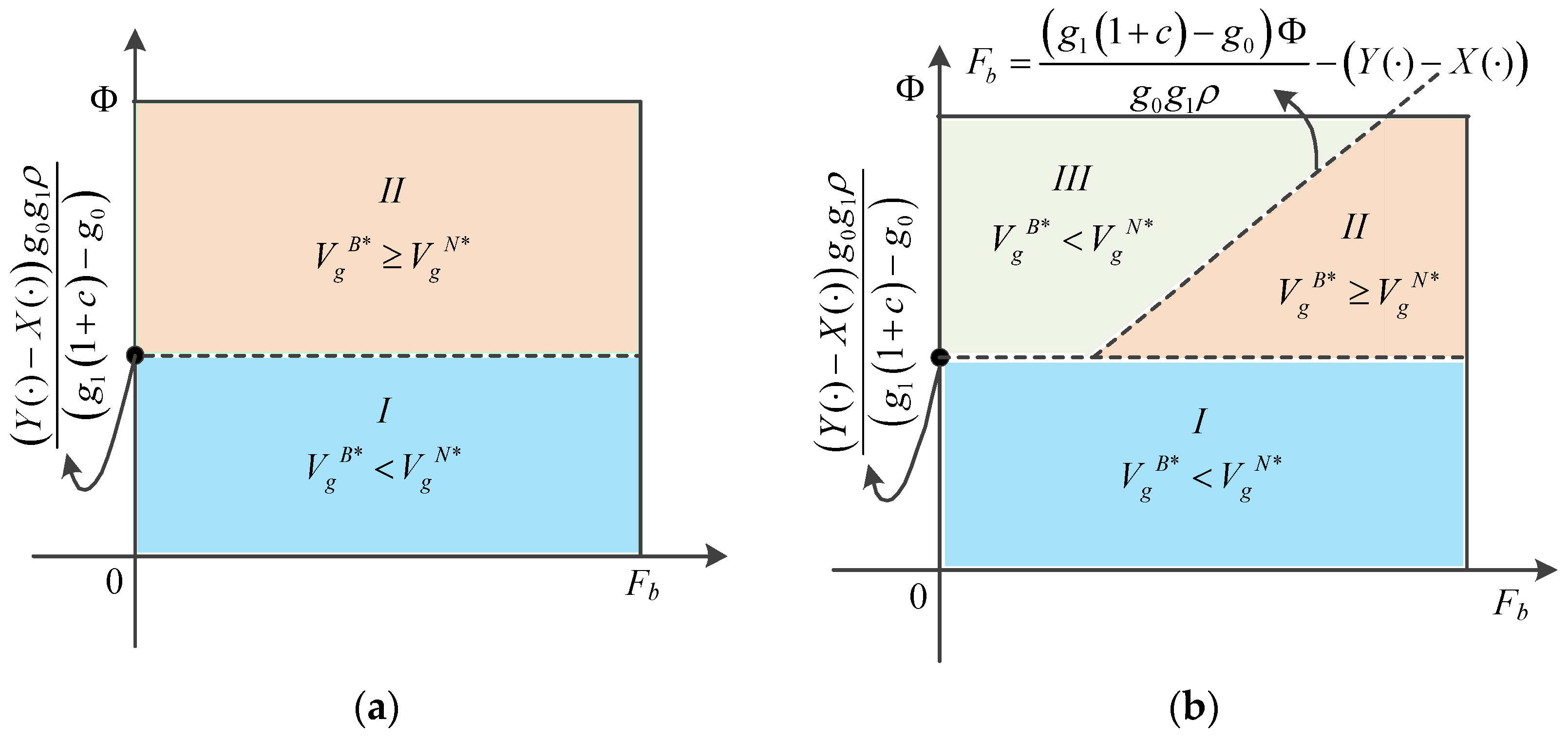
5.4. Values of Blockchain Technology and Carbon Trading Policy
- (i)
- When ignoring the fixed cost of establishing the blockchain (as a sunk cost), i.e., Fb = 0, we have
- (ii)
- when considering the fixed cost of establishing the blockchain, that is, Fb > 0, we have
- (i)
- When the unit operation cost of implementing blockchain is ignored, that is, Cb = 0, we have
- (ii)
- When considering the unit operation cost of implementing the blockchain, that is, Cb > 0, we have
6. Numerical Analysis
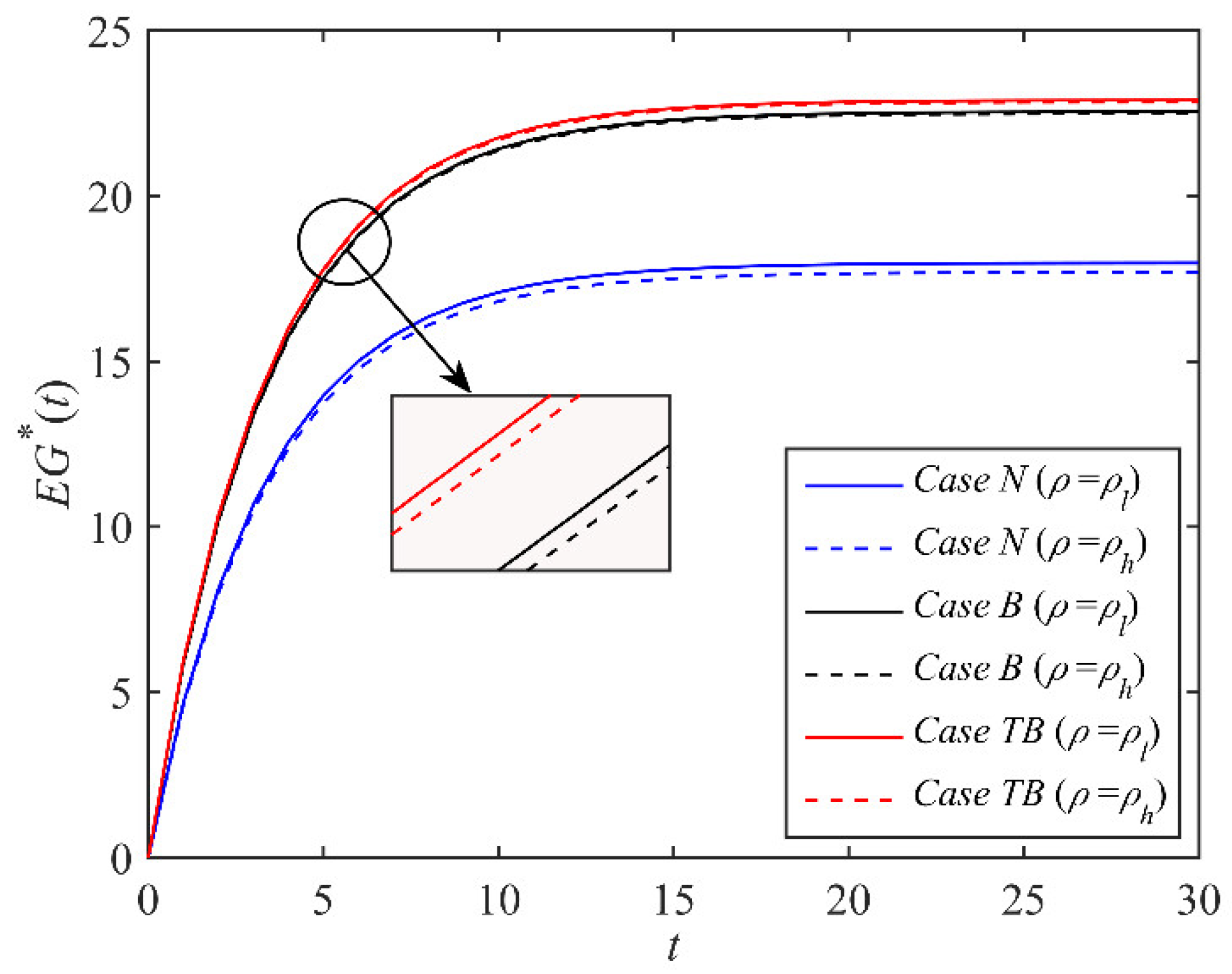
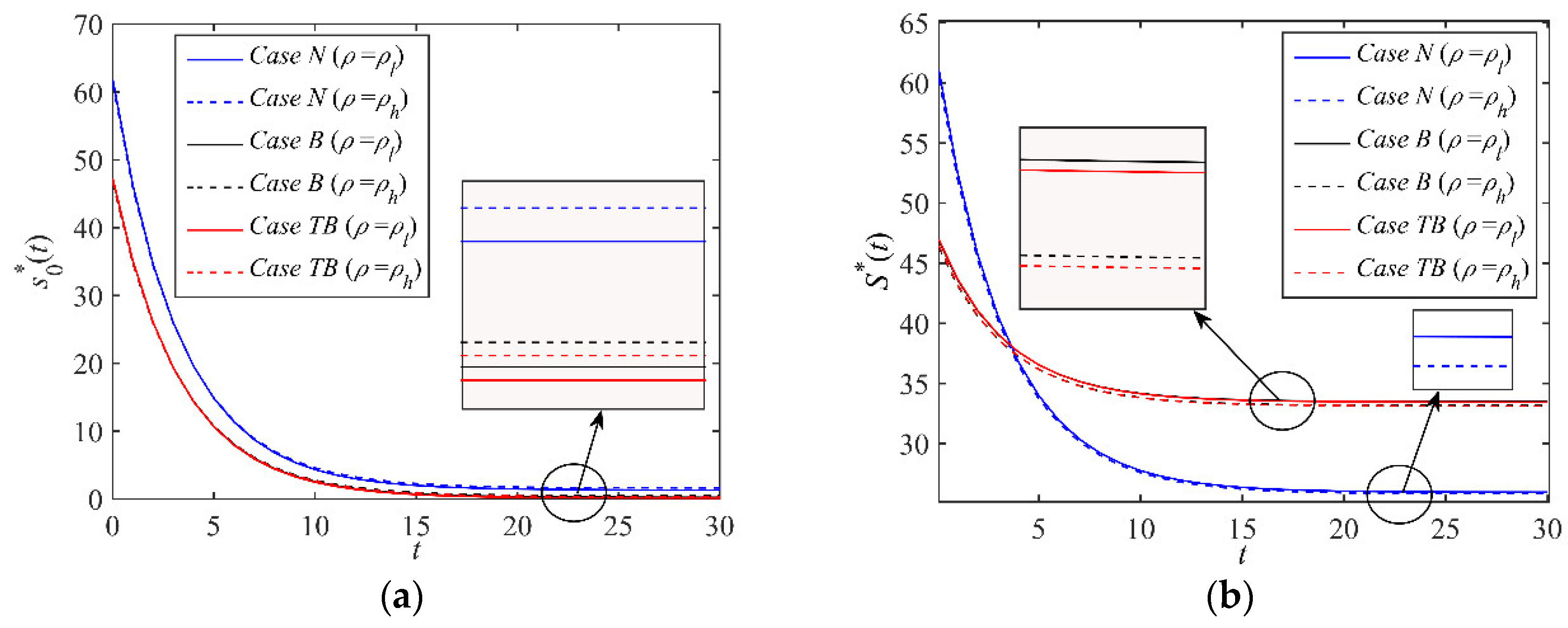
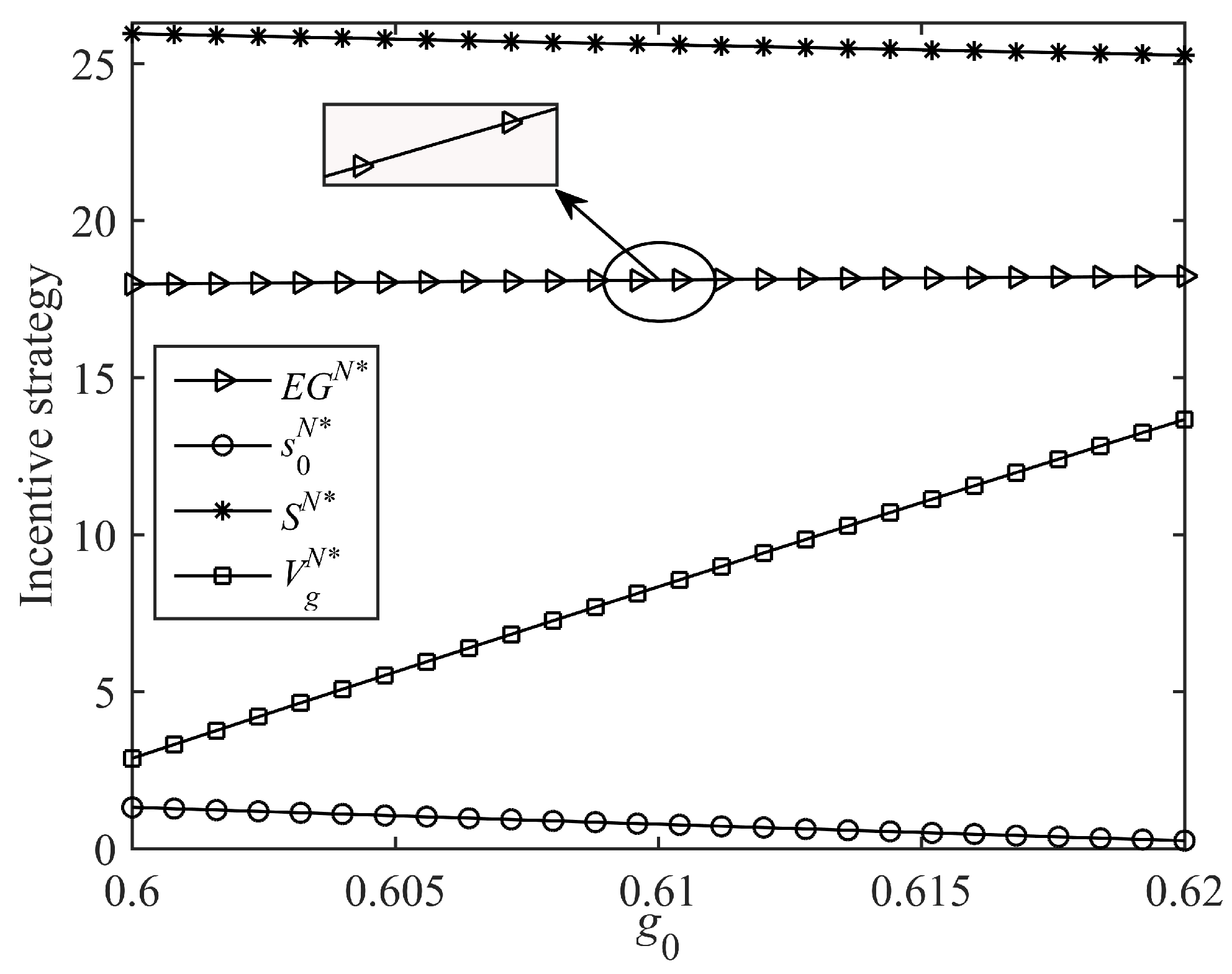
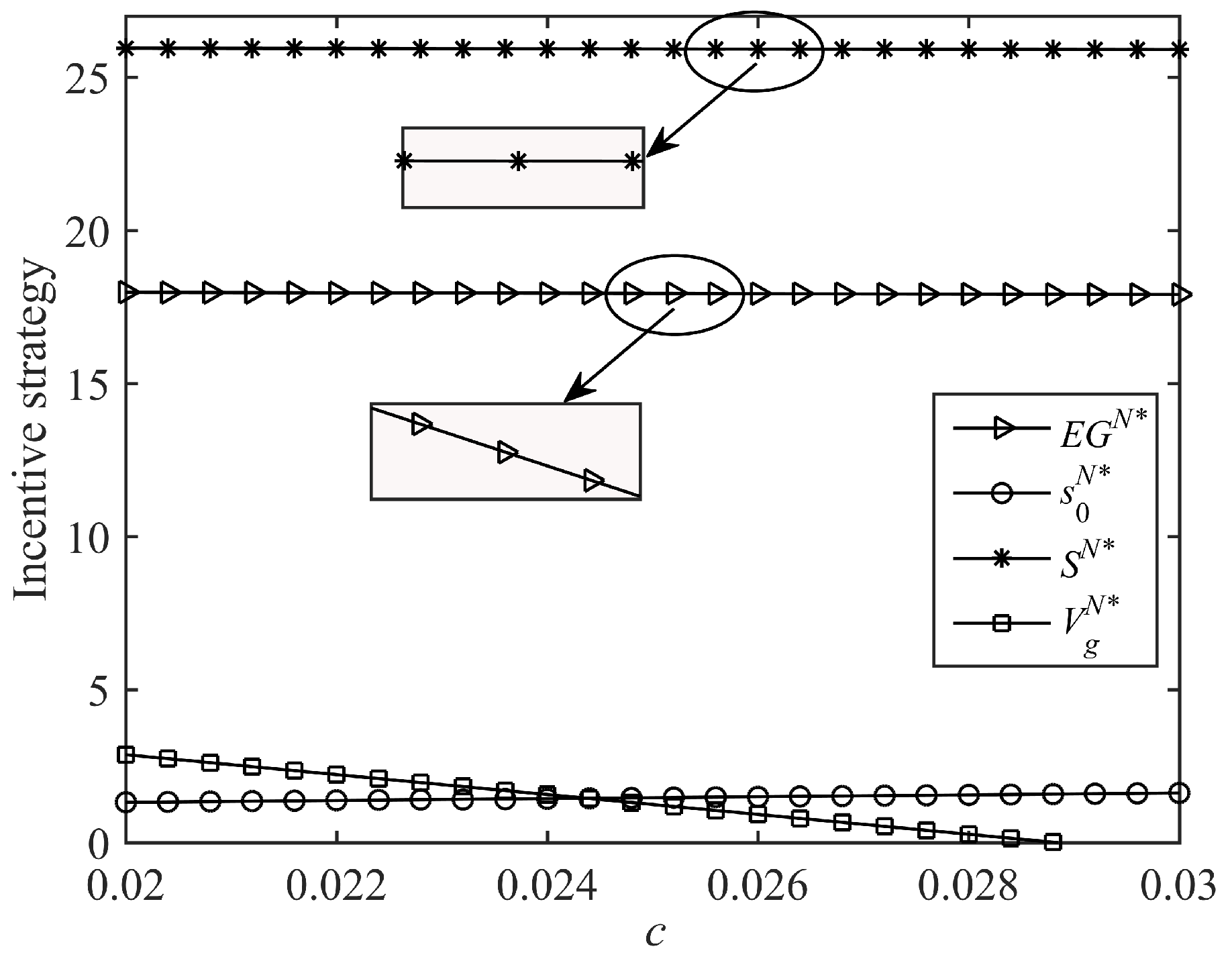
6.1. The Optimal Dynamic Trajectories of Government Incentive Strategy
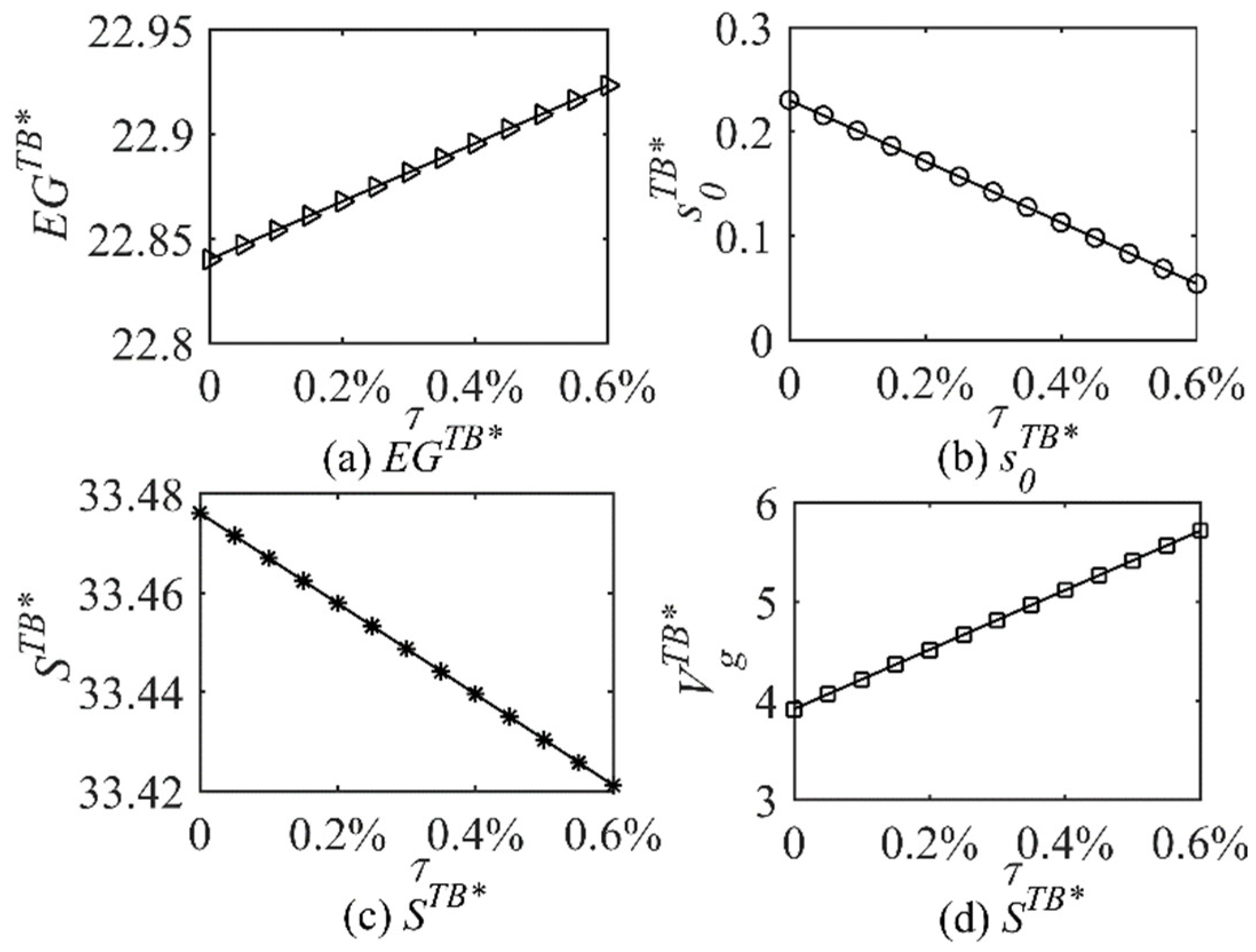
6.2. Impacts of Key Parameters on the Government Dynamic Incentive Strategy
7. Conclusions
7.1. Key Findings
- (1)
- This paper determines the optimal dynamic trajectory change rules of the government’s incentive strategy for port emission reduction under different cases (see Propositions 1–3). We find that under the government dynamic incentive contract, the optimal dynamic trajectory of port VERs in different cases will first monotonously increase and then tend to steady state with the passage of time. However, the optimal dynamic trajectories of the government’s fixed subsidy for port enterprises, the incentive contract, and the discount value of the government’s expected benefit are different in different cases. Especially after the implementation of the blockchain, the government’s dynamic incentive strategy for port emission reduction is related to the unit operating cost of the blockchain. After the carbon trading policy is launched, the government’s dynamic incentive strategy is not only related to the unit operating cost of the blockchain, but also related to the price of the carbon trading market.
- (2)
- This paper reveals the impacts of relevant parameters on the equilibrium solutions of the government and port enterprise in different cases (see Propositions 4–7). We find that the equilibrium solutions in different cases are positively correlated with the influencing factor of the investment level of port emission reduction on its emission reductions, the monetary expression of the social benefit generated by unit emission reduction, and the contract execution efficiency, while they are negatively correlated with the variance of market random disturbance factor, the degree of risk aversion and the contract execution cost. In addition, when the port service price increases, the optimal ERI level and VERs of port enterprises in different cases will increase, while the optimal unit subsidy in the government dynamic incentive contract will decrease. Under blockchain technology, the equilibrium solutions of the government and port enterprise are positively correlated with the green trust coefficient of shipping customers to port ERI level and the disclosure degree of blockchain to market information. Moreover, the optimal ERI level and VERs of port enterprises are negatively correlated with the unit operating cost of blockchain, while the government’s optimal unit subsidy has nothing to do with the unit operating cost of blockchain. When considering carbon trading policy, the increase in carbon trading market price will positively affect the optimal ERI level and VERs of port enterprises, but will not affect the optimal unit subsidy of the government.
- (3)
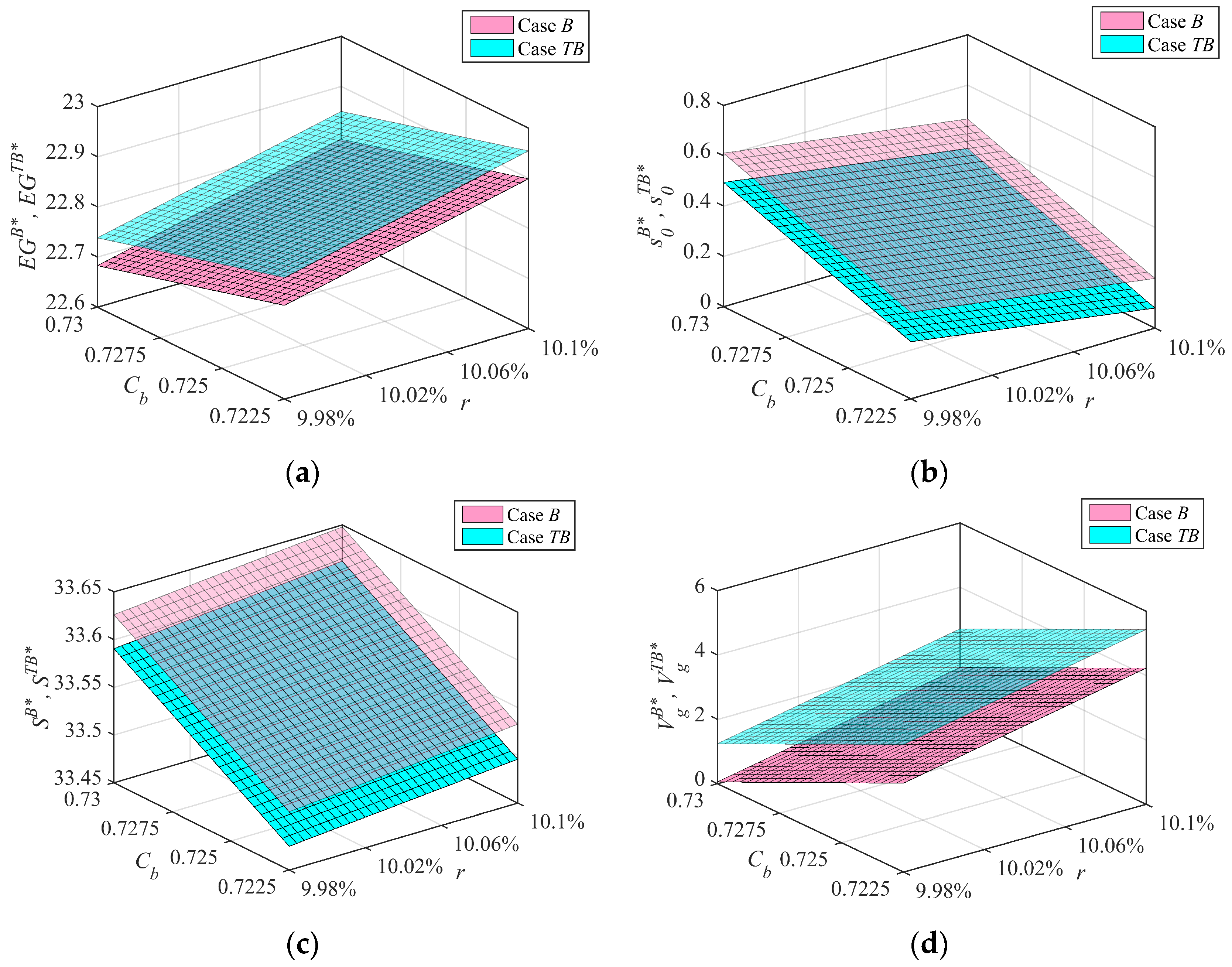
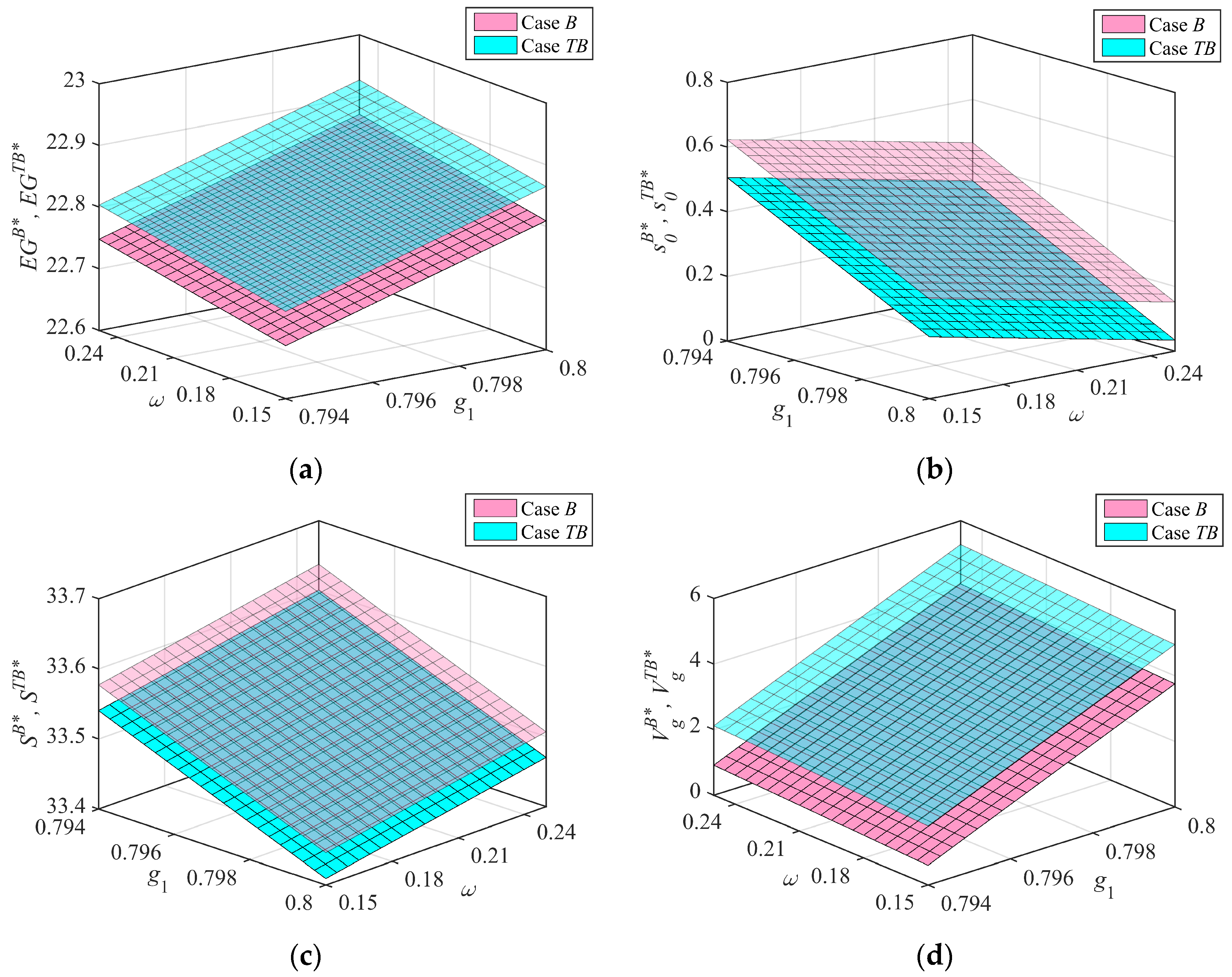
- This paper compares and analyzes the equilibrium solutions in different cases, and gives the effects of blockchain and carbon trading policy on the optimal decisions of the government and port enterprises (see Propositions 8–9). We find that compared with the traditional mode without blockchain, the government’s optimal unit subsidy under blockchain technology will increase. Moreover, if the unit operation cost of blockchain is ignored, the optimal ERI level and VERs of port enterprises will also increase. However, if the unit operation cost of blockchain is considered, the optimal ERI level and VERs of port enterprises will not necessarily increase. In addition, compared with Case B of blockchain technology, the optimal ERI level and VERs of port enterprises will increase under the TB case of considering carbon trading under blockchain technology, while the optimal unit subsidy of the government will remain unchanged.
- (4)
- This paper determines the influencing factors and specific conditions for the government to implement the blockchain and start the carbon trading policy (see Propositions 10–11). We find that when the fixed cost of establishing blockchain is ignored, only if the opportunity cost Φ of port enterprise is greater than a critical point, the expected benefit of the government under blockchain technology will be higher than that under the traditional mode without blockchain. However, when the fixed cost of blockchain is considered, only if the opportunity cost Φ is greater than a certain threshold and the fixed cost of blockchain is less than a certain threshold are simultaneously satisfied, the expected benefit of the government under blockchain technology will be higher than that under the traditional mode without blockchain. In addition, when the unit operation cost of implementing the blockchain is ignored, only if the critical value of carbon emission reduction of port enterprises is small, the expected benefit of the government under the carbon trading policy is higher than that under the carbon-free trading policy. However, when the unit operation cost of blockchain is considered, only if the critical value is small and the unit operation cost of the blockchain is small, the expected benefit of the government under the carbon trading policy is higher than that of the carbon-free trading.
- (5)
- Through the numerical simulation, we confirm that the reasonable implementation of blockchain technology and carbon trading policy will help to improve the VERs of port enterprise and the expected benefit of the government, and the government’s incentive strategy for port emission reduction is sensitive to the changes of relevant parameters under different cases, especially the increase in carbon trading market price is usually conducive to promoting the enthusiasm of port emission reduction and improving the expected benefit of the government.
7.2. Managerial Insights
7.3. Limitations and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbol | Description |
| ERI | Emission reduction investment |
| CERs | Carbon emission reductions |
| VERs | Verified emission reductions |
| v | Market random disturbance factor, v~N(0, δ2) |
| δ2 | Variance of random disturbance factor v |
| η | The investment cost coefficient of port enterprise |
| θ | Degree of risk aversion |
| σ | Attenuation rate of port emission reduction |
| ρ | Discount rate |
| β | Influence factor of port ERI on CERs |
| g | Contract execution efficiency |
| c | Unit execution cost of contract |
| Cb | Unit operation cost of blockchain |
| Fb | Fixed cost of blockchain |
| r | Green trust coefficient of customers on port ERI |
| h | Monetary expression of social benefits generated by unit CERs |
| γ | Impact of port’s CERs on shipping customer demand |
| ξ | Service price of port |
| Φ | Opportunity cost of ERI in port enterprise |
| τ | Carbon trading market price |
| ψ | A critical value of carbon emission reduction to achieve carbon trading |
| ω | Disclosure degree of blockchain for port emission reduction market information |
| I | The port’s ERI level (decision variable) |
| s0 | Fixed subsidy paid by the government to port enterprise (decision variable) |
| s1 | Unit subsidy paid by the government to port enterprise (decision variable) |
| G | CERs of port enterprise |
| EG | VERs of port enterprise |
| S | Dynamic incentive contract of government (S = s0 + s1⋅G) |
| πp | Expected revenue of port enterprise |
| πg | Government expected benefit |
| Vp | Expected discounted profit of port enterprise |
| Vg | Discount value of government expected benefit |
Appendix A. Proofs
References
- Alamoush, A.S.; Ölçer, A.I.; Ballini, F. Ports’ Role in Shipping Decarbonisation: A Common Port Incentive Scheme for Shipping Greenhouse Gas Emissions Reduction. Clean. Logist. Supply Chain 2022, 3, 100021. [Google Scholar] [CrossRef]
- Dulebenets, M.A. Multi-Objective Collaborative Agreements amongst Shipping Lines and Marine Terminal Operators for Sustainable and Environmental-Friendly Ship Schedule Design. J. Clean. Prod. 2022, 342, 130897. [Google Scholar] [CrossRef]
- Xiao, G.; Wang, T.; Chen, X.; Zhou, L. Evaluation of Ship Pollutant Emissions in the Ports of Los Angeles and Long Beach. J. Mar. Sci. Eng. 2022, 10, 1206. [Google Scholar] [CrossRef]
- Ahmad, R.W.; Hasan, H.; Jayaraman, R.; Salah, K.; Omar, M. Blockchain Applications and Architectures for Port Operations and Logistics Management. Res. Transp. Bus. Manag. 2021, 41, 100620. [Google Scholar] [CrossRef]
- Shen, B.; Xu, X.; Yuan, Q. Selling Secondhand Products through an Online Platform with Blockchain. Transp. Res. Part E Logist. Transp. Rev. 2020, 142, 102066. [Google Scholar] [CrossRef]
- Xin, X.; Liu, M.; Wang, X.; Chen, H.; Chen, K. Investment Strategy for Blockchain Technology in a Shipping Supply Chain. Ocean Coast. Manag. 2022, 226, 106263. [Google Scholar] [CrossRef]
- Kapnissis, G.; Vaggelas, G.K.; Leligou, H.C.; Panos, A.; Doumi, M. Blockchain Adoption from the Shipping Industry: An Empirical Study. Marit. Transp. Res. 2022, 3, 100058. [Google Scholar] [CrossRef]
- Zhang, N.; Sun, Q.; Yang, L.; Li, Y. Event-Triggered Distributed Hybrid Control Scheme for the Integrated Energy System. IEEE Trans. Ind. Inform. 2022, 18, 835–846. [Google Scholar] [CrossRef]
- Yang, L.; Li, X.; Sun, M.; Sun, C. Hybrid Policy-Based Reinforcement Learning of Adaptive Energy Management for the Energy Transmission-Constrained Island Group. IEEE Trans. Ind. Inform. 2023, 99, 1–12. [Google Scholar] [CrossRef]
- Choi, T.-M. Blockchain-Technology-Supported Platforms for Diamond Authentication and Certification in Luxury Supply Chains. Transp. Res. Part E Logist. Transp. Rev. 2019, 128, 17–29. [Google Scholar] [CrossRef]
- Sun, Z.; Xu, Q.; Shi, B. Price and Product Quality Decisions for a Two-Echelon Supply Chain in the Blockchain Era. Asia Pac. J. Oper. Res. 2022, 39, 2140016. [Google Scholar] [CrossRef]
- Shen, B.; Dong, C.; Minner, S. Combating Copycats in the Supply Chain with Permissioned Blockchain Technology. Prod. Oper. Manag. 2022, 31, 138–154. [Google Scholar] [CrossRef]
- Liu, S.; Hua, G.; Kang, Y.; Edwin Cheng, T.C.; Xu, Y. What Value Does Blockchain Bring to the Imported Fresh Food Supply Chain? Transp. Res. Part E Logist. Transp. Rev. 2022, 165, 102859. [Google Scholar] [CrossRef]
- Guo, Q.; Zhao, P.; Cheng, S.; Ahmed, M. Two-Period Price Competition of Second-Hand Product Platforms with or without Blockchain under Different Supply and Demand Levels. Comput. Ind. Eng. 2023, 178, 109131. [Google Scholar] [CrossRef]
- Xu, L.; Luo, Y.; Pu, X. Information Acquisition from Data-Driven Analytics: A Perspective of Blockchain Service in a Duopoly Market. Comput. Ind. Eng. 2023, 176, 108994. [Google Scholar] [CrossRef]
- Ying, W.; Jia, S.; Du, W. Digital Enablement of Blockchain: Evidence from HNA Group. Int. J. Inf. Manag. 2018, 39, 1–4. [Google Scholar] [CrossRef]
- Ramirez-Peña, M.; Sánchez Sotano, A.J.; Pérez-Fernandez, V.; Abad, F.J.; Batista, M. Achieving a Sustainable Shipbuilding Supply Chain under I4.0 Perspective. J. Clean. Prod. 2020, 244, 118789. [Google Scholar] [CrossRef]
- Pu, S.; Lam, J.S.L. Blockchain Adoptions in the Maritime Industry: A Conceptual Framework. Marit. Policy Manag. 2021, 48, 777–794. [Google Scholar] [CrossRef]
- Balci, G.; Surucu-Balci, E. Blockchain Adoption in the Maritime Supply Chain: Examining Barriers and Salient Stakeholders in Containerized International Trade. Transp. Res. Part E Logist. Transp. Rev. 2021, 156, 102539. [Google Scholar] [CrossRef]
- Meng, Z.W.; Wang, X.G. Research on benefit allocation mechanism of shipping alliance transportation capacity sharing based on blockchain. Appl. Res. Comput. 2021, 38, 1631–1636. (In Chinese) [Google Scholar]
- Chen, Y.; Yang, B. Analysis on the Evolution of Shipping Logistics Service Supply Chain Market Structure under the Application of Blockchain Technology. Adv. Eng. Inform. 2022, 53, 101714. [Google Scholar] [CrossRef]
- Wang, X.G.; Yin, M. Research on Two-stage Pricing of Shipping Supply Chain under Blockchain Platform. Comput. Eng. Appl. 2023, 59, 319–327. (In Chinese) [Google Scholar]
- Zhao, H.D.; Liu, J.G.; Wang, J.J.; Li, J. Research on investment strategy of shipping supply chain based on blockchain technology. J. Ind. Eng. Eng. Manag. 2022, 36, 117–128. (In Chinese) [Google Scholar]
- Acciaro, M.; Ghiara, H.; Cusano, M.I. Energy Management in Seaports: A New Role for Port Authorities. Energy Policy 2014, 71, 4–12. [Google Scholar] [CrossRef]
- Innes, A.; Monios, J. Identifying the Unique Challenges of Installing Cold Ironing at Small and Medium Ports—The Case of Aberdeen. Transp. Res. Part D Transp. Environ. 2018, 62, 298–313. [Google Scholar] [CrossRef]
- Poulsen, R.T.; Sampson, H. A Swift Turnaround? Abating Shipping Greenhouse Gas Emissions via Port Call Optimization. Transp. Res. Part D Transp. Environ. 2020, 86, 102460. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Q.; Wang, L.; Chen, Y.; Wang, J. A Review of the Port Carbon Emission Sources and Related Emission Reduction Technical Measures. Environ. Pollut. 2023, 320, 121000. [Google Scholar] [CrossRef]
- Zhou, C.; Huang, H.; Liu, Z.; Ding, Y.; Xiao, J.; Shu, Y. Identification and Analysis of Ship Carbon Emission Hotspots Based on Data Field Theory: A Case Study in Wuhan Port. Ocean Coast. Manag. 2023, 235, 106479. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, L.; Di, Z.; Xu, L. Subsidy or Punishment: An Analysis of Evolutionary Game on Implementing Shore-Side Electricity. Reg. Stud. Mar. Sci. 2021, 48, 102010. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, K.; Li, Z.-C.; Fu, X.; Felix, T.S. Chan. Subsidy or Minimum Requirement? Regulation of Port Adaptation Investment under Disaster Ambiguity. Transp. Res. Part B Methodol. 2021, 150, 457–481. [Google Scholar] [CrossRef]
- Meng, L.; Wang, J.; Yan, W.; Han, C. A Differential Game Model for Emission Reduction Decisions between Ports and Shipping Enterprises Considering Environmental Regulations. Ocean Coast. Manag. 2022, 225, 106221. [Google Scholar] [CrossRef]
- Meng, L.; Liu, K.; He, J.; Han, C.; Liu, P. Carbon Emission Reduction Behavior Strategies in the Shipping Industry under Government Regulation: A Tripartite Evolutionary Game Analysis. J. Clean. Prod. 2022, 378, 134556. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, S.; Dai, L.; Zhang, Z.; Hu, H. Shore Side Electricity Subsidy Policy Efficiency Optimization: From the Game Theory Perspective. Ocean Coast. Manag. 2022, 228, 106324. [Google Scholar] [CrossRef]
- Song, Z.; Tang, W.; Zhao, R.; Zhang, G. Implications of Government Subsidies on Shipping Companies’ Shore Power Usage Strategies in Port. Transp. Res. Part E Logist. Transp. Rev. 2022, 165, 102840. [Google Scholar] [CrossRef]
- Tan, Z.; Zeng, X.; Wang, T.; Wang, Y.; Chen, J. Capacity Investment of Shore Power Berths for a Container Port: Environmental Incentive and Infrastructure Subsidy Policies. Ocean Coast. Manag. 2023, 239, 106582. [Google Scholar] [CrossRef]
- Zhong, H.; Hu, Z.; Yip, T.L. Carbon Emissions Reduction in China’s Container Terminals: Optimal Strategy Formulation and the Influence of Carbon Emissions Trading. J. Clean. Prod. 2019, 219, 518–530. [Google Scholar] [CrossRef]
- Yang, L.; Cai, Y.; Wei, Y.; Huang, S. Choice of Technology for Emission Control in Port Areas: A Supply Chain Perspective. J. Clean. Prod. 2019, 240, 118105. [Google Scholar] [CrossRef]
- Zhong, H.; Chen, W.; Gu, Y. A System Dynamics Model of Port Hinterland Intermodal Transport: A Case Study of Guangdong-Hong Kong-Macao Greater Bay Area under Different Carbon Taxation Policies. Res. Transp. Bus. Manag. 2023, 49, 100987. [Google Scholar] [CrossRef]
- Li, S.; Liu, J.; Wu, J.; Hu, X. Spatial Spillover Effect of Carbon Emission Trading Policy on Carbon Emission Reduction: Empirical Data from Transport Industry in China. J. Clean. Prod. 2022, 371, 133529. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Zhao, Z.; Ren, J.; Chen, X. Research on Carbon Emission Reduction Effect of China’s Regional Digital Trade under the “Double Carbon” Target—Combination of the Regulatory Role of Industrial Agglomeration and Carbon Emissions Trading Mechanism. J. Clean. Prod. 2023, 405, 137049. [Google Scholar] [CrossRef]
- Holmstrom, B.; Milgrom, P. Aggregation and Linearity in the Provision of Intertemporal Incentives. Econometrica 1987, 55, 303. [Google Scholar] [CrossRef]
- Zhou, X.; Swan, P.L. Performance Thresholds in Managerial Incentive Contracts. J. Bus. 2003, 76, 665–696. [Google Scholar] [CrossRef]
- Yu, Y.; Kong, X. Robust Contract Designs: Linear Contracts and Moral Hazard. Oper. Res. 2020, 68, 1457–1473. [Google Scholar] [CrossRef]
- Gao, X.; Tian, J. Multi-Period Incentive Contract Design in the Agent Emergency Supplies Reservation Strategy with Asymmetric Information. Comput. Ind. Eng. 2018, 120, 94–102. [Google Scholar] [CrossRef]
- Gao, J.; Fan, H.; Cao, B.; Wang, N. Quality Incentive Contracts Considering Asymmetric Product Manufacturability Information: Piece Rate vs. Tournament. Comput. Ind. Eng. 2020, 144, 106446. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Q. Proportional Incentive Contracts in Live Streaming Commerce Supply Chain Based on Target Sales Volume. Electron. Commer. Res. 2023, 3, 1–29. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Q.; Zhang, G. Optimal Contracts with Moral Hazard and Adverse Selection in a Live Streaming Commerce Market. J. Retail. Consum. Serv. 2023, 74, 103419. [Google Scholar] [CrossRef]
- Barbos, A. Dynamic Contracts with Random Monitoring. J. Math. Econ. 2019, 85, 1–16. [Google Scholar] [CrossRef]
- Hori, K.; Osano, H. Dynamic Contract and Discretionary Termination Policy under Loss Aversion. J. Econ. Dyn. Control 2020, 111, 103794. [Google Scholar] [CrossRef]
- Szydlowski, M.; Yoon, J.H. Ambiguity in Dynamic Contracts. J. Econ. Theory 2021, 199, 105229. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, Z.; Wang, P.; Du, C. A Dynamic Incentive and Reputation Mechanism for Energy-Efficient Federated Learning in 6g. Digit. Commun. Netw. 2022, 1–10. [Google Scholar] [CrossRef]
- Xie, Y.; Ding, C.; Li, Y.; Wang, K. Optimal Incentive Contract in Continuous Time with Different Behavior Relationships between Agents. Int. Rev. Financ. Anal. 2023, 86, 102521. [Google Scholar] [CrossRef]
- Tan, R.; Wu, Y.; Su, P.; Liao, R.; Zhang, J. Optimal Dynamic Incentive Mechanism Design for Construction and Demolition Waste Recycling with Bayesian Learning. J. Clean. Prod. 2023, 412, 137371. [Google Scholar] [CrossRef]
- Ma, D.; Hu, J.; Wang, W. Differential Game of Product–Service Supply Chain Considering Consumers’ Reference Effect and Supply Chain Members’ Reciprocity Altruism in the Online-To-Offline Mode. Ann. Oper. Res. 2021, 304, 263–297. [Google Scholar] [CrossRef]
- Hong, Z.; Guo, X. Green Product Supply Chain Contracts Considering Environmental Responsibilities. Omega 2019, 83, 155–166. [Google Scholar] [CrossRef]
- Chai, Q.; Sun, M.; Lai, K.; Xiao, Z. The Effects of Government Subsidies and Environmental Regulation on Remanufacturing. Comput. Ind. Eng. 2023, 178, 109126. [Google Scholar] [CrossRef]
- Chen, F. Salesforce Incentives, Market Information, and Production/Inventory Planning. Manag. Sci. 2005, 51, 60–75. [Google Scholar] [CrossRef]
- Zhang, T.; Dong, P.; Chen, X.; Gong, Y. The Impacts of Blockchain Adoption on a Dual-Channel Supply Chain with Risk-Averse Members. Omega 2023, 114, 102747. [Google Scholar] [CrossRef]
- Choi, T.-M.; Guo, S.; Liu, N.; Shi, X. Optimal Pricing in On-Demand-Service-Platform-Operations with Hired Agents and Risk-Sensitive Customers in the Blockchain Era. Eur. J. Oper. Res. 2020, 284, 1031–1042. [Google Scholar] [CrossRef]
- Gottlieb, D.; Moreira, H. Simple Contracts with Adverse Selection and Moral Hazard. Theor. Econ. 2022, 17, 1357–1401. [Google Scholar] [CrossRef]
- Pun, H.; Swaminathan, J.M.; Hou, P. Blockchain Adoption for Combating Deceptive Counterfeits. Prod. Oper. Manag. 2021, 30, 864–882. [Google Scholar] [CrossRef]


| References | Blockchain Adoption | Shipping Industry | Port Emission Reduction | Government Subsidy | Carbon Trading Policy | |
|---|---|---|---|---|---|---|
| Dynamic Incentive | Static Incentive | |||||
| [27,28] | No | No | Yes | No | No | No |
| [29,33] | No | No | Yes | No | Yes | No |
| [20,21,22,23] | Yes | Yes | No | No | No | No |
| [10,11,12,13,14] | Yes | No | No | No | No | No |
| [51,52] | No | No | No | Yes | No | No |
| [39] | No | No | Yes | No | Yes | Yes |
| [36,37,40] | No | No | Yes | No | No | Yes |
| [31,32] | No | No | Yes | Yes | No | No |
| This paper | Yes | Yes | Yes | Yes | Yes | Yes |
| Parameters | β | 0.39925 | 0.3995 | 0.39975 | 0.4 | 0.4 | 0.4 | 0.4 |
|---|---|---|---|---|---|---|---|---|
| h | 1.495 | 1.495 | 1.495 | 1.495 | 1.4975 | 1.5 | 1.5025 | |
| Case N | EGN* | 17.876 | 17.899 | 17.922 | 17.945 | 17.958 | 17.971 | 17.983 |
| s0N* | 1.590 | 1.541 | 1.491 | 1.441 | 1.389 | 1.336 | 1.284 | |
| SN* | 25.980 | 25.964 | 25.948 | 25.932 | 25.939 | 25.947 | 25.955 | |
| VgN* | 0.015 | 0.525 | 1.034 | 1.544 | 2.097 | 2.651 | 3.206 | |
| Case B | EGB* | 22.705 | 22.728 | 22.751 | 22.774 | 22.802 | 22.829 | 22.856 |
| s0B* | 0.487 | 0.457 | 0.426 | 0.396 | 0.327 | 0.258 | 0.189 | |
| SB* | 33.399 | 33.403 | 33.407 | 33.412 | 33.438 | 33.465 | 33.492 | |
| VgB* | 1.312 | 1.617 | 1.921 | 2.226 | 2.929 | 3.633 | 4.338 | |
| Case TB | EGTB* | 22.760 | 22.783 | 22.807 | 22.830 | 22.857 | 22.885 | 22.912 |
| s0TB* | 0.370 | 0.340 | 0.309 | 0.279 | 0.210 | 0.140 | 0.071 | |
| STB* | 33.362 | 33.367 | 33.371 | 33.375 | 33.402 | 33.429 | 33.456 | |
| VgTB* | 2.503 | 2.809 | 3.115 | 3.421 | 4.126 | 4.832 | 5.538 |
| Parameters | ξ | 0.9975 | 0.998 | 0.9985 | 0.9990 | 0.9990 | 0.9990 | 0.9990 |
|---|---|---|---|---|---|---|---|---|
| γ | 1.1970 | 1.1970 | 1.1970 | 1.1970 | 1.1975 | 1.198 | 1.1985 | |
| Case N | EGN* | 17.924 | 17.929 | 17.934 | 17.940 | 17.944 | 17.948 | 17.952 |
| s0N* | 1.529 | 1.507 | 1.486 | 1.465 | 1.447 | 1.429 | 1.411 | |
| SN* | 26.098 | 26.083 | 26.068 | 26.054 | 26.041 | 26.029 | 26.017 | |
| VgN* | 0.587 | 0.815 | 1.043 | 1.271 | 1.462 | 1.652 | 1.843 | |
| Case B | EGB* | 22.758 | 22.766 | 22.774 | 22.783 | 22.789 | 22.796 | 22.803 |
| s0B* | 0.437 | 0.416 | 0.396 | 0.375 | 0.358 | 0.341 | 0.323 | |
| SB* | 33.566 | 33.557 | 33.548 | 33.539 | 33.532 | 33.524 | 33.517 | |
| VgB* | 1.784 | 1.997 | 2.209 | 2.422 | 2.599 | 2.777 | 2.955 | |
| Case TB | EGTB* | 22.814 | 22.822 | 22.830 | 22.838 | 22.845 | 22.852 | 22.859 |
| s0TB* | 0.320 | 0.299 | 0.279 | 0.258 | 0.241 | 0.223 | 0.206 | |
| STB* | 33.530 | 33.521 | 33.512 | 33.503 | 33.495 | 33.488 | 33.480 | |
| VgTB* | 2.979 | 3.192 | 3.405 | 3.618 | 3.796 | 3.974 | 4.152 |
| Parameters | δ2 | 1.0252 | 1.052 | 1.0752 | 1.12 | 1.12 | 1.12 | 1.12 |
|---|---|---|---|---|---|---|---|---|
| θ | 0.19 | 0.19 | 0.19 | 0.19 | 0.1925 | 0.195 | 0.1975 | |
| Case N | EGN* | 17.977 | 17.951 | 17.925 | 17.898 | 17.890 | 17.882 | 17.874 |
| s0N* | 1.310 | 1.450 | 1.592 | 1.738 | 1.780 | 1.823 | 1.865 | |
| SN* | 25.949 | 25.967 | 25.986 | 26.004 | 26.010 | 26.015 | 26.021 | |
| VgN* | 2.899 | 2.218 | 1.522 | 0.811 | 0.604 | 0.396 | 0.189 | |
| Case B | EGB* | 22.841 | 22.817 | 22.791 | 22.766 | 22.758 | 22.751 | 22.743 |
| s0B* | 0.226 | 0.323 | 0.421 | 0.521 | 0.550 | 0.580 | 0.609 | |
| SB* | 33.4757 | 33.4860 | 33.4966 | 33.507 | 33.510 | 33.514 | 33.517 | |
| VgB* | 3.937 | 3.356 | 2.761 | 2.153 | 1.975 | 1.798 | 1.620 | |
| Case TB | EGTB* | 22.897 | 22.872 | 22.847 | 22.821 | 22.814 | 22.807 | 22.799 |
| s0TB* | 0.109 | 0.205 | 0.304 | 0.404 | 0.433 | 0.463 | 0.492 | |
| STB* | 33.4391 | 33.4495 | 33.4601 | 33.471 | 33.474 | 33.477 | 33.480 | |
| VgTB* | 5.137 | 4.555 | 3.960 | 3.352 | 3.174 | 2.996 | 2.818 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Xu, Q.; Liu, J. Dynamic Incentive Contract of Government for Port Enterprises to Reduce Emissions in the Blockchain Era: Considering Carbon Trading Policy. Sustainability 2023, 15, 12148. https://doi.org/10.3390/su151612148
Sun Z, Xu Q, Liu J. Dynamic Incentive Contract of Government for Port Enterprises to Reduce Emissions in the Blockchain Era: Considering Carbon Trading Policy. Sustainability. 2023; 15(16):12148. https://doi.org/10.3390/su151612148
Chicago/Turabian StyleSun, Zhongmiao, Qi Xu, and Jinrong Liu. 2023. "Dynamic Incentive Contract of Government for Port Enterprises to Reduce Emissions in the Blockchain Era: Considering Carbon Trading Policy" Sustainability 15, no. 16: 12148. https://doi.org/10.3390/su151612148
APA StyleSun, Z., Xu, Q., & Liu, J. (2023). Dynamic Incentive Contract of Government for Port Enterprises to Reduce Emissions in the Blockchain Era: Considering Carbon Trading Policy. Sustainability, 15(16), 12148. https://doi.org/10.3390/su151612148








