Mathematical Modeling and Analysis of Capacitor Voltage Balancing for Power Converters with Fewer Switches
Abstract
1. Introduction
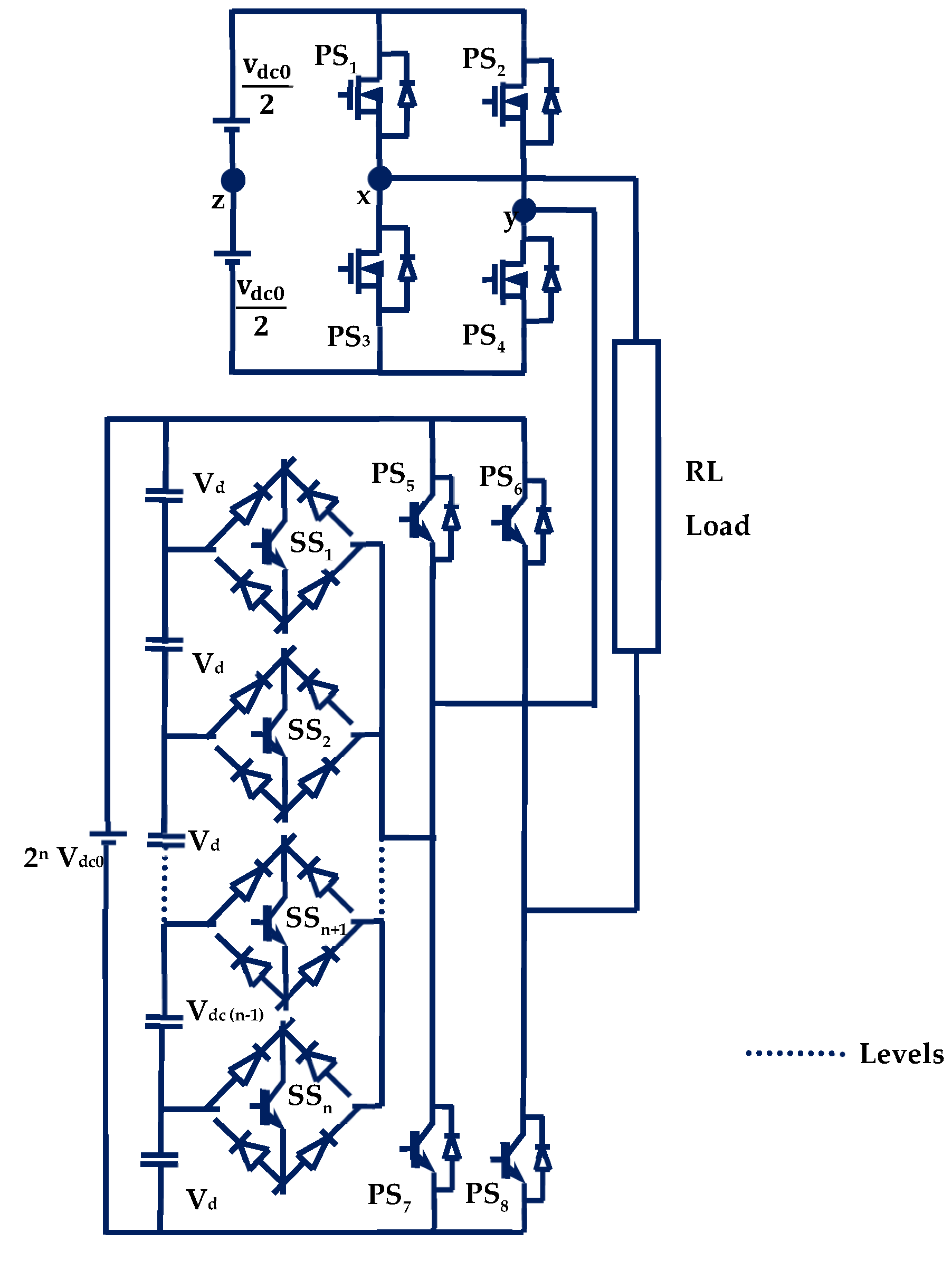
2. Proposed Cascaded H-Bridge MLI
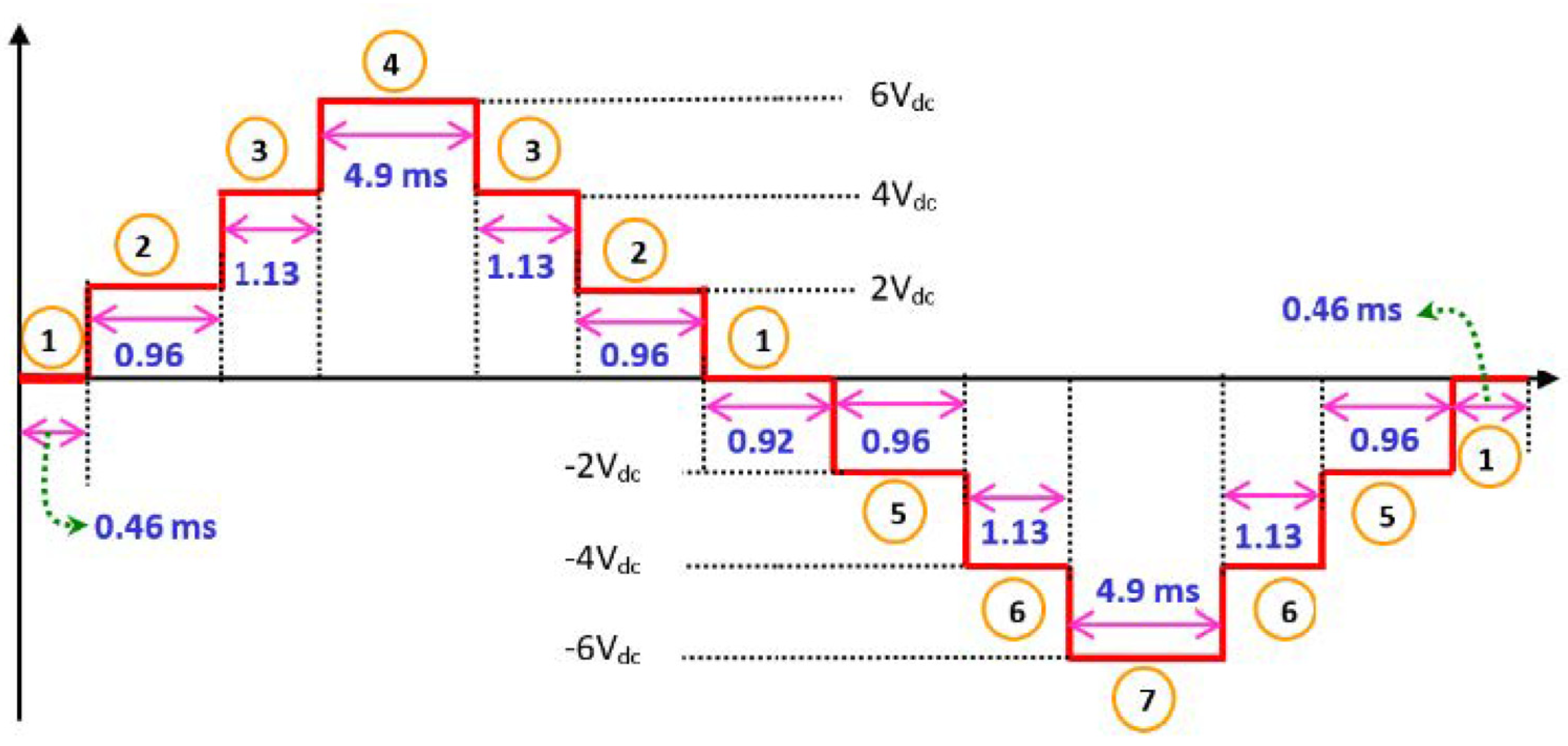
2.1. Modes of Operation
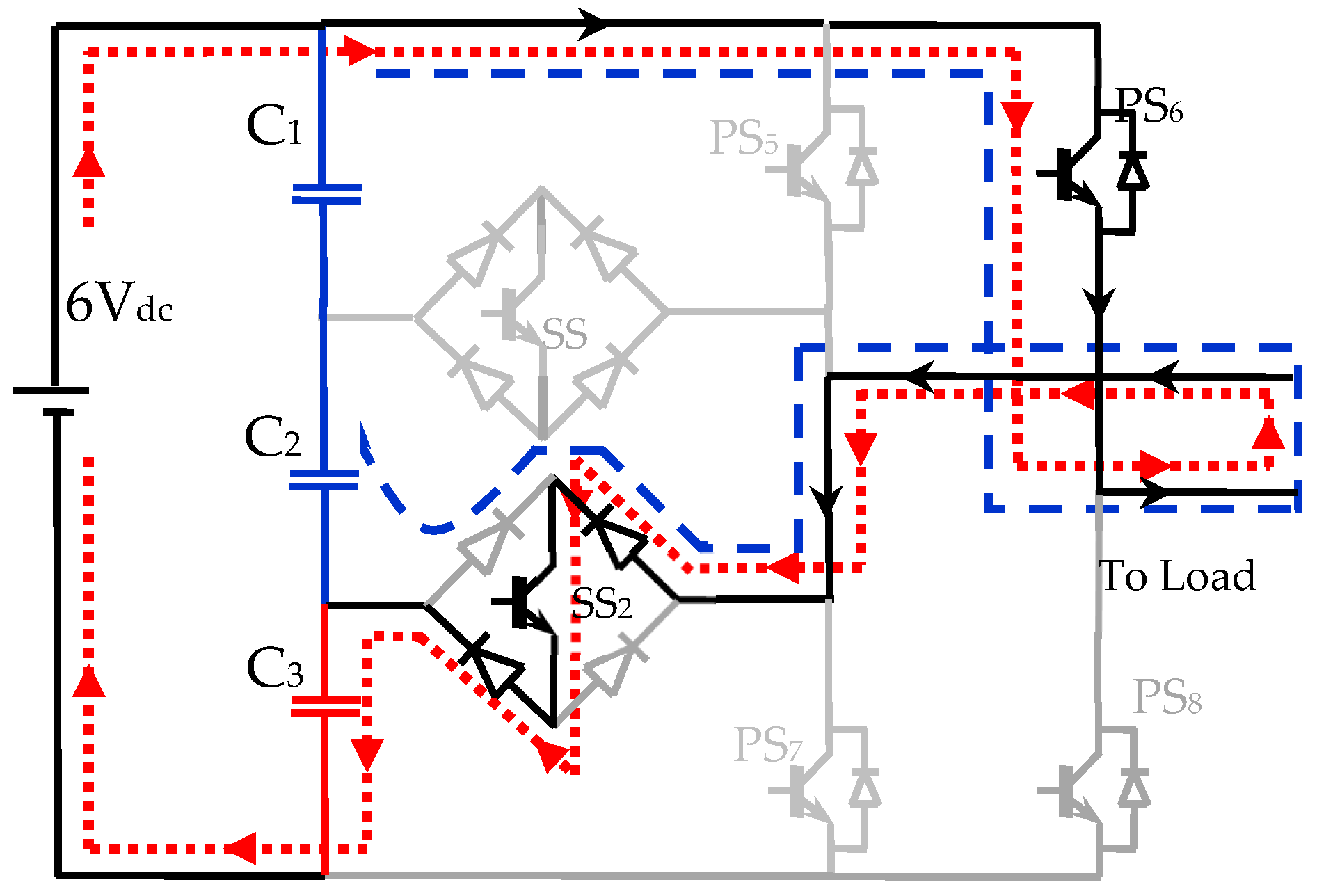
2.2. Capacitor States of Bottom H Bridge Inverter
- C1 and C3 total charging time = 4.18 milli seconds;
- C1 and C3 total discharging time = 4.18 milli seconds;
- C2 total charging time = 3.84 milli seconds;
- C2 total discharging time = 4.52 milli seconds.
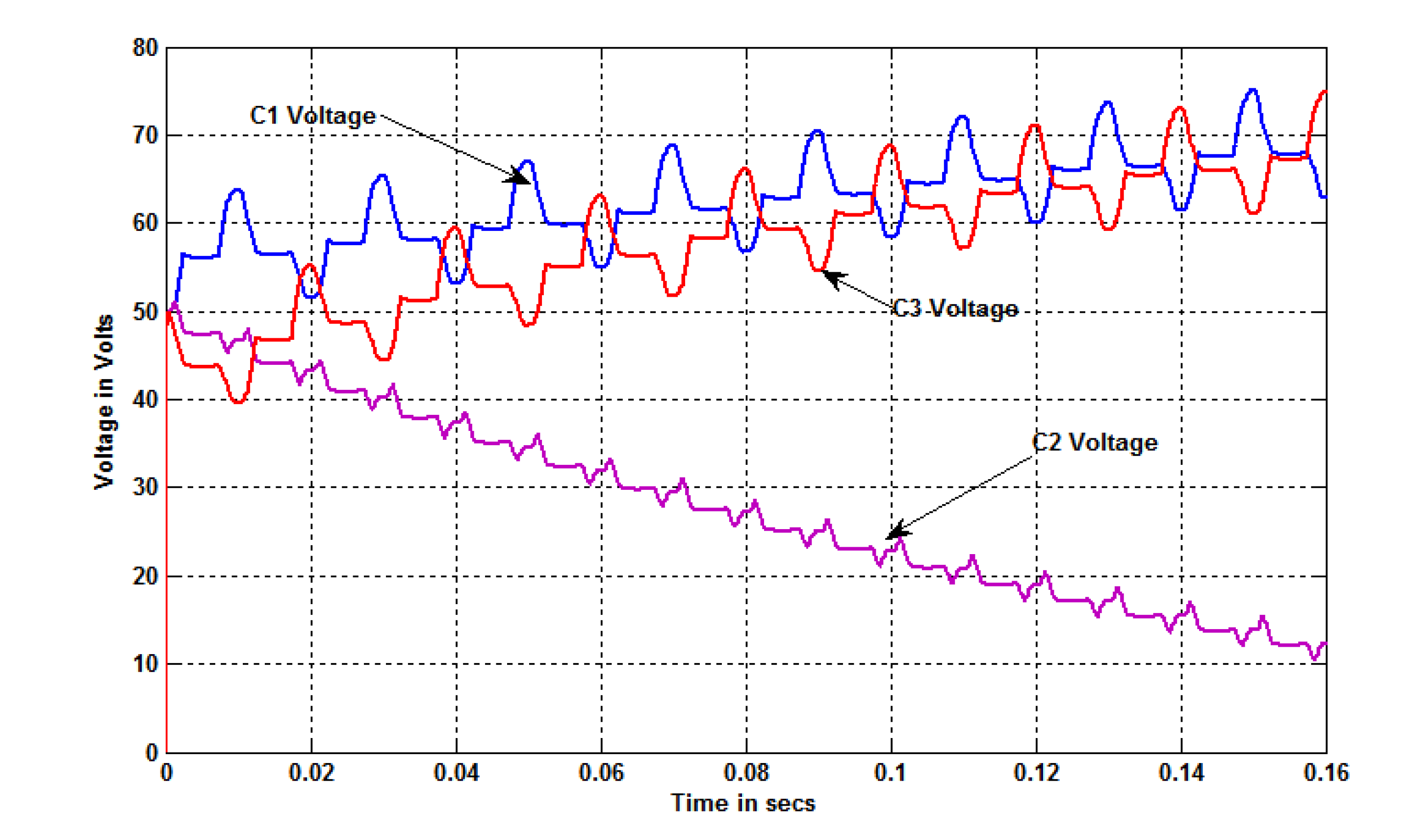
3. Capacitor Voltage Balancing in the Proposed Inverter
4. Modeling of PWM Pulses for Proposed Cascaded Multilevel Inverter
- Step 1.
- Form a set:
- Step 2.
- Write the permutation P on
- Step 3.
- Eliminate the final column in the above permutation P1 and rework as
- Step 4.
- We can develop the switching signals for the secondary switches calculated from the above equation. The first and last columns of the matrix are responsible for establishing the switching patterns for the initial and final secondary switches, respectively. The equations for SS1 and SSn are also included.
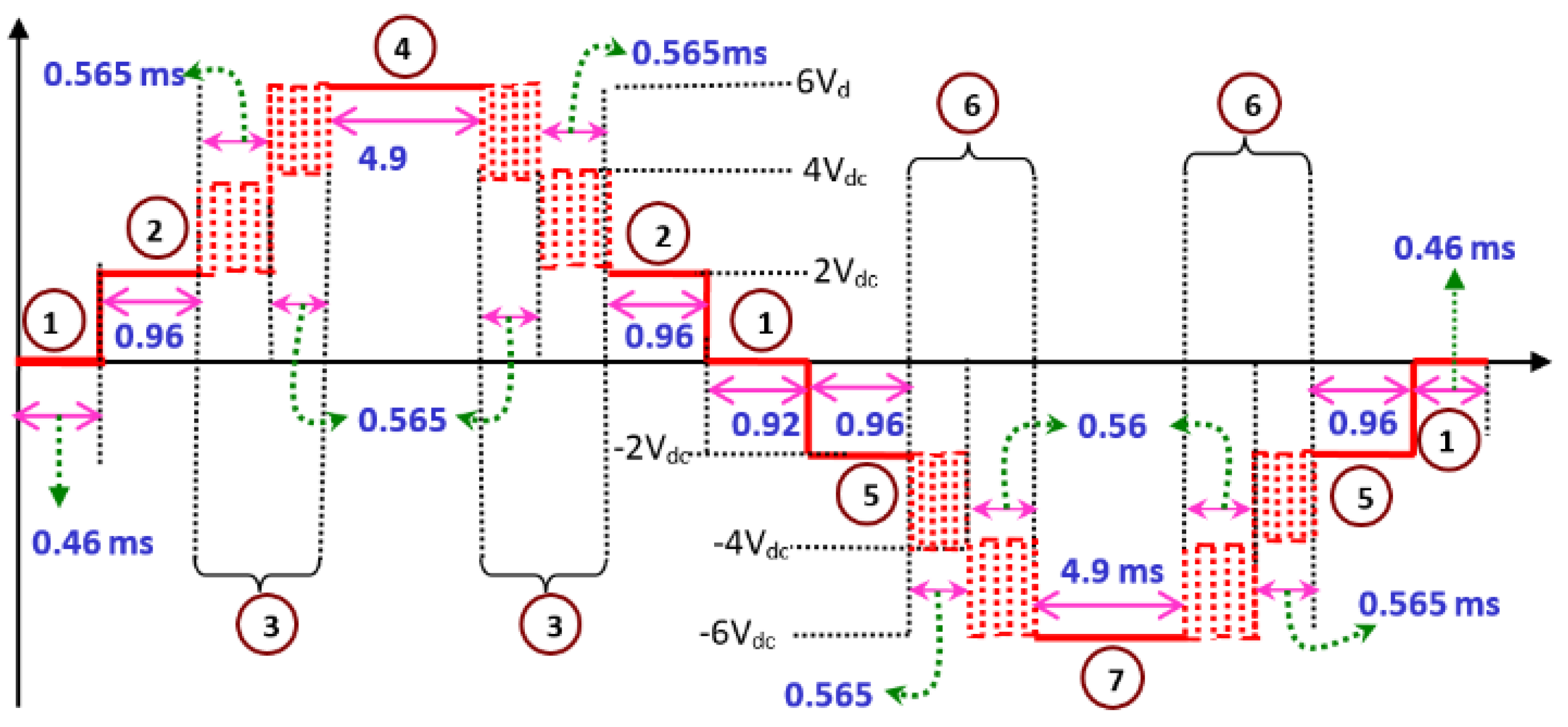
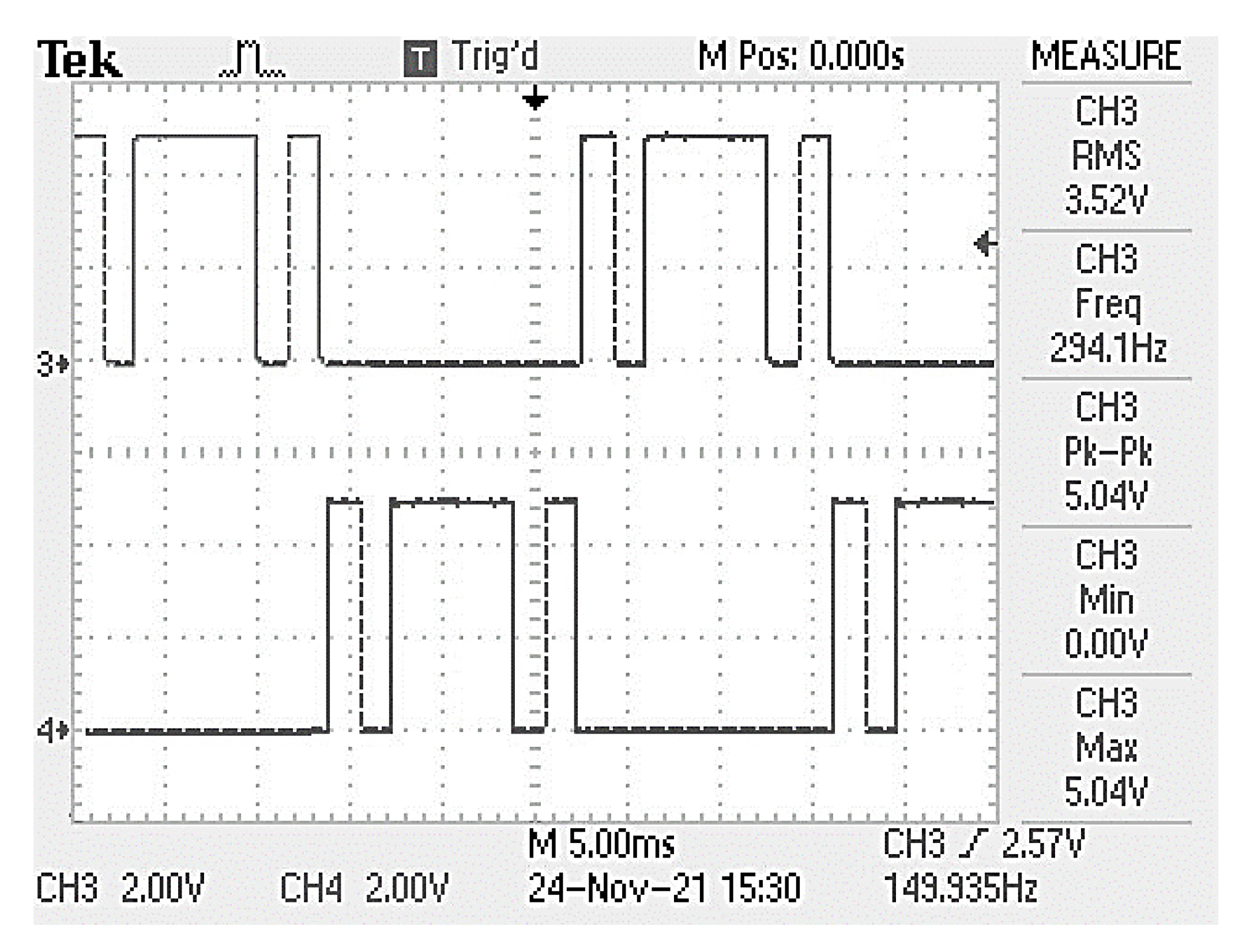
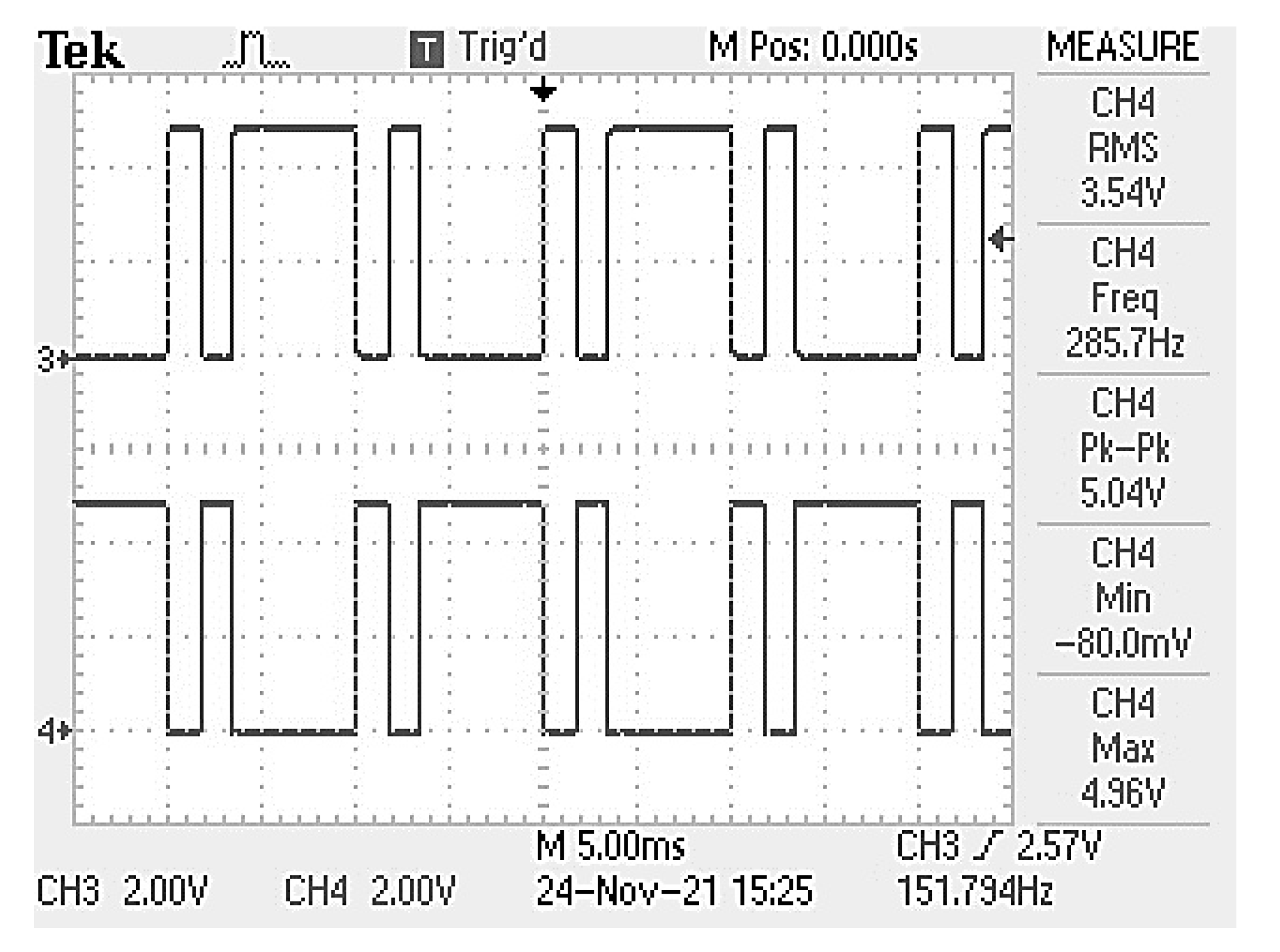
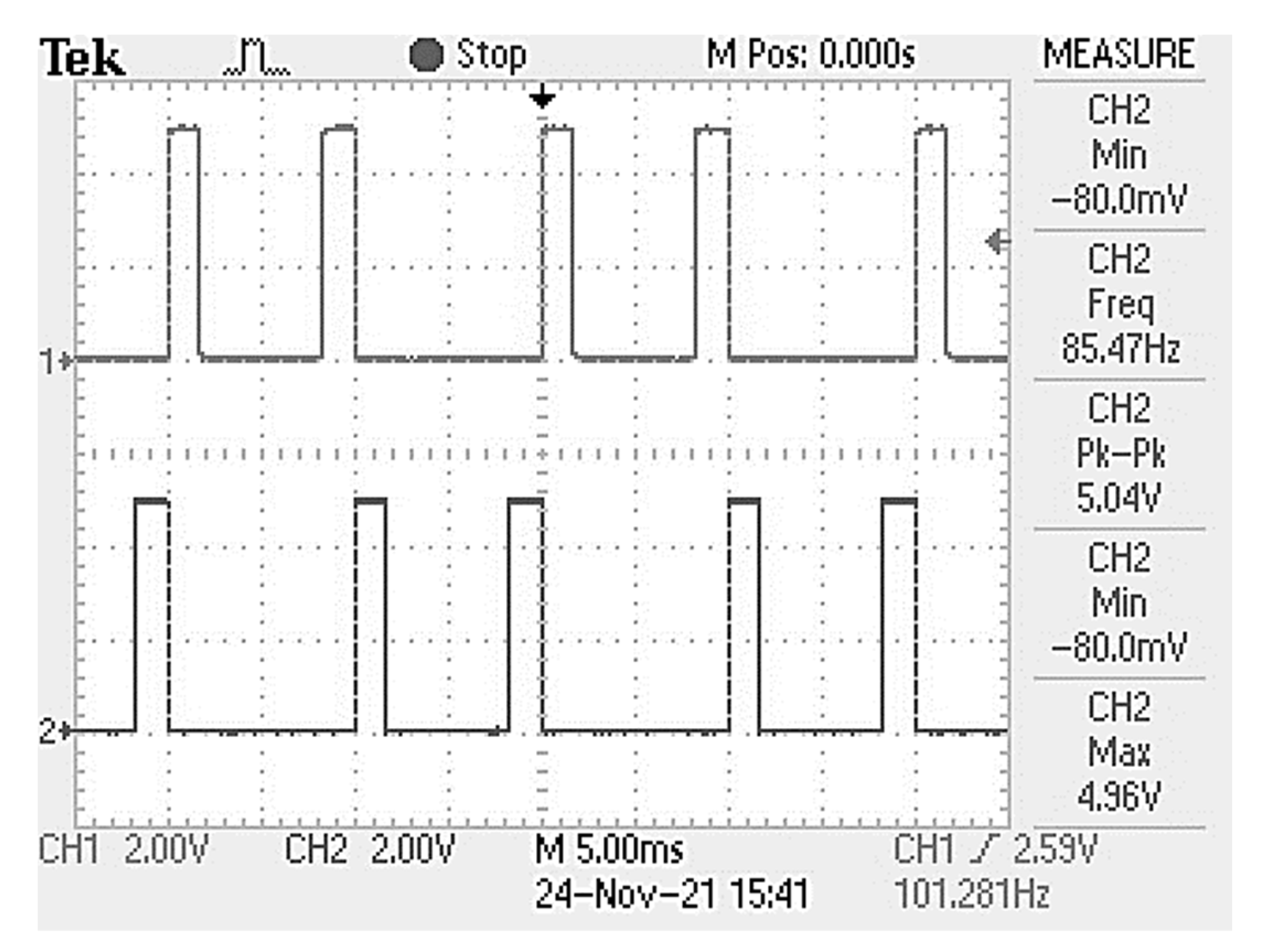
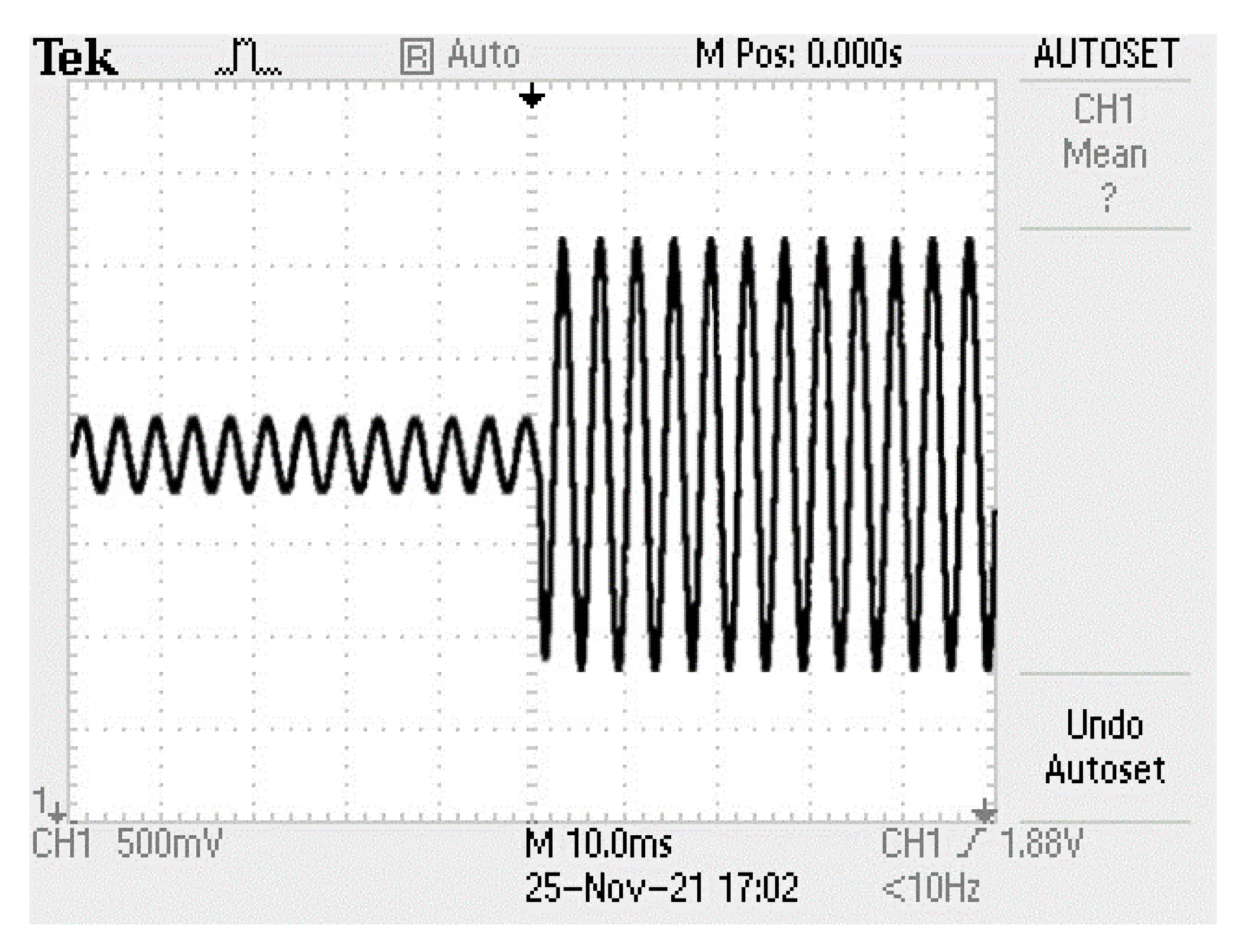
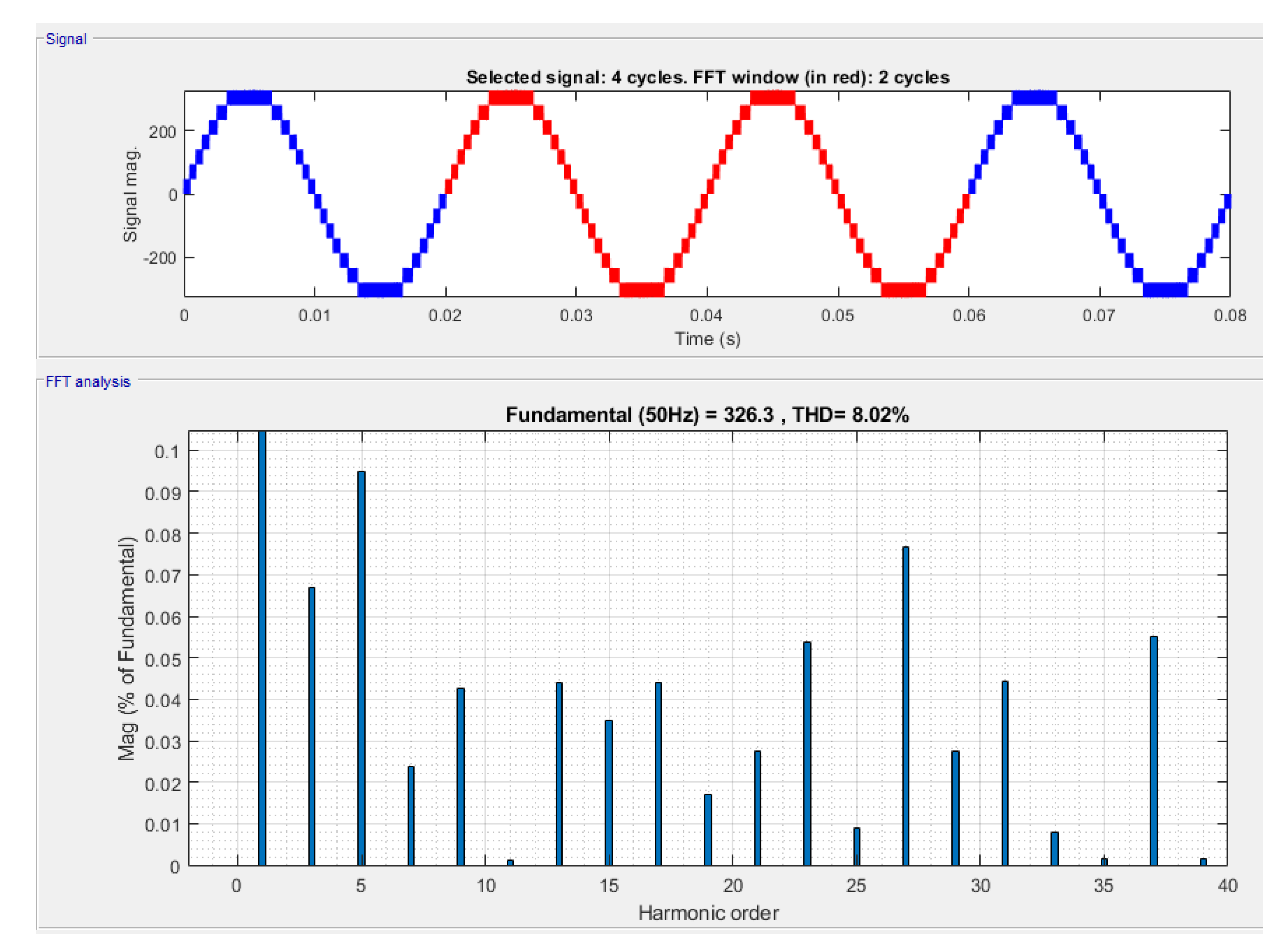
5. Results and Discussion
6. Hardware Validation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Almehizia, A.A.; Al-Masri, H.M.; Ehsani, M. Feasibility Study of sustainable energy sources in a fossil fuel rich country. IEEE Trans. Ind. Appl. 2019, 55, 4433–4440. [Google Scholar] [CrossRef]
- Kumar, B.R.; Sundararaju, K.; Saravanan, S.; Senthil Kumar, R. Mboa based PV array interconnection scheme for enlarging the harvested power under PS condition. Int. J. Electron. 2022, 110, 26–53. [Google Scholar]
- Podder, A.K.; Roy, N.K.; Pota, H.R. MPPT methods for solar PV systems: A critical review based on tracking nature. IET Renew. Power Gener. 2019, 13, 1615–1632. [Google Scholar] [CrossRef]
- Alzahrani, A.; Ramu, S.K.; Devarajan, G.; Vairavasundaram, I.; Vairavasundaram, S. A review on hydrogen-based hybrid microgrid system: Topologies for hydrogen energy storage, integration, and energy management with solar and wind energy. Energies 2022, 15, 7979. [Google Scholar] [CrossRef]
- Ramu, S.K.; Paramasivam, S.; Muthusamy, S.; Panchal, H.; Sadasivuni, K.K.; Noorollahi, Y. A novel design of switched boost action based multiport converter using dsPIC controller for Renewable Energy Applications. Energy Sources Part A Recovery Util. Environ. Eff. 2021, 44, 75–90. [Google Scholar] [CrossRef]
- Rong, F.; Gong, X.; Huang, S. A novel grid-connected PV system based on MMC to get the maximum power under partial shading conditions. IEEE Trans. Power Electron. 2017, 32, 4320–4333. [Google Scholar] [CrossRef]
- Farivar, G.; Hredzak, B.; Agelidis, V.G. A DC-side sensorless cascaded H-bridge multilevel converter-based Photovoltaic System. IEEE Trans. Ind. Electron. 2016, 63, 4233–4241. [Google Scholar] [CrossRef]
- Can, E. Mathematical algorithm of Fuzzy Logic Controller for multilevel inverter creating vertical divided voltage. Acta Polytech. 2019, 59, 1–11. [Google Scholar] [CrossRef]
- Can, E. Novel high multilevel inverters investigated on simulation. Electr. Eng. 2016, 99, 633–638. [Google Scholar] [CrossRef]
- Bendyk, M.S.; Luk, P.C.-K.; Alkhafaji, M.H. Control strategy for a modified Cascade multilevel inverter with dual DC source for enhanced Drivetrain Operation. IEEE Trans. Ind. Appl. 2017, 53, 4655–4664. [Google Scholar] [CrossRef]
- Can, E.; Sayan, H.H. A novel SSPWM controlling inverter running nonlinear device. Electr. Eng. 2016, 100, 39–46. [Google Scholar] [CrossRef]
- Yu, Y.; Konstantinou, G.; Hredzak, B.; Agelidis, V.G. Power balance of cascaded H-bridge multilevel converters for large-scale photovoltaic integration. IEEE Trans. Power Electron. 2016, 31, 292–303. [Google Scholar] [CrossRef]
- Yu, Y.; Konstantinou, G.; Hredzak, B.; Agelidis, V.G. Operation of cascaded H-bridge multilevel converters for large-scale photovoltaic power plants under bridge failures. IEEE Trans. Ind. Electron. 2015, 62, 7228–7236. [Google Scholar] [CrossRef]
- Kaliamoorthy, M.; Rajasekaran, V.; Raj, I.G.C. Single-phase fifteen-level grid-connected inverter for photovoltaic system with evolutionary programming based MPPT algorithm. Sol. Energy 2014, 105, 314–329. [Google Scholar] [CrossRef]
- Kaliamoorthy, M.; Rajasekaran, V.; Christopher Raj, I.G.; Hubert Tony Raj, L. Generalised hybrid switching topology for a single-phase Modular Multilevel Inverter. IET Power Electron. 2014, 7, 2472–2485. [Google Scholar] [CrossRef]
- Ramu, S.K.; Irudayaraj, G.C.; Paramasivam, S.K.; Murugesan, R.; Muthusamy, S.; Sundararajan, S.C.; Panchal, H.; Sadasivuni, K.K.; Meena, R.S. A simplified methodology for renewable energy integration and harmonic current reduction in Hybrid Micro Grid. Energy Sources Part A Recovery Util. Environ. Eff. 2021, 44, 8357–8379. [Google Scholar] [CrossRef]
- Hu, P.; Teodorescu, R.; Wang, S.; Li, S.; Guerrero, J.M. A currentless sorting and selection-based capacitor-voltage-balancing method for modular multilevel converters. IEEE Trans. Power Electron. 2019, 34, 1022–1025. [Google Scholar] [CrossRef]
- Peftitsis, D.; Tolstoy, G.; Antonopoulos, A.; Rabkowski, J.; Jang-Kwon, L.; Bakowski, M.; Ängquist, L.; Nee, H. High-power modular multilevel converters with SIC JFETs. IEEE Trans. Power Electron. 2012, 27, 28–36. [Google Scholar] [CrossRef]
- Can, E.; Sayan, H.H. Development of fractional sinus pulse width modulation with β gap on three step signal processing. Int. J. Electron. 2022, 110, 527–546. [Google Scholar] [CrossRef]
- Can, E. A new multi-level inverter with reverse connected dual DC to DC converter at simulation. Int. J. Model. Simul. 2020, 42, 34–46. [Google Scholar] [CrossRef]
- Can, E.; Sayan, H.H. Investigation of the effect of the gap at the zero-crossing point of pwms creating the first level voltage in a multi-level inverter. J. Eng. Res. 2022. [Google Scholar] [CrossRef]
- Anand, I.; Senthilkumar, S.; Biswas, D.; Kaliamoorthy, M. Dynamic Power Management System employing a single-stage power converter for standalone solar PV applications. IEEE Trans. Power Electron. 2018, 33, 10352–10362. [Google Scholar] [CrossRef]
- Hinago, Y.; Koizumi, H. A single-phase multilevel inverter using switched series/parallel DC voltage sources. IEEE Trans. Ind. Electron. 2010, 57, 2643–2650. [Google Scholar] [CrossRef]
- Sabyasachi, S.; Borghate, V.B.; Karasani, R.R.; Maddugari, S.K.; Suryawanshi, H.M. Hybrid control technique-based three-phase cascaded multilevel inverter topology. IEEE Access 2017, 5, 26912–26921. [Google Scholar] [CrossRef]
- Agrawal, N.; Bansal, P. A new 21-level asymmetrical multilevel inverter topology with different PWM techniques. In Proceedings of the 2017 Recent Developments in Control, Automation & Power Engineering (RDCAPE), Noida, India, 26–27 October 2017. [Google Scholar]
- Reddy, V.P.; Muralikumar, K.; Ponnambalam, P.; Mahapatra, A. Asymmetric 15-level multilevel inverter with fuzzy controller using super imposed carrier PWM. In Proceedings of the 2017 Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 21–22 April 2017. [Google Scholar]
- Saravanan, S.; Senthil Kumar, R.; Prakash, A.; Chinnadurai, T.; Tiwari, R.; Prabaharan, N.; Chitti Babu, B. Photovoltaic array reconfiguration to extract maximum power under partially shaded conditions. In Distributed Energy Resources in Microgrids; Academic Press: Cambridge, MA, USA, 2019; pp. 215–241. [Google Scholar]
- Sarasvathy, K.; Luciana, M.L.; Kumar, R.S. Comparison of sine, hysteresis, SVPWM and predictive PWM techniques for shunt active power filter. In Proceedings of the 2017 IEEE International Conference on Electrical, Instrumentation and Communication Engineering (ICEICE), Karur, India, 27–28 April 2017. [Google Scholar]
- Alghaythi, M.L.; O’Connell, R.M.; Islam, N.E.; Khan, M.M.S.; Guerrero, J.M. A High Step-Up Interleaved DC–DC Converter with Voltage Multiplier and Coupled Inductors for Renewable Energy Systems. IEEE Access 2020, 8, 123165–123174. [Google Scholar] [CrossRef]
- Alghaythi, M.L.; O’Connell, R.M.; Islam, N.E. Design of a High Step-up DC-DC Power Converter with Voltage Multiplier Cells and Reduced Losses on Semiconductors for Photovoltaic Systems. In Proceedings of the 2019 IEEE Electric Ship Technologies Symposium (ESTS), Arlington, VA, USA, 14–16 August 2019; pp. 214–218. [Google Scholar]
- Najwan Hamidi, M.; Ishak, D.; Ammirrul Atiqi Mohd Zainuri, M.; Ai Ooi, C.; Tarmizi, T. Asymmetrical multi-level DC-link inverter for PV Energy System with perturb and observe based voltage regulator and capacitor compensator. J. Mod. Power Syst. Clean Energy 2021, 9, 199–209. [Google Scholar] [CrossRef]






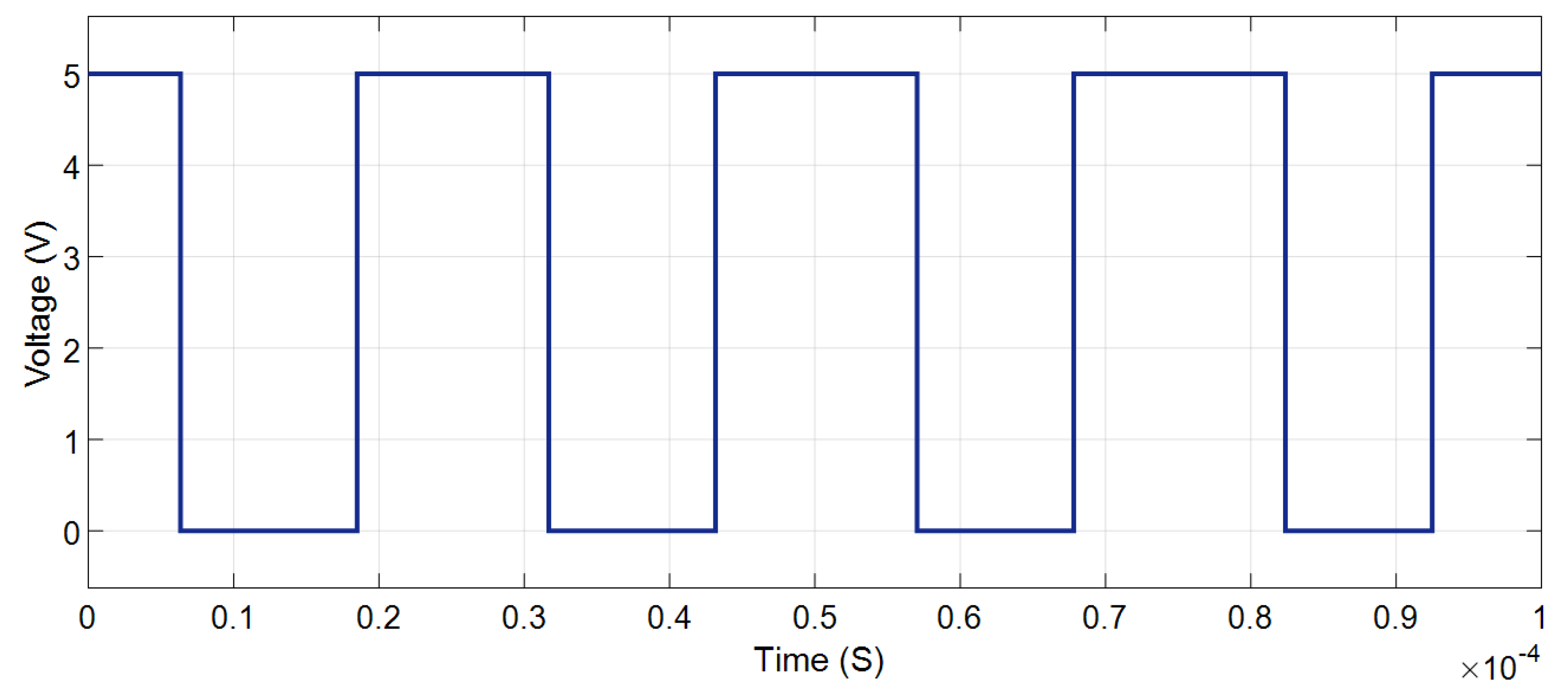
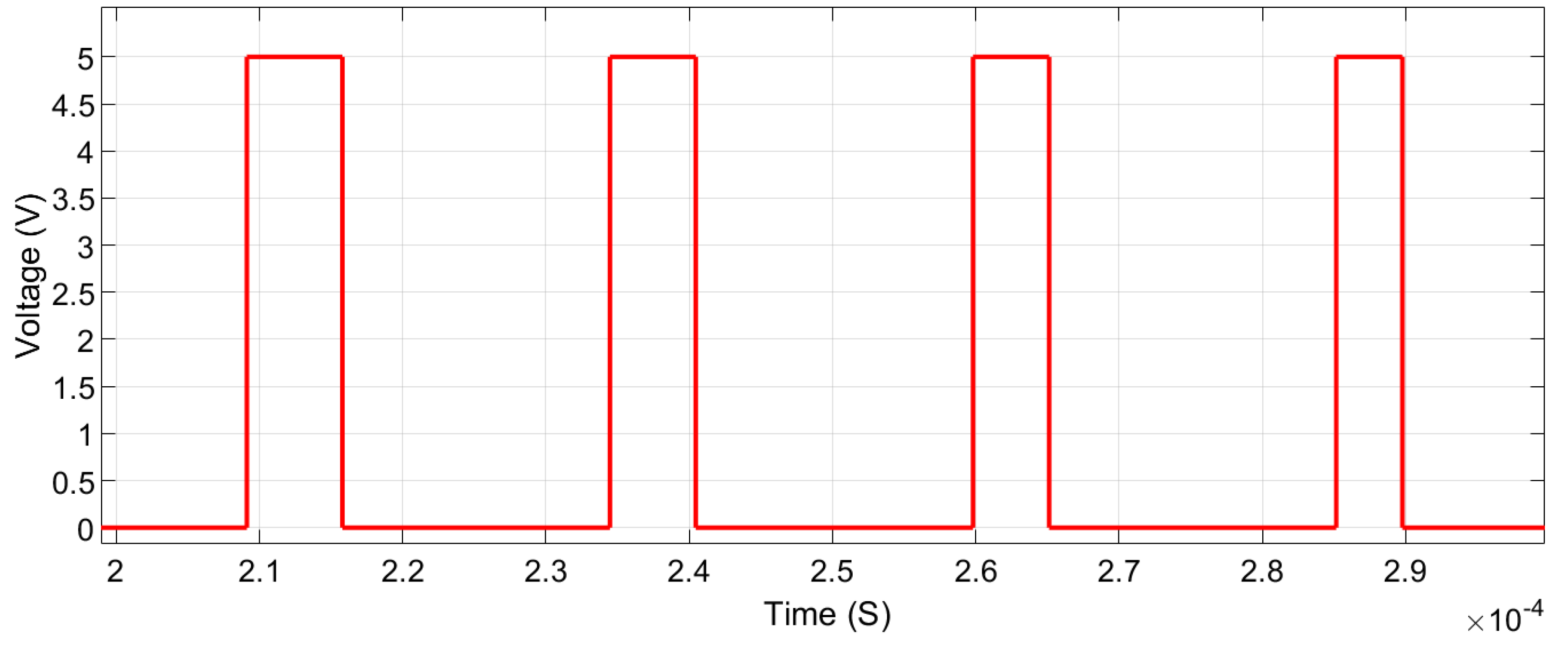
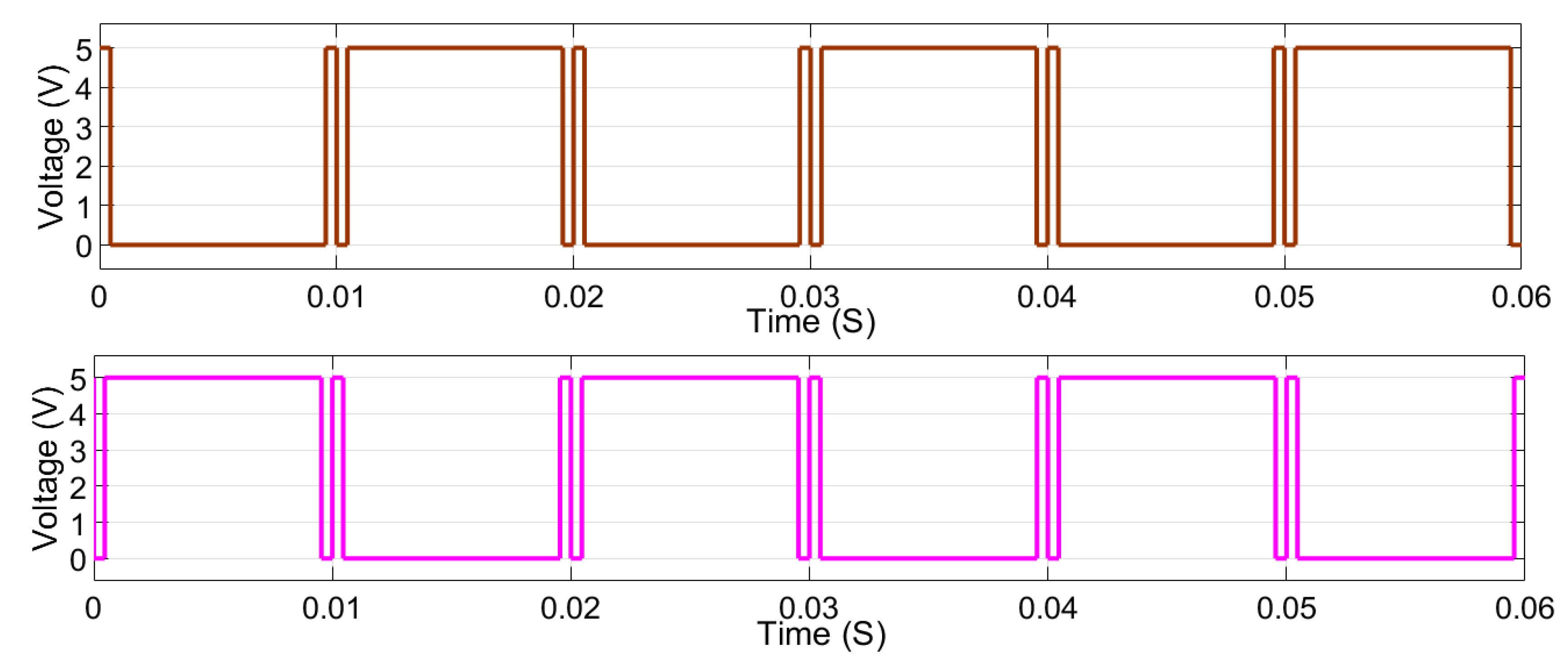










| Switching Mode | PS5 | PS6 | PS7 | PS8 | SS1 | SS2 | Voltage Obtained | Reference |
|---|---|---|---|---|---|---|---|---|
| 1 | ✓ | ✓ | ✖ | ✖ | ✖ | ✖ | 0 | Figure 2a |
| ✖ | ✖ | ✓ | ✓ | ✖ | ✖ | 0 | Figure 2b | |
| 2 | ✖ | ✖ | ✖ | ✓ | ✖ | ✓ | 2 Vdc0 | Figure 2c |
| 3 | ✖ | ✖ | ✖ | ✓ | ✓ | ✖ | 4 Vdc0 | Figure 2d |
| 4 | ✓ | ✖ | ✖ | ✓ | ✖ | ✖ | 6 Vdc0 | Figure 2e |
| 5 | ✖ | ✓ | ✖ | ✖ | ✓ | ✖ | −2 Vdc0 | Figure 2f |
| 6 | ✖ | ✓ | ✖ | ✖ | ✖ | ✓ | −4 Vdc0 | Figure 2g |
| 7 | ✖ | ✓ | ✓ | ✖ | ✖ | ✖ | −6 Vdc0 | Figure 2h |
| ✖—OFF|✓—ON | ||||||||
| Switching Mode | PS5 | PS6 | PS7 | PS8 | SS1 | SS2 | Status of Capacitors | Time Duration | ||
|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | ||||||||
| 1 | ✓ | ✓ | ❌ | ❌ | ❌ | ❌ | UC | UC | UC | 1.84 ms |
| ❌ | ❌ | ✓ | ✓ | ❌ | ❌ | UC | UC | UC | ||
| 2 | ❌ | ❌ | ❌ | ✓ | ❌ | ✓ | ↑ | ↑ | ↓ | 1.92 ms |
| 3 | ❌ | ❌ | ❌ | ✓ | ✓ | ❌ | ↑ | ↓ | ↓ | 2.26 ms |
| 4 | ✓ | ❌ | ❌ | ✓ | ❌ | ❌ | UC | UC | UC | 4.9 ms |
| 5 | ❌ | ✓ | ❌ | ❌ | ✓ | ❌ | ↓ | ↑ | ↑ | 1.92 ms |
| 6 | ❌ | ✓ | ❌ | ❌ | ❌ | ✓ | ↓ | ↓ | ↑ | 2.26 ms |
| 7 | ❌ | ✓ | ✓ | ❌ | ❌ | ❌ | UC | UC | UC | 4.9 ms |
| ❌—OFF|✓—ON|UC—Unchanged | 20 ms | |||||||||
| Top H Bridge Switches | Bottom H Bridge Switches | Mode | Output Load Voltage | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PS1 | PS2 | PS3 | PS4 | PS5 | PS6 | PS7 | PS8 | SS1 | SS2 | Vtop | Vbottom | Vtotal = Vtop + Vbottom | |
| ✓ | ✖ | ✖ | ✓ | ✓ | ✖ | ✖ | ✓ | ✖ | ✖ | I | 6 Vdc0 | ||
| ✖ | ✓ | ✓ | ✖ | ✓ | ✖ | ✖ | ✓ | ✖ | ✖ | II | 6 Vdc0 | ||
| ✓ | ✖ | ✖ | ✓ | ✖ | ✖ | ✖ | ✓ | ✓ | ✖ | III | |||
| ✖ | ✓ | ✓ | ✖ | ✖ | ✖ | ✖ | ✓ | ✓ | ✖ | IV | |||
| ✓ | ✖ | ✖ | ✓ | ✖ | ✖ | ✖ | ✓ | ✖ | ✓ | V | 2 Vdc0 | ||
| ✖ | ✓ | ✓ | ✖ | ✖ | ✖ | ✖ | ✓ | ✖ | ✓ | VI | 2 Vdc0 | ||
| ✓ | ✖ | ✖ | ✓ | ✓ | ✓ | ✖ | ✖ | ✖ | ✖ | VII | 0 | ||
| ✖ | ✓ | ✓ | ✖ | ✖ | ✖ | ✓ | ✓ | ✖ | ✖ | VIII | 0 | ||
| ✓ | ✖ | ✖ | ✓ | ✖ | ✓ | ✖ | ✖ | ✓ | ✖ | IX | −2 Vdc0 | ||
| ✖ | ✓ | ✓ | ✖ | ✖ | ✓ | ✖ | ✖ | ✓ | ✖ | X | −2 Vdc0 | ||
| ✓ | ✖ | ✖ | ✓ | ✖ | ✓ | ✖ | ✖ | ✖ | ✓ | XI | |||
| ✖ | ✓ | ✓ | ✖ | ✖ | ✓ | ✖ | ✖ | ✖ | ✓ | XII | |||
| ✓ | ✖ | ✖ | ✓ | ✖ | ✓ | ✓ | ✖ | ✖ | ✖ | XIII | −6 Vdc0 | ||
| ✖ | ✓ | ✓ | ✖ | ✖ | ✓ | ✓ | ✖ | ✖ | ✖ | XIV | −6 Vdc0 | ||
| ✖—OFF|✓—ON | |||||||||||||
| PARAMETERS | LEVEL 11 | LEVEL 15 |
|---|---|---|
| Top inverter voltage | 65 V | 47 V |
| Bottom inverter voltage | 130 V | 94 V |
| Load resistance = 100 Ω and load inductance = 30 mH. | ||
| Levels | No. of Primary Switches in the Top Inverter | No. of Primary Switches in the Bottom Inverter | No. of Secondary Switches in the Bottom | Current THD in % |
|---|---|---|---|---|
| 15 | 4 | 4 | 2 | 0.88 |
| 11 | 4 | 4 | 1 | 2.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alghaythi, M.L.; Irudayaraj, G.C.R.; Ramu, S.K.; Govindaraj, P.; Vairavasundaram, I. Mathematical Modeling and Analysis of Capacitor Voltage Balancing for Power Converters with Fewer Switches. Sustainability 2023, 15, 10698. https://doi.org/10.3390/su151310698
Alghaythi ML, Irudayaraj GCR, Ramu SK, Govindaraj P, Vairavasundaram I. Mathematical Modeling and Analysis of Capacitor Voltage Balancing for Power Converters with Fewer Switches. Sustainability. 2023; 15(13):10698. https://doi.org/10.3390/su151310698
Chicago/Turabian StyleAlghaythi, Mamdouh L., Gerald Christopher Raj Irudayaraj, Senthil Kumar Ramu, Praveenraj Govindaraj, and Indragandhi Vairavasundaram. 2023. "Mathematical Modeling and Analysis of Capacitor Voltage Balancing for Power Converters with Fewer Switches" Sustainability 15, no. 13: 10698. https://doi.org/10.3390/su151310698
APA StyleAlghaythi, M. L., Irudayaraj, G. C. R., Ramu, S. K., Govindaraj, P., & Vairavasundaram, I. (2023). Mathematical Modeling and Analysis of Capacitor Voltage Balancing for Power Converters with Fewer Switches. Sustainability, 15(13), 10698. https://doi.org/10.3390/su151310698







