Developing a Generalized Multi-Level Inverter with Reduced Number of Power Electronics Components
Abstract
:1. Introduction
- The proposed basic module has a lesser number of switches, which by generalizing the basic module, the proposed extended structure is realized.
- As the number of switches decreases, the axillary circuit number of devices, including the number of gate drivers, snubber circuits, heat sinks, etc., decreases as well, which reduces the cost and volume of the suggested inverter.
- The voltage stress of the recommended basic module switches is low.
- The maximum number of conducting switches in the current path of each voltage level is low for the proposed structure. Thus, the switches total conduction losses are reduced and the efficiency increased.
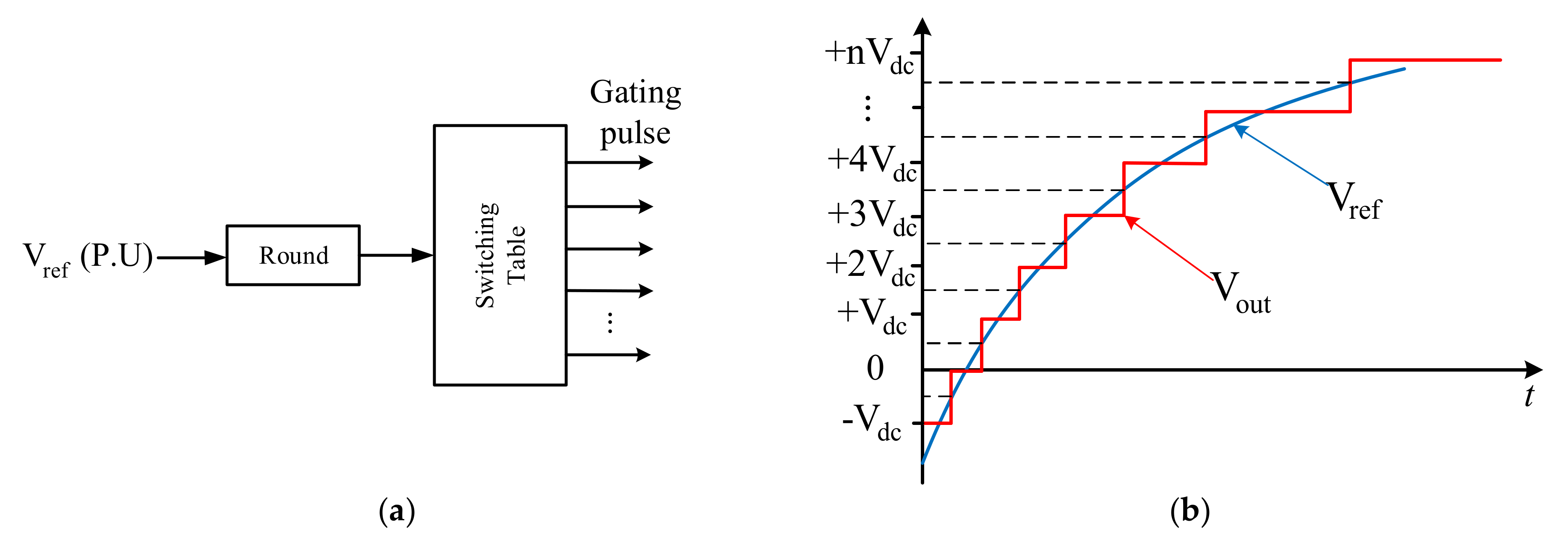
2. Suggested Structure
2.1. The Reduced Switch Basic Module
2.2. Blocking Voltage of the Proposed Reduced Switch Basic Module
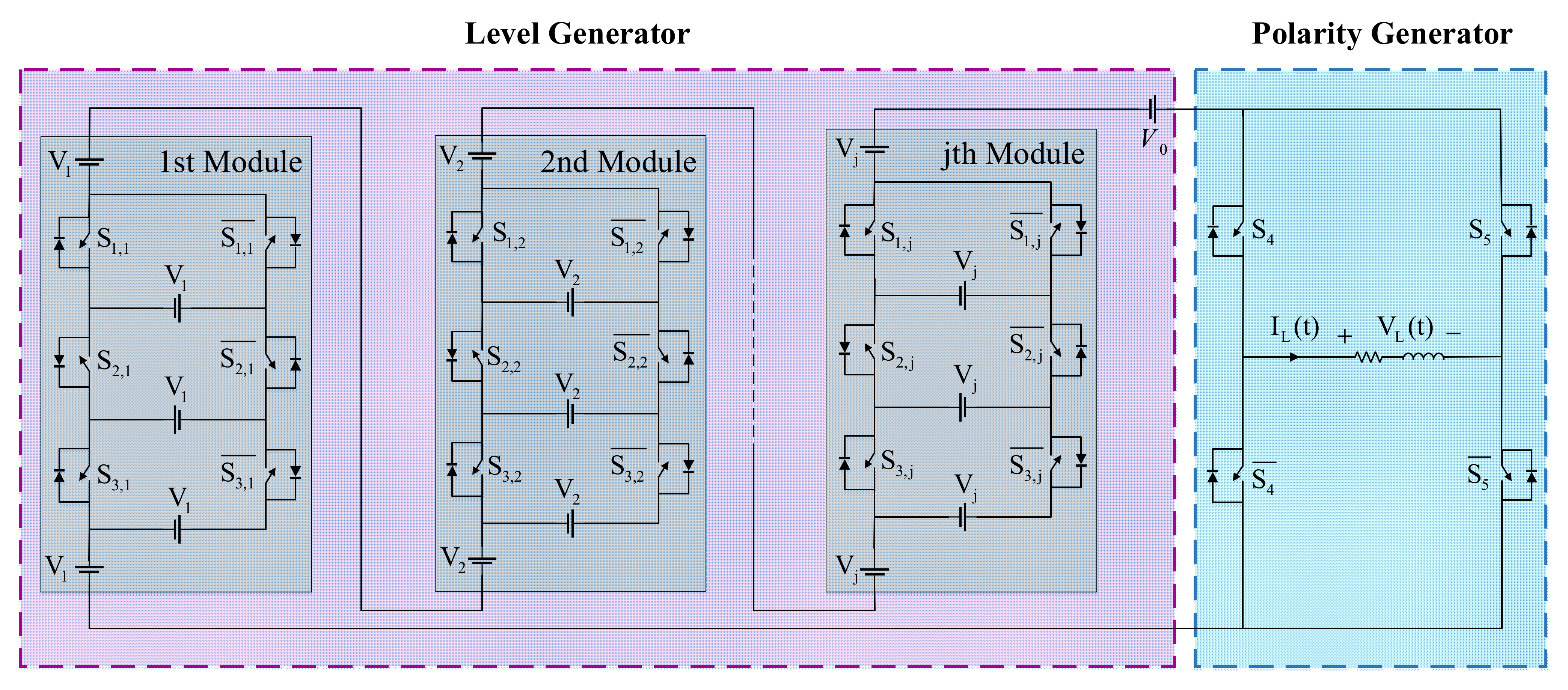
2.3. The Proposed Generalized Inverter Structure
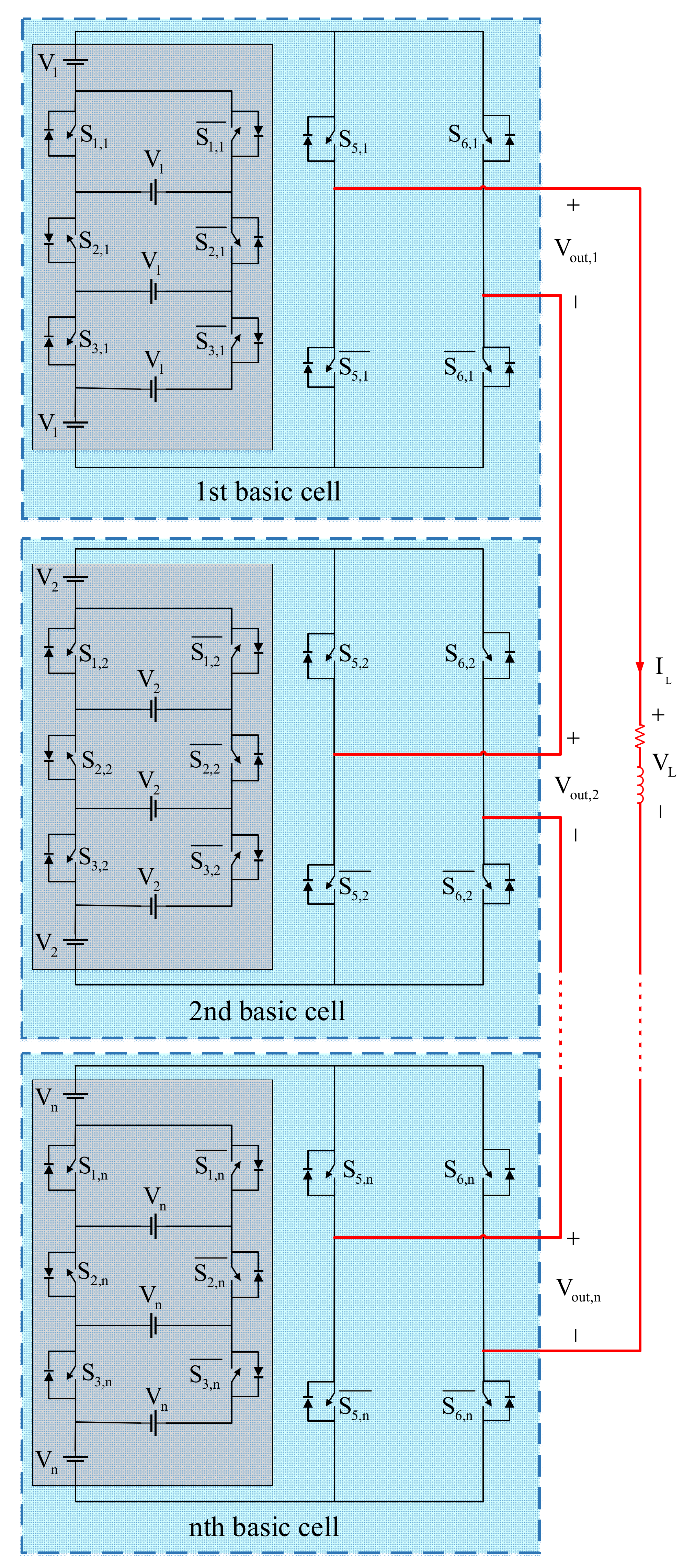
2.4. The Proposed Multi-Level Inverter Structure
3. Efficiency Calculation
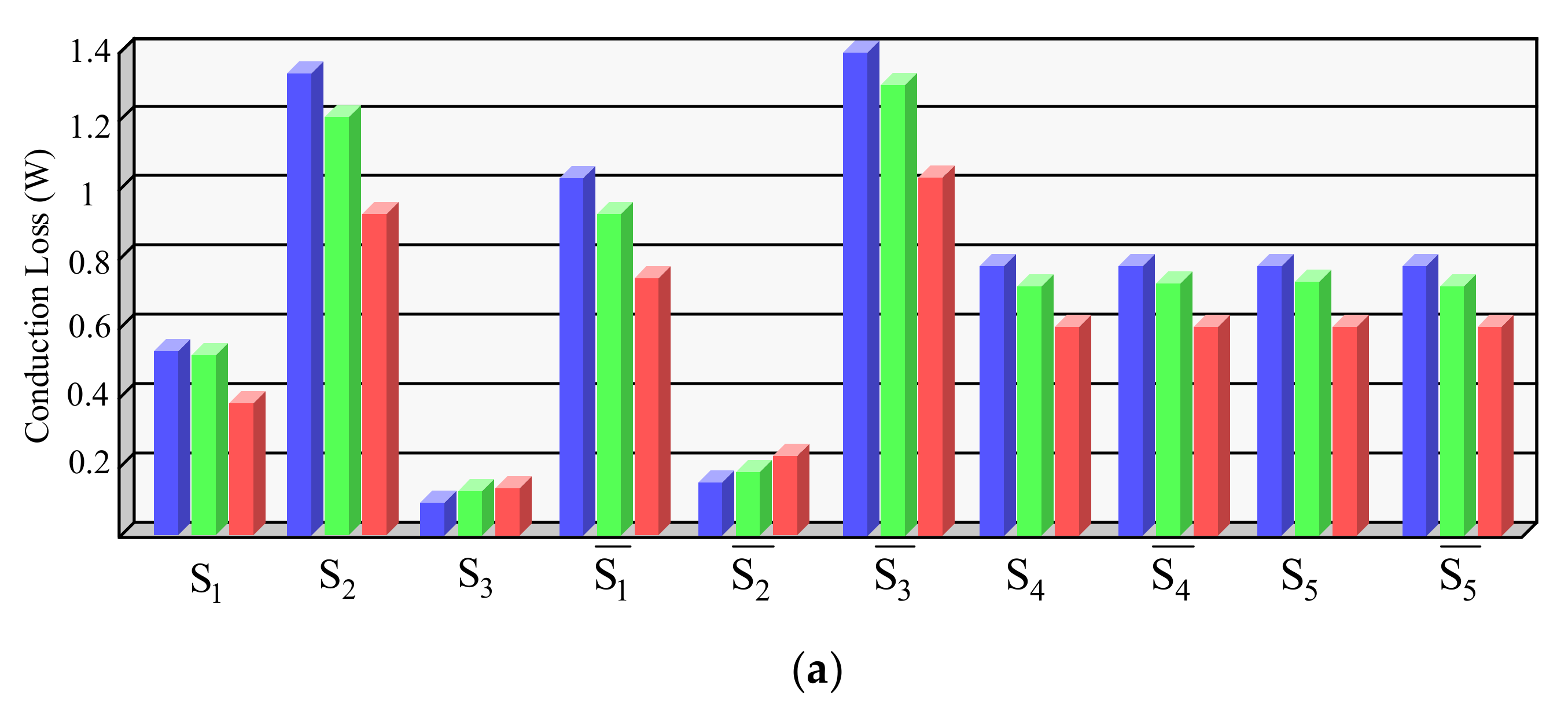
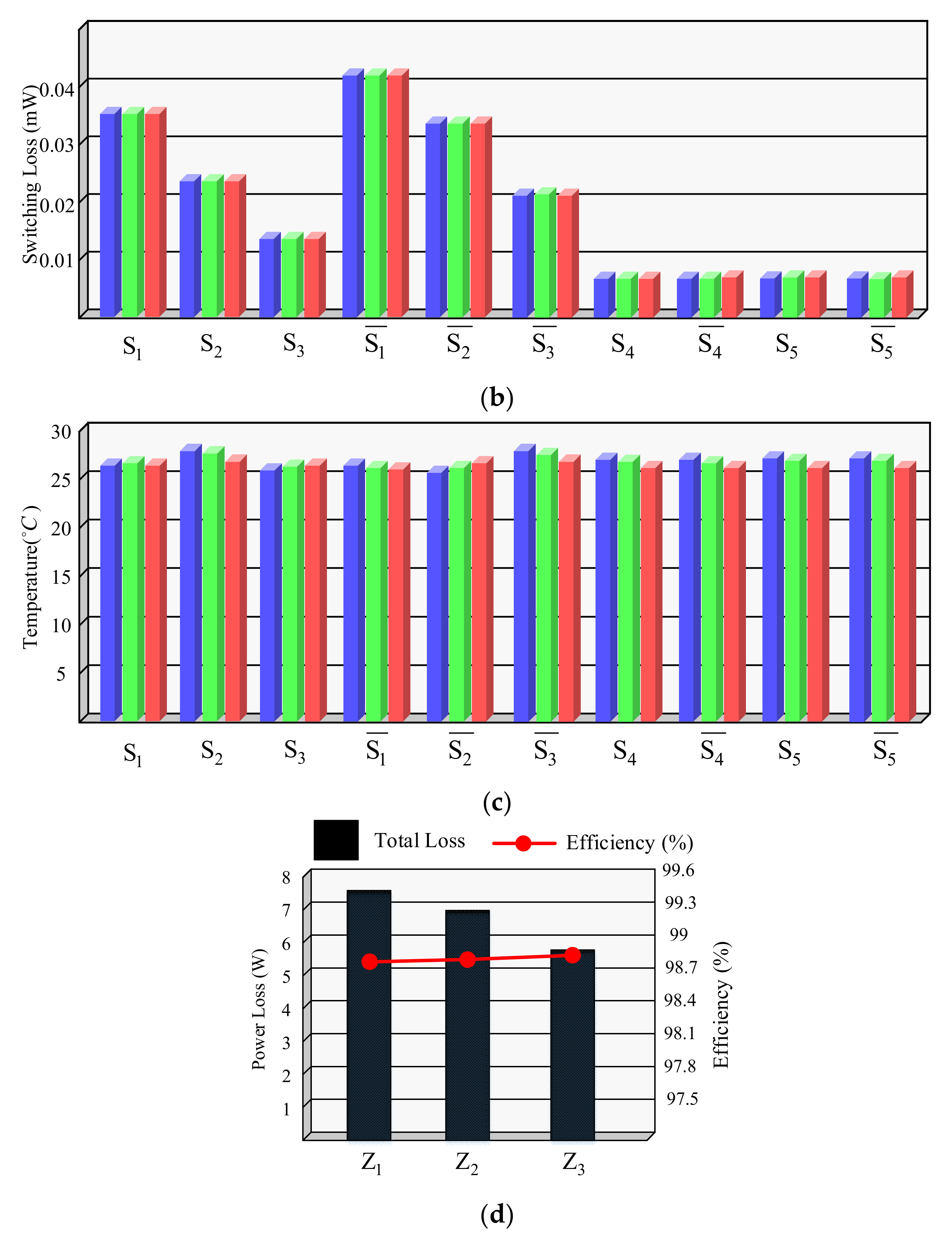
3.1. Conduction Losses
3.2. Switching Losses
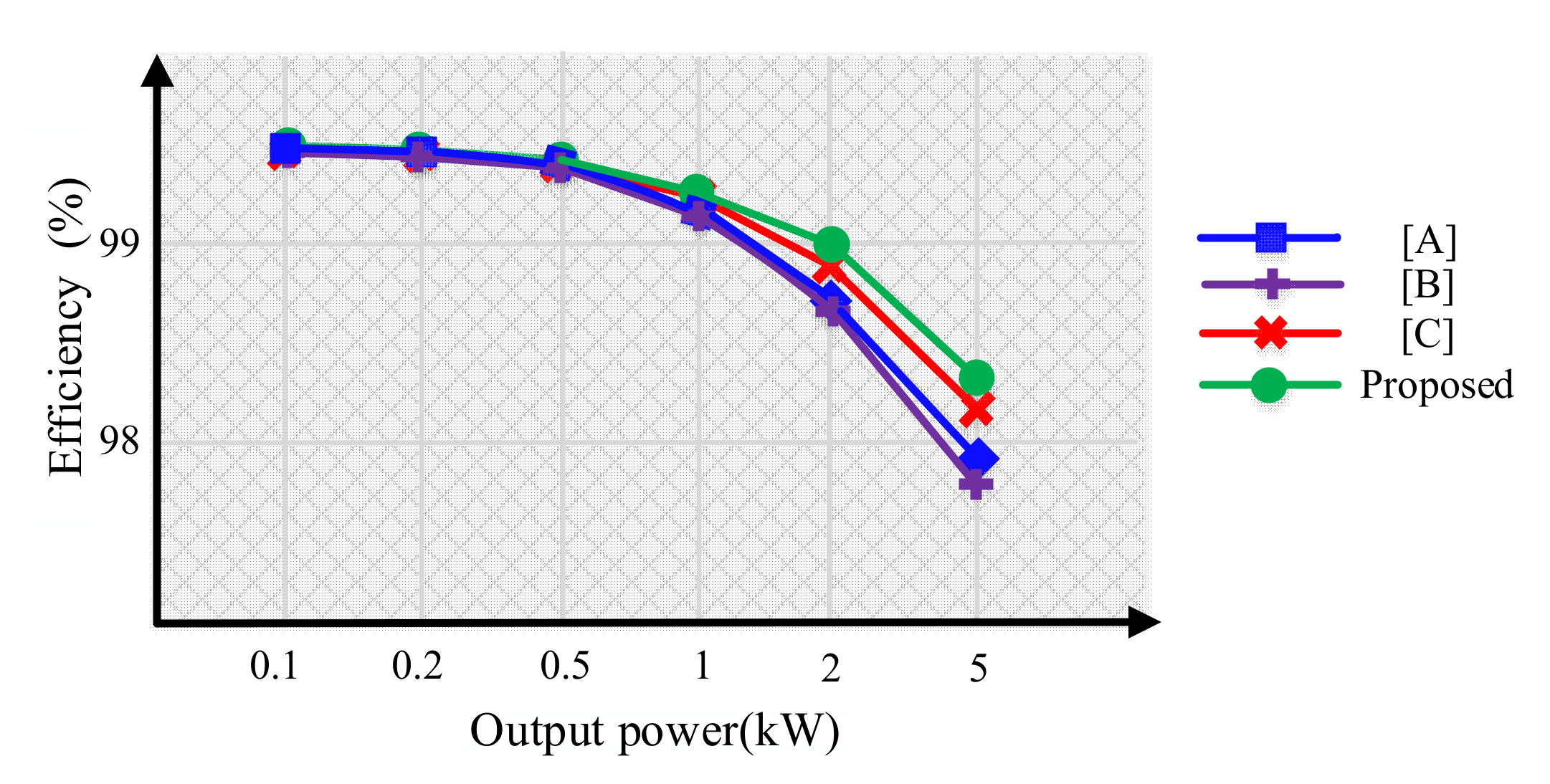
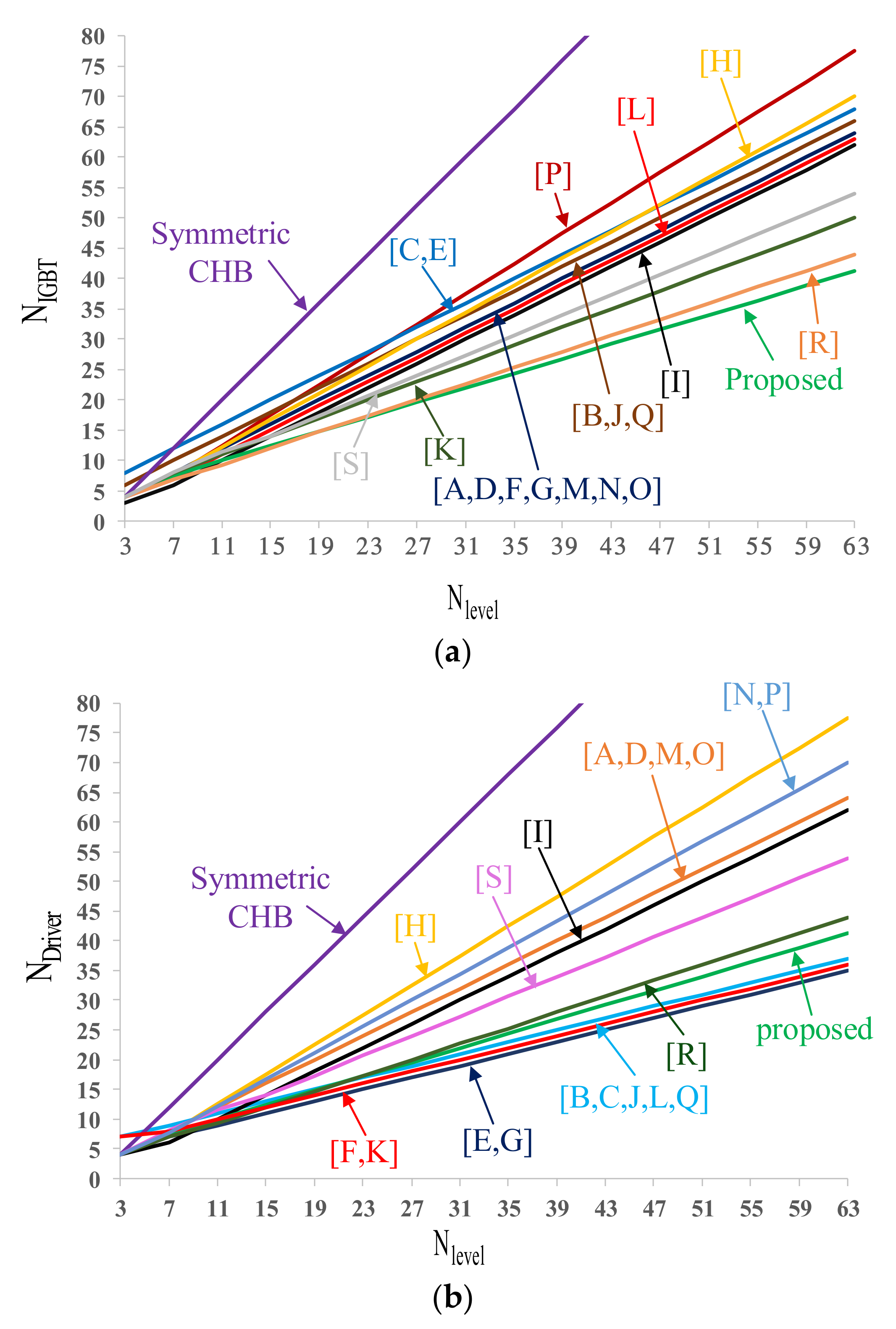
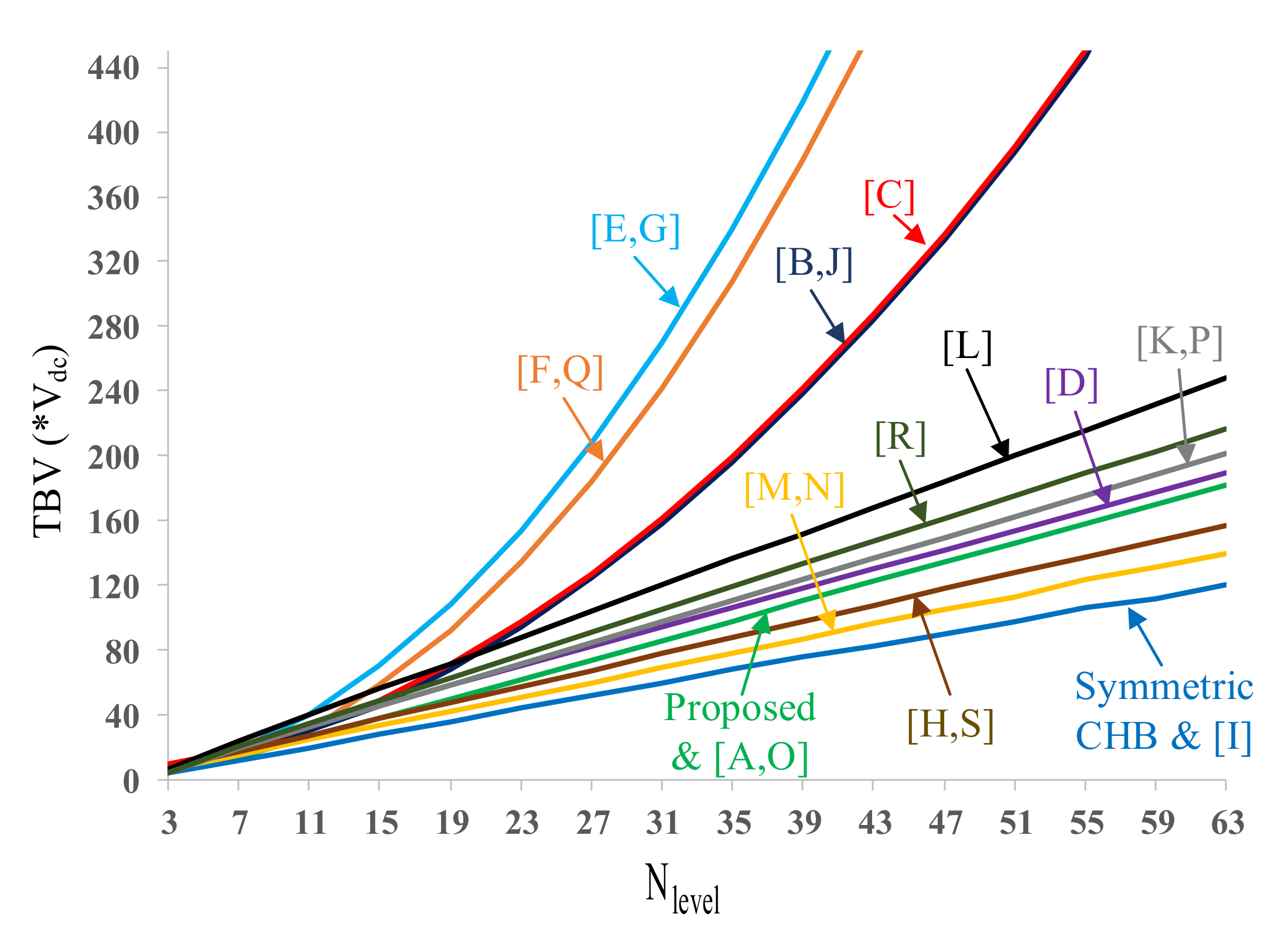
4. Comparative Study
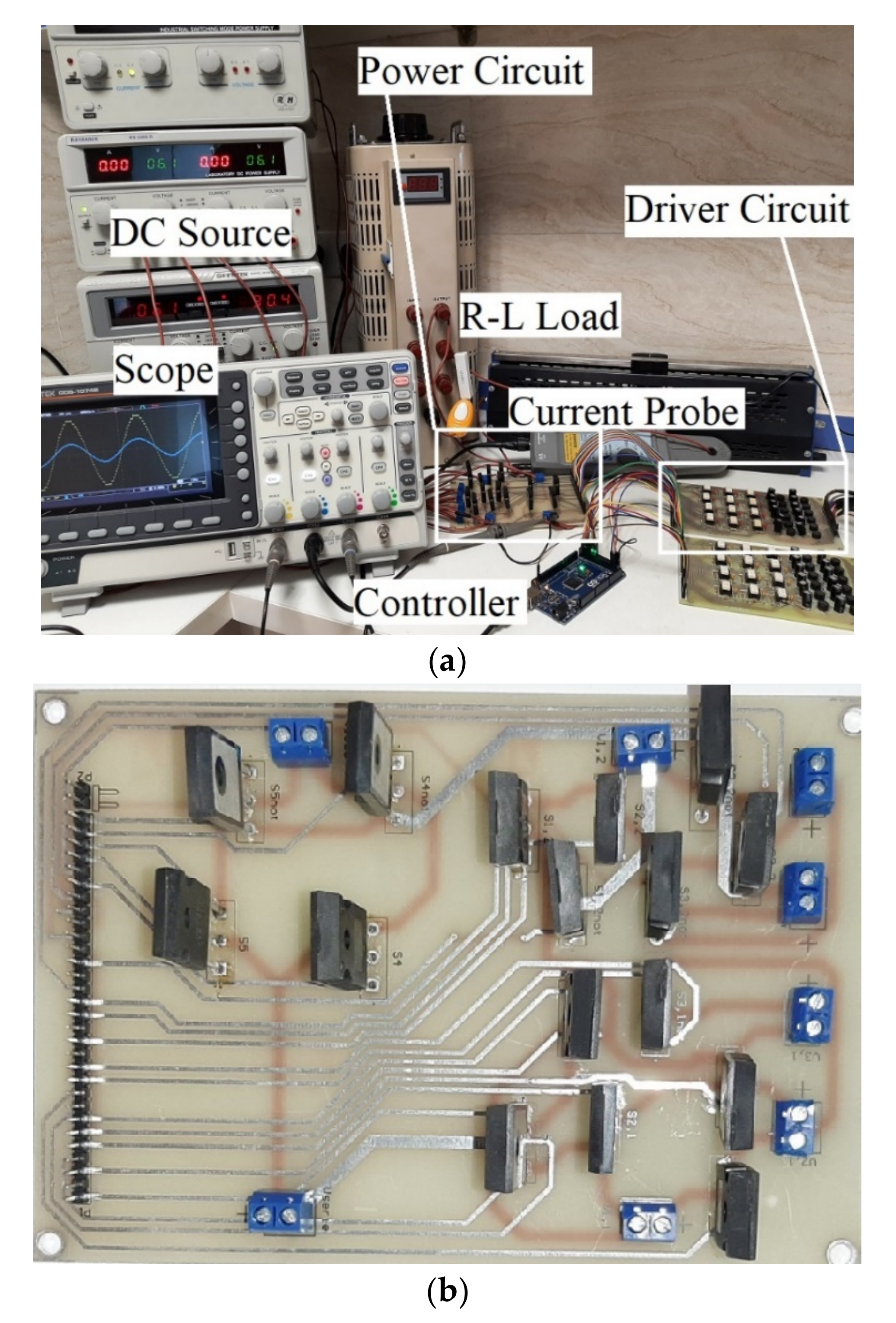
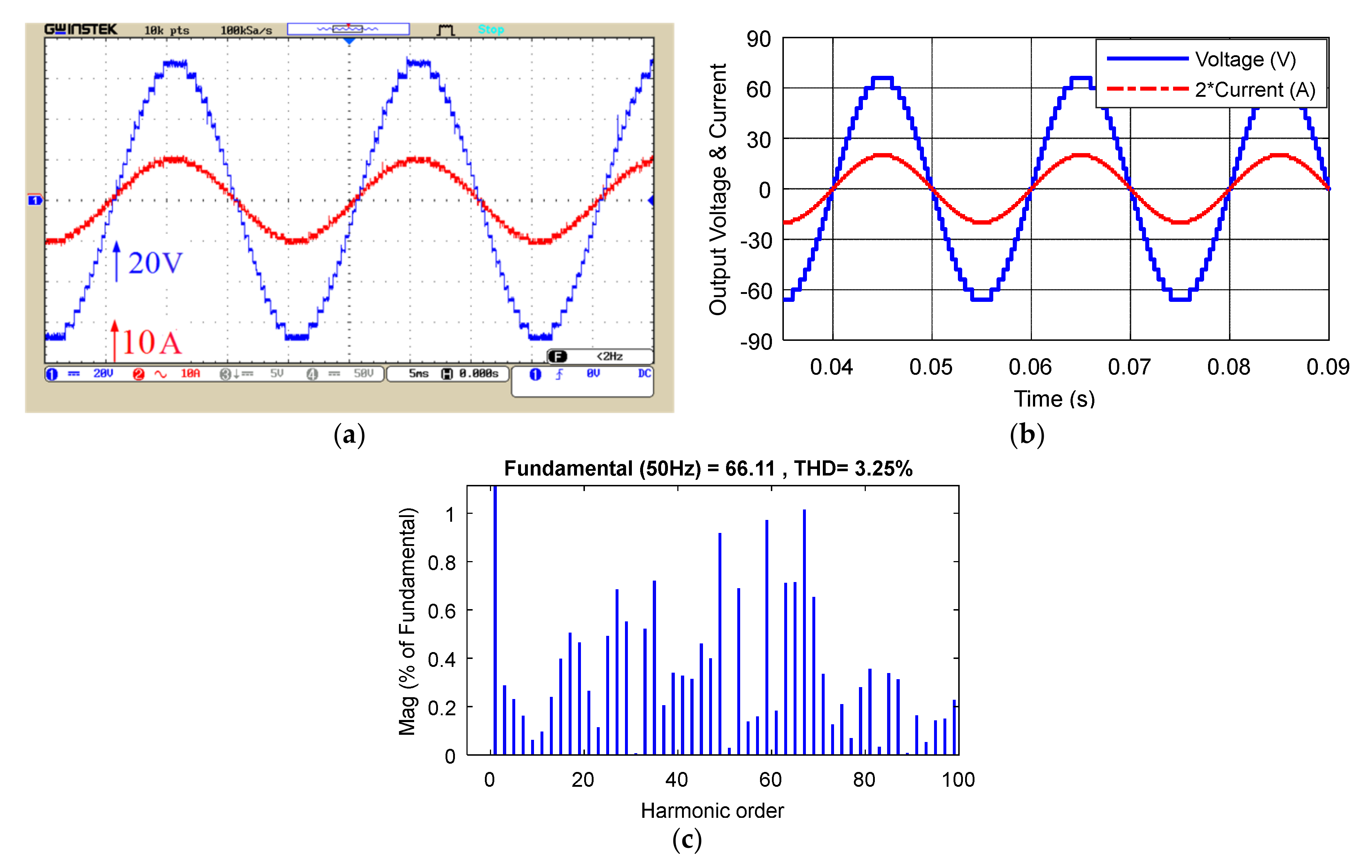
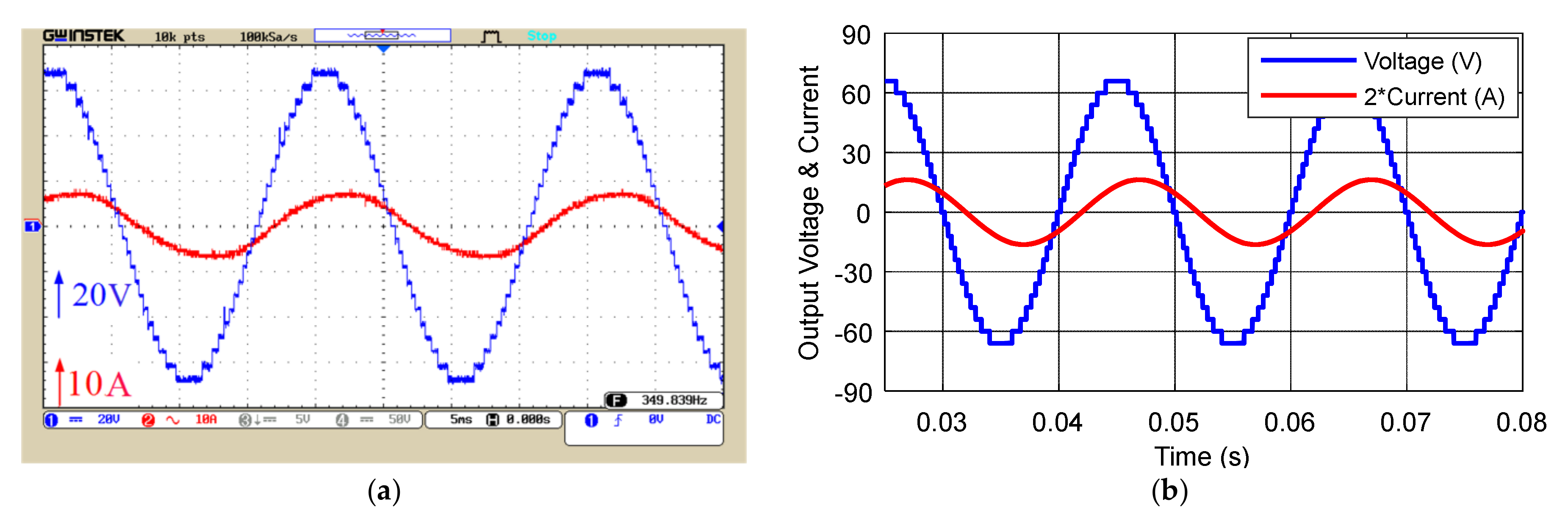
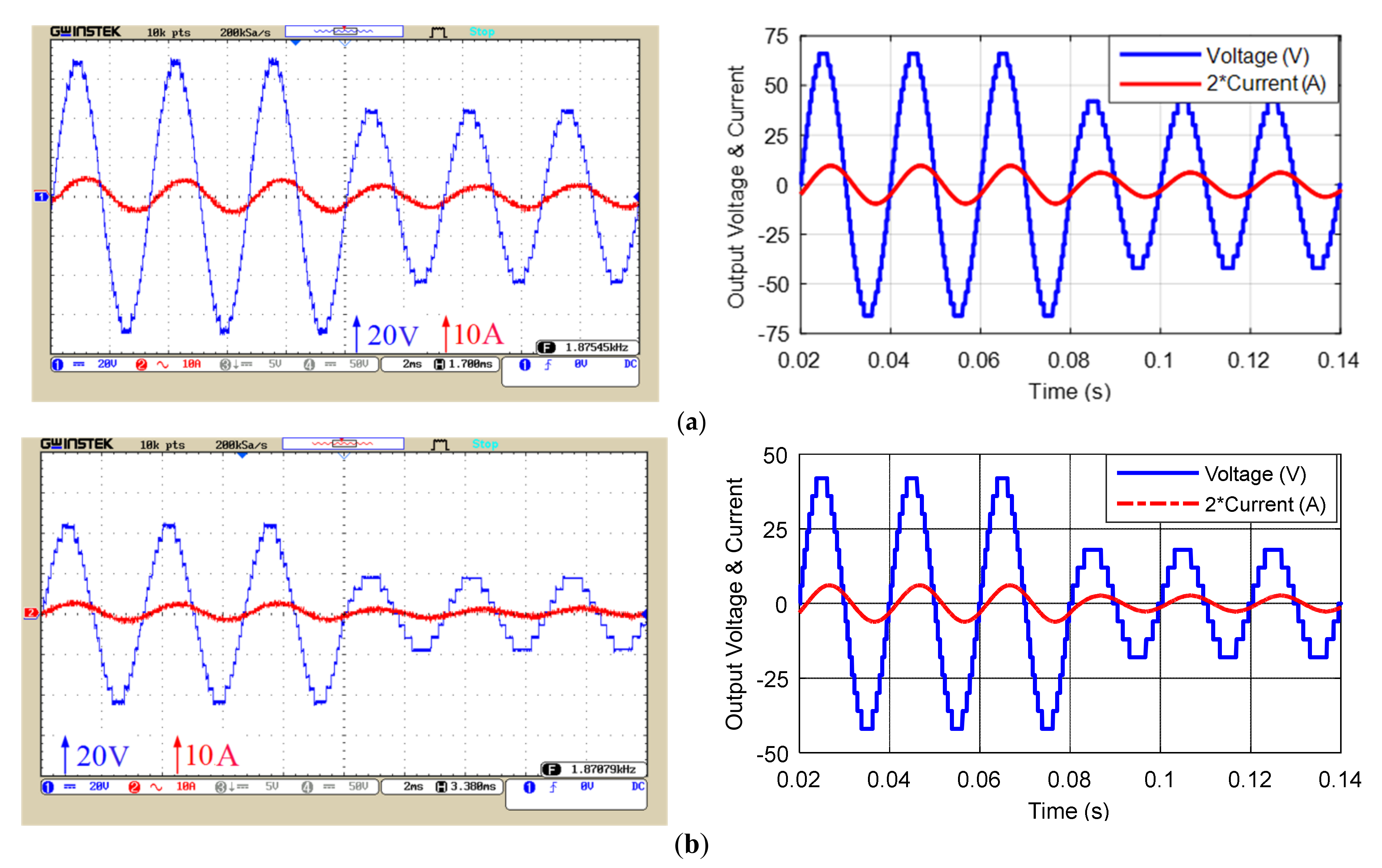
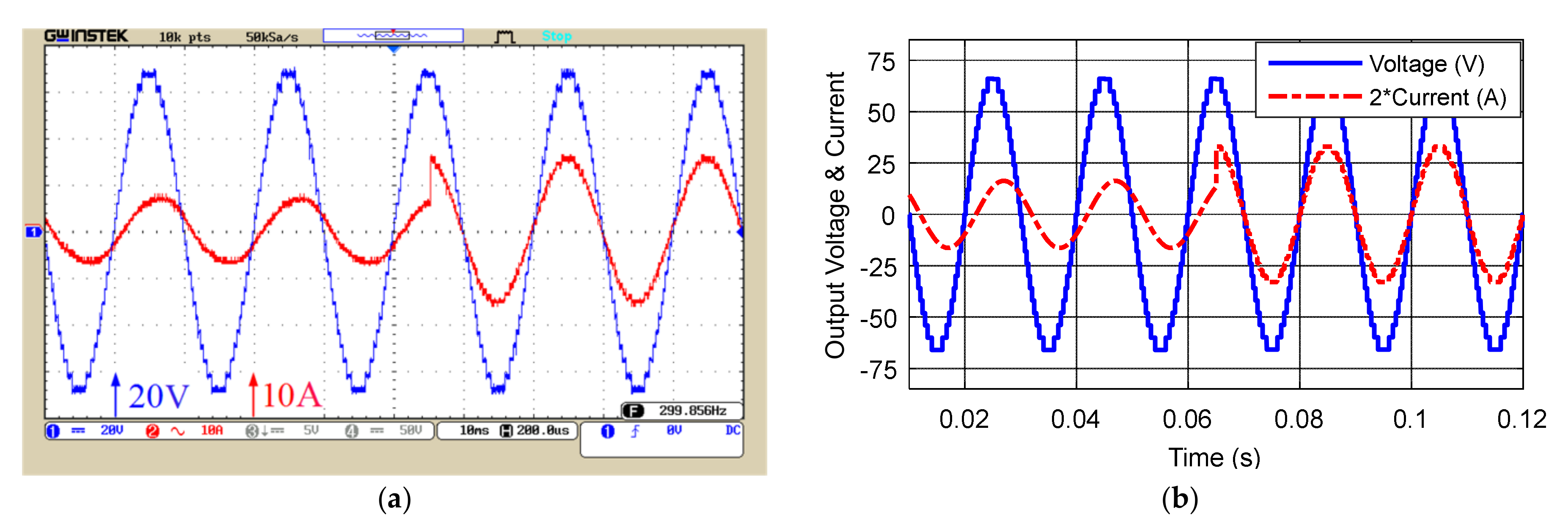
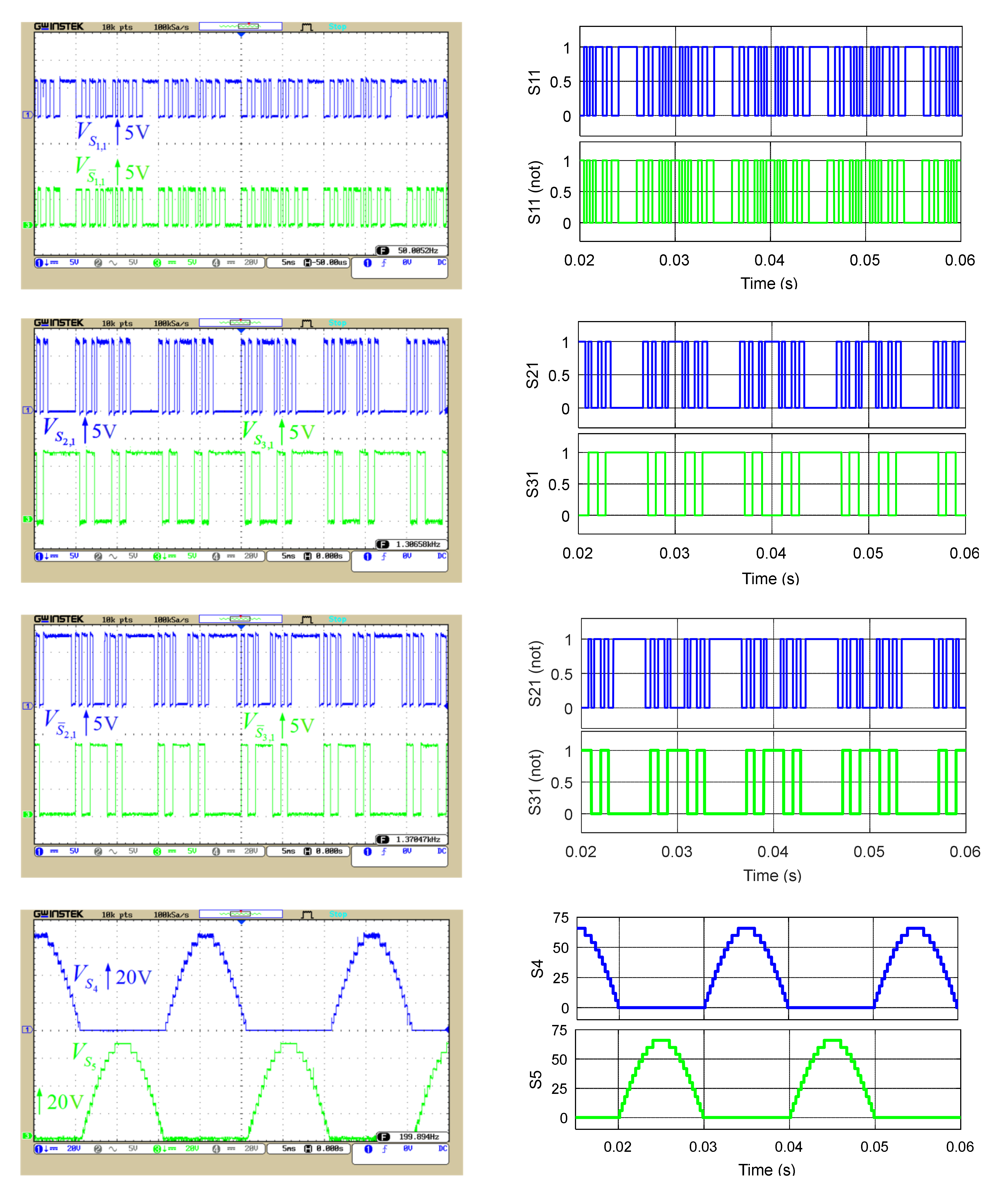
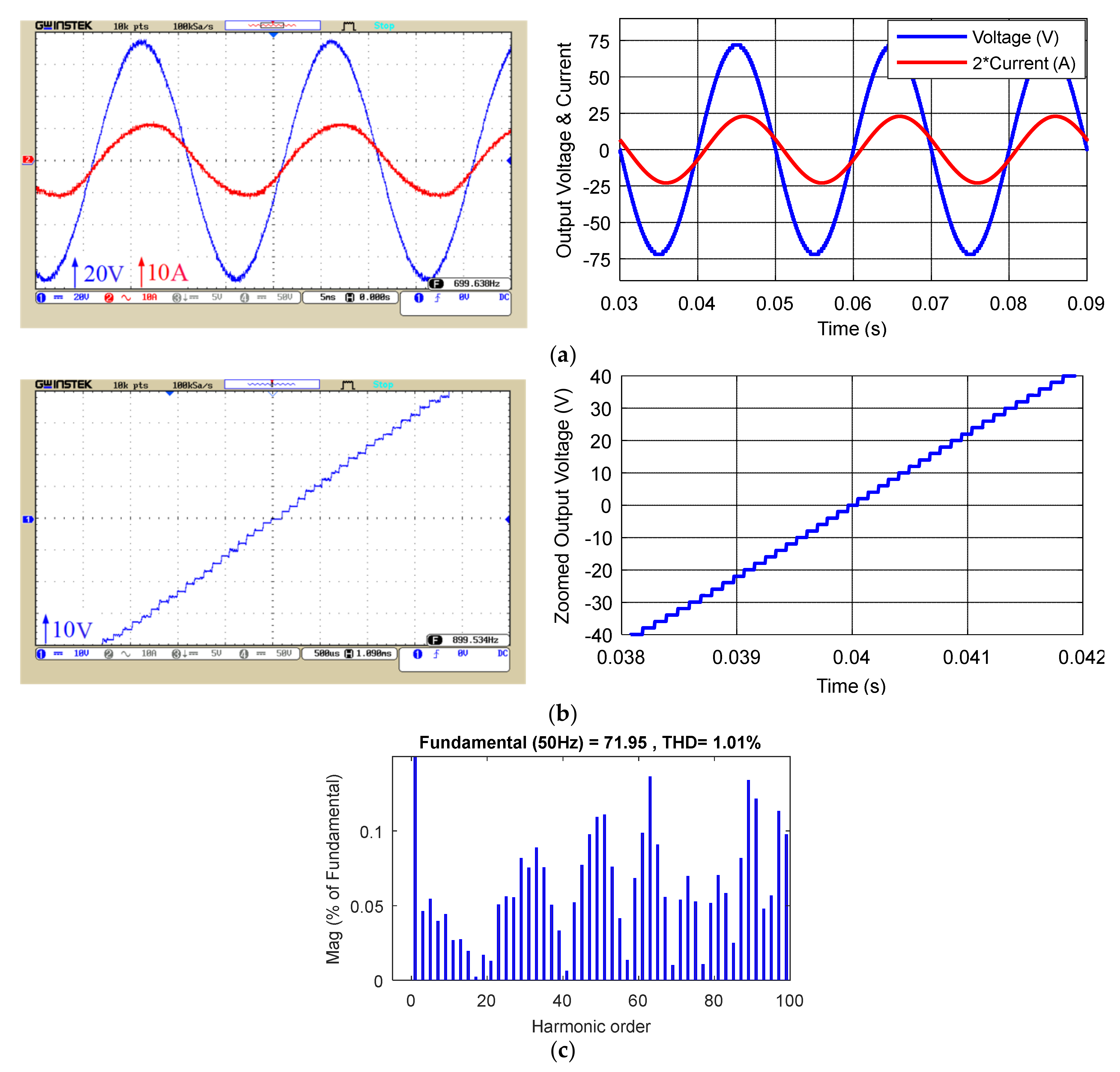
5. Simulation and Laboratory Results of the Proposed Structure
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sunddararaj, S.P.; Srinivasarangan Rangarajan, S. An extensive review of multilevel inverters based on their multifaceted structural configuration, triggering methods and applications. Electronics 2020, 9, 433. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, S.A.M.; Abd El Sattar, M. Dynamic Performance and Effectiveness of Voltage Disturbances on the Improvement of Power Quality for Grid-Connected DFIG System Based Wind Farm. J. Electr. Eng. Electron. Control. Comput. Sci. 2019, 5, 25–30. Available online: https://jeeeccs.net/index.php/journal/article/view/126 (accessed on 3 September 2019).
- Ahmed, S.A.M. Performance Analysis of Power Quality Improvement for Standard IEEE 14-Bus Power System based on FACTS Controller. J. Electr. Eng. Electron. Control Comput. Sci. 2019, 5, 11–18. Available online: https://jeeeccs.net/index.php/journal/article/view/134 (accessed on 3 December 2019).
- Sorlei, I.S.; Bizon, N.; Thounthong, P.; Varlam, M.; Carcadea, E.; Culcer, M.; Iliescu, M.; Raceanu, M. Fuel Cell Electric Vehicles—A Brief Review of Current Topologies and Energy Management Strategies. Energies 2021, 14, 252. [Google Scholar] [CrossRef]
- Benbouhenni, H.; Bizon, N. Improved Rotor Flux and Torque Control Based on the Third-Order Sliding Mode Scheme Applied to the Asynchronous Generator for the Single-Rotor Wind Turbine. Mathematics 2021, 9, 2297. [Google Scholar] [CrossRef]
- Shahzad, U. Significance of Smart Grids in Electric Power Systems: A Brief Overview. J. Electr. Eng. Electron. Control. Comput. Sci. 2020, 6, 7–12. Available online: https://jeeeccs.net/index.php/journal/article/view/141 (accessed on 3 February 2020).
- Onyishi, D.U.; Ofualagba, G. Analysis of the Electricity Distribution Supply in Eastern Nigeria: Current Challenges and Possible Solutions. J. Electr. Eng. Electron. Control Comput. Sci. 2021, 7, 1–8. Available online: https://jeeeccs.net/index.php/journal/article/view/209 (accessed on 3 September 2021).
- Seifi, A.; Hosseinpour, M.; Dejamkhooy, A. A switch-source cell-based cascaded multilevel inverter topology with minimum number of power electronics components. Trans. Inst. Meas. Control 2021, 43, 1212–1225. [Google Scholar] [CrossRef]
- Sarebanzadeh, M.; Hosseinzadeh, M.A.; Garcia, C.; Babaei, E.; Hosseinpour, M.; Seifi, A.; Rodriguez, J. A 15-Level Switched-Capacitor Multilevel Inverter Structure with Self-Balancing Capacitor. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 1477–1481. [Google Scholar] [CrossRef]
- Hosseinpour, M.; Seifi, A.; Dejamkhooy, A.; Sedaghati, F. Switch count reduced structure for symmetric bi-directional multilevel inverter based on switch-diode-source cells. IET Power Electron. 2020, 13, 1675–1686. [Google Scholar] [CrossRef]
- Esmaeilzadeh, R.; Ajami, A.; Banaei, M.R. Two-Stage Inverter Based on Combination of High Gain DC-DC Converter and Five-Level Inverter for PV-Battery Energy Conversion. J. Oper. Autom. Power Eng. 2018, 6, 101–110. Available online: http://joape.uma.ac.ir/article_641.html (accessed on 29 February 2018).
- Siddique, M.D.; Mekhilef, S.; Shah, N.M.; Sarwar, A.; Memon, M.A. A new single-phase cascaded multilevel inverter topology with reduced number of switches and voltage stress. Int. Trans. Electr. Energy Syst. 2020, 30, 12191. [Google Scholar] [CrossRef]
- Oskuee, M.R.; Karimi, M.; Ravadanegh, S.N.; Gharehpetian, G.B. An innovative scheme of symmetric multilevel voltage source inverter with lower number of circuit devices. IEEE Trans. Ind. Electron. 2015, 62, 6965–6973. [Google Scholar] [CrossRef]
- Alishah, R.S.; Bertilsson, K.; Vosoughi Kurdkandi, N.; Hosseini, S.H.; Gharehkoushan, A.Z.; Ali, J.S. A New Switched-Ladder Multilevel Converter Structure with Reduced Power Electronic Components. J. Circuits Syst. Comput. 2021, 30, 2150217. [Google Scholar] [CrossRef]
- Jayabalan, M.; Jeevarathinam, B.; Sandirasegarane, T. Reduced switch count pulse width modulated multilevel inverter. IET Power Electron. 2017, 10, 10–17. [Google Scholar] [CrossRef]
- Ponraj, R.P.; Sigamani, T.; Subramanian, V. A developed H-bridge cascaded multilevel inverter with reduced switch count. J. Electr. Eng. Technol. 2021, 16, 1445–1455. [Google Scholar] [CrossRef]
- Peddapati, S. A generalized symmetrical MLI topology with improved commutation. Electr. Eng. 2020, 102, 2617–2635. [Google Scholar] [CrossRef]
- Siddique, M.D.; Mekhilef, S.; Shah, N.M.; Memon, M.A. Optimal design of a new cascaded multilevel inverter topology with reduced switch count. IEEE Access 2019, 7, 24498–24510. [Google Scholar] [CrossRef]
- Samsami, H.; Taheri, A.; Samanbakhsh, R. New bidirectional multilevel inverter topology with staircase cascading for symmetric and asymmetric structures. IET Power Electron. 2017, 10, 1315–1323. [Google Scholar] [CrossRef]
- Dhanamjayulu, C.; Meikandasivam, S. Implementation and comparison of symmetric and asymmetric multilevel inverters for dynamic loads. IEEE Access 2017, 6, 738–746. [Google Scholar] [CrossRef]
- Gohari, A.; Afjei, E.S.; Torkaman, H. Novel symmetric modular hybrid multilevel inverter with reduced number of semiconductors and low-voltage stress across switches. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 4297–4305. [Google Scholar] [CrossRef]
- Alishah, R.S.; Hosseini, S.H.; Babaei, E.; Sabahi, M. A new general multilevel converter topology based on cascaded connection of submultilevel units with reduced switching components, DC sources, and blocked voltage by switches. IEEE Trans. Ind. Electron. 2016, 63, 7157–7164. [Google Scholar] [CrossRef]
- Hosseinpour, M.; Seifi, A.; Rahimian, M.M. A bidirectional diode containing multilevel inverter topology with reduced switch count and driver. Int. J. Circuit Theory Appl. 2020, 48, 1766–1785. [Google Scholar] [CrossRef]
- Hosseini Montazer, B.; Olamaei, J.; Hosseinpour, M.; Mozafari, B. A generalized diode containing bidirectional topology for multilevel inverter with reduced switches and power loss. Int. J. Circuit Theory Appl. 2021, 49, 2959–2978. [Google Scholar] [CrossRef]
- Selvaraj, S.; Kumaresan, G.; Sathik, M.A. Modified “K”-type multilevel inverter topology with reduced switches, DC sources, and power loss. Int. Trans. Electr. Energy Syst. 2020, 30, 12345. [Google Scholar] [CrossRef]
- Meraj, S.T.; Hasan, K.; Masaoud, A. A novel configuration of cross-switched T-type (CT-type) multilevel inverter. IEEE Trans. Power Electron. 2019, 35, 3688–3696. [Google Scholar] [CrossRef]
- Ponraj, R.P.; Sigamani, T. A novel design and performance improvement of symmetric multilevel inverter with reduced switches using genetic algorithm. Soft Comput. 2021, 25, 4597–4607. [Google Scholar] [CrossRef]
- Lee, S.S.; Sidorov, M.; Idris, N.R.; Heng, Y.E. A symmetrical cascaded compact-module multilevel inverter (CCM-MLI) with pulsewidth modulation. IEEE Trans. Ind. Electron. 2017, 65, 4631–4639. [Google Scholar] [CrossRef]
- Siddique, M.D.; Mekhilef, S.; Shah, N.M.; Sarwar, A.; Iqbal, A.; Memon, M.A. A new multilevel inverter topology with reduce switch count. IEEE Access 2019, 7, 58584–58594. [Google Scholar] [CrossRef]
- Ali, J.S.; Alishah, R.S.; Krishnasamy, V. A new generalized multilevel converter topology with reduced voltage on switches, power losses, and components. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 7, 1094–1106. [Google Scholar] [CrossRef]
- Seifi, A.; Hosseinpour, M.; Dejamkhooy, A.; Sedaghati, F. Novel reduced switch-count structure for symmetric/asymmetric cascaded multilevel inverter. Arab. J. Sci. Eng. 2020, 45, 6687–6700. [Google Scholar] [CrossRef]

| S3 | Vout | ||
|---|---|---|---|
| 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | Vdc |
| 1 | 1 | 1 | 2Vdc |
| 0 | 1 | 1 | 3Vdc |
| 1 | 1 | 0 | 4Vdc |
| 0 | 1 | 0 | 5Vdc |
| Proposed Algorithm | Magnitude of dc Voltage Sources | NIGBT | NL | ND |
|---|---|---|---|---|
| 1st proposed algorithm | ||||
| 2nd proposed algorithm | ||||
| 3rd proposed algorithm | ||||
| 4th proposed algorithm |
| NIGBT | NGD | NL | NDC | TBV(* Vdc) | ND | NIGBT,ON | NIGBT/NL | |
|---|---|---|---|---|---|---|---|---|
| [13] | 10 | 10 | 9 | 4 | 22 | 0 | 5 | 1.11 |
| [14] | 12 | 10 | 9 | 4 | 24 | 0 | 7 | 1.33 |
| [15] | 12 | 9 | 7 | 3 | 18 | 0 | 7 | 1.71 |
| [16] | 10 | 10 | 7 | 3 | 20 | 0 | 5 | 1.42 |
| [17] | 10 | 7 | 7 | 3 | 21 | 1 | 4 | 1.42 |
| [18] | 8 | 7 | 7 | 3 | 14 | 0 | 4 | 1.14 |
| [19] | 8 | 7 | 7 | 3 | 18 | 0 | 4 | 1.14 |
| [20] | 5 | 5 | 3 | 2 | 9 | 4 | 2 | 1.66 |
| [21] | 6 | 6 | 7 | 4 | 12 | 0 | 3 | 0.85 |
| [22] | 12 | 10 | 9 | 4 | 24 | 0 | 7 | 1.33 |
| [23] | 11 | 10 | 11 | 5 | 31 | 1 | 5 | 1 |
| [24] | 11 | 10 | 11 | 5 | 31 | 2 | 4 | 1 |
| [25] | 8 | 8 | 7 | 3 | 12 | 0 | 3 | 1.14 |
| [26] | 10 | 8 | 9 | 4 | 20 | 0 | 4 | 1.11 |
| [27] | 10 | 10 | 9 | 4 | 20 | 0 | 5 | 1.11 |
| [28] | 10 | 7 | 7 | 3 | 20 | 0 | 3 | 1.42 |
| [29] | 10 | 9 | 7 | 3 | 14 | 0 | 4 | 1.42 |
| [30] | 10 | 9 | 9 | 4 | 18 | 0 | 4 | 1.11 |
| [31] | 9 | 9 | 9 | 4 | 22 | 1 | 5 | 1 |
| Proposed | 10 | 10 | 13 | 5 | 30 | 0 | 5 | 0.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shayeghi, H.; Seifi, A.; Hosseinpour, M.; Bizon, N. Developing a Generalized Multi-Level Inverter with Reduced Number of Power Electronics Components. Sustainability 2022, 14, 5545. https://doi.org/10.3390/su14095545
Shayeghi H, Seifi A, Hosseinpour M, Bizon N. Developing a Generalized Multi-Level Inverter with Reduced Number of Power Electronics Components. Sustainability. 2022; 14(9):5545. https://doi.org/10.3390/su14095545
Chicago/Turabian StyleShayeghi, Hossein, Ali Seifi, Majid Hosseinpour, and Nicu Bizon. 2022. "Developing a Generalized Multi-Level Inverter with Reduced Number of Power Electronics Components" Sustainability 14, no. 9: 5545. https://doi.org/10.3390/su14095545
APA StyleShayeghi, H., Seifi, A., Hosseinpour, M., & Bizon, N. (2022). Developing a Generalized Multi-Level Inverter with Reduced Number of Power Electronics Components. Sustainability, 14(9), 5545. https://doi.org/10.3390/su14095545








