Study on Stope Stability in Continuous Mining of Long-Dip, Thin Orebody by Room–Pillar Method
Abstract
:1. Introduction
2. The Particularity of Mining Long-Dip, Thin Orebody
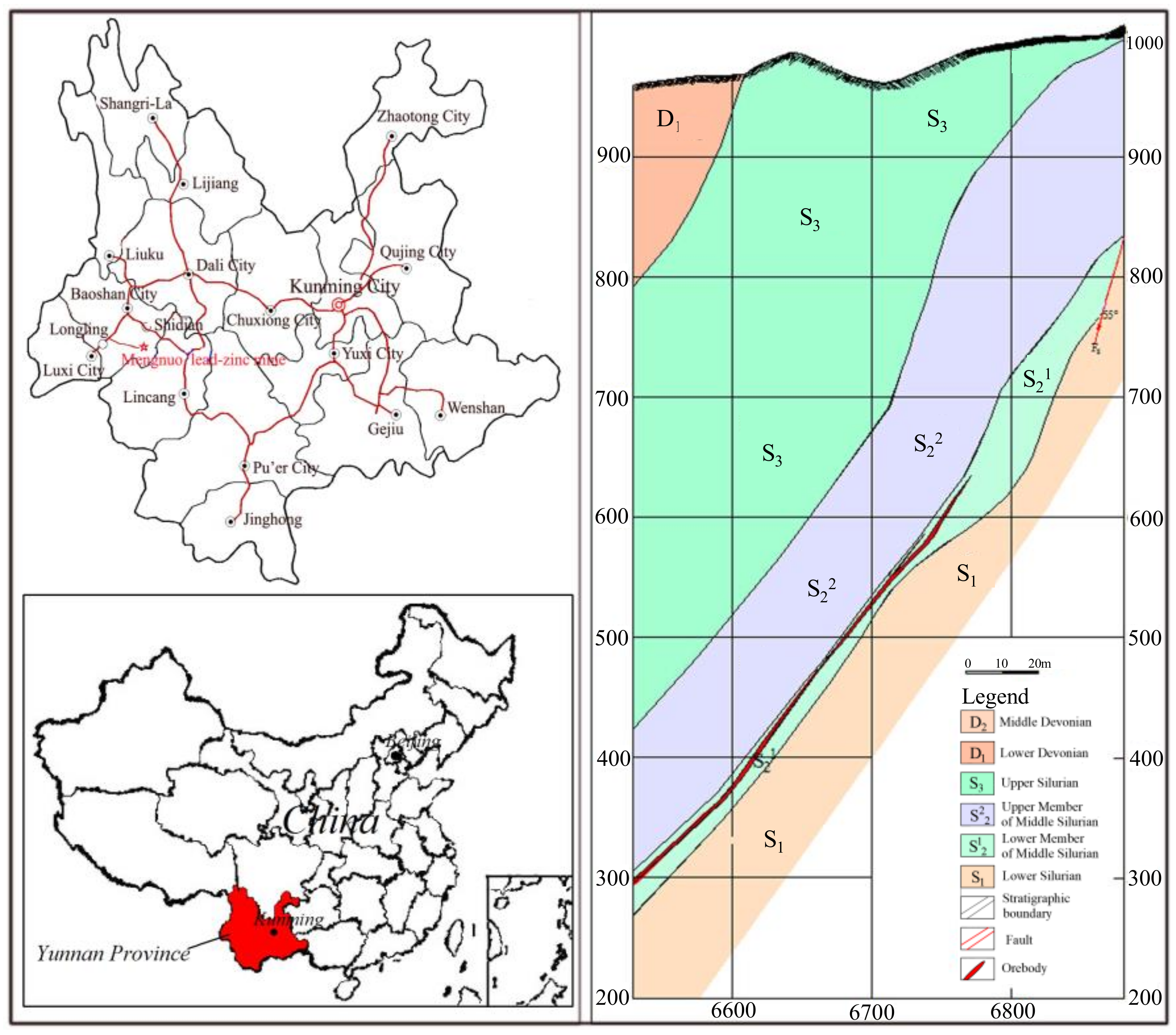
3. Engineering Situation
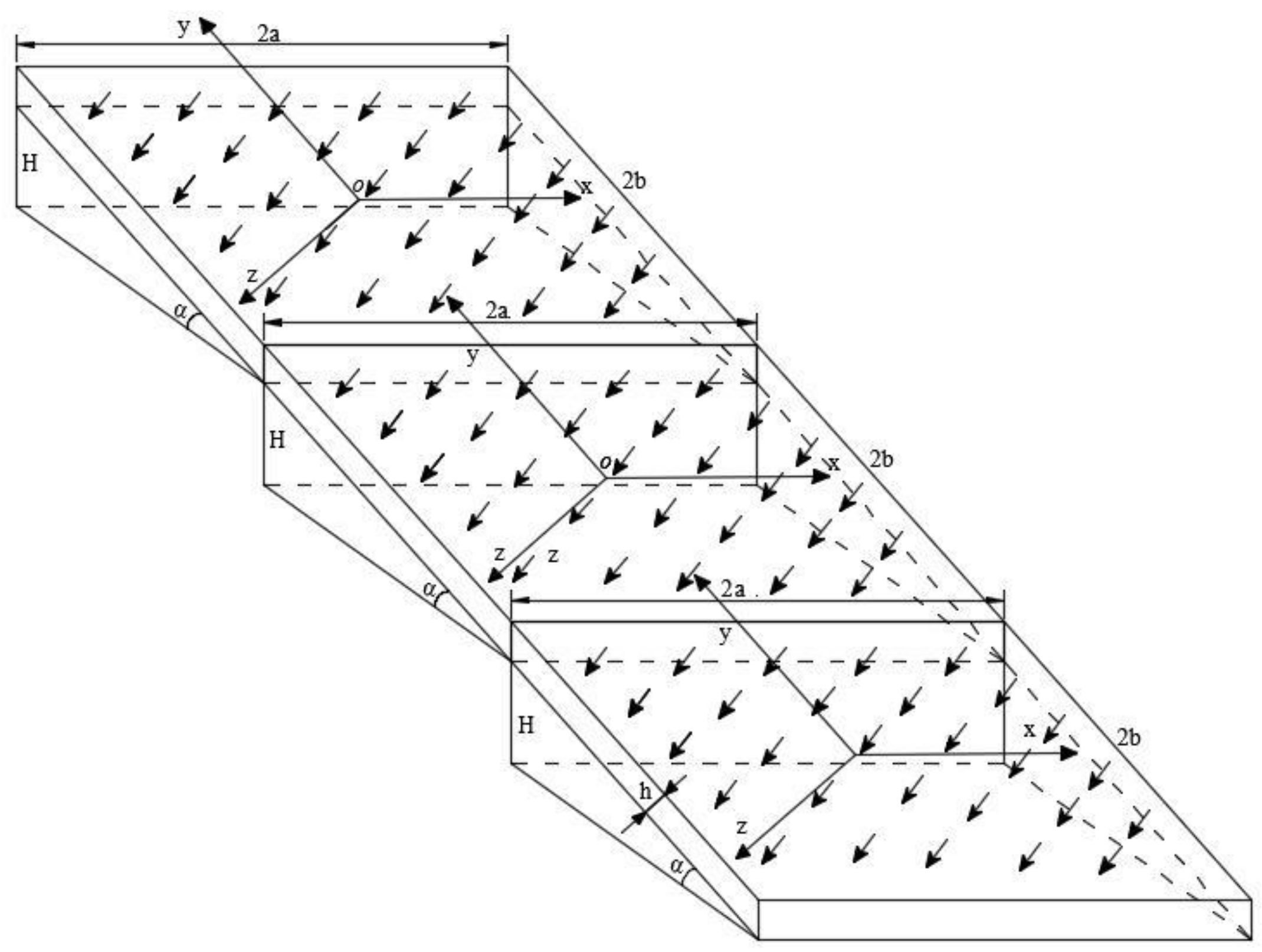
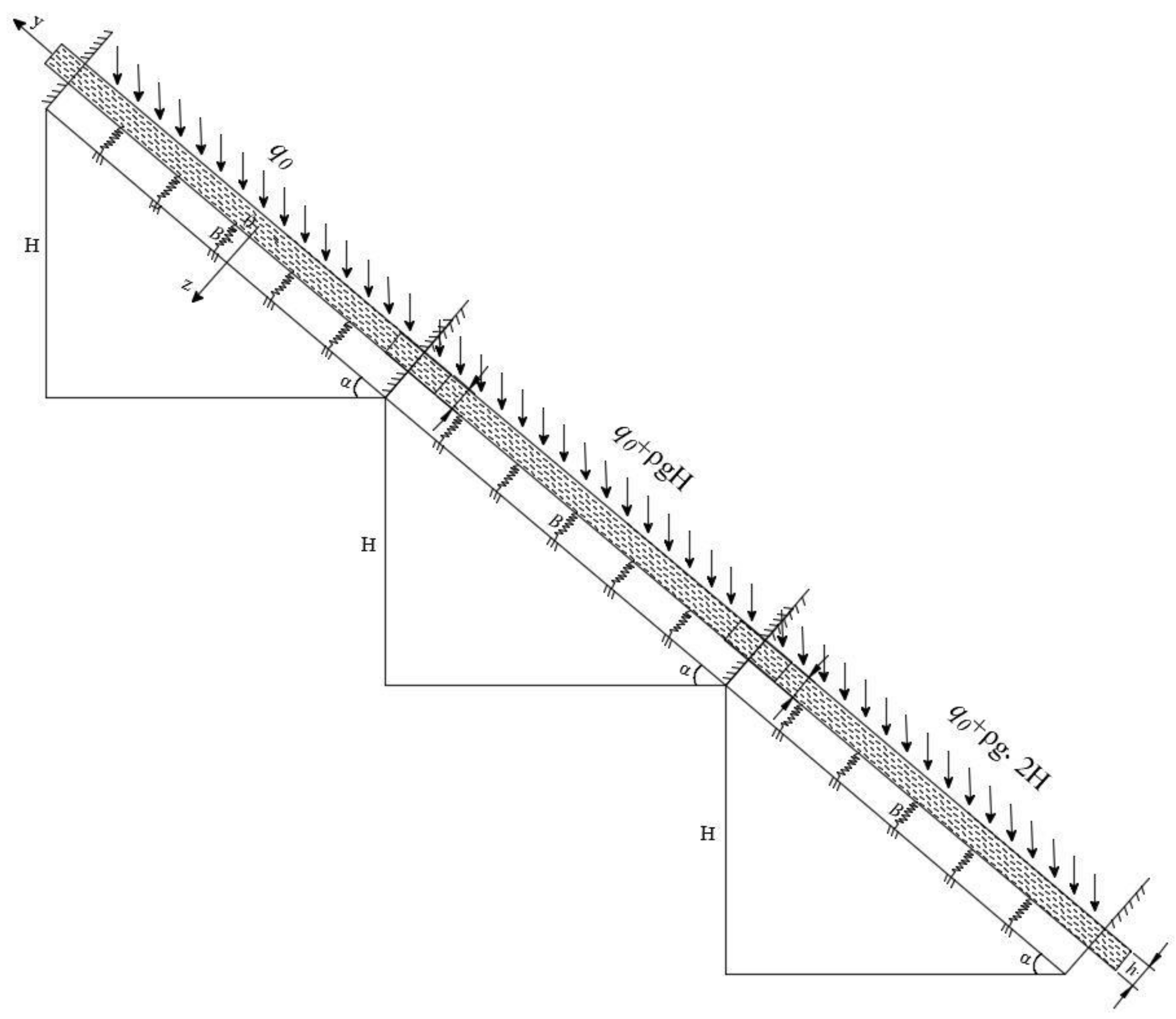
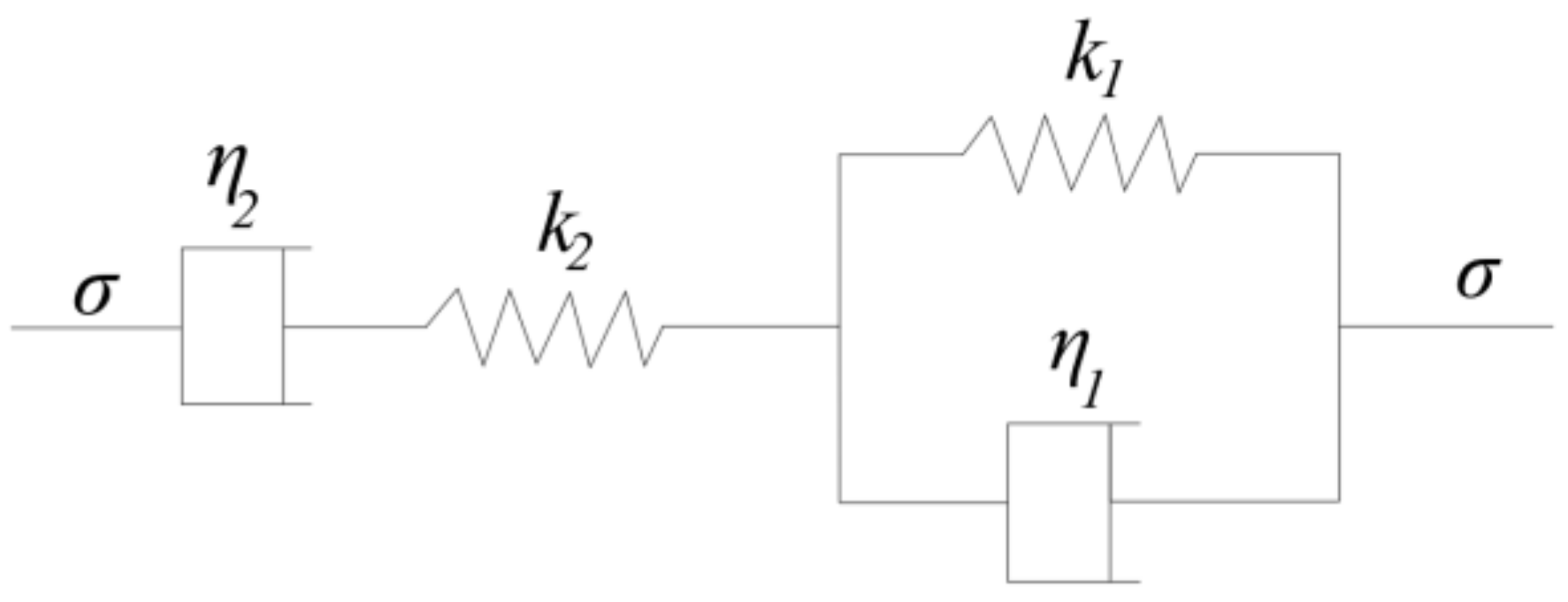
4. Stope Mechanical Model of Room-and-Pillar Mining in Long-Dip, Thin Orebody
5. Numerical Simulation of Stope Stability of Continuous Mining in Long-Dip, Thin Orebody
5.1. Justification of the Geomechanical Model
5.2. Computational Scheme
5.3. Analysis of Calculation Results
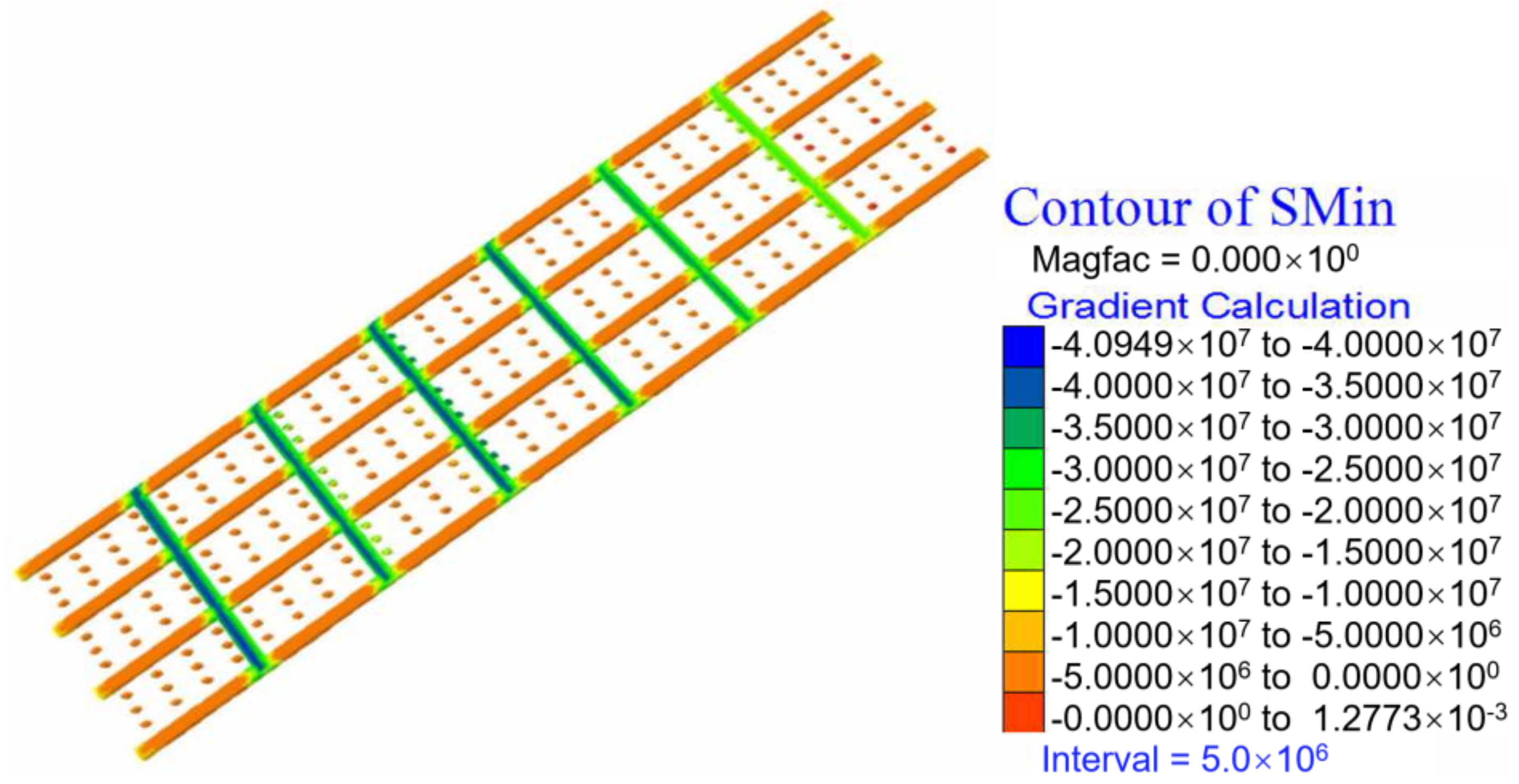
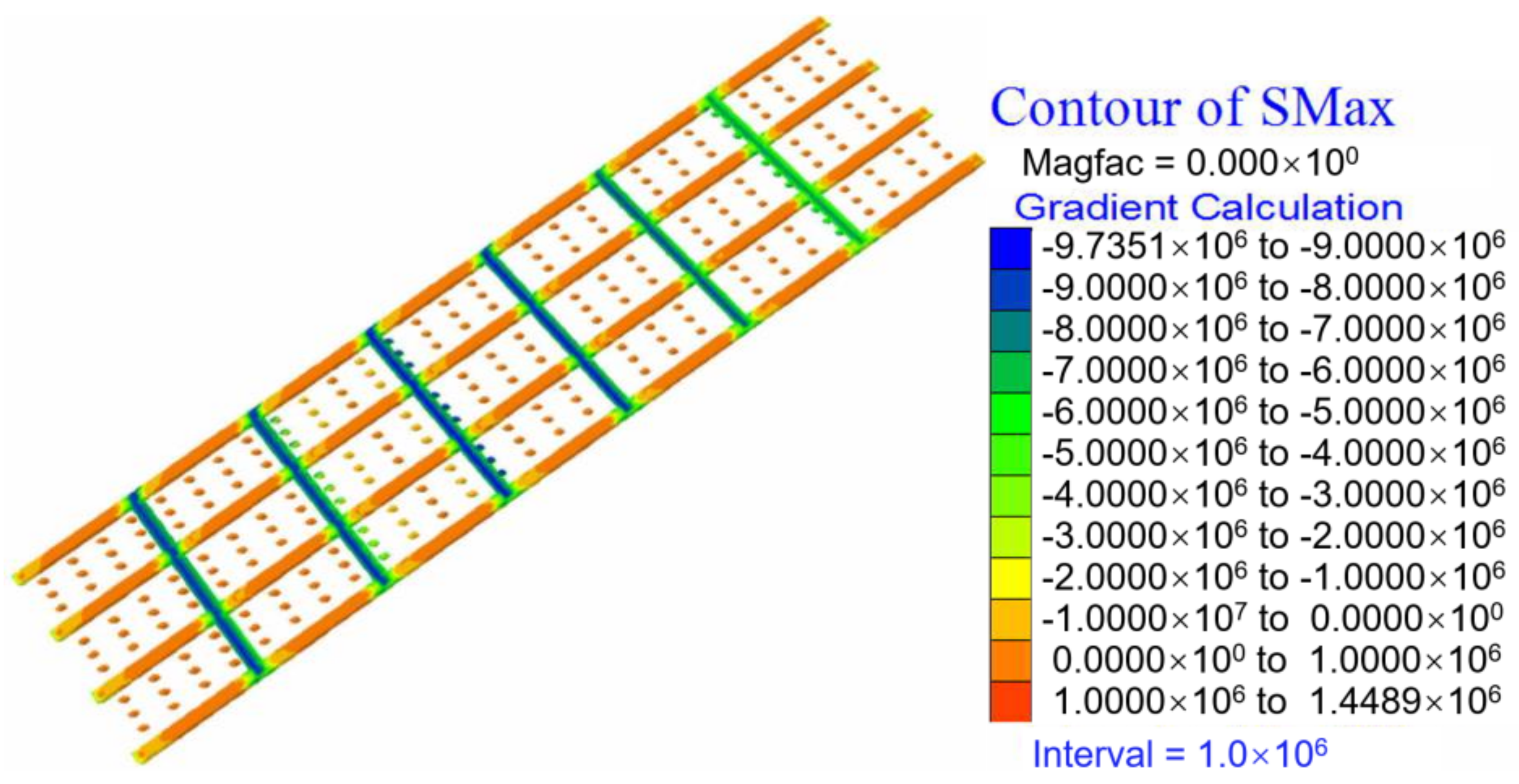
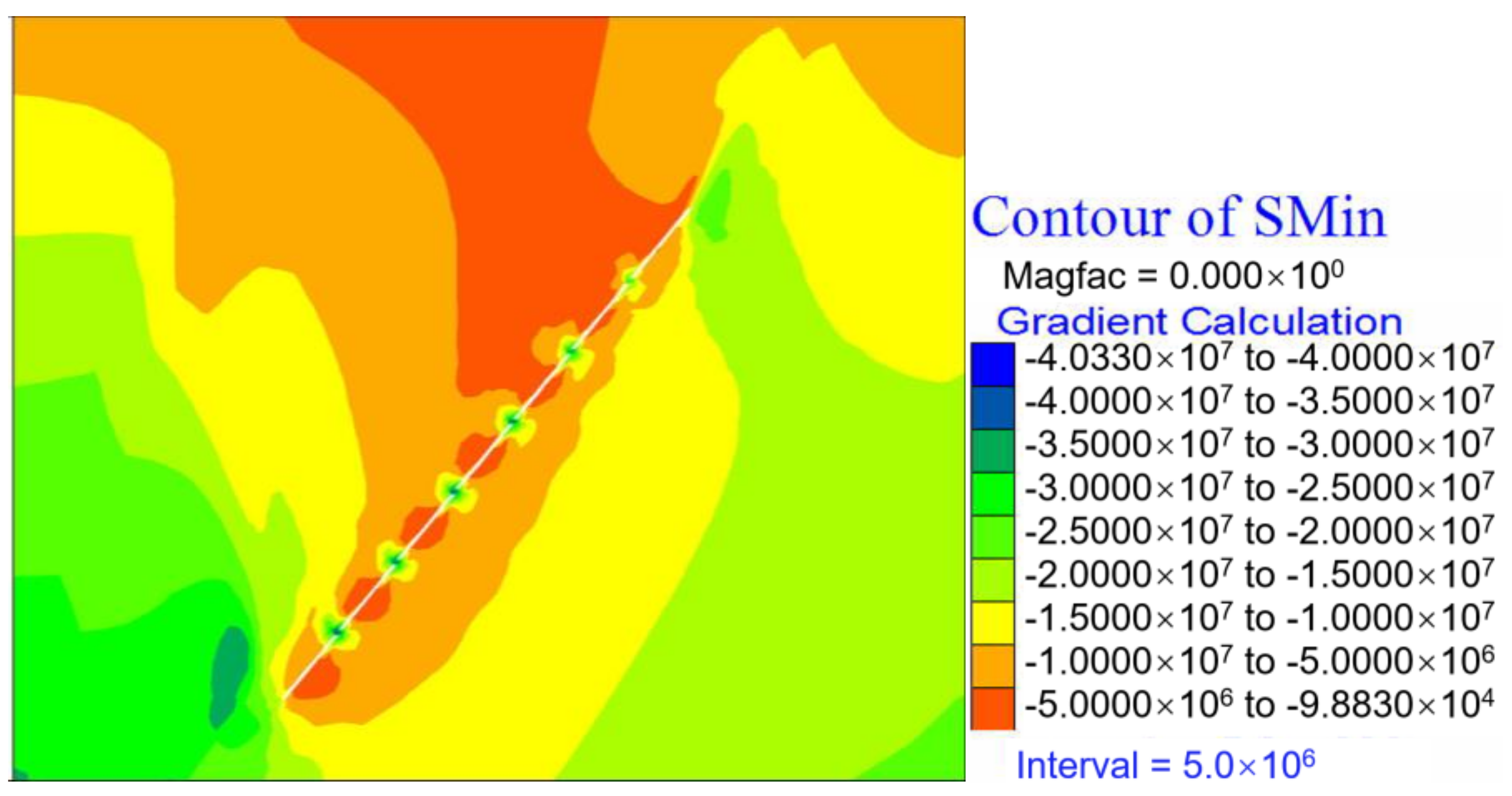
5.3.1. Stress Analysis
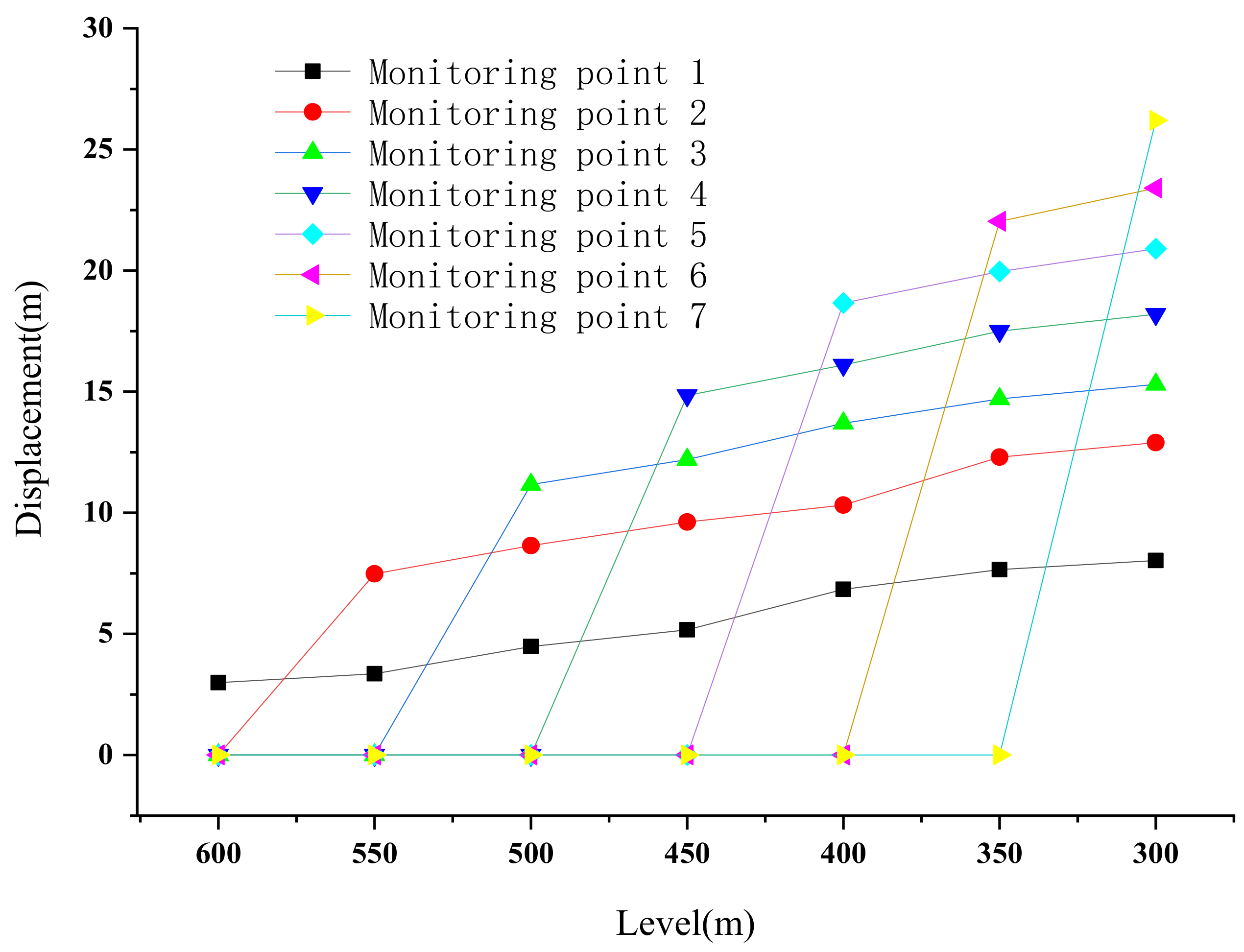
5.3.2. Displacement Analysis
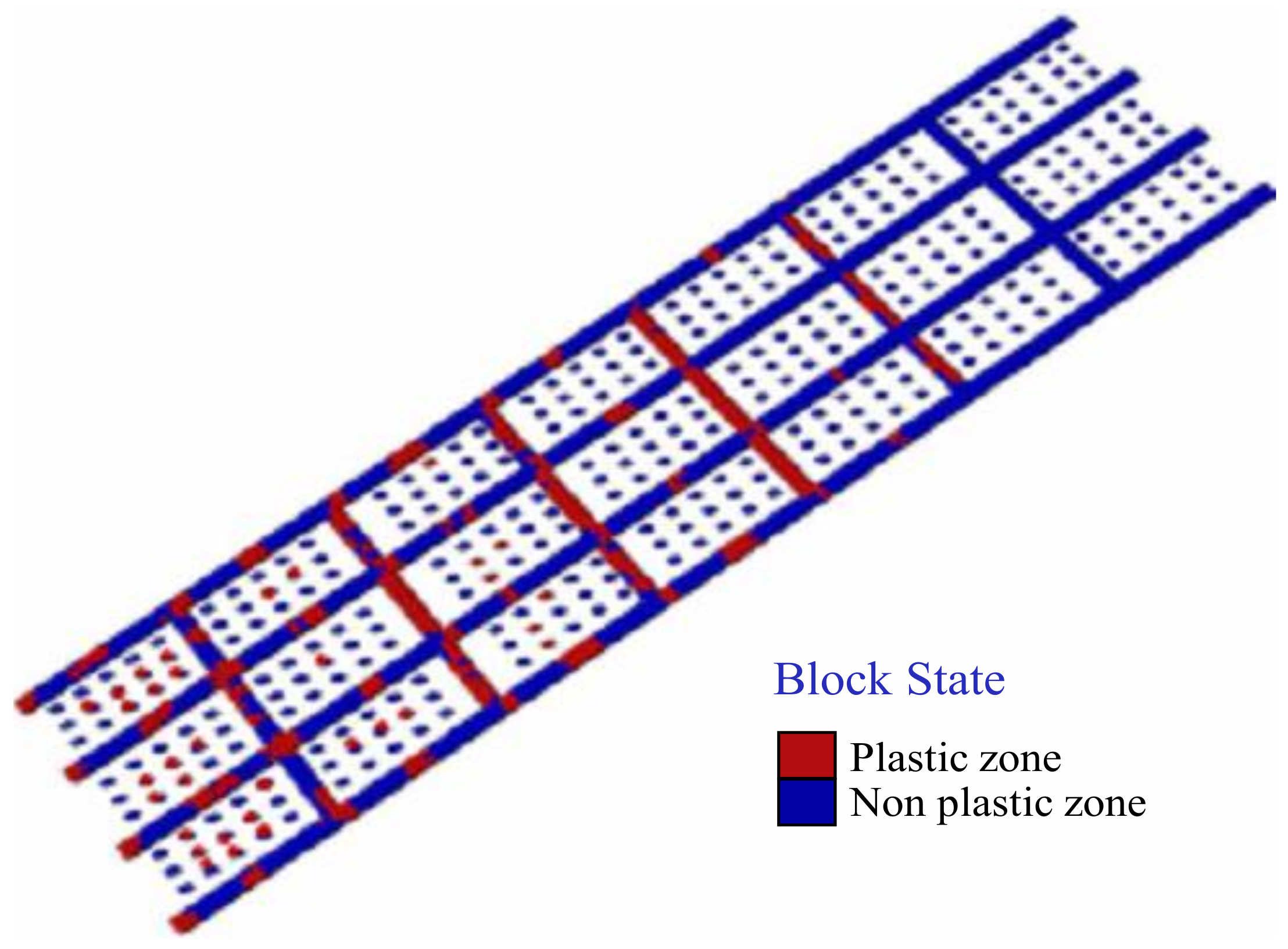
5.3.3. Plastic Zone Analysis
6. Proposals for Continuous Mining of Long-Dip, Thin Orebody by Room–Pillar Method
7. Conclusions
- (1)
- The Burgers model of rock mechanics is introduced into the mining of a long-inclined, thin orebody, the failure mechanism of the goaf roof of the long-inclined, thin orebody is studied, and the rheological mechanical model of the stope of the long-inclined, thin orebody is established, providing a theoretical foundation for the optimization of the stope design and stope support of this kind of orebody.
- (2)
- In the room–pillar mining of thin orebodies with a greater tendency to extend, the roof displacement of the stope is proportional to the mining depth, that is, the deeper the stope is buried, the larger the roof subsidence. For instance, the roof subsidence is only 2.99 mm, while the displacement of the roof increases to 26.2 mm after level 300 is mined. With the continuation of mining, the roof displacement of the upper stope that has been finished will not stop, but will continue to increase, with the increasing range becoming smaller and smaller.
- (3)
- When the same stope structural parameters are used to extract long-dip orebodies, as mining depth increases, the compressive stress on the pillars and roofs obviously increases. For example, the maximum principal stress increases from 15 MPa to 40.95 MPa, and the maximum tensile stress increases from 0.53 MPa to 1.449 MPa. As the stope continuously advances, the plastic zone scope becomes wider and wider. The failure mechanism of the rock mass also presents a variety of failure modes from single-compression shear failure to compression shear failure, tension shear failure, and so on. This shows that the stability of the stope tends to decline under the existing stope structural parameters.
- (4)
- For long-dip, thin orebodies mined with the room-and-pillar method similar to the Mengnuo Lead–Zinc Mine, although its mining conditions are different from those of pure deep mining, the influence of the continuous variation of mining depth on the stability of the stope should also be noticed. When mining the lower part of the orebody, the existing stope structural parameters should be adjusted appropriately, such as reducing the spacing of the room or pillar, increasing the size of the point pillars, and increasing the width of the room and bottom pillars and the continuous pillars, so as to ensure the long-term stability of the stope surrounding rock.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, M.C.; Xie, H.P.; Peng, S.P.; Jiang, Y.D. Study on rock mechanics in deep mining engineering. Chin. J. Rock Mech. Eng. 2005, 24, 2803–2813. [Google Scholar]
- Davide, E.; Doug, S. An integrated numerical modeling-discrete fracture network approach applied to the characterization of rock mass strength of naturally fractured pillars. Rock Mech. Rock Eng. 2010, 43, 3–19. [Google Scholar]
- Tesarik, D.; Seymour, J.; Yanske, T. Post-failure behavior of two mine pillars confined with backfill. Int. J. Rock Mech. Min. Sci. 2003, 40, 221–232. [Google Scholar] [CrossRef]
- Swift, G.M.; Reddish, D.J. Stability problems associated with an abandoned ironstone mine. Bulletin Eng. Geol. Environ. 2002, 61, 227–239. [Google Scholar]
- Martin, C.D.; Chander, N.A. The progressive fracture of Lacdu Bonnet granite. Int. J. Rock Mech. Min. 1994, 31, 643–659. [Google Scholar] [CrossRef]
- Dong, J.K.; Feng, X.T.; Zhang, X.W.; Zhang, Z.H. Stability evaluation and param eter optim ization on the fractured rockmass around underground stope. J. Northeast. Univ. 2013, 34, 1322–1326. [Google Scholar]
- Zhang, Q.L.; Cao, X.G.; Wang, Y.L.; Liu, H.Q. Stability analysis of stope roof-pillar based on cusp catastrophe model. China Saf. Sci. J. 2011, 21, 52–57. [Google Scholar]
- Xu, W.B.; Song, W.D.; Cao, S.; Jiang, G.J.; Wu, F. Stopes stability in underground mine and its control technique. J. Min. Saf. Eng. 2015, 32, 658–664. [Google Scholar]
- Liu, H.Q.; Zhang, Q.L.; Pan, C.J.; Kang, Q. Analysis of the failure law and stability of the pillar in open stope mining. J. Min. Saf. Eng. 2011, 28, 138–143. [Google Scholar]
- Tao, G.Q.; Ren, Q.Y.; Luo, H.; Liu, Z.D. Stability analysis of stope in pillarless sublevel caving. Rock Soil Mech. 2011, 32, 3768–3799. [Google Scholar]
- Sun, Y.; Luo, L.M.; Deng, W.H. Stability Analysis and Parameter Optimization of Stope in Deep Metal Mines. Gold Sci. Technol. 2017, 25, 99–105. [Google Scholar]
- Chen, T.; Mitri, H.S. Strategic sill pillar design for reduced hanging wall overbreak in longhole mining. Int. J. Min. Sci. Technol. 2021, 31, 975–982. [Google Scholar] [CrossRef]
- Bazaluk, O.; Petlovanyi, M.; Zubko, S.; Lozynskyi, V.; Sai, K. Instability Assessment of Hanging Wall Rocks during Underground Mining of Iron Ores. Minerals 2021, 11, 858. [Google Scholar] [CrossRef]
- Takhanov, D.; Muratuly, B.; Rashid, Z.; Kydrashov, A. Geomechanics substantiation of pillars development parameters in case of combined mining the contiguous steep ore bodies. Min. Miner. Depos. 2021, 15, 50–58. [Google Scholar] [CrossRef]
- Garza-Cruz, T.; Pierce, M.; Board, M. Effect of Shear Stresses on Pillar Stability: A Back Analysis of the Troy Mine Experience to Predict Pillar Performance at Montanore Mine. Rock Mech. Rock Eng. 2019, 52, 4979–4996. [Google Scholar] [CrossRef]
- Guo, Y.H.; Luo, L.; Xu, H.H.; Zhu, C. Analysis of the Regularity and Mechanism of Fault Activation Caused by Deep Continuous Mining of Shizishan Copper Mine, China. Adv. Mater. Sci. Eng. 2022, 2022, 4027231. [Google Scholar] [CrossRef]
- Guo, Y.; Luo, L. Monitoring and Analysis of Deformation Evolution Law of Fault Activation Caused by Deep Mining in Shizishan Copper Mine, China. Appl. Sci. 2022, 12, 6863. [Google Scholar] [CrossRef]
- Guo, Y.H.; Hou, K.P. Loose Circle Test and Active-passive Combined Support Technology for Deep Buried Carbonaceous Phyllite Tunnel. Chin. J. Undergr. Sp. Eng. 2021, 17, 214–221. [Google Scholar]
- Potyondy, D.O. Simulating stress corrosion with a bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 677–691. [Google Scholar] [CrossRef]
- Vyazmensky, A.; Stead, D.; Elmo, D.; Moss, A. Numerical Analysis of Block Caving-Induced Instability in Large Open Pit Slopes: A Finite Element/Discrete Element Approach. Rock Mech. Rock Eng. 2009, 43, 21–39. [Google Scholar] [CrossRef]
- Yu, G.B.; Yang, P.; Chen, Z.C. Study on surrounding rock stability of pillar extraction in thin gently inclined ore body. J. China Coal Soc. 2013, 38, 294–298. [Google Scholar]
- Wang, J.A.; Shang, X.C.; Liu, H.; Hou, Z.Y. Study on fracture mechanism and catastrophic collapse of strong roof strata above the mined area. J. China Coal Soc. 2008, 33, 850–855. [Google Scholar]
- Ghasemi, E.; Ataei, M.; Shahriar, K.; Sereshki, F.; Jlali, S.E.; Ramazanzadeh, A. Assessment of roof fall risk during retreat mining in room and pillar coal mines. Int. J. Rock Mech. Min. 2012, 12, 80–89. [Google Scholar] [CrossRef]
- Singh, G.S.P.; Singh, U.K.; Murthy, V.M.S.R. Application of numerical modeling for strata control in mines. Geotech. Geol. Eng. 2010, 513–524. [Google Scholar] [CrossRef]
- Ghasemi, E.; Shahriar, K. A new coal pillars design method in order to enhance safety of the retreat mining in room and pillar mines. Saf. Sci. 2012, 50, 579–585. [Google Scholar] [CrossRef]



| Lithology | Density (g/cm3) | Uniaxial Tensile Strength (MPa) | Elasticity Modulus (GPa) | Cohesion (MPa) | Friction Angle (°) | Poisson Ratio |
|---|---|---|---|---|---|---|
| Orebody | 4.15 | 1.2494 | 55.1 | 0.7036 | 33.93 | 0.319 |
| Sandstone | 2.71 | 0.8922 | 18.4 | 0.6659 | 49.19 | 0.084 |
| Lamellar limestone | 2.75 | 0.9801 | 21.1 | 0.5242 | 30.43 | 0.103 |
| Crystalline limestone | 2.82 | 0.9314 | 67.5 | 0.5443 | 33.32 | 0.309 |
| Phyllite | 2.64 | 0.5498 | 13.2 | 0.4448 | 32.05 | 0.300 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Miao, Y. Study on Stope Stability in Continuous Mining of Long-Dip, Thin Orebody by Room–Pillar Method. Sustainability 2022, 14, 9601. https://doi.org/10.3390/su14159601
Guo Y, Miao Y. Study on Stope Stability in Continuous Mining of Long-Dip, Thin Orebody by Room–Pillar Method. Sustainability. 2022; 14(15):9601. https://doi.org/10.3390/su14159601
Chicago/Turabian StyleGuo, Yanhui, and Yichen Miao. 2022. "Study on Stope Stability in Continuous Mining of Long-Dip, Thin Orebody by Room–Pillar Method" Sustainability 14, no. 15: 9601. https://doi.org/10.3390/su14159601
APA StyleGuo, Y., & Miao, Y. (2022). Study on Stope Stability in Continuous Mining of Long-Dip, Thin Orebody by Room–Pillar Method. Sustainability, 14(15), 9601. https://doi.org/10.3390/su14159601






