Reliability Assessment Method for Simply Supported Bridge Based on Structural Health Monitoring of Frequency with Temperature and Humidity Effect Eliminated
Abstract
:1. Introduction
2. Basic Theory of Verification Coefficient
2.1. Verification Coefficient of Deflection
2.2. Verification Coefficient of Frequency
2.3. Deflection Verification Coefficient Based on Frequency
3. Temperature and Humidity Effect Elimination
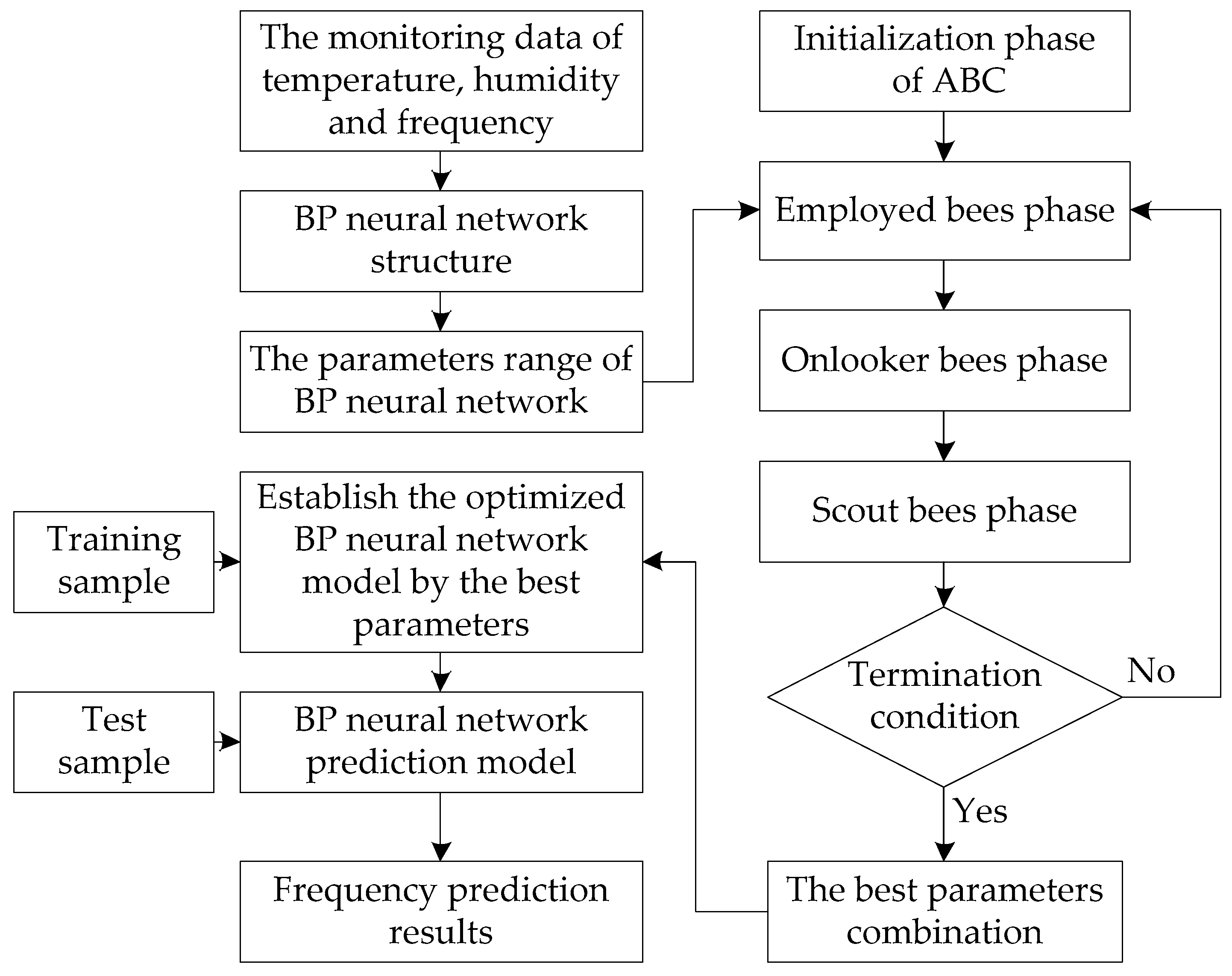
3.1. BP Neural Network
3.2. Artificial Bee Colony Algorithm
- (1)
- Initialization phase
- (2)
- Employed bees phase
- (3)
- Onlooker bees phase
- (4)
- Scout bees phase
3.3. BP Neural Network Optimized by ABC Algorithm
3.4. Temperature and Humidity Effect Elimination of Bridge Modal Frequency
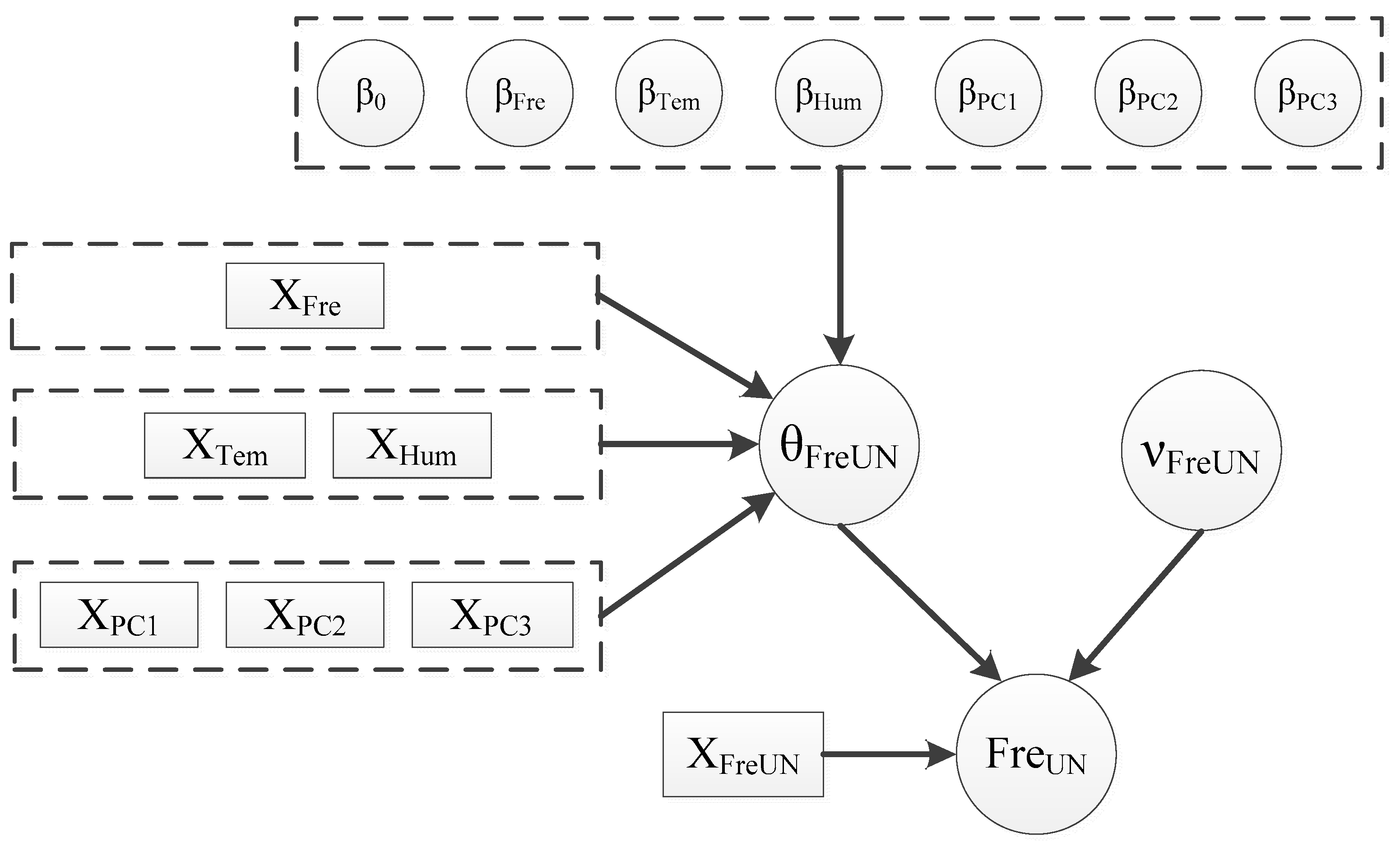
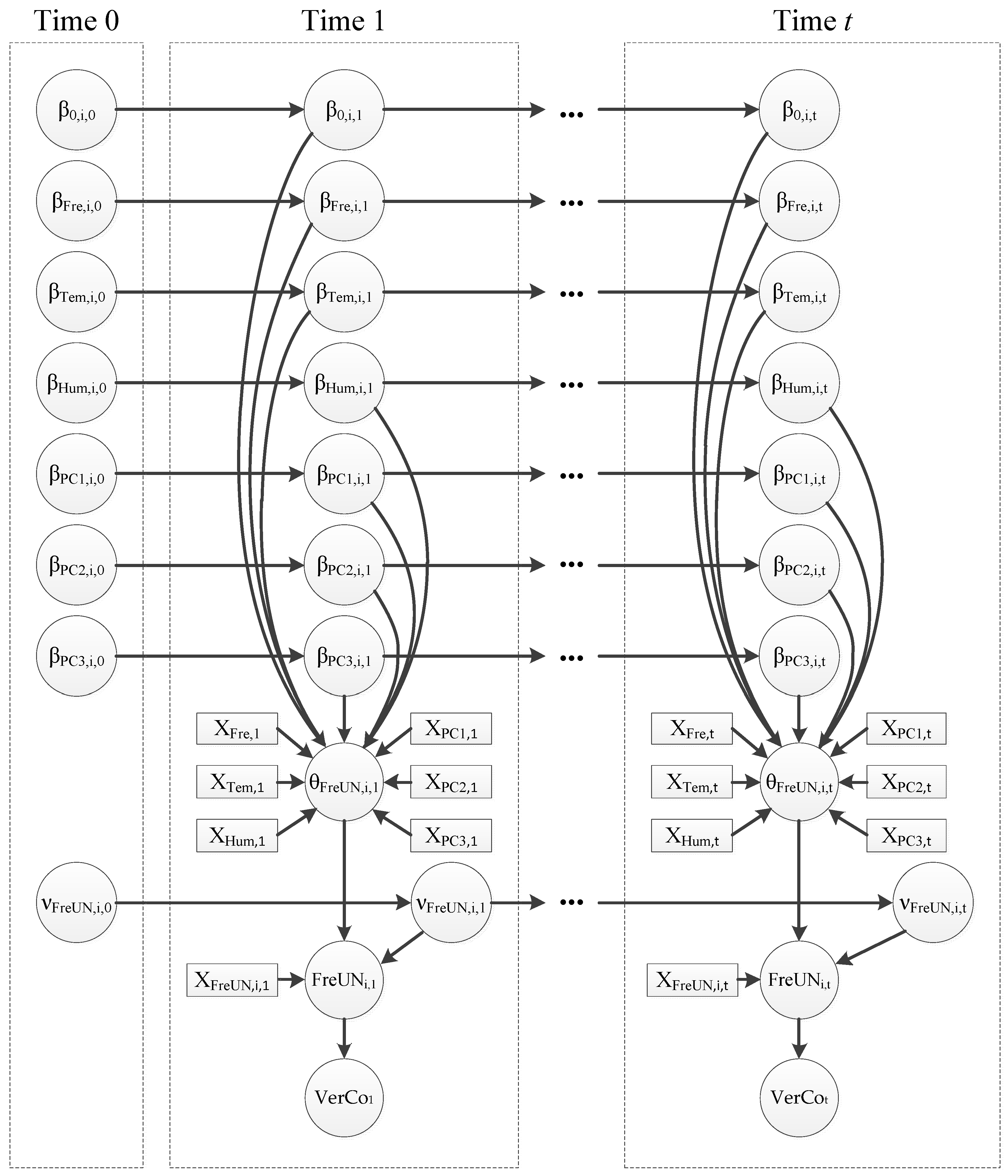
4. Dynamic Bayesian Network Model
5. Experimental Test
5.1. Simply Supported Bridge
5.2. Structural Health Monitoring System
5.2.1. Modal Frequency Monitoring System
5.2.2. Temperature and Humidity Monitoring System
6. Results and Discussion
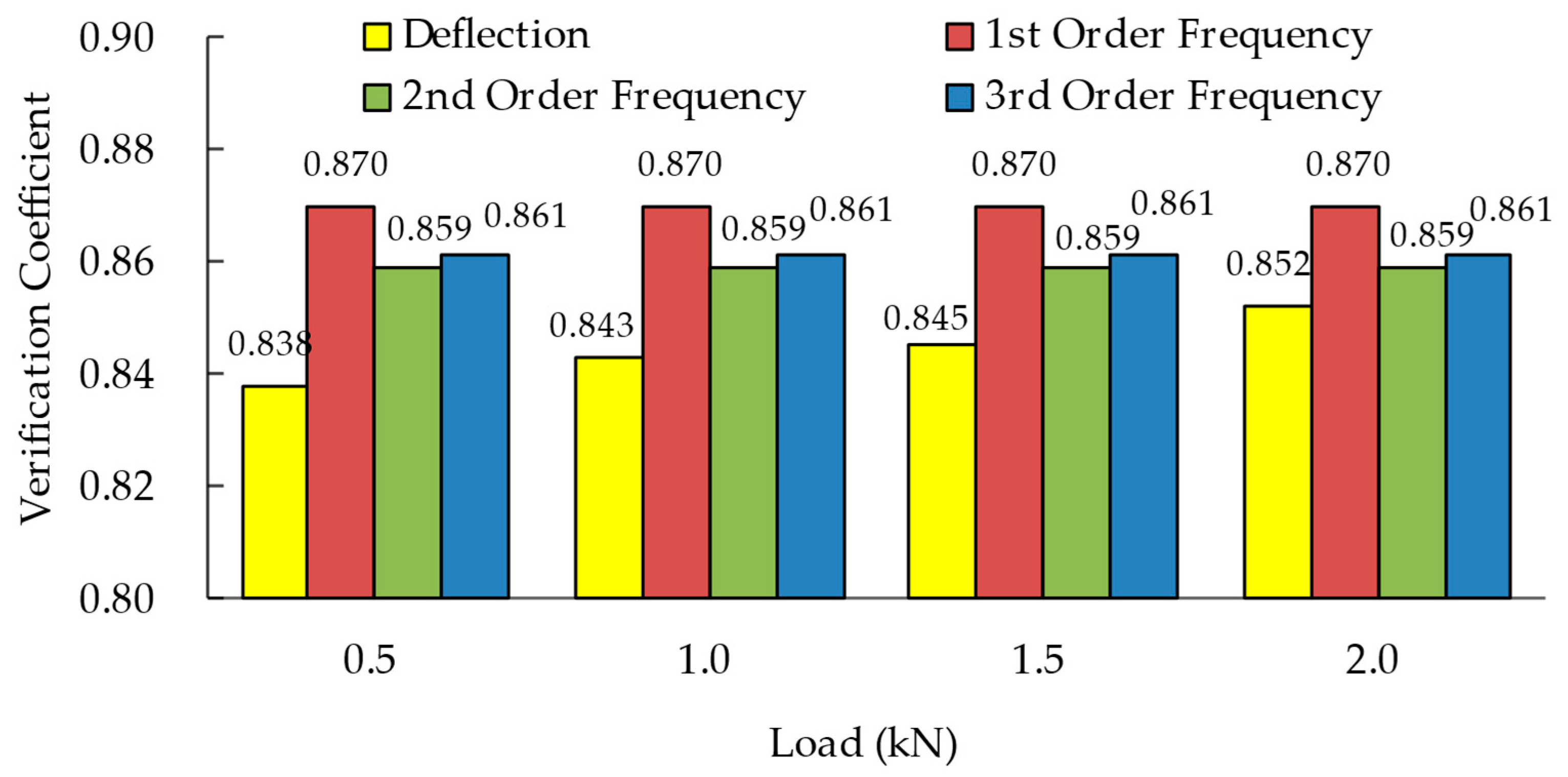
6.1. Validation of Bridge Verification Coefficient Based on Modal Frequency
6.2. Bridge Frequency with the Effect of Temperature and Humidity Eliminated
6.3. Dynamic Bayesian Network Analysis
6.4. Bridge Reliability Analysis Based on Verification Coefficient
7. Conclusions
- (1)
- The relationship between modal frequency and verification coefficient was obtained through theoretical derivation. Through the comparation between static test and dynamic test, it verified the verification coefficient calculation method based on modal frequency. The results demonstrated that the verification coefficient computed by the proposed method coincided with that obtained through the static test. The first three modal of frequencies can be used for deflection verification coefficient calculation;
- (2)
- The BP neural network optimized by an artificial bee colony algorithm has high fitting precision, which is adopted for the influence of temperature and humidity on the monitoring frequency elimination method. The bridge frequency does not change with temperature and humidity; rather, it only fluctuates slightly near the expected frequency and gradually approaches the expected value;
- (3)
- According to the results analyzed using the dynamic Bayesian network, bridge internal temperature possesses the greatest influence on the bridge frequency, and ambient temperature and humidity also clearly affect the bridge frequency. However, the change of bridge frequency is mainly influenced by temperature. With more monitoring data, the posterior information of bridge frequency demonstrated that the proposed method reduced the uncertainty of bridge frequency with the temperature and humidity effect eliminated, and showed that it is closer to the real probability distribution parameter;
- (4)
- The bridge reliability calculation results reveal that the reliability indices have a great difference before and after the temperature and humidity effects are eliminated. When the temperature and humidity effects are eliminated, the variations of bridge reliability are independent of temperature and humidity. The bridge performance cannot be accurately estimated without the temperature and humidity effects being eliminated. The proposed method in this paper provides a new theoretical basis and technical support for bridge SHM.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mu, H.; Zheng, Z.; Wu, X.; Su, C. Bayesian Network-Based Modal Frequency–Multiple Environmental Factors Pattern Recognition for the Xinguang Bridge Using Long-Term Monitoring Data. J. Low Freq. Noise Vib. Act. Control. 2018, 39, 545–559. [Google Scholar] [CrossRef]
- Sun, S.; Liang, L.; Li, M.; Li, X. Bridge Performance Evaluation via Dynamic Fingerprints and Data Fusion. J. Perform. Constr. Fac. 2019, 33, 04019004. [Google Scholar] [CrossRef]
- Hasan, S.; Elwakil, E. Knowledge-driven stochastic reliable modeling for steel bridge deck condition rating prediction. J. Struct. Integr. Main. 2021, 6, 91–98. [Google Scholar] [CrossRef]
- Xia, Y.; Jian, X.; Yan, B.; Su, D. Infrastructure Safety Oriented Traffic Load Monitoring Using Multi-Sensor and Single Camera for Short and Medium Span Bridges. Remote Sens. 2019, 11, 2651. [Google Scholar] [CrossRef] [Green Version]
- Lei, X.; Sun, L.; Xia, Y.; He, T. Vibration-Based Seismic Damage States Evaluation for Regional Concrete Beam Bridges Using Random Forest Method. Sustainability 2020, 12, 5106. [Google Scholar] [CrossRef]
- Whitlow, R.D.; Haskins, R.; McComas, S.L.; Crane, C.K.; Howard, I.L.; McKenna, M.H. Remote Bridge Monitoring Using Infrasound. J. Bridge Eng. 2019, 24, 04019023. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Experimental Validation of Cost-Effective Vision-Based Structural Health Monitoring. Mech. Syst. Signal Process. 2017, 88, 199–211. [Google Scholar] [CrossRef]
- Prakash, G. A Deflection-Based Practicable Method for Health Monitoring of In-Service Bridges. Meas. Sci. Technol. 2021, 32, 075108. [Google Scholar] [CrossRef]
- Farreras-Alcover, I.; Chryssanthopoulos, M.K.; Andersen, J.E. Regression Models for Structural Health Monitoring of Welded Bridge Joints Based on Temperature, Traffic and Strain Measurements. Struct. Health Monit. 2015, 14, 648–662. [Google Scholar] [CrossRef] [Green Version]
- Pan, C.; Yu, L.; Liu, H. Identification of Moving Vehicle Forces on Bridge Structures via Moving Average Tikhonov Regularization. Smart Mater. Struct. 2017, 26, 085041. [Google Scholar] [CrossRef]
- Seo, J.; Hu, J.W.; Lee, J. Summary Review of Structural Health Monitoring Applications for Highway Bridges. J. Perform. Constr. Fac. 2016, 30, 04015072. [Google Scholar] [CrossRef]
- Whelan, M.J.; Gangone, M.V.; Janoyan, K.D.; Jha, R. Real-Time Wireless Vibration Monitoring for Operational Modal Analysis of An Integral Abutment Highway Bridge. Eng. Struct. 2009, 31, 2224–2235. [Google Scholar] [CrossRef]
- Tan, C.; Uddin, N.; Obrien, E.J.; McGetrick, P.J.; Kim, C.W. Extraction of Bridge Modal Parameters Using Passing Vehicle Response. J. Bridge Eng. 2019, 24, 04019087. [Google Scholar] [CrossRef]
- Lee, L.S.; Karbhari, V.M.; Sikorsky, C. Structural Health Monitoring of CFRP Strengthened Bridge Decks Using Ambient Vibrations. Struct. Health Monit. 2007, 6, 199–214. [Google Scholar] [CrossRef]
- Liu, C.; DeWolf, J.T.; Kim, J.H. Development of A Baseline for Structural Health Monitoring for A Curved Post-Tensioned Concrete Box-Girder Bridge. Eng. Struct. 2009, 31, 3107–3115. [Google Scholar] [CrossRef]
- Li, J.; Zhu, X.; Law, S.; Samali, B. Time-Varying Characteristics of Bridges under the Passage of Vehicles Using Synchroextracting Transform. Mech. Syst. Signal Process. 2020, 140, 106727. [Google Scholar] [CrossRef]
- Nandan, H.; Singh, M.P. Effects of Thermal Environment on Structural Frequencies: Part I—A Simulation Study. Eng. Struct. 2014, 81, 480–490. [Google Scholar] [CrossRef]
- He, H.; Wang, W.; Zhang, X. Frequency Modification of Continuous Beam Bridge Based on Co-Integration Analysis Considering the Effect of Temperature and Humidity. Struct. Health Monit. 2019, 18, 376–389. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, Y.; Wei, Z.; Zhu, H.; Zhou, X. Variation of Structural Vibration Characteristics Versus Non-Uniform Temperature Distribution. Eng. Struct. 2011, 33, 146–153. [Google Scholar] [CrossRef] [Green Version]
- Teng, J.; Tang, D.-H.; Hu, W.; Lu, W.; Feng, Z.; Ao, C.; Liao, M. Mechanism of the Effect of Temperature on Frequency Based on Long-Term Monitoring of An Arch Bridge. Struct. Health Monit. 2021, 20, 1716–1737. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, K.; Ye, Z.; Liu, C.; Lu, K.; Wang, L. Influence of Temperature on the Natural Vibration Characteristics of Simply Supported Reinforced Concrete Beam. Sensors 2021, 21, 4242. [Google Scholar] [CrossRef] [PubMed]
- Kromanis, R.; Kripakaran, P. Data-Driven Approaches for Measurement Interpretation: Analysing Integrated Thermal and Vehicular Response in Bridge Structural Health Monitoring. Adv. Eng. Inform. 2017, 34, 46–59. [Google Scholar] [CrossRef] [Green Version]
- Deng, Y.; Li, A.; Feng, D. Probabilistic Damage Detection of Long-Span Bridges Using Measured Modal Frequencies and Temperature. Int. J. Struct. Stab. Dy. 2018, 18, 1850126. [Google Scholar] [CrossRef]
- Wang, Z.; Yi, T.; Yang, D.; Li, H.; Liu, H. Eliminating the Bridge Modal Variability Induced by Thermal Effects Using Localized Modeling Method. J. Bridge Eng. 2021, 26, 04021073. [Google Scholar] [CrossRef]
- Gonen, S.; Soyoz, S. Reliability-based seismic performance of masonry arch bridges. Struct. Infrastruct. Eng. 2021, 2021, 1–16. [Google Scholar] [CrossRef]
- Dissanayake, P.B.R.; Karunananda, P.A.K. Reliability Index for Structural Health Monitoring of Aging Bridges. Struct. Health Monit. 2008, 7, 175–183. [Google Scholar] [CrossRef]
- Newhook, J.P.; Edalatmanesh, R. Integrating Reliability and Structural Health Monitoring in the Fatigue Assessment of Concrete Bridge Decks. Struct. Infrastruct. Eng. 2013, 9, 619–633. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Eldiasty, M.; Hu, J.W. Safety and Reliability Evaluations of Bridge Behaviors under Ambient Truck Loads through Structural Health Monitoring and Identification Model Approaches. Measurement 2021, 187, 110234. [Google Scholar] [CrossRef]
- Catbas, F.N.; Susoy, M.; Frangopol, D.M. Structural health monitoring and reliability estimation: Long span truss bridge application with environmental monitoring data. Eng. Struct. 2008, 30, 2347–2359. [Google Scholar] [CrossRef]
- Fan, X.P.; Liu, Y.F. Time-variant reliability prediction of bridge system based on BDGCM and SHM data. Struct. Control Health Monit. 2018, 25, e2185. [Google Scholar] [CrossRef]
- Xu, X.; Ren, Y.; Huang, Q.; Zhao, D.; Tong, Z.; Chang, W. Thermal response separation for bridge long-term monitoring systems using multi-resolution wavelet-based methodologies. J. Civ. Struct. Health 2020, 10, 527–541. [Google Scholar] [CrossRef]
- Bhattacharya, B.; Li, D.; Chajes, M.; Hastings, J. Reliability-Based Load and Resistance Factor Rating Using In-Service Data. J. Bridge Eng. 2005, 10, 530–543. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Fan, X. Gaussian Copula–Bayesian Dynamic Linear Model–Based Time-Dependent Reliability Prediction of Bridge Structures Considering Nonlinear Correlation between Failure Modes. Adv. Mech. Eng. 2016, 8, 1687814016681372. [Google Scholar] [CrossRef]
- Chen, C.; Wang, Z.; Wang, Y.; Wang, T.; Luo, Z. Reliability Assessment for PSC Box-Girder Bridges Based on SHM Strain Measurements. J. Sens. 2017, 2017, 8613659. [Google Scholar] [CrossRef] [Green Version]
- Kaloop, M.R.; Kim, K.H.; Elbeltagi, E.; Jin, X.; Hu, J.W. Service-Life Evaluation of Existing Bridges Subjected to Static and Moving Trucks Using Structural Health Monitoring System: Case Study. KSCE J. Civ. Eng. 2020, 24, 1593–1606. [Google Scholar] [CrossRef]
- Liu, H.; He, X.; Jiao, Y.; Wang, X. Reliability Assessment of Deflection Limit State of a Simply Supported Bridge Using Vibration Data and Dynamic Bayesian Network Inference. Sensors 2019, 19, 837. [Google Scholar] [CrossRef] [Green Version]
- Kaloop, M.R.; Elsharawy, M.; Abdelwahed, B.; Hu, J.W.; Kim, D. Performance Assessment of Bridges Using Short-Period Structural Health Monitoring System: Sungsu Bridge Case Study. Smart Struct. Syst. 2020, 26, 667–680. [Google Scholar] [CrossRef]
- Jamali, S.; Chan, T.H.T.; Nguyen, A.; Thambiratnam, D.P. Reliability-Based Load-Carrying Capacity Assessment of Bridges Using Structural Health Monitoring and Nonlinear Analysis. Struct. Health Monit. 2019, 18, 20–34. [Google Scholar] [CrossRef] [Green Version]
- Gehl, P.; D’Ayala, D. Development of Bayesian Networks for the Multi-Hazard Fragility Assessment of Bridge Systems. Struct. Saf. 2016, 60, 37–46. [Google Scholar] [CrossRef]
- Morales-Napoles, O.; Steenbergen, R.D.J.M. Analysis of Axle and Vehicle Load Properties through Bayesian Networks Based on Weigh-In-Motion Data. Reliab. Eng. Syst. Safe. 2014, 125, 153–164. [Google Scholar] [CrossRef]
- Research Institute of Highway Ministry of Transport of China. Specification for Inspection and Evaluation of Load-Bearing Capacity of Highway Bridges, 1st ed.; China Communications Press: Beijing, China, 2011. (In Chinese)
- Wang, X.; Miao, C.; Wang, X. Prediction analysis of deflection in the construction of composite box-girder bridge with corrugated steel webs based on MEC-BP neural networks. Structures 2021, 32, 691–700. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B. A comparative study of Artificial Bee Colony algorithm. Appl. Math. Comput. 2009, 214, 108–132. [Google Scholar] [CrossRef]
- Pham, D.T.; Castellani, M. Benchmarking and comparison of nature-inspired population-based continuous optimisation algorithms. Soft Comput. 2014, 18, 871–903. [Google Scholar] [CrossRef]
- Tan, G.; Liu, Z. Temperature Effect Analysis of Bridge Natural Frequency Based on Particle Swarm Optimized Neural Network. In Proceedings of the 7th IEEE Annual International Conference on CYBER Technology in Automation, Control and Intelligent Systems, Honolulu, HI, USA, 31 July 2017. [Google Scholar]
- Fan, X. Bridge extreme stress prediction based on Bayesian dynamic linear models and non-uniform sampling. Struct. Health Monit. 2017, 16, 253–261. [Google Scholar] [CrossRef]
- Sen, D.; Erazo, K.; Zhang, W.; Nagarajaiah, S.; Sun, L. On the effectiveness of principal component analysis for decoupling structural damage and environmental effects in bridge structures. J. Sound Vib. 2019, 457, 280–298. [Google Scholar] [CrossRef]
- Ntzoufras, I. Bayesian Modeling Using WinBUGS, 1st ed.; John Wiley & Sons Publication: Hoboken, NJ, USA, 2009; pp. 151–166. [Google Scholar]




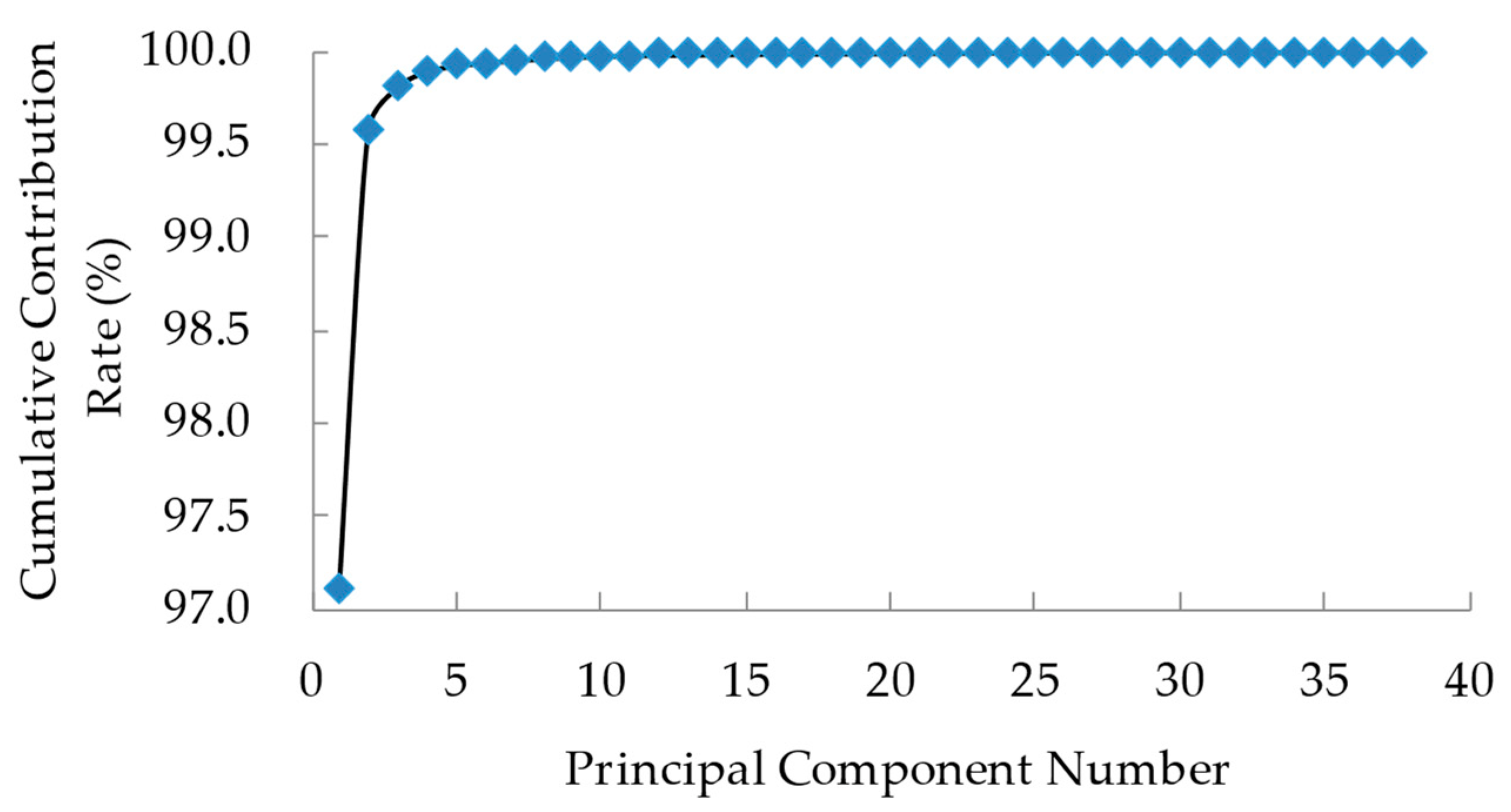
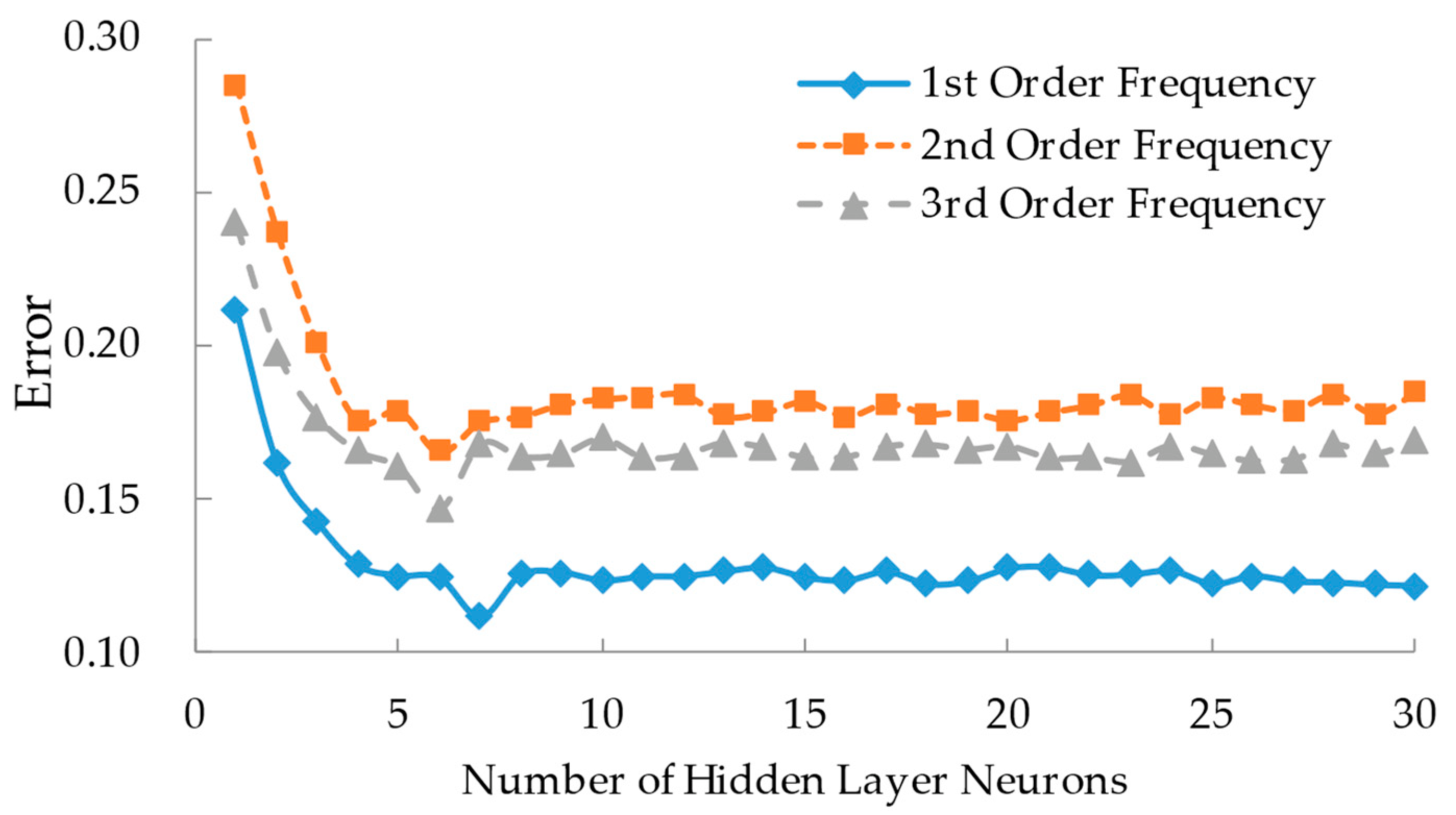
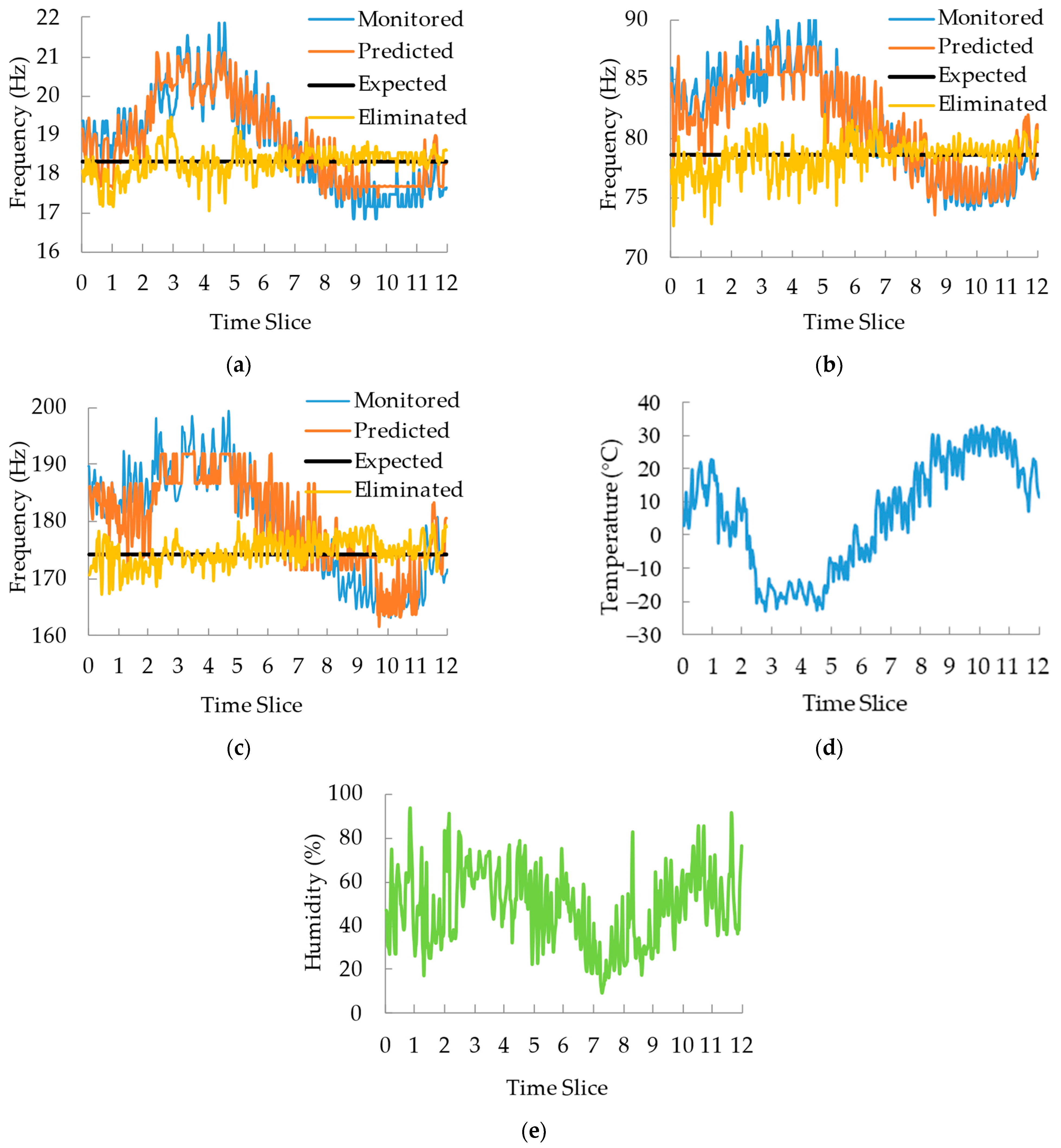


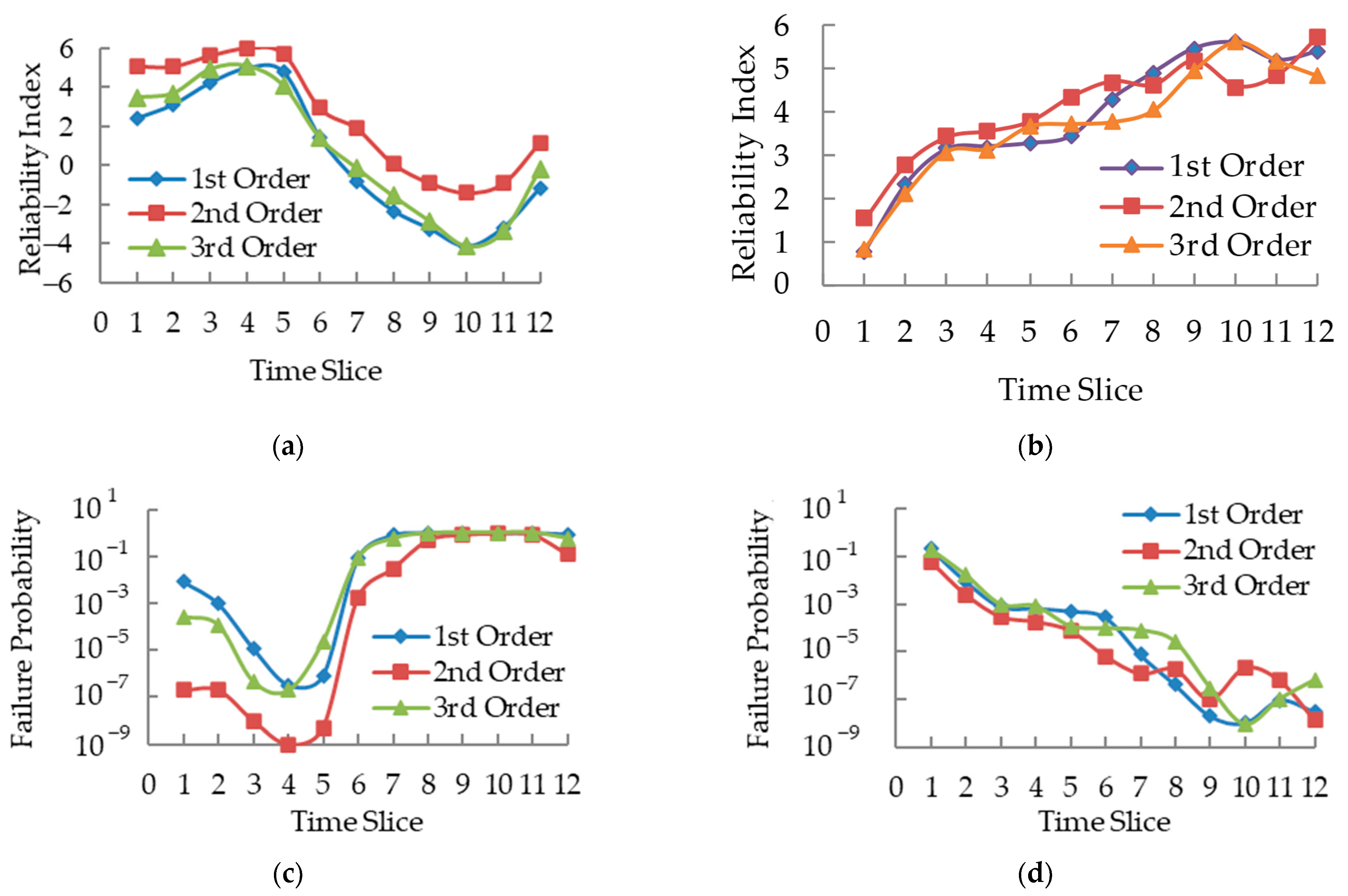
| Material | Unit | Proportions |
|---|---|---|
| Cement | kg/m3 | 378 |
| Coarse aggregate | kg/m3 | 1230 |
| Fine aggregate | kg/m3 | 607 |
| Water | kg/m3 | 185 |
| Water/cement ratio | — | 0.49 |
| Load P Level (kN) | Theoretical Values (mm) | Measured Values (mm) | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | Mean | Coefficient of Variation | ||
| 0.5 | 0.111 | 0.10 | 0.10 | 0.09 | 0.08 | 0.093 | 0.1035 |
| 1.0 | 0.223 | 0.17 | 0.20 | 0.19 | 0.19 | 0.188 | 0.0671 |
| 1.5 | 0.329 | 0.26 | 0.29 | 0.28 | 0.28 | 0.278 | 0.0453 |
| 2.0 | 0.432 | 0.35 | 0.37 | 0.38 | 0.37 | 0.368 | 0.0342 |
| Modal Order | Theoretical Values (Hz) | Measured Values (Hz) | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | Mean | Coefficient of Variation | ||
| 1st order | 18.304 | 19.688 | 19.750 | 19.375 | 19.688 | 19.625 | 0.0086 |
| 2nd order | 76.617 | 82.511 | 82.900 | 83.132 | 82.133 | 82.669 | 0.0053 |
| 3rd order | 174.330 | 187.769 | 188.408 | 188.927 | 186.481 | 187.896 | 0.0056 |
| Variables | First Order | Second Order | Third Order | Distribution Type | |||
|---|---|---|---|---|---|---|---|
| Mean Value | Standard Deviation | Mean Value | Standard Deviation | Mean Value | Standard Deviation | ||
| 34.5100 | 2.8180 | 146.400 | 25.5500 | 240.5000 | 37.4600 | Normal istribution | |
| −0.8250 | 0.1478 | −0.8431 | 0.3032 | −0.3431 | 0.2026 | ||
| −0.0093 | 0.0101 | −0.0526 | 0.0508 | −0.1116 | 0.1020 | ||
| 0.0021 | 0.0018 | 0.0229 | 0.0095 | −0.0138 | 0.0188 | ||
| −0.0995 | 0.0321 | −0.9589 | 0.1973 | 0.1528 | 0.3525 | ||
| 2.7850 | 1.9560 | −52.5800 | 9.6580 | 22.8300 | 19.2700 | ||
| −0.2917 | 0.1678 | −0.9816 | 0.8333 | −5.7380 | 1.6160 | ||
| 18.4800 | 0.0250 | 78.3200 | 0.1241 | 176.2000 | 0.2494 | ||
| 0.2218 | 0.0193 | 1.0990 | 0.0956 | 2.2080 | 0.1934 | Gamma distribution | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Tan, G.; Chu, W.; Zhang, S.; Wei, X. Reliability Assessment Method for Simply Supported Bridge Based on Structural Health Monitoring of Frequency with Temperature and Humidity Effect Eliminated. Sustainability 2022, 14, 9600. https://doi.org/10.3390/su14159600
He X, Tan G, Chu W, Zhang S, Wei X. Reliability Assessment Method for Simply Supported Bridge Based on Structural Health Monitoring of Frequency with Temperature and Humidity Effect Eliminated. Sustainability. 2022; 14(15):9600. https://doi.org/10.3390/su14159600
Chicago/Turabian StyleHe, Xin, Guojin Tan, Wenchao Chu, Sufeng Zhang, and Xueliang Wei. 2022. "Reliability Assessment Method for Simply Supported Bridge Based on Structural Health Monitoring of Frequency with Temperature and Humidity Effect Eliminated" Sustainability 14, no. 15: 9600. https://doi.org/10.3390/su14159600
APA StyleHe, X., Tan, G., Chu, W., Zhang, S., & Wei, X. (2022). Reliability Assessment Method for Simply Supported Bridge Based on Structural Health Monitoring of Frequency with Temperature and Humidity Effect Eliminated. Sustainability, 14(15), 9600. https://doi.org/10.3390/su14159600








