Modeling and Simulation of Multipumping Photovoltaic Irrigation Systems
Abstract
:1. Introduction
Objectives and Organization of the Article
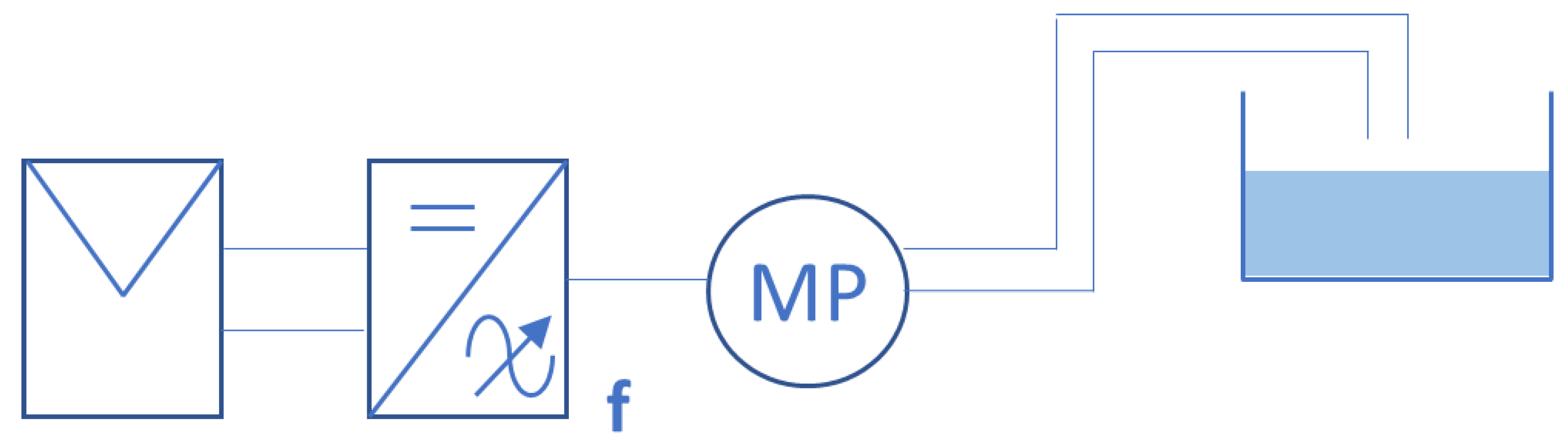
2. Materials and Methods
- The active pumps of the first group operate synchronized with each other at a fixed frequency (typically, it corresponds to the nominal frequency or the frequency at which maximum efficiency is achieved), and the active pumps of the second group operate synchronized with each other at a variable frequency;
- The pumps in both groups operate at a variable frequency, and this frequency may be different in each group but equal within the same group.
3. Modeling of the Multipumping PV Irrigation Systems
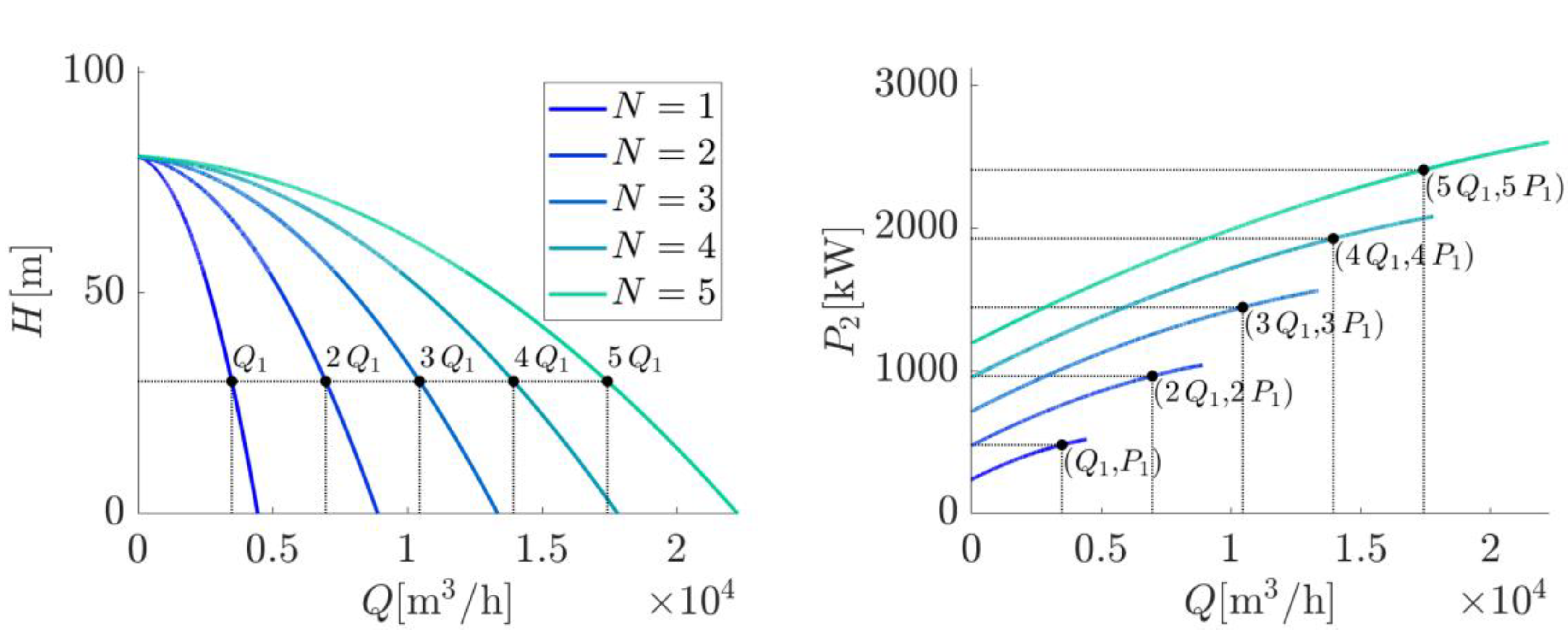
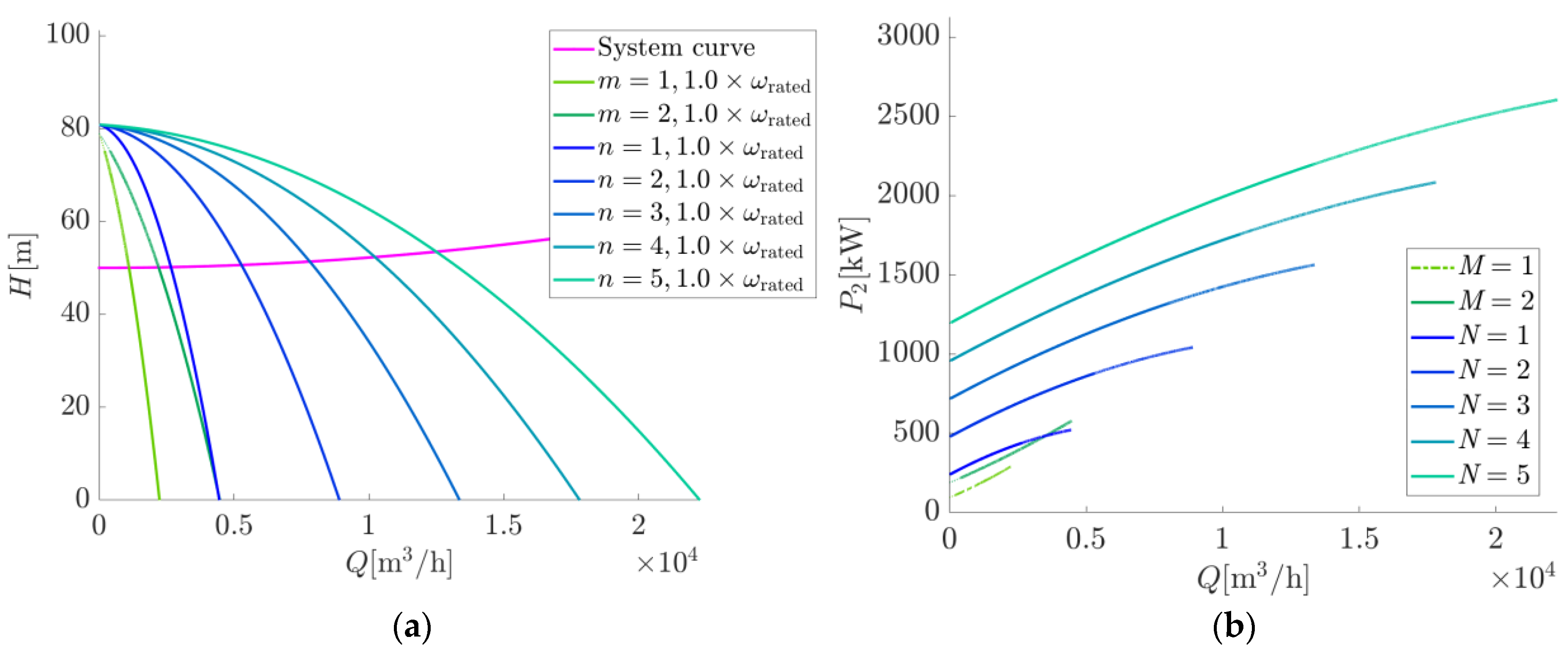
3.1. Configuration 1: Multipump PVIS Made up of a Group of N Equal Motor Pumps, in Parallel and Synchronized in Frequency
- Determine the power P2 demanded by the equivalent pump at a certain working point Q-H;
- Obtain PDC at the input of the frequency converter corresponding to that P2, assuming that the motors of all pumps are identical;
- Select the combination of active pumps that maximizes the flow rate pumped given the available PV power PDC,mpp.
3.1.1. Calculation of P2 for Any Q-H Working Point
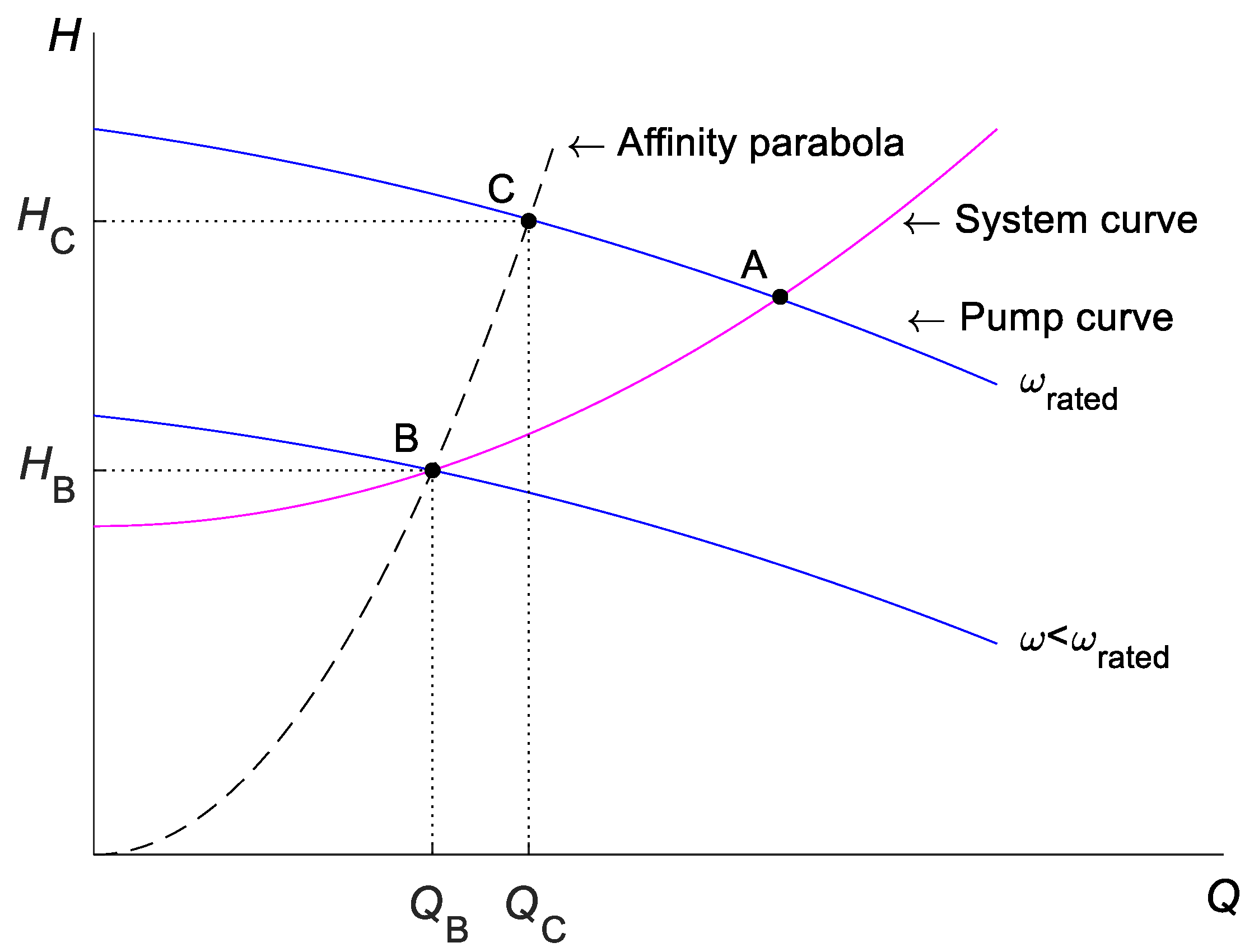
- 1.
- Calculate the required flow QB as the real positive root for Equation (3): obtaining point B (QB, HB) at frequency .
- 2.
- Determine the affinity parabola (H = + Q2) that passes through point B, where = 0, . The affinity parabola connects the points of equal efficiency.
- 3.
- Calculate the intersection of the affinity parabola and Q-H characteristic curve of the pump at rated frequency, , to obtain point C (QC, HC).
- 4.
- Determine the hydraulic power at point C, PHC = ·HC·QC, where is a constant value that depends on the water density and gravity.
- 5.
- Determine P2 at point C, P2C(QC) using Equation (4).
- 6.
- Calculate pump efficiency at point C, ηPC = PHC/P2(QC), which is equal to the efficiency at point B, ηPB = ηPC.
- 7.
- Calculate the hydraulic power at point B, PHB.
- 8.
- Finally, determine P2 at point B as P2B = PHB/ηPB.
3.1.2. Calculation of PDC at the Input of the Frequency Converter
- Determine the power at the input of the motor (P1) at point B: P1B = P2B/ηM(P2B), ηM(P2B) being the efficiency of the motor at P2B.
- Determine the power at the output of the frequency converter (PAC), given the AC wiring losses WAC at P1: PAC,B = P1B/WAC(P1B).
- Determine PDC: PDC,B = PAC,B/ηFC(PAC,B), ηFC(PAC,B) being the efficiency of the frequency converter at the load PAC,B.
3.1.3. Selection of the Combination of Active Pumps That Maximizes the Pumped Water Flow
- The minimum DC power of the equivalent pump (PDCmin) that is determined by the minimum cooling water flow of the pumps (Qmin) that its manufacturer requires. This restriction disables some combinations of pumps. It should be noted that Qmin of the equivalent pump is different from N times the minimum one of the individual pump due to the higher working head in the system curve.
- The maximum DC power of the equivalent pump (PDCmax), which is determined by the maximum operating frequency of each individual pump (). The equivalent pump is still eligible but is limited to this maximum operating frequency even if more power is available (PDC,mpp > PDCmax). Again, note that the power demanded at this by the equivalent pump is different from N times that of an individual pump, also due to the higher working head in the system curve.
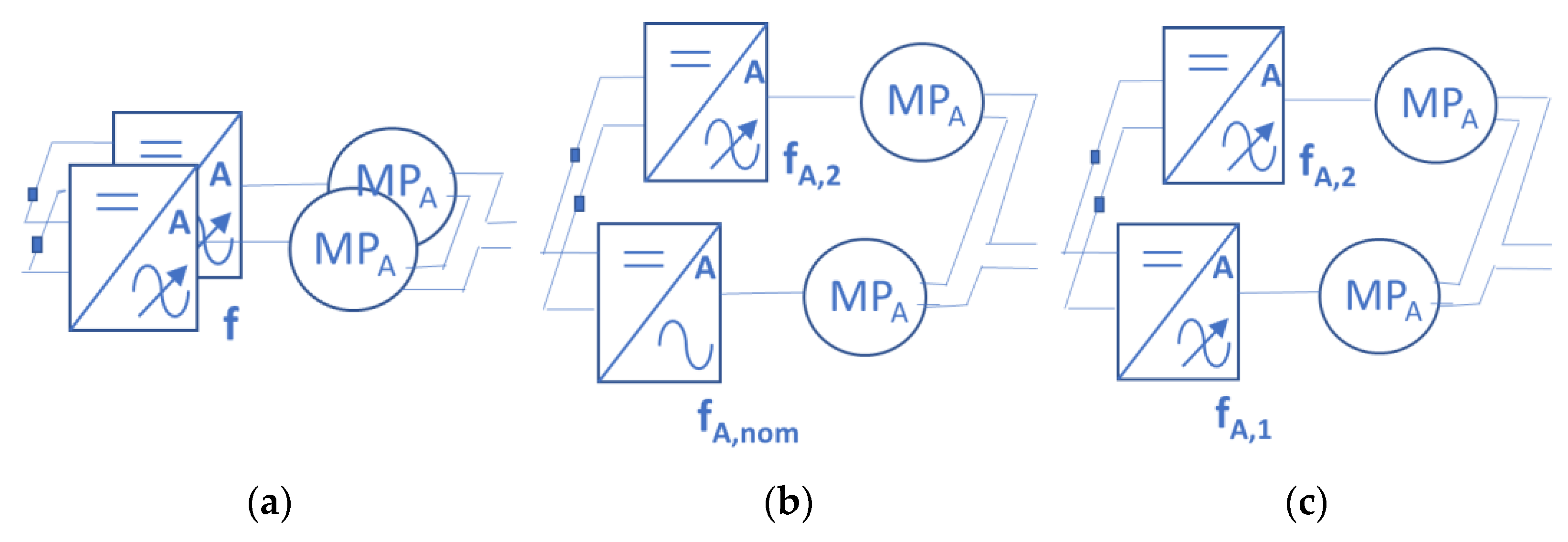
3.2. Configuration 2: Group of N Equal Pumps + Group of M Equal Pumps
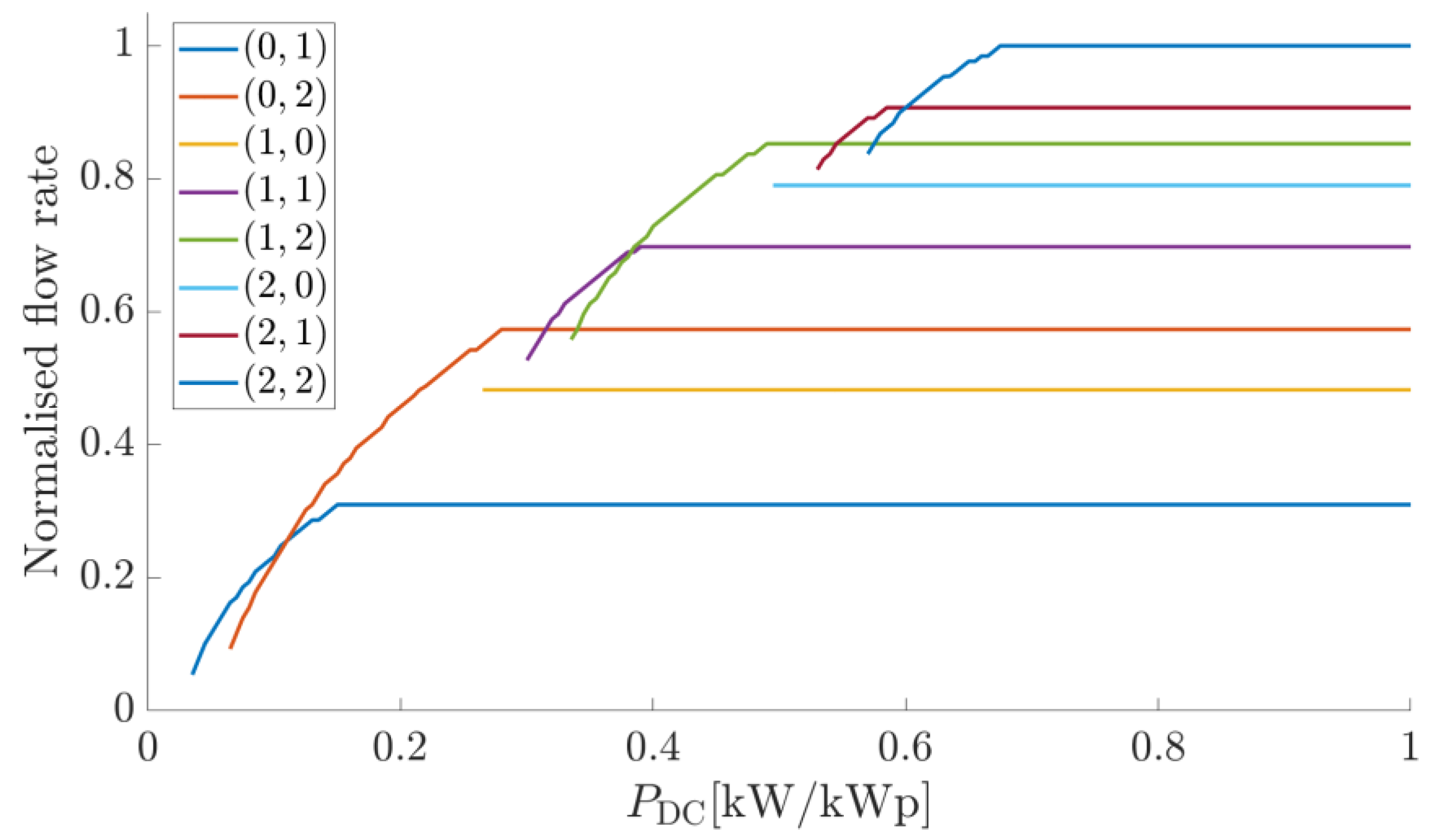
3.2.1. Selection of the Combination of Pumps
3.2.2. Subconfiguration 2.1: A First Group of N Pumps at Fixed Frequency and a Second Group of M Pumps at Variable Frequency
3.2.3. Subconfiguration 2.2: Two (or More) Groups of Pumps Working at Variable Frequency
4. Results and Discussion
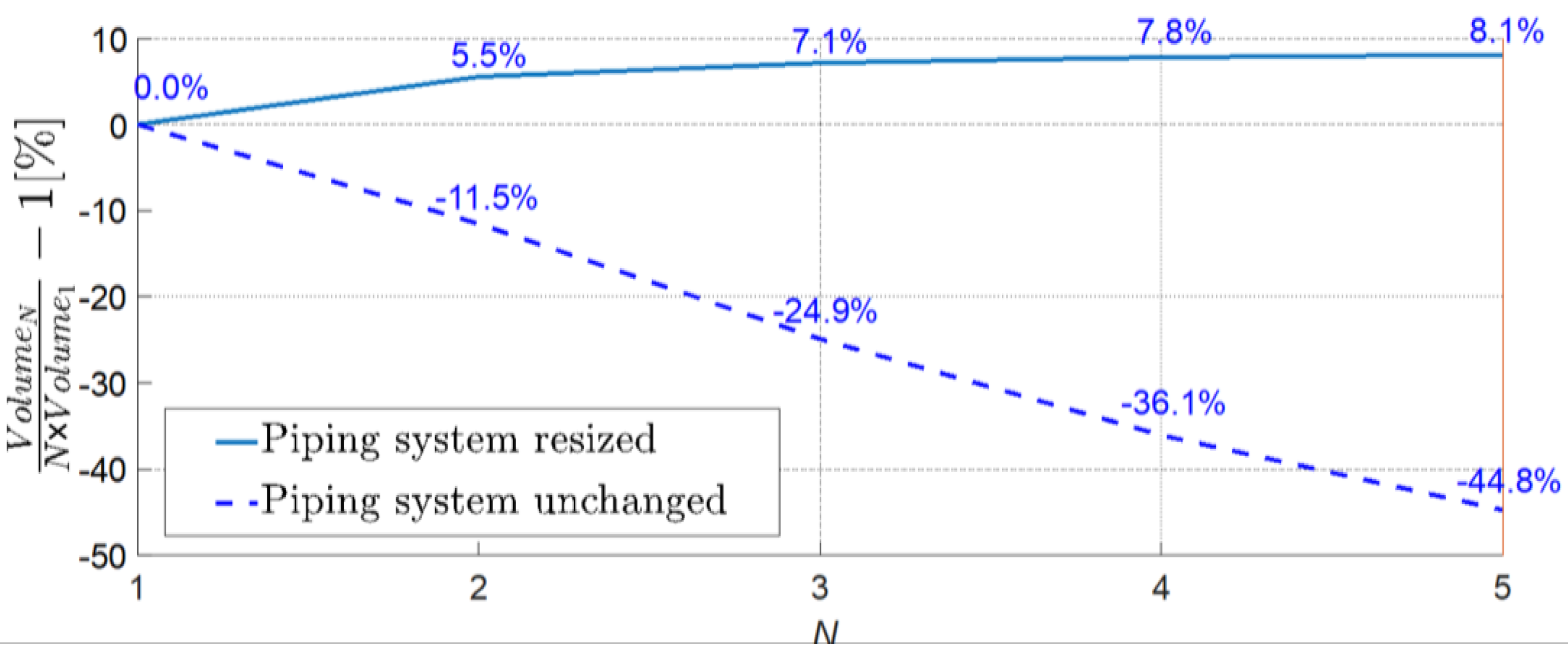
4.1. Independent PV Generators vs. Shared PV Generator
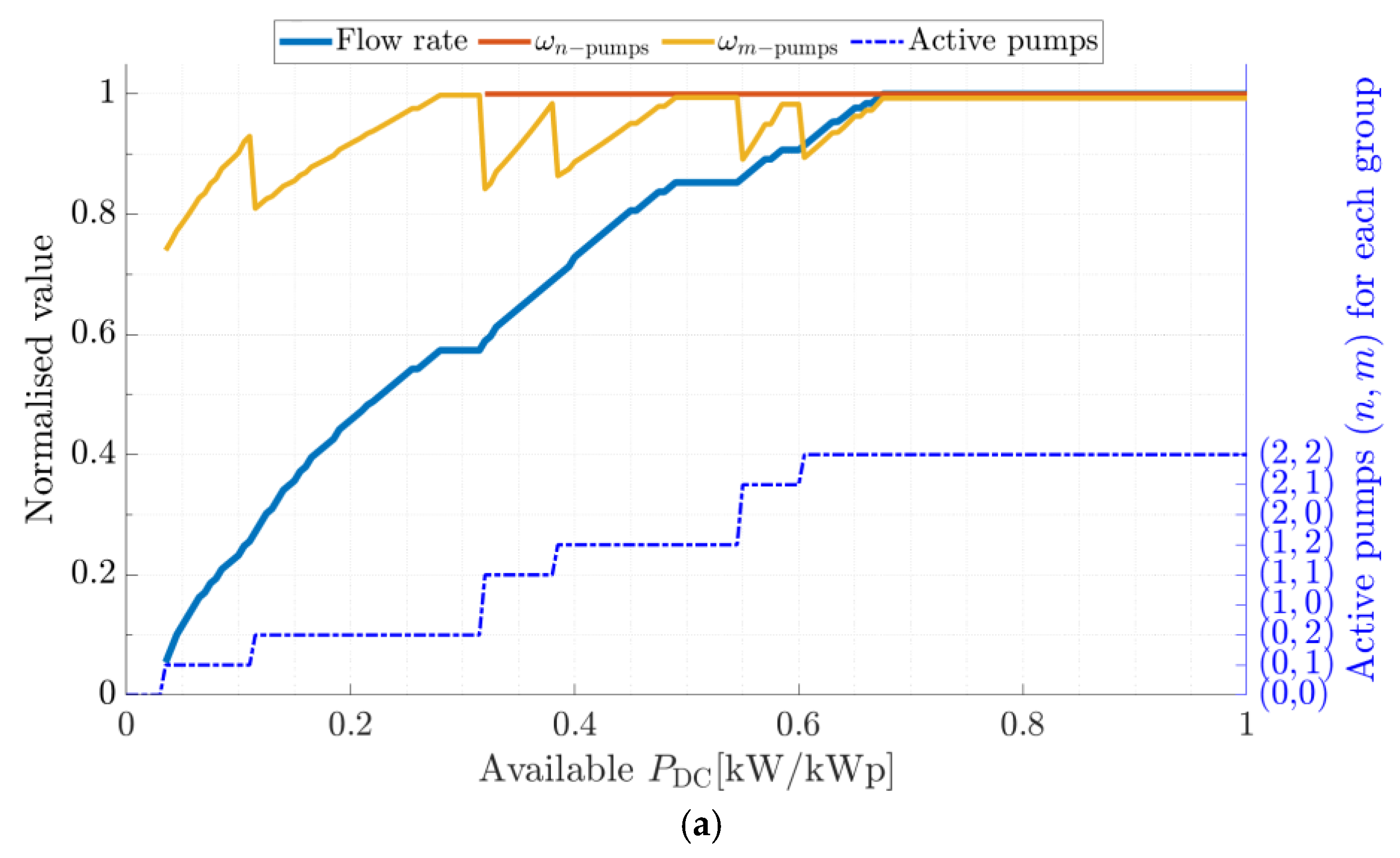
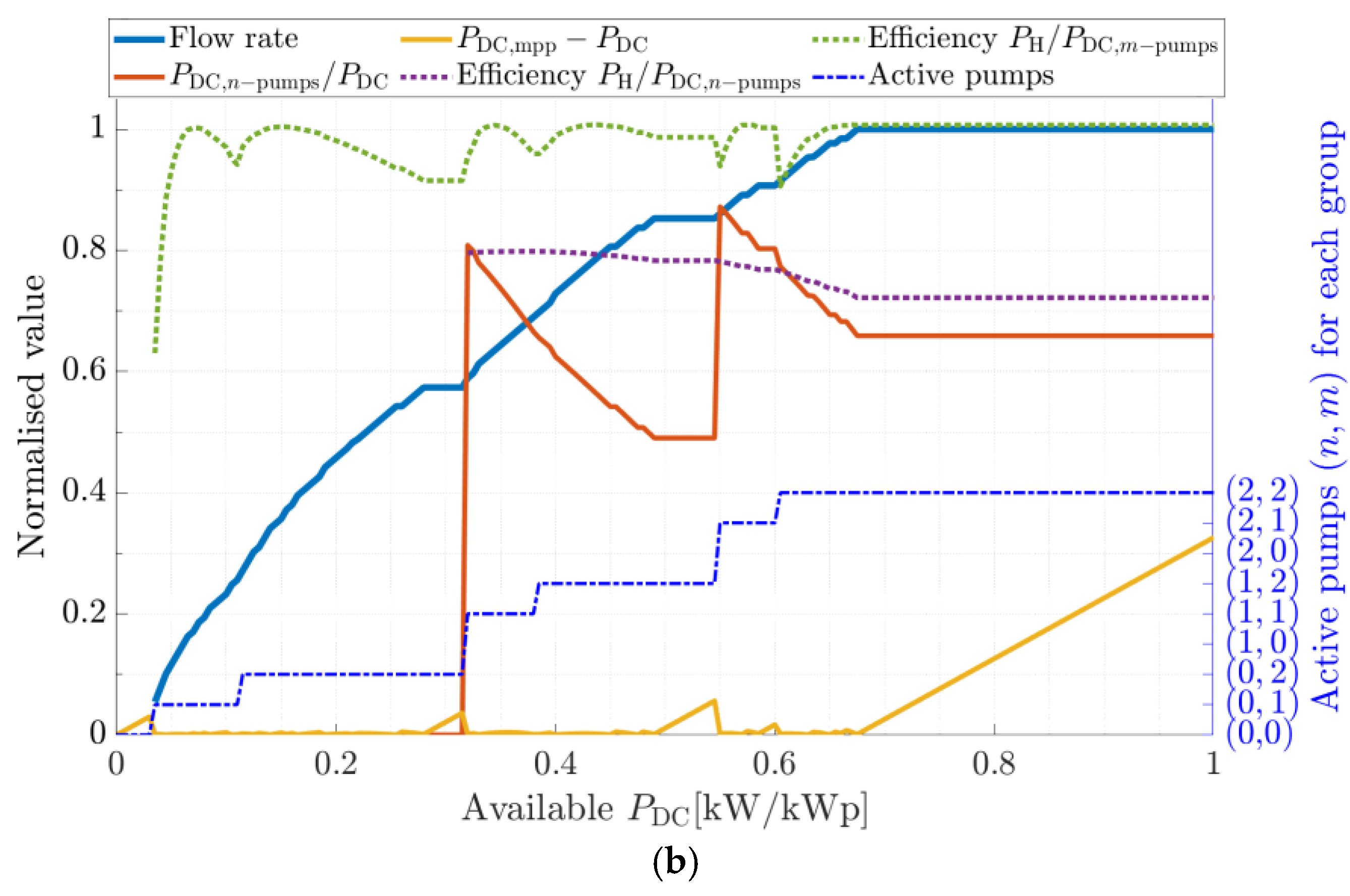
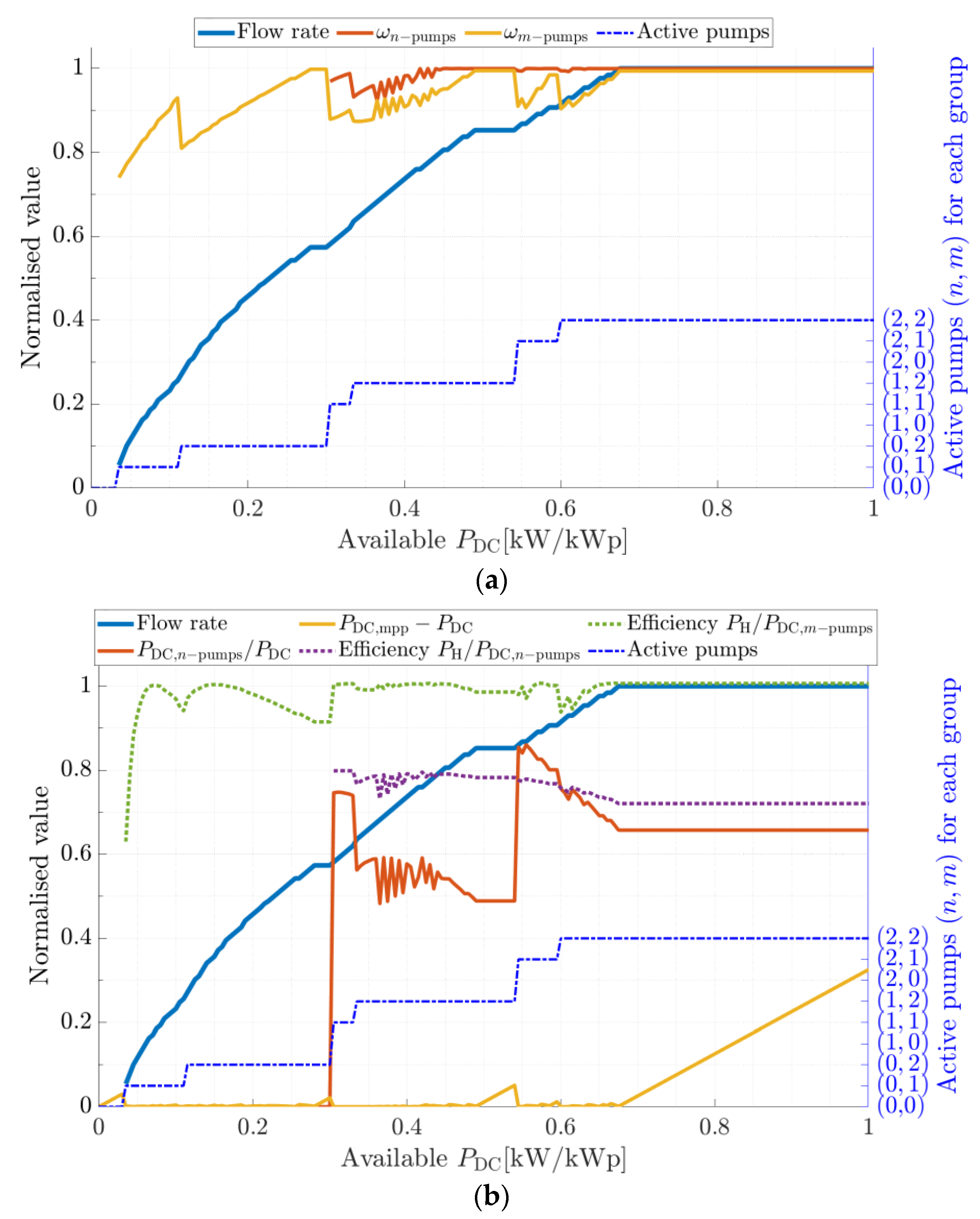
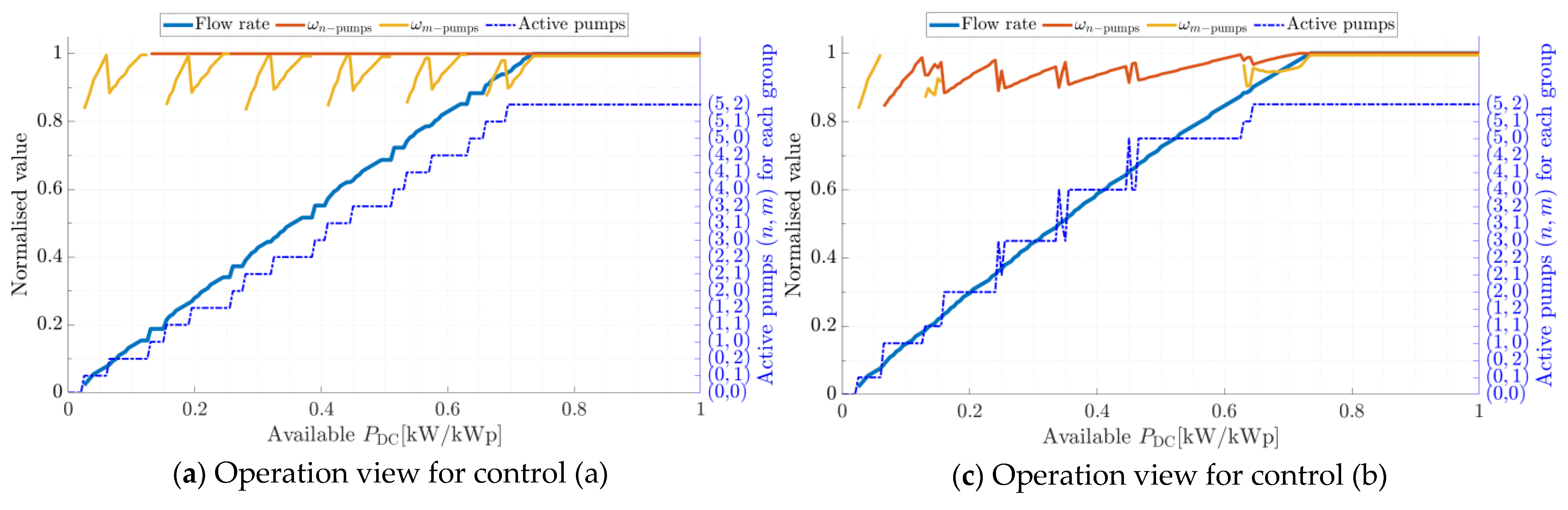
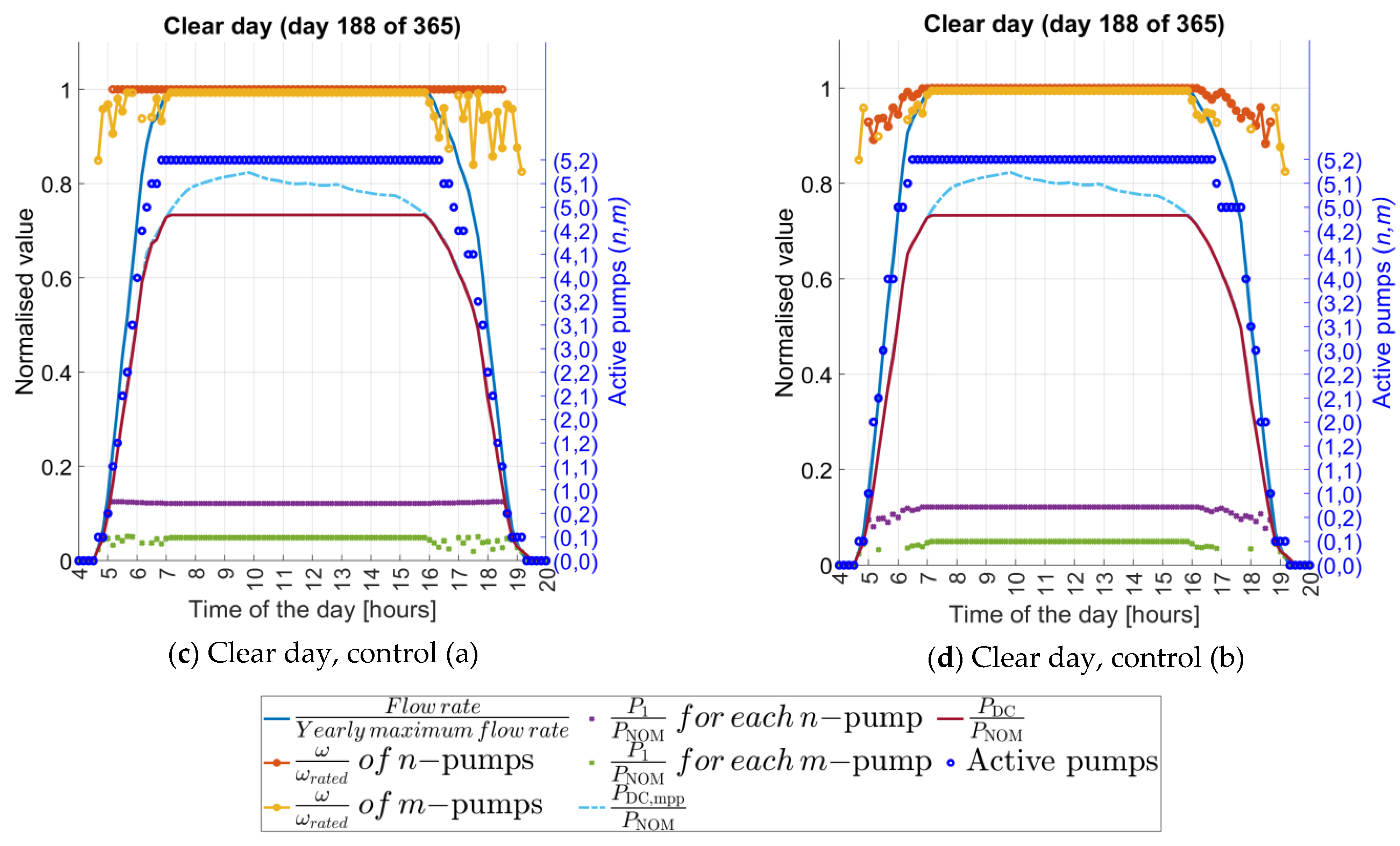
4.2. Performance vs. Type of Frequency Control
- In control (b), there is a larger range of PDC,mpp values that cannot be fully exploited, mainly because there is not enough power available yet to start the large pump at its nominal frequency while the small pump is already operating at its nominal frequency.
- The efficiency of the converter, wiring, motor, and pump assembly is different for each duty point. In case (c), there are duty points corresponding to two pumps working at different frequencies that provide more total water flow than the other duty points with frequency restrictions (either one pump is forced to nominal frequency or both pumps are forced to equal frequencies). In other words, the higher efficiency of one pump can compensate for the worse efficiency of the other pump and overcome the combination where both pumps must operate at the same efficiency. The final gain is small compared to control (a) but appreciable. This gain improves if the number of pumps is increased. In the literature, some studies can be found in which this gain is neglected and the PDC,mpp is assumed to be equally distributed between both pumps, perhaps due to the impossibility of predicting a different distribution, as this requires a solution such as the one proposed in this work, using dynamic programming.
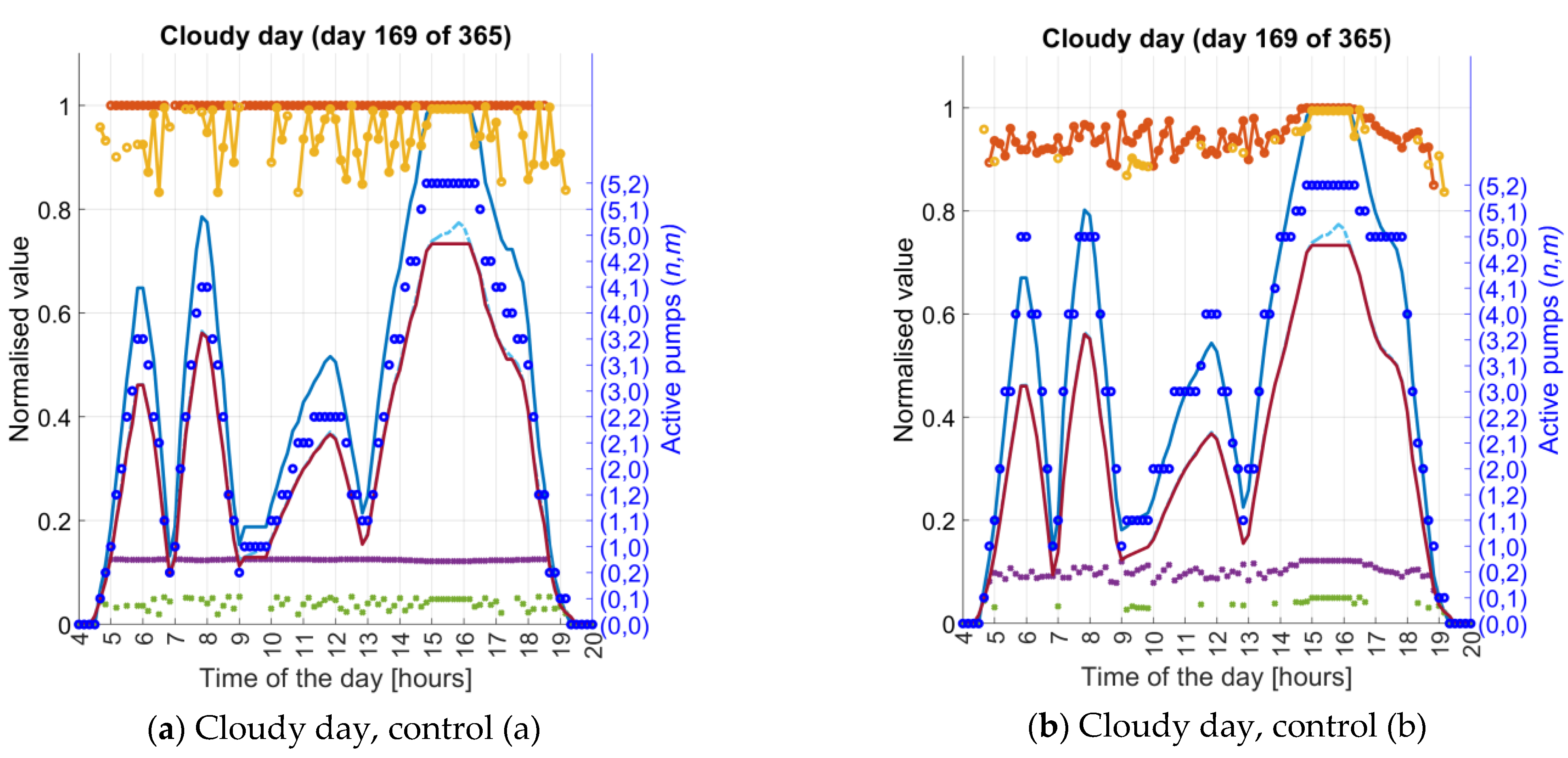
4.3. Performance of a Study Case N = 5 and M = 2
5. Conclusions
- Better selecting the large and small pumps in each group to seek greater complementarity in order to minimize the number of pump starts/stops;
- Better withstanding fades in irradiance due to the passage of clouds;
- Better adapting to the climate of the site;
- Taking advantage of all the energy that the PV generator can produce at its maximum power point;
- Limiting the working point of the pumps to efficiency ranges close to their best efficiency point;
- Reducing the number of frequency variators required;
- Combining several of these objectives, sometimes conflicting, as long as the required pumped water flow during the irrigation period can be met.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| DP | Dynamic programming | PDC,B | DC power at point B |
| E1 | AC energy yield at the motor-pump input | PDC,z | Demanded DC power by a single pump while pumping a water flow Qz at Hs |
| EDC | DC energy yield | PDC,z−1 | Demanded DC power of the rest of z − 1 active pumps, PDC,z−1, pumping the rest of water flow, Qs − Qz at Hs |
| EDC,MPP | Potential DC energy yield (at MPP) | PDC,mpp | Available PV power |
| EH | Hydraulic energy yield | PDCmax | Maximum DC power of the equivalent pump |
| f, ω | Frequency | PDCmin | Minimum DC power of the equivalent pump |
| fz−1(x) | Cost of the rest of the path, in this case, the demanded DC power of the rest of z − 1 active pumps, PDC,z−1, pumping the rest of water flow, Qs − Qz at Hs | PHB | Hydraulic power at point B |
| gz(x) | State cost function, for this case, the demanded DC power by a single pump while pumping a water flow Qz at Hs | PHC | Hydraulic power at point C |
| H | Pumping head | PV | Photovoltaic |
| HB | Pumping head at a certain duty point not included in the Q-H curve at nominal frequency | PVIS | Photovoltaic irrigation system |
| kb0,1, kb1,1, kb2,1 | Parameters that fit the Q-H curve of the individual pump | Q | Water flow |
| kb0,N, kb1,N, kb2,N | Parameters that fit the Q-H curve of the equivalent pump of N equal pumps | Q1 | Water flow of the individual pump |
| kp0,1, kp1,1, kp2,1 | Parameters that fit the Q-P2 curve of the individual pump | QB | Water flow at a certain duty point not included in the rated-frequency Q-H curve |
| kp0,N, kp1,N, kp2,N | Parameters that fit the Q-P2 curve of the equivalent pump of N equal pumps | Qmin | Minimum cooling water flow of the pumps |
| ks0, ks2 | Parameters that fit the system curve | QN | Water flow of the equivalent pump of N pumps |
| Parameters that fit the “pseudo system curves” | Qs | Required water flow at the system curve discretized in S samples (0 < Qz < Qs) | |
| m | Number of active motor pumps in the second group | Qs,max | Maximum required water flow at the system curve discretized in S samples |
| M | Number of motor pumps in the second group | S | Number of samples from the system curve |
| MP | Motor pump | WAC | AC wiring losses |
| n | Number of active motor pumps in the first group | x | Constrained state variable |
| N | Number of motor pumps in the first group | Z | Number of equivalent pumps resulting from the possible combinations of N pumps |
| P1 | Demanded power at the input of the motor | z | Each combination of active pumps |
| P1B | P1 at point B | ηFC | Frequency converter efficiency |
| P2 | Demanded power at the pump input (1 pump) | ηPB | Pump efficiency at point B |
| P2,N | Demanded power at the pump input (N pumps) | ηPC | Pump efficiency at point C |
| P2B | P2 at point B | θ | Constant value that depends on the water density and gravity |
| PAC | Power at the output of the frequency converter | ωmax | Maximum operating frequency of each individual pump |
| PAC,B | Power at the output of the frequency converter at point B | ωrated | Rated frequency |
| PDC | DC power |
References
- Palz, W. The French Connection: The rise of the PV water pump. Refocus—Int. Renew. Energy Mag. 2001, 2, 46–47. [Google Scholar]
- Enochian, R.V. Solar- and Wind-Powered Irrigation Systems; United States Department of Agriculture: Washington, DC, USA, 1982. [Google Scholar]
- Halcrow, W. Small-Scale Solar-Powered Irrigation Pumping Systems—Technical and Economical Review; World Bank: Washington, DC, USA, 1981. [Google Scholar]
- Barlow, R.; McNelis, B.; Derrick, A. Solar Pumping: An Introduction and Update on the Technology, Performance, Costs, and Economics; World Bank Technical Paper Number 168; World Bank: Washington, DC, USA, 1993. [Google Scholar]
- Fedrizzi, M.C.; Sauer, I.L. Bombeamento Solar Fotovoltaico, histórico, características e projetos. In Encontro de Energia no Meio Rural, 4; UNICAMP: Campinas, Brazil, 2002; Available online: http://www.proceedings.scielo.br/scielo.php?script=sci_arttext&pid=MSC0000000022002000100034&lng=en&nrm=iso (accessed on 1 March 2021).
- Van Campen, B.; Guidi, D.; Best, G. Solar Photovoltaics for Sustainable Agriculture and Rural Development; FAO: Rome, Italy, 2000. [Google Scholar]
- Abella, M.A.; Lorenzo, E.; Chenlo, F. PV Water Pumping Systems Based on Standard Frequency Converters. Prog. Photovolt.—Res. Appl. 2003, 11, 179–191. [Google Scholar] [CrossRef]
- Ghoneim, A.A. Design optimization of photovoltaic powered water pumping systems. Energy Convers. Manag. 2006, 47, 1449–1463. [Google Scholar] [CrossRef]
- Campana, P.E.; Li, H.; Yan, J. Dynamic modelling of a PV pumping system with special consideration on water demand. Appl. Energy 2013, 112, 635–645. [Google Scholar] [CrossRef] [Green Version]
- Renu; Bora, B.; Prasad, B.; Sastry, O.; Kumar, K.; Bangar, M. Optimum sizing and performance modeling of Solar Photovoltaic (SPV) water pumps for different climatic conditions. Solar Energy 2017, 155, 1326–1338. [Google Scholar] [CrossRef]
- Muhsen, D.H.; Ghazali, A.B.; Khatib, T. Multiobjective differential evolution algorithm-based sizing of a standalone photovoltaic water pumping system. Energy Convers. Manag. 2016, 118, 32–43. [Google Scholar] [CrossRef]
- Bouzidi, B. New sizing method of PV water pumping systems. Sustain. Energy Technol. Assess. 2013, 4, 1–10. [Google Scholar] [CrossRef]
- Bakelli, Y.; Arab, A.H.; Azouic, B. Optimal sizing of photovoltaic pumping system with water tank storage using LPSP concept. Sol. Energy 2011, 85, 288–294. [Google Scholar] [CrossRef]
- Muhsen, D.H.; Khatib, T.; Abdulabbas, T.E. Sizing of a standalone photovoltaic water pumping system using hybrid multi-criteria decision making methods. Solar Energy 2018, 159, 1003–1015. [Google Scholar] [CrossRef]
- Olcan, C. Multi-objective analytical model for optimal sizing of stand-alone photovoltaic water pumping systems. Energy Convers. Manag. 2015, 100, 358–369. [Google Scholar] [CrossRef]
- Yahyaoui, I.; Atieh, A.; Serna, A.; Tadeo, F. Sensitivity analysis for photovoltaic water pumping systems: Energetic and economic studies. Energy Convers. Manag. 2017, 135, 402–415. [Google Scholar] [CrossRef] [Green Version]
- Monís, J.I.; López-Luque, R.; Reca, J.; Martínez, J. Multistage Bounded Evolutionary Algorithm to Optimize the Design of Sustainable Photovoltaic (PV) Pumping Irrigation Systems with Storage. Sustainability 2020, 12, 1026. [Google Scholar] [CrossRef] [Green Version]
- Suehrcke, H.; Appelbaum, J.; Reshef, B. Modelling a permanent magnet DC motor/centrifugal pump assembly in a photovoltaic energy system. Solar Energy 1997, 59, 37–42. [Google Scholar] [CrossRef]
- Hamidat, A.; Benyoucef, B. Mathematic models of photovoltaic motor-pump systems. Renew. Energy 2008, 33, 933–942. [Google Scholar] [CrossRef]
- Gherbi, A.D.; Arab, A.H.; Salhi, H. Improvement and validation of PV motor-pump model for PV pumping system performance analysis. Solar Energy 2017, 144, 310–320. [Google Scholar] [CrossRef]
- Mayer, O.; Baumeister, A.; Festl, T. Design, simulation and diagnosis of photovoltaic pumping systems with DASTPVPS. In Proceedings of the 13th European Photovoltaic Solar Energy Conference, Nice, France, 23–27 October 1995. [Google Scholar]
- Grundfos. Available online: http://de.grundfos.com/grundfos-wincaps.html (accessed on 4 November 2021).
- COMPASS. Available online: https://www.lorentz.de/en/products/submersible-solar-pumps.html (accessed on 4 November 2021).
- SOLARPACK. Available online: http://tools.franklin-electric.com/solar/ (accessed on 4 November 2021).
- Hydraulic Calculation Tool. Available online: http://www.netafim.com/service/hydrocalc-pro (accessed on 4 November 2021).
- GESTAR. SETUP GESTAR. 2016. Available online: http://www.acquanalyst.com/contenido.php?modulo=descargas&cat=2 (accessed on 4 November 2021).
- Estrada, C.; González; Aliod, R.; Paño, J. Improved pressurized pipe network hydraulic solver for applications in irrigation systems. J. Irrig. Drain. Eng. 2009, 135, 421–430. [Google Scholar] [CrossRef]
- FAO. Land & Water. Available online: http://www.fao.org/nr/water/infores_databases_cropwat.html (accessed on 4 November 2021).
- Langarita, R.; Chóliz, J.S.; Sarasa, C.; Duarte, R.; Jiménez, S. Electricity costs in irrigated agriculture: A case study for an irrigation sheme in Spain. Renew. Sustain. Energy Rev. 2016, 68, 1008–1019. [Google Scholar] [CrossRef]
- Knecht, R.; Baumgartner, F.P. PV-Battery and Diesel Hybrid System for Irrigation of a Farm in Patagonia. In Proceedings of the 33rd European Photovotaic Solar Energy Conference and Exhibition, Amsterdam, The Netherlands, 25–29 September 2017. [Google Scholar]
- Carrêlo, I.B.; Almeida, R.H.; Narvarte, L.; Martínez-Moreno, F.; Carrasco, L.M. Comparative analysis of the economic feasibility of five large-power. Renew. Energy 2020, 145, 2671–2682. [Google Scholar] [CrossRef]
- Herraiz, J.I.; Fernández-Ramos, J.; Almeida, R.H.; Báguena, E.; Castillo-Cagigal, M.; Narvarte, L. On the tuning and performance of Stand-Alone Large-Power PV irrigation systems. Energy Convers. Adn Manag. X 2022, 13, 100175. [Google Scholar] [CrossRef]
- Almeida, R.H.; Carrêlo, I.B.; Lorenzo, E.; Narvarte, L.; Fernández-Ramos, J.; Martinez-Moreno, F.; Carrasco, L.M. Development and Test of Solutions to Enlarge the Power of PV Irrigation and Application to a 140 kW PV-Diesel Representative Case. Energies 2018, 11, 3538. [Google Scholar] [CrossRef] [Green Version]
- Innovagri. El Riego Solar, una Alternativa para Rentabilizar el Consumo Energético. 2016. Available online: https://www.innovagri.es/comunidad/el-riego-solar-una-alternativa-para-rentabilizar-la-energia.html (accessed on 10 May 2018).
- Energías Renovables. Powen Instala en el Campo de Albacete un Bombeo Solar para Autoconsumo de Casi Doscientos Kilovatios. 2017. Available online: https://www.energias-renovables.com/fotovoltaica/powen-instala-en-el-campo-de-albacete-20171023 (accessed on 10 May 2018).
- EIP Water. European Innovation Partnership Water—Strategic Implementation Plan; European Commission: Brussels, Belgium, 2012. [Google Scholar]
- Ramos, J.F.; Fernandez, L.N.; de Almeida, R.H.T.; Carrêlo, I.B.; Moreno, L.M.C.; Pigueiras, E.L. Method and Control Device for Photovoltaic Pumping Systems. Spain Patent ES 2 607 253 B2, 1 March 2018. [Google Scholar]
- Gasque, M.; González-Alltozano, P.; Gutiérrez-Colomer, R.P.; García-Marí, E. Optimisation of the distribution of power from a photovoltaic generator between two pumps working in parallel. Solar Energy 2020, 198, 324–334. [Google Scholar] [CrossRef]
- Olszewski, P. Genetic optimization and experimental verification of complex parallel pumping station with centrifugal pumps. Appl. Energy 2016, 178, 527–539. [Google Scholar] [CrossRef]
- Da Costa Bortoni, E.; de Almeida, R.A.; Carvalho Viana, A.N. Optimization of parallel variable-speed-driven centrifugal pumps operation. Energy Effic. 2008, 1, 167–173. [Google Scholar] [CrossRef]
- Munoz, J.; Carrillo, J.; Martínez-Moreno, F.; Carrasco, L.; Narvarte, L. Modeling and simulation of large PV pumping systems. In Proceedings of the 31th European Photovoltaic Solar Energy Conference and Exhibition, Hamburg, Germany, 14–18 September 2015. [Google Scholar]
- Bellman, R.E. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Casti, R.L.a.J. Principles of Dynamic Programming, Part I; Dekker: New York, NY, USA, 1979. [Google Scholar]
- Viholainen, J.; Tamminen, J.; Ahonen, T.; Ahola, J.; Vakkilainen, E.; Soukka, R. Energy-efficient control strategy for variable speed-driven parallel pumping systems. Energy Effic. 2013, 6, 495–509. [Google Scholar] [CrossRef]








| Frequency Control Type | |||
|---|---|---|---|
| Control (a) N = 2 (Variable) | Control (b) N = 1 (Nominal) M = 1 (Variable) | Control (c) N = 1 (Variable) M = 1 (Variable) | |
| Potential DC energy yield at MPP, EDC,MPP (kWh/kWp) | 2057.9 | 2057.9 | 2057.9 |
| DC energy yield, EDC (kWh/kWp) | 1936.3 | 1924.0 | 2036.9 |
| EDC/EDC,MPP ratio | 0.950 | 0.935 | 0.990 |
| AC energy yield at the motor-pump input, E1 (kWh/kWp) | 1859.7 | 1747.7 | 1860.5 |
| Mechanical energy yield at the pump input, E2 (kWh/kWp) | 1690.0 | 1567.1 | 1690.7 |
| Hydraulic energy yield, EH (kWh/kWp) | 1439.5 | 1326.2 | 1440.1 |
| Annual water volume yield (m3/kWp) | 9868 | 9141 | 9872 |
| Control (a) | Control (b) | |
|---|---|---|
| Potential DC energy yield (at MPP), EDC,MPP (kWh/kWp) | 2057.9 | 2057.9 |
| DC energy yield (MPP), EDC (kWh/kWp) | 1990.3 | 2000.1 |
| EDC,MPP/EDC ratio | 0.967 | 0.972 |
| AC energy yield at the motor-pump input, E1 (kWh/kWp) | 1922.5 | 1936.2 |
| Hydraulic energy yield, EH (kWh/kWp) | 1553.1 | 1586.3 |
| Annual water volume yield (m3/kWp) | 10,741 | 10,962 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ledesma, J.R.; Almeida, R.H.; Narvarte, L. Modeling and Simulation of Multipumping Photovoltaic Irrigation Systems. Sustainability 2022, 14, 9318. https://doi.org/10.3390/su14159318
Ledesma JR, Almeida RH, Narvarte L. Modeling and Simulation of Multipumping Photovoltaic Irrigation Systems. Sustainability. 2022; 14(15):9318. https://doi.org/10.3390/su14159318
Chicago/Turabian StyleLedesma, Javier R., Rita H. Almeida, and Luis Narvarte. 2022. "Modeling and Simulation of Multipumping Photovoltaic Irrigation Systems" Sustainability 14, no. 15: 9318. https://doi.org/10.3390/su14159318
APA StyleLedesma, J. R., Almeida, R. H., & Narvarte, L. (2022). Modeling and Simulation of Multipumping Photovoltaic Irrigation Systems. Sustainability, 14(15), 9318. https://doi.org/10.3390/su14159318






