Damage Simulation Analysis of Canal Concrete Lining Plates Based on Temperature-Stress-Water Load Coupling
Abstract
:1. Introduction
- (i)
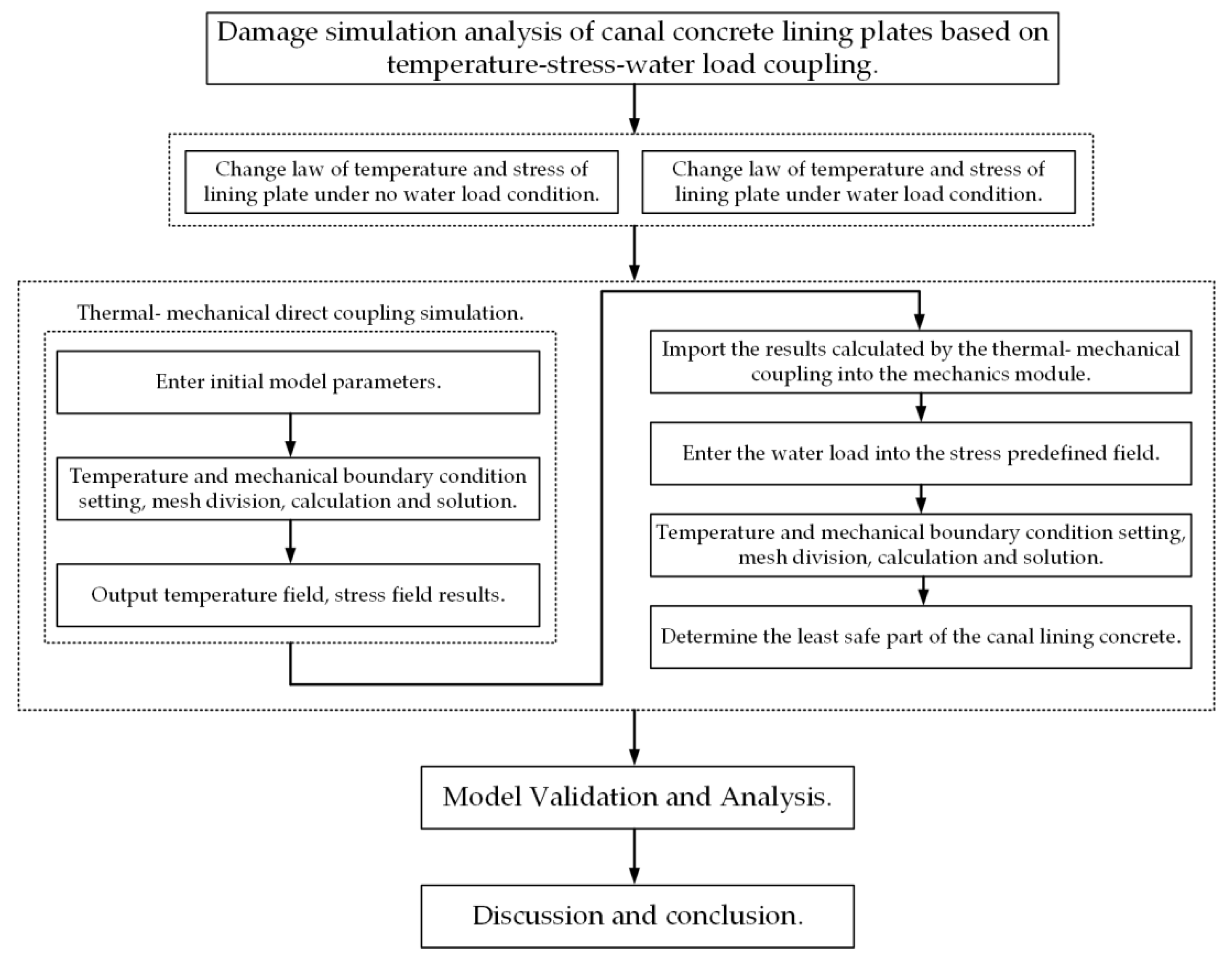
- A considerable number of research studies focus on the numerical analysis of the canal concrete lining under the action of frost heave, and there are few studies on simulating the temperature and stress changes of the lining plate under the coupling action of different temperatures and water loads. This paper takes an engineering project as an example, and ABAQUS finite element software was used to calculate, analyze and summarize the changes and distribution rules of the temperature and stress fields of the canal lining plate under the action of multi-factor coupling.
- (ii)
- The stress concentration position of the entire canal concrete lining plate is determined by simulation, and the most likely position of damage to the canal concrete lining plate under the coupling action of temperature and load is determined. This can be used as a reference for further research on canal concrete lining construction quality control.
- (iii)
- Utilizing the in situ test of canal lining carried out by other scholars, the numerical model of this paper is verified. The results show that the simulated value is in close agreement with the field measured value, which establishes the validity and rationality of the model in this paper.
2. Project Overview
3. Numerical Simulation
3.1. Basic Assumptions and Theories
3.1.1. Basic Assumptions
- (1)
- Through the collection of geological data in this region, it was found that the groundwater at the bottom of the canal is located at depth and it is difficult for the groundwater to migrate into the canal foundation soil so the migration of groundwater is not considered.
- (2)
- The concrete lining plate of the canal is simplified as a thin shell structure, and the self-weight of the concrete lining plate of the canal is not considered in the analysis.
- (3)
- The heat transfer mode of canal foundation soil is heat conduction, and the heat released during water phase transformation in the canal lining is not considered during freezing in winter.
3.1.2. Theory of Temperature Field Calculation
- (1)
- Boundary conditions of the first kind.
- (2)
- Boundary conditions of the second kind.
- (3)
- Boundary conditions of the third kind.
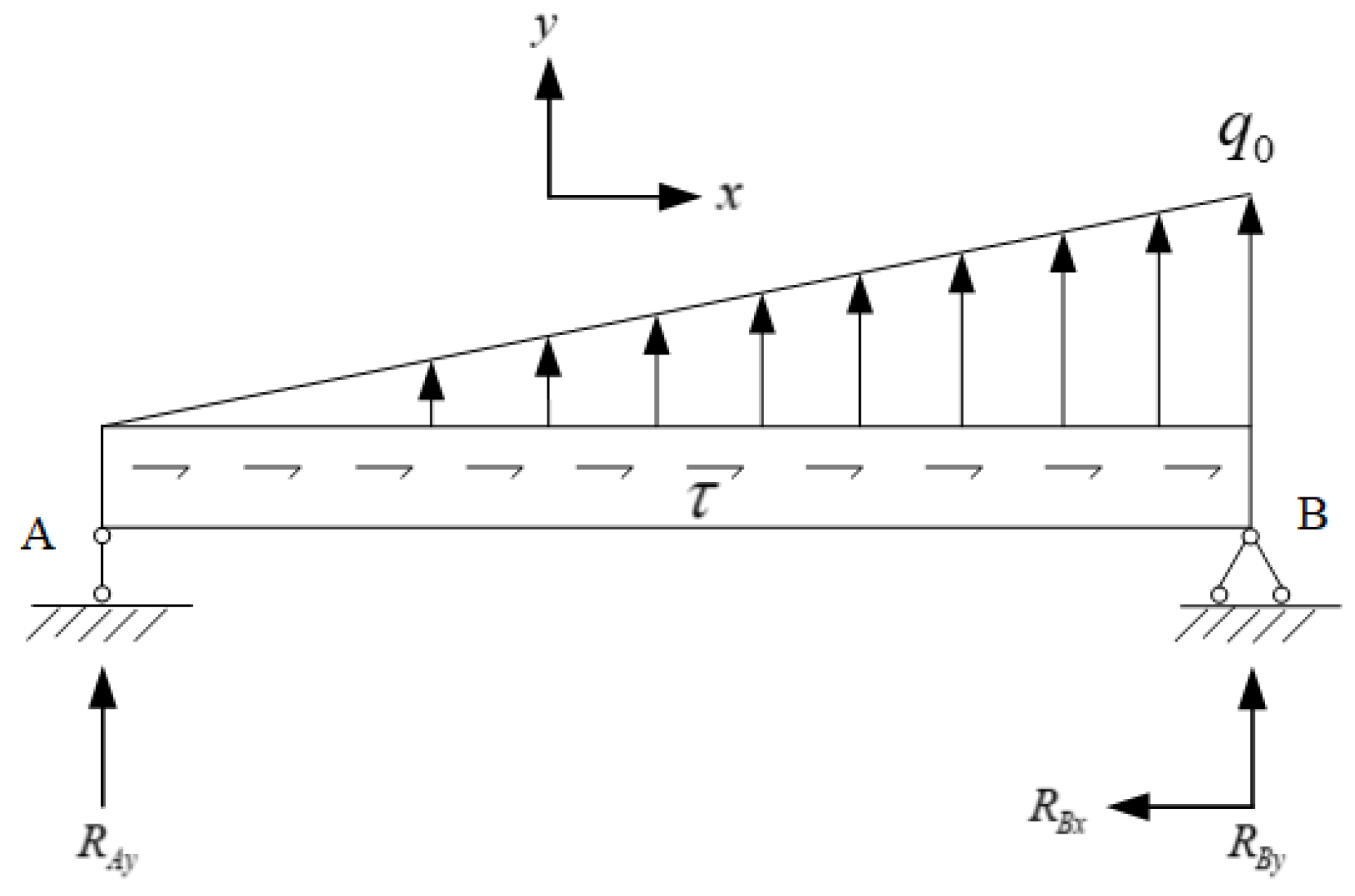
3.1.3. Water Load
3.1.4. Constitutive Model of Materials
- (1)
- Constitutive model of silty soil
- (2)
- Constitutive model of concrete.
3.2. Establishing a Numerical Model
3.2.1. Selection of the Numerical Model and Related Parameters
- (1)
- Determine the boundary and value range of the numerical model.
- (2)
- Determine the calculation parameters of silt.
- (3)
- Determine the calculation parameters of concrete.
- (4)
- Determine the surface heat release coefficient of concrete.
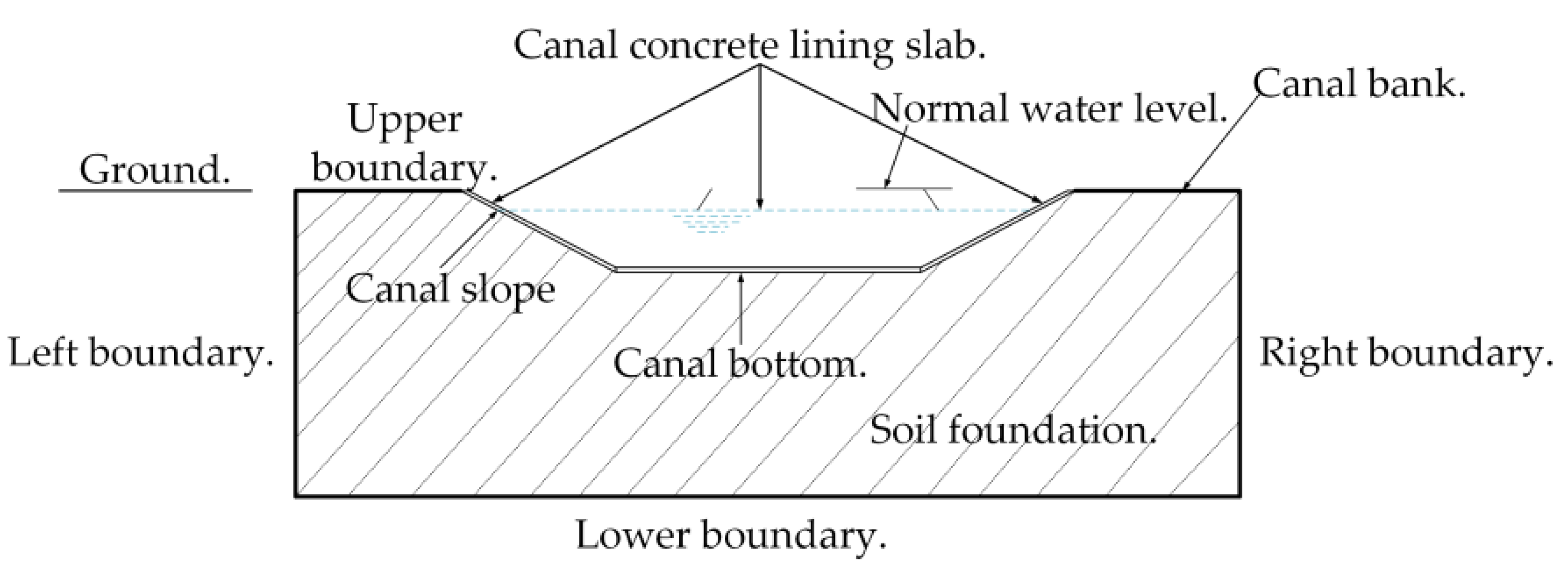
3.2.2. Determine Geometric Dimensions
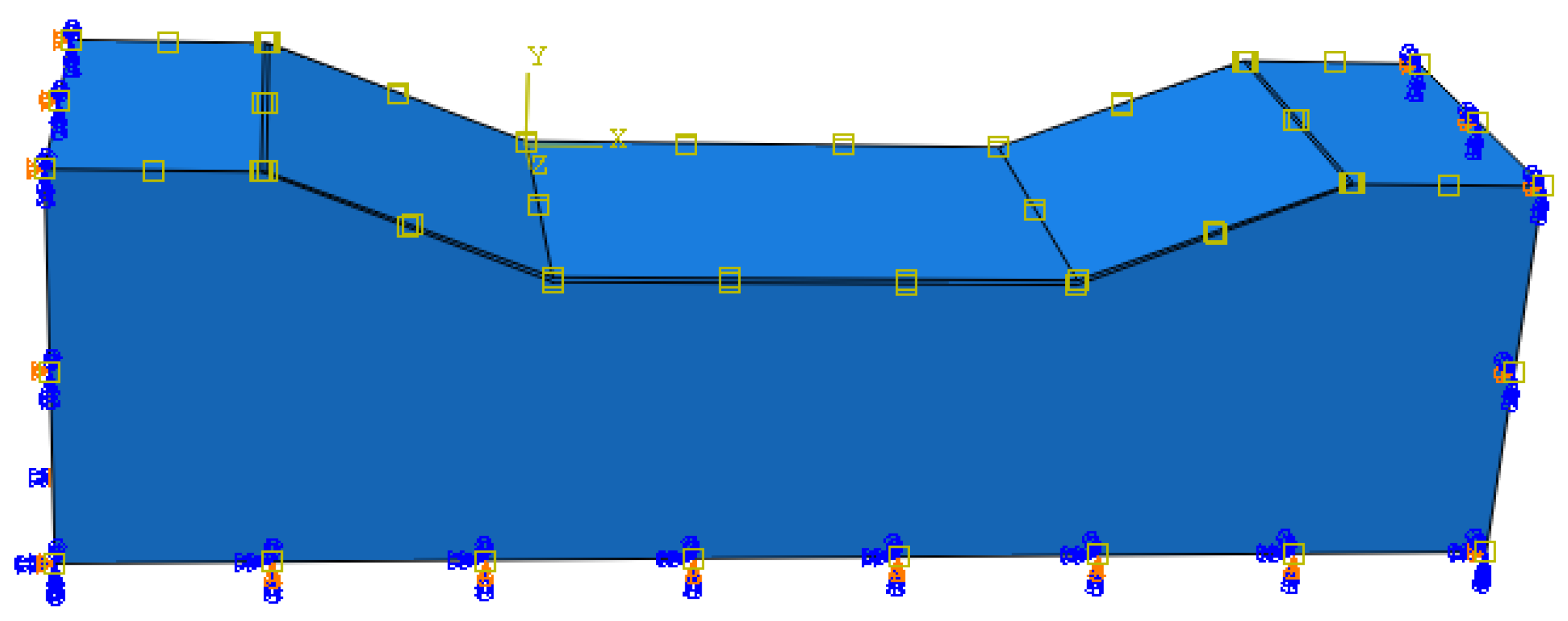
3.2.3. Determine Boundary Conditions
3.2.4. Determine the Calculation Conditions
- (1)
- Temperature and stress changes in the concrete lining plate of the canal under no water condition during the construction and maintenance period.
- (2)
- Temperature and stress changes in the concrete lining plate of the canal under water-filled conditions during the operation period.
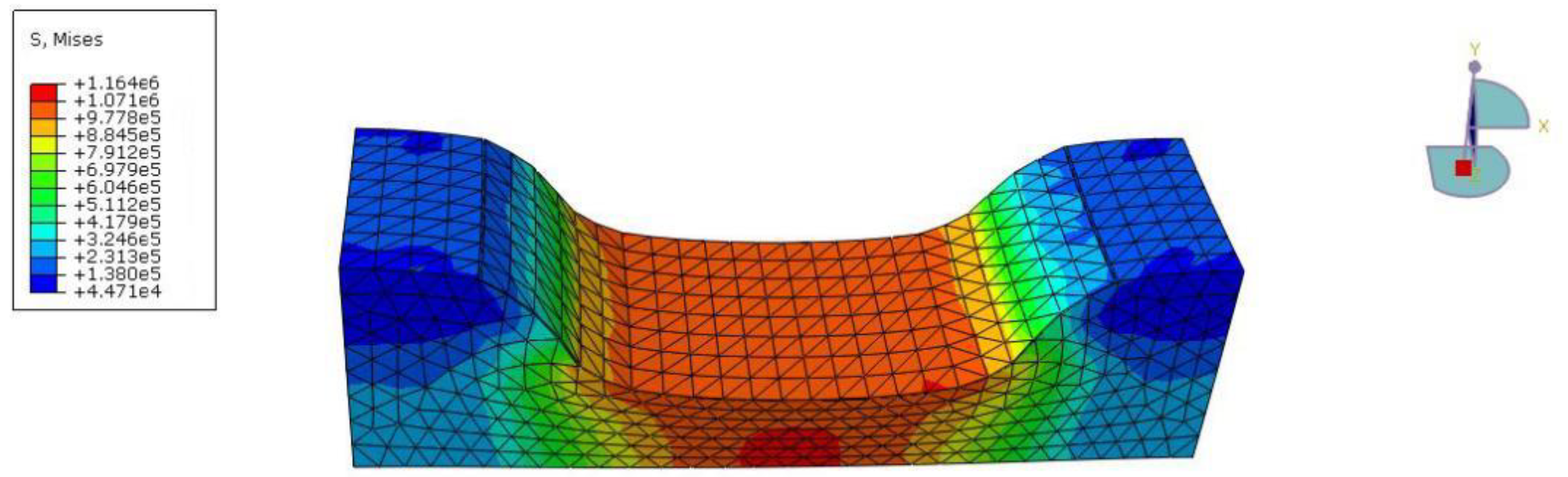
3.3. Results and Analysis
- (1)
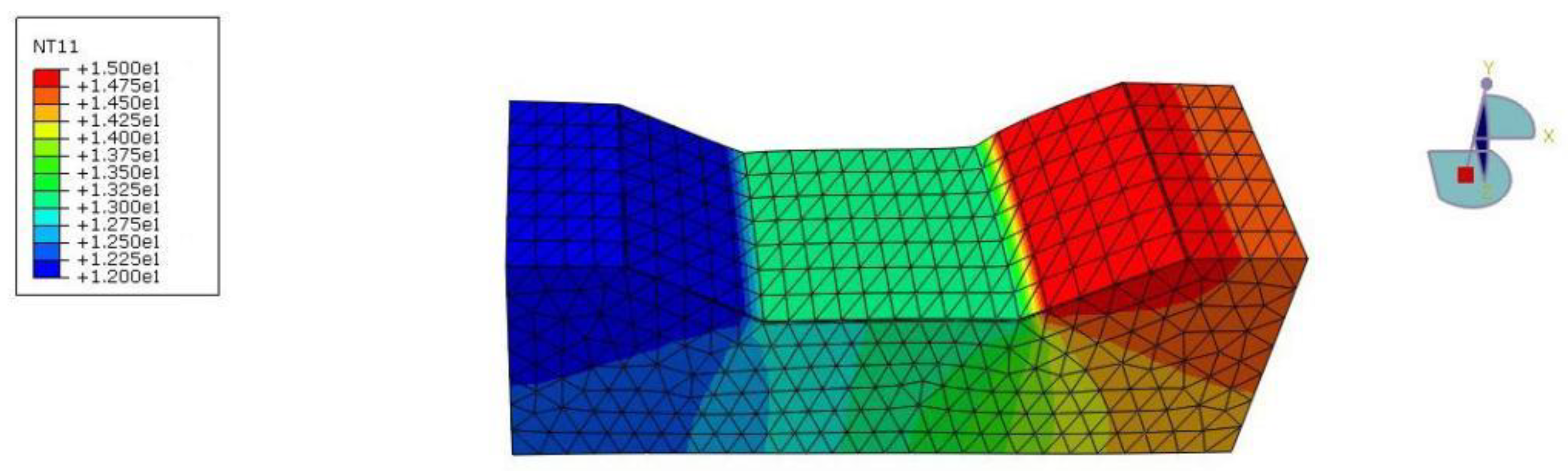
- Temperature field
- (2)
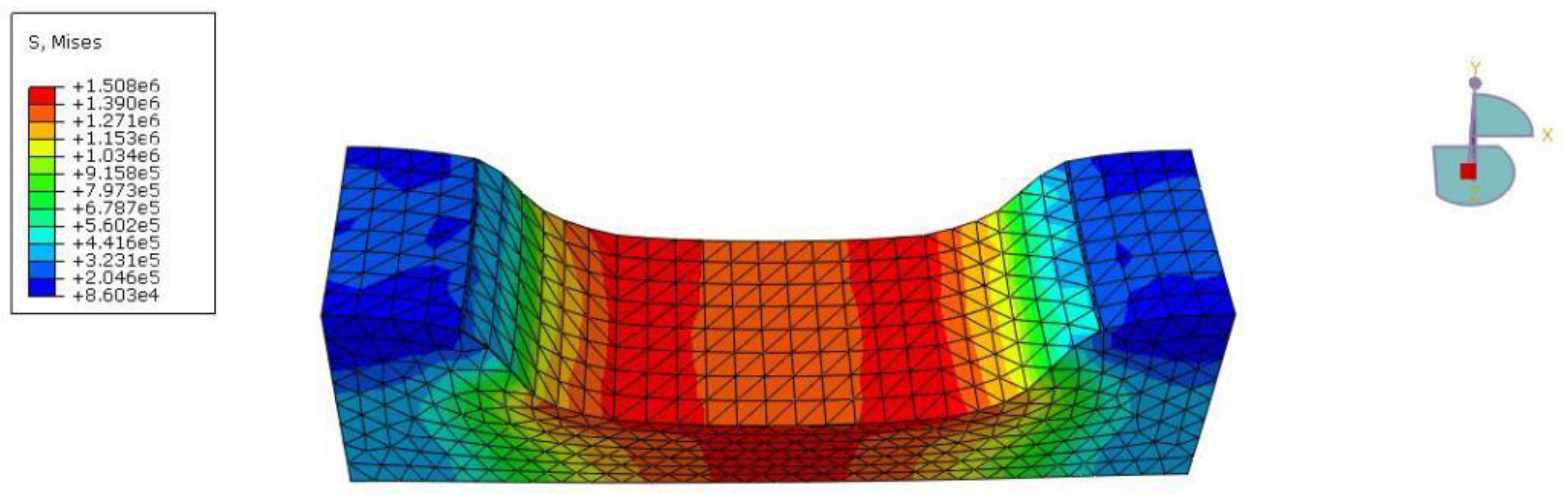
- Stress field.
- (1)
- The reaction force at the support.
- (2)
- Axial force of slope plate.
- (3)
- Slope plate shear force.
- (4)
- Bending moment of slope plate.
3.4. Sensitivity Analysis of the Model to Changes in Input Parameters
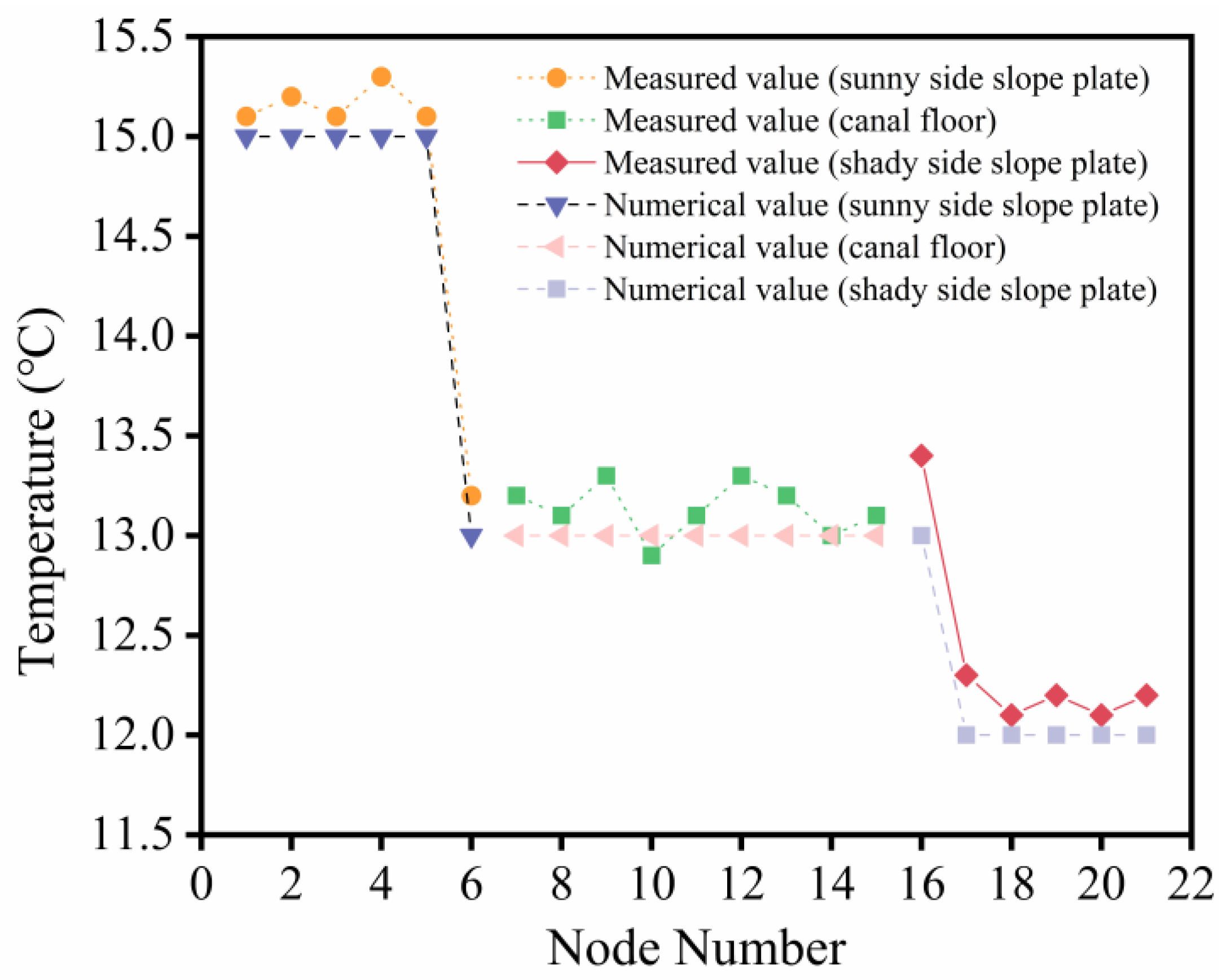
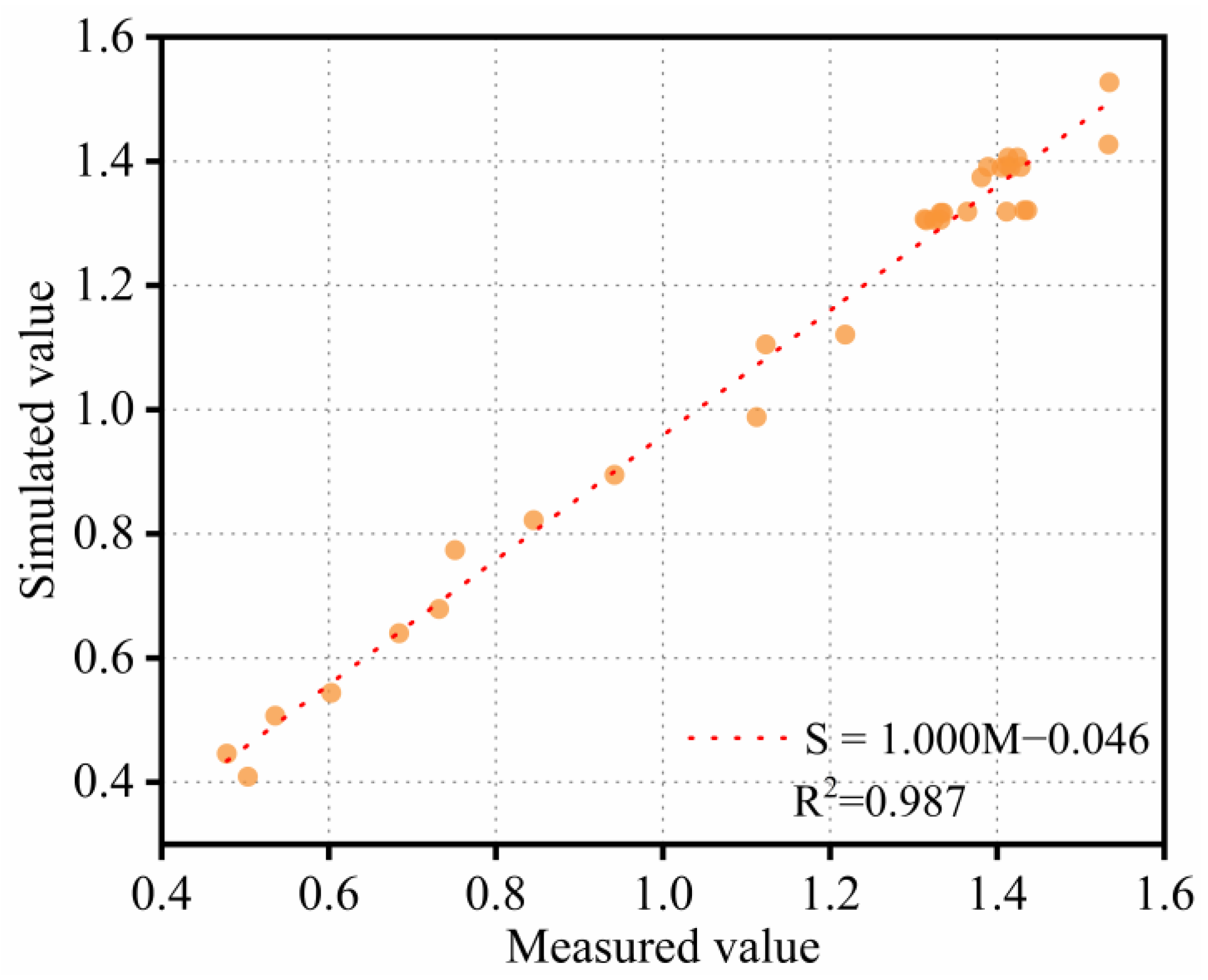
3.5. Model Validation
4. Discussion and Conclusions
- (1)
- Under the condition of no water load, the temperature distribution in the middle of the canal floor is more uniform, and the overall temperature of the sunny side slope plate is higher than that of the shady side slope plate. Under the action of water load, it is found that the variation of temperature field is consistent with that under the action of no water load, and the overall trend of plate temperature on the sunny side slope is higher than that of the shady side slope.
- (2)
- In the case of no water load, the variation of the stress field of the canal lining was analyzed. According to the established numerical model of canal concrete lining, the stress of the lining plate at the foot of two sides of the slope is large, and the stress of the middle canal bottom plate is small. The shady side slope plate was selected for analysis, and it was found that from the bottom to the top, the stress value on the canal slope gradually decreased, and reached the maximum value at the foot of the lining plate slope. Simplified analysis with mechanical knowledge shows that the shear force and axial force of the lining plate reach the maximum at the slope foot, and the maximum bending moment occurs at the lining plate near the slope foot. In order to prevent the maximum tensile strain of the concrete lining plate at the slope toe from exceeding its allowable tensile strain and causing expansion cracks in the lining plate, special attention should be paid to its prevention.
- (3)
- The load conditions were set to 1/2, 2/3 of the canal water filling depth and full load (i.e., 1/2 canal depth, 2/3 canal depth, full load), and the simulation analysis was carried out. The maximum stress position is located in the middle of the canal slope toe and the canal bottom. Once these stresses exceed the allowable stress value of the concrete plate itself, damage results, and these are the weakest positions of the entire canal concrete lining plate. In the later stages of design, construction, and maintenance, relevant technical measures should be taken to consolidate the structure at these locations.
- (4)
- In order to verify the accuracy of the model, the method of comparing error values is used for verification. The results show that the temperature and stress values output by the model are in close agreement with the in situ test results, and the correlation between the measured value and the simulated value is above 0.98 (Correlation coefficient R2). The proposed model is reasonable and correct, and can be successfully used in practical cases.
- (5)
- When the input parameters change, in order to determine the influence of each parameter on the sensitivity of the model, the maximum stress of the canal concrete lining plate is used as the evaluation index to analyze the sensitivity of the model. The results show that the factors affecting the sensitivity of the numerical model from strong to weak are: Elastic modulus > Poisson’s ratio > Coefficient of thermal expansion > Coefficient of thermal conductivity > Specific heat capacity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Serial Number | Influencing Factors | ||||
|---|---|---|---|---|---|
| Elastic Modulus (A) | Poisson’s Ratio (B) | Specific Heat Capacity (C) | Coefficient of Thermal Conductivity (D) | Coefficient of Thermal Expansion (E) | |
| 1 | 33,600 | 0.24 | 0.312 | 3000 | 0.0036 |
| 2 | 33,600 | 0.22 | 0.286 | 2750 | 0.0033 |
| 3 | 33,600 | 0.2 | 0.26 | 2500 | 0.003 |
| 4 | 33,600 | 0.18 | 0.234 | 2250 | 0.0027 |
| 5 | 30,800 | 0.24 | 0.286 | 2500 | 0.0027 |
| 6 | 30,800 | 0.22 | 0.312 | 2250 | 0.003 |
| 7 | 30,800 | 0.2 | 0.234 | 3000 | 0.0033 |
| 8 | 30,800 | 0.18 | 0.26 | 2750 | 0.0036 |
| 9 | 28,000 | 0.24 | 0.26 | 2250 | 0.0033 |
| 10 | 28,000 | 0.22 | 0.234 | 2500 | 0.0036 |
| 11 | 28,000 | 0.2 | 0.312 | 2750 | 0.0027 |
| 12 | 28,000 | 0.18 | 0.286 | 3000 | 0.003 |
| 13 | 25,200 | 0.24 | 0.234 | 2750 | 0.003 |
| 14 | 25,200 | 0.22 | 0.26 | 3000 | 0.0027 |
| 15 | 25,200 | 0.2 | 0.286 | 2250 | 0.0036 |
| 16 | 25,200 | 0.18 | 0.312 | 2500 | 0.0033 |
References
- Li, Q.F.; Zhou, H.D.; Ma, Q.; Lu, L.F. Evaluation of serviceability of canal lining based on AHP—Simple correlation function method–cloud model: A case study in Henan Province, China. Sustainability 2021, 13, 12314. [Google Scholar] [CrossRef]
- Li, Q.; Guo, L.; Zhou, H. Construction Quality Evaluation of Large-Scale Concrete Canal Lining Based on Statistical Analysis, FAHM, and Cloud Model. Sustainability 2022, 14, 7663. [Google Scholar] [CrossRef]
- Wang, B.; Tian, J.C.; Zhou, J.J. Effect of different concrete properties on frost heave crack in U-shaped canal lining and joint. Phys. Chem. Earth 2021, 121, 102983. [Google Scholar] [CrossRef]
- Li, Z.; Liu, S.H.; Feng, Y.T.; Liu, K.; Zhang, C.C. Numerical study on the effect of frost heave prevention with different canal lining structures in seasonally frozen ground regions. Cold Reg. Sci. Technol. 2013, 85, 242–249. [Google Scholar] [CrossRef]
- Wang, Y.H.; Si, N. Numerical simulation of anti-frost heave effect of U-shaped FRP canal. J. Inner. Mongolia Univ. Sci. Technol. 2014, 33, 409–412. [Google Scholar]
- Yan, C.C.; Wang, Z.Z.; Liu, X.D.; Chen, L.J. Preliminary study on anti-frost heave performance of glass fiber reinforced plastic anti-seepage canal in seasonal frozen soil area. Yellow River 2011, 33, 140–142. [Google Scholar]
- Cheng, C.S.; Tian, J.C.; Wang, B.; Gao, J. Study on frost heave resistance of U-shaped FRP and concrete canals in arid and cold regions. J. Water Res. Water Eng. 2015, 26, 173–177. [Google Scholar]
- Wu, Y.; Zhou, C.; He, N.; He, J.C.; Wu, Y. Numerical simulation of canal frost heave mitigation with waste tire flexible bank protection. Chin. J. Undergr. Space Eng. 2014, 10, 1777–1781, 1793. [Google Scholar]
- Li, J.J.; He, X.L.; Qiu, L.C.; Liu, R.Q.; Zhou, B.L. Numerical simulation of frost heave cracking of concrete lining canal based on thermal coupling. Chin. J. Comput. Mech. 2019, 36, 278–283. [Google Scholar]
- Chen, R.K.; Song, L.; Wei, P.; Du, M.R. Numerical simulation of frost heave of water conveyance canals in winter considering the influence of water in the canal. J. Shihezi Univ. 2018, 36, 220–225. [Google Scholar]
- Wang, Z.Z.; Chen, L.J.; Mu, S.Y.; Li, J.L. Frost heave simulation of polymer coating and asphalt concrete lining canal. J. Liaoning Univ. Eng. Technol. 2009, 28, 961–964. [Google Scholar]
- Chen, L.K.; Cai, X.Y.; Wang, Z.Z.; Niu, Y.H.; Hua, W. Frost heave simulation of composite geomembrane and nano-concrete lining canal. China Rural. Water Conserv. Hydropower 2010, 8, 106–109. [Google Scholar]
- An, P.; Xing, Y.C.; Zhang, A.J.; Zhu, P.T. Research on design method and numerical simulation of anti-frost heave cushion for canal. Geotech. Mech. 2013, 34, 257–271. [Google Scholar]
- Zhang, R.; Wang, Z.Z.; Mou, S.Y.; Liu, X. Numerical simulation of frost heave for U-shaped channel based on transversely isotropic frozen soil. J. Appl. Basic Eng. Sci. 2010, 18, 773–783. [Google Scholar]
- Chen, L.J.; Wang, Z.Z.; Liu, X.D.; Li, J.L. Numerical simulation of frost heave resistance of lining structures of irrigation and drainage canals with high groundwater level. J. Yangtze River Acad. Sci. 2009, 26, 66–70. [Google Scholar]
- Wang, Z.Z.; Liu, X.D.; Chen, L.J.; Li, J.L. Numerical simulation of the frost heave reduction effect of different longitudinal joints in rigid lining canals. Chin. J. Agric. Eng. 2009, 25, 1–7. [Google Scholar]
- Asl, R.H.; Salmasi, F.; Arvanaghi, H. Numerical investigation on geometric configurations affecting seepage from unlined earthen channels and the comparison with field measurements. Eng. Appl. Comp. Fluid 2020, 14, 236–253. [Google Scholar] [CrossRef]
- Eltarabily, M.G.; Eldin, M.H.; Negm, A.M. Assessment of slope instability of canal with standard incomat concrete-filled geotextile mattresses lining. Alex. Eng. J. 2019, 58, 1385–1397. [Google Scholar] [CrossRef]
- El-Molla, D.A.; El-Molla, M.A. Reducing the conveyance losses in trapezoidal canals using compacted earth lining. Ain Shams Eng. J. 2021, 12, 2453–2463. [Google Scholar] [CrossRef]
- Cui, J.H.; Xie, Z.Q.; Xiao, H.J. Cause analysis on the cracks in concrete plate of canal lining. Appl. Mech. Mater. 2013, 405, 2596–2599. [Google Scholar] [CrossRef]
- Han, X.; Wang, X.; Zhu, Y.; Wu, J.; Huang, J. Effects of canal damage characteristics on canal seepage based on a three-dimensional numerical model. J. Hydrol. 2022, 605, 127295. [Google Scholar] [CrossRef]
- Zhang, H.C.; Li, Z.; Zhang, M.L.; Yao, Z.P.; Zhu, X.L.; Wang, M.Y. Numerical simulation of frost heave damage of trapezoidal canal lining in cold and arid regions. Yellow River 2019, 41, 156–160. [Google Scholar]
- Zhao, C.; Zhou, W.; Chen, X.Y.; Wu, Q.Y.; Ma, G.; Wang, Q. Mesoscopic analysis of heat and moisture coupled transfer in concrete considering phase change under frost action. J. Build Eng. 2022, 57, 104888. [Google Scholar] [CrossRef]
- Li, G.X. Advanced Soil Mechanics, 2nd ed.; Tsinghua University Press: Beijing, China, 2016. [Google Scholar]
- Guo, Z.H. Principles of Reinforced Concrete; Tsinghua University Press: Beijing, China, 2013. [Google Scholar]
- Wang, H.B.; Yang, P.; He, Z.Y. Effects of porosity and saturation on thermal conductivity of silt. J. Nanjing For. Univ. 2012, 36, 42–46. [Google Scholar]
- GB 50010-2010; Design Code for Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China, China Construction Industry Press: Beijing, China, 2010.
- Du, Y.C. Prototype Test and Numerical Analysis of Canal Rubber Concrete Lining Structure. Master’s Thesis, Zhengzhou University, Zhengzhou, China, 2016. [Google Scholar]
- Yang, Y.Q.; Gong, L.; Wang, H.; Kang, C.T.; Wang, Z.H. Frost heave damage analysis and numerical simulation of trapezoidal canal lining in dry and cold regions. Gansu Water Conserv. Hydropower Technol. 2020, 56, 21–26. [Google Scholar]
- Wang, Z.Z. Study on the mechanical model of frost heave failure of trapezoidal canal concrete lining. Chin. J. Agric. Eng. 2004, 3, 24–29. [Google Scholar]
- Chen, T.; Wang, Z.Z.; Zhang, A.J. Experimental study on frost heave mechanism of large U-shaped canal. J. Irrig. Drain 2006, 2, 8–11. [Google Scholar]
- Lu, L.; Ma, Q.; Hu, J.; Li, Q. Mechanical Properties, Curing Mechanism, and Microscopic Experimental Study of Polypropylene Fiber Coordinated Fly Ash Modified Cement–Silty Soil. Materials 2021, 14, 5441. [Google Scholar] [CrossRef]
- Stern, F.; Wilson, R.; Coleman, H.; Paterson, E.G. Comprehensive approach to verification and validation of CFD simulations—Part 1: Methodology and procedures. J. Fluids Eng. 2001, 123, 793–802. [Google Scholar] [CrossRef]
- Nowoświat, A.; Olechowska, M. Experimental Validation of the Model of Reverberation Time Prediction in a Room. Buildings 2022, 12, 347. [Google Scholar] [CrossRef]
- Garcíaa, B.F.; Mousaviraadb, M.; Saraji, S. Verification and validation for microfluidic CFD simulations of Newtonian and non-Newtonian flows. Appl. Math. Model. 2022, 107, 557–573. [Google Scholar] [CrossRef]





| Elastic Modulus (MPa) | Poisson’s Ratio | Shear Modulus (MPa) | Coefficient of Thermal Expansion | Specific Heat Capacity | |
|---|---|---|---|---|---|
| 20 | 0.33 | 8 | 641.5 | 0.2 × 10−2 | 0.1 × 10−3 |
| Elastic Modulus (MPa) | Poisson’s Ratio | Specific Heat Capacity | Coefficient of Thermal Conductivity | Coefficient of Thermal Expansion |
|---|---|---|---|---|
| 2.8 × 104 | 0.2 | 0.26 | 2.5 × 103 | 0.3 × 10−2 |
| Serial Number | Maximum Stress (MPa) |
|---|---|
| 1 | 1.34 |
| 2 | 1.28 |
| 3 | 1.22 |
| 4 | 1.19 |
| 5 | 1.23 |
| 6 | 1.21 |
| 7 | 1.20 |
| 8 | 1.23 |
| 9 | 1.18 |
| 10 | 1.17 |
| 11 | 1.16 |
| 12 | 1.17 |
| 13 | 1.14 |
| 14 | 1.12 |
| 15 | 1.11 |
| 16 | 1.09 |
| Calculated Index | Result Value | ||||
|---|---|---|---|---|---|
| A | B | C | D | E | |
| S1j | 5.03 | 4.89 | 4.8 | 4.83 | 4.85 |
| S2j | 4.87 | 4.78 | 4.79 | 4.81 | 4.75 |
| S3j | 4.68 | 4.69 | 4.75 | 4.71 | 4.74 |
| S4j | 4.46 | 4.68 | 4.7 | 4.69 | 4.7 |
| n | 4 | 4 | 4 | 4 | 4 |
| s1j | 1.2575 | 1.2225 | 1.2 | 1.2075 | 1.2125 |
| s2j | 1.2175 | 1.195 | 1.1975 | 1.2025 | 1.1875 |
| s3j | 1.17 | 1.1725 | 1.1875 | 1.1775 | 1.185 |
| s4j | 1.115 | 1.17 | 1.175 | 1.1725 | 1.175 |
| Rj | 0.1425 | 0.0525 | 0.025 | 0.035 | 0.0375 |
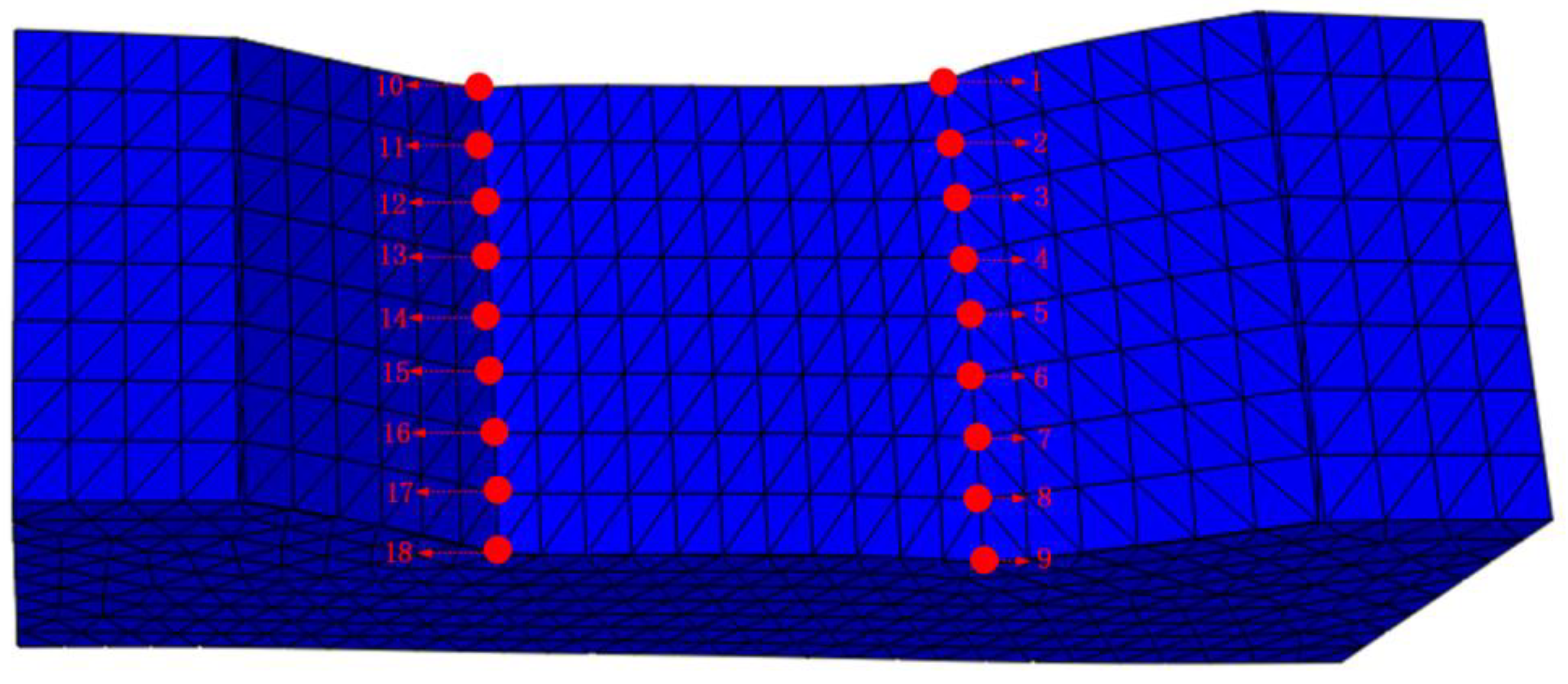
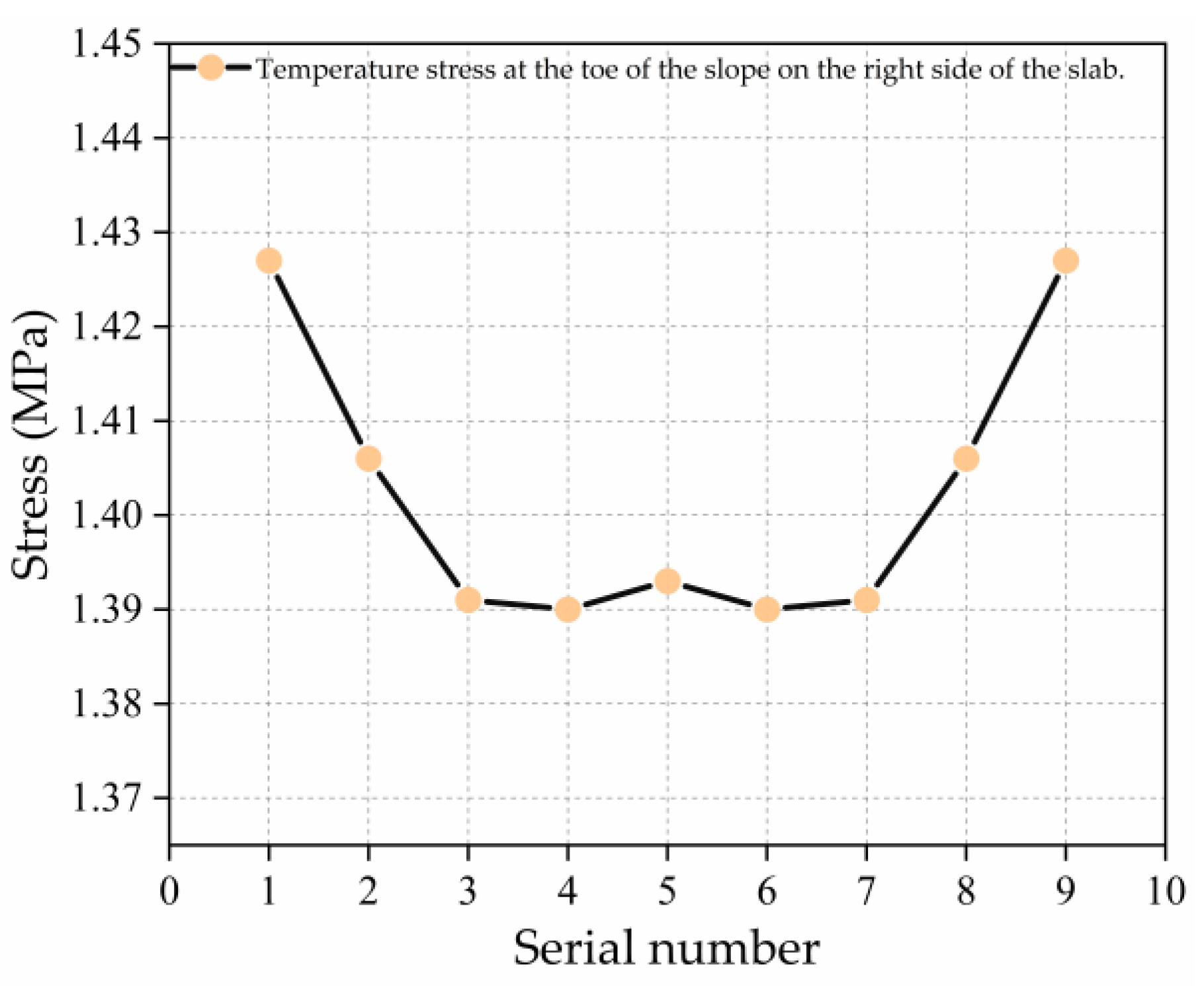
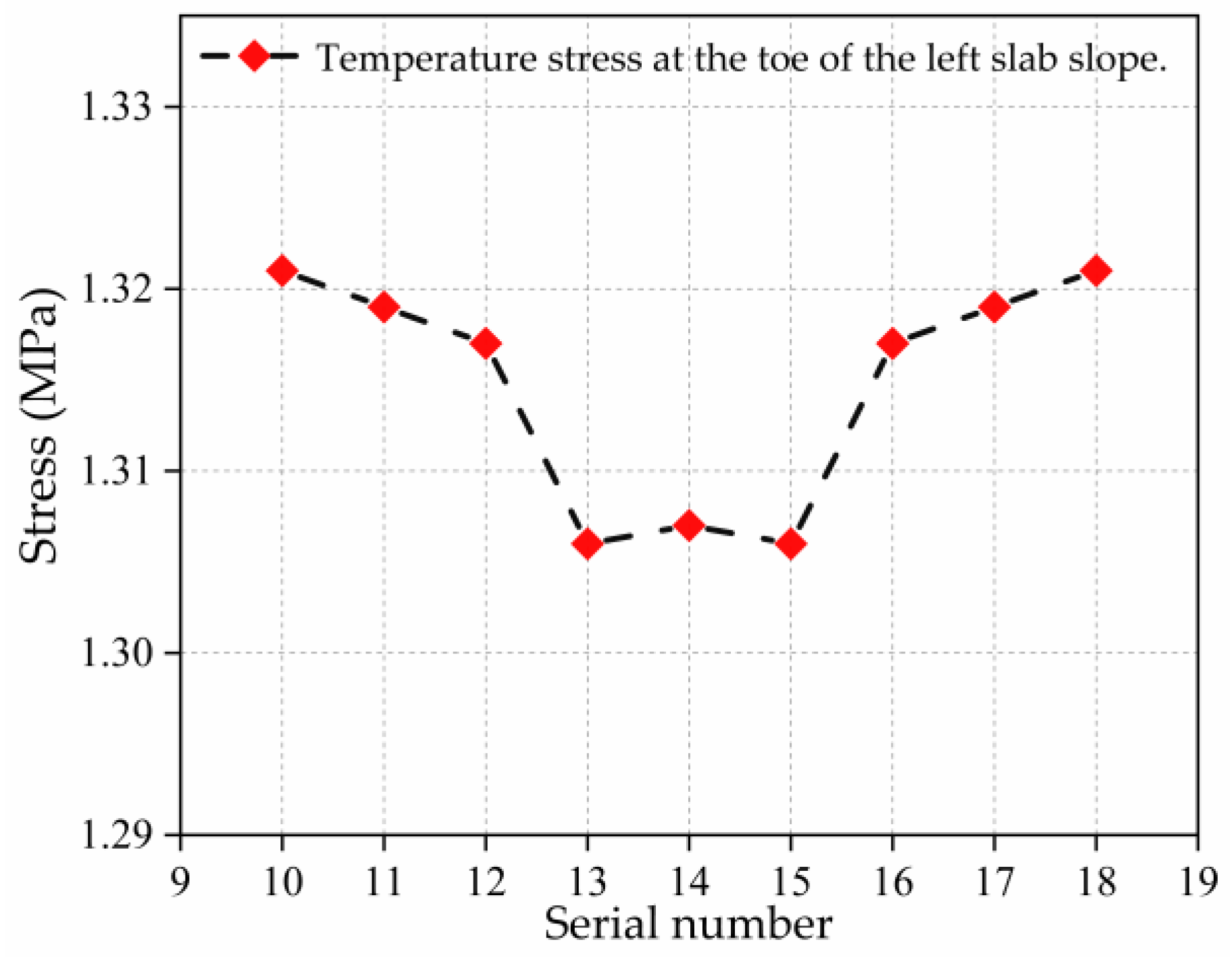
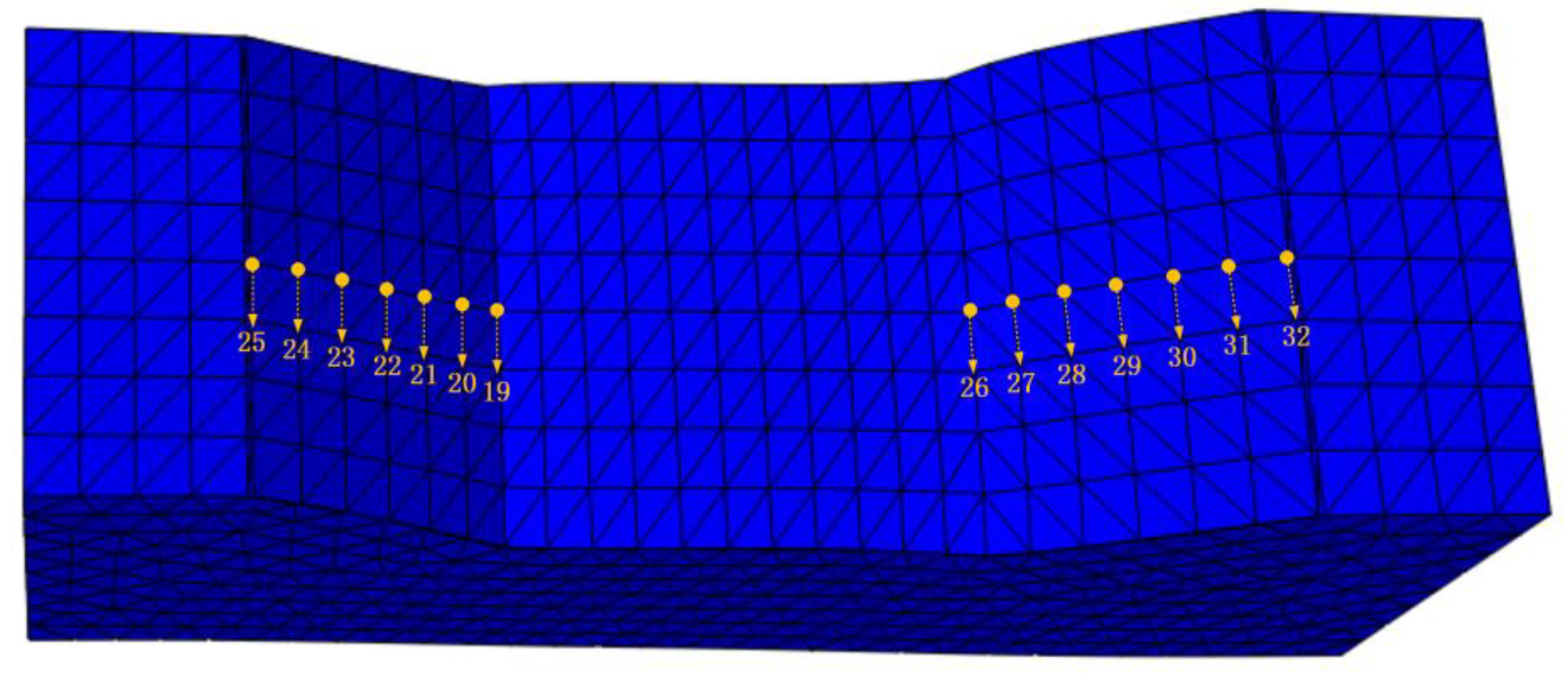
| Number (Location) | Simulated Value (MPa) | Measured Value [28] (MPa) | Validation Error |
|---|---|---|---|
| 1 (left side slope toe) | 1.527 | 1.534 | 0.007 |
| 2 (left side slope toe) | 1.406 | 1.424 | 0.018 |
| 3 (left side slope toe) | 1.391 | 1.428 | 0.037 |
| 4 (left side slope toe) | 1.39 | 1.416 | 0.026 |
| 5 (left side slope toe) | 1.393 | 1.412 | 0.019 |
| 6 (left side slope toe) | 1.39 | 1.405 | 0.015 |
| 7 (left side slope toe) | 1.391 | 1.389 | −0.002 |
| 8 (left side slope toe) | 1.406 | 1.413 | 0.007 |
| 9 (left side slope toe) | 1.427 | 1.533 | 0.106 |
| 10 (right side slope toe) | 1.321 | 1.432 | 0.111 |
| 11 (right side slope toe) | 1.319 | 1.411 | 0.092 |
| 12 (right side slope toe) | 1.317 | 1.332 | 0.015 |
| 13 (right side slope toe) | 1.306 | 1.332 | 0.026 |
| 14 (right side slope toe) | 1.307 | 1.313 | 0.006 |
| 15 (right side slope toe) | 1.306 | 1.324 | 0.018 |
| 16 (right side slope toe) | 1.317 | 1.335 | 0.018 |
| 17 (right side slope toe) | 1.319 | 1.364 | 0.045 |
| 18 (right side slope toe) | 1.321 | 1.436 | 0.115 |
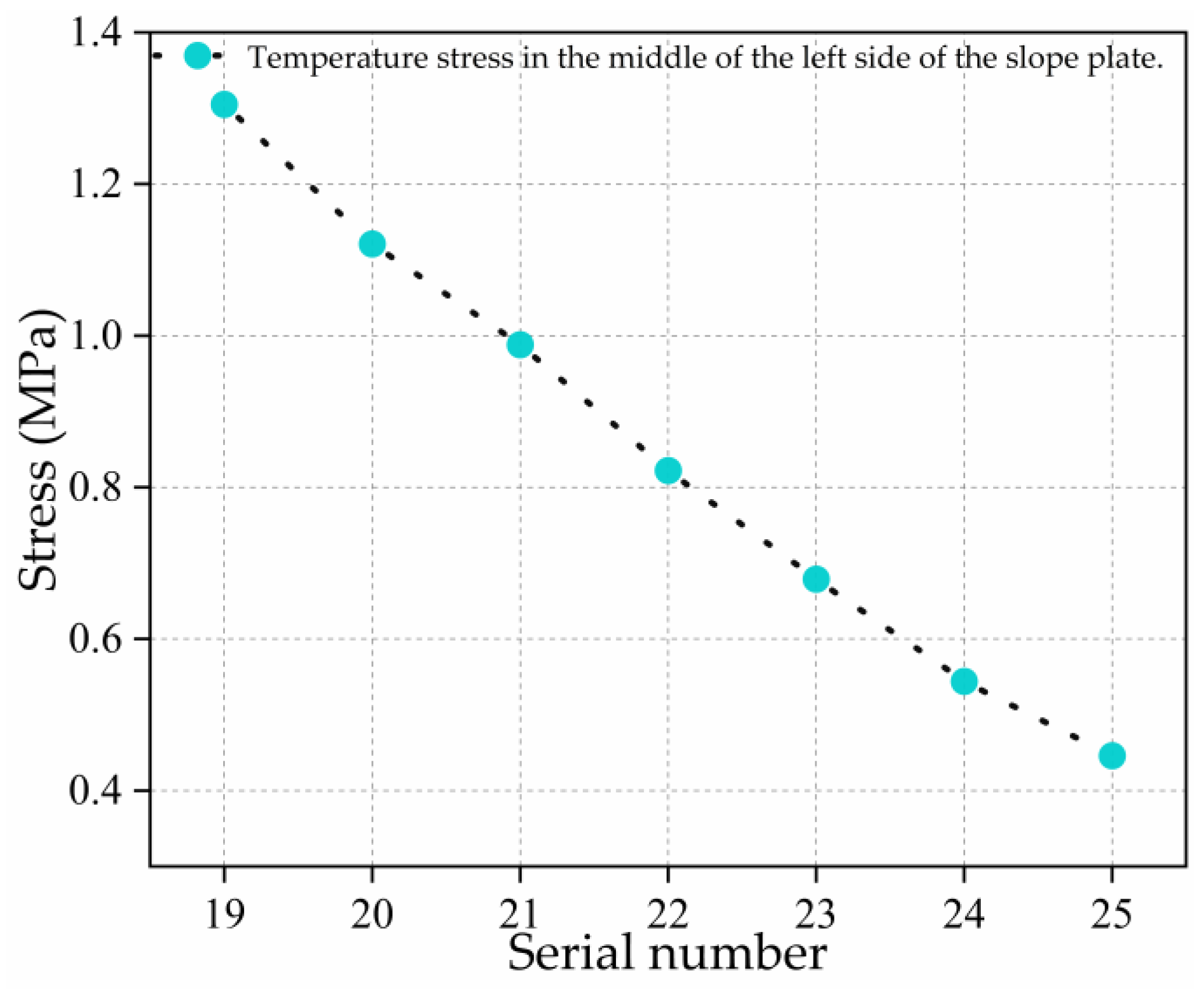
| 19 (left side slope plate) | 1.305 | 1.315 | 0.01 |
| 20 (left side slope plate) | 1.121 | 1.218 | 0.097 |
| 21 (left side slope plate) | 0.988 | 1.112 | 0.124 |
| 22 (left side slope plate) | 0.822 | 0.845 | 0.023 |
| 23 (left side slope plate) | 0.679 | 0.732 | 0.053 |
| 24 (left side slope plate) | 0.544 | 0.603 | 0.059 |
| 25 (left side slope plate) | 0.446 | 0.478 | 0.032 |
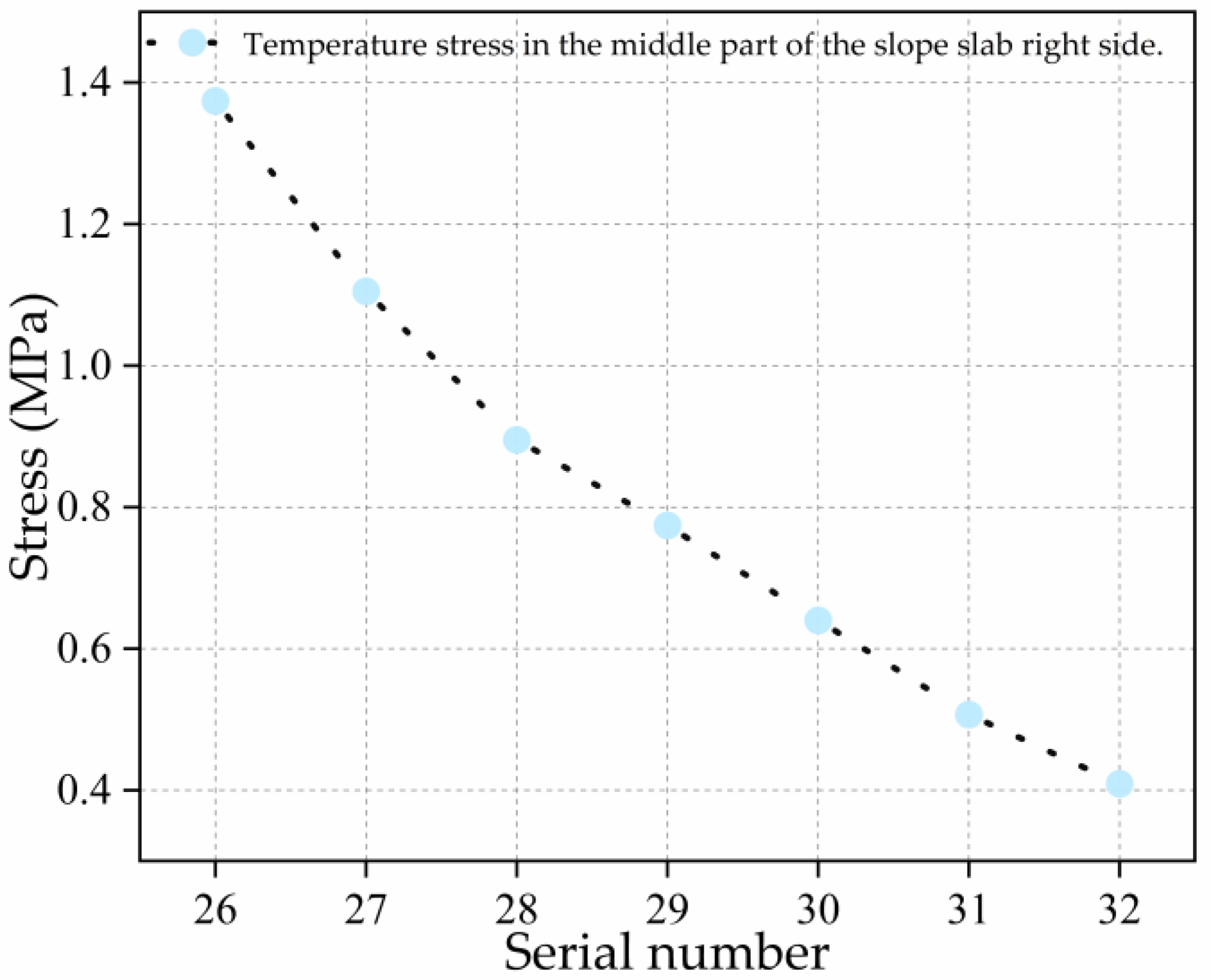
| 26 (right side slope plate) | 1.374 | 1.381 | 0.007 |
| 27 (right side slope plate) | 1.105 | 1.123 | 0.018 |
| 28 (right side slope plate) | 0.895 | 0.942 | 0.047 |
| 29 (right side slope plate) | 0.774 | 0.751 | −0.023 |
| 30 (right side slope plate) | 0.64 | 0.684 | 0.044 |
| 31 (right side slope plate) | 0.507 | 0.536 | 0.029 |
| 32 (right side slope plate) | 0.409 | 0.503 | 0.094 |
| Number (Location) | Parameters of Error (%) | Value of Error (%) | |
|---|---|---|---|
| 1 (left side slope toe) | 1.54 | 0.46 | 1.08 |
| 2 (left side slope toe) | 1.96 | 1.26 | 0.70 |
| 3 (left side slope toe) | 1.75 | 2.59 | 0.84 |
| 4 (left side slope toe) | 1.29 | 1.84 | 0.54 |
| 5 (left side slope toe) | 1.70 | 1.35 | 0.36 |
| 6 (left side slope toe) | 2.08 | 1.07 | 1.02 |
| 7 (left side slope toe) | 1.29 | 0.14 | 1.14 |
| 8 (left side slope toe) | 1.28 | 0.50 | 0.79 |
| 9 (left side slope toe) | 1.54 | 6.91 | 5.37 |
| 10 (right side slope toe) | 1.54 | 7.75 | 6.21 |
| 11 (right side slope toe) | 1.54 | 6.52 | 4.98 |
| 12 (right side slope toe) | 1.28 | 1.13 | 0.16 |
| 13 (right side slope toe) | 1.28 | 1.95 | 0.67 |
| 14 (right side slope toe) | 1.45 | 0.46 | 1.00 |
| 15 (right side slope toe) | 1.29 | 1.36 | 0.07 |
| 16 (right side slope toe) | 1.31 | 1.35 | 0.04 |
| 17 (right side slope toe) | 1.28 | 3.30 | 2.01 |
| 18 (right side slope toe) | 2.07 | 8.01 | 5.93 |
| 19 (left side slope plate) | 1.32 | 0.76 | 0.56 |
| 20 (left side slope plate) | 1.81 | 7.96 | 6.15 |
| 21 (left side slope plate) | 1.73 | 11.15 | 9.42 |
| 22 (left side slope plate) | 1.97 | 2.72 | 0.76 |
| 23 (left side slope plate) | 1.01 | 7.24 | 6.23 |
| 24 (left side slope plate) | 2.59 | 9.78 | 7.19 |
| 25 (left side slope plate) | 1.21 | 6.69 | 5.48 |
| 26 (right side slope plate) | 1.31 | 0.51 | 0.80 |
| 27 (right side slope plate) | 1.68 | 1.60 | 0.08 |
| 28 (right side slope plate) | 1.96 | 4.99 | 3.03 |
| 29 (right side slope plate) | 2.62 | 3.06 | 0.44 |
| 30 (right side slope plate) | 2.59 | 6.43 | 3.84 |
| 31 (right side slope plate) | 2.60 | 5.41 | 2.81 |
| 32 (right side slope plate) | 2.63 | 18.69 | 16.06 |
| Number (Location) | Uncertainty of Measurement and Simulation (%) | Uncertainty (%) | |
|---|---|---|---|
| 1 (left side slope toe) | 1.54 | 0.46 | 3.05 |
| 2 (left side slope toe) | 1.96 | 1.26 | 4.05 |
| 3 (left side slope toe) | 1.75 | 2.59 | 4.30 |
| 4 (left side slope toe) | 1.29 | 1.84 | 3.13 |
| 5 (left side slope toe) | 1.70 | 1.35 | 3.60 |
| 6 (left side slope toe) | 2.08 | 1.07 | 4.22 |
| 7 (left side slope toe) | 1.29 | 0.14 | 2.52 |
| 8 (left side slope toe) | 1.28 | 0.50 | 2.57 |
| 9 (left side slope toe) | 1.54 | 6.91 | 7.55 |
| 10 (right side slope toe) | 1.54 | 7.75 | 8.32 |
| 11 (right side slope toe) | 1.54 | 6.52 | 7.18 |
| 12 (right side slope toe) | 1.28 | 1.13 | 2.76 |
| 13 (right side slope toe) | 1.28 | 1.95 | 3.19 |
| 14 (right side slope toe) | 1.45 | 0.46 | 2.89 |
| 15 (right side slope toe) | 1.29 | 1.36 | 2.87 |
| 16 (right side slope toe) | 1.31 | 1.35 | 2.90 |
| 17 (right side slope toe) | 1.28 | 3.30 | 4.15 |
| 18 (right side slope toe) | 2.07 | 8.01 | 8.98 |
| 19 (left side slope plate) | 1.32 | 0.76 | 2.70 |
| 20 (left side slope plate) | 1.81 | 7.96 | 8.72 |
| 21 (left side slope plate) | 1.73 | 11.15 | 11.66 |
| 22 (left side slope plate) | 1.97 | 2.72 | 4.72 |
| 23 (left side slope plate) | 1.01 | 7.24 | 7.51 |
| 24 (left side slope plate) | 2.59 | 9.78 | 11.02 |
| 25 (left side slope plate) | 1.21 | 6.69 | 7.10 |
| 26 (right side slope plate) | 1.31 | 0.51 | 2.61 |
| 27 (right side slope plate) | 1.68 | 1.60 | 3.67 |
| 28 (right side slope plate) | 1.96 | 4.99 | 6.30 |
| 29 (right side slope plate) | 2.62 | 3.06 | 5.98 |
| 30 (right side slope plate) | 2.59 | 6.43 | 8.20 |
| 31 (right side slope plate) | 2.60 | 5.41 | 7.43 |
| 32 (right side slope plate) | 2.63 | 18.69 | 19.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Wu, B.; Zhou, H. Damage Simulation Analysis of Canal Concrete Lining Plates Based on Temperature-Stress-Water Load Coupling. Sustainability 2022, 14, 9202. https://doi.org/10.3390/su14159202
Li Q, Wu B, Zhou H. Damage Simulation Analysis of Canal Concrete Lining Plates Based on Temperature-Stress-Water Load Coupling. Sustainability. 2022; 14(15):9202. https://doi.org/10.3390/su14159202
Chicago/Turabian StyleLi, Qingfu, Binghui Wu, and Huade Zhou. 2022. "Damage Simulation Analysis of Canal Concrete Lining Plates Based on Temperature-Stress-Water Load Coupling" Sustainability 14, no. 15: 9202. https://doi.org/10.3390/su14159202
APA StyleLi, Q., Wu, B., & Zhou, H. (2022). Damage Simulation Analysis of Canal Concrete Lining Plates Based on Temperature-Stress-Water Load Coupling. Sustainability, 14(15), 9202. https://doi.org/10.3390/su14159202





