Procurement Strategies and Auction Mechanism for Heterogeneous Service Providers in a Service Supply Chain

Abstract

This paper examines competition between two heterogeneous service providers (SPs) in a service procurement market. We investigate a service supply chain consisting of one service integrator (SI), and two SPs who compete the SI’s order with their own reservation profits. To select the favorable SP and centralize the total system, we propose an auction mechanism in symmetric and asymmetric information scenarios and find that channel coordination can be achieved by means of an efficient auction mechanism, hence, Pareto improvement conditions can be clearly illustrated. In addition, we characterize the effects of information asymmetry on optimal decisions and derive some important managerial insights into the value of information.

1. Introduction

In recent years, service supply chain management has received increasing attention in the operations management and operations research literature as the world economy has grown increasingly service oriented. Due to fierce market competition, many manufacturing enterprises have gradually expanded their products range from physical products to value-added services. This trend is called “product servitization” in [1]. Service supply chain systems can be subdivided into two categories based on the specific form of the product, the service-only supply chain, and the product service supply chain. For example, in many well-established service industries such as healthcare body checking, psychology advice, and financial consultancy, the respective supply chains are service-only supply chain [2]. Likewise, we can find the product service supply chain in restaurant and food retail supply chain, product design, and logistics supply chain.

To benefit the channel members, cooperation is one of the most effective means to improve channel members’ or a supply chain’s operational performance, and a service supply chain is no exception. So far, most studies on supply chain coordination mechanisms have investigated the issue of how to establish game theory models and design contracts among supply chain members [3,4,5]. By contrast, little work was done on auctions for supply chain coordination. Actually, it is known that an auction can provide an ideal and important market mechanism for the competitive allocation of the price for goods or services. In a service supply chain, an auction offers direct access to numerous competitive SPs at a relatively low cost. For the SP, the auction offers a transparent form of competition that depends on quantitatively defined terms such as price, delivery time, and service quality. Meanwhile, the auction could facilitate supply chain coordination and has a significant influence on the supply chain performance. In order to minimize procurement costs, many companies purchase via reverse auctions or employ online bidding systems instead of traditional procurement contracts. For instance, Wal-Mart uses a reverse auction mechanism to choose competitive manufacturers so as to save purchasing costs, and hence increase Wal-Mart’s profit. In another instance, eBay, the largest consumer-oriented auction site, attains nearly half of the gross merchandise via auction transactions.

When it comes to demand uncertainty, the supply chain often inevitably suffers from the risk of the trade-off between overstocks and stock-outs. Moreover, there are many other factors inducing supply failures such as earthquakes, floods, and climate environment. Therefore, in the face of uncertain demand, it is necessary to take participants’ risk preferences into consideration. Nowadays, risk analysis and management have drawn much attention from both the industry and academia in uncertain environments (Choi and Andrzej [6], Choi et al. [7], Choi and Andrzej [8]). At present, based on probability and statistics, value at risk (VaR) is one of the most widely and frequently employed models for risk measure in risk management (Olson and Wu [9], Paul et al. [10]). VaR can be characterized as a maximum expected loss, given some time horizon and within a given confidence interval, which is suitable for our model setting. Inspired by real business problems, this study considers a service supply chain consisting of two heterogeneous SPs, with different reservation profits, who competitively provide service to a single risk-averse SI measured by VaR. Under such a context, the contract must be designed to offer the SPs no less than their own reservation profits. Specifically, the research questions are: whether or not an appropriate auction mechanism can be regarded as a service supply chain coordination mechanism? How do the critical system factors, especially reservation profits and information asymmetry, affect the optimal outcomes and contract decisions?

Our specific research questions related to the impacts of information asymmetry and auction schemes on service competition in a service supply chain in which SI chooses the favorable SP and coordinates the whole service supply chain. Toward that end, we develop a duopoly competition model in an asymmetric information case to examine whether auction and contracting mechanisms can be served as a coordination mechanism in a service supply chain considering participants’ different risk preferences and individual reservation profit. Several managerial insights about how participants’ risk preferences and cost variation influence their own optimal decisions and system optimums are presented. The main contributions of this paper can be summarized as follows:

(1)

For the purpose of encouraging the SP to cooperate fully with the SI, and satisfying their reservation profits at the same time, proper auction and contracting mechanisms are established to ensure that the SP and the SI are inclined to get involved.

(2)

In certain circumstances, the optimal decisions deduced by the auction and contracting mechanisms are exactly the same as channel coordination optimums. Furthermore, Pareto improvement conditions are also clearly illustrated.

(3)

We characterize the impact of the SP’s cost variation on the optimal decisions and total supply chain profits. We find that the high-cost SP is always motivated to truthfully announce rather than distort exact cost information with the SI. This conclusion is consistent with the outcome of separate equilibrium in a signal game.

(4)

We derive more practical insights into the relationship between the decision makers’ risk preferences and policies. We also perform some comprehensive comparisons of the channel coordination optimums obtained in the risk-neutral system and the risk-averse one.

In addition to offering insights into the service competition in a service supply chain, our results extend the results of the literature that examines firm competition using service price. First, proper auction contracting, as opposed to a traditional coordination contract, achieves service supply chain coordination. In particular, Pareto improvement conditions ensure every member is a voluntary participant in auction contracting. Second, as compared with a risk-neutral case in which the SI is risk-neutral and maximizes one’s own expected profit, we find that the risk-averse SI has a lower service price and higher order quantity. Additionally, in the presence of information asymmetry, we find that the high-cost SP may be worse off if encountered with a high cost variation.

The rest of the paper is organized as follows. We briefly present the relevant literature in Section 2. In Section 3, information symmetric case is studied. Section 4 presents the optimal auction mechanism in asymmetric information cases and explores the value of information. In Section 5, the comparative analyses among different risk preferences of the SI are conducted. Numerical experiments and sensitivity analyses are performed to validate and enrich our analytical results in Section 6. Section 7 concludes this study. Detail proof is displayed in Appendix A.

2. Literature Review

The body of research closely related to this work can be divided into three broad sets. The first set studies service supply chain coordination. The second set refers to the effects of information asymmetry on the decision maker’s policies in supply chain management. The third set includes the literature on auction mechanisms in operations management.

There is considerable literature devoted to service supply chain coordination. Here, we define coordination as the mechanism used to achieve the best performance in a service supply chain system, which is consistent with the existing literature [11,12,13,14,15]. A widely accepted structure of a service supply chain is: “Service Provider (SP)-Service Integrator (SI)-Customers” [16]. Usually, the SI has stronger control power and outsources the functional service to SPs in order to maintain a competitive advantage. Bernstein and Federgruen [17] examined supply chain coordination with price and service competition. They found that with an exogenous service level, a simple linear wholesale pricing contract can be designed so as to achieve service supply chain coordination. However, with the endogenous service level, they proved that a simple linear wholesale pricing contract cannot achieve coordination. Sethi et al. [18] examined a two-stage service supply chain with information updating. They identified the optimal order quantity and studied the effect of order cancellations in such a service supply chain. They employed the buyback contract to coordinate the supply chain. Sieke et al. [19] proposed several service-level-based supply contracts to achieve supply chain coordination. They identified the optimal service level contracts. Xiao and Xu [20] studied the service level in a supply chain under the vendor-managed inventory. They identified the equilibrium prices and service quality under both centralized and decentralized cases and found that a revenue-sharing contract can achieve supply chain coordination. Heydari [21] investigated a coordination mechanism in a supply chain taking customer service level into consideration and found that stochastic lead time may harm the customer service level. However, different from the above-mentioned literature, this study designed auction contracting as a coordination mechanism.

In addition, we are aware of several studies in the supply chain literature that explore the impacts of cost/demand information asymmetry on supply chain performance. Cakanyildirim et al. [22] concluded that information asymmetry alone does not necessarily induce loss in channel efficiency and designed the optimal contract for coordination. Chiu et al. [4] proposed a PRR (price, rebate, and returns) contract to coordinate a decentralized supply chain with both additive and multiplicative price-dependent demands and presented the fact that multiple equilibrium policies for channel coordination existed. Ha [23] designed a contract to maximize the supplier’s profit with asymmetric cost information in a one-supplier-one-buyer relationship for a short-life-cycle product. Ha et al. [24] investigated contracting and information sharing in two competing supply chains, in which each consisting of one manufacturer and one retailer. They evaluated the value of information sharing and fully characterized the equilibrium information sharing decisions under different investment costs. In this study, we investigate the impact of service cost variation on the optimal service price, optimal order quantity, and participants’ profits.

This study specifically relates to the literature on auction mechanisms in operations management in a competitive context. Previous studies have examined how an auction is utilized to award supply contracts to a selected group of suppliers. Auctions find successful applications in the electricity procurement market, which attracts a great number of researchers to make further investigation into the market mechanism. Ryzin and Vulcano [25] studied the inventory management for items sold through forward (selling) auctions. Abhishek et al. [26] studied the problem of selling a resource through an auction mechanism. Jain et al. [27] proposed the multi-stage auction mechanism by analyzing two-way competitions, a Bertrand and Cournot competition. Huang et al. [28] proved that the PT-BOCR method is a useful tool for risk aversion buyers to avoid losses and for suppliers to win the bids. Chen et al. [29] investigated keyword auctions for advertising. Another research stream in procurement auctions analyzed auctions in a more complicated supply chain setting. Ivengar and Kumar [30] proposed an optimal auction mechanism for a buyer that sources from suppliers with different capacity limits and production costs. Chen and Vulcano [31] compared the first- and the second-price auctions as mechanisms for two competing retailers to procure capacity from a supplier. Multi-attribute procurement auction mechanism was also extensively studied. Che [32] studied the two-attribute auction in which price and quality are the two attributes under consideration. Branco [33] extended Che’s model to allow a correlation in the suppliers’ costs. Parkes and Kalagnanam [34] provided an iterative auction design for an important special case of the multi-attribute allocation problem. Recently, there is also some research on auction coordination mechanisms for procurement. Chen [35] investigated the auction coordination mechanism for the supply chain with one manufacturer and multiple competing suppliers in the electronic market.

In this study, we consider the channel participants’ risk preferences and reservation profits, and the main differences between our paper and the literature mentioned above can be summarized as follows. Firstly, in consideration of individual reservation profit, we employ an auction and contracting mechanism for channel coordination for a service supply chain in which traditional contracts are generally used such as two-part contracts, cost-sharing contracts, risk-sharing contracts, etc. Our findings also provide a useful tool for firms to deal with supplier selection and channel coordination. Secondly, we investigate the impacts of production cost variation and the value of information on the participants’ profits and preferences in contrast to associated optimal policies in symmetric and asymmetric situations, which rarely appeared in the existing literature.

3. Symmetric Information Case

In this section, we consider a supply chain consisting of one SI and two competitive SPs providing services to the SI with different costs. We begin this section with some notations used throughout this paper in

Table 1. List of Notations.

Notation	Definition
r:	service price;
q:	order quantity;
c:	the SI’s holding cost;
$L_i$:	side payment of SP i, for $i=l,h$;
$w_i$:	the SP i’s wholesale price;
$s_i$:	the SP i’s service cost, $s_l$ stands for low cost, $s_h$ stands for high cost, $s_l\le s_h$;
${\Pi }_i$:	the SI’s profit when $i=R$; the entire supply chain’s profit when $i=SC$;
	the low-(high-)cost SP’s profit when $i=S_{l(h)}$;
$\alpha$:	the confidence level for the SI’s risk measure;
$k_{S_i}$:	the SP i’s reservation profit, $i=l,h$.

.

For the demand in the system, we assume a stochastic and price-dependent demand function (Arcelus et al. [36], Leng et al. [37])

$$D_d=g{r}^{-b}x,forg>0,b>1,$$

where x denotes a random variable with a finite mean $\mu$ that follows a density function $f(·)$ and a cumulative distribution function $F(·)$. Denote the inverse function of $F(·)$ by $F^{-1}(·)$. Then, the SI’s profit can be expressed as

$${\Pi }_R(r,q)=\left\{\begin{array}{cc}g{r}^{-b+1}x-(c+w)q,\hfill & \mathrm{i}\mathrm{f}x\le \frac{q{r}^b}{g},\hfill \\ (r-c-w)q,\hfill & \mathrm{i}\mathrm{f}x>\frac{q{r}^b}{g}.\hfill \end{array}\right.$$

Consider the case that the SI follows the VaR criterion to determine the optimal order quantity and optimal service price. Then, the SI’s profit with VaR is defined as

$$\underset{r,q\ge 0}{max}\left\{T\right|P({\Pi }_R(r,q)\le T)\le \alpha \}$$

(1)

where T is the SI’s reservation profit, and $0<\alpha <1$ denotes the confidence level which reflects the degree of risk-aversion for the SI. The optimization problem (1) with a chance constraint that maximizes the SI’s profit turns out to be the main challenge.

Lemma 1.

For the VaR model, the optimal price, optimal order quantity, and optimal profit of the SI are

$$\left\{\begin{array}{c}{r}^{★}=\frac{b}{b-1}(c+w),\hfill \\ q^{★}={\mathsf{\Phi }}_{\alpha }g{b}^{-b}{(b-1)}^b{(c+w)}^{-b},\hfill \\ T^{★}={\mathsf{\Phi }}_{\alpha }g{b}^{-b}{(b-1)}^{b-1}{(c+w)}^{-b+1},\hfill \end{array}\right.$$

(2)

respectively.

From

$$\frac{d{\mathsf{\Phi }}_{\alpha }}{d_{\alpha }}=\frac{d{F}^{-1}(1-\alpha )}{d_{\alpha }}=-\frac{1}{\frac{dF\left({\mathsf{\Phi }}_{\alpha }\right)}{d{\mathsf{\Phi }}_{\alpha }}}=-\frac{1}{f\left(F^{-1}(1-\alpha )\right)}<0,$$

we have $\frac{d{q}^{★}}{d\alpha }<0$ and $\frac{d{T}^{★}}{d\alpha }<0$, then $q^{★}$ and $T^{★}$ decrease with respect to $\alpha$. The lower the risk tolerance of managers, the less order quantity as a security strategy, hence, the SI’s profit decreases accordingly.

Now, consider the situation where the symmetric information case including the SPs’ service cost $(s_l,s_h)$, reservation profit $(k_l,k_h)$. Without loss of generality, we assume that $s_l<s_h$, and the market imposes a competitive requirement $s_h\le \frac{c+b{s}_l}{b-1}$ on the costs of the two SPs. There is a twofold explanation for imposing this assumption. Firstly, the high-cost SP’s cost should not be too high compared to the low-cost SP’s cost in order to make the market more competitive. Secondly, this requirement is aimed at making both the SI and SPs have incentives to join in the two-part contract auction.

3.1. Supply Chain Coordination Model with Symmetric Information

For channel coordination issues, we can obtain the following optimization problem

$$\begin{array}{cc}\underset{w}{max}{\pi }_{SC,\alpha }\hfill & ={\pi }_{R,\alpha }+{\pi }_{R,\alpha }\hfill \\ & ={\mathsf{\Phi }}_{\alpha }g{b}^{-b}{(b-1)}^{b-1}{(c+w_i)}^{-b+1}+(w_i-s_i){\mathsf{\Phi }}_{\alpha }g{b}^{-b}{(b-1)}^b{(c+w_i)}^{-b}.\hfill \end{array}$$

For this problem, by Equation (2), we have the following conclusion.

Lemma 2.

For the channel, the optimal order quantity, optimal service price, and coordinated supply chain profit are respectively

$$\left\{\begin{array}{c}{r}_{R,\alpha }^{★}=\frac{b}{b-1}(c+s_i),\hfill \\ q_{R,\alpha }^{★}={\mathsf{\Phi }}_{\alpha }g{b}^{-b}{(b-1)}^b{(c+s_i)}^{-b},\hfill \\ {\pi }_{R,\alpha }^{★}={\mathsf{\Phi }}_{\alpha }g{b}^{-b}{(b-1)}^{b-1}{(c+s_i)}^{-b+1}.\hfill \end{array}\right.$$

Next, we consider the decentralized case where the SPs and the SI are independent of each other, that is, both of the two SPs determine the optimal wholesale price from their viewpoints. Therefore, the SI will set the service price and order quantity to maximize its profit. For the SP in the decentralized case, the optimal wholesale price $w^{★}$ can be derived from the following optimization problem

$$\underset{w_i}{max}{\pi }_{S_i,\alpha }=(w_i-s_i){\mathsf{\Phi }}_{\alpha }g{b}^{-b}{(b-1)}^b{(c+w_i)}^{-b},i=l,h$$

Lemma 3.

For the decentralized case, the optimal wholesale price of the SP is

$$w_i^{★ind}=\frac{c+b{s}_i}{b-1},i=l,h.$$

From Lemma 3, one has

$$\left\{\begin{array}{c}{\pi }_{S_i,\alpha }^{★ind}={\mathsf{\Phi }}_{\alpha }g{b}^{-2b}{(b-1)}^{2b-1}{(c+s_i)}^{-b+1},\hfill \\ {\pi }_{R,\alpha }^{★ind}={\mathsf{\Phi }}_{\alpha }g{b}^{-2b+1}{(b-1)}^{2b-2}{(c+s_i)}^{-b+1},\hfill \\ {\pi }_{SC,\alpha }^{★ind}={\mathsf{\Phi }}_{\alpha }g{b}^{-2b}{(b-1)}^{2b-2}(2b-1){(c+s_i)}^{-b+1},\hfill \end{array}\right.$$

where ${\pi }_{S_i,\alpha }^{★ind}$, ${\pi }_{R,\alpha }^{★ind}$, ${\pi }_{SC,\alpha }^{★ind}$ are respectively, the SP’s optimal profit, the SI’s optimal profit, and the total supply chain profit for the decentralized case.

By comparing ${\pi }_{SC,\alpha }^{★}$ and ${\pi }_{SC,\alpha }^{★ind}$, we find that $\frac{{\pi }_{SC,\alpha }^{★}}{{\pi }_{SC,\alpha }^{★ind}}=\frac{b^b}{{(b-1)}^{b-1}(2b-1)}>1$. As a consequence of Lemma 3, the total supply chain profit cannot achieve the system optimums. Therefore, designing the supply chain coordination mechanism becomes particularly important. On the other hand, it should be noted that, in the channel coordination, the SI possesses the total profit of the supply chain system–in other words, the SP has no profit. Although the supply chain optimum is achieved, the SP has no incentive to cooperate with the SI because of no profit. Consequently, it is quite necessary to design an effective supply chain coordination mechanism to ensure the efficient operation of the entire supply chain.

3.2. Two-Part Contract Auction with Symmetric Information

In this subsection, we define a two-part contract auction as follows, also illustrated in Figure 1.

(1)

The SI announces an order quantity function and a service price function

$$q={\mathsf{\Phi }}_{\alpha }g{(c+w)}^{-b},r=c+w.$$

(3)

(2)

Given that reservation profit $k_{S_i}$ respectively, each SP in the two-part contract proposes a wholesale price $w_i^{★}$ and a side payment $L_i^{★}$ to the SI.

(3)

The SI selects the more profitable contract and then makes decisions on its order quantity and service price.

Likewise, we use $w_i^{★tca}$, $r_{R,\alpha }^{★tca}$, $q_{R,\alpha }^{★tca}$, ${\pi }_{R,\alpha }^{★tca}$, ${\pi }_{S_i,\alpha }^{★tca}$, ${\pi }_{SC,\alpha }^{★tca}$ to denote the optimal wholesale price of the SP i, $i=l,h$, the optimal service price, the optimal quantity, the SI’s optimal profit, the SP’s optimal profit and the total supply chain profit in the two-part contract auction, respectively. Notice that both the service price function and order quantity function of the SI are related to the SP’s wholesale price. In this setting, it offers the SI more flexibility to make decisions. From the definition of q and r in Equation (3), the two SPs can determine the wholesale price by solving the problem as follows

$$\underset{w}{max}{\pi }_{S_i,\alpha }=(w_i-s_i){\mathsf{\Phi }}_{\alpha }g{(c+w_i)}^{-b},i=l,h.$$

As mentioned above, the optimal wholesale price of the SP is

$$w_i^{★tca}=\frac{c+b{s}_i}{b-1},i=l,h$$

For the SP’s reservation profit $k_{s_i}(i=l,h)$, only when the profit that the SP gets from the contract is greater than its reservation profit, the SP will accept the contract and cooperate with the SI, otherwise, they will not.

Proposition 1.

For the symmetric information case, the profit of the total supply chain under a two-part contract auction is the same as the one in channel coordination optimum.

A nice consequence of Proposition 1 is that the two-part contract auction guarantees the channel coordination optimum in a symmetric information scenario.

Proposition 2.

For any given $k_{S_i}={\mathsf{\Phi }}_{\alpha }g{b}^{-2b}{(b-1)}^{2b-1}{(c+s_i)}^{-b+1}$, which is the profit of the SP $i=l,h$ in decentralized case, each SP’s profit under the two-part contract auction ${\pi }_{S_i,\alpha }^{★tca}$ is always greater than that in decentralized case.

From Proposition 2, compared with the decentralized case, the SP’s profit in the two-part contract auction can be improved. Therefore, both of them have an incentive to participate in the designed auction mechanism. Combining Propositions 1 and 2 yields the following Parato improvement conditions.

Proposition 3.

For the SI’s profit under the two-part contract auction, it holds that

(1) 

If the SI cooperates with the high-cost SP, then the SI’s profit under two-part contract auction is greater than that in the decentralized case provided that

$$k_{S_l}<{\mathsf{\Phi }}_{\alpha }g{b}^{-b}{(b-1)}^{b-1}[{(c+s_l)}^{-b+1}-{(\frac{b-1}{b})}^{b-1}{(c+s_h)}^{-b+1}];$$

(2) 

If the SI cooperates with the low-cost SP, then the SI’s profit under two-part contract auction is greater than that in the decentralized case provided that

$$k_{S_h}<{\mathsf{\Phi }}_{\alpha }g{b}^{-b}{(b-1)}^{b-1}[{(c+s_h)}^{-b+1}-{(\frac{b-1}{b})}^{b-1}{(c+s_l)}^{-b+1}];$$

(3) 

For the case

$$k_{S_i}={\mathsf{\Phi }}_{\alpha }g{b}^{-2b}{(b-1)}^{2b-1}{(c+s_i)}^{-b+1},i=l,h$$

if the SI cooperates with the low-cost SP, the SI’s profit under two-part contract auction is greater than that in the decentralized case provided that

$$\frac{{(c+s_h)}^{-b+1}}{{(c+s_l)}^{-b+1}}<\frac{1-{(\frac{b-1}{b})}^b}{{(\frac{b-1}{b})}^{b-1}};$$

if the SI cooperates with the low-cost SP, the SI’s profit under two-part contract auction is greater than that in the decentralized case provided that

$$\frac{{(c+s_l)}^{-b+1}}{{(c+s_h)}^{-b+1}}<\frac{1-{(\frac{b-1}{b})}^b}{{(\frac{b-1}{b})}^{b-1}}.$$

Proposition 3 clearly characterizes Pareto improvement conditions in which every participant’s profit can be improved under the two-part contract auction strategy in comparison with that in the decentralized case. Therefore, both of them have an incentive to voluntarily participate in this auction mechanism.

4. Supply Chain System with Asymmetric Information

4.1. Supply Chain Coordination Model with Asymmetric Information

In this section, we focus on the case where the SPs hold asymmetric cost $s_i$. The SI assumes that the two SPs’ marginal costs both follow a uniform distribution on the interval $[\overline{s}-\epsilon ,\overline{s}+\epsilon ]$ and have a prior probability density function $g\left(s\right)$ and a cumulative distribution function $G\left(s\right)$, where $\epsilon$ denotes cost variation.

Similar to the discussion in Section 3, let ${\tilde{q}}_{R,\alpha }^{★}$, ${\tilde{r}}_{R,\alpha }^{★}$ and ${\tilde{\pi }}_{SC,\alpha }^{★}$ be the optimal order quantity, optimal service price and optimal expected profit of the supply chain system in the asymmetric case.

Lemma 4.

In the asymmetric information case,

(1) 

when the low-cost SP wins the contract, the expected optimal service price, order quantity, and profit of the entire supply chain are

$$\begin{array}{ccccc}& & \hfill E[{\tilde{r}}_{R,\alpha }^{★}]& =\frac{b}{b-1}[c+2{\int }_{\overline{s}-\epsilon }^{\overline{s}+\epsilon }s(1-G\left(s\right))g\left(s\right)ds]\hfill & \end{array}$$

(4)

$$\begin{array}{cccc}& & \hfill E[{\tilde{q}}_{R,\alpha }^{★}]& =2{\mathsf{\Phi }}_{\alpha }g{b}^{-b-1}{(b-1)}^b{\int }_{\overline{s}-\epsilon }^{\overline{s}+\epsilon }{s}^{-\frac{1}{b}}(1-G(s^{-\frac{1}{b}}-c))g(s^{-\frac{1}{b}}-c)ds\hfill \end{array}$$

(5)

$$E[{\tilde{\pi }}_{SC,\alpha }^{★}]=2{\mathsf{\Phi }}_{\alpha }g{b}^{-b-1}{(b-1)}^{b-2}{\int }_{\overline{s}-\epsilon }^{\overline{s}+\epsilon }{s}^{-\frac{1}{b-1}}(1-G(s^{-\frac{1}{b-1}}-c))g(s^{-\frac{1}{b-1}}-c)ds$$

(6)

(2) 

when the high-cost SP wins the contract, the expected optimal service price, order quantity, and profit of the entire supply chain are

$$\begin{array}{ccccc}& & \hfill E[{\tilde{r}}_{R,\alpha }^{★}]& =\frac{b}{b-1}[c+2{\int }_{\overline{s}-\epsilon }^{\overline{s}+\epsilon }sG\left(s\right)g\left(s\right)ds]\hfill & \end{array}$$

(7)

$$\begin{array}{ccccc}& & \hfill E[{\tilde{q}}_{R,\alpha }^{★}]& =2{\mathsf{\Phi }}_{\alpha }g{b}^{-b-1}{(b-1)}^b{\int }_{\overline{s}-\epsilon }^{\overline{s}+\epsilon }{s}^{-\frac{1}{b}}G(s^{-\frac{1}{b}}-c)g(s^{-\frac{1}{b}}-c)ds\hfill & \end{array}$$

(8)

$$\begin{array}{cccc}& & \hfill E[{\tilde{\pi }}_{SC,\alpha }^{★}]& =2{\mathsf{\Phi }}_{\alpha }g{b}^{-b-1}{(b-1)}^{b-2}{\int }_{\overline{s}-\epsilon }^{\overline{s}+\epsilon }{s}^{-\frac{1}{b-1}}G(s^{-\frac{1}{b-1}}-c)g(s^{-\frac{1}{b-1}}-c)ds\hfill \end{array}$$

(9)

4.2. Two-Part Contract Auction with Asymmetric Information Case

Now, we introduce the two-part auction mechanism for asymmetric information cases so as to achieve channel coordination optimums.

(1)

An order quantity function and a service price function w.r.t. wholesale price w announced by the SI as follows:

$$q={\mathsf{\Phi }}_{\alpha }g{(\widehat{k}+w)}^{-b},r=\widehat{k}+w,$$

where $\widehat{k}$ is an unknown parameter decided by the channel system.

(2)

The SPs compete in this two-part contract auction, in which each of them proposes a wholesale price of $w_i^{★}$ and a side payment of $L_i^{★}$ to the SI.

(3)

The SI chooses the more profitable contract and determines the order quantity and service price on $w_i^{★}$.

If the low-cost SP wins the auction, one needs to determine the optimal wholesale price by solving the following optimization

$$\underset{w}{max}{\pi }_{S_l,\alpha }=(w-min(s_l,s_h)){\mathsf{\Phi }}_{\alpha }g{(\widehat{k}+w)}^{-b}.$$

There exists a unique optimal wholesale price

$$w_l^{★tca}=\frac{\widehat{k}+bmin(s_l,s_h)}{b-1},$$

and hence

$$\begin{array}{c}{\widehat{q}}_{R,\alpha }^{★tca}={\mathsf{\Phi }}_{\alpha }g{b}^{-b}{(b-1)}^b{(\widehat{k}+min(s_l,s_h))}^{-b},\hfill \\ {\widehat{r}}_{R,\alpha }^{★tca}=\frac{b}{b-1}(\widehat{k}+min(s_l,s_h)),\hfill \end{array}$$

where ${\tilde{r}}_{R,\alpha }^{★}$, ${\tilde{q}}_{R,\alpha }^{★}$ and ${\tilde{\pi }}_{SC,\alpha }^{★}$ denote the optimal service price, order quantity and profit of the supply chain under two-part asymmetric information case.

Lemma 5.

There may not exist any other values but $\widehat{k}=c$ which can improve the total supply chain profit.

Lemma 5 implies that the best choice of the parameter $\widehat{k}=c$, from the viewpoint of improving the system efficiency, which shows that, under the two-part auction setting, the SI’s profit completely comes from the SP’s side payment.

Proposition 4.

For asymmetric information cases, the supply chain can achieve coordination in a two-part contract auction.

Likewise, Proposition 4 shows that for asymmetric service cost information, channel coordination can be achieved in the two-part contract auction as well.

Proposition 5.

For any given $k_{S_i}={\mathsf{\Phi }}_{\alpha }g{b}^{-2b}{(b-1)}^{2b-1}{(c+E[s_i])}^{-b+1},i=l,h$, which is the profit of the SP obtained in the decentralized case, the SP’s expected profit in this two-part contract auction is more than that in decentralized case.

Proposition 5 shows us, in contrast to the decentralized case, the SP has an incentive to join the two-part contracting auction. In practice, to stimulate every participant’s incentive to join the two-part contract, we need to explicitly clarify the Pareto improvement conditions.

Proposition 6.

For the SI’s profit in a two-part contract auction, it holds that

(1) 

If the SI cooperates with the high-cost SP, then the SI’s profit under two-part contract auction is greater than that in the decentralized case provided that

$$\begin{array}{cc}\hfill k_{S_l}<& 2{\mathsf{\Phi }}_{\alpha }g{b}^{-b}{(b-1)}^{b-2}[{\int }_{\overline{s}-\epsilon }^{\overline{s}+\epsilon }{s}^{-\frac{1}{b-1}}(1-G(s^{-\frac{1}{b-1}}-c))g(s^{-\frac{1}{b-1}}-c)ds-\hfill \\ & {(\frac{b-1}{b})}^{b-1}{\int }_{\overline{s}-\epsilon }^{\overline{s}+\epsilon }{s}^{-\frac{1}{b-1}}G(s^{-\frac{1}{b-1}}-c)g(s^{-\frac{1}{b-1}}-c)ds].\hfill \end{array}$$

(2) 

If the SI cooperates with the low-cost SP, then the SI’s profit under two-part contract auction is greater than that in the decentralized case provided that

$$\begin{array}{cc}\hfill k_{S_h}<& 2{\mathsf{\Phi }}_{\alpha }g{b}^{-b}{(b-1)}^{2b-2}[{\int }_{\overline{s}-\epsilon }^{\overline{s}+\epsilon }{s}^{-\frac{1}{b-1}}(1-G(s^{-\frac{1}{b-1}}-c))g(s^{-\frac{1}{b-1}}-c)ds-\hfill \\ & {(\frac{b-1}{b})}^{b-1}{\int }_{\overline{s}-\epsilon }^{\overline{s}+\epsilon }{s}^{-\frac{1}{b-1}}G(s^{-\frac{1}{b-1}}-c)g(s^{-\frac{1}{b-1}}-c)ds].\hfill \end{array}$$

(3) 

Specially, for the case that

$$k_{S_l}=2{\mathsf{\Phi }}_{\alpha }g{b}^{-2b}{(b-1)}^{2b-2}{\int }_{\overline{s}-\epsilon }^{\overline{s}+\epsilon }{s}^{-\frac{1}{b-1}}(1-G(s^{-\frac{1}{b-1}}-c))g(s^{-\frac{1}{b-1}}-c)ds,$$

which is the profit of the low-cost SP in the decentralized case. The SI’s profit under two-part contract auction is greater than that in the decentralized case if and only if

$$\frac{{\int }_{\overline{s}-\epsilon }^{\overline{s}+\epsilon }{s}^{-\frac{1}{b-1}}G(s^{-\frac{1}{b-1}}-c)g(s^{-\frac{1}{b-1}}-c)ds}{{\int }_{\overline{s}-\epsilon }^{\overline{s}+\epsilon }{s}^{-\frac{1}{b-1}}(1-G(s^{-\frac{1}{b-1}}-c))g(s^{-\frac{1}{b-1}}-c)ds}<\frac{1-{(\frac{b-1}{b})}^b}{{(\frac{b-1}{b})}^{b-1}}.$$

For the case that

$$k_{S_h}=2{\mathsf{\Phi }}_{\alpha }g{b}^{-2b}{(b-1)}^{2b-2}{\int }_{\overline{s}-\epsilon }^{\overline{s}+\epsilon }{s}^{-\frac{1}{b-1}}G(s^{-\frac{1}{b-1}}-c)g(s^{-\frac{1}{b-1}}-c)ds,$$

which is the profit of the high-cost SP in the decentralized case. The SI’s profit under two-part contract auction is greater than that in the decentralized case if and only if

$$\frac{{\int }_{\overline{s}-\epsilon }^{\overline{s}+\epsilon }{s}^{-\frac{1}{b-1}}(1-G(s^{-\frac{1}{b-1}}-c))g(s^{-\frac{1}{b-1}}-c)ds}{{\int }_{\overline{s}-\epsilon }^{\overline{s}+\epsilon }{s}^{-\frac{1}{b-1}}G(s^{-\frac{1}{b-1}}-c)g(s^{-\frac{1}{b-1}}-c)ds}<\frac{1-{(\frac{b-1}{b})}^b}{{(\frac{b-1}{b})}^{b-1}}.$$

Therefore, when the above conditions hold, both the SP’s and the SI’s profit can be improved in this two-part contract auction strategy compared with the decentralized case. Therefore, both of them have an incentive to join in this contracting and auction mechanism. Note that, the formulations under the symmetric and asymmetric cases are quite different. Therefore, it is necessary to explore the impacts of the SP’s service cost variation on optimal decisions.

4.3. Value of Information

In order to explore the value of information, we compare participants’ optimal decisions and profits under both symmetric and asymmetric information cases and analyze the difference between different cases.

Proposition 7.

Suppose the low-cost SP wins the contract, then

(a) 

for the service’s optimal decisions, it holds that

(a.1) 

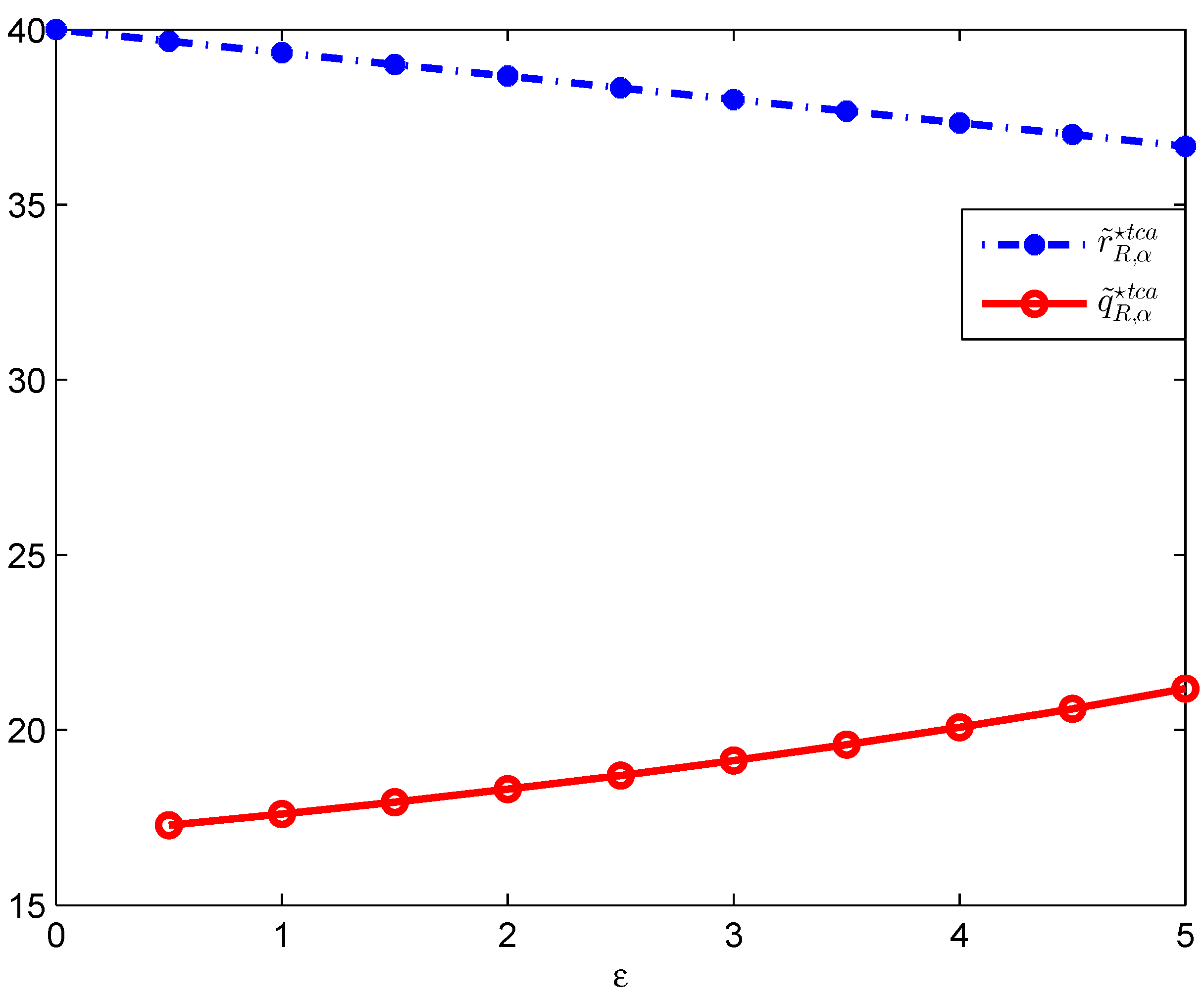
the optimal service price decreases w.r.t. the low-cost SP’s cost variation (ε);

(a.2) 

the optimal order quantity increases w.r.t. the low-cost SP’s cost variation (ε);

(a.3) 

the greater the level of the low-cost SP’s cost variation, the larger the difference of service prices under information symmetry and information asymmetry cases;

(a.4) 

the greater the level of the low-cost SP’s cost variation, the smaller the difference of the optimal order quantity under both symmetric and asymmetric information cases.

(b) 

For the SI’s profit, it holds that

(b.1) 

the SI’s profit decreases with the low-cost SP’s cost variation (ε);

(b.2) 

the greater the level of the low-cost SP’s cost variation, the larger the difference of the SI’s profits under both symmetric and asymmetric information cases.

(c) 

For the low-cost SP’s profit, it holds that

(c.1) 

the low-cost SP’s profit increases with its own cost variation (ε);

(c.2) 

the greater the level of the low-cost SP’s cost variation, the smaller the difference between the low-cost SP’s profit under both symmetric and asymmetric information cases;

(d) 

and for the supply chain’s profit, it holds that

(d.1) 

the supply chain’s profit increases with the low-cost SP’s cost variation (ε);

(d.2) 

the greater the level of the low-cost SP’s cost variation, the smaller the difference in the supply chain’s profit under both symmetric and asymmetric information cases.

For ease of exposition, we can use a table to clearly illustrate the results of Proposition 7.

Proposition 8.

When the high-cost SP wins the contract,

(a) 

for the service’s optimal decisions we have that

(a.1) 

the optimal service price increases with the high-cost SP’s cost variation (ε);

(a.2) 

the optimal order quantity decreases with the high-cost SP’s cost variation (ε);

(a.3) 

the greater the level of the high-cost SP’s cost variation (large ε), the smaller the difference of the service price under both symmetric and asymmetric information cases (two cases for short).

(a.4) 

the greater the level of the high-cost SP’s cost variation (large ε), the larger the difference of the optimal order quantity under two cases.

(b) 

for the SI’s profit we have that

(b.1) 

the SI’s profit increases with the high-cost SP’s cost variation (ε);

(b.2) 

the greater the level of the high-cost SP’s cost variation (large ε), the smaller the difference of the SI’s profit under two cases.

(c) 

for the low-cost SP’s profit we have that

(c.1) 

the low-cost SP’s profit decreases with its own cost variation (ε);

(c.2) 

the greater the level of the high-cost SP’s cost variation (large ε), the larger the difference of the low-cost SP’s profit under two cases.

(d) 

for the supply chain’s profit we have that

(d.1) 

the supply chain’s profit decreases with the high-cost SP’s cost variation (ε);

(d.2) 

the greater the level of the high-cost SP’s cost variation (large ε), the larger the difference of the supply chain’s profit under two cases.

Likewise, for ease of exposition, we can use a table to clearly illustrate the results of Proposition 8.

Observing from

Table 2. Results of Proposition 7 “↑” increasing; “↓” decreasing.

	${\tilde{r}}_{R,\alpha }^{★tca}$	${\tilde{q}}_{R,\alpha }^{★tca}$	$E[{\tilde{\pi }}_{R,\alpha }^{★tca}]$	$E[{\tilde{\pi }}_{S_i,\alpha }^{★tca}]$	$E[{\tilde{\pi }}_{SC,\alpha }^{★tca}]$
$\epsilon \uparrow$	↓	↑	↓	↑	↑
	$\mathsf{\Delta }{\tilde{r}}_{R,\alpha }^{★tca}$	$\mathsf{\Delta }{\tilde{q}}_{R,\alpha }^{★tca}$	$\mathsf{\Delta }E[{\tilde{\pi }}_{R,\alpha }^{★tca}]$	$\mathsf{\Delta }E[{\tilde{\pi }}_{S_i,\alpha }^{★tca}]$	$\mathsf{\Delta }E[{\tilde{\pi }}_{SC,\alpha }^{★tca}]$
$\epsilon \uparrow$	↑	↓	↑	↓	↓

and

Table 3. Results of Proposition 8 “↑” increasing; “↓” decreasing.

	${\tilde{r}}_{R,\alpha }^{★tca}$	${\tilde{q}}_{R,\alpha }^{★tca}$	$E[{\tilde{\pi }}_{R,\alpha }^{★tca}]$	$E[{\tilde{\pi }}_{S_i,\alpha }^{★tca}]$	$E[{\tilde{\pi }}_{SC,\alpha }^{★tca}]$
$\epsilon \uparrow$	↑	↓	↑	↓	↓
	$\mathsf{\Delta }{\tilde{r}}_{R,\alpha }^{★tca}$	$\mathsf{\Delta }{\tilde{q}}_{R,\alpha }^{★tca}$	$\mathsf{\Delta }E[{\tilde{\pi }}_{R,\alpha }^{★tca}]$	$\mathsf{\Delta }E[{\tilde{\pi }}_{S_i,\alpha }^{★tca}]$	$\mathsf{\Delta }E[{\tilde{\pi }}_{SC,\alpha }^{★tca}]$
$\epsilon \uparrow$	↓	↑	↓	↑	↑

, we find that information asymmetry benefits the low-cost SP, however, the SI may be worse off without the SP’s full cost information. On the contrary, information asymmetry benefits SI when the high-cost SP wins the contract, but the high-cost SP may be worse off if encountered with high cost variation. Therefore, the high-cost SP is always motivated to truthfully announce rather than distort his exact cost information. This conclusion is somewhat similar to separate equilibrium in a signal game.

5. The Case with a Risk Neutral SI

In this section, we consider the optimal service price, the optimal order quantity, and supply chain profits when the participants are all risk-neutral. The relationship between the risk-neutral agent case and at least one risk-averse agent case will also be explored.

In the risk-neutral agent system, facing the announced wholesale price, the SI needs to solve the following optimization to determine his optimal service price and order quantity

$$\underset{r>c,q\ge 0}{max}E[{\Pi }_R(r,q)]$$

where,

$$\begin{array}{ccc}\hfill E[{\Pi }_R(r,q)]& =& \begin{array}{c}rE[min(g{r}^{-b}x,q)]-(c+w)q\hfill \end{array}\hfill \\ & =& \begin{array}{c}r[q(1-F(\frac{q}{g}{r}^b))+{\int }_0^{\frac{q}{g}{r}^b}(g{r}^{-b}x)f(x)dx]-(c+w)q\hfill \end{array}\hfill \\ & =& \begin{array}{c}r[q(1-F(\frac{q}{g}{r}^b))+g{r}^{-b}(\frac{q}{g}{r}^{b}F(\frac{q}{g}{r}^b))-{\int }_0^{\frac{q}{g}{r}^b}F(x)dx]-(c+w)q\hfill \end{array}\hfill \\ & =& \begin{array}{c}r(q-g{r}^{-b}{\int }_0^{\frac{q}{g}{r}^b}F(x)dx)-(c+w)q.\hfill \end{array}\hfill \end{array}$$

Thus

$$E[{\Pi }_{SC}(r,q)]=r(q-g{r}^{-b}{\int }_0^{\frac{q}{g}{r}^b}F(x)dx)-(c+s)q.$$

Differentiate $E[{\Pi }_{SC}(r,q)]$ w.r.t. q and r, and denote $\frac{dE[{\Pi }_{SC}(r,q)]}{dq}=\frac{dE[{\Pi }_{SC}(r,q)]}{dr}=0$, which yields the optimal values $q_N^{★}$ and $r_N^{★}$, where

$$q_N^{★}=g{(r_N^{★})}^{-b}{F}^{-1}(\frac{r_N^{★}-c-s}{r_N^{★}})$$

(10)

$$(b-1)g{(r_N^{★})}^{-b}{\int }_0^{F^{-1}(\frac{r_N^{★}-c-s}{r_N^{★}})}F(x)dx+q_N^{★}(1-b(\frac{r_N^{★}-c-s}{r_N^{★}}))=0,$$

(11)

From which we can obtain

$$(b-1){\int }_0^{F^{-1}(\frac{r_N^{★}-c-s}{r_N^{★}})}F(x)dx+F^{-1}(\frac{r_N^{★}-c-s}{r_N^{★}})(1-b(\frac{r_N^{★}-c-s}{r_N^{★}}))=0.$$

Let $SL(r)=\frac{r-c-s}{r},\alpha =1-SL(r_N^{★})$. Then

$$F^{-1}(\frac{r_N^{★}-c-s}{r_N^{★}})=F^{-1}(1-\alpha )={\mathsf{\Phi }}_{\alpha }.$$

The following theorem illustrates the relationship between service prices and order quantities in agents’ risk-neutral cases and risk-averse cases.

Proposition 9.

For any $0<\alpha <1$, it holds that $r_{\alpha }^{★}\le r_N^{★}$ and $q_{\alpha }^{★}\ge q_N^{★}$.

Note that even though we are unable to obtain a closed-form expression of the optimal order quantity and optimal service price in the risk-neutral SI case, Proposition 9 theoretically proves the relationship between the optimal service price and optimal order quantity between the cases with a risk-neutral and a risk-averse SI, respectively. To be specific, Proposition 9 shows that a risk-averse SI tends to set a service price higher than that set by a risk-neutral SI and induce a lower order quantity than that induced by a risk-neutral SI, which accounts for how decisions might adapt with respect to the degree of risk aversion. This is an important and neat analytical result.

6. Numerical Examples and Illustrations

In order to verify the efficiency of the obtained results, we take a numerical experiment on some practical industrial productions. We assume that Foxconn and Quanta are two competing manufacturing service SPs for the SI Apply Company, which plays the role of an SI. As stated in literature (Mathewson and Winter [38], Gans and King [39]), pricing power endows the SI first mover advantage. The exponential and stochastic demand function is shown as follows:

$$D_d=g{r}^{-b}x,g>0,b>1.$$

For the parameters involved in the model, we take g = 10,000, $b=2$, $\epsilon =5$, low-cost and high-cost are denoted as $s_l$ and $s_h$, respectively, $10\le s_l$, $s_h\le 20$. The reservation profits of the SPs are $k_{S_l}$, $k_{s_h}$ respectively, $200\le k_{S_l}\le 500$, $100\le k_{S_h}\le 400$.

To test the effect of the SP costs on the optimal order quantity, the optimal service price, and the profits of the supply chain under a different situation, $\lambda =1$. the probability density function and the cumulative distribution function of x are respectively

$$f_1(x)=e^{-x},x\ge 0,F_1(x)=1-e^{-x},x\ge 0.$$

Hence $F_1^{-1}(\alpha )=-ln(1-x)$, and

$${\mathsf{\Phi }}_{1,\alpha }=F_1^{-1}(\alpha )=-ln(1-\alpha )$$

Next, we assume that the variable representing the disturbance in the demand $D_d$ follows a normal distribution with $\mu =4$ and variance ${\sigma }^2=1$. In other words, the probability density function and the cumulative distribution function of x are

$$f_2(x)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{{(x-4)}^2}{2}}$$

$$F_2(x)={\int }_{-\infty }^x\frac{1}{\sqrt{2\pi }}{e}^{-\frac{{(y-4)}^2}{2}}dy={\int }_{-\infty }^{x-4}\frac{1}{\sqrt{2\pi }}{e}^{-\frac{y^2}{2}}dy$$

respectively. Hence ${\mathsf{\Phi }}_{2,\alpha }$ is defined by

$${\mathsf{\Phi }}_{2,\alpha }=F_2^{-1}(1-\alpha )$$

Thus ${\int }_{-\infty }^{{\mathsf{\Phi }}_{2,\alpha }}\frac{1}{\sqrt{2\pi }}{e}^{-\frac{y^2}{2}}dy=\alpha$. We divide the SI’s risk preferences into three cases (i) $\alpha =0.9$, (ii) $\alpha =0.95$, (iii) $\alpha =0.99$.

6.1. Comparisons of Optimal Decisions under the Symmetric and Asymmetric Information Cases

In the case of symmetric information, we assume that the service costs of the SPs $s_i,i=l,h$ is either 10 or 15, the SI knows that the service costs of the SPs follow a uniform distribution on the interval $[10,20]$ and thus, the expected cost $E[s_i]$ is 15. The probability density function and the cumulative distribution function of $s_i$ are

$$g(s)=\left\{\begin{array}{c}0.1,10\le s\le 20,\hfill \\ 0,\mathrm{otherwise},\hfill \end{array}\right.G(s)=\left\{\begin{array}{c}0,0\le s\le 10\hfill \\ 0.1(s-10),10\le s\le 20\hfill \\ 1,s>20\hfill \end{array}\right.$$

respectively. Thus,

$$f_{min}(s)=F_{min}^{{}^{\prime }}(s)=2(1-G(s))g(s)=\left\{\begin{array}{cc}0.02(20-s),\hfill & 10\le s\le 20\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

$$f_{max}(s)=F_{max}^{{}^{\prime }}(s)=2G(s)g(s)=\left\{\begin{array}{cc}0.02(s-10),\hfill & 10\le s\le 20\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

Let $q_{R,\alpha }^{★}$ and $r_{R,\alpha }^{★}$, ${\tilde{q}}_{R,\alpha }^{★}$ and ${\tilde{r}}_{R,\alpha }^{★}$ denote the optimal order quantity and service price under the symmetric information and asymmetric information cases with risk preference. We consider two cases where the demand disturbance follows the exponential distribution and the normal distribution, respectively. When the SI cooperates with the low-cost SP, we have

$$\begin{array}{ccc}\hfill E[{\tilde{q}}_{R,\alpha }^{★}]& =& \begin{array}{c}{\mathsf{\Phi }}_{\alpha }g{b}^{-b}{(b-1)}^{b}E[{(c+min(s_l,s_h))}^{-b}]\hfill \end{array}\hfill \\ & =& \begin{array}{c}{\mathsf{\Phi }}_{\alpha }\times 10000\times 0.25\times 0.00317\hfill \end{array}\hfill \\ & =& \begin{array}{c}7.7925{\mathsf{\Phi }}_{\alpha }\hfill \end{array}\hfill \end{array}$$

$$E[{\tilde{r}}_{R,\alpha }^{★}]=\frac{110}{3}=36.67.$$

When the SI cooperates with the low-cost SP, we have

$$\begin{array}{ccc}\hfill E[{\tilde{q}}_{R,\alpha }^{★}]& =& \begin{array}{c}{\mathsf{\Phi }}_{\alpha }g{b}^{-b}{(b-1)}^{b}E[{(c+max(s_l,s_h))}^{-b}]\hfill \end{array}\hfill \\ & =& \begin{array}{c}{\mathsf{\Phi }}_{\alpha }\times 10000\times 0.25\times 0.002217\hfill \end{array}\hfill \\ & =& \begin{array}{c}5.5425{\mathsf{\Phi }}_{\alpha }\hfill \end{array}\hfill \end{array}$$

$$E[{\tilde{r}}_{R,\alpha }^{★}]=\frac{130}{3}=43.33.$$

Detail results are illustrated in

Table 4. Comparison of the optimal ordering quantities and optimal service prices obtained under the complete information and asymmetric information situations when the SI cooperates with low-cost SP (g = 10,000, $b=2$, $c=5$).

Cooperation		Demand Disturbance∼Exponential				Demand Disturbance∼Normal
with the		Symmetric		Asymmetric		Symmetric		Asymmetric
Low-Cost SP		Information		Information		Information		Information
$\mathit{\alpha }$	${\mathit{s}}_{\mathbf{1}}$	${\mathit{q}}_{\mathit{R},\mathit{\alpha }}^{★}$	${\mathit{r}}_{\mathit{R},\mathit{\alpha }}^{★}$	${\overline{\mathit{q}}}_{\mathit{R},\mathit{\alpha }}^{★}$	${\overline{\mathit{r}}}_{\mathit{R},\mathit{\alpha }}^{★}$	${\mathit{q}}_{\mathit{R},\mathit{\alpha }}^{★}$	${\mathit{r}}_{\mathit{R},\mathit{\alpha }}^{★}$	${\overline{\mathit{q}}}_{\mathit{R},\mathit{\alpha }}^{★}$	${\overline{\mathit{r}}}_{\mathit{R},\mathit{\alpha }}^{★}$
0.9	10	25.58	30.00	17.94	36.67	58.67	30.00	41.14	36.67
	12	19.92	34.00			45.67	34.00
	14	15.95	38.00			36.57	38.00
0.95	10	33.29	30.00	23.34		62.67	30.00	43.95
	12	25.91	34.00			48.79	34.00
	14	20.75	38.00			39.06	38.00
0.99	10	51.17	30.00	35.89		70.33	30.00	49.33
	12	39.84	34.00			54.76	34.00
	14	31.89	38.00			43.84	38.00

and

Table 5. Comparison of the optimal ordering quantities and optimal service prices obtained under the complete information and asymmetric information situations when the SI cooperates with high-cost SP (g = 10,000, $b=2$, $c=5$).

Cooperation		Demand Disturbance∼Exponential				Demand Disturbance∼Normal
with the		Symmetric		Asymmetric		Symmetric		Asymmetric
High-Cost SP		Information		Information		Information		Information
$\mathit{\alpha }$	${\mathit{s}}_{\mathbf{1}}$	${\mathit{q}}_{\mathit{R},\mathit{\alpha }}^{★}$	${\mathit{r}}_{\mathit{R},\mathit{\alpha }}^{★}$	${\overline{\mathit{q}}}_{\mathit{R},\mathit{\alpha }}^{★}$	${\overline{\mathit{r}}}_{\mathit{R},\mathit{\alpha }}^{★}$	${\mathit{q}}_{\mathit{R},\mathit{\alpha }}^{★}$	${\mathit{r}}_{\mathit{R},\mathit{\alpha }}^{★}$	${\overline{\mathit{q}}}_{\mathit{R},\mathit{\alpha }}^{★}$	${\overline{\mathit{r}}}_{\mathit{R},\mathit{\alpha }}^{★}$
0.9	16	13.05	42.00	12.76	43.33	29.93	42.00	29.26	43.33
	18	10.88	46.00			24.95	46.00
	20	9.21	50.00			21.12	50.00
0.95	16	16.98	42.00	16.60	43.33	31.97	42.00	31.26	43.33
	18	14.16	46.00			26.65	46.00
	20	11.98	50.00			22.56	50.00
0.99	16	26.11	42.00	25.52		35.88	42.00	35.08
	18	21.76	46.00			29.91	46.00
	20	18.42	50.00			25.32	50.00

.

6.2. The Impact of Service Cost Variation

In this section, we use a numerical example to explore the service cost variation’s effect on the SI’s optimal decisions and profit, SP’s profit, and supply chain’s profit. Thus, to compare the performances of service cost variation in this section, we use normal distribution density functions to present the demand disturbances with $\mu =4$ and variance ${\sigma }^2=1$. For the SI’s risk preference, we let $\alpha =0.9$. Then Figure 2, Figure 3, Figure 4 and Figure 5 depict the impact of parameter $\epsilon$ on the SI and the SP under the information asymmetry.

From Figure 2, Figure 3, Figure 4 and Figure 5, information asymmetry benefits SP when the low-cost SP wins the contract, but the SI may be worse off without the SP’s full cost information. To be specific, the optimal service price and the SI’s profit decrease with the low-cost SP’s cost variation, while the optimal order quantity, the low-cost SP’s profit, and the supply chain’s profit increase with the low-cost SP’s cost variation. When the high-cost SP wins the contract, the result is opposite to that when the low-cost SP wins the contract.

7. Conclusions, Practical Implications and Future Research Directions

In this study, we design the procurement auction and contracting mechanism and demonstrate it would be served as a channel coordination mechanism incorporating parties’ risk preferences and individual reservation profit and further, analytically provide new insights on the bidding and auction strategies in both symmetric information and asymmetric information, respectively. We characterize the Pareto improvement conditions and find that the high-cost SP may be worse off if encountered with high cost variation. Therefore, the high-cost SP is always motivated to truthfully announce his cost information. With risk-averse agents, we show that the obtained results have lower service prices and higher order quantity when compared with the supply chain with risk-neutral agents case.

Several important practical implications are derived from this study. (1) When the SI practitioner is engaged in service procurement from heterogeneous SPs, an appropriate auction and contracting mechanism can be employed for SP selection. Our study underscores the importance of the auction mechanism in the competitive bidding environment, as shown in the main body, which can be taken as a successful channel coordination strategy. (2) In practice, the SIs with various risk preferences have different decision-making abilities. Notably, the agents’ risk preferences are therefore important and non-negligible influencing factors in a service procurement supply chain. (3) In an asymmetric information environment, relative high-cost SP should strive for avoiding cost variation, i.e., to truthfully share exact cost information with the SI.

Our work leaves many interesting directions for future research. It would be interesting to develop a multi-period auction and contracting mechanism for multi-product service supply chain coordination. It is also an intriguing question to understand how much the production deviation cost of the two SPs differs in optimal decision-making and policy.