An Experimental Study on the Dynamic Evolution Characteristics of Soil Arching and the Rational Spacing of Anti-Slide Piles
Abstract
:1. Introduction
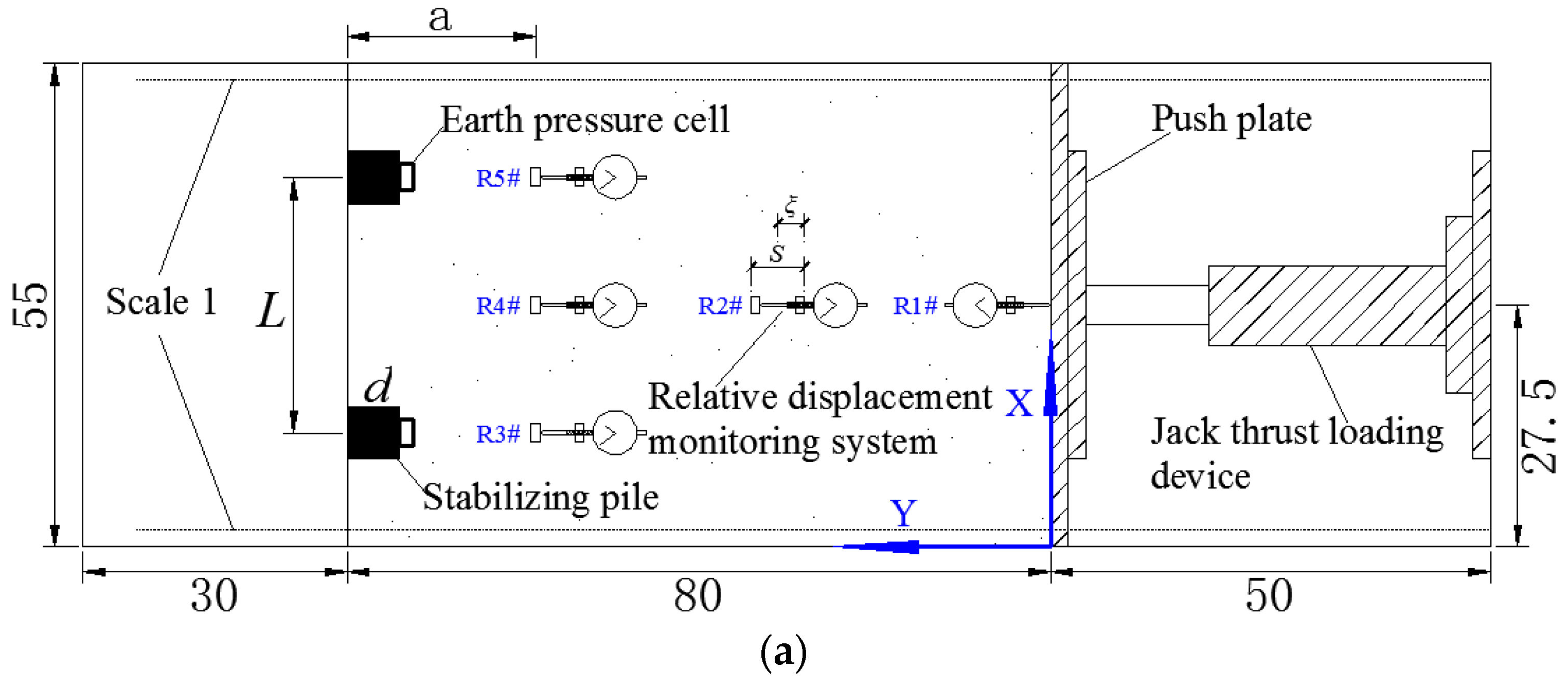
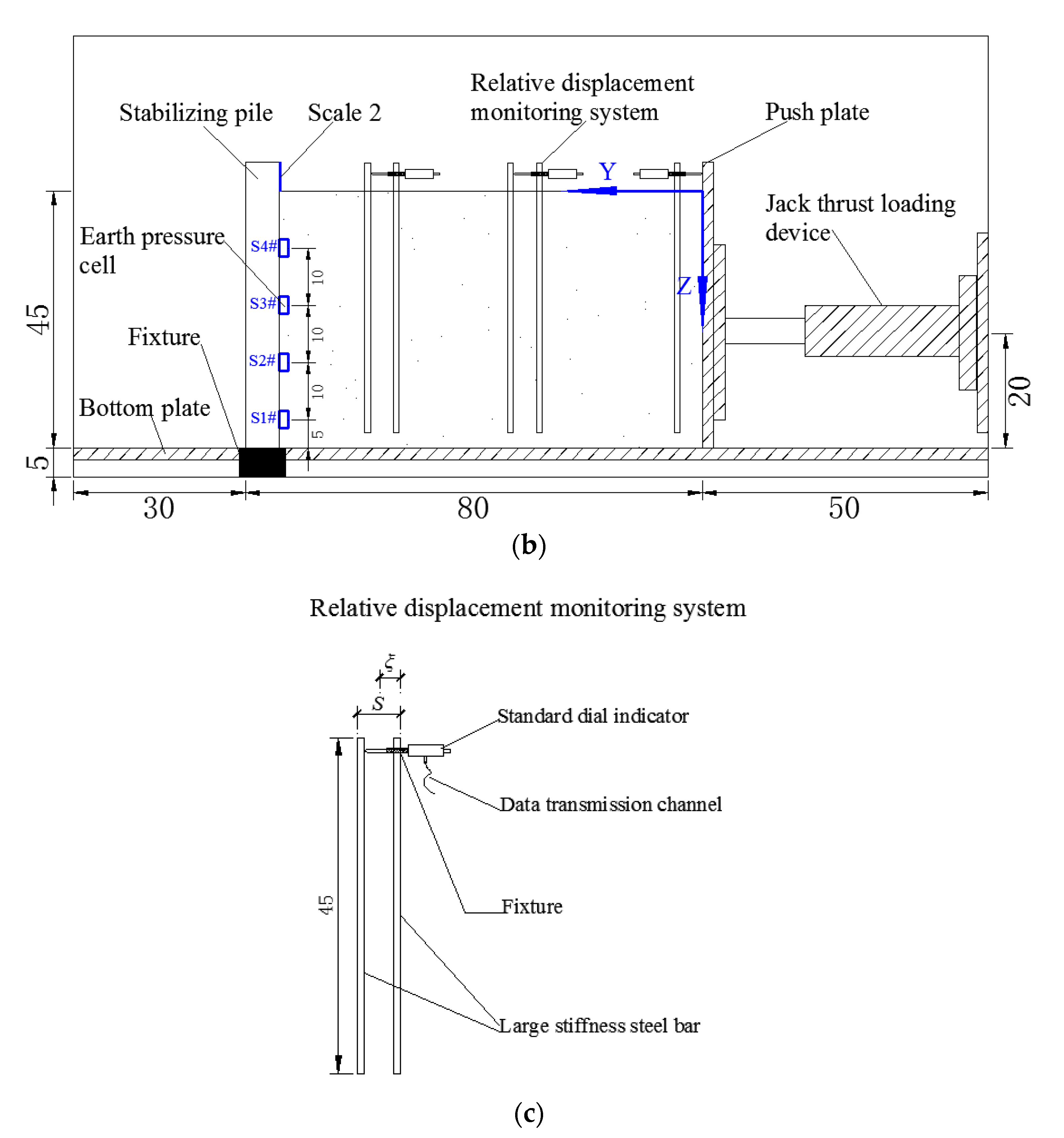
2. Laboratory Model Tests
2.1. Test Setup
2.2. Testing Material
2.3. Monitoring System
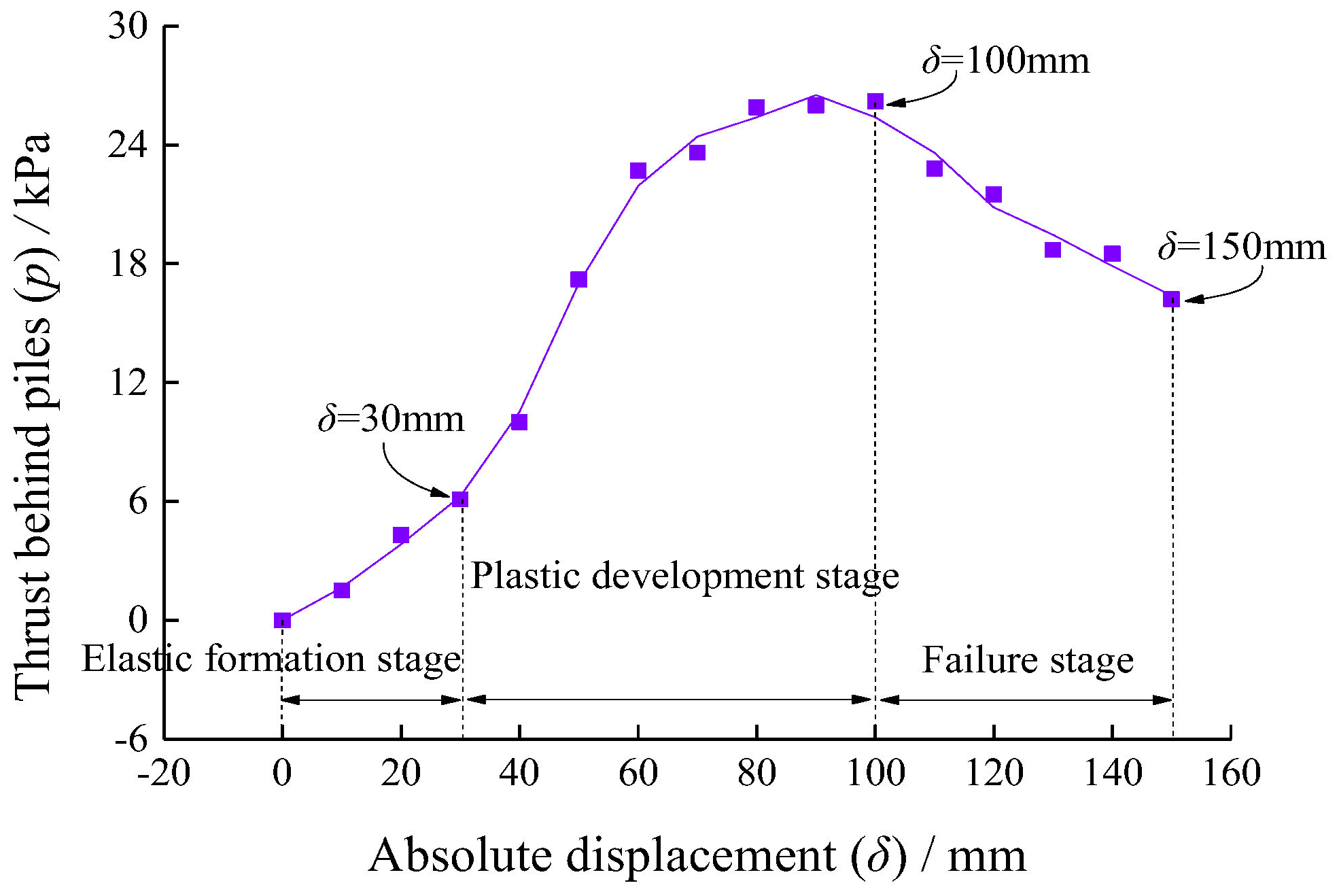
2.4. Loading Design
3. Results and Analysis
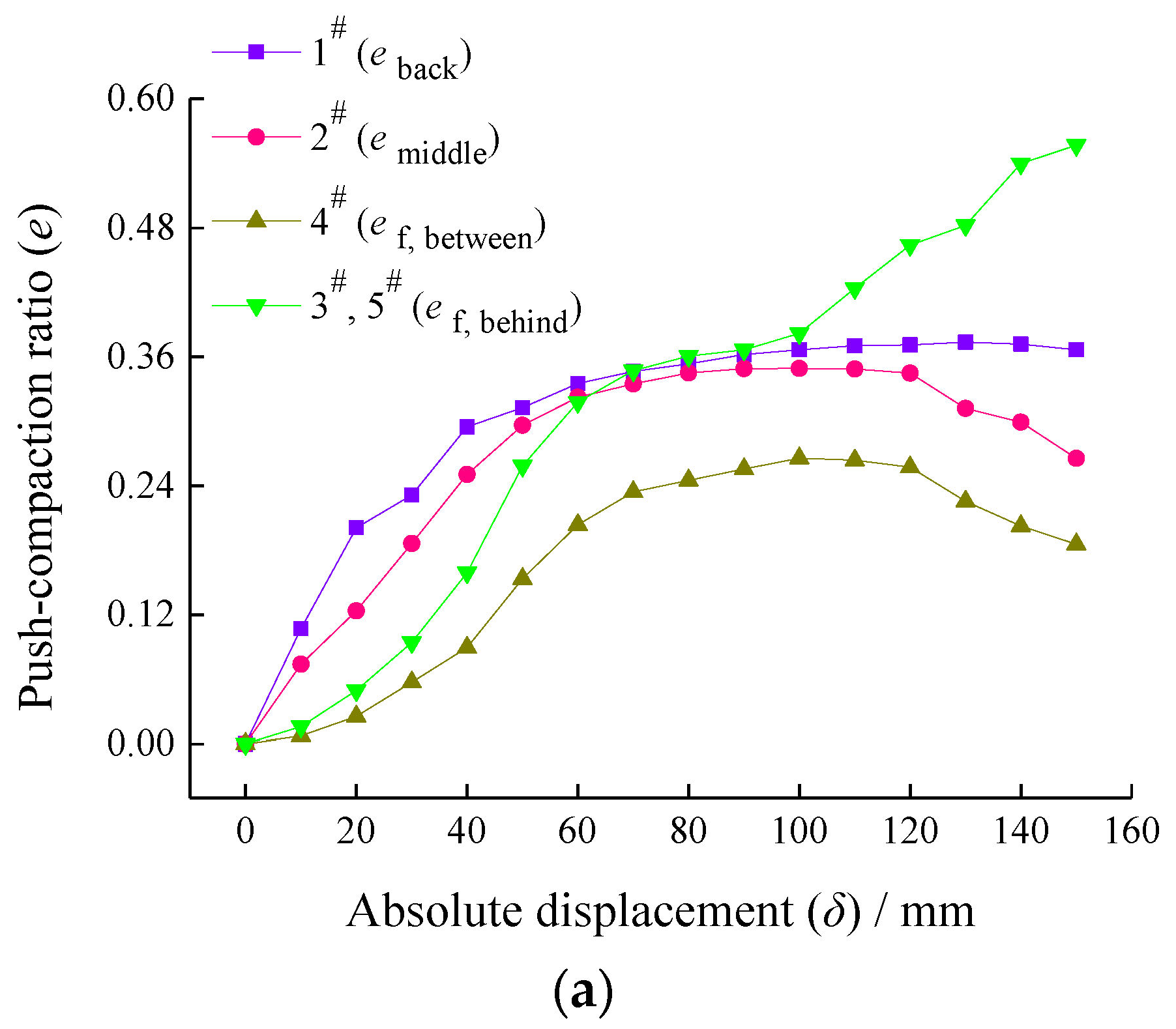
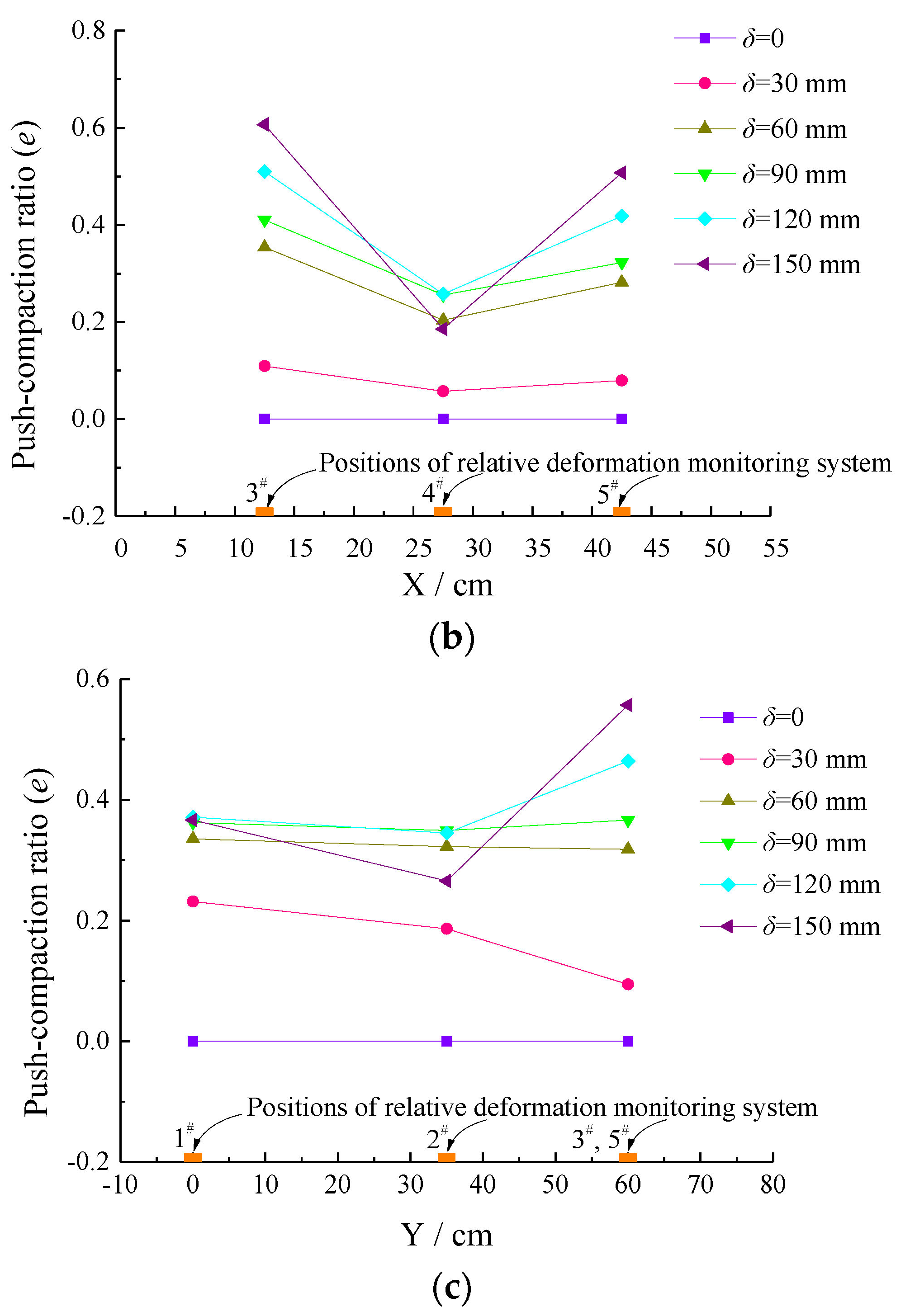
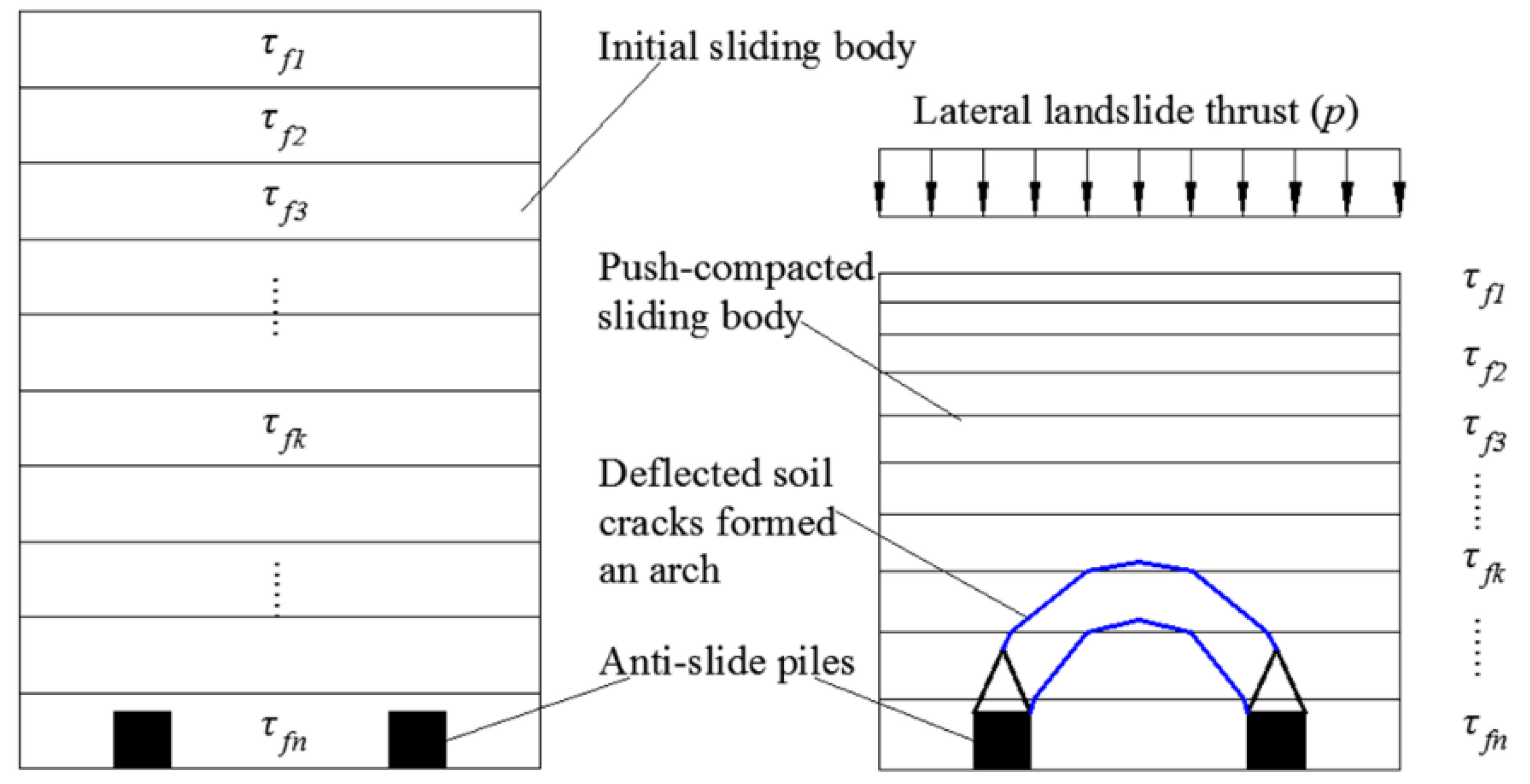
3.1. Evolution Characteristics of Soil Arching
3.2. Strengthening Effect of Shear Strength Parameters
4. Discussion
4.1. Evolution Mechanism of Soil Arching
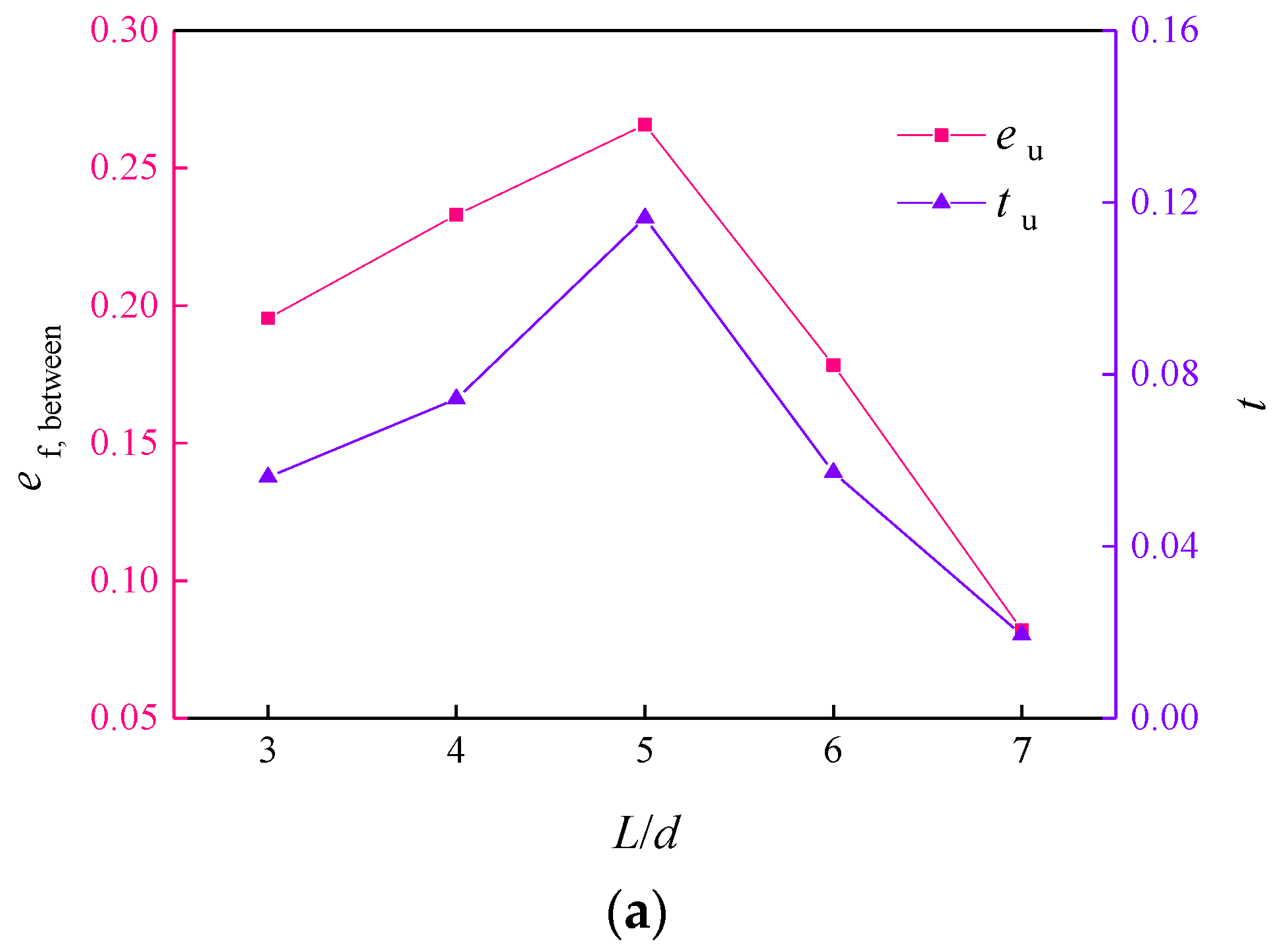
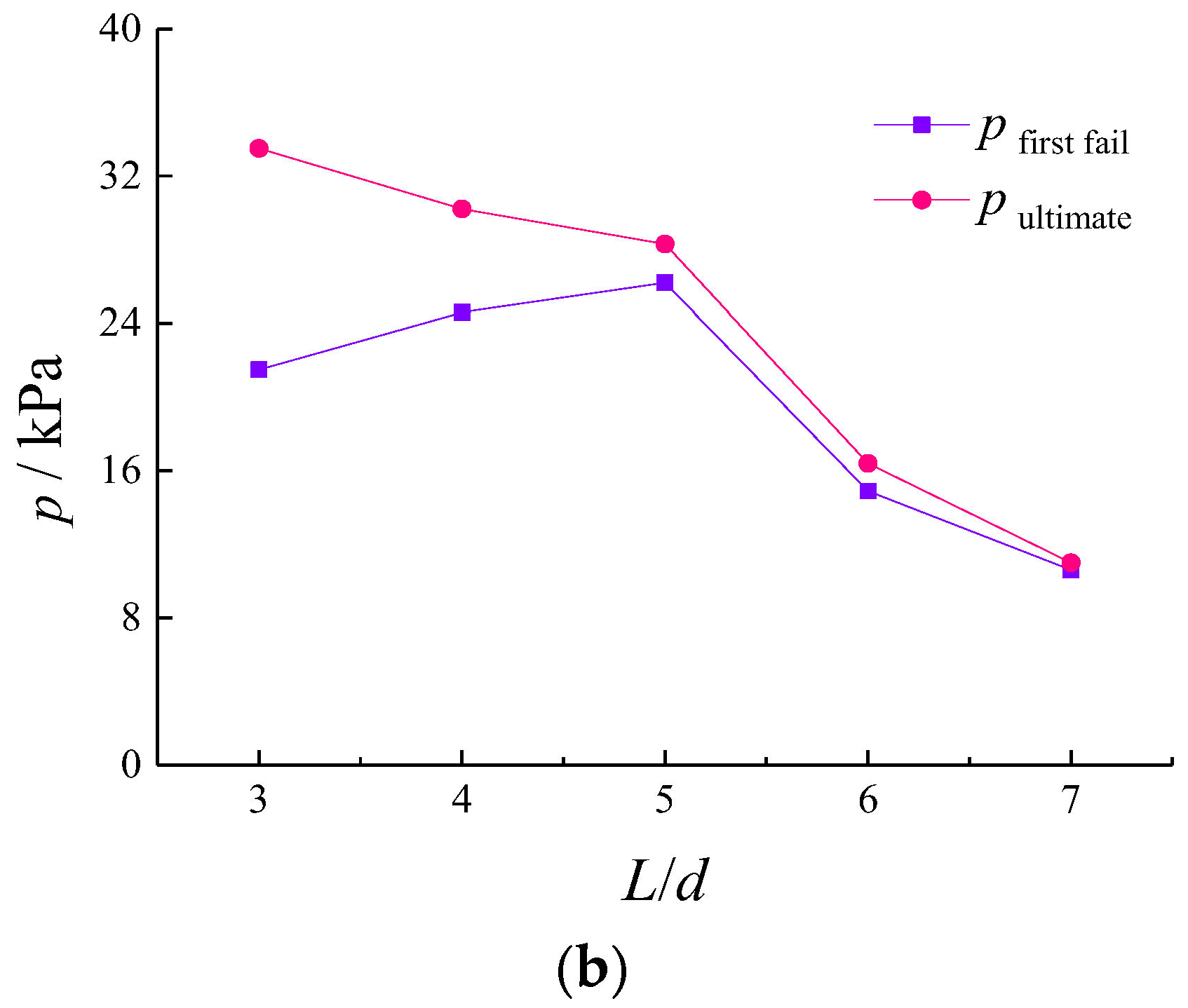
4.2. Discussion of Rational Spacing between Adjacent Piles
5. Conclusions
6. Limitations and Recommendations
Author Contributions
Funding
Conflicts of Interest
References
- Ashour, M.; Ardalan, H. Analysis of pile stabilized slopes based on soil–pile interaction. Comput. Geotech. 2012, 39, 85–97. [Google Scholar] [CrossRef]
- Bi, Z.; Gong, Q.; Guo, P.; Cheng, Q. Experimental study of the evolution of soil arching effect under cyclic loading based on trapdoor test and particle image velocimetry. Can. Geotech. J. 2020, 57, 903–920. [Google Scholar] [CrossRef]
- Cai, F.; Ugai, K. Numerical Analysis of the Stability of a Slope Reinforced with Piles. Soils Found. 2000, 40, 73–84. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.T.; Poulos, H.G.; Hull, T.S. Model tests on pile groups subjected to lateral soil movement. Soils Found. 1997, 37, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.Y.; Martin, G.K. Soil–structure interaction for landslide stabilizing piles. Comput. Geotech. 2002, 29, 363–386. [Google Scholar] [CrossRef]
- Chevalier, B.; Combe, G.; Villard, P. Load transfers and arching effects in granular soil layer. In Proceedings of the 18ème Congrès Français de Mécanique, Grenoble, France, 27–31 August 2007. [Google Scholar]
- Das, B.M. Advanced Soil Mechanics, 4th ed.; CRC Press: Boca Raton, FL, USA, 2014; pp. 403–507. [Google Scholar]
- Handy, R.L. The arch in soil arching. J. Geotech. Eng. 1985, 111, 302–318. [Google Scholar] [CrossRef]
- He, G.-F.; Li, Z.-G.; Yuan, Y.; Li, X.-H.; Hu, L.-H.; Zhang, Y. Optimization analysis of the factors affecting the soil arching effect between landslide stabilizing piles. Nat. Resour. Model. 2018, 31, e12148. [Google Scholar] [CrossRef]
- He, Y.; Hazarika, H.; Yasufuku, N.; Teng, J.; Jiang, Z.; Han, Z. Estimation of lateral force acting on piles to stabilize landslides. Nat. Hazards 2015, 79, 1981–2003. [Google Scholar] [CrossRef]
- Huang, R.Q. Some catastrophic landslides since the twentieth century in the southwest of China. Landslides 2009, 6, 69–81. [Google Scholar] [CrossRef]
- Kang, G.-C.; Song, Y.-S.; Kim, T.-H. Behavior and stability of a large-scale cut slope considering reinforcement stages. Landslides 2009, 6, 263–272. [Google Scholar] [CrossRef]
- Li, C.D.; Tang, H.M.; Hu, X.L.; Wang, L.Q. Numerical modelling study of the load sharing law of anti-sliding piles based on the soil arching effect for Erliban landslide, China. KSCE J. Civ. Eng. 2013, 17, 1251–1262. [Google Scholar] [CrossRef]
- Li, C.D.; Wu, J.J.; Tang, H.M.; Wang, J.; Chen, F.; Liang, D.M. A novel optimal plane arrangement of stabilizing piles based on soil arching effect and stability limit for 3D colluvial landslides. Eng. Geol. 2015, 195, 236–247. [Google Scholar] [CrossRef]
- Li, G.X. Advanced Soil Mechanics, 2nd ed.; Tsinghua University Press: Beijing, China, 2016; pp. 137–212. (In Chinese) [Google Scholar]
- Liang, R.; Zeng, S.P. Numerical study of soil arching mechanism in drilled shafts for slope stabilization. Soils Found. 2002, 42, 83–92. [Google Scholar] [CrossRef] [Green Version]
- Lin, Z.P.; Liu, Z.Q.; Shang, Q.T. Research on soil arch of anti-slide pile structure with methods of separation and combination. Rock Soil Mech. 2012, 33, 3109–3114. (In Chinese) [Google Scholar] [CrossRef]
- Lirer, S. Landslide stabilizing piles: Experimental evidences and numerical interpretation. Eng. Geol. 2012, 149–150, 70–77. [Google Scholar] [CrossRef]
- Liu, J.; Iskander, M.G. Modelling capacity of transparent soil. Can. Geotech. J. 2010, 47, 451–460. [Google Scholar] [CrossRef]
- Al-Naddaf, M.; Han, J.; Xu, C.; Jawad, S.; Abdulrasool, G. Experimental investigation of soil arching mobilization and degradation under localized surface loading. J. Geotech. Geoenviron. Eng. 2019, 145, 1–17. [Google Scholar] [CrossRef]
- Mujah, D.; Hazarika, H.; Watanabe, N.; Ahmad, F. Soil arching effect in sand reinforced with micropiles under lateral load. Soil Mech. Found. Eng. 2016, 53, 152–157. [Google Scholar] [CrossRef]
- Pardo, G.S.; Sáez, E. Experimental and numerical study of arching soil effect in coarse sand. Comput. Geotech. 2014, 57, 75–84. [Google Scholar] [CrossRef]
- Pulko, B.; Majes, B.; Mikoš, M. Reinforced concrete shafts for the structural mitigation of large deep-seated landslides: An experience from the Macesnik and the Slano blato landslides (Slovenia). Landslides 2014, 11, 81–91. [Google Scholar] [CrossRef]
- Shen, Y.J.; Yang, M.; Cui, H.H.; Xiang, Z.L.; Li, Y.Z.; Wen, K. Distribution characteristics and influence factors of soil arching ring behind stabilizing piles. Appl. Mech. Mater. 2015, 744–746, 474–478. [Google Scholar] [CrossRef]
- Sun, H.Y.; Wong, L.N.Y.; Shang, Y.Q.; Shen, Y.J.; Qing, L. Evaluation of drainage tunnel effectiveness in landslide control. Landslides 2012, 7, 445–454. [Google Scholar] [CrossRef]
- Sun, S.W.; Ma, N.; Hu, J.B.; Zhu, B.Z. Evolution characteristics and mechanism analysis of soil arch of anti-slide pile. J. Railw. Eng. Soc. 2019, 254, 7–12. (In Chinese) [Google Scholar]
- Terzaghi, K. Stress distribution in dry and in saturated sand above a yielding trap-door. In Proceedings of the 1st Conference of Soil Mechanics and Foundation Engineering, Boston, MA, USA, 22–26 July 1936; Cambridge Press: Cambridge, UK; pp. 307–316. [Google Scholar]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley & Sons: New York, NY, USA, 1943; pp. 76–85. [Google Scholar]
- Vardoulakis, L.; Graf, B.; Gudehus, G. Trap-door problem with dry sand: A statical approach based upon model test kinematics. Int. J. Numer. Anal. Methods Geomech. 1981, 5, 57–78. [Google Scholar] [CrossRef]
- Wang, F.W.; Sassa, K. Landslide simulation by a geotechnical model combined with a model for apparent friction change. Phys. Chem. Earth 2010, 35, 149–161. [Google Scholar] [CrossRef]
- Wang, G.H.; Sassa, K. Pore-pressure generation and movement of rainfall-induced landslides: Effects of grain size and fine-particle content. Eng. Geol. 2003, 69, 109–125. [Google Scholar] [CrossRef]
- Wang, G.L.; Ran, L.B.; Zhang, L. Discrete element simulation and evolution pattern of three-dimension soil arching between anti-slide piles. J. Civ. Environ. Eng. 2019, 41, 1–8. (In Chinese) [Google Scholar] [CrossRef]
- Wei, X.-L.; Chen, N.-S.; Cheng, Q.-G.; He, N.; Deng, M.-F.; Tanoli, J.I. Long-term activity of earthquake-induced landslides: A case study from Qionghai Lake Basin, Southwest of China. J. Mt. Sci. 2014, 11, 607–624. [Google Scholar] [CrossRef]
- Wu, J.J.; Li, C.D.; Liu, Q.T.; Fan, F.S. Optimal isosceles trapezoid cross section of laterally loaded piles based on friction soil arching. KSCE J. Civ. Eng. 2017, 21, 2655–2664. [Google Scholar] [CrossRef]
- Xu, C.J.; Liang, L.J.; Chen, Q.Z.; Luo, W.J.; Chen, Y.F. Experimental study of soil arching effect under seepage condition. Acta Geotech. 2019, 14, 2031–2044. [Google Scholar] [CrossRef]
- Zhao, X.Y.; Li, K.P.; Xiao, D. A simplified method to analyze the load on composite retaining structures based on a novel soil arch model. Bull. Eng. Geol. Environ. 2020, 79, 3483–3496. [Google Scholar] [CrossRef]




| Material | Proportion by Mass? (%) | |
|---|---|---|
| 1 | Barite grains | 17.34 |
| 2 | Silty clay | 58.40 |
| 3 | Mixed sand | 16.06 |
| 4 | Washing powder | 1.98 |
| 5 | Talcum powder | 6.22 |
| Characteristic | Value | |
|---|---|---|
| 1 | Unit weight, γ (kN/m3) | 19.5 |
| 2 | Cohesion, c (kPa) | 11.44 |
| 3 | Friction angle, φ (°) | 32.89 |
| 4 | Poisson ratio, μ | 0.26 |
| 5 | Elastic modulus, E (kPa) | 31,058 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, W.; Zhang, S.; He, N. An Experimental Study on the Dynamic Evolution Characteristics of Soil Arching and the Rational Spacing of Anti-Slide Piles. Sustainability 2022, 14, 8566. https://doi.org/10.3390/su14148566
Zhong W, Zhang S, He N. An Experimental Study on the Dynamic Evolution Characteristics of Soil Arching and the Rational Spacing of Anti-Slide Piles. Sustainability. 2022; 14(14):8566. https://doi.org/10.3390/su14148566
Chicago/Turabian StyleZhong, Wei, Shuai Zhang, and Na He. 2022. "An Experimental Study on the Dynamic Evolution Characteristics of Soil Arching and the Rational Spacing of Anti-Slide Piles" Sustainability 14, no. 14: 8566. https://doi.org/10.3390/su14148566
APA StyleZhong, W., Zhang, S., & He, N. (2022). An Experimental Study on the Dynamic Evolution Characteristics of Soil Arching and the Rational Spacing of Anti-Slide Piles. Sustainability, 14(14), 8566. https://doi.org/10.3390/su14148566






