Ticket Allocation Optimization of Fuxing Train Based on Overcrowding Control: An Empirical Study from China

Abstract

At the peak of passenger flow, some passengers extend travel sections, which will be likely to lead to overcrowding of high-speed railway (HSR) trains. Therefore, the problem of train overcrowding control needs to be considered in ticket allocation. Firstly, by simulating the passenger demand function and utility function, an optimization model of ticket allocation for multiple trains and multiple stops with the goal of maximizing revenue is constructed. Secondly, the concepts of the travel extension coefficient and risk coefficient are introduced, the number of passengers is estimated under the risk coefficient as the probability, and the total number of passengers on the train arriving at any station is obtained. Thus, preventing the number of passengers on the train from exceeding the train capacity is introduced to the ticket allocation optimization model of multiple trains and multiple stops as a constraint. Finally, this model is solved by the particle swarm optimization algorithm (PSO). The research results show that the idea of controlling passenger numbers so as not to exceed train capacity based on ticket allocation proposed in this paper has strong practical feasibility. By reasonably and accurately allocating the tickets to the departure terminal section and long-distance terminal sections, it can ensure that, even if there are some passengers extending their travel section, the train will not be overcrowded under a certain probability, improving the train safety and passenger travel experiences.

1. Introduction

High-speed railway is a kind of green, environmentally friendly, and sustainable transportation, which is favored by passengers. The factors that impact the sustainability of high-speed railways are mainly economic and safety. High-speed railways can operate well only by ensuring the revenue of tickets is greater than the cost. Therefore, the goal of ticket allocation is to maximize revenue. On the other hand, the safety of HSR trains is important for sustainability as well. However, during the peak period of railway transportation such as holidays, passengers cannot buy tickets for the section they want to take. As a response, passengers will purchase any origin–destination (OD) pair ticket from their current station in order to get on the train first and then buy another continuing OD pair ticket, which could allow them to extend their travel sections to the target station (terminal station). If there are too many passengers extending their travel section (OD pair) in the above manner, the number of passengers on the train will be likely to exceed the train capacity when the train arrives at some stations. This phenomenon is called “overcrowding”, which will affect the safety of train operation and cause the train to be delayed or even shut down [1]. Therefore, overcrowding especially for the Fuxing train is not conducive to the sustainable development of high-speed railway (HSR) in China.

When the train experiences “overcrowding”, the conductor should let the passengers who extend their travel section through buying tickets after getting on the train get off; however, the cost is too high in practice, and it is easy to risk negative public opinion. One possible solution to solve the train overcrowding problem is to consider how to avoid train overcrowding when allocating tickets. This means allocating tickets reasonably and accurately under the constraint of controlling passenger numbers so as not to exceed train capacity. Therefore, this paper studies how to avoid train overcrowding through ticket allocation, so as to ensure the safety of train operation.

Literature Review and Innovation of This Paper

Ticket allocation of HSR trains is mainly borrowed from the aviation field, because these two fields both take revenue maximization as the objective function. However, there are still many differences between them [2,3]. What is more important is that ticket allocation in HSR is more complex than aviation seat allocation. Thus, according to the difference in complexity and constraints of the application scenarios, ticket allocation in HSR presents a different research focus:

(1)

Single-train ticket allocation is the most basic research entry. Ciancimino et al. [4] first proposed treating different classes of carriages as different train products, so the problem of train ticket allocation can be transformed into a seat control problem in single trains, with multiple sections and a single ticket price. Some studies [5] assumed that the passenger demand obeys an independent normal distribution and used the particle swarm optimization algorithm (PSO) to solve the final optimization model. Shan et al. [6] predicted the passenger flow by adopting time series firstly. Then, they obtained a ticket allocation method through the formulation of rules such as long distance before short distance, seat before no seat, and allocating tickets in advance by quantity and then by proportion. Gopalakrishnan et al. [7] mainly considered the long-distance passenger demand of Indian railways and studied the utilization method of single-train seat capacity.

(2)

Ticket allocation involving multiple trains is further complicated on the basis of single-train ticket allocation. Jiang et al. [8] integrated the short-term passenger flow demand forecasting method into the railway multi-train ticket allocation model, which solved the situation that some stations were short of tickets and other stations were rich in tickets. Yan et al. [9] developed a seat allocation model for multiple HSR trains with flexible train formation. Jiang et al. [10] proposed a dynamic adjustment method for ticket allocation. Zhao et al. [11] proposed a probabilistic nonlinear programming model for the problem of railway passenger ticket allocation. Deng et al. [12] focused on the joint pricing and ticket allocation problem for multiple HSR trains with different stop patterns. Luo et al. [13] developed a multi-train seat inventory control model based on revenue management theory. The above was discussed with respect to the complexity of ticket allocation.

(3)

Customer choice behavior plays an important role in estimating customer demand, which has also been more discussed in ticket allocation in recent years. It is an obvious research conclusion that there are many factors influencing customer choice behavior, and these factors can be divided mainly into two aspects, personal attributes and trip attributes, in a great deal of the literature [14,15,16,17]. As for the method describing passenger choice behavior, Wang et al. [18] described different passenger needs through the Logit model and established a multi-stage random ticket allocation model under passenger selection behavior.

(4)

In the two most important sub-studies of revenue management, ticket allocation is always constrained by ticket prices. However, it is unfortunate that in the past few years, pricing and ticket allocation issues have always been treated separately, and there is a gap in the research regarding joint pricing and ticket allocation models [2,19]. Weatherford [20] first stressed the importance of considering prices and suggested them as decision variables for the ticket allocation problem. After Weatherford’s contribution, we can see more and more research that has optimized ticket allocation and ticket prices at the same time. Hetrakul et al. [19] put forward a comprehensive optimization model of dynamic ticket pricing and ticket allocation based on the impact of passenger heterogeneity on ticket allocation. Some of the literature regards ticket allocation as the basis of dynamic pricing and gives priority to solving the problem of ticket allocation while solving dynamic pricing [21,22,23,24].

In summary, we found that there are many scholars who have researched ticket allocation based on revenue maximization, but few scholars have studied how to avoid train overcrowding through ticket allocation. As

Table 1. Comparison of our research with the literature in ticket allocation.

References	Revenue Maximization			Overcrowding Control
	Single Train	Multiple Trains	Pricing
[4,5,6,7]	√	×	×	×
[8,9,10,11,12,13]	×	√	×	×
[2,19,20,21,22,23,24]	×	×	√	×
This paper	×	√	×	√

shows, the above studies about ticket allocation only take revenue maximization as the objective function of ticket allocation, but lack the consideration of combining the problem of “train overcrowding” with ticket allocation. Therefore, as the most significant innovation, this paper integrates the problem of “train overcrowding” into the ticket allocation model as a constraint. Our research introduces a “risk coefficient” as the probability boundary and a “travel extension coefficient” to describe the proportion of passengers who extend their travel section out of the total number of passengers, then constructs and solves the ticket allocation optimization model by taking into account the goal of maximizing the expected revenue of multiple trains and multiple stops under the constraint that the train will not experience “overcrowding” under a certain probability. This is exactly the innovation of this paper and the original intention of writing this paper. It also enriches the research dimension of ticket allocation and sustainable operations and management of railway systems at the same time.

This paper proceeds as follows: Part 2 lists the model assumptions and the variable definition and then constructs a mathematical model formulation; Part 3 provides the algorithms to solve the model; Part 4 shows the numerical experiments; Part 5 concludes the paper.

2. Research Methodology and Process

2.1. Model Assumptions and Notations

Suppose a high-speed railway line contains $l$ stations and involves $K$ trains, $k=1,2\dots K$. Each train has different stopping plans and serves the travel demand of a set of OD pairs on the line. Two adjacent stations on the line form a section, named the $h$ section, and in total, $h=1,2\dots l-1$.

To simplify the problem, we make the following reasonable assumptions:

(1)

Passengers whose requests are fulfilled will not cancel their reservations or change their ticket.

(2)

Take the second-class seat of HSR as the research object.

(3)

If passengers need to extend their travel section after getting on the train, they only make up the tickets to the terminal. The travel section that extends from the boarding station to the terminal is called the “target travel section (OD pair)”. In order to get on the train first, passengers buy a short OD pair ticket, and the travel section corresponding to these tickets is called the “short travel section (OD pair)”. A target travel section corresponds to several short travel sections.

To simplify the description of the problem, the notations in

Table 2. Notations.

Symbols	Definition	Unit
	Variable or Parameters
$(r,s)$	$\mathrm{Origin}–\mathrm{destination}\mathrm{pair}\mathrm{in}\mathrm{the}\mathrm{transportation}\mathrm{service},\mathrm{which}\mathrm{is}\mathrm{composed}\mathrm{of}\mathrm{the}\mathrm{train}\mathrm{stops},\mathrm{from}\mathrm{station}r\mathrm{to}\mathrm{station}s$	/
$t$	$\mathrm{Station}\mathrm{serial}\mathrm{number},\mathrm{the}\mathrm{train}\mathrm{arrives}\mathrm{at}\mathrm{the}t\mathrm{th}\mathrm{station}$	/
$h$	$\mathrm{Section}\mathrm{serial}\mathrm{number},h=1,2\dots l-1$	/
$k$	$\mathrm{Train}\mathrm{serial}\mathrm{number},k=1,2\dots K$	/
$p_{rs}^{(k)}$	$\mathrm{Price}\mathrm{of}\mathrm{train}k$$\mathrm{between}(r,s)$	CNY
${\eta }_{rs}^{\left(k\right)}$	$\mathrm{The}0–1\mathrm{binary}\mathrm{parameter}\mathrm{denoting}\mathrm{whether}\mathrm{train}k$$\mathrm{can}\mathrm{provide}\mathrm{services}\mathrm{between}(r,s)$	/
$t_{rs}^{\left(k\right)}$	$\mathrm{Travel}\mathrm{time}\mathrm{of}\mathrm{train}k$$\mathrm{between}(r,s)$	min
${\alpha }_1,{\alpha }_2$	Parameters of utility function	/
$U_{rs}^{\left(k\right)}$	$\mathrm{Total}\mathrm{utility}\mathrm{of}\mathrm{train}k$$\mathrm{for}\mathrm{passengers}\mathrm{between}(r,s)$	/
$w_{rs}^{\left(k\right)}$	$\mathrm{Probability}\mathrm{of}\mathrm{train}k$$\mathrm{chosen}\mathrm{by}\mathrm{passengers}\mathrm{between}(r,s)$	%
$Q_{rs}$	$\mathrm{Expected}\mathrm{sales}\mathrm{volume}\mathrm{between}(r,s)$	/
$C_k$	$\mathrm{Capacity}\mathrm{of}\mathrm{train}k$	passengers
$q_t^{\left(k\right)}$	$\mathrm{Total}\mathrm{number}\mathrm{of}\mathrm{passengers}\mathrm{on}\mathrm{train}k$$\mathrm{arriving}\mathrm{at}\mathrm{station}t$	passengers
$q_{t·}^{\left(k\right)}$	$\mathrm{The}\mathrm{number}\mathrm{of}\mathrm{passengers}\mathrm{boarding}\mathrm{train}k$$\mathrm{when}\mathrm{arriving}\mathrm{at}\mathrm{station}t$	passengers
${\widehat{q}}_t^{\left(k\right)}$	$\mathrm{The}\mathrm{number}\mathrm{of}\mathrm{passengers}\mathrm{who}\mathrm{get}\mathrm{on}\mathrm{train}k$$\mathrm{before}\mathrm{station}t$$\mathrm{and}\mathrm{get}\mathrm{off}\mathrm{the}\mathrm{train}\mathrm{after}\mathrm{station}t$	passengers
$q_{·t}^{\left(k\right)}$	$\mathrm{For}\mathrm{train}k$$,\mathrm{the}\mathrm{number}\mathrm{of}\mathrm{passengers}\mathrm{who}\mathrm{should}\mathrm{get}\mathrm{off}\mathrm{before}\mathrm{station}t,\mathrm{but}\mathrm{are}\mathrm{still}\mathrm{on}\mathrm{the}\mathrm{train}\mathrm{after}\mathrm{extending}\mathrm{their}\mathrm{travel}\mathrm{section}$	passengers
$g_{rs}$	$\mathrm{The}\mathrm{number}\mathrm{of}\mathrm{passengers}\mathrm{who}\mathrm{buy}\mathrm{tickets}\mathrm{between}(r,s),\mathrm{but}\mathrm{extend}\mathrm{the}\mathrm{travel}\mathrm{section}\mathrm{to}\mathrm{the}\mathrm{terminal}$	passengers
${\beta }_{rs}$	Parameter, travel extension coefficient	/
$\gamma$	Parameter, risk coefficient	/
$x_{rl}$	$\mathrm{Passenger}\mathrm{demand}\mathrm{under}\gamma$$\mathrm{for}\mathrm{target}\mathrm{travel}\sec \mathrm{tion}(r,l)$	/
$F_{rl}^{-1}(x)$	$\mathrm{Inverse}\mathrm{function}\mathrm{of}\mathrm{cumulative}\mathrm{probability}\mathrm{function}\mathrm{of}\mathrm{passenger}\mathrm{demand}\mathrm{for}\mathrm{target}\mathrm{travel}\sec \mathrm{tion}(r,l)$	/
	Decision Variable
$b_{rs}^{\left(k\right)}$	$\mathrm{The}\mathrm{number}\mathrm{of}\mathrm{tickets}\mathrm{allocated}\mathrm{to}\mathrm{train}k$$\mathrm{between}(r,s)$	/

will be used in the formulation.

2.2. Model Formulation

For any given OD pair, the probability function of passenger demand can be fitted by normal distribution [25]. Then, passenger demand between $(r,s)$ obeys an independent normal distribution as follows:

$$f_{rs}(x)=\frac{\exp (-\frac{{(x-{\mu }_{rs})}^2}{2{\sigma }_{rs}^2})}{\sqrt{2\pi }{\sigma }_{rs}},1\le r<s\le l$$

(1)

${\mu }_{rs}$ is the expectation of passenger demand, while ${\sigma }_{rs}$ is the standard deviation of passenger demand. $F_{rs}^{}(x)$ is the cumulative probability function of passenger demand. ${\eta }_{rs}^{(k)}$ is the service parameter of train $k$. $b_{rs}^{\left(k\right)}$ is the number of tickets allocated to train $k$. If train $k$ provides a transportation service between $(r,s)$, ${\eta }_{rs}^{\left(k\right)}=1$, $b_{rs}^{\left(k\right)}\ge 0$. Otherwise, ${\eta }_{rs}^{\left(k\right)}=0$, $b_{rs}^{\left(k\right)}=0$. Set ${\displaystyle \sum _{k=1}^K{\eta }_{rs}^{(k)}}·b_{rs}^{(k)}=B_{rs}^{(k)}$. Finally, the expected ticket sales volume between $(r,s)$ can be described as below:

$$Q_{rs}={\displaystyle \underset{0}{\overset{B_{rs}^{(k)}}{\int }}x{f}_{rs}(x)}dx+B_{rs}^{(k)}·{\displaystyle {\int }_{B_{rs}^{(k)}}^{\infty }{f}_{rs}(x)}dx$$

(2)

When passengers choose a train between $(r,s)$, they will mainly focus on two factors: ticket price and travel time. The utility obtained by passengers choosing train $k$ can be expressed as the following formula:

$$U_{rs}^{\left(k\right)}={\alpha }_1\frac{p_{rs}^{\left(k\right)}}{\lambda }+{\alpha }_2·T_{rs}^{\left(k\right)},{\alpha }_1<0,{\alpha }_2<0$$

(3)

${\alpha }_1$ and ${\alpha }_2$ are parameters of the utility function. $p_{rs}^{\left(k\right)}$ and $T_{rs}^{\left(k\right)}$ are ticket price and travel time for train $k$ between $(r,s)$. λ is revised average monthly passenger income [19]. Passengers will choose each train based on utility. Then, we can define the probability of passengers choosing train $k$ between $(r,s)$ by the Logit model as

$$w_{rs}^{\left(k\right)}=\frac{{\eta }_{rs}^{\left(k\right)}\exp (U_{rs}^{\left(k\right)})}{{\displaystyle \sum _{k=1}^K{\eta }_{rs}^{\left(k\right)}\exp (U_{rs}^{\left(k\right)})}}$$

(4)

With the goal of maximizing the overall expected revenue, the following objective function is obtained for the ticket allocation of HSR:

$$R=\max {\displaystyle \sum _{k=1}^K{\displaystyle \sum _{(r,s)}^{}{Q}_{rs}(b_{rs}^{\left(k\right)})}·w_{rs}^{(k)}·p_{rs}^{(k)}},1\le r<s\le l$$

(5)

The following constraints shall also be taken into account for ticket allocation:

(1)

Train capacity constraints: the ticket number allocated for each train between $(r,s)$ cannot exceed their capacity constraint. $C_k$ is the capacity of train $k$

$${\displaystyle \sum _{r=1}^h{\displaystyle \sum _{s=h+1}^l{b}_{rs}^{\left(k\right)}}}\le C_k,h=1,2\dots l-1$$

(6)

(2)

Train service constraints:

$$\{\begin{array}{l}{\eta }_{rs}^{\left(k\right)}=1,b_{rs}^{\left(k\right)}>0,b_{rs}^{\left(k\right)}\in Z^{+}\\ {\eta }_{rs}^{\left(k\right)}=0,b_{rs}^{\left(k\right)}=0\end{array}$$

(7)

2.3. Train Overcrowding Control

In the peak period of the railway, due to the lack of sufficient train capacity, some of the passengers who want to reach the terminal will first buy tickets that can allow them to get on the train from the current station and then make up tickets on the train to extend their travel section to the terminal. Through the above alternative approach, passengers can achieve the goal of getting off at the terminal without buying the target travel section tickets. Although such passengers’ behavior can increase train revenue for railway transport enterprises, it will also bring a problem: overcrowding. This paper estimates the number of passengers on the train when arriving at each station to ensure that the passenger number does not exceed the train capacity for a certain probability. When train $k$ arrives at station $t$, $1<t<l$, the number of passengers on the train at this time is $q_t^{\left(k\right)}$.

$$q_t^{\left(k\right)}=q_{t·}^{\left(k\right)}+{\stackrel{⌢}{q}}_t^{\left(k\right)}+q_{·t}^{\left(k\right)}$$

(8)

In Formula (8), $q_{t·}^{\left(k\right)}$ indicates passengers boarding train $k$ at station $t$:

$$q_{t·}^{\left(k\right)}={\displaystyle \sum _{(r,s)}^{}\min [Q_{rs}}·w_{rs}^{\left(k\right)},b_{rs}^{\left(k\right)}],\forall (r,s)|t=r<s\le l$$

(9)

${\hat{q}}_t^{\left(k\right)}$ represents the number of passengers who get on train $k$ before station $t$ and get off the train after station $t$. These passengers are still on the train at this time.

$${\widehat{q}}_t^{\left(k\right)}={\displaystyle \sum _{(r,s)}\min [Q_{rs}}·w_{rs}^{\left(k\right)},b_{rs}^{\left(k\right)}],\forall (r,s)|1\le r<t<s\le l$$

(10)

$q_{·t}^{\left(k\right)}$ means the number of passengers who should have disembarked at station $t$ or before station $t$, but are still on the train due to the extension of the travel section through buying a continued OD pair of tickets. This is this segment of passengers that may cause the train overcrowding.

$$q_{·t}^{\left(k\right)}={\displaystyle \sum _{(r,s)}\min [g_{rs}}·w_{rs}^{\left(k\right)},b_{rs}^{\left(k\right)}],\forall (r,s)|1\le r<s\le t$$

(11)

$$g_{rs}={\beta }_{rs}·(x_{rl}-{\displaystyle \sum _{k=1}^K{b}_{rl}^{\left(k\right)}}),\forall (r,s)|1\le r<s\le t$$

(12)

$${\beta }_{rl}={\displaystyle \sum _{(r,s)}{\beta }_{rs}},\forall (r,s)\in (r,l)$$

(13)

$$x_{rl}=F_{rl}^{-1}(\gamma ),\forall (r,s)|1\le r<s\le t,0<\gamma <1$$

(14)

Equation (12) shows that when the passenger demand $x_{rl}$ in the target section $(r,l)$ exceeds the supply capacity ${\displaystyle \sum _{k=1}^K{b}_{rl}^{\left(k\right)}}$, the phenomenon of extending the travel section will occur in all short travel sections $(r,s)$. ${\beta }_{rs}$ is the travel extension coefficient, which is used to describe the proportion between the passengers extending their travel section and the excess demand $x_{1l}-{\displaystyle \sum _{k=1}^K{b}_{rl}^{\left(k\right)}}$ in the target travel section $(r,l)$. Equation (14) is used to calculate the corresponding number of passengers under the risk coefficient $\gamma$. $F_{rl}^{-1}(x)$ is the inverse function of the cumulative probability function of passenger demand (the inverse function of the cumulative probability function of the normal distribution in this paper). For the Fuxing train as a representative product of HSR, it is more important to ensure that it is not overcrowded rather than increasing revenue in the actual operation process, which will not affect the train’s operation safety and weaken the passenger riding experience. For a given scheme of ticket allocation, when train $k$ arrives at station $t$, it needs to satisfy:

$$q_t^{\left(k\right)}\le C_k,1<\forall t<l$$

(15)

Finally, we construct the ticket allocation optimization model of the Fuxing train considering solving the problem of train overcrowding caused by passengers extending their travel sections:

$$\begin{array}{l}R=\max {\displaystyle \sum _{k=1}^K{\displaystyle \sum _{(r,s)}^{}{Q}_{rs}(b_{rs}^{(k)})}·w_{rs}^{(k)}·p_{rs}^{(k)}},1\le r<s\le l\\ s.t.\\ q_t^{\left(k\right)}\le C_k,1<\forall t<l\\ {\displaystyle \sum _{r=1}^h{\displaystyle \sum _{s=h+1}^l{b}_{rs}^{\left(k\right)}}}\le C_k,h=1,2\dots l-1\\ \{\begin{array}{l}{\eta }_{rs}^{\left(k\right)}=1,b_{rs}^{\left(k\right)}>0,b_{rs}^{\left(k\right)}\in Z^{+}\\ {\eta }_{rs}^{\left(k\right)}=0,b_{rs}^{\left(k\right)}=0\end{array}\end{array}$$

(16)

3. Solution Algorithm

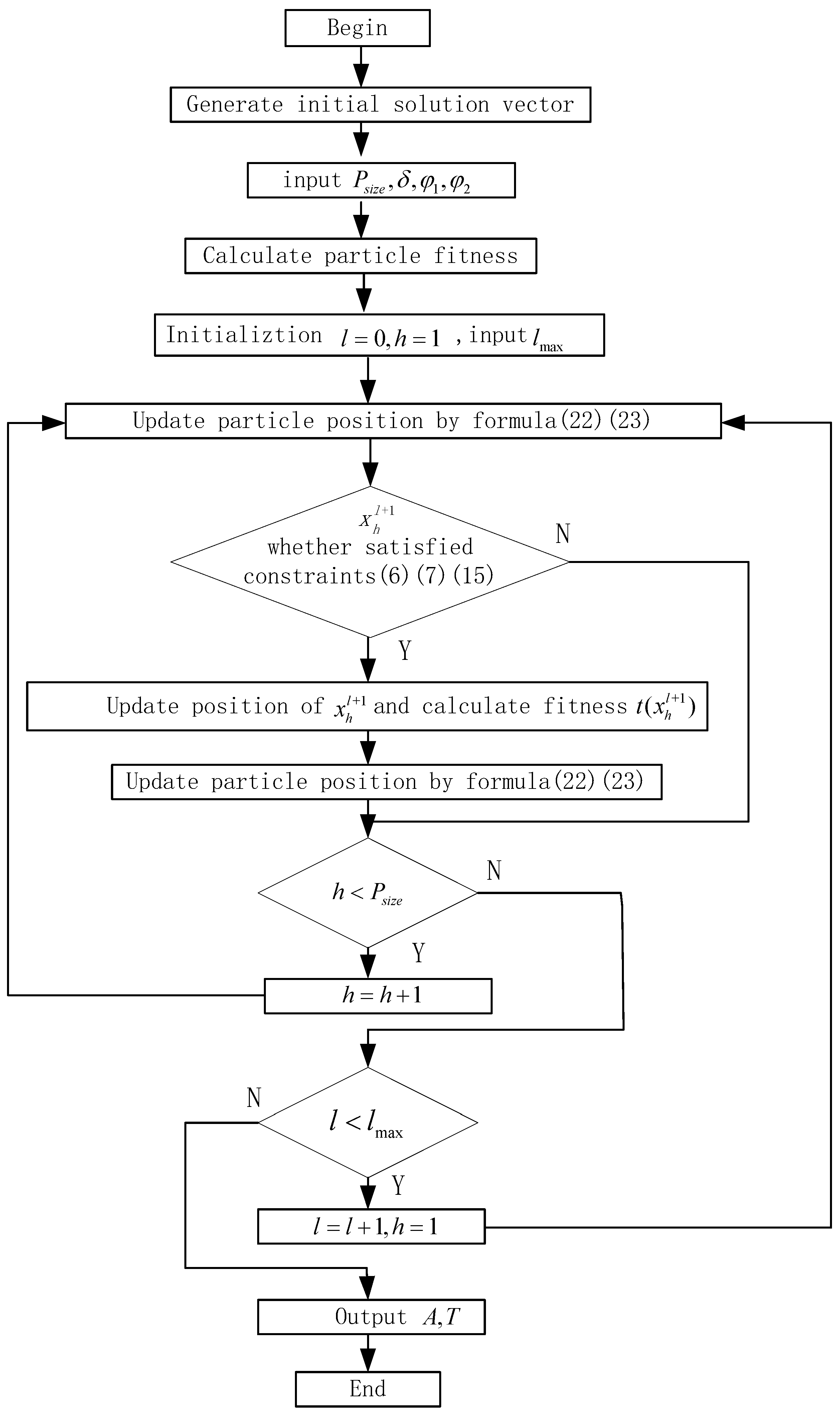
Because the optimization model proposed in this paper is a mixed-integer nonlinear programming model (MINLP) with several constraints (Equation (16)), it cannot calculate the maximum value directly by derivation. Therefore, we chose the heuristic algorithm to solve Model (16). The PSO algorithm is one of the heuristic algorithms that is simple and easy to implement and has fewer parameters, all of which lead to faster convergence speed, and it requires only small computer memory. Moreover, the leap of the PSO algorithm makes it easier to find the global optimal value without being trapped in the local optimal value.

Setting the initial solution vector $\mathit{A}$, if train $k$ provides service for ${\displaystyle \sum _{(r,s)}{\eta }_{rs}^{\left(k\right)}}$ OD pairs, $\mathit{A}$ is the ${\displaystyle \sum _{k=1}^K{\displaystyle \sum _{(r,s)}{\eta }_{rs}^{\left(k\right)}}}$ dimension vector. We convert Equation (16) into the following equivalent model [2,26]:

$$\begin{array}{l}\max {\displaystyle \sum _{k=1}^K{\displaystyle \sum _{(r,s)}{b}_{rs}^{\left(k\right)}}}·p_{rs}^{\left(k\right)},1\le r<s\le l\\ s.t.\\ q_t^k\le C_k,1<\forall t\le l\\ {\displaystyle \sum _{r=1}^h{\displaystyle \sum _{s=h+1}^l{b}_{rs}^{\left(k\right)}}}\le C_k,h=1,2\dots l-1\\ \{\begin{array}{l}{\eta }_{rs}^{\left(k\right)}=1,b_{rs}^{\left(k\right)}>0,b_{rs}^{\left(k\right)}\in Z^{+}\\ {\eta }_{rs}^{\left(k\right)}=0,b_{rs}^{\left(k\right)}=0\end{array}\end{array}$$

(17)

Equation (17) is a linear programming model, and $b_{rs}^{\left(k\right)}$ can be solved directly. Setting $\mathit{A}=(b_{12}^{\left(1\right)},b_{13}^{\left(1\right)},\dots ,b_{rs}^{\left(k\right)})$, this is the initial solution. $P_{size}$ is the particle size, and the initial position of the $h$th particle is recorded as ${\mathit{x}}_{\mathit{h}}^{\mathbf{0}}$, $h=1,2,3\dots P_{size}$.

$${\mathit{x}}_{\mathit{h}}^{\mathbf{0}}=A+{\mathit{g}}_{\mathit{h}}$$

(18)

In the above formula, ${\mathit{g}}_{\mathit{h}}$ is a vector with the same dimension of $A$, and each component obeys the uniform distribution of $(-d,d)$.

${\mathit{x}}_{\mathit{h}}^{\mathit{l}}$ is the position at the $l$th iteration. $l_{\max }$ represents the maximum number of iterations, $1\le l\le l_{\max }$. $t({\mathit{x}}_{\mathit{h}}^{\mathit{l}})$ can reflect the fitness of ${\mathit{x}}_{\mathit{h}}^{\mathit{l}}$, and then:

$$t({\mathit{x}}_{\mathit{h}}^{\mathit{l}})=T({\mathit{A}}_{\mathit{h}}^{\mathit{l}})$$

(19)

${\mathit{A}}_{\mathit{h}}^{\mathit{l}}$ is the vector for which each component of ${\mathit{x}}_{\mathit{h}}^{\mathit{l}}$ is tested by Constraints (6), (7), and (15) and rounded. $T({\mathit{A}}_{\mathit{h}}^{\mathit{l}})$ represents the output that inputs ${\mathit{A}}_{\mathit{h}}^{\mathit{l}}$ into the objective function (16).

We set ${\mathit{v}}_{\mathit{h}}^{\mathit{l}\mathbf{+}\mathbf{1}}$ as the velocity of the $h$th particle at the $l$th iteration. ${\mathit{x}}_{\mathit{h}}^{\mathit{l}}$ is the updated position of the $h$th particle after the $l$th iteration. ${\mathit{y}}_{\mathit{h}}^{\mathit{l}}$ is described as the best historical position at the $l$th iteration of the $h$th particle. ${\mathit{y}}_{\mathit{g}}^{\mathit{l}}$ represents the historical position of all particles at the $l$th iteration. The above process can be expressed as follows [19]:

$${\mathit{v}}_{\mathit{h}}^{\mathit{l}\mathbf{+}\mathbf{1}}=\delta {\mathit{v}}_{\mathit{h}}^{\mathit{l}}+{\phi }_1{\mathit{r}}_{\mathit{h}\mathbf{1}}^{\mathit{l}}({\mathit{y}}_{\mathit{h}}^{\mathit{l}}-{\mathit{x}}_{\mathit{h}}^{\mathit{l}})+{\phi }_2{\mathit{r}}_{\mathit{h}\mathbf{2}}^{\mathit{l}}({\mathit{y}}_{\mathit{g}}^{\mathit{l}}-{\mathit{x}}_{\mathit{h}}^{\mathit{l}})$$

(20)

$${\mathit{x}}_{\mathit{h}}^{\mathit{l}\mathbf{+}\mathbf{1}}={\mathit{x}}_{\mathit{h}}^{\mathit{l}}+{\mathit{v}}_{\mathit{h}}^{\mathit{l}\mathbf{+}\mathbf{1}}$$

(21)

$${\mathit{y}}_{\mathit{h}}^{\mathit{l}\mathbf{+}\mathbf{1}}={\mathit{A}}_{\mathit{h}}^{\mathit{l}\mathbf{+}\mathbf{1}},T_h=t({\mathit{y}}_{\mathit{h}}^{\mathit{l}\mathbf{+}\mathbf{1}}),\forall t({\mathit{x}}_{\mathit{h}}^{\mathit{l}\mathbf{+}\mathbf{1}})\le T_h$$

(22)

$${\mathit{y}}_{\mathit{g}}^{\mathit{l}\mathbf{+}\mathbf{1}}={\mathit{A}}_{\mathit{h}}^{\mathit{l}\mathbf{+}\mathbf{1}},T=t({\mathit{y}}_{\mathit{g}}^{\mathit{l}\mathbf{+}\mathbf{1}}),\forall t({\mathit{x}}_{\mathit{h}}^{\mathit{l}\mathbf{+}\mathbf{1}})\le T,h=1,2\dots P_{size}$$

(23)

$T_h$ is the fitness of the best historical position of the $h$th particle. $T$ is the fitness of the best historical position of all particles. ${\mathit{r}}_{\mathit{h}\mathbf{1}}^{\mathit{l}}$ and ${\mathit{r}}_{\mathit{h}\mathbf{2}}^{\mathit{l}}$ have the same dimensions as vector A and obey the uniform distribution of $(0,1)$. $\delta ,{\phi }_1,{\phi }_2$ are control parameters. Finally, the solving process of this paper is as follows (Figure 1).

4. Results and Analysis

4.1. Basic Data

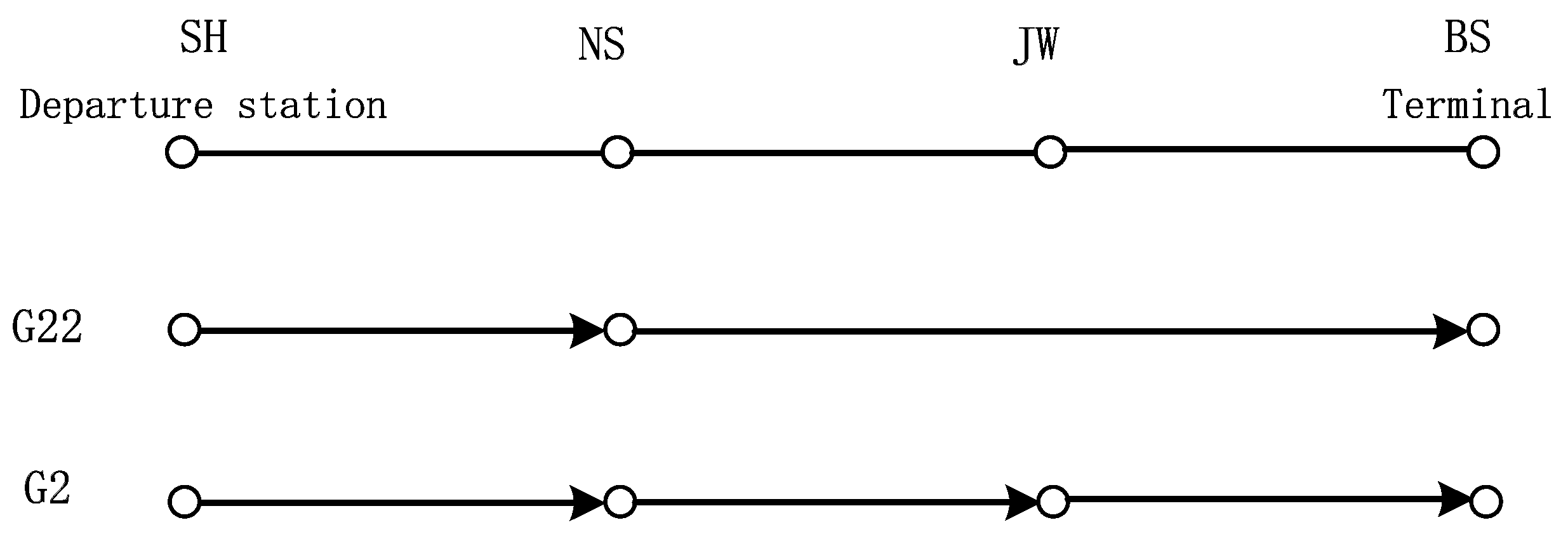
We chose the Shanghai–Beijing line in China as an example to verify the validity and applicability of the model in this paper. For the situation of multiple trains and multiple stops, there are two trains, G2 and G22, providing service between Shanghai Hongqiao station and Beijing South station. The total second-class seat capacity of each of the trains is set at 1113. Like the Fuxing train, G2 and G22 have few stops and a short travel time (Figure 2), which are deeply favored by passengers. The seat occupation rate of these two trains is higher than the average level of all the trains on the same line. During the peak period of passenger flow, such as holidays, many passengers take these two trains and extend their travel section by purchasing continued OD pair tickets, which is likely to increase the risk of overcrowding. The train stops and travel times are shown in

Table 3. Train stops and travel times.

Train	Factors of Passengers Choice	OD
		(SH, BS)	(SH, NS)	(SH, JW)	(NS, BS)	(NS, JW)	(JW, BS)
G2	Price (CNY)	553	134.5	398.5	443.5	279	184.5
	Travel time (min)	268	60	179	206	117	87
G22	Price (CNY)	553	134.5	/	443.5	/	/
	Travel time (min)	258	60	/	196	/	/

. “/” means the train does not provide service between the OD pair. There are four stations on the line, namely, Shanghai Hongqiao (SH), Nanjing South (NS), Jinan West (JW), and Beijing South (BS).

We take the actual number of passengers of the two trains from 30 September 2019 to 7 October 2019 and from 30 September 2020 to 7 October 2020 as a case for empirical analysis. Then, the estimated values of the main parameters of the passenger demand function are obtained as in

Table 4. Main parameter values of passenger demand function.

Parameter	OD
	(SH, BS)	(SH, NS)	(SH, JW)	(NS, BS)	(NS, JW)	(JW, BS)
${\mu }_{rs}$	1701.4	170	89.6	277	13.4	96.6
${\sigma }_{rs}$	222.5	92.4	68.7	142.4	14	70.3

.

The parameter value of the utility function is obtained according to the literature [25]: ${\alpha }_1=-2.24$, ${\alpha }_2=-0.0113$, and $\lambda =190$. Referring to the finance risk control theory, the confidence interval of the VaR method is generally 95%, and then, $\gamma =0.95$. The values of other parameters for the example are as follows: $P_{size}=25$, $l_{\max }=100$, $\delta =0.5$, ${\phi }_1=2$, and ${\phi }_2=2$.

The behaviors of extending travel sections occur in all the corresponding short travel sections. It can be seen from Table 2 that both two trains will terminate at BS. For train G2, the target travel sections are (SH, BS) and (NS, BS). Train G22 only has one target travel section (SH, BS). Therefore, the short travel sections (SH, NS) and (SH, JW) belong to the target travel section (SH, BS). Similarly, (NS, BS) has only one short travel section (NS, JW). All travel extension coefficients of each of the short travel sections are shown in

Table 5. Travel extension coefficient values.

Arrive at the Station t	NS	JW
Target travel section	(SH, BS)	(NS, BS)	(SH, BS)
Short travel section	(SH, BS)	(NS, JW)	(SH, NS)	(SH, JW)
$\mathrm{Travel}\mathrm{extension}\mathrm{coefficient}{\beta }_{rs}$	0.065	0.1	0.065	0.035

:

4.2. Computational Results

We used the Python language programming to solve the model. The final ticket allocation details (Scheme I) are shown in

Table 6. Ticket allocation results (Scheme I).

Train	OD	Number of Tickets Finally Allocated
G2	(SH, BS)	833
G2	(SH, NS)	110
G2	(SH, JW)	117
G2	(NS, BS)	153
G2	(NS, JW)	43
G2	(JW, BS)	160
G22	(SH, BS)	919
G22	(SH, NS)	184
G22	(NS, BS)	184

, and the total expected revenue of the two trains is CNY 1,084,120. As can be seen from Table 5, most tickets are allocated to departure terminal section (SH, BS) for both G2 and G22.

If the aim is not train overcrowding control, just allocating tickets with the goal of maximizing overall revenue (remove Constraints (15)), we can obtain the ticket allocation optimization model under general constraints as a comparison scheme, and the results of the comparison scheme (Scheme II) by solving the model are shown in

Table 7. Ticket allocation results of comparison scheme (Scheme II).

Train	OD	Number of Tickets Finally Allocated
G2	(SH, BS)	833
G2	(SH, NS)	75
G2	(SH, JW)	131
G2	(NS, BS)	139
G2	(NS, JW)	64
G2	(JW, BS)	195
G22	(SH, BS)	888
G22	(SH, NS)	225
G22	(NS, BS)	225

.

Through the comparative analysis of the ticket allocation results of the two schemes, it can be summarized that, in order to prevent the train from overcrowding, the goal of maximizing the revenue of the trains will be weakened. At the same time, 1752 tickets were allocated for the departure terminal OD pair (SH, BS) in Scheme I, 31 more than the comparison scheme, and more tickets were allocated to the long-distance terminal sections such as (NS, BS) compared with Scheme II. In contrast to long-distance terminal sections, midway short sections such as (NS, JW) or the short departure section (SH, NS) are given more tickets in Scheme II, which will give passengers more opportunities to extend their travel section. It is indicated that, for the sake of controlling the passengers not exceeding the train capacity, the tickets should be given to the departure terminal sections or long-distance terminal sections instead of allocating a large number of tickets to the short sections or short departure sections.

5. Conclusions

Different from the general research on ticket allocation, this paper took the risk coefficient as the lower limit of probability and reasonably and scientifically allocated the tickets to each travel section of the train to prevent the number of passengers from exceeding the train capacity resulting from too many passengers extending their travel sections, so as to solve the problem of train overcrowding. After numerical verification, the conclusions of this paper demonstrated that in the peak period of passenger flow, such as some holidays, in order to control the number of passengers on the train so as not to exceed the capacity, railway operation departments should allocate more tickets to the departure terminal and the long-distance terminal sections, while reducing the number of tickets for the short-distance or the short departure sections and, finally, achieve a balance between revenue maximization and passenger riding experiences, which is crucial for the sustainable development and operation of the HSR [27]

Compared with those ticket allocation literature works that only aim to maximize revenue, this paper provided a new way of thinking about the railway operation department to reasonably allocate tickets so as to solve the problem of train overcrowding, which is an innovation for and supplement to ticket allocation theory. At the same time, preventing train overcrowding can effectively improve the safety of train operation, which is beneficial to the promotion of passenger experiences. It is of great significance to the management and operation of railway enterprises and to enhance their market competitiveness. However, the research conclusions of this paper are based on the assumption that all passengers only extend their travel to the terminal station and there are no passengers extending travel in other sections. The situation in real life is obviously more complex than that. In addition, the optimization model proposed in this paper is a mixed-integer nonlinear programming model (MINLP) with several constraints. This model is complex and difficult to solve directly by derivation. We chose the PSO algorithm to solve the model. The iterative process of the PSO algorithm takes much more time, and there is a small probability of falling into local optimization.