A Graphical Method for Designing the Horizontal Alignment and the Cant in High-Speed Railway Lines Aimed at Mixed-Speed Traffic
Abstract
:1. Introduction and Motivation
- What is the role of the cant in mixed-speed traffic operations? To solve this, we will analyze several cant designs for the same radius. The decision of which cant should be used affects comfort, train speed, maintenance, and many other issues of the railway system that are very difficult to handle all together. The railway manuals and civil engineering schools usually deal with those parameters in a separate way (see, for example, Esveld [12] and Lopez-Pita [13]).
- What factors should be addressed when running freight trains with a high cant excess mixed with trains with a high cant deficiency? An equilibrium between safety and maintenance should be reached, and at least, the authors of this work have not found any work that explicitly deals with this topic.
- Which cant–radius pair should we design for shared operations established in terms of curving performance and wheel–rail interaction between high-speed passenger and low-speed freight vehicles? Up to now, the technicians that write the standards have solved the problem by recommending the use of a certain cant law, but without carrying out an in-depth analysis of the consequences (see, for example, Adif [6]).
2. Theoretical Analysis of the Horizontal Alignment Parameters and Constraints
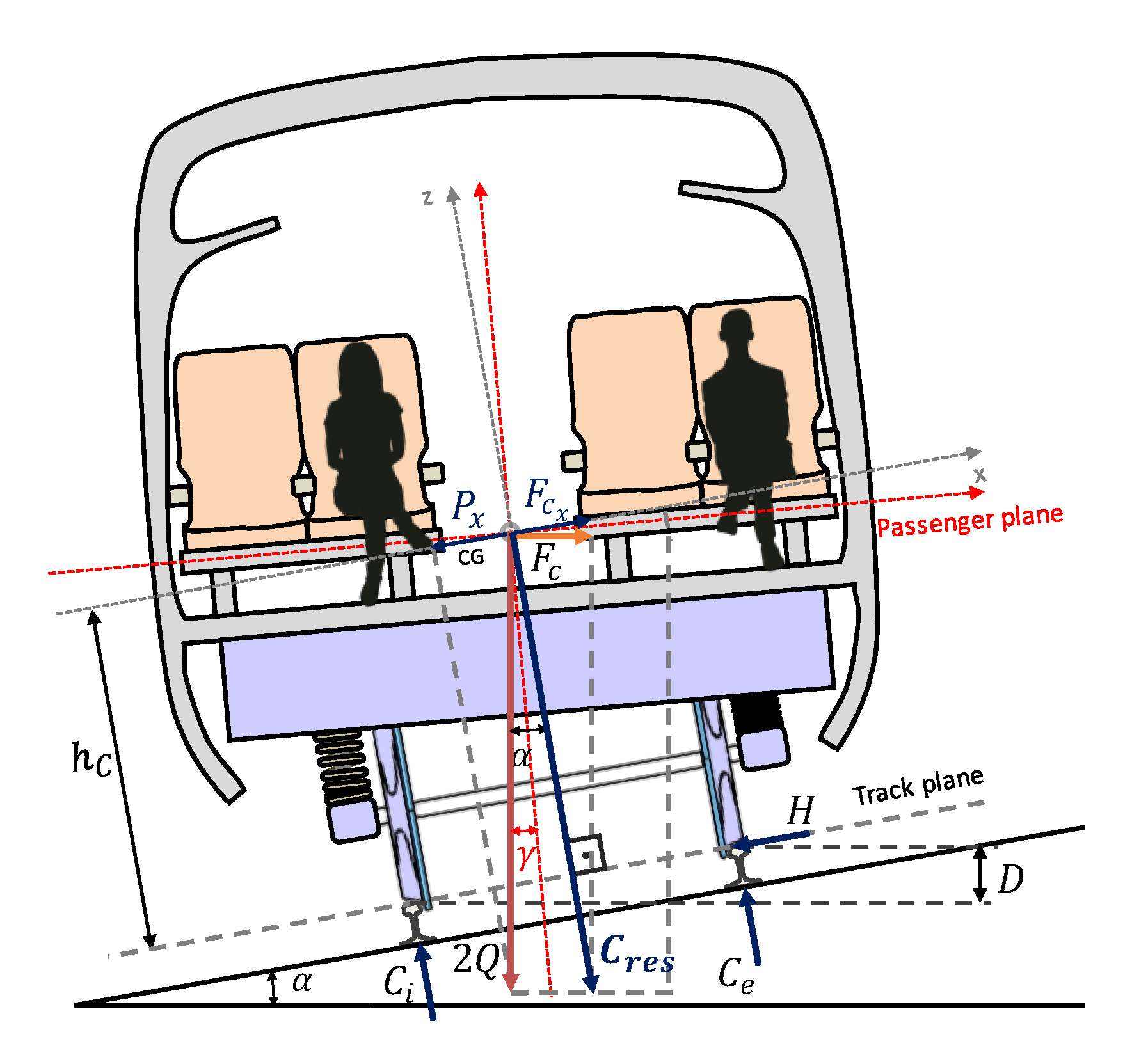
2.1. Design Parameters for Railway Track Curves
2.1.1. Parameters Involved to Define the Radii
Cant
| e (mm) | |||
|---|---|---|---|
| R (m) | V (km/h) | 1500 | 1740 |
| 7700 | 100 | 15.3 | 17.8 |
| 7700 | 250 | 95.9 | 111.2 |
| 7700 | 300 | 138.0 | 160.1 |
| 7700 | 350 | 187.9 | 218 |
Cant Deficiency
The Cant Excess
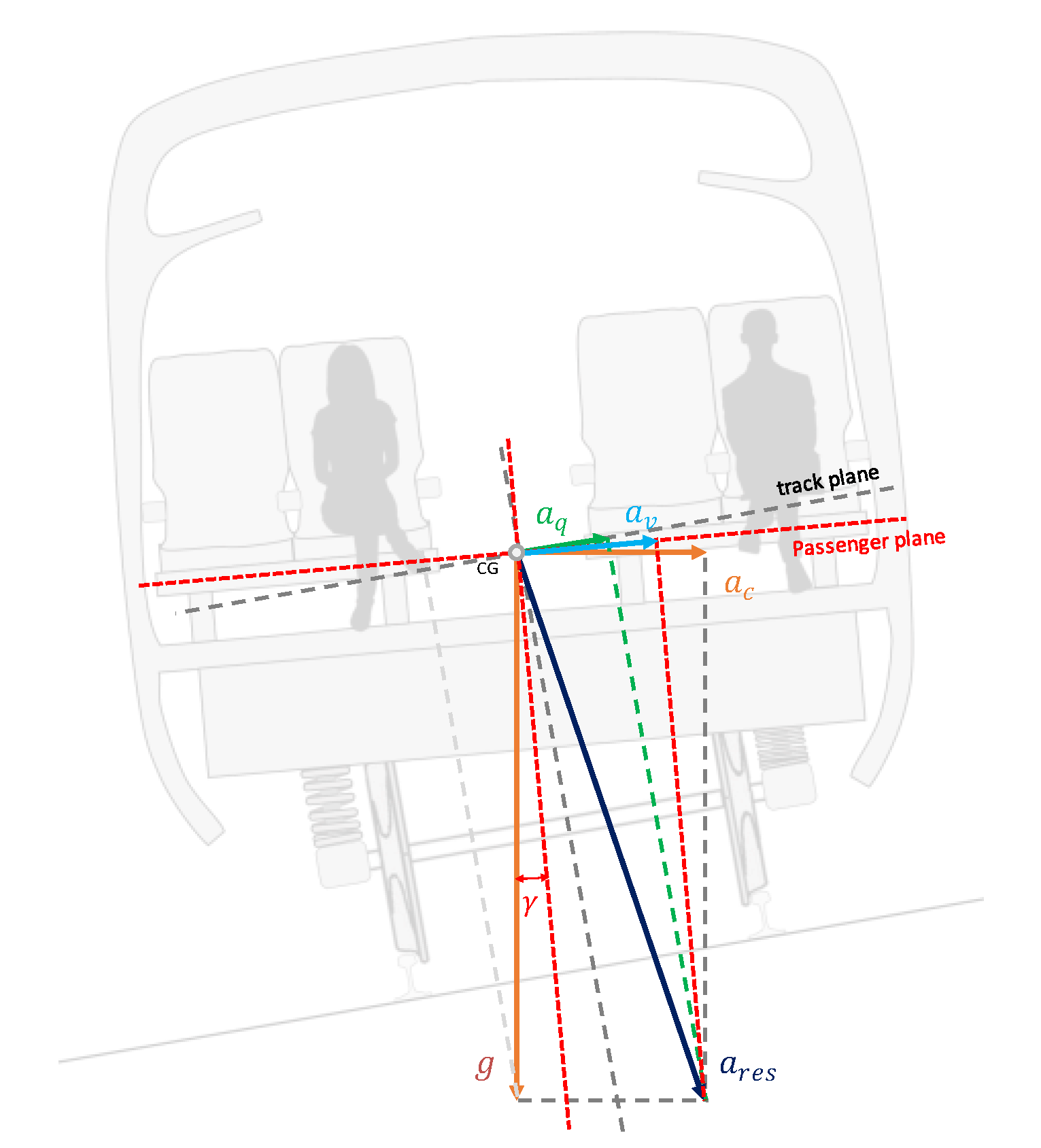
The Uncompensated Lateral Acceleration
2.1.2. Parameters Involved in Defining the Transition Curve (Clothoid)
2.2. Design Constraints for Railway Track Curves
2.2.1. The Passenger Comfort
2.2.2. The Lateral Stability
- Quasistatic forces mainly derived from unbalanced cant and thermal loads,
- Dynamic reasons mainly derived from the track quality, and
- The crosswind that may appear.
2.2.3. Maintenance Cost
- Static load , which is simply the static weight of the train in this case, and for convenience, measured by wheel .
- Quasistatic loads , which are the loads appearing while the train travels around a bend such that (see Table 2).
| Inner Rail Load (Ci,a) | Outer Rail Load (Ce,a) | |
|---|---|---|
| If cant deficiency (I) | ||
| If cant excess (E) |
2.3. Design Constraints for Railway Track Clothoid
- Geometrical limitations:
- ○
- It must be tangent to the straight for one side and to the circular curve on the other.
- ○
- It must have the same curvature as the straight (0) and the curve (1/R).
- ○
- It must have a continuous change in curvature.
- ○
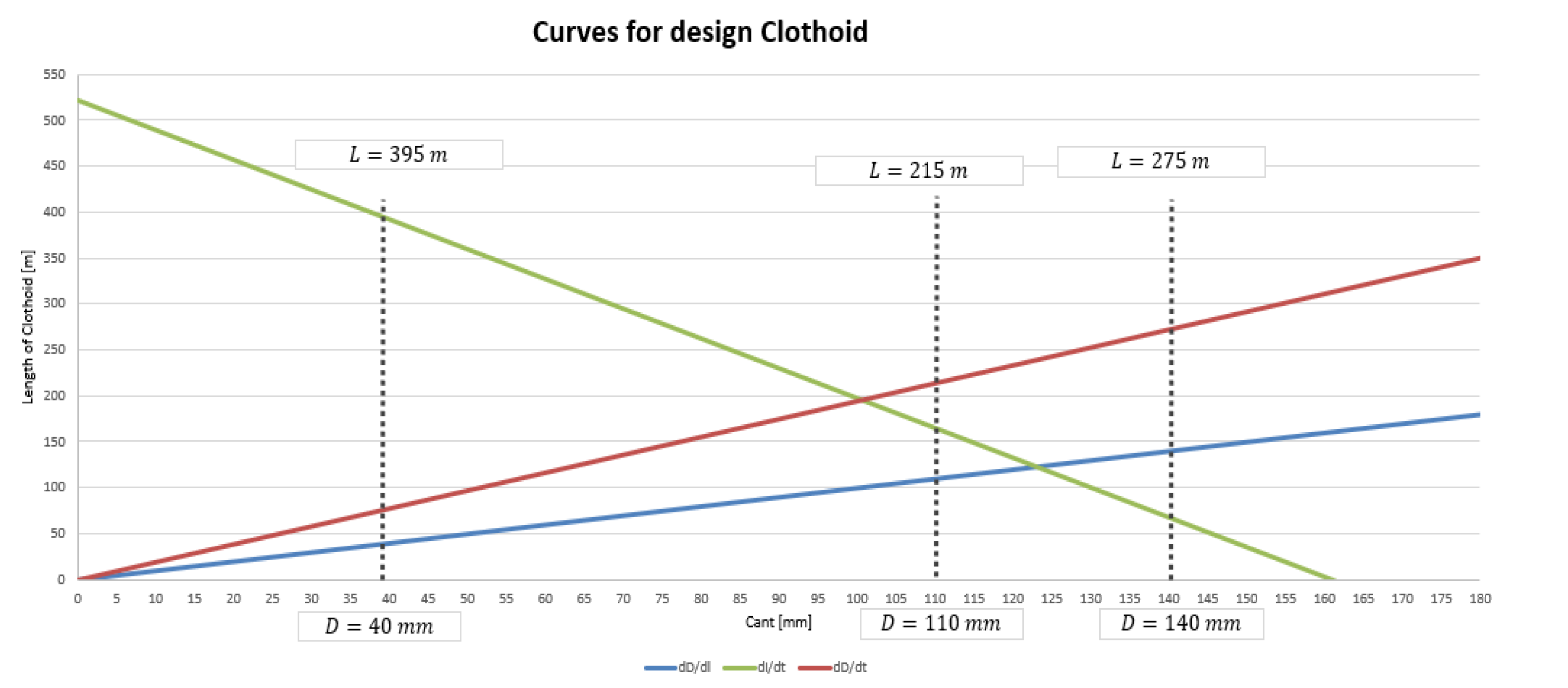
- The length of the clothoid must be defined to minimize the cant wrap at the end of the transition, and for this, a limit for the cant gradient ( [mm/m]) must be set. For this:
- Functional conditions:
- ○
- To avoid both dynamic problems with the rolling stock and comfort problems with passengers, the ascendent speed ( [mm/s]) of the train’s outer wheel during the transition must be limited. Therefore:
- ○
- To ensure a smooth variation in uncompensated acceleration, the variation in this parameter with time is limited. In other words, the rate of cant deficiency variation ( [mm/s]) is limited. Therefore:
| Parameter | Parameter Value | Clothoid Length for D = 140 mm | Clothoid Length for D = 100 mm |
|---|---|---|---|
| 1 mm/m | 140 m | 100 m | |
| 50 mm/s | 272 m | 195 m | |
| 30 mm/s | 193 m | 323 m |
2.4. Review of the Design Parameters Limitation of Several Technical Standards
- Spain, according to Spanish standards (Adif [6]).
- The USA, Germany, France, Japan, and Sweden, according to (Rakoczy et al.) [3].
- Technical Specification for Interoperability (TSI) (European Association for Railway Interoperability (AEIF) [28]).
- Committee for European Standardization (CEN) (European Committee for Standardization (CEN) [29]).
- Rail Baltic (railway infrastructure project to link Estonia, Latvia, and Lithuania with Poland) (Ernst and Young [30]).
- (Russia, Slovakia, Ukraine) from Contact Group of the Organization for Cooperation between Railways (OSJD) with the European Union Agency for Railways (ERA) (OSJD and (ERA)), [31].
3. The Proposed Methodology
- Propose a number of alignment alternatives to be developed with a proper design software (in the case of this paper, we used Istram-Ispol). For each one:
- The first step should be to decide which cant law have to be used; i.e., a relationship that provides a cant as a function of the radius of the curve. This decision and the project speed will condition the value of the design parameters including the radii and also the clothoids.
- In the second step, a novel graphical representation to decide which radii should better fit with the requirements of the design is presented. With it, we intend to have a single picture of all the parameters, equations, and constraints involved in the design, which will allow us to make better decisions.
- Once the radius and the cant of the curve are decided, the third step is intended to design the clothoid. For this, another graphical method is proposed in order to design a flexible clothoid while taking into account not only the current traffic conditions, but also that it should fit with future possible scenarios.
- Compare the alternatives using some quantitative figures to finally decide which one is the best. These figures can be those noted in Section 2.
3.1. Defining the Criteria to Design the Cant
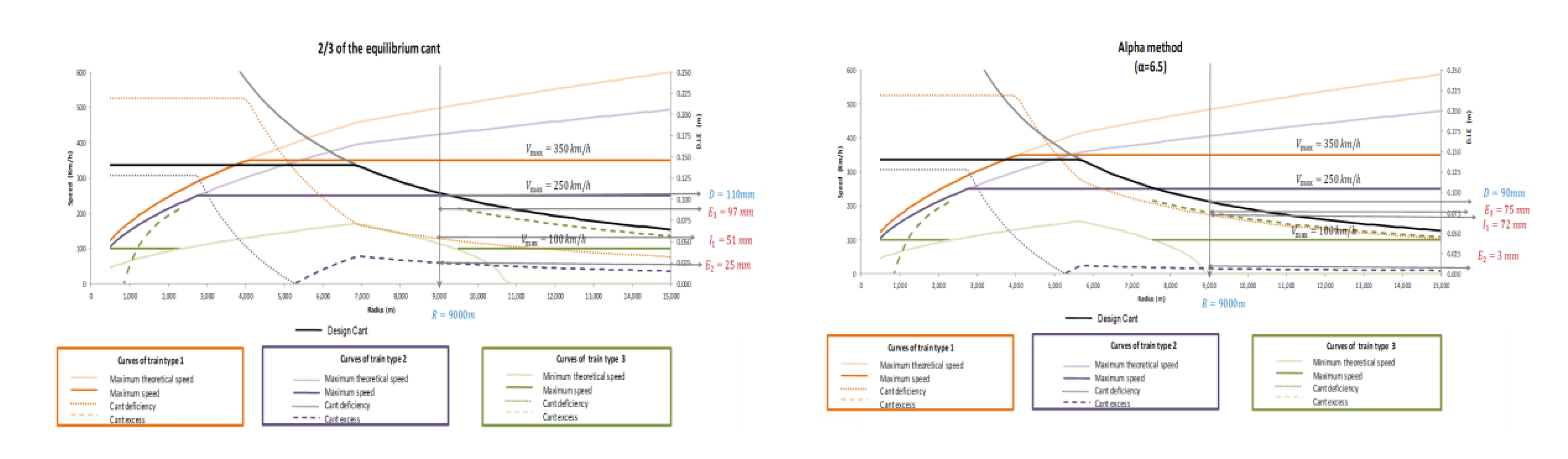
3.1.1. The 2/3 of the Equilibrium Cant Method
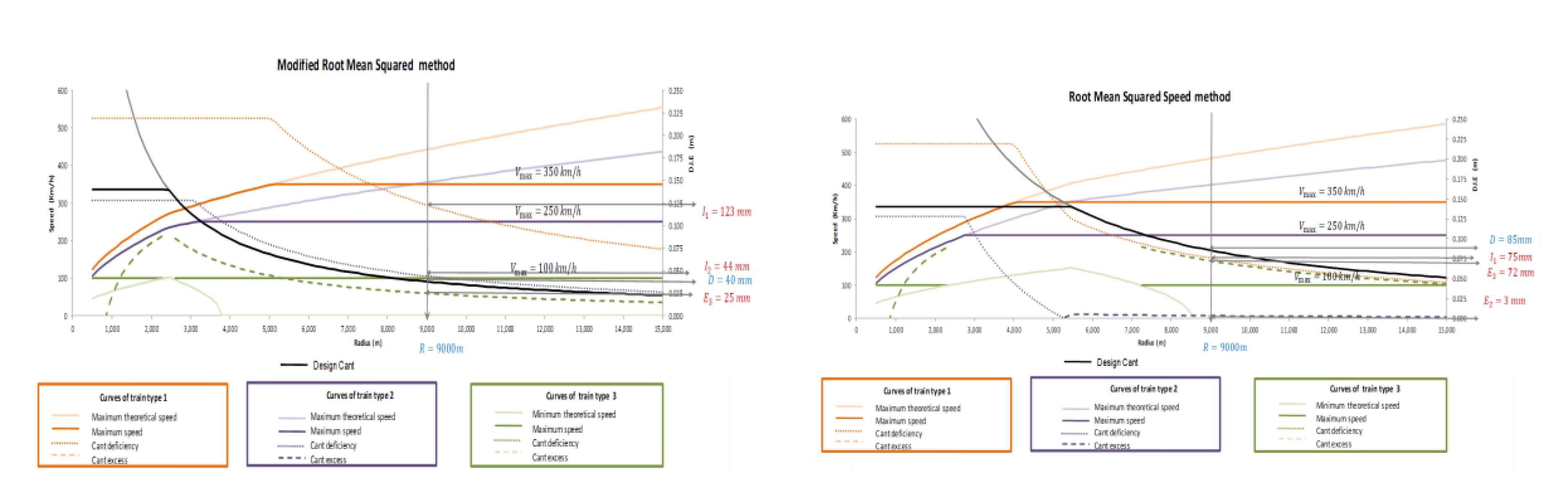
3.1.2. The Root-Mean-Squared Speed Method
3.1.3. The Alpha Method
3.1.4. The Modified Root-Mean-Squared Method
3.2. Graphical Representation to Define the Cant and the Radii
- The black line represents the proposed design cant as a function of the radii and according to one of the criteria defined in Section 3.1. In this particular case, 2/3 of the equilibrium cant method is represented. Note that since , the line has 2 parts:
- The orange lines represent the design curves for the high-speed trains used as the design cant for the curve in (17). Particularly:
- ○
- The solid orange line represents the maximum allowed speed for this train () as a function of the radii according to Equation (6) and assuming . Again, and due to the maximum speed for this type of train, this line has two parts:
- ○
- The resultant cant deficiency is a dashed orange line according to Equation (2). In this case, the curve has three parts:
- The purple lines represent the design curves for the shuttle train also using Equation (13) as the cant criteria. Specifically:
- ○
- The maximum allowed speed as a function of the radii is represented as a solid line that also has two parts with the same expressions as in Equation (18), but using instead . Note that in this case, because instead of , the maximum allowed speed has to be lower to meet the limit of . In any case, when designing high-speed railway lines, this limit is never reached, no matter the type of train, due to the high cant deficiency obtained for those combinations of , and , having then to increase the radius to decrease
- ○
- The resultant cant deficiency is a dashed line according to Equation (2). Note that for this type of train with , and since , the shape of the curve has some interesting features, and four sections can be defined as follows:
- The green lines represent the design curves for the freight trains. For the sake of simplicity, we have avoided the analysis of small radii, where cant deficiency may appear for slow trains:
- ○
- From Equation (9) and assuming a certain limit for the cant excess (), the minimum allowed speed is represented as a light solid line according to the expressions below:
- ○
- The resultant cant excess is a long dashed line, according to Equation (3).
- By supposing that the slowest train travels at, for example, 180 km/h, which is the maximum of the minimum speed curve (the green light curve). However, it may be difficult for rail freight transport to be profitable at those speeds.
- By changing the limit value of the cant excess imposed by the standard, the invalid radii would be reduced. This may have other consequences; for example, Equation (9). The last solution is to modify all the designs and change the cant definition criteria.
| Criterium to Define the Cant | |||||
|---|---|---|---|---|---|
| Parameter to Analyze | 2/3 of the Equilibrium Cant | Alpha Method | Root-Mean-Squared Speed Method | Modified Root-Mean-Squared Method | |
| Cant | D (mm) | 110 | 90 | 85 | 40 |
| Coefficient maintenance cost | 1.17 | 1.13 | 1.12 | 1.03 | |
| High-speed train (V1 = 350 km/h) | |||||
| Cant deficiency | (mm) | 51 | 72 | 75 | 123 |
| Uncompensated acceleration | (m/s2) | 0.33 | 0.46 | 0.49 | 0.80 |
| Uncompensated acceleration in the passenger | (m/s2) | 0.23 | 0.32 | 0.35 | 0.56 |
| Coefficient lateral stability | 1.80 | 1.73 | 1.71 | 1.57 | |
| Shuttle train (V2 = 250 km/h) | |||||
| Cant deficiency | (mm) | - | - | - | 44 |
| Cant excess | (mm) | 25 | 6 | 3 | - |
| Uncompensated acceleration | (m/s2) | 0.18 | 0.05 | 0.02 | 0.29 |
| Uncompensated acceleration in the passenger | (m/s2) | 0.22 | 0.06 | 0.02 | 0.35 |
| Coefficient lateral stability | 2.39 | 2.53 | 2.56 | 2.59 | |
| Freight train (V3 = 100 km/h) | |||||
| Cant excess | (mm) | 97 | 75 | 72 | 25 |
| Uncompensated acceleration | (m/s2) | 0.63 | 0.50 | 0.47 | 0.16 |
| Coefficient lateral stability | 3.02 | 3.57 | 3.37 | 4.33 | |
3.3. Graphical Representation to Define the Length of the Clothoid
4. Case Study
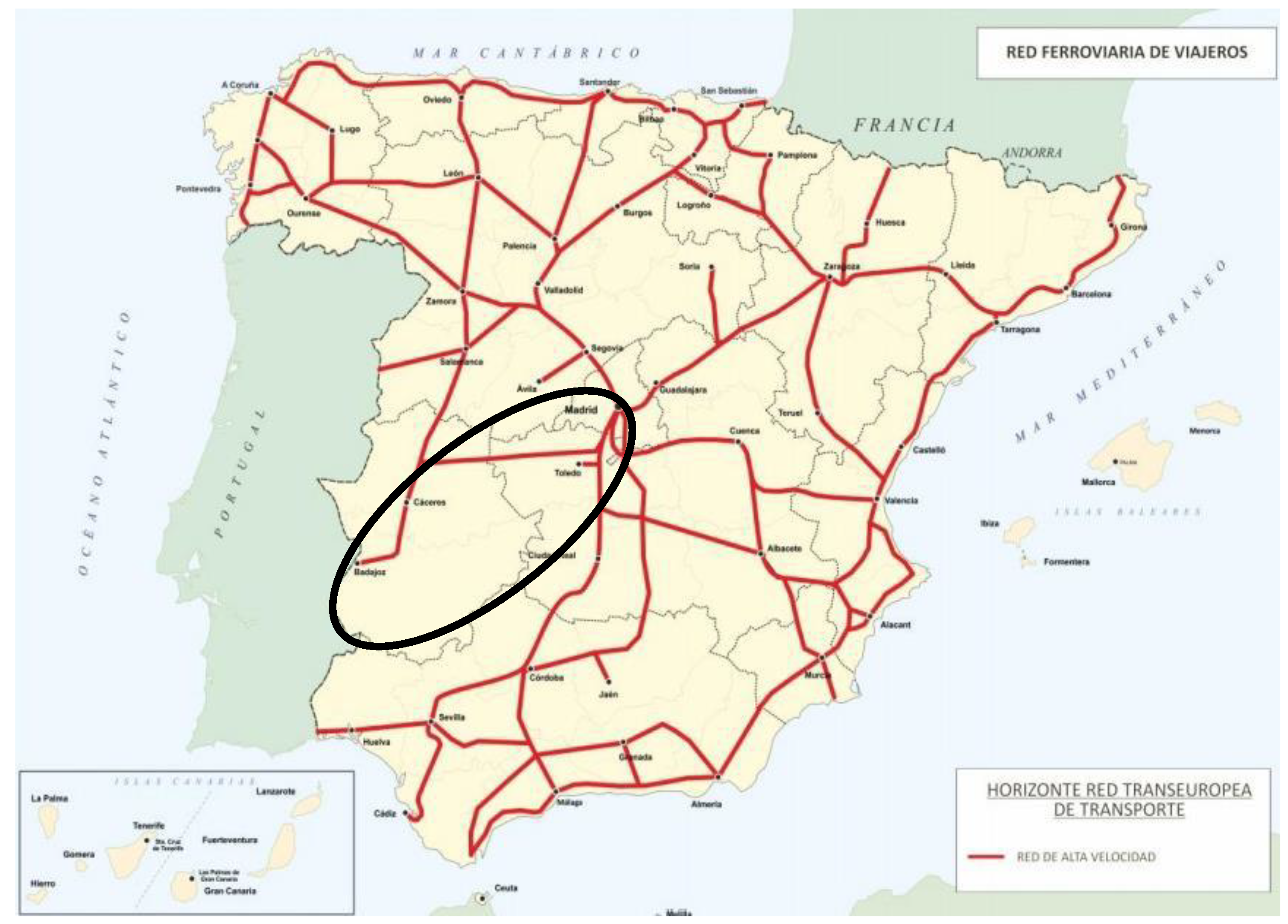
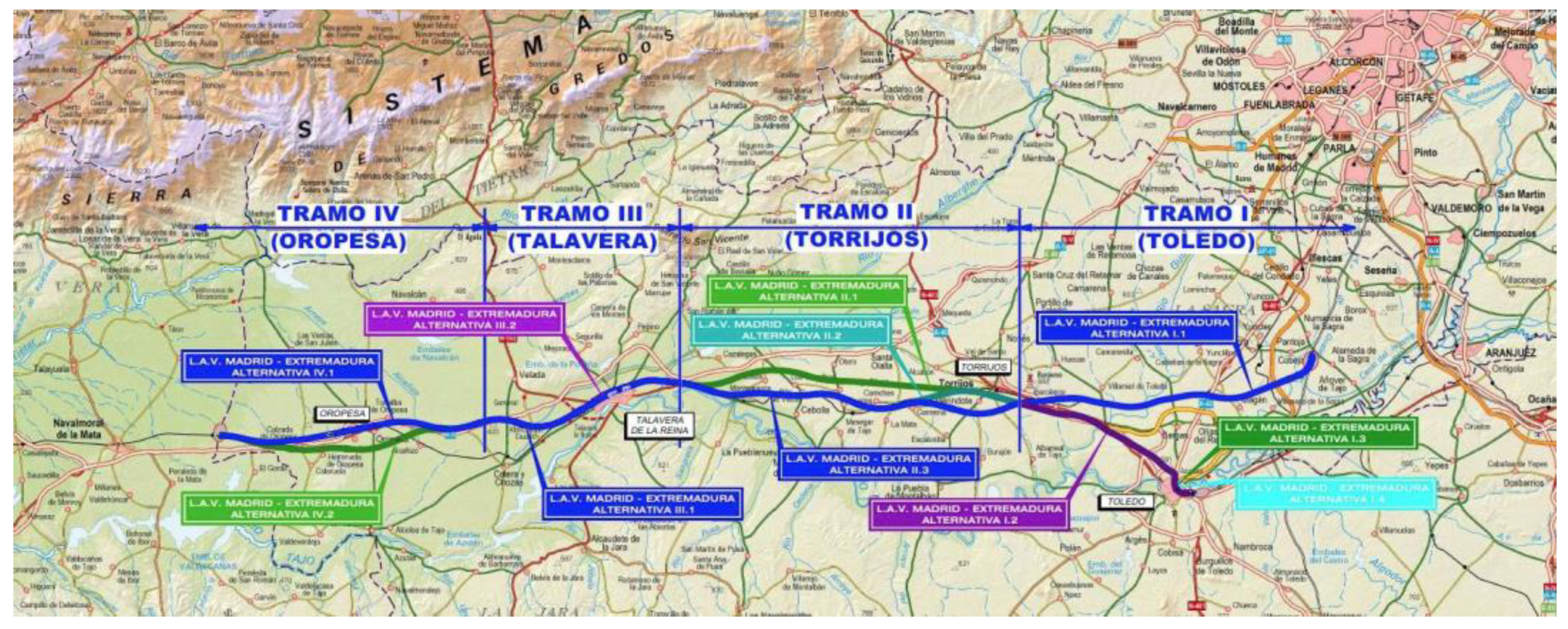
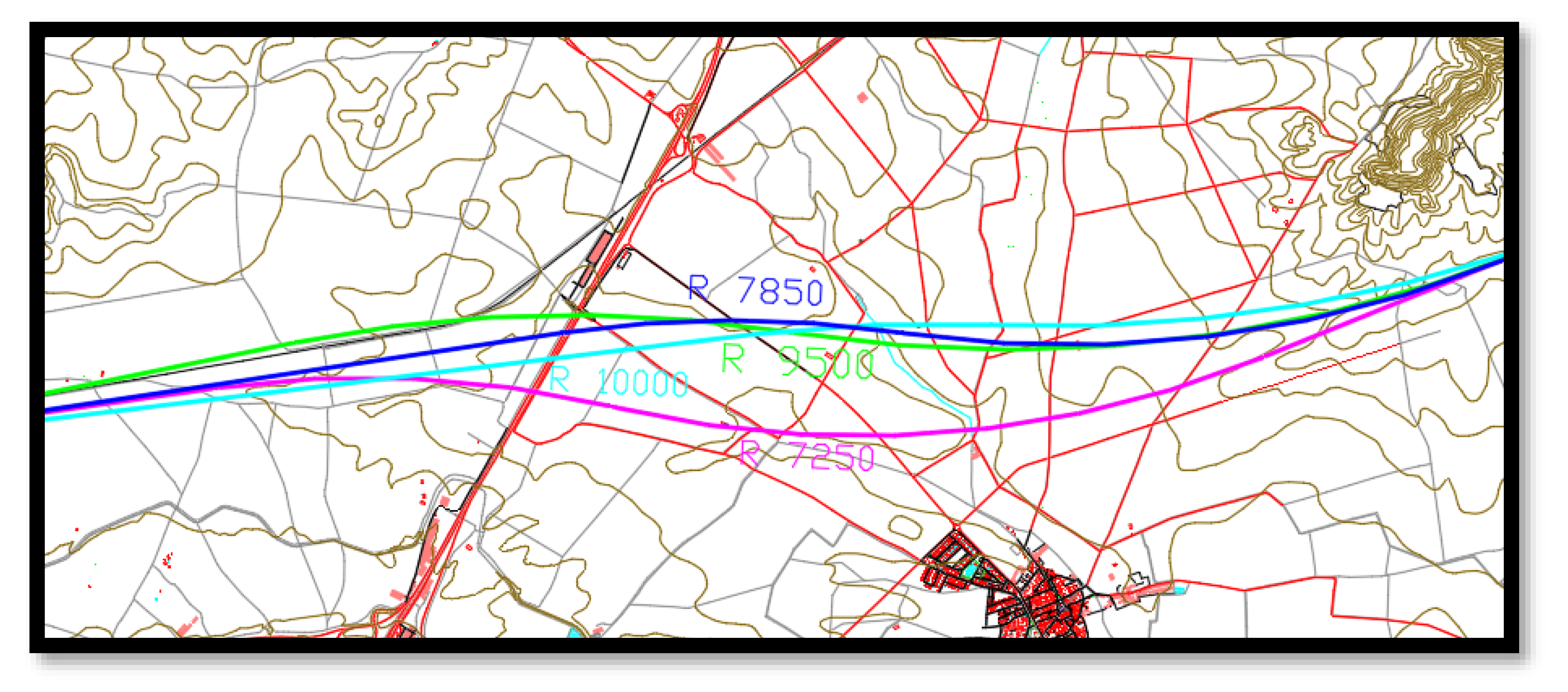
4.1. Location and Description of the Considered Section
- Alternative I.1. Corresponding with the blue line of Section I. This section connects with the high-speed line Madrid–Sevilla and finishes in Torrijos.
- Alternative II.3. Corresponding with the blue line of Section II, we studied just the first half of this section. It connects with Alternative I.1 in Torrijos and finishes in Talavera de la Reina.
- The trains that will operate the corridor will be the Renfe’s S-102 series (Talgo T350) for high-speed services (AVE), and the S-114 series for shuttle services (Avant). In addition, we included freight trains. The characteristics of those trains are given in Table 5.
- The capacity of the trains was 320 passengers for S-102 and 230 for S-114.
- The mean occupancy grade for both AVE and Avant trains was 60%.
- The effective schedule for traveler trains will be from 6:00 a.m. to 10:00 p.m. (16 effective hours); therefore, between 10:00 p.m. and 6:00 a.m., freight trains could use the line while respecting at least 3 h daily for maintenance. With this, the estimated traffic is shown in Table 7. Regarding freights trains, we understand that the Lisbon–Madrid corridor is an important one because it could join some Portuguese ports with Madrid and the rest of Europe. So, freight transport by train could be very competitive, and therefore we estimated 8 freight trains each way per day in this line for 2030 and 10 for 2050.
4.2. Proposing Some Alternatives to Be Compared with the Original Project
4.2.1. Alternative 0: The Proposed Alternative in the Original Project
4.2.2. Alternative 1: The Proposed Alignment from the Original Project but a Different Cant Law
4.2.3. Alternative 2: Designing Using the 2/3 of the Equilibrium Cant Method
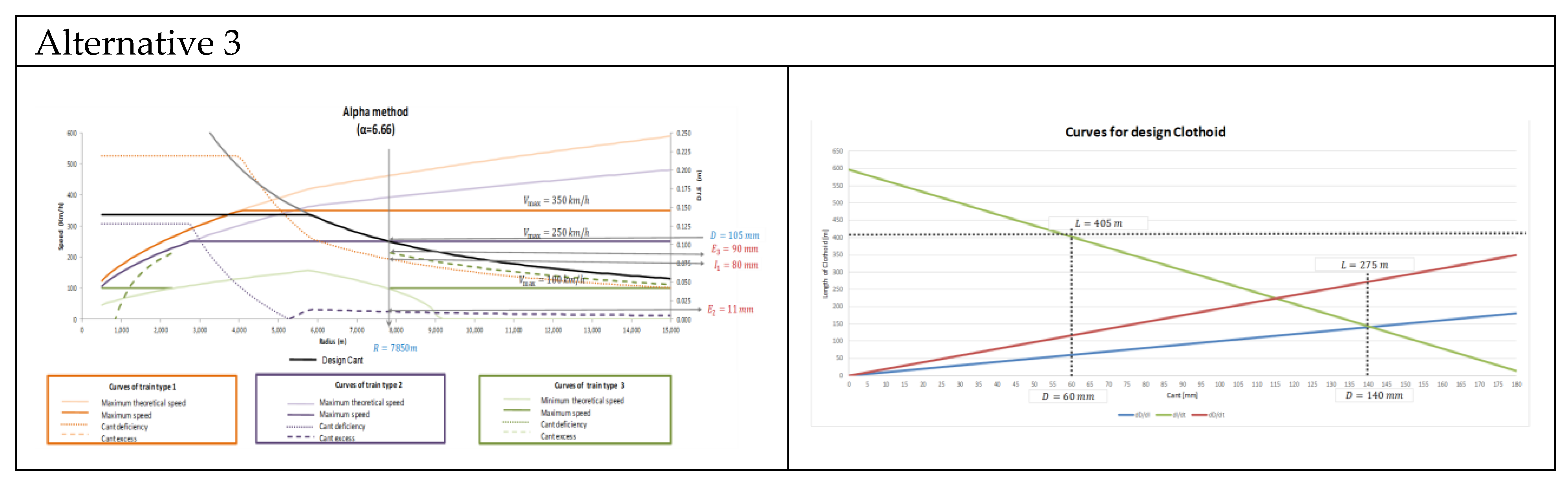
4.2.4. Alternative 3: Designing Using the Alpha Method
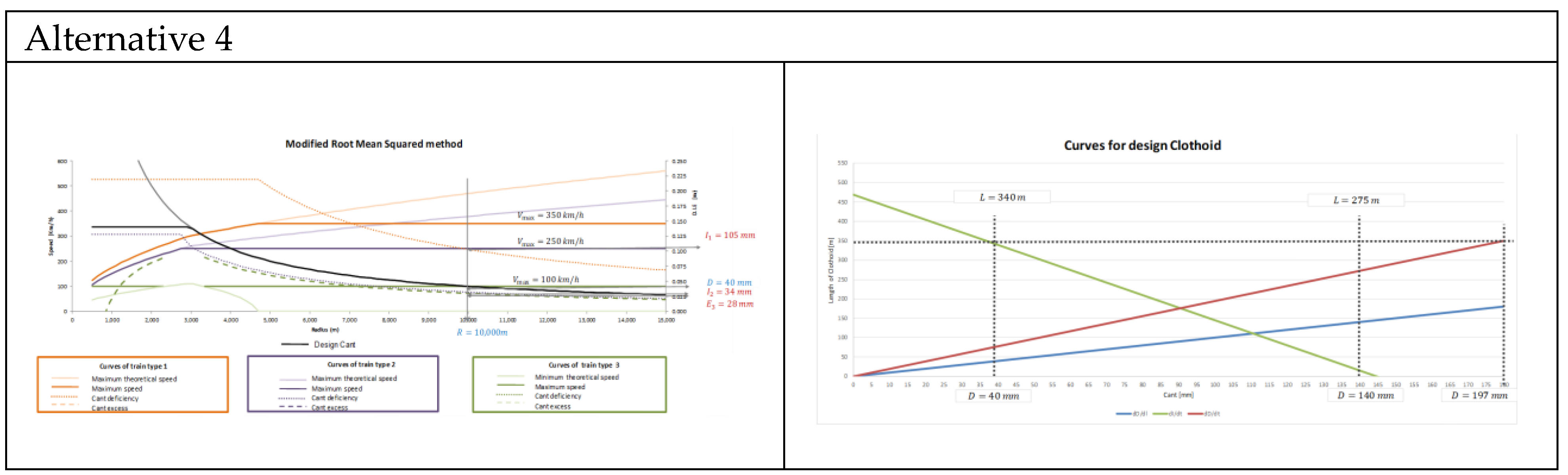
4.2.5. Alternative 4: Designing Using the Modified Root-Mean-Squared Method
4.3. Comparing Alternatives
| Parameter to Analyze | # of Alternative | |||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | ||
| Alpha Method | 2/3 of the Equilibrium Cant | Alpha Method | Modified Root-Mean-Squared Method | |||
| Cant | D (mm) | 140 | 105 | 105 | 105 | 40 |
| Radius | R (mm) | 7250 | 7250 | 9500 | 7850 | 10,000 |
| Clothoid | L (mm) | 460 | 460 | 300 | 405 | 340 |
| Coefficient maintenance cost | 1.27 | 1.19 | 1.21 | 1.19 | 1.07 | |
| = 350 km/h) | ||||||
| Cant deficiency | (mm) | 60 | 95 | 47 | 80 | 105 |
| Uncompensated acceleration | (m/s2) | 0.39 | 0.42 | 0.31 | 0.52 | 0.68 |
| Uncompensated acceleration in the passenger | (m/s2) | 0.27 | 0.43 | 0.22 | 0.36 | 0.48 |
| Coefficient lateral stability | 1.89 | 1.76 | 1.94 | 1.70 | 1.73 | |
| = 250 km/h) | ||||||
| Cant deficiency | (mm) | − | − | − | − | 34 |
| Cant excess | (mm) | 38 | 3 | 27 | 11 | − |
| Uncompensated acceleration | (m/s2) | 0.25 | 0.02 | 0.18 | 0.07 | 0.22 |
| Uncompensated acceleration in the passenger | (m/s2) | 0.30 | 0.02 | 0.21 | 0.09 | 0.27 |
| Coefficient lateral stability | 2.32 | 2.56 | 2.39 | 2.50 | 2.35 | |
| = 100 km/h) | ||||||
| Cant Excess | (mm) | 124 | 90 | 93 | 90 | 28 |
| Uncompensated acceleration | (m/s2) | 0.81 | 0.55 | 0.60 | 0.59 | 0.18 |
| Coefficient lateral stability | 2.71 | 3.12 | 3.07 | 3.11 | 4.24 | |
5. Conclusions and Future Research
- ○
- The graphic method allowed us to see all the design parameters and their limitations in the same figure, and modifications in terms of changing the criteria to design the cant could be very easily analyzed. So, it was very powerful when looking for some alignment alternatives.
- ○
- We pointed out the importance of explicitly evaluating the passenger comfort, the train lateral stability in curves, and the maintenance cost when designing the curves of the alignment. In particular, nowadays, the maintenance cost for high-speed railway lines can amount to about EUR 3 million per km and year (see, for example, Campos Méndez et al. [37] and Normas Técnicas Vía ADIF [38]). Therefore, taking into account this point in this early phase of the lifetime of the infrastructure is a key point.
- ○
- The proposed method to define the length of clothoids took into account not only that it must meet the standard for the proposed radius–cant pair, but also the possibility to be valid for an eventual change of the cant that adapts the railway track to a new traffic operation. This is not an evident aspect, because if the length is not well chosen, the speed limit for high-speed trains and/or freight trains might be modified.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation
| Symbol | Unit | Description |
| m2 | Clothoid parameter | |
| m/s2 | Total acceleration | |
| m/s2 | Compensated acceleration by cant | |
| m/s2 | Uncompensated acceleration in the track plane | |
| m/s2 | Uncompensated acceleration in the passenger | |
| mm/m | Geometric limitation (cant ramp) | |
| mm/s | Dynamic limitation (ascent speed) | |
| mm/s | Rate of change cant deficiency with time | |
| Tn | Vertical reaction force in the inner rail | |
| Tn | Vertical reaction force in the outer rail | |
| Tn | Resultant force | |
| Center of gravity | ||
| mm | Cant | |
| mm | Equilibrium cant | |
| mm | Theoretical equilibrium cant | |
| mm | Cant excess | |
| E | mm | Track width (the distance between the centerline of two rails) |
| Tn | Centrifugal force | |
| m/s2 | Gravity acceleration (9.8 m/s2) | |
| Tn | Horizontal reaction force in one of the rails | |
| Tn | Transversal load | |
| Tn/axle | Wind load | |
| m | Distance between the rail axis and the center of gravity | |
| mm | Cant deficiency | |
| m | Length of transition curve (clothoid) | |
| Tn/axle | Minimum load that the track will support | |
| MSR | Medium-speed railway | |
| HSR | High-speed railway | |
| Number of axles of each composition | ||
| Tn | Train weight per wheel | |
| Tn | Static loads per wheel | |
| Tn | Quasistatic loads per wheel | |
| Tn | Dynamic overloads per wheel | |
| m | Radius of the curve | |
| Km/h | Speed | |
| Km/h | Equilibrium speed | |
| Km/h | Root-mean-squared speed | |
| Km/h | Weighted root-mean-squared speed | |
| Inclination angle | ||
| Coefficient to take care of track maintenance, and layout of tracks | ||
| Safety factor of lateral track stability | ||
| Coefficient for maintenance cost | ||
| P | Passenger train | |
| F | Freight train |
References
- Watson, I.; Ali, A.; Bayyati, A. Freight transport using high-speed railways. Int. J. Transp. Dev. Integr. 2019, 3, 103–116. [Google Scholar] [CrossRef]
- Biancardo, S.A.; Avella, F.; Di Lisa, E.; Chen, X.; Abbondati, F.; Dell’Acqua, G. Multiobjective Railway Alignment Optimization Using Ballastless Track and Reduced Cross-Section in Tunnel. Sustainability 2021, 13, 10672. [Google Scholar] [CrossRef]
- Cant Excess for Freight Train Operations on Shared Track (Report No: DOT/FRA/ORD-20/05). Available online: https://railroads.dot.gov/elibrary/cant-excess-freight-train-operations-shared-track (accessed on 24 May 2022).
- Lazarević, L.; Popović, Z.; Vilotijević, M.; Mirković, N. Track alignment parameters on modern railway lines for mixed traffic. In Proceedings of the XVIII Scientific-Expert Conference on Railways in RAILCON ’18, Niš, Serbia, 11–12 October 2018; pp. 77–80. [Google Scholar]
- Mixed Freight and Higher-Speed Passenger Trains: Framework for Superelevation Design. (Report No: DOT/FRA/ORD-19/42). Available online: https://railroads.dot.gov/elibrary/mixed-freight-and-higher-speed-passenger-trains-framework-superelevation-design (accessed on 24 May 2022).
- Adif, NAP 1-2-1.0 Meteorología Para el Diseño del Trazado Ferroviario. Available online: http://descargas.adif.es/ade/u18/GCN/NormativaTecnica (accessed on 3 June 2022).
- High-Speed Rail Freight Sub-Report in Efficient Train Systems for Freight Transport. Available online: https://www.kth.se/polopoly_fs/1.87134!/Menu/general/column-content/attachment/0512_inlaga.pdf (accessed on 24 February 2022).
- Investigating Technical Challenges and Research Needs Related to Shared Corridors for High-Speed Passenger and Railroad Freight Operations. Available online: http://www.fra.dot.gov (accessed on 17 February 2022).
- Ambrósio, J.; Rauter, F.; Pombo, J.; Pereira, M.S. A flexible multibody pantograph model for the analysis of the catenary-pantograph contact. Comput. Methods Appl. Sci. 2011, 23, 1–27. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Ronnquist, A.; Navik, P.; Liu, Z. Contact Wire Irregularity Stochastics and Effect on High-Speed Railway Pantograph-Catenary Interactions. IEEE Trans. Instrum. Meas. 2020, 69, 8196–8206. [Google Scholar] [CrossRef]
- Superelevation Optimization for Mixed Freight and Higher-Speed Passenger Trains. Available online: https://railtec.illinois.edu/wp/wp-content/uploads/2019/01/Dick-et-al-2016-AREMA.pdf (accessed on 4 July 2022).
- Guillén, M.F. The Limits of Convergence: Globalization and Organizational Change in Argentina, South Korea, and Spain; Anthony, W.P., Stephen, H., Robert, K.S., Eds.; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Maganti, H.C.; Manju, Y.; Akula, N.S.D.K. Dynamic behaviour mainly on performances, environmental, safety and health benefits of european highspeed trains (madrid-barcelona highspeed line). Int. J. Eng. Appl. Sci. Technol. 2021, 5, 247–253. [Google Scholar]
- Brustad, T.F.; Dalmo, R. Infrastructures Railway Transition Curves: A Review of the State-of-the-Art and Future Research. Infrastructures 2020, 5, 43. [Google Scholar] [CrossRef]
- Investigation of Ride Comfort and Comfort Disturbance on Transition and Circular Curves. Available online: https://trid.trb.org/view/696691 (accessed on 3 June 2022).
- Esveld, C. Modern Railway Track, 2nd ed.; Zwarthoed, D., Nieuwenhuizen, V., Eds.; MRT-Productions: Zaltbommel, The Netherlands, 2001. [Google Scholar]
- López Pita, A. Infraestructura Ferroviaria, 2nd ed.; Universitat Politecnica de Catalunya: Barcelona, Spain, 2006; Volume 12. [Google Scholar]
- Renfe’s-S102/112. Available online: https://www.renfe.com/es/en/renfe-group/renfe-group/fleet-of-trains/s-102-112 (accessed on 19 April 2022).
- Yu, M.; Jiang, R.; Zhang, Q.; Zhang, J. Crosswind Stability Evaluation of High-Speed Train Using Different Wind Models. Chin. J. Mech. Eng. 2019, 32, 40. [Google Scholar] [CrossRef] [Green Version]
- Historical Wind Speed Equivalents of the Beaufort Scale, 1850–1950. Available online: https://www.knmi.nl/kennis-en-datacentrum/publicatie/historical-wind-speed-equivalents-of-the-beaufort-scale-1850-1950 (accessed on 3 June 2022).
- Hasan, N. Lateral Stability of a Ballasted Curved Track. J. Transp. Eng. Part A Syst. 2020, 146, 1–6. [Google Scholar] [CrossRef]
- Gallego, I.; Álvarez-Bazo, F.; Sanchez-Cambronero, S.; Rivas, A. State of the Art: Deterioration Models of Railway Ballasts and Subgrades. Recommendations and Applications. Glob. J. Eng. Sci. 2020, 4, 1–15. [Google Scholar] [CrossRef]
- Grossoni, I.; Powrie, W.; Zervos, A.; Bezin, Y.; le Pen, L. Modelling railway ballasted track settlement in vehicle-track interaction analysis. Transp. Geotech. 2021, 26, 100433. [Google Scholar] [CrossRef]
- Gallego, I.; Munoz, J.; Rivas, A.; Sanchez-Cambronero, S. Vertical Track Stiffness as a New Parameter Involved in Designing High-Speed Railway Infrastructure. J. Transp. Eng. 2011, 137, 971–979. [Google Scholar] [CrossRef]
- Gallego, I.; Muñoz, J.; Sánchez-Cambronero, S.; Rivas, A. Recommendations for Numerical Rail Substructure Modeling Considering Nonlinear Elastic Behavior. J. Transp. Eng. 2013, 139, 1–34. [Google Scholar] [CrossRef]
- Balmaseda, L.; Gallego, I.; Sánchez-Cambronero, S.; Rivas, A. Importance of vertical rail track stiffness on dynamic overloading: Limitations of the Eisenmann formulation. 360 Rev. Alta Velocidad 2018, 5, 301–311. [Google Scholar]
- Meek, D.S.; Walton, D.J. A note on finding clothoids. J. Comput. Appl. Math. 2004, 170, 433–453. [Google Scholar] [CrossRef] [Green Version]
- Moving Europe Towards a Sustainable and Safe Railway System without Frontiers (ERA/Activities). Technical Specification for Interoperability (TSI). Available online: https://www.era.europa.eu/activities/technical-specifications-interoperability_en (accessed on 3 June 2022).
- European Committee for Standardization (CEN), Railway Application—Track Alignment Design Parameters—Track Gauges 1435 and Wider—Part 1: Plain Line [EN 13803-1:2010, CEN/TC256/WC15]. Available online: https://standards.iteh.ai/catalog/standards/cen/9565785d-11ef-4b9d-9831-a5a6e5551119/en-13803-1-2010 (accessed on 23 February 2022).
- Design Guidelines Railway Alignment. Available online: https://www.railbaltica.org/wp-content/uploads/2021/06/RBDG-MAN-013-0105_RailwayAlignment.pdf (accessed on 3 June 2022).
- Analysis of the Basic Parameters for Maintaining Technical and Operational Compatibility. Available online: https://www.era.europa.eu/sites/default/files/agency/docs/analysis_1520_inf_en.pdf (accessed on 3 June 2022).
- Renfe. Available online: https://www.renfe.com/es/es/grupo-renfe/grupo-renfe/flota-de-trenes (accessed on 3 June 2022).
- Estudio Informativo del Proyecto de Línea Ferroviaria de Alta Velocidad Madrid-Extremadura: Tramo Madrid-Oropesa | Ministerio de Transportes, Movilidad y Agenda Urbana. Available online: https://www.mitma.gob.es/ferrocarriles/estudios-en-tramite/estudios-y-proyectos-en-tramite/madrid-oropesa (accessed on 11 April 2022).
- Istram, Software Para Ingeniería Civil, Desarrollo Inteligente. Available online: https://istram.net/ (accessed on 11 May 2022).
- Adif -IGP-3 Instrucciones Y Recomendaciones Sobre Trazado Índice. Available online: https://tinyurl.com/yfshvdwm (accessed on 3 June 2022).
- Datosclima.es-Base de Datos Meteorológica. Red Principal Estaciones Meteorológicas de AEMET. Available online: https://datosclima.es/ (accessed on 11 April 2022).
- Campos Méndez, J.; de Rus Mendoza, G.; Barrón de Angoiti, I. El transporte ferroviario de alta velocidad. Una visión económica. Fund. BBVA 2009, 3, 15–24. [Google Scholar]
- Normas Técnicas via ADIF. Available online: http://descargas.adif.es/ade/u18/GCN/NormativaTecnica.nsf/v0/51C52AFFBF10BF52C12573AA003ECE4A/$FILE/NAV%207151.pdf?OpenElement (accessed on 25 June 2022).




| Standard | Traffic Type | Gauge (mm) | Vmax (km/h) | max (mm) | (mm) | Emax (mm) | dD/dt (mm/s) | dD/dl (mm/m) | (m/s2) |
|---|---|---|---|---|---|---|---|---|---|
| France | MSRs HSRs | 1435 | ≤250 ≥300 | 160 180 | 150 100 | 70–100 | 30 | 0.5–0.7 | 1–2 |
| Germany | HSRs | 1435 | ≥300 | 180 | 150 | 70–110 | 30 | 0.5–0.7 | 1–2 |
| Spain | MSRs HSRs | 1435 | 250 350 | 140 | 60 80 | 90 | 50 | 1 | 0.52 0.39 |
| Sweden | HSRs F | 1435 | 300 120 | 100 | 150 100 | 100 | 55 46 | - | 0.98 0.43 |
| Belarus | MSRs | 1520 | 140 | 150 | 115 | - | - | 0.5 | 0.7 |
| Latvia | P + F | 1435 | 250 + (120) | 90 | 100 | 90 | 30 | 2.5 | 1 |
| Lithuania | P + F | 1435 | 250 + (120) | 90 | 100 | 90 | 30 | 2.5 | 1 |
| Russia | MSRs | 1520 | 140 | 150 | 115 | - | - | 0.5 | 0.7 |
| Slovakia | MSRs | 1520 | 200 | 150 | 115 | - | - | 0.5 | 0.7 |
| Ukraine | MSRs | 1520 | 140 | 150 | 115 | - | - | 0.5 | 0.7 |
| Estonia | P + F | 1435 | 250 + (120) | 90 | 100 | 90 | 30 | 2.5 | 1 |
| Poland | MSRs | 1520 | 200 | 150 | 100 | - | 30 | - | 0.7 |
| USA | HSRs F | 1435 | 300 120 | 150 | 76 50 | - | - | - | 0.9–1.2 |
| Japan | HSRs | 1435 | 500 | 200 | - | - | - | - | - |
| TSI | HSRs | 1435 | 300 | 180–190 | 80 | 110 | 60 | - | - |
| CEN | HSRs | 1435 | 300 | 180 | 100 | 110 | 60 | - | - |
| Type of Train | Characteristic | Value |
|---|---|---|
| High-speed train Talgo T350 (S-102 class) 4 circulations/way | # Cars | 12 |
| 350 | ||
| s | −0.3 | |
| hc (m) | 1.2 | |
| # Axles | 21 | |
| Weight per axle (Tn/axle) | 16 | |
| Shuttle train (S-114 class) 10 circulations/way | # Cars | 4 |
| 250 | ||
| s | 0.2 | |
| hc (m) | 1.5 | |
| # Axles | 16 | |
| Weight per axle (Tn/axle) | 17 | |
| Freight train 5 circulations/way | # Wagons | 35 |
| 100 | ||
| hc (m) | 1.5 | |
| # Axles | 140 | |
| Weight per axle (Tn/axle) | 20 |
| Year | Service | Estimated Demand | # Trains Each Way |
|---|---|---|---|
| 2030 | AVE Madrid–Lisbon | 2,022,050 passengers/year | 15 |
| Avant Madrid–Talavera | 399,646 passengers/year | 4 | |
| Freight | - | 8 | |
| 2050 | AVE Madrid–Lisbon | 2,471,893 passengers/year | 18 |
| Avant Madrid–Talavera | 488,555 passengers/year | 5 | |
| Freight | - | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alqatawna, A.; Sánchez-Cambronero, S.; Gallego, I.; López-Morales, J.M. A Graphical Method for Designing the Horizontal Alignment and the Cant in High-Speed Railway Lines Aimed at Mixed-Speed Traffic. Sustainability 2022, 14, 8377. https://doi.org/10.3390/su14148377
Alqatawna A, Sánchez-Cambronero S, Gallego I, López-Morales JM. A Graphical Method for Designing the Horizontal Alignment and the Cant in High-Speed Railway Lines Aimed at Mixed-Speed Traffic. Sustainability. 2022; 14(14):8377. https://doi.org/10.3390/su14148377
Chicago/Turabian StyleAlqatawna, Ali, Santos Sánchez-Cambronero, Inmaculada Gallego, and Juan Miguel López-Morales. 2022. "A Graphical Method for Designing the Horizontal Alignment and the Cant in High-Speed Railway Lines Aimed at Mixed-Speed Traffic" Sustainability 14, no. 14: 8377. https://doi.org/10.3390/su14148377
APA StyleAlqatawna, A., Sánchez-Cambronero, S., Gallego, I., & López-Morales, J. M. (2022). A Graphical Method for Designing the Horizontal Alignment and the Cant in High-Speed Railway Lines Aimed at Mixed-Speed Traffic. Sustainability, 14(14), 8377. https://doi.org/10.3390/su14148377







