Reliability of Relative Permeability Measurements for Heterogeneous Rocks Using Horizontal Core Flood Experiments
Abstract
1. Introduction
1.1. Literature Review
- The large body of multiphase flow studies, particularly relative permeability in oil/water and gas/liquid systems, provides a good starting point for understanding CO2/brine systems;
- As the fluid properties of the CO2/water system are very different from those of the oil/water system, and because of the fundamentally empirical nature of the relative permeability concept, studies are needed to establish similarities and differences between multiphase flow oil/water and CO2/brine systems;
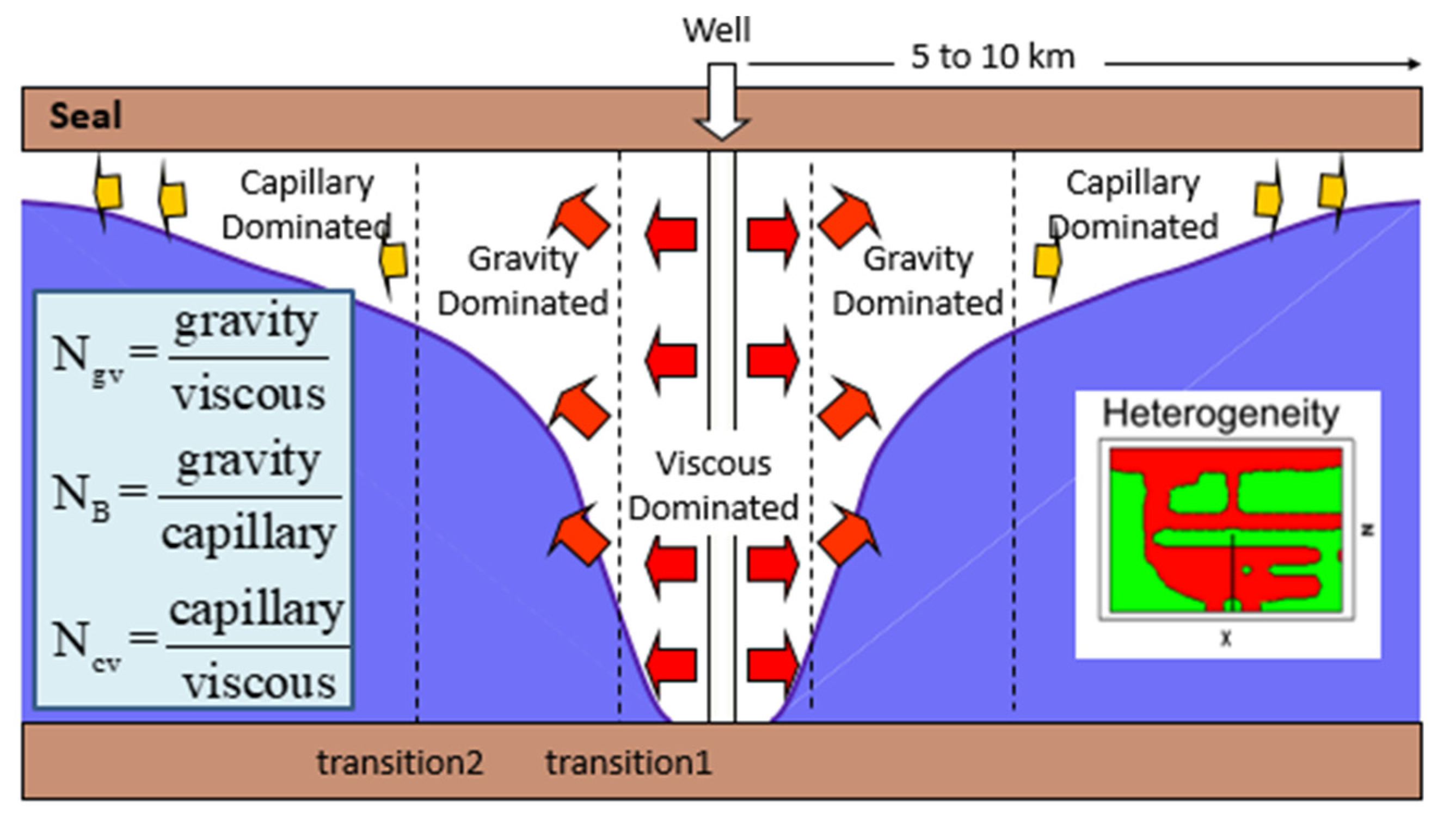
- Potential and unresolved influences of flow rate, capillary number, and small-scale heterogeneity on relative permeability in CO2/brine systems need to be investigated;
- The end effect is an important factor that could lead experimental error. If we want to investigate the flow rate dependence on relative permeability curves, the end effect must be carefully understood and compensated for;
- Based on recent studies of heterogeneity, the effect of heterogeneity may be the reason for the observed dependence of relative permeability on flow rate;
- As the experiments to measure the influence of heterogeneity on relative permeability are time consuming, numerical simulations can be used to simulate, understand, and interpret laboratory experiments of multiphase flow in typical reservoir rocks.
1.2. Summary of the Previous Work
1.3. General Rule of Thumb for Reliable Relative Permeability Measurements
2. Materials and Methods
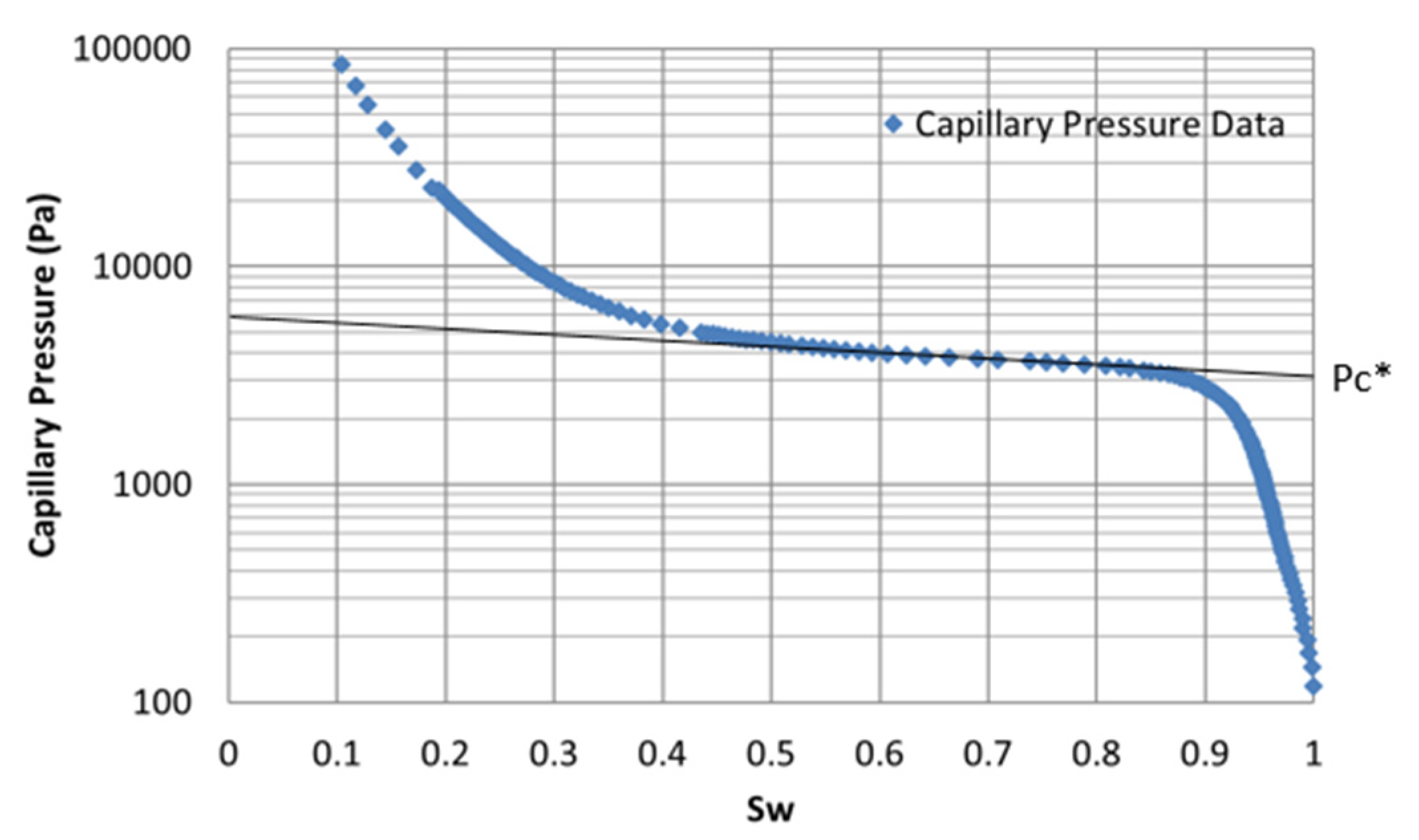
2.1. Simulation
2.2. Boundary Conditions
2.3. Simulated Synthetic Relative Permeability Data Sets
3. Results
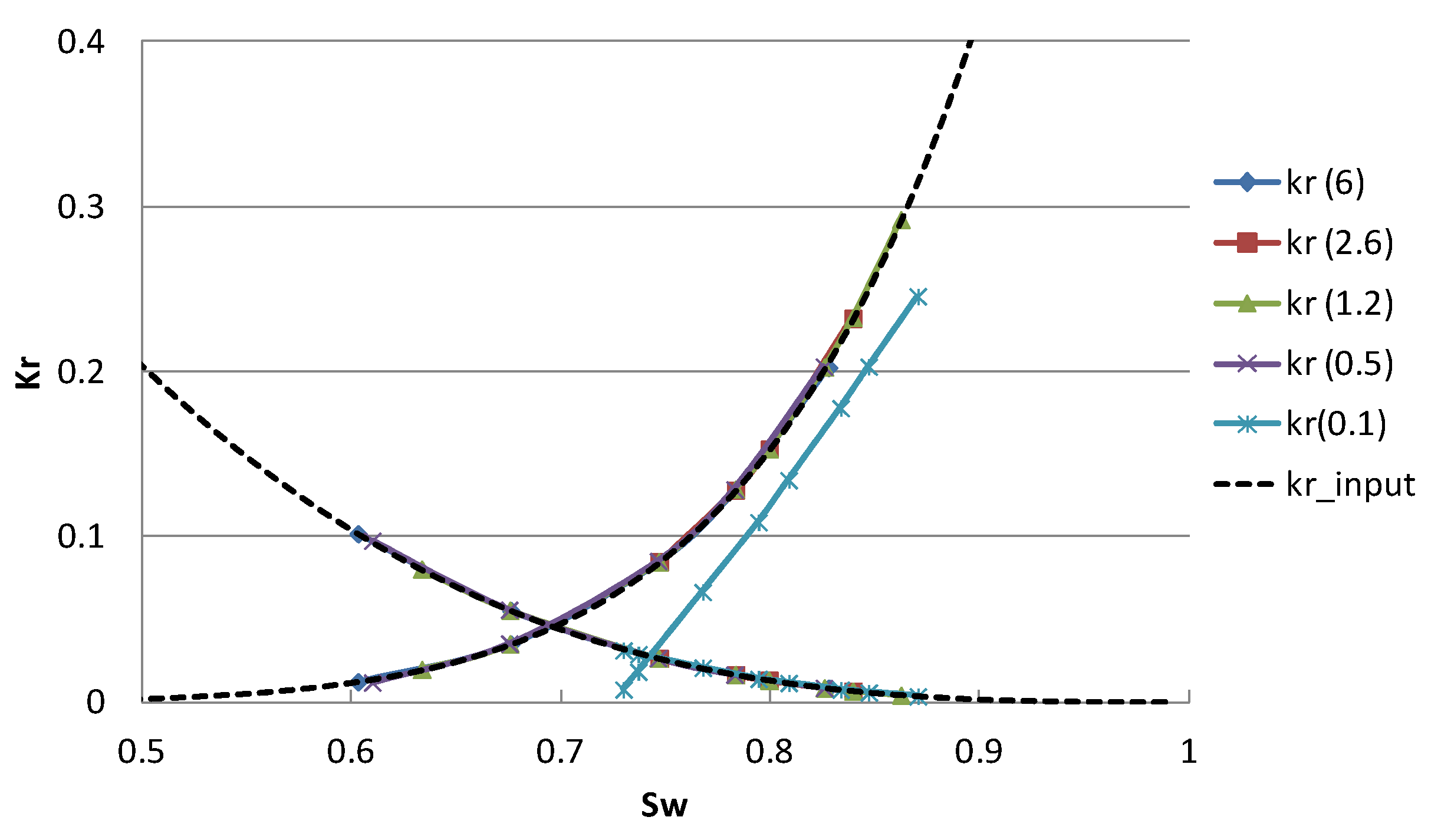
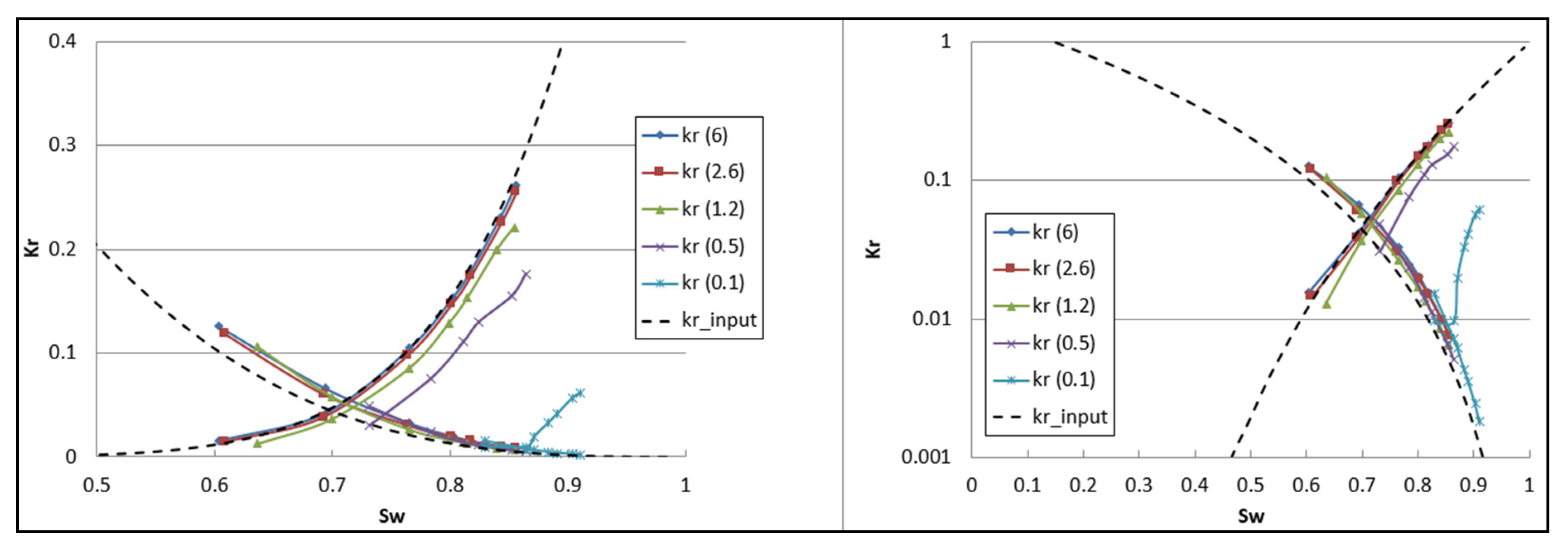
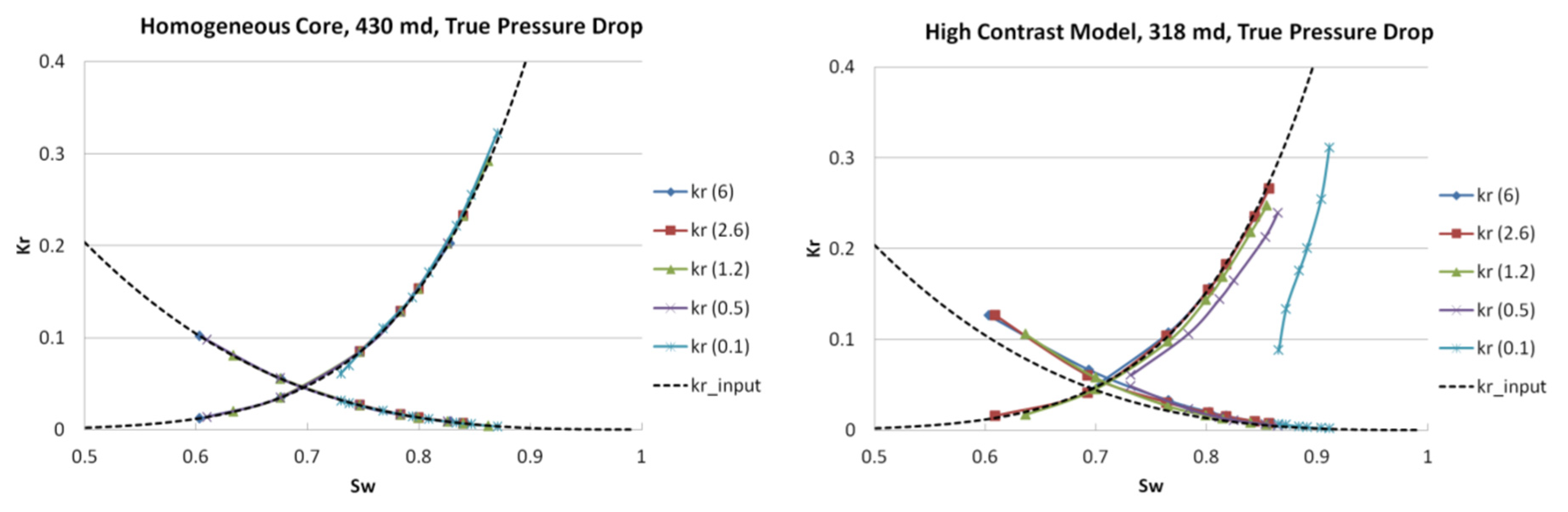
3.1. Relative Permeability Calculated When ΔPw = ΔPCO2
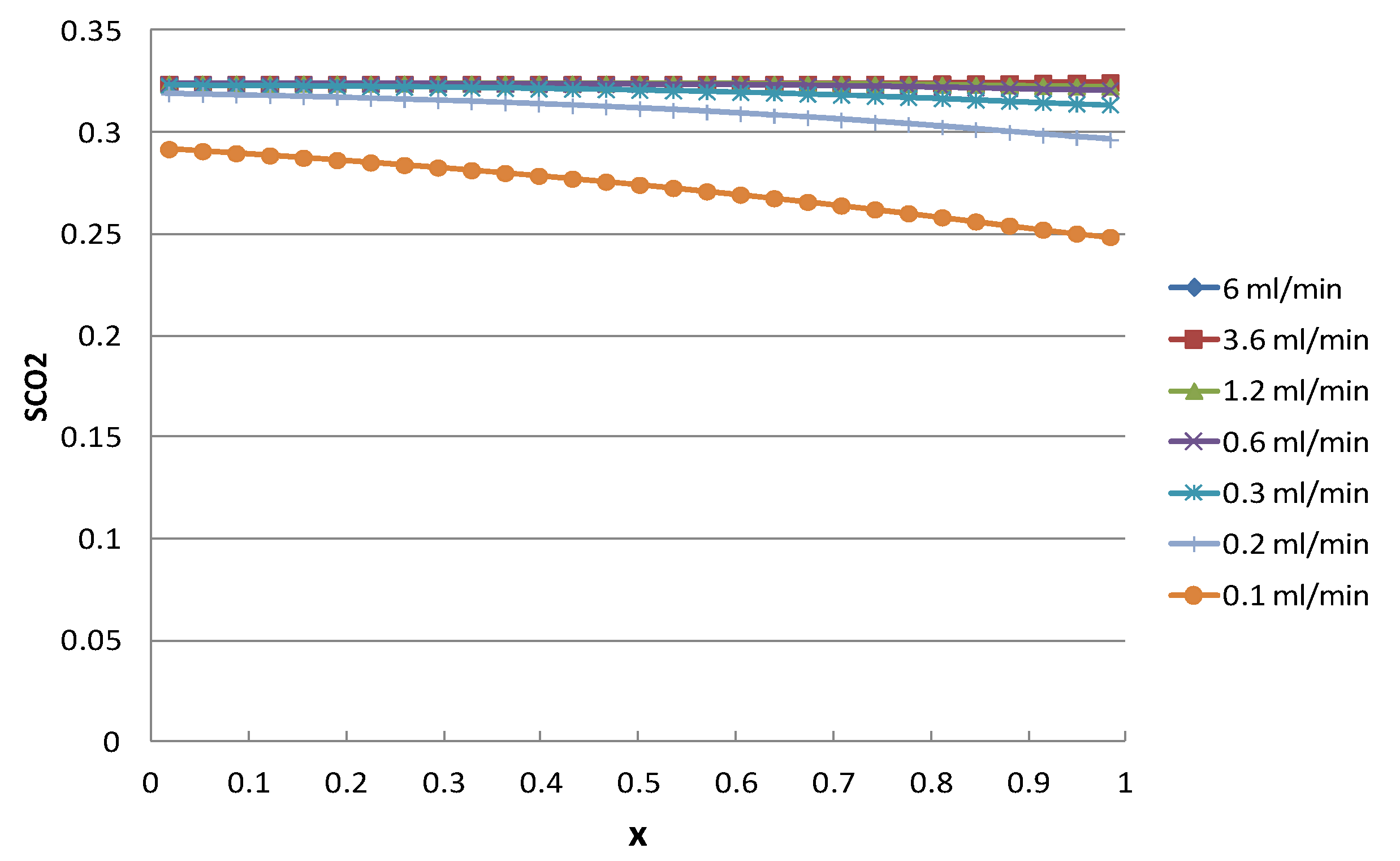
3.1.1. Homogeneous Cores (σlnk’ = 0)
3.1.2. Heterogeneous Core (High Contrast Model, σlnk’ = 0.96)
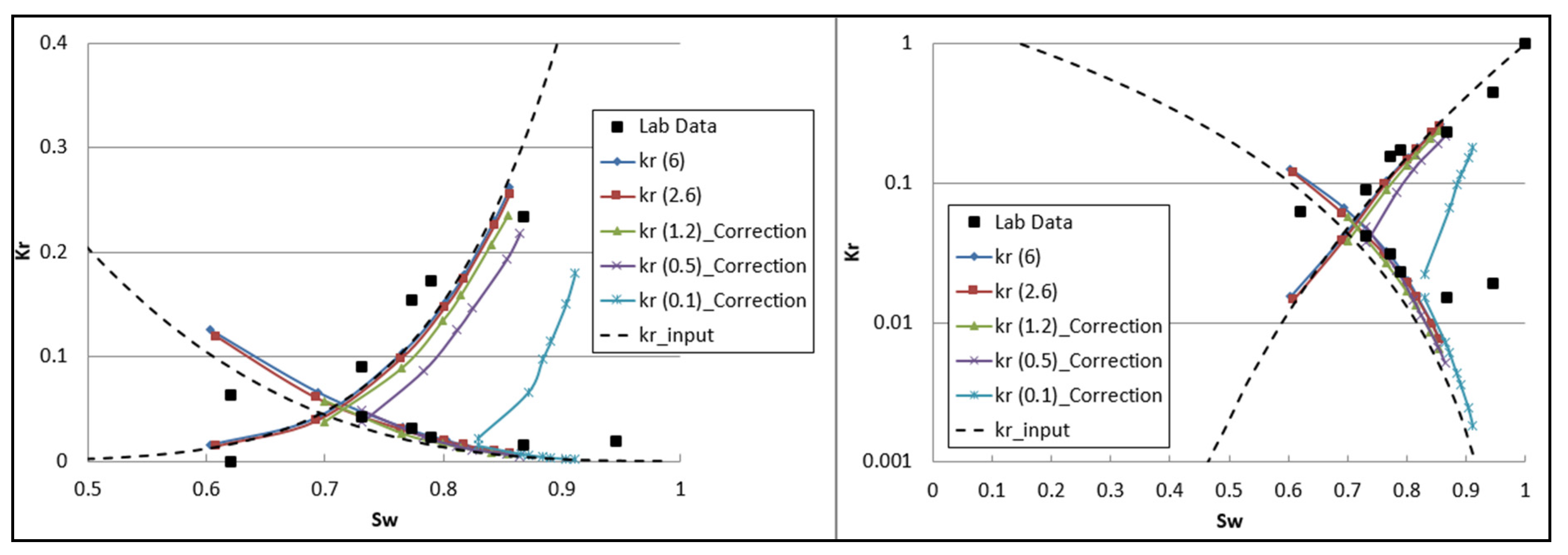
3.2. Relative Permeability Calculated by Using Corrected Pressure Drops
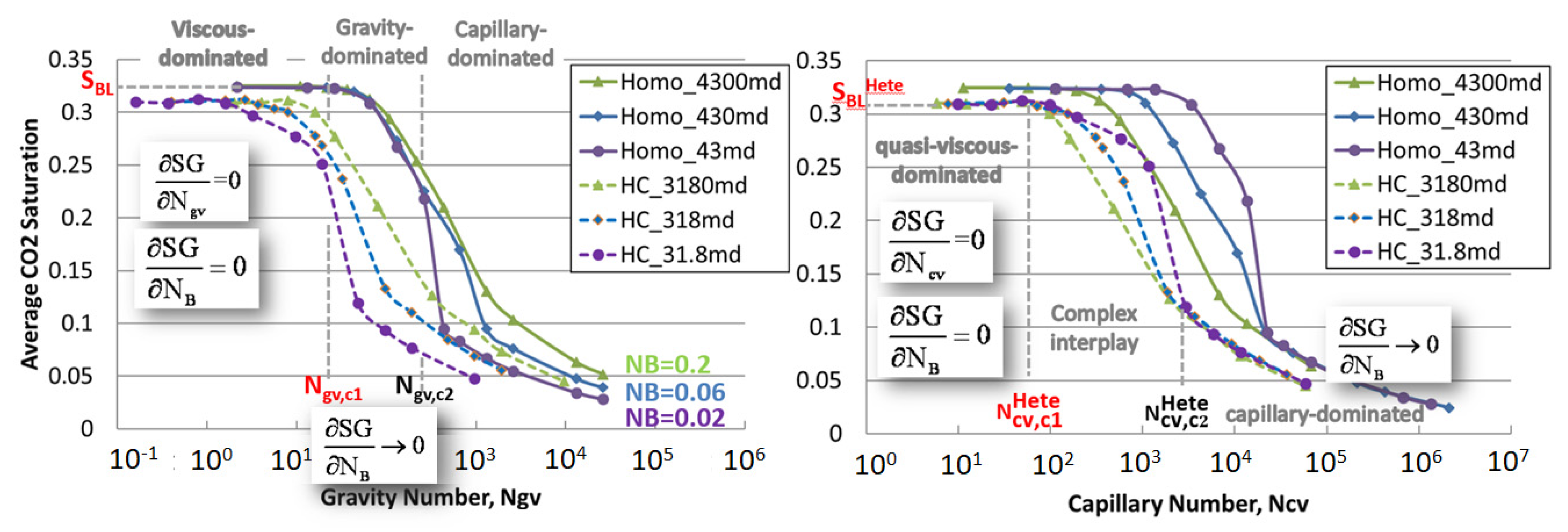
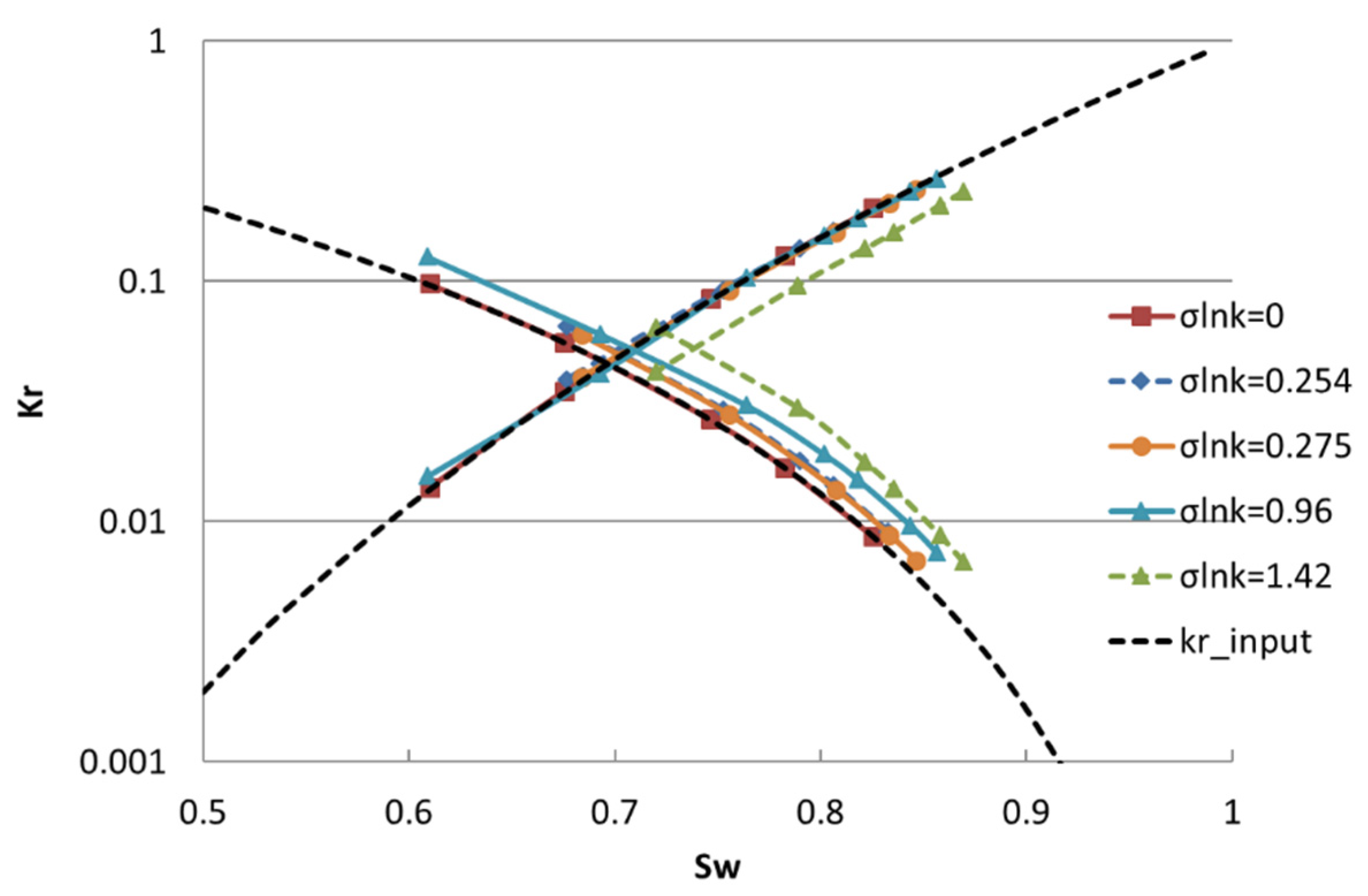
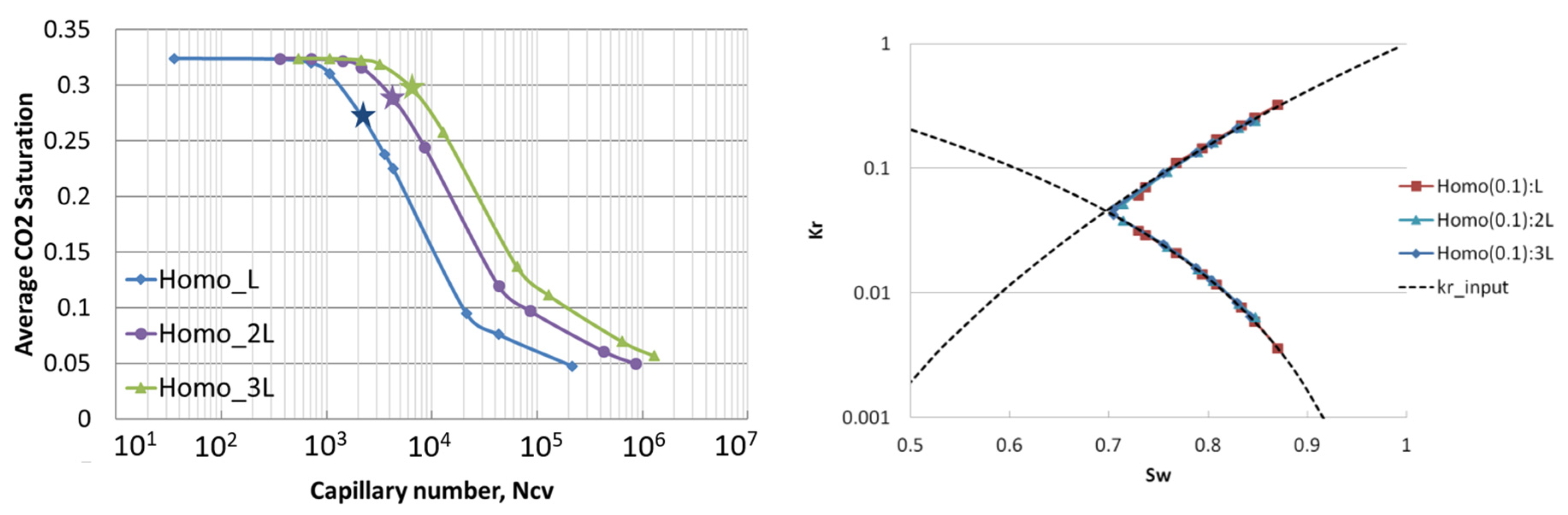
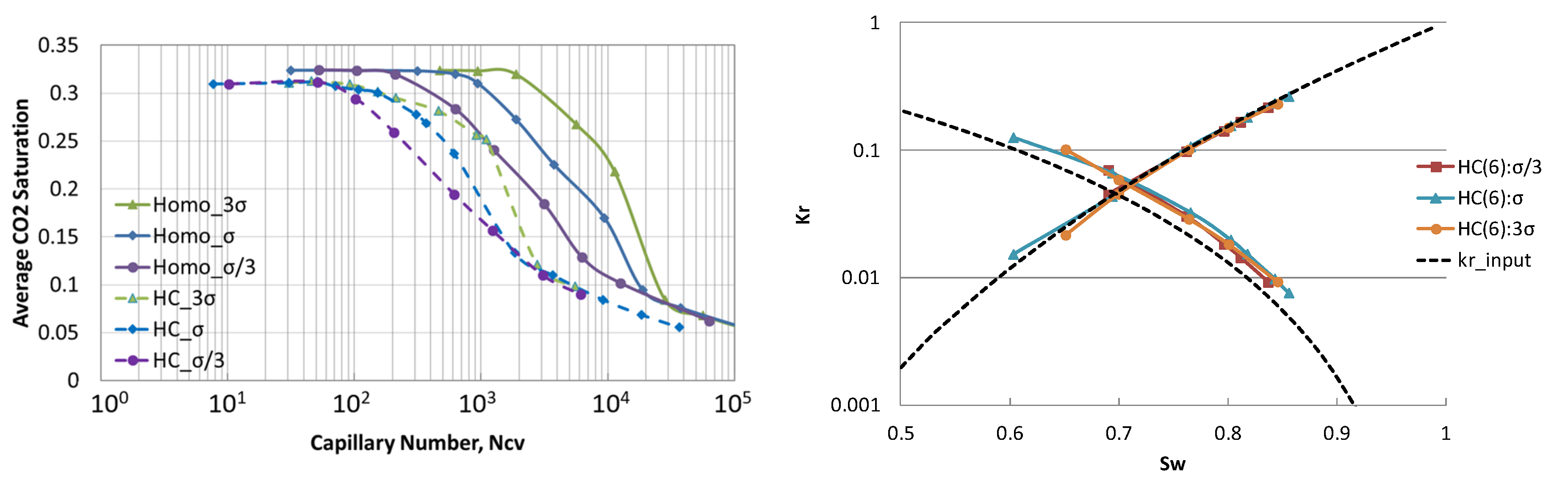
3.3. Sensitivity Studies for Different Core Properties
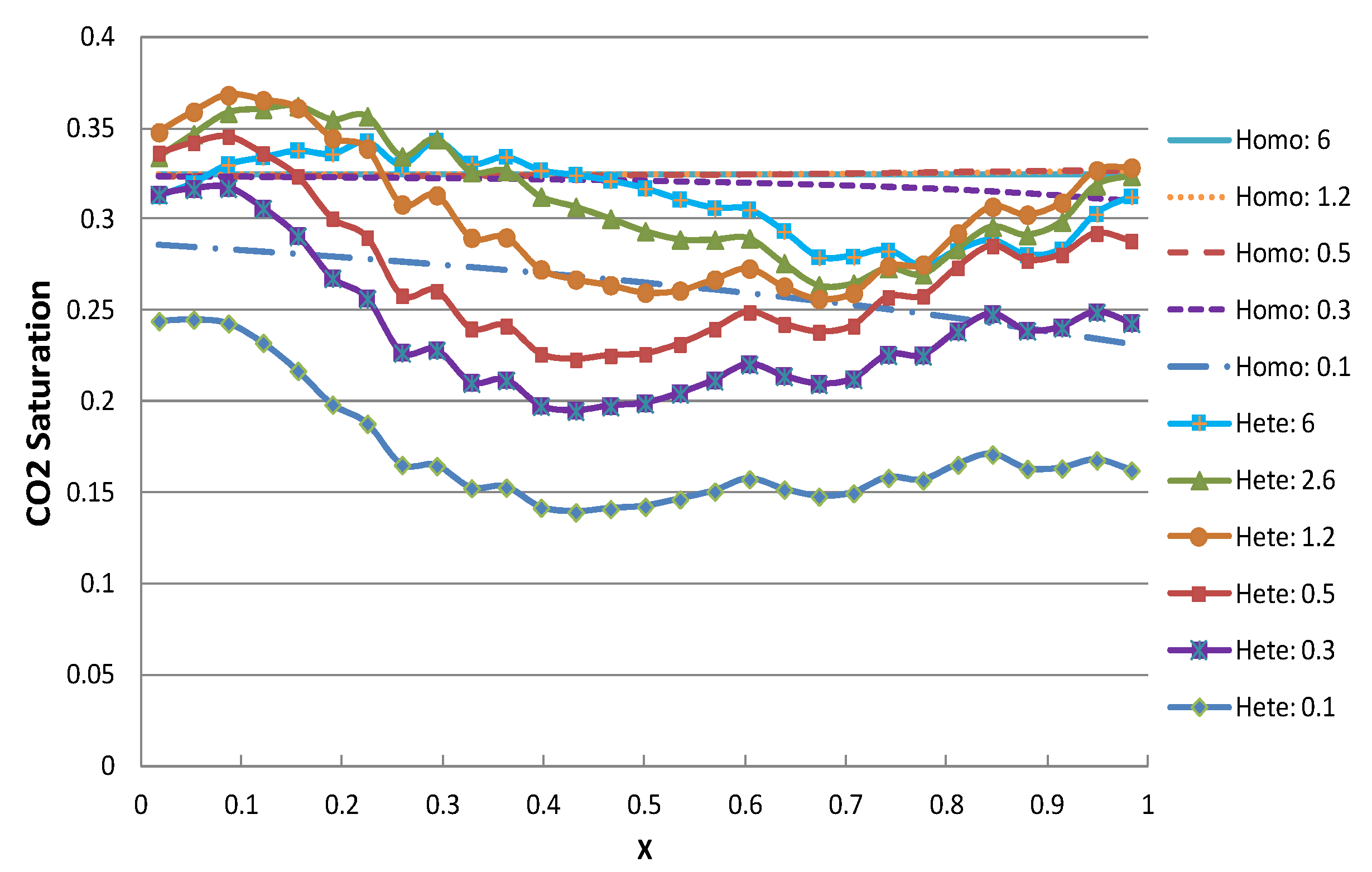
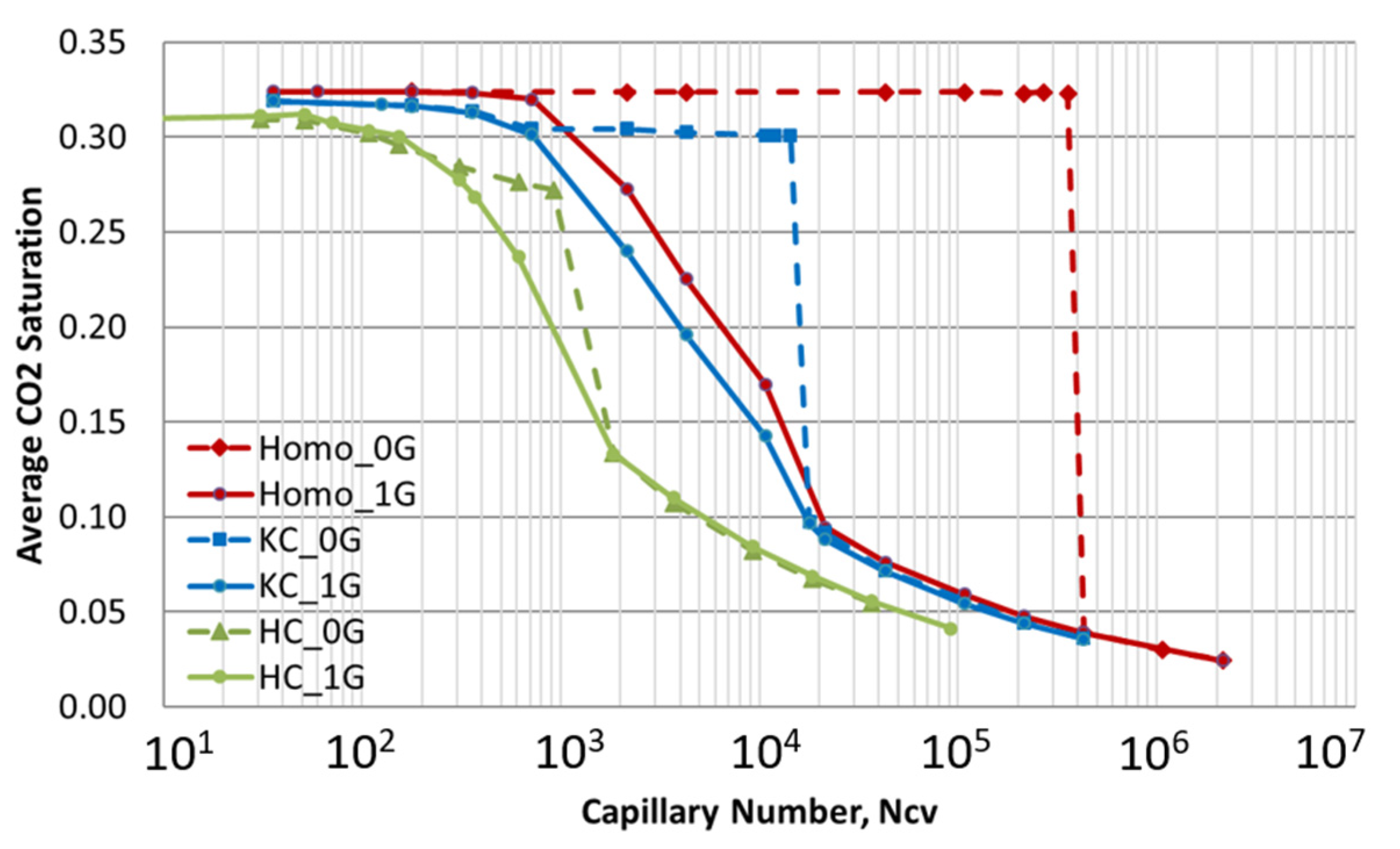
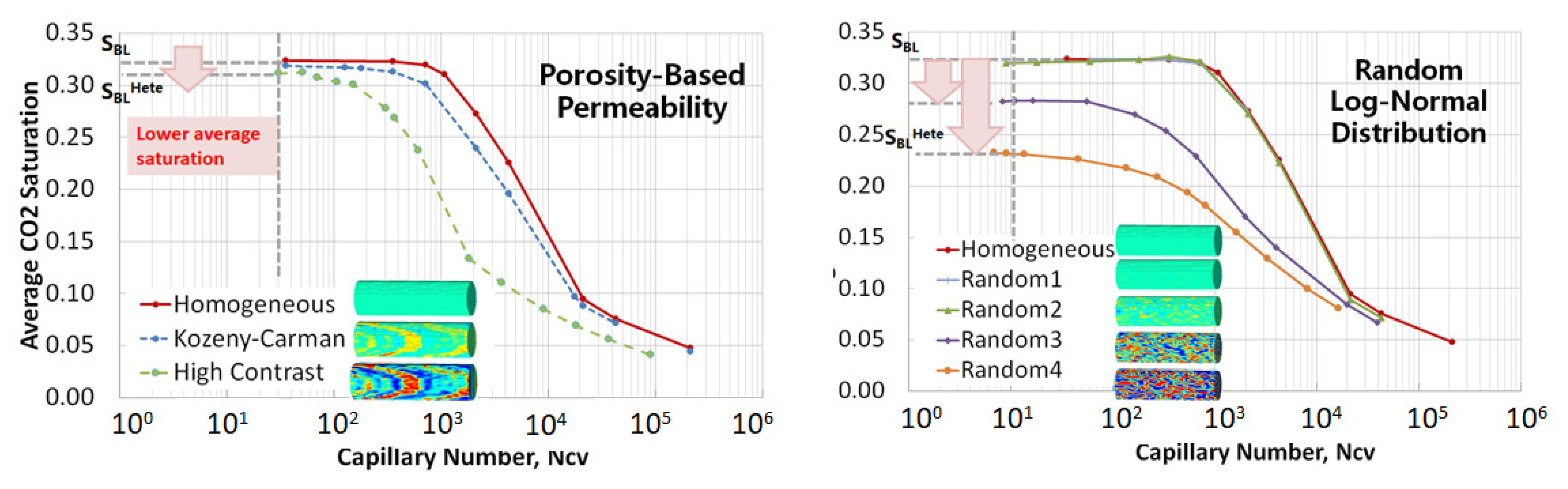
3.3.1. Effects of Heterogeneity
3.3.2. Effects of Core Length (15.24–45.72 cm)
3.3.3. Effects of Interfacial Tension (7.49–67.41 mN/m)
3.3.4. Effects of Gravity
4. Discussion
4.1. Observations from the Numerical and Semi-Analytical Models
4.2. Conditions for Reliable Effective Relative Permeability Measurements
- (i)
- If the core is known as relatively homogeneous (τ ~ 1 and SBLHete ~ SBL)
- (ii)
- If the core is very heterogeneous,
4.3. Permeability Heterogeneity Parameter τ
4.4. Initial Guess of Critical Flow Rate
4.5. Practical Application
- Conduct steady-state drainage core-flooding experiment with initial injection rate qc,max (Equation (35)).
- can be calculated based on the design of experiment.
- Equation (25) would give the lower bound of =.
- Change the initial rate up and down, and measure the corresponding core pressure drop of CO2 () and average CO2 saturation for each injection rate.
- could be obtained once saturation becomes constant.
- The permeability heterogeneity parameter τ could be obtained based on Equation (31).
5. Conclusions
- Despite the presence of heterogeneity, it is possible to obtain the accurate effective relative permeability measurements for heterogeneous cores. The incomplete fluid displacement is primarily due to the heterogeneity and unfavorable mobility ratio, not gravity segregation, but with a sufficiently high flow rate, these effects can be overcome.
- The critical flowrate for making these accurate measurements was identified based on the properties of the core, and most notably on heterogeneity (Equations (22) and (28)). Increasing the flow rate results in minimizing the saturation gradient caused by the combined effects of capillary, viscous, and gravity forces; hence, the relative permeability approaches the maximum value asymptotically and stabilizes when the uniform saturation is achieved.
- The simulation results shown here indicate that the flow-rate dependent saturation occurs not only in the heterogeneous core, but also in homogeneous cores. In addition, we show that the capillary heterogeneity will increase the flow-rate dependency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | cross-section area of the core [m2] | f | fractional flow |
| H | height of the core [m] | g | acceleration [m/s2] |
| L | length of the core [m] | k | average permeability [md] |
| Rl | aspect ratio, L/H | kr | relative permeability |
| NB | Bond number, ΔρgH/pc* | q | volumetric flow rate [mL/min] |
| Ncv | capillary number, nLpc*/H2μg ut | p | pressure [Pa] |
| Ngv | gravity number, ΔρgL/Hμg ut | pc* | characteristic capillary pressure [Pa] |
| Δρ | density difference between CO2 and brine [kg/m3] | u | Darcy velocity [m/s] |
| μ | viscosity [cp] | θ | contact angle, 0° |
| φ | porosity | τ | heterogeneity parameter |
| σ | CO2–brine interfacial tension [N/m] or standard deviation | ||
| ΔP | pressure difference between the average inlet and the outlet slice values | ||
References
- The Intergovernmental Panel on Climate Change (IPCC). IPCC Special Report on Carbon Dioxide Capture and Storage; Metz, B., Davidson, O., de Coninck, H.C., Loos, M., Meyer, L.A., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2005. [Google Scholar]
- Ide, S.T.; Jessen, K.; Orr, F.M., Jr. Storage of CO2 in saline aquifers: Effects of gravity, viscous, and capillary forces on amount and timing of trapping. J. Greenh. Gas Control. 2007, 1, 481–491. [Google Scholar]
- Kopp, A.; Class, H.; Helmig, R. Investigations on CO2 storage capacity in saline aquifers—Part 1: Dimensional analysis of flow processes and reservoir characteristics. Int. J. Greenh. Gas Control 2009, 3, 263–276. [Google Scholar] [CrossRef]
- Bryant, S.L.; Lakshiminarasimhan, S.; Pope, G.A. Buoyancy-dominated multiphase flow and its impact on geological sequestration of CO2. In Proceedings of the SPE/DOE Symposium on Improved Oil Recovery, Tulsa, OK, USA, 22–26 April 2006. [Google Scholar]
- Juanes, R.; Spiteri, E.J.; Orr, F.M., Jr.; Blunt, M.J. Impact of relative permeability hysteresis on geological CO2 storage. Water Resour Res. 2006, 42, W12418. [Google Scholar] [CrossRef]
- Flett, M.; Gurton, R.; Weir, G. Heterogeneous saline formations for carbon dioxide disposal: Impact of varying heterogeneity on containment and trapping. J. Pet. Sci. Eng. 2007, 57, 106–118. [Google Scholar] [CrossRef]
- Han, W.S.; Kim, K.Y.; Esser, R.P.; Park, E.; McPherson, B.J. Sensitivity Study of Simulation Parameters Controlling CO2 Trapping Mechanisms in Saline Formations. Transp. Porous Med. 2011, 90, 807–829. [Google Scholar] [CrossRef]
- Krause, M.H.; Perrin, J.C.; Benson, S.M. Modeling Permeability Distributions in a Sandstone Core for History Matching Coreflood Experiments. SPE J. 2011, 16, 768–777. [Google Scholar] [CrossRef]
- Kuo, C.W.; Perrin, J.C.; Benson, S.M. Effect of gravity, flow Rate, and small scale heterogeneity on multiphase flow of CO2 and brine. In Proceedings of the SPE Western Regional Meeting, Anaheim, CA, USA, 27–29 May 2010. [Google Scholar]
- Shi, J.Q.; Xue, Z.; Durucan, S. Supercritical CO2 core flooding and imbibition in Tako sandstone—Influence of sub-core scale heterogeneity. Int. J. Greenh. Gas Control 2011, 5, 75–87. [Google Scholar] [CrossRef]
- Kuo, C.W.; Benson, S.M. Analytical Study of Effects of Flow Rate, Capillarity, and Gravity on CO2/Brine Multiphase-Flow System in Horizontal Corefloods. SPE J. 2013, 18, 708–720. [Google Scholar] [CrossRef]
- Muskat, M. The Flow of Homogeneous Fluids through Porous Media; McGraw-Hill Book Company: New York, NY, USA; London, UK, 1937. [Google Scholar]
- Morse, R.A.; Terwilliger, P.K.; Yuster, S.T. Relative permeability measurements on small core samples. Oil Gas J. 1947, 46, 109–125. [Google Scholar]
- Osoba, J.S.; Richardson, J.G.; Kerver, J.K.; Hafford, J.A.; Blair, P.M. Laboratory measurements of relative permeability. J. Pet. Technol. 1951, 3, 47–56. [Google Scholar] [CrossRef]
- Abaci, S.; Edwards, J.S.; Whittaker, B.N. Relative permeability measurements for two phase flow in unconsolidated sands. Mine Water Environ. 1992, 11, 11–16. [Google Scholar] [CrossRef]
- Perrin, J.C.; Benson, S. An experimental study on the influence of sub-core scale heterogeneities on CO2 distribution in reservoir rocks. Transp. Porous Media 2010, 82, 93–109. [Google Scholar] [CrossRef]
- Krevor, S.C.M.; Pini, R.; Li, B.; Benson, S.M. Capillary heterogeneity trapping of CO2 in a sandstone rock at reservoir conditions. Geophys. Res. Lett. 2011, 38, L15401. [Google Scholar] [CrossRef]
- Welge, H.J. A simplified method for computing oil recovery by gas or water drive. Trans. AIME 1952, 195, 91–98. [Google Scholar] [CrossRef]
- Johnson, E.F.; Bossler, D.P.; Naumann, V.O. Calculation of relative permeability from displacement experiments. Trans. AIME 1959, 216, 370–372. [Google Scholar] [CrossRef]
- Bennion, D.B.; Bachu, S. Dependence on temperature, pressure, and salinity of the IFT and relative permeability displacement characteristics of CO2 injected in deep saline aquifers. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006. [Google Scholar]
- Chalbaud, C.A.; Lombard, J.M.N.; Martin, F.; Robin, M.; Bertin, H.J.; Egermann, P. Two Phase Flow Properties of Brine-CO2 Systems in a Carbonate Core: Influence of Wettability on P c and k r. In Proceedings of the SPE/EAGE Reservoir Characterization and Simulation Conference, Abu Dhabi, UAE, 28–31 October 2007. [Google Scholar]
- Avraam, D.G.; Payatakes, A.C. Generalized relative permeability coefficients during steady-state two-phase flow in porous media, and correlation with the flow mechanisms. Transp. Porous Media 1995, 20, 135–168. [Google Scholar] [CrossRef]
- Bennion, B.; Bachu, S. Relative Permeability Characteristics for Supercritical CO2 Displacing Water in a Variety of Potential Sequestration Zones. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 9–12 October 2005. [Google Scholar]
- Bennion, D.B.; Bachu, S. The impact of interfacial tension and pore size distribution/capillary pressure character on CO2 relative permeability at reservoir conditions in CO2-Brine systems. In Proceedings of the SPE/DOE Symposium on Improved Oil Recovery, Tulsa, OK, USA, 22–26 April 2006. [Google Scholar]
- Bennion, D.B.; Bachu, S. Permeability and relative permeability measurements at reservoir conditions for CO2-Water systems in ultra low permeability confining caprocks. In Proceedings of the EUROPEC/EAGE Conference and Exhibition, London, UK, 11–14 June 2007. [Google Scholar]
- Bennion, B.; Bachu, S. Drainage and imbibition relative permeability relations for supercritical CO2/brine and H2S/brine systems in intergranular sandstone, carbonate, shale, and anhydrite rocks. SPE Reserv. Eval. Eng. 2008, 11, 487–496. [Google Scholar] [CrossRef]
- Bennion, D.B.; Bachu, S. Drainage and imbibition CO2/Brine relative permeability curves at reservoir conditions for high-permeability carbonate rocks. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010. [Google Scholar]
- Bachu, S.; Bennion, B. Effects of in-situ conditions on relative permeability characteristics of CO2–brine systems. Environ. Geol. 2007, 54, 1707–1722. [Google Scholar] [CrossRef]
- Akbarabadi, M.; Piri, M. Relative permeability hysteresis and capillary trapping characteristics of supercritical CO2/brine systems: An experimental study at reservoir conditions. Adv. Water Resour. 2013, 52, 190–206. [Google Scholar] [CrossRef]
- Krevor, S.C.M.; Pini, R.; Zuo, L.; Benson, S.M. Relative permeability and trapping of CO2 and water in sandstone rocks at reservoir conditions. Water Resour. Res. 2012, 48, W02532. [Google Scholar] [CrossRef]
- Müller, N. Supercritical CO2-brine relative permeability experiments in Reservoir Rocks—Literature Review and Recommendations. Transp. Porous Med. 2011, 87, 367–383. [Google Scholar] [CrossRef]
- Benson, S.; Pini, R.; Reynolds, C.; Krevor, S. Relative Permeability Analysis to Describe Multi-Phase Flow in CO2 Storage Reservoirs; Global CCS Institute Targeted Report No. 2; Global CCS Institute: Melbourne, Australia, 2013. [Google Scholar]
- Benson, S.M.; Hingerl, F.; Zuo, L.; Krevor, S.; Pini, R.; Reynolds, C.; Niu, B.; Calvo, R.; Niemi, A. Relative Permeability for Multi-Phase Flow in CO2 Storage Reservoirs: Part II. Resolving Fundamental Issues and Resolving Data Gaps. Global CCS Institute Targeted Report; Stanford University: Stanford, CA, USA, 2015. [Google Scholar]
- Leverett, M.C. Capillary behavior in porous solids. Trans. AIME 1941, 142, 152–169. [Google Scholar] [CrossRef]
- Caudle, B.H.; Slobod, R.L.; Brownscombe, E.R. Further developments in the laboratory determination of relative permeability. Trans. AIME 1951, 192, 145–150. [Google Scholar] [CrossRef]
- Kyte, J.R.; Rapoport, L.A. Linear waterflood behavior and end effects in water-wet porous media. Trans. AIME 1958, 213, 423–426. [Google Scholar] [CrossRef]
- Henderson, G.D.; Danesh, A.; Tehrani, D.H.; Peden, J.M. The effect of velocity and interfacial tension on relative permeability of gas condensate fluids in the wellbore region. J. Pet. Sci. Eng. 1997, 17, 265–273. [Google Scholar] [CrossRef]
- Sandberg, C.R.; Gournay, L.S.; Sippel, R.F. The effect of fluid-flow rate and viscosity on laboratory determinations of oil-water relative permeabilities. Trans. AIME 1958, 213, 36–43. [Google Scholar] [CrossRef]
- Fulcher, R.A.; Ertekin, T.; Stahl, C.D. Effect of capillary number and its constituents on two-phase relative permeability curves. J. Petrol. Technol. 1985, 37, 249–260. [Google Scholar] [CrossRef]
- Henderson, J.H.; Yuster, S.T. Studies in relative permeability. World Oil 1948, 3, 139–144. [Google Scholar]
- Skauge, A.; Hydro, N.; Poulsen, S. Rate effects on centrifuge drainage relative permeability. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 1–4 October 2000. [Google Scholar]
- Virnovsky, G.A.; Friis, H.A.; Lohne, A. A steady-state upscaling approach for immiscible two-phase flow. Transp. Porous Media 2004, 54, 167–192. [Google Scholar] [CrossRef]
- Ringrose, P.S.; Sorbie, K.S.; Corbett, P.W.M.; Jensen, J.L. Immiscible flow behavior in laminated and cross-bedded sandstones. J. Pet. Sci. Eng. 1993, 9, 103–124. [Google Scholar] [CrossRef]
- Honarpour, M.M.; Cullick, A.S.; Saad, N.; Humphreys, N.V. Effect of Rock Heterogeneity on Relative Permeability: Implications for Scale-up. J. Pet. Technol. 1995, 47, 980–986. [Google Scholar] [CrossRef]
- Dale, M.; Ekrann, S.; Mykkeltveit, J.; Virnovsky, G. Effective relative permeability and capillary pressure for one-dimensional heterogeneous media. Transp. Porous Media 1997, 26, 229–260. [Google Scholar] [CrossRef]
- Pickup, G.E.; Stephen, K.D. An assessment of steady-state scale-up for small-scale geological models. Pet. Geosci. 2000, 6, 203–210. [Google Scholar] [CrossRef]
- Pickup, G.; Ringrose, P.S.; Sharif, A. Steady-state upscaling: From lamina-scale to full-field model. SPE J. 2000, 5, 208–217. [Google Scholar] [CrossRef]
- Lohne, A.; Virnovsky, G.A.; Durlofsky, L.J. Two-stage upscaling of two-phase flow: From core to simulation scale. SPE J. 2006, 11, 304–316. [Google Scholar] [CrossRef]
- Jonoud, S.; Jackson, M.D. New criteria for the validity of steady-state upscaling. Transp. Porous Media 2008, 71, 53–73. [Google Scholar] [CrossRef]
- Skauge, A.; Haskjold, G.; Thorsen, T.; Aarra, M. Accuracy of gas-oil relative permeability from two-phase flow experiments. Soc. Core Anal. 1997, 9707. Available online: http://www.jgmaas.com/SCA/1997/SCA1997-07.pdf (accessed on 4 February 2021).
- Chang, Y.B.; Lim, M.T.; Pope, G.A.; Sepehrnoori, K. CO2 flow patterns under multiphase flow: Heterogeneous field-scale conditions. SPE Reserv. Eng. 1994, 9, 208–216. [Google Scholar] [CrossRef]
- Rossen, W.R.; van Duijn, C.J. Gravity segregation in steady-state horizontal flow in homogeneous reservoirs. J. Pet. Sci. Eng. 2004, 43, 99–111. [Google Scholar] [CrossRef]
- Hesse, M.A.; Orr, F.M., Jr.; Tchelepi, H.A. Gravity currents with residual trapping. J. Fluid Mech. 2008, 611, 35–60. [Google Scholar] [CrossRef]
- Cinar, Y.; Jessen, K.; Berenblyum, R.; Juanes, R.; Orr, F.M., Jr. An experimental and numerical investigation of crossflow effects in two-phase displacements. SPE J. 2006, 11, 216–226. [Google Scholar] [CrossRef][Green Version]
- Hamon, G.; Roy, C. Influence of heterogeneity, wettability and coreflood design on relative permeability curves. In Proceedings of the 2000 International Symposium of the Society of Core Analysts, Dallas, TX, USA, 4–7 June 2000. [Google Scholar]
- Ataie-Ashtiani, B.; Hassanizadeh, S.M.; Celia, M.A. Effects of heterogeneities on capillary pressure-saturation-relative permeability relationships. J. Contam. Hydrol. 2002, 56, 175–192. [Google Scholar] [CrossRef]
- Chaouche, M.; Rakotomalala, N.; Salin, D.; Xu, B.; Yortsos, Y.C. Capillary effects in drainage in heterogeneous porous media: Continuum modelling, experiments and pore network simulations. Chem. Eng. Sci. 1994, 49, 2447–2466. [Google Scholar] [CrossRef]
- Oloruntobi, O.S.; LaForce, T. Effect of aquifer heterogeneity on CO2 sequestration. In Proceedings of the EUROPEC/EAGE Conference and Exhibition, Amsterdam, The Netherlands, 8–11 June 2009. [Google Scholar]
- Jackson, S.J.; Agada, S.; Reynolds, C.A.; Krevor, S. Characterizing drainage multiphase flow in heterogeneous sandstones. Water Resour. Res. 2018, 54, 3139–3161. [Google Scholar] [CrossRef]
- Kuo, C.W.; Benson, S.M. Numerical and Analytical Study of Effects of Small Scale Heterogeneity on CO2/Brine Multiphase Flow System in Horizontal Corefloods. Adv. Water Resour. 2015, 79, 1–17. [Google Scholar] [CrossRef]
- Li, B.; Benson, S.M. Influence of small-scale heterogeneity on upward CO2 plume migration in storage aquifers. Adv. Water Resour. 2015, 83, 389–404. [Google Scholar] [CrossRef]
- Pini, R.; Krevor, S.C.M.; Benson, S.M. Capillary pressure and heterogeneity for the CO2/water system in sandstone rocks at reservoir conditions. Adv. Water Resour. 2012, 38, 48–59. [Google Scholar] [CrossRef]
- Rabinovich, A.; Darkwah, E.A.; Mishra, A.M. Determining characteristic relative permeability from coreflooding experiments: A simplified model approach. Water Resour. Res. 2019, 55, 8666–8690. [Google Scholar] [CrossRef]
- Pruess, K.; Oldenburg, C.; Moridis, G. TOUGH2 User’s Guide V.2.0; Lawrence Berkeley National Laboratory Report LBNL-43134: Berkeley, CA, USA, 1999.
- Pruess, K. ECO2N: A TOUGH2 Fluid Property Module for Mixtures of Water, NaCl, and CO2; Lawrence Berkeley National Laboratory Report LBNL-57952: Berkeley, CA, USA, 2005.
- Perrin, J.C.; Krause, M.; Kuo, C.W.; Miljkovic, L.; Charob, E.; Benson, S.M. Core-scale experimental study of relative permeability properties of CO2 and brine in reservoir rocks. Energy Procedia 2009, 1, 3515–3522. [Google Scholar] [CrossRef]
- Benson, S.M.; Perrin, J.-C.; Krause, M.; Kuo, C.-W.; Miljkovic, L. Experimental Investigations of Multiphase Flow and Trapping in Saline Aquifer—Annual Report 2007; Stanford University: Stanford, CA, USA, 2008. [Google Scholar]
- Geffen, T.M.; Owens, W.W.; Parrish, D.R.; Morse, R.D. Experimental investigation of factors affecting laboratory relative permeability measurements. Trans. AIME 1951, 192, 99–110. [Google Scholar] [CrossRef]
- Huppler, J.D. Numerical Investigation of the Effects of Core Heterogeneities on Waterflood Relative Permeabilities. SPE J. 1970, 10, 381–392. [Google Scholar] [CrossRef]
- Rabinovich, A. Analytical Corrections to Core Relative Permeability for Low-Flow-Rate Simulation. SPE J. 2018, 23, 1851–1865. [Google Scholar] [CrossRef]
- Corey, A.T.; Rathjens, C.H. Effect of stratification on relative permeability. J. Pet. Technol. 1956, 8, 69–71. [Google Scholar] [CrossRef]
- Honarpour, M.M.; Cullick, A.S.; Saad, N. Influence of Small-Scale Rock Laminations on Core Plug Oil/Water Relative Permeability and Capillary Pressure. In Proceedings of the University of Tulsa Centennial Petroleum Engineering Symposium, Tulsa, OK, USA, 29–31 August 1994. [Google Scholar]
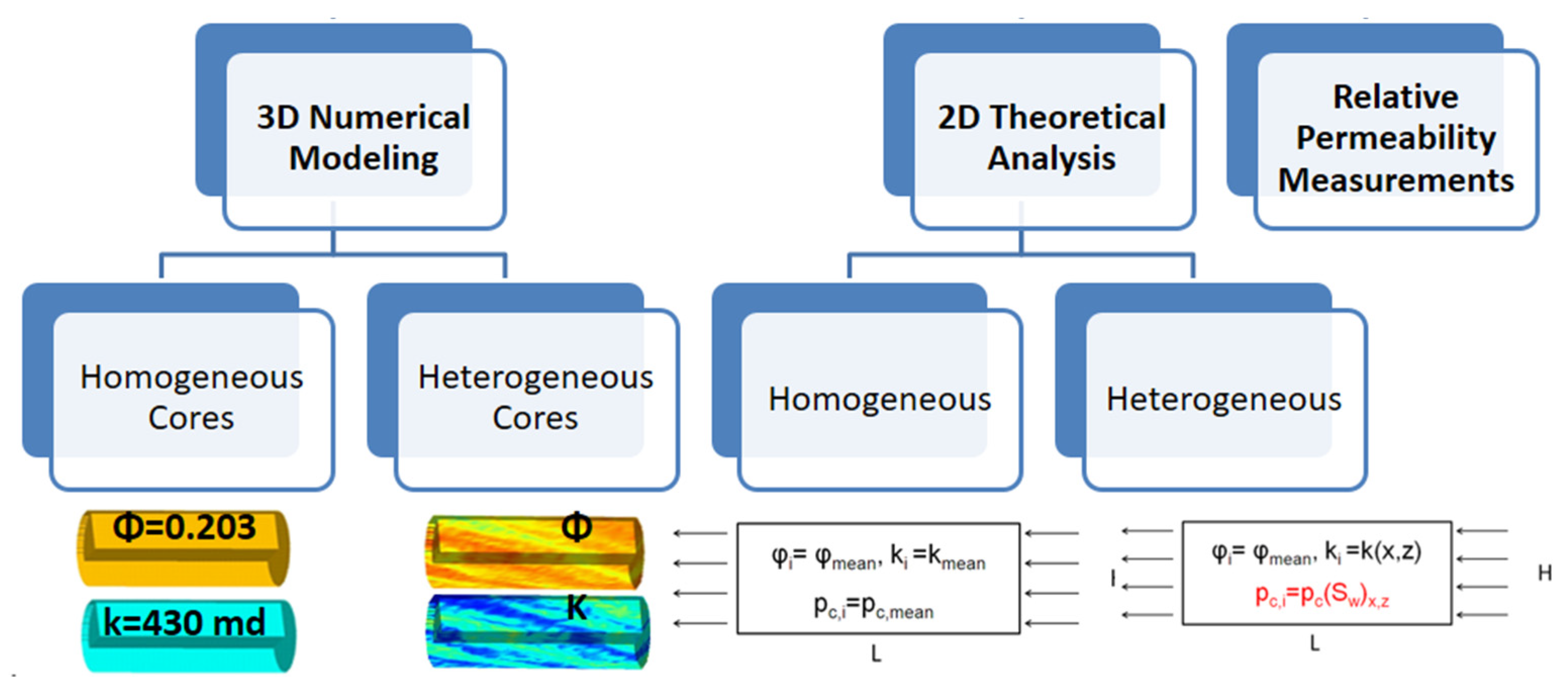
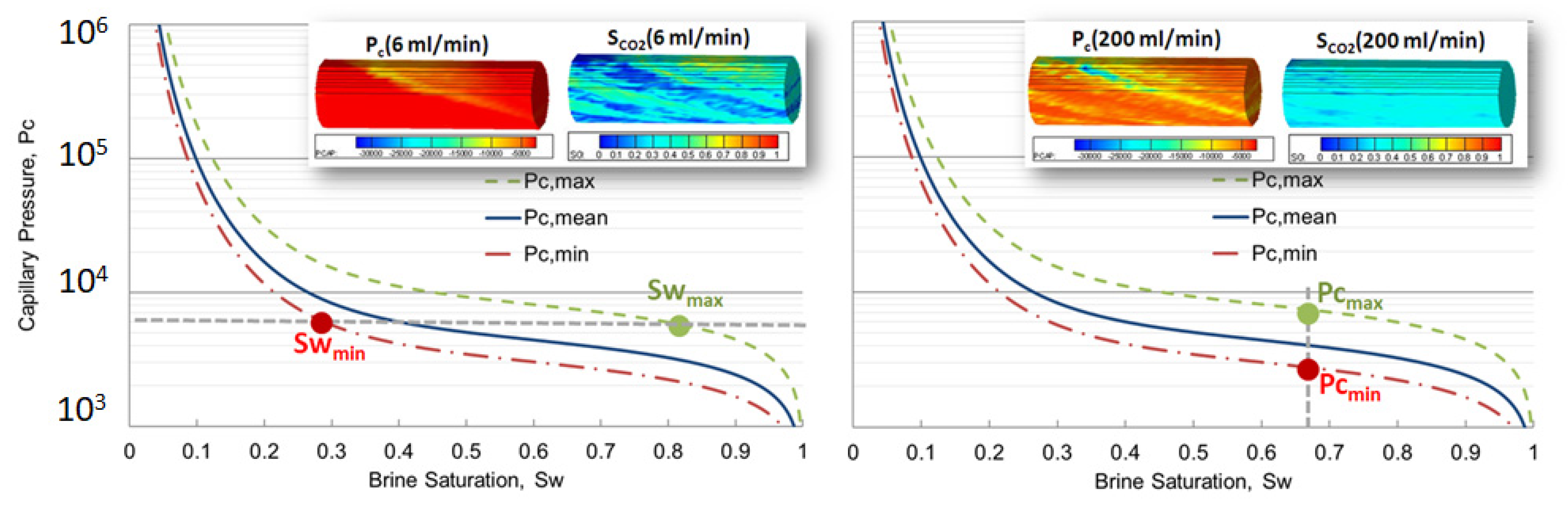

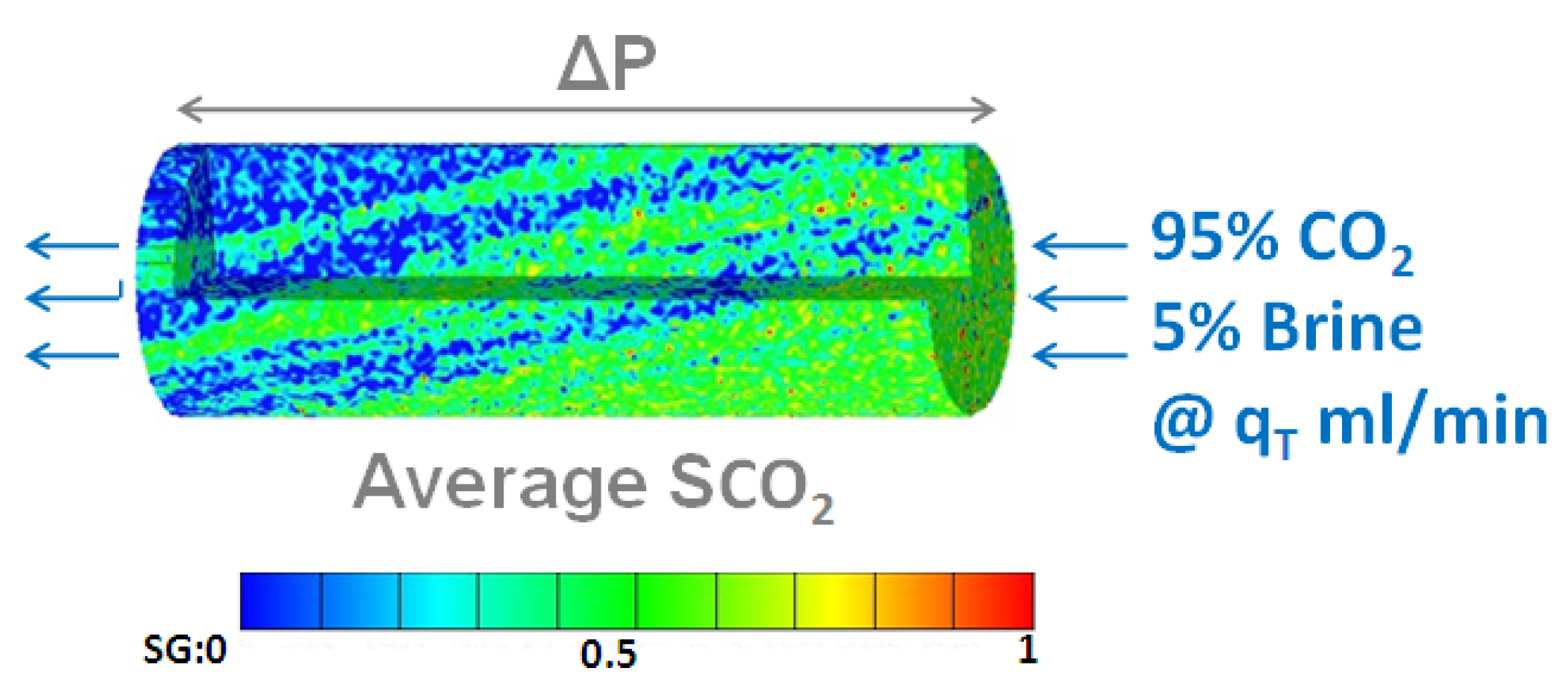

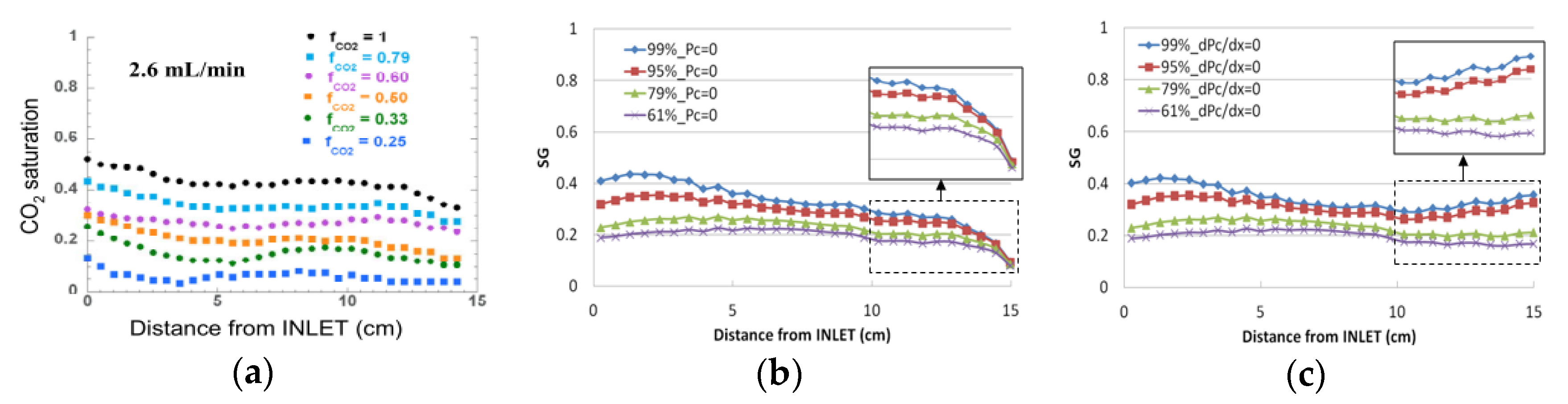
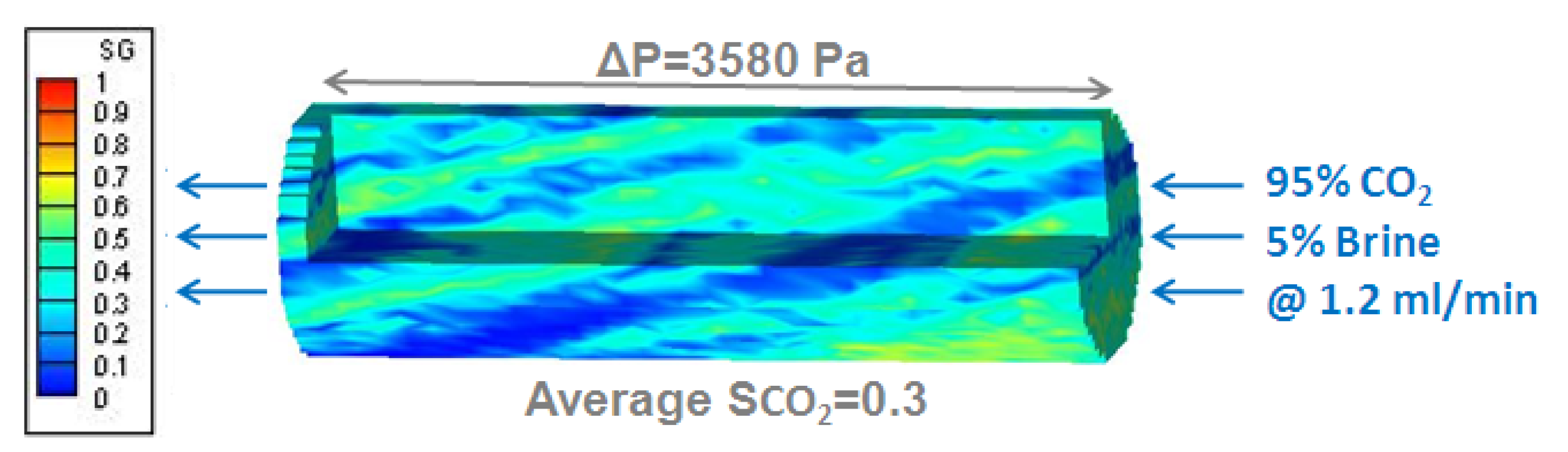
| σlnk’ | Porosity | Permeability (md) | Capillary Pressure (Pa) | Input Relative Permeability | |
|---|---|---|---|---|---|
| Homogeneous Model | 0 | φi = φmean | ki = kmean | Measured Pc Curve | power-law functions |
| Kozeny–Carman Model | 0.27 | φi | φi3/(1 − φi)2 | power-law functions | |
| High Contrast Model | 0.96 | φi | exp(64φi4)  | power-law functions |
| Inlet Slice | Rock Slices (29 Slices) | Outlet Slice |
|---|---|---|
| φmean, | φi, | φmean, |
| kmean: Anisotropic | ki: Isotropic | kmean: Isotropic |
| (kz = ky = 100kx) | Dirichlet boundary condition | |
| Pc = Pc,mean | dPc/dx = 0 |
| Degree of Heterogeneity σlnk’ | Injection Flow Rate q, mL/min | qcritical, mL/min | Regime | |
|---|---|---|---|---|
| Homo | 0 | 0.5 | 0.24 | Viscous-dominated |
| Random 2 | 0.254 | 0.5 | 0.25 | Viscous-dominated |
| KC | 0.275 | 1.2 | 0.37 | Viscous-dominated |
| HC | 0.96 | 2.6 | 0.97 | Viscous-dominated |
| Random 3 | 1.42 | 6 | 1.19 | Viscous-dominated |
| SBL/ SBLHete | krCO2(SBL)/ krCO2(SBLHete) | qcritical [mL/min] from the Simulation Results | |
|---|---|---|---|
| Homogeneous core | 0.324 | 0.0554 | around 0.3 |
| High contrast model | 0.30 | 0.0483 | around 1.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuo, C.-W.; Benson, S.M. Reliability of Relative Permeability Measurements for Heterogeneous Rocks Using Horizontal Core Flood Experiments. Sustainability 2021, 13, 2744. https://doi.org/10.3390/su13052744
Kuo C-W, Benson SM. Reliability of Relative Permeability Measurements for Heterogeneous Rocks Using Horizontal Core Flood Experiments. Sustainability. 2021; 13(5):2744. https://doi.org/10.3390/su13052744
Chicago/Turabian StyleKuo, Chia-Wei, and Sally M. Benson. 2021. "Reliability of Relative Permeability Measurements for Heterogeneous Rocks Using Horizontal Core Flood Experiments" Sustainability 13, no. 5: 2744. https://doi.org/10.3390/su13052744
APA StyleKuo, C.-W., & Benson, S. M. (2021). Reliability of Relative Permeability Measurements for Heterogeneous Rocks Using Horizontal Core Flood Experiments. Sustainability, 13(5), 2744. https://doi.org/10.3390/su13052744






