Abstract
Demand has increased for analytical solutions to determine the velocities and dispersion coefficients that describe solute transport with spatial, temporal, or spatiotemporal variations encountered in the field. However, few analytical solutions have considered spatially, temporally, or spatiotemporally dependent dispersion coefficients and velocities. The proposed solutions consider eight cases of dispersion coefficients and velocities: both spatially dependent, both spatiotemporally dependent, both temporally dependent, spatiotemporally dependent dispersion coefficient with spatially dependent velocity, temporally dependent dispersion coefficient with constant velocity, both constant, spatially dependent dispersion coefficient with spatiotemporally dependent velocity, and constant dispersion coefficient with temporally dependent velocity. The spatial dependence is linear, while the temporal dependence may be exponential, asymptotical, or sinusoidal. An advection–dispersion equation with these variable coefficients was reduced to a non-homogeneous diffusion equation using the pertinent coordinate transform method. Then, solutions were obtained in an infinite medium using Green’s function. The proposed analytical solutions were validated against existing analytical solutions or against numerical solutions when analytical solutions were unavailable. In this study, we showed that the proposed analytical solutions could be applied for various spatiotemporal patterns of both velocity and the dispersion coefficient, shedding light on feasibility of the proposed solution under highly transient flow in heterogeneous porous medium.
1. Introduction
The dispersion coefficient and pore velocity in an advection-dispersion process have generally been treated as constants in previous studies [1,2,3,4,5]. However, recharge rates vary regionally and temporally, and therefore groundwater velocity can change over time and space. Specifically, groundwater flow around a river can shift between river-to-land and land-to-river flow patterns due to changes in rainfall and evapotranspiration conditions. Moreover, groundwater levels near the sea fluctuate continuously due to tides. Groundwater flow can vary spatially due to pumping and injection for contaminant remediation [6,7]. Groundwater velocity can also vary with distance under steady recharge conditions [8,9], and similar spatially varying velocity can be observed in open channel flows where water velocity increases proportional to distance due to steady lateral inflow that is uniformly distributed over its whole length [10]. Additionally, velocity may change temporally in response to the rainy season or tidal effects [11,12]. In all of these situations, the groundwater velocity in a system may change temporally, spatially, or spatiotemporally. Therefore, the dispersion coefficient may also change temporally, spatially, or spatiotemporally.
In various previous studies, groundwater velocity has often been treated as a constant mean value [13,14,15,16,17,18,19]. In theoretical and field analyses, longitudinal dispersivity is scale-dependent due to the influence of natural heterogeneities that produce irregular flow patterns at the field scale [20,21,22]. On the other hand, temporally variable dispersion coefficients have also been considered by many researchers [23,24,25,26,27]. Field experiments and numerous theoretical studies have demonstrated that dispersion coefficients are functions of time or travel distance [15,23]. Following Rehfeldt and Gelhar [21], dispersivity in transient flow is a function of both the spatial and temporal variability through the interrelation of bulk hydraulic conductivity and the flow factor.
Accordingly, in order to account for situations characterized by various spatiotemporal patterns of both velocity and the dispersion coefficient, many researchers have provided analytical solutions under specific types of both velocity and dispersion coefficient they hypothesized. For example, Su et al. [15], Basha and El-Habel [28], and Aral and Liao [25] provided analytical solutions for a temporally dependent dispersion coefficient with a uniform flow field, and these analytical solutions were compared to the breakthrough curves observed in laboratory testing by Su et al. [15]. Selvadurai [29] provided an analytical solution with a constant diffusion coefficient and time-dependent velocity for the situation in which transient flow is induced at the inflow boundary. Unlike either constant velocity or dispersion coefficients as above, Huang et al. [30], Zamani and Bombardelli [12] and Suk [31] assumed both the dispersion coefficient and velocity to be spatially, temporally, and spatiotemporally dependent, respectively, for solving their problems, and provided analytical solutions. Furthermore, in order to analyze the effects of velocity fluctuations on dispersive mixing in a porous medium, Sternberg et al. [32] used a spatiotemporally dependent dispersion coefficient. Besides, in order to explain solute transport behavior in much less permeable layers (such as a rock matrix or aquitard) of a stratified multi-layer system, Zhou et al. [33] applied the concept of a scale-dependent diffusion coefficient.
Demand for consideration of various velocities and dispersion coefficients measured under actual field conditions is increasing, but few analytical solutions are available that consider spatiotemporal variation in both velocity and the dispersion coefficient [31,34,35,36], although many analytical solutions exist [9,15,25,28,29,32,37,38,39,40,41,42,43,44,45,46,47,48,49,50]. Specifically, Kumar et al. [34] and Sanskrityayn et al. [35] employed a dispersion coefficient proportional to the square of the velocity, while Sanskrityayn al. [36] and Suk [31] allowed for a linear relationship between the dispersion coefficient and advection velocity. However, situations in which the dispersion coefficient is linearly proportional to velocity are of great hydrological importance in the groundwater literature, and therefore a linear relationship between the dispersion coefficient and velocity has been widely applied in numerous previous studies. Suk [31] proposed an analytical solution with spatiotemporal variations in both velocity and the dispersion coefficient in a homogeneous aquifer based on a linear relationship between velocity and the dispersion coefficient, but did not consider velocity variability in a heterogeneous aquifer. In addition, the analytical solution obtained by Sanskrityayn et al. [36] with both temporal and spatial dependency was limited to only three cases: both dispersion coefficient and velocity spatially dependent, both spatiotemporally dependent, and both temporally dependent.
However, the present proposed analytical solution considers eight types of analytical solutions for various dispersion coefficients and velocities, as shown in Table 1: dispersion coefficient and velocity both spatially dependent, both spatiotemporally dependent, both temporally dependent, spatiotemporally dependent dispersion coefficient with spatially dependent velocity, temporally dependent dispersion coefficient with constant velocity, both dispersion coefficient and velocity constant, spatially dependent dispersion coefficient with spatiotemporally dependent velocity, and constant dispersion coefficient with temporally dependent velocity. Accordingly, the analytical solutions proposed in this study are an extension of those in Sanskrityayn et al. [36]. Furthermore, the proposed analytical solutions can be degenerated to other existing analytical solutions, including those of Basha and El-Habel [28], Sanskrityayn et al. [36], Yeh [51], De Marsily [52], Selvadurai [29], and Singh et al. [11], as shown in Table 1 and described in Section 3.

Table 1.
Application areas of the proposed analytical solution.
The objective of this study is to present analytical solutions for various types of dispersion coefficients and velocities to meet the requirement for consideration of various dispersion coefficients and velocities under field conditions. In this study, the spatial dependence is assumed to be linear and the temporal dependence to be exponential, asymptotical, or sinusoidal. To solve those problems, a general form of the advection dispersion equation (ADE) with spatially, temporally, or spatiotemporally dependent parameters was reduced into a diffusion equation with a constant diffusion coefficient using appropriate transformation equations. Then, Green’s function method (GFM) was employed to obtain analytical solutions because it can handle easily a non-homogeneous boundary value problem. GFM is based on the superposition principle and provides a solution to an inhomogeneous differential equation with a driving term that is delta function. In addition, GFM is a convenient method for solving more complicated non-homogeneous diffusion equation and Green’s function can easily be obtained through Fourier transform in infinite medium.
2. Mathematical Formulation and Analytical Solution
The general form of the linear ADE in a one-dimensional infinite medium [53] can be written as:
where , , , and are the concentration, dispersion coefficient, pore velocity, and the sink/source term, respectively, at position and time . Initially, the domain is assumed to be solute free. For the initial conditions,
We used the following expressions for the dispersion coefficient and pore velocity:
where and are the dispersion coefficient and pore velocity obtained at the local scale, respectively, and is the spatial dependence parameter, such that is dimensionless. , , and are dimensionless time functions determined by the user. The dimensionless function in Equation (4) is determined from , , and through derivation of the pertinent transformation under some restrictions: the spatial dependence parameter cannot exceed the range of 0.05 to 0.1 for porous medium [40], the local-scale dispersion coefficient is limited to values of less than 1, the local-scale velocity of is sufficiently greater than 0, and the temporal dependent function is limited to exponential, asymptotical, or sinusoidal.
Using the dispersion coefficient and velocity expressed in Equations (3) and (4), respectively, Equation (1) becomes:
The first-order term is eliminated using the transformation
Equation (5) becomes:
where denotes the dummy variable. The initial condition in Equation (2) becomes:
The following two coordinate transformation equations were developed (for details, see Appendix A):
and
where
in Equation (4) is obtained as follows (see Appendix A):
where prime marks are used to denote differentiation with respect to . Using the transformations expressed in Equations (9) and (10), Equation (7) is reduced to a non-homogeneous diffusion equation with a constant coefficient, as follows:
where . Here, . and are new spatial and temporal variables, respectively. The initial condition for the diffusion equation becomes:
Using GFM [28,51,54], the analytical solution of the diffusion Equation (13), subject to the initial conditions described by Equation (14), can be obtained as:
where and are dummy variables. Using the transformations in Equations (6) and (9), and (10), the solution of concentration can be written as:
where , , and .
2.1. Instantaneous Point Injection
An instantaneous point source in Equation (1) was assumed to be injected at · can be defined as:
where is the injected pollutant mass per unit area in the porous medium and is the Dirac delta function. An analytical solution can be obtained in the case of an instantaneous source using Equation (16), as follows:
2.2. Continuous Point Injection
A continuous source injected at at a groundwater velocity of can be defined as
where is the injected concentration The analytical solution for solute transport in the case of a continuous source as defined in Equation (19) can be obtained using Equation (16) as
2.3. Specific Cases of Dispersion Coefficient and Velocity
The analytical solutions for both instantaneous and continuous sources are presented here for eight specific cases of dispersion coefficient and velocity variations (Table 1). The first case is a spatiotemporally dependent dispersion coefficient and spatially dependent velocity. The second case represents both the dispersion coefficient and velocity being spatially dependent. The third case involves a spatially dependent dispersion coefficient with spatiotemporally dependent velocity. In the fourth case, both the dispersion coefficient and velocity are spatiotemporally dependent. These four cases can be degenerated into the following additional four cases using a very small value of the spatial dependence parameter, namely a temporally dependent coefficient with constant flow, both dispersion coefficient and velocity constant, constant dispersion coefficient with temporally dependent velocity, and both dispersion coefficient and velocity temporally dependent (Table 1). The second and fourth cases were also explored by Sanskrityayn et al. [36] and therefore the analytical solution proposed in this study is an extension of that of Sanskrityayn et al. [36]. In Appendix B, the present analytical solution is mathematically derived as a generalization of the analytical solution of Sanskrityayn et al. [36].
2.3.1. Case 1: Spatiotemporally Dependent Dispersion Coefficients and Spatially Dependent Velocities
In the case of , and , is determined as using Equation (12). The spatial dependence parameter cannot exceed the range of 0.05 to 0.1 for a porous medium [40]. If the local-scale dispersion coefficient is limited to values of less than 1, the local-scale velocity of is sufficiently greater than 0, and is limited to exponential, asymptotical, or sinusoidal functions, then . Under the assumptions , , , and , the dispersion coefficient and velocity are and based on Equations (3) and (4), respectively. In this case, a spatiotemporally dependent dispersion coefficient and spatially dependent velocity are considered. From Equations (18) and (20), the respective solutions for an instantaneous source and continuous source injected at become:
and
Furthermore, four expressions of can be considered, as can the corresponding expressions for the new time variable in Equations (21) and (22), as follows:
- (i)
- and .
- (ii)
- and .
- (iii)
- and .
- (iv)
- and .
From Equations (21) and (22), an analytical solution can easily be obtained for a temporally dependent dispersion coefficient with uniform flow with an instantaneous source and a continuous source, respectively. If , then and . Basha and El-Habel [28] provided an analytical solution for a temporally dependent dispersion coefficient with uniform flow in the case of . The analytical solutions of Basha and El-Habel [28] for instantaneous and continuous sources can be obtained using Equations (21) and (22) for , respectively.
2.3.2. Case 2: Both Dispersion Coefficient and Velocity Spatially Dependent
In the case of and , is determined as using Equation (12). If the local-scale dispersion coefficient is limited to less than 1 and , then for values of the spatial dependence parameter from 0.05 to 0.1 [40]. Under such
, , , and conditions, the spatially dependent dispersion coefficient and velocity are and based on Equations (3) and (4), respectively. The corresponding analytical solution with the dispersion coefficient and velocity described above can be obtained using Equation (18) for an instantaneous source:
where . An analytical solution for a continuous source injected at can be obtained using Equation (20):
If , and in Equation (23), then , , , and . Accordingly, the solution of Equation (23) applies to the case of both a constant dispersion coefficient and velocity given by Yeh [51], Haberman [54], and Basha and El-Habel [28] for an instantaneous source. In other words, if and in Equation (24), the expression approaches and becomes . Accordingly, the solution of Equation (24) for a continuous source is as follows:
De Marsily [52] obtained an analytical solution using both the dispersion coefficient and velocity constant in a semi-infinite homogeneous medium for a continuous source injected at , which is equivalent to Equation (25). Assuming in Equation (25), we can obtain the solutions of Yeh [51], Beck et al. [55], and Yeh and Yeh [56] with both the dispersion coefficient and velocity constant and a continuous point source at the origin.
2.3.3. Case 3: Spatially Dependent Dispersion Coefficient with Spatiotemporally Dependent Velocity
In the case of , , is determined as using Equation (12). If the local-scale dispersion coefficient of is limited to values less than 1, and , then for the range of from 0.05 to 0.1 [40]. Under such , , , and conditions, the dispersion coefficient and velocity are and , respectively. In this case, the dispersion coefficient is spatially dependent and velocity is spatiotemporally dependent, and Equations (18) and (20) for the instantaneous and continuous sources, respectively, can be rewritten as follows.
and
where and . In accordance with the previous section, exponentially decelerating, asymptotically decelerating and asymptotically accelerating forms of are considered and corresponding expressions for the new time variable and can be obtained as follows:
- (i)
- . Using Equations (10) and (11), we obtain and .
- (ii)
- , and thus and .
- (iii)
- ; therefore, and .
If , the analytical solution with a constant dispersion coefficient, temporally dependent velocity, and continuous source can be obtained from Equation (27), which is the same as the analytical solution provided by Selvadurai [29].
2.3.4. Case 4: Both Dispersion Coefficient and Velocity Spatiotemporally Dependent
In the case of , is calculated as using Equation (12). If the local-scale dispersion coefficient of is limited to values of less than 1, , and is limited to exponential, asymptotical, or sinusoidal functions, then for the range of from 0.05 to 0.1 [40]. Under such , , , and conditions, the dispersion coefficient and velocity are given by and , respectively. Accordingly, the dispersion coefficient and velocity are both spatiotemporally dependent. Using Equation (10), the new time variable can be expressed as , and can be obtained using Equation (11). The solutions for an instantaneous source and a continuous source can be obtained using Equations (18) and (20), respectively, as:
In accordance with previous sections, exponentially decelerating, asymptotically decelerating, asymptotically accelerating, and sinusoidal forms of are considered and the corresponding expressions for the new time variable and can be obtained as follows:
- (i)
- , and thus .
- (ii)
- , and thus .
- (iii)
- , and thus .
- (iv)
- , and thus .
By setting , analytical solutions for solute transport from instantaneous and continuous sources in the case of both temporally dependent dispersion coefficients and velocity can be obtained simply from Equations (28) and (29), respectively. Notably, dispersion coefficients and velocities corresponding to were used by Singh et al. [11] to obtain analytical solutions with temporal dependence of both dispersion coefficients and velocity for a continuous source, which can be obtained from Equation (29) by substituting and . Similarly, the analytical solutions for a continuous source given by Zamani and Bombardelli [12] under conditions of both dispersion coefficients and velocity being temporally dependent, corresponding to , can be obtained using Equation (29) with substitutions of and . In Zamani and Bombardelli [12], m (day−1) defines the seasonal fluctuation frequency of groundwater. In tropical regions, recharge into the aquifer is maximal after the rainy season and is minimal in summer.
3. Verification and Discussion
This section describes the verification of the proposed analytical solutions through comparison against either existing analytical solutions or the numerical solution from two-dimensional subsurface flow, fate and transport of microbes and chemicals (2DFATMIC) [57]. When existing analytical solutions were available, we compared the proposed solutions against existing analytical solutions; otherwise, comparison was performed against the numerical solutions of 2DFATMIC. To guarantee that the numerical solution had negligible numerical error, 2DFATMIC employed a sufficiently fine grid and small time step ( = 0.005 m and = 0.01 day) to maintain low Courant and Peclet numbers. To assess the performance of the proposed analytical solution with various dispersion coefficients and velocities, concentration distributions were calculated for eight different dispersion coefficients and velocities, as described above (Table 2). All input parameters used for all cases are presented in Table 2. A schematic diagram of the flow region including initial condition, boundary domains, and sink/sources for solute transport is shown in Figure 1.

Table 2.
Parameters used for analysis of all examples.
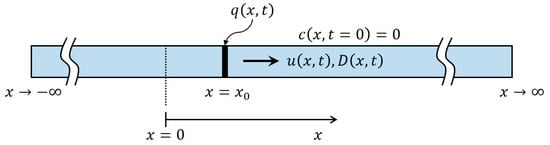
Figure 1.
A schematic diagram of the flow domain including initial condition, boundary domains, and sinks/sources for solute transport. is the concentration, is dispersion coefficient, is pore velocity, is the sink/source term, and is the location of sinks/sources.
In this study, the effect of spatial dependence on solute transport is reflected using two values of (m−1). The larger value of the spatial dependence parameter (m−1) represents a heterogeneous medium and the smaller value of the spatial dependence parameter (m−1) is too small for the dispersion coefficient or velocity to vary with position, and thus represents a homogeneous medium. Therefore, we determined the dispersion coefficient and velocity for the heterogeneous case using the larger value of , and for the homogeneous case using a very small .
Figure 2 shows the proposed analytical solutions obtained with a spatiotemporally dependent dispersion coefficient and spatially dependent velocity, representing Case 1 in Section 2.3.1. In this case, no previous analytical solution exists, and therefore verification was performed through comparison with the numerical solution of 2DFATMIC. To describe solute transport for a spatiotemporally dependent dispersion coefficient and spatially dependent velocity under Case 1 from an introduced instantaneous source, solutions of Equation (21) for both the dispersion coefficient and velocity are shown for two dispersion coefficient expressions, and , and for two spatial values , 0.1 m−1 and 0.0001 m−1. The input parameters used for the proposed analytical solution illustrated in Figure 2 are indicated in Table 2. The effect of temporal dependence of the dispersion coefficient is illustrated in Figure 2, which shows solutions to Equation (21) for asymptotically accelerating expressions of and asymptotically decelerating expressions of , described by cases (ii) and (iii) in Section 2.3.1, respectively. As shown in the upper-left subfigure of Figure 2, the asymptotically accelerating form of increases over time, but the asymptotically decelerating form of decreases over time. Accordingly, the dispersion coefficient for the accelerating form increases over time, while that for the decelerating form decreases over time. Because the dispersion coefficient is higher for the accelerating form than for the decelerating form at any time , the peak concentration is lower for the accelerating function than for the decelerating function with both values of , as shown in Figure 2.
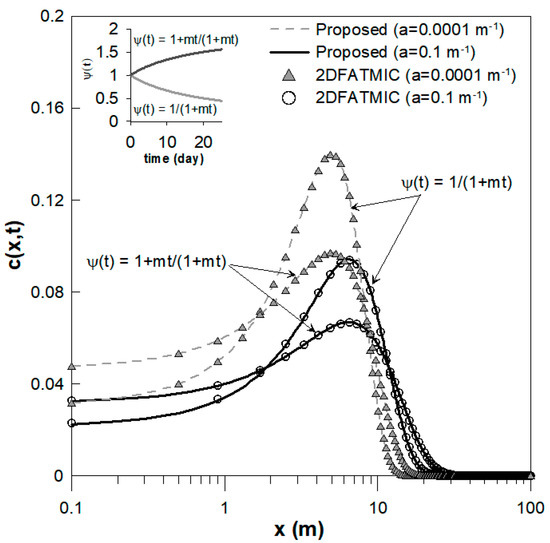
Figure 2.
Comparison of analytical solutions for an instantaneous source from Equation (21) with a spatiotemporally dependent dispersion coefficient and spatially dependent velocity (a = 0.1 m−1) shown as solid curves and with a temporally dependent dispersion coefficient and constant velocity (a = 0.0001 m−1) shown as dashed curves, with numerical solutions of 2DFATMIC at t = 25 days. Temporal values are shown in the upper-left subfigure for asymptotically decelerating and asymptotically accelerating temporal functions, respectively.
In addition, to assess the effects of spatial dependence of the dispersion coefficient and velocity, two values of were applied in a heterogeneous medium (0.1 m−1) and a homogeneous medium (0.0001 m−1). As shown in Figure 2, at all positions in the heterogeneous medium (0.1 m−1), the dispersion coefficient and velocity were higher than in the homogeneous medium (0.0001 m−1), and thus solute transport was faster in the heterogeneous medium (0.1 m−1) than in the homogeneous medium ( 0.0001 m−1). In addition, the peak concentrations were lower in a heterogeneous medium than in a homogeneous medium. As shown in Figure 2, the numerical solutions obtained using 2DFATMIC aligned well with the proposed solutions for the cases described above.
In Figure 3a,b, the proposed analytical solutions were obtained for a temporally dependent dispersion coefficient with uniform flow from instantaneous and continuous sources, respectively. A temporally dependent dispersion coefficient with uniform flow is a special case of Case 1, described in Section 2.3.1, which is obtained using a very small value of 0.0001 m−1. Using the asymptotically accelerating temporal expression of , the solutions for an instantaneous source described by Equation (21) and for a continuous source expressed in Equation (22) are compared with existing solutions corresponding to Equations (28) and (29) of Basha and El-Habel [28], respectively, in Figure 3. As shown in the upper-left subfigures of Figure 3a,b, the asymptotically accelerating temporal function increases over time, but the slope of decreases with (day). For example, in the case of days, is maximized, whereas in the case of days, is minimized. Accordingly, the dispersion coefficient is maximized at days, and minimized at days. Because the dispersion coefficient is higher in the case of days than for days and days, the plumes are more widely spread and the peak concentrations are lower at days, as shown Figure 3a,b.
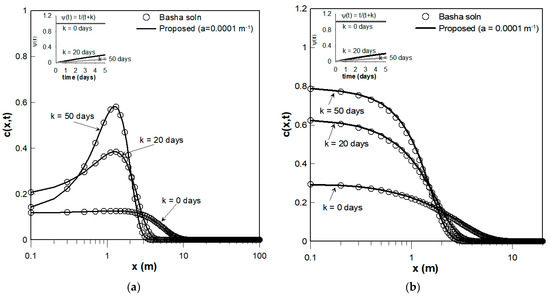
Figure 3.
Comparison of the proposed analytical solutions (shown as solid curves) with a temporally dependent dispersion coefficient and constant velocity ( 0.0001 m−1) at t = 5 days (a) for an instantaneous source based on Equation (21) and (b) for a continuous source described by Equation (22), together with the solutions at t = 5 days obtained by Basha and El-Habel [28]) (indicated with circles). The temporal values of the asymptotically accelerating temporal function are shown in the upper-left subfigure for k = 0, 20, and 50 days, respectively.
Figure 3a,b show that the proposed solutions align perfectly with the existing solutions of Basha and El-Habel [28] for instantaneous and continuous sources, respectively, with a temporally dependent dispersion coefficient and constant velocity. The temporally dependent dispersion coefficient and constant velocity have been commonly applied to solute transport considering the influence of natural heterogeneity, which produces irregular flow patterns at the field scale [23,24,25,26,27,28].
For Case 2, with spatial dependence of both the dispersion coefficient and velocity, as described in Section 2.3.2, the parameter values listed in Table 2 are used to solve Equation (23) for an instantaneous source, as shown in Figure 4. Both the dispersion coefficient and velocity increase linearly across space, depending on the spatial dependence parameter (m−1). To represent heterogeneous and homogeneous media, two values of the spatial dependence parameter (m−1) are employed, as before. In a heterogeneous medium (= 0.1 m−1), the dispersion coefficient and velocity increase across space, while in a homogeneous medium (= 0.0001 m−1), the dispersion coefficient and velocity change little spatially, and thus remain at almost constant values. Therefore, as the travel distance increases, the dispersion coefficient and velocity increase more sharply in a heterogeneous medium ( 0.1 m−1) than in a homogeneous medium (= 0.0001 m−1). Accordingly, as shown in Figure 4, as the travel distance increases, the plumes migrate faster in a heterogeneous medium (= 0.1 m−1) than in a homogenous medium ( = 0.0001 m−1), as the velocity is greater in the heterogeneous medium than in the homogeneous medium. In addition, peak concentrations are lower in a heterogeneous medium than in a homogeneous medium, as the dispersion coefficient is greater in the heterogeneous medium than in the homogenous medium. Lastly, all analytical solutions proposed for these cases are identical to the solutions of Sanskrityayn et al. [36], as shown in Figure 4.
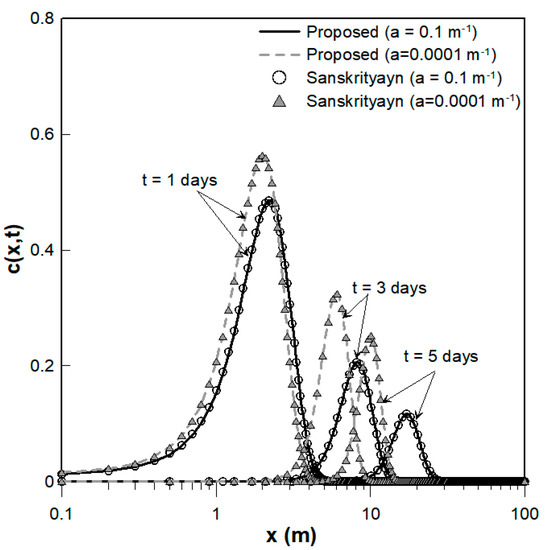
Figure 4.
Comparison of the proposed analytical solutions at t = 1, 3, and 5 days for an instantaneous source described in Equation (23) with spatial dependence of both the dispersion coefficient and velocity (a = 0.1 m−1), shown as solid curves, and with both the dispersion coefficient and velocity (a = 0.0001 m−1) constant, shown as dashed curves, along with the solutions obtained by Sanskrityayn et al. [36] at t = 1, 3, and 5 days.
To validate the proposed analytical solution of Equation (25) for solute transport with a constant dispersion coefficient and velocity assumed to be 0 m−1 for a continuous source, the analytical solution of De Marsily [52] was used for comparison, as shown in Figure 5. The detailed input parameters for these analytical solutions are listed in Table 2. In addition, the proposed analytical solution of Equation (24) with spatial dependence of both the dispersion coefficient and velocity for a continuous source was verified against the analytical solutions of Zoppou and Knight [10], as shown in Figure 5. The detailed input parameters for these analytical solutions are listed in Table 2. Note that in the analytical solution of De Marsily [52], the velocity was assumed to be constant, whereas in Zoppou and Knight [10] the velocity was assumed to increase with travel distance. Accordingly, the analytical solution for the concentration distribution reported by De Marsily [52] shows a flat trend around the source point, while that of Zoppou and Knight [10] decreases rapidly from the source point, as shown in Figure 5. Moreover, the proposed analytical solutions for a constant dispersion coefficient and velocity, as well as for spatial dependence of both the dispersion coefficient and velocity with a continuous source align well with the analytical solutions of De Marsily [52] and Zoppou and Knight [10], respectively, as shown in Figure 5.
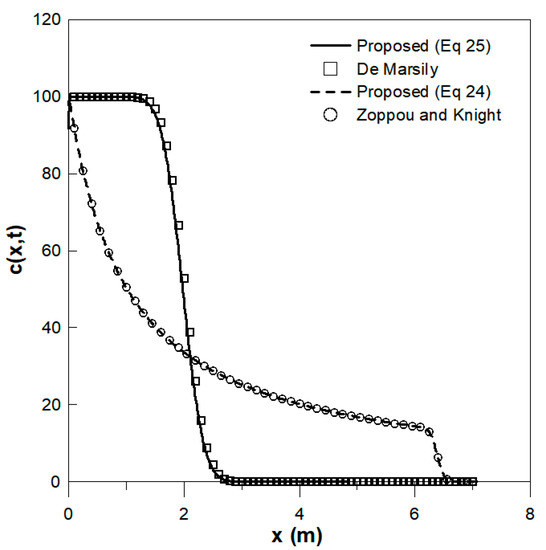
Figure 5.
Comparison of the proposed analytical solution (shown as a solid line) obtained using Equation (25) with a constant dispersion coefficient and velocity for a continuous source with the analytical solution (indicated by squares) of De Marsily [52]. Comparison of the proposed analytical solution (shown as a dashed line) of Equation (24) with a spatially dependent dispersion coefficient and velocity for a continuous source with the analytical solution (indicated by circles) of Zoppou and Knight [10] is also shown.
To verify the analytical solutions of Equation (26) for an instantaneous source with a spatially dependent dispersion coefficient and spatiotemporally dependent velocity, as described for Case 3 in Section 2.3.3, against the numerical solutions of 2DFATMIC, a comparison was conducted, as shown in Figure 6a.
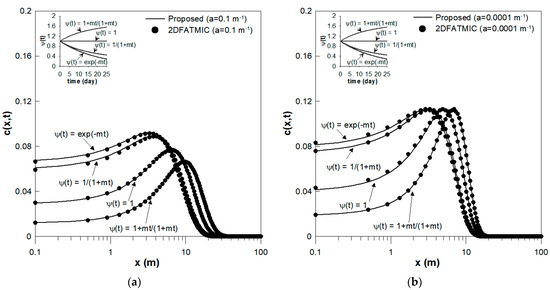
Figure 6.
Comparison of the proposed analytical solutions at t = 25 days for an instantaneous source described in Equation (26) with the numerical solutions of 2DFATMIC, when (a) the dispersion coefficient is spatially dependent and velocity is spatiotemporally dependent (a = 0.1 m−1), and when (b) the dispersion coefficient is constant and velocity is temporally dependent (a = 0.0001 m−1). The temporal values are shown in the upper-left subfigure for the constant, exponentially decelerating, asymptotically decelerating, and asymptotically accelerating forms.
The temporal dependence of velocity was considered using the exponentially decelerating, asymptotically accelerating, and asymptotically decelerating expressions of described in Section 2.3.3, as well as a constant value of . As shown in the upper-left subfigure of Figure 6a, the asymptotically accelerating form of increases over time, whereas the asymptotically and exponentially decelerating forms of and both decrease over time. Accordingly, velocity increases over time when using the asymptotically accelerating form, but decreases over time with the exponentially and asymptotically decelerating forms. Thus, in Figure 6a, transport is faster with the asymptotically accelerating form of than with the constant expression of , while transport is slower with the asymptotically and exponentially decelerating forms of and than with the constant expression of . In turn, solute transport is fastest when the asymptotically accelerating function is applied, and slowest with the exponentially decelerating function, as shown in Figure 6a.
The analytical solutions obtained using a constant dispersion coefficient with temporally dependent velocity for an instantaneous source can be obtained from Equation (26) using 0.0001 m−1. As described above, to verify the analytical solutions, analytical solutions were obtained for a homogeneous medium ( 0.0001 m−1) and compared to the numerical solutions of 2DFATMIC, as shown in Figure 6b. Depending on the function of used, as described in Section 2.3.3, transport values were obtained that followed a similar trend as the values with a spatially dependent dispersion coefficient, spatiotemporally dependent velocity, and an instantaneous source obtained previously. Namely, solute transport is fastest with an asymptotically accelerating function, while an exponentially decelerating function results in the slowest transport value.
Peak concentrations with a constant dispersion coefficient, temporally dependent velocity and an instantaneous source showed little difference in behavior relative to those obtained with a spatially dependent dispersion coefficient, spatiotemporally dependent velocity and an instantaneous source, as demonstrated by comparison of Figure 6a,b. As shown in Figure 6b, the peak concentrations are almost identical for all four expressions of , due to the constant dispersion coefficients used in all four expressions. On the other hand, as shown in Figure 6a, the peak concentrations varied among expressions of . The peak concentration was minimal with the asymptotically accelerating form of , and maximal with the exponentially decelerating form of , as the dispersion coefficient for the asymptotically accelerating form with the longest travel distance is greatest, whereas the dispersion coefficient for the exponentially decelerating form with the smallest travel distance is lowest with the spatially dependent dispersion coefficients shown in Figure 6a.
All analytical solutions obtained using a spatially dependent dispersion coefficient with spatiotemporally dependent velocity, i.e., Case 3 in Section 2.3.3, for an instantaneous source, as well as those obtained with a constant dispersion coefficient and temporally dependent velocity, aligned well with numerical solutions obtained from 2DFATMIC, as shown in Figure 6a,b, respectively.
In addition to the case of a constant dispersion coefficient and temporally dependent velocity for an instantaneous source discussed above, the analytical solutions of Equation (27) for a continuous source were validated through comparison with the analytical solution obtained by Selvadurai [29] under the assumption of an exponentially decelerating velocity over time and a constant diffusion coefficient. The analytical solution of Selvadurai [29] simulated one-dimensional solute transport under advective-dispersive conditions encountered in column flow, which was characterized by exponential decay of the velocity over time and a constant dispersion coefficient. The proposed analytical solution was obtained using Equation (27) with a very small value of = 0.0001 m−1 and compared to the analytical solution of Selvadurai [29]. As shown in Figure 7, the proposed analytical solution was identical to that of Selvadurai [29].
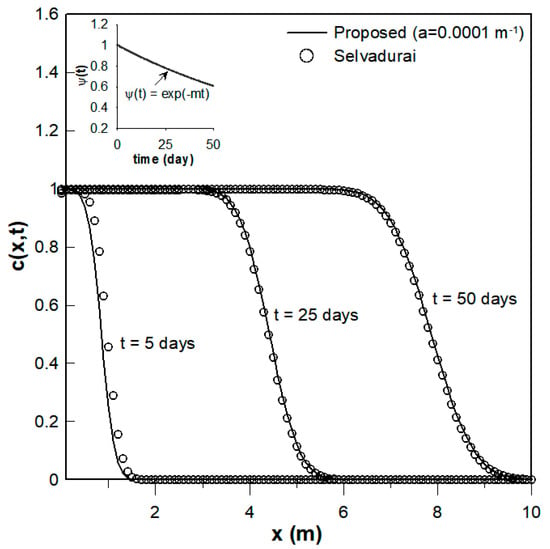
Figure 7.
Comparison of the proposed analytical solution (shown as a solid curve) for a continuous source described by Equation (27) with a constant dispersion coefficient and temporally dependent velocity (a = 0.0001 m−1) to the analytical solution (indicated with circles) obtained by Selvadurai [29] using a constant diffusion coefficient with exponentially decelerating velocity. The temporal value of the exponentially decelerating temporal function are shown in the upper-left subfigure.
To describe solute transport from an instantaneous source with spatiotemporal dependence of both the dispersion coefficient and velocity, as well as with temporal dependence of both the dispersion coefficient and velocity, as described for Case 4 in Section 2.3.4, Equation (28) was employed to obtain concentration distributions in a heterogeneous medium ( 0.1 m−1) and a homogeneous medium ( 0.0001 m−1). Figure 8a,b show the concentration distributions in a heterogeneous medium and a homogeneous medium, respectively, for three temporal dependence forms of described as (i)–(iii) in Section 2.3.4 and a constant value of = 1. The three temporal dependence forms of are the exponentially decelerating expression , the asymptotically accelerating expression and the asymptotically decelerating expression , as shown in Figure 6a,b. Therefore, in Figure 8a,b, transport is faster in the case of than with , as the velocity is greater when using the asymptotically accelerating form than with . On the other hand, transport with or is slower than with , as the velocities are slower for the asymptotically and exponentially decelerating forms than for . In addition, as illustrated in Figure 8a,b, the peak concentrations are lower for than for , as the dispersion coefficients are larger for the asymptotically accelerating form than for . Meanwhile, peak concentrations are higher for and than for , as the asymptotically and exponentially decelerating forms have smaller dispersion coefficients than .
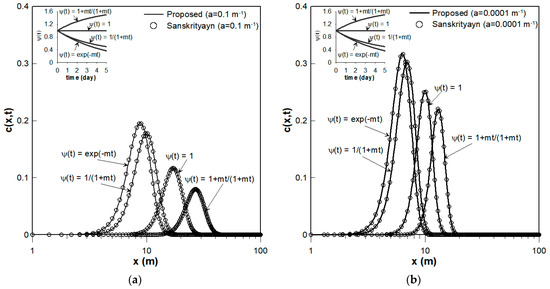
Figure 8.
Comparison of the proposed analytical solutions for an instantaneous source based on Equation (28) with the analytical solutions of Sanskrityayn et al. [36] when (a) the dispersion coefficient and velocity are spatiotemporally dependent (a = 0.1 m−1), and when (b) the dispersion coefficient and velocity are temporally dependent (a = 0.0001 m−1), at t = 5 days. The temporal values of are shown in upper-left subfigure for the constant, exponentially decelerating, asymptotically decelerating, and asymptotically accelerating forms, respectively.
Furthermore, the transport rates for all temporal functions when both the dispersion coefficient and velocity are temporally dependent in a homogeneous system, as illustrated in Figure 8b, are slower than the transport rates for all temporal functions when both the dispersion coefficient and velocity are spatiotemporally dependent in a heterogeneous system, as illustrated in Figure 8a. This difference arises because the advection velocities are smaller for all temporal functions in a homogeneous system than in a heterogeneous system. The reason why the advection velocities for all temporal functions in a homogeneous system are low is apparent from the advection expressions listed in Table 2: in the homogeneous system, the advection velocities do not increase with distance, while in the heterogeneous system, the advection velocities increase with travel distance. Furthermore, Figure 8a,b clearly show that the peak concentrations for all temporal functions when both the dispersion coefficient and velocity are temporally dependent in a homogeneous system, as illustrated in Figure 8b, are higher than the peak concentrations for all temporal functions when both the dispersion coefficient and velocity are spatiotemporally dependent in a heterogeneous system, as shown in Figure 8a. This difference can be attributed to differences in the dispersion coefficients between the cases in which both dispersion coefficient and velocity are temporally dependent and both are spatiotemporally dependent. The dispersion coefficients of all temporal functions with a temporally dependent dispersion coefficient and velocity in a homogeneous system are smaller than the coefficients of all temporal functions with a spatiotemporally dependent dispersion coefficient and velocity in a heterogeneous system, which is apparent from the dispersion coefficient expressions in Table 2. Specifically, in a homogeneous system, the dispersion coefficients do not increase with distance, while dispersion coefficients in a heterogeneous system increase with travel distance.
As shown in Figure 8a,b, all proposed analytical solutions of Equation (28) for solute transport from an instantaneous source with spatiotemporal dependence of both the dispersion coefficient and velocity or temporal dependence of both the dispersion coefficient and velocity, described as Case 4 in Section 2.3.4, are identical to the analytical solutions of Sanskrityayn et al. [36].
Finally, in contrast to the proposed analytical solution for an instantaneous source with both the velocity and dispersion coefficient temporally dependent, which is a special case of Case 4 in Section 2.3.4, the proposed analytical solution for a continuous source with both the velocity and dispersion coefficient temporally dependent, another special case of Case 4 described in Section 2.3.4, were compared with the solutions of Singh et al. [11] and Zamani and Bombardelli [12]. Singh et al. [11] provided analytical solutions of solute transport in an aquifer where flow velocity and the dispersion coefficient decreased exponentially over time. Zamani and Bombardelli [12] provided analytical solutions for solute transport in an aquifer where groundwater flow changed sinusoidally over time. The sinusoidal form can be used to represent seasonal rainfall variations in tropical regions or to indicate monthly or daily tidal variations. Accordingly, Singh et al. [11] and Zamani and Bombardelli [12] provided analytical solutions for a continuous source with temporal dependence of both the velocity and dispersion coefficients, but employed velocity and dispersion coefficients with different temporal dependences. As shown in Figure 9a,b, the proposed analytical solutions obtained using Equation (29) with a = 0.0001 m−1 agree well with those of Singh et al. [11] and Zamani and Bombardelli [12], respectively.
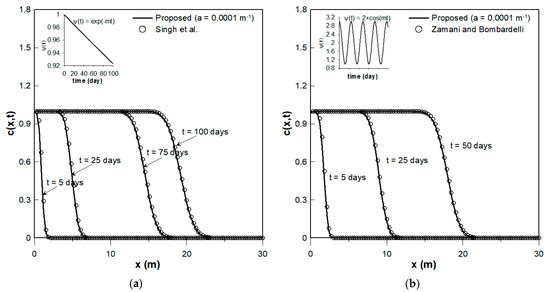
Figure 9.
Comparison of the proposed analytical solutions (shown as solid curves) for a continuous source obtained using Equation (29) with temporally dependent dispersion coefficient and velocity (a = 0.0001 m−1), to (a) the solutions of Singh et al. [11] (indicated with circles) with temporally exponential decelerating dispersion coefficients and velocity, and (b) the solution of Zamani and Bombardelli [12] (indicated with circles) with temporally sinusoidal dispersion coefficients and velocity.
4. Conclusions
Numerous classical analytical solutions have been applied under limited circumstances where the velocity or dispersion coefficient can be considered constant. To increase the utility of such analytical solutions and support consideration of various dispersion coefficient and velocity types, we generalized the analytical solutions for one-dimensional solute transport under various conditions of the flow regime and dispersion coefficients. The generalized analytical solutions consider solute transport from instantaneous and continuous point sources with eight types of dispersion coefficient and velocity. In addition, the flow velocity and dispersion coefficient can vary temporally, spatially, or spatiotemporally.
In this study, the eight velocity and dispersion coefficient patterns were considered to account for various situation encountered in the field. The spatial dependencies of velocity and dispersion coefficients are linear, while their temporal dependencies include asymptotically accelerating, asymptotically decelerating, exponentially decelerating, and sinusoidal forms. The ADE with various spatiotemporally variable coefficients was reduced to a solvable form through pertinent coordinate transformations, together with definition of new spatial and temporal variables. The transformed equation was solved using the Green’s function method. This study showed that the proposed analytical solution could be used to accurately describe the distinctive features of the observed breakthrough curve at various locations in laboratory test, to provide a solution of solute transport with highly transient flow rates induced from the inflow source, and to analyze the effects of velocity fluctuation on dispersive mixing in a porous medium.
Previous analytical solutions developed for special cases with various spatiotemporal variations in the velocity and dispersion coefficients employed in this study were used to validate the proposed analytical solutions [10,11,12,28,29]. Furthermore, when no analytical solutions were available, the proposed analytical solutions were verified through comparison with the numerical solutions of 2DFATMIC. In addition, mathematical derivation was used to demonstrate that the analytical solutions proposed in this study are an extension and generalization of previously reported analytical solutions.
Finally, the analytical solutions presented here are not only applicable to specific situations, such as solute transport under seasonal rainfall variations and monthly or daily variations due to tidal effects in areas near a river or sea, but could also be used to validate numerical solutions that account for complicated situations characterized by various spatiotemporal patterns of both velocity and the dispersion coefficient.
Author Contributions
Conceptualization, A.S.; methodology, A.S.; software, A.S. and H.S.; validation, A.S. and H.S.; formal analysis, A.S. and H.S.; investigation, J.-S.C.; resources, E.P.; data curation, A.S.; writing—original draft preparation, A.S. and H.S.; writing—review and editing, A.S., H.S., J.-S.C. and E.P.; visualization, A.S. and H.S.; supervision, J.-S.C. and E.P.; project administration, J.-S.C. and E.P.; funding acquisition, H.S., J.-S.C. and E.P. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the project titled “Research on rock properties in deep environment for HLW geological disposal (GP2020–002; 21–3115)” funded by the Ministry of Science and ICT, Korea.
Data Availability Statement
Data is not publicly available, though the data may be made available on request from the corresponding author.
Acknowledgments
This study was performed through the Korea Institute of Geosciences and Mineral resources (KIGAM). We also appreciate support by the project titled “Research on rock properties in deep environment for HLW geological disposal (GP2020–002; 21–3115)” funded by the Ministry of Science and ICT, Korea.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A
To reduce the variable coefficients of the ADE in Equation (7) and obtain the diffusion equation with a constant coefficient, as expressed in Equation (13), the coordinate transformation equations in Equations (9) and (10) are derived as follows:
Given that
Using Equation (A1), Equation (7) can be rewritten as:
where
If Equation (A2) is equivalent to the diffusion equation in Equation (13), then
Substituting Equation (A4) into Equation (A5), Equation (A5) is obtained, as follows:
Integrating Equation (A4) with respect to , we obtain
Using Equation (A7), Equation (A6) can be rewritten as follows:
Using the terms and from Equations (3) and (4), Equation (A8) can be expressed as
Equating the coefficients of and from both sides of Equation (A9), we obtain
and
From Equation (A11), can be obtained as
From Equation (A12), we can express in terms of and as:
where
Using Equations (A3) and (A13), we can obtain a new temporal variable as follows:
From Equations (A7) and (A13), we can obtain the new spatial variable as follows:
Equation (A16) is the same as Equation (9). Using Equations (A10) and (A11), we can obtain an expression of as:
Appendix B
To verify that the present analytical solution can be degenerated into the analytical solution of Sanskrityayn et al. [36], consider: , and . Using , , , and Equation (12), we determine as follows:
Using Equations (3), (4), and (A18), we obtain the dispersion coefficient and velocity as
References
- Shi, X.; Lei, T.; Yan, Y.; Zhang, F. Determination and impact factor analysis of hydrodynamic dispersion coefficient within a gravel layer using an electrolyte tracer method. Int. Soil Water Conserv. Res. 2016, 4, 87–92. [Google Scholar] [CrossRef]
- Pérez Guerrero, J.S.; Pontedeiro, E.M.; van Genuchten, M.T.; Skaggs, T.H. Analytical solutions of the one-dimensional advection–dispersion solute transport equation subject to time-dependent boundary conditions. Chem. Eng. J. 2013, 221, 487–491. [Google Scholar] [CrossRef]
- Chen, J.-S.; Lai, K.-H.; Liu, C.-W.; Ni, C.-F. A novel method for analytically solving multi-species advective–dispersive transport equations sequentially coupled with first-order decay reactions. J. Hydrol. 2012, 420–421, 191–204. [Google Scholar] [CrossRef]
- Clement, T.P. Generalized solution to multispecies transport equations coupled with a first-order reaction network. Water Resour. Res. 2001, 37, 157–163. [Google Scholar] [CrossRef]
- Clement, T.P.; Srinivasan, V. Analytical solutions for sequentially coupled one-dimensional reactive transport problems—Part I: Mathematical derivations. Adv. Water Resour. 2008, 31, 203–218. [Google Scholar] [CrossRef]
- Corniello, A.; Ducci, D.; Sellerino, M. The hydrogeological monitoring of an experimental site in Campania focused at the evaluation of the contaminants transfer from the soil. Rend. Online Soc. Geol. Ital. 2019, 47, 24–30. [Google Scholar] [CrossRef]
- Kihm, J.-H.; Hwang, G. Numerical simulation of water table drawdown due to groundwater pumping in a contaminated aquifer system at a shooting test site, Pocheon, Korea. Econ. Environ. Geol. 2021, 54, 247–257. [Google Scholar] [CrossRef]
- De Josselin de Jong, G. Longitudinal and transverse diffusion in granular deposits. Trans. Am. Geophys. Union 1958, 39, 67–74. [Google Scholar] [CrossRef]
- Serrano, S.E. The form of the dispersion equation under recharge and variable velocity, and its analytical solution. Water Resour. Res. 1992, 28, 1801–1808. [Google Scholar] [CrossRef]
- Zoppou, C.; Knight, J.H. Analytical solutions for advection and advection-diffusion equations with spatially variable coefficients. J. Hydraul. Eng. 1997, 123, 144–148. [Google Scholar] [CrossRef]
- Singh, M.K.; Singh, V.P.; Singh, P.; Shukla, D. Analytical solution for conservative solute transport in one-dimensional homogeneous porous formations with time-dependent velocity. J. Eng. Mech. 2009, 135, 1015–1021. [Google Scholar] [CrossRef]
- Zamani, K.; Bombardelli, F.A. Analytical solutions of nonlinear and variable-parameter transport equations for verifications of numerical solvers. Environ. Fluid Mech. 2014, 14, 711–742. [Google Scholar] [CrossRef]
- Kinzelbach, W.; Ackerer, P. Modelisation de la propogation d’ un champ d’ écoulement transitoire. Hydrogeology 1986, 2, 197–206. (In French) [Google Scholar]
- Sposito, G.; Weeks, S.W. Tracer advection by steady groundwater flow in a stratified aquifer. Water Resour. Res. 1998, 34, 1051–1059. [Google Scholar] [CrossRef]
- Su, N.; Sander, G.C.; Liu, F.; Anh, V.; Barry, D.A. Similarity solutions for solute transport in fractal porous media using a time- and scale dependent dispersivity. Appl. Math. Model. 2005, 29, 852–870. [Google Scholar] [CrossRef]
- Pang, L.; Hunt, B. Solutions and verification of a scale-dependent dispersion model. J. Contam. Hydrol. 2001, 53, 21–39. [Google Scholar] [CrossRef]
- Moranda, A.; Cianci, R.; Paladino, O. Analytical solutions of one-dimensional contaminant transport in soils with source production-decay. Soil Syst. 2018, 2, 40. [Google Scholar] [CrossRef]
- Paladino, O.; Moranda, A.; Massabò, M.; Robbins, G.A. Analytical solutions of three-dimensional contaminant transport models with exponential source decay. Groundwater 2017, 56, 96–108. [Google Scholar] [CrossRef]
- Stoppiello, M.G.; Lofrano, G.; Carotenuto, M.; Viccione, G.; Guarnaccia, C.; Cascini, L. A comparative assessment of analytical fate and transport models of organic contaminants in unsaturated soils. Sustainability 2020, 12, 2949. [Google Scholar] [CrossRef]
- Gelhar, L.W.; Welty, C.; Rehfeldt, K.R. A critical review of data on field-scale dispersion in aquifers. Water Resour. Res. 1992, 28, 1955–1974. [Google Scholar] [CrossRef]
- Rehfeldt, K.R.; Gelhar, L.W. Stochastic analysis of dispersion in unsteady flow in heterogeneous aquifers. Water Resour. Res. 1992, 28, 2085–2099. [Google Scholar] [CrossRef]
- Neuman, S.P. Universal scaling of hydraulic conductivities and dispersivities in geologic media. Water Resour. Res. 1990, 26, 1749–1758. [Google Scholar] [CrossRef]
- Dagan, G. Solute transport in heterogeneous porous formations. J. Fluid Mech. 1984, 145, 151–177. [Google Scholar] [CrossRef]
- Dagan, G. Time-dependent macrodispersion for solute transport in anisotropic heterogeneous aquifers. Water Resour. Res. 1988, 24, 1491–1500. [Google Scholar] [CrossRef]
- Aral, M.M.; Liao, B. Analytical solutions for two–dimensional transport equations with time-dependent dispersion coefficients. J. Hydrol. Eng. 1996, 1, 20–32. [Google Scholar] [CrossRef]
- Zoua, S.; Ma, J.; Koussis, A.D. Analytical solutions to non-Fickian subsurface dispersion in uniform groundwater flow. J. Hydrol. 1996, 179, 237–258. [Google Scholar] [CrossRef]
- Sposito, G.; Barry, D.A. On the Dagan model of solute transport in groundwater: Foundational aspects. Water Resour. Res. 1987, 23, 1867–1875. [Google Scholar] [CrossRef]
- Basha, H.A.; El-Habel, F.S. Analytical solution of the one-dimensional time dependent transport equation. Water Resour. Res. 1993, 29, 3209–3214. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S. On the advective-diffusive transport in porous media in the presence of time-dependent velocities. Geo. Res. Lett. 2004, 31, 1–5. [Google Scholar] [CrossRef]
- Huang, C.-S.; Tong, C.; Hu, W.-S.; Yeh, H.-D.; Yang, T. Analysis of radially convergent tracer test in a two-zone confined aquifer with vertical dispersion effect: Asymmetrical and symmetrical transports. J. Hazard. Mater. 2019, 377, 8–16. [Google Scholar] [CrossRef] [PubMed]
- Suk, H. Semi-analytical solution of land-derived solute transport under tidal fluctuation in a confined aquifer. J. Hydrol. 2017, 554, 517–531. [Google Scholar] [CrossRef]
- Sternberg, S.P.K.; Cushman, J.H.; Greenkorn, R.A. Laboratory observation of nonlocal dispersion. Trans. Porous Media 1996, 13, 123–151. [Google Scholar] [CrossRef]
- Zhou, R.; Zhan, H.; Chen, K.; Peng, X. Transport in a fully coupled asymmetric stratified system: Comparison of scale dependent and independent dispersion schemes. J. Hydrol. X 2018, 1, 100001. [Google Scholar] [CrossRef]
- Kumar, A.; Jaiswal, D.K.; Kumar, N. Analytical solutions to one-dimensional advection-diffusion equation with variable coefficients in semi-infinite media. J. Hydrol. 2010, 380, 330–337. [Google Scholar] [CrossRef]
- Sanskrityayn, A.; Suk, H.; Kumar, N. Analytical solutions for solute transport in groundwater and riverine flow using Green’s function method and pertinent coordinate transformation method. J. Hydrol. 2017, 547, 517–533. [Google Scholar] [CrossRef]
- Sanskrityayn, A.; Kumar, V.; Kumar, N. Solute transport due to spatio-temporally dependent dispersion coefficient and velocity: Analytical solutions. J. Hydrol. Eng. 2018, 23, 04018009. [Google Scholar] [CrossRef]
- You, K.; Zhan, H. New solutions for solute transport in a finite column with distance-dependent dispersivities and time-dependent solute sources. J. Hydrol. 2013, 487, 87–97. [Google Scholar] [CrossRef]
- Van Genuchten, M.T.; Alves, W.J. Analytical Solutions of the One-Dimensional Convective Dispersive Solute Transport Equations; Technical Bulletin No. 1661; U.S. Department of Agriculture: Washington, DC, USA, 1982.
- Javandel, I.; Doughty, C.; Tsang, C.F. Groundwater Transport Hand Book of Mathematical Models. In AGU Water Resources Monograph Series 10; AGU: Washington, DC, USA, 1984. [Google Scholar]
- Pickens, J.F.; Grisak, G.E. Scale-dependent dispersion in stratified granular aquifer. Water Resour. Res. 1981, 17, 1191–1211. [Google Scholar] [CrossRef]
- Yates, S.R. An Analytical solution for one-dimensional transport in heterogeneous porous media. Water Resour. Res. 1990, 26, 2331–2338. [Google Scholar] [CrossRef]
- Gao, G.; Zhan, H.; Feng, S.; Fu, B.; Ma, Y.; Huang, G. A new mobile-immobile model for reactive solute transport with scale-dependent dispersion. Water Resour. Res. 2010, 46, W08533. [Google Scholar] [CrossRef]
- Hunt, B. Contaminant source solutions with scale-dependent dispersivities. J. Hydrol. Eng. 1998, 3, 268–275. [Google Scholar] [CrossRef]
- Chen, J.S.; Ni, C.F.; Liang, C.P. Analytical power series solution to the two-dimensional advection-dispersion equation with distance-dependent dispersivites. Hydrol. Process. 2008, 22, 4670–4678. [Google Scholar] [CrossRef]
- Chen, J.S.; Ni, C.F.; Liang, C.P.; Chiang, C.C. Analytical power series solution for contaminant transport with hyperbolic asymptotic distance-dependent dispersivity. J. Hydrol. 2008, 362, 142–149. [Google Scholar] [CrossRef]
- Zamani, K.; Bombardelli, F.A. One-dimensional, mass conservative, spatially-dependent transport equation: New analytical solution. In Proceedings of the 12th Pan-American Congress of Applied Mechanics, Port of Spain, Trinidad, 2–6 January 2012. [Google Scholar]
- Kumar, A.; Jaiswal, D.K.; Kumar, N. Analytical solutions of one dimensional advection diffusion equation with variable coefficients in a finite domain. J. Earth Syst. Sci. 2009, 118, 539–549. [Google Scholar] [CrossRef]
- Sanskrityayn, A.; Kumar, N. Analytical solution of advection-diffusion equation in heterogeneous infinite medium using Green’s function method. J. Earth Syst. Sci. 2016, 125, 1713–1723. [Google Scholar] [CrossRef]
- Suk, H. Developing semianalytical solutions for multispecies transport coupled with a sequential first-order reaction network under variable flow velocities and dispersion coefficients. Water Resour. Res. 2013, 49, 3044–3048. [Google Scholar] [CrossRef]
- Suk, H. Generalized semi-analytical solutions to multispecies transport equation coupled with sequential first-order reaction network with spatially or temporally variable transport and decay coefficients. Adv. Water Resour. 2016, 94, 412–423. [Google Scholar] [CrossRef]
- Yeh, G.T. AT123D: Analytical Transient One-, Two-, and Three-Dimensional Simulation of Waste Transport in the Aquifer System; Environmental Sciences Division 1439 Report ORNL-5602; Oak Ridge Natl Lab: Oak Ridge, TN, USA, 1981.
- De Marsily, G. Quantitative Hydrogeology: Groundwater Hydrology for Engineers; Academic Press, Inc.: San Diego, CA, USA, 1986. [Google Scholar]
- Matheron, G.; De Marsily, G. Is transport in porous media always diffusive? A counterexample. Water Resour. Res. 1980, 16, 901–917. [Google Scholar] [CrossRef]
- Haberman, R. Elementry Applied Partial Differential Equations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1987. [Google Scholar]
- Beck, J.V.; Cole, K.D.; Litkouhi, B. Heat Conduction Using Green’s Functions; Hemisphere Publishing Corporation: Washington, DC, USA, 1992. [Google Scholar]
- Yeh, H.D.; Yeh, G.T. Analysis of point-source and boundary-source solutions of one-dimensional groundwater transport equation. J. Environ. Eng. 2007, 133, 1032–1041. [Google Scholar] [CrossRef][Green Version]
- Yeh, G.T.; Cheng, J.R. 2DFATMIC: User’s Manual of a Two-Dimensional Subsurface Flow, Fate and Transport of Microbes and Chemical Model Version 1.0. EPA/600/R-97/052; U.S. Environmental Protection Agency: Washington, DC, USA, 1997.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).