Tuning Deep Neural Networks for Predicting Energy Consumption in Arid Climate Based on Buildings Characteristics

Abstract

The dramatic growth in the number of buildings worldwide has led to an increase interest in predicting energy consumption, especially for the case of residential buildings. As the heating and cooling system highly affect the operation cost of buildings; it is worth investigating the development of models to predict the heating and cooling loads of buildings. In contrast to the majority of the existing related studies, which are based on historical energy consumption data, this study considers building characteristics, such as area and floor height, to develop prediction models of heating and cooling loads. In particular, this study proposes deep neural networks models based on several hyper-parameters: the number of hidden layers, the number of neurons in each layer, and the learning algorithm. The tuned models are constructed using a dataset generated with the Integrated Environmental Solutions Virtual Environment (IESVE) simulation software for the city of Buraydah city, the capital of the Qassim region in Saudi Arabia. The Qassim region was selected because of its harsh arid climate of extremely cold winters and hot summers, which means that lot of energy is used up for cooling and heating of residential buildings. Through model tuning, optimal parameters of deep learning models are determined using the following performance measures: Mean Square Error (MSE), Root Mean Square Error (RMSE), Regression (R) values, and coefficient of determination (R${}^2$). The results obtained with the five-layer deep neural network model, with 20 neurons in each layer and the Levenberg–Marquardt algorithm, outperformed the results of the other models with a lower number of layers. This model achieved MSE of 0.0075, RMSE 0.087, R and R${}^2$ both as high as 0.99 in predicting the heating load and MSE of 0.245, RMSE of 0.495, R and R${}^2$ both as high as 0.99 in predicting the cooling load. As the developed prediction models were based on buildings characteristics, the outcomes of the research may be relevant to architects at the pre-design stage of heating and cooling energy-efficient buildings.

1. Introduction

Over the past decade, there has been a rapid increase in the number of residential buildings, which has raised worldwide interest on climate change, global carbon emission [1,2], global warming, urban growth, and fast construction development. In Saudi Arabia, all building sectors are accountable for around 70% of the total energy consumption, and about 50% of that is used by residential buildings [3,4]. Many residential buildings in Saudi Arabia are detached or semidetached types, which demand more cooling and heating loads than typical flat apartments.

The Qassim region has a very harsh arid weather condition. The region has a dry climate characterized by hot summers and cold winters. Thus, energy in buildings is used primarily for their heating during winter and their cooling during summer. In fact, almost 76% of the total energy consumption in residential buildings goes for their heating and cooling load [4].

Surprisingly, the effectiveness of energy consumption is not well documented in this region. Following the Saudi vision 2030 [5] to enhance energy efficiency, this study proposes a predictive model for energy consumption of residential buildings in the Qassim region based on a typical condition of building characteristics.

Building characteristics, such as form orientation, roof type and wall insulation, among others, are essential elements that determine energy consumption by residential buildings. Different terms have been used to identify building characteristics. The building characteristics or building envelope are the key influential design parameter that significantly affects the energy consumption of buildings [6]. Therefore, architects and designers must impose proactive energy prediction strategies for a better future of built environments development and buildings energy efficiency enhancement.

Many studies have addressed building prediction modeling for energy consumption [7,8,9,10,11,12,13]. However, their developed prediction models were based mainly on historical data or recorded data of building energy consumption [8] while building characteristics were ignored. Most of the current studies that consider buildings characteristics mostly apply machine learning methods, although deep learning is rarely used. Deep neural networks which are considered as extension of the conventional artificial neural networks, allow multi-task learning [14] and have been proved to extract features automatically from the related datasets. The majority of the existent studies are based on the benchmark dataset (of 768 records) created by Tsanas and Xifara [15], whose relatively small size is not appropriate for deep learning models.

To fill the identified gap in energy consumption prediction, for this study, a larger dataset of 3840 instances was first generated and deep neural networks models were then developed. The dataset was generated for the capital of the Qassim region in Saudi Arabia, the city of Buraydah. To get the optimum prediction model, deep neural network models are tuned using different combinations of the hyper-parameters: number of hidden layers, number of neurons per layer and training algorithm.

The hyper-parameter tuning is fully described in Section 3.2. As such, the main goal of this study is to identify the optimal parameters of deep learning models for energy consumption prediction based on buildings’ characteristics. Such models are very useful to guide the predesign stage of heating and cooling energy efficient buildings.

The main contributions of this study are:

• A generated dataset for predicting energy loads based on buildings characteristics in arid climate, i.e., Qassim region, Saudi Arabia.
  Unlike the datasets available in the literature, the generated dataset is larger in size, and also dedicated to arid climate;
• Deep neural network models with different parameter tunings to predict buildings energy consumption. In fact, previous studies of buildings’ energy consumption mostly depended on typical machine learning methods rather than deep learning method. This point is further elaborated in Section 2;
• Development of energy consumption models to predict heating and cooling loads of buildings in arid climate. In contrast to the majority of the state of the art studies, the prediction models in this study are based on the buildings characteristics rather than the historical data of energy consumption.

The rest of the paper is organized as follows. Section 2 briefly reviews literature related works and identifies research gaps. Detail descriptions of methods, dataset generation and the hyper-parameter tuning of the proposed deep neural networks models are described in Section 3. Section 4 reports on the experimental results and performance comparison among the tuned models and with the state of the art models. Section 5 discusses the obtained results and Section 6 concludes the paper.

2. Related Work

Numerous studies in the existing literature have addressed building prediction modeling for energy consumption. However, the majority of them do not consider building characteristics to be the most important predictors but historical data of energy consumption or, in some cases, historical data with climate data. Despite the significance of these studies’ outcomes, there is still a lack of studies on prediction models based on the building characteristics, known as building envelope, data. Building envelope refers to wall materials, roof materials, the window to wall ratio, and facade orientation [16]. Energy prediction based on buildings characteristics allows architects and designers to optimize the building’s design at an early stage. Table 1 summarizes the related studies that have used building’s characteristics as predictors for energy consumption in terms of the prediction method used, the classification method used, either machine learning (ML) or deep learning (DL), the dataset used, and the location of the study.

Table 1. Summary of the related studies.

Ref	Prediction Method	ML/ DL	Dataset	Location
[17]	RF ANN	ML	Self-generated	U.S. Midwest
[18]	XGBoost	ML	Tsanas and Xifara [15]	Athens, Greece
[19]	ANN LSTM	ML and DL	Self-generated	N/A
[20]	ELM OSELM B-ELM	ML	Tsanas and Xifara [15]	California
[21]	ELM ANN GP	ML	Self-generated	Istanbul
[22]	Octahedric regression IRLS RF	ML	Tsanas and Xifara [15]	Alicante, Spain
[23]	DNN with SA	DL	Tsanas and Xifara [15]	Athens, Greece
[24]	SVM RF NN GP GBRT XGBoost	ML	Tsanas and Xifara [15]	Athens, Greece
[25]	ANN	ML	Self-generated	Montreal, Canada
[26]	ANN LSTM	ML and DL	Self-generated	Brussels, Belgium
[27]	ENMIM	ML	Tsanas and Xifara [15]	Ho Chi Minh City, Viet Nam
[28]	MLP ABC-MLP PSO-ELM	ML	Tsanas and Xifara [15]	NM

In the following, a summary of the related works is provided.

Al Tarhuni et al. [17] predicted each month’s natural gas energy consumption based on integrating the physics-based approach and data energy system characteristics. Adding to that, meteorological data and historical energy consumption for all residences were used. Results of the study indicate that 36% of energy consumption reduction can be achieved with efficient energy prediction.

Al-Rakhami et al. [18] introduced an ensemble learning approach, via the XGBoost method to solve overfitting issues, to design an efficient prediction model. With a dataset containing 768 samplings of building attributes, in comparison to previous studies, they obtained a lower mean square error and better accuracy for cooling and heating energy prediction. The study by Navarro-Gonzalez and Villacampa [22] also addressed the overfitting issue using the Octahedric regression method with lower computational complexity. Because of the high demand of industrial and residential buildings for efficient smart energy techniques, Reference [29] proposed a system that utilized an ensemble deep learning-based approach to predict energy consumption via chronological dependencies. The study used benchmark, residential UCI, and local Korean commercial building datasets. The data is being passed to the proposed ensemble model to extract hybrid discriminative features via convolution neural network (CNN), stacked, and bi-directional long-short term memory (LSTM) architectures. The study is being concluded by showing a lower error rate.

A component-based approach with two construction and zone levels was proposed by Geyer and Singaravel [19] to improve the machine learning models in the whole building design. They showed that high quality of estimation could be achieved with lower error rate of 3.7% and 3.9% for cooling and heating respectively.

Different machine learning approaches for energy load estimation, including Extreme Learning Machine (ELM), Online Sequential ELM (OSELM), and Bidirectional ELM (B-ELM), were proposed by Kumar et al. [20]. Substantial improvement of energy prediction based on ELM and B-ELM were achieved. Besides, a faster learning rate was also observed for the new proposed model compared to SVR, RF and ANNs. ELM was introduced by Naji et al. [21] for building energy consumption estimation using building materials thickness and thermal insulation capability. The results showed improvement in prediction accuracy with ELM compared to Genetic Programming (GP) and ANNs.

Sadeghi et al. [23] applied DNNs, with Multi-Layer Perceptron (MLP) network, to predict heating load and cooling load for a variety of structures. With various extensive testing of data pre-processing techniques, DNNs enhanced previous ANN models.

Seyedzadeh et al. [24] generated two datasets in two different simulation software to investigate ML accuracy in predicting buildings heating and cooling loads. A grid-search coupled with a cross-validation method was used to study the model parameters combinations. Among the five models studied, the outcomes indicated that the Gradient Boosted Regression Trees (GBRT) provides the best accuracy prediction results based on the RMSE. However, NNs was found to be the best for complex data sets.

Sharif and Hammad [25] focused on developing an ANN model to predict energy consumption with a large and complicated dataset generated by the SBMO model. The findings of this study revealed that the suggested ANN models was capable of accurately predicting Total Energy Consumption (TEC), Life Cycle Assessment (LCA), and Life Cycle Cost (LCC) for entire building re-modeling scenarios that included the building envelope, HVAC, and lighting systems.

Singaravel et al. [26] compared the deep learning model with building performance simulation using 201 design cases. The deep learning model showed high accuracy for cooling prediction with an R${}^2$ of 0.983. The model recorded an error for heating prediction with an R${}^2$ of 0.848, which can be resolved using more heating data from a better sampling model. The study confirmed that the simulation results using the deep learning model could be acquired in 0.9 s, which is considered high computation speed on buildings performance simulation.

Tran et al. [27] used real data from residential buildings to develop an evolutionary Neural Machine Inference Model (ENMIM) for energy consumption prediction. Their new ensemble model integrates two single supervised learning machines: the Least Squares Support Vector regression (LSSVR) and the Radial Basis Function Neural Network (RBFNN). The developed model has better accuracy than other compared artificial intelligence techniques for predicting energy consumption.

The study of Zhou et al. [28] uses the Artificial Bee Colony (ABC) and Particle Swarm Optimization (PSO) metaheuristic algorithms to optimize the MLP NN in order to predict the heating and cooling loads of energy-efficient buildings for residential usage. To do so, they used a dataset with eight independent variables: relative compactness, surface area, wall area, roof area, overall height, orientation, glazing area, and glazing area distribution. Their results indicate that using ABC and PSO algorithms improves the MLP performance. Furthermore, they determined that PSO was better than the ABC in terms of MLP performance enhancement.

The above literature review evidences the successful use of machine learning models to address problems related to buildings energy prediction. However, the following research gaps were observed:

• There is a little information on how to use deep learning models and how to tune them to meet the task at hand for the best predictive accuracy and consistency. While machine learning methods are used by most studies, deep learning is rarely used.
• Many of the studies that use building characteristics as inputs to the prediction model are based on the benchmark dataset of 786 records by Tsanas and Xifara [15]. Other self-generated datasets are kept private and are not available for experimental replication.
• Most of the studies are conducted in non-arid climates such as Spain, Greece, the USA, Canada and China.

This paper, therefore, lays out an applicable approach to tuning deep learning models to building energy data using a larger open-access self-generated dataset in Qassim, a typical arid climate region.

3. Method

This section presents the dataset generated to train the DNN models and the tuning of the models using several hyper-parameters.

3.1. Dataset Description

Figure 1 shows a snapshot of the based model: a typical detached family house located in many cities in the Qassim region. The total area of the house is 145.87 m${}^2$, while the total volume is 408.42 m${}^3$. Table 2 shows details of the building envelope. Typical heavy construction was applied to build the house. Concrete is the primary material used in walls and roof. A thermal layer (10 mm) was used in the top roof; 4 mm of double clear glass was installed in the windows. Plasterboard was applied as the exterior finishing of the building.

Figure 1. A snapshot of the case study in IESVE.

Table 2. Envelope construction features of the selected case study.

House Features	Description
Location	Buraydah (Coordinates: 26°22′17.8″ N 43°51′29.4″ E)
Orientation	Front elevation facing South
Shape	Typical Square and Rectangular combination of spaces
Ceiling Height	2.8 m
Floor Area	93.83 m${}^2$ (Ground Floor); 52.04 m${}^2$ (First Floor)
Window Wall Ratio	10–15%
Exterior Walls	15 mm Plaster (Dense) + 10 mm Cement + 200 mm Concrete Block (Medium) + 10 mm Cement + 15 mm Plaster (Lightweight)
Roof	10 mm Ceramic tiles + 30 mm Concrete layer + 10 mm Extruded Polystyrene + 150 mm Reinforced Concrete (Dense)
Windows	4 mm Double clear glass

The thermal dataset was generated in the Integrated Environmental Solutions Virtual Environment (IESVE) simulation software [30]. IESVE simulation software has been recognized as the building performance simulation by LEED (Leadership in Energy and Environmental Design), BREEAM (Building Research Establishment Environmental Assessment Method) and Green Mark. The dataset contained eight attributes as inputs and two response variables as outputs. For the input variables, the dataset included two building areas with two different floor heights, five glazing areas, six glazing U-values, four roof U-values and eight wall U-values, which equated to 3840 data series. While for the output variables, the dataset included heating and cooling, which referred to the sensible cooling load through the spaces envelope (wall, window and roof) calculated by kWh per year. Five Window to Wall Ratio (WWR), obtained dividing the total glazing area in all the walls divided by the total wall area, with two floor heights were used. Table 3 and Table 4 summarize the physical and thermal characteristics of the input and output variables in the model simulation, respectively. The generated dataset is available at [31].

Table 3. Descriptions of input variables in the model simulation.

Features	Description	Values
Building Size	Spaces in the house subjected to air-conditioning	145.86 m${}^2$ 184.53 m${}^2$
Floor Height	Internal ceiling height of spaces	2.8 m 3.0 m
Glazing Area	Net area of windows	23.25 m${}^2$ 24.15 m${}^2$ 69.75 m${}^2$ 72.46 m${}^2$ 116.24 m${}^2$ 120.76 m${}^2$ 162.74 m${}^2$ 169.07 m${}^2$ 209.24 m${}^2$ 217.37 m${}^2$
Wall Area	Gross exterior opaque wall area	217.37 m${}^2$ 209.24 m${}^2$ 169.07 m${}^2$ 162.74 m${}^2$ 120.76 m${}^2$ 116.24 m${}^2$ 72.46 m${}^2$ 69.75 m${}^2$ 24.15 m${}^2$ 23.25 m${}^2$
WWR	Window to wall ratio of all the external walls that exposed to outdoor in all sides	10% 30% 50% 70% 90%
Win Glazing U-value	Thermal properties of glazing window which measured by (W/m${}^2$K)	0.97 1.63 2.87 3.23 4.61 5.60
Roof U-value	Thermal properties of the covering of the specified spaces in the model measured by (W/m${}^2$K)	0.13 0.22 0.35 0.47
External Wall U-value	Wall envelop for the specified spaces measured by (W/m${}^2$K)	0.26 0.34 0.60 1.03 1.62 2.11 2.82 3.34

Table 4. Descriptions of output variables in the model simulation.

Variable	Description
Cooling Load	Refers to the sensible cooling load through the spaces envelope (wall, window, and roof) measured by kWh per year
Heating Load	Refers to the sensible heating load through the spaces envelope (wall, window, and roof) measured by kWh per year

The selection of wall and roof materials should achieve the sustainable approach based on energy and environmental aspects [32]. Thickness also plays a key role in the thermal performance inside the buildings [33]. Motivated by [34,35,36,37,38], the wall and roof U-values have been obtained according to the materials and insulation types and thicknesses. For instance, a wall U-value of 3.34 W/m${}^2$K, as shown in Table 3, is constructed with reinforced concrete (125 mm) covered by inside plaster (10 mm) and exterior render (10 mm). By increasing the reinforced concrete to 250 mm, the U-value improves to 2.82 W/m${}^2$K. Adding 10 mm of cavity enhanced the wall U-value to 2.11 W/m${}^2$K, while adding 100 mm of expended polystyrene as insulation and another layer of reinforced concrete (125 mm) achieved a wall U-value of 0.26 W/m${}^2$K. The roof U-value of 0.47 W/m${}^2$K is obtained with concrete deck (150 mm), polystyrene insulation (10 mm), tiles and cement finishing (8 mm). The U-value is improved to 0.35 W/m${}^2$K by increasing the thickness of the insulation from 10 to 60 mm. The U-value 0.13 W/m${}^2$K is achieved using white roof coatings as a final top finishing layer. All construction details mentioned above are used as an example for achieving the required U-value for each simulation; however, it is worth highlighting that different location, climate, and local resources could affect the availability of the materials for construction. Therefore, any materials should be obtained according to the local authorities, codes and regulations.

3.2. Hyper-Parameter Tuning of Deep Neural Networks Models

This study is based on a self-generated dataset for predicting heating and cooling load based on building characteristics. The dataset contains 3840 observations and eight building characteristics. To achieve the aim of developing an accurate prediction model, sixteen experiments with different configurations have been designed (See Table 5). Three parameters have been tuned: the number of hidden layers (2, 3, 4, 5), the number of neurons in each hidden layer (10, 20), and the backpropagation algorithm (LM algorithm; and SCG algorithm. The single-layer model was excluded as the scope of this study is to tune deep neural networks with two and more hidden layers.

Table 5. The different configurations of the models’ parameters.

Experiment	No. of Hidden Layers	No. of Neurons per Layer	Training Algorithm (Backpropagation Algorithm)
1	2	10	Levenberg–Marquardt algorithm (LM)
2	2	10	Scaled Conjugate Gradient (SCG)
3	2	20	Levenberg–Marquardt algorithm (LM)
4	2	20	Scaled Conjugate Gradient (SCG)
5	3	10	Levenberg–Marquardt algorithm (LM)
6	3	10	Scaled Conjugate Gradient (SCG)
7	3	20	Levenberg–Marquardt algorithm (LM)
8	3	20	Scaled Conjugate Gradient (SCG)
9	4	10	Levenberg–Marquardt algorithm (LM)
10	4	10	Scaled Conjugate Gradient (SCG)
11	4	20	Levenberg–Marquardt algorithm (LM)
12	4	20	Scaled Conjugate Gradient (SCG)
13	5	10	Levenberg–Marquardt algorithm (LM)
14	5	10	Scaled Conjugate Gradient (SCG)
15	5	20	Levenberg–Marquardt algorithm (LM)
16	5	20	Scaled Conjugate Gradient (SCG)

Figure 2 shows the implemented methodology. First, the building dataset is generated using the IESVE software. Second, the dataset is randomly split in (see Table 6): 70% for training, 15% for testing, and 15% for validation. Third, the training phase adjust the network according to its error. Fourth, the testing phase measures the network performance during and after training. Five, in the validation phase, samples are used to measure the generalizability of the proposed network. It is also used to stop training when there is no more improvement in the network generalization.

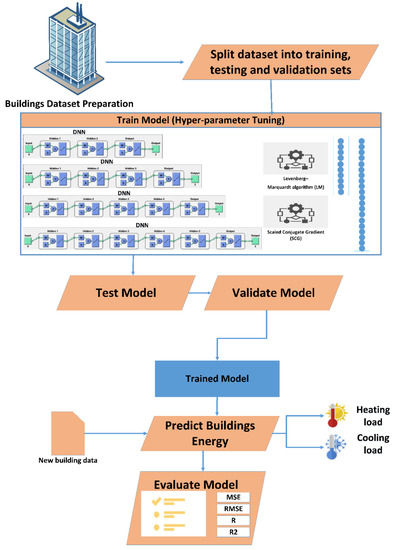
Figure 2. The overall methodology followed in this study.

Table 6. Number of samples for training, testing and validation.

Type of Data	Number of Samples
Training data	2688 (70%)
Testing data	576 (15%)
Validation data	576 (15%)

For model evaluation, four metrics were used to measure the performance of the proposed network: Mean Square Error (MSE), Root Mean Square Error (RMSE), Regression (R) values and coefficient of determination (R${}^2$).

The MSE is the average squared difference between predicted and actual variables, i.e., heating and cooling loads. The lower values, the better.

$$\mathrm{MSE}=\left(\frac{1}{n}\right)\times \sum _{i=1}^n{|p_i-y_i|}^2$$

(1)

RMSE calculates the average square error of prediction and is useful when capturing large differences between predicted and actual outputs. Like MSE, low values for RMSE indicate better model performance.

$$\mathrm{RMSE}=\sqrt{\left(\frac{1}{n}\right)\times \sum _{i=1}^n{\left[p_i-y_i\right]}^2}$$

(2)

The R value measures the correlation between predicted and actual variables. For closer the R value to 1, the stronger relationship and higher performance model.

$$\mathrm{R}=\sqrt{1-\frac{{\sum }_{i=1}^n{(y_i-p_i)}^2}{{\sum }_{i=1}^n{(y_i-\overline{y})}^2}}$$

(3)

R${}^2$ measures the proportion of variance in the dependent variable that is predictable via the independent variables. The closer the R${}^2$ value 1, the stronger relationship and higher performance model.

$${\mathrm{R}}^2=1-\frac{{\sum }_{i=1}^n{(y_i-p_i)}^2}{{\sum }_{i=1}^n{(y_i-\overline{y})}^2}$$

(4)

where $p_i$ identifies the predicted value for sample i, $y_i$ identifies the actual value for sample i, n is the sample size, $\overline{y}$ indicates the mean of the predicted values.

4. Experimental Results

The experiments were carried out on a computer device with Intel i-7 9700K 3.6 GHz CPU, 16 GB RAM, and NVIDIA GeForce RTX 2060 8 GB GPU.

4.1. Prediction Results of Energy Consumption

Table 7 shows the MSE, RMSE, R, and R${}^2$ values obtained for the different models to predict heating and cooling loads collectively. It is worth mentioning that almost all tuned models performed well in terms of R and R${}^2$. However, they performed completely different in terms of MSE and RMSE. This disparity indicates the importance of choosing the corresponding weights.

Table 7. Results of tuning the DNN models of the generated dataset.

Exp	No. of Layers	No. of Neurons	Alg.	MSE			RMSE			R			R2
				Train	Val	Test	Train	Val	Test	Train	Val	Test	Train	Val	Test
1	2	10	LM	19.538	9.505	12.006	4.420	3.083	3.465	1.000	1.000	1.000	0.999	1.000	1.000
2	2	10	SCG	656.647	737.697	638.550	25.625	27.161	25.270	0.991	0.990	0.991	0.983	0.980	0.983
3	2	20	LM	12.083	5.329	4.257	3.476	2.308	2.063	1.000	1.000	0.999	1.000	1.000	0.999
4	2	20	SCG	32.55	25.373	27.725	5.705	5.037	5.265	1.000	1.000	1.000	0.999	0.999	0.999
5	3	10	LM	46.385	85.997	104.928	6.811	9.273	10.243	0.999	0.999	0.999	0.999	0.998	0.997
6	3	10	SCG	1258	1077.6	1211.7	35.468	32.827	34.809	0.983	0.986	0.983	0.966	0.972	0.967
7	3	20	LM	44.732	29.045	89.665	6.688	5.389	9.469	0.999	1.000	0.999	0.999	0.999	0.998
8	3	20	SCG	121.512	287.097	327.378	11.023	16.944	18.094	0.998	0.996	0.996	0.997	0.993	0.991
9	4	10	LM	31.869	55.962	56.282	5.645	7.481	7.502	1.000	0.999	0.999	0.999	0.999	0.998
10	4	10	SCG	337.808	314.332	410.841	18.38	17.729	20.269	0.995	0.996	0.995	0.991	0.991	0.989
11	4	20	LM	0.216	64.616	0.435	0.465	8.038	0.660	1.000	0.999	1.000	1.000	0.998	1.000
12	4	20	SCG	645.138	673.653	749.034	25.4	25.955	27.368	0.991	0.991	0.990	0.983	0.982	0.980
13	5	10	LM	13.09	5.897	6.664	3.618	2.428	2.581	1.000	1.000	1.000	1.000	1.000	1.000
14	5	10	SCG	503.603	454.754	641.240	22.441	21.325	25.323	0.991	0.989	0.991	0.982	0.978	0.982
15	5	20	LM	0.875	7.456	5.122	0.936	2.731	2.263	1.000	1.000	1.000	1.000	1.000	1.000
16	5	20	SCG	103.56	109.755	90.484	10.176	10.476	9.512	0.999	0.999	0.999	0.997	0.997	0.998

By grouping the experiments based on the number of hidden layers (Figure 3), it is obvious that the best configuration in all groups was: 20 neurons in the hidden layers and LM as the learning algorithm (shaded in Table 7).

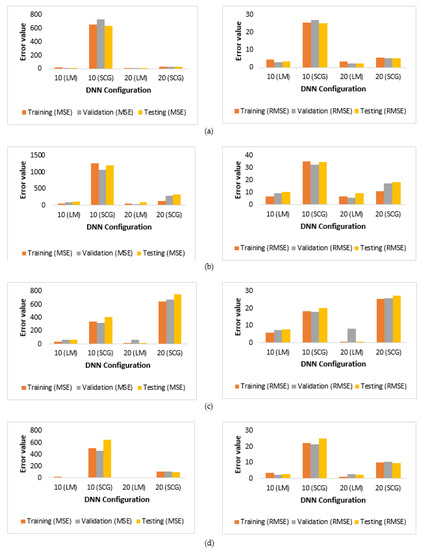
Figure 3. Prediction results, in terms of MSE and RMSE, for the DNN models with different combinations of hyper parameters: (a) two-layer DNN (experiment 3), (b) three-layer DNN (experiment 7), (c) four-layer DNN (experiment 11), and (d) five-layer DNN (experiment 15).

Based on the results, the best two performing models are those used in experiment 3 (two hidden layers of 20 neurons with the LM training algorithm) and experiment 15 (five hidden layers of 20 neurons with the LM algorithm). These two models are comparatively better than all other models and thus are further investigated and compared in the following section. The comparison is made in terms of performance and computation time predicting the heating load and the cooling load independently.

4.2. The Best-Performed Model for Predicting Building Heating and Cooling Loads Independently

Models utilized in experiment 3 and experiment 15 are represented in Figure 4. To examine the difference between the two model, the same tuned hyper parameters were employed in further experiments predicting the heating and cooling loads independently rather than collectively. The prediction results as well as the computation times are shown in Table 8. Remarkably, the time to train these models was disparate. The time required to train the five-layer model in experiment 3 is lower than time required to train the two-layer model.

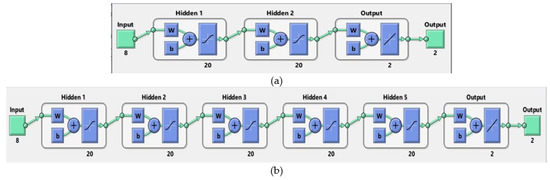
Figure 4. Graphical representation of the best performed models: (a) two-layer model (experiment 3) and (b) five-layer model (experiment 15).

Table 8. Results of the best performed DNN models for predicting heating load and cooling load separately.

Model	Output	Computation Time (min)	MSE			RMSE
			Train	Valid	Test	Train	Valid	Test
DNN (2)	Heating load	1.37	0.011	0.016	0.014	0.106	0.127	0.119
	Cooling load	1.23	9.836	141.976	12.989	3.136	11.915	3.604
DNN (5)	Heating load	1.03	0.000	0.008	0.006	0.016	0.087	0.079
	Cooling load	1.05	0.080	0.245	0.421	0.282	0.495	0.649

Based on MSE and RMSE measures, the two models performed well predicting both heating load and cooling load independently. However, both models achieved better performance predicting heating load than predicting cooling load. The five-layer DNN performed better than the two-layer DNN in all training, validation and testing datasets. The heating and cooling prediction results of the two models are further illustrated using four kinds of plots: how the models performance improved during training (Figure 5), the corresponding error histogram for the two models (Figure 6), the regression plots that shows the values predicted by the models against the simulated heating and cooling loads (Figure 7), and a sample of the actual and predicted values for both models (Figure 8).

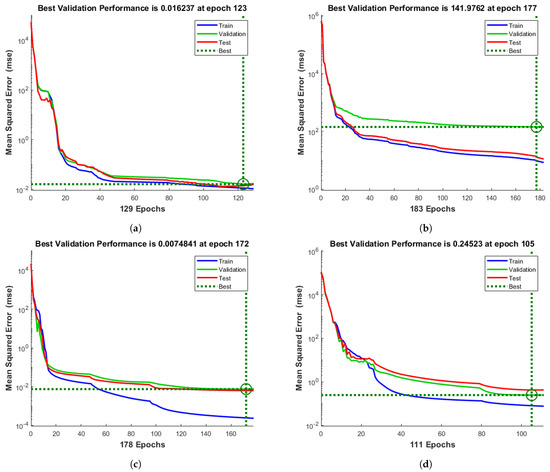
Figure 5. Evaluation of the best-performed model based on MSE measure in predicting (a) heating load of two-layer DNN, and (b) cooling load of two-layer DNN, (c) heating load of five-layer DNN, and (d) cooling load of five-layer DNN.

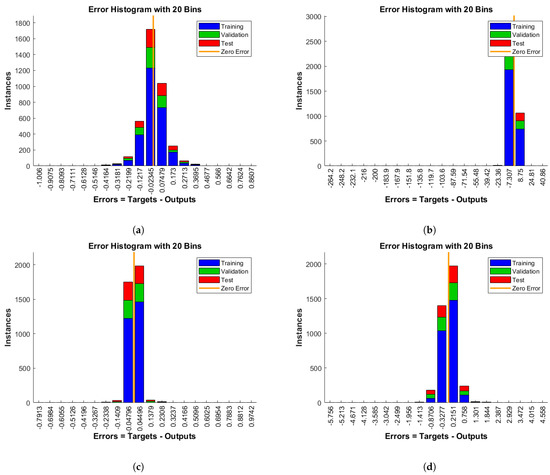
Figure 6. Error histogram of the best-performed model in predicting (a) heating load of two-layer DNN, and (b) cooling load of two-layer DNN, (c) heating load of five-layer DNN, and (d) cooling load of five-layer DNN.

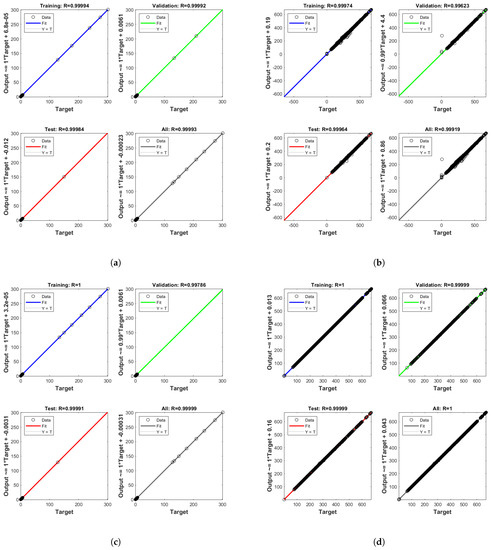
Figure 7. Regression plot of the best-performed model (a) heating load of two-layer DNN, and (b) cooling load of two-layer DNN, (c) heating load of five-layer DNN, and (d) cooling load of five-layer DNN.

Figure 8. The actual and predicted values of energy consumption (a) heating load using the two-layer DNN model, (b) cooling load using the two-layer DNN model, (c) heating load using the five-layer DNN model, and (d) cooling load using the five-layer DNN model.

Figure 5 depicts the MSE performance for the training, validation, and test datasets for the two models in log scale. The final network is the network that performed best on the validation set. The five-layer model MSE decreased rapidly as the network was trained to predict both heating and cooling loads and achieved smaller error values than the two-layer model. Based on the validation dataset, the five-layer model achieved an MSE as low as 0.007 at epoch 172 when predicting the heating load (Figure 5c) and 0.245 at epoch 105 when predicting the cooling load (Figure 5d).

Figure 6 shows the error histogram of the two models on the training, testing and validation datasets. The histogram shows the errors between the target values and the predicted values after training the DNN models. As these error values indicate how predicted values are above/below the target values, they can be positive or negative. The bins in the histogram are the number of vertical bars shown in the graph. The total error range is divided into 20 smaller bins. The heating prediction errors obtained with the two-layer model were higher than with the five-layer model. In particular, the highest bin corresponded to error −0.02345, while the height of that bin for the training dataset lies above but close to 1200. For the validation and test datasets, it lies between 1300 and 1600. This means that many samples from the different datasets have an error that lies in that small range. Besides, the zero error falls under the bin just before −0.02345. As most errors are near zero, this indicates that the model performed very well in predicting the heating load and the cooling load.

Another measure of how well the model has fit the data is the regression plot. The regression was plotted in Figure 7 across all samples: training, validation, and testing. The regression plot shows the actual model outputs plotted in terms of the associated target values. As the figure depicts, the linear fit to the output-target relationship is closely intersected. This indicates that the model has learned to fit the data well.

As an example of the prediction results using the two best performing models, Figure 8 shows the actual and predicted values of the cooling load for both models. The actual and predicted cooling loads follow similar trends using the two models. This means that, a specific high configuration of inputs will result in an increased output of cooling load. However, it is obvious that the heating and the cooling prediction results of the five-layer DNN were more accurate than the prediction results of the two-layer DNN.

5. Discussion

Based on the results presented in the previous section, we draw the following conclusions:

• Results of energy performance prediction depend on the parameters’ tuning of the DNNs.
• The prediction model preforms better for the higher number of neurons in each hidden layer.
• The LM Algorithm results in a more accurate prediction model than the SCG algorithm. A possible explanation of this is that the dataset used may considered of small size (less than 10,000 samples) for which the LM is known to perform well when compared to other training algorithms.
• The two-layer and the five-layer models with 20 neurons and LM training algorithm achieved comparable results for predicting the heating and cooling loads collectively. However, for predicting the heating and cooling loads independently, the five layer-model was the more accurate and also faster than the two-layer model

Table 9 presents the previous studies reported performance measures when predicting the heating and cooling loads in the context of buildings. The results are compared with the outcomes of the best model of our study: the five-layer model with 20 neurons and the LM training algorithm. To keep the comparison fair, the buildings characteristics utilized in the studies are also presented. Our best-performed model outperformed the state of the art models in terms of MSE and RMSE for both heating and cooling loads. Also, it achieved comparative results with previous studies in terms of R and R${}^2$ for both predicting heating load and cooling load. This evidences the merit of our model for arid climate to predict the energy consumption of residential buildings.

Table 9. A comparison of the proposed model and the previous DNN-based studies in terms of heating and cooling loads.

Reference	Building Characteristics	Heating Load				Cooling Load
		MSE	RMSE	R	R${}^2$	MSE	RMSE	R	R${}^2$
[19]	Length Width WWR Wall U-value Glazing U-value Roof U-value Orientation			9.349	87.400			9.930	98.6
[23]	Relative compactness Surface Area Wall area Roof area Overall Height Orientation Glazing area Glazing area distribution	0.069	0.263	1.000	1.000	0.476	0.69	0.997	0.994
[26]	Length Width WWR Orientation Wall U-value Glazing U-value Roof U-value			0.995	0.990			0.999	0.999
This study	Building Size Floor Height Glazing Area Wall Area WWR Win Glazing U-value Roof U-value External Wall U-value	0.008	0.087	0.998	0.996	0.245	0.495	1.000	1.000

6. Conclusions

Buildings’ energy consumption has a strong influence on the environmental and economic aspects of many developed and developing countries. This study highlighted the importance of tuning DNNs to achieve the best predictive performance of heating and cooling loads for a given use case. The predictive models were trained on a dataset generated by the authors for the extremely arid climate region of Qassim, in Saudi Arabia.

Experimental results of different DNNs showed that the model with higher number of hidden layers and number of neurons using the LM training algorithm outperformed other models in terms of predicting heating and cooling loads independently. Specifically, this model, which contained five layers, with 20 neurons in each layer and the Levenberg–Marquardt algorithm, outperformed the other models and achieved MSE of 0.0075 and RMSE 0.087 in predicting the heating load, and MSE of 0.245 and RMSE of 0.495 in predicting the cooling load.

These results support the effectiveness of deep learning with appropriate weight choosing on the area of buildings energy consumption. The outcomes of the research can help architects of new energy-efficient design buildings in the synthesis and predesign stages. Building regulations authorities could refer to this model for more improvement of local code.