Food System Sustainability Metrics: Policies, Quantification, and the Role of Complexity Sciences
Abstract
1. Introduction
2. Sustainability Definition and Measuring Challenges
2.1. SD and Sustainability Definitions
2.2. Sustainability Frameworks, Indices, Indicators, and Metrics
2.3. Robustness, Resilience, and Sustainability
2.4. Quantifying Sustainability
- Under those ex ante and uncertain conditions, the sustainability criterion can only be met with some probability;
- Depending on whether this probability is associated with a notion of maintaining an aggregate wealth or welfare or with the maintenance of separate critical stocks and services above some minimum levels, we can speak, respectively, of a weak, or strong, notion of sustainability.
3. Sustainable Food System Policy Design and Control
3.1. Toward Sustainable Food Systems
- The properties of diversity and fluxes relate to the diversity and transparency attributes, allowing for timely and reliable access to information;
- The mechanism of building blocks (simple parts, or modules, that can be reused and articulated in different ways) is closely linked to the modularity attribute;
- The mechanism of internal models provides a way for the exploration of alternatives, leading to innovation;
- The previous properties and mechanisms and the additional properties of aggregation (facilitating the generation of meta-agents and model building) and nonlinearity (resulting in more complex interactions), together with the tagging mechanism (underlying the system’s organization), lead to the continuous search for fitness (or congruence) of the system’s complex adaptive process.
3.2. Food System Sustainability Quantification Developments
3.3. Policy Design and Control of Diverse, Complex, Multi-Scale, and Multi-Level SESs
3.4. Prediction, Intangibles, and Uncertainty
- Decision theory (use of “available information to make optimal decisions under uncertainty”);
- Threshold approach (“focusing attention on critical boundaries that have major consequences if crossed” and thus of the utmost relevance to sustainability);
- Scenario planning (based on “sets of plausible stories, supported with data and simulations, about how the future might unfold”);
- Resilience thinking (which “focuses on critical thresholds for system performance, [and] the capacity to adapt [and] transform”).
4. Complexity Sciences’ Contributions to SD
4.1. Articulating the Macro, Meso, and Micro Levels
- The micro concept to characterize individual agent interactions, with specific and fine-grain rules, providing detailed levels of description;
- The macro concept to address the higher-level overall aggregations of groups (of groups) of agents, using whole encompassing and coarse concepts, providing the more general and abstract level of description; and
- The meso concept to describe the intermediate individual and group of agents’ interactions, using linking concepts related to observed patterns, behavioral regularities, and shared rules, providing intermediate levels of description built through new lenses applied to the micro-level interactions and incorporated at the more abstract macro level.
4.2. The role of Multiple and Independent Modeling Frameworks
4.3. The Contribution of Complexity Sciences’ Theories and Tools
5. Case-Study: Sheep Grazing Policymaking and Management of a Rangeland System
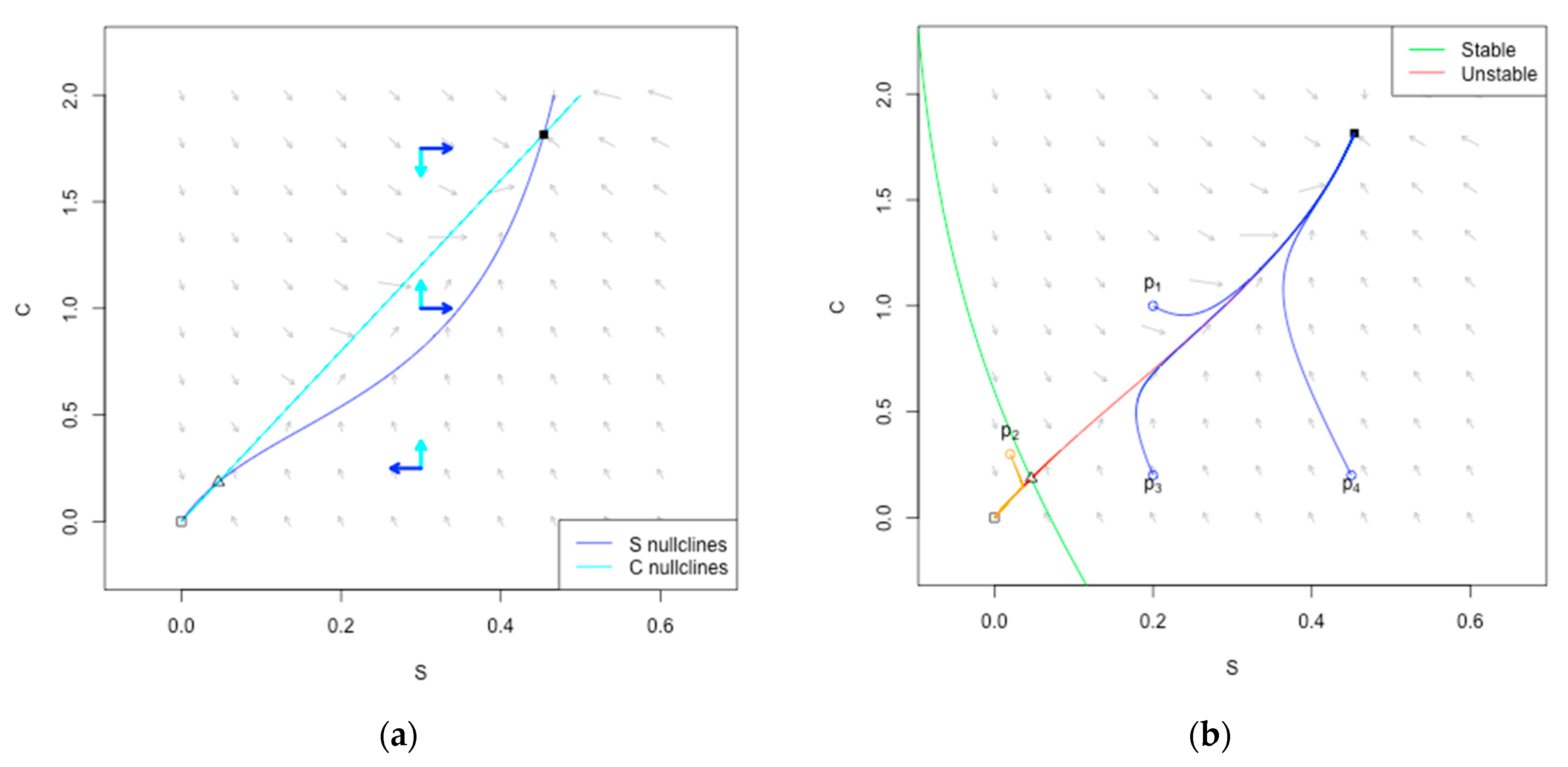
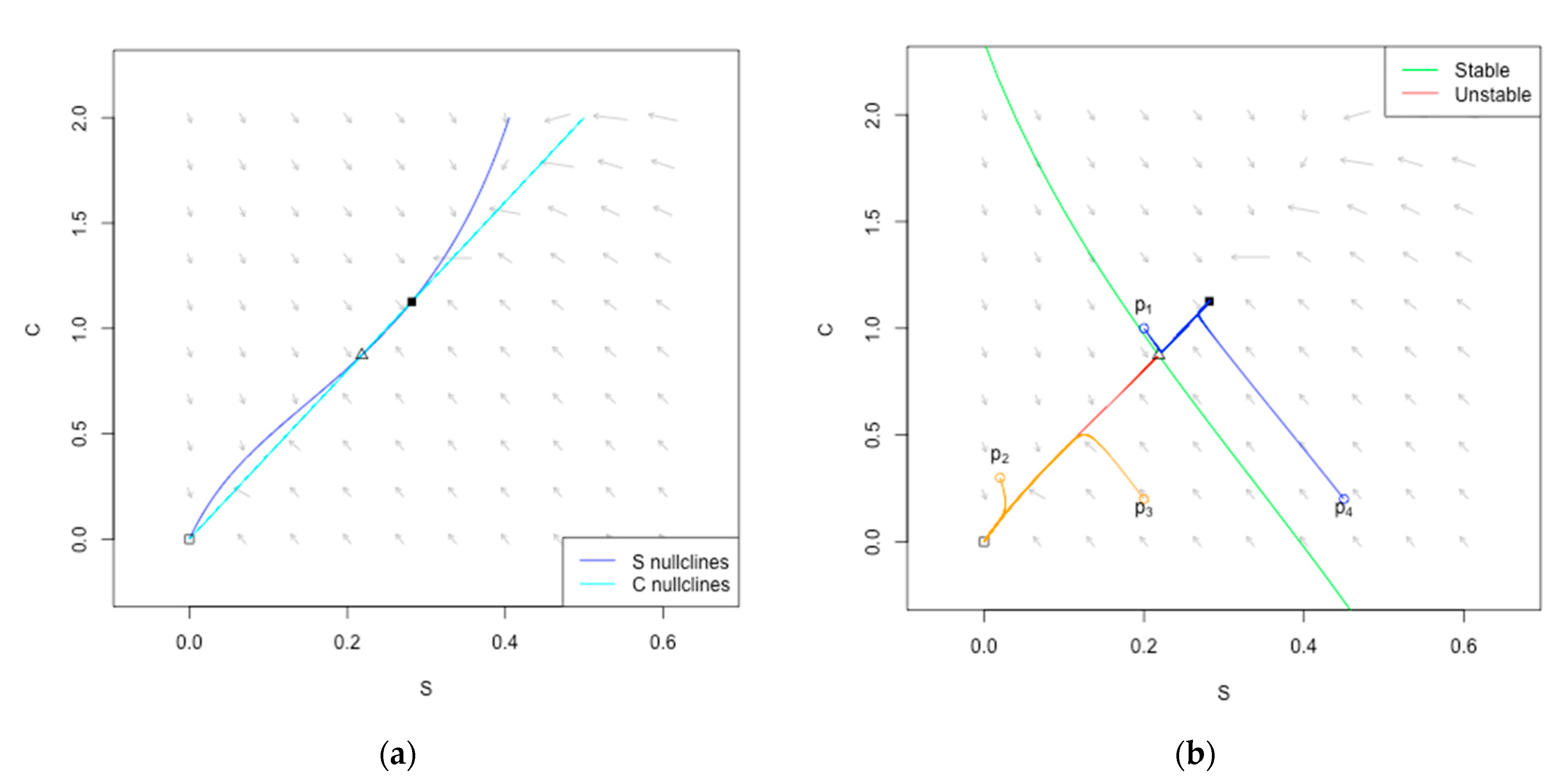
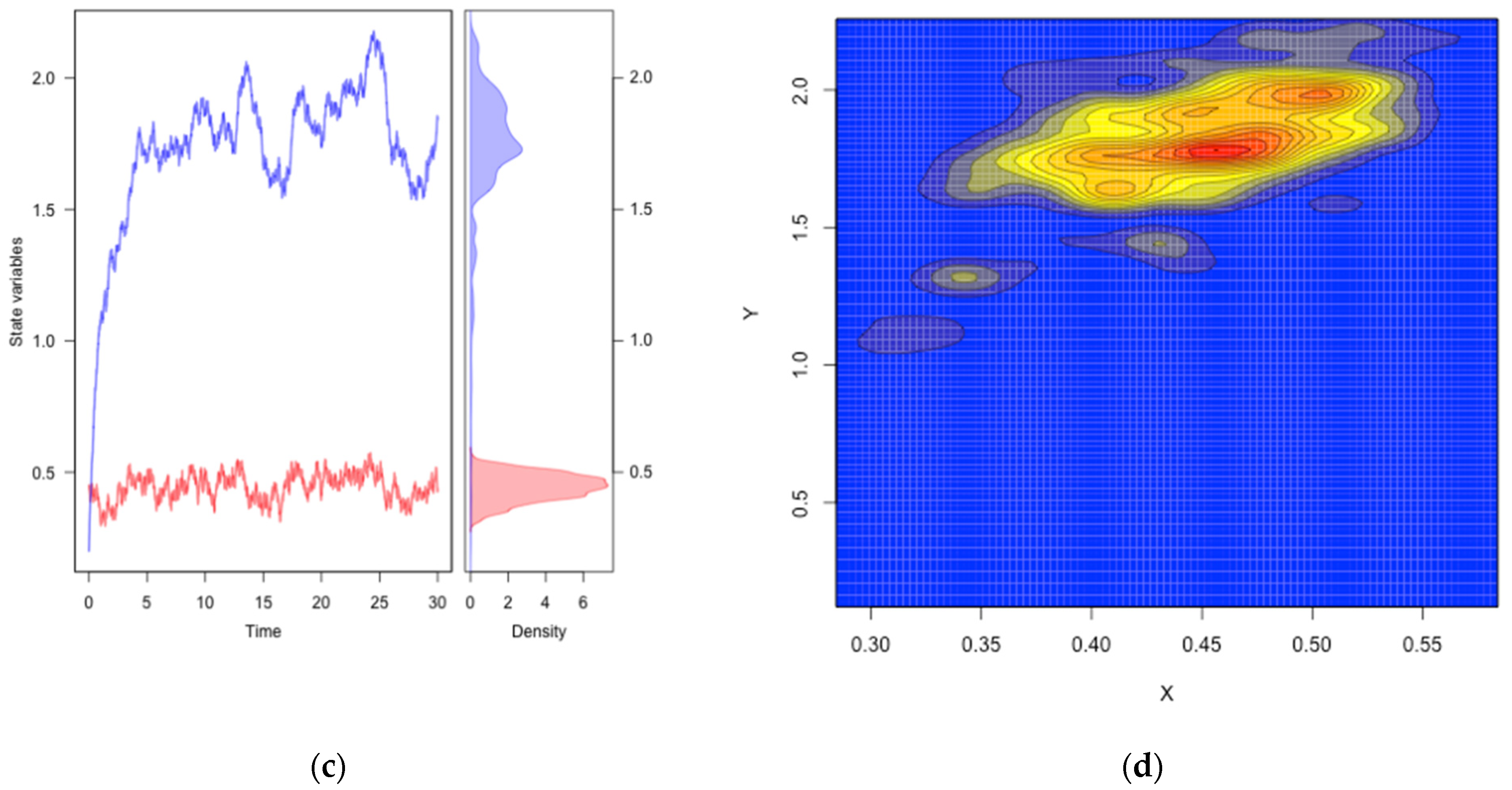
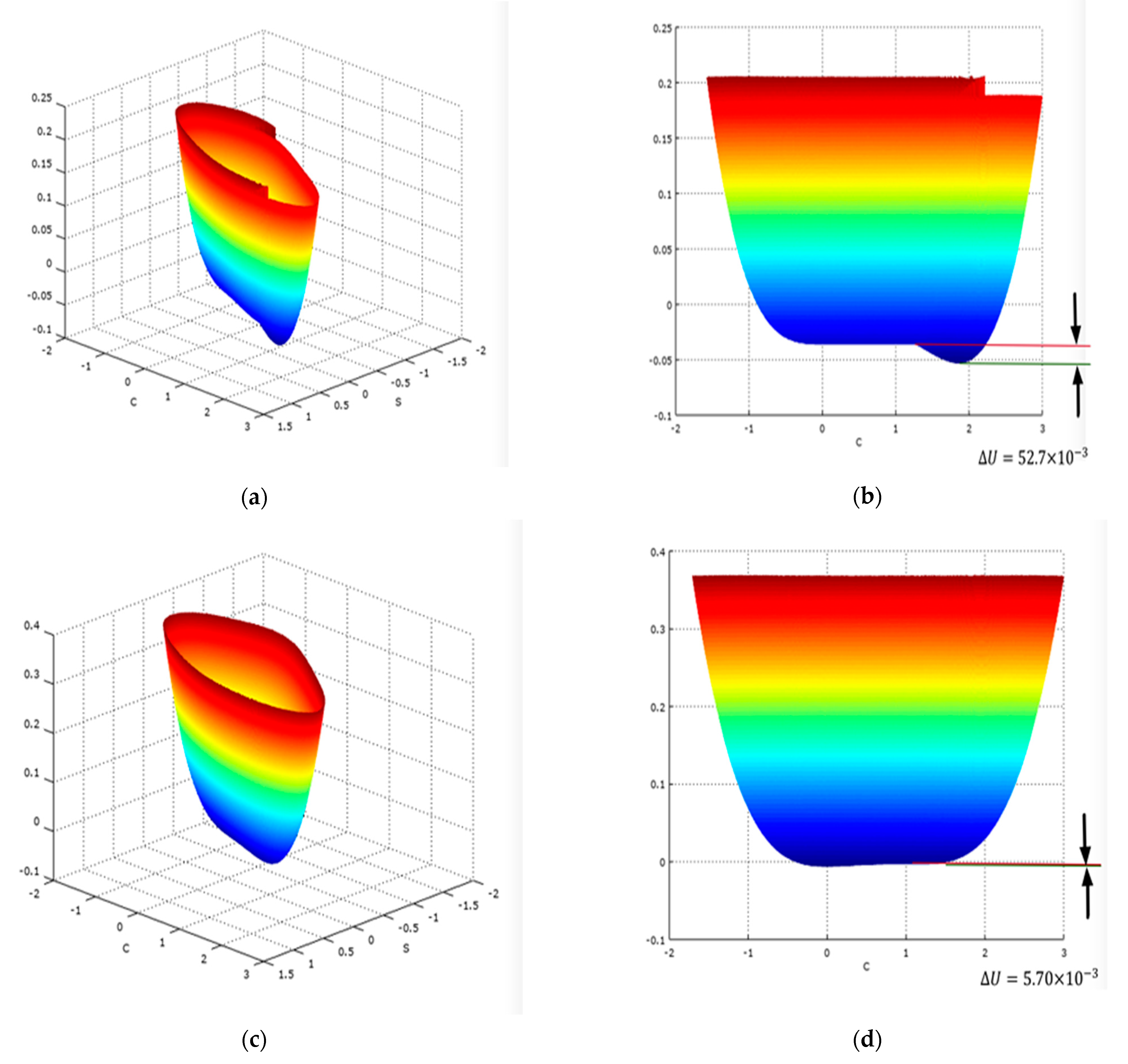
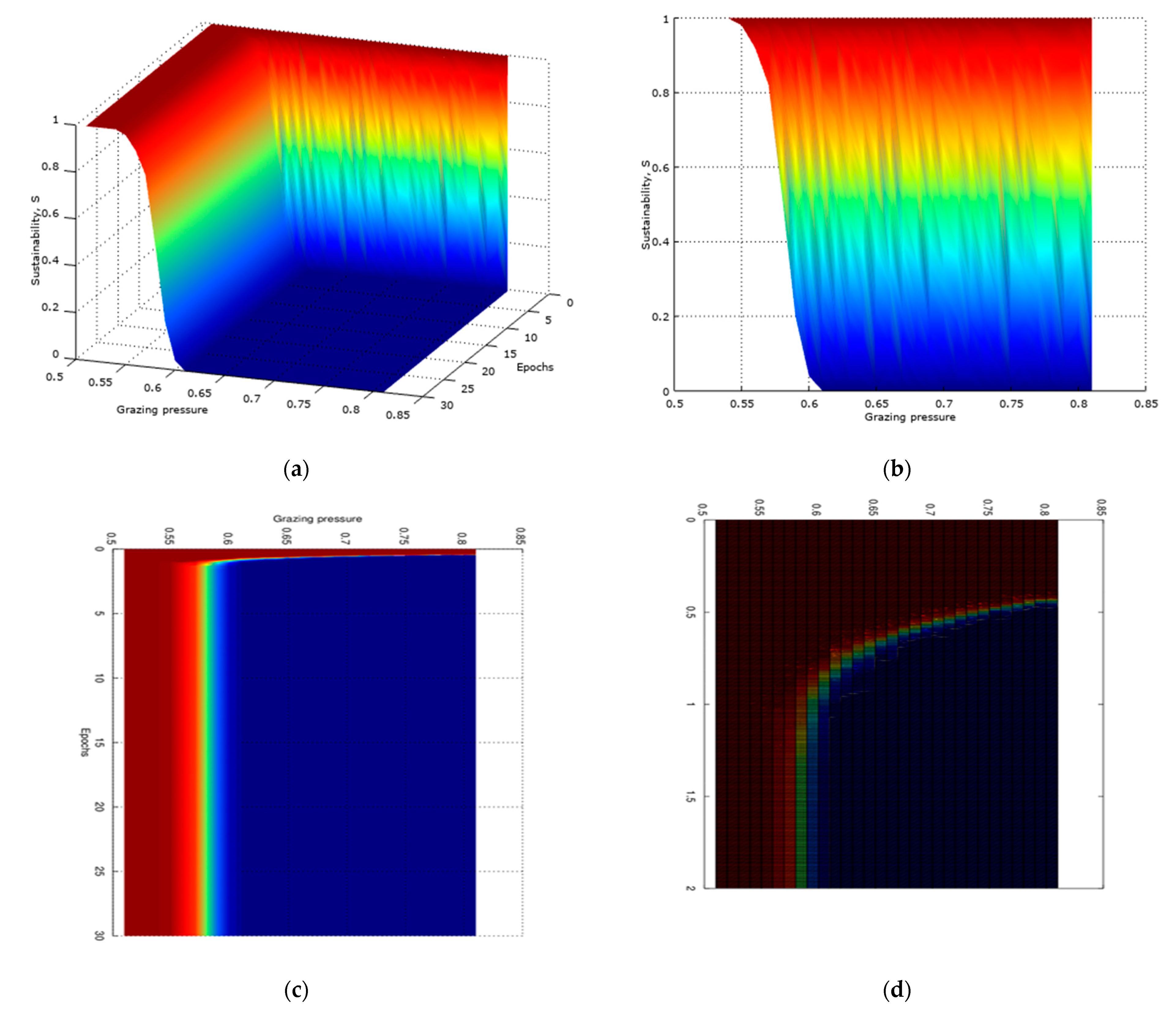
5.1. Macro-Level Modeling of System Dynamics
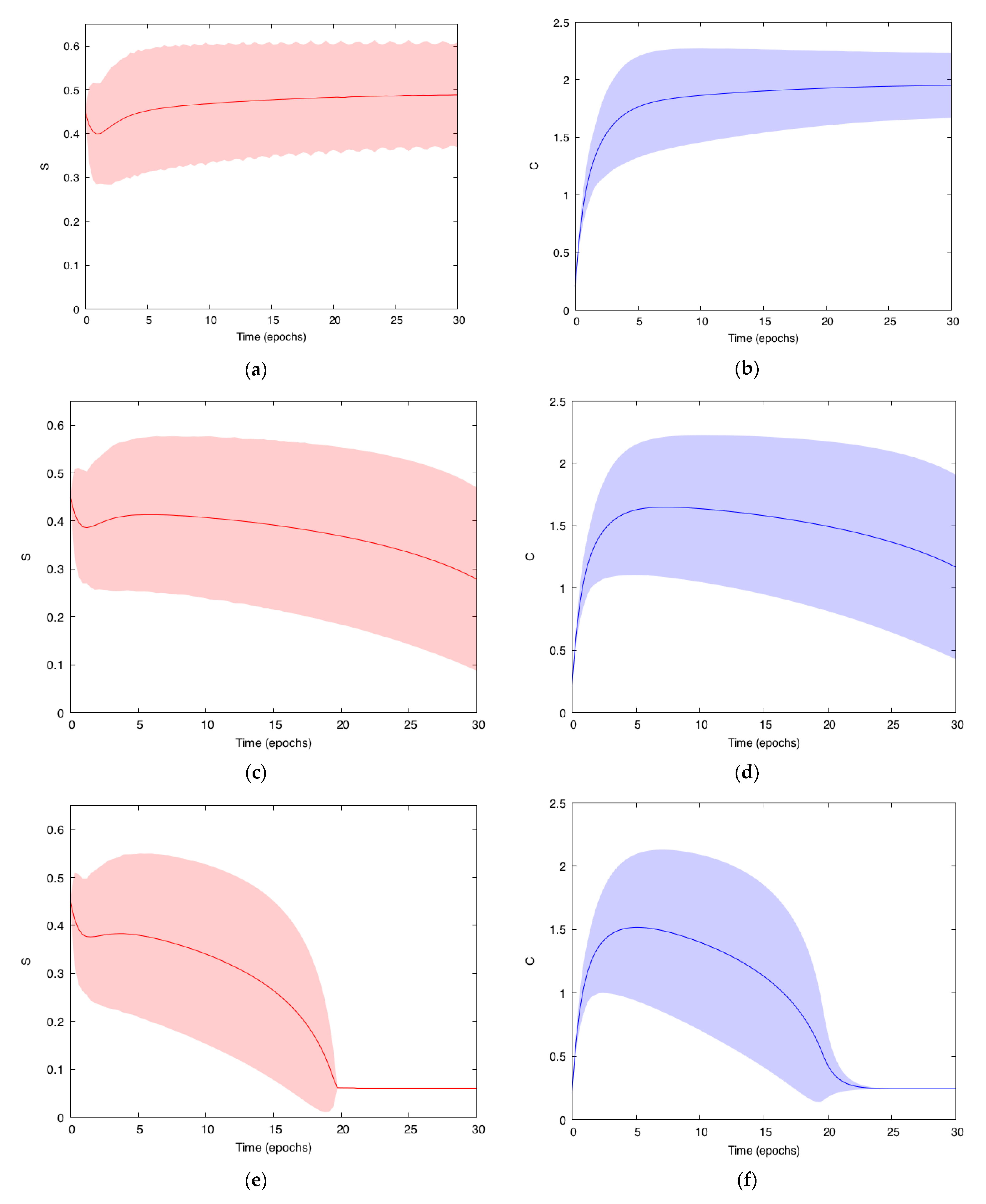
- A strong, nonlinear relation between the sustainability and consumption pressure values (see Figure 9b);
- For the larger values of consumption pressure, the stability point is below the sustainability threshold value, which leads to dramatically low values of sustainability, even for short time horizons. On the other hand, for the smaller values of consumption pressure of sustainability, it keeps close to one even with long time horizons (see Figure 9c,d);
- The initial state of the system (with above the sustainability threshold value ) provides a “sustainability buffer” for the system for some (even if very limited) time (see Figure 9c,d).
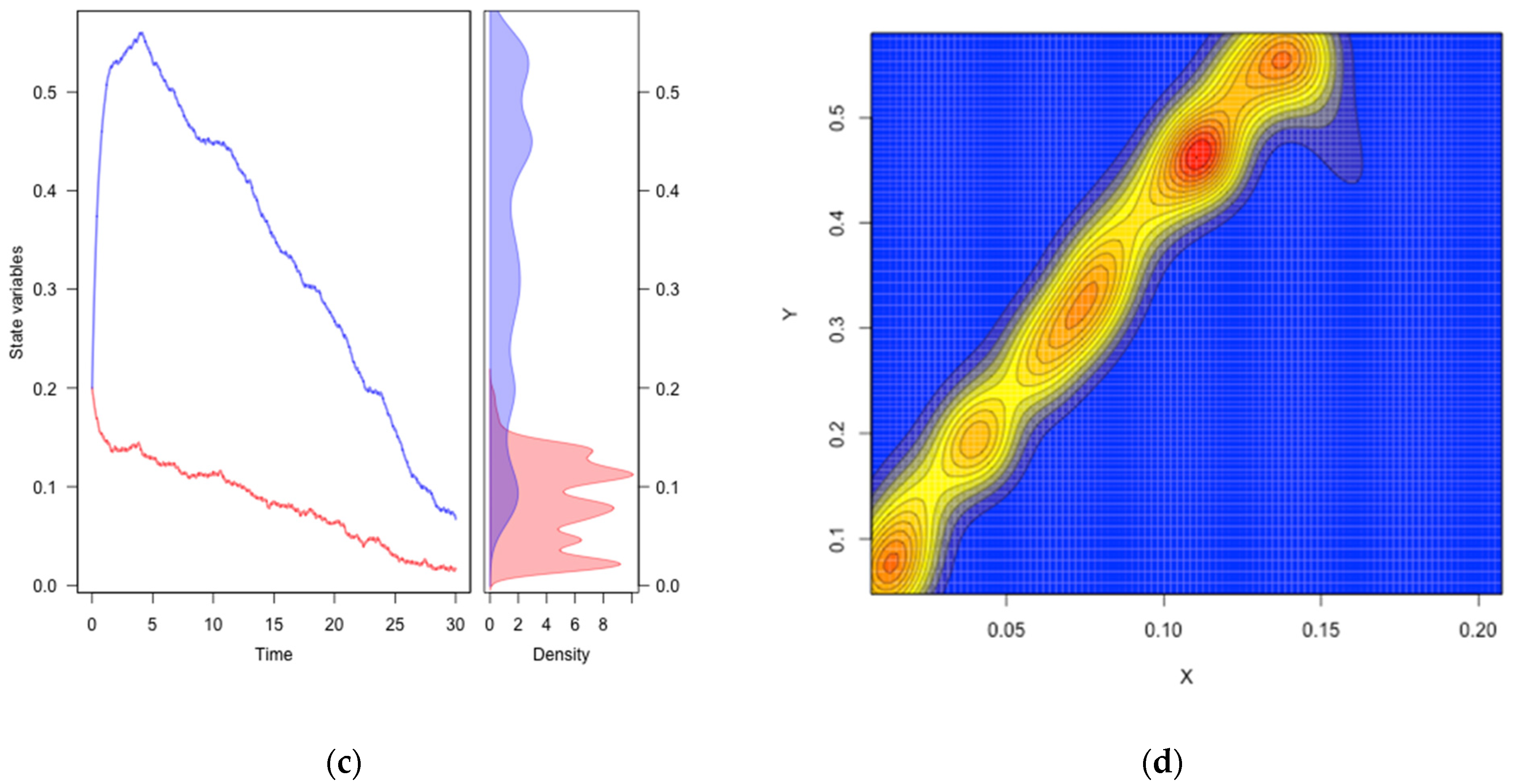
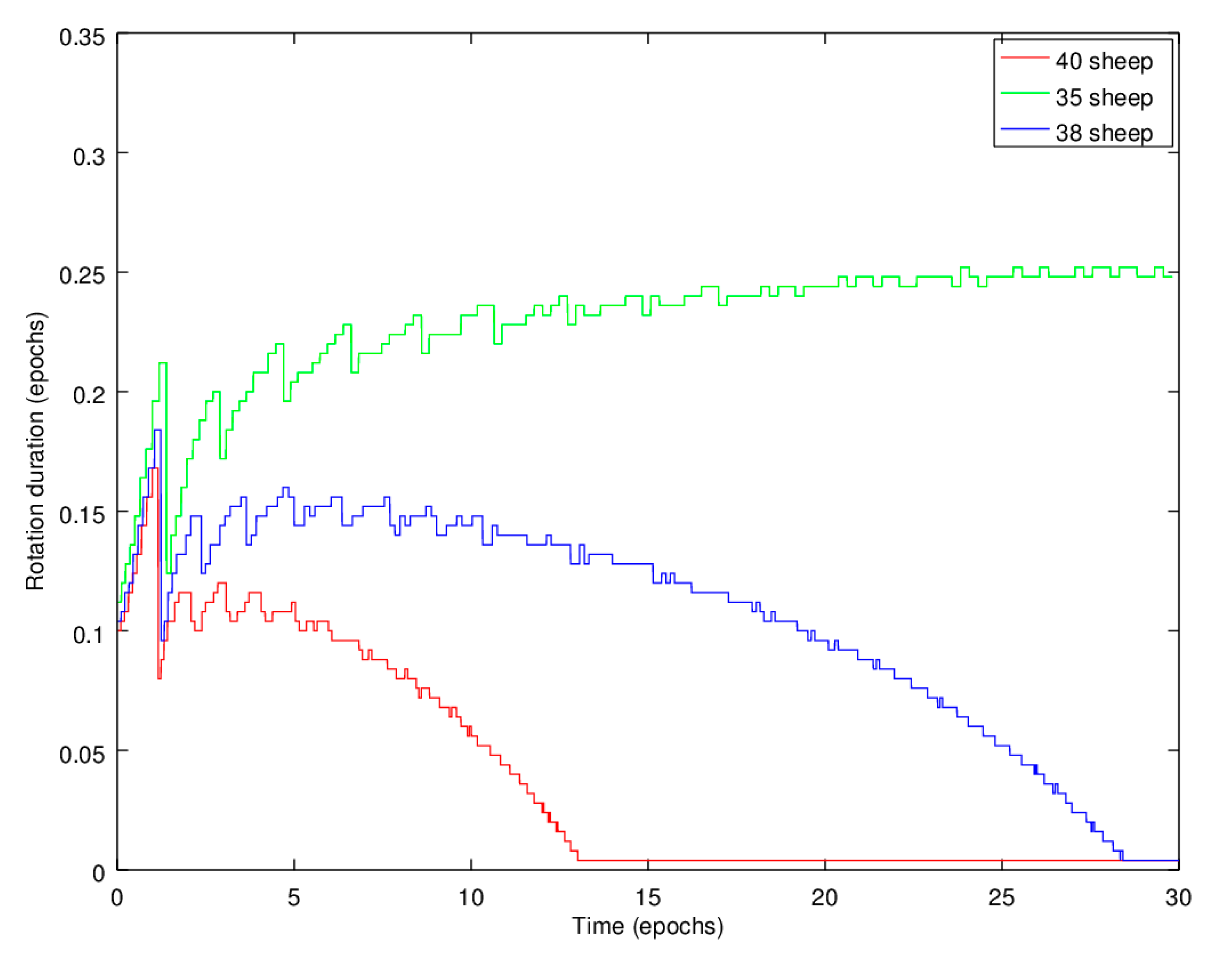
5.2. Agent-Based Modeling of System Dynamics
- The rangeland of total area is modeled via atomic area units of area , in a bidimensional grid;
- Each atomic area unit is defined by its coordinates (i, j) in the grid and their crowns’, , and shoots’ biomass value , at time t;
- The rangeland field management is based on a sheep grazing patch rotation policy: (1) the rangeland is divided in equally sized patches, each one including atomic area units; (2) at each time the herd is allowed to graze in a single patch; (3) when the mean value of the shoots’ biomass is below a threshold value, , the herd is moved to the patch with the highest shoots’ biomass mean value;
- The herd is composed of sheep, with individual behavior;
- Each sheep has a nutritional requirement, , that it tries to meet by grazing in the current patch consuming shoot biomass until its nutritional requirement is met or the shoot biomass at its current location (an atomic unit area) is below a threshold value, ; in the latter case, the sheep moves randomly within the limits of the current patch.
6. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- United Nations Sustainable Development. Agenda 21. UN General Assembly. Available online: https://sustainabledevelopment.un.org/content/documents/Agenda21.pdf (accessed on 17 May 2021).
- Transforming Our World: The 2030 Agenda for Sustainable Development|Department of Economic and Social Affairs. Available online: https://sdgs.un.org/2030agenda (accessed on 17 May 2021).
- Comm/dg/Unit. A European Green Deal. Available online: https://ec.europa.eu/info/strategy/priorities-2019-2024/european-green-deal_en (accessed on 17 May 2021).
- European Commission. A Farm to Fork Strategy for a Fair, Healthy and Environmentally-Friendly Food System COM(2020) 381 Final. Available online: https://ec.europa.eu/food/farm2fork_en (accessed on 17 May 2021).
- Vázquez, P.; Del Río, J.A.; Cedano, K.G.; Martínez, M.; Jensen, H.J. An Entangled Model for Sustainability Indicators. PLoS ONE 2015, 10, e0135250. [Google Scholar] [CrossRef]
- Parris, T.M.; Kates, R.W. Characterizing and measuring sustainable development. Annu. Rev. Environ. Resour. 2003, 28, 559–586. [Google Scholar] [CrossRef]
- Böhringer, C.; Jochem, P.E. Measuring the immeasurable—A survey of sustainability indices. Ecol. Econ. 2007, 63, 1–8. [Google Scholar] [CrossRef]
- Wilson, J.; Tyedmers, P.; Pelot, R. Contrasting and comparing sustainable development indicator metrics. Ecol. Indic. 2007, 7, 299–314. [Google Scholar] [CrossRef]
- Stoycheva, S. The History of Sustainability: A Critical Assessment of Metrics and Their Changes. In International Conference on Management, Leadership & Governance; Academic Conferences International Limited, APR: Kidmore End, UK, 2016; pp. 475–480. [Google Scholar]
- Anderies, J.M.; Folke, C.; Walker, B.; Ostrom, E. Aligning Key Concepts for Global Change Policy: Robustness, Resilience, and Sustainability. Ecol. Soc. 2013, 18. [Google Scholar] [CrossRef]
- Bell, S.; Morse, S. Sustainability Indicators: Measuring the Immeasurable? 2nd ed.; Earthscan: Oxon, UK, 2008. [Google Scholar]
- Levine, S. Assessing Resilience: Why Quantification Misses the Point; Humanitarian Policy Group: London, UK, 2014. [Google Scholar]
- Cash, D.W.; Adger, W.N.; Berkes, F.; Garden, P.; Lebel, L.; Olsson, P.; Pritchard, L.; Young, O. Scale and Cross-Scale Dynam-ics: Governance and Information in a Multilevel World. Ecol. Soc. 2006, 11, 8. Available online: https://www.ecologyandsociety.org/vol11/iss2/art8/ (accessed on 3 August 2021). [CrossRef]
- Folke, C.; Biggs, R.; Norström, A.V.; Reyers, B.; Rockström, J. Social-ecological resilience and biosphere-based sustainability science. Ecol. Soc. 2016, 21, 41. [Google Scholar] [CrossRef]
- Stefanovic, L.; Freytag-Leyer, B.; Kahl, J. Food System Outcomes: An Overview and the Contribution to Food Systems Transformation. Front. Sustain. Food Syst. 2020, 4, 156. [Google Scholar] [CrossRef]
- Rockström, J.; Steffen, W.; Noone, K.; Persson, Å.; Chapin, F.S.; Lambin, E.F.; Lenton, T.M.; Scheffer, M.; Folke, C.; Schellnhuber, H.J.; et al. A safe operating space for humanity. Nature 2009, 461, 472–475. [Google Scholar] [CrossRef]
- Ericksen, P.J. Conceptualizing food systems for global environmental change research. Glob. Environ. Chang. 2008, 18, 234–245. [Google Scholar] [CrossRef]
- Eakin, H.; Connors, J.P.; Wharton, C.; Bertmann, F.; Xiong, A.; Stoltzfus, J. Identifying attributes of food system sustainability: Emerging themes and consensus. Agric. Hum. Values 2016, 34, 757–773. [Google Scholar] [CrossRef]
- Beratan, K.K.; Kabala, S.J.; Loveless, S.M.; Martin, P.J.; Spyke, N.P. Sustainability Indicators as a Communicative Tool: Building Bridges in Pennsylvania. Environ. Monit. Assess. 2004, 94, 179–191. [Google Scholar] [CrossRef] [PubMed]
- Moldan, B.; Janoušková, S.; Hak, T. How to understand and measure environmental sustainability: Indicators and targets. Ecol. Indic. 2012, 17, 4–13. [Google Scholar] [CrossRef]
- Steward, F. Breaking the Boundaries: Transformative Innovation for the Global Good. NESTA 2008, Provocation 7. Available online: https://media.nesta.org.uk/documents/breaking_the_boundaries.pdf (accessed on 18 August 2020).
- HM Government. Securing the Future: The UK Government Sustainable Development Strategy; The Stationery Office: London, UK, 2005.
- United Nations. Report of the World Commission on Environment and Development, A/42/427, 4 August 1987, Annex “Our Common Future”. Available online: https://digitallibrary.un.org/record/139811 (accessed on 17 May 2021).
- Barnosky, A.D.; Hadly, E.A.; Bascompte, J.; Berlow, E.L.; Brown, J.H.; Fortelius, M.; Getz, W.; Harte, J.; Hastings, A.; Marquet, P.; et al. Approaching a state shift in Earth’s biosphere. Nature 2012, 486, 52–58. [Google Scholar] [CrossRef]
- Scheffer, M.; Bascompte, J.; Brock, W.A.; Brovkin, V.; Carpenter, S.R.; Dakos, V.; Held, H.; van Nes, E.H.; Rietkerk, M.; Sugihara, G. Early-warning signals for critical transitions. Nature 2009, 461, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Scott, E.M.; Cocchi, D.; Gemmell, J.C. Defining a fit for purpose statistically reliable sustainability indicator. Sustain. Account. Manag. Policy J. 2014, 5, 262–267. [Google Scholar] [CrossRef]
- Münnich, R.T.; Seger, J.G. Impact of survey quality on composite indicators. Sustain. Account. Manag. Policy J. 2014, 5, 268–291. [Google Scholar] [CrossRef]
- Global SDG Indicators Database. United Nations Statistics Division. Available online: https://unstats.un.org/sdgs/indicators/database/ (accessed on 12 November 2020).
- European Commission. Eurostat: Sustainable Development Indicators–Main Tables. Available online: https://ec.europa.eu/eurostat/web/sdi/main-tables (accessed on 3 August 2021).
- United Nations. Sustainable Development Goals Progress Chart 2021. Available online: https://unstats.un.org/sdgs/report/2021/progress-chart-2021.pdf (accessed on 3 August 2021).
- Geniaux, G.; Bellon, S.; Deverre, C.; Powell, B. 2009 Sustainable Development Indicator Frameworks and Initiatives, Report No.49, SEAMLESS integrated project, EU 6th Framework Programme, contract no. 010036-2. Available online: www.SEAMLESS-IP.org (accessed on 3 August 2021).
- Martins, A.A.; Mata, T.M.; Costa, C.A.V. Framework for Sustainability Metrics. Ind. Eng. Chem. Res. 2007, 46, 2962–2973. [Google Scholar] [CrossRef]
- Organization for Economic Co-Operation and Development. Handbook on Constructing Composite Indicators: Methodology and User Guide; OECD Publications: Paris, France, 2008. [Google Scholar]
- Machado, C.G.; Lima, E.P.; Costa, S.E.G.; Cestari, J.M.A.P.; Kluska, R.A.; Hundzinski, L.N. Indicators formulation process for sustainable development operations management. In Proceedings of the International Conference on Production Research–ICPR Americas, Bahía Blanca, Argentina, 8–10 July 2012. [Google Scholar]
- Convertino, M.; Baker, K.; Vogel, J.; Lu, C.; Suedel, B.; Linkov, I. Multi-criteria decision analysis to select metrics for design and monitoring of sustainable ecosystem restorations. Ecol. Indic. 2013, 26, 76–86. [Google Scholar] [CrossRef]
- Reed, M.S.; Fraser, E.D.; Dougill, A. An adaptive learning process for developing and applying sustainability indicators with local communities. Ecol. Econ. 2006, 59, 406–418. [Google Scholar] [CrossRef]
- Holling, C.S. Resilience and Stability of Ecological Systems. Annu. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar] [CrossRef]
- Davoudi, S.; Shaw, K.; Haider, L.J.; Quinlan, A.E.; Peterson, G.; Wilkinson, C.; Fünfgeld, H.; McEvoy, D.; Porter, L. Resilience: A Bridging Concept or a Dead End? “Reframing” Resilience: Challenges for Planning Theory and Practice Interacting Traps: Resilience Assessment of a Pasture Management System in Northern Afghanistan Urban Resilience: What Does it Mean in Planning Practice? Resilience as a Useful Concept for Climate Change Adaptation? The Politics of Resilience for Planning: A Cautionary Note. Plan. Theory Pr. 2012, 13, 299–333. [Google Scholar] [CrossRef]
- Carpenter, S.; Walker, B.; Anderies, J.M.; Abel, N. From metaphor to measurement: Resilience of what to what? Ecosystems 2001, 4, 765–781. [Google Scholar] [CrossRef]
- Carpenter, S.R.; Westley, F.; Turner, M.G. Surrogates for Resilience of Social–Ecological Systems. Ecosystems 2005, 8, 941–944. [Google Scholar] [CrossRef]
- Walker, B.; Holling, C.S.; Carpenter, S.R.; Kinzig, A. Resilience, adaptability and transformability in social-ecological sys-tems. Ecol. Soc. 2004, 9, 5. Available online: http://www.ecologyandsociety.org/vol9/iss2/art5/ (accessed on 17 January 2014). [CrossRef]
- Jen, E. Stable or robust? What’s the difference? In Robust Design; Oxford University Press: New York, NY, USA, 2005; pp. 7–20. [Google Scholar]
- Anderies, J.M.; Janssen, M.A.; Ostrom, E. A Framework to analyze the robustness of social-ecological systems from an in-stitutional perspective. Ecol. Soc. 2004, 9, 18. Available online: https://www.ecologyandsociety.org/vol9/iss1/art18/ (accessed on 21 May 2021). [CrossRef]
- Folke, C. Resilience: The emergence of a perspective for social–ecological systems analyses. Glob. Environ. Chang. 2006, 16, 253–267. [Google Scholar] [CrossRef]
- Derissen, S.; Quaas, M.; Baumgaertner, S. The relationship between resilience and sustainability of ecological-economic systems. Ecol. Econ. 2011, 70, 1121–1128. [Google Scholar] [CrossRef]
- Marchese, D.; Reynolds, E.; Bates, M.E.; Morgan, H.; Clark, S.S.; Linkov, I. Resilience and sustainability: Similarities and differences in environmental management applications. Sci. Total Environ. 2018, 613-614, 1275–1283. [Google Scholar] [CrossRef]
- Redman, C.L. Should sustainability and resilience be combined or remain distinct pursuits? Ecol. Soc. 2014, 19, 37. Available online: https://www.ecologyandsociety.org/vol19/iss2/art37/ (accessed on 1 March 2021). [CrossRef]
- Goerner, S.J.; Dyck, R.G.; Lagerroos, D. The New Science of Sustainability: Building a Foundation for Great Change; Triangle Center for Complex Systems: Chapel Hill, NC, USA, 2008. [Google Scholar]
- Baumgärtner, S.; Quaas, M. Ecological-economic viability as a criterion of strong sustainability under uncertainty. Ecol. Econ. 2009, 68, 2008–2020. [Google Scholar] [CrossRef]
- Krakovská, H.; Kuehn, C.; Longo, I.P. Resilience of Dynamical Systems (preprint). arXiv 2021, arXiv:2015.10592v1. Available online: https://arxiv.org/pdf/2105.10592.pdf (accessed on 7 June 2021).
- Nolting, B.C.; Abbott, K.C. Balls, cups, and quasi-potentials: Quantifying stability in stochastic systems. Ecology 2015, 97, 850–864. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Anderies, J.M.; Janssen, M.A.; Walker, B.H. Grazing Management, Resilience, and the Dynamics of a Fire-driven Rangeland System. Ecosystems 2002, 5, 23–44. [Google Scholar] [CrossRef]
- Martin, S. The cost of restoration as a way of defining resilience: A viability approach applied to a model of lake eutrophica-tion. Ecol. Soc. 2004, 9, 8. Available online: https://www.ecologyandsociety.org/vol9/iss2/art8/ (accessed on 17 January 2014). [CrossRef]
- Aubin, J.P. Viability Theory; Birkhäuser: Boston, MA, USA, 1991. [Google Scholar]
- Martin, S.; Deffuant, G.; Calabrese, J.M. Defining Resilience Mathematically: From Attractors To Viability. In Viability and Resilience of Complex Systems; Springer: Berlin/Heidelberg, Germany, 2011; pp. 15–36. [Google Scholar] [CrossRef]
- Boin, A.; van Eeten, M.J.G. The resilient organization. Public Manag. Rev. 2013, 15, 429–445. [Google Scholar] [CrossRef]
- Goerner, S.J.; Lietaer, B.; Ulanowicz, R.E. Quantifying economic sustainability: Implications for free-enterprise theory poli-cy and practice. Ecol. Econ. 2009, 69, 76–81. [Google Scholar] [CrossRef]
- Ulanowicz, R.E.; Goerner, S.J.; Lietar, B.; Gomez, R. Quantifying sustainability: Resilience, efficiency and the return of in-formation theory. Ecol. Complexity 2009, 6, 27–36. [Google Scholar] [CrossRef]
- Bellwood, D.R.; Hughes, T.; Hoey, A.S. Sleeping Functional Group Drives Coral-Reef Recovery. Curr. Biol. 2006, 16, 2434–2439. [Google Scholar] [CrossRef]
- United Nations. World Population Projected to Reach 9.8 Billion in 2050, and 11.2 Billion in 2100. Available online: https://www.un.org/en/desa/world-population-projected-reach-98-billion-2050-and-112-billion-2100 (accessed on 19 August 2021).
- Food and Agriculture Organization of the United Nations. Strategic Framework 2022-2031. Available online: http://www.fao.org/3/ne577en/ne577en.pdf (accessed on 19 August 2021).
- Food and Agriculture Organization of the United Nations (FAO). The State of Food Security and Nutrition in the World (SOFI). Available online: http://www.fao.org/documents/card/en/c/ca9692en (accessed on 22 February 2021).
- European Commission-Food and Agriculture Organization Food Security Programme. An Introduction to the Basic Con-cepts of Food Security. 2008. Available online: http://www.fao.org/3/al936e/al936e.pdf (accessed on 19 August 2021).
- Holland, J.H. Hidden Order: How Adaptation Builds Complexity; Addison-Wesley: Reading, MA, USA, 1995. [Google Scholar]
- Fang, K.; Song, S.; Heijungs, R.; de Groot, S.; Dong, L.; Song, J.; Wiloso, E.I. The footprint’s fingerprint: On the classification of the footprint family. Curr. Opin. Environ. Sustain. 2016, 23, 54–62. [Google Scholar] [CrossRef]
- Smetana, S.M.; Bornkessel, S.; Heinz, V. A Path From Sustainable Nutrition to Nutritional Sustainability of Complex Food Systems. Front. Nutr. 2019, 6, 39. [Google Scholar] [CrossRef] [PubMed]
- Liobikiene, G.; Chen, X.; Streimikiene, D.; Balezentis, T. The trends in bioeconomy development in the European Union: Exploiting capacity and productivity measures based on the land footprint approach. Land Use Policy 2020, 91, 104375. [Google Scholar] [CrossRef]
- Stegmann, P.; Londo, M.; Junginger, M. The circular bioeconomy: Its elements and role in European bioeconomy clusters. Resour. Conserv. Recycl. X 2020, 6, 100029. [Google Scholar] [CrossRef]
- Tendall, D.; Joerin, J.; Kopainsky, B.; Edwards, P.; Shreck, A.; Le, Q.; Kruetli, P.; Grant, M.; Six, J. Food system resilience: Defining the concept. Glob. Food Secur. 2015, 6, 17–23. [Google Scholar] [CrossRef]
- Holling, C.S. Understanding the Complexity of Economic, Ecological, and Social Systems. Ecosystems 2001, 4, 390–405. [Google Scholar] [CrossRef]
- Pereira, L.M.; Drimie, S.; Maciejewsky, K.; Tonissen, P.B.; Biggs, R. Food system transformation: Integrating a politi-cal-economy and social-ecological approach to regime shifts. Int. J. Environ. Res. Public Health 2020, 17, 1313. Available online: https://www.mdpi.com/1660-4601/17/4/1313 (accessed on 1 March 2021). [CrossRef] [PubMed]
- Kusch-Brandt, S. Towards more sustainable food systems—14 lessons learned. Int. J. Environ. Res. Public Health 2020, 17, 4005. Available online: https://www.mdpi.com/1660-4601/17/11/4005 (accessed on 1 March 2021). [CrossRef]
- Chaudhary, A.; Gustafson, D.; Mathys, A. Multi-indicator sustainability assessment of global food systems. Nat. Commun. 2018, 9, 1–13. [Google Scholar] [CrossRef]
- Béné, C.; Fanzo, J.; Prager, S.D.; Achicanoy, H.A.; Mapes, B.R.; Toro, P.A.; Cedrez, C.B. Global drivers of food system (un)sustainability: A multi-country correlation analysis. PLoS ONE 2020, 15, e0231071. [Google Scholar] [CrossRef]
- Peano, C.; Tecco, N.; Dansero, E.; Girgenti, V.; Sottile, F. Evaluating the Sustainability in Complex Agri-Food Systems: The SAEMETH Framework. Sustainability 2015, 7, 6721–6741. [Google Scholar] [CrossRef]
- Scheffer, M.; Carpenter, S.R.; Lenton, T.M.; Bascompte, J.; Brock, W.; Dakos, V.; van de Koppel, J.; van de Leemput, I.A.; Levin, S.A.; van Nes, E.H.; et al. Anticipating Critical Transitions. Science 2012, 338, 344–348. [Google Scholar] [CrossRef] [PubMed]
- Suweis, S.; D’Odorico, P. Early Warning Signs in Social-Ecological Networks. PLoS ONE 2014, 9, e101851. [Google Scholar] [CrossRef] [PubMed]
- Allen, T.; Prosperi, P. Modeling Sustainable Food Systems. Environ. Manag. 2016, 57, 956–975. [Google Scholar] [CrossRef]
- Sneessens, I.; Sauvée, L.; Randrianasolo-Rakotobe, H.; Ingrand, S. A framework to assess the economic vulnerability of farming systems: Application to mixed crop-livestock systems. Agric. Syst. 2019, 176, 102658. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0308521×18309363 (accessed on 20 September 2020). [CrossRef]
- Meuwissen, M.P.M.; Feindt, P.H.; Spiegel, A.; Termeer, C.J.A.M.; Mathijs, E.; de Mey, Y.; Finger, R.; Balmann, A.; Wauters, E.; Urquhart, J.; et al. A framework to assess the resilience of farming systems. Agric. Syst. 2019, 176, 102656. Available online: https://www.sciencedirect.com/science/article/pii/S0308521X19300046 (accessed on 20 September 2020). [CrossRef]
- Rosin, C.; Campbell, H.; Reid, J. Metrology and sustainability: Using sustainability audits in New Zealand to elaborate the complex politics of measuring. J. Rural. Stud. 2017, 52, 90–99. [Google Scholar] [CrossRef]
- Hubbard, D.W. How to Measure Anything: Finding the Values of “Intangibles” in Business, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Fiksel, J. Sustainability and resilience: Toward a systems approach. Sustain. Sci. Pr. Policy 2006, 2, 14–21. [Google Scholar] [CrossRef]
- Schouten, M.A.; van der Heide, C.M.; Heijman, W.J.; Opdam, P.F. A resilience-based policy evaluation framework: Application to European rural development policies. Ecol. Econ. 2012, 81, 165–175. [Google Scholar] [CrossRef]
- Morgan, M.G.; Henrion, M. Uncertainty: A Guide to Dealing with Uncertainty in Quantitative Risk and Policy Analysis, 1st ed.; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Innerarity, D. O Futuro e os Seus Inimigos: Uma Defesa da Esperança Política, 1st ed.; Teorema: Alfragide, Portugal, 2011. [Google Scholar]
- Alchian, A.A. Uncertainty, evolution, and economic theory. J. Political Econ. 1950, 58, 211–221. [Google Scholar] [CrossRef]
- ISO 7708:1995(en). Air Quality—Particle Size Fraction Definitions for Health-Related Sampling. Available online: https://www.iso.org/obp/ui#iso:std:iso:7708:ed-1:v1:en (accessed on 16 September 2020).
- Polasky, S.; Carpenter, S.; Folke, C.; Keeler, B. Decision-making under great uncertainty: Environmental management in an era of global change. Trends Ecol. Evol. 2011, 26, 398–404. [Google Scholar] [CrossRef]
- Watkins, G.P.; Knight, F.H. Knight’s Risk, Uncertainty and Profit. Q. J. Econ. 1922, 36, 682. [Google Scholar] [CrossRef]
- Stirling, A. Keep it complex. Nature 2010, 468, 1029–1031. [Google Scholar] [CrossRef]
- Anderies, J.M.; Rodriguez, A.A.; Janssen, M.A.; Cifdaloz, O. Panaceas, uncertainty, and the robust control framework in sustaina-bility science. PNAS 2007, 109, 15194–15199. [Google Scholar] [CrossRef]
- Schwartz, P. The Art of the Long View: Planning for the Future in an Uncertain World; John Wiley & Sons: Chichester, West Sussex, UK, 1998. [Google Scholar]
- Tetlock, P.; Gardner, D. Superforecasting: The Art and Science of Prediction, 1st ed.; Random House Books: London, UK, 2015. [Google Scholar]
- Hubbard, D.W. The Failure of Risk Management: Why it’s Broken and How to Fix it; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Hubbard, D.W.; Seiersen, R. How to Measure Anything in Cybersecurity Risk; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Brock, W.A.; Durlauf, S.N.; West, K.D. Model uncertainty and policy evaluation: Some theory and empirics. J. Econ. 2007, 136, 629–664. [Google Scholar] [CrossRef]
- Landerrechte, O.; Leiva, B.; Vivanco, D.; López, I. Welcoming uncertainty: A probabilistic approach to measure sustainabil-ity. Ecol. Indicators 2017, 72, 586–596. [Google Scholar] [CrossRef]
- Miller, J.H.; Page, S.E. Complex Adaptive Systems: An Introduction to Computational Models of Social Life; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Coleman, J.S. Foundations of Social Theory; The Belknap Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Ylikoski, P. Thinking with the Coleman boat. In The IAS Working Paper Series 2016:1; Linköping University: Sweden, 2016. [Google Scholar]
- Schillo, M.; Fischer, K.; Klein, C.T. The Micro-Macro Link in DAI and Sociology; Springer: Berlin/Heidelberg, Germany, 2000; pp. 133–148. [Google Scholar] [CrossRef]
- Dopfer, K.; Foster, J.; Potts, J. Micro-meso-macro. J. Evolut. Econ. 2004, 14, 263–279. [Google Scholar] [CrossRef]
- Bergström, J.; Dekker, S.W.A. Bridging the Macro and the Micro by Considering the Meso: Reflections on the Fractal Nature of Resilience. Ecol. Soc. 2014, 19. [Google Scholar] [CrossRef]
- Holland, J.H. Emergence: From Chaos to Order; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Geels, F. Technological transitions as evolutionary reconfiguration processes: A multi-level perspective and a case-study. Res. Policy 2002, 31, 1257–1274. [Google Scholar] [CrossRef]
- Geels, F. The multi-level perspective on sustainability transitions: Responses to seven criticisms. Environ. Innov. Soc. Transit. 2011, 1, 24–40. [Google Scholar] [CrossRef]
- Luketina, R.; El Bilali, H.; Berjan, S.; Wurzinger, M. SUSTAINABILITY TRANSITIONS IN BOSNIAN AGRO-FOOD SYSTEM. J. Agric. For. 2018, 64. [Google Scholar] [CrossRef]
- Gaitán-Cremaschi, D.; Klerkx, L.; Duncan, J.; Trienekens, J.H.; Huenchuleo, C.; Dogliotti, S.; Contesse, M.E.; Rossing, W.A.H. Characterizing diversity of food systems in view of sustainability transitions. A review. Agron. Sustain. Dev. 2018, 39, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Tetlock, P.E. Expert Political Judgement: How Good Is It? How Can We Know? Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]
- Page, S.E. The Difference: How the Power of Diversity Creates Better Groups, Firms, Schools, and Societies; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Norberg, J.; Cumming, G.S. Complexity theory for a sustainability future: Conclusions and Outlook. In Complexity Theory for a Sustainability Future; Norberg, J., Cumming, G.S., Eds.; Columbia University Press: New York, NY, USA, 2008. [Google Scholar]
- Juarrero, A. Complex Dynamical Systems Theory. Cognitive Edge 2010. Available online: https://narrate.co.uk/wp-content/uploads/2010/11/100608-complex_dynamical_systems_theory.pdf (accessed on 26 August 2021).
- Auyang, S.Y. Foundations of Complex-System Theories in Economics, Evolutionary Biology, and Statistical Physics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Mitchell, M. Complexity: A Guided Tour; Oxford University Press: New York, NY, USA, 2009. [Google Scholar]
- Holland, J.H. Signals and Boundaries: Building Blocks for Complex Adaptive Systems; The MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Siegenfeld, A.F.; Bar-Yam, Y. An Introduction to Complex Systems Science and Its Applications. Complexity 2020, 2020, 6105872. [Google Scholar] [CrossRef]
- Shalizi, C.R. Methods and techniques of complex systems science: An overview. In Complex Systems Science in Biomedicine; Deisboeck, T.S., Kresh, J.Y., Eds.; Springer: Boston, MA, USA, 2006. [Google Scholar]
- Gilbert, N.; Teoitzsch, K.G. Simulation for the Social Scientist, 2nd ed.; Open University Press: Berkshire, UK, 2005. [Google Scholar]
- Espinosa, A.; Harnden, R.; Walker, J. A complexity approach to sustainability–Stafford Beer revisited. Eur. J. Oper. Res. 2008, 187, 636–651. [Google Scholar] [CrossRef]
- Gutowitz, H. Cellular Automata: Theory and Experiment; The MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Wolfram, S. A New Kind of Science; Wolfram Media Inc.: Champaign, IL, USA, 2002. [Google Scholar]
- Bandini, S.; Pavesi, G. A model based on cellular automata for the simulation of plant populations. In Proceedings of the 2nd International Congress of Environmental Modelling and Software, Osnabrück, Germany, 1 July 2004; p. 160. Available online: https://scholarsarchive.byu.edu/cgi/viewcontent.cgi?article=3447&context=iemssconference (accessed on 8 February 2021).
- Grayling, M.J. phaseR: An R Package for Phase Plane Analysis of Autonomous ODE Systems. R J. 2014, 6, 43–51. [Google Scholar] [CrossRef]
- Moore, C.M.; Stieha, C.R.; Nolting, B.C.; Cameron, M.K.; Abbott, K.C. QPot: An R Package for Stochastic Differential Equa-tion Quasi-Potential Analysis. R J. 2016, 8, 19–38. [Google Scholar] [CrossRef]
- Wilensky, U. NetLogo. In Center for Connected Learning and Computer-Based Modeling; Northwestern University: Evanston, IL, USA, 1999; Available online: http://ccl.northwestern.edu/netlogo/ (accessed on 1 March 2021).
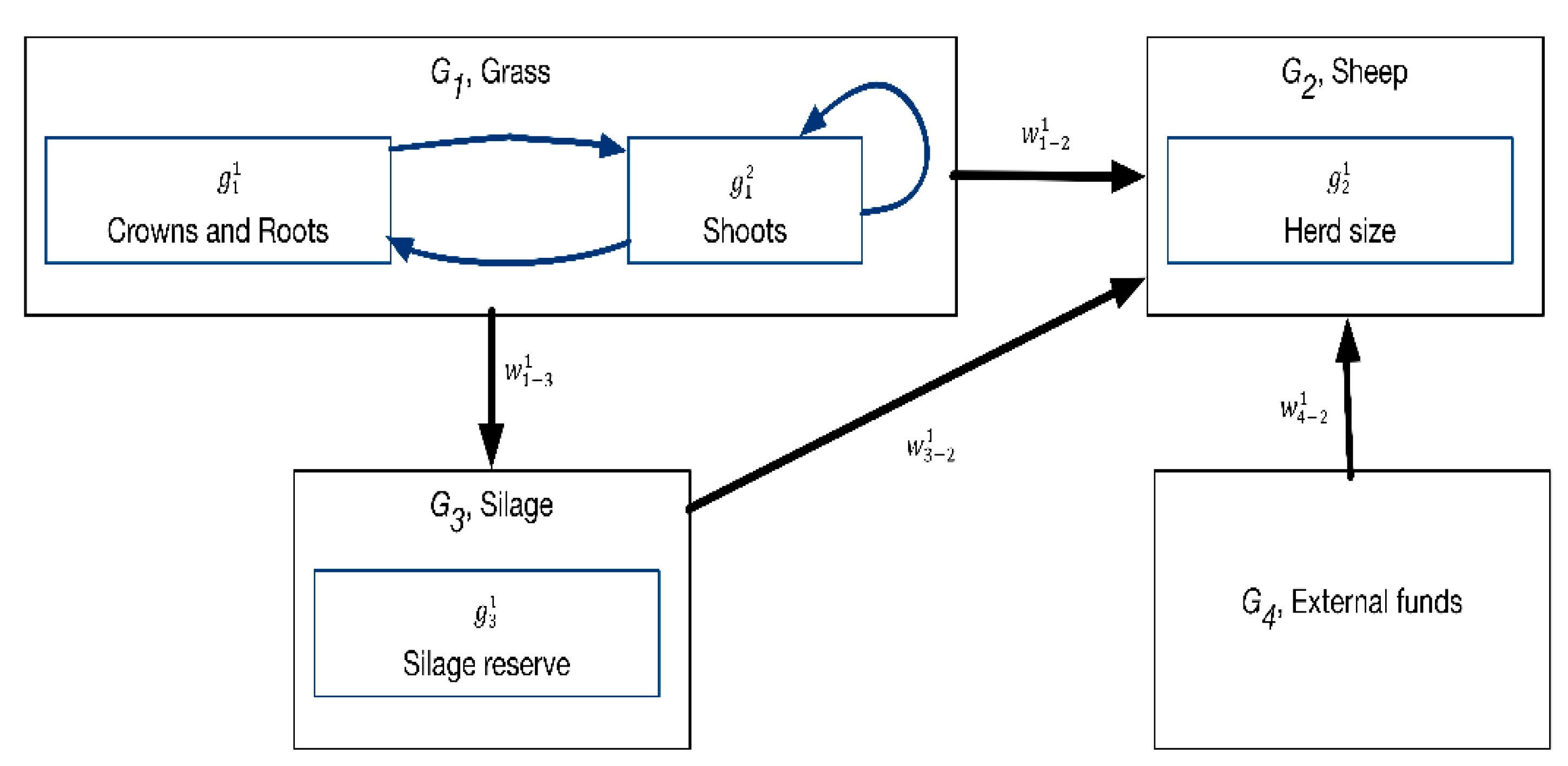





| , grass Rangeland grazed by sheep and harvested for silage. | , crowns and roots. Rangeland crowns’ and roots’ available biomass. Measured in dry matter (DM) kilogram equivalents available per unit area and epoch. , shoots. Rangeland shoots’ available biomass. Measured in dry matter (DM) kilogram equivalents available per unit area and epoch. |
| , sheep Herd to be raised. | , number of sheep. Herd, measured by the number of adult sheep in the herd. |
| , silage | , silage reserve. Dry matter (DM) kilogram equivalents available from silage. |
| , external funds. External funds (e.g., dry pellets) that may need to be acquired for herd nutritional needs. Modeled in the simplified system as an inexhaustible fund, thus having no associated variables. | |
| , dry matter (DM) equivalents Provision of the required dry matter equivalents in order to meet the herd’s feed requirements. | , grazing. Dry matter equivalents grazed by the herd. Measured in DM kilograms grazed per unit area and epoch. , harvesting. Dry matter equivalents harvested for silage. Measured in DM kilograms harvested per unit area and epoch. , silage consumption. Dry matter equivalents of silage consumed by the herd. Measured in DM kilograms consumed per epoch. , external feeding. Dry matter equivalents of food from external sources (e.g., pellets) consumed by the herd. Measured in DM kilograms consumed per epoch. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matos, J.V.; Lopes, R.J. Food System Sustainability Metrics: Policies, Quantification, and the Role of Complexity Sciences. Sustainability 2021, 13, 12408. https://doi.org/10.3390/su132212408
Matos JV, Lopes RJ. Food System Sustainability Metrics: Policies, Quantification, and the Role of Complexity Sciences. Sustainability. 2021; 13(22):12408. https://doi.org/10.3390/su132212408
Chicago/Turabian StyleMatos, José V., and Rui J. Lopes. 2021. "Food System Sustainability Metrics: Policies, Quantification, and the Role of Complexity Sciences" Sustainability 13, no. 22: 12408. https://doi.org/10.3390/su132212408
APA StyleMatos, J. V., & Lopes, R. J. (2021). Food System Sustainability Metrics: Policies, Quantification, and the Role of Complexity Sciences. Sustainability, 13(22), 12408. https://doi.org/10.3390/su132212408






