Analysis of Rainfall Time Series with Application to Calculation of Return Periods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study of Probabilities of Extreme Events
2.1.1. Generalized Extreme Value (GEV) Distribution
2.1.2. Peak over Threshold (POT) Pareto Distribution
2.2. Determination of Return Periods
- -
- Modification of hydrological channels;
- -
- Variation of flows;
- -
- River basin typology;
- -
- Variation in land use in the area potentially affected by flooding;
- -
- Infrastructure located in the analysis area;
- -
- Climatological variability (effects of climate change);
- -
- Orography of the study area;
- -
- Geological characterization of the terrain in the analysis area;
- -
- Links with other hydrological basins or nearby environment.
2.3. Numerical Model of Rainfall Time Series
- Transform the original dataset, including only those days when : there are many observations with zero value, which generates a distortion when calculating the mean values to compare non-zero data;
- Calculate monthly averages: In order to estimate the global trend (see next section), it is necessary to minimize the variance of the data considered. One way is to consider monthly groupings of the data, since this represents a period long enough for several rainfall episodes to appear and short enough so that the possible trend does not affect the calculated averages too much;
- Eliminate global trends: from the averages grouped by month calculated in the previous step, a linear regression is performed to obtain an overall trend;
- Remove seasonal effects of the time series from the median values of the monthly data grouped in step 2: once the medians (which are less sensitive than means to extreme values) of the monthly values are calculated, the difference between these values and the medians are used to study the seasonal components;
- Once the data are treated in steps 1–4, use the extreme values of distribution to determine the characteristics of the distribution using the TOP approach: Steps 1–3 attempt to eliminate the main random values appearing in Expression (11). Once the global and seasonal components of the original signal are discounted, we can make the approximation . The analysis of extremes is performed on this modified data;
- From the distribution obtained in step 5, calculate the return periods for different extreme values: once the distribution parameter estimates are obtained by POT, they can be used for return period forecasting;
3. Results
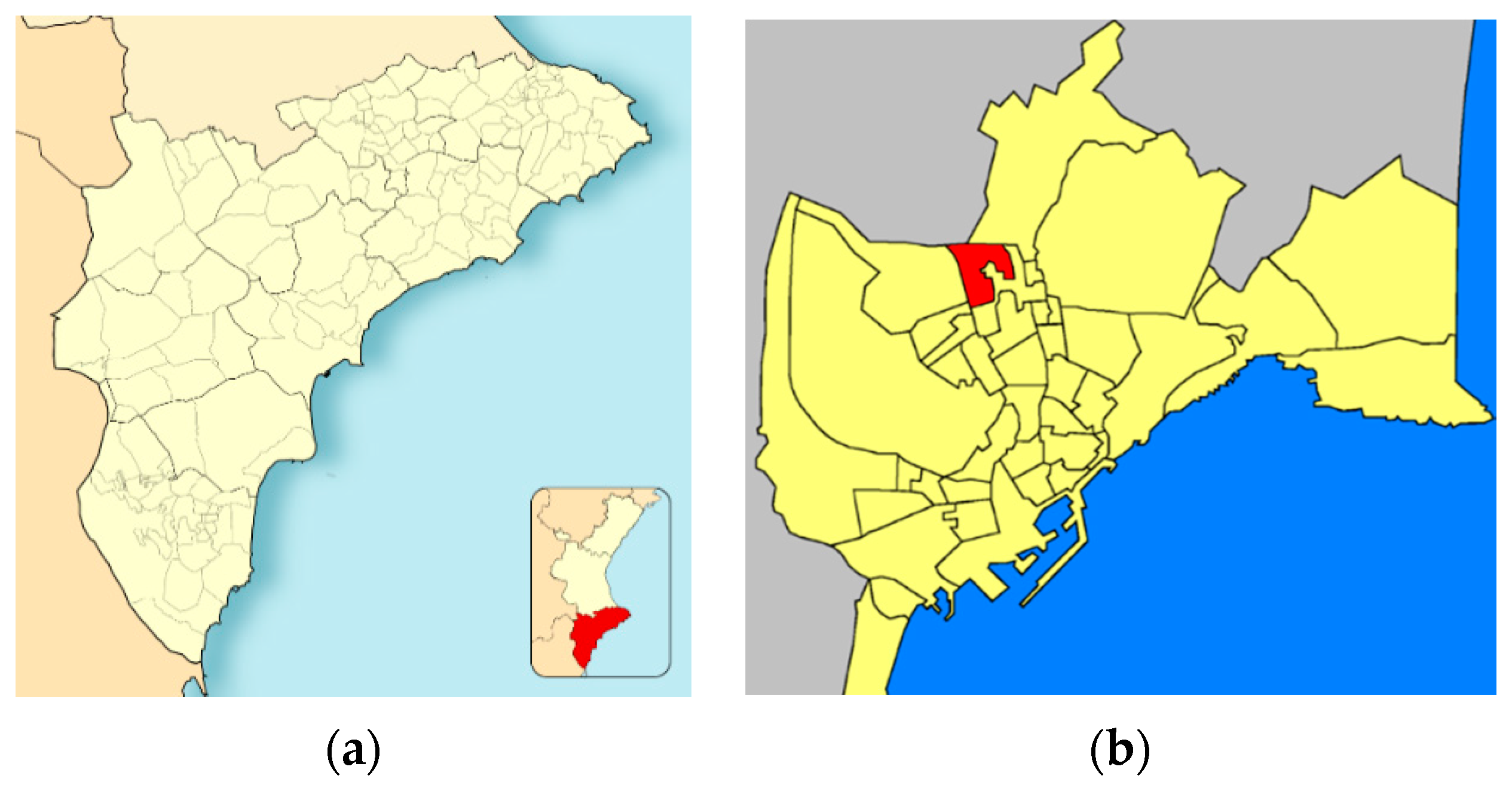
3.1. Introduction to the Rainfall Series of Ciudad Jardin Dataset
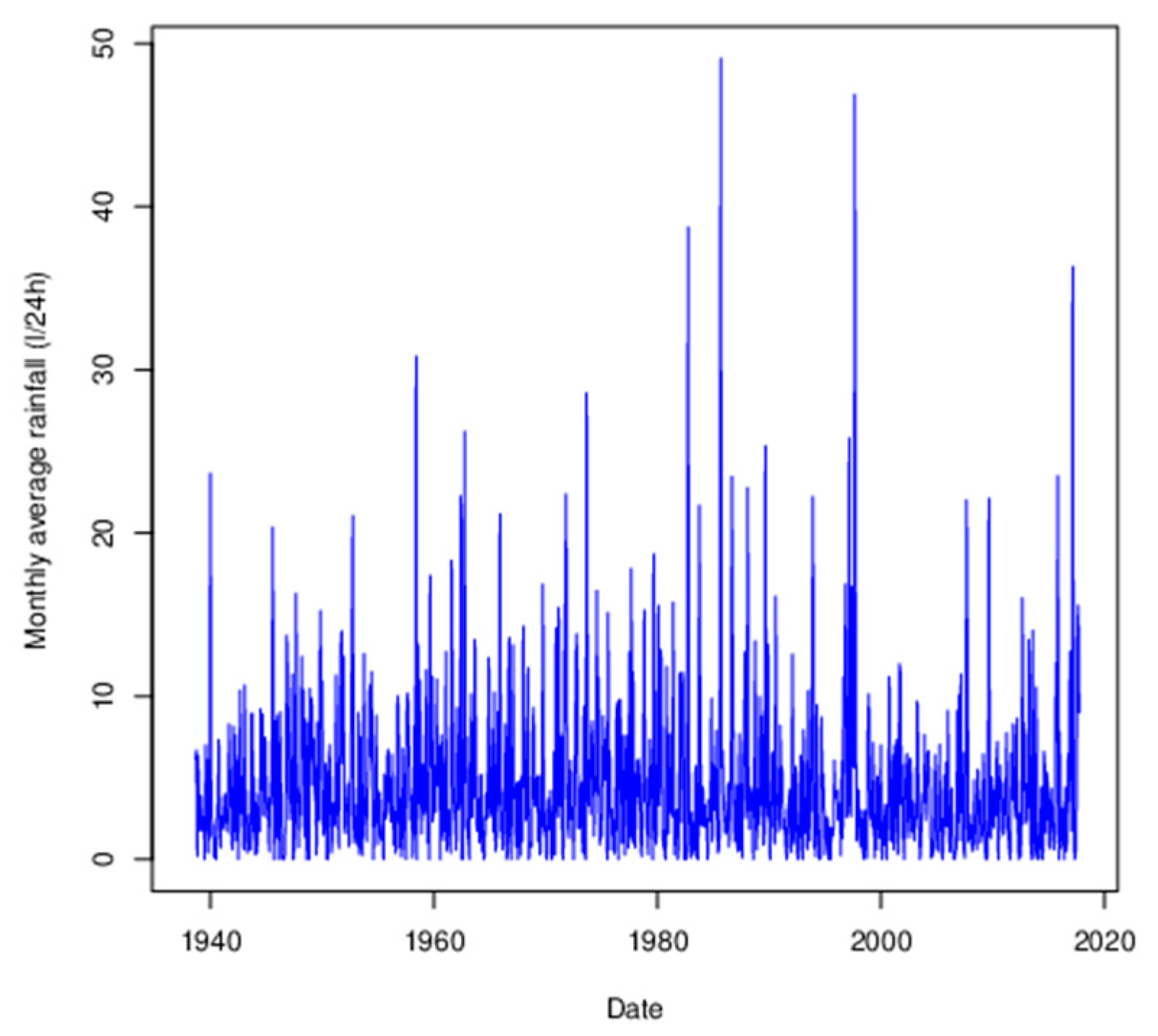
3.2. Filtering of Global Trends and Seasonal Components
3.2.1. General Trend
3.2.2. Seasonal Analysis
3.3. Fitting of Distribution of Extreme Value Probabilities
3.3.1. POT Analysis
3.3.2. Return Period
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zorraquino Junquera, C. El modelo SQRT-ET MAX. Rev. Obras Públicas 2004, 151, 33–37. [Google Scholar]
- Álvarez, M.; Puertas Agudo, J.; Soto, B.; Díaz-Fierros, F. Análisis regional de las precipitaciones máximas en Galicia mediante el método del índice de avenida. Ing. Agua 1999, 6, 379–386. [Google Scholar] [CrossRef] [Green Version]
- Valero, F.; Luna, M.Y.; Martín, M.L.; Morata, A.; González-Rouco, F. Coupled modes of large-scale climatic variables and regional precipitation in the Western Mediterranean in autumn. Clim. Dyn. 2004, 22, 307–323. [Google Scholar] [CrossRef]
- Martín, M.L.; Luna, M.Y.; Morata, A.; Valero, F. North Atlantic teleconnection patterns of low-frequency variability and their links with springtime precipitation in the Western Mediterranean. Int. J. Climatol. 2004, 24, 213–230. [Google Scholar] [CrossRef]
- Serrano, A.; García, J.A.; Mateos, V.L.; Cancillo, M.L.; Garrido, J. Monthly Modes of Variation of Precipitation over the Iberian Peninsula. J. Clim. 1999, 12, 2894–2919. [Google Scholar] [CrossRef]
- García, J.A.; Serrano, A.; Gallego, M.C. A spectral analysis of the Iberian Peninsula monthly rainfall. Theor. Appl. Clim. 2002, 71, 77–95. [Google Scholar] [CrossRef]
- Estrela, M.J.; Miró, J.J.; Millán, M. Análisis de tendencia de la precipitación por situaciones convectivas en la Comunidad Valenciana (1959–2004). In Proceedings of the V Congreso Internacional de la Asociación Española de Climatología, Zaragoza, Spain, 18–21 September 2006; Cuadrat Prats, J.M., Saz Sánchez, M.A., Vicente Serrano, S.M., Lanjeri, S., de Luis Arrillaga, M., González-Hidalgo, J.C., Eds.; Clima, Sociedad y Medio Ambiente, Asociación Española de Climatología: Zaragoza, Spain, 2006; pp. 1–12. [Google Scholar]
- Salas, J.D.; Obeysekera, J. Revisiting the Concepts of Return Period and Risk for Nonstationary Hydrologic Extreme Events. J. Hydrol. Eng. 2014, 19, 554–568. [Google Scholar] [CrossRef] [Green Version]
- Rodrigo, F.S.; Trigo, R.M. Trends in daily rainfall in the Iberian Peninsula from 1951 to 2002. Int. J. Climatol. J. R. Meteorol. Soc. 2007, 27, 513–529. [Google Scholar] [CrossRef]
- Goodess, C.M.; Jones, P.D. Links between circulation and changes in the characteristics of Iberian rainfall. Int. J. Climatol. 2002, 22, 1593–1615. [Google Scholar] [CrossRef]
- Millán, M.; Estrela, M.J.; Sanz, M.J.; Mantilla, E.; Martín, M.; Pastor, F.; Salvador, R.; Vallejo, R.; Alonso, L.; Gangoiti, G.; et al. Climate feedbacks and desertification: The Mediterranean model. J. Clim. 2005, 18, 684–701. [Google Scholar] [CrossRef] [Green Version]
- Millán, M.M.; Estrela, M.J.; Miró, J. Rainfall Components: Variability and spatial distribution in a Mediterranean area (Valencia Region). J. Clim. 2005, 18, 2682–2705. [Google Scholar] [CrossRef]
- Pardo, M.A.; Pérez-Montes, A.; Moya-Llamas, M.J. Using reclaimed water in dual pressurized water distribution networks. Cost analysis. J. Water Process Eng. 2021, 40, 101766. [Google Scholar] [CrossRef]
- Navarro-Gonzalez, F.J.; Villacampa, Y.; Picazo, M.Á.P.; Cortés-Molina, M. Optimal load scheduling for off-grid photovoltaic installations with fixed energy requirements and intrinsic constraints. Process Saf. Environ. 2021, 149, 476–484. [Google Scholar] [CrossRef]
- Jato-Espino, D.; Charlesworth, S.M.; Perales-Momparler, S.; Andrés-Doménech, I. Prediction of Evapotranspiration in a Mediterranean Region Using Basic Meteorological Variables. J. Hydrol. Eng. 2017, 22, 04016064. [Google Scholar] [CrossRef] [Green Version]
- Lelieveld, J.; Hadjinicolaou, P.; Kostopoulou, E.; Chenoweth, J.; El Maayar, M.; Giannakopoulos, C.; Hannides, C.; Lange, M.A.; Tanarhte, M.; Tyrlis, E.; et al. Climate change and impacts in the Eastern Mediterranean and the Middle East. Clim. Chang. 2012, 114, 667–687. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tramblay, Y.; Somot, S. Future evolution of extreme precipitation in the Mediterranean. Clim. Chang. 2018, 151, 289–302. [Google Scholar] [CrossRef]
- Ribes, A.; Thao, S.; Vautard, R.; Dubuisson, B.; Somot, S.; Colin, J.; Planton, S.; Soubeyroux, J.M. Observed increase in extreme daily rainfall in the French Mediterranean. Clim. Dynam. 2019, 52, 1095–1114. [Google Scholar] [CrossRef]
- Ruti, P.M.; Somot, S.; Giorgi, F.; Dubois, C.; Flaounas, E.; Obermann, A.; Dell’Aquila, A.; Pisacane, G.; Harzallah, A.; Lombardi, E.; et al. MED-CORDEX initiative for Mediterranean climate studies. Bull. Am. Meteorol. Soc. 2016, 97, 1187–1208. [Google Scholar] [CrossRef] [Green Version]
- Millán, M.; Estrela, M.J.; Caselles, V. Torrential precipitations on the Spanish east coast: The role of the Mediterranean Sea surface temperature. Atmos Res. 1995, 36, 1–16. [Google Scholar] [CrossRef]
- Kang, J.-N.; Wei, Y.-M.; Liu, L.-C.; Han, R.; Yu, B.-Y.; Wang, J.-W. Energy systems for climate change mitigation: A systematic review. Appl. Energy 2020, 263, 114602. [Google Scholar] [CrossRef]
- Barkhordarian, A.; Von Storch, H.; Bhend, J. The expectation of future precipitation change over the Mediterranean region is different from what we observe. Clim. Dyn. 2013, 40, 225–244. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Puebla, C.; Encinas, A.H.; Nieto, S.; Garmendia, J. Spatial and temporal patterns of annual precipitation variability over the Iberian Peninsula. Int. J. Climatol. 1998, 18, 299–316. [Google Scholar] [CrossRef]
- Martin-Vide, J.; Lopez-Bustins, J.-A. The Western Mediterranean Oscillation and rainfall in the Iberian Peninsula. Int. J. Climatol. 2006, 26, 1455–1475. [Google Scholar] [CrossRef]
- De Luis, M.; González-Hidalgo, J.C.; Longares, L.A.; Štepánek, P. Seasonal precipitation trends in the Mediterranean Iberian Peninsula in second half of 20th century. Int. J. Climatol. 2008, 29, 1312–1323. [Google Scholar] [CrossRef]
- Parracho, A.C.; Melo-Gonçalves, P.; Rocha, A. Regionalisation of precipitation for the Iberian Peninsula and climate change. Phys. Chem. Earth 2016, 94 Pt A/B/C, 146–154. [Google Scholar] [CrossRef]
- Ruiz García, J.A.; Nuñez Mora, J.A. Sobre los periodos de retorno de las precipitaciones extraordinarias en la Comunidad Valenciana. In Delegación AEMET Comunidad Valenciana; Agencia Estatal de Meteorología: Madrid, Spain, 2011. Available online: http://hdl.handle.net/20.500.11765/2465 (accessed on 7 April 2021).
- Pereyra-Díaz, D.; Pérez-Sesma, J.A.A.; Gómez-Romero, L. Ecuaciones que estiman las curvas intensidad-duración-periodo de retorno de la lluvia. Geos 2004, 24, 46–56. [Google Scholar]
- Rodríguez Solà, R.; Casas Castillo, M.C.; Navarro, X.; Redaño, A. A study of the scaling properties of rainfall in Spain and its appropriateness to generate intensity-duration-frequency curves from daily records. Int. J. Climatol. 2017, 37, 770–780. [Google Scholar] [CrossRef]
- Acosta Castellanos, P.M.; Sierra Aponte, L.X. Evaluación de métodos de construcción de curvas IDF a partir de distribuciones de probabilidad y parámetros de ajuste. Rev. Fac. Ing. 2013, 22, 25–33. [Google Scholar] [CrossRef] [Green Version]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis, Forecasting and Control; Holden Day: San Francisco, CA, USA, 1970. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis, Forecasting and Control; Holden Day: San Francisco, CA, USA, 1974. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Revised ed.; Holden Day: San Francisco, CA, USA, 1976. [Google Scholar]
- Contreras, J.; Espinola, R.; Nogales, F.J.; Conejo, A.J. ARIMA models to predict next-day electricity prices. IEEE T. Power Syst. 2003, 18, 1014–1020. [Google Scholar] [CrossRef]
- Ariyo Adebiyi, A.; Adewumi, A.; Ayo, C. Stock price prediction using the ARIMA model. In Proceedings of the 2014 UKSim-AMSS 16th International Conference on Computer Modelling and Simulation, Cambridge, UK, 26–28 March 2014; pp. 106–112. [Google Scholar] [CrossRef] [Green Version]
- Meyler, A.; Kenny, G.; Quinn, T. Forecasting Irish Inflation Using ARIMA Models; Project Forecasting Inflation in Ireland; The Central Bank of Ireland: Doublin, Ireland, 1998. [Google Scholar]
- Moayedi, H.Z.; Masnadi-Shirazi, M.A. Arima model for network traffic prediction and anomaly detection. In Proceedings of the IEEE 2008 International Symposium on Information Technology, Kuala Lumpur, Malaysia, 26–28 August 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Somvanshi, V.K.; Pandey, O.P.; Agrawal, P.K.; Kalanker, N.V.; Prakash, M.R.; Chand, R. Modeling and prediction of rainfall using artificial neural network and ARIMA techniques. J. Ind. Geophys. Union 2006, 10, 141–151. [Google Scholar]
- Chattopadhyay, S.; Chattopadhyay, G. Univariate modelling of summer-monsoon rainfall time series: Comparison between ARIMA and ARNN. Comptes Rendus Geosci. 2010, 342, 100–107. [Google Scholar] [CrossRef]
- Abdul-Aziz, A.R.; Anokye, M.; Kwame, A.; Munyakazi, L.; Nsowah-Nuamah, N.N.N. Modeling and forecasting rainfall pattern in Ghana as a seasonal ARIMA process: The case of Ashanti region. Int. J. Humanit. Soc. Sci. 2013, 3, 224–233. [Google Scholar]
- Unnikrishnan, P.; Jothiprakash, V. Hybrid SSA-ARIMA-ANN model for forecasting daily rainfall. Water Resour. Manag. 2020, 34, 3609–3623. [Google Scholar] [CrossRef]
- Poměnková, J.; Fidrmuc, J.; Korhonen, I. China and the World Economy: Wavelet Spectrum Analysis of Business Cycles. Appl. Econ. Lett. 2014, 21, 1309–1313. [Google Scholar] [CrossRef] [Green Version]
- Qin, W.J.B. Energy demand forecasting model in China based on wavelet-neural network. J. Syst. Sci. Math. Sci. 2009, 11, 1542–1551. [Google Scholar]
- Raihan, S.M.; Wen, Y.; Zeng, B. Wavelet: A New Tool for Business Cycle Analysis; Working Papers 2005-050; Federal Reserve Bank of St. Louis: St. Louis, MO, USA, 2005. [Google Scholar]
- Razdan, A. Wavelet correlation coefficient of ‘strongly correlated’time series. Phys. A Stat. Mech. Its Appl. 2004, 333, 335–342. [Google Scholar] [CrossRef] [Green Version]
- Ju, K.; Zhou, D.; Zhou, P.; Wu, J. Macroeconomic effects of oil price shocks in China: An empirical study based on Hilbert–Huang transform and event study. Appl. Energ. 2014, 136, 1053–1066. [Google Scholar] [CrossRef]
- Li, M.; Huang, Y. Hilbert–Huang Transform based multifractal analysis of China stock market. Phys. A Stat. Mech. Its Appl. 2014, 406, 222–229. [Google Scholar] [CrossRef]
- Liu, H.Y.; Lin, Z.S.; Zhang, M.Y. Analysis on the fluctuation of grain output in China and its causes at multi-time scale based on empirical mode decomposition method. J. Nat. Resour. 2005, 20, 745–751. [Google Scholar] [CrossRef]
- Oladosu, G. Identifying the oil price–macroeconomy relationship: An empirical mode decomposition analysis of US data. Energy Policy 2009, 37, 5417–5426. [Google Scholar] [CrossRef]
- Zhang, X.; Lai, K.K.; Wang, S.Y. A new approach for crude oil price analysis based on empirical mode decomposition. Energy Econ. 2008, 30, 905–918. [Google Scholar] [CrossRef]
- Zhu, B.; Wang, P.; Chevallier, J.; Wei, Y. Carbon price analysis using empirical mode decomposition. Comput. Econ. 2015, 45, 195–206. [Google Scholar] [CrossRef]
- Fisher, R.A.; Tippett, L.H.C. Limiting forms of the frequency distribution of the largest or smallest member of a sample. Math. Proc. Camb. 1928, 24, 180–190. [Google Scholar] [CrossRef]
- Valdes-Abellan, J.; Pardo, M.A.; Tenza-Abril, A.J. Observed precipitation trend changes in the western Mediterranean region. Int. J. Climatol. 2017, 37, 1285–1296. [Google Scholar] [CrossRef]
- De Kokoo, C.C. BY-SA 3.0. Available online: https://commons.wikimedia.org/w/index.php?curid=1759109 (accessed on 4 February 2021).
- Ribatet, M.A. User’s Guide to the PoT Package (Version 1.4); University of Quebec: Montreal, QC, Canada, 2006; p. 31. [Google Scholar]
- Northrop, P.J.; Coleman, C.L. Improved threshold diagnostic plots for extreme value analyses. Extremes 2014, 17, 289–303. [Google Scholar] [CrossRef] [Green Version]
- Benhamrouche, A.; Martín-Vide, J. Avances metodológicos en el análisis de la concentración diaria de la precipitación en la España Peninsular. An. Geogr. Univ. Complut. 2012, 32, 11–27. [Google Scholar] [CrossRef] [Green Version]

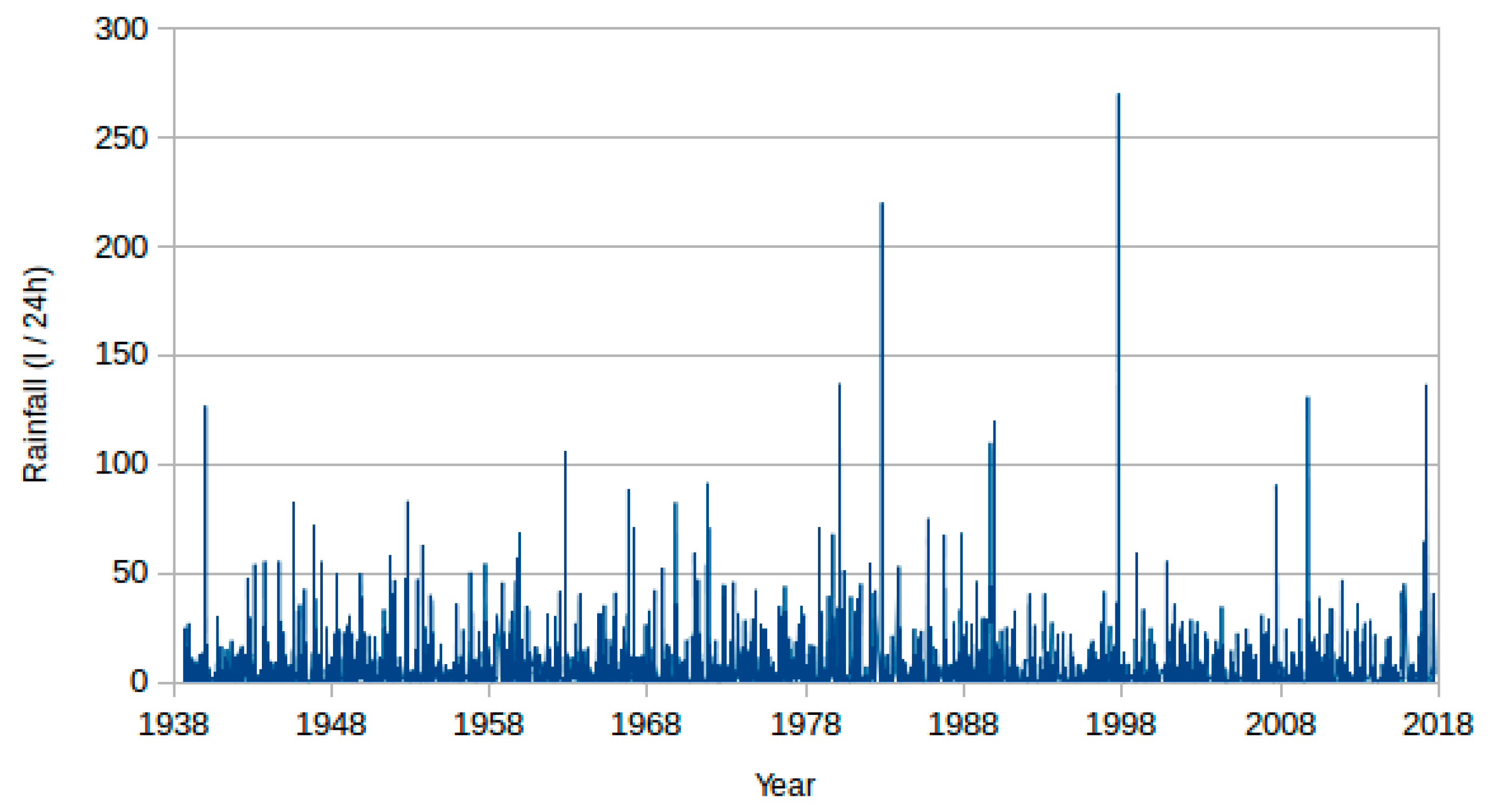



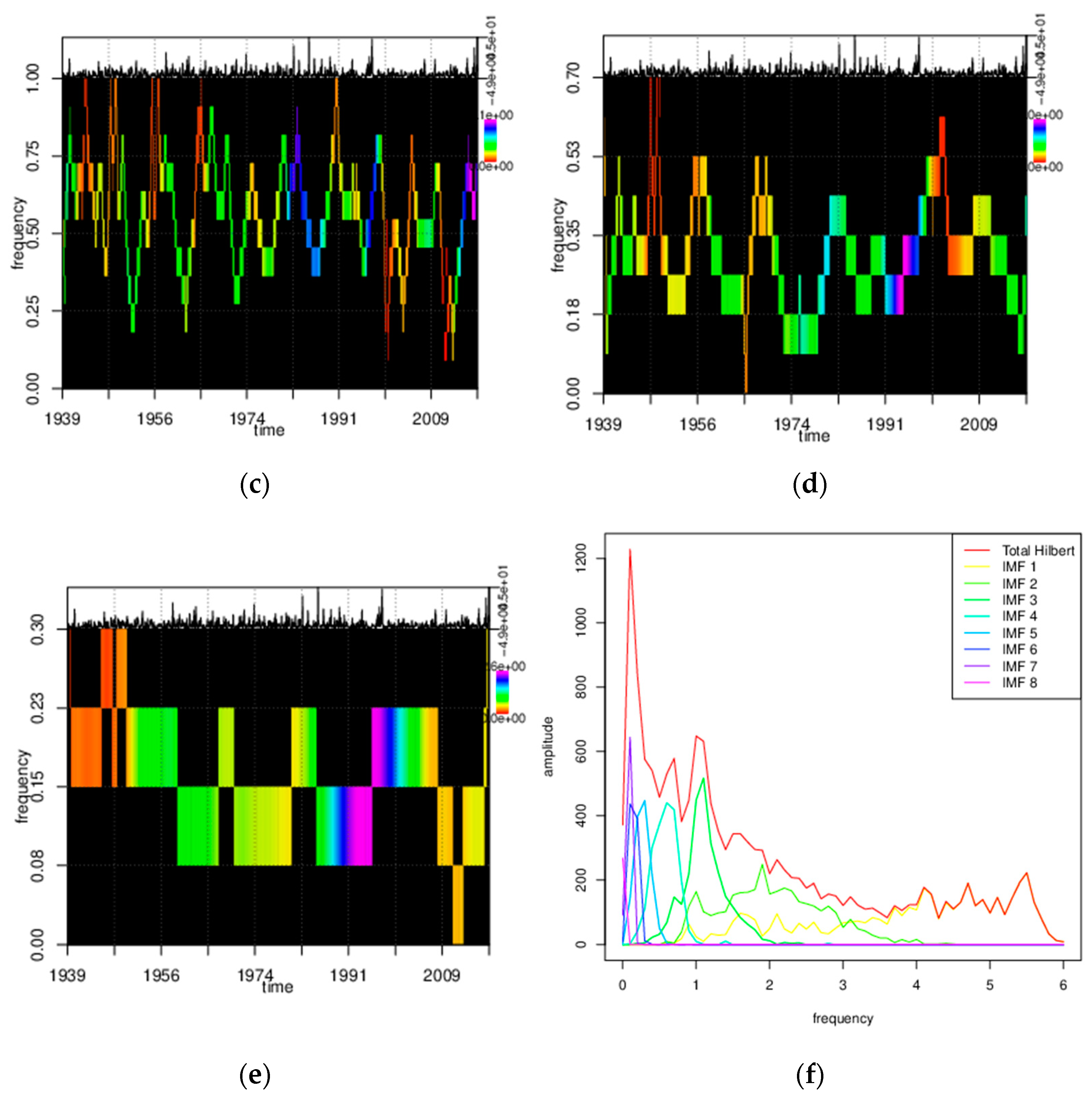


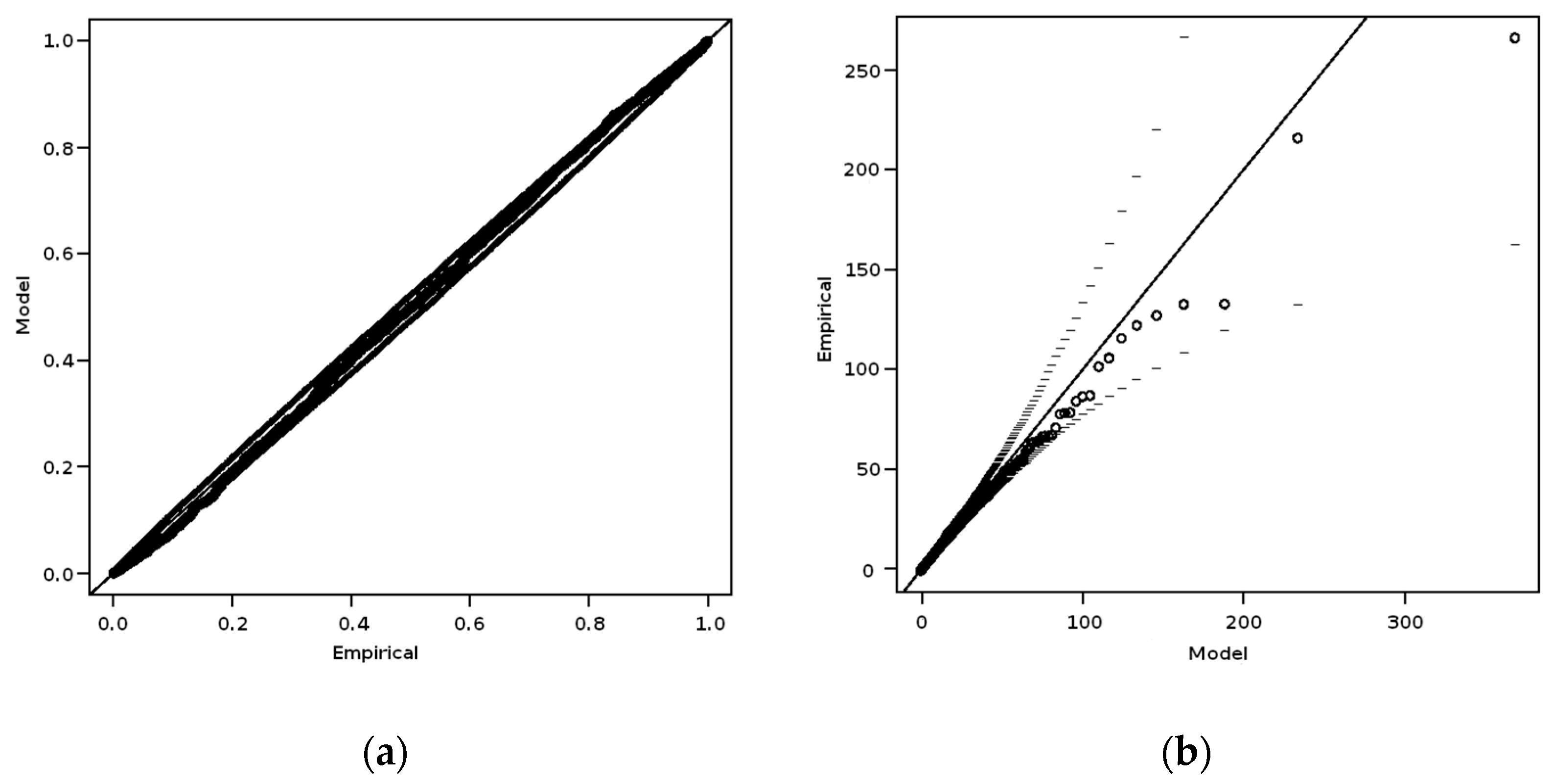

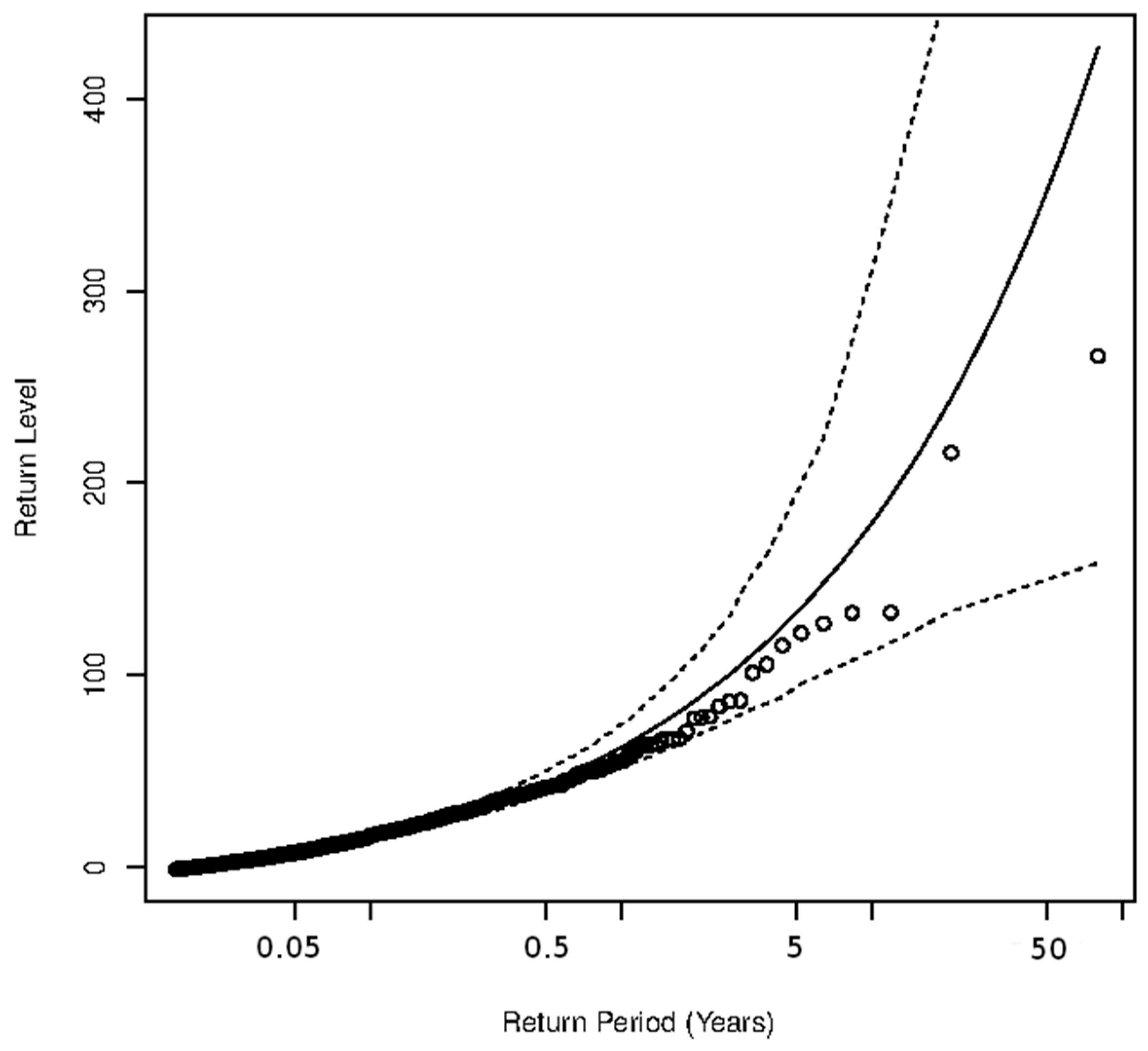

| Date | Rainfall (L/24 h) | Effective Rainfall (L/24 h) | |
|---|---|---|---|
| Minimum | 1 September 1938 | 0 | 0.1 |
| Maximum | 31 January 2017 | 270.2 1 | 270.2 1 |
| Median | - | 0 | 1.7 |
| Average | - | 0.8922 | 5.4694 |
| Std. Dev. | - | 4.9678 | 11.3687 |
| NCD | |
|---|---|
| Maximum | 10 1 |
| Average | 1.7115804807 |
| Std. Dev. | 1.0895069514 |
| Estimate | t Value Pr(>|t|) 1 | |
|---|---|---|
| 34.826622 | 0.00747 ** | |
| −0.014934 | 0.02245 * |
| Estimator | Scale Std. Error | Shape Std. Error | ||
|---|---|---|---|---|
| MLE | 6.2516 | 0.3927 | 0.26519 | 0.03597 |
| PWMU | 6.3134 | 0.3709 | 0.26627 | 0.03934 |
| PWMB | 6.3184 | 0.3704 | 0.26631 | 0.03928 |
| Pickands | 5.9410 | 0.5127 | – | – |
| MDPD | 6.0974 | 0.4245 | – | – |
| MPLE | 6.2677 | 0.3892 | 0.26486 | 0.03553 |
| Estimator | ||||
|---|---|---|---|---|
| MLE | 5.731855 | 6.771363 | 0.3221609 | 0.4631557 |
| PWMU | 5.791555 | 6.835303 | 0.2938097 | 0.4480322 |
| PWMB | 5.796462 | 6.840393 | 0.2934333 | 0.4474126 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Egea Pérez, R.; Cortés-Molina, M.; Navarro-González, F.J. Analysis of Rainfall Time Series with Application to Calculation of Return Periods. Sustainability 2021, 13, 8051. https://doi.org/10.3390/su13148051
Egea Pérez R, Cortés-Molina M, Navarro-González FJ. Analysis of Rainfall Time Series with Application to Calculation of Return Periods. Sustainability. 2021; 13(14):8051. https://doi.org/10.3390/su13148051
Chicago/Turabian StyleEgea Pérez, Ramón, Mónica Cortés-Molina, and Francisco J. Navarro-González. 2021. "Analysis of Rainfall Time Series with Application to Calculation of Return Periods" Sustainability 13, no. 14: 8051. https://doi.org/10.3390/su13148051
APA StyleEgea Pérez, R., Cortés-Molina, M., & Navarro-González, F. J. (2021). Analysis of Rainfall Time Series with Application to Calculation of Return Periods. Sustainability, 13(14), 8051. https://doi.org/10.3390/su13148051







