3D Numerical Analysis of the Natural Ventilation Behavior in a Colombian Greenhouse Established in Warm Climate Conditions
Abstract
1. Introduction
2. Materials and Methods
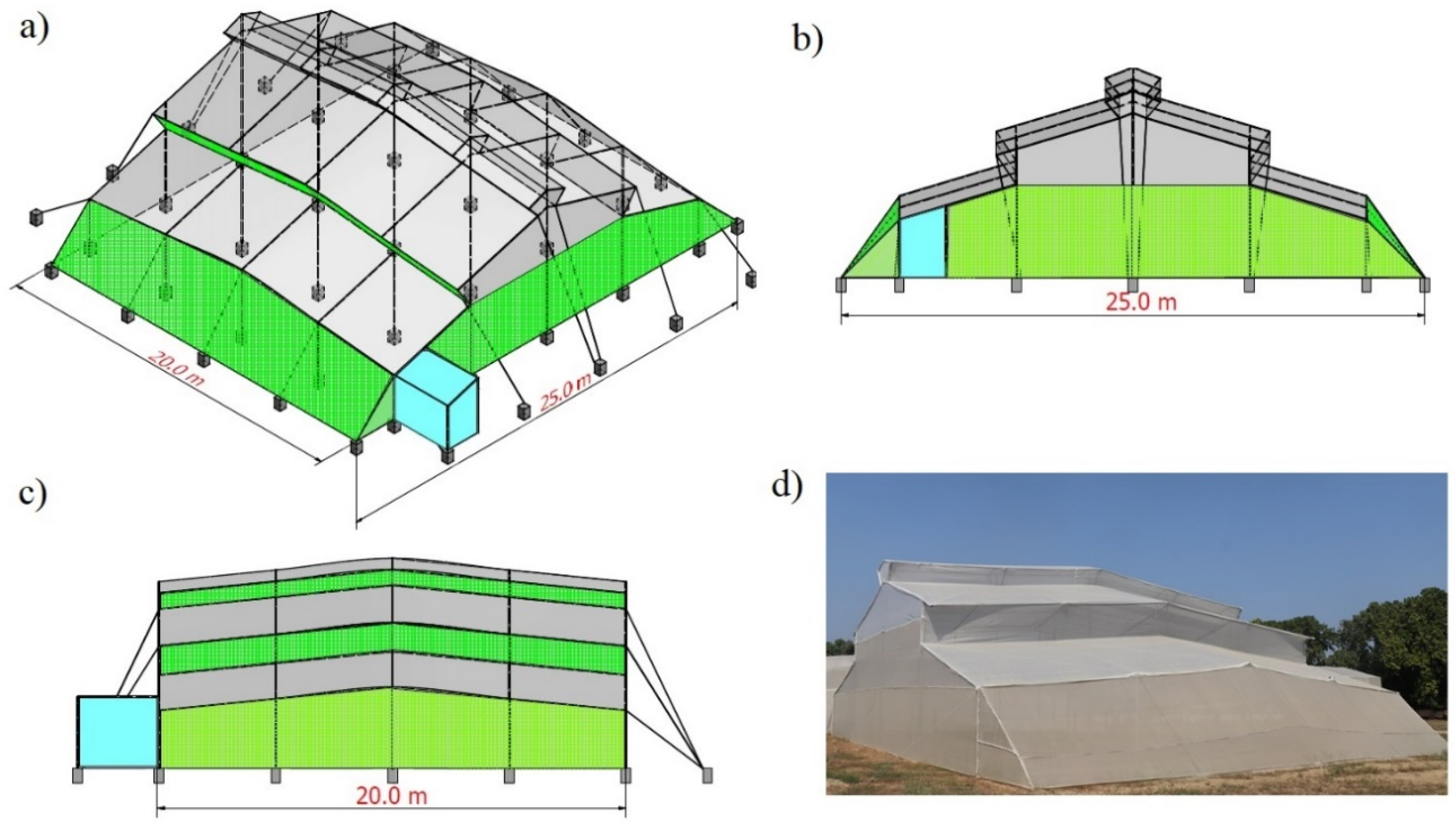
2.1. Description of the Greenhouse
2.2. Numerical Model and Governing Equations
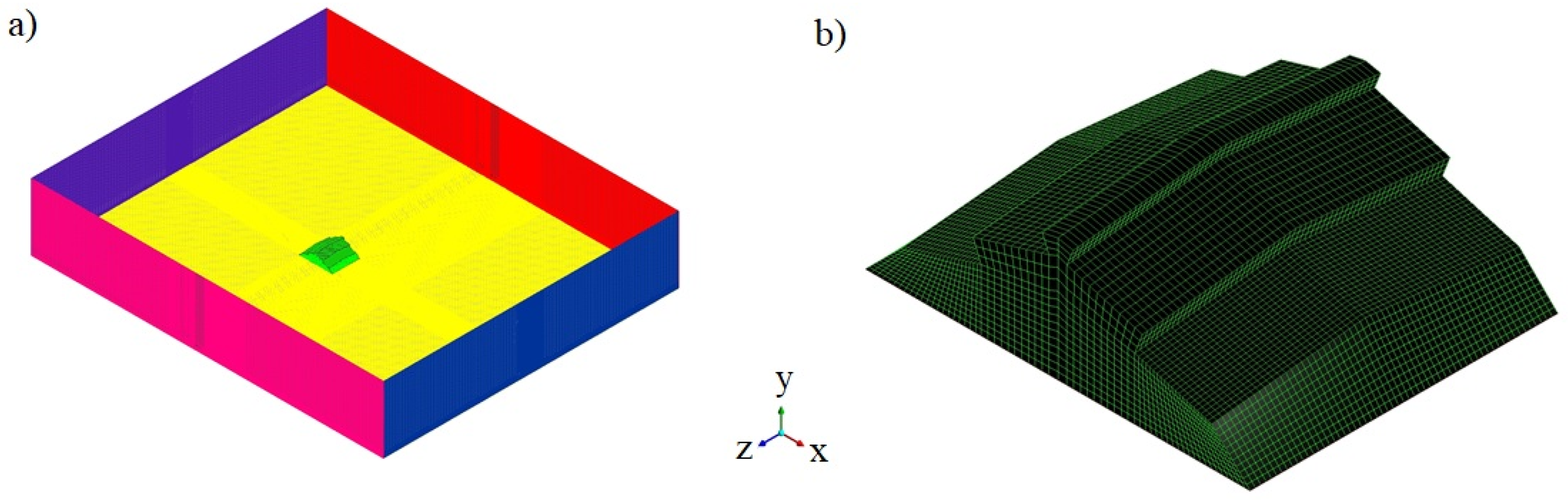
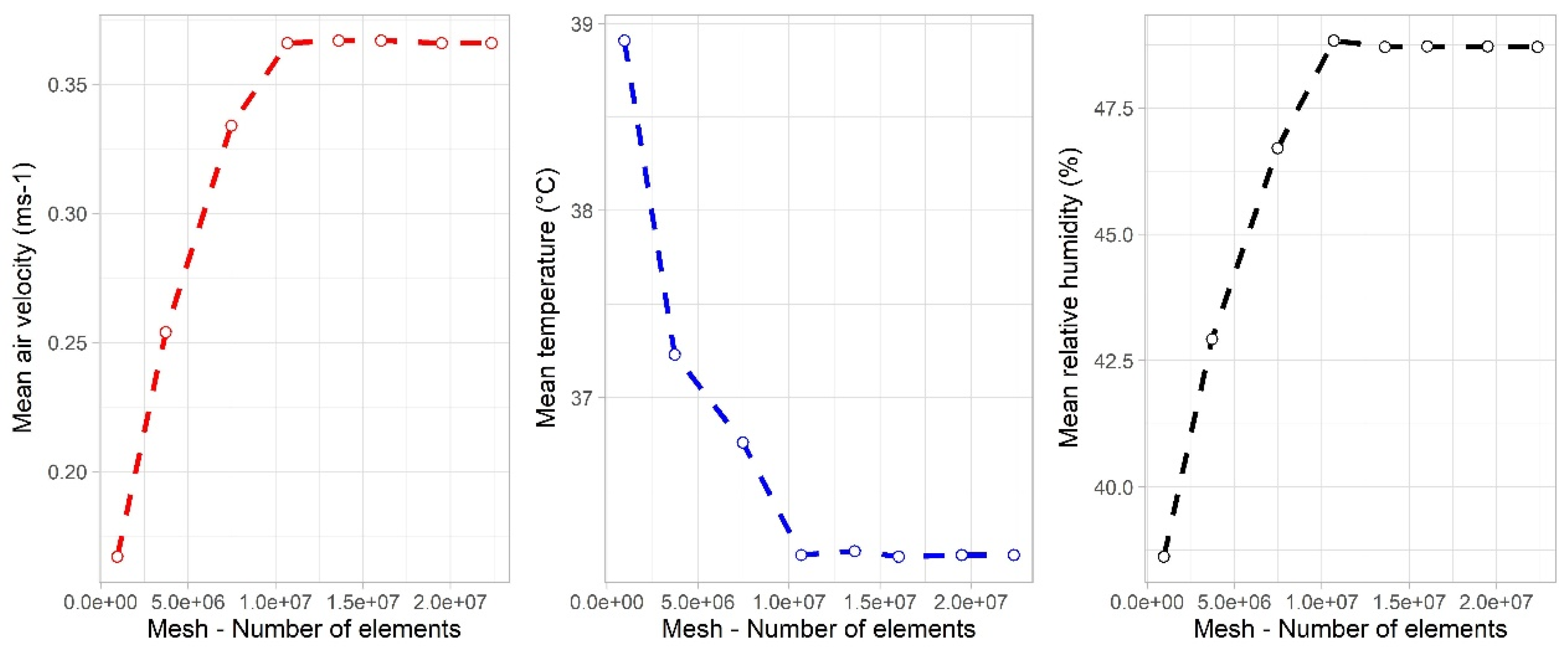
2.3. Computational Domain and Meshing Process
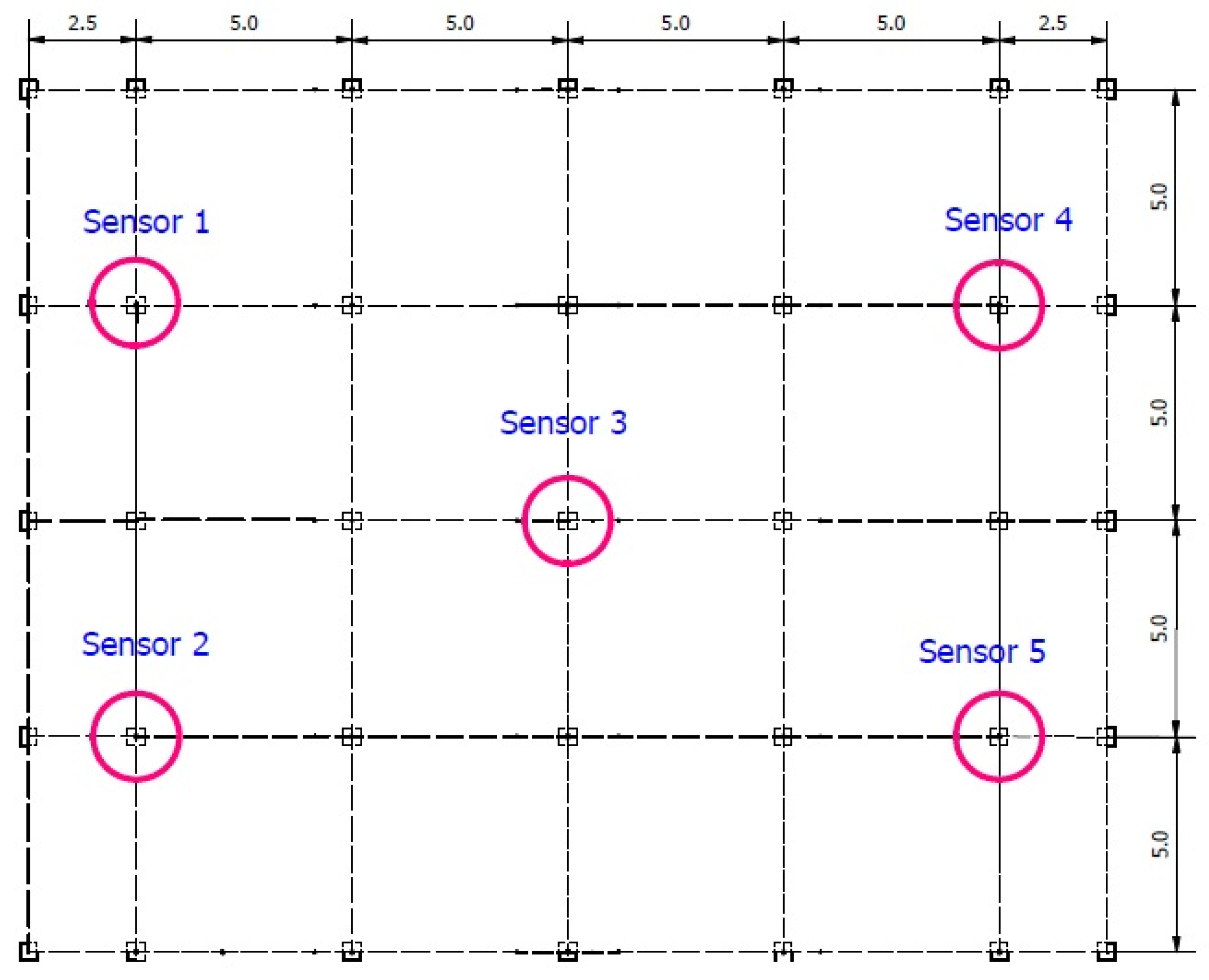
2.4. Validation of the CFD Model and Simulated Scenarios
3. Results
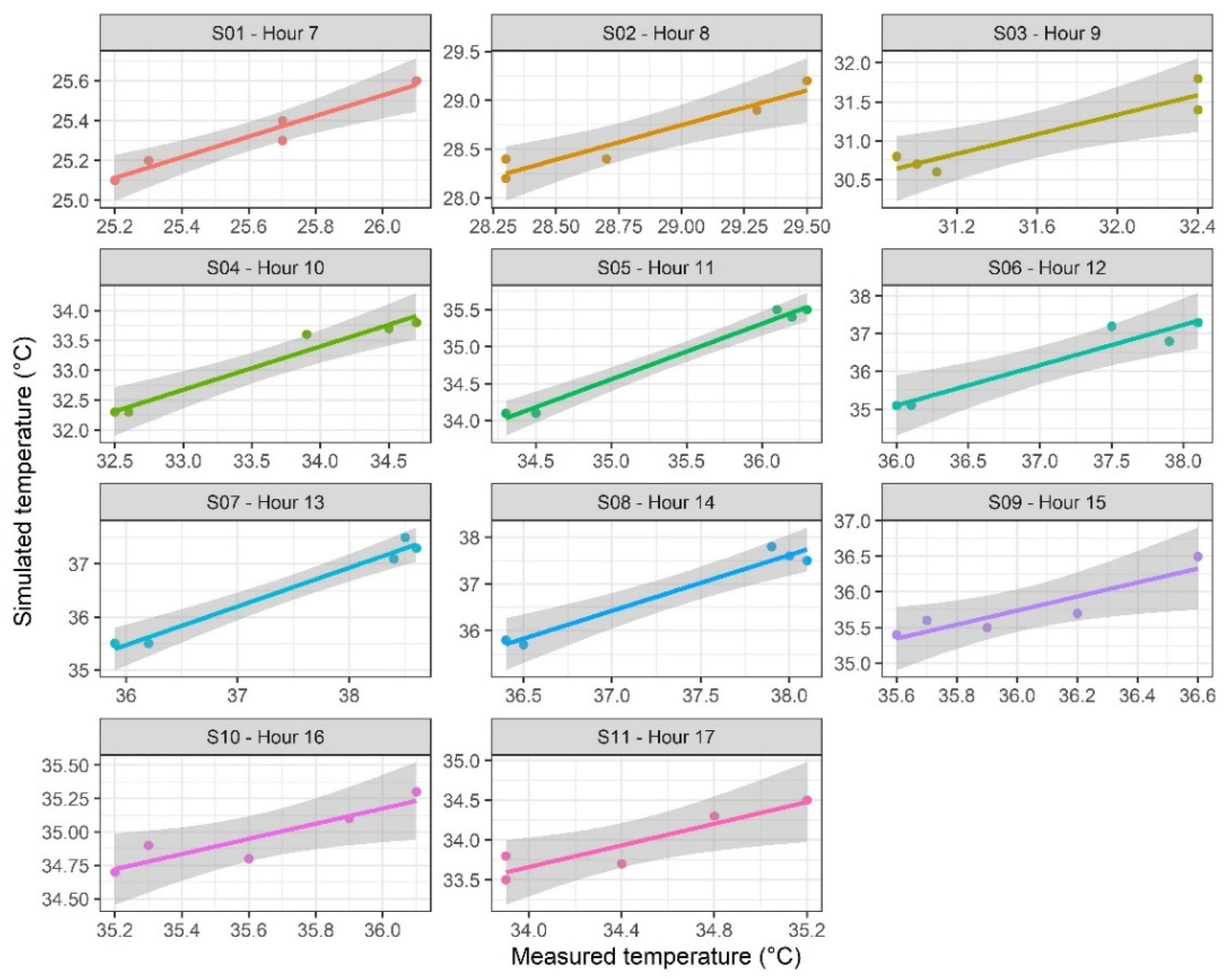
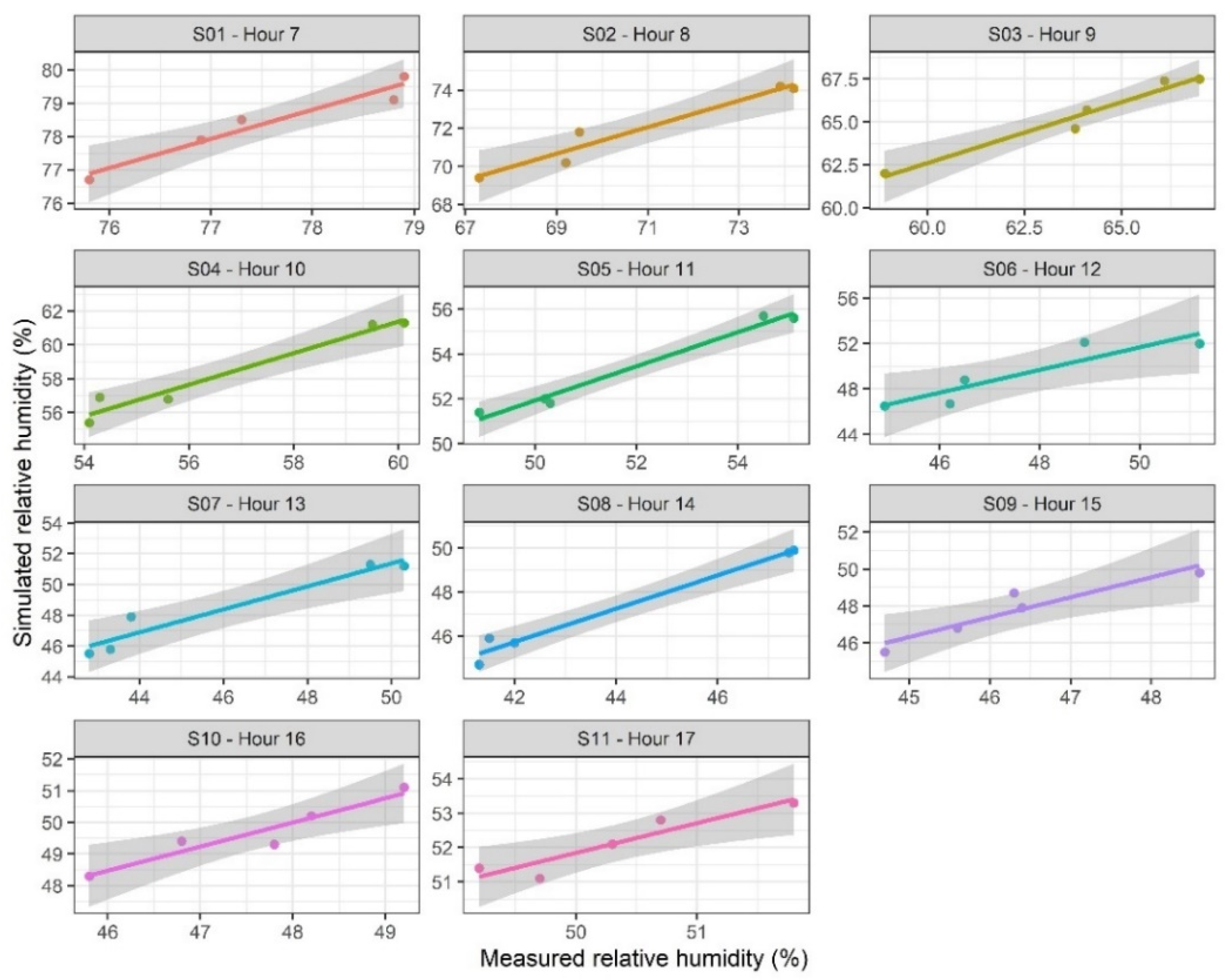
3.1. Data and Model Validation
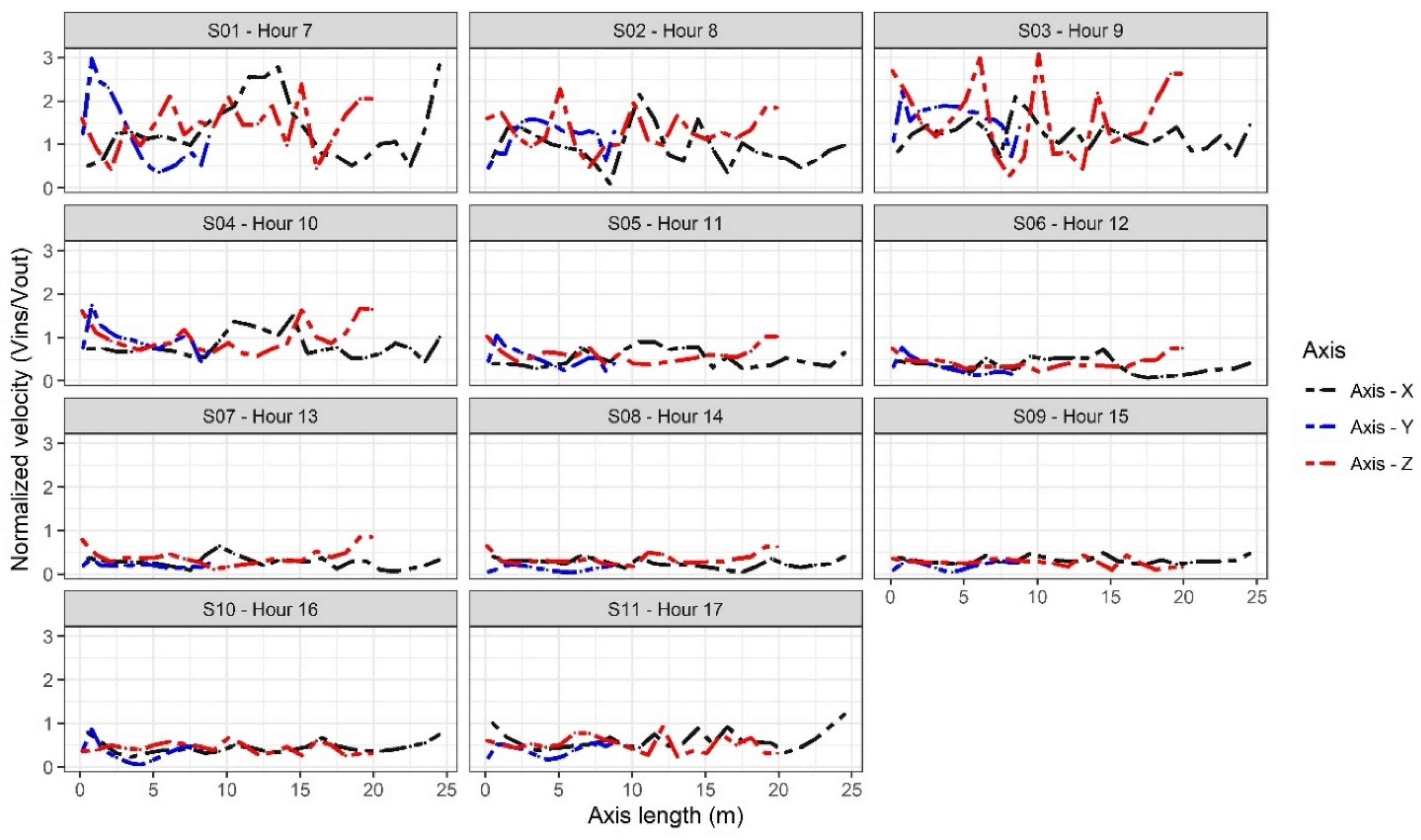
3.2. Airflow Pattern Simulations
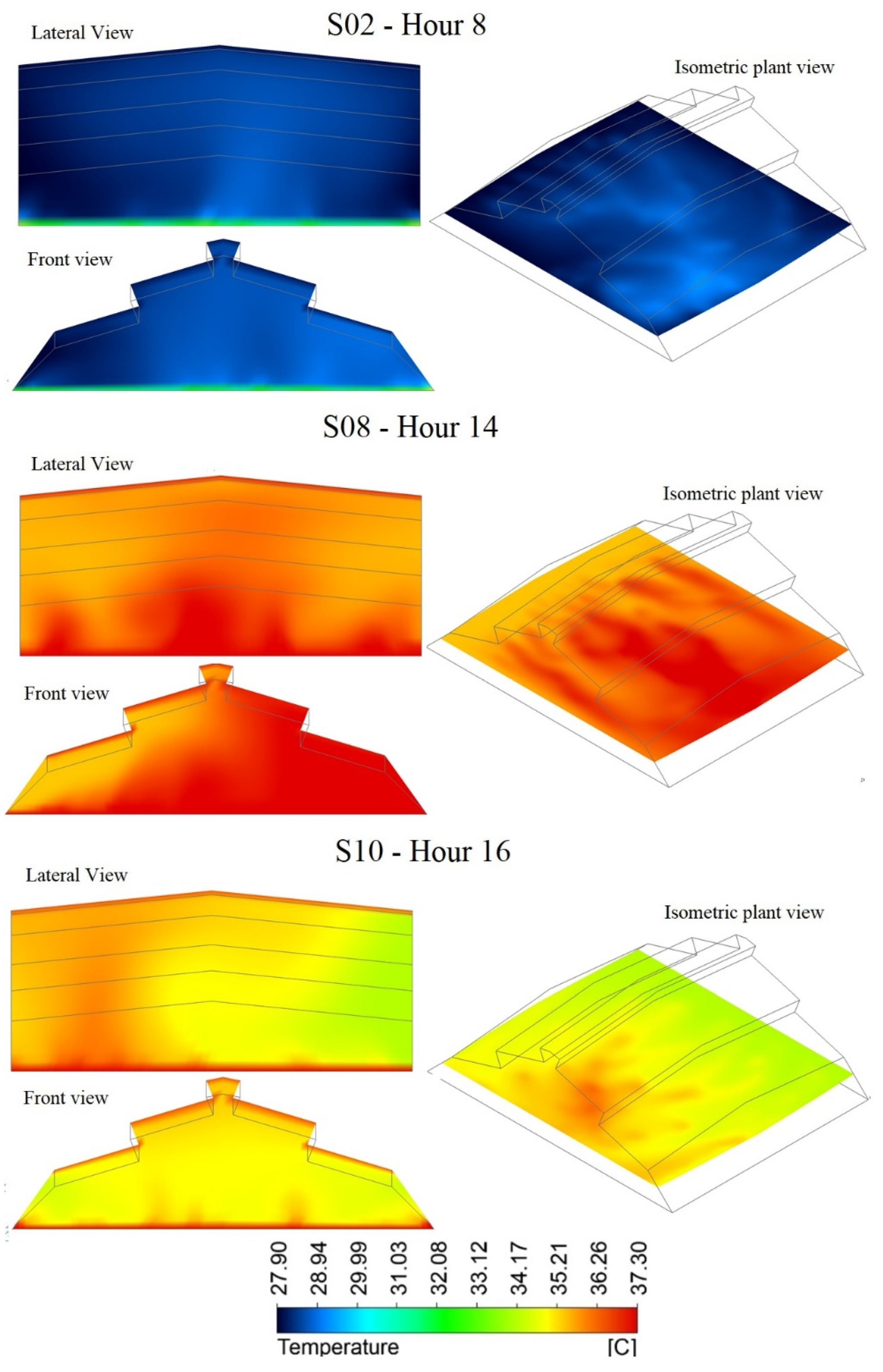
3.3. Spatial Temperature Distribution
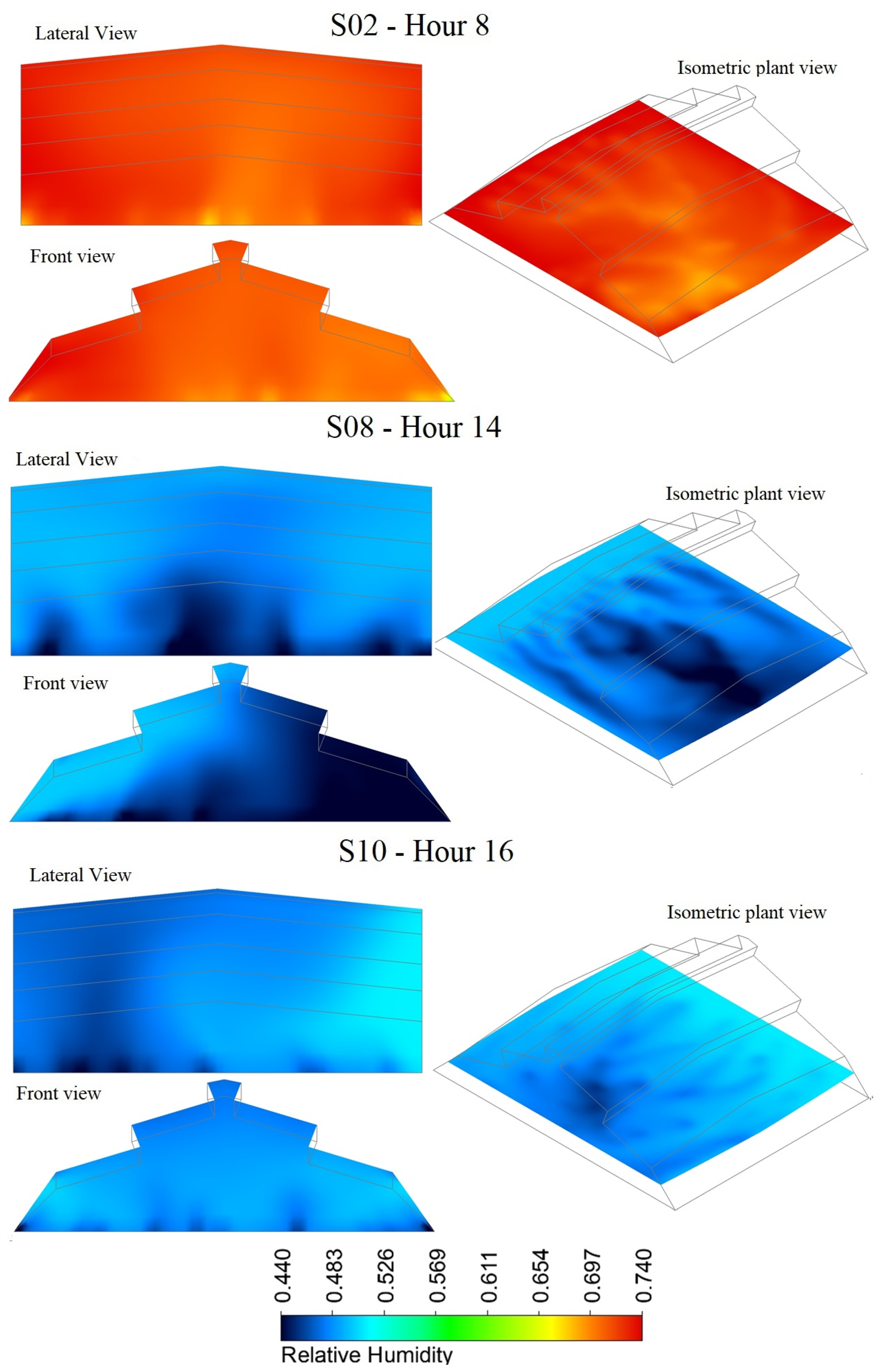
3.4. Spatial Distribution of Relative Humidity
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- United Nations. World Population Prospects The 2017 Revision Key Findings and Advance Tables ESA/P/WP/248, 2017. Available online: https://population.un.org/wpp/Publications/Files/WPP2017_KeyFindings.pdf (accessed on 3 January 2020).
- Sarkodie, S.A.; Strezov, V.; Weldekidan, H.; Asamoah, E.F.; Owusu, P.A.; Doyi, I.N.Y. Environmental sustainability assessment using dynamic Autoregressive-Distributed Lag simulations—Nexus between greenhouse gas emissions, biomass energy, food and economic growth. Sci. Total. Environ. 2019, 668, 318–332. [Google Scholar] [CrossRef] [PubMed]
- Armanda, D.T.; Guinée, J.B.; Tukker, A. The second green revolution: Innovative urban agriculture’s contribution to food security and sustainability—A review. Glob. Food Sec. 2019, 22, 13–24. [Google Scholar] [CrossRef]
- Sarkar, D.; Kar, S.K.; Chattopadhyay, A.; Rakshit, A.; Tripathi, V.K.; Dubey, P.K.; Abhilash, P.C. Low input sustainable agriculture: A viable climate-smart option for boosting food production in a warming world. Ecol. Indic. 2020, 115, 106412. [Google Scholar] [CrossRef]
- Hemming, S.; de Zwart, F.; Elings, A.; Righini, I.; Petropoulou, A. Remote control of greenhouse vegetable production with artificial intelligence—Greenhouse climate, irrigation, and crop production. Sensors 2019, 19, 1807. [Google Scholar] [CrossRef]
- Jha, S.; Kaechele, H.; Lana, M.; Amjath-Babu, T.S.; Sieber, S. Exploring Farmers’ Perceptions of Agricultural Technologies: A Case Study from Tanzania. Sustainability 2020, 12, 998. [Google Scholar] [CrossRef]
- Simon, X.; Montero, M.; Romero, Ó. Advancing food security through agroecological technologies: The implementation of the biointensive method in the dry corridor of Nicaragua. Sustainability 2020, 12, 844. [Google Scholar] [CrossRef]
- Bowles, T.M.; Mooshammer, M.; Socolar, Y.; Calderón, F.; Cavigelli, M.A.; Culman, S.W.; Harkcom, W.S. Long-Term Evidence Shows that Crop-Rotation Diversification Increases Agricultural Resilience to Adverse Growing Conditions in North America. One Earth 2020, 2, 284–293. [Google Scholar] [CrossRef]
- Liu, C.H.; Ay, C.; Tsai, C.Y.; Lee, M.T. The application of passive radiative cooling in greenhouses. Sustainability 2019, 11, 6703. [Google Scholar] [CrossRef]
- Akrami, M.; Salah, A.H.; Javadi, A.A.; Fath, H.E.; Hassanein, M.J.; Farmani, R.; Negm, A. Towards a Sustainable Greenhouse: Review of Trends and Emerging Practices in Analysing Greenhouse Ventilation Requirements to Sustain Maximum Agricultural Yield. Sustainability 2020, 12, 2794. [Google Scholar] [CrossRef]
- Martin, M.; Molin, E. Environmental assessment of an urban vertical hydroponic farming system in Sweden. Sustainability 2019, 11, 4124. [Google Scholar] [CrossRef]
- Maraveas, C. Environmental Sustainability of Greenhouse Covering Materials. Sustainability 2019, 11, 6129. [Google Scholar] [CrossRef]
- Eyhorn, F.; Muller, A.; Reganold, J.P.; Frison, E.; Herren, H.R.; Luttikholt, L.; Smith, P. Sustainability in global agriculture driven by organic farming. Nat. Sustain. 2019, 2, 253–255. [Google Scholar] [CrossRef]
- Reyes-Rosas, A.; Molina-Aiz, F.D.; Valera, D.L.; López, A.; Khamkure, S. Development of a single energy balance model for prediction of temperatures inside a naturally ventilated greenhouse with polypropylene soil mulch. Comput. Electron. Agric. 2017, 142, 9–28. [Google Scholar] [CrossRef]
- Yang, N.W.; Zang, L.S.; Wang, S.; Guo, J.Y.; Xu, H.X.; Zhang, F.; Wan, F.H. Biological pest management by predators and parasitoids in the greenhouse vegetables in China. Biol. Control. 2014, 68, 92–102. [Google Scholar] [CrossRef]
- Reyes-Rosas, A.; Molina-Aiz, F.D.; López, A.; Valera, D.L. A simple model to predict air temperature inside a Mediterranean greenhouse. Acta Hortic. 2017, 1182, 95–104. [Google Scholar] [CrossRef]
- Chu, C.R.; Lan, T.W. Effectiveness of ridge vent to wind-driven natural ventilation in monoslope multi-span greenhouses. Biosyst. Eng. 2019, 186, 279–292. [Google Scholar] [CrossRef]
- Graamans, L.; Baeza, E.; Van Den Dobbelsteen, A.; Tsafaras, I.; Stanghellini, C. Plant factories versus greenhouses: Comparison of resource use efficiency. Agric. Syst. 2018, 160, 31–43. [Google Scholar] [CrossRef]
- Espinoza, K.; López, A.; Valera, D.L.; Molina-Aiz, F.D.; Torres, J.A.; Pena, A. Effects of ventilator configuration on the flow pattern of a naturally-ventilated three-span Mediterranean greenhouse. Biosyst. Eng. 2017, 164, 13–30. [Google Scholar] [CrossRef]
- Reynafarje, X.; Villagrán, E.A.; Bojacá, C.R.; Gil, R.; Schrevens, E. Simulation and validation of the airflow inside a naturally ventilated greenhouse designed for tropical conditions. Acta Hortic. 2020, 1271, 55–62. [Google Scholar] [CrossRef]
- Villagrán, E.A.; Bojacá, C.R. Effects of surrounding objects on the thermal performance of passively ventilated greenhouses. J. Agric. Eng. 2019, 50, 20–27. [Google Scholar] [CrossRef]
- Bournet, P.E.; Khaoua, S.O.; Boulard, T.; Migeon, C.; Chassériaux, G. Effect of Roof and Side Opening Combinations on the Ventilation of a Greenhouse Using Computer Simulation. Trans. ASABE 2007, 50, 201–212. [Google Scholar] [CrossRef]
- Chu, C.R.; Lan, T.W.; Tasi, R.K.; Wu, T.R.; Yang, C.K. Wind-driven natural ventilation of greenhouses with vegetation. Biosyst. Eng. 2017, 164, 221–234. [Google Scholar] [CrossRef]
- Bournet, P.E.; Boulard, T. Effect of ventilator configuration on the distributed climate of greenhouses: A review of experimental and CFD studies. Comput. Electron. Agric. 2010, 74, 195–217. [Google Scholar] [CrossRef]
- Baxevanou, C.; Fidaros, D.; Bartzanas, T.; Kittas, C. Yearly numerical evaluation of greenhouse cover materials. Comput. Electron. Agric. 2017, 149, 54–70. [Google Scholar] [CrossRef]
- Molina-Aiz, F.D.; Fatnassi, H.; Boulard, T.; Roy, J.C.; Valera, D.L. Comparison of finite element and finite volume methods for simulation of natural ventilation in greenhouses. Comput. Electron. Agric. 2010, 72, 69–86. [Google Scholar] [CrossRef]
- Perén, J.I.; van Hooff, T.; Leite, B.C.C.; Blocken, B. CFD simulation of wind-driven upward cross ventilation and its enhancement in long buildings: Impact of single-span versus double-span leeward sawtooth roof and opening ratio. Build. Environ. 2016, 96, 142–156. [Google Scholar] [CrossRef]
- Baeza, E.J.; Pérez-Parra, J.J.; Montero, J.I.; Bailey, B.J.; López, J.C.; Gázquez, J.C. Analysis of the role of sidewall vents on buoyancy-driven natural ventilation in parral-type greenhouses with and without insect screens using computational fluid dynamics. Biosyst. Eng. 2009, 104, 86–96. [Google Scholar] [CrossRef]
- Villagrán, E.A.; Romero, E.J.B.; Bojacá, C.R. Transient CFD analysis of the natural ventilation of three types of greenhouses used for agricultural production in a tropical mountain climate. Biosyst. Eng. 2019, 188, 288–304. [Google Scholar] [CrossRef]
- Vanthoor, B.H.E.; Stanghellini, C.; Van Henten, E.J.; De Visser, P.H.B. A methodology for model-based greenhouse design: Part 1, a greenhouse climate model for a broad range of designs and climates. Biosyst. Eng. 2011, 110, 363–377. [Google Scholar] [CrossRef]
- Righini, I.; Vanthoor, B.; Verheul, M.J.; Naseer, M.; Maessen, H.; Persson, T.; Stanghellini, C. A greenhouse climate-yield model focussing on additional light, heat harvesting and its validation. Biosyst. Eng. 2020, 194, 1–15. [Google Scholar] [CrossRef]
- Jung, D.H.; Kim, H.S.; Jhin, C.; Kim, H.J.; Park, S.H. Time-serial analysis of deep neural network models for prediction of climatic conditions inside a greenhouse. Comput. Electron. Agric. 2020, 173, 105402. [Google Scholar] [CrossRef]
- Choab, N.; Allouhi, A.; El Maakoul, A.; Kousksou, T.; Saadeddine, S.; Jamil, A. Review on greenhouse microclimate and application: Design parameters, thermal modeling and simulation, climate controlling technologies. Sol. Energy. 2019, 191, 109–137. [Google Scholar] [CrossRef]
- Valera-Martínez, D.L.; Belmonte-Ureña, L.J.; Molina-Aiz, F.D.; López-Martinez, A. Greenhouse agriculture in Almeria. In A Comprehensive Techno-Economic Analysis; Cajamar, Caja Rural: Almeria, Spain, 2016; p. 409. [Google Scholar]
- Pakari, A.; Ghani, S. Airflow assessment in a naturally ventilated greenhouse equipped with wind towers: Numerical simulation and wind tunnel experiments. Energy Build. 2019, 199, 1–11. [Google Scholar] [CrossRef]
- Tong, G.; Christopher, D.M.; Zhang, G. New insights on span selection for Chinese solar greenhouses using CFD analyses. Comput. Electron. Agric. 2018, 149, 3–15. [Google Scholar] [CrossRef]
- Flores-Velázquez, J.; Mejía-Saenz, E.; Montero-Camacho, J.I.; Rojano, A. Análisis numérico del clima interior en un invernadero de tres naves con ventilación mecánica. Agrociencia 2011, 45, 545–560. [Google Scholar]
- Molina-Aiz, F.D.; Valera, D.L.; Pena, A.A.; Alvarez, A.J.; Gil, J.A. Analysis of the effect of rollup vent arrangement and wind speed on Almería-type greenhouse ventilation performance using computational fluid dynamics. Acta Hortic. 2006, 719, 173–180. [Google Scholar] [CrossRef]
- Baeza, E.J.; Pérez-Parra, J.J.; Lopez, J.C.; Montero, J.I. CFD study of the natural ventilation performance of a parral type greenhouse with different numbers of spans and roof vent configurations. Acta Hortic. 2006, 719, 333–340. [Google Scholar] [CrossRef]
- Benni, S.; Tassinari, P.; Bonora, F.; Barbaresi, A.; Torreggiani, D. Efficacy of greenhouse natural ventilation: Environmental monitoring and CFD simulations of a study case. Energy Build. 2016, 125, 276–286. [Google Scholar] [CrossRef]
- Li, K.; Xue, W.; Mao, H.; Chen, X.; Jiang, H.; Tan, G. Optimizing the 3D Distributed Climate inside Greenhouses Using Multi-Objective Optimization Algorithms and Computer Fluid Dynamics. Energies 2019, 12, 2873. [Google Scholar] [CrossRef]
- He, X.; Wang, J.; Guo, S.; Zhang, J.; Wei, B.; Sun, J.; Shu, S. Ventilation optimization of solar greenhouse with removable back walls based on CFD. Comput. Electron. Agric. 2017, 149, 16–25. [Google Scholar] [CrossRef]
- Fatnassi, H.; Boulard, T.; Poncet, C.; Chave, M. Optimisation of greenhouse insect screening with computational fluid dynamics. Biosyst. Eng. 2006, 93, 301–312. [Google Scholar] [CrossRef]
- Khaoua, S.O.; Bournet, P.E.; Migeon, C.; Boulard, T.; Chassériaux, G. Analysis of Greenhouse Ventilation Efficiency based on Computational Fluid Dynamics. Biosyst. Eng. 2006, 95, 83–98. [Google Scholar] [CrossRef]
- Villagrán, E.A.; Bojacá, C.R. CFD simulation of the increase of the roof ventilation area in a traditional Colombian greenhouse: Effect on air flow patterns and thermal behavior. Int. J. Heat Technol. 2019, 37, 881–892. [Google Scholar] [CrossRef]
- Mesmoudi, K.; Meguallati, K.H.; Bournet, P.E. Effect of the greenhouse design on the thermal behavior and microclimate distribution in greenhouses installed under semi-arid climate. Heat Transf. Asian Res. 2017, 46, 1294–1311. [Google Scholar] [CrossRef]
- Piscia, D.; Muñoz, P.; Panadès, C.; Montero, J.I. A method of coupling CFD and energy balance simulations to study humidity control in unheated greenhouses. Comput. Electron. Agric. 2015, 115, 129–141. [Google Scholar] [CrossRef]
- ANSYS-Fluent User’s Guide. ANSYS FLUENT Theory Guide, Release 18.2. 2013. Available online: https://www.afs.enea.it/project/neptunius/docs/fluent/html/th/main_pre.htm (accessed on 12 January 2020).
- Wang, X.W.; Luo, J.Y.; Li, X.P. CFD based study of heterogeneous microclimate in a typical Chinese greenhouse in central China. J. Integr. Agric. 2013, 12, 914–923. [Google Scholar] [CrossRef]
- Aich, W.; Kolsi, L.; Borjini, M.N.; Aissia, H.B.; Öztop, H.F.; Abu-Hamdeh, N. Three dimensional CFD analysis of Buoyancy-driven natural ventilation and entropy generation in a prismatic greenhouse. Therm. Sci. 2018, 22, 73–85. [Google Scholar] [CrossRef]
- Flores-Velazquez, F.; Guerrero, F.V.; Lopez, I.L.; Montero, J.I.; Piscia, D. 3-Dimensional thermal analysis of a screenhouse with plane and multispan roof by using computational fluid dynamics (CFD). Acta Hortic. 2013, 1008, 151–158. [Google Scholar] [CrossRef]
- Valera, D.L.; Álvarez, A.J.; Molina, F.D. Aerodynamic analysis of several insect-proof screens used in greenhouses. Span. J. Agric. Res. 2006, 4, 273–279. [Google Scholar] [CrossRef]
- Flores-Velazquez, J.; Ojeda, W.; Villarreal-Guerrero, F.; Rojano, A. Effect of crops on natural ventilation in a screenhouse evaluated by CFD simulations. Acta Hortic. 2017, 1170, 95–101. [Google Scholar] [CrossRef]
- Akrami, M.; Javadi, A.A.; Hassanein, M.J.; Farmani, R.; Dibaj, M.; Tabor, G.R.; Negm, A. Study of the effects of vent configuration on mono-span greenhouse ventilation using computational fluid dynamics. Sustainability 2020, 12, 986. [Google Scholar] [CrossRef]
- Villagrán, E.A.; Bojacá, C.R. Study of natural ventilation in a Gothic multi-tunnel greenhouse designed to produce rose (Rosa spp.) in the high-Andean tropic. Ornam. Hortic. 2019, 25, 133–143. [Google Scholar] [CrossRef]
- Wu, T.; Lei, C. CFD simulation of the thermal performance of an opaque water wall system for Australian climate. Sol. Energy 2016, 133, 141–154. [Google Scholar] [CrossRef]
- Baxevanou, C.; Bartzanas, T.; Fidaros, D.; Kittas, C. Solar radiation distribution in a tunnel greenhouse. Acta Hortic. 2008, 801, 855–862. [Google Scholar] [CrossRef]
- Senhaji, A.; Mouqallid, M.; Majdoubi, H. CFD Assisted Study of Multi-Chapels Greenhouse Vents Openings Effect on Inside Airflow Circulation and Microclimate Patterns. Open J. Fluid Dyn. 2019, 9, 119–139. [Google Scholar] [CrossRef]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Perén, J.I.; Van Hooff, T.; Ramponi, R.; Blocken, B.; Leite, B.C.C. Impact of roof geometry of an isolated leeward sawtooth roof building on cross-ventilation: Straight, concave, hybrid or convex? J. Wind Eng. Ind. Aerodyn. 2015, 145, 102–114. [Google Scholar] [CrossRef]
- Franke, J.; Hellsten, A.; Schlunzen, H.A.; Carissimo, B. The Best Practise Guideline for the CFD simulation of flows in the urban environment: An outcome of COST 732. In Proceedings of the The Fifth International Symposium on Computational Wind Engineering, Chapel Hill, NC, USA, 23–27 May 2010. [Google Scholar]
- Toghraie, D.; Abdollah, M.M.D.; Pourfattah, F.; Akbari, O.A.; Ruhani, B. Numerical investigation of flow and heat transfer characteristics in smooth, sinusoidal and zigzag-shaped microchannel with and without nanofluid. J. Therm. Anal. Calorim. 2018, 131, 1757–1766. [Google Scholar] [CrossRef]
- Román-Roldán, N.I.; López-Ortiz, A.; Ituna-Yudonago, J.F.; García-Valladares, O.; Pilatowsky-Figueroa, I. Computational fluid dynamics analysis of heat transfer in a greenhouse solar dryer “chapel-type” coupled to an air solar heating system. Energy Sci. Eng. 2019, 7, 1123–1139. [Google Scholar] [CrossRef]
- Richards, P.J.; Hoxey, R.P. Unsteady flow on the sides of a 6 m cube. J. Wind Eng. Ind. Aerodyn. 2002, 90, 1855–1866. [Google Scholar] [CrossRef]
- King, M.F.; Gough, H.L.; Halios, C.; Barlow, J.F.; Robertson, A.; Hoxey, R.; Noakes, C.J. Investigating the influence of neighbouring structures on natural ventilation potential of a full-scale cubical building using time-dependent CFD. J. Wind Eng. Ind. Aerodyn. 2017, 169, 265–279. [Google Scholar] [CrossRef]
- Sase, S. Air movement and climate uniformity in ventilated greenhouses. Acta Hortic. 2006, 719, 313–323. [Google Scholar] [CrossRef]
- Teitel, M.; Montero, J.I.; Baeza, E.J. Greenhouse design: Concepts and trends. Acta Hortic. 2012, 952, 605–620. [Google Scholar] [CrossRef]
- Katsoulas, N.; Bartzanas, T.; Boulard, T.; Mermier, M.; Kittas, C. Effect of Vent Openings and Insect Screens on Greenhouse Ventilation. Biosyst. Eng. 2006, 93, 427–436. [Google Scholar] [CrossRef]
- Semple, L.; Carriveau, R.; Ting, D.S.K. A techno-economic analysis of seasonal thermal energy storage for greenhouse applications. Energy Build. 2017, 154, 175–187. [Google Scholar] [CrossRef]
- Villagrán Munar, E.A.; Bojacá Aldana, C.R. Simulación del microclima en un invernadero usado para la producción de rosas bajo condiciones de clima intertropical. Chil. J. Agric. Anim. Sci. 2019, 35, 137–150. [Google Scholar] [CrossRef]
- Villagran, E.; Bojacá, C. Analysis of the microclimatic behavior of a greenhouse used to produce carnation (Dianthus caryophyllus L.). Ornam. Hortic. 2020, 26, 109–204. [Google Scholar] [CrossRef]
- Taki, M.; Ajabshirchi, Y.; Ranjbar, S.F.; Rohani, A.; Matloobi, M. Modeling and experimental validation of heat transfer and energy consumption in an innovative greenhouse structure. Inf. Process. Agric. 2016, 3, 157–174. [Google Scholar] [CrossRef]
- Zorzeto, T.Q.; Leal, P.A.M.; Nunes, E.F.; de Araújo, H.F. Homogeneity of temperature and relative humidity of air in greenhouse. Int. Proc. Chem. Biol. Environ. Eng. (IPCBEE) 2014, 79, 25–29. [Google Scholar] [CrossRef]
- Rabbi, B.; Chen, Z.H.; Sethuvenkatraman, S. Protected cropping in warm climates: A review of humidity control and cooling methods. Energies 2019, 12, 2737. [Google Scholar] [CrossRef]
- Bournet, P.E. Assessing greenhouse climate using CFD: A focus on air humidity issues. Acta Hortic. 2014, 1037, 971–986. [Google Scholar] [CrossRef]
- Teitel, M.; Liran, O.; Tanny, J.; Barak, M. Wind driven ventilation of a mono-span greenhouse with a rose crop and continuous screened side vents and its effect on flow patterns and microclimate. Biosyst. Eng. 2008, 101, 111–122. [Google Scholar] [CrossRef]
- Villagran Munar, E.A.; Bojacá Aldana, C.R.; Rojas Bahamon, N.A. Determinación del comportamiento térmico de un invernadero espacial colombiano mediante dinámica de fluidos computacional. Rev. UDCA Actual. Divulg. Científica 2018, 21, 415–426. [Google Scholar] [CrossRef]
- Saberian, A.; Sajadiye, S.M. The effect of dynamic solar heat load on the greenhouse microclimate using CFD simulation. Renew. Energy 2019, 138, 722–737. [Google Scholar] [CrossRef]
- Mesmoudi, K.; Meguellati, K.; Bournet, P.E. Thermal analysis of greenhouses installed under semi arid climate. Int. J. Heat Technol. 2017, 35, 474–486. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Y.; Lü, E. Numerical simulation of temperature decrease in greenhouses with summer water-sprinkling roof. Energies 2019, 12, 2435. [Google Scholar] [CrossRef]
- Baptista, F.J.; Bailey, B.J.; Meneses, J.F. Effect of nocturnal ventilation on the occurrence of Botrytis cinerea in Mediterranean unheated tomato greenhouses. Crop Prot. 2012, 32, 144–149. [Google Scholar] [CrossRef]
- Rojano, F.; Flores-Velázquez, J.; Villarreal-Guerrero, F.; Rojano, A. Dynamics of climatic conditions in a greenhouse: Two locations in Mexico. Acta Hortic. 2014, 1037, 955–962. [Google Scholar] [CrossRef]
- Villagran, E.A.; Noreña, J.E. Microclimatic behavior of a screen house proposed for horticultural production in low-altitude tropical climate conditions. Comununicata. Sci. 2020, 11, e3350. [Google Scholar] [CrossRef]
- Villagran, E.; Ramirez, R.; Rodriguez, A.; Pacheco, R.L.; Jaramillo, J. Simulation of the thermal and aerodynamic behavior of an established screenhouse under warm tropical climate conditions: A numerical approach. Int. J. Sustain. Dev. Plan 2020. [Google Scholar] [CrossRef]
- Molina-Aiz, F.D.; Valera, D.L. Configuration by evaluating ventilation efficiency based on computational fluid dynamics. Acta Hortic. 2009, 893, 669–677. [Google Scholar] [CrossRef]
- Molina-Aiz, F.D.; Valera, D.L.; López, A. Airflow at the openings of a naturally ventilated Almería-type greenhouse with insect-proof screens. Acta Hortic. 2011, 893, 545–552. [Google Scholar] [CrossRef]
- López, A.; Valera, D.L.; Molina-Aiz, F. Sonic anemometry to measure natural ventilation in greenhouses. Sensors 2011, 11, 9820–9838. [Google Scholar] [CrossRef] [PubMed]
- López, A.; Molina-Aiz, F.D.; Valera, D.L.; Peña, A. Wind tunnel analysis of the airflow through insect-proof screens and comparison of their effect when installed in a mediterranean greenhouse. Sensors 2016, 16, 690. [Google Scholar] [CrossRef]
- McCartney, L.; Orsat, V.; Lefsrud, M.G. An experimental study of the cooling performance and airflow patterns in a model Natural Ventilation Augmented Cooling (NVAC) greenhouse. Biosyst. Eng. 2018, 174, 173–189. [Google Scholar] [CrossRef]
- Rasheed, A.; Lee, J.W.; Kim, H.T.; Lee, H.W. Efficiency of Different Roof Vent Designs on Natural Ventilation of Single-Span Plastic Greenhouse. Prot. Hortic. Plant Fact. 2019, 28, 225–233. [Google Scholar] [CrossRef]
- Fernández, M.D.; Bonachela, S.; Orgaz, F.; Thompson, R.; López, J.C.; Granados, M.R.; Fereres, E. Measurement and estimation of plastic greenhouse reference evapotranspiration in a Mediterranean climate. Irrig. Sci. 2010, 28, 497–509. [Google Scholar] [CrossRef]
- Bartzanas, T.; Boulard, T.; Kittas, C. Numerical simulation of the airflow and temperature distribution in a tunnel greenhouse equipped with insect-proof screen in the openings. Comput. Electron. Agric. 2002, 34, 207–221. [Google Scholar] [CrossRef]
- Majdoubi, H.; Boulard, T.; Fatnassi, H.; Bouirden, L. Airflow and microclimate patterns in a one-hectare Canary type greenhouse: An experimental and CFD assisted study. Agric. Meteorol. 2009, 149, 1050–1062. [Google Scholar] [CrossRef]
| Physical and Optical Properties of the Materials | ||||
|---|---|---|---|---|
| Air | Ground | Polyethylene | Porous Screen | |
| Density (ρ, kg m−3) | 1.225 | 1.400 | 920 | 910 |
| Thermal conductivity (k, W/m °K) | 0.0242 | 1.5 | 0.33 | 0.31 |
| Specific heat (Cp, J/°K kg) | 1006.43 | 1.738 | 2600 | 1.800 |
| Coefficient of thermal expansion (1/K) | 0.0033 | |||
| Absorptivity | 0.19 | 0.9 | 0.06 | 0.2 |
| Scattering coefficient | 0 | −15 | 0 | 0 |
| Refractive index | 1 | 3 | 1.53 | 0.05 |
| Emissivity | 0.9 | 0.95 | 0.70 | 0.45 |
| Hour | Temperature (°C) | Relative Humidity (%) | Solar Radiation (W/m2) | Wind Speed (m/s) | Wind Direction |
|---|---|---|---|---|---|
| S01—Hour 7 | 24.9 | 81.4 | 46.6 | 0.2 | WNW |
| S02—Hour 8 | 27.8 | 75.6 | 177.8 | 0.2 | WNW |
| S03—Hour 9 | 30.1 | 68.6 | 376.7 | 0.2 | W |
| S04—Hour 10 | 31.9 | 62.4 | 580.8 | 0.4 | W |
| S05—Hour 11 | 33.5 | 56.6 | 713.7 | 0.7 | W |
| S06—Hour 12 | 34.8 | 53.1 | 792.1 | 1.01 | W |
| S07—Hour 13 | 35.2 | 52.2 | 802.7 | 1.22 | W |
| S08—Hour 14 | 35.4 | 50.8 | 719.4 | 1.31 | W |
| S09—Hour 15 | 34.9 | 50.2 | 547.6 | 1.13 | N |
| S10—Hour 16 | 34.1 | 51.8 | 347.9 | 0.72 | N |
| S11—Hour 17 | 33.1 | 54.6 | 184.6 | 0.51 | N |
| Scenario | Sensor | T-M * | T-S * | RH-M * | RH-S * | Scenario | Sensor | T-M * | T-S * | RH-M * | RH-S |
|---|---|---|---|---|---|---|---|---|---|---|---|
| S01—Hour 7 | 1 | 25.2 | 25.1 | 78.8 | 79.1 | S07—Hour 13 | 1 | 35.9 | 35.5 | 50.3 | 51.2 |
| S01—Hour 7 | 2 | 25.3 | 25.2 | 78.9 | 79.8 | S07—Hour 13 | 2 | 36.2 | 35.5 | 49.5 | 51.3 |
| S01—Hour 7 | 3 | 26.1 | 25.6 | 75.8 | 76.7 | S07—Hour 13 | 3 | 38.4 | 37.1 | 43.8 | 47.9 |
| S01—Hour 7 | 4 | 25.7 | 25.3 | 76.9 | 77.9 | S07—Hour 13 | 4 | 38.5 | 37.5 | 43.3 | 45.8 |
| S01—Hour 7 | 5 | 25.7 | 25.4 | 77.3 | 78.5 | S07—Hour 13 | 5 | 38.6 | 37.3 | 42.8 | 45.5 |
| S02—Hour 8 | 1 | 28.3 | 28.2 | 73.9 | 74.2 | S08—Hour 14 | 1 | 36.4 | 35.8 | 47.5 | 49.9 |
| S02—Hour 8 | 2 | 28.3 | 28.4 | 74.2 | 74.1 | S08—Hour 14 | 2 | 36.5 | 35.7 | 47.4 | 49.8 |
| S02—Hour 8 | 3 | 29.3 | 28.9 | 69.2 | 70.2 | S08—Hour 14 | 3 | 38.1 | 37.5 | 41.3 | 44.7 |
| S02—Hour 8 | 4 | 28.7 | 28.4 | 69.5 | 71.8 | S08—Hour 14 | 4 | 38.0 | 37.6 | 41.5 | 45.9 |
| S02—Hour 8 | 5 | 29.5 | 29.2 | 67.3 | 69.4 | S08—Hour 14 | 5 | 37.9 | 37.8 | 42.0 | 45.7 |
| S03—Hour 9 | 1 | 30.9 | 30.8 | 67.0 | 67.5 | S09—Hour 15 | 1 | 35.7 | 35.6 | 48.6 | 49.8 |
| S03—Hour 9 | 2 | 31.0 | 30.7 | 66.1 | 67.4 | S09—Hour 15 | 2 | 35.6 | 35.4 | 46.4 | 47.9 |
| S03—Hour 9 | 3 | 32.4 | 31.8 | 58.9 | 62.0 | S09—Hour 15 | 3 | 36.2 | 35.7 | 45.6 | 46.8 |
| S03—Hour 9 | 4 | 31.1 | 30.6 | 64.1 | 65.7 | S09—Hour 15 | 4 | 35.9 | 35.5 | 46.3 | 48.7 |
| S03—Hour 9 | 5 | 32.4 | 31.4 | 63.8 | 64.6 | S09—Hour 15 | 5 | 36.6 | 36.5 | 44.7 | 45.5 |
| S04—Hour 10 | 1 | 32.5 | 32.3 | 60.1 | 61.3 | S10—Hour 16 | 1 | 35.3 | 34.9 | 47.8 | 49.3 |
| S04—Hour 10 | 2 | 32.6 | 32.3 | 59.5 | 61.2 | S10—Hour 16 | 2 | 35.2 | 34.7 | 49.2 | 51.1 |
| S04—Hour 10 | 3 | 34.5 | 33.7 | 54.1 | 55.4 | S10—Hour 16 | 3 | 35.9 | 35.1 | 46.8 | 49.4 |
| S04—Hour 10 | 4 | 33.9 | 33.6 | 55.6 | 56.8 | S10—Hour 16 | 4 | 35.6 | 34.8 | 48.2 | 50.2 |
| S04—Hour 10 | 5 | 34.7 | 33.8 | 54.3 | 56.9 | S10—Hour 16 | 5 | 36.1 | 35.3 | 45.8 | 48.3 |
| S05—Hour 11 | 1 | 34.5 | 34.1 | 54.5 | 55.7 | S11—Hour 17 | 1 | 33.9 | 33.8 | 50.3 | 52.1 |
| S05—Hour 11 | 2 | 34.3 | 34.1 | 55.1 | 55.6 | S11—Hour 17 | 2 | 33,9 | 33.5 | 51.8 | 53.3 |
| S05—Hour 11 | 3 | 36.1 | 35.5 | 50.3 | 51.8 | S11—Hour 17 | 3 | 34.8 | 34.3 | 49.7 | 51.1 |
| S05—Hour 11 | 4 | 36.2 | 35.4 | 48.9 | 51.4 | S11—Hour 17 | 4 | 34.4 | 33.7 | 50.7 | 52.8 |
| S05—Hour 11 | 5 | 36.3 | 35.5 | 50.2 | 52.0 | S11—Hour 17 | 5 | 35.2 | 34.5 | 49.2 | 51.4 |
| S06—Hour 12 | 1 | 36.1 | 35.1 | 48.9 | 52.1 | ||||||
| S06—Hour 12 | 2 | 36.0 | 35.1 | 51.2 | 52.0 | ||||||
| S06—Hour 12 | 3 | 37.9 | 36.8 | 46.5 | 48.8 | ||||||
| S06—Hour 12 | 4 | 37.5 | 37.2 | 46.2 | 46.7 | ||||||
| S06—Hour 12 | 5 | 38.1 | 37.3 | 44.9 | 46.5 | ||||||
| F Test to Compare Two Variances | H0: σ(Dm)2 = σ(Ds)2 o H1: σ(Dm)2 ≠ σ(Ds)2 | |
| Temperature | Relative Humidity | |
| F | 1.095 | 1.101 |
| p-value | 0.750 | 0.724 |
| 95% confidence interval | {0.636,1.870} | {0.642,1.888} |
| The null hypothesis (H0) is accepted. | ||
| Two Sample t-test | H0: µDm = µDs o H1: µDm ≠ µDs | |
| Temperature | Relative Humidity | |
| T | 0.740 | −0.847 |
| p-value | 0.460 | 0.398 |
| 95% confidence interval | {−0.869,1.905} | {−5.829,2.338} |
| Mean (µ) | µDm = 33.92 °C µDs = 33.40 °C | µDm = 54.77% µDs = 56.51% |
| The null hypothesis (H0) is accepted. | ||
| Temperature (°C) | Relative Humidity (%) | |||||
|---|---|---|---|---|---|---|
| MAE* | RMSE* | R2 | MAE | RMSE | R2 | |
| S01—Hour 7 | 0.28 | 0.32 | 0.94 | 0.86 | 0.91 | 0.93 |
| S02—Hour 8 | 0.24 | 0.26 | 0.91 | 1.16 | 1.46 | 0.94 |
| S03—Hour 9 | 0.50 | 0.58 | 0.87 | 1.46 | 1.71 | 0.96 |
| S04—Hour 10 | 0.50 | 0.57 | 0.95 | 1.62 | 1.72 | 0.95 |
| S05—Hour 11 | 0.56 | 0.60 | 0.97 | 1.52 | 1.68 | 0.97 |
| S06—Hour 12 | 0.82 | 0.86 | 0.92 | 1.68 | 1.94 | 0.84 |
| S07—Hour 13 | 0.94 | 1.02 | 0.97 | 2.42 | 2.68 | 0.91 |
| S08—Hour 14 | 0.51 | 0.56 | 0.96 | 3.25 | 3.36 | 0.96 |
| S09—Hour 15 | 0.26 | 0.30 | 0.82 | 1.42 | 1.52 | 0.87 |
| S10—Hour 16 | 0.66 | 0.68 | 0.81 | 2.10 | 2.18 | 0.96 |
| S11—Hour 17 | 0.48 | 0.52 | 0.83 | 1.82 | 1.88 | 0.88 |
| X-Axis | |||||
| Scenario | Vin (m/s) | Vnor (%) | Scenario | Vin (m/s) | Vnor (%) |
| S01—Hour 7 | 0.26 ± 0.14 | 132 ± 43.1 | S07—Hour 13 | 0.33 ± 0.15 | 27.1 ± 12.9 |
| S02—Hour 8 | 0.21 ± 0.09 | 101 ± 13.2 | S08—Hour 14 | 0.32 ± 0.13 | 24.2 ± 11.2 |
| S03—Hour 9 | 0.24 ± 0.07 | 122 ± 33.2 | S09—Hour 15 | 0.35 ± 0.13 | 23.9 ± 4.2 |
| S04—Hour 10 | 0.32 ± 0.11 | 81.3 ± 27.2 | S10—Hour 16 | 0.31 ± 0.11 | 44.1 ± 13.8 |
| S05—Hour 11 | 0.36 ± 0.13 | 51.4 ± 19.3 | S11—Hour 17 | 0.32 ± 0.12 | 61.2 ± 21.2 |
| S06—Hour 12 | 0.35 ± 0.17 | 35.2 ± 16.5 | |||
| Y-Axis | |||||
| Scenario | Vin (m/s) | Vnor (%) | Scenario | Vin (m/s) | Vnor (%) |
| S01—Hour 7 | 0.23 ± 0.16 | 119 ± 67.1 | S07—Hour 13 | 0.23 ± 0.06 | 19.5 ± 5.6 |
| S02—Hour 8 | 0.24 ± 0.07 | 121 ± 34.2 | S08—Hour 14 | 0.15 ± 0.08 | 12.3 ± 6.5 |
| S03—Hour 9 | 0.35 ± 0.08 | 161 ± 35.1 | S09—Hour 15 | 0.22 ± 0.09 | 19.1 ± 8.3 |
| S04—Hour 10 | 0.37 ± 0.12 | 44.3 ± 28.2 | S10—Hour 16 | 0.24 ± 0.14 | 33.5 ± 21.8 |
| S05—Hour 11 | 0.35 ± 0.15 | 51.1 ± 21.3 | S11—Hour 17 | 0.20 ± 0.07 | 61.2 ± 13.2 |
| S06—Hour 12 | 0.31 ± 0.16 | 32.1 ± 18.2 | |||
| Z-Axis | |||||
| Scenario | Vin (m/s) | Vnor (%) | Scenario | Vin (m/s) | Vnor (%) |
| S01—Hour 7 | 0.29 ± 0.10 | 141 ± 47.1 | S07—Hour 13 | 0.40 ± 0.18 | 33.4 ± 16.1 |
| S02—Hour 8 | 0.26 ± 0.08 | 132 ± 34.2 | S08—Hour 14 | 0.46 ± 0.18 | 35.6 ± 13.5 |
| S03—Hour 9 | 0.32 ± 0.18 | 157 ± 45.6 | S09—Hour 15 | 0.29 ± 0.11 | 26.9 ± 9.1 |
| S04—Hour 10 | 0.33 ± 0.14 | 82.5 ± 29.2 | S10—Hour 16 | 0.30 ± 0.09 | 42.5 ± 11.2 |
| S05—Hour 11 | 0.43 ± 0.15 | 60.1 ± 14.3 | S11—Hour 17 | 0.27 ± 0.08 | 51.5 ± 18.2 |
| S06—Hour 12 | 0.44 ± 0.17 | 42.4 ± 15.7 | |||
| X-Axis | |||||
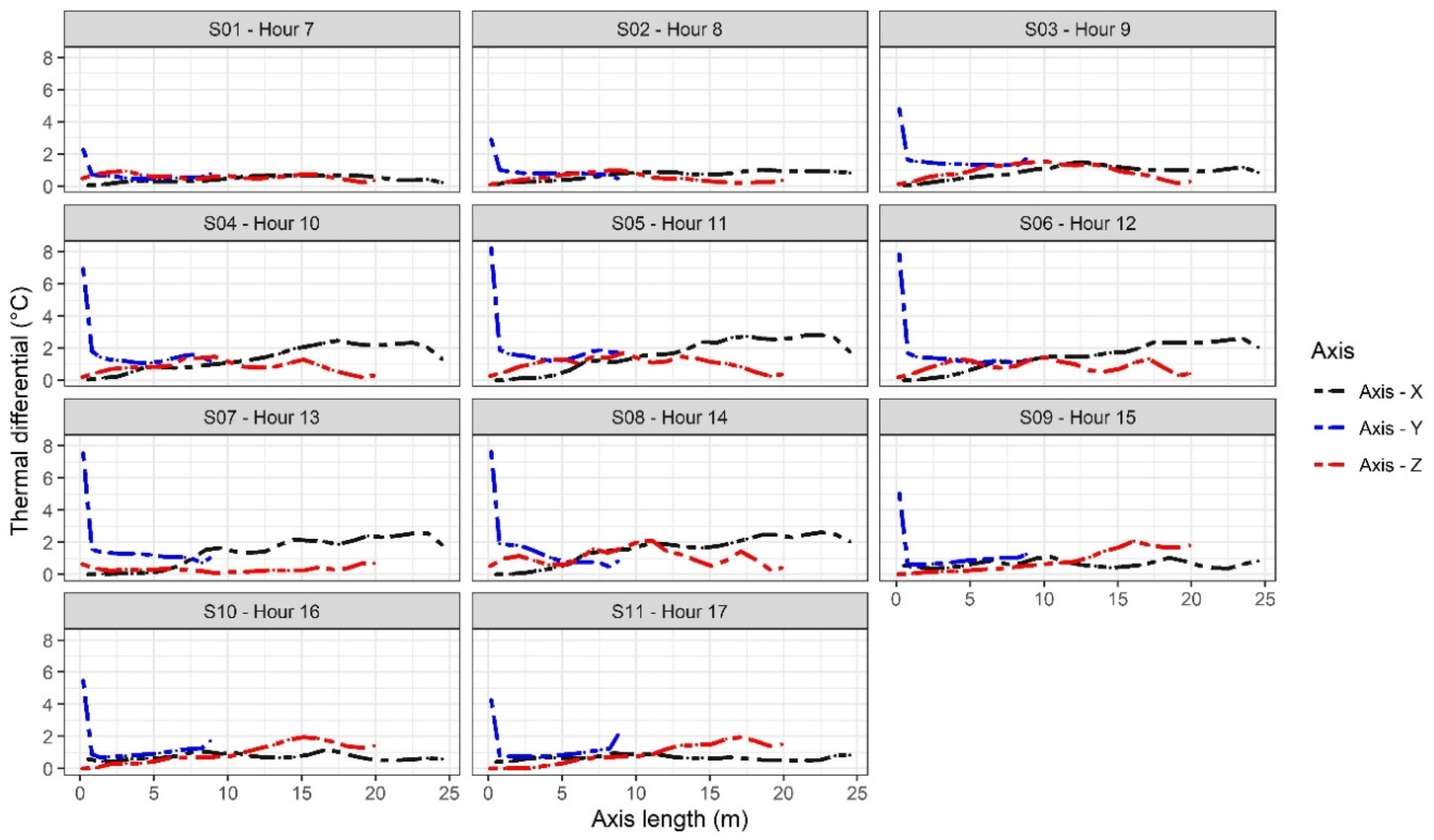
| Scenario | Tin (°C) | ΔTm (°C) | Scenario | Tin (°C) | ΔTm (°C) |
| S01—Hour 7 | 25.4 ± 0.19 | 0.44 ± 0.19 | S07—Hour 13 | 35.6 ± 0.24 | 0.42 ± 0.24 |
| S02—Hour 8 | 28.5 ± 0.26 | 0.70 ± 0.26 | S08—Hour 14 | 36.9 ± 0.13 | 1.56 ± 11.2 |
| S03—Hour 9 | 31.0 ± 0.39 | 0.90 ± 0.34 | S09—Hour 15 | 35.5 ± 0.21 | 0.65 ± 0.21 |
| S04—Hour 10 | 33.3 ± 0.77 | 1.40 ± 0.77 | S10—Hour 16 | 34.8 ± 0.20 | 0.73 ± 0.20 |
| S05—Hour 11 | 35.1 ± 0.97 | 1.62 ± 0.97 | S11—Hour 17 | 33.7 ± 0.15 | 0.67 ± 0.15 |
| S06—Hour 12 | 36.3 ± 0.82 | 1.48 ± 0.82 | |||
| Eje Y | |||||
| Scenario | Tin (°C) | ΔTm (°C) | Scenario | Tin (°C) | ΔTm (°C) |
| S01—Hour 7 | 25.6 ± 0.43 | 0.70 ± 0.43 | S07—Hour 13 | 36.7 ± 1.61 | 1.50 ± 1.61 |
| S02—Hour 8 | 28.7 ± 0.55 | 0.91 ± 0.55 | S08—Hour 14 | 36.9 ± 1.69 | 1.52 ± 1.69 |
| S03—Hour 9 | 31.7 ± 0.86 | 1.62 ± 0.86 | S09—Hour 15 | 36.0 ± 1.06 | 1.12 ± 1.06 |
| S04—Hour 10 | 33.6 ± 1.42 | 1.71 ± 1.42 | S10—Hour 16 | 35.4 ± 1.15 | 1.28 ± 1.15 |
| S05—Hour 11 | 35.4 ± 1.69 | 1.91 ± 1.69 | S11—Hour 17 | 34.3 ± 0.90 | 1.18 ± 0.90 |
| S06—Hour 12 | 36.5 ± 1.66 | 1.67 ± 1.66 | |||
| Eje Z | |||||
| Scenario | Tin (°C) | ΔTm (°C) | Scenario | Tin (°C) | ΔTm (°C) |
| S01—Hour 7 | 25.5 ± 0.17 | 0.58 ± 0.17 | S07—Hour 13 | 36.1 ± 0.37 | 0.93 ± 0.37 |
| S02—Hour 8 | 28.3 ± 0.26 | 0.49 ± 0.26 | S08—Hour 14 | 36.5 ± 0.51 | 1.06 ± 0.51 |
| S03—Hour 9 | 31.0 ± 0.47 | 0.89 ± 0.47 | S09—Hour 15 | 35.8 ± 0.69 | 0.86 ± 0.69 |
| S04—Hour 10 | 32.7 ± 0.37 | 0.82 ± 0.37 | S10—Hour 16 | 35.1 ± 0.60 | 0.95 ± 0.60 |
| S05—Hour 11 | 34.5 ± 0.42 | 1.02 ± 0.42 | S11—Hour 17 | 34.0 ± 0.65 | 0.90 ± 0.65 |
| S06—Hour 12 | 35.7 ± 0.36 | 0.86 ± 0.36 | |||
| X-Axis | |||||
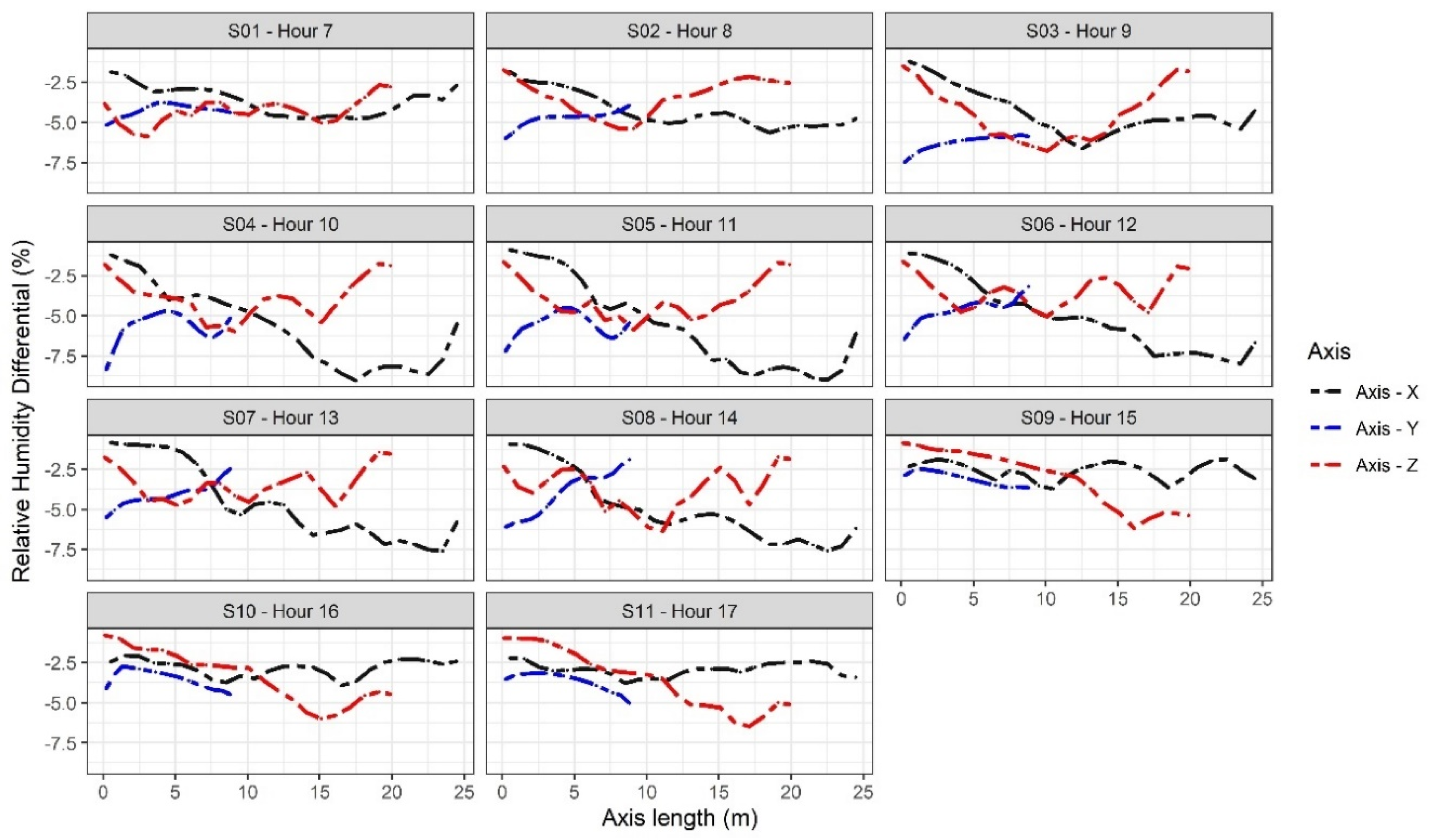
| Scenario | RHin (%) | ΔRHm (%) | Scenario | RHin (%) | ΔRHm (%) |
| S01—Hour 7 | 77.8 ± 0.90 | −3.63 ± 0.90 | S07—Hour 13 | 47.4 ± 2.39 | −4.64 ± 2.39 |
| S02—Hour 8 | 71.3 ± 1.11 | −4.26 ± 1.11 | S08—Hour 14 | 45.8 ± 2.14 | −4.95 ± 2.14 |
| S03—Hour 9 | 64.2 ± 1.44 | −4.35 ± 1.44 | S09—Hour 15 | 47.6 ± 0.55 | −2.54 ± 0.55 |
| S04—Hour 10 | 56.7 ± 2.46 | −5.71 ± 2.46 | S10—Hour 16 | 48.9 ± 0.53 | −2.83 ± 0.53 |
| S05—Hour 11 | 50.9 ± 2.78 | −5.61 ± 2.78 | S11—Hour 17 | 51.6 ± 0.42 | −2.94 ± 0.42 |
| S06—Hour 12 | 48.1 ± 2.19 | −5.08 ± 2.19 | |||
| Y-Axis | |||||
| Scenario | RHin (%) | ΔRHm (%) | Scenario | RHin (%) | ΔRHm (%) |
| S01—Hour 7 | 77.1 ± 0.40 | −4.29 ± 0.40 | S07—Hour 13 | 48.0 ± 0.75 | −4.09 ± 0.75 |
| S02—Hour 8 | 70.8 ± 0.49 | −4.79 ± 0.49 | S08—Hour 14 | 46.8 ± 1.40 | −3.94 ± 1.40 |
| S03—Hour 9 | 62.3 ± 0.48 | −6.26 ± 0.48 | S09—Hour 15 | 47.1 ± 0.42 | −3.09 ± 0.42 |
| S04—Hour 10 | 56.7 ± 0.96 | −5.69 ± 0.96 | S10—Hour 16 | 48.3 ± 0.56 | −3.51 ± 0.56 |
| S05—Hour 11 | 51.0 ± 0.76 | −4.60 ± 0.76 | S11—Hour 17 | 50.9 ± 0.57 | −3.68 ± 0.57 |
| S06—Hour 12 | 48.6 ± 0.77 | −4.09 ± 0.77 | |||
| Z-Axis | |||||
| Scenario | RHin (%) | ΔRHm (%) | Scenario | RHin (%) | ΔRHm (%) |
| S01—Hour 7 | 77.1 ± 0.81 | −4.28 ± 0.81 | S07—Hour 13 | 48.6 ± 1.03 | −3.40 ± 1.03 |
| S02—Hour 8 | 72.2 ± 1.12 | −3.39 ± 1.12 | S08—Hour 14 | 47.0 ± 1.31 | −3.72 ± 1.31 |
| S03—Hour 9 | 64.2 ± 1.74 | −4.37 ± 1.74 | S09—Hour 15 | 47.1 ± 1.78 | −3.10 ± 1.78 |
| S04—Hour 10 | 58.5 ± 1.27 | −3.86 ± 1.27 | S10—Hour 16 | 48.4 ± 1.61 | −3.39 ± 1.61 |
| S05—Hour 11 | 52.6 ± 1.26 | −3.94 ± 1.26 | S11—Hour 17 | 51.0 ± 1.89 | −3.57 ± 1.89 |
| S06—Hour 12 | 49.7 ± 1.01 | −3.48 ± 1.01 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villagran, E.; Leon, R.; Rodriguez, A.; Jaramillo, J. 3D Numerical Analysis of the Natural Ventilation Behavior in a Colombian Greenhouse Established in Warm Climate Conditions. Sustainability 2020, 12, 8101. https://doi.org/10.3390/su12198101
Villagran E, Leon R, Rodriguez A, Jaramillo J. 3D Numerical Analysis of the Natural Ventilation Behavior in a Colombian Greenhouse Established in Warm Climate Conditions. Sustainability. 2020; 12(19):8101. https://doi.org/10.3390/su12198101
Chicago/Turabian StyleVillagran, Edwin, Rommel Leon, Andrea Rodriguez, and Jorge Jaramillo. 2020. "3D Numerical Analysis of the Natural Ventilation Behavior in a Colombian Greenhouse Established in Warm Climate Conditions" Sustainability 12, no. 19: 8101. https://doi.org/10.3390/su12198101
APA StyleVillagran, E., Leon, R., Rodriguez, A., & Jaramillo, J. (2020). 3D Numerical Analysis of the Natural Ventilation Behavior in a Colombian Greenhouse Established in Warm Climate Conditions. Sustainability, 12(19), 8101. https://doi.org/10.3390/su12198101






