False Alarms Analysis of Wind Turbine Bearing System
Abstract
1. Introduction
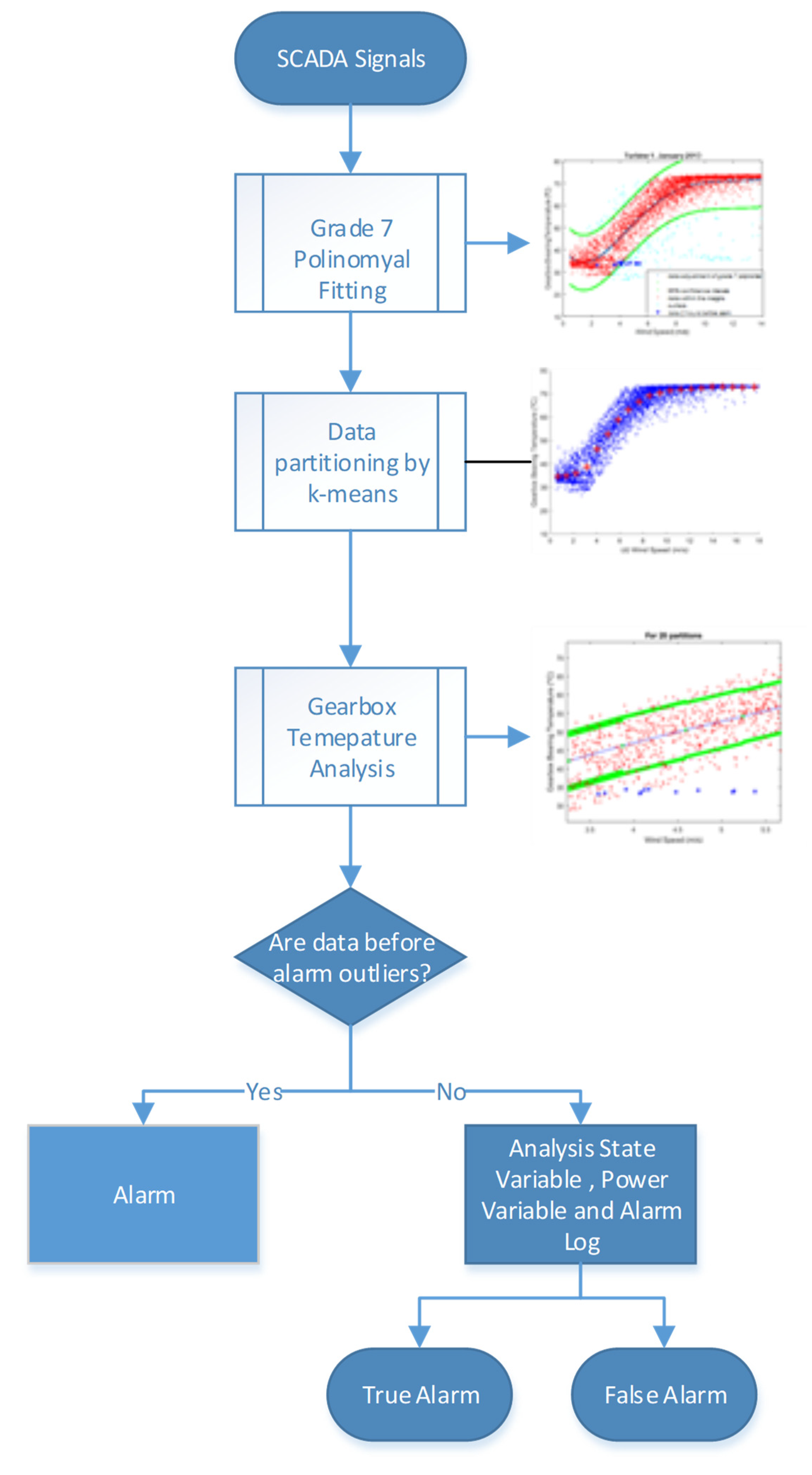
2. Approach
- Calculating the distances from each observation to each center and designating each observation to its nearest centroid.
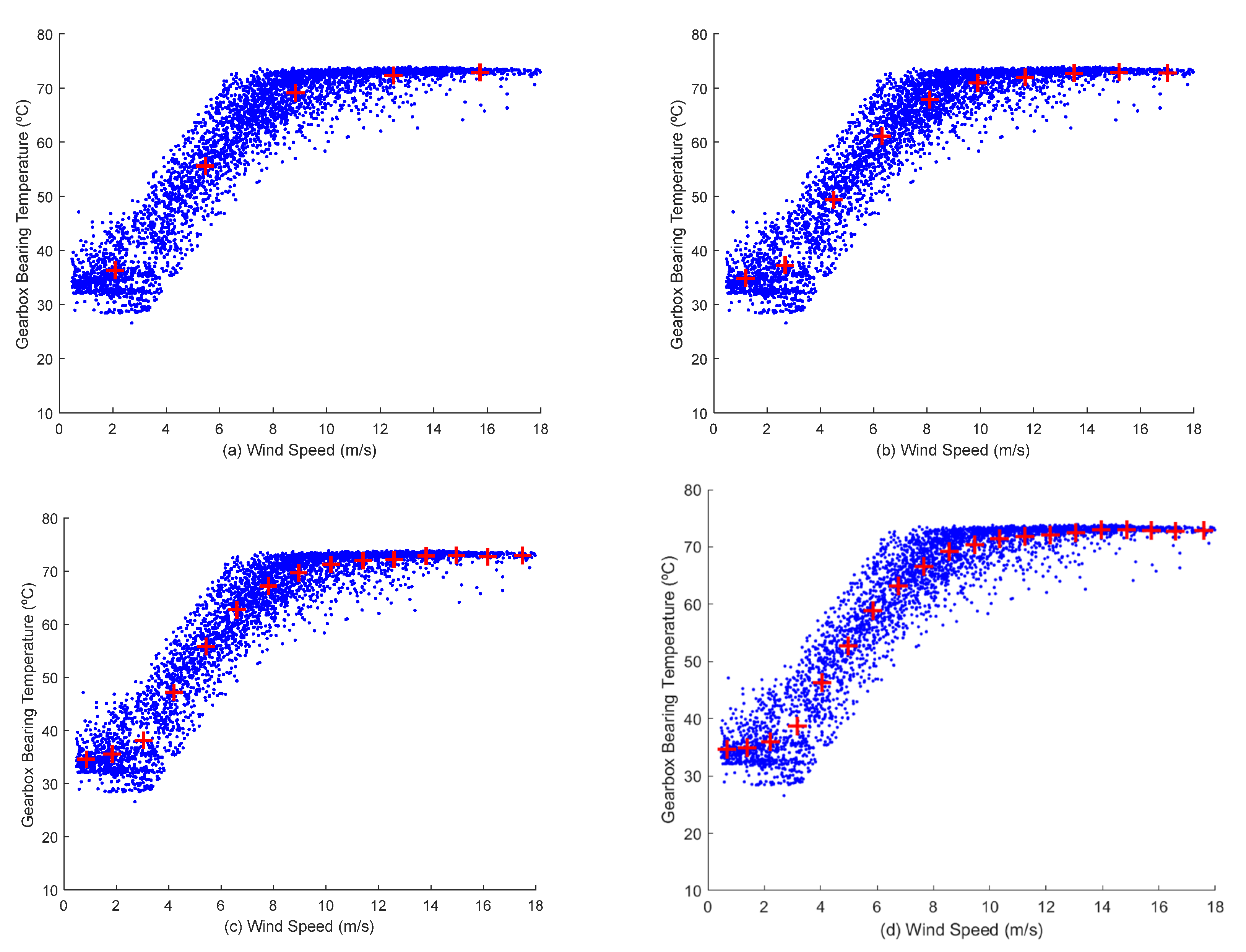
- For m = 1,...,n and p = 1,...,j − 1, choosing centroid j at random from wind speed with probability according to the Equation (2), where is the set of all observations nearest to centroid , and xm fits to .
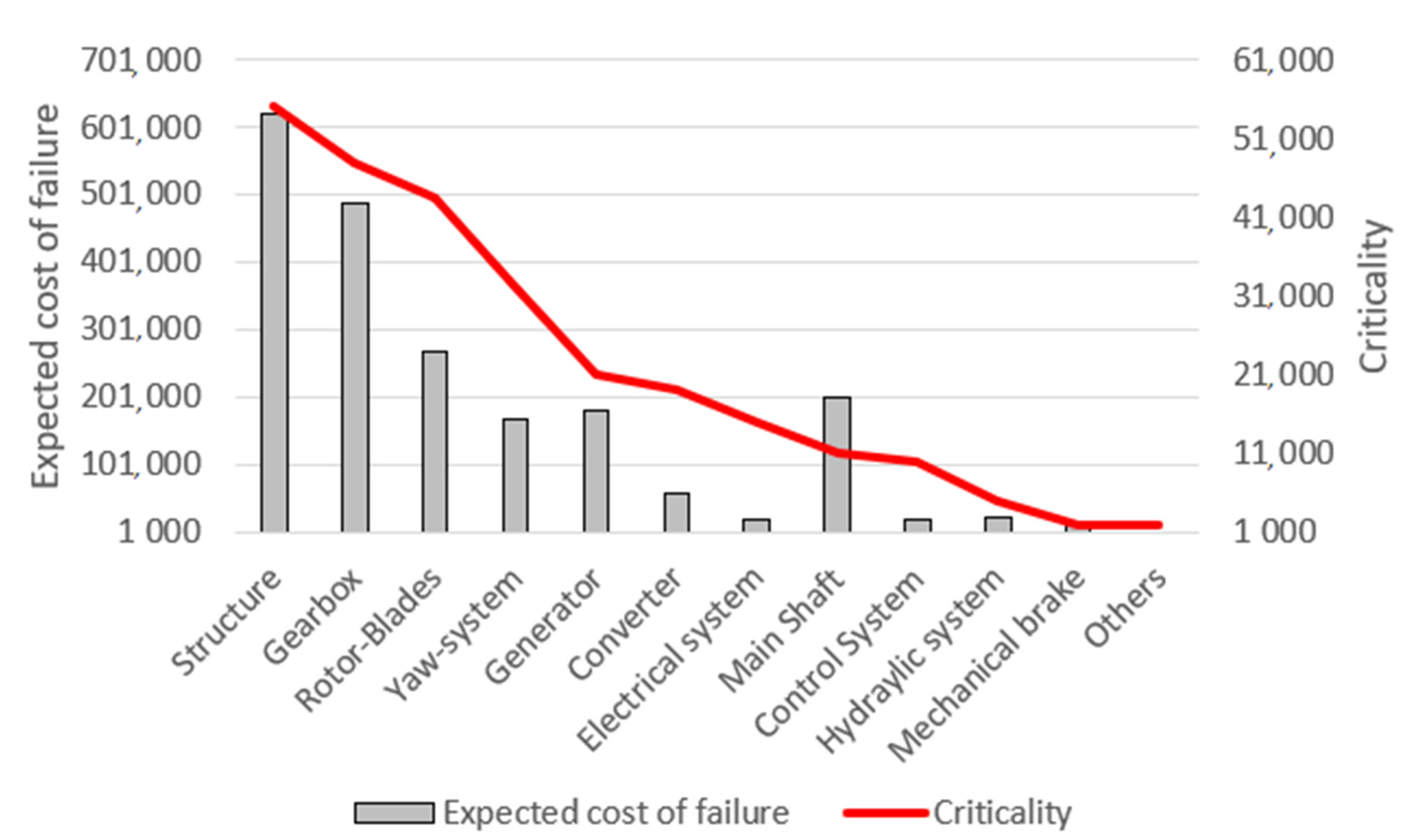
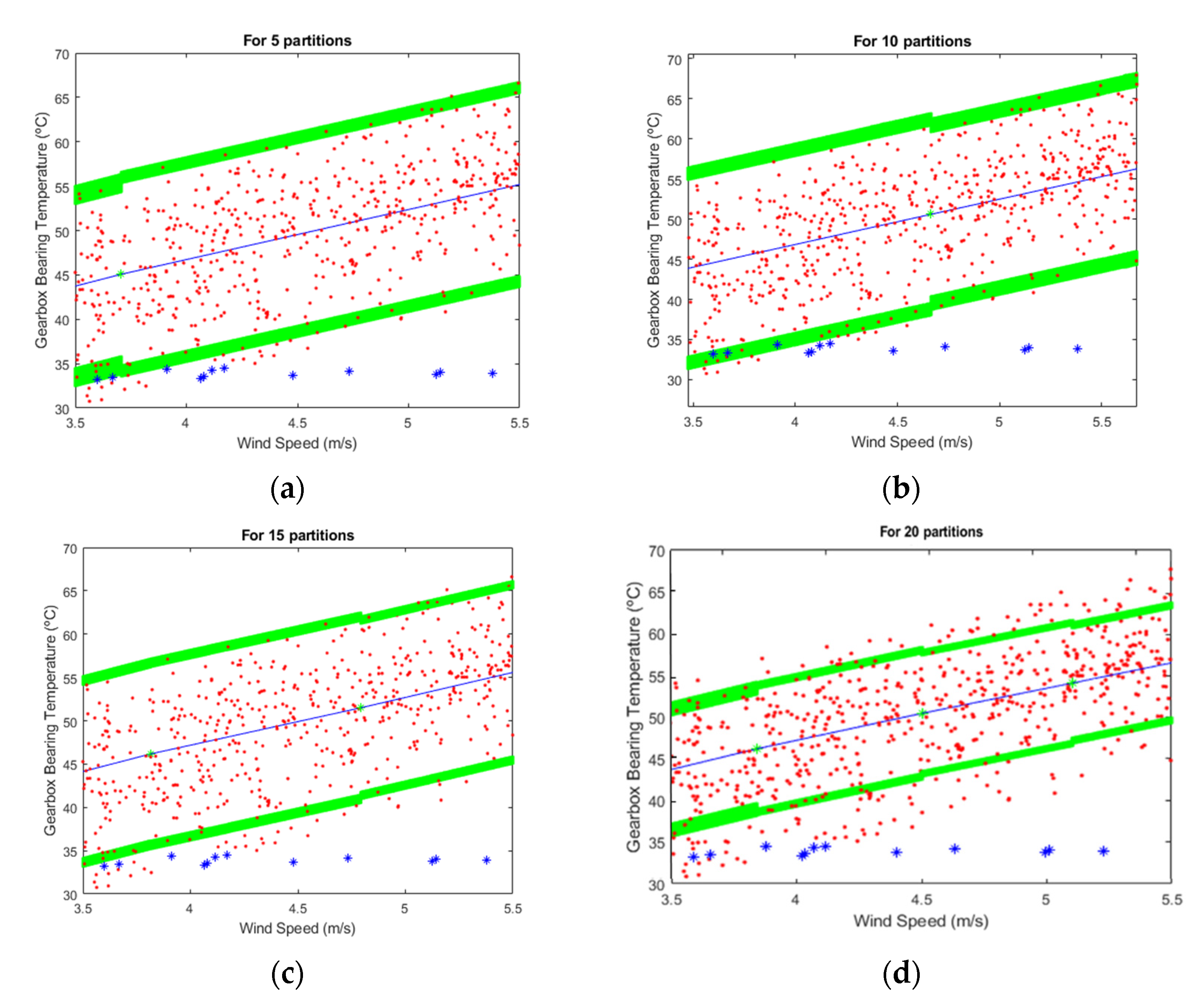
3. Real Case Study and Results
- 1
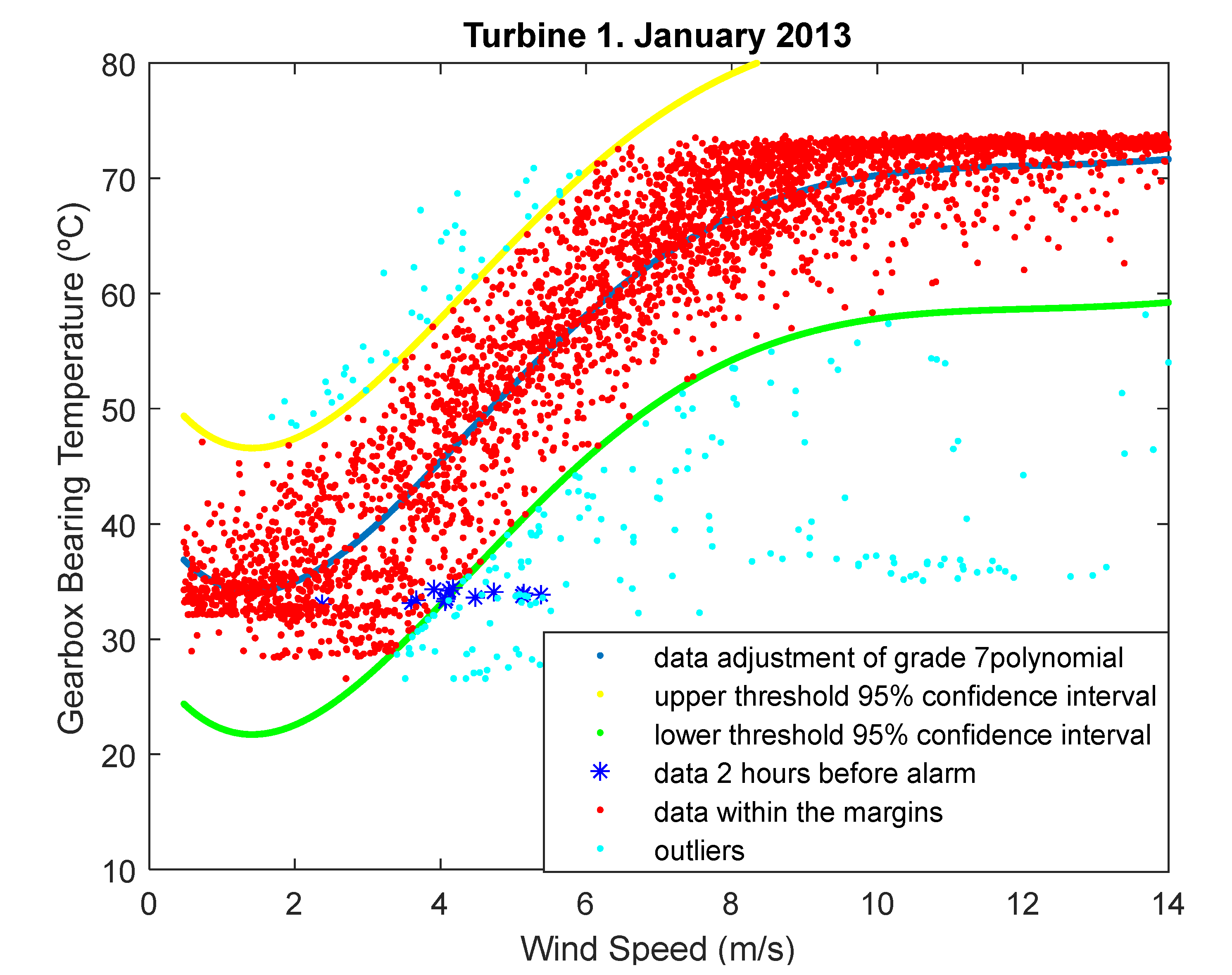
- The first alarm is produced due to a low temperature of the gearbox oil. The alarm is activated 15 h after the WT is turned off and starts working without any maintenance operations. There is no information in the state variable for determining the WT stop, although this variable indicates that the WT has been stopped due to “atmospheric conditions” at least 12 h. There are outliers before the shutdown (blue points in Figure 4), but no alarms have been activated at that time. The main hypothesis is the delay of the alarm, and this alarm is related to the outliers detected with the methodology. Another possible cause is the decreasing of the gearbox temperature due to low environmental temperatures for 15 h. The results are not convincing, and more data are required to check the cause and the classification of the alarm.
- 2
- The alarms 2 and 4 occur at the same time for WTs 1 and 2. Both WTs coincide in downtime periods and the state variable provides the same information. The alarm activation time is reduced, about 2 min. The system has not enough time to react and there are no maintenance activities carried out, and this alarm is set as false.
- 3
- The third alarm has an abnormal behavior, with 23 alarms in an interval of 5 s. The state variable indicates emergency, implying that the reset must be manual and local, then the state variable indicates that there are maintenance actions for more than one hour. When the alarms are activated, the SCADA system takes nonsense measures, being evidence that an anomaly is occurring. The gearbox system alarm is not caused by a failure in the gearbox, because the alarms triggered belong to different components and alarm systems. The maintenance time is insufficient to perform maintenance on the gearbox itself. With the data obtained and analyzed, it can be stated that this is a SCADA system failure and not a gearbox failure.
- 4
- The alarm 5 is activated and deactivated in five times in an interval of time of 40 min. The SCADA system offers null values before and after the alarm appears for all SCADA variables, and the maintenance activities are carried out.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lin, B.; Xu, M. Regional differences on CO2 emission efficiency in metallurgical industry of China. Energy Policy 2018, 120, 302–311. [Google Scholar] [CrossRef]
- Dube, K.; Nhamo, G. Climate change and the aviation sector: A focus on the Victoria Falls tourism route. Environ. Dev. 2019, 29, 5–15. [Google Scholar] [CrossRef]
- Lo, P.L.; Martini, G.; Porta, F.; Scotti, D. The determinants of CO2 emissions of air transport passenger traffic: An analysis of Lombardy (Italy). Transp. Policy 2020, 91, 108–119. [Google Scholar] [CrossRef]
- Abioye, O.F.; Dulebenets, M.A.; Pasha, J.; Kavoosi, M. A Vessel Schedule Recovery Problem at the Liner Shipping Route with Emission Control Areas. Energies 2019, 12, 2380. [Google Scholar] [CrossRef]
- Dulebenets, M.A.; Moses, R.; Ozguven, E.E.; Vanli, A. Minimizing Carbon Dioxide Emissions Due to Container Handling at Marine Container Terminals via Hybrid Evolutionary Algorithms. IEEE Access 2017, 5, 8131–8147. [Google Scholar] [CrossRef]
- Andersson, F.N.; Opper, S.; Khalid, U. Are capitalists green? Firm ownership and provincial CO emissions in China. Energy Policy 2018, 123, 349–359. [Google Scholar] [CrossRef]
- Zhang, N.; Liu, G.; Chen, C.; Zhang, Y.; Hao, Y.; Casazza, M. Medium-to-long-term coupled strategies for energy efficiency and greenhouse gas emissions reduction in Beijing (China). Energy Policy 2019, 127, 350–360. [Google Scholar] [CrossRef]
- W.H. OFFICE. Wind Power Capacity Worldwide Reaches 597 GW, 50,1 GW added in 2018. Available online: https://wwindea.org/blog/2019/02/25/wind-power-capacity-worldwide-reaches-600-gw-539-gw-added-in-2018/ (accessed on 17 February 2020).
- Zhao, H.-S.; Zhang, X.-T. Early Fault Prediction of Wind Turbine Gearbox Based on Temperature Measurement. In Proceedings of the 2012 IEEE International Conference on Power System Technology (POWERCON), Auckland, New Zealand, 30 October–2 November 2012; pp. 1–5. [Google Scholar]
- Márquez, F.P.G.; Karyotakis, A.; Papaelias, M. Renewable Energies: Business Outlook 2050; Springer: Geneva, Switzerland, 2018. [Google Scholar]
- Patel, K.K.; Patel, S.M. Internet of things-IOT: Definition, characteristics, architecture, enabling technologies, application & future challenges. Int. J. Eng. Sci. Comput. 2016, 6. [Google Scholar] [CrossRef]
- Márquez, F.P.G.; Marugán, A.P.; Pérez, J.M.P.; Hillmansen, S.; Papaelias, M. Optimal Dynamic Analysis of Electrical/Electronic Components in Wind Turbines. Energies 2017, 10, 1111. [Google Scholar] [CrossRef]
- Jiménez, A.A.; Márquez, F.P.G.; Moraleda, V.B.; Muñoz, C.Q.G. Linear and nonlinear features and machine learning for wind turbine blade ice detection and diagnosis. Renew. Energy 2019, 132, 1034–1048. [Google Scholar] [CrossRef]
- Gomez, C.Q.; Garcia, F.P.; Arcos, A.; Cheng, L.; Kogia, M.; Papaelias, M. Calculus of the defect severity with EMATs by analysing the attenuation curves of the guided waves. Smart Struct. Syst. 2017, 19, 195–202. [Google Scholar] [CrossRef]
- Jiménez, A.A.; Zhang, L.; Muñoz, C.Q.G.; Márquez, F.P.G. Maintenance management based on Machine Learning and nonlinear features in wind turbines. Renew. Energy 2020, 146, 316–328. [Google Scholar] [CrossRef]
- Márquez, F.P.G.; Ramírez, I.S.; Pliego-Marugán, A. Decision Making using Logical Decision Tree and Binary Decision Diagrams: A Real Case Study of Wind Turbine Manufacturing. Energies 2019, 12, 1753. [Google Scholar] [CrossRef]
- Márquez, F.P.G.; Tobias, A.M.; Pérez, J.M.P.; Papaelias, M. Condition monitoring of wind turbines: Techniques and methods. Renew. Energy 2012, 46, 169–178. [Google Scholar] [CrossRef]
- Marugán, A.P.; Márquez, F.P.G. Advanced analytics for detection and diagnosis of false alarms and faults: A real case study. Wind. Energy 2019, 22, 1622–1635. [Google Scholar] [CrossRef]
- Tazi, N.; Châtelet, E.; Bouzidi, Y. Using a Hybrid Cost-FMEA Analysis for Wind Turbine Reliability Analysis. Energies 2017, 10, 276. [Google Scholar] [CrossRef]
- Carroll, J.; Koukoura, S.; McDonald, A.; Charalambous, A.; Weiss, S.; McArthur, S.D.J. Wind turbine gearbox failure and remaining useful life prediction using machine learning techniques. Wind. Energy 2018, 22, 360–375. [Google Scholar] [CrossRef]
- Mandic, G.; Nasiri, A.; Muljadi, E.; Oyague, F. Active Torque Control for Gearbox Load Reduction in a Variable-Speed Wind Turbine. IEEE Trans. Ind. Appl. 2012, 48, 2424–2432. [Google Scholar] [CrossRef]
- Muñoz, C.Q.G.; Márquez, F.P.G.; Crespo, B.H.; Makaya, K. Structural health monitoring for delamination detection and location in wind turbine blades employing guided waves. Wind. Energy 2019, 22, 698–711. [Google Scholar] [CrossRef]
- Kusiak, A.; Verma, A. Analyzing bearing faults in wind turbines: A data-mining approach. Renew. Energy 2012, 48, 110–116. [Google Scholar] [CrossRef]
- Abdusamad, K.B.; Gao, D.W.; Muljadi, E. A Condition Monitoring System for Wind Turbine Generator Temperature by Applying Multiple Linear Regression Model. In Proceedings of the 2013 North American Power Symposium (NAPS), Manhattan, KS, USA, 22–24 September 2013; pp. 1–8. [Google Scholar]
- Cambron, P.; Masson, C.; Tahan, A.; Pelletier, F. Control chart monitoring of wind turbine generators using the statistical inertia of a wind farm average. Renew. Energy 2018, 116, 88–98. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Márquez, F.P.G.; Ramírez, I.S.; Mohammadi-Ivatloo, B.; Marugán, A.P. Reliability Dynamic Analysis by Fault Trees and Binary Decision Diagrams. Information 2020, 11, 324. [Google Scholar] [CrossRef]
- Ouyang, T.; Kusiak, A.; He, Y. Modeling wind-turbine power curve: A data partitioning and mining approach. Renew. Energy 2017, 102, 1–8. [Google Scholar] [CrossRef]
- Jiménez, A.A.; Muñoz, C.Q.G.; Márquez, F.P.G. Machine Learning for Wind Turbine Blades Maintenance Management. Energies 2017, 11, 13. [Google Scholar] [CrossRef]
- Márquez, F.P.G.; García-Pardo, I.P. Principal component analysis applied to filtered signals for maintenance management. Qual. Reliab. Eng. Int. 2009, 26, 523–527. [Google Scholar] [CrossRef]
- Márquez, F.P.G.; Muñoz, J.M.C. A pattern recognition and data analysis method for maintenance management. Int. J. Syst. Sci. 2012, 43, 1014–1028. [Google Scholar] [CrossRef]
- Lydia, M.; Kumar, S.S.; Kumar, K.V.; Kumar, G.E.P. A comprehensive review on wind turbine power curve modeling techniques. Renew. Sustain. Energy Rev. 2014, 30, 452–460. [Google Scholar] [CrossRef]
- Muñoz, C.Q.G.; Jiménez, A.A.; Márquez, F.P.G. Wavelet transforms and pattern recognition on ultrasonic guides waves for frozen surface state diagnosis. Renew. Energy 2018, 116, 42–54. [Google Scholar] [CrossRef]
- Márquez, F.P.G.; Muñoz, C.Q.G. A New Approach for Fault Detection, Location and Diagnosis by Ultrasonic Testing. Energies 2020, 13, 1192. [Google Scholar] [CrossRef]
- Marugán, A.P.; Chacón, A.M.P.; Márquez, F.P.G. Reliability analysis of detecting false alarms that employ neural networks: A real case study on wind turbines. Reliab. Eng. Syst. Saf. 2019, 191, 106574. [Google Scholar] [CrossRef]
- Pérez, J.M.P.; Márquez, F.P.G.; Ruiz-Hernandez, D. Economic viability analysis for icing blades detection in wind turbines. J. Clean. Prod. 2016, 135, 1150–1160. [Google Scholar] [CrossRef]
- Muñoz, C.Q.G.; Márquez, F.P.G.; Jiménez, A.A.; Cheng, L.; Kogia, M.; Mohimi, A.; Papaelias, M. A heuristic method for detecting and locating faults employing electromagnetic acoustic transducers. Ekspolatacja Niezawodn. Maint. Reliab. 2017, 19, 493–500. [Google Scholar] [CrossRef]
- Márquez, F.P.G. An Approach to Remote Condition Monitoring Systems Management. In Proceedings of the IET International Conference on Railway Condition Monitoring, Birmingham, UK, 29–30 November 2006; pp. 156–160. [Google Scholar]
- Márquez, F.P.G. A new method for maintenance management employing principal component analysis. Struct. Durab. Health Monit. 2010, 6, 89–99. [Google Scholar]
- Jiménez, A.A.; Muñoz, C.Q.G.; Márquez, F.P.G. Dirt and mud detection and diagnosis on a wind turbine blade employing guided waves and supervised learning classifiers. Reliab. Eng. Syst. Saf. 2019, 184, 2–12. [Google Scholar] [CrossRef]
- Ahmed, K.; Izadi, I.; Chen, T.; Joe, D.; Burton, T. Similarity Analysis of Industrial Alarm Flood Data. IEEE Trans. Autom. Sci. Eng. 2013, 10, 452–457. [Google Scholar] [CrossRef]
- Chacón, A.M.P.; Zhang, L.; Márquez, F.P.G. Maintenance Management in Wind Turbines by Monitoring the Bearing Temperature. In Advances in Intelligent Systems and Computing; Springer Science and Business Media LLC: Berlin, Germany, 2019; pp. 678–687. [Google Scholar]
- Arthur, D.; Vassilvitskii, S. k-means++: The Advantages of Careful Seeding, Stanford 2006. Available online: http://ilpubs.stanford.edu:8090/778/ (accessed on 17 February 2020).
- Har-Peled, S.; Sadri, B. How Fast Is the k-Means Method? Algorithmica 2004, 41, 185–202. [Google Scholar] [CrossRef]
- Seber, G.A. Multivariate Observations; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 252. [Google Scholar]
- Yang, X.; Yang, M.; Zeng, X.; Zhu, Y.; Zhou, Y. Fault Warning of Pitch System of Wind Turbine Based on Kernel Density Estimation. In Proceedings of the 8th Renewable Power Generation Conference (RPG 2019), Shanghai, China, 24–25 October 2019; pp. 1–5. [Google Scholar]
- Pandit, R.; Infield, D. SCADA-based wind turbine anomaly detection using Gaussian process models for wind turbine condition monitoring purposes. IET Renew. Power Gener. 2018, 12, 1249–1255. [Google Scholar] [CrossRef]
- Pandit, R.; Infield, D.; Carroll, J. Incorporating air density into a Gaussian process wind turbine power curve model for improving fitting accuracy. Wind Energy 2018, 22, 302–315. [Google Scholar] [CrossRef]
| Alarm Number | WT Analysed | Alarm Description | State Variable | Number of Activations of Other Alarms |
|---|---|---|---|---|
| 1 | 1 | Low temperature of gearbox oil | Pause | 3 |
| 2 | 1 | Gearbox frequency converter no feedbackGearbox oil flow no feedback | Stop | 5 |
| 3 | 1 | Gearbox bearing 1 PT100 error | Emergency | 23 |
| 4 | 2 | Gearbox bearing 1 PT 100 error Gearbox oil flow no feedback | Stop Fault | 6 |
| 5 | 3 | Gearbox frequency converter no feedback | I/O timeout Fault Stop | 11 |
| Alarm | Description Causes | Alarm |
|---|---|---|
| 1 | The WT is stopped for more than 14 h before the alarm occurs. The gearbox temperature decreases because it tends to equalize with the ambient temperature. | N/A |
| 2 | Due to the short period of activation of the alarm, the system could not react. | False |
| 3 | Fault in the SCADA measurement system, sensors give unreal values | False |
| 4 | Due to the short period of activation of the alarm, the system could not react. Dependence on turbine 1 and 2, because these alarms occur at the same time, for no obvious reason. | False |
| 5 | SCADA system provides measurements in null and zero value intervals. 11 different alarms arise in half an hour, since the alarm system detects faults, although they are failures of the SCADA system itself and not of the WT components. | False |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chacón, A.M.P.; Ramírez, I.S.; Márquez, F.P.G. False Alarms Analysis of Wind Turbine Bearing System. Sustainability 2020, 12, 7867. https://doi.org/10.3390/su12197867
Chacón AMP, Ramírez IS, Márquez FPG. False Alarms Analysis of Wind Turbine Bearing System. Sustainability. 2020; 12(19):7867. https://doi.org/10.3390/su12197867
Chicago/Turabian StyleChacón, Ana María Peco, Isaac Segovia Ramírez, and Fausto Pedro García Márquez. 2020. "False Alarms Analysis of Wind Turbine Bearing System" Sustainability 12, no. 19: 7867. https://doi.org/10.3390/su12197867
APA StyleChacón, A. M. P., Ramírez, I. S., & Márquez, F. P. G. (2020). False Alarms Analysis of Wind Turbine Bearing System. Sustainability, 12(19), 7867. https://doi.org/10.3390/su12197867







