1. Introduction
The world is engulfed in a pandemic of the new coronavirus SARS-CoV2 and the respiratory illness COVID-19 it causes. The virus was first identified in Wuhan, China, and in three months spread throughout the entire world. To reduce the spread of the virus and prevent overload of local health systems, most nations have introduced measures such as physical distancing, movement restrictions, and temporary lockdown of both business and social activities. The global airline industry has been hit particularly hard by the pandemic. Revenue passenger kilometers have temporarily dropped by more than 90% in some regions and are only slowly recovering. Overall, the International Civil Aviation Organization (ICAO) expects an unprecedented drop in passenger demand and a crisis in the industry unseen before [
1]. Air travel should be considered critical, as this globally well-connected transport network could be part of new transmission chains to remote locations. The confined space conditions inside the aircraft require a small physical distance between passengers and may, therefore, encourage virus transmission. Current research and studies indicate that there is only a low probability of transmission in aircraft, but also point out that activities before and after the flight could also contribute significantly to the spread of disease.
Unlike the first coronavirus now referred to as SARS-CoV1, the new coronavirus SARS-CoV2 cannot be annihilated any more. With more than 5 million confirmed infections worldwide at the end of May 2020 and probably a three to tenfold higher number of unaccounted infected, complete extinction of the virus is unlikely until a vaccination exists. Most affected nations have introduced measures to control the spread and minimize the number of new infections. These measures are primarily aimed at increasing the distance between people so that the virus cannot be transmitted. Most governments have advocated a strategy of maximum containment until either a vaccine is available or an effective medication is available to prevent a large number of seriously sick people from overburdening the local health system. A particular feature of SARS-CoV2 and COVID-19 is that infected persons become contagious before they develop the first symptoms [
2]. The isolation of apparently sick people (e.g., by measuring their body temperature) therefore does not sufficiently reduce the spread. Early analyses have shown that about half of the infections occur before the infected person develops symptoms. Another difficulty is that many people do not develop any symptoms at all, but are still highly contagious [
3]. Also, an effective containment strategy must be pursued for at least one month, which will have a significant negative impact on (inter-) national economies if this strategy has to be continued in the longer term.
We assume in our contribution that air travel will be re-established between regions that have a sufficiently controlled situation with a low number of new infections. These regions will accept passengers from other equally affected regions if two main conditions can be met (a) prevent as far as technically possible the transport of infected people to prevent the start of new transmission chains at their destination, and (b) minimize the risk that undetected infected persons transmit the virus to other passengers during the travel and by that have “super-spreading” event with multiple infection chains starting from a particular flight. The first condition can be met by looking for symptoms like cough or fever and denying access to these affected passengers. This reduces the probability of having infected people on board but does not fully eliminate it. A further step can be the use of contact tracking technologies, as already introduced in some Asian countries (especially in China), to identify possible transmission chains in advance. The safest measure would be the actual testing of passengers before each flight. Current laboratory test methods based on polymerase chain reaction (PCR) require roughly 4 to 6 hrs for processing if the (logistic) process is optimized [
4]. But the costs for these tests are substantial, Vienna airport offers a test for arriving passengers at 190 EUR (May 2020).
The development of appropriate capacities for rapid, reliable, and cost-effective testing is urgently needed. Currently, there are many rapid tests on the market, but they mainly target antigen and therefore only indicate whether someone has been exposed to SARS-CoV2 [
5]. More affordable PCR-based virus tests are currently under development to provide reliable results within one hour, making them applicable to air travel [
6]. If physical distance can be maintained during a flight, the multiple testing of each passenger and the associated costs and time-consuming procedures could be avoided. Flying in airplanes has the advantage over other means of transport that passengers can be tracked down more easily because all passengers are thoroughly registered. When the physical distance is required over an entire flight, the capacity of a standard single-aisle aircraft shrinks by 33% when the middle seats are not used, or even more when only every second row is allowed. This would prevent airlines from operating flights economically.
1.1. Review of Research on Virus Transmission in Aircraft
SARS-CoV2 is not the first pandemic disease that has confronted the modern world. Aircraft are relevant for modern pandemics in two ways. First, they have always been identified as relevant for transporting a disease through the entire world within a matter of days. Second, an aircraft may act as a place of “super spreading”, enabling many transmissions from a single infected person. Both factors combined mean that air travel during pandemic conditions is risky for containment and restricting air travel is usually one of the first things done. Nevertheless, travel from the Wuhan region in China is likely the way how SARS-CoV2 has arrived in Europe and North America, probably as early as mid to late January. As the first step a few terms are introduced:
Index Case: the first case of an infection chain.
Secondary Attack Rate: the percentage of people infected out of the number of all contacts. A measure of how contagious a disease is, different from reproduction number R, which describes how many people an infected person infects on average.
Pre-symptomatic: positively confirmed person, but before developing symptoms.
Symptomatic: an infected person has apparent illness symptoms like fever, coughing and other
Asymptomatic: positively confirmed the infected person who does not recognize any symptoms.
An overview study reviewed the knowledge regarding disease spreading in an aircraft [
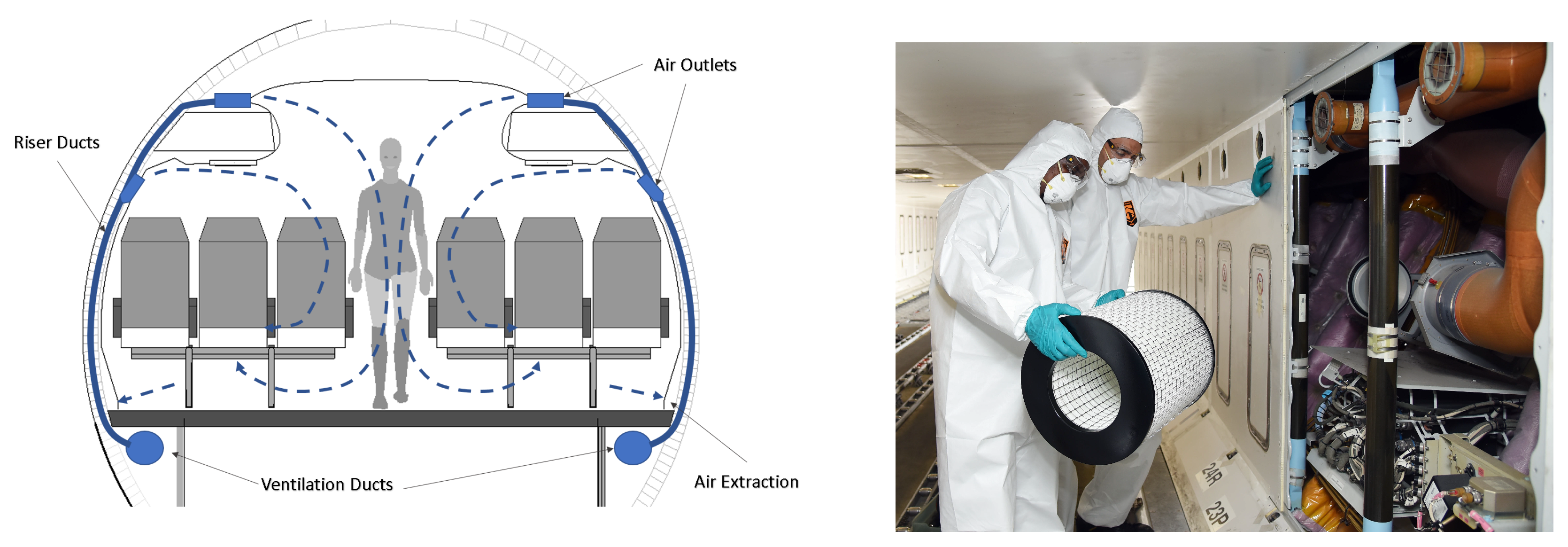
7]. The learning is that there is no proven model of how a disease spreads in an aircraft. A comparable virus is the influenza virus, which is also transmitted via droplets. The study shows that transmissions have been occurred in both cases seated close to and seated far away from the index case. The most important finding is that the flight event itself is only one possible source of infection, the upstream and downstream processes (contacts in the airport, boarding and deboarding, baggage collection) could similarly lead to infectious contacts. The cited studies used contact tracing after the flights and the actual relevant point of contact can usually not be re-enacted. A key technical fact is that cabin air is constantly re-circulated at a high rate [
4,
7]. The recirculated air passes through High Efficiency Particulate Air (HEPA) filters that remove above 99.9% of all virus and bacteria attached to droplets (see
Figure 1). The assumption is that as long as the environmental control system of the aircraft is running in normal mode, the pure physical distance is not the key criterion that matters.
A detailed study on SARS-CoV1 shows how different infection spreads can be [
8]. The study looked at three flights with contagious passengers. On the first flight, no additional infection was identified, and only one new infection was reported on the second flight. But on the third flight, 22 new infections were counted, which could be traced back to the index passenger. In this case, the physical proximity to the index patient was related to the transmission. This was also indicated by a study, which confirms a higher chance of infection when being seated within 2 rows of the index case [
9] and study focusing on inflight transmission of influenza during passenger movements [
10]. However, the probability of other passengers still reached about one-third of those being seated within two rows. Thus, as a commonly accepted rule of thumb, each passenger seated two seats and two rows around the index case shall be contacted for disease containment.
A very recent study documented the travel of a symptomatic index case flying a 15 h trip in economy class [
11]. All 25 passengers being seated within a range of 2 m of the index case were contacted and closely monitored after the trip. Some of these developed symptoms, however, none of those were tested positive for SARS-CoV2 (that particular time of the year sees many respiratory illnesses). The study specifically mentions the relevance of other shared events before the flight and during boarding and deboarding. Another study from China reports 11 aircraft transmissions [
12]. There are no further details provided. Yet another study from France suspected the infection of a patient happened during a flight. This is not confirmed yet [
13]. The IATA in contrast states that 1.100 infected people flying have been traced and no secondary cases have been identified [
4]. The probability of infection while being seated appears to be rather low, up to being non-existing following some research [
4]. Contributing factors to this observation are listed in the following.
- -
The airflow in an aircraft cabin is from above downwards (see
Figure 1), reducing the probability that virus-laden air is ingested by other passengers,
- -
The air in an aircraft cabin is exchanged rather frequently, about 20 times an hour.
- -
The recirculated air is run through HEPA (High Efficiency Particulate Air) filters.
- -
The air is quite dry at cruising altitude, which is problematic for Corona-type viruses.
However, most of these observations are only valid when the ventilation system is running, and some characteristics (like dry air) are only found when the aircraft is in cruise. When standing at the gate, the cabin ventilation needs to be activated and this generally requires the auxiliary power unit to run. This is usually not desired as it creates lots of environmental impact at the airport (e.g., noise, air pollution), but in times of a pandemic, it might be a sensible operational procedure without too much additional cost or other repercussions.
1.2. Passenger Boarding
Comprehensive overviews are provided for aircraft ground operations, passenger boarding, and corresponding economic impact [
14,
15,
16,
17,
18,
19,
20]. A common goal of simulation-based approaches for passenger boarding is to minimize boarding time. Thus, the efficiency of different boarding strategies was focus of the research activities [
21,
22,
23,
24,
25,
26,
27,
28]. These models are based on cellular automaton or analytical approaches, but also other models were developed: mixed integer linear program [
29], statistical mechanics [
30], power law rule [
31,
32], cellular discrete-event system specification [
33], stochastic approach covering individual passenger behavior and aircraft/airline operational constraints [
16,
26].
The quantity and quality of hand luggage determine the duration of boarding significantly. Thus, research was conducted with a particular focus on the physique of passengers (maximum speed), the quantity of hand luggage, and individually preferred distance [
34], seat assigned passengers with regards to hand luggage [
28,
35,
36,
37]. Furthermore, the fact that passengers travel in groups has an impact on the boarding efficiency [
16,
38]. Other research is aiming at the evaluation of pre-boarding areas [
39,
40], consideration of passenger expectations [
41], use of apron busses [
42], real-time seat allocation [
43,
44]. The aircraft cabin layout and design with regards to their impact of passenger boarding were focused on the following studies: aircraft interior design (seat pitch and passengers per row) [
45], aircraft seating layouts and alternative designs single and twin-aisle configuration [
46,
47], impact of aircraft cabin modifications [
48], novel aircraft configurations and seating concepts [
49,
50], dynamic change of the cabin infrastructure [
51].
Only a few experimental tests were conducted to provide data for the calibration of input parameters and validation of simulation results, e.g., using a mock Boeing 757 fuselage [
52], small-scale laboratory tests [
53], or a field trial configuration to get real operational and passenger data [
54]. Particular test setups were used to provide data for the time to store hand luggage items in the overhead compartments [
55] or to evaluate passenger perceptions during boarding/deboarding [
56].
1.3. Previous Fields of Applications
We use a stochastic, cellular automata approach to model passenger interactions and operational constraints in the aircraft cabin. Details of the model are presented in
Section 3. This particular model was already applied in several fields of scientific and applied research. These fields are namely the analysis and evaluation of common group dynamic behaviors, the modeling of passenger processes at the airport in regular and exceptional conditions, the egress characteristics of railway coaches, and evaluation of infrastructural adaptations in the aircraft cabin during passenger boarding. The dedicated model extension with a module for the evaluation of the transmission probability is built upon these previous developments.
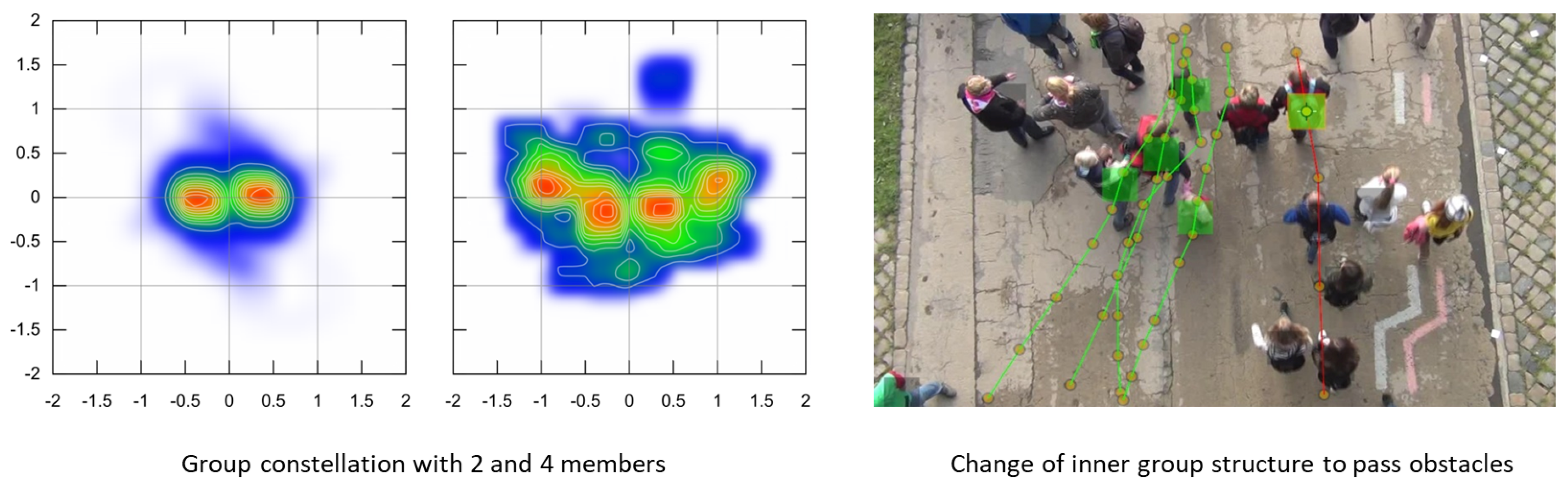
Pedestrian flows consist of mainly independent pedestrians possess a more homogeneous density distribution and individually higher flexibility to change the speed and the direction of motion, compared to flows consists of pedestrian groups [
57]. Data conducted in the field point out that the individual movement characteristic of each group member depends on the group constellation (e.g., size, age). This results in a coordinated group movement (e.g., distance keeping, collision avoidance) and a granular flow structure.
Figure 2 depicts the position of individuals on a free flow (left side) and congested environment (right side). In contrast to the classical V-formation of birds, the social interactions of group members lead to a reversed V-formation, where everyone can communicate from face to face (not behind one’s back, literally). If the group has to avoid obstacles, the positions of the individuals change, with larger groups tending to split up and come back together after passing.
The coordinated group movement is often a result of a non-verbal, iterative consideration of observations and anticipated behavior of group members around [
57]. Pedestrians become passengers in the context of transportation and use corresponding infrastructures and vehicles to reaching their destinations. The tactical behavior enables (modeled) passengers to act with environmental anticipation, including knowledge about processes, infrastructure layout (navigation), and perception/processing of provided information [
58,
59,
60]. Using the model of visual human perception and modeling the necessary properties of signage components (see
Figure 3) allows for a valuable extension of the operational motion behavior approach.
The model was also applied to non-normal situations (egress) where people cannot draw on their experience. This is further complicated by the fact that special procedures usually have to be applied to these situations. For example, during evacuations, emergency exits must be used that no one had previously used since they are not part of standard movement areas. In the case of fire, the fractional effective dose model (FED [
61]) allows the consideration of the human response in a toxic gas atmosphere.
Figure 4 shows the implementation of both the numerical simulation of a toxic atmosphere during a fire and the passenger movement model inside a double-deck railway coach.
The model and the simulation environment have been continuously improved and now also enable the systematic development of appropriate passenger handling processes to take full advantage of future technologies [
51,
62]. As an example, future aircraft cabins may contain dynamically adjustable seat rows to provide a wider aisle if the corresponding seats are not in use at the current time (see the concept of the Side-Slip in
Figure 5). This additional space allows two passengers to pass each other comfortably or offers the possibility to use more easily accessible seats for passengers with reduced mobility (e.g., use of wheelchairs). Finally, integrated technology and process development open up a further field of application for improving operating concepts and testing innovative products. The on-going (data) revolution in aviation urgently requires these integrated approaches to unlock to potential of fully-digital, connected technologies, and corresponding business models.
1.4. Focus and Structure of the Document
We provide an evaluation of current concepts of operations of passenger boarding with a special focus on the transmission of SARS-CoV2 in the cabin. Therefore we derive a transmission model to determine the individual transmission probability during several standard boarding procedures, such as random or outside-in boarding strategies. Furthermore, we investigated the impact of limiting the number of hand luggage items and the use of a second door for boarding. The results are based on a reliable simulation environment, which was validated in the field and extended by the derived transmission model. Our contribution is structured as follows. After the introduction and summary of modeling the dynamic behavior of human beings in
Section 1, we provide an overview of the current knowledge about virus transmission in the context of transportation. Furthermore, we extend a transmission model to our use case of passenger boarding in
Section 2 and show the general mechanism. In
Section 3 the derived transmission model is implemented in a fast stochastic model to provide a high number of simulation runs for each selected scenario. The results of the scenario analysis are presented in
Section 4. Finally, our contribution ends with a conclusion and outlook (
Section 5).
2. Derivation of Transmission Model
Knowledge about the characteristics of SARS-CoV2 is evolving quickly as more studies become available. In this section, we derive a model for the transmission probability, based on three early studies on SARS-CoV2 propagation and general characteristics.
2.1. Understanding of SARS-CoV2
In a study from Germany, a small cluster was researched in depth [
63]. The relevant finding was that the overall secondary attack rate was below 10% for close contacts. Even prolonged meeting situations left some people without a transmission, while on another occasion a transmission happened when a pre-symptomatic person sat back to back with another person and handed over a salt dispenser. This demonstrates the relevance of even short contacts to contagious people. In particular, the contagious person was pre-symptomatic and would not have been rejected for air travel by symptom-based detection strategies. A study on the outbreak of COVID19 in the Italian town of Vò shows that the number of asymptomatic cases was at roughly 45% out of the entire number of cases [
64]. This means that even if symptomatic passengers are rejected from flying, the probability of having contagious passengers is still considering if the virus is active in a population. This is considered the most problematic characteristic of SARS-CoV2, next to the fact that also pre-symptomatic passengers are contagious. A study from Guangzhou and Hong Kong estimated the incubation period as 5.2 days on average and—more importantly—the onset of infectiousness 2 days before the start of symptoms [
2]. The peak of infectiousness is estimated at half a day before symptoms onset. Thus, contagious people are likely to travel despite their best intentions and pose a similar or even higher danger than infected people with clear illness symptoms.
In general, the coronavirus will survive for some time on surfaces, especially metal and synthetic material [
65]. The contagiousness of surfaces touched by multiple passengers is hence of concern. However, the virus load of asymptomatic or pre-symptomatic passengers likely puts on surfaces is limited, as he does not cough or sneeze. The overall contribution of contact transmission to the overall transmission is currently deemed low.
Key parameters of epidemic spread were analyzed to evaluate the contribution of different transmission routes [
66]. Therefore, a transmission rate of 45% from pre-symptomatic events and 5% from the asymptomatic event was assumed. The study further assumed the transmission risk from contaminated surfaces at 10%. Consequently, a counter-infection strategy relying primarily on eliminating contact infection (for example through repeated disinfection of the cabin interiors) will not reduce infection risk sufficiently. However, the reduction of contact infections remains an effective element of a comprehensive containment strategy and will also help to prevent the transmission of other diseases.
2.2. Modelling Approach
Agent-based models allow for an efficient implementation of individual interactions in simulation environments. Transmission models require several parameters, foremost the distance between agents and the duration of the interaction [
67,
68].
A comparable work has been published, in which an agent-based mobility model of an entire city was used to show the spread of SARS-CoV2 as a function of different public distancing measures [
69]. The problem encountered was that the character of the individual contacts could not be modeled in its entirety. That is, the time and distance between agents when being in the same place (e.g., in an office or a public transport vehicle) is based on probabilities.
Our approach of an agent-based model provides a more profound estimation of the quality of the contact between passengers. The initial idea of the transmission model [
67] is shown in Equation (
1) and specifically useful for diseases that spread via droplets or aerosols, such as SARS-CoV2.
The sum is performed for each person n over all contagious persons m, with the following variables and parameters.
- -
the probability of the person n to receive an infectious dose. This shall not be understood as “infection probability”, because this strongly depends on the immune response by the affected person.
- -
the calibration factor for the specific disease
- -
the shedding rate, the amount of virus the person m spreads during the time step t
- -
the intensity of the contact between n and m, which corresponds to their distance
- -
the time the person n interacts with person m during the time step t
The resulting probability has to be understood as a possible transmission event, or dangerous contact. It is not the infection probability. Unfortunately, current research does not provide any data to calibrate the model parameters for the SARS-CoV2 case. Besides the distance between the passengers, further factors could impact the transmission and should be reflected carefully to derive a reasonable parameter setting.
- -
If the cabin ventilation is active (which is highly desirable and probably mandatory in times of pandemic air travel) the air is circulated and quickly replaced. The exhale of a person does not remain in a place for very long. Hence the distance threshold is set lower than for other interior settings.
- -
Droplets sink to the ground, and the cabin ventilation also injects fresh air into the upper part of the cabin and extracts at floor level. Hence a passenger located at a lower position is more susceptible to the virus exhaled from a passenger being located higher than vice versa. This is relevant when people in the aisle pass seated passengers.
- -
The virus load increases with physical activity simply as more air is exchanged in the lungs. Talking (especially very loud, or even singing) also increases virus load in the exhale. Hence, the model considers moving passengers as having a higher shedding rate than seated passengers. Shedding rates are even higher when passengers store luggage in overhead bins or squeeze themselves into window seats.
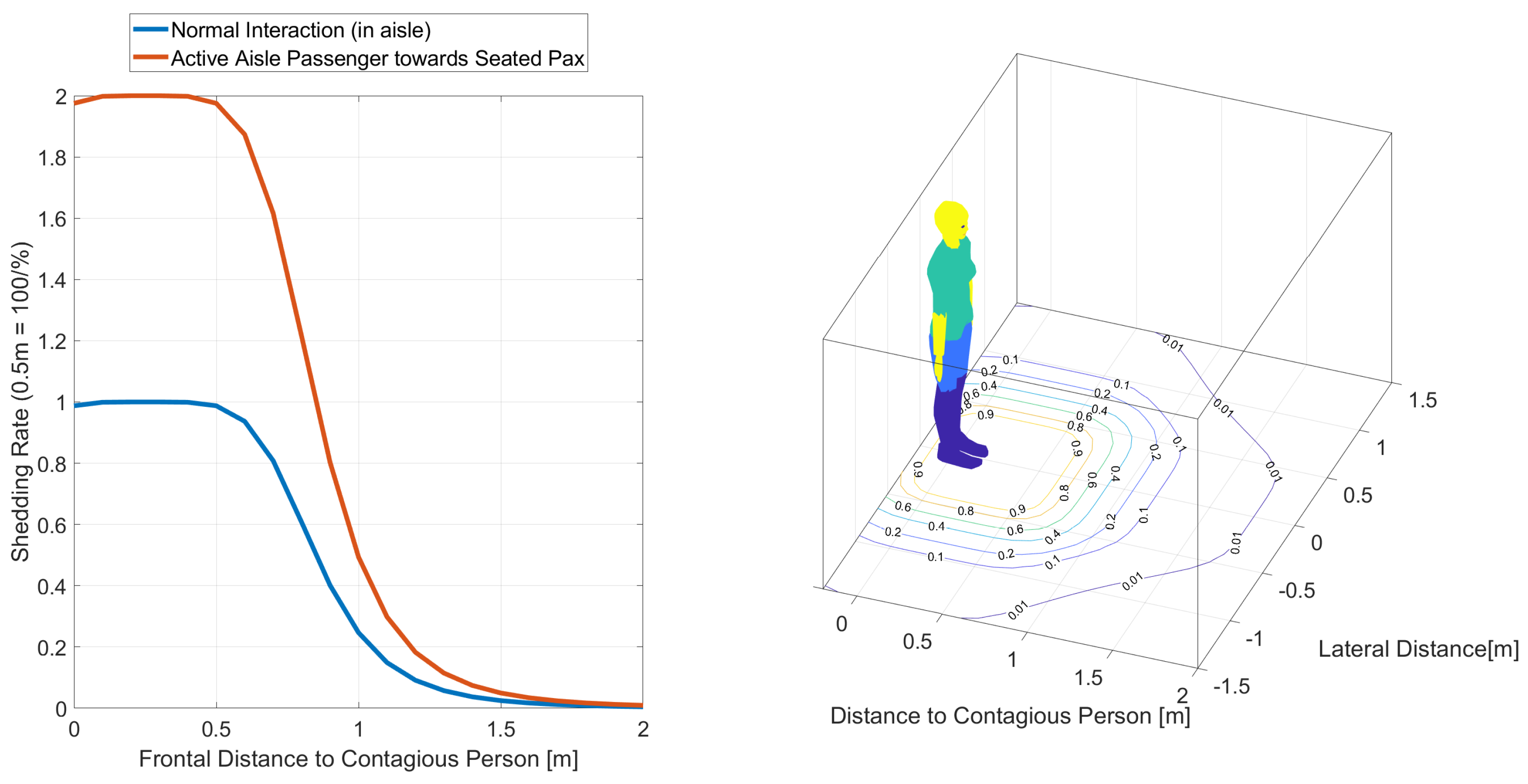
In this context, the shedding rate and hence the infection probability is considerably higher, when a passenger stands in the aisle, stowing his bulky carry-on luggage, in contrast to a seated passenger at an aisle seat. The airflow characteristics of the aircraft cabin would further transport the exhale of the standing passengers along with the seated one. The used boarding simulation offers the advantage that it considers these events with increased detail due to their relevance for normal boarding operations. In our approach, we define the shedding rate
as a normalized bell-shaped function (Equation (
2)) with
for both longitudinal and lateral dimensions, respectively.
The parameters are
a (scaling factor),
b (slope of leading and falling edge), and
c (offset) to determine the shape of the curve. The parameters have been initially set to
,
,
,
,
, and
. This provides the spread in y-direction (lateral) a slightly smaller footprint than in x-direction (longitudinal). The spread in x-direction is higher in front of the index case than behind it (see
Figure 6).
Finally, the individual probability for virus transmission
is corresponds to
, the specific intensity (dose) per time step (Equation (
3)). As an example, if a passenger should reach a probability of 1 after standing 10 s in the closest distance in front of an infected passenger (SR
)
has to be set to a value of
.
2.3. Calibration of Transmission Model
The behavior of actual diseases is deterministic and the model needs to be calibrated so that for a combination of time and intensity (corresponding to distance) the transmission probability can be set. Additional to the limited understanding of SARS-CoV2 transmissions in operational environments comes the fact that different individual immune responses exist (some people are more susceptible than other, for example as exposure to other corona-type virus has created a base immunity). This implies that we are more likely to derive an estimated range for the input parameters than to provide a well-founded calibration of the model. For this attempt, we use the case of Air China Flight 112 from 15 March 2003. On this flight from Hong Kong to Peking 22 passengers were being infected by a single index case [
8]. This particular flight was responsible for a considerable spread of SARS-CoV1 throughout Asia and is considered a super spreading event. But unfortunately, little is known about this flight: 3 h trip length, Boeing 737-300 aircraft, no information about equipage with HEPA filter. The subsequent contact tracing determined later that the transmission for all passengers most likely happened during this flight event. There is no way to determine whether the infection happened during the flight, during the boarding, or during any process before or afterward (for example when boarded with buses).
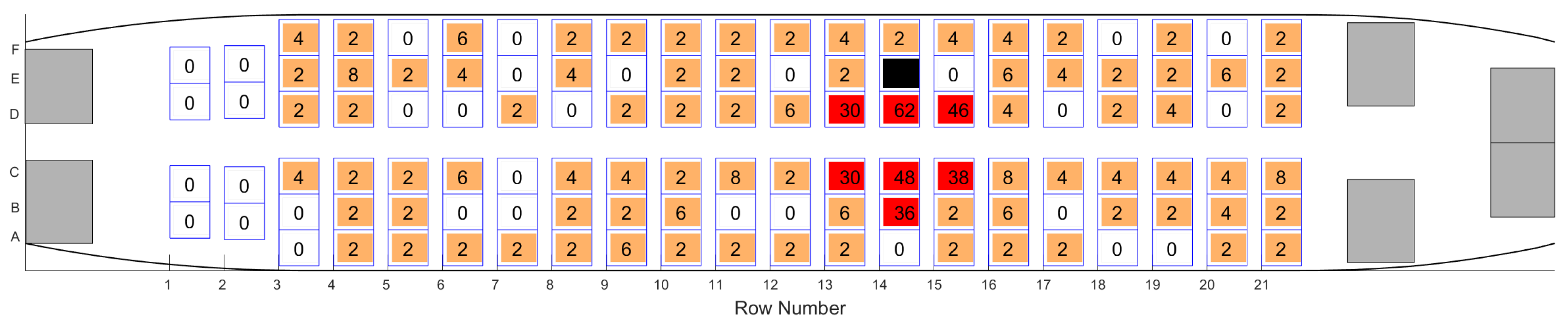
For our calibration approach, we decided to have one index case seated at 14E in a virtual Boeing 737-300 (
Figure 7). The initial values of the input parameters (see Equation (
2)) are chosen to ensure that about one-third of the total infections are probable. This setup was tested for 50 boarding-deboarding scenarios and the results confirm both assumptions: (a) transmissions do happen far away from the index case, and (b) the majority of infections would happen in proximity to the index case. Finally, the value for
is set to
while the other parameters remain unchanged at their original values. Furthermore, we will assume a doubled shedding rate during the storage of hand luggage items and entering the seat row, since these are physical activities with a short distance to surrounding passengers.
We are aware of the fact, that our calibration is a straightforward approach. Several assumptions were taken and it is not proven that Air China Flight 112 is the single source for all transmissions. It shall be stressed again that the resulting number is not the transmission probability, but a measure of impact if the index case is highly contagious. This means that below a threshold of 100% we consider a transmission as unlikely. If a person becomes infected depends on many factors beyond the viral load itself.
In the following analyses, we consider always a single index case per aircraft, which is a 174 seat single-aisle aircraft (29 rows). If the infection rate in a population is about 5 persons per week and 100,000 people (average rate in Germany between 18th and 25th of May 2020), the probability of having an infectious person on board a fully booked 174 seat aircraft can be assumed to be less than 5%. This considers the absence of apparently ill people but considers the pre-symptomatic and asymptomatic cases. It further does not account for any contact tracing and subsequent quarantine. This rough calculation is not provided herein detail as it does not influence the result, it is provided to explain why we do not assume more than a single index case.
3. Passenger Boarding Model Using Operational and Individual Constraints
In our contribution, we use a cellular automata model, which is based on individual transition probabilities to move to adjacent positions around the current position [
70]. The model was developed to provide a stochastic approach covering short (e.g., avoid collisions, group behavior [
57]) and long-range interactions (e.g., tactical wayfinding) [
59].
3.1. Operational Constraints and Rules of Movement
To reflect operational conditions of aircraft and airlines (e.g., seat load factor, compliance to the boarding procedure) as well as the non-deterministic nature of the underlying processes (e.g., amount and distribution of hand luggage) a stochastic model was developed [
46,
71] and calibrated [
54,
72]. Herein, the passenger boarding can be understood as a stochastic, forward-directed, one-dimensional, and discrete (time and space) process, which is mapped to a regular grid. An appropriate mapping of the aircraft seat layout is shown in
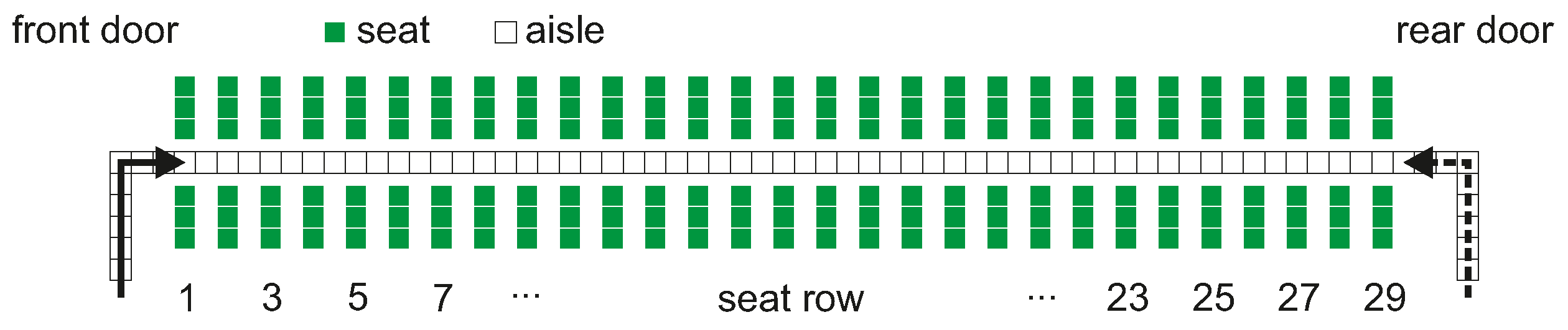
Figure 8 (Airbus A320, 29 rows, 174 seats). This regular grid consists of equal cells with a size of 0.4 × 0.4 m, whereas a cell can either be empty or contain exactly one passenger.
The boarding progress consists of a simple set of rules for the passenger movement: (a) enter the aircraft at the assigned door (based on the current boarding scenario), (b) move forward from cell to cell along the aisle until reaching the assigned seat row, and (c) store the baggage (aisle is blocked for other passengers) and take the seat. The storage time for the hand luggage depends on the individual number of hand luggage items. The seating process depends on the constellation of already used seats in the corresponding row. The stochastic nature of the boarding model requires a minimum of simulation runs for each selected scenario to derive reliable simulation results. In this context, a simulation scenario is mainly defined by the underlying seat layout, the number of passengers to board (seat load factor, default: 85%), the arrival frequency of the passengers at the aircraft, the number of available doors (default 1 door), the specific boarding strategy (default: random) and the compliance of passengers in following the current strategy (default: 85%). Further details regarding the model and the simulation environment are available at [
16].
In the simulation environment, the boarding process is implemented as follows. Depending on the seat load, a specific number of randomly chosen seats are used for boarding. For each seat, a passenger (agent) is created. The agent contains individual parameters, such as the number of hand luggage items, maximum walking speed in the aisle (set for all agents to 0.8 m/s [
43,
54]), seat coordinates, time to store the hand luggage and arrival time at the aircraft door. To create the time needed to store the hand luggage, a stochastic distribution is used. The agents are sequenced concerning their seats and the current boarding strategy. From this sequence, a given percentage of agents are taken out of the sequence (non-compliant behavior) and inserted into a position, which contradicts the current strategy (e.g., inserted into a different boarding block).
According to the exponential arrival time distribution and the boarding sequence, each agent gets a timestamp to appear on the aircraft door queue. When the simulation starts, the first agent of the queue always enters the aircraft by moving from the queue to the entry cell of the aisle grid (aircraft door), if this cell is free. In each simulation step, all agents located in the row are moved to the next cell, if possible (free cell and not arrived at the seat row), using a shuffled sequential update procedure (emulate parallel update behavior [
59,
70]). If the agent arrives at the assigned seat row, he blocks this position as long as the time needed to store the hand luggage. Depending on the seat row condition (e.g., blocked aisle or middle seat or both), additional time is added to perform the seating process (seat shuffle). The aisle is blocked for passing during the whole seating process. Each boarding scenario is simulated 125,000 times, to derive statistically relevant results defined by average boarding time (start with the first passenger arrives the aircraft and finished when the last passenger is seated) and standard deviation of the boarding time.
In general, boarding strategies follow three basic approaches: boarding per rows (aggregated to blocks), boarding per seat (window, middle, aisle), and sequences of specific seats.
Figure 9 (left) depicts how the boarding strategies and operational constraints are implemented in the boarding model. The seats are color-coded to emphasize the order of aircraft seats. In our contribution we will consider six different boarding strategies (and deboarding): random, back-to-front (based on 2 boarding blocks), optimized block (based on 6 boarding blocks), outside-in (window seats first, aisle seats last), reverse pyramid (back-to-front plus outside-in with 6 blocks), and individual seating. These strategies cover the most relevant operational and scientific approaches for passenger boarding. For the random boarding, passengers arrive with no specific chronological order. Finally, the individual boarding strategy is a specific solution of the optimized block (alternating rows) and outside-in strategy, where each block contains only one seat.
Figure 9 (right) additionally emphasizes how the operational constraints of 1st class seats, passenger compliance to the boarding strategy, seat load factor, and the existence of groups are covered by the boarding model.
3.2. Model Adaption
The actual model for passenger boarding has to be adapted for considering different approaches addressing a reduced transmission probability during boarding. These approaches primarily focus on the two major concepts of distance keeping and reduction of contact times, where both concepts result in a lower chance to get in close contact with a probably infected passenger. To get an initial picture and a valid baseline about interactions in the aircraft cabin, all interactions between passengers will be counted. The idea is to identify the number of individual contacts and the duration of these contacts. The following rules are applied.
- -
A passenger is moving forward in the aisle, except the next position is blocked by another passenger. This blocking is counted as interaction for both passengers.
- -
Entering the seat row demands a minimum of movements to reach the seat, which depends on the already used seats. All involved passengers are marked as interacting.
- -
Each interaction is only counted one time (at the first appearance), to derive the number of individual contacts.
Counting the individual contacts will provide the first indication about potential ways of infections, but as introduced in
Section 2, the severity (measured by distance) and the duration of an individual contact have to be considered as well. Thus the introduced infection model provides an additional quantification.
4. Scenario Analyses and Results
Before different boarding (de-boarding) strategies are evaluated, a baseline setup will be introduced (cf. [
16]). As
Table 1 exhibits, each boarding strategy results in a specific boarding time, which is measured by an average time value and standard deviation of the boarding time. The boarding time mainly depends on the number of passengers and their interactions in the aircraft cabin. Thus, an increased amount of interactions (contacts) also increase the boarding time. The random boarding is taken as the reference case and points out an average of 3.5 individual contacts per passenger during boarding with a corresponding relative standard deviation (RSD) of 36%. The RSD is defined as the standard deviation divided by the average value. If block-based strategies are applied, the average number of contacts only slightly changes from the random boarding. More complex strategies addressing a minimized interaction during the seating process (outside-in) and combination of both block and seat consideration (reverse pyramid) result in a decrease to approx. 2.7 contacts on average. Finally, the approach for the individual-based sequence results in 2.2 contacts (RSD of 53). The deboarding case exhibits a significantly higher amount of individual contacts since the passengers stand near the aisle and take their hand luggage out of the overhead compartments whereas other passengers passing. This specific contact is counted for both passengers standing, whereas passing seated passengers is not considered as direct individual contact in this simplified approach. These indirect contacts (passing seated passengers) are considered in
Section 4.3, where the introduced transmission model is applied for a more accurate evaluation of the overall transmission probability.
4.1. Distance Keeping
As already introduced and analyzed in detail [
59,
70,
73], social and long-range interaction could be reliably modeled by using a floor field. This field contains information about preceding passengers, which allows for a long-range interaction even considering adjacent cells around the actual position. So each passenger will leave a trace with a given length during movement to block the corresponding cells and indicate the minimum distance required. As
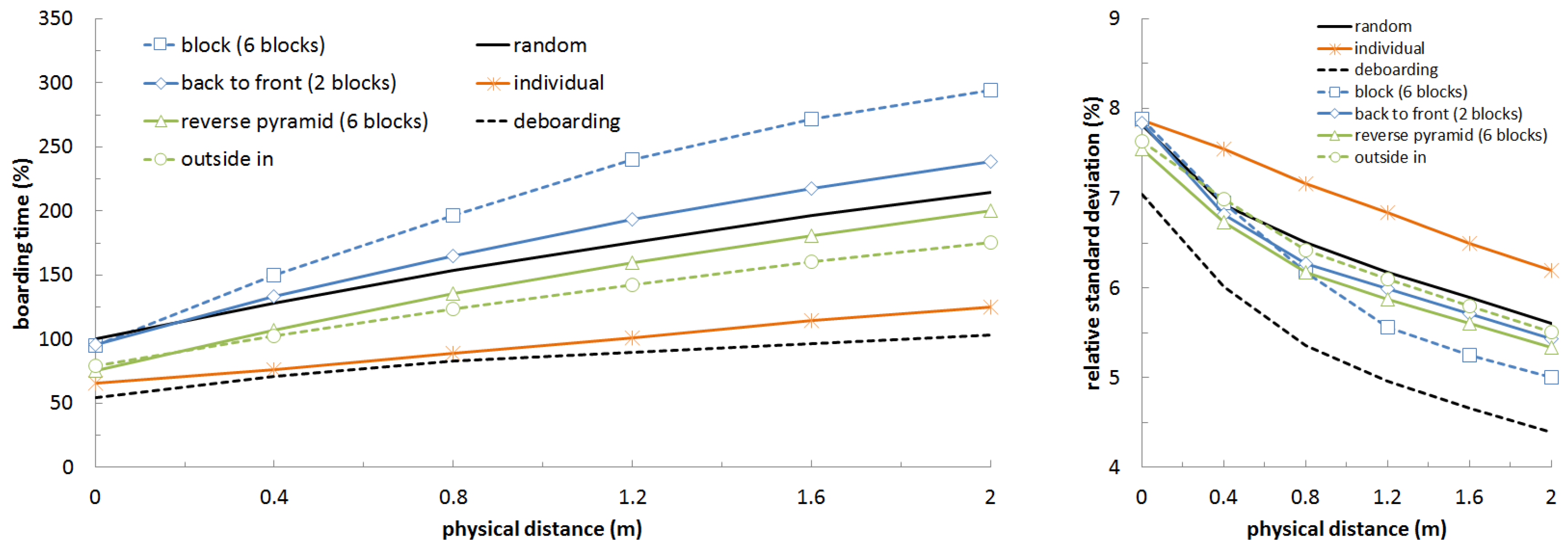
Figure 10 exhibits, an increasing physical distance results and in a longer boarding time accompanied by a decreased standard deviation. Assuming a minimum distance of 1.6 m, which corresponds to 4 grid cells in the stochastic model, the boarding time is nearly doubled for random boarding.
The effect of physical distance superimposes all advantages by a significantly reduced arrival rate and the completely coupling of the individual passenger movements. This is also indicated by the reduced relative standard deviations, as depicted in
Figure 10 (right). Furthermore, the increased distance between passengers results in a worse performance of block-based boarding strategies. This would be also true for the individual boarding, which follows the idea that each row is a block and this block should be boarded with window seat first and aisle seat last (outside-in). The distance of subsequently following blocks has to be adapted according to the required distance of the passengers. Finally, each (optimized) block-based strategy will converge to this individual approach.
On the positive side, the introduced physical distance reduces the direct contact of a passenger in the aisle to zero. As
Table 2 shows, the remaining individual contacts result from the seating process. When a passenger arrives at the seat row and some seats already used by other passengers then these passengers have to stand up to allow entering the row if necessary, e.g., window seat to be taken and the middle seat is occupied. This process is time-consuming, because the aisle is normally blocked during this seat shuffle, and consists of close distances between the involved passengers. The implementation of the outside-in boarding strategy leads to a minimum of these time-consuming shuffles, because here first the window seats, then the middle seats, and finally the aisle seats are being taken. As mentioned in
Section 3, the passenger compliance to the boarding strategies will be not 100% since passengers arrive late or family members will not be separated. Therefore the number of contacts in
Table 2 still show a value different from zero for all strategies.
4.2. Reduction of Hand Luggage Items
It will be assumed that the amount of hand luggage will be significantly reduced by the airline to ensure a shorten time storing the hand luggage in the overhead compartment. If the average number of hand luggage is reduced by 50%, the boarding time decreased by approx. 20% using random passenger sequences [
16]. Since we expect all SARS-CoV2 related modification of the boarding process will have a negative impact, we will implement a significant reduction of hand luggage items (50%) in our scenarios to ensure that each passenger can store his items in the corresponding overhead compartment at any time. As
Table 2 points out, the average number of individual contacts is significantly reduced but at the cost of the doubled boarding time. Thus, the random and block-based strategies lead to an average of 0.9 contacts with an RSD of approx 85% (standard deviation of approx. 0.8). The seat-based strategies only show 0.2 individual contacts associated with RSD value higher than 200% (standard deviation of approx. 0.5). The number of direct contacts during deboarding is only reduced by 0.3 points.
The approach to limit the number of hand luggage items to 50% of the standard amount mitigates the effect of longer boarding times. In conclusion, the boarding time of today random boarding strategy could be reached with 1.6 m distance rule, using a passenger-wise, time-consuming presorting, and 50% reduction of hand luggage items. The boarding time for the random strategy increases by 54% under the same conditions.
The often mentioned approach of having a free middle seat will also result in less interaction during seating but also result in a 33% reduced seat load, which may result in efficient airline operations from an ecological and economic perspective. This scenario could not be compared directly to the random strategy since the number of passengers is intentionally reduced, which consequently reduces the direct contacts as well.
4.3. Transmission Approach
At this stage, the interactions between passengers are only individually counted but not evaluated against their probability to get passengers infected. Therefore Equations (
2) and (
3) are implemented using the following parameters for longitudinal
x (in the direction of motion) and lateral propagation
y (across to the direction of motion):
,
,
,
;
,
,
,
;
, one randomly selected passenger as SARS-CoV2 source. Furthermore, we introduce an amplification factor of 2 to reflect the higher intensity of interactions during the hand luggage storage and seating process. This factor is active if the infected passengers start to store his luggage until he is finally seated. This approach opens up a more detailed assessment, but also contains a high degree of uncertainty, because although we have chosen a reasonable approach, it is not based on a reliable data set or scientific validation. We hope that upcoming research will help us to gain additional insights into this highly dynamic process.
In the following
Table 3 the necessity to distinguish between the simplified approach of counting individual contacts in the aisle and the more differentiated approach of assessing possible transmissions around an infected passenger is emphasized. In particular, the implemented back-to-front strategy exhibits lower values for the transmission probability than the optimized block strategy. If passengers board in blocks from the back to the front, the chance of passing an infected person is reduced to a minimum, as confirmed by the calculated reduction of the transmission probability. This effect is also a root cause of the low transmission probabilities of outside-in, reverse pyramid, and individual boarding strategy. The table shows also the impact of distance keeping and reduction of hand luggage, e.g., the reference case of random boarding initially shows an average value of 5.9 possible transmissions which could be reduced by both operational changes finally to 1.1 possible transmissions. All these reductions are accompanied by an increase in the RSD values. Again, deboarding shows only minor changes.
4.4. Two Door Operations (Front and Rear Door)
The left front door is regularly used during standard boarding procedures at gate positions. Apron positions or special gate positions allow for the use of two doors for boarding and deboarding. The approach of using two doors accelerates the boarding progress and also results in reduced values for possible transmissions.
Table 4 exhibits that the boarding time for two-door operations with a reduction of 50% hand luggage items reaches the reference time for random boarding using one door.
5. Discussion and Outlook
The new coronavirus SARS-CoV2 has demonstrated high contagiousness even before infected people show any symptoms. Surface disinfection does not reduce the infection risk sufficiently as the majority of transmission is observed as droplet-based. However, the transmission probability during the flight itself is currently deemed low due to the airflow patterns in a cabin, the dry air, and the effectiveness of filtering systems in the aircraft. Research on previous diseases has further shown the relevance of the pre- and post-flight processes, such as boarding and deboarding. In our contribution, we address this issue using a stochastic cellular automata model and a transmission model, which was calibrated using an event from the previous SARS epidemic. The resulting transmission probabilities are likely to be conservative (means: higher than in actual life). We are not considering face masks in our model approach. The boarding and deboarding simulation were performed using a single-aisle aircraft with 174 seats, representative for the majority of Airbus A320 and Boeing B737 family aircraft in service. Several different boarding strategies are applied. There is a single infected person among the passengers, its seat position and entry position are randomly set and the result averaged over 125,000 simulation runs.
The standard random boarding without additional distances and normal carry-on luggage results in about 5–6 critical contacts between passengers. Changing the boarding procedure reduces the number of contacts by more than half. Introducing a distancing of 1.6 m reduces the number of critical contacts for the random boarding to about 1–2. Hence, distancing alone does not eliminate these contacts. Carry-on luggage influences the time spent in the aisle at a high physical workload (high shedding rate). Reducing the luggage by 50% reduces the number of critical contacts to about 1 for the random boarding. Boarding procedures like outside-in or reverse pyramid have a profound effect and reduce the number of critical contacts substantially below 1, even with normal carry-on luggage. Particularly, the use of the rear door will reduce the transmission probability significantly for all boarding strategies.
The transmission probability during deboarding is only slightly influenced since physical distancing is difficult if not impossible to impose. The number of contacts and the transmission probability remain at a high level, which indicates deboarding as the critical process in the aircraft cabin. To reduce the transmission probability, the timing of passengers entering the aisle during deboarding would need to be controlled. Further measures like having active ventilation after engine shutdown should be discussed with experts on cabin ventilation. This study does make any statements regarding the risk during normal seating. Cited studies have shown that the infection risk is very low, also with normal seating densities. Reducing the risk through boarding and deboarding provides the advantage, that remaining infection risk is limited to the passengers directly around the index case.
The used transmission model is not sufficiently calibrated to make a strong conclusion about actual transmission probabilities. Therefore we introduce the term critical contacts. We interpret our simulation results as such that we recommend boarding procedures that minimize interactions between passengers. The application of seat-based boarding procedures recovers some of the additional boarding time needed through the introduced physical distancing. The use of two doors for boarding will provide a good solution for a reduced transmission risk inside and outside the cabin if near apron stands could be used and passengers could walk from the terminal to the aircraft. This kind of walk boarding also prevents passengers from standing in the badly ventilated jetway during the boarding. Deboarding is difficult to control through procedures and passengers have demonstrated little discipline and high eagerness to leave the aircraft. We think this event should be given increased attention, and either procedural or technical solutions considered.
Carry-on luggage has substantial influence. It should be considered to limit the carry-on to the amount which can be put into the overhead bins with little effort or increasing the carry-on capacity in the cabin. Assigning a place in the overhead bin for each passenger with carry-on may further reduce the storage time and reduce contacts. This should also have a favorable effect on the boarding times, also after the pandemic has ended. Removing the carry-on luggage entirely could be an option, but there is also a diametrical effect of increased interaction before and after the flight. Although not modeled or discussed here, other hygienic measures need also to be considered. SARS-CoV2 is not specifically known to easily transmit via contaminated surfaces. Therefore advanced hygienic measures shall be applied, and shall be focused in places where passenger interaction happens frequently, foremost the lavatories. This is specifically relevant for longer-range flights, and would also help to contain other infectiousness diseases.
The infection risk of boarding and deboarding is substantial but can be addressed. This contributes to the effort to ensure a very low and overall acceptable risk of infection when traveling by aircraft. The procedural measures that are recommended do not add any cost or unacceptable inconvenience to passengers. The reduction of critical contacts by additional physical distance alone does not eliminate the risk if random boarding is continued. Distance and different boarding procedures remove the risk for the boarding process. The not regulated passenger deboarding remains an issue. Carry-on luggage and deboarding as a whole should receive further attention. The suggested changes to the boarding process would also enhance the travel experience and reduce turnaround time in the hopefully not too distant future when the pandemic has ended.
Author Contributions
Conceptualization, M.S. and J.F.; methodology, M.S. and J.F.; software, M.S. and J.F.; validation, M.S. and J.F.; formal analysis, M.S. and J.F.; investigation, M.S. and J.F.; writing—review and editing, M.S. and J.F.; visualization, M.S. and J.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- ICAO. Effects of Novel Coronavirus (COVID-19) on Civil Aviation; Technical Report; International Civil Aviation Organisation: Montreal, QC, Canada, 2020. [Google Scholar]
- He, X.; Lau, E.H.; Wu, P.; Deng, X.; Wang, J.; Hao, X.; Lau, Y.C.; Wong, J.Y.; Guan, Y.; Tan, X.; et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med. 2020. [Google Scholar] [CrossRef]
- Gandhi, M.; Yokoe, D.S.; Havlir, D.V. Asymptomatic Transmission, the Achilles’ Heel of Current Strategies to Control Covid-19. New Engl. J. Med. 2020. [Google Scholar] [CrossRef]
- IATA. Restarting Aviation Following COVID-19; IATA: Montreal, QC, Canada, 2020. [Google Scholar]
- Vandenberg, O. Development and potential usefulness of the COVID-19 Ag Respi-Strip diagnostic assay in a pandemic context. medRxiv 2020. [Google Scholar] [CrossRef]
- Waltz, E. How Do Coronavirus Tests Work? IEEE Spectrum, 3 April 2020. [Google Scholar]
- Mangili, A.; Gendreau, M.A. Transmission of infectious diseases during commercial air travel. Lancet 2005, 365. [Google Scholar] [CrossRef]
- Olsen, S.J.; Chang, H.L.; Cheung, T.Y.Y.; Tang, A.F.Y.; Fisk, T.L.; Ooi, S.P.L.; Kuo, H.W.; Jiang, D.D.S.; Chen, K.T.; Lando, J.; et al. Transmission of the severe acute respiratory syndrome on aircraft. N. Engl. J. Med. 2003, 349, 2416–2422. [Google Scholar] [CrossRef]
- Hertzberg, V.S.; Weiss, H. On the 2-Row Rule for Infectious Disease Transmission on Aircraft. Ann. Glob. Health 2016, 82, 819–823. [Google Scholar] [CrossRef] [PubMed]
- Hertzberg, V.S.; Weiss, H.; Elon, L.; Si, W.; Norris, S.L. Behaviors, movements, and transmission of droplet-mediated respiratory diseases during transcontinental airline flights. Proc. Natl. Acad. Sci. USA 2018, 115, 3623–3627. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, K.L.; Murti, M.; Finkelstein, M.; Leis, J.A.; Fitzgerald-Husek, A.; Bourns, L.; Meghani, H.; Saunders, A.; Allen, V.; Yaffe, B.; et al. Lack of COVID-19 transmission on an international flight. Can. Med Assoc. J. 2020, 192. [Google Scholar] [CrossRef] [PubMed]
- Qian, G.Q.; Yang, N.B.; Ding, F.; Ma, A.H.Y.; Wang, Z.Y.; Shen, Y.F.; Shi, C.W.; Lian, X.; Chu, J.G.; Chen, L.; et al. Epidemiologic and Clinical Characteristics of 91 Hospitalized Patients with COVID-19 in Zhejiang, China: A retrospective, multi-centre case series. QJM Int. J. Med. 2020, hcaa089. [Google Scholar] [CrossRef] [PubMed]
- Eldin, C.; Lagier, J.C.; Mailhe, M.; Gautret, P. Probable aircraft transmission of Covid-19 in-flight from the Central African Republic to France. Travel Med. Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Schmidt, M. A review of aircraft turnaround operations and simulations. Prog. Aerosp. Sci. 2017, 92, 25–38. [Google Scholar] [CrossRef]
- Jaehn, F.; Neumann, S. Airplane boarding. Eur. J. Oper. Res. 2015, 244, 339–359. [Google Scholar] [CrossRef]
- Schultz, M. Implementation and application of a stochastic aircraft boarding model. Transp. Res. Part C Emerg. Technol. 2018, 90, 334–349. [Google Scholar] [CrossRef]
- Nyquist, D.C.; McFadden, K.L. A study of the airline boarding problem. J. Air Transp. Manag. 2008, 14, 197–204. [Google Scholar] [CrossRef]
- Mirza, M. Economic Impact of Airplane Turn-Times. Aero Q. 2008, 4, 14–19. [Google Scholar]
- Cook, A.; Tanner, G. European Airline Delay Cost Reference Values—Updated and Extended Values (Version 4.1); Technical Report; EUROCONTROL Performance Review Unit: Brussels, Belgium, 2015. [Google Scholar]
- Delcea, C.; Cotfas, L.A.; Paun, R. Agent-Based Evaluation of the Airplane Boarding Strategies’ Efficiency and Sustainability. Sustainability 2018, 10, 1879. [Google Scholar] [CrossRef]
- Marelli, S.; Mattocks, G.; Merry, R. The Role of Computer Simulation in Reducing Airplane Turn Time. Boeing AERO Mag. 2018, 1. [Google Scholar]
- Van Landeghem, H.; Beuselinck, A. Reducing passenger boarding time in airplanes: A simulation based approach. Eur. J. Oper. Res. 2002, 142, 294–308. [Google Scholar] [CrossRef]
- Ferrari, P.; Nagel, K. Robustness of Efficient Passenger Boarding Strategies for Airplanes. Transp. Res. Rec. 2005, 1915, 44–54. [Google Scholar] [CrossRef]
- van den Briel, M.H.L.; Villalobos, J.R.; Hogg, G.L.; Lindemann, T.; Mulé, A.V. America West Airlines Develops Efficient Boarding Strategies. INFORMS J. Appl. Anal. 2005, 35, 191–201. [Google Scholar] [CrossRef]
- Bachmat, E.; Elkin, M. Bounds on the performance of back-to-front airplane boarding policies. Oper. Res. Lett. 2008, 36, 597–601. [Google Scholar] [CrossRef]
- Schultz, M.; Schulz, C.; Fricke, H. Efficiency of Aircraft Boarding Procedures. In Proceedings of the 3rd International Conference on Research in Airport Transportation, Fairfax, VA, USA, 1–4 June 2008; pp. 371–377. [Google Scholar]
- Bachmat, E.; Khachaturov, V.; Kuperman, R. Optimal back-to-front airplane boarding. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2013, 87, 062805. [Google Scholar] [CrossRef] [PubMed]
- Steffen, J.H. Optimal boarding method for airline passengers. J. Air Transp. Manag. 2008, 14, 146–150. [Google Scholar] [CrossRef]
- Bazargan, M. A linear programming approach for aircraft boarding strategy. Eur. J. Oper. Res. 2007, 183, 394–411. [Google Scholar] [CrossRef]
- Steffen, J.H. A statistical mechanics model for free-for-all airplane passenger boarding. Am. J. Phys. 2008, 76, 1114–1119. [Google Scholar] [CrossRef]
- Frette, V.; Hemmer, P.C. Time needed to board an airplane: A power law and the structure behind it. Phys. Review. E Stat. Nonlinear Soft Matter Phys. 2012, 85, 011130. [Google Scholar] [CrossRef]
- Bernstein, N. Comment on “Time needed to board an airplane: A power law and the structure behind it”. Phys. Review. E Stat. Nonlinear Soft Matter Phys. 2012, 86, 023101. [Google Scholar] [CrossRef]
- Jafer, S.; Mi, W. Comparative Study of Aircraft Boarding Strategies Using Cellular Discrete Event Simulation. Aerospace 2017, 4, 57. [Google Scholar] [CrossRef]
- Tang, T.Q.; Wu, Y.H.; Huang, H.J.; Caccetta, L. An aircraft boarding model accounting for passengers’ individual properties. Transp. Res. Part C Emerg. Technol. 2012, 22, 1–16. [Google Scholar] [CrossRef]
- Qiang, S.J.; Jia, B.; Xie, D.F.; Gao, Z.Y. Reducing airplane boarding time by accounting for passengers’ individual properties: A simulation based on cellular automaton. J. Air Transp. Manag. 2014, 40, 42–47. [Google Scholar] [CrossRef]
- Milne, R.J.; Salari, M. Optimization of assigning passengers to seats on airplanes based on their carry-on luggage. J. Air Transp. Manag. 2016, 54, 104–110. [Google Scholar] [CrossRef]
- Milne, R.J.; Kelly, A.R. A new method for boarding passengers onto an airplane. J. Air Transp. Manag. 2014, 34, 93–100. [Google Scholar] [CrossRef]
- Zeineddine, H. A dynamically optimized aircraft boarding strategy. J. Air Transp. Manag. 2017, 58, 144–151. [Google Scholar] [CrossRef]
- Steiner, A.; Philipp, M. Speeding up the airplane boarding process by using pre-boarding areas. In Proceedings of the 9th Swiss Transport Research Conference, Ascona, Switzerland, 9–11 September 2009; p. 30. [Google Scholar]
- Wallace, R. The Flying Carpet. Available online: http://the-flying-carpet.com/wp-content/uploads/2013/11/The-Flying-Carpet-Information-Brochure.pdf (accessed on 29 June 2020).
- Wittmann, J. Customer-oriented optimization of the airplane boarding process. J. Air Transp. Manag. 2019, 76, 31–39. [Google Scholar] [CrossRef]
- Milne, R.J.; Delcea, C.; Cotfas, L.A.; Salari, M. New methods for two-door airplane boarding using apron buses. J. Air Transp. Manag. 2019, 80, 101705. [Google Scholar] [CrossRef]
- Schultz, M. Fast Aircraft Turnaround Enabled by Reliable Passenger Boarding. Aerospace 2018, 5, 8. [Google Scholar] [CrossRef]
- Yazdani, D.; Omidvar, M.N.; Deplano, I.; Lersteau, C.; Makki, A.; Wang, J.; Nguyen, T.T. Real-time seat allocation for minimizing boarding/alighting time and improving quality of service and safety for passengers. Transp. Res. Part C Emerg. Technol. 2019, 103, 158–173. [Google Scholar] [CrossRef]
- Bachmat, E.; Berend, D.; Sapir, L.; Skiena, S.; Stolyarov, N. Analysis of Airplane Boarding Times. Oper. Res. 2009, 57, 499–513. [Google Scholar] [CrossRef]
- Schultz, M.; Kunze, T.; Fricke, H. Boarding on the critical path of the turnaround. In Proceedings of the 10th USA/Europe Air Traffic Management Research and Development Seminar, Chicago, IL, USA, 10–13 June 2013. [Google Scholar]
- Chung, C. Simulation Design Approach for the Selection of Alternative Commercial Passenger Aircraft Seating Configurations. J. Aviat. Technol. Eng. 2012, 2. [Google Scholar] [CrossRef]
- Fuchte, J.C. Enhancement of Aircraft Cabin Design Guidelines with Special Consideration of Aircraft Turnaround and Short Range Operations. Ph.D. Thesis, Technische Universität Hamburg-Harburg, Hamburg, Germany, 2014. [Google Scholar]
- Schmidt, M.; Nguyen, P.; Hornung, M. Novel Aircraft Ground Operation Concepts Based on Clustering of Interfaces; SAE Technical Paper 2015-01-2401; SAE International: Warrendale, PA, USA, 2015; ISSN 0148-7191, 2688-3627. [Google Scholar] [CrossRef]
- Schmidt, M.; Heinemann, P.; Hornung, M. Boarding and Turnaround Process Assessment of Single- and Twin-Aisle Aircraft. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, AIAA SciTech Forum, American Institute of Aeronautics and Astronautics, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Schultz, M. Dynamic change of aircraft seat condition for fast boarding. Transp. Res. Part C Emerg. Technol. 2017, 85, 131–147. [Google Scholar] [CrossRef]
- Steffen, J.H.; Hotchkiss, J. Experimental test of airplane boarding methods. J. Air Transp. Manag. 2012, 18, 64–67. [Google Scholar] [CrossRef]
- Gwynne, S.M.V.; Senarath Yapa, U.; Codrington, L.; Thomas, J.R.; Jennings, S.; Thompson, A.J.L.; Grewal, A. Small-scale trials on passenger microbehaviours during aircraft boarding and deplaning procedures. J. Air Transp. Manag. 2018, 67, 115–133. [Google Scholar] [CrossRef]
- Schultz, M. Field Trial Measurements to Validate a Stochastic Aircraft Boarding Model. Aerospace 2018, 5, 27. [Google Scholar] [CrossRef]
- Kierzkowski, A.; Kisiel, T. The Human Factor in the Passenger Boarding Process at the Airport. Procedia Eng. 2017, 187, 348–355. [Google Scholar] [CrossRef]
- Miura, A.; Nishinari, K. A passenger distribution analysis model for the perceived time of airplane boarding/deboarding, utilizing an ex-Gaussian distribution. J. Air Transp. Manag. 2017, 59, 44–49. [Google Scholar] [CrossRef]
- Schultz, M.; Rößger, L.; Fricke, H.; Schlag, B. Group Dynamic Behavior and Psychometric Profiles as Substantial Driver for Pedestrian Dynamics. In Pedestrian and Evacuation Dynamics 2012; Springer International Publishing: Cham, Switzerland, 2013; pp. 1097–1111. [Google Scholar] [CrossRef]
- Schultz, M.; Schulz, C.; Fricke, H. Enhanced Information Flow and Guidance in Airport Terminals using best Passenger‘s Visual Perception. In Proceedings of the 6th EUROCONTROL Innovative Research Workshop, Bretigny-sur-Orge, France, 4–6 December 2007; pp. 149–156. [Google Scholar]
- Schultz, M. Entwicklung eines individuenbasierten Modells zur Abbildung des Bewegungsverhaltens von Passagieren im Flughafenterminal. Ph.D. Thesis, Technische Universität Dresden, Faculty of Transport and Traffic Sciences “Friedrich List”, Dresden, Germany, 2010. [Google Scholar]
- Schultz, M.; Fricke, H. Managing Passenger Handling at Airport Terminal. In Proceedings of the 9th USA/Europe Air Traffic Management Research and Development Seminar, Berlin, Germany, 14–17 June 2011. [Google Scholar]
- Speitel, L.C. Fractional effective dose model for post-crash aircraft survivability. Toxicology 1996, 115, 167–177. [Google Scholar] [CrossRef]
- Schultz, M. Faster aircraft boarding enabled by infrastructural changes. In Proceedings of the 2017 Winter Simulation Conference (WSC), Las Vegas, NV, USA, 3–6 December 2017. [Google Scholar] [CrossRef]
- Böhmer, M.M.; Buchholz, U.; Corman, V.M.; Hoch, M.; Katz, K.; Marosevic, D.V.; Böhm, S.; Woudenberg, T.; Ackermann, N.; Konrad, R.; et al. Outbreak of COVID-19 in Germany Resulting from a Single Travel-Associated Primary Case. Lancet Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Lavezzo, E.; Franchin, E.; Ciavarella, C.; Cuomo-Dannenburg, G.; Barzon, L.; Del Vecchio, C.; Rossi, L.; Manganelli, R.; Loregian, A.; Navarin, N.; et al. Suppression of COVID-19 outbreak in the municipality of Vo’, Italy. medRxiv 2020. [Google Scholar] [CrossRef]
- Van Doremalen, N.; Bushmaker, T.; Morris, D.H.; Holbrook, M.G.; Gamble, A.; Williamson, B.N.; Tamin, A.; Harcourt, J.L.; Thornburg, N.J.; Gerber, S.I.; et al. Aerosol and Surface Stability of SARS-CoV-2 as Compared with SARS-CoV-1. N. Engl. J. Med. 2020, 382, 1564–1567. [Google Scholar] [CrossRef]
- Ferretti, L.; Wymant, C.; Kendall, M.; Zhao, L.; Nurtay, A.; Abeler-Dörner, L.; Parker, M.; Bonsall, D.; Fraser, C. Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science 2020. [Google Scholar] [CrossRef]
- Smieszek, T. A mechanistic model of infection: Why duration and intensity of contacts should be included in models of disease spread. Theor. Biol. Med. Model. 2009, 6. [Google Scholar] [CrossRef] [PubMed]
- Smieszek, T. Models of Epidemics: How Contact Characteristics Shape the Spread of Infectious Diseases. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2010. [Google Scholar] [CrossRef]
- Müller, S.A.; Balmer, M.; Neumann, A.; Nagel, K. Mobility traces and spreading of COVID-19. medRxiv 2020. [Google Scholar] [CrossRef]
- Schultz, M. Stochastic Transition Model for Pedestrian Dynamics. In Pedestrian and Evacuation Dynamics 2012; Springer International Publishing: Cham, Switzerland, 2013; pp. 971–985. [Google Scholar] [CrossRef]
- Schultz, M.; Fricke, H. Improving Aircraft Turnaround Reliability. In Proceedings of the 3rd International Conference on Research in Airport Transportation, Fairfax, VA, USA, 1–4 June 2008; pp. 335–343. [Google Scholar]
- Schultz, M. Aircraft Boarding—Data, Validation, Analysis. In Proceedings of the 12th USA/Europe Air Traffic Management Research and Development Seminar, Seattle, WA, USA, 27–30 June 2017. [Google Scholar]
- Schultz, M.; Fricke, H. Stochastic Transition Model for Discrete Agent Movements. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; pp. 506–512. [Google Scholar] [CrossRef]
Figure 1.
(Left) Air ventilation pattern in a single-aisle cabin, here an Airbus A320. Note that other types have similar flow patterns. (Right) High Efficiency Particulate Air (HEPA) filters being removed in an Airbus A380 aircraft from Emirates.
Figure 1.
(Left) Air ventilation pattern in a single-aisle cabin, here an Airbus A320. Note that other types have similar flow patterns. (Right) High Efficiency Particulate Air (HEPA) filters being removed in an Airbus A380 aircraft from Emirates.
Figure 2.
Position of individuals in groups depends on environmental conditions: free flow (left) and congestion (right).
Figure 2.
Position of individuals in groups depends on environmental conditions: free flow (left) and congestion (right).
Figure 3.
Navigation in complex environments (airport terminal) under regular operational conditions, such as path finding with limited information.
Figure 3.
Navigation in complex environments (airport terminal) under regular operational conditions, such as path finding with limited information.
Figure 4.
Modeling and simulation of egress behavior considering fractional effective dose, a measure of airborne contaminants absorbed. A fire starts at the lower-deck of the third coach and smoke spreads through the whole coach. Passengers escape to the adjacent coaches. Affected passengers are color-coded from green (less impacted) to red (toxic dose), blue indicates no impact.
Figure 4.
Modeling and simulation of egress behavior considering fractional effective dose, a measure of airborne contaminants absorbed. A fire starts at the lower-deck of the third coach and smoke spreads through the whole coach. Passengers escape to the adjacent coaches. Affected passengers are color-coded from green (less impacted) to red (toxic dose), blue indicates no impact.
Figure 5.
Implementation of technologies for active control of aircraft cabin environment and development of corresponding boarding procedures.
Figure 5.
Implementation of technologies for active control of aircraft cabin environment and development of corresponding boarding procedures.
Figure 6.
(Left) Shedding rate of infected person. The increased rate is due to the relative positioning and increased physical activity. (Right) Virus load depicted as contour plot around person as function of distance.
Figure 6.
(Left) Shedding rate of infected person. The increased rate is due to the relative positioning and increased physical activity. (Right) Virus load depicted as contour plot around person as function of distance.
Figure 7.
Calibrated viral load using the Air China Flight 112 from 15 March 2003. The numbers show the infection probability 50 boarding-deboarding runs. Note that infections have occurred even in remote seats, albeit the highest probability is close to the index case in 14E. The transmission probability is color-coded with white (no-contact), orange (minor probability), red (highly probable), and black (index case).
Figure 7.
Calibrated viral load using the Air China Flight 112 from 15 March 2003. The numbers show the infection probability 50 boarding-deboarding runs. Note that infections have occurred even in remote seats, albeit the highest probability is close to the index case in 14E. The transmission probability is color-coded with white (no-contact), orange (minor probability), red (highly probable), and black (index case).
Figure 8.
Grid-based simulation environment—Airbus A320 as reference.
Figure 8.
Grid-based simulation environment—Airbus A320 as reference.
Figure 9.
Overview of different boarding strategies: darker seats are boarded first, followed by black, blue, and green (left). Implementation of operational constraints: darker seats are boarded first (right).
Figure 9.
Overview of different boarding strategies: darker seats are boarded first, followed by black, blue, and green (left). Implementation of operational constraints: darker seats are boarded first (right).
Figure 10.
Characteristic of boarding time (left) and relative standard deviation of boarding time (right) with increasing physical distance between passengers.
Figure 10.
Characteristic of boarding time (left) and relative standard deviation of boarding time (right) with increasing physical distance between passengers.
Table 1.
Baseline simulation to determine regular boarding time and number of individual contacts by using average values and relative standard deviation (RSD).
Table 1.
Baseline simulation to determine regular boarding time and number of individual contacts by using average values and relative standard deviation (RSD).
| | Boarding Strategy | Boarding Time (%) | Number of Contacts (%) |
|---|
| | | Average | RSD | Average | RSD |
|---|
| reference | random | 100.0 | 7.3 | 3.5 | 36 |
| by block | back-to-front (2 blocks) | 95.9 | 7.3 | 3.5 | 36 |
| | optimized block (6 blocks) | 95.3 | 7.3 | 3.3 | 35 |
| by seat | outside-in | 79.5 | 7.1 | 2.8 | 39 |
| | reverse pyramid | 75.2 | 7.0 | 2.7 | 40 |
| | individual | 65.8 | 7.4 | 2.2 | 53 |
| | deboarding | 54.5 | 6.5 | 5.3 | 35 |
Table 2.
Impact of physical distance rules (1.6 m) on the number of individual contacts, boarding time, and compensation of boarding time by 50% less hand luggage item. The reference boarding time equals 100% (random strategy), which corresponds to airline-specific implementations and reaches values between 10 and 20 min [
54].
Table 2.
Impact of physical distance rules (1.6 m) on the number of individual contacts, boarding time, and compensation of boarding time by 50% less hand luggage item. The reference boarding time equals 100% (random strategy), which corresponds to airline-specific implementations and reaches values between 10 and 20 min [
54].
| | Reference | Keeping 1.6 m Minimum Distance in Aisle |
|---|
| Boarding Strategy | Number of Contacts | Number of Contacts | Average Boarding Time (%) |
|---|
| | Average | RSD (%) | Average | RSD (%) | 100% Carry-on | 50% Carry-on |
|---|
| random | 3.5 | 36 | 0.9 | 85 | 198 | 154 |
| back-to-front (2 blocks) | 3.5 | 36 | 0.9 | 86 | 220 | 169 |
| optimized block (6 blocks) | 3.3 | 35 | 0.9 | 85 | 279 | 210 |
| outside-in | 2.8 | 39 | 0.2 | 227 | 161 | 116 |
| reverse pyramid | 2.7 | 39 | 0.2 | 261 | 185 | 128 |
| individual | 2.2 | 53 | 0.2 | 271 | 114 | 104 |
| deboarding | 5.3 | 35 | 5.0 | 36 | 97 | 68 |
Table 3.
Evaluation of possible transmissions assuming one SARS-CoV2 passenger in the cabin and one door operations (front door).
Table 3.
Evaluation of possible transmissions assuming one SARS-CoV2 passenger in the cabin and one door operations (front door).
| | Possible Transmissions |
|---|
| | 0 m Distance | 1.6 m Distance |
|---|
| | 100% Carry-on | 50% Carry-on | 100% Carry-on | 50% Carry-on |
|---|
| Boarding Strategy | Average | RSD | Average | RSD | Average | RSD | Average | RSD |
|---|
| | Value | (%) | Value | (%) | Value | (%) | Value | (%) |
|---|
| random | 5.9 | 68 | 4.2 | 83 | 1.6 | 124 | 1.1 | 145 |
| back-to-front (2 blocks) | 5.6 | 65 | 3.9 | 81 | 1.4 | 123 | 1.0 | 144 |
| optimized block (6 blocks) | 6.5 | 67 | 4.8 | 77 | 2.3 | 116 | 1.5 | 134 |
| outside-in | 3.5 | 62 | 1.7 | 97 | 0.4 | 226 | 0.2 | 329 |
| reverse pyramid | 3.0 | 56 | 1.3 | 99 | 0.2 | 291 | 0.1 | 467 |
| individual | 2.0 | 92 | 0.8 | 154 | 0.2 | 301 | 0.1 | 489 |
| deboarding | 10.0 | 36 | 8.0 | 42 | 9.7 | 34 | 7.8 | 43 |
Table 4.
Evaluation of possible transmissions (Transm.) and boarding time assuming one SARS-CoV2 passenger in the cabin and two door operations (front and rear door).
Table 4.
Evaluation of possible transmissions (Transm.) and boarding time assuming one SARS-CoV2 passenger in the cabin and two door operations (front and rear door).
| | 0 m Distance | 1.6 m Distance |
|---|
| | Carry-on | Carry-on | Carry-on | Carry-on |
|---|
| | 100% | 50% | 100% | 50% |
|---|
| Boarding Strategy | Average | Average | Average | Boarding | Average | Boarding |
|---|
| (Two Doors) | Transm. | Transm. | Transm. | Time (%) | Transm. | Time (%) |
|---|
| random | 4.3 | 2.5 | 1.4 | 133 | 1.0 | 103 |
| back-to-front (2 blocks) | 3.9 | 2.4 | 1.2 | 153 | 0.8 | 116 |
| optimized block (6 blocks) | 5.5 | 3.4 | 1.5 | 166 | 1.0 | 125 |
| outside-in | 1.9 | 0.6 | 0.3 | 107 | 0.1 | 77 |
| reverse pyramid | 1.7 | 0.5 | 0.2 | 119 | 0.1 | 82 |
| individual | 1.0 | 0.3 | 0.2 | 103 | 0.1 | 74 |
| deboarding | 7.9 | 6.2 | 7.6 | 52 | 6.0 | 36 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).