A Price-Forecast-Based Irrigation Scheduling Optimization Model under the Response of Fruit Quality and Price to Water
Abstract
1. Introduction
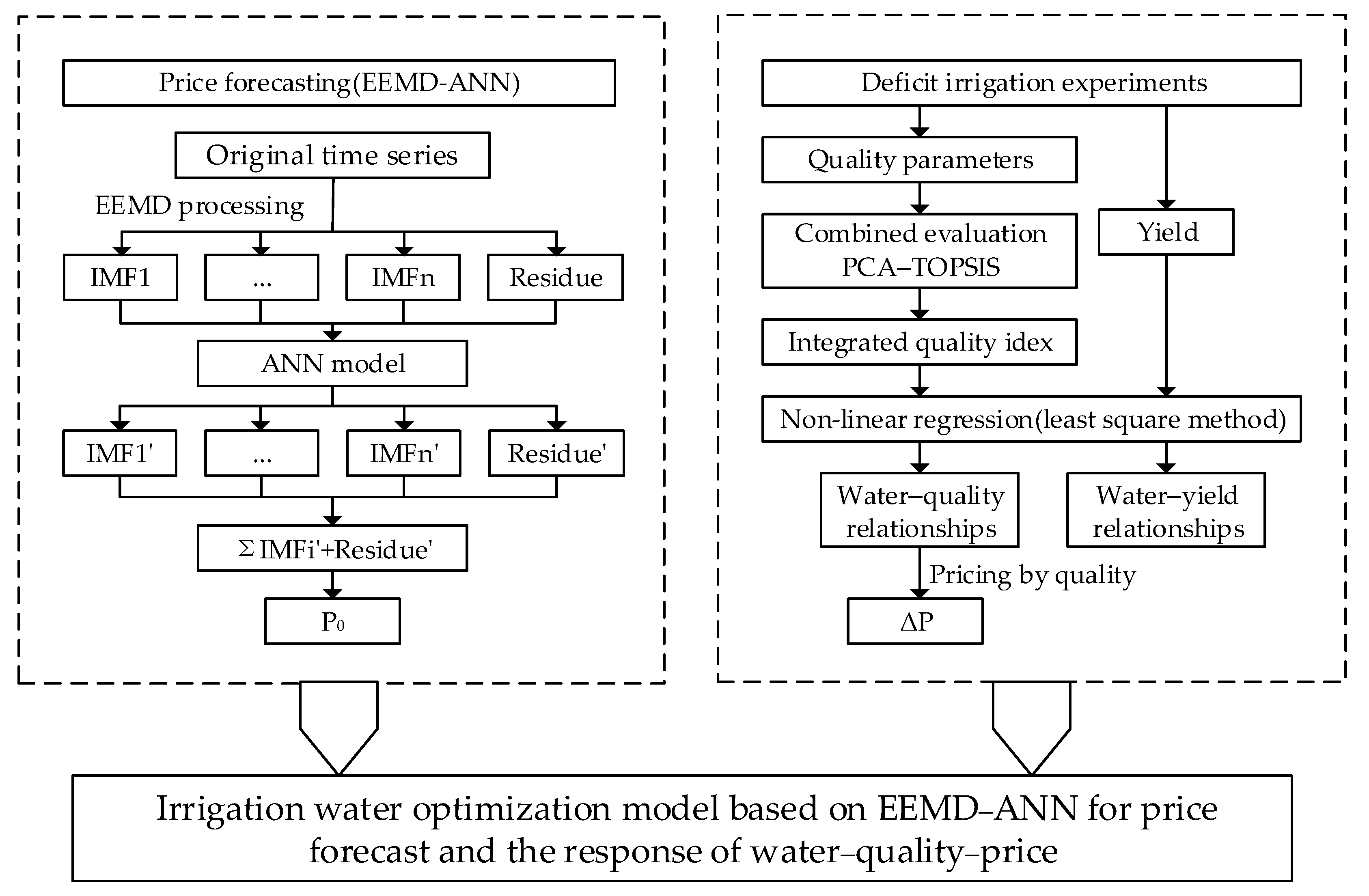
2. Methodology
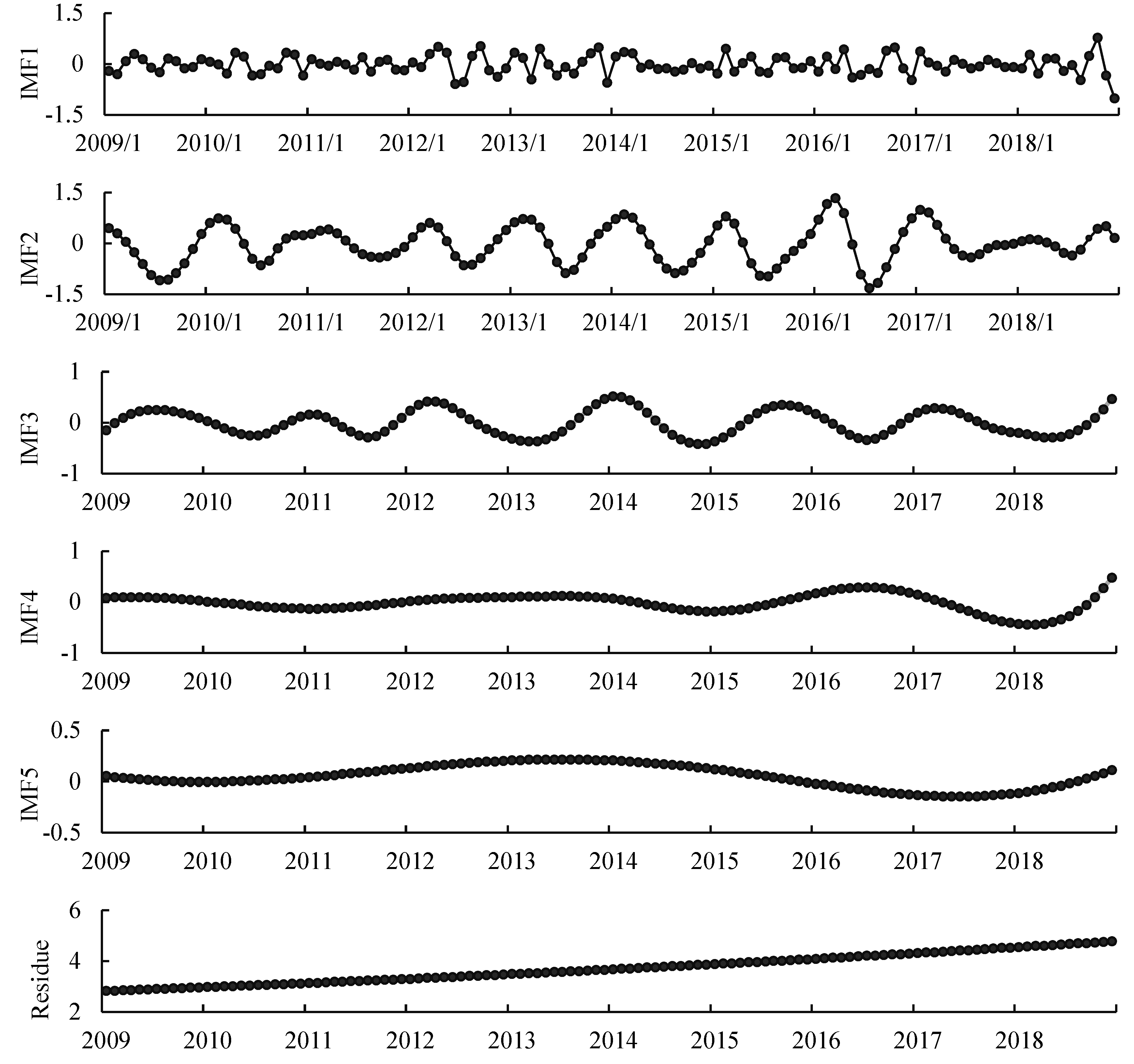
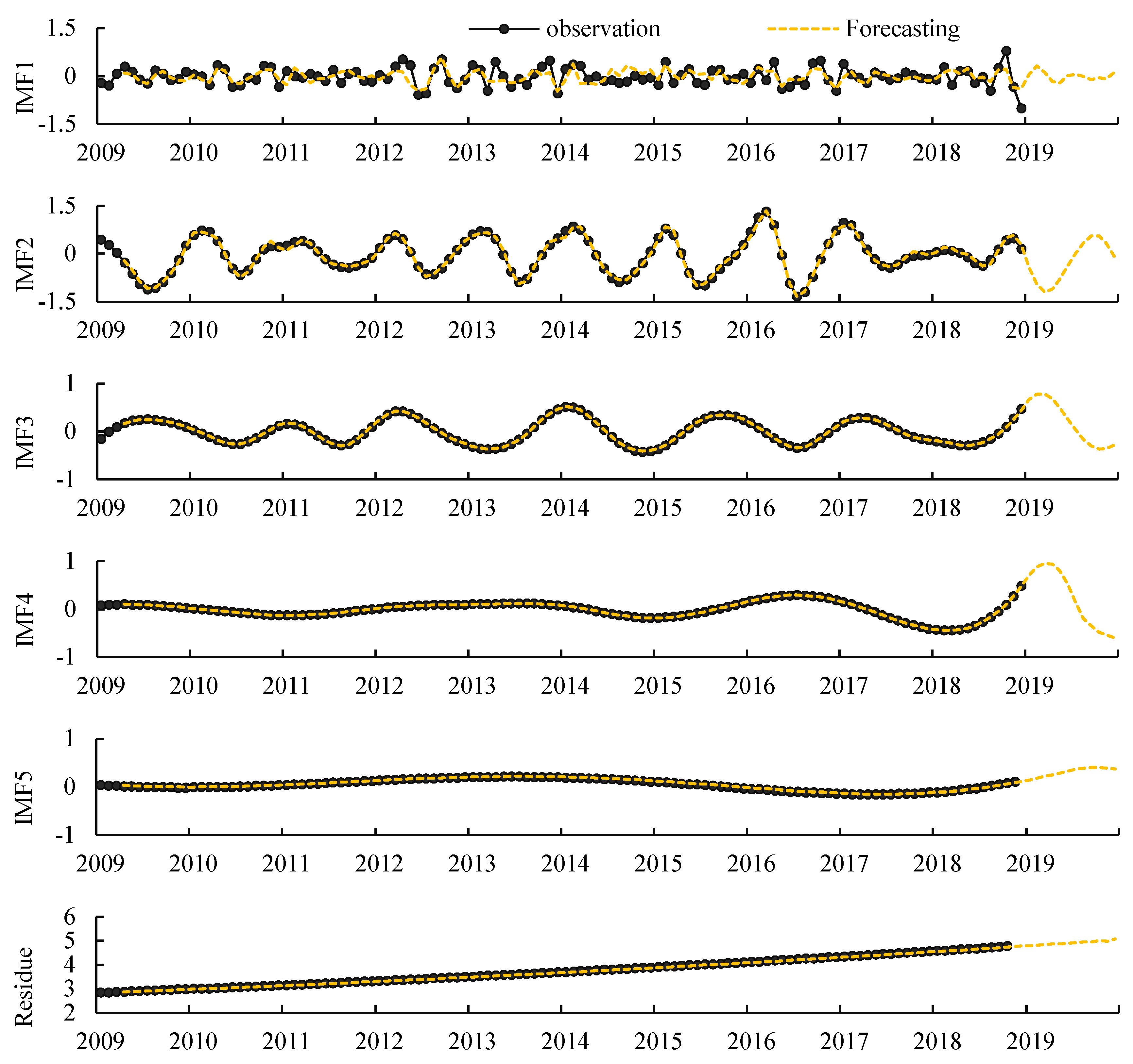
2.1. EEMD-ANN for Forecasting
2.2. Intergrated Evaluation Method
2.2.1. Factor Analysis (FA)
- (1)
- Standardization:where and denote the mean and standard deviation, respectively; is the j-th value of the standardized variable.
- (2)
- Calculate the coefficient matrix R of matrix Z.
- (3)
- Calculate the eigenvalues and eigenvectors of matrix R.
- (4)
- Calculate the principal factor load and perform a varimax rotation [30].
- (5)
- Computation of factor scores for each observation , where K is the number of main factors.
- (6)
- Calculate the comprehensive index.where and are the maximum and minimum values of the k-th factor of the K main factors, respectively; is the ratio of the k-th variance contribution rate to the cumulative variance contribution rate after rotation; is the comprehensive evaluation index of the i-th alternatives by FA and .
2.2.2. TOPSIS
- (1)
- Standardization.
- (2)
- Obtain positive ideal solution (PIS) and negative ideal solution (NIS).where is benefit criteria (larger is better) and is cost criteria (smaller is better).
- (3)
- Calculate the separation.The third step is to calculate the separation from the PIS and the NIS between alternatives. The separation values can be measured using the Euclidean distance, which is given as:where is the weight coefficient.
- (4)
- Similarities to the PISwhere is comprehensive index by TOPSIS and .
2.2.3. FA-TOPSIS
2.3. Modeling Relations of Yield and Quality with Water Deficit at Different Growth Stage
2.3.1. Water–Yield Model
- (1)
- Jensen model:
- (2)
- Stewart model:
- (3)
- Blank model:
- (4)
- Rao model:where i is the growth stage; n is the number of growth stages; is the crop yield of deficit irrigation treatments; is the crop yield of full irrigation treatment; is actual crop evapotranspiration at the i-th growth stage of deficit irrigation treatments; is maximum crop evapotranspiration at the i-th growth stage of full irrigation treatment; , , , and are the water deficit sensitivity index of crop yield at the i-th growth stage of Jensen model, Stewart model, Blank model, and Rao model, respectively.
2.3.2. Water–Fruit Quality Model
- (1)
- The multiplicative model adapted from the model by Jensen is given as
- (2)
- The additive model adapted from the model by Stewart et al. is given as
- (3)
- The exponential model is given aswhere is the comprehensive quality of deficit irrigation treatments; represents the comprehensive quality from full irrigation treatment; , , and are the water deficit sensitivity index of fruit quality at the i-th growth stage of the multiplicative model, additive model, and exponential model, respectively.
2.3.3. Pricing by Quality
3. Case Study
3.1. Data Collection
3.1.1. Field Experimental Data Collection
3.1.2. Other Data
3.2. Irrigation Water Optimization Model
3.2.1. Objective Function
3.2.2. Constraints
4. Results and Discussion
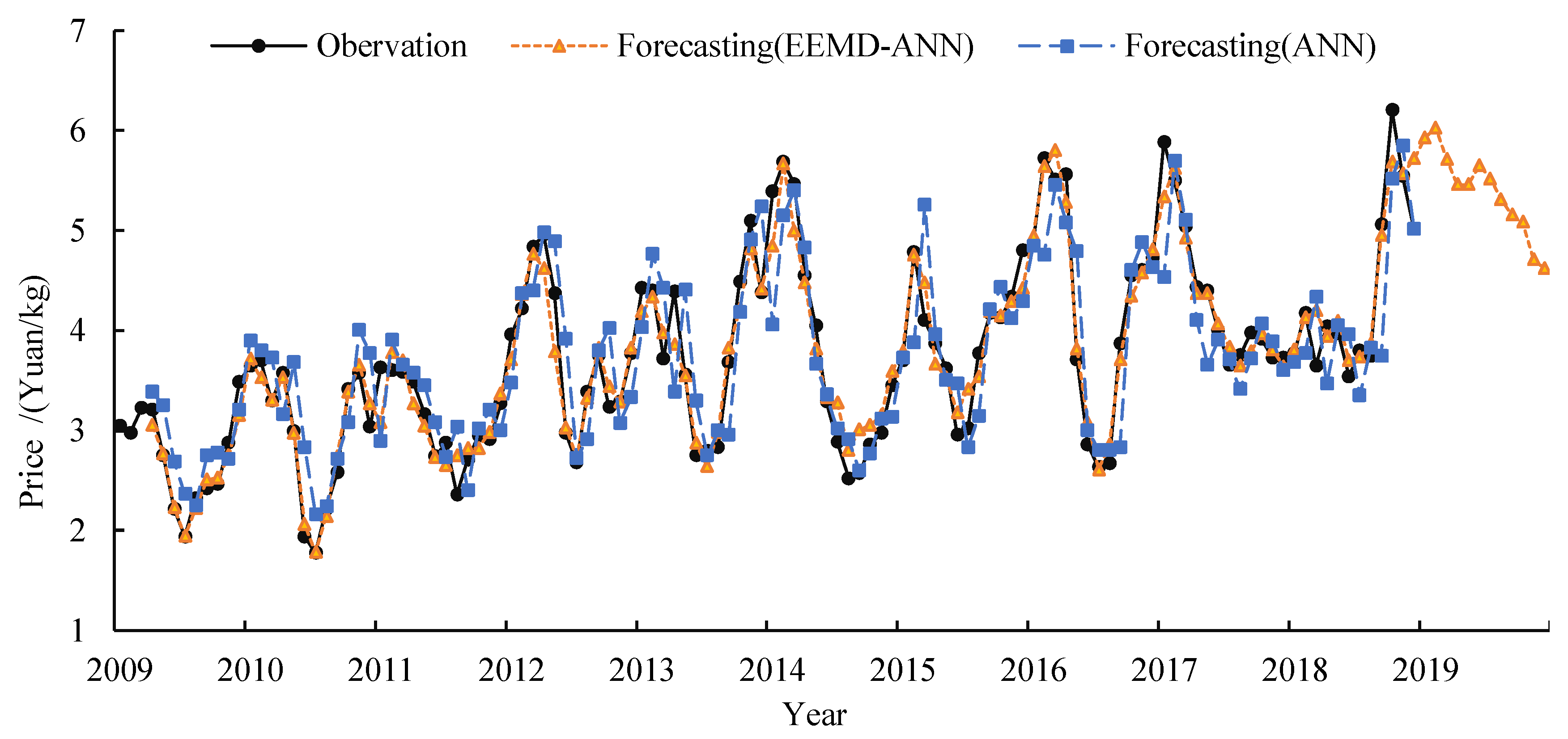
4.1. The Results of Basic Price Forecasting by EEMD-ANN
4.2. The Solutions of FA-TOPSIS
4.3. Non-Linear Regression Results
4.3.1. Water–Yield Relationships
4.3.2. Water–Fruit Quality Relationships
4.4. Optimal Results and Discussion
4.4.1. Optimization MODEL
4.4.2. Optimal Solution of WYQ
4.4.3. Discussion
5. Conclusions
- (1)
- For the monthly forecast of tomato price, the EEMD-ANN model can significantly improve forecast accuracy compared with ANN method.
- (2)
- In the WYQ model, it can be found that Stages II and III of tomato are more important than Stage I, and meeting their water requirement should be a priority.
- (3)
- Considering the economic mechanism of market price changes with fruit quality, the irrigation scheduling optimization model can achieve the purposes of saving water resources, improving net benefit, increasing quality, and improving water-use efficiency.
Author Contributions
Funding
Conflicts of Interest
References
- Li, M.; Fu, Q.; Singh, V.P.; Ma, M.; Liu, X. An intuitionistic fuzzy multi-objective non-linear programming model for sustainable irrigation water allocation under the combination of dry and wet conditions. J. Hydrol. 2017, 555, 80–94. [Google Scholar] [CrossRef]
- Zhang, C.; Fan, Z.; Guo, S.; Xiao, L.; Ping, G. Inexact nonlinear improved fuzzy chance-constrained programming model for irrigation water management under uncertainty. J. Hydrol. 2018, 556, 397–408. [Google Scholar] [CrossRef]
- Behboudian, M.H.; Lawes, G.S.; Griffiths, K.M. The influence of water deficit on water relations, photosynthesis and fruit growth in Asian pear (Pyrus serotina Rehd.). Sci. Horticult. 1994, 60, 89–99. [Google Scholar] [CrossRef]
- Mills, T.M.; Behboudian, M.H.; Clothier, B.E. Water Relations, Growth, and the Composition of ‘Braeburn’ Apple Fruit under Deficit Irrigation. J. Am. Soc. Horticult. Sci. 1996, 121, 286–291. [Google Scholar] [CrossRef]
- Pomper, K.W.; Breen, P.J. Expansion and Osmotic Adjustment of Strawberry Fruit during Water Stress. J. Am. Soc. Horticult. Sci. 1997, 122, 183–189. [Google Scholar] [CrossRef]
- Shellie, K.C. Vine and berry response of Merlot (vitis vinifera L.) to differential water stress. Am. J. Enol. Viticult. 2006, 57, 514–518. [Google Scholar]
- Marouelli, W.A.; Silva, W.L.C. Water tension thresholds for processing tomatoes under drip irrigation in Central Brazil. Irrig. Sci. 2007, 25, 411–418. [Google Scholar] [CrossRef]
- Chen, J.; Kang, S.; Du, T.; Qiu, R.; Guo, P.; Chen, R. Quantitative response of greenhouse tomato yield and quality to water deficit at different growth stages. Agric. Water Manag. 2013, 129, 152–162. [Google Scholar] [CrossRef]
- Sensoy, S.; Ertek, A.; Gedik, I.; Kucukyumuk, C. Irrigation frequency and amount affect yield and quality of field-grown melon (Cucumis melo L.). Agric. Water Manag. 2007, 88, 269–274. [Google Scholar] [CrossRef]
- Leib, B.G.; Caspari, H.W.; Redulla, C.A.; Andrews, P.K.; Jabro, J.J. Partial rootzone drying and deficit irrigation of ‘Fuji’ apples in a semi-arid climate. Irrig. Sci. 2006, 24, 85–99. [Google Scholar]
- Du, T.; Kang, S. Efficient water-saving irrigation theory based on the response of water and fruit quality for improving quality of economic crops. J. Hydr. Eng. 2011, 42, 245–252. [Google Scholar]
- Chen, J.; Kang, S.; Du, T.; Guo, P.; Qiu, R.; Chen, R.; Gu, F. Modeling relations of tomato yield and fruit quality with water deficit at different growth stages under greenhouse condition. Agric. Water Manag. 2014, 146, 131–148. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, H.; Wang, M. A Forecast Model of Agricultural and Livestock Products Price. Appl. Mech. Mater. 2010, 20–23, 1109–1114. [Google Scholar] [CrossRef]
- Chenglong, Z.; Engel, B.A.; Ping, G. An Interval-based Fuzzy Chance-constrained Irrigation Water Allocation model with double-sided fuzziness. Agric. Water Manag. 2018, 210, 22–31. [Google Scholar]
- Pastori, M.; Udias, A.; Bouraoui, F.; Bidoglio, G. A Multi-Objective Approach to Evaluate the Economic and Environmental Impacts of Alternative Water and Nutrient Management Strategies in Africa. J. Environ. Inform. 2015, 29, 16–28. [Google Scholar] [CrossRef]
- Wang, W.C.; Chau, K.W.; Qiu, L.; Chen, Y.B. Improving forecasting accuracy of medium and long-term runoff using artificial neural network based on EEMD decomposition. Environ. Res. 2015, 139, 46–54. [Google Scholar] [CrossRef]
- Tan, Q.-F.; Lei, X.-H.; Wang, X.; Wang, H.; Wen, X.; Ji, Y.; Kang, A.-Q. An adaptive middle and long-term runoff forecast model using EEMD-ANN hybrid approach. J. Hydrol. 2018, 567, 767–780. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Huang, N.E.; Zheng, S.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Chi, C.T.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z. A review on Hilbert-Huang transform: Method and its applications to geophysical studies. Rev. Geophys. 2008, 46, L13705. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Rojas, R. Neural Networks: A Systematic Introduction; Springer Science & Business Media: Berlin, Germany, 1996. [Google Scholar]
- Chen, J.S.; Chen, W.G.; Li, J.; Sun, P. A generalized model for wind turbine faulty condition detection using combination prediction approach and information entropy. J. Environ. Inform. 2018, 32, 14–24. [Google Scholar] [CrossRef]
- Chen, J. Modeling Fruit Growth and Sugar Accumulation and Optimizing Irrigation Scheduling for Improving Water Use Efficiency and Fruit Quality of Tomato. Ph.D. Thesis, China Agricultural University, Beijing, China, 2016. [Google Scholar]
- Wang, F.; Du, T.; Qiu, R. Deficit irrigation scheduling of greenhouse tomato based on quality principle component analysis. Trans. CSAE 2011, 27, 75–80. [Google Scholar]
- Tong, L.; Wang, C.; Chen, H. Optimization of multiple responses using principal component analysis and technique for order preference by similarity to ideal solution. Int. J. Adv. Manuf. Technol. 2005, 27, 407–414. [Google Scholar] [CrossRef]
- Gumus, A.T. Evaluation of hazardous waste transportation firms by using a two step fuzzy-AHP and TOPSIS methodology. Expert Syst. Appl. 2009, 36, 4067–4074. [Google Scholar] [CrossRef]
- Jia, W.; He, J. Application of Principal Component Analysis and Factor Analysis in Evaluating Regional Economic Development Level. Modern Manag. Sci. 2007, 19–21. [Google Scholar] [CrossRef]
- Liu, C.-W.; Lin, K.-H.; Kuo, Y.-M. Application of factor analysis in the assessment of groundwater quality in a blackfoot disease area in Taiwan. Sci. Total Environ. 2003, 313, 77–89. [Google Scholar] [CrossRef]
- Kaiser, H.F. The varimax criterion for analytic rotation in factor analysis. Psychometrika 1958, 23, 187–200. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Yoon, K. Multiple Attribute Decision Making, Methods and Applications. Lecture Notes in Economics and Mathematical Systems; Springer: New York, NY, USA, 1981. [Google Scholar]
- Tzeng, G.-H.; Huang, J.-J. Multiple Attribute Decision Making: Methods and Applications; Chapman and Hall/CRC: Boca Raton, FL, USA, 2011. [Google Scholar]
- Jensen, M.E. Water consumption by agricultural plants. In Plant Water Consumption and Response. Water Deficits and Plant Growth, 1st ed.; Kozlowski, T.T., Ed.; Academic Press: New York, NY, USA, 1968; Volume 2, pp. 1–22. [Google Scholar]
- Stewart, J.I.; Misra, R.D.; Puritt, W.O.; Hagan, R.M. Irrigating Corn and Grain Sorphum with a Deficient Water Supply. Trans. ASAE 1975, 18, 260–270. [Google Scholar] [CrossRef]
- Blank, H.G. Optimal Irrigation Decisions with Limited Water, unpublished. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 1975. [Google Scholar]
- Rao, N.H.; Sarma, P.B.S.; Chander, S. A simple dated water-production function for use in irrigated agriculture. Agric. Water Manag. 1988, 13, 25–32. [Google Scholar] [CrossRef]
- Zhao, M.; Li, Y. Discussion on the specific method of quality. Price Theory Pract. 1991, 6, 31–33. [Google Scholar]
- Wang, F. Response of Greenhouse Tomato Yield and Quality to Water Stress and the Irrigation Index for Water Saving & Fruit Quality Improving. Ph.D. Thesis, China Agricultural University, Beijing, China, 2016. [Google Scholar]
- Favati, F.; Lovelli, S.; Galgano, F.; Miccolis, V.; Di Tommaso, T.; Candido, V. Processing tomato quality as affected by irrigation scheduling. Sci. Horticult. 2009, 122, 562–571. [Google Scholar] [CrossRef]
- Patanè, C.; Cosentino, S.L. Effects of soil water deficit on yield and quality of processing tomato under a Mediterranean climate. Agric. Water Manag. 2010, 97, 131–138. [Google Scholar] [CrossRef]
- Machado, R.M.; Maria do Rosàrio, G.O. Tomato root distribution, yield and fruit quality under different subsurface drip irrigation regimes and depths. Irrig. Sci. 2005, 24, 15–24. [Google Scholar] [CrossRef]
- Zheng, J.; Huang, G.; Jia, D.; Wang, J.; Mota, M.; Pereira, L.S.; Huang, Q.; Xu, X.; Liu, H. Responses of drip irrigated tomato (Solanum lycopersicum L.) yield, quality and water productivity to various soil matric potential thresholds in an arid region of Northwest China. Agric. Water Manag. 2013, 129, 181–193. [Google Scholar] [CrossRef]
- Qiu, R.; Kang, S.; Li, F.; Du, T.; Tong, L.; Wang, F.; Chen, R.; Liu, J.; Li, S. Energy partitioning and evapotranspiration of hot pepper grown in greenhouse with furrow and drip irrigation methods. Sci. Horticult. 2011, 129, 790–797. [Google Scholar] [CrossRef]
- Hagan, M.T.; Menhaj, M.B. Training feedforward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef] [PubMed]

| Cropping Season | Treatment | ETa (mm) | Yield (t/ha) | |||
|---|---|---|---|---|---|---|
| Stage I | Stage II | Stage III | Whole Season | |||
| 2008–2009 | V1/3 | 56.1 | 61.8 | 141.5 | 259.4 | 118.2 |
| V2/3 | 42.1 | 83.9 | 144.5 | 270.5 | 119.2 | |
| F1/3 | 52.2 | 40.2 | 134.9 | 227.3 | 103.6 | |
| F2/3 | 58.3 | 64.7 | 139.9 | 262.9 | 109.6 | |
| R1/3 | 53.0 | 74.1 | 74.1 | 201.2 | 102.2 | |
| R2/3 | 71.7 | 59.4 | 100.7 | 231.8 | 106.5 | |
| CK | 65.2 | 63.4 | 140.0 | 268.6 | 113.8 | |
| 2009–2010 | F1/3 | 68.8 | 39.8 | 126.8 | 235.4 | 114.7 |
| F2/3 | 67.9 | 66.6 | 134.0 | 268.6 | 121.5 | |
| R1/3 | 69.3 | 82.2 | 61.0 | 212.5 | 111.0 | |
| R2/3 | 71.2 | 80.1 | 94.4 | 245.2 | 120.7 | |
| CK | 68.4 | 82.1 | 134.0 | 284.5 | 128.1 | |
| 2011 | F8/9R8/9 | 26.1 | 85.3 | 189.8 | 301.2 | 136.9 |
| F7/9R7/9 | 28.8 | 80.1 | 185.1 | 294.0 | 119.4 | |
| F6/9R6/9 | 27.0 | 76.5 | 158.4 | 261.8 | 110.3 | |
| F5/9R5/9 | 26.3 | 67.0 | 125.7 | 218.9 | 97.5 | |
| F4/9R4/9 | 26.9 | 61.7 | 103.5 | 192.0 | 88.2 | |
| CK | 28.9 | 95.9 | 205.0 | 329.9 | 138.0 | |
| 2012–2013 | F1/3 | 58.8 | 62.2 | 140.9 | 262.0 | 84.2 |
| F2/3 | 52.6 | 78.2 | 146.6 | 277.4 | 95.2 | |
| R1/3 | 57.8 | 98.7 | 66.1 | 222.7 | 75.6 | |
| R2/3 | 51.6 | 97.3 | 114.4 | 263.3 | 92.2 | |
| F2/3R2/3 | 59.6 | 74.1 | 98.4 | 232.0 | 84.6 | |
| F2/3R1/3 | 59.4 | 74.8 | 80.4 | 214.6 | 80.6 | |
| F1/3R2/3 | 54.6 | 57.2 | 100.3 | 212.2 | 81.4 | |
| F1/3R1/3 | 56.8 | 53.8 | 60.8 | 171.3 | 64.6 | |
| CK | 58.3 | 98.2 | 146.6 | 303.1 | 96.9 | |
| Cropping Season | Treatment | TSS (°rix) | RS (g 100 g/FW) | OA (g 100 g/FW) | SAR | VC (mg kg/FW) | Fn (kg/m2) | CI |
|---|---|---|---|---|---|---|---|---|
| 2008–2009 | V1/3 | 4.57 | 3.44 | 0.432 | 7.96 | 73.60 | 5.25 | 32.3 |
| V2/3 | 4.50 | 3.47 | 0.436 | 7.96 | 73.60 | 5.36 | 33.9 | |
| F1/3 | 5.06 | 4.08 | 0.486 | 8.40 | 85.80 | 5.93 | 35.0 | |
| F2/3 | 4.64 | 3.60 | 0.449 | 8.02 | 78.10 | 5.62 | 34.3 | |
| R1/3 | 4.98 | 4.07 | 0.482 | 8.44 | 101.10 | 6.19 | 36.5 | |
| R2/3 | 4.88 | 3.67 | 0.454 | 8.06 | 86.80 | 5.64 | 35.9 | |
| CK | 4.66 | 3.38 | 0.438 | 7.72 | 72.80 | 5.23 | 30.2 | |
| 2009–2010 | F1/3 | 6.02 | 2.91 | 0.311 | 9.36 | 183.60 | 8.26 | 35.8 |
| F2/3 | 5.44 | 2.55 | 0.273 | 9.34 | 176.40 | 7.90 | 33.5 | |
| R1/3 | 6.16 | 3.29 | 0.300 | 10.99 | 217.40 | 8.37 | 35.4 | |
| R2/3 | 5.91 | 2.82 | 0.285 | 9.91 | 199.20 | 7.96 | 33.8 | |
| CK | 5.55 | 2.60 | 0.283 | 9.20 | 163.20 | 7.39 | 31.3 | |
| 2011 | F8/9R8/9 | 4.86 | 2.45 | 0.374 | 6.53 | 167.50 | 5.45 | 33.4 |
| F7/9R7/9 | 5.51 | 2.59 | 0.398 | 6.52 | 179.10 | 5.84 | 35.8 | |
| F6/9R6/9 | 5.67 | 2.86 | 0.407 | 7.01 | 185.50 | 5.94 | 36.3 | |
| F5/9R5/9 | 5.76 | 3.17 | 0.423 | 7.50 | 198.70 | 5.92 | 36.7 | |
| F4/9R4/9 | 6.11 | 3.64 | 0.440 | 8.27 | 204.90 | 6.05 | 37.4 | |
| CK | 4.99 | 2.46 | 0.376 | 6.55 | 166.40 | 5.43 | 32.5 | |
| 2012–2013 | F1/3 | 5.70 | 3.76 | 0.452 | 8.32 | 143.60 | 4.58 | 37.8 |
| F2/3 | 5.33 | 3.39 | 0.417 | 8.15 | 120.70 | 4.27 | 36.5 | |
| R1/3 | 6.33 | 4.63 | 0.435 | 10.24 | 150.20 | 4.71 | 41.1 | |
| R2/3 | 5.28 | 3.44 | 0.400 | 8.58 | 136.40 | 4.00 | 36.4 | |
| F2/3R2/3 | 5.90 | 3.83 | 0.431 | 8.89 | 141.10 | 4.16 | 39.1 | |
| F2/3R1/3 | 5.78 | 4.20 | 0.457 | 9.48 | 150.60 | 4.75 | 38.9 | |
| F1/3R2/3 | 6.22 | 4.42 | 0.445 | 9.93 | 148.40 | 4.49 | 39.1 | |
| F1/3R1/3 | 6.63 | 4.79 | 0.452 | 10.59 | 151.70 | 4.91 | 40.1 | |
| CK | 5.22 | 3.34 | 0.402 | 7.98 | 117.60 | 3.95 |
| Soil Water Holding Capacity | (cm3/cm3) | 0.36 | Fixed cost | (Yuan/ha) | 30,420.4 |
| Initial Soil Moisture Content | (cm3/cm3) | 0.29 | Basic water price | (Yuan/ha) | 30.0 |
| Lower Limit of Volumetric Water Content | (cm3/cm3) | 0.16 | Metered water price | (Yuan/m3) | 0.157 |
| Planned Wet Layer Depth | (m) | 0.5 |
| Model | RMSE (Yuan/kg) | MARE (%) | R | NSEC |
|---|---|---|---|---|
| ANN | 0.491 | 10.36 | 0.856 | 0.732 |
| EEMD-ANN | 0.224 | 4.40 | 0.972 | 0.944 |
| Variable | Factor 1 | Factor 2 | Factor 3 |
|---|---|---|---|
| TSS | 0.214 | 0.402 | −0.380 |
| RS | 0.542 | 0.100 | −0.450 |
| OA | −0.432 | 1.233 | −0.489 |
| SAR | 0.914 | −0.479 | −0.309 |
| VC | 0.259 | −0.368 | 0.363 |
| Fn | −0.434 | 0.248 | 0.549 |
| CI | −0.416 | −0.524 | 1.319 |
| Percent of variance (%) | 38.130 | 29.748 | 27.423 |
| Cumulative percent of variance (%) | 38.130 | 67.878 | 95.301 |
| Cropping Season | Treatment | Factor Score | Ranking | Ranking | Ranking | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Factor 1 | Factor 2 | Factor 3 | ||||||||
| 2008–2009 | V1/3 | −0.066 | −1.030 | −0.581 | 0.372 | 6 | 0.105 | 6 | 0.239 | 6 |
| V2/3 | −0.631 | −1.249 | 0.618 | 0.401 | 5 | 0.156 | 5 | 0.278 | 5 | |
| F1/3 | 1.154 | 1.863 | −1.087 | 0.660 | 2 | 0.455 | 2 | 0.557 | 2 | |
| F2/3 | −0.567 | −0.351 | 0.607 | 0.465 | 4 | 0.233 | 4 | 0.349 | 4 | |
| R1/3 | 1.052 | 0.610 | 1.084 | 0.732 | 1 | 0.569 | 1 | 0.651 | 1 | |
| R2/3 | −0.250 | −0.357 | 1.264 | 0.532 | 3 | 0.354 | 3 | 0.443 | 3 | |
| CK | −0.693 | 0.514 | −1.905 | 0.365 | 7 | 0.054 | 7 | 0.209 | 7 | |
| 2009–2010 | F1/3 | −1.713 | 2.085 | 0.872 | 0.539 | 2 | 0.336 | 3 | 0.438 | 2 |
| F2/3 | −0.797 | −1.544 | 1.052 | 0.406 | 4 | 0.146 | 4 | 0.276 | 4 | |
| R1/3 | 2.020 | −0.096 | 0.205 | 0.675 | 1 | 0.616 | 1 | 0.645 | 1 | |
| R2/3 | 0.611 | −0.620 | 0.076 | 0.518 | 3 | 0.342 | 2 | 0.430 | 3 | |
| CK | −0.121 | 0.175 | −2.206 | 0.372 | 5 | 0.054 | 5 | 0.213 | 5 | |
| 2011 | F8/9R8/9 | −0.303 | −1.093 | −0.726 | 0.332 | 6 | 0.052 | 6 | 0.192 | 6 |
| F7/9R7/9 | −1.280 | 0.154 | 0.969 | 0.468 | 4 | 0.245 | 4 | 0.356 | 4 | |
| F6/9R6/9 | −0.534 | 0.258 | 0.885 | 0.531 | 3 | 0.368 | 3 | 0.450 | 3 | |
| F5/9R5/9 | 0.454 | 0.403 | 0.509 | 0.621 | 2 | 0.544 | 2 | 0.582 | 2 | |
| F4/9R4/9 | 1.679 | 0.901 | −0.025 | 0.735 | 1 | 0.745 | 1 | 0.740 | 1 | |
| CK | −0.016 | −0.624 | −1.613 | 0.341 | 5 | 0.054 | 5 | 0.197 | 5 | |
| 2012–2013 | F1/3 | −1.549 | 1.607 | 0.147 | 0.496 | 5 | 0.401 | 6 | 0.448 | 6 |
| F2/3 | −1.310 | 0.023 | −0.487 | 0.356 | 8 | 0.143 | 8 | 0.249 | 8 | |
| R1/3 | 1.157 | −0.779 | 1.443 | 0.619 | 2 | 0.780 | 2 | 0.699 | 2 | |
| R2/3 | 0.234 | −1.921 | −0.287 | 0.375 | 7 | 0.234 | 7 | 0.305 | 7 | |
| F2/3R2/3 | −0.152 | −0.399 | 0.389 | 0.484 | 6 | 0.416 | 5 | 0.450 | 5 | |
| F2/3R1/3 | −0.319 | 1.050 | 0.480 | 0.586 | 4 | 0.611 | 4 | 0.599 | 4 | |
| F1/3R2/3 | 1.076 | 0.317 | −0.295 | 0.617 | 3 | 0.674 | 3 | 0.646 | 3 | |
| F1/3R1/3 | 1.446 | 0.747 | 0.194 | 0.724 | 1 | 0.842 | 1 | 0.783 | 1 | |
| CK | −0.583 | −0.646 | −1.585 | 0.277 | 9 | 0.054 | 9 | 0.165 | 9 | |
| Model | |||||
|---|---|---|---|---|---|
| Stage I | Stage II | Stage III | Simulation | Verification | |
| Jenson | 0.058 | 0.257 | 0.286 | 0.764 | 0.878 |
| Stewart | 0.108 | 0.287 | 0.344 | 0.810 | 0.808 |
| Blank | 0.281 | 0.349 | 0.402 | 0.809 | 0.727 |
| Rao | 0.107 | 0.295 | 0.347 | 0.783 | 0.838 |
| Model | |||||
|---|---|---|---|---|---|
| Stage I | Stage II | Stage III | Simulate | Verify | |
| Multiplication | −1.507 | −0.806 | −1.392 | 0.838 | 0.547 |
| Additive | 2.643 | 1.629 | 3.793 | 0.914 | 0.713 |
| Exponential | 1.709 | 0.880 | 1.947 | 0.852 | 0.645 |
| Models | Optimal Irrigation Water in the Whole Season (mm) | Net Benefits (104 Yuan) | Water Use Efficiency (Yuan/m3) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| P01 | P02 | P03 | P01 | P02 | P03 | P01 | P02 | P03 | |
| WY | 238.1 | 238.1 | 238.1 | 55.3 | 49.1 | 41.7 | 232.5 | 206.4 | 175.1 |
| WYQ (Δd = 0.5) | 237.0 | 231.3 | 224.4 | 55.3 | 49.2 | 41.8 | 233.5 | 212.6 | 186.2 |
| WYQ (Δd = 1.0) | 210.0 | 209.0 | 209.0 | 56.4 | 50.4 | 43.2 | 268.3 | 241.2 | 206.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, B.; Guo, P.; Guo, S.; Li, Z. A Price-Forecast-Based Irrigation Scheduling Optimization Model under the Response of Fruit Quality and Price to Water. Sustainability 2019, 11, 2124. https://doi.org/10.3390/su11072124
Shan B, Guo P, Guo S, Li Z. A Price-Forecast-Based Irrigation Scheduling Optimization Model under the Response of Fruit Quality and Price to Water. Sustainability. 2019; 11(7):2124. https://doi.org/10.3390/su11072124
Chicago/Turabian StyleShan, Baoying, Ping Guo, Shanshan Guo, and Zhong Li. 2019. "A Price-Forecast-Based Irrigation Scheduling Optimization Model under the Response of Fruit Quality and Price to Water" Sustainability 11, no. 7: 2124. https://doi.org/10.3390/su11072124
APA StyleShan, B., Guo, P., Guo, S., & Li, Z. (2019). A Price-Forecast-Based Irrigation Scheduling Optimization Model under the Response of Fruit Quality and Price to Water. Sustainability, 11(7), 2124. https://doi.org/10.3390/su11072124






