A Multi-Objective and Multi-Dimensional Optimization Scheduling Method Using a Hybrid Evolutionary Algorithms with a Sectional Encoding Mode
Abstract
1. Introduction
2. Problem Description and Mathematical Model
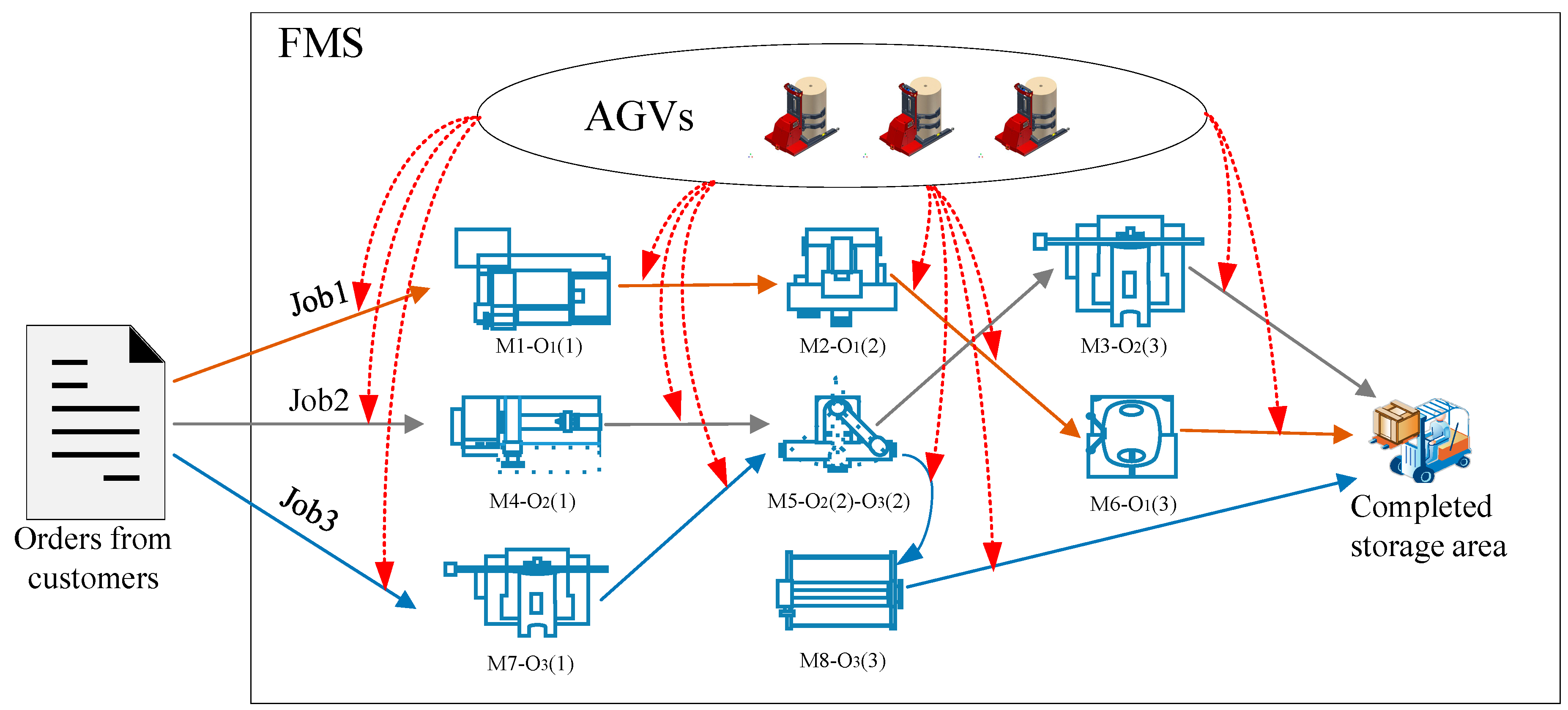
2.1. Problem Description
- All AGVs have a unit-load capacity.
- There are no battery charge problems on any AGV.
- AGVs and machines operate continuously without breakdown.
- There are no traffic problems, collision, deadlock.
- AGV loading and unloading times are fixed and considered as travel times.
- AGVs can always park at their unloading locations.
- The velocity of AGVs is constant.
- The start point (SP) of each job is in the home position (H) of the AGV.
- The machine-to-machine distances and SP-to-machine distances are known.
- Each machine operates only one product at a time.
- The setup times are included in the time of production.
2.2. Mathematical Model
3. Algorithm Design
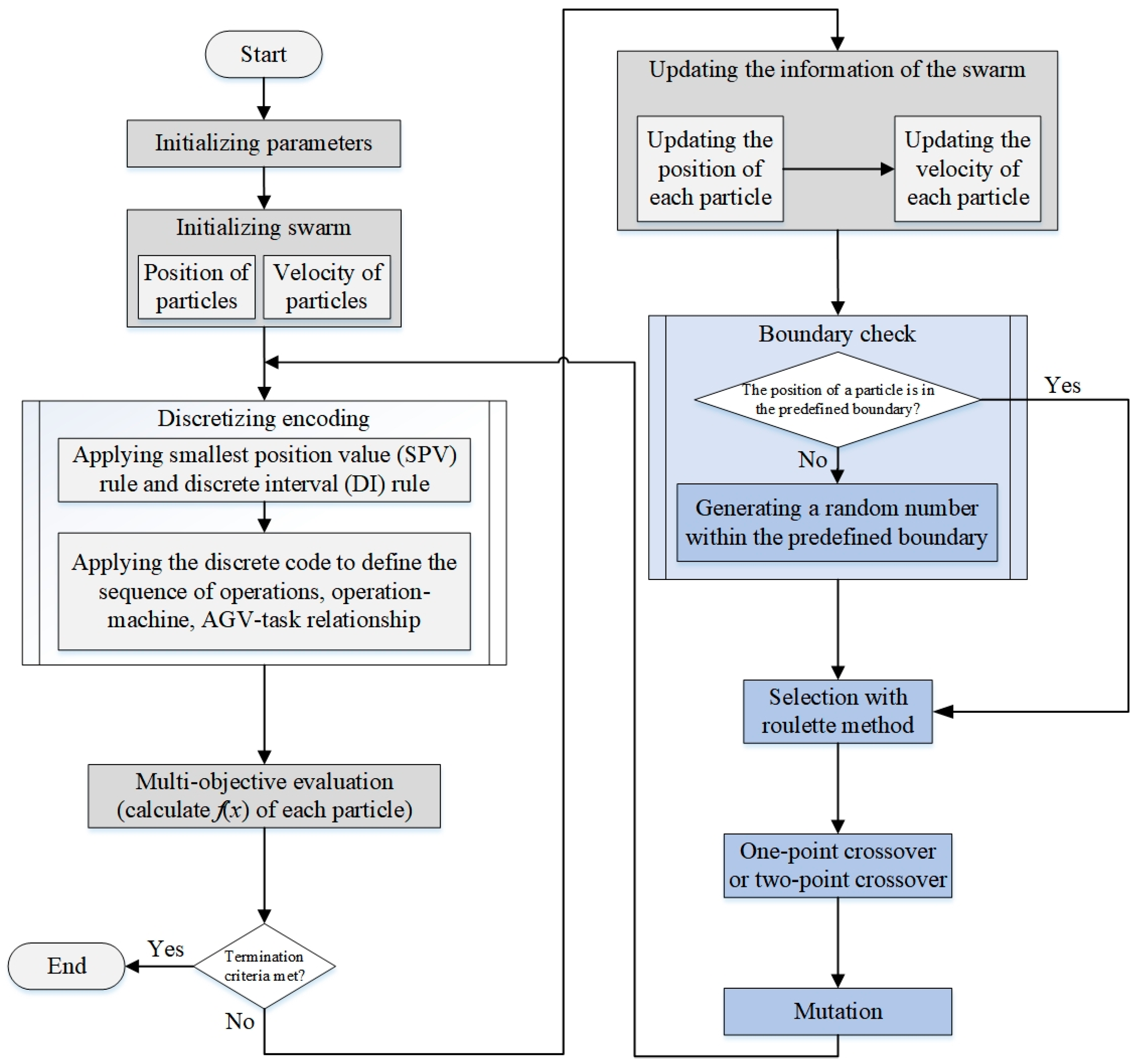
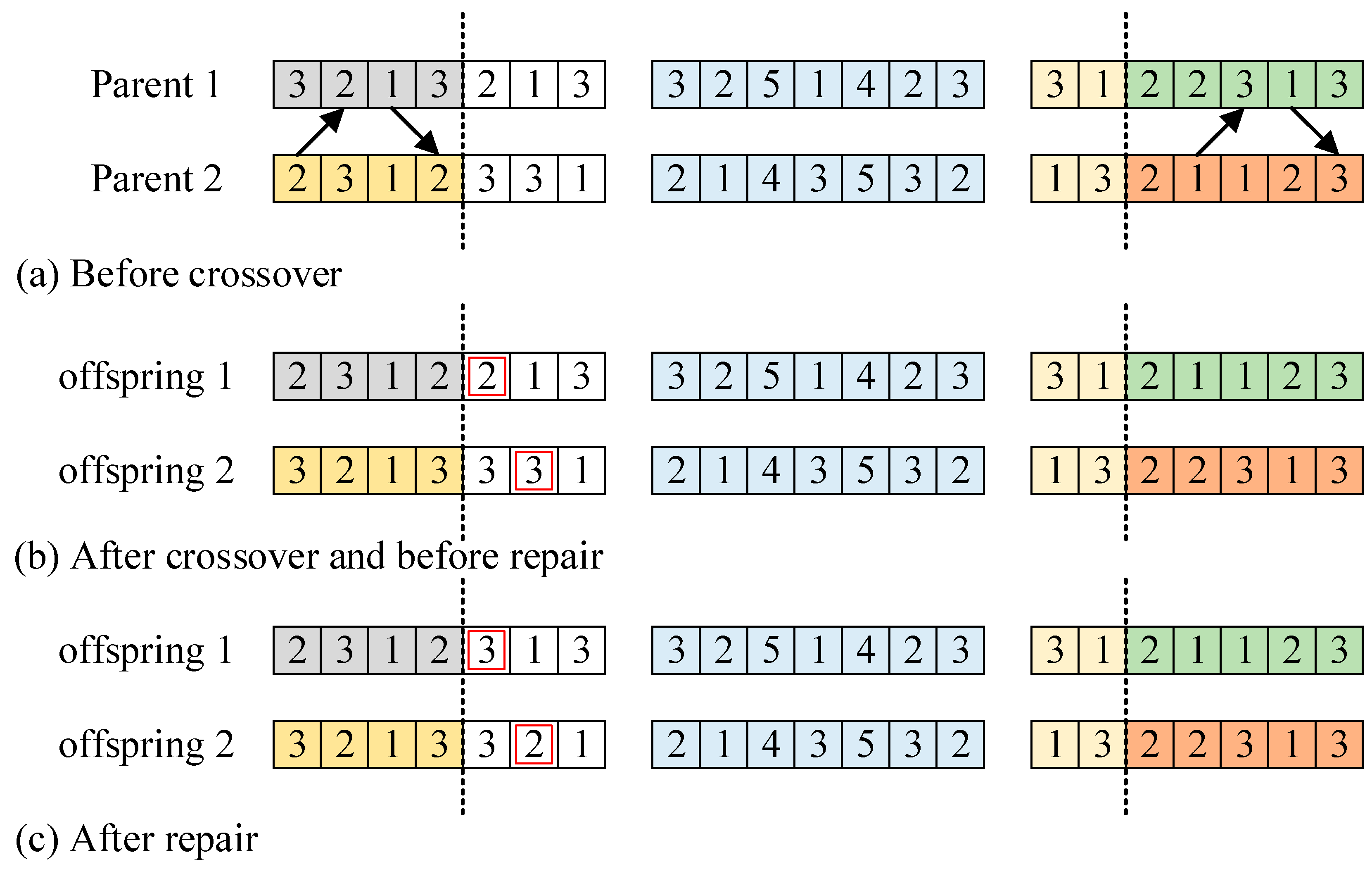
3.1. Sectional Encoding Genetic Algorithm
3.2. Sectional Encoding Discrete Particle Swarm Optimization
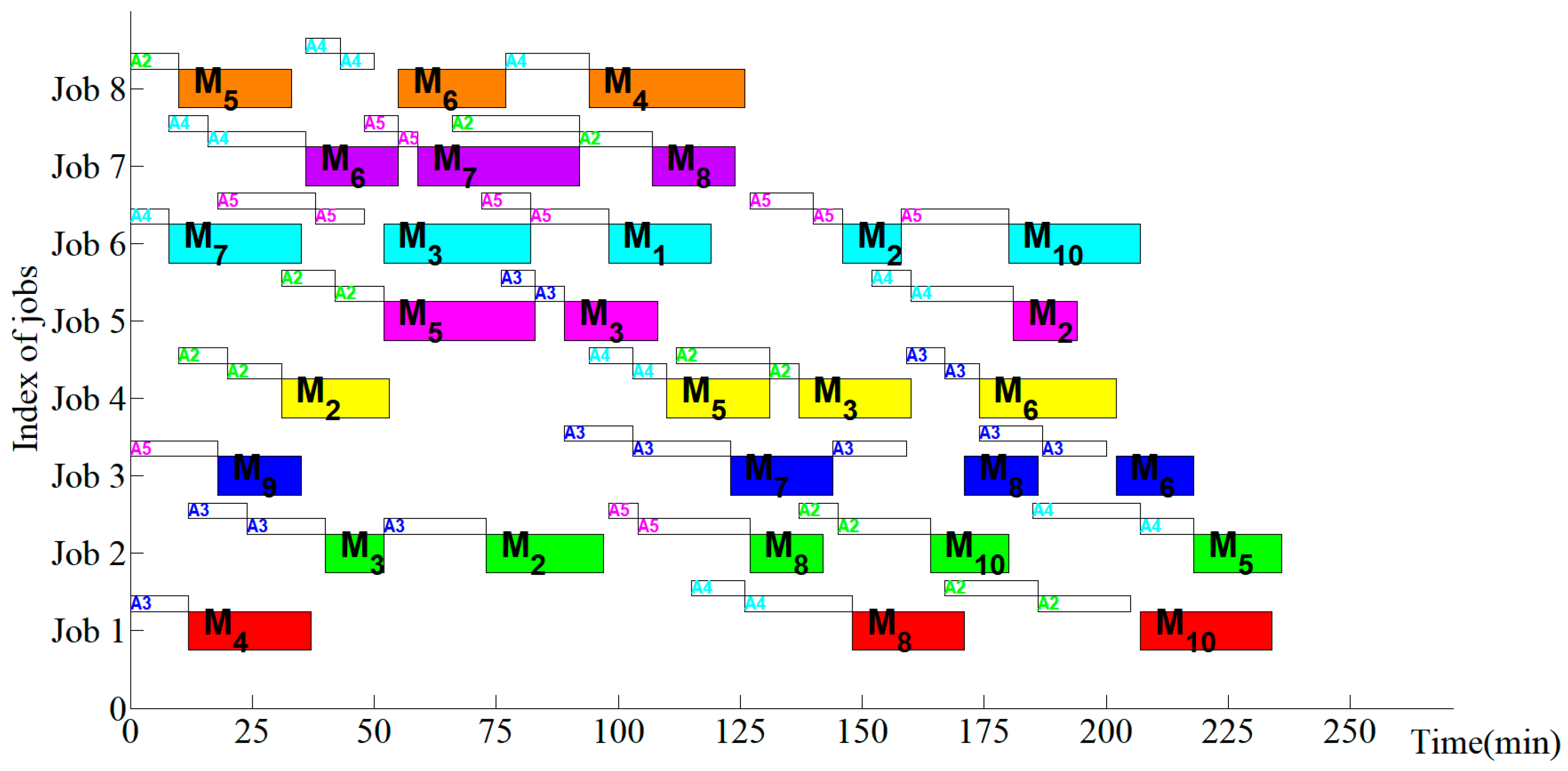
4. Simulation Experiments and Discussion
4.1. Initial Data
4.2. Parameters of the Algorithms Setting
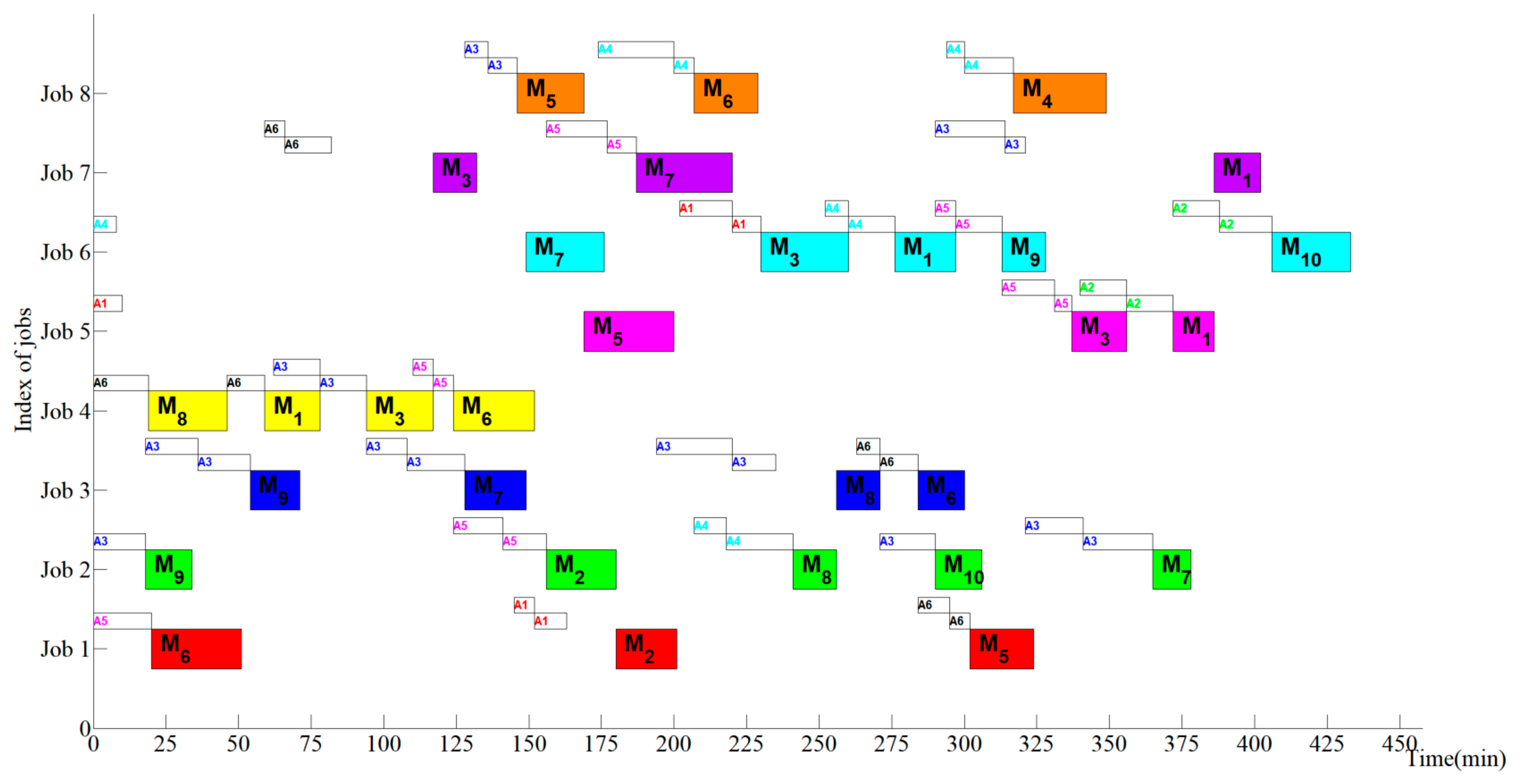
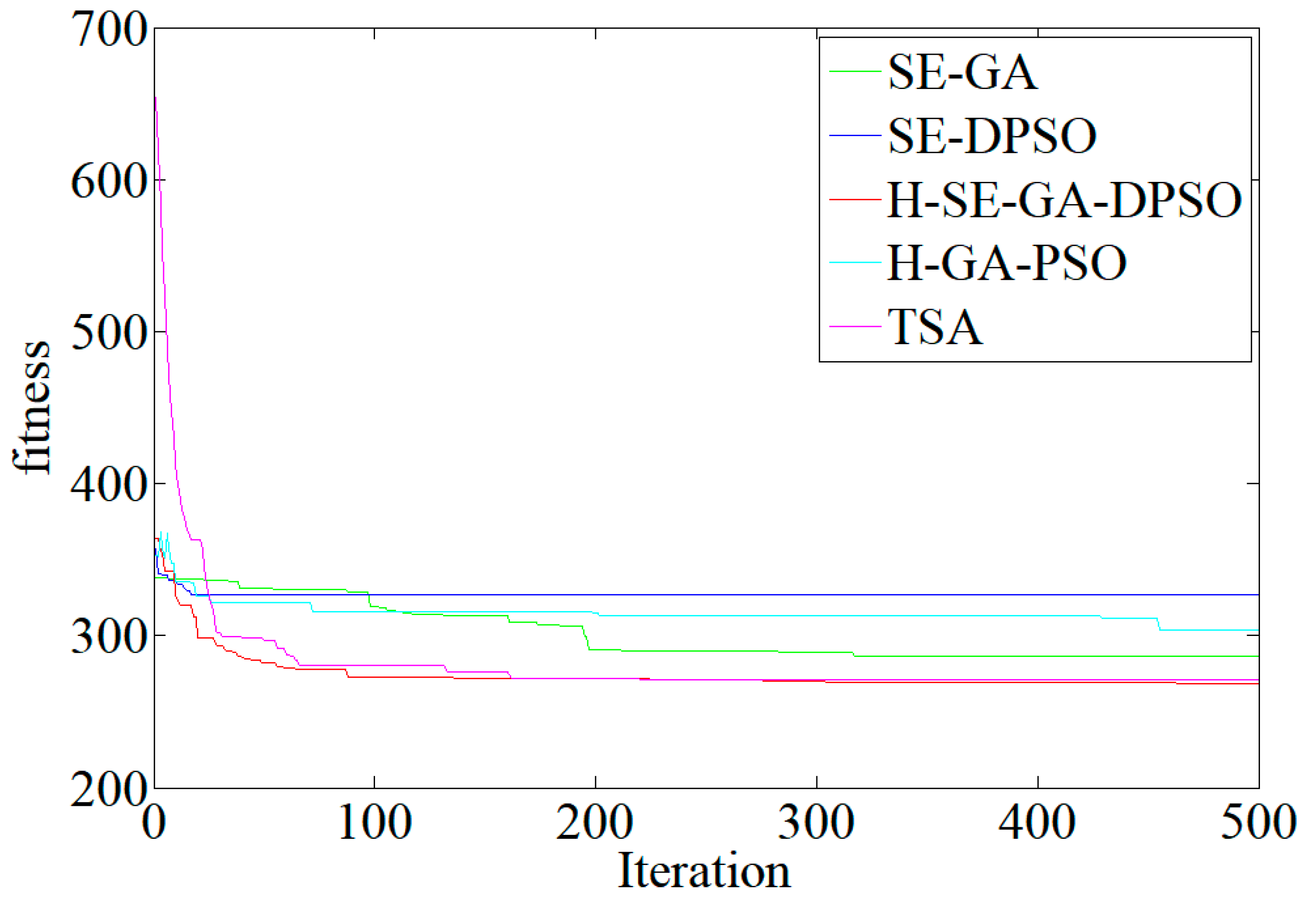
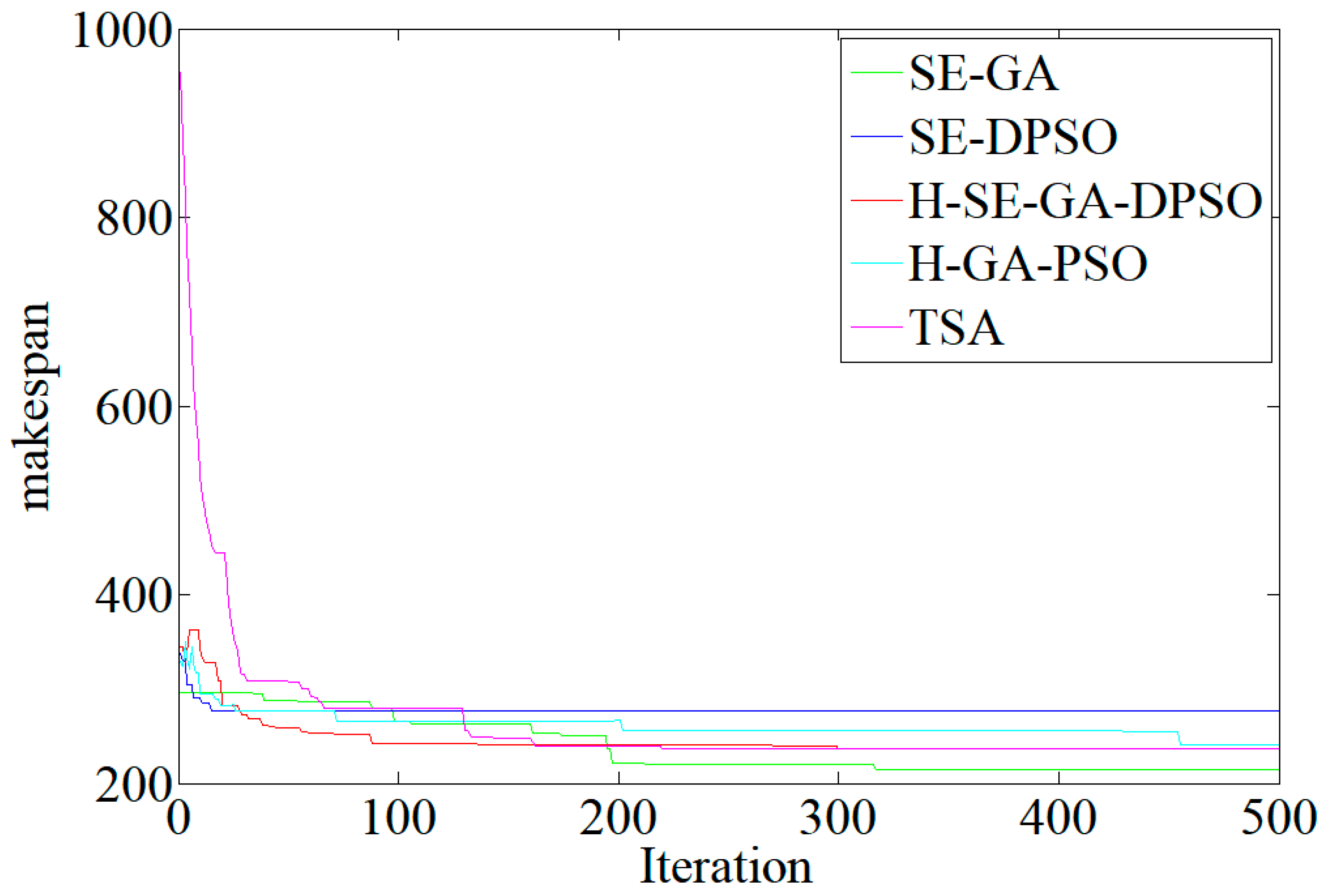
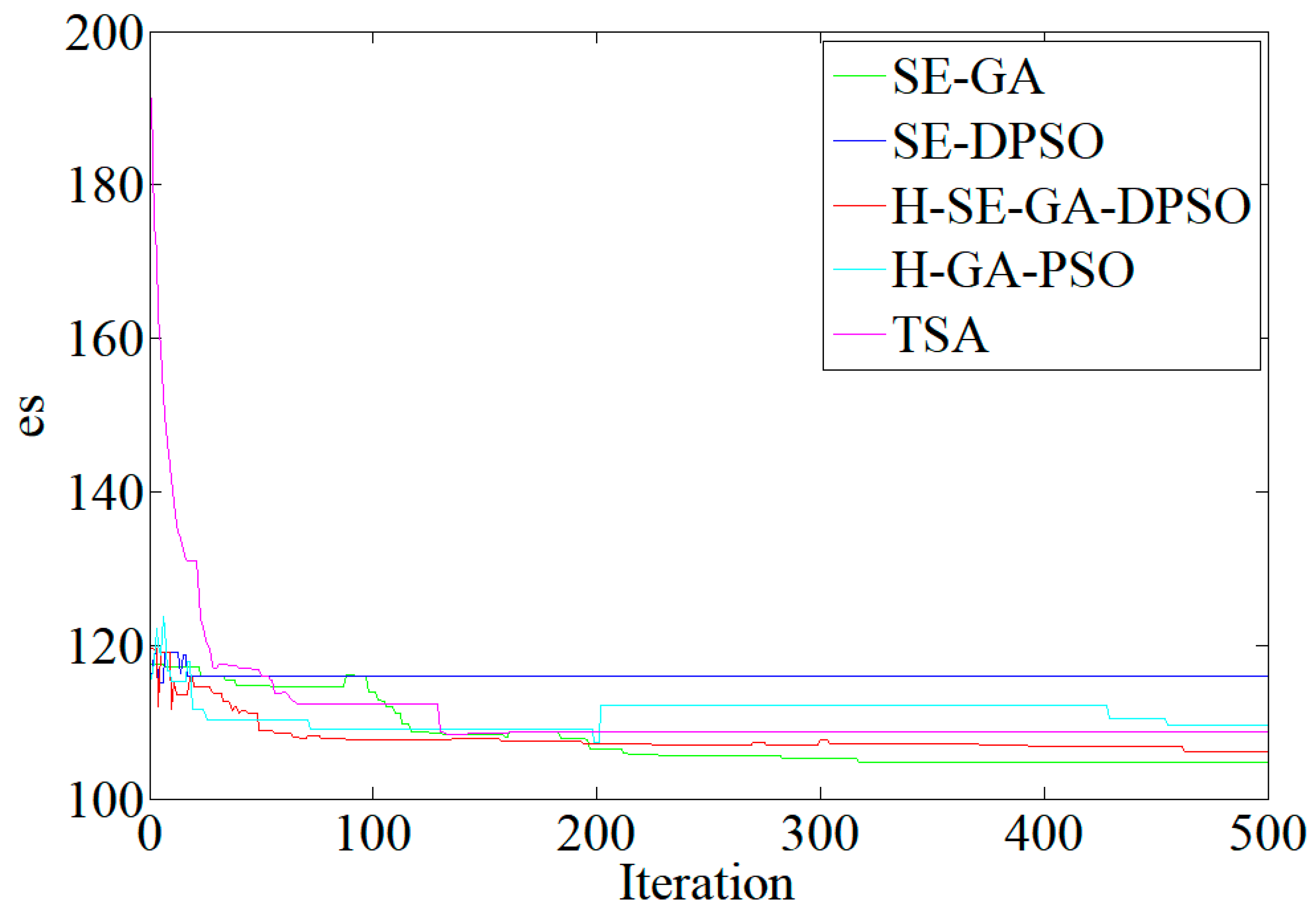
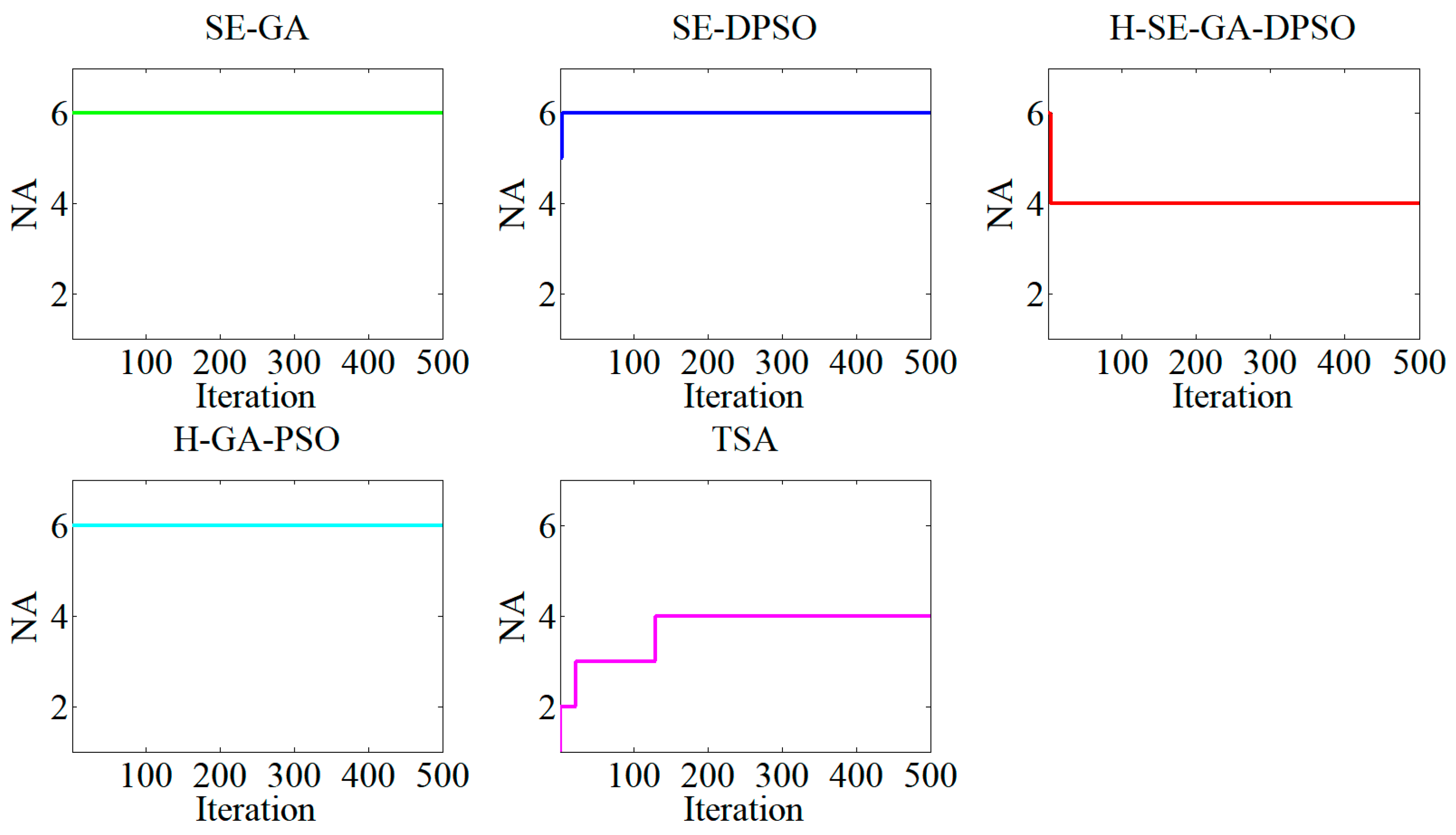
4.3. Experiment Results and Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| i | Index of jobs |
| j | Index of operations in a job |
| k | Index of machines |
| l | Index of AGVs |
| n | Number of jobs |
| mi | Number of operations for Job number i |
| s | Number of machines |
| NA | Number of AGVs |
| Ji | Job number i |
| Oi(j) | Operation number j of job i |
| Mk | Machine number k |
| Mi(j) | Assigned machine for Oi(j) |
| Al | AGV number l |
| Ai(j) | Assigned AGV for traveling task of Oi(j) |
| H | Home of AGVs |
| Nk | Number of operations assigned to Mk |
| p | Index of operations assigned to Mk |
| Ts(k,p) | Start time of executing operation number p assigned to Mk |
| Te(k,p) | End time of executing operation number p assigned to Mk |
| T(k,p) | Executing time of operation number p assigned to Mk |
| WT(k,p) | Waiting time before executing operation number p and after executing operation number p-1 assigned to Mk |
| es(k,p) | Energy consumption of operation number p assigned to Mk |
| wesu(k) | Standby energy consumption of Mk in unit time |
| Nl | Number of traveling tasks assigned to Al |
| q | Index of traveling tasks assigned to Al |
| Ts(l,q) | Start time of executing task number q assigned to Al |
| Te(l,q) | End time of executing task number q assigned to Al |
| T(l,q) | Traveling time of task number q assigned to Al |
| WT (l,q) | Waiting time before executing the traveling task number q and after executing the traveling task number q-1 assigned to Al |
| ots(i,j) | Start time of executing Oi(j) |
| ote(i,j) | End time of executing Oi(j) |
| ot(i,j) | Executing time of Oi(j) |
| otw(i,j) | Waiting time before executing operation number j and after executing operation number j-1 |
| ot(i) | Finish time of operations of Ji |
| TAij | Related traveling task to Oi(j) (Moving from the previous point of AGV to Mi(j-1) and then to Mi(j) or H to Mi(j)) |
| tts(i,j) | Start traveling time of executing TAij |
| tte(i,j) | End traveling time of executing TAij |
| tt(i,j) | Traveling time of executing TAij |
| ttw(i,j) | Waiting time before executing TAij and after executing TAi(j-1) |
| tt(i) | Finish time of traveling of Ji |
| es(i,j) | Energy consumption of executing Oi(j) |
| esw(k) | Standby energy consumption of Mk |
| ese(k) | Energy consumption of executing operations of Mk |
| esw | Standby energy consumption |
| ese | Energy consumption of executing operations |
| ES | Energy consumption of all jobs |
| AFTl | Finish time of traveling tasks assigned to Al |
| MFTk | Finish time of operations assigned to Mk |
| MS, DT | Makespan, Time of delivery |
References
- Guo, Q.; Zhang, M. A novel approach for multi-agent-based Intelligent Manufacturing System. Inf. Sci. 2009, 179, 3079–3090. [Google Scholar] [CrossRef]
- Kang, H.S.; Ju, Y.L.; Choi, S.S.; Kim, H.; Park, J.; Son, J.; Kim, B.; Noh, S. Smart manufacturing: Past research, present findings, and future directions. Int. J. Precis. Eng. Manuf. Green Technol. 2016, 3, 111–128. [Google Scholar] [CrossRef]
- Huang, S.; Guo, Y.; Zha, S.; Wang, F.; Fang, W. A Real-time Location System Based on RFID and UWB for Digital Manufacturing Workshop. Procedia CIRP 2017, 63, 132–137. [Google Scholar] [CrossRef]
- Confessore, G.; Fabiano, M.; Liotta, G. A network flow based heuristic approach for optimising AGV movements. J. Intell. Manuf. 2013, 24, 405–419. [Google Scholar] [CrossRef]
- Srivastava, S.C.; Choudhary, A.K.; Kumar, S.; Tiwari, M.K. Development of an intelligent agent-based AGV controller for a flexible manufacturing system. Int. J. Adv. Manuf. Technol. 2008, 36, 780. [Google Scholar] [CrossRef]
- Singh, N.; Sarngadharan, P.V.; Pal, P.K. AGV scheduling for automated material distribution: A case study. J. Intell. Manuf. 2011, 22, 219–228. [Google Scholar] [CrossRef]
- Ramana, B.; Reddy, S.S.; Ramprasad, B. Quantitative Analysis of AGV System in FMS Cell Layout. Def. Sci. J. 2013, 47, 75–81. [Google Scholar] [CrossRef]
- Murata, T. Makespan Minimization of Machines and Automated Guided Vehicles Schedule Using Binary Particle Swarm Optimization. In Proceedings of the Proceedings of the International Multiconference of Engineers and Computer Scientists, Hong Kong, China, 17–19 March 2010; pp. 268–272. [Google Scholar]
- Zheng, Y.; Xiao, Y.; Seo, Y. A tabu search algorithm for simultaneous machine/AGV scheduling problem. Int. J. Prod. Res. 2014, 52, 5748–5763. [Google Scholar] [CrossRef]
- Deroussi, L.; Gourgand, M.; Tchernev, N. A simple metaheuristic approach to the simultaneous scheduling of machines and automated guided vehicles. Int. J. Prod. Res. 2008, 46, 2143–2164. [Google Scholar] [CrossRef]
- Lacomme, P.; Larabi, M.; Tchernev, N. Job-shop based framework for simultaneous scheduling of machines and automated guided vehicles. Int. J. Prod. Econ. 2013, 143, 24–34. [Google Scholar] [CrossRef]
- Baruwa, O.T.; Piera, M.A. A coloured Petri net-based hybrid heuristic search approach to simultaneous scheduling of machines and automated guided vehicles. Int. J. Prod. Res. 2016, 54, 1–20. [Google Scholar] [CrossRef]
- Udhayakumar, P.; Kumanan, S. Task scheduling of AGV in FMS using non-traditional optimization techniques. Int. J. Simul. Model. 2010, 9, 28–39. [Google Scholar] [CrossRef]
- Pan, X.Y.; Wu, J.; Zhang, Q.W.; Lai, D.; Xie, H.; Zhang, Z. A Case Study of AGV Scheduling for Production Material Handling. Appl. Mechan. Mater. 2013, 411–414, 2351–2354. [Google Scholar] [CrossRef]
- Mousavi, M.; Yap, H.J.; Musa, S.N.; Tahriri, F.; Dawal, S.Z.M. Multi-objective AGV scheduling in an FMS using a hybrid of genetic algorithm and particle swarm optimization. PLoS ONE 2017, 12, e0169817. [Google Scholar] [CrossRef] [PubMed]
- Mousavi, M.; Yap, H.J.; Musa, S.N. A fuzzy hybrid GA-PSO algorithm for multi-objective AGV scheduling in FMS. Int. J. Simul. Model. 2017, 16, 58–71. [Google Scholar] [CrossRef]
- Cai, Q.; Tang, D.; Zheng, K.; Zhu, H.; Wu, X.; Lu, X. Multi-AGV scheduling optimization based on: Neuro-endocrine coordination mechanism. Int. J. Smart Sens. Intell. Syst. 2013, 7, 1613–1630. [Google Scholar] [CrossRef]
- Novas, J.M.; Henning, G.P. Integrated scheduling of resource-constrained flexible manufacturing systems using constraint programming. Expert Syst. Appl. 2014, 41, 2286–2299. [Google Scholar] [CrossRef]
- Mchaney, R. Modelling battery constraints in discrete event automated guided vehicle simulations. Int. J. Prod. Res. 2007, 33, 3023–3040. [Google Scholar] [CrossRef]
- Kabir, Q.S.; Suzuki, Y. Increasing manufacturing flexibility through battery management of automated guided vehicles. Comput. Ind. Eng. 2018, 117, 225–236. [Google Scholar] [CrossRef]
- Yan, R.; Jackson, L.M.; Dunnett, S.J. Automated guided vehicle mission reliability modelling using a combined fault tree and Petri net approach. Int. J. Adv. Manuf. Technol. 2017, 92, 1825–1837. [Google Scholar] [CrossRef]
- Tao, F.; Hu, Y.; Zhou, Z. Correlation-aware resource service composition and optimal-selection in manufacturing grid. Eur. J. Oper. Res. 2010, 201, 129–143. [Google Scholar] [CrossRef]
- Guo, S.; Du, B.; Peng, Z.; Huang, X.; Li, Y. Manufacturing resource combinatorial optimization for large complex equipment in group manufacturing: A cluster-based genetic algorithm. Mechatronics 2015, 31, 101–115. [Google Scholar] [CrossRef]
- Du, B.; Guo, S.; Huang, X.; Li, Y.; Guo, J. A Pareto supplier selection algorithm for minimum the life cycle cost of complex product system. Expert Syst. Appl. 2015, 42, 4253–4264. [Google Scholar] [CrossRef]
- Wang, L.; Guo, S.; Li, X.; Du, B.; Xu, W. Distributed manufacturing resource selection strategy in cloud manufacturing. Int. J. Adv. Manuf. Technol. 2018, 94, 3375–3388. [Google Scholar] [CrossRef]
- Udhayakumar, P.; Kumanan, S. Integrated scheduling of flexible manufacturing system using evolutionary algorithms. Int. J. Adv. Manuf. Technol. 2012, 61, 621–635. [Google Scholar] [CrossRef]
- Caridá, V.F.; Morandin, O.; Tuma CC, M. Approaches of fuzzy systems applied to an AGV dispatching system in a FMS. Int. J. Adv. Manuf. Technol. 2015, 79, 615–625. [Google Scholar] [CrossRef]
- Chang, H.C.; Liu, T.K. Optimisation of distributed manufacturing flexible job shop scheduling by using hybrid genetic algorithms. J. Intell. Manuf. 2017, 28, 1973–1986. [Google Scholar] [CrossRef]
- Rifai, A.P.; Nguyen, H.T.; Aoyama, H.; Dawal, S.Z.M.; Masruroh, N.A. Non-dominated sorting biogeography-based optimization for bi-objective reentrant flexible manufacturing system scheduling. Appl. Soft Comput. 2018. [Google Scholar] [CrossRef]
- Proth, J.M.; Sauer, N.; Xie, X. Optimization of the number of transportation devices in a flexible manufacturing system using event graphs. IEEE Trans. Ind. Electron. 2006, 44, 298–306. [Google Scholar] [CrossRef]
- Saidi-Mehrabad, M.; Dehnavi-Arani, S.; Evazabadian, F.; Mahmoodian, V. An Ant Colony Algorithm (ACA) for solving the new integrated model of job shop scheduling and conflict-free routing of AGVs. Comput. Ind. Eng. 2015, 86, 2–13. [Google Scholar] [CrossRef]
- Pjevcevic, D.; Nikolic, M.; Vidic, N.; Vukadinovic, K. Data envelopment analysis of AGV fleet sizing at a port container terminal. Int. J. Prod. Res. 2017, 55, 4021–4034. [Google Scholar] [CrossRef]
- Vivaldini, K.; Rocha, L.F.; Martarelli, N.J.; Becker, M.; Moreira, A.P. Integrated tasks assignment and routing for the estimation of the optimal number of AGVS. Int. J. Adv. Manuf. Technol. 2016, 82, 719–736. [Google Scholar] [CrossRef]
- Yan, H.E. Job scheduling model of machining system for green manufacturing. Chin. J. Mech. Eng. 2007, 43, 27–33. [Google Scholar]
- Govindan, K.; Diabat, A.; Shankar, K.M. Analyzing the drivers of green manufacturing with fuzzy approach. J. Clean. Prod. 2015, 96, 182–193. [Google Scholar] [CrossRef]
- Singh, A.; Philip, D.; Ramkumar, J.; Das, M. A simulation based approach to realize green factory from unit green manufacturing processes. J. Clean. Prod. 2018, 182, 67–81. [Google Scholar] [CrossRef]
- Liang, Y.; Lin, L.; Gen, M.; Chien, C. A hybrid evolutionary algorithm for fms optimization with AGV dispatching. Comput. Ind. Eng. 2012, 2, 1115–1128. [Google Scholar]
- Chen, R.M.; Shen, Y.M. Dynamic search control-based particle swarm optimization for project scheduling problems. Adv. Mech. Eng. 2016, 8, 1687814016641837. [Google Scholar] [CrossRef]
- Lu, H.; Zhou, R.; Fei, Z.; Shi, J. A multi-objective evolutionary algorithm based on Pareto prediction for automatic test task scheduling problems. Appl. Soft Comput. 2018. [Google Scholar] [CrossRef]
- Wang, Z.; Si, L.; Tan, C.; Liu, X. A Novel Approach for Shearer Cutting Load Identification through Integration of Improved Particle Swarm Optimization and Wavelet Neural Network. Adv. Mech. Eng. 2014, 2014, 521629. [Google Scholar] [CrossRef]
- Giagkiozis, I.; Fleming, P.J. Methods for multi-objective optimization: An analysis. Inf. Sci. 2015, 293, 338–350. [Google Scholar] [CrossRef]
- Han, D.; Yang, B.; Li, J.; Wang, J.; Sun, M.; Zhou, Q. A multi-agent-based system for two-stage scheduling problem of offshore project. Adv. Mech. Eng. 2017, 9, 1–17. [Google Scholar] [CrossRef]
- Kim, J.W.; Sang, W.K. New Encoding/Converting Methods of Binary GA/Real-Coded GA. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2005, 88, 1554–1564. [Google Scholar] [CrossRef]
- Yamamoto, H.; Qudeiri, J.A.; Yamada, T.; Rizauddin, R. Production layout design system by GA with one by one encoding method. Artif. Life Robot. 2008, 13, 234–237. [Google Scholar] [CrossRef]
- Wang, H.F.; Hsu, H.W. A closed-loop logistic model with a spanning-tree based genetic algorithm. Comput. Oper. Res. 2010, 37, 376–389. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, M. An improved genetic algorithm encoded by adaptive degressive ary number. Soft Comput. 2018, 22, 6861–6875. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, C.H.; Cui, N.X. PSO algorithm-based parameter optimization for HEV powertrain and its control strategy. Int. J. Automot. Technol. 2008, 9, 53–59. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Amjad, M.; Mekhilef, S. An Improved Particle Swarm Optimization (PSO)-Based MPPT for PV With Reduced Steady-State Oscillation. IEEE Trans. Power Electron. 2012, 27, 3627–3638. [Google Scholar] [CrossRef]
- Tian, Y.; Liu, D.; Yuan, D.; Wang, K. A discrete PSO for two-stage assembly scheduling problem. Int. J. Adv. Manuf. Technol. 2013, 66, 481–499. [Google Scholar] [CrossRef]
- Shi, X.H.; Liang, Y.C.; Leeb, H.P.; Lu, C.; Wang, L.M. An improved GA and a novel PSO-GA-based hybrid algorithm. Inf. Process. Lett. 2005, 93, 255–261. [Google Scholar] [CrossRef]
- Li, J.; Yang, B.; Zhang, D.; Zhou, Q.; Li, L. Development of a multi-objective scheduling system for offshore projects based on hybrid non-dominated sorting genetic algorithm. Adv. Mech. Eng. 2015, 7, 1687814015573785. [Google Scholar] [CrossRef]
- Su, Y.; Chu, X.; Zhang, Z.; Chen, D. Process planning optimization on turning machine tool using a hybrid genetic algorithm with local search approach. Adv. Mech. Eng. 2015, 7, 1687814015581241. [Google Scholar] [CrossRef]

| SE-GA (C1) | Chromosome (Cr) | Operations (Oi(j)) | |||||
| SgSo | SgOm | SgAt | |||||
| Gene Number (Ge) | Gene Code (g) | Gene Number (Ge) | Gene Code (g) | Gene Number (Ge) | Gene Code (g) | ||
| G1 | 1 | Gθ+1 | 1 | G2θ+1 | 1 | O1(1) | |
| G2 | 1 | Gθ+2 | 3 | G2θ+2 | 3 | O1(2) | |
| … | … | … | … | … | … | ||
| Gm1 | 1 | Gθ+m1 | 2 | G2θ+m1 | 2 | O1(m1) | |
| 2 | s | 5 | O2(1) | ||||
| … | … | … | … | ||||
| 2 | 5 | 4 | O2(m2) | ||||
| … | … | … | … | ||||
| n | k | NA | On(1) | ||||
| … | … | … | … | ||||
| Gθ | n | G2θ | 4 | G3θ | l | On(mn) | |
| SE-DPSO (P1) | Particle (Pr) | Operations (Oi(j)) | |||||
| SgSo | SgOm | SgAt | |||||
| Dimension Number (dn) | Dimension Code (dc) | Code of Dimension (dc) | |||||
| 1 | 2 | 1 | 1 | O1(1) | |||
| 2 | 3 | 3 | 3 | O1(2) | |||
| … | … | … | … | … | |||
| m1 | c | 2 | 2 | O1(m1) | |||
| … | … | s | 5 | O2(1) | |||
| … | … | … | |||||
| 5 | 4 | O2(m2) | |||||
| θ | … | … | … | ||||
| … | k | NA | On(1) | ||||
| … | … | … | |||||
| θ | 1 | 4 | l | On(mn) | |||
| SgSo | Particle example | 0.21 | 0.32 | 0.43 | 0.18 | 0.66 | 0.89 |
| Applying SPV rule | 2 | 3 | 4 | 1 | 5 | 6 | |
| Job codes | 1 | 1 | 2 | 1 | 2 | 2 | |
| Corresponding operations in each job | O1(1) | O1(2) | O2(1) | O1(3) | O2(2) | O2(3) | |
| SgOm | 0.1 | 0.3 | 0.5 | 0.7 | 0.3 | 0.7 | |
| Corresponding machines | M1, M2, M3 | M2, M3 | M2 | M1, M3 | M2, M3 | M1, M2 | |
| Applying DI rule (Index of machines) | 1 | 2 | 2 | 3 | 2 | 2 | |
| Corresponding operations in each job | O1(1) | O1(2) | O1(3) | O2(1) | O2(2) | O2(3) | |
| SgAt | 0.93 | 0.21 | 0.49 | 0.37 | 0.86 | 0.18 | |
| Applying DI rule (Index of AGVs) | 6 | 2 | 3 | 3 | 6 | 2 | |
| Corresponding operations in each job | O1(1) | O1(2) | O1(3) | O2(1) | O2(2) | O2(3) |
| Job(Ji) | Mk/ ot(i,j)/ ec(i,j)/ wecu(k) | ||||
|---|---|---|---|---|---|
| Oi(1) | Oi(2) | Oi(3) | Oi(4) | Oi(5) | |
| J1 | M1/28/3.22/0.012 M4/25/2.91/0.012 M6/31/3.84/0.017 | M2/21/3.82/0.015 M8/23/3.15/0.014 | M5/22/2.67/0.011 M7/25/3.08/0.016 M10/27/2.72/0.021 | ||
| J2 | M3/12/2.15/0.020 M9/16/2.23/0.019 | M2/24/2.53/0.015 | M1/11/1.79/0.012 M8/15/1.93/0.014 | M10/16/2.37/0.021 | M5/18/2.44/0.011 M7/13/2.21/0.016 |
| J3 | M9/17/3.22/0.019 | M2/18/2.78/0.015 M5/23/3.62/0.011 M7/21/2.50/0.016 | M4/19/3.14/0.012 M8/15/2.93/0.014 | M1/13/2.34/0.012 M6/16/2.45/0.017 | |
| J4 | M2/22/3.25/0.015 M8/27/3.23/0.014 | M1/19/3.33/0.012 M5/21/3.32/0.011 | M3/23/3.67/0.020 M10/21/3.52/0.021 | M6/28/4.13/0.017 M7/33/4.21/0.016 | |
| J5 | M5/31/3.67/0.011 M10/27/3.55/0.021 | M3/19/2.21/0.020 M4/24/2.32/0.012 M8/22/2.24/0.014 | M1/14/2.54/0.012 M2/13/2.56/0.015 M9/16/2.63/0.019 | ||
| J6 | M4/25/3.11/0.012 M7/27/3.23/0.016 | M3/30/4.11/0.020 | M1/21/3.76/0.012 M5/18/3.68/0.011 | M2/12/1.97/0.015 M9/15/1.91/0.019 | M10/27/3.41/0.021 |
| J7 | M3/15/2.23/0.020 M6/19/2.27/0.017 | M4/30/3.95/0.012 M7/33/3.87/0.016 | M1/16/2.08/0.012 M8/17/2.11/0.014 | ||
| J8 | M5/23/3.54/0.011 M10/21/3.42/0.021 | M3/25/3.73/0.020 M6/22/3.82/0.017 | M2/27/4.21/0.015 M4/32/4.33/0.012 | ||
| Time(min) | H | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| H | 0 | 7 | 11 | 16 | 12 | 10 | 20 | 8 | 19 | 18 | 23 |
| M1 | 7 | 0 | 6 | 16 | 21 | 14 | 6 | 7 | 13 | 16 | 20 |
| M2 | 11 | 6 | 0 | 21 | 9 | 7 | 11 | 18 | 23 | 15 | 22 |
| M3 | 16 | 16 | 21 | 0 | 14 | 6 | 7 | 10 | 8 | 14 | 11 |
| M4 | 12 | 21 | 9 | 14 | 0 | 11 | 17 | 13 | 22 | 5 | 19 |
| M5 | 10 | 14 | 7 | 6 | 11 | 0 | 7 | 26 | 19 | 18 | 11 |
| M6 | 20 | 6 | 11 | 7 | 17 | 7 | 0 | 4 | 13 | 17 | 18 |
| M7 | 8 | 7 | 18 | 10 | 13 | 26 | 4 | 0 | 15 | 20 | 24 |
| M8 | 19 | 13 | 23 | 8 | 22 | 19 | 13 | 15 | 0 | 13 | 19 |
| M9 | 18 | 16 | 15 | 14 | 5 | 18 | 17 | 20 | 13 | 0 | 18 |
| M10 | 23 | 20 | 22 | 11 | 19 | 11 | 18 | 24 | 19 | 18 | 0 |
| Levels | Factors | |||||||
|---|---|---|---|---|---|---|---|---|
| PS | CR | MR | c1 | c2 | wmin | wmax | σ | |
| 1 | 100 | 0.2 | 0.05 | 0.01 | 0.3 | 0.01 | 0.3 | 0.2 |
| 2 | 150 | 0.4 | 0.08 | 0.05 | 0.5 | 0.05 | 0.5 | 0.4 |
| 3 | 200 | 0.6 | 0.1 | 0.1 | 0.7 | 0.1 | 0.7 | 0.6 |
| 4 | 300 | 0.8 | 0.2 | 0.2 | 0.9 | 0.2 | 0.9 | 0.8 |
| Index | PS | CR | MR | c1 | c2 | wmin | wmax | σ | Fitnesses | Time |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 100 | 0.2 | 0.05 | 0.01 | 0.3 | 0.01 | 0.3 | 0.2 | 274.93 | 84.67 |
| 2 | 100 | 0.4 | 0.08 | 0.05 | 0.5 | 0.05 | 0.5 | 0.4 | 273.90 | 85.12 |
| 3 | 100 | 0.6 | 0.1 | 0.1 | 0.7 | 0.1 | 0.7 | 0.6 | 271.24 | 85.18 |
| 4 | 100 | 0.8 | 0.2 | 0.2 | 0.9 | 0.2 | 0.9 | 0.8 | 299.52 | 85.37 |
| 5 | 150 | 0.2 | 0.05 | 0.05 | 0.5 | 0.1 | 0.7 | 0.8 | 276.37 | 120.07 |
| 6 | 150 | 0.4 | 0.08 | 0.01 | 0.3 | 0.2 | 0.9 | 0.6 | 272.72 | 117.92 |
| 7 | 150 | 0.6 | 0.1 | 0.2 | 0.9 | 0.01 | 0.3 | 0.4 | 273.69 | 119.26 |
| 8 | 150 | 0.8 | 0.2 | 0.1 | 0.7 | 0.05 | 0.5 | 0.2 | 272.06 | 124.39 |
| 9 | 200 | 0.2 | 0.08 | 0.1 | 0.9 | 0.01 | 0.5 | 0.6 | 272.02 | 168.32 |
| 10 | 200 | 0.4 | 0.05 | 0.2 | 0.7 | 0.05 | 0.3 | 0.8 | 273.08 | 168.21 |
| 11 | 200 | 0.6 | 0.2 | 0.01 | 0.5 | 0.1 | 0.9 | 0.2 | 268.01 | 169.05 |
| 12 | 200 | 0.8 | 0.1 | 0.05 | 0.3 | 0.2 | 0.7 | 0.4 | 271.51 | 168.23 |
| 13 | 300 | 0.2 | 0.08 | 0.2 | 0.7 | 0.1 | 0.9 | 0.4 | 275.29 | 247.08 |
| 14 | 300 | 0.4 | 0.05 | 0.1 | 0.9 | 0.2 | 0.7 | 0.2 | 263.67 | 249.13 |
| 15 | 300 | 0.6 | 0.2 | 0.05 | 0.3 | 0.01 | 0.5 | 0.8 | 270.88 | 251.51 |
| 16 | 300 | 0.8 | 0.1 | 0.01 | 0.5 | 0.05 | 0.3 | 0.6 | 269.30 | 249.74 |
| 17 | 100 | 0.2 | 0.2 | 0.01 | 0.9 | 0.05 | 0.7 | 0.4 | 276.15 | 82.77 |
| 18 | 100 | 0.4 | 0.1 | 0.05 | 0.7 | 0.01 | 0.9 | 0.2 | 275.87 | 96.53 |
| 19 | 100 | 0.6 | 0.08 | 0.1 | 0.5 | 0.2 | 0.3 | 0.8 | 270.46 | 92.71 |
| 20 | 100 | 0.8 | 0.05 | 0.2 | 0.3 | 0.1 | 0.5 | 0.6 | 272.73 | 93.06 |
| 21 | 150 | 0.2 | 0.2 | 0.05 | 0.7 | 0.2 | 0.3 | 0.6 | 267.76 | 131.14 |
| 22 | 150 | 0.4 | 0.1 | 0.01 | 0.9 | 0.1 | 0.5 | 0.8 | 285.97 | 125.89 |
| 23 | 150 | 0.6 | 0.08 | 0.2 | 0.3 | 0.05 | 0.7 | 0.2 | 277.42 | 146.37 |
| 24 | 150 | 0.8 | 0.05 | 0.1 | 0.5 | 0.01 | 0.9 | 0.4 | 271.09 | 151.61 |
| 25 | 200 | 0.2 | 0.1 | 0.1 | 0.3 | 0.05 | 0.9 | 0.8 | 276.93 | 174.32 |
| 26 | 200 | 0.4 | 0.2 | 0.2 | 0.5 | 0.01 | 0.7 | 0.6 | 273.46 | 169.82 |
| 27 | 200 | 0.6 | 0.05 | 0.01 | 0.7 | 0.2 | 0.5 | 0.4 | 272.31 | 168.94 |
| 28 | 200 | 0.8 | 0.08 | 0.05 | 0.9 | 0.1 | 0.3 | 0.2 | 277.92 | 170.27 |
| 29 | 300 | 0.2 | 0.1 | 0.2 | 0.5 | 0.2 | 0.5 | 0.2 | 280.28 | 259.37 |
| 30 | 300 | 0.4 | 0.2 | 0.1 | 0.3 | 0.1 | 0.3 | 0.4 | 272.58 | 246.45 |
| 31 | 300 | 0.6 | 0.05 | 0.05 | 0.9 | 0.05 | 0.9 | 0.6 | 274.05 | 247.34 |
| 32 | 300 | 0.8 | 0.08 | 0.01 | 0.7 | 0.01 | 0.7 | 0.8 | 277.16 | 252.66 |
| 33 | 100 | 0.2 | 0.08 | 0.01 | 0.9 | 0.01 | 0.5 | 0.6 | 272.94 | 95.31 |
| Algorithms | Parameters |
|---|---|
| SE-GA | PS = 150, CR = 0.2, MR = 0.2 |
| SE-DPSO | PS = 150, c1 = 0.05, c2 = 0.7, wmin = 0.2, wmax = 0.3, σ = 0.6 |
| H-SE-GA-DPSO | PS = 150, CR = 0.2, MR = 0.2, c1 = 0.05, c2 = 0.7, wmin = 0.2, wmax = 0.3, σ = 0.6 |
| H-GA-PSO | PS = 150, CR = 0.2, MR = 0.2, c1 = 0.05, c2 = 0.7, wmin = 0.2, wmax = 0.3, σ = 0.6 |
| TSA | Based on the related literature [9] |
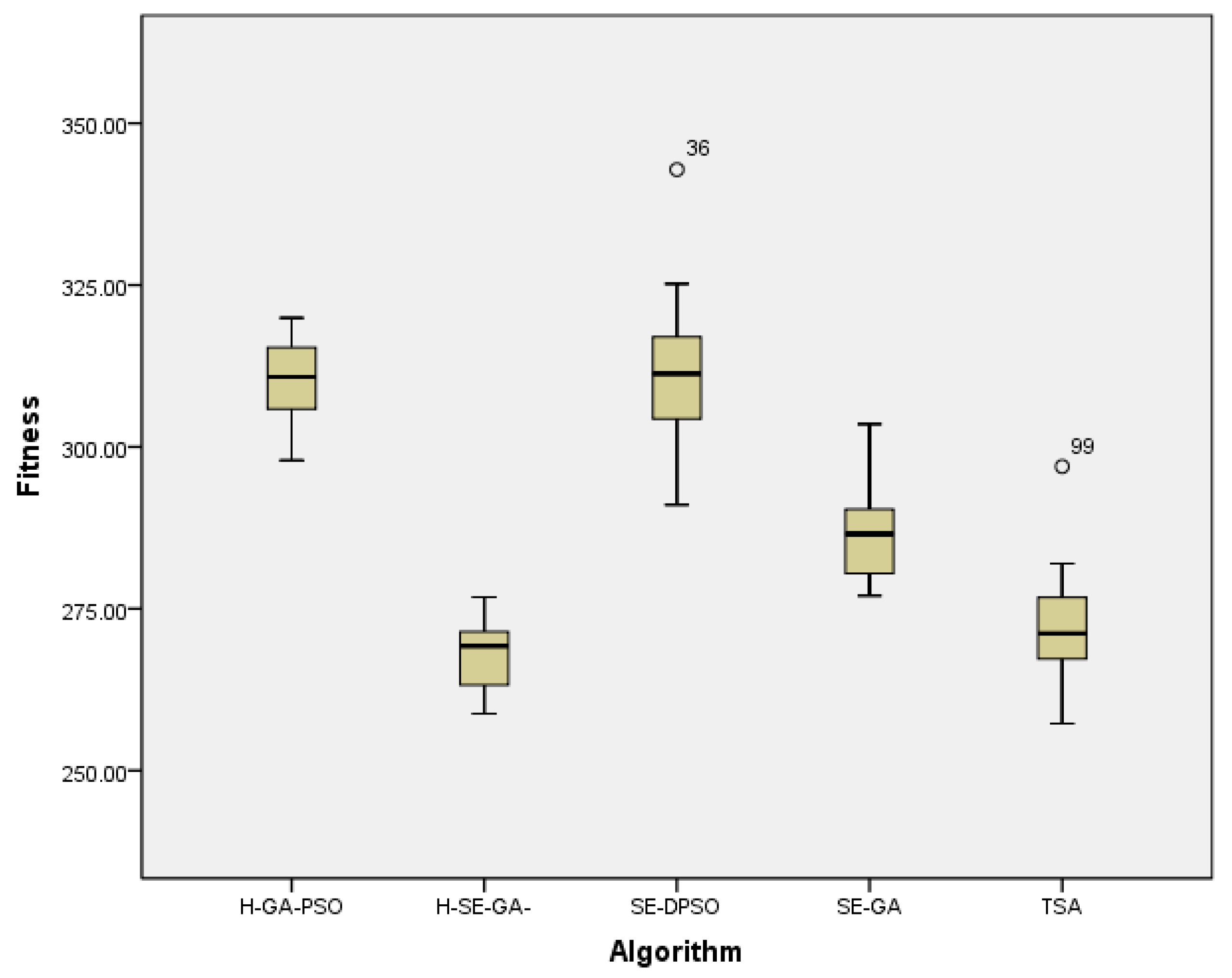
| Algorithms | Average Values of Fitness | Average Values of Makespan | Average Values of Energy Consumption | Average Numbers of AGVs | Values of Mean Computational Time |
|---|---|---|---|---|---|
| SE-GA | 286.76 | 241.40 | 109.05 | 4.90 | 82.33 |
| SE-DPSO | 311.43 | 263.45 | 111.87 | 5.65 | 96.16 |
| H-SE-GA-DPSO | 267.76 | 211.85 | 104.95 | 4.85 | 131.14 |
| H-GA-PSO | 310.13 | 253.00 | 111.19 | 5.95 | 137.86 |
| TSA | 272.45 | 216.95 | 106.60 | 4.90 | 148.69 |
| Group Numbers | SE-GA | SE-DPSO | H-SE-GA-DPSO | H-GA-PSO | TSA | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Fitness Values | NA | Fitness Values | NA | Fitness Values | NA | Fitness Values | NA | Fitness Values | NA | |
| 1 | 283.97 | 5 | 302.61 | 6 | 267.02 | 5 | 311.34 | 6 | 268.14 | 4 |
| 2 | 288.22 | 5 | 303.77 | 6 | 272.47 | 5 | 303.71 | 6 | 268.05 | 4 |
| 3 | 280.47 | 5 | 297.10 | 6 | 264.84 | 5 | 319.92 | 6 | 257.24 | 5 |
| 4 | 290.13 | 5 | 314.55 | 6 | 272.16 | 5 | 298.77 | 6 | 274.32 | 6 |
| 5 | 286.47 | 5 | 304.89 | 6 | 262.00 | 5 | 308.00 | 6 | 266.79 | 5 |
| 6 | 286.60 | 4 | 318.13 | 5 | 270.36 | 5 | 297.91 | 6 | 272.21 | 5 |
| 7 | 288.38 | 5 | 305.45 | 5 | 271.25 | 5 | 318.64 | 6 | 259.46 | 5 |
| 8 | 297.83 | 6 | 317.55 | 6 | 260.91 | 5 | 312.78 | 6 | 276.08 | 5 |
| 9 | 303.52 | 5 | 325.18 | 6 | 271.62 | 5 | 311.86 | 6 | 262.57 | 5 |
| 10 | 279.32 | 5 | 316.09 | 5 | 264.26 | 4 | 309.95 | 6 | 270.11 | 4 |
| 11 | 283.85 | 5 | 299.63 | 6 | 274.43 | 5 | 303.21 | 6 | 276.49 | 4 |
| 12 | 277.01 | 5 | 322.33 | 6 | 261.51 | 4 | 309.85 | 6 | 275.45 | 6 |
| 13 | 283.42 | 4 | 291.04 | 6 | 269.45 | 5 | 310.76 | 6 | 267.69 | 4 |
| 14 | 290.57 | 6 | 316.45 | 6 | 258.78 | 5 | 315.64 | 6 | 281.90 | 5 |
| 15 | 279.99 | 4 | 309.10 | 6 | 266.22 | 5 | 315.64 | 6 | 281.97 | 6 |
| 16 | 290.95 | 6 | 342.85 | 4 | 270.40 | 5 | 315.07 | 6 | 281.75 | 5 |
| 17 | 280.45 | 5 | 307.36 | 5 | 276.77 | 4 | 316.68 | 6 | 268.66 | 4 |
| 18 | 289.96 | 5 | 314.90 | 5 | 262.12 | 5 | 310.88 | 5 | 266.19 | 5 |
| 19 | 277.39 | 4 | 313.54 | 6 | 268.98 | 5 | 302.03 | 6 | 296.97 | 6 |
| 20 | 296.76 | 4 | 306.07 | 6 | 269.60 | 5 | 309.90 | 6 | 277.03 | 5 |
| Data items | Numbers of Available AGVs | ||||
|---|---|---|---|---|---|
| 6 | 7 | 8 | 9 | 10 | |
| Average values of fitness | 267.76 | 268.11 | 270.20 | 273.45 | 276.03 |
| Average numbers of AGV | 4.85 | 4.95 | 5.15 | 5.20 | 5.40 |
| Number of AGVs | 4(3), 5(17) | 4(2), 5(17), 6(1) | 4(1), 5(15), 6(4) | 5(16), 6(4) | 4(2), 5(10), 6(6), 7(2) |
| Algorithms | SE-GA | SE-DPSO | H-SE-GA-DPSO | H-GA-PSO | TSA |
|---|---|---|---|---|---|
| Significance (p-value) | 0.319 | 0.388 | 0.599 | 0.335 | 0.365 |
| Levene Statistic | degree of Freedom 1 (df1) | degree of Freedom 2 (df2) | p-Value |
|---|---|---|---|
| 2.743 | 4 | 95 | 0.033 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Guo, S. A Multi-Objective and Multi-Dimensional Optimization Scheduling Method Using a Hybrid Evolutionary Algorithms with a Sectional Encoding Mode. Sustainability 2019, 11, 1329. https://doi.org/10.3390/su11051329
Xu W, Guo S. A Multi-Objective and Multi-Dimensional Optimization Scheduling Method Using a Hybrid Evolutionary Algorithms with a Sectional Encoding Mode. Sustainability. 2019; 11(5):1329. https://doi.org/10.3390/su11051329
Chicago/Turabian StyleXu, Wenxiang, and Shunsheng Guo. 2019. "A Multi-Objective and Multi-Dimensional Optimization Scheduling Method Using a Hybrid Evolutionary Algorithms with a Sectional Encoding Mode" Sustainability 11, no. 5: 1329. https://doi.org/10.3390/su11051329
APA StyleXu, W., & Guo, S. (2019). A Multi-Objective and Multi-Dimensional Optimization Scheduling Method Using a Hybrid Evolutionary Algorithms with a Sectional Encoding Mode. Sustainability, 11(5), 1329. https://doi.org/10.3390/su11051329





