An Evidential Model for Environmental Risk Assessment in Projects Using Dempster–Shafer Theory of Evidence

Abstract

One of the goals of sustainable development is to achieve economic and social growth according to environmental criteria. Nowadays, impact assessment is an efficient decision making method in planning and management with environmental perspectives. Environmental risk assessment is a tool to reduce the impacts and consequences of various activities on the environment in order to achieve sustainable development. One of the commonly used environmental risk assessment methods is the probability–impact matrix method, which is known as a quantitative method for risk assessment of projects. In this method, numerical estimates of probability and impact of risk occurrence are very difficult, and these factors are associated with uncertainty. When uncertainty exists, data integration is of great importance, for which the fuzzy inference system and evidence theory are known as effective methods. Unavailability of experts’ opinion and the exponential growth of the number of required fuzzy rules associated with the risk factors are two drawbacks of fuzzy inference. Dempster–Shafer’s theory of evidence is one of the popular theories used in intelligent systems for modeling and reasoning under uncertainty and inaccuracy. In this paper, an evidential model for project environmental risk assessment is proposed based on the Dempster–Shafer theory, which is capable of taking into account the uncertainties. The proposed model is used to assess the environmental risks of Maroon oil pipelines in Isfahan. In addition, the proposed model is used in the case of tunneling risk assessment taken from the subject literature. To evaluate the validity of the proposed evidential model, the results are compared in two case studies, with the results of the conventional risk assessment method and the fuzzy inference system method. The comparative results show that the proposed model has a high potential for project risk assessment under an uncertain environment.

1. Introduction

1.1. Project Risk Assessment under Uncertainty

Risk is an uncertain event or state that, if it occurs, may influence at least one of the objectives of the project. Objectives may include timing, cost, quality, or performance. Each risk may have one or more causes that will result in one or more of the effects. Any cause can be a need, limitation, or condition that can produce negative or positive outcomes. For example, causes may include the need for an environmental permission to carry out work, personnel constraints, etc. In this case, the risk may include issues such as prolonged licensing by the licensing authority over the scheduled status, or the limitation of the allocation and provision of personnel for the work to be done on-time. If any of such uncertainty events occur, they may affect the cost, scheduling, quality, or performance of the project [1].

The source of the project risk is the uncertainties in these projects. Known risks are those that are identified and analyzed, and there is the potential for planning in response to them, while it is not possible to perform preventive management regarding the unknown risks, and the project team provides a feasible plan. Organizations have found that risk is a threat to project success or an opportunity for effective and efficient project success. Risks that present a threat to the project may be accepted if they are balanced by the results of risk-taking.

The nature of the construction projects is one of the most complex and hazardous industries in the field of safety due to the large number of variables in it, and with the simultaneous shift of the two factors of the labor force and work environment in such projects. Therefore, there exists high uncertainty in construction projects. Consequently, the lack of attention to the assessment of risks in the construction industry will cause irreparable problems and impose heavy costs on the project. Different methods have been employed to evaluate the risk of projects. The probability–impact matrix is one of the traditional methods for risk assessment. Winch [2] believes that for efficient applications, quantitative risk management is difficult and complex, and requires accurate data. Therefore, selecting an effective risk assessment method plays an important role in the economic evaluation phase of projects [3]. Unfortunately, obtaining such data is either difficult or not available in many projects. In addition, using these data is difficult to illustrate with uncertainties. The nature of construction projects has uncertainties in which the risk analysis process relates to individual thinking. This prevents the use of many risk assessment methods. The aim of this paper is to propose an evidential model based on the Dempster–Shafer (DS) theory of evidence for project risk assessment. The proposed DS method helps us to assess the risks of projects in the cases where there exist uncertainties in the data. For instance, the data for the probability of occurrence and the impacts of risk events in the probability–impact method are associated with uncertainty. Therefore, this paper reflects this uncertainty in the process of risk assessment by the concept of theory of evidence.

1.2. Background

Fuzzy multi-criteria decision making methods and the fuzzy inference system are widely used tools for managing and handling complex issues in projects. Application of fuzzy multi-criteria decision making methods for project risk assessment can be seen in several researches. In a study, fuzzy logic was used to assess the risk of construction projects [4]. Nieto and Ruz-Vila [5] used fuzzy theory to assess the risk of construction projects. In this research, the fuzzy hierarchy process analysis method was used to evaluate the risk in construction projects. In one recent paper, Tylan et al. [6] used the five risk criteria to evaluate construction projects. They evaluated 30 projects using the fuzzy analytic hierarchy process (AHP) and the fuzzy technique for order of preference by similarity to ideal solution (TOPSIS). In this study, time risk, cost risk, safety risk, quality risk, and environmental sustainability risk are used as effective risk factors for construction projects.

Valipour et al. [7] proposed a novel framework based on the step-wise weight assessment ratio analysis (SWARA) and complex proportional assessment (COPRAS) methods to assess the existing risks in the excavation projects. Their proposed model enables decision makers to consider uncertainties in the risk assessment process. Seker and Zavadskas [8] extracted the employed fuzzy decision making trial and evaluation laboratory (DEMATEL) to assess occupational risks in the construction industry by considering the interrelationship among risk factors. EI-Shayegh and Mansour [9] assessed the risk of freeway construction projects in the United Arab Emirates. The authors used the likelihood and effect matrix to evaluate projects based on internal and external risk factors. Wang et al. [10] introduced a risk assessment framework for assessing the risk of submarine routes in China. Time risk was considered to evaluate the risks arising from external factors. In addition, the risks associated with decision-makers’ behavior are also considered within the proposed evaluation framework. Samantra et al. [11] introduced an integrated risk assessment methodology based on fuzzy theory to assess the risk of urban construction projects. The authors used a hierarchical structure to identify and classify risks. Then, they defined the risk rate as a function of the possibility of the occurrence of the risk and severity of the occurrence of the risk and, accordingly, assessed the risk of subway stations.

Islam et al. [12] used Bayesian fuzzy networks to assess the risk of construction projects. In their research, the authors first investigated risk assessment methods in construction projects. The authors concluded that the use of Bayesian fuzzy networks could be considered as an effective tool for risk assessment. In another study, Chau et al. [13] identified risk patterns in bridge building and road construction projects in Vietnam. In this research, using the questionnaire and collecting the views of the contractors, the existing risks of bridge building and road construction projects were identified and classified into four categories of contractor risks, project risks, owner-risk, and external risk. Then, the authors identified the probability and impact of each identified risk for a variety of small, medium, and large bridge building and road construction projects. Ghasemi et al. [14] proposed Bayesian network methodology for modeling and analyzing portfolio risks a construction company. Chatterjee et al. [15] introduced the analytic network process in the D number and an extended multi-attributive border approximation area comparison (MABAC) method in D number to prioritize and select the best alternative risk response strategy. Hatefi and Tamošaitienė [16] introduced an integrated fuzzy DEMATEL–fuzzy analytic network process (ANP) model for evaluating construction projects by considering interrelationships among risk factors. The authors utilized the proposed model to evaluate five construction projects based on 22 risk factors.

Fuzzy inference system is a useful method for risk assessment in different domains. In a recent study, the risks were first identified in tunneling projects, and then a fuzzy inference system was designed to evaluate and prioritize the risks involved in tunneling projects. In this research, using the experts’ opinion, 25 fuzzy if-then rules are considered in the fuzzy inference system [17]. Jamshidi et al. [18] designed a fuzzy inference system to assess the risk of pipelines. In the proposed fuzzy inference system, 14 fuzzy if-then rules are considered using experts’ opinions. In another study conducted in this area, a fuzzy inference system containing 25 fuzzy if-then rules designed to assess the safety of oil and gas pipelines. Jaderi et al. [19] designed a fuzzy inference system for risk assessment in the petrochemical industry. Using the Mamdani inference System and the 20 fuzzy if-then rules, the authors perform the risk assessment.

As pointed out in the above-mentioned articles, the fuzzy if-then rules are used for the inference mechanism in the fuzzy inference system, that is a state-of-the-art method for risk assessment, and these rules are determined by the opinions of the experts. Therefore, the correct writing of the fuzzy if-then rules and determining their number can play an important role in the results of risk assessment. Unavailability of experts’ opinion and the exponential growth of the number of needed fuzzy rules with the risk factors are two drawbacks of fuzzy inference systems used for risk assessment, while their ability to model the uncertainty of experts and values is their main advantage. In order to address these problems, a new model based on the Dempster–Shafer (DS) theory of evidence [20] is proposed in this article. This proposed method, similar to fuzzy inference systems, can model the uncertainty involved in the projects and, contrary to fuzzy inference systems, does not need any predefined experts’ rules. This makes the proposed model scalable and efficient.

The DS theory of evidence was applied in different problems and showed promising results. For example, Basir and Yuan [21] utilized the DS theory for engine fault diagnosis and Wahab et al. [22] proposed a DS-based model for detecting misbehaving vehicles. Basiri et al. [23] exploited the DS theory for predicting the sentiment of users from their comments and Nemati and Naghsh-Nilchi [24,25] used DS theory in multimodal affective video retrieval. More recently, Basiri and Kabiri [26] used the DS theory for aggregating sentiment labels and combining supervised and unsupervised machine learning classifier results for sentiment analysis [27].

The remainder of the article is organized as follows. Risk assessment with the fuzzy inference system for is described in Section 2 where the architecture of this system is first introduced and then, their main components are reviewed. A brief overview of the DS theory of evidence and the proposed DS-based model is represented in Section 3. Experimental results and discussions are presented in Section 4 and finally Section 5 sets out the conclusion and identifies some research directions for the future work.

2. Fuzzy Inference System

The fuzzy logic was first introduced by Professor Lotfizadeh in 1965 and became operational in the 1970s. Fuzzy logic is a successful application in the context of fuzzy sets in which variables are linguistic rather than numerical. The fuzzy logic is in contrast to binary or Aristotelian logic that sees everything in two or more ways; yes or no, black or white, zero or one. The values in this logic change between zero and one. In Figure 1, the architecture of the fuzzy inference system is shown.

Figure 1. The structure of a fuzzy inference system, adapted from Urbina and Aoyama [17].

As it is clear, the fuzzy inference system is generally made up of the following components:

• Fuzzifier
• Knowledge-based and fuzzy rules
• Fuzzy inference engine
• Defuzzifier

In the following, components of a fuzzy inference system are described for risk assessment based on Yazdani et al. [28]. The process of transforming explicit variables into linguistic variables is called fuzzifying. In a fuzzy inference system, the inputs and outputs of the fuzzy inference system must first be fuzzy. The probability of occurrence and the severity of the risk effect are considered as the two inputs and the risk level is considered as the output of the fuzzy inference system. Linguistic expressions and fuzzy sets used to fuzzify inputs and outputs of the fuzzy inference system are presented in Table 1 and Figure 1, Figure 2 and Figure 3, in the risk assessment. Further details are presented in Yazdani-Chamzini [28].

Table 1. Linguistic terms and definitions of risk factors.

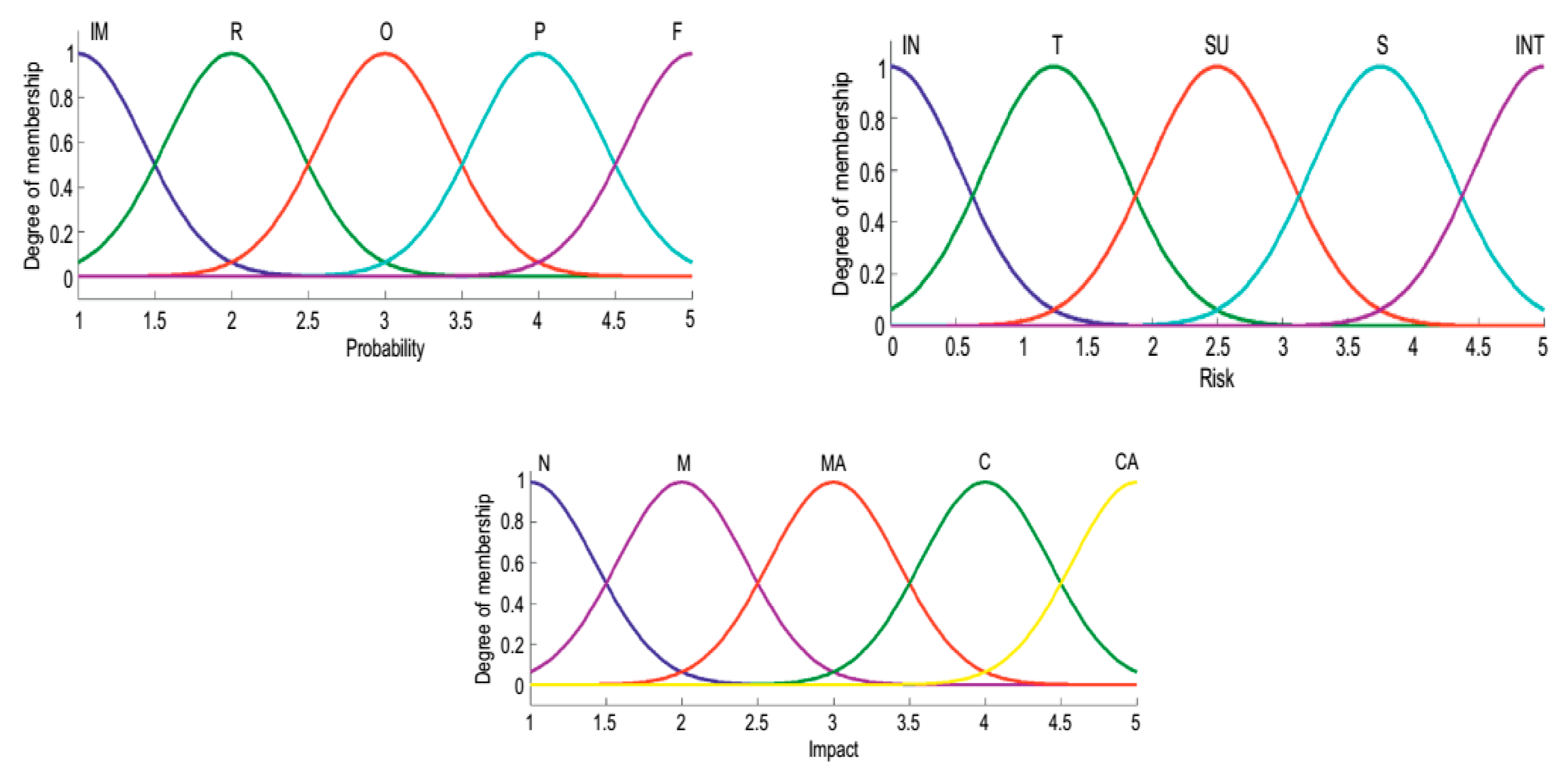
Inputs and Output	Linguistic Terms	Definitions	Crisp Rating
Probability levels (Input 1)	Improbable (IM)	So unlikely event, it may not be experienced	1
	Remote (R)	Unlikely to occur during the lifetime	2
	Occasional (O)	Likely to occur during the lifetime	3
	Probable (P)	May occur several times	4
	Frequent (F)	Will occur frequently	5
Impact levels (Input 2)	Negligible (N)	Highly have no impact on the process	1
	Minor (M)	Have no critical impact on the process	2
	Major (MA)	Have no substantial impact on the process	3
	Critical (C)	Have a certain impact on the performance	4
	Catastrophic (CA)	Have a highly impact on the performance	5
Risk levels (Output)	Insignificant (IN)	Risk is tolerable without any mitigation	(1–4)
	Tolerable (T)	Some partial mitigation may be needed	(5–8)
	Substantial (SU)	Mitigation may be needed	(9–12)
	Significant (S)	Mitigation should be implemented to reduce risk	(13–16)
	Intolerable (INT)	Mitigation that reduces risk must be implemented	(17–25)

Figure 2. Membership functions for probability of occurrence, impact level, and risk level [28].

Figure 3. Ranking results of environmental risks obtained by the proposed method and the fuzzy inference system.

The second component of the designed fuzzy inference system for risk assessment is a knowledge base and fuzzy rules, which includes 25 fuzzy if-then rules, which are presented in the Table 2.

Table 2. Fuzzy if-then rules [28].

		Probability
		IM	R	O	P	F
Impact	N	IN	IN	T	T	T
	M	IN	T	T	SU	SU
	MA	T	SU	SU	S	S
	C	T	SU	S	S	IN
	CA	SU	S	S	IN	IN

The third component of the designed fuzzy inference system for risk assessment is the fuzzy inference engine. The inference engine evaluates and inferences the rules using inference algorithms, and, after aggregating the output rules by a defuzzifier unit, it is converted into an explicit or numerical value. Often, the Mamdani and Sugno methods are used for inference. The fuzzy inference engine used by Yazdani-Chamzini [28] is the Mamdani algorithm. The maximum method is used to aggregate the outputs and the center of gravity method is used for defuzzification.

3. The Proposed DS-Based Model

In this section, a brief overview of DS theory is first given, and then its similarities and differences with the fuzzy systems are discussed. Finally, the process of applying the DS theory in risk assessment is described in detail.

3.1. Dempster–Shafer Theory of Evidence

The Dempster–Shafer theory is a theory of uncertainty that is presented to determine the degree of support for an information source from a proposition [19]. In fact, this theory is a substitute for the classical probability theory that lets combining and neglecting evidence, too Basiri et al. [23]. This theory was originally presented by Dempster [29], and then Shafer completed it in his book “A mathematical theory of evidence” [30]. In this theory, the scope of the problem is determined by using a non-empty set of bounded and mutually exclusive sets of hypotheses called the frame of discernment, which is represented by θ, and is defined as:

$$\theta =\left\{{\theta }_1,{\theta }_2,\cdots ,{\theta }_n\right\},$$

(1)

where 2^θ is the power set of θ, which contains all possible subsets of θ. If θ has n members, then there are 2ⁿ elements in 2^θ.

The amount of evidence support from each member, such as A ⊆ θ, of this set is characterized by a function called the mass function, which is represented by m(A). In other words, each mass function is a basic probability assignment (BPA) to each member of the set θ. This numeric function returns a number in the interval [0, 1] and has the following properties:

$$m:P\left(X\right)\to \left[0,1\right];$$

(2)

m(∅)=0;

(3)

$${{\displaystyle \sum }}_{A\in 2^{\theta }}m\left(A\right)=1.$$

(4)

where m(A) can be interpreted as the amount of belief in A based on existing evidence.

The Dempster’s fundamental operator that uses various sources to integrate evidence, is the Dempster’s rule of combination [30]. It can be used to combine two evidences provided that both are defined on the same frame of discernment. This operator, sometimes represented by the symbol ⊕, and also called the orthogonal sum, can be used for the combination of two BPAs, such as $m^1$ and $m^2$, as follows:

$$m\left(A\right)=m_{1,2}\left(A\right)=(m_1\oplus m_2)\left(A\right)=\{\begin{array}{ll}\frac{{{\displaystyle \sum }}_{X{\displaystyle \cap }Y=A}{m}_1\left(X\right)m_2\left(Y\right)}{1-K_{12}}& A\ne \varnothing \\ 0& A=\varnothing \end{array},$$

(5)

$$K_{12}={\displaystyle \sum }_{X{\displaystyle \cap }Y=\varnothing }{m}_1\left(X\right)m_2\left(Y\right).$$

(6)

In this relationship, $K_{12}$ is a balancing factor that ensures that the composition of $m_1\oplus m_2$ remains BPA. This factor is also called the contradiction factor, and indicates the degree of contradiction between the two sources of evidence. If $K_{12}=0$, then there is no contradiction between evidence, and $K_{12}=1$ denotes the complete conflict. Further evidence is combined as follows:

$$(m_1\oplus m_2\oplus \dots \oplus m_n)\left(A\right)=\frac{{{\displaystyle \sum }}_{{{\displaystyle \cap }}_{i=1}^n{X}_i=A}({{\displaystyle \prod }}_{j=1}^n{m}_j\left(X_i\right))}{1-{{\displaystyle \sum }}_{{{\displaystyle \cap }}_{i=1}^n{X}_i=\varnothing }({{\displaystyle \prod }}_{j=1}^n{m}_j\left(X_i\right))}.$$

(7)

3.2. Applying DS Theory of Evidence in Risk Assessment

Before describing the steps for applying the DS theory in risk assessment, the reason for choosing this theory is presented. First, the DS method is a more general form of the Bayesian approach which has all its benefits. For instance, in the DS method, like the Bayesian method, the available prior information can be incorporated in the inexact inference of the uncertain indicators and inferential results. However, the use of prior information in the DS method is not mandatory. This matter is one of the merits of the DS method. Furthermore, DS theory similar to Bayesian decision theory can provide a framework in which the initial inferential results of the uncertain indicators are related to the final decision analysis. Second, compared to other probabilistic methods such as Bayesian method, in the DS method calculation of the prior probability is not required. Third, it has a flexible and understandable mass function. Forth, creating the mass function is easy and convenient. Fifth, the computational complexity of this method is much less than that of the Bayesian method. Sixth, such as the fuzzy inference system, it is usable in cases where uncertainty exists.

The first step in using Dempster’s theory in each problem is to define the propositions [23,24]. In the proposed model, each proposition indicates the amount of belief in the evidence for the relevant risk factor, which is a real number in the range $\left[1,5\right]$ as:

$$A=f_i\in \left[1,5\right]\mathrm{and}i=\left\{1,2\right\}.$$

(8)

In Equation (8), i has only two possible values because we intend to aggregate just two evidences. The second step in using Dempster’s theory is to define the evidence [23]. In the current study, following the natural way in which experts make a decision, we consider the impact and probability as evidence for the final risk value.

After defining the evidence, the third step in using Dempster’s theory is to define the mass function [31]. For this purpose, we use the normalized values of impact and probability as follows:

$$m\left(A\right)=\frac{f_i-maxF}{maxF-minF},$$

(9)

where $\max F=max\left\{f_j|j\in \left[1,n\right]\right\}$, $\mathrm{minF}=min \left\{f_j|j\in \left[1,n\right]\right\}$, and n is the number of risks in the problem.

In order to see a working example of applying the proposed method for obtaining the risk value, suppose the impact and probability scores has the values 4.535 and 1.350, respectively. Based on these two values and according to Equation (9), $m_1\left(A\right)$ and $m_2\left(A\right)$ are 0.0875 and 0.88375, respectively. Now these two BPAs may be aggregated using Equations (5) and (6) as follows:

$$\begin{gathered} K_{12}={{\displaystyle \sum }}_{X{\displaystyle \cap }Y=\varnothing }{m}_1\left(X\right)m_2\left(Y\right)=0.0875\times \left(1-0.88375\right)+0.88375\times \left(1-0.0875\right)=0.8166, \\ m\left(A\right)=m_{1,2}\left(A\right)=(m_1\oplus m_2)\left(A\right)=\frac{{{\displaystyle \sum }}_{X{\displaystyle \cap }Y=A}{m}_1\left(X\right)m_2\left(Y\right)}{1-K_{12}}=\frac{0.0875\times 0.88375}{1-0.8166}=2.686 \end{gathered}$$

(10)

As could be seen in the above example, the amount of belief in evidence is considered as propositions. Thus, in the nominator of Equation (5), the values for $m_1\left(A\right)$ and $m_2\left(A\right)$ are multiplied, while in the denominator, $K_{12}$ is calculated using the multiplication of each evidence in the complement of that evidence.

4. Experiments and Results

4.1. Environmental Risk Assessment of Maroon–Isfahan Pipeline

Pipelines seem to be one of the most effective and economical means for the transportation of hazardous and flammable materials such as natural gas, crude oil, and its derivatives that cannot be transported through a railway or rail transport line. In most countries, the system of pipelines is expanding and increasing gas and oil consumption, and they constantly need these materials and safe operation facilities. Additionally, due to combustible materials, explosion and diffusion are normal. In transmission pipelines, due to the dispersal of gas or natural gas through failure or leakage, it creates a risk of explosion or fire as a precursor position.

Isfahan region is located 10 km north of the city of Isfahan and near the refinery in the city at an altitude of 1697 m above sea level. The region is responsible for the transfer of crude oil from the Maroon oil field in Omidieh, Khuzestan province, to the Isfahan oil refinery. The characteristics of the Isfahan area are exploitation and maintenance of the strategic Maroon oil pipeline, 430 km from Omidieh, in Khuzestan to the Isfahan refinery, which is known as the Maroon–Isfahan pipeline. The minimum height of the pipeline is 74 m and the highest elevation is 2700 m above sea level. Due to the Maroon-Isfahan pipeline is located in impassable mountainous areas, it is considered as one of the most damaging pipelines in the world. Despite frequent problems, such as intermittent falls and landslides and seasonal floods, maintenance of this pipeline is in good demand and all pipelines in this area are monitored day-to-day with advanced electronic systems and manpower.

The first and second columns of Table 3 show the notations and the environmental risk events identified in the Maroon–Isfahan pipeline.

Table 3. Comparison of the priority of risks between the proposed model and the fuzzy inference system.

No	Risk Event	Probability	Impact	Conventional Method		Fuzzy Inference System Method		Proposed Method
				Risk	Rank	Risk	Rank	Risk	Rank
1	2	3	4	5	6	7	8	9	10
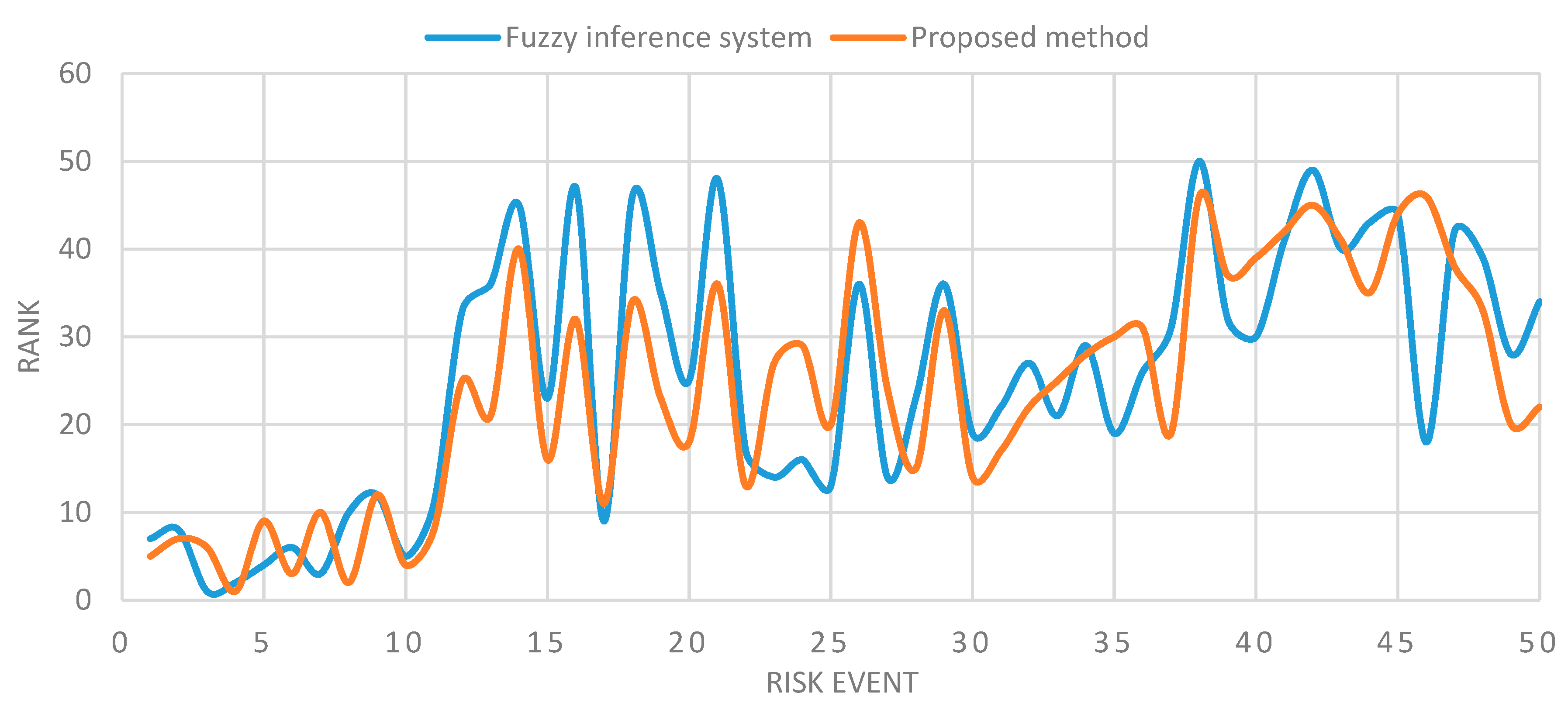
R1	Water and environment pollution due to leakage of crude oil from the pipeline through the lake	2.050	4.705	9.65	9	3.29	7	4.269	5
R2	Water-taking and tearing of the pathway of the Dooplan River	1.900	4.680	8.89	10	3.15	8	4.078	7
R3	The penetration of welding at the site of the half pipe, patched to the pipeline and piercing it	4.000	3.180	12.72	5	3.48	1	4.129	6
R4	Rupture and breaking of the pipeline due to burnout	4.000	4.050	16.20	1	3.45	2	4.624	1
R5	Breaking the tube due to underwater flows	3.750	3.250	12.19	6	3.41	4	3.955	9
R6	Rupture of the line or cracking of the reservoir due to the drift of the ground	3.750	4.120	15.45	2	3.38	6	4.545	3
R7	Line tearing due to falling mountain	3.800	3.150	11.97	7	3.43	3	3.922	10
R8	Difference in pressure and line tearing at the point of decay due to the closure of the valve	3.550	4.268	15.15	3	3.07	10	4.548	2
R9	Reservoir corrosion due to dewatering delay	1.900	4.338	8.24	11	2.73	12	3.376	12
R10	Failure to procure parts due to sanctions	3.050	4.421	13.48	4	3.39	5	4.445	4
R11	Fire due to material release to turbine exhaust through hole line	1.550	4.800	7.44	12	2.89	11	4.007	8
R12	Abrupt stopping of turbines and reverse pressure on the transmission line	2.700	2.600	7.02	17	2.04	33	2.32	25
R13	Inability to check and visit the transit line	3.000	2.400	7.20	15	1.87	36	2.4	21
R14	Defective cable and failure to send and receive electricity	2.200	2.180	4.80	44	1.51	45	1.608	40
R15	Material leakage from the reservoir due to corrosion	1.350	4.535	6.12	30	2.37	23	2.686	16
R16	Line break due to inappropriate design	2.700	2.070	5.59	34	1.45	47	1.85	32
R17	Environmental pollution due to human wastewater transfer	2.500	4.250	10.63	8	3.11	9	3.889	11
1	2	3	4	5	6	7	8	9	10
R18	Abrupt stopping of turbines and reverse pressure on the transmission line	2.500	2.040	5.10	37	1.46	46	1.696	34
R19	Damage to lines due to the impact of machinery	3.400	2.020	6.87	22	1.88	35	2.357	23
R20	The collision with the tube and its deterioration due to the redundancy	1.750	3.980	6.97	18	2.29	25	2.611	18
R21	Disrupting the measurement of technical quantities due to the presence of water	2.500	2.000	5.00	39	1.43	48	1.667	36
R22	Corrosion of the pipeline due to the release of corrosive materials	1.200	4.828	5.79	32	2.52	17	3.155	13
R23	Valve fracture, due to existence of water inside it	2.200	3.110	6.84	23	2.62	14	2.294	27
R24	Drop of personnel due to freezing stairs	2.050	3.200	6.56	28	2.56	16	2.213	29
R25	The creation of an anode cathode flow due to the lack of tank cover	2.200	3.250	7.15	16	2.72	13	2.421	20
R26	Breakdown of tubes or lines by cold weather	1.050	4.375	4.59	45	1.87	36	1.256	43
R27	Crash of passing cars	2.100	3.295	6.92	20	2.62	14	2.352	24
R28	The collision of agricultural equipment with the pipeline	1.650	4.220	6.96	19	2.37	23	2.779	15
R29	The creation of decay and corrosion in the facility due to the presence of water	1.250	4.178	5.22	36	1.87	36	1.82	33
R30	Disruption of the cathodic system	1.750	4.170	7.30	14	2.43	19	2.874	14
R31	Cable tear and collision with residential building	1.900	3.855	7.32	13	2.39	22	2.68	17
R32	Machine failure and equipment collapse during repair	1.800	3.713	6.68	26	2.27	27	2.38	22
R33	The destruction of the coating on the pipe due to inappropriate area around (water, growing plants, and etc.)	1.935	3.470	6.71	25	2.41	21	2.32	25
R34	Decrease in the life of the devices considering their standard	1.800	3.565	6.42	29	2.24	29	2.235	28
R35	Oil spill due to lack of repair of tank floor plates	1.935	3.060	5.92	31	2.43	19	1.979	30
R36	Line damage due to earthquake	1.800	3.140	5.65	33	2.28	26	1.894	31
R37	The collapse of local people while crossing the pipeline	4.000	1.660	6.64	27	2.11	31	2.489	19
R38	Lack of timely implement of relief valves	1.000	3.660	3.66	49	1.41	50	1	46
R39	Drop of personnel due to freezing stairs	1.650	3.000	4.95	40	2.1	32	1.65	37
R40	Misdiagnosis regarding the required repair site	1.800	2.690	4.84	43	2.13	30	1.618	39
R41	Delay in the expropriation of land from residents	1.350	3.100	4.19	47	1.69	41	1.383	42
R42	Tensions and pressures caused by building materials	1.050	3.280	3.44	50	1.42	49	1.066	45
R43	Local threats	1.800	2.450	4.41	46	1.8	40	1.498	41
1	2	3	4	5	6	7	8	9	10
R44	Bursting the stopper during welding	4.000	1.260	5.04	38	1.58	43	1.69	35
R45	The emission of toxic gases SO2 and CO2 in the operation of tank repair due to environmental factors	1.250	3.000	3.75	48	1.57	44	1.25	44
R46	Fire during welding due to the presence of petroleum products	1.000	4.950	4.95	40	2.47	18	1	46
R47	Failure to transfer petroleum products due to equipment inefficiency	3.800	1.300	4.94	42	1.63	42	1.636	38
R48	Failure of the pipeline due to the impact on it	3.800	1.460	5.55	35	1.84	39	1.931	33
R49	Damage to personnel’s hearing system at the place of material pumping	3.800	1.780	6.76	24	2.26	28	2.444	20
R50	Environmental pollution due to its correlation	3.550	1.940	6.89	21	2.03	34	2.403	22

The third and fourth columns of Table 3 show the probability of occurrence and the impact of risk events. In order to obtain the probability and impact of risk events, 22 employees of Isfahan oil pipelines and Telecommunication Company identified the environmental risks of the Maroon–Isfahan pipeline and then the probability of the occurrence and severity of the effect of each of the risks was evaluated. To determine the probability of the occurrence and severity of the effect of each identified risk, each expert person first presented his/her views on the likelihood of occurrence and the severity of the effect using Table 1. Then the collected comments were converted to crisp numbers according to the last column of Table 1. At the end, the average scores of the 22 expert opinions were calculated for the probability of the occurrence and severity of the effect of each of the risks and were reported in the third and fourth columns of Table 3.

Columns 5 to 10 of Table 3 show the risk score and rank of risk events, which were obtained by the conventional risk assessment method, the fuzzy inference method, and the proposed method, respectively. In the conventional risk assessment method, the risk score reported in column 5 of Table 3 is derived from the multiplication of the probability of occurrence of risk in the severity of the risk effect. The sixth column of Table 3 shows the rank of risk events obtained using the conventional risk assessment methodology.

The seventh and eighth columns, respectively, represent the risk score and the rank of risk events calculated by implementing the fuzzy inference system. To do this end, according to Yazdani-Chamzini [16], for each type of risk event presented in Table 3, the level of probability and its impact based on the values given in Table 1 are determined by an expert team, including seven assessors with a high degree of knowledge in the area of risk management. Therefore, risk levels are extracted from these numerical values, as represented in Table 3. For each risk event, its probability and impact values are considered as the inputs of the fuzzy inference system. The fuzzy inference engine is applied on both of these inputs and the fuzzy rules represented in Table 2 are evaluated based on the Mamdani algorithm. After evaluating each fuzzy rule, the output of each fuzzy rule is obtained. In the next stage, the outputs of fuzzy rules are aggregated by maximum method and then they are defuzzified by the center of gravity method and converted into the numerical values, which are reported in the seventh column of Table 3.

The last two columns of Table 3 also show the risk score and the rank of risk events obtained by using the proposed Dempster–Shafer method. For obtaining the results of the proposed Dempster–Shafer method, several steps must be performed. In the first step, the propositions and the amount of belief are obtained based on formulation (8). In the second step, the probability and the impact are considered as two evidences for each risk event and their mass functions are provided according to formulation (9). After that, formulations (5) and (6) are applied to combine their respected mass functions, which show the risk score reported in the ninth column of Table 3. Figure 3 graphically depicted the ranks of risk events extracted by the proposed method and fuzzy inference system method.

As Table 3 and Figure 3 show, the risk of "rupture and failure of the pipeline due to burnout", or R4, has been ranked first by the proposed method. This risk factor gained the first and second rank, respectively, by implementing conventional risk assessment methods and the method of the fuzzy inference system. R8 with the title “Making a difference in line pressure at the point of decay due to closure of the valve” was ranked second, third, and tenth, respectively, by using the proposed method, conventional risk assessment method, and fuzzy inference system. The risk of R6, entitled “Rupture of the line or rubbing the reservoir due to landslide”, assigned the third, second, and sixth rank, respectively, using the proposed method, conventional risk assessment method, and fuzzy inference system method. The risk of R10, entitled “Inability to Supply Components Due to Boosts”, was ranked fourth among the top 50 risks by using the proposed method. The risk rating of R10 was four and five using conventional risk assessment methods and the fuzzy inference system, respectively.

4.2. Tunneling Risk Assessment

In this section, the proposed method is used to evaluate tunneling risks and the results are compared with those obtained by the fuzzy inference system method and the conventional risk assessment method. Yazdani-Chamzini [28] proposed a fuzzy inference system to evaluate 47 tunneling risks and compared the results with the conventional risk assessment method. Data on the probability of occurrence and the severity of the effect of each of the tunnel risks are presented. The results of conventional risk assessment and the method of fuzzy inference system and the proposed DS method are reported in Table 4.

Table 4. Comparison results of tunneling risk assessment methods.

No.	Risk Events	Conventional Method		Fuzzy Inference System Method		Proposed Method
		Risk	Rank	Risk	Rank	Risk	Rank
1	2	3	4	5	6	7	8
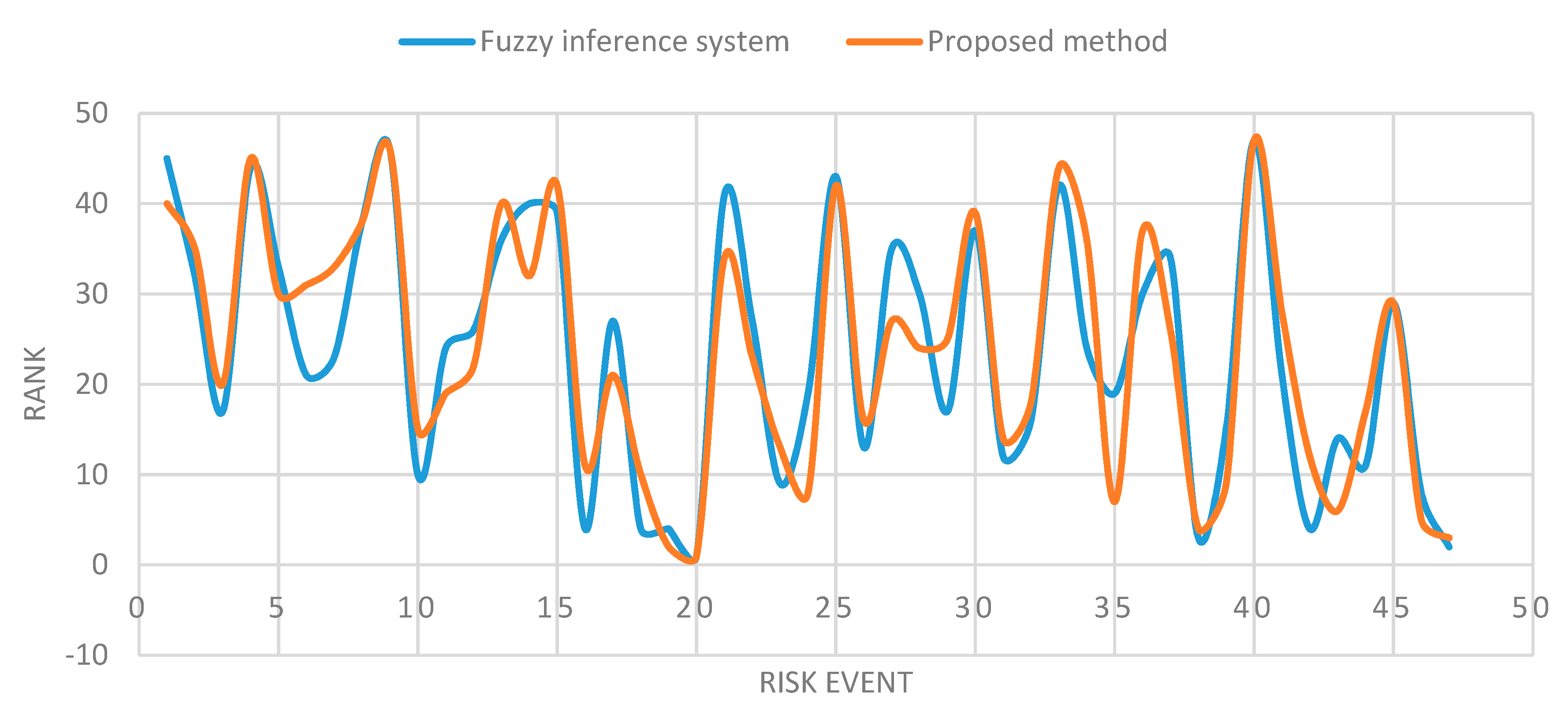
R1	Land acquisition problem	6	30	1.56	45	2.03	40
R2	Difficulty in cooperation with related government	6	30	2.56	32	2.38	35
R3	Public opposition	8	23	2.89	17	3.56	20
R4	Unscientific planning of tunnel construction	4	44	1.57	44	1.33	45
R5	Inadequate design specification and documentation	8	23	2.50	33	2.73	30
R6	Over break	6	30	2.75	21	2.54	31
R7	Inaccurate survey data	6	30	2.69	23	2.45	33
R8	Design mistakes	5	42	2.31	38	2.05	38
R9	Lack of experienced designers	3	46	1.53	46	1.19	46
R10	Conflict designs on interface between adjacent a	12	7	3.53	10	3.96	15
R11	Water inflow	8	23	2.65	24	3.65	19
R12	Tunnel walls instability	9	19	2.61	26	3.16	22
R13	Tunnel face instability	6	30	2.38	36	2.03	40
R14	Fault zone	6	30	1.99	40	2.53	32
R15	Squeezing	6	30	2.24	39	1.96	42
R16	Collapse	12	7	3.67	4	4.18	11
R17	Rock burst	5	42	2.59	27	3.27	21
R18	Roof fall	12	7	3.67	4	4.25	10
R19	Collisions	15	4	3.67	4	4.7	2
R20	Toxic gas leakage	20	1	4.34	1	4.97	1
R21	Poor ventilation	6	30	1.91	41	2.44	34
R22	Fire in tunnel	8	23	2.59	27	3.15	23
R23	Disturbance to the residents near the construction	12	7	3.6	9	4.05	13
R24	Physical damage to workers	10	16	2.88	19	4.30	8
R25	Ecological constraints	6	30	1.68	43	1.96	42
1	2	3	4	5	6	7	8
R26	Surface subsidence	12	7	3.44	13	3.86	16
R27	Noise	8	23	2.41	35	2.88	27
R28	Air pollution	9	19	2.57	30	3.08	24
R29	Interference of different operations	8	23	2.89	17	3.01	25
R30	Inconsistent schedule in intersections	6	30	2.32	37	2.04	39
R31	Damage to the foundation of adjacent buildings	12	7	3.46	12	3.98	14
R32	Inappropriate machine and equipment selection	12	7	3.16	16	3.75	18
R33	Rough and incomplete construction program	4	44	1.82	42	1.69	44
R34	Inappropriate material selection	6	30	2.65	24	2.36	36
R35	Machinery breakdown	10	16	2.88	19	4.39	7
R36	Poor workmanship	6	30	2.57	30	2.24	37
R37	Poor construction programming	9	19	2.47	34	2.95	26
R38	Delay of materials supply	16	2	3.71	3	4.59	4
R39	Managerial inability	10	16	3.25	15	4.28	9
R40	Lack of experienced professional consultants	3	46	1.41	47	1.05	47
R41	Change of key personnel	8	23	2.75	21	2.86	28
R42	Workers’ strike	12	7	3.67	4	4.17	12
R43	High tender price	15	4	3.35	14	4.44	6
R44	Material price escalation	12	7	3.49	11	3.82	17
R45	Labor cost escalation	9	19	2.58	29	2.75	29
R46	Delay in contractual progress payment	16	2	3.66	8	4.48	5
R47	Financing difficulties	15	4	3.77	2	4.66	3

The second column of Table 4 shows the risk factors for tunneling. The third and fourth columns show the risk score and the risk rating of the tunnel using the conventional risk assessment method. Fifth and sixth columns show the results of the implementing the fuzzy inference system. In addition, the risk scores and their ranks are shown in columns 7 and 8 in Table 4, which are obtained by the proposed Dempster–Shafer method. Furthermore, the ranking results of the proposed method and fuzzy inference system are depicted in Figure 4.

Figure 4. Ranking results of tunneling risks obtained by the proposed method and the fuzzy inference system [28].

The results reported in Table 4 and Figure 4 show that the R20 entitled “Toxic gas leakage” had the first rank among the tunneling risks using the proposed method, conventional risk assessment method and fuzzy inference system method. The R19 risk, “Collisions”, ranked second with the proposed method, while this risk factor was ranked fourth in the conventional risk assessment method and fuzzy inference system. The risk of R47, entitled “Financing difficulties,” was ranked third by the proposed method. This risk factor was ranked fourth and second, using the conventional risk assessment method and fuzzy inference system, respectively.

5. Discussion

As mentioned earlier, the DS theory of evidence and the fuzzy inference system were two efficient and applicable methods for modeling uncertainty in project risk assessment. Unavailability of experts’ opinion and the exponential growth of the number of needed fuzzy rules with respect to the risk factors are two drawbacks of fuzzy inference systems used for risk assessment. Fortunately, the DS theory of evidence overcomes to these drawbacks. When the DS method is compared with the probabilistic methods such as the Bayesian method, it has the several merits. Unlike the Bayesian method, the DS method does not require the prior probability. The computational complexity of the DS method is less than that of the Bayesian method. Furthermore, it has a flexible and easy-to-use mass function.

In order to validate the proposed DS method for risk assessment, two cases including the environmental risk assessment of the Maroon–Isfahan pipeline and tunneling risk assessment were considered and the respected results were compared with those obtained by the fuzzy inference system. For doing so, we used the Spearman correlation coefficient. The Spearman correlation coefficient shows the correlation between two ordinal variables. In the first case, which is the environmental risk assessment of the Maroon–Isfahan pipeline, the correlation coefficient between the risk rating in the proposed method and the conventional risk assessment method is 0.946. This correlation coefficient indicates that there is a high correlation between the results of the proposed method and the conventional risk assessment method. Furthermore, the Spearman’s correlation coefficient between the proposed risk rating and the fuzzy inference system method is 0.823. This coefficient shows that there is a high correlation between the results of the proposed method and the method of the fuzzy inference system.

In the case of tunneling risk assessment, the correlation coefficient between the risk rating in the proposed method and the conventional risk assessment method is 0.922. This correlation coefficient indicates that there is a high correlation between the results of the proposed method and the conventional risk assessment method. In addition, the Spearman’s correlation coefficient between the proposed risk rating and the method of the fuzzy inference system is 0.911. This coefficient shows that there is a high correlation between the results of the proposed method and the two methods of fuzzy inference system and conventional risk assessment for the evaluation of tunnel risks. According to the aforementioned results, the proposed method has a high potential for risk assessment in the aforementioned projects. The proposed DS method can be considered as the extension of the probability–impact method for risk assessment in the cases where uncertainty exists. Therefore, the proposed DS method can be utilized for risk assessment in an uncertain environment instead of the conventional probability–impact method.

6. Conclusions

Due to the uncertain nature of experts’ opinions about the probability of occurrence and impact level of risks, this paper proposed an evidential model for environmental risk assessment using the Dempster–Shafer theory of evidence. The proposed evidential model enables us to consider uncertainty in the environmental risk assessment process and, contrary to the fuzzy inference system, does not require any predefined experts’ rules. The proposed evidential model is used to assess the existing risks in two cases. The first case refers to the environmental risk assessment of the Maroon–Isfahan pipeline, where 50 environmental risks are considered to be evaluated. The second case is taken from the literature review in which 47 tunneling risks are assessed [28]. The proposed evidential model is employed to assess the existing risks in the two mentioned cases and the obtained results are compared with those obtained by the conventional risk assessment method and the fuzzy inference system method. The validity of the proposed model is investigated by the Spearman correlation coefficient in two cases. The Spearman correlation coefficient between the results of our proposed method and those obtained by the fuzzy inference system are 0.823 and 0.911, in the pipeline and tunneling risk assessment cases, respectively. Furthermore, these coefficients are 0.946 and 0.922 when comparing our proposed method with the conventional risk assessment method in two studied cases, respectively. According to the results, it can be concluded that the results of proposed evidential model have high consistency with those obtained by the conventional risk assessment method and the fuzzy inference system method.

The DS theory of evidence is an efficient and applicable tool to solve decision making problems under uncertainty. Evaluating construction projects based on the risk factors under uncertainty is an important topic in the field of construction risk management [16]. Therefore, applying DS theory of evidence to solve the construction project evaluation problem under uncertainty is an interesting topic for future research. The existence of conflicts among evidences is one of the limitations of applying the DS method, which may lead to unreliable results. Therefore, proposing a modified DS method for project risk assessment in the case where there exist conflicts among evidences is an important topic for future research.